Batch process particle separation using surface acoustic waves (SAW): integration of travelling and standing SAW

Abstract

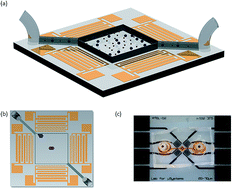
Acoustic fields offer a versatile and non-contact method for particle and cell manipulation, where several acoustofluidic systems have been developed for the purpose of sorting. However, in almost all cases, these systems utilize a steady flow to either define the exposure time to the acoustic field or to counteract the acoustic forces. Batch-based systems, within which sorting occurs in a confined volume, are compatible with smaller sample volumes without the need for externally pumped flow, though remain relatively underdeveloped. Here, the effects of utilizing a combination of travelling and standing waves on particles of different sizes are examined. We use a pressure field combining both travelling and standing wave components along with a swept excitation frequency, to collect and isolate particles of different sizes in a static fluid volume. This mechanism is employed to demonstrate size-based deterministic sorting of particles. Specifically, 5.1 μm and 7 μm particles are separated using a frequency range from 60 MHz to 90 MHz, and 5.1 μm particles are separated from 3.1 μm using an excitation sweeping between 70 MHz and 120 MHz.