Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Capacitive deionization in organic solutions: case study using propylene carbonate†
S. Poradaa,
G. Fengb,
M. E. Sussc and
V. Presser*ad
aINM-Leibniz Institute for New Materials, Campus D2 2, 66123 Saarbrücken, Germany. E-mail: volker.presser@leibniz-inm.de
bState Key Laboratory of Coal Combustion, School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan, China
cFaculty of Mechanical Engineering, Technion-Israel Institute of Technology, Haifa, Israel
dDepartment of Materials Science and Engineering, Saarland University, Campus D2 2, 66123 Saarbrücken, Germany
First published on 8th January 2016
Abstract
Capacitive deionization (CDI) is an emerging technology for the energy-efficient removal of dissolved ions from aqueous solutions. Expanding this technology to non-aqueous media, we present an experimental characterization of a pair of porous carbon electrodes towards electrosorption of dissolved ions in propylene carbonate. We demonstrate that application of CDI technology for treatment of an organic solution with an electrochemical stability window beyond 1.2 V allows for a higher salt removal capacity and higher charge efficiency as compared to CDI applied for treatment of aqueous electrolytes. Further, we show that using conductivity measurements of the stream emerging from the CDI cell combined with an equilibrium electric double-layer structure model, we can gain insights into charge compensation mechanisms and ion distribution in carbon nanopores.
Electrosorption is a process whereby ionic electrolyte species are electrostatically confined near to charged solid–liquid interfaces, enabling fast energy storage and recovery via electric double-layer capacitors (or supercapacitors)1 and water desalination via capacitive deionization (CDI).2 In such applications, a pair of porous carbon electrodes (or stacks thereof) is charged, and ions are electrosorbed onto the pore surfaces, residing in electric double-layers (EDLs). One important difference between supercapacitors and CDI is the operation at very different ionic strength: CDI is employed at low concentrations, typically in the range of 100 mM or lower, while supercapacitors operate at 1 M or higher (depending on the electrolyte system).3 Also, while the field of CDI has been focused almost entirely on the study and application of water desalination (ion removal from aqueous electrolytes),4 supercapacitors can store energy with aqueous electrolytes, organic electrolytes, and solvent-free systems based on ionic liquids.
While it is well known that CDI can separate a feed water stream into potable water and a separate brine stream, recently, CDI has been investigated as a promising tool for other separations in aqueous solutions, including between ionic species with different valencies,5 and in separations for microfluidic sample purification.6 A key property of CDI is the potential for energy efficient separation when using relatively dilute electrolyte solutions (i.e., where the molecules of water outnumber by roughly three or more orders of magnitude the number of ions).7 Despite CDI's many benefits, a fundamental limitation to the usable cell voltage range is the narrow electrochemical stability window of water.4 As a consequence, the maximum voltage in typical CDI systems does not exceed 1.2 to 1.4 V.4,8 At electric potentials above this level, water decomposition occurs at the electrodes via water electrolysis, which acts as a parasitic energy loss and a source of unwanted gas generation. Thus, the maximum NaCl adsorption capacity for CDI systems based on capacitive electrodes remains limited to roughly 20 mgNaCl gcarbon−1, when normalized by the mass of the highly porous carbon electrodes (typically with around 1500–2000 m2 g−1 specific surface area).9–12
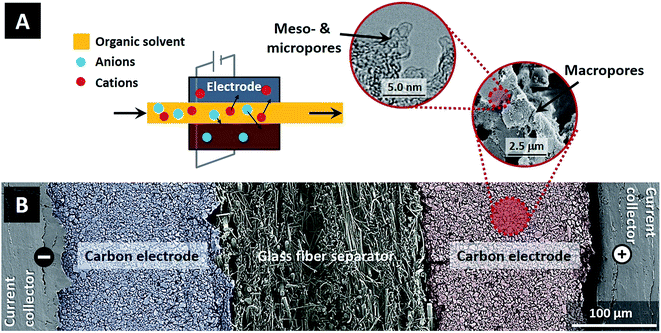
While CDI has been proven to be a versatile and powerful tool for separation processes in aqueous solutions, little attention has been paid to separations achievable by CDI in electrolyte systems using organic solvents. This is despite the enormous amount of electrolyte-based separations performed in organic solvents throughout the chemical and pharmaceutical industries.13 In this study, using a proof-of-concept system, we demonstrate for the first time that CDI can be a useful tool for the large field of separations in organic solvents. Within the family of electrosorption technologies, CDI in organic solvents combines the use of organic solvents typical to supercapacitors with operation at low ion concentration typical to CDI, thus establishing a new operational regime for these technologies (see Fig. 1A).
To compare electrosorption properties of carbon electrodes for ion removal from aqueous and organic electrolytes, two identical cells were constructed where the electrolyte flows in-between a pair of electrodes (flow-between geometry). One cell was for CDI electrosorption with the aqueous electrolyte of NaCl, and the second for the organic electrolyte system, where we use tetraethylammonium tetrafluoroborate salt dissolved in propylene carbonate (TEA-BF4/PC), see Fig. 1A. Materials used in this study were graphite current collectors (Sigraflex Z, SGL Carbon, Germany), carbon composite electrodes with a thickness of ∼250 μm consisting of 90 wt% of activated carbon (YP50-F, Kuraray Chemical, Japan; see ESI Fig. S1†) and 10 wt% of polyvinylidene fluoride (Kynar HSV 900, Arkema Inc., USA), and a glass fiber spacer (Millipore, Ireland, thickness ∼ 250 μm). Fig. 1B shows a scanning electron micrograph (SEM) of the cross-section of the CDI cell, as well as an SEM image of the electrode macropore structure, and a transmission electron microscope (TEM) micrograph of the meso- and micropore structure. Carbon electrodes were fabricated using similar procedure as outlined in ref. 14. In this study we used a flow-between cell containing four pairs of carbon electrodes with total activated carbon mass equal to ∼3.6 g. A constant flow rate of Φ = 7.5 mL min−1 per flow channel is used throughout this work (total flow of Φ = 30 mL min−1). Electrochemical measurements were carried out with a potentiostat (VSP30 from Bio-Logic, France) using chronoamperometry (CAM) at several different levels of applied cell voltage, while salt concentration is measured on-line via conductivity sensor (856 conductivity module coupled with 5 ring conductivity measuring cells, Metrohm AG, Switzerland). The measured conductivity was converted to salt concentration using a calibration function (see ESI Fig. S2†). The salt adsorption capacity and the measured charge are defined as per mass of active material in both electrodes. Electric charge was calculated from the discharge current after correcting for the leakage current measured at the end of each desorption step.
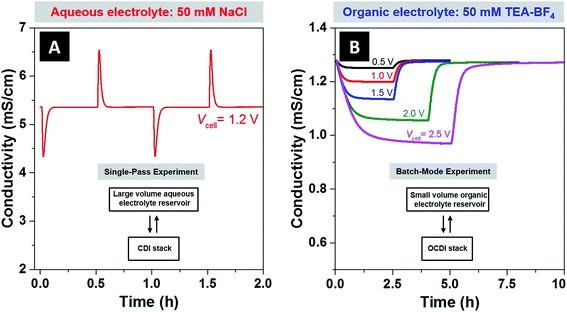
The NaCl/H2O system was operated in a single-pass mode, which is where the feed passes through the cell a single time and is then mixed into a large reservoir (10.5 L), with negligible change in the reservoir ionic strength. The TEA-BF4/PC system was operated in a batch-mode, where the electrolyte in the small-volume reservoir of ∼98 mL and 566 mL for 5 mM and 50 mM feeds, respectively, was recirculated through the cell until a steady effluent conductivity was reached (so reservoir ionic strength was significantly changed). For more details on batch versus single-pass experimental modes see ref. 4, or the schematics provided in Fig. 2A (for single pass mode) and Fig. 2B (for batch mode). CDI experiments with organic electrolyte were performed in batch mode operation due to the slow ion electrosorption kinetics of this system. In order to probe the physical source of the slow kinetics observed, we performed molecular dynamics simulations which show that the diffusivity of TEA-BF4 in PC is about one order of magnitude lower than for NaCl in water when both systems are at a concentration of 50 mM (see ESI Fig. S3 and Tables S1 and S2†). This large difference in predicted diffusivity is likely the cause of the slow ion electrosorption rate observed when TEA-BF4 in PC was studied.
In Fig. 2A, we provide experimental effluent conductivity data taken form NaCl/H2O system during single-pass charge–discharge cycling, and in Fig. 2B the data taken from the TEA-BF4/PC system during batch-mode cycling. For the CDI experiments with aqueous electrolyte, we used experimental conditions typical to ion removal from aqueous electrolyte studies, with 1.2 V applied during charging, 0 V applied during discharging, and a feed with 50 mM NaCl solution. Two full charge–discharge cycles are shown, characterized by the sharp dip in conductivity upon initiating cell charging, and sharp rise in conductivity upon shorting the electrodes. For the CDI experiments with an organic solvent, applied voltages varied from 0.5 V to 2.5 V, and the ion concentration of TEA-BF4 in PC was 50 mM. At 2.5 V, low leakage current of 0.3 mA (which was about 2% of the initial current) demonstrates the near absence of parasitic side-reactions at voltages well outside the water stability window in our CDI system. The reduction in feed conductivity at equilibrium was roughly 2% for 0.5 V, 11% for 1.5 V, and 24% for 2.5 V, demonstrating a large increase in achieved ion sorption when accessing higher voltages.
In Fig. 3, we show several commonly reported CDI performance metrics,2 and use these metrics to contrast the performance of the NaCl/H2O and TEA-BF4/PC systems. In Fig. 3A we present the charge storage capacity as function of applied cell voltage. We find that at 1 V, the charge stored is approximately 15 C g−1 for both systems tested. For TEA-BF4/PC system, due to wider electrochemical stability window,15 the measured charge storage capacity attains higher values than that of the aqueous system, up to about 49 C g−1 at 2.5 V. Further, as shown in Fig. 3A, we observed a nonlinear increase of the charge stored (an increase in cell specific capacitance) with cell voltage, with specific capacitance increasing from about 44 F g−1 for voltages which were under 1.5 V to 78 F g−1 at Vcell = 2.5 V for the TEA-BF4/PC system.
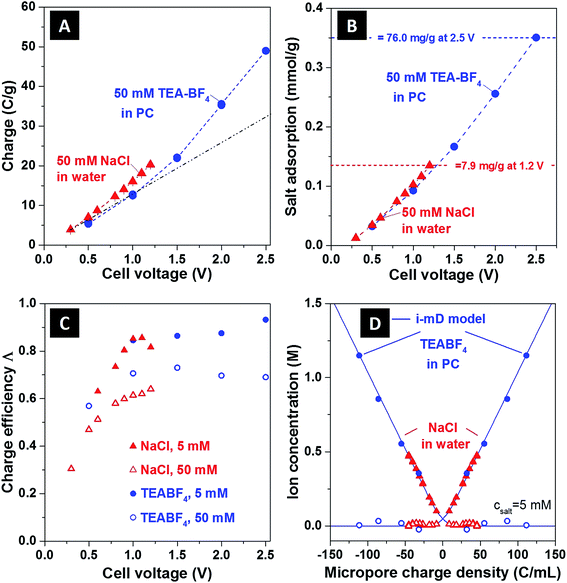 | ||
| Fig. 3 Comparison between (A) charge storage, (B) salt adsorption, (C) charge efficiency as function of cell voltage, and (D) ion concentration as function of ionic charge density of aqueous and organic CDI systems, (assuming E = 200 kT mM−1,12 vpore = 0.736 mL g−1). In panel (B), salt adsorption data are expressed in mmol g−1, where mmol refers to either NaCl or TEA-BF4. For the maximum sorption values, corresponding values in mg g−1 are given; also, see ESI Fig. S4† for a full representation in mg g−1. The black dashed line in (A) is a line of best fit through the organic system data points less than 1.5 V (blue circles), extrapolated to 2.5 V, in order to show clearly the non-linear increase in measured charge stored at >1.5 V. The blue dashed lines in A and B follow the data points for the organic system in order to guide the eye, and the solid blue line in (D) are the i-mD model results. | ||
In Fig. 3B, we show the equilibrium salt adsorption capacity (eq-SAC) versus applied cell voltage for the case of 50 mM ion concentration. The metric eq-SAC is widely used in the field of CDI to quantify the electrosorption performance of CDI electrodes, and is typically measured experimentally through NaCl electrosorption.2 The maximum eq-SAC achieved by state-of-the-art capacitive CDI electrodes is roughly 15 mg g−1 for the NaCl/H2O electrolyte.2 Since we want to compare NaCl/H2O and TEA-BF4/PC systems, using eq-SAC with units mg g−1 is not an adequate metric due to the significantly higher molar mass of TEA-BF4 compared to NaCl (roughly four times higher). Rather, a better metric which eliminates the effect of ion mass is eq-SAC using units of mmol g−1. As can be seen in Fig. 3B, the NaCl/H2O system achieves about 0.135 mmol g−1 at 1.2 V, whereas the TEA-BF4/PC system achieves over 0.35 mmol g−1 at 2.5 V. Further, the eq-SAC in mmol g−1 of both systems roughly overlaps at voltages between 0 and 1.2 V, whereas the eq-SAC of the TEA-BF4 system continues to increase after 1.2 V due to the extended voltage window. Thus, we here observe that it is possible to achieve nearly three times higher salt sorption when using electrolyte with extended electrochemical stability window. In ESI Fig. S4,† we provide a comparison between TEA-BF4/PC and NaCl/H2O in terms of eq-SAC with units of mg g−1, showing that the TEA-BF4/PC system can achieve up to 76 mg g−1.
In Fig. 3C we plot the charge efficiency (Λ) versus applied cell voltage for both systems (see also ESI Fig. S5A†). The charge efficiency Λ is defined as the ratio of charge (ions) removed from the feed stream to electrode surface charge at the end of the charge step, where measured Λ is less than unity due to the effect of co-ion expulsion from the carbon nanopores.16,17 This metric is of high importance in CDI as the electrical energy consumption per ion removed scales as 1/Λ.4 As can be seen in Fig. 3C, for NaCl/H2O and TEA-BF4/PC, the measured Λ generally increases with cell voltage and decreasing ionic strength. However, as TEA-BF4/PC can achieve higher voltage regimes, the attained Λ (and so attained energy efficiency) is also slightly higher, with Λ ≈ 92% at 5 mM and 2.5 V for CDI with organic solvent (compared to ∼85% for CDI at 1.1 V and 5 mM).
In Fig. 3D, we show the equilibrium concentration of counterions and co-ions in the carbon nanopores derived from experimental data, as functions of electric charge normalized by the nanopore volume. The data is shown for both NaCl/H2O and TEA-BF4/PC at an initial concentration of 5 mM (see ESI Fig. S5B† for 50 mM data). We further compare the experimentally derived data with the results of an improved modified Donnan (i-mD) model, which captured the data well (see ESI† and ref. 18 for details on the i-mD model). The data was obtained using the i-mD model to calculate initial micropore concentration,12 and the measured ion removal from solution at equilibrium from effluent conductivity measurements (see ESI† for more details). For the aqueous system at Vcell = 1.2 V, we calculate from measured data that the counterion concentration is ∼0.47 M, while for organic system at a cell voltage of Vcell = 2.5 V this value can be as high as 1.15 M, more than 23-times higher than initial concentration in the initially uncharged electrodes.
To advance the field of electrosorption technologies, significant research has been recently conducted in the field of in situ electrochemical characterization of supercapacitors. Advanced tools, such as nuclear magnetic resonance (NMR) spectroscopy,19,20 electrochemical quartz crystal microbalance (eQCM),21–23 electrochemical in situ small-angle X-ray scattering,24 in situ infrared spectroelectrochemistry,25 in situ ion concentration neutron imaging, and combination of such techniques,26 have been successfully employed to probe the ion concentration and redistribution dynamics in carbon nanopores undergoing electric charge compensation (during charging). One important result demonstrated by these studies is that at high concentrations (≥1 M), during cell charging and discharging, ion populations inside porous carbon particles typically do not significantly change because charge compensation is mostly accomplished by ion swapping (i.e., exchanging one cation with one anion to accommodate two negative electric charges).27,28 These findings are relevant for high ionic concentrations; yet, at lower salt concentrations (<100 mM), another mechanism needs to be considered: preferred counterion adsorption.29 The latter can occur when the initial concentration of ions in carbon nanopores is too low to accommodate the increased electric charge via ion swapping, and this mechanism can be leveraged towards energy-efficient ion removal (as in CDI). We note that the transition between these charge-compensation electrosorption mechanisms may not only vary as a function of state-of-charge and initial ion concentration, but also is sensitive to the type of salt and solvent system, and the co-ion and counterion kinetics.23,30
The measurement technique demonstrated here to capture the equilibrium ion concentration in carbon nanopores can give insights into the ion compensation mechanisms without the use of highly complex NMR or eQCM measurements. For example, the data in Fig. 3D shows quantitatively that the mechanism of counterion adsorption dominates and co-ion expulsion also occurs to a more limited extent. As the charge (cell voltage) is increased, the counterion concentration in the pore is greatly increased while the co-ion is reduced to near-zero concentration. Effectively, we see that counterion adsorption only dominates when the reservoir of co-ions becomes depleted. Thus, taken as a whole, the technique coupling the i-mD model and effluent conductivity measurements allows us to link key parameters of the porous carbons, such as charge storage, non-electrostatic attraction energy, and pore volume, to the ion distribution in the nanopores. We note that the i-mD model neglected the effects of steric ion exclusion on electrode capacitance. This effect has, to our knowledge, never been incorporated into CDI theory as CDI typically uses small ions, such as sodium and chloride, which are assumed to be able to enter unobstructed into the entire distribution of carbon nanopores. Here, for organic electrolyte, we use larger TEA+ ions, which can be sterically excluded from pores below around 0.7 nm.31 We expect that the latter effect will result in asymmetric systems, with differing nanopore volumes available to the larger TEA+ and smaller BF4− ions during cell charging (see ESI Table S1 and Fig. S1†).
Further insights can be gained on the local environment in carbon nanopores when considering the ratio of ion volume to available pore volume (the micropore volume of the carbon particles used in our electrodes). This ratio is shown in ESI Fig. S6,† and the obtained results suggest that ion desolvation during charging has to be considered for CDI system with TEA-BF4 in PC (at least for the ionic system used in our study). The presence of significant ion desolvation has previously been inferred in porous carbon systems from works studying the influence of average pore size on the charge storage ability of supercapacitors,31,32 and has been demonstrated via molecular dynamics model results.33,34
In conclusion, our study demonstrates the potential of CDI technology for the application of ion-based separations in electrolytes using organic solvents. Our work demonstrated a first time extension of the CDI voltage window to 2.5 V due to the use of organic solvents with >2 V decomposition potentials. We also provided an experimental study of ion removal at voltages beyond the water electrolysis window, showing higher salt adsorption is possible in CDI applied to aqueous electrolytes. Finally, we demonstrated a simple and insightful method to link commonly reported properties of carbon electrodes, such as salt adsorption capacity, with ion concentrations inside nanopores as a function of applied cell voltage. While our proof-of-concept system uses the salt/solvent system of tetraethylammonium tetrafluoroborate salt (TEA-BF4) dissolved in propylene carbonate (PC), the same concept can be performed with a wide variety of organic solvents, charged molecules, and applications (such as lithium recovery or recycling or organic solvents used for purification of synthesis product and cleaning of equipment in the chemical industry).35,36 Especially the possibility to employ CDI for reducing the amount of needed organic solvent in the pharmaceutical industry is of great interest, considering that solvents account for 80–90 mass% of the total utilized materials.37
Acknowledgements
S. P. acknowledges financial support of the Alexander von Humboldt Foundation (AVH). V. P. acknowledges financial support by the German Research Foundation via the Heinz Maier-Leibnitz Prize. S. P. and V. P. thank Prof. Eduard Arzt (INM) for his continuing support. The authors thank Dr Maarten Biesheuvel (Wetsus) and Dr Daniel Weingarth (INM) for their support and value discussion. The authors also thank Marco Zeiger (INM) for his help with Raman spectroscopy and electron microscopy, and Nicolas Jäckel (INM) for his support with gas sorption analysis.References
- H. Wang, T. K. J. Köster, N. M. Trease, J. Ségalini, P.-L. Taberna, P. Simon, Y. Gogotsi and C. P. Grey, J. Am. Chem. Soc., 2011, 133, 19270–19273 CrossRef PubMed.
- M. E. Suss, S. Porada, X. Sun, P. M. Biesheuvel, J. Yoon and V. Presser, Energy Environ. Sci., 2015, 8, 2296–2319 CAS.
- P. M. Biesheuvel and M. Z. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031502 CrossRef PubMed.
- S. Porada, R. Zhao, A. van der Wal, V. Presser and P. M. Biesheuvel, Prog. Mater. Sci., 2013, 58, 1388–1442 CrossRef CAS.
- R. Zhao, M. van Soestbergen, H. H. M. Rijnaarts, A. van der Wal, M. Z. Bazant and P. M. Biesheuvel, J. Colloid Interface Sci., 2012, 384, 38–44 CrossRef PubMed.
- S. H. Roelofs, B. Kim, J. C. Eijkel, J. Han, A. van den Berg and M. Odijk, Lab Chip, 2015, 15, 1458–1464 RSC.
- R. Zhao, S. Porada, P. M. Biesheuvel and A. van der Wal, Desalination, 2013, 330, 35–41 CrossRef CAS.
- H.-H. Jung, S.-W. Hwang, S.-H. Hyun, K.-H. Lee and G.-T. Kim, Desalination, 2007, 216, 377–385 CrossRef CAS.
- X. Xu, L. Pan, Y. Liu, T. Lu, Z. Sun and D. H. C. Chua, Sci. Rep., 2015, 5, 8458 CrossRef CAS PubMed.
- X. Xu, Z. Sun, D. H. C. Chua and L. Pan, Sci. Rep., 2015, 5, 11225 CrossRef CAS PubMed.
- P. M. Biesheuvel, M. E. Suss and H. V. M. Hamelers, 2015, Arxiv, 1506.03948.
- T. Kim, J. E. Dykstra, S. Porada, A. van der Wal, J. Yoon and P. M. Biesheuvel, J. Colloid Interface Sci., 2015, 446, 317–326 CrossRef CAS PubMed.
- P. Marchetti, M. F. Jimenez Solomon, G. Szekely and A. G. Livingston, Chem. Rev., 2014, 114, 10735–10806 CrossRef CAS PubMed.
- D. Weingarth, M. Zeiger, N. Jäckel, M. Aslan, G. Feng and V. Presser, Adv. Energy Mater., 2014, 4, 1400316 Search PubMed.
- F. Markoulidis, C. Lei, C. Lekakou, D. Duff, S. Khalil, B. Martorana and I. Cannavaro, Carbon, 2014, 68, 58–66 CrossRef CAS.
- P. M. Biesheuvel, R. Zhao, S. Porada and A. van der Wal, J. Colloid Interface Sci., 2011, 360, 239–248 CrossRef CAS PubMed.
- J.-B. Lee, K.-K. Park, H.-M. Eum and C.-W. Lee, Desalination, 2006, 196, 125–134 CrossRef CAS.
- P. M. Biesheuvel, S. Porada, M. Levi and M. Z. Bazant, J. Solid State Electrochem., 2014, 18, 1365–1376 CrossRef CAS.
- H. Wang, A. C. Forse, J. M. Griffin, N. M. Trease, L. Trognko, P.-L. Taberna, P. Simon and C. P. Grey, J. Am. Chem. Soc., 2013, 135, 18968–18980 CrossRef CAS PubMed.
- Z. X. Luo, Y. Z. Xing, Y. C. Ling, A. Kleinhammes and Y. Wu, Nat. Commun., 2015, 6, 6358 CrossRef CAS PubMed.
- M. D. Levi, G. Salitra, N. Levy, D. Aurbach and J. Maier, Nat. Mater., 2009, 8, 872–875 CrossRef CAS PubMed.
- M. D. Levi, N. Levy, S. Sigalov, G. Salitra, D. Aurbach and J. Maier, J. Am. Chem. Soc., 2010, 132, 13220–13222 CrossRef CAS PubMed.
- W.-Y. Tsai, P.-L. Taberna and P. Simon, J. Am. Chem. Soc., 2014, 136, 8722–8728 CrossRef CAS PubMed.
- C. Prehal, D. Weingarth, E. Perre, R. T. Lechner, H. Amenitsch, O. Paris and V. Presser, Energy Environ. Sci., 2015, 8, 1725–1735 CAS.
- F. W. Richey, B. Dyatkin, Y. Gogotsi and Y. A. Elabd, J. Am. Chem. Soc., 2013, 135, 12818–12826 CrossRef CAS PubMed.
- J. M. Griffin, A. C. Forse, W. Y. Tsai, P. L. Taberna, P. Simon and C. P. Grey, Nat. Mater., 2015, 14, 812–819 CrossRef CAS PubMed.
- M. Deschamps, E. Gilbert, P. Azais, E. Raymundo-Piñero, M. R. Ammar, P. Simon, D. Massiot and F. Béguin, Nat. Mater., 2013, 12, 351–358 CrossRef CAS PubMed.
- S. Kondrat, P. Wu, R. Qiao and A. A. Kornyshev, Nat. Mater., 2014, 13, 387–393 CrossRef CAS PubMed.
- J. M. Griffin, A. C. Forse, H. Wang, N. M. Trease, P. L. Taberna, P. Simon and C. P. Grey, Faraday Discuss., 2015, 176, 49–68 RSC.
- C. Péan, C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, B. Daffos, M. Salanne and P. Simon, ACS Nano, 2014, 8, 1576–1583 CrossRef PubMed.
- J. Chmiola, C. Largeot, P.-L. Taberna, P. Simon and Y. Gogotsi, Angew. Chem. Int. Ed., 2008, 47, 3392–3395 CrossRef CAS PubMed.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760–1763 CrossRef CAS PubMed.
- D. Jiang, Z. Jin, D. Henderson and J. Wu, J. Phys. Chem. Lett., 2012, 3, 1727–1731 CrossRef CAS PubMed.
- D. Jiang, Z. Jin and J. Wu, Nano Lett., 2011, 11, 5373–5377 CrossRef CAS PubMed.
- Y. Liu, L. Pan, X. Xu, T. Lu and Z. Sun, RSC Adv., 2013, 3, 16932–16935 RSC.
- T. Ryu, D.-H. Lee, J. C. Ryu, J. Shin, K.-S. Chung and Y. H. Kim, Hydrometallurgy, 2015, 151, 78–83 CrossRef CAS.
- D. J. C. Constable, C. Jimenez-Gonzalez and R. K. Henderson, Org. Process Res. Dev., 2007, 11, 133–137 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra20786j |
| This journal is © The Royal Society of Chemistry 2016 |