π⁺–π⁺ stacking of imidazolium cations enhances molecular layering of room temperature ionic liquids at their interfaces

Abstract

The interfacial structure of room temperature ionic liquids (RTILs) controls many of the unique properties of RTILs, such as the high capacitance of RTILs and the efficiency of charge transport between RTILs and electrodes. RTILs have been experimentally shown to exhibit interfacial molecular layering structures over a 10 Å length scale. However, the driving force behind the formation of these layered structures has not been resolved. Here, we report ab initio molecular dynamics simulations of imidazolium RTIL/air and RTIL/graphene interfaces along with force field molecular dynamics simulations. We find that the π⁺–π⁺ interaction of imidazolium cations enhances the layering structure of RTILs, despite the electrostatic repulsion. The length scales of the molecular layering at the RTIL/air and RTIL/graphene interfaces are very similar, manifesting the limited effect of the substrate on the interfacial organization of RTILs.

---

1. Introduction

Room temperature ionic liquids (RTILs) constitute a class of salts, which are in the liquid state at room temperature. Intermolecular ionic interactions between their cations and anions differentiate RTILs from non-ionic liquids, and render RTILs unique solvents:^1,2 RTILs are environmentally friendly solvents thanks to their low vapor pressure. Moreover, owing to their ionic nature, RTILs have potential applications in supercapacitors, as battery electrolytes, and as catalysts for generating graphene sheets from graphite.^3–5 The interfacial properties of RTILs govern their performance in supercapacitors and in the graphene exfoliation process. Unveiling and understanding the local structure of RTILs at their interfaces is therefore crucial for designing and optimizing the physical and chemical properties of RTILs.

Experimentally, the interfacial structures of RTILs have been investigated by X-ray spectroscopy,^6–11 neutron reflectivity,^12,13 atomic force microscopy,¹⁴ sum-frequency generation (SFG) spectroscopy,^15–19 and surface force measurements.^20,21 Owing to its selection rules, SFG spectroscopy is specifically sensitive to the near-surface region in which the symmetry of the molecular arrangement is broken. The SFG spectra recorded from the RTIL/air^15–17 and RTIL/graphene interfaces^18,19 evidence that the imidazolium ring of the RTIL cations are oriented parallel to the interface. Starting from this planar orientation of the RTIL cations at the topmost RTIL layer, cation-rich and anion-rich layers appear alternately. X-ray spectroscopy revealed that this RTIL layering continues over a length scale of ∼10 Å.^6–11 However, it is not clear how the repeated cation-rich and anion-rich layers are stabilized near the RTIL interfaces.

Since computational approaches based on the force field/ab initio molecular dynamics (MD) simulation allow us to visualize the molecular structures of RTILs, they have been frequently used for connecting both the bulk^22–37 and interfacial structures^38–44 of RTILs with their physical and chemical properties. The non-polarizable force field MD (NP-FFMD) simulation was the first to be applied to RTILs. NP-FFMD can reproduce the structural properties of RTILs such as the radial distribution function and density, whereas dynamical properties such as the diffusion constant and viscosity were poorly reproduced, because of the slow RTIL dynamics in the NP-FFMD simulation.^22–25 To improve the description of the dynamical properties of RTILs, polarizable force field MD has been applied for RTILs.^26,33–37 The molecular polarizability of RTILs in the polarizable force field MD (P-FFMD) simulation screens the electrostatic interactions, accelerating the RTIL dynamics.²⁶ Furthermore, the interfacial structure of RTILs at the RTIL/air interface was examined using P-FFMD.⁴² The comparison of P-FFMD and NP-FFMD shows that the molecular polarizability randomizes the specific orientation of the imidazolium cation.⁴² However, both FFMD simulations are known to have serious drawbacks for balancing various types of intermolecular interactions such as the electrostatic interactions, π⁺–π⁺ interactions, and hydrogen bond interactions.²⁷ Both the inclusion of dispersion corrections⁴⁵ and the interplay between π⁺–π⁺ interactions and hydrogen bonding⁴⁶ are of importance to stabilize the cation–cation arrangements in the RTIL bulk system. However, the role of π⁺–π⁺ interactions at the interface of RTILs is still not clear.

Here, by using the ab initio MD (AIMD) simulation with the van der Waals corrections and comparing AIMD data with NP- and P-FFMD data, we explore the RTIL layering at the RTIL/air and RTIL/graphene interfaces. Our simulation indicates that the RTIL interfacial structure results from the competing effects of electrostatic forces (causing layering), the molecular polarizability (disordering the interface) and π⁺–π⁺ interactions (giving rise to additional layering and ordering). Furthermore, the very similar length scale of molecular layering at the RTIL/air and RTIL/graphene interfaces reveals that the molecular layering is governed by the intrinsic RTIL interactions and is not strongly influenced by the substrate.

2. Simulation details

2.1. Ab initio MD simulations

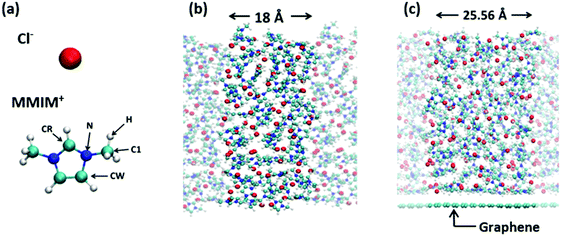
We employed the Becke–Lee–Yang–Parr (BLYP)^47,48 and Perdew–Burke–Ernzerhof (PBE)⁴⁹ exchange–correlation functionals for the AIMD simulation at the 1,3-dimethylimidazolium chloride [MMIM⁺][Cl⁻]/air interface and the BLYP exchange–correlation functional for the AIMD simulation at the [MMIM⁺][Cl⁻]/graphene interface. We used the triple-zeta valence plus two polarization (TZV2P) basis sets and the real-space density cutoff of 400 Ry. The core electrons were described by the Goedecker–Teter–Hutter pseudopotential.⁵⁰ The van der Waals correction was included via the Grimme's D3 method.⁵¹ We prepared an 18 Å × 18 Å × 65 Å simulation cell, which contained 70 [MMIM⁺][Cl⁻] pairs. The cell size for the RTIL/graphene interface simulation was set to 25.56 Å × 24.595 Å × 65 Å, which contained 120 [MMIM⁺][Cl⁻] pairs. Periodic boundary conditions were used. In this study, we used the deuterium atom instead of the hydrogen atom for [MMIM⁺], which is denoted as [d-MMIM⁺]. The molecular structures of the [MMIM⁺] and [Cl⁻] are shown in Fig. 1(a). The time step for integrating the equation of motion was set to 0.6 fs. The AIMD simulation employing the QUICKSTEP⁵² method was performed by using the CP2K code.⁵³

Fig. 1 (a) Molecular structure of [MMIM⁺] and [Cl⁻]. (b) A snapshot of the RTIL/air interface. The width of 18 Å indicates the cell width. (c) A snapshot of the RTIL/graphene interface. The width of 25.56 Å indicates the cell width.

We started the BLYP + D3-AIMD simulation at 450 K using four different initial conformations for the RTIL/air interface, while we ran the BLYP + D3-AIMD simulation at 450 K with one initial conformation for the RTIL/graphene interface. Note that since the melting temperature of [MMIM⁺][Cl⁻] is 398.15 K,⁵⁴ our system is in liquid phase. For these initial configurations, we conducted 5 ps AIMD simulations in the NVT ensemble for equilibrating the systems. We used the canonical sampling through a velocity rescaling (CSVR) thermostat⁵⁵ to control the temperature. Sequential >25 ps AIMD runs were performed for sampling the AIMD trajectories, and finally we obtained total 123.4 ps AIMD trajectories for the RTIL/air interface and 28.6 ps AIMD trajectory for the RTIL/graphene interface. The snapshots of the simulated RTIL/air interface and RTIL/graphene interface are shown in Fig. 1(b) and (c), respectively.

For the PBE + D3-AIMD simulation at the RTIL/air interface, we used the same MD simulation conditions, and the same initial configurations as the BLYP + D3-AIMD simulation. We used the four different initial configurations for the PBE + D3-AIMD simulation. These initial configurations were the same as used in the BLYP + D3-AIMD simulation. For the simulation at 450 K, we performed 5 ps PBE + D3-AIMD runs for equilibrating the systems and then performed over 27 ps AIMD runs for obtaining the MD trajectories. The total 109 ps AIMD trajectories were used for analyzing the data. More detailed information on the simulation is given in the ESI.†

2.2. Force field MD simulations

For the NP-FFMD simulation of the [d-MMIM⁺][Cl⁻]/air interface, we employed the OPLS-AA-based force field model developed by Canongia Lopes, Deschamps and Pádua.⁵⁶ The C–D (C–H) bond lengths were fixed by using the SHAKE algorithm. A time step of 1 fs was used for integrating the equation of motion. We used the same simulation cell size and the same number of ion pairs in the NP-FFMD run. Periodic boundary conditions were used. We ran a 5 ns NP-FFMD simulation in the NVT ensemble to equilibrate the systems at 450 K. The temperature was controlled by the Andersen temperature coupling scheme in the production run.⁵⁷ Subsequently, we performed a 38 ns MD run at 450 K to obtain the trajectories, which were used for analyzing the data. The NP-FFMD simulation was performed by using the PMEMD module of the Amber14 package.⁵⁸

For the P-FFMD simulation of the [d-MMIM⁺][Cl⁻]/air interface, we used the SANDER module of the Amber14 software package.⁵⁸ The parameters for the intermolecular interactions, point charges, and Lennard-Jones parameters were the same as those used in the NP-FFMD simulation. In the P-FFMD simulation, we added the atomic polarizability models to the NP-FFMD simulation. One model was the Amber polarizability model which is designed to apply for any atom species.⁵⁹ The other was the polarizability model optimized by the imidazolium room temperature ionic liquids (the Voth model²⁶). The electrostatic interactions were calculated within the Applequist model.⁶⁰ The target temperature was set to 450 K. The other simulation conditions were the same as the NP-FFMD simulation. We ran 5 ns P-FFMD runs to equilibrate the systems. Subsequently, we performed a 20 ns P-FFMD run for the Amber polarizability model and a 19 ns P-FFMD run for the Voth polarizability model at 450 K to obtain the P-FFMD trajectories, which were used for analyzing the data.

2.3. Geometry-definitions of stacked, displaced and T-shaped conformations

We analyzed the π⁺–π⁺ configurations of cations from the MD trajectories using distinct geometry-based definitions. These geometry-based definitions are based on the relative configuration of a pair of [d-MMIM⁺], for which we calculated the three vectors, , , 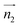and ; and are the normal of the planes formed by the three carbon atoms of the imidazolium rings of two cations, while 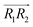is the vector pointing from R₁ to R₂ where R₁ and R₂ are the centers of mass of three carbon atoms of the imidazolium rings. These are schematically shown in Fig. 2.

Fig. 2 (Left) The definition of three vectors: , and , based on the geometry of a pair of [d-MMIM⁺]. The red, blue, sky blue, and white spheres denote the chloride ion, nitrogen atom, carbon atom, and deuterium atom, respectively. (Right) A schematic representation of three π⁺–π⁺ interactions of imidazolium cations.

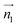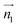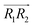We evaluated the π⁺–π⁺ interaction configuration pairs of [d-MMIM⁺] using the following conditions: for the stacked π⁺–π⁺ configuration (1), we set the criteria of φ < 30°, , ψ₁ < 30°, and ψ₂ < 30°, where φ, ψ₁, and ψ₂ denote the angles formed by and , and , and , respectively. φ, ψ₁, and ψ₂ have values between 0° and 90°, and when φ, ψ₁, and ψ₂ are more than 90°, these should be replaced by 180° − φ, 180° − ψ₁, and 180° − ψ₂, respectively. For the displaced π⁺–π⁺ configuration (2), we used the criteria of φ < 30°, , 30° < ψ₁ < 60°, and 30° < ψ₂ < 60°. For the T-shaped π⁺–π⁺ configuration (3), we used the criteria of φ > 60°, 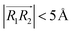. Furthermore, the pairs should satisfy ψ₁ > 60° or ψ₂ > 60°. The positions of these pairs are represented by the midpoints of R₁ and R₂. By using these geometry-based definitions, we quantified the propensity of the different cation–cation conformations through the π⁺–π⁺ interactions.

3. Results

3.1. Layering structure of RTILs at the RTIL/air interface

We calculated the number densities of [MMIM⁺] and [Cl⁻] (denoted by ρ₊ and ρ₋, respectively) at the RTIL/air interface. The axial profiles of the number densities, ρ₊, ρ₋, and the difference of the densities, (ρ₊ − ρ₋), are plotted in Fig. 3(a–d). These indicate that near the RTIL/air interface, the anion-rich and cation-rich layers appear repeatedly. The (ρ₊ − ρ₋) data also show that the alternating anion-rich and cation-rich layers decay towards the bulk, consistent with the previous NP-FFMD simulation studies.^43,44

Fig. 3 (a–d) Axial profiles of the RTIL number densities at the RTIL/air interface. We obtained the data by averaging the number density at the two RTIL/air interfaces in the slab models. The origin point (z = 0 Å) is set to the Gibbs dividing surface. The areas of (ρ₊ − ρ₋), ΔS(z), are filled with red (blue) color, when the peak is positive (negative). (e) Comparison of ΔS obtained from different models. The fit function is given by Δf(z) = f₀(1 − exp(−(z − c)/λ))exp(−z/ξ). The data were normalized to the maximum value of the fits. The fit parameters are summarized in Table 1.

To quantify the decay of (ρ₊ − ρ₋) between AIMD, P-FFMD and NP-FFMD simulations, we plot the normalized area of the positive and negative (ρ₊ − ρ₋), that is, we integrated the function of (ρ₊ − ρ₋) between adjacent zero crossings, and took the absolute value of the integrals. This results in a discrete function ΔS, which represents the successive areas filled with red and blue colors in Fig. 3(a–d). ΔS is plotted as a function of the peak maxima in Fig. 3(e). This figure shows that ΔS decays more quickly in the P-FFMD simulation than in the NP-FFMD simulation. This indicates that the molecular polarizability, which is accounted for in P-FFMD but not in NP-FFMD, substantially randomizes the RTIL layering structure near the RTIL/air interface. On the other hand, the AIMD simulation indicates a much slower decay of ΔS than the P-FFMD simulation, although both the AIMD and P-FFMD simulations include the effects of the molecular polarizability. Surprisingly, (ρ₊ − ρ₋) is similar for the AIMD and NP-FFMD simulations. This raises the question why the AIMD simulation predicts more extensive RTIL layering than the P-FFMD simulation.

ΔS can be described well by a phenomenological function Δf(z) = f₀(1 − exp(−(z − c)/λ))exp(−z/ξ), where the term exp(−z/ξ) represents the decay of (ρ₊ − ρ₋) with a length scale of ξ (Lorentzian model¹⁰). The term (1 − exp(−(z − c)/λ)) represents the rapid density increase at the interface and different surface activity of the cation and anion; c and λ denote the coordinate shift from the Gibbs dividing surface and the decay constant of the surface modulation (λ < ξ), respectively. f₀ is the amplitude of Δf(z). We obtained λ from global fitting for all the NP-FFMD, P-FFMD, and AIMD simulations, while ξ, c, and f₀ were allowed to vary between the different simulations. The normalized fit curves Δf(z) are also plotted in Fig. 3(e). The decay constant of the density oscillation in the AIMD simulation amounts to ξ = 10.4 Å, about twice as large as that inferred from the P-FFMD simulation (ξ = 6.2 Å for Amber polarizability model and ξ = 4.2 Å for the Voth polarizability model), but remarkably similar to the ξ = 9.6 Å of the NP-FFMD simulation.

3.2. π⁺–π⁺ conformations at the RTIL/air interface

To elucidate the mechanism for enhanced RTIL layering in the AIMD simulation against the structure randomization due to the molecular polarizability, we consider the effect of π⁺-interactions on the RTIL interfacial structure. In fact, the ion pairs interact substantially through the π⁺–anion interactions in the AIMD simulation, while they do not interact in the FFMD simulation.^29–31 However, quantifying the π⁺–π⁺ interactions of [MMIM⁺] is not straightforward, since these π⁺–π⁺ interactions mediated by [Cl⁻] can have several different conformations – stacked, displaced, and T-shaped conformations.^61–63

The axial profiles of the π⁺–π⁺ conformations calculated from the AIMD trajectory, P-FFMD trajectory using the Amber polarizability model, and NP-FFMD trajectory are displayed in Fig. 4(a)–(c). The AIMD simulation shows that at the RTIL/air interface, the stacked conformation is dominant and substantially more prevalent at the interface than in the bulk. In contrast, the displaced and T-shaped conformations are not prominent at the interface. This trend differs from that inferred from the NP-FFMD and P-FFMD simulations; these three conformations show similar distributions and no preferable stacked conformation at the interface. This highlights the importance of the π⁺–π⁺ interaction of imidazolium cations through the stacked conformation at the RTIL/air interface, despite the cations being electrostatically repulsive.

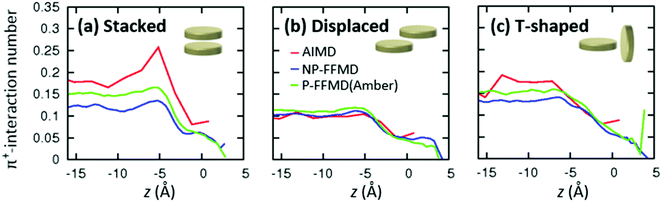Fig. 4 Axial profiles of the relative prevalence of different π⁺–π⁺ conformations, obtained by AIMD, NP-FFMD and P-FFMD simulations.

3.3. Layering structure of RTILs at the RTIL/graphene interface

We have discussed the molecular layering of RTILs at the RTIL/air interface. To demonstrate that the ∼10 Å molecular layering distance is intrinsic to the nature of RTILs, we also investigated the RTIL/graphene interface. The number density profiles at the RTIL/graphene interface are displayed in Fig. 5(a). The amplitude of the (ρ₊ − ρ₋) peak area is much larger at the RTIL/graphene interface than that at the RTIL/air interface, indicating that the graphene sheet has strong templating effects on the RTILs. This is consistent with the previous NP-FFMD simulation.^64–68 The peak area of (ρ₊ − ρ₋), ΔS, at the RTIL/graphene interface is plotted in Fig. 5(b) together with ΔS at the RTIL/air interface. The normalized fit curves of Δf(z) are also displayed in Fig. 5(b), while the fit parameters are summarized in Table 1. These plots show very similar decay lengths for both the RTIL/air and RTIL/graphene interfaces, illustrating that the range of the molecular layering is not affected by the RTIL–substrate interactions but is governed by the nature of the RTIL.

Table 1 The fit parameters of Δf(z) = f₀(1 − exp(−(z − c)/λ))exp(−z/ξ) for the AIMD (BLYP + D3), NP-FFMD, and P-FFMD simulations at the RTIL/air interface (Fig. 3(a–d)) and the AIMD simulation at the RTIL/graphene interface (Fig. 5(a)). λ was obtained from global fits to all the data, yielding λ = 4.0 Å. The standard deviations of S₀, c, and ξ for the RTIL/air interface are at most 5%, while those for the RTIL/graphene interface are at most 15%

	RTIL/air				RTIL/graphene
	AIMD(BLYP + D3)	NP-FFMD	P-FFMD (amber)	P-FFMD (Voth)	AIMD(BLYP + D3)
f 0 (nm^−2)	0.92	0.74	0.91	0.95	1.26
c (Å)	−1.00	−0.88	−0.52	−0.92	−1.48
ξ (Å)	10.4	9.6	6.2	4.2	10.2

---

Fig. 5 (a) Axial profiles of the RTIL number densities at the RTIL/graphene interface in the AIMD simulation. The number density of graphene (shown in black) was divided by 50. The origin point (z = 0 Å) was set to the position of the first peak position of ρ₊. (b) Normalized ΔS(z), of the RTIL/graphene and RTIL/air interfaces in the AIMD simulation. The fitting function is given by Δf(z) = f₀(1 − exp(−(z − c)/λ))exp(−z/ξ), and the fit parameters are given in Table 1.

Fig. 6 Axial profiles of the number of the π⁺–π⁺ conformations obtained by the AIMD simulation at the BLYP + D3/TZV2P and PBE + D3/TZV2P levels of theory. The origin point (z = 0 Å) is the Gibbs dividing surface. The BLYP + D3 data are the same as given in Fig. 4.

3.4. π⁺–π⁺ conformations with PBE XC functional

Above, we showed the comparison of interfacial RTIL structures predicted by the AIMD and FFMD simulations and found that the π⁺–π⁺ stacked conformation is essential for the layering structure of RTILs at the RTIL interfaces. In this section, by comparing the RTIL layering structures predicted using the BLYP + D3 and PBE + D3 methods, we again demonstrate that the rich π⁺–π⁺ stacked conformation at the RTIL/air interface is very sensitive to the π⁺–π⁺ interaction energy. Here, a key property is that the PBE + D3 level of theory significantly lowers the binding energy of the stacked conformation relative to the BLYP + D3 level of theory.⁵¹ Therefore, one can expect that the PBE + D3-AIMD simulation provides much less stacked conformations compared with the BLYP + D3-AIMD simulation.

The axial profiles of the stacked conformations calculated using the PBE + D3-AIMD simulation are displayed in Fig. 6. Indeed, the comparison of the PBE + D3 and BLYP + D3 levels of theory in Fig. 6 shows that more stacked conformations are observed in the BLYP + D3-AIMD simulation. This illustrates that, as expected, the π⁺–π⁺ stacked conformations are very sensitive to the π⁺–π⁺ interaction energy.

3.5. Consistency between simulation and experiment

Finally, we discuss the consistency of the current simulation and experimental data. We show that the π⁺–π⁺ interaction of imidazolium cations stabilizes the RTIL layering structure, against both electrostatic repulsion and the molecular polarizability, which both serve to reduce the molecular layering near the RTIL interface. As a result, the AIMD simulation coincidentally shows a very similar length scale of molecular layering as the NP-FFMD simulation. A good agreement between the NP-FFMD and experimental data has been reported; both X-ray scattering and NP-FFMD show 10 Å length of molecular layering for the [BMIM⁺][NTf₂⁻]/mica⁷ and [EMIM⁺][NTf₂⁻]/sapphire⁸ interfaces. The NP-FFMD simulation gets the correct length scale for the wrong reasons: our finding indicates that a coincidental cancellation of the lack of the π⁺–π⁺ interaction and molecular polarizability results in a good agreement of the NP-FFMD simulation and the experiment. Furthermore, a similar length scale of RTIL layering at the mica⁷ and sapphire⁸ interfaces also suggests that the molecular layering structure is less influenced by the substrate, consistent with our findings.

4. Conclusion

We studied the length scale of the molecular layering for imidazolium RTILs at the RTIL/air and RTIL/graphene interfaces, by using the AIMD simulation. Comparison of the AIMD, NP-FFMD, and P-FFMD simulation data indicates the competing effects of the randomization of RTILs due to the molecular polarizability and the enhanced molecular layering due to the π⁺–π⁺ interactions of the imidazolium rings. A very similar length scale of RTIL layering at the RTIL/air and RTIL/graphene interfaces shows that the length scale of the molecular layering structure is dictated by the RTIL–RTIL interactions and is not affected by the substrates. Our study highlights the importance of π⁺–π⁺ interactions of the cation imidazolium rings in stabilizing the surface structure of the imidazolium RTILs, which is essential, for example, for the charge transport properties in the RTILs and between the RTILs and the electrodes.

Competing financial interests

The authors declare no competing financial interests.

Acknowledgements

We are grateful to Dr Johannes Hunger and Dr Markus Metzger for fruitful discussion and critical reading of the manuscript. This project was supported by TRR146 through the German Science Foundation.

References

1. E. W. Castner, J. F. Wishart and H. Shirota, Acc. Chem. Res., 2007, 40, 1217–1227.
2. T. W. P. Wasserscheid, Ionic Liquids in Synthesis, Wiley Online Library, 2003.
3. K. R. K. Seddon, J. Chem. Technol. Biotechnol., 1997, 68, 351–356.
4. D. R. Macfarlane, M. Forsyth, P. C. Howlett, J. M. Pringle, J. Sun, G. Annat, W. Neil and E. I. Izgorodina, Acc. Chem. Res., 2007, 40, 1165–1173.
5. M. Matsumoto, Y. Saito, C. Park, T. Fukushima and T. Aida, Nat. Chem., 2015, 7, 730–736.
6. M. Mezger, H. Schröder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schöder, V. Honkimäki, M. Deutsch, B. M. Ocko, J. Ralston, M. Rohwerder, M. Stratmann and H. Dosch, Science, 2008, 322, 424–428.
7. H. Zhou, M. Rouha, G. Feng, S. S. Lee, H. Docherty, P. Fenter, P. T. Cummings, P. F. Fulvio, S. Dai, J. McDonough, V. Presser and Y. Gogotsi, ACS Nano, 2012, 6, 9818–9827.
8. Z. Brkljača, M. Klimczak, Z. Miličevic, M. Weisser, N. Taccardi, P. Wasserscheid, D. M. Smith, A. Magerl and A. S. Smith, J. Phys. Chem. Lett., 2015, 6, 549–555.
9. M. Mezger, B. M. Ocko, H. Reichert and M. Deutsch, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3733–3737.
10. M. Mezger, S. Schramm, H. Schröder, H. Reichert, M. Deutsch, E. J. De Souza, J. S. Okasinski, B. M. Ocko, V. Honkimäki and H. Dosch, J. Chem. Phys., 2009, 131, 94701.
11. N. Nishi, K. Kasuya and T. Kakiuchi, J. Phys. Chem. C, 2012, 116, 5097–5102.
12. J. Bowers, M. C. Vergara-Gutierrez and J. R. P. Webster, Langmuir, 2004, 20, 309–312.
13. D. Wakeham, P. Niga, G. G. Warr, M. W. Rutland and R. Atkin, Langmuir, 2010, 26, 8313–8318.
14. R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426.
15. C. Aliaga and S. Baldelli, J. Phys. Chem. B, 2007, 111, 9733–9740.
16. C. S. Santos and S. Baldelli, J. Phys. Chem. B, 2007, 111, 4715–4723.
17. T. Iimori, T. Iwahashi, K. Kanai, K. Seki, J. Sung, D. Kim, H. Hamaguchi and Y. Ouchi, J. Phys. Chem. B, 2007, 111, 4860–4866.
18. S. Xu, S. Xing, S.-S. Pei and S. Baldelli, J. Phys. Chem. B, 2014, 118, 5203–5210.
19. S. Xu, S. Xing, S.-S. Pei, V. Ivaništšev, R. Lynden-Bell and S. Baldelli, J. Phys. Chem. C, 2015, 119, 26009–26019.
20. M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679.
21. M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437.
22. Y. Zhang and E. J. Maginn, J. Phys. Chem. B, 2012, 116, 10036–10048.
23. K. G. Sprenger, V. W. Jaeger and J. Pfaendtner, J. Phys. Chem. B, 2015, 119, 5882–5895.
24. C. Cadena, Q. Zhao, E. J. Maginn and R. Q. Snurr, J. Phys. Chem. B, 2006, 110, 2821–2832.
25. F. Dommert, K. Wendler, R. Berger, L. Delle Site and C. Holm, ChemPhysChem, 2012, 13, 1625–1637.
26. T. Yan, C. J. Burnham, M. G. Del Pópolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 11877–11881.
27. R. S. Paton and J. M. Goodman, J. Chem. Inf. Model., 2009, 49, 944–955.
28. J. N. Canongia Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898.
29. B. L. Bhargava and S. Balasubramanian, Chem. Phys. Lett., 2006, 417, 486–491.
30. M. G. Del Pópolo, R. M. Lynden-Bell and J. Kohanoff, J. Phys. Chem. B, 2005, 109, 5895–5902.
31. M. Bühl, A. Chaumont, R. Schurhammer and G. Wipff, J. Phys. Chem. B, 2005, 109, 18591–18599.
32. B. Kirchner, O. Hollóczki, J. N. Canongia Lopes and A. A. H. Pádua, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 202–214.
33. M. Salanne, L. J. A. Siqueira, A. P. Seitsonen, P. A. Madden and B. Kirchner, Faraday Discuss., 2012, 154, 171.
34. M. Salanne, B. Rotenberg, S. Jahn, R. Vuilleumier, C. Simon and P. A. Madden, Theor. Chem. Acc., 2012, 131, 1–16.
35. A. Dequidt, J. Devémy and A. A. H. Pádua, J. Chem. Inf. Model., 2016, 56, 260–268.
36. O. Borodin, J. Phys. Chem. B, 2009, 113, 11463–11478.
37. K. Bica, M. Deetlefs, C. Schröder and K. R. Seddon, Phys. Chem. Chem. Phys., 2013, 15, 2703–2711.
38. B. Heggen, W. Zhao, F. Leroy, A. J. Dammers and F. Müller-Plathe, J. Phys. Chem. B, 2010, 114, 6954–6961.
39. B. L. Bhargava and S. Balasubramanian, J. Am. Chem. Soc., 2006, 128, 10073–10078.
40. A. Sanmartín Pensado, P. Malfreyt and A. A. H. Pádua, J. Phys. Chem. B, 2009, 113, 14708–14718.
41. X. Paredes, J. Fernández, A. A. H. Pádua, P. Malfreyt, F. Malberg, B. Kirchner and A. S. Pensado, J. Phys. Chem. B, 2012, 116, 14159–14170.
42. T. Yan, S. Li, W. Jiang, X. Gao, B. Xiang and G. A. Voth, J. Phys. Chem. B, 2006, 110, 1800–1806.
43. S. S. Sarangi, S. G. Raju and S. Balasubramanian, Phys. Chem. Chem. Phys., 2011, 13, 2714–2722.
44. A. S. Pensado, M. F. Costa Gomes, J. N. Canongia Lopes, P. Malfreyt and A. A. H. Pádua, Phys. Chem. Chem. Phys., 2011, 13, 13518–13526.
45. A. S. Pensado, M. Brehm, J. Thar, A. P. Seitsonen and B. Kirchner, ChemPhysChem, 2012, 13, 1845–1853.
46. H. Weber and B. Kirchner, J. Phys. Chem. B, 2016, 120, 2471–2483.
47. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
48. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
50. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B, 1996, 54, 1703–1710.
51. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
52. J. Vandevondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
53. The CP2K developer groups, http://www.cp2k.org.
54. S. Zhang, N. Sun, X. He, X. Lu and X. Zhang, J. Phys. Chem. Ref. Data, 2006, 35, 1475–1517.
55. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 14101.
56. J. N. Canongia Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047.
57. H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393.
58. D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, AMBER 14, University of California, San Francisco, 2014.
59. P. Cieplak, F. Dupradeau, Y. Duan and J. Wang, J. Phys.: Condens. Matter, 2009, 21, 333102.
60. J. Applequist, J. R. Carl and K.-K. Fung, J. Am. Chem. Soc., 1972, 94, 2952–2960.
61. S. K. Panja, N. Dwivedi, H. Noothalapati, S. Shigeto, A. K. Sikder, A. Saha, S. S. Sunkari and S. Saha, Phys. Chem. Chem. Phys., 2015, 17, 18167–18177.
62. R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2014, 16, 3238–3253.
63. R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2015, 17, 14437–14453.
64. S. A. Kislenko, I. S. Samoylov and R. H. Amirov, Phys. Chem. Chem. Phys., 2009, 11, 5584–5590.
65. A. S. Pensado, F. Malberg, M. F. C. Gomes, A. A. H. Padua, J. Fernandez and B. Kirchner, RSC Adv., 2014, 4, 18017–18024.
66. M. V. Fedorov and R. M. Lynden-Bell, Phys. Chem. Chem. Phys., 2012, 14, 2552–2556.
67. S. Wang, S. Li, Z. Cao and T. Yan, J. Phys. Chem. C, 2010, 114, 990–995.
68. S. Aparicio and M. Atilhan, J. Phys. Chem. C, 2012, 116, 12055–12065.

---

Footnote

† Electronic supplementary information (ESI) available: NP-FFMD simulation for generating initial conformations of the AIMD simulation, further details about the AIMD simulation, density profiles of RTILs, and discussion on the simulation cell size. See DOI: 10.1039/c6cp07034e

---