Microfluidic in situ mechanical testing of photopolymerized gels
Camille
Duprat
*ab,
Hélène
Berthet†
b,
Jason S.
Wexler‡
b,
Olivia
du Roure
*b and
Anke
Lindner
b
aLaboratoire d'Hydrodynamique (LadHyx), Ecole Polytechnique, 91128 Palaiseau, France. E-mail: camille.duprat@ladhyx.polytecnhique.fr
bPhysique et Mécanique des Milieux Hétérogènes (PMMH), UMR 7636 CNRS – ESPCI ParisTech – Université Pierre et Marie Curie Université Paris Diderot 10, rue Vauquelin, 75231 Paris Cedex 05, France. E-mail: olivia.duroure@espci.fr
First published on 24th October 2014
Abstract
Gels are a functional template for micro-particle fabrication and microbiology experiments. The control and knowledge of their mechanical properties is critical in a number of applications, but no simple in situ method exists to determine these properties. We propose a novel microfluidic based method that directly measures the mechanical properties of the gel upon its fabrication. We measure the deformation of a gel beam under a controlled flow forcing, which gives us a direct access to the Young's modulus of the material itself. We then use this method to determine the mechanical properties of poly(ethylene glycol) diacrylate (PEGDA) under various experimental conditions. The mechanical properties of the gel can be highly tuned, yielding two order of magnitude in the Young's modulus. The method can be easily implemented to allow for an in situ direct measurement and control of Young's moduli under various experimental conditions.
1. Introduction
Photopolymerized hydrogels have found numerous applications in biology, chemistry, physics or mechanics. In particular, they provide a functional template for micro-particles, which can then be used as model colloids,1 responsive materials,2 micro reactors, biology tools,3 model suspensions,4 or microflow sensors.5,6 These gels are also widely used for biomedical applications such as drug delivery7,8 or tissue engineering.9–11Often, microfluidics provides a versatile and precise technique for fabricating gel particles, capsules or fibers through complex flow patterns12,13 or flow lithography,14,15 as well as patterned gel substrates.16
The mechanical properties of the gels are paramount to many applications, in particular for cellular biology studies. The elasticity of the gel can be used to initiate differentiated reaction in cells.11 In addition, the elastic modulus of the gel can be used to measure the distance between two adjacent crosslinks and hence a measure of the size of the mesh, i.e. the space available between the macromolecular chains, e.g. for drug diffusion.8 Knowledge of the evolution of the mechanical properties of the gel during cross-linking also allows for a more precise design of fabrication methods under flow,17 and fundamental studies of the transport of flexible objects under flow requires an exact knowledge of their modulus.18
Synthetic hydrogels, such as poly(ethylene glycol) (PEG)-based gels, are among the most commonly used for these applications as their properties (in particular their mechanical properties) can be highly tuned. A common and robust approach to synthesize PEG hydrogels is the photopolymerization of macromolecular PEG chains. The photo-polymerized gel properties can be controlled synthetically (by modifying the monomer structure by adding acrylate or methacrylate groups, or changing the concentration of solvent) and with experimentally tunable parameters such as UV light intensity, exposure time or photoinitiator concentration/structure. Cross-linked gels exhibit entropy-driven elasticity, commonly called rubber elasticity, with a characteristic elastic modulus, which determines their deformation under a given force or flow. The modulus of PEG based gel varies highly with these parameters; consequently, values reported in the literature vary from a couple of kPa to over 10 MPa.19–21
Microfluidic fabrication of gel particles has been widely developed over the past few years, and it is thus important to have a robust method to determine their mechanical properties. Since gel properties are highly dependent on their composition, on the exact fabrication conditions and on their environment, i.e. are extremely set-up dependent, there is a need of a reliable method to assess the mechanical properties of these gels directly in situ, in the conditions of the application. Currently, several methods are employed to characterize gels, but generally require to remove the gel from its environment. Macroscopic tests, such as uniaxial compression or tensile tests, or measurements with a rheometer, require large samples of the gel in a dry environment, which is not always compatible with a microfluidic fabrication. AFM and nanoindentation20,21 or rheology are useful and accurate tools, but require external equipment and the extraction of the gel particle outside of the micro-channel. There is thus a need to access the global mechanical properties, such as the Young's modulus or the average mesh size, of the gel, with an in situ microfluidic method.
Microfluidics has been extensively used for rheological measurements,22 but much less to provide information on the mechanical properties of soft materials such as gels. We have developed a novel microfluidic based method that directly access the mechanical properties of a gel upon its fabrication. We designed a microfluidic channel containing slots filled with a solution of oligomers and photoinitiator. A free standing beam of precisely controlled rectangular shape is fabricated in situ within these slots (Fig. 1(a–b)), using the stop-flow microscope-based projection photolithography method.15,23 It will be used as a probe to measure the mechanical properties of the gel cured in different conditions. When a flow of the uncured solution is imposed in the channel, the beam is pushed into contact with the edges of the slot. The solution then flows over the beam, applying an hydrodynamic force on the gel that deforms accordingly (Fig. 1(c)). Mechanical properties of the gel are deduced from the measurement of the deformation of the beam in response to the flow. This method, where both the load applied to the beam and its geometry are precisely controlled and known, gives a direct access to the Young's modulus of the material. Furthermore, the gel remains in its own solution, thus preventing any swelling or conformation changes and ensuring an accurate determination of its mechanical properties as used in the application.
2. Implementation of microfluidic-based mechanical measurements
2.1. Channel and fiber fabrication
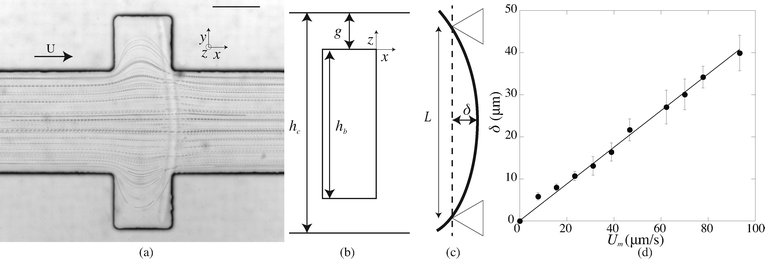
We fabricate all-PDMS (polydimethylsiloxane, Sylgard 184, Corning) microfluidic devices with traditional soft-lithography techniques. The channels are straight with regularly spaced slots. Their typical dimensions are width L = 200 μm, height hc = 40–70 μm, slots length L = 120 μm and channel length of a few centimeters. In order to fabricate hydrogel beams of controlled geometry, we use the stop-flow microscope-based projection photolithography process23 described in Fig. 2(a). The microfluidic channel is filled with a solution of oligomer and photo-initiator and placed on an inverted microscope equipped with a UV light source. The channel is exposed to a pulse of UV light through a lithography mask placed in the field-stop position of the microscope. The shape prescribed by the mask is thus projected into the microchannel. By focusing the light in the center of the microchannel we initiate the cross linking of the solution and we obtain an hydrogel object whose shape is determined by the shape of the mask. We take advantage of the permeability of PDMS to dioxygen that inhibits the polymerization, leaving a non-polymerized lubricating layer of constant thickness along the walls of the channel24 (Fig. 1(b)).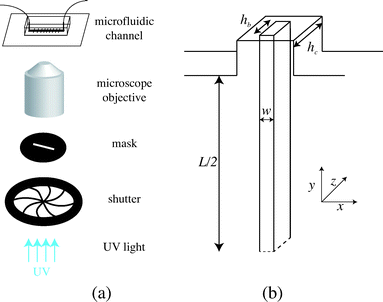 | ||
| Fig. 2 (a) Principle of stop-flow photo-polymerization. (b) Schematic of the beam and channel geometries. | ||
We use an inverted microscope (Zeiss Axio Observer) equipped with a UV light source (Lamp HBO 130W) and an external computer-controlled shutter (Shutter Uniblitz V25). The shutter opening time, tuv, can be precisely controlled. The UV light intensity is kept constant in our experiments. The UV light is filtered through a narrow-UV-excitation filter set (11004v2 Chroma) and is then projected into the channel through a beam-shaped mask. There is a reduction in size between the printed mask and the actual object of width w formed in the channel; the reduction factor corresponds to the magnification of the objective corrected by a factor from the tube lens. With our 10× objective, this reduction factor is about 4. The photo polymerization method requires to focus the projected light into the channel, which is different than visible light. Practically, this means the channel will appear out of focus. The height of the fiber hb is set by the channel height and the height of the inhibition layer. For our channels, this layer is constant and of order 4–6.5 μm. The resulting geometry is described in Fig. 2(b). We explore different geometries listed in Table 1. For a fixed constant channel height, the height of the beam hc is constant and we vary both the width w of the beam and the width L of the channel. We then connect the microfluidic device with rigid tubing to a long syringe (Hamilton 50 μL) mounted on a precision pump (Nemesys, Cetoni) in order to impose well-controlled flow rates Q with a range 0.1 nL s−1 < Q <10 nL s−1. Once the flow is established, no significant fluctuations are observed.
| h c (μm) | h b (μm) | w (μm) | L (μm) |
|---|---|---|---|
| 42 ± 1 | 34 ± 2 | 29 ± 2 | 300 ± 2 |
| 68 ± 1 | 55 ± 2 | 22 ± 2 | 210 ± 2 |
| 265 ± 2 | |||
| 300 ± 2 | |||
| 345 ± 2 | |||
| 27 ± 2 | 345 ± 2 | ||
| 47 ± 2 | 215 ± 2 | ||
| 265 ± 2 |
In principle, the method described here could be applied to any gel obtained from a free-radical reaction. Here, we use polyethylene glycol diacrylate (PEGDA) which is a very common hydrogel used in a large variety of applications. We use a solution PEGDA (Aldrich) of average molecular weight 575 with Darocur 1173 (2-hydroxy-2-methylpropriophenone, Sigma) as a photoinitiator at a concentration [PI] varying from 2 to 10 vol%. The viscosity of the uncured solution is η = 47 mPa s, measured with a capillary rheometer at 20 °C.
2.2. Flow-induced deformation
After fabrication of the probe beam, we impose a small flow rate in order for the beam to be gently pushed into contact with the edges of the slot. The Hele-Shaw geometry creates a plug flow that we visualize by adding particles to the solution (Fig. 3(a)). As the flow approaches the beam, the particles flow through the gap between the top and bottom channel walls and the beam and accelerate due to the confinement. This creates a viscous drag on the fiber. The particle paths show that the presence of a slot does not affect the flow over a large distance, and in particular the streamlines are almost parallel when passing over the fiber. The flow is thus uniform with a constant speed Um = Q/(hcL) over the entire length of the fiber. When the flow is increased, the beam deforms and bends in the direction of the flow with a maximum deflection δ at its center (Fig. 3(c)). The boundary conditions on the edge of the slots correspond to simply supported conditions: the position of the beam is imposed and the beam remains moment-free at the ends. At a critical flow rate, the deformation of the beam is too large and it escapes in the channel. We measure the maximum deflection δ as a function of the flow rate, corresponding to the average flow speed in the channel Um. For a given geometry, we repeat this experiment for several fibers (10 on average) and using at least two different polymer solutions in order to ensure the reproducibility of the system. We perform experiments for various fibers and channel geometries (w = 16.5–42 μm, L = 190–270 μm, see Table 1), and increasing or decreasing flow rate. Once the flow is turned on, the beam takes a couple of seconds to reach a steady shape, due to the delay in fully establishing the flow and possibly the viscoelasticity of the gel. Measurements are only taken once the shape is steady and the deflection is constant. Measuring the deflection for increasing or decreasing flow rate shows that there are no plasticity effects. We observe that, for small flow rates, the deflection varies linearly with the flow speed (Fig. 3(d)). As the flow speed (hence the applied load) is increased, the deflection departs from its linear behavior (data not shown) as expected for large deflections of a simply supported beam under a uniform load.25 We only focus here on the low speed linear region, in which we can extract a Young's modulus for the gel. For given experimental conditions, decreasing the beam length L or increasing the beam width w all lead to a decrease of the deflection δ. Since both the hydrodynamic force and the beam deformation are linked to the channel and fiber geometries, and can not be decoupled, we need to rationalize our observations using analytical modeling of both the hydrodynamic force and the bending of the beam.2.3. Modelling
The force acting on the beam originates from the pressure difference Δp across the width of the beam and the viscous stress σxz applied by the flow on the top and bottom sides of the beam. The flow of interest occurs in the (x, z) plane, in a region of height g = (hc − hb)/2 (Fig. 3(b)). We use the lubrication approximation and assume that the velocity profile ux (z) is constant over the entire length of the beam on the y axis. The velocity of the fluid is given by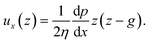 | (1) |
The flow rate per unit length is thus given by
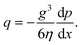 | (2) |
We can estimate the pressure gradient across the width of the beam as
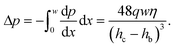 | (3) |
This pressure gradient generates a force per unit length on the fiber fp = Δphb. The viscous stress on one fiber side is given by
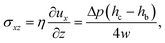 | (4) |
| f = fp + fv = ληUm, | (5) |
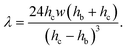 | (6) |
The ratio of the pressure to viscous forces is
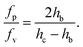 | (7) |
As the confinement increases, i.e. hc − hb decreases, the pressure force becomes predominant. In our case, both forces are of the same order of magnitude, although the pressure force dominates (fp/fv ≃ 8).
We only consider the flow rates where the deflection of the beam varies linearly with the applied force (Fig. 3(d)) and thus the elastomeric beam obeys Hooke's law. Assuming that the load applied on the beam is constant along the length L and equal to f, and considering a slender beam (w ≪ L), we can thus solve the Euler–Bernoulli equation for the beam displacement v(y)
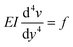 | (8) |
| v(0) = v(L) = 0 | (9) |
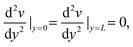 | (10) |
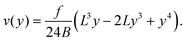 | (11) |
The maximum deflection is given by
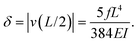 | (12) |
Using expression eqn (5) for the load f, we find finally
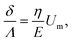 | (13) |
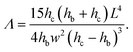 | (14) |
The equations can be made non dimensional using Y = y/L and V = v/δ, which gives for the profile
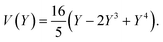 | (15) |
2.4. Validation of the method
For a first validation of our method we compare the experimental shapes of the beam to the theoretical prediction. We obtain the shape of the beam under different flow conditions and for different geometries by image analysis. Typical profiles are shown in Fig. 4(a). Rescaling the profile with the maximum deflection δ and the length of the beam L, all the profiles collapse onto a universal shape (Fig. 4(b)), in very good agreement with eqn (15). This indicates that our description of the gel beam as a linearly elastic beam, simply supported at both sides and under constant load along its length is valid.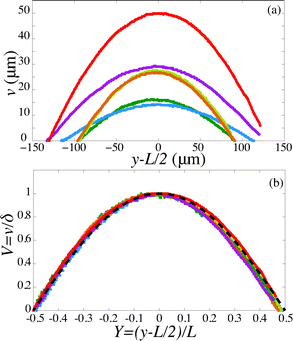 | ||
| Fig. 4 (a) Fiber shapes under different experimental conditions: 5% PI, tuv = 750 ms, L = 220 μm, Q = 50 nl s−1 (red); 5% PI, tuv = 750 ms, L = 220 μm, Q = 25 nL s−1 (purple); tuv = 200 ms, L = 190 μm, Q = 0.8 nL s−1 (yellow/orange); 10% PI, tuv = 350 ms, L = 190 μm, Q = 30 nL s−1 (green); 10% PI, 10% PI, tuv = 250 ms, L = 230 μm, Q = 1.7 nL s−1 (blue). (b) Rescaled shapes v/δ as a function of y/L. Dashed line is eqn (15). | ||
Second, we measure the maximum deflection as a function of the flow speed for various geometries under identical experimental conditions, and for a given solution ([PI] = 10 vol%, tuv = 250 ms). We report the renormalized deflection δ/Λ in Fig. 5. All the data collapse onto a single line, in agreement with our prediction eqn (13). The collapse of our data for a large set of geometries confirms the validity of our analytical approach. The only unknown parameter, the Young's modulus E, is obtained by measuring the slope of this line. In the case presented here, we obtain a Young's modulus of E = 690 ± 70 kPa.
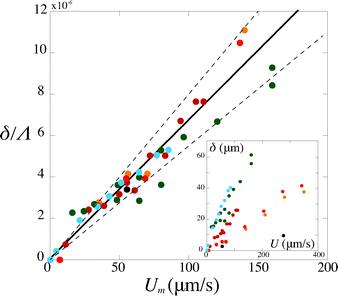 | ||
| Fig. 5 Rescaled deflection δ/Λ as a function of the flow speed Umoy for 10% PI, tuv = 250 ms, and all fiber and channel geometries listed in Table 1. The black line is a fit of the experimental data giving a slope η/E = (6.8 ± 0.7) × 10−8 s, hence a Young's modulus E = 690 ± 70 kPa. Inset: dimensional data. | ||
3. Results
3.1. Mechanical properties of PEG-DA
We now use our method to measure the mechanical properties of PEG-diacrylate as a function of the experimental conditions and the solution composition. In this paper, we use solutions of the commonly used PEG-DA with molecular weight Mw = 575. We vary the concentration in photo initiator [PI] (2–10 vol%) as well as the exposure time tuv (from 200 to 900 ms) which are easily tunable parameters. We consider only polymer melts, i.e. we do not add water to the solution, and thus obtain an highly cross-linked material.A region of the parameter space is not accessible in the experiments. Indeed, below a critical exposure time, the reaction does not initiate and no gel can be formed. For slightly longer times, above the gel point, a beam starts to form but the resulting beam does not match the shape of the mask, and rather resemble a thin filament. We denote tstart the time at which a solid hydrogel beam of the shape prescribed by the mask is formed in the channel. The time tstart slightly decreases with increasing [PI], but looking at the gelation point is beyond the scope of our study. All measurements are taken above tstart, which also ensures that the elastomer is more homogeneous, which is crucial since our method allows for the determination of the average properties of the gel and which is confirmed by the shape adopted by the beams (Fig. 4).
For a given PI concentration, the evolution of the modulus with tuv is reported in Fig. 6. We note that the Young's modulus increases with increasing exposure time. The modulus increases rapidly with tuv, then saturates and reaches a constant value E = 12.5 ± 1 MPa. In this limit of large exposure times, the Young's modulus does not depend on the UV light intensity, [PI], or exposure time. We can thus compare this saturation value to measurements obtained using conventional measurement techniques. We perform measurements of the mechanical properties of our gel, cured in a UV chamber, using a micro indentation tester (CSM instruments MHT). We obtain a value of E = 11.7 ± 1.5 MPa, which is in good agreement with the value obtained in the microfluidic channel.
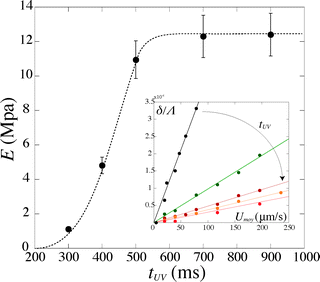 | ||
| Fig. 6 Evolution of the Young's modulus with exposure time tuv for [PI] = 6%. Inset: corresponding evolution of the deflection δ/Λ with the flow speed Umoy. | ||
Increasing the photoinitiator concentration does not change the qualitative evolution of the modulus with exposure time, nor the saturation value. With higher [PI], the modulus increases faster, i.e. an identical value is reached for shorter exposure times tuv. In our experiments, we keep the photoinitiator concentration [PI] ≥ 2%, such that the saturation value of ≃12 MPa is always reached at large exposure times, i.e. the PI concentration is never the limiting factor. However, below a certain threshold of this concentration, the maximum value of the modulus will depend on the photoinitiator concentration as it affects the degree of cross-linking. Drira and Yadavalli21 give AFM measurement of the Young's modulus of dry samples of PEG-DA575. For a concentration [PI] = 1.5%, they report a value of E ≃ 12 MPa, which is in good agreement with our measurements. However, they find a value of E ≃ 4 MPa for lower PI concentrations ([PI] ≤ 1%). We can thus estimate a threshold value of [PI] ≃ 1%; above this threshold, the value of the concentration only affects the dynamics of cross-linking.
We measure a wide range of Young's moduli, from 77 kPa to 14 MPa (Fig. 7). We can obtain over two decades in Young's modulus by simply adjusting the UV exposure time, which is easily and precisely varied with a computer-controlled shutter. This provides a convenient control parameter to obtain a gel of desired modulus. PEGDA is thus a versatile material with highly tunable mechanical properties; a single solution with one polymer chain length leads to several decades in moduli. The strong dependence of the modulus on the exposure time also emphasizes the need for an accurate method to measure the Young's modulus in the precise conditions of the experiment.
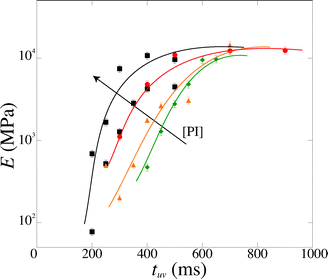 | ||
| Fig. 7 Magnitude of the Young's modulus as a function of exposure time tuv for various photoinitiator concentration [PI] (4, 5, 6 and 10 vol%). The lines are guide to the eyes. | ||
3.2. Discussion
These results can be rationalized by studying the polymerization reaction. The polymerization process is a free-radical reaction. A simplified reaction mechanism is presented in Table 2. First, the photoinitiator reacts with UV light and produces two free radical species (photolysis). These radicals react with an acrylate group of the polymer to form a reactive alkyl monomer radical (initiation). The radicals react in chain with other polymer molecules (propagation) and the gel crosslinks. Finally, the radicals interact and recombine to give neutral species (termination). Following the classical description of such reaction,26 we consider that the termination speed is equal to the initiation speed (stationary state), and is much smaller than the propagation speed (kp ≪ kt). Practically, this means that the reaction stops quickly after the UV light is turned off, and so the exposure time is a good approximation for the polymerization reaction time. The degree of cross-linking of the gel increases with increasing reaction time, i.e. the average molecular weight Mc between cross-links decreases, and the elastic modulus increases according to classical rubber elasticity.27 Specifically, the elastic modulus can be written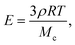 | (16) |
| Step | Rate constant | Reaction |
|---|---|---|
| Photolysis | PI + hν → PI* → Ṙ | |
| Initiation | Ṙ + M → RṀ | |
| Propagation | k p | RM n + M → RM |
| Termination | k t | RM n + RMm → RMnMm |
The maximum value of the modulus is reached when Mc = Mw, i.e. there is exactly one monomer chain between two cross-links. For the PEG-DA 575 used in our experiments, this maximum Young's modulus is E ≃ 14.2 MPa, in good agreement with the experimental value. The slight overestimation arises from the assumption that the chain length is constant (although there is a distribution of monomer chain lengths in the original solution); furthermore, network imperfections lead to a lower value of the average modulus.
We can rationalize the effect of [PI] by looking at the kinetics of the reaction.26 The rate at which the monomer is consumed is given by
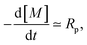 | (17) |
The propagation, initiation and termination are second order reactions, and the polymerization speed Rp is given by
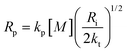 | (18) |
| Ri = 2ϕεI[PI]h | (19) |
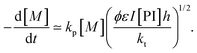 | (20) |
The initial concentration of monomer at t = 0 is noted [M]0, and eqn (20) can be solved to give
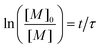 | (21) |
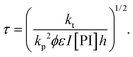 | (22) |
In order to take into account the effect of the concentration of photoinitiator, we write τ = β[PI]−1/2, with a setup constant β. We thus use tuv[PI]1/2 to rescale our experiments (Fig. 8). All the data from different [PI] concentrations reasonably collapse onto a single curve. As the reaction time increases, the number of consumed monomers increases according to eqn (21). This directly corresponds to a decrease in the average molecular mass between cross-links Mc, and thus an increase in Young's modulus, with the same characteristic time τ.
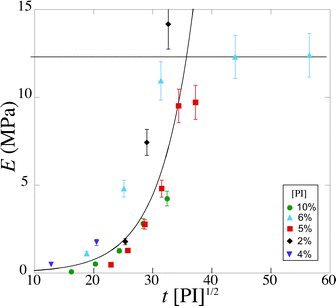 | ||
| Fig. 8 Evolution of the Young's modulus with rescaled exposure time tuv [PI]1/2 for various [PI] concentrations (2, 4, 6, 8, 10 vol%). | ||
Experimentally, we find that, before saturation, our data are well described by an exponential law
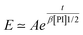 | (23) |
We can further infer the effect of the light intensity on the Young's modulus using eqn (22). The effect is similar as the effect of the PI concentration, i.e. only affects the dynamics of polymerization. For example, a decrease in intensity by a factor 4 leads to an increase in τ by a factor 2, hence an important decrease in E for the same UV exposure time, which explains the high variations of modulus values in different experiments. Previous experiments, on a similar set-up and with a similar PEG-DA solution, albeit with a different light source, were used to give an estimation of the Young's modulus of 63 ± 22 kPa.6 By taking the ratio of the light intensities between the two experiments, and assuming all conditions to be identical, we can predict a modulus of 100 kPa in fair agreement with these previous estimations.
In addition, the average mesh size ξ can be estimated from the Young's modulus with the relation E = 3kT/ξ3, which gives for our highly cross-linked gels typical mesh sizes between 1 and 5 nm.
3.3. Practical application
On a given setup, the method can be implemented as follows: the microfluidic channel used in the application is designed with a specific part dedicated to the measurement of the intrinsic mechanical properties of the gel, i.e. with a slot where a beam will be fabricated. Alternatively, a separate channel can be designed to be used on the same setup. The value of the Young's modulus measured with the beam remains valid for any particle fabricated under the same UV light conditions.The design of the channel and the choice of the shape of the beam are based on the order of magnitude of the Young's modulus of the material and the viscosity of the oligomer solution, with a design parameter Λ given by eqn (14) that can be adjusted to adapt to the value of the Young's modulus as described in §2.4. In order to keep a constant inhibition layer, the channel has to be all-PDMS. The inhibition layer is measured by letting the beam fall on its side (Fig. 1(b)).
For a given channel (i.e. a given height hc) and a constant inhibition layer (hc − hb)/2, one can first tune the width L of the channel to reach a specific range of moduli, since the parameter Λ rapidly varies with the length of the beam, i.e. the width of the channel (Λ ∝ L4). Then, the width of the beam can be easily and externally adjusted by modifying the mask to probe different moduli (Λ ∝ w−2) as long as the beam remains slender (w ≪ L). Reducing the depth of the channel hc allows to probe smaller moduli. Finally, we can note that the confinement has a strong effect (Λ ∝ (hc − hb)−3); the thickness of the inhibition layer could be tuned by changing the thickness of the PDMS channel,24 although this is not straightforward. Nevertheless, adjusting both length and width allows for the measurement of Young's moduli over several decades, from kPa to MPa.
The fabrication of the beam is identical as the one used in the application (i.e. same light intensity, filters, objective). A controlled flow is then applied, and the deflection δ is measured for increasing fluid velocity in the linear region, i.e. the deflection remains small (δ ~ w). A linear fit of the data directly gives the Young's modulus according to eqn (13). Adjustments of the exposure time tuv, and respective measurements of the deflection, allows to target a specific modulus as needed in the application. In addition, we provide a characteristic kinetics time scale τ that can be obtained by an exponential fit of the data. This setup constant allows for a prediction of the modulus for a given exposure time, which in turn can be measured accurately with the beam method.
4. Conclusion
We have shown that PEGDA is a versatile polymer whose mechanical properties can be highly tuned. The range of Young's moduli can be even further extended by adding solvent (water) to the solution. Different saturation values can be achieved by changing the molecular weight of the initial solution according to eqn (16). We provide a simple control parameter, e.g. the exposure time tuv, to have a great control over the network properties (i.e. E and ξ). The value of the Young's modulus E depends on the experimental conditions; thus, a calibration directly on the setup used for the application is necessary. A quantitative value of the properties of the formed gel can be obtained using our in situ method.This technique can thus be used to both choose the conditions to obtain a target Young's modulus and accurately measure the gel properties under specific conditions. Finally, we believe our method is a convenient tool to study the reaction kinetics of photo-polymerized gels and the dependance of their mechanical properties on various parameters; in particular, the evolution of the modulus with solvent concentration and/or swelling could be directly investigated with our micro-channel.
Acknowledgements
We thank Dominique Hourdet for helpful discussion, Ludovic Pauchard (FAST Laboratory, Orsay) for the micro indentation measurements, and ANR DeFHy for financial support.References
- B. R. Saunders and B. Vincent, Adv. Colloid Interface Sci., 1999, 80, 1–25 CrossRef CAS.
- M. A. Cohen Stuart, W. T. S. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113 CrossRef CAS PubMed.
- J. Heo, K. J. Thomas, G. H. Seong and R. M. Crooks, Anal. Chem., 2003, 75, 22–26 CrossRef CAS.
- H. Berthet, M. Fermigier and A. Lindner, Phys. Fluids, 2013, 25, 103601 CrossRef PubMed.
- R. Attia, D. C. Pregibon, P. S. Doyle, J.-L. Viovy and D. Bartolo, Lab Chip, 2009, 9, 1213–1218 RSC.
- J. S. Wexler, P. H. Trinh, H. Berthet, N. Quennouz, O. du Roure, H. E. Huppert, A. Linder and H. A. Stone, J. Fluid Mech., 2013, 720, 517–544 CrossRef.
- A. S. Hoffman, Adv. Drug Delivery Rev., 2002, 54, 3–12 CrossRef CAS.
- N. A. Peppas, J. Z. Hilt, A. Khademhosseini and R. Langer, Adv. Mater., 2006, 18, 1345–1360 CrossRef CAS.
- K. Y. Lee and D. J. Mooney, Chem. Rev., 2001, 101, 1869–1880 CrossRef CAS PubMed.
- B. G. Chung, K.-H. Lee, A. Khademhosseini and S.-H. Lee, Lab Chip, 2012, 12, 45–59 RSC.
- M. Verhulsel, M. Vignes, S. Descroix, L. Malaquin, D. M. Vignjevic and J.-L. Viovy, Biomaterials, 2014, 35, 1816–1832 CrossRef CAS PubMed.
- R. Shah, H. Shum, A. Rowat, D. Lee, J. Agresti, A. Utada, L. Chu, J. Kim, A. Fernandez-Nieves and C. Martinez, Mater. Today, 2008, 11, 18–27 CrossRef CAS.
- J. K. Nunes, S. S. H. Tsai, J. Wan and H. A. Stone, J. Phys. D: Appl. Phys., 2013, 46, 114002 CrossRef PubMed.
- D. Dendukuri, K. Tsoi, T. A. Hatton and P. S. Doyle, Langmuir, 2005, 21, 2113–2116 CrossRef CAS PubMed.
- D. Dendukuri, D. C. Pregibon, J. Collins, T. A. Hatton and P. S. Doyle, Nat. Mater., 2006, 5, 365–369 CrossRef CAS PubMed.
- J. A. Burdick, A. Khademhosseini and R. Langer, Langmuir, 2004, 20, 8–11 CrossRef.
- J. K. Nunes, H. Constantin and H. A. Stone, Soft Matter, 2013, 9, 4227 RSC.
- H. Berthet, Ph.D. thesis, UPMC, 2012 Search PubMed.
- J. S. Temenoff, K. A. Athanasiou, R. G. Lebaron and A. G. Mikos, J. Biomed. Mater. Res., 2002, 59, 429–437 CrossRef CAS PubMed.
- A. M. Kloxin, C. J. Kloxin, C. N. Bowman and K. S. Anseth, Adv. Mater., 2010, 22, 3484–3494 CrossRef CAS PubMed.
- Z. Drira and V. K. Yadavalli, J. Mech. Behav. Biomed. Mater., 2013, 18, 20–28 CrossRef CAS PubMed.
- C. J. Pipe and G. H. McKinley, Mech. Res. Commun., 2009, 36, 110–120 CrossRef PubMed.
- D. Dendukuri, S. S. Gu, D. C. Pregibon, T. A. Hatton and P. S. Doyle, Lab Chip, 2007, 7, 818–828 RSC.
- D. Dendukuri, P. Panda, R. Haghgooie, J. M. Kim, T. A. Hatton and P. S. Doyle, Macromolecules, 2008, 41, 8547–8556 CrossRef CAS.
- T. M. Wang, Int. J. Nonlinear Mech., 1969, 4, 389–395 CrossRef.
- G. Odian, Principles of polymerization, John Wiley & Sons, 2004 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer physics, Oxford university press, Oxford, New York, 2003 Search PubMed.
Footnotes |
| † Current address: TOTAL, Avenue Larribau, 64000 Pau, France. |
| ‡ Current address: Princeton University, Mechanical and Aerospace Engineering, Princeton NJ 08540, USA. |
| § The intensity is expressed in E/(m3 s) where E denotes Einsteins, i.e. mol of light, and the molar extinction coefficient is expressed in m3 (mol−1 m−1). |
| This journal is © The Royal Society of Chemistry 2015 |