Open Access Article
Open Access ArticleOn the breakdown of Förster energy transfer theory due to solvent effects: atomistic simulations unveil distance-dependent dielectric screening in calmodulin†
Daniel
Gonzalo
 ab,
Lorenzo
Cupellini
ab,
Lorenzo
Cupellini
 c and
Carles
Curutchet
c and
Carles
Curutchet
 *ab
*ab
aDepartament de Farmàcia i Tecnologia Farmacèutica, i Fisicoquímica, Facultat de Farmàcia i Ciències de l'Alimentació, Universitat de Barcelona (UB), Barcelona, Spain. E-mail: carles.curutchet@ub.edu
bInstitut de Química Teòrica i Computacional (IQTCUB), Universitat de Barcelona (UB), Barcelona, Spain
cDipartimento di Chimica e Chimica Industriale, Università di Pisa, 56126 Pisa, Italy
First published on 29th January 2025
Abstract
Förster resonance energy transfer (FRET) is a powerful technique used to investigate the conformational preferences of biosystems, and molecular simulations have emerged as an ideal complement to FRET due to their ability to provide structural models that can be compared with experiments. This synergy is however hampered by the approximations underlying Förster theory regarding the electronic coupling between the participating dyes: a dipole–dipole term attenuated by a simple dielectric screening factor 1/n2 that depends on the refractive index of the medium. Whereas the limits of the dipole approximation are well-known, detailed insights on how environment effects deviate from the 1/n2 assumption and modify the R−6 distance dependence that characterizes FRET as a spectroscopic ruler are still not well understood, especially in biosystems characterized by significant structural disorder. Here we address this using a rigorous theoretical framework based on electrostatic potential-fitted transition charges coupled to an atomistic polarizable classical environment, which allows investigation of dielectric screening in atomic detail in extended simulations of disordered systems. We apply this strategy to investigate the conformational preferences of calmodulin, a protein that plays a major role in the transmission of calcium signals. Our results indicate that dielectric screening displays an exponential decay at donor/acceptor separations below 20 Å, significantly modifying the R−6 distance dependence widely adopted in FRET studies. Screening appears to be maximized at separations ∼15 Å, a situation in which the fluorophores are partially excluded from the solvent and thus screening is dictated by the more polarizable protein environment.
1. Introduction
Förster resonance energy transfer (FRET) describes the non-radiative transfer of electronic excitation energy between a donor (D) and an acceptor (A) molecule mediated by dipole–dipole coulombic interactions. Over 70 years ago, Theodor Förster developed the practical expressions that allow describing the transfer rate from purely spectroscopic observables and the distance separating the donor and the acceptor.1–3 This expression is the foundation of the FRET technique, which is widely used as a spectroscopic ruler to measure distances in biological systems and has had an enormous impact in life sciences.4,5 FRET is used for example to detect protein–protein interactions, to observe protein folding, or the investigate the conformational ensembles of nucleic acids or disordered proteins, even in vivo and for single molecules. Compared to other techniques, single molecule FRET (smFRET) allows detailed insights into the dynamical aspects of biological structure, including subpopulations and interconversion kinetics, and has been applied to characterize the conformational and substrate-binding dynamics of enzymes, the structural dynamics of DNA, the conformational ensembles and folding dynamics of RNA enzymes and proteins, and many other molecular mechanisms.6–13The FRET ruler, however, gives access to one-dimensional structural information, so this technique needs to be complemented with other approaches to fully characterize three-dimensional structures and give insights into the function of relevant conformational states. Besides other biophysical and photophysical techniques, molecular dynamics (MD) simulations represent one of the most powerful tools to investigate biomolecular dynamics thanks to its ability to explore complex energy landscapes and provide thermodynamic and kinetic data of the relevant states of a system in atomic detail. A variety of studies in the last decade have thus combined FRET experiments with MD simulations to unveil the properties of proteins, disordered amyloid-β monomers, single stranded DNA and RNA, and many other biosystems.14–28 This synergistic exchange allows the interpretation of FRET data in terms of atomic models but also the refinement of the classical potentials determining energy landscapes in MD simulations. The comparison between FRET data and MD ensembles, however, typically relies on the various approximations underlying Förster theory regarding D/A electronic coupling: a dipole–dipole term attenuated by a simple dielectric screening factor 1/n2 that depends on the refractive index of the medium. In some cases, the dipole interaction is further approximated adopting an orientation factor κ2 = 2/3, corresponding to the isotropic average obtained if D and A are free to rotate, a reasonable approximation when dyes are attached through long and flexible linkers to the biomolecule.15
If dyes are explicitly included in the MD, the dipole approximation can be overcome by evaluating the coupling for specific D/A arrangements sampled along an MD trajectory using a more rigorous theoretical model, for example using transition densities derived from quantum mechanical (QM) calculations.29 Breakdown of the dipole approximation at distances comparable to dye dimensions is well-known, and most studies acknowledge the fact that, besides distance between the dyes, FRET efficiency depends also on their orientation and dynamics. How screening effects impact FRET studies in disordered proteins and peptides, however, remains largely unknown.16 In Förster theory, screening effects are described by adding a 1/n2 prefactor in the dipole coupling entering the rate expression:
 | (1) |
The 1/n2 screening prefactor leads to a dramatic fourfold attenuation of the FRET rate in typical biological environments, where n2 is often assumed a value of 2, representing the optical component of the dielectric constant of the medium (εopt).30 Förster derived this simple screening factor by assuming a continuum dielectric embedding the D/A point dipoles. Some refinements can be introduced if one assumes that the molecules are placed in spherical cavities inside the dielectric. This leads to screening factors ranging from 3/(2εopt + 1) for dipolar transitions to 2/(εopt + 1) for high-order multipoles.31 More realistic models have later been developed coupling a QM description of the chromophores to modern continuum solvation models like the integral equation formalism of the polarizable continuum model (IEFPCM), which allows to account for the molecular-shaped cavities enclosing the molecules in the dielectric, or by adopting an atomistic polarizable molecular mechanics (MMPol) description of the environment in a quantum/molecular mechanics (QM/MMPol) framework.29,32,33
The application of multiscale QM/classical models has allowed unprecedented details on the impact of screening effects in FRET processes occurring in a variety of biological systems.34 Application of the QM/IEFPCM model to pigment pairs from photosynthetic complexes of cyanobacteria, higher plants and cryptophyte algae, showed that screening is exponentially attenuated at D/A separations below 20 Å, thus modifying the well-known R−6 distance dependence of Förster FRET rate, a behavior occurring when the pigments start to form a common cavity inside the dielectric.35,36 In turn, QM/MMPol calculations allow taking into account the screening by highly anisotropic environments such as protein cavities. Application of the QM/MMPol model to photosynthetic complexes, nucleic acids and protein-ligand complexes,34 indicated that the heterogeneous nature of the environment polarizability often leads to important deviations from the 1/εopt Förster prefactor, profoundly tuning by a factor up to ∼4 energy migration rates compared to the average continuum dielectric view that has been historically assumed.37 Recently, Eder and Renger applied extensive Poisson-TrEsp calculations to study photosystem I trimers, concluding that exponential distance dependence only contributes to the dielectric screening in chlorophyll pairs with in-line dipole arrangements.38 In disordered proteins, the exchange between folded and more solvent-exposed extended structures means both effects – distance-dependent screening and dielectric heterogeneity – could play an important role in energy transfer processes underlying FRET structural studies.
Here, we assess how environment effects deviate from Förster 1/εopt assumption in a disordered system, and how this approximation biases the characterization of the underlying conformational ensemble. The cost associated to multiscale QM/MMPol models has so far precluded its application to the colossal number of conformations needed to describe, for example, a disordered protein. Here we address this challenge using a rigorous theoretical framework that overcomes Förster limits adopting a TrESP/MMPol approach, which describes the fluorophores through electrostatic potential-fitted transition charges (TrESP) coupled to a polarizable molecular mechanics (MMPol) description of the environment.39 While this approach allows an efficient processing of thousands of structures extracted from extensive MD simulations, it allows to retain the accurate description of screening effects provided by more costly QM/MMPol calculations. We apply this strategy to investigate the impact of Förster approximations on the Ca2+-dependent conformational preferences of calmodulin (CaM), a protein that plays a major role in the transmission of calcium signals in eukaryotes.40,41 In particular, we simulate the FRET properties of holo CaM tagged with Alexa Fluor 488 and Texas Red dyes, shown in Fig. 1, which was investigated by the Johnson group using time-resolved and single-molecule fluorescence spectroscopy.42 Our results indicate a profound impact of dielectric screening on CaM FRET distributions. Strong distance-dependent screening effects induce an important shift on fluorescence lifetime distributions, leading to corrections much larger than those due to breakdown of the dipole approximation, especially at close D/A separations. Interestingly, our results warn that the common practice of ignoring distance-dependent screening effects masks the common tendency of classical force fields to overstabilize compact folded structures, with important consequences in the refinement and validation of classical potentials for disordered proteins based on FRET data.
2. Methods
2.1 Multiscale MD/TrESP-MMPol approach
We adopt a multiscale pipeline based on performing classical MD simulations and postprocessing the trajectories with extensive calculations of FRET electronic couplings based on the TrESP/MMPol method.39 Compared to using other multiscale approaches like QM/IEFPCM, based on a continuum solvation model, this strategy allows to account for heterogeneities in the polarizability of the environment in the calculation of FRET couplings by using an atomistic polarizable description of the protein-water environment. On the other hand, it allows estimating couplings with similar quality compared to the QM/MMPol approach at a much cheaper cost by using TrESP charges precomputed from QM calculations, thus avoiding to perform QM/MM calculations on many structures. In the following we describe the expressions adopted to estimate FRET properties and couplings using this protocol, as well as the details of the MD and TrESP/MMPol calculations performed.2.2 Förster resonance energy transfer theory
Förster theory can be formulated in the weak coupling limit adopting the point dipole approximation (PDA) as shown in eqn (1).34 Alternatively, Förster rate can be formulated from spectroscopic data measured for the non-interacting dyes, | (2) |
 | (3) |
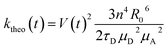 | (4) |
FRET efficiencies were estimated considering the orientational dynamics of the dyes using this expression, which allows to incorporate static and dynamic disorder by separating slow and fast fluctuations in instantaneous transfer rates:16
 | (5) |
 | (6) |
| I = 〈e−(kD+〈ktheo(t)〉fast)t〉slow | (7) |
2.3 TrESP-MMPol model
The electronic coupling for singlet–singlet energy transfer involving bright states is dominated by coulombic and environment-mediated contributions:| V = VCoul + Venv | (8) |
From these terms one can then define a screening factor s and an effective dielectric constant for the environment as
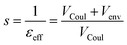 | (9) |
Then the total coupling can be expressed as V = sVCoul, providing a direct link to the coulombic term and the screening factor in the Förster expression V ≈ sVPDA = 1/εopt·VPDA. The limits of the dipole approximation at close separations are well-known.29,43 Here we overcome this limits using the TrESP-MMPol model,39 in which atomic transition charge models are fitted to reproduce the electrostatic potential generated by QM-derived transition densities,44 and the Coulomb interaction between such charges is computed in the presence of a polarizable molecular mechanics (MMPol) description of the environment, leading to the following expressions:
 | (10) |
 | (11) |
2.4 MD simulations
The simulated systems were prepared starting from the human holo structure of CaM solved at 1.7 Å resolution (PDB ID 1CLL).45 We considered mutations T34C and T110C and labelled CaM at these positions with donor/acceptor dyes Alexa Fluor 488 C5 maleimide (AF488) and Texas Red C2 maleimide (TRC2). We run a total of 3 × 5 μs replicas for each system CaM-AF488-TRC2 and CaM-TRC2-AF488 using the GAFF2 force field for the dyes,46 the Amber ff14SB protein force field,47 the TIP3P water model,48 the Joung–Cheatham parameters for monovalent ions49 and the Li-Merz parameters for Ca2+.50 All simulations were performed using the Amber20 software.512.5 Electronic coupling calculations
We performed extensive calculations of TrESP/MMPol electronic couplings every 20 ps of the MD trajectories using the Trespcoup software,52 leading to a total of 750![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 calculations for each system CaM-AF488-TRC2 and CaM-TRC2-AF488. In these calculations, the MMPol environment was described using the Amber pol12 AL polarizable force field,53,54 whereas the dyes were described using atom-centered TrESP charges. To make our approach cost-effective, TrESP charges were precomputed once for optimized structures of the chromophores. TrESP charges were fitted to reproduce the electrostatic potential obtained from TD-CAM-B3LYP/6-31G(d)/IEFPCM transition densities using the TraDA tool.55 In this way, we account for the effect of the environment on the transition densities themselves. Alternatively, one can also train a regression model from multiple QM/MMPol calculations able to derive the charges directly from the dye MD geometries.39 Because here FRET rates are estimated through eqn (4), in which couplings are effectively normalized by the transition dipoles of D and A, results are not expected to be much sensitive to fluctuations in TrESP charges. To ensure their reliability, TrESP/MMPol couplings were nevertheless benchmarked with TD-DFT QM/MMPol calculations performed using a locally modified development version of the Gaussian package.56 Finally, FRET rates were obtained using a refractive index n2 = 2,57 a critical Förster radius R0 = 54 Å
000 calculations for each system CaM-AF488-TRC2 and CaM-TRC2-AF488. In these calculations, the MMPol environment was described using the Amber pol12 AL polarizable force field,53,54 whereas the dyes were described using atom-centered TrESP charges. To make our approach cost-effective, TrESP charges were precomputed once for optimized structures of the chromophores. TrESP charges were fitted to reproduce the electrostatic potential obtained from TD-CAM-B3LYP/6-31G(d)/IEFPCM transition densities using the TraDA tool.55 In this way, we account for the effect of the environment on the transition densities themselves. Alternatively, one can also train a regression model from multiple QM/MMPol calculations able to derive the charges directly from the dye MD geometries.39 Because here FRET rates are estimated through eqn (4), in which couplings are effectively normalized by the transition dipoles of D and A, results are not expected to be much sensitive to fluctuations in TrESP charges. To ensure their reliability, TrESP/MMPol couplings were nevertheless benchmarked with TD-DFT QM/MMPol calculations performed using a locally modified development version of the Gaussian package.56 Finally, FRET rates were obtained using a refractive index n2 = 2,57 a critical Förster radius R0 = 54 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 42 and a fluorescence lifetime for AF488 τD = 4 ns.58 Transition dipole moments for the AF488 donor and TRC2 acceptor equal to μD = 7.56 D and μA = 10.19 D were extracted from the TD-DFT calculations used to parametrize the TrESP charges.
42 and a fluorescence lifetime for AF488 τD = 4 ns.58 Transition dipole moments for the AF488 donor and TRC2 acceptor equal to μD = 7.56 D and μA = 10.19 D were extracted from the TD-DFT calculations used to parametrize the TrESP charges.
3. Results and discussion
3.1 Conformational ensembles of CaM
The structure of CaM is characterized by two lobes connected by a linker, each domain containing two E–F hands. Ca2+ binding to the E–F hands then leads to the exposure of the lobe's hydrophobic interfaces, which allows CaM to bind a variery of protein targets in a Ca2+ dependent manner. The flexible linker allows binding targets of different size anchored to the N and C-terminal domains, but the lobes are also flexible, and both structural data and MD simulations suggest that the C-lobe is more flexible and provides more selectivity.59 In Fig. 1, we show an illustration of the MD ensembles we obtained for holo CaM-TRC2-AF488 and CaM-AF488-TRC2, which correspond to a total of 15 μs per system. For clarity, we only display the superposition of a subset of the structures sampled, but this suffices to illustrate the conformational heterogeneity of CaM, which leads the dyes to explore a rich variety of relative arrangements, in line with previous MD simulations59–64 and FRET studies that show distinct configurations of the N- and C-lobes about the central linker, which is crucial for target recognition and binding.42,58,65The structural heterogeneity underlying the MD ensembles leads to a distribution of radius of gyration with values from 15 to 25 Å, as shown in Fig. 2A, with average Rg equal to 19.8 Å, slightly underestimating the experimental Rg 21.5 Å.66 This could arise from an overpopulation of compact structures, an ongoing problem in classical force fields, but is also affected by the limited sampling in our simulations. To obtain clearer insights into the conformational ensemble, we performed a clustering analysis to determine the four more populated structures, with the aim of relating them to the four main FRET states identified in experimental lifetime distributions by DeVore and co-workers.42 In Fig. 2C we display representative structures for the clusters, along with their Rg values, which allows to characterize the structures underlying the Rg distribution in Fig. 2A. The most populated Cluster 1 (51%) has an Rg value of 21.2 Å, thus it accounts for the peak centered around the experimental value in Fig. 2C, together with a minor contribution from Cluster 4 (12%). In these clusters, the linker keeps the two CaM domains spatially separated, resembling the main conformation of holo CaM displayed in crystal structures, although in Cluster 4 the linker helix is bent. In contrast, Clusters 2 and 3, which amount to a total 37% population, display Rg values of 16.9 Å and 17.7 Å. Thus, these subpopulations account for the band centered at ∼17.5 Å and the minor peak at ∼15.5 Å in Fig. 2A and display a structural collapse of the extended crystal arrangement leading to compact shapes like those observed in complexes of CaM with peptides.62
 | ||
| Fig. 2 (A) Distribution of radius of gyration computed along the MD trajectories of holo CaM-AF488-TRC2 and CaM-TRC2-AF488 compared to the experimental value.66 (B) Intramolecular contact map averaged over the MD showing the folding patterns of the two domains in CaM. (C) Major clusters for the structural ensemble of CaM. For each cluster we draw the most representative structure (centroid) and report its population, the MD-averaged radius of gyration and the intramolecular contact map relative to the ensemble-averaged contact map shown in panel B. Blue and red contacts indicate those populated more and less frequently than the average, respectively. The C34–C110 Cα–Cα distances between Cys residues linking the AF488 and TRC2 dyes in the centroid structures are also reported and represented by dashed lines. | ||
Because in this study we aim at characterizing CaM states observed through FRET, it is interesting to examine the D/A separations in the centroids of the clusters. We estimate this separation using the C34–C110 Cα–Cα distance (the Cys residues linking the AF488 and TRC2 dyes), as the specific position of the dyes among members of the cluster can vary considerably. The resulting distances in the extended Clusters 1 and 4 are similar to the more compact Cluster 3, with values ∼49 Å, suggesting similar FRET data can be obtained for them despite remarkable differences in terms of overall CaM structure. In contrast, Cluster 2 adopts a different mutual arrangement of the N and C-lobes, leading to a closer distance of 16.8 Å between Cys34 and Cys110 which allows the dyes to come in contact. We expect these conformations to explain the states characterized by the largest FRET efficiencies and shortest fluorescence lifetimes, as will be discussed in the next sections.
3.2 Beyond Förster coupling: dipole approximation
The limits of the PDA have been extensively studied for a variety of systems, and a usual role of thumb indicates breakdown of the PDA at separations close to the dye's dimensions.43 Here we analyzed this issue by comparing Coulomb couplings based on the PDA or the more rigorous model based on transition charges (TrESP). Our results, shown in Fig. S5 of the ESI,† confirm the common knowledge that more significant deviations are found at close separations below 30 Å, were VPDA/VTrESP ratios significantly depart from one. Nevertheless, analysis of the average ratios computed at different D/A separations indicates that the PDA tends to slightly overestimate the Coulomb term for all range of D/A separations in CaM.3.3 Beyond Förster coupling: dielectric screening effects
Beyond the dipole approximation, the R−6 dependence of FRET rates also relies on the validity of the 1/n2 screening prefactor in eqn (1), which describes how the interaction between D/A dipoles is screened by the polarizable environment. As discussed in the introduction, the accurate yet efficient formulation of the TrESP/MMPol model allows us to investigate the impact of dielectric screening over long timescale MD trajectories in atomistic detail. In Fig. 3, we plot the distribution of environment screening factors computed according to eqn (9)–(11) from these atomistic calculations. | ||
| Fig. 3 (A) Density distribution of screening factors as a function of D/A separation derived from TrESP/MMPol electronic couplings computed for holo CaM-AF488-TRC2 and CaM-TRC2-AF488 systems along MD trajectories. Empirically fitted functions are compared to estimates from the Onsager model s = 3/(2εopt + 1) using εopt values of 2.0 and 1.776 for protein and water environments, respectively.35,36 (B) Graphical representation of water and amino acid (residue) contributions to the MMPol environment-mediated term (eqn (11)) in the electronic coupling between AF488 (lime) and TRC2 (orange) for two limiting cases at short and long D/A separations. Blue colored residues contribute to screen the interactions, whereas red ones reinforce the Coulomb interaction between D and A. | ||
Our results display a strong attenuation of screening effects at D/A separations below 20 Å, where s values start from about ∼1 (i.e. no screening) at very short distances reaching ∼0.6 at 15 Å. Beyond 30 Å, s increases again to ∼0.7. The dependence of dielectric screening on D/A separation has been previously examined in studies of photosynthetic pigment–protein complexes35,36,38,67 and to analyze single-molecule experiments on a polyproline helix.16 Quite strikingly the initial decay until ∼10 Å observed in our atomistic simulations strongly resembles the behavior in those studies, suggesting a universal trend.35,36 This is somewhat unexpected, as here we deal with different dye molecules, the dyes are significantly more solvent-exposed than the pigments in photosynthetic complexes, and instead of a continuum model we adopt an atomistic description of the environment, which is able to account for heterogeneities in the protein and solvent. Our findings thus reinforce the notion that distance-dependent dielectric screening alters the R−6 distance dependence of FRET (eqn (1) and (2)).
We then fitted our results to an exponentially decaying empirical screening function that other researchers can use to account for dielectric screening, albeit in an approximate way. In analogy with previous studies, we first fitted our results to the following expression:35,36
s = 30.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−0.61R + 0.70 e−0.61R + 0.70 | (12) |
Recently, Eder and Renger applied extensive Poisson-TrEsp calculations to study photosystem I, concluding that exponential decay only contributes to the screening in chlorophyll pairs with in-line dipole arrangements. Thus, they proposed a modified version of eqn (12) in which the A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−βR term only survives for geometries with a κ dipole orientation factor above a certain threshold.38 We then examined the dependence of screening factors on κ in our simulations on CaM, and compared exponential decaying functions fitted for specific subsets of data characterized by different ranges of orientation factors (Group 1 0.0 ≤ κ ≤ 0.6; Group 2 0.6 ≤ κ ≤ 1.2; Group 3 1.2 ≤ κ ≤ 2.0). Although the results (see Fig. S3 of the ESI†) suggest a somewhat steeper exponential decay for in-line geometries (Group 3), all subsets clearly show the exponential decay, so we choose not to include any explicit dependence of the empirical screening function on κ.
e−βR term only survives for geometries with a κ dipole orientation factor above a certain threshold.38 We then examined the dependence of screening factors on κ in our simulations on CaM, and compared exponential decaying functions fitted for specific subsets of data characterized by different ranges of orientation factors (Group 1 0.0 ≤ κ ≤ 0.6; Group 2 0.6 ≤ κ ≤ 1.2; Group 3 1.2 ≤ κ ≤ 2.0). Although the results (see Fig. S3 of the ESI†) suggest a somewhat steeper exponential decay for in-line geometries (Group 3), all subsets clearly show the exponential decay, so we choose not to include any explicit dependence of the empirical screening function on κ.
Beyond the exponential decay, however, our data indicates that screening is maximized at separations ∼15 Å, where s values adopt a minimum ∼0.6, increasing to ∼0.7 at distances beyond ∼30 Å. We ascribe this trend to the decreased polarizability of water compared to the protein environment, given that at distances >30 Å the dyes are more exposed to the water solvent, as exemplified by the structures shown in Fig. 3B. In contrast, in more compact conformations in the 15–25 Å range, the interaction of the dyes with the protein becomes more important. In Fig. S4 (ESI)† we report the contribution of the dyes to the total solvent-accessible surface area (SASA) of the system, which confirms this increased solvent exposure beyond 30 Å. In Fig. 3A we then indicate as dashed lines the Onsager screening factor estimated for protein and water environments (εopt 2.0 and 1.776, respectively), which illustrate the fact that a smaller screening is expected in water. It is also worth noting that, although our data tends to the Onsager factor at long separations, the screening factor s strongly deviates from Förster's 1/εopt assumption at all distance ranges.
To account for the minimum at ∼15 Å, in which the fluorophores are partially excluded from the solvent and thus screening is dictated by the more polarizable protein environment, we decided to add an R−3 term, leading to this modified fitted empirical function:
s = 37.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−0.40R − 668R−3 + 0.72 e−0.40R − 668R−3 + 0.72 | (13) |
We recall nevertheless the approximate nature of this empirical expression, as screening effects also depend on the local environment and D/A orientation, as visible in the distribution of values in Fig. 3A that deviate from the fitted curve. We expect the position of the minimum to effectively depend on the system, as this minimum arises from the difference between protein and water environment.
To illustrate the origin of the screening distance depencence, in Fig. 3B we graphically represent the environment-mediated contributions estimated using the atomistic TrESP-MMPol model for two limiting cases at short and long separations (R = 8.4 Å and s = 0.92; R = 64 Å and s = 0.71). In the top picture with R = 8.4 Å, screening is largely attenuated, as blue regions that contribute to screen the interaction, located surrounding the dyes, are counterbalanced by other surrounding red residues that significantly enhance the interaction. For example, Asn111 contributes with −13 cm−1 to the MMPol environment-mediated coupling term Venv. In contrast, in the R = 64 Å case, blue residues contributing to the screening of the interaction are located in between the AF488 and TRC2 dyes, including residues Arg106, Lys115 and Leu116 near TRC2 and a water molecule next to AF488. In contrast, red residues enhancing the interaction like Asn111, Leu112 and Gly113 show in this case smaller contributions, thus leading to an overall significant screening effect.
3.4 Beyond Förster coupling: deviations from the ideal isotropic distribution
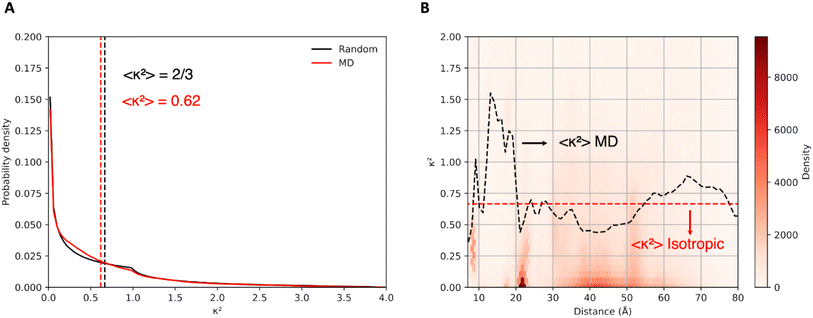
In cases where the specific relative orientation between D and A is unknown, it is common to assume an isotropic distribution, in which the dyes randomly adopt all possible mutual orientations, leading to κ2 = 2/3. This allows to simplify eqn (1) and derive eqn (2) and (3), which allows to extract D/A distances directly from FRET efficiencies, an approximation that typically performs well for flexible linkers. The atomistic detail of MD simulations, however, allows direct calculation of the orientation factors and also tackling eventual correlations between κ and R dictated by dye and protein dynamics.20 Thus, to examine this further assumption in Förster description of the coupling, in Fig. 4A we report the distribution of orientation factors sampled along the MD trajectories, which turns to be very close to the random isotropic distribution, with an average κ2 = 0.62 close to the isotropic limit. As shown in Fig. 4B, however, at D/A separations below 20 Å we find significant deviations from the isotropic average value. This is probably due to the more compact structures adopted by CaM in this separation range, which restrict the orientational freedom of the dyes.3.5 Fluorescence lifetime and efficiency distributions
In the previous sections, we have shown how screening effects impact FRET couplings at all distance ranges, whereas the dipole approximation and the isotropic assumption lead to significant deviations only at short D/A separations. Here, we examine how all these effects impact the analysis of FRET data. We first analyze how they impact distance distributions derived from smFRET efficiencies.68 To this end, we simulate a smFRET experiment that corresponds exactly to our MD ensemble: the distribution of FRET efficiencies is the one calculated by TrESP/MMPol. We then use the approximate expression eqn (3) to transform these efficiencies to D/A distances. We compare the actual MD distances with the ones estimated from efficiencies in Fig. S6 (ESI).† The estimated distances display a global shift to lower D/A separations compared to the actual MD data, suggesting that eqn (3) results in systematically underestimated distances. This bias arises from the overestimation of screening effects in Förster theory, as shown in Fig. 3, thus leading to a concomitant underestimation of the D/A distances. For example, the average D/A separation derived from FRET efficiencies is 38.6 Å, which is 2.7 Å lower than the value 41.3 Å directly measured along the MD.On the other hand, it is also interesting to investigate how Förster approximations impact the simulation of FRET distributions. We focus on FRET efficiency histograms and fluorescence lifetime distributions. The latter also reflect the underlying FRET distribution because energy transfer decreases the donor fluorescence lifetime. We then compare both distributions to the experimental data measured from donor fluorescence decays and smFRET.42
The results in Fig. 5A and B allow us to gauge the performance of different electronic coupling models in describing the lifetime distributions, which were generated using the expressions in eqn (4) and (6). To dissect the impact of errors due to dielectric screening or the PDA approximation, we compare several models of increasing accuracy (PDA, TrESP, PDA-MMPol and TrESP-MMPol), where PDA/TrESP indicates the method used to compute the Coulomb term, whereas MMPol indicates that atomistic screening factors obtained from TrESP-MMPol calculations are used. Thus, how the breakdown of the dipole approximation impacts results can be assessed by comparing the PDA and TrESP curves, or alternatively the PDA-MMPol and TrESP-MMPol curves in Fig. 5A and B. Adopting the PDA leads to small changes in the theoretical lifetime distributions, especially in the sub-ps lifetime region of CaM-TRC2-AF488, where close donor/acceptor separations are expected to worsen the performance of the PDA. These short lifetimes are rare, hardly contributing to the overall fluorescence decay, and anyway shorter than the typical time resolution of fluorescence experiments.69 Thus, even though significant deviations were observed in the ratios VPDA/VTrESP shown in Fig. S5,† the actual outcome of these deviations in terms of lifetime distributions is rather small.
 | ||
| Fig. 5 Distribution of fluorescence lifetimes computed for holo CaM-AF488-TRC2 and CaM-TRC2-AF488 systems using different electronic coupling models (PDA: point dipole approximation + Förster screening factor. PDA-MMPol: point dipole approximation + MMPol screening factor. TrESP: TrESP coulombic term + Förster screening factor. TrESP-MMPol: TrESP coulombic term + MMPol screening factor): (A) Holo CaM-AF488-TRC2, (B) Holo CaM-TRC2-AF488 and (C) Holo CaM-AF488-TRC2 + CaM-TRC2-AF488 versus experiment.42 Note that experiments contain a mixture of both D–A and A–D systems due to unselective dye labelling. (D) Distribution of FRET efficiencies computed for the two CaM systems using the PDA and the TrESP-MMPol model. | ||
In stark contrast, the adoption of Förster screening factor s = 1/εopt significantly shifts the complete lifetime distributions compared to results that incorporate atomistic MMPol screening effects estimated from eqn (9)–(11). Overall, Förster model overestimates screening effects, leading to underestimated FRET rates and efficiencies, and longer lifetimes. We can observe this trend when comparing PDA and TrESP-MMPol lifetimes in Fig. 5C, or by comparing the efficiency distributions plotted in Fig. 5D. In both cases, the incorporation of atomistic screening effects improves the agreement with experimental data. The average efficiency obtained with TrESP-MMPol (E = 0.79) is closer to the experimental distribution, which displays a maximum near ∼0.8.42,68
In addition, in Fig. 5C, the relative intensity of the main FRET states suggested by the experimental lifetime distributions improves when MMPol effects are included, as FRET states with lifetimes near 0.1 ns and 0.4 ns increase their probability. This comparison, however, must be done with care, given that the experimental distribution is derived from a fitting of fluorescence decays using classic maximum entropy (cMEM) analysis. Because only 4 FRET populations were recovered in these fits, the experimental distribution only displays these peaks, but this probably does not reflect the complete distribution and misses intermediate states. Beyond the overall agreement of simulations in terms of average efficiency and shape of the lifetime distribution in the 0.1–4 ns range, Fig. 5C gives the impression that our simulations describe a set of rather compact conformations not observed experimentally. Significant populations are observed of efficient FRET states with lifetimes <10 ps, whereas experimentally the fastest component of the decay was fitted to a lifetime of 100 ps. This disagreement however could arise from the fact that fluorescence decays were measured with an instrument response function (IRF) with a full width at half-maximum <50 ps, so it is unlikely to observe those fast components in this experimental set-up. Comparison of simulated and experimental decays (see Fig. S8 in the ESI†) nevertheless clearly indicates that the overall MD ensemble of CaM is too compact, leading to a decay slightly faster than in experiments. However, this problem also arises, for example, from the underestimation of populations with lifetimes ∼3–4 ns, as shown in Fig. 5C, and not only from the states with lifetimes <10 ps.
Current additive force fields widely used for the simulation of proteins tend to introduce a bias that favors folded states, thus breaking the balance between compact and more extended or disordered states, and this could still be happening here for CaM. Because of this, important efforts are being carried out to refine protein force fields for disordered systems.70,71 Our findings are an illustrative example of the potential of FRET and MD to refine current force fields, as simulations provide rather accurate ensemble properties, like FRET efficiencies, but the sub-ensemble lifetime distributions suggest the presence of a set of compact states that could be unrealistic. More accurate experiments would be needed to confirm this hypothesis, as discussed above. Interestingly, such compact states are in agreement with the hypothesis put forward by DeVore and co-workers, suggesting that the TRC2 dye, in contrast to other acceptors, may stabilize a compact conformation of CaM by conformational selection.42 Nevertheless, our results show that it becomes particularly important to account for atomistic screening effects if FRET is used to examine the balance between extended and folded conformations, given the strong attenuation of screening effects at close separations. Neglecting this distance-dependence contribution in the PDA model artificially reduces the coupling found for compact structures, in this way counteracting their overestimated interaction and masking possible disagreements between simulations and experiment.
4. Conclusions
In summary, we have examined for the first time how the heterogeneous environment impacts dielectric screening effects and thus the determination of the conformational properties of a partially disordered protein, CaM, studied combining MD and FRET. This was made possible by the adoption of a rigorous yet efficient theoretical method that describes the fluorophores through distributed atomic transition charges coupled to a polarizable atomistic description of the protein and solvent environment. While this approach allows an efficient processing of thousands of structures extracted from extensive MD simulations, it retains the accurate description of screening effects provided by more costly QM/MMPol calculations. Our results indicate that the Förster dielectric screening approximation introduces systematic deviations much larger than those caused by the point dipole approximation, which mostly breaks down at short D/A separations where FRET lifetimes are anyway very short. In particular, we find a strong exponential attenuation of screening effects at D/A separations below 20 Å, which is in striking agreement with the behavior previously observed in pigment pairs of photosynthetic complexes from calculations based on continuum solvent models, despite the fact that we deal with different dye molecules located in a different protein-solvent environment, and more importantly, we describe the environment in atomic detail. Our findings thus indicate that dielectric screening alters the well-known R−6 distance dependence of Förster energy transfer rate, which affects the practical derivation of structural information in FRET experiments. These effects seem to be of particular relevance to describe the balance between folded and unfolded conformations, characterized by either short or large interdye separations. In this context, our results warn that the common practice of ignoring distance-dependent screening effects masks the tendency of classical force fields to overstabilize compact folded structures, with consequences in the refinement and validation of classical potentials for disordered proteins based on FRET data.Data availability
The input files needed to prepare and run the MD simulations and the TrESP charges of the dyes can be found on Zenodo at DOI: https://doi.org/10.5281/zenodo.11108574. The TrADA and Trespcoup codes used to fit TrESP charges and compute TrESP-MMPol calculations can be found at DOI: https://doi.org/10.5281/zenodo.10966411 and https://doi.org/10.5281/zenodo.10966391.Author contributions
CC conceived this research. CC and LC developed the methodology. DG performed the simulations. DG, LC and CC analyzed the results. CC supervised the work. All authors wrote the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge access to computer resources at MareNostrum and the technical support provided by the Barcelona Supercomputing Center (QCM-2018-3-0042, QSB-2019-2-0001). Financial support from the State Research Agency/Spanish Ministry of Science, Innovation and Universities (AEI/10.13039/501100011033; grants PID2020-115812GB-I00, PID2023-151584NB-I00, MDM-2017-0767 and CEX2021-001202-M) and the Catalan Agència de Gestió d’Ajuts Universitaris i de Recerca from Generalitat de Catalunya (GENCAT; 2021SGR00671) is acknowledged.Notes and references
- H. E. A. Kramer and P. Fischer, ChemPhysChem, 2011, 12, 555–558 CrossRef CAS PubMed.
- S. E. Braslavsky, E. Fron, H. B. Rodríguez, E. S. Román, G. D. Scholes, G. Schweitzer, B. Valeur and J. Wirz, Photochem. Photobiol. Sci., 2008, 7, 1444 CrossRef CAS PubMed.
- D. Beljonne, C. Curutchet, G. D. Scholes and R. J. Silbey, J. Phys. Chem. B, 2009, 113, 6583–6599 CrossRef CAS PubMed.
- W. R. Algar, N. Hildebrandt, S. S. Vogel and I. L. Medintz, Nat. Methods, 2019, 16, 815–829 CrossRef CAS PubMed.
- FRET – Förster Resonance Energy Transfer: From Theory to Applications, ed. I. Medintz and N. Hildebrandt, WILEY-VCH Verlag, Weinheim, 2014 Search PubMed.
- E. Lerner, T. Cordes, A. Ingargiola, Y. Alhadid, S. Chung, X. Michalet and S. Weiss, Science, 2018, 359, eaan1133 CrossRef PubMed.
- L. A. Metskas and E. Rhoades, Annu. Rev. Phys. Chem., 2020, 71, 391–414 CrossRef CAS PubMed.
- A. Chowdhury, D. Nettels and B. Schuler, Annu. Rev. Biophys., 2023, 52, 433–462 CrossRef CAS PubMed.
- I. Nasir, P. L. Onuchic, S. R. Labra and A. A. Deniz, Biochim. Biophys. Acta Protein Proteonomics, 2019, 1867, 980–987 CrossRef CAS PubMed.
- E. D. Holmstrom, A. Holla, W. Zheng, D. Nettels, R. B. Best and B. Schuler, in Methods in Enzymology, Academic Press Inc., 2018, vol. 611, pp. 287–325 Search PubMed.
- G. N. Gomes and C. C. Gradinaru, Biochim. Biophys. Acta Protein Proteonomics, 2017, 1865, 1696–1706 CrossRef CAS PubMed.
- B. Schuler, A. Soranno, H. Hofmann and D. Nettels, Annu. Rev. Biophys., 2016, 45, 207–231 CrossRef CAS PubMed.
- P. R. Banerjee and A. A. Deniz, Chem. Soc. Rev., 2014, 43, 1172–1188 RSC.
- F. Meng, M. M. J. Bellaiche, J.-Y. Kim, G. H. Zerze, R. B. Best and H. S. Chung, Biophys. J., 2018, 114, 870–884 CrossRef CAS PubMed.
- I. Reinartz, C. Sinner, D. Nettels, B. Stucki-Buchli, F. Stockmar, P. T. Panek, C. R. Jacob, G. U. Nienhaus, B. Schuler and A. Schug, J. Chem. Phys., 2018, 148, 123321 CrossRef PubMed.
- E. Sobakinskaya, M. Schmidt am Busch and T. Renger, J. Phys. Chem. B, 2018, 122, 54–67 CrossRef CAS PubMed.
- K. K. Grotz, M. F. Nueesch, E. D. Holmstrom, M. Heinz, L. S. Stelzl, B. Schuler and G. Hummer, J. Phys. Chem. B, 2018, 122, 11626–11639 CrossRef CAS PubMed.
- P. Prakash, D. Litwin, H. Liang, S. Sarkar-Banerjee, D. Dolino, Y. Zhou, J. F. Hancock, V. Jayaraman and A. A. Gorfe, Biophys. J., 2019, 116, 179–183 CrossRef CAS PubMed.
- B. Schuler, E. A. Lipman, P. J. Steinbach, M. Kumke and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 2754–2759 CrossRef CAS PubMed.
- D. B. VanBeek, M. C. Zwier, J. M. Shorb and B. P. Krueger, Biophys. J., 2007, 92, 4168–4178 CrossRef CAS PubMed.
- K. A. Merchant, R. B. Best, J. M. Louis, I. V Gopich and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 1528–1533 CrossRef CAS PubMed.
- E. Dolghih, A. E. Roitberg and J. L. Krause, J. Photochem. Photobiol., A, 2007, 190, 321–327 CrossRef CAS.
- A. K. Wozniak, G. F. Schroeder, H. Grubmueller, C. A. M. Seidel and F. Oesterhelt, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18337–18342 CrossRef CAS PubMed.
- L. R. Allen and E. Paci, J. Chem. Phys., 2009, 131, 1–6 CrossRef PubMed.
- E. Dolghih, W. Ortiz, S. Kim, B. P. Krueger, J. L. Krause and A. E. Roitberg, J. Phys. Chem. A, 2009, 113, 4639–4646 CrossRef CAS PubMed.
- A. L. Speelman, A. Muñoz-Losa, K. L. Hinkle, D. B. VanBeek, B. Mennucci and B. P. Krueger, J. Phys. Chem. A, 2011, 115, 3997–4008 CrossRef CAS PubMed.
- R. Kellner, H. Hofmann, A. Barducci, B. Wunderlich, D. Nettels and B. Schuler, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13355–13360 CrossRef CAS PubMed.
- K. Walczewska-Szewc and B. Corry, Phys. Chem. Chem. Phys., 2014, 16, 12317–12326 RSC.
- C. Curutchet and B. Mennucci, Chem. Rev., 2017, 117, 294–343 CrossRef CAS PubMed.
- R. S. Knox and H. van Amerongen, J. Phys. Chem. B, 2002, 106, 5289–5293 CrossRef CAS.
- C.-P. Hsu, G. R. Fleming, M. Head-Gordon and T. Head-Gordon, J. Chem. Phys., 2001, 114, 3065 CrossRef CAS.
- C. Curutchet, A. Munoz-Losa, S. Monti, J. Kongsted, G. D. Scholes and B. Mennucci, J. Chem. Theory Comput., 2009, 5, 1838–1848 CrossRef CAS PubMed.
- M. F. Iozzi, B. Mennucci, J. Tomasi and R. Cammi, J. Chem. Phys., 2004, 120, 7029–7040 CrossRef CAS PubMed.
- L. Cupellini, M. Corbella, B. Mennucci and C. Curutchet, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2019, 9, e1392 CrossRef.
- C. Curutchet, G. D. Scholes, B. Mennucci and R. Cammi, J. Phys. Chem. B, 2007, 111, 13253–13265 CrossRef CAS PubMed.
- G. D. Scholes, C. Curutchet, B. Mennucci, R. Cammi and J. Tomasi, J. Phys. Chem. B, 2007, 111, 6978–6982 CrossRef CAS PubMed.
- C. Curutchet, J. Kongsted, A. Muñoz-Losa, H. Hossein-Nejad, G. D. Scholes and B. Mennucci, J. Am. Chem. Soc., 2011, 133, 3078–3084 CrossRef CAS PubMed.
- M. Eder and T. Renger, Int. J. Mol. Sci., 2024, 25, 9006 CrossRef CAS PubMed.
- E. Cignoni, L. Cupellini and B. Mennucci, J. Phys. Condens. Matter, 2022, 34, 304004 CrossRef CAS PubMed.
- P. Kursula, Amino Acids, 2014, 46, 2295–2304 CrossRef CAS PubMed.
- C. K. Johnson, Biochemistry, 2006, 45, 14233–14246 CrossRef CAS PubMed.
- M. S. DeVore, A. Braimah, D. R. Benson and C. K. Johnson, J. Phys. Chem. B, 2016, 120, 4357–4364 CrossRef CAS PubMed.
- A. Muñoz-Losa, C. Curutchet, B. P. Krueger, L. R. Hartsell and B. Mennucci, Biophys. J., 2009, 96, 4779–4788 CrossRef PubMed.
- M. E. Madjet, A. Abdurahman and T. Renger, J. Phys. Chem. B, 2006, 110, 17268–17281 CrossRef CAS PubMed.
- R. Chattopadhyaya, W. E. Meador, A. R. Means and F. A. Quiocho, J. Mol. Biol., 1992, 228, 1177–1192 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- P. Li, B. P. Roberts, D. K. Chakravorty and K. M. Merz, J. Chem. Theory Comput., 2013, 9, 2733–2748 CrossRef CAS PubMed.
- D. A. Case, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, V. Man, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, A. Onufriev, F. Pan, S. Pantano, R. Qi, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, L. Wilson, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, M. York and P. A. Kollman, AMBER 2020, University of California, San Francisco, 2020 Search PubMed.
- L. Cupellini, F. Lipparini and E. Cignoni, Trespcoup – Software to compute TrEsp couplings, Zenodo, 2024, DOI:10.5281/zenodo.10966391.
- J. Wang, P. Cieplak, J. Li, T. Hou, R. Luo and Y. Duan, J. Phys. Chem. B, 2011, 115, 3091–3099 CrossRef CAS PubMed.
- J. Wang, P. Cieplak, J. Li, J. Wang, Q. Cai, M. Hsieh, H. Lei, R. Luo and Y. Duan, J. Phys. Chem. B, 2011, 115, 3100–3111 CrossRef CAS PubMed.
- L. Cupellini, S. Jurinovich and B. Mennucci, TraDA - Transition Density Analyzer, Zenodo, 2024, DOI:10.5281/zenodo.10966411.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, B. G. Janesko, F. Lipparini, G. Zheng, J. L. Sonnenberg, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven Jr. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, T. Staroverov, T. Keith, R. Kobayashi, K. Normand, J. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, P. V. Parandekar, N. J. Mayhall, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox. Gaussian development version, Revision H.36. Wallingford CT: Gaussian, Inc. 2010 Search PubMed.
- X. J. Jordanides, M. J. Lang, X. Song and G. R. Fleming, J. Phys. Chem. B, 1999, 103, 7995–8005 CrossRef CAS.
- B. D. Slaughter, M. W. Allen, J. R. Unruh, R. J. Bieber Urbauer and C. K. Johnson, J. Phys. Chem. B, 2004, 108, 10388–10397 CrossRef CAS.
- A. M. Westerlund and L. Delemotte, PLoS Comput. Biol., 2018, 14, e1006072 CrossRef PubMed.
- W. Wriggers, E. Mehler, F. Pitici, H. Weinstein and K. Schulten, Biophys. J., 1998, 74, 1622–1639 CrossRef CAS PubMed.
- Y. Komeiji, Y. Ueno and M. Uebayasi, FEBS Lett., 2002, 521, 133–139 CrossRef CAS PubMed.
- C. M. Shepherd and H. J. Vogel, Biophys. J., 2004, 87, 780–791 CrossRef CAS PubMed.
- G. Fiorin, R. R. Biekofsky, A. Pastore and P. Carloni, Proteins: Struct., Funct., Bioinf., 2005, 61, 829–839 CrossRef CAS PubMed.
- D. Shukla, A. Peck and V. S. Pande, Nat. Commun., 2016, 7, 10910 CrossRef CAS PubMed.
- K. Wang, A. Sachdeva, D. J. Cox, N. W. Wilf, K. Lang, S. Wallace, R. A. Mehl and J. W. Chin, Nat. Chem., 2014, 6, 393–403 CrossRef CAS PubMed.
- I. Bertini, A. Giachetti, C. Luchinat, G. Parigi, M. V. Petoukhov, R. Pierattelli, E. Ravera and D. I. Svergun, J. Am. Chem. Soc., 2010, 132, 13553–13558 CrossRef CAS PubMed.
- T. Renger and F. Müh, Photosynth. Res., 2012, 111, 47–52 CrossRef CAS PubMed.
- B. D. Slaughter, J. R. Unruh, M. W. Allen, R. J. B. Urbauer and C. K. Johnson, Biochemistry, 2005, 44, 3694–3707 CrossRef CAS PubMed.
- B. Crockett, J. van Howe, N. Montaut, R. Morandotti and J. Azaña, Laser Photon. Rev., 2022, 16, 2100635 CrossRef.
- P. Robustelli, S. Piana and D. E. Shaw, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4758–E4766 CrossRef CAS PubMed.
- R. B. Best, W. Zheng and J. Mittal, J. Chem. Theory Comput., 2014, 10, 5113–5124 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The complete methods and computational details, tables of structural and FRET properties along MD trajectories, and figures with benchmark coupling results, screening factors, dyes SASA values, PDA/TrESP coupling ratios, distances, distributions of electronic couplings and fluorescence decays. See DOI: https://doi.org/10.1039/d4sc07679f |
| This journal is © The Royal Society of Chemistry 2025 |