Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical analysis of the OH-initiated atmospheric oxidation reactions of imidazole†
Thomas
Golin Almeida
 *ab,
Carles
Martí
*ab,
Carles
Martí
 c,
Theo
Kurtén
ab,
Judit
Zádor
c,
Theo
Kurtén
ab,
Judit
Zádor
 c and
Sommer L.
Johansen
*c
c and
Sommer L.
Johansen
*c
aDepartment of Chemistry, University of Helsinki, Helsinki 00014, Finland. E-mail: thomas.golin@helsinki.fi
bInstitute for Atmospheric and Earth System Research/Chemistry, University of Helsinki, Helsinki 00014, Finland
cCombustion Research Facility, Sandia National Laboratories, Livermore 94550, California, USA. E-mail: sljohan@sandia.gov
First published on 29th July 2024
Abstract
Imidazoles are present in Earth's atmosphere in both the gas-phase and in aerosol particles, and have been implicated in the formation of brown carbon aerosols. The gas-phase oxidation of imidazole (C3N2H4) by hydroxyl radicals has been shown to be preferentially initiated via OH-addition to position C5, producing the 5-hydroxyimidazolyl radical adduct. However, the fate of this adduct upon reaction with O2 in the atmospheric gas-phase is currently unknown. We employed an automated approach to investigate the reaction mechanism and kinetics of imidazole's OH-initiated gas-phase oxidation, in the presence of O2 and NOx. The explored mechanism included reactions available to first-generation RO2 radicals, as well as alkoxyl radicals produced from RO2 + NO reactions. Product distributions were obtained by assembling and solving a master equation, under conditions relevant to the Earth's atmosphere. Our calculations show a complex, branched reaction mechanism, which nevertheless converges to yield two major closed-shell products: 4H-imidazol-4-ol (4H-4ol) and N,N′-diformylformamidine (FMF). At 298 K and 1 atm, we estimate the yields of 4H-4ol and FMF from imidazole oxidation initiated via OH-addition to position C5 to be 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 66, 12
66, 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 85 and 2
85 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95 under 10 ppt, 100 ppt and 1 ppb of NO respectively. This work also revealed O2-migration pathways between the α-N-imino peroxyl radical isomers. This reaction channel is fast for the first-generation RO2 radicals, and may be important during the atmospheric oxidation of other unsaturated organic nitrogen compounds as well.
95 under 10 ppt, 100 ppt and 1 ppb of NO respectively. This work also revealed O2-migration pathways between the α-N-imino peroxyl radical isomers. This reaction channel is fast for the first-generation RO2 radicals, and may be important during the atmospheric oxidation of other unsaturated organic nitrogen compounds as well.
1 Introduction
Imidazole is a five-membered aromatic heterocycle with two nitrogen atoms in meta positions: one that is pyrrole-like (>NH) and one that is pyridine-like (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–). Alongside other organic nitrogen compounds,1 imidazole and its derivatives (hence referred to as imidazoles) have been observed in the Earth's atmosphere, both in the gas-phase2,3 and in aerosol particles.4–7 Recently, imidazole's presence in the atmosphere has garnered attention due to its potential influence on the planet's climate.4,8–10 More generally, imidazole is ubiquitous in nature due to its role in biochemistry,11 where it can act as a versatile catalyst in enzyme active sites.12
N–). Alongside other organic nitrogen compounds,1 imidazole and its derivatives (hence referred to as imidazoles) have been observed in the Earth's atmosphere, both in the gas-phase2,3 and in aerosol particles.4–7 Recently, imidazole's presence in the atmosphere has garnered attention due to its potential influence on the planet's climate.4,8–10 More generally, imidazole is ubiquitous in nature due to its role in biochemistry,11 where it can act as a versatile catalyst in enzyme active sites.12
The majority of atmospheric imidazoles are thought to be secondary in origin, i.e., formed in the atmosphere from reaction of precursor compounds. Numerous experimental and theoretical studies report that imidazoles can be formed from α-dicarbonyl compounds, such as glyoxal, reacting with ammonia or primary amines in aqueous aerosol particles.13–20 Other possible sources of imidazoles to the atmosphere include anthropogenic emissions from industrial activities,4 biomass burning,21 and riverine water–air interface reactions.22 This latter source, involving oxidation of organic compounds by ozone at the river surface microlayer, may be a possible source of imidazole emissions directly into the atmospheric gas-phase. Although most studies investigating atmospheric imidazoles focus on condensed-phase chemistry, recent field experiments in the Hyytiälä boreal forest research station in Finland reported the detection of these compounds also in the gas-phase,2,3 with concentrations of up to ∼183 ppt, which is comparable to the typical concentration of abundant amines.23
Concerning their impact on the atmosphere, imidazoles have received much attention due to their role as components of brown carbon, in which they strongly affect the aerosol optical properties.4,24,25 Moreover, studies show that imidazoles may act as photosensitizers, promoting accelerated aerosol particle growth via gas-particle interface reactions.8,26,27 Aerosols still constitute one of the largest sources of uncertainty in climate model predictions,28 largely due to insufficient understanding of the molecular-level processes controlling the formation, growth, ageing, composition, and physical properties of atmospheric aerosol particles.9,29 Among these processes is the degradation of aerosol precursor species by atmospheric oxidation, which may lead to several different products, oftentimes with widely different properties.
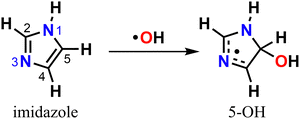
Either in the gas-phase or dissolved in aqueous aerosol particles, imidazoles can react with OH radicals, the main atmospheric oxidant,30–35 yet knowledge of their fate upon oxidation is limited. The mechanism for imidazole reaction with OH radical in aqueous solution has been previously investigated with experiments32,33 and theory,35 revealing that oxidation is preferentially initiated via electrophilic addition to position C5 leading to the 5-hydroxyimidazolyl radical adduct (5-OH) (Scheme 1).
There are only few studies investigating imidazole's gas-phase atmospheric chemistry.31,36,37 A rate coefficient for the reaction of imidazole with OH radical was reported to be k(298 K) = 3.8 × 10−11 cm3 molecule−1 s−1,31 as measured with flash photolysis-resonance fluorescence. Subsequent theoretical studies predicted that just like in the aqueous-phase, OH-addition to position C5 is favored (∼88% yield), while addition to position C2 is a minor channel.36,37 However, no study has explored the atmospherically important reactions of the 5-OH product, an alkyl (C-centered) radical, with O2.
Alkyl radicals formed in the atmosphere are prone to react fast with O2, yielding peroxyl radical (RO2) products:
| R˙ + O2 → RO2˙ | (1) |
RO2 unimolecular reactions such as intramolecular H-shifts,
| RO2˙ → R′˙OOH | (2) |
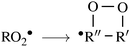 | (3) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double-bond,41 may lead to propagation of the oxidative chain by reforming a C-centered radical, allowing for addition of a second O2 molecule, in what are called autoxidation channels.40,42,43 These channels may eventually produce highly functionalized, low-volatility products, contributing to enhanced aerosol particle growth.44
C double-bond,41 may lead to propagation of the oxidative chain by reforming a C-centered radical, allowing for addition of a second O2 molecule, in what are called autoxidation channels.40,42,43 These channels may eventually produce highly functionalized, low-volatility products, contributing to enhanced aerosol particle growth.44
If, however, a N-centered radical is formed (e.g., via H-shift from an amino group), subsequent reactions typically lead to termination of the oxidative chain. Their reactions with O2 leads to the formation of a closed-shell imine plus HO2,45
RCH(–N˙R′)R′′ + O2 → RC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR′)R′′ + HO2˙ NR′)R′′ + HO2˙ | (4) |
| RN˙R′ + NOx˙ → RN(–NOx)R′ | (5) |
Other RO2 unimolecular channels may also lead to an early termination of the oxidative chain, such as HO2-elimination reactions, in which a concerted H-shift from a β-peroxyl C, N or O atom (1,4 shift) and C–O(O) bond scission produces a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N or C
N or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O π-bond plus HO2. In general, HO2-elimination involving concerted H-shift from a carbon is negligible in the atmosphere,48,51 whereas it becomes competitive, or even predominant, when it involves H-shift from a nitrogen48,52–54
O π-bond plus HO2. In general, HO2-elimination involving concerted H-shift from a carbon is negligible in the atmosphere,48,51 whereas it becomes competitive, or even predominant, when it involves H-shift from a nitrogen48,52–54
RO2˙ → R′C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NR′′′)R′′ + HO2˙ NR′′′)R′′ + HO2˙ | (6) |
RO2˙ → R′C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)R′′ + HO2˙ O)R′′ + HO2˙ | (7) |
Relevant bimolecular channels of RO2 include reaction with NO, NO2, HO2, and self- or cross-reaction with another R′O2 radical.38 These channels are often barrierless (or nearly so), since they involve radical recombination, and therefore their competitiveness is largely dictated by the favorability of unimolecular channels, as well as the concentration of reaction partners. For instance, typical NOx concentrations in pristine environments are on the order of 1–10 ppt, where unimolecular, RO2 + HO2 and RO2 + R′O2 reactions can compete, while in more polluted conditions NOx concentrations may be 3 orders of magnitude higher (1–10 ppb), and thus RO2 + NO reactions tend to dominate.56 Reaction of a RO2 radical with NO leads predominantly to the formation of NO2 plus the corresponding alkoxyl radical (RO),
| RO2˙ + NO˙ → RO˙ + NO2˙ | (8) |
RO˙ → R′C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)R′′ + R′′′˙ O)R′′ + R′′′˙ | (9) |
Since peroxyl radicals derived from cyclic compounds tend to be, in general, less prone to react via unimolecular pathways than acyclic analogues,58 RO2 + NO reactions could be important during imidazole oxidation even under lower NO concentrations. The rigid structure of a cyclic RO2 imposes constraints on the orientation of functional groups, thus hindering or completely preventing access to some sites for intramolecular –OO˙ radical attack. On the other hand, the presence of a nitrogen in the ring allows for the possibility of HO2-elimination with imine formation, reaction which can be fast even for cyclic reactants.48,54,59 Furthermore, aromatic homocyclic compounds display some mechanistic peculiarities during atmospheric oxidation, such as a prevalence of RO2 endo-cyclization pathways (Reaction (3)) producing bicyclic endoperoxides.39,60,61 The mechanism of heterocyclic aromatic atmospheric oxidation is less understood, and so far it is uncertain whether the homocyclic reactivity trends apply also for these compounds, or if they follow entirely different pathways.
To gain fundamental understanding of imidazoles in the atmosphere, we investigate the mechanism of imidazole gas-phase oxidation initiated by OH radical addition to position C5, and follow its chemistry upon the formation of RO2 in the presence of NO (Reactions (1)–(8)). The explored oxidation mechanism also includes the further reactions available to RO radicals produced viareaction (8). We employ automated high-level quantum chemistry methods to explore the reaction pathways involved in the oxidation mechanism systematically, calculate reaction rate coefficients, and explore the overall reaction kinetics to predict product distributions under a range of atmospherically relevant conditions.
2 Methods
2.1 Potential energy surface exploration
Unimolecular isomerization and decomposition reactions were explored using KinBot,59,62,63 a workflow code for automated gas-phase reaction search and kinetics. KinBot automatically creates and submits calculations to explore and characterize the relevant regions of a potential energy surface (PES) as described below. Overall, starting from an initial reactant structure well (e.g. RO2), KinBot proposes the set of unimolecular isomerization and dissociation reactions that this species can undergo, and generates a guess for the related transition state geometries based on reaction templates. After filtering out the invalid reactions and the ones with barriers above a user-defined energy cutoff, the process is repeated for each new well, until no more new stationary points are found.Stationary point geometries were first optimized at the L1 = B3LYP/6-31+G* level of theory.64–69 We discarded all reactions with an L1 barrier above a threshold, for which we found that 20 kcal mol−1 relative to the initial reactant was a meaningful choice in all cases. Additionally, intrinsic reaction coordinate (IRC) calculations were used for each of the remaining saddle points to identify the connected minima. Saddle-points are discarded if neither or both of the connected minima corresponded to the reactant. KinBot searched the conformational space of each stationary point at the L1 level. Subsequently, all unique conformers with a Boltzmann factor larger than 0.05 at 300 K were re-optimized at the L2 = ωB97X-D/aug-cc-pVTZ level of theory.70–73 Finally, single-point L3 = ROHF-ROCCSD(T)-F12a/cc-pVDZ-F1274,75 calculations were done for the lowest energy conformers of each stationary point. As is recommended for this type of calculation,75 we changed the value of the geminal Slater exponent β to 0.9, using the keyword “gem_beta = 0.9”. In order to understand the uncertainties associated with our choice of method for L3, we performed ROHF-ROCCSD(T)-F12a/cc-pVTZ-F1275 and ROHF-UCCSD(T)-F12a/cc-pVDZ-F12 single-point calculations on a subset of important species. Comparison of the results obtained is shown in Table S11 (ESI†).
We selected the lowest energy structures in two ways, based on the zero-point energy (ZPE) corrected energies and based on the 300-K free-energy. The former definition was used in the multi-conformer transition state theory (MC-TST) calculations, while the latter was used to select the structure in the master-equation, where we used a single conformer for each stationary point. Note that in the MC-TST calculations we applied the same L3//L2 energy correction to the higher energy conformers as to the lowest one.
The L1 and L2 calculations were done via KinBot's atomic simulation environment (ASE)76 interface to Gaussian,77 while Molpro v2022.278–80 was used for the L3 energies offline with automatically generated inputs.
For a few reactions, such as bimolecular reactions connecting successive parts of the oxidation mechanism, the PES was explored manually. In those cases, conformer search was performed with the Spartan v2081 software, employing the Merck-molecular force field (MMFF94) method.82
2.2 Reaction kinetics
We estimated thermal rate coefficients for each unimolecular reaction using transition state theory (TST),83 both using only the lowest-energy conformer and a multi-conformer approach (MC-TST),73 assuming rigid-rotor-harmonic-oscillator (RRHO) partition functions for each structure. Product yields were estimated by assembling and solving a master equation, using the Master Equation Solver for Multi-Energy well Reactions (MESMER) software version 7.084 using the lowest-free energy conformers only.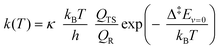 | (10) |
In order to assess the effect of multiple conformations on reaction rates, we also used a MC-TST approach73 to estimate k(T) values using a sum of Boltzmann-weighed conformer contributions.
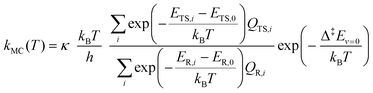 | (11) |
Unimolecular reactions (isomerizations and dissociations) were modelled with standard Rice–Ramsperger–Kassel–Marcus (RRKM) theory, using the Eckart tunnelling correction.85 Each dissociation transition state was assumed to be connected by isomerization to a post-reactive complex (PC), whose decomposition into bimolecular products was modelled in a separate, irreversible and barrierless reaction step, using ILT with a rate coefficient of 10−10 cm3 molecule−1 s−1 corresponding to the reverse association reaction. Finally, RO2 + NO reactions were modelled as simple bimolecular sinks, with a rate coefficient value of 2.7 × 10−12 exp(+360 K/T) cm3 molecule−1 s−1.88
In the simulations a high concentration of OH radicals (1015 molecules cm−3cf ∼ 106 molecules cm−3 ambient OH concentration) was used with the intent of starting the oxidative chain within ∼1 μs. This enabled us to see reactive intermediates on short time-scales and resolve low-yield intermediates better in the numerical simulations, but it did not affect any other reaction step in the master equation. For O2, a mixing ratio of 0.20946 (5.16 × 1018 molecules cm−3 at 1 atm, 298 K) was used. The RRKM-ME calculations were done in the 250–350 K temperature range and using three NO concentrations (10 ppt, 100 ppt and 1 ppb). We extrapolated the range of investigated temperatures beyond realistic atmospheric conditions, especially towards the hotter end, with the intention of gaining further insight into the kinetics of oxidation.
We employed the single exponential down model to treat collisional energy transfer, using a 〈ΔE〉down parameter value of 225 cm−1. Lennard-Jones parameters for modelled wells were calculated from pure-compound critical properties,89,90 which were in turn estimated with the Joback group-additivity method.91 N2 was set as the bath gas, with Lennard-Jones parameters ε/kB = 91.85 K and σ = 3.919. We employed 50 cm−1 energy grains, which spanned a maximum energy of 20 kBT above the highest-energy stationary point. Test calculations done with a smaller energy grain size (30 cm−1) resulted in negligible differences in product yields (maximum difference of ∼0.04%). The time evolution of species distributions was obtained by summing over populations in energy grains at each time step. We used the quad-double (qd) numerical precision in all ME calculations.
Once the product distributions from the reaction of first-generation RO2 radicals were obtained, we explored the reaction pathways available to the open-shell products with significant yields, using KinBot and repeating the computational routine described above (PES exploration and RRKM-ME simulation), with a few differences. The fate of each major alkoxyl radical product was investigated with a separate RRKM-ME calculation, setting the parent RO2 radical as the initial reactant. Formation of the alkoxyl radical occurs with two steps, both modelled with standard ILT: first, RO2 + NO reaction produces a ROONO adduct, which then dissociates into RO + NO2 in a second step. We set the NO and NO2 concentrations to 100 ppt. An O2 addition reaction step is added for each possible alkyl radical intermediate, but this time modelled as simple bimolecular sinks. Once a major, second-generation RO2 product is identified, the RRKM-ME calculation is run again, but this time treating the corresponding O2-addition channel with standard ILT, and including subsequent unimolecular reaction steps.
Finally, to assess the uncertainty of calculated product yields due to the uncertainty in RRKM-ME model parameters and the calculated PES, we employed the automated procedure present in KinBot.59 Here the approach was adapted for the MESMER code. A detailed description for this procedure is given in the ESI.†
3 Results and discussion
3.1 First generation peroxyl radicals
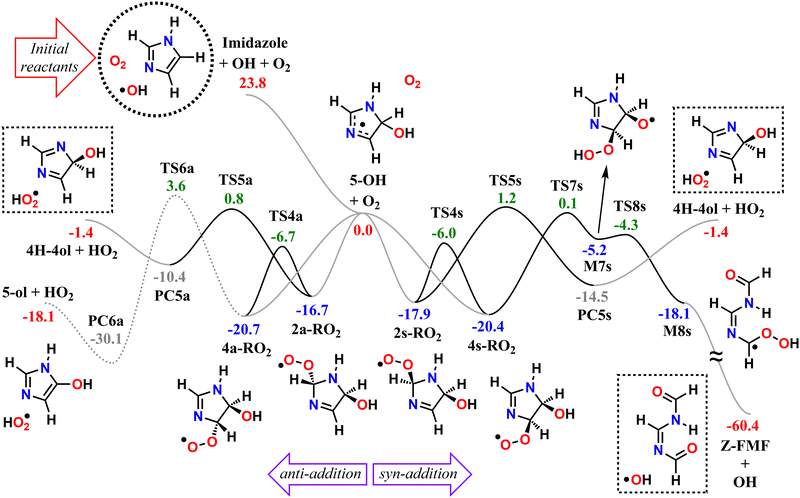
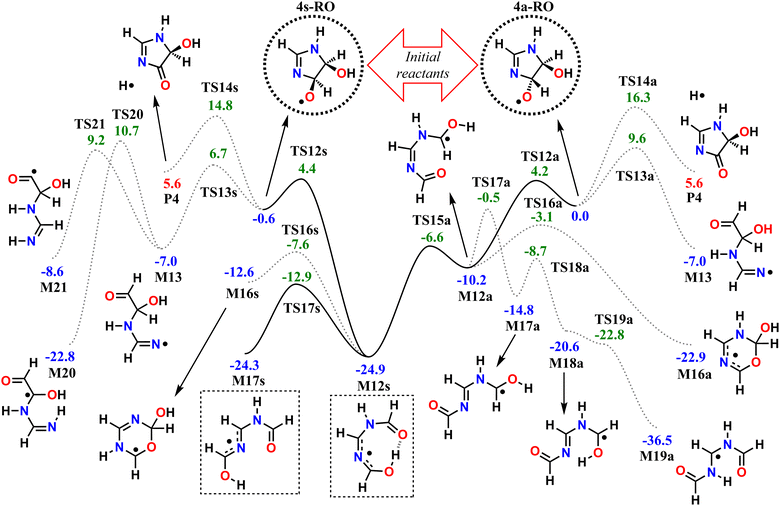
We start by exploring the fate of imidazole after initial OH radical addition to position C5, producing the C-centered alkyl radical, 5-OH. Adduct 5-OH has no unimolecular reaction channel that is able to compete with O2-addition, as the only pathway found during reaction search (within the 20 kcal mol−1 energy barrier cutoff) was dissociation back to reactants (imidazole + OH). Direct H-abstraction from C5 by O2, leading to the aromatic species 1H-imidazol-5-ol (5-ol), is also unable to compete with O2-addition. The calculated energy barrier for this reaction is 9.93 kcal mol−1, and the associated rate coefficient value estimated with TST is 1.14 × 10−21 cm3 molecule−1 s−1.Reaction of O2 with 5-OH may initially lead to the formation of one of four different RO2 isomers. The odd-electron density in 5-OH is delocalized over two carbon atoms, C2 and C4, due to resonance stabilization, thus the addition of O2 may occur at either of these positions. Moreover, depending on the side of the ring at which the O2 attack occurs, addition to positions C2 and C4 may lead to two RO2 stereoisomers each. Anti-addition (relative to the OH moiety) may lead to peroxyl radicals 2a-RO2 or 4a-RO2, while syn-addition may lead to peroxyl radicals 2s-RO2 or 4s-RO2. The stationary points on the PES, including O2-addition reactions, as well as the unimolecular reaction pathways available to each of the RO2 species, are shown in Fig. 1.
The 4-RO2 adducts are 3–4 kcal mol−1 more stable than their 2-RO2 counterparts. This difference can be explained by the hyperconjugative interaction between the amine nitrogen's lone-pair and the imine's π-antibonding orbital (nN → πCN*), which is retained in the C4-addition products (in the amidine group), but lost upon O2-addition to position C2. The energy differences between syn- and anti-adducts are smaller, and the reasons are less obvious. Unlike in anti-isomers, the peroxyl and hydroxyl groups in syn-isomers are able to interact via an intramolecular H-bond, albeit a weak one, since ring-strain prevents an optimal O–H–O orientation. The 2s-RO2 isomer is therefore 0.8 kcal mol−1 lower in energy compared to 2a-RO2. However, the opposite trend is observed for the 4-isomers: 4s-RO2 is 0.4 kcal mol−1 higher in energy than 4a-RO2. Here, destabilization brought by steric repulsion between the neighboring peroxyl and hydroxyl groups, which is significant with β-OH syn-substitution, overcomes the stabilizing effect of the H-bond.
In the 2-RO2 isomers, the peroxyl group is bonded to an α-amino C, and thus both of these species may undergo HO2-elimination (1,4 H-shift from the nitrogen concerted with cleavage of the C–O(O) bond), resulting in C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double-bond formation via transition states TS5a or TS5s. These two HO2-elimination pathways have similar reaction barrier heights, differing by about 0.4 kcal mol−1, and lead to the same products, the cyclic diimine 4H-imidazol-4-ol (4H-4ol) plus HO2 radical. In contrast, the reaction channels which are available to the 4-RO2 isomers depend on the reactant's stereochemistry that determines which moieties are accessible for attack of the peroxyl group. Unlike the syn isomer 4s-RO2, the anti isomer 4a-RO2 may also react via HO2-elimination (via transition state TS6a), but in this case with concerted H-transfer from the α-hydroxyl carbon, producing the aromatic species 1H-imidazol-5-ol (5-ol) plus HO2 radical. Even though this channel recovers the aromaticity of the heterocycle, leading to a product that is more stable than 4H-4ol by 16.7 kcal mol−1, its reaction barrier is the highest among the ones studied here for first-generation RO2 species.
N double-bond formation via transition states TS5a or TS5s. These two HO2-elimination pathways have similar reaction barrier heights, differing by about 0.4 kcal mol−1, and lead to the same products, the cyclic diimine 4H-imidazol-4-ol (4H-4ol) plus HO2 radical. In contrast, the reaction channels which are available to the 4-RO2 isomers depend on the reactant's stereochemistry that determines which moieties are accessible for attack of the peroxyl group. Unlike the syn isomer 4s-RO2, the anti isomer 4a-RO2 may also react via HO2-elimination (via transition state TS6a), but in this case with concerted H-transfer from the α-hydroxyl carbon, producing the aromatic species 1H-imidazol-5-ol (5-ol) plus HO2 radical. Even though this channel recovers the aromaticity of the heterocycle, leading to a product that is more stable than 4H-4ol by 16.7 kcal mol−1, its reaction barrier is the highest among the ones studied here for first-generation RO2 species.
The peroxyl group in the syn isomer 4s-RO2 has access to the alcohol group, and this species may react via an 1,5 H-shift (via TS7s), producing the hydroperoxy-alkoxyl radical (HOOQO) M7s. This channel has a slightly lower reaction barrier height than the HO2-elimination pathways, and it initiates a cascade of exothermic unimolecular reaction steps, ultimately leading to the formation of another closed-shell product, (Z)-N,N′-diformylformamidine (Z-FMF), plus OH radical. Most substituted RO radicals may undergo fast β-scission, producing a carbonyl and a C-centered radical. Species M7s is especially prone to react in this manner (via TS8s) because the reaction barrier associated with β-scission is only 0.9 kcal mol−1. Release of ring-strain and the development of a high degree of electron delocalization in TS8s may explain the increased reactivity observed. The (HOO)C–C(O) distance in M7s is also abnormally large (∼2 Å), and for this reason, this part of the PES was calculated manually. The product of this β-scission, species M8s, is an α-OOH alkyl radical, a class of intermediates which are known to undergo spontaneous OH radical elimination,92 producing a closed-shell carbonyl compound
RC˙(–OOH)R′ → RC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)R′ + ˙OH O)R′ + ˙OH | (12) |
Since most conformations of the reactant spontaneously decompose into the products (Z-FMF and OH radical) during geometry optimization, we assumed that dissociation of M8s occurs without a barrier.
Finally, O2-migration reaction steps connect the two anti-isomers (2a-RO2 ⇄ 4a-RO2) and the two syn-isomers (2s-RO2 ⇄ 4s-RO2), via TS4a and TS4s respectively, with the lowest energy barriers among the RO2 unimolecular channels. These reactions resemble endo-cyclization steps (Reaction (3)), but involving a concerted attack of the peroxyl group on the C-terminus of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double-bond and C–O(O) bond cleavage. As a result, the peroxyl group and the C
N double-bond and C–O(O) bond cleavage. As a result, the peroxyl group and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double-bond exchange positions.
N double-bond exchange positions.
We note that T1 diagnostics and the percentage of triples (T) contribution to the total atomization energy %TAE[(T)]93,94 suggest that transition states TS4a, TS4s, TS5a, TS5s, TS6a, TS7s, and TS8s have a mild degree of multi-configurational character (see Section S9 in the ESI†). Test calculations with a unrestricted coupled-cluster wavefunction (ROHF-UCCSD(T)-F12a/cc-pVDZ-F12) show a substantially lower (∼2.1 kcal mol−1) relative energy for TS7s, in comparison to the restricted open-shell method used for L3 (see Table S11, ESI†). However, since this difference does not change the order of importance among exit reaction channels, uncertainties associated with the use of a ROCCSD(T) method (as opposed to UCCSD(T)95) are not expected to significantly affect branching ratios.
While the formation of electronically-excited RO2 intermediates directly from the association of an alkyl radical with O2 may be possible,96 a thorough exploration of excited-state reaction mechanisms is beyond the scope of this study. We argue, however, that if excited RO2 species are formed from association of 5-OH and O2, the likely major outcome is fast relaxation to the electronic ground state via internal conversion.97 Further discussion is presented in Section S8 of the ESI† alongside test calculations.
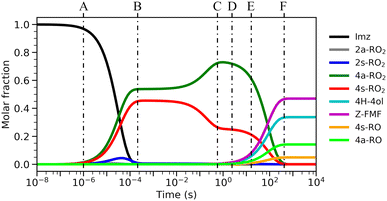
The calculated reaction barrier heights and associated thermal rate coefficients, estimated with TST, for each unimolecular reaction described above are shown in Table 1. To capture the chemical evolution of the first-generation RO2 system, we invoked an RRKM-ME model, in which we also included the reaction of each RO2 radical with NO (Reaction (8)) as loss terms as described in the Methods section, to determine the competition between unimolecular and bimolecular channels. The alkoxyl radicals produced this way are 4a-RO, 4s-RO, 2a-RO and 2s-RO. The simulation results (298 K and 10 ppt NO) are summarized in Fig. 2.
| Reaction step | Description | Δ‡Ev=0 (kcal mol−1) | k LC-TST (s−1) | k MC-TST (s−1) | k MC/kLC | Q TS/QR | κ |
|---|---|---|---|---|---|---|---|
| 2a-RO2 → 4a-RO2 | O2-Migration | 10.05 | 1.69 × 105 | 8.24 × 104 | 0.49 | 0.61 | 1.04 |
| 2a-RO2 → PC5a | HO2-Elimination | 17.57 | 4.14 | 3.05 | 0.74 | 1.67 | 3.02 |
| 4a-RO2 → 2a-RO2 | O2-Migration | 14.04 | 2.01 × 102 | 30.94 | 0.49 | 0.47 | 1.04 |
| 4a-RO2 → PC6a | HO2-Elimination | 24.29 | 1.78 × 10−5 | 5.54 × 10−6 | 0.31 | 1.04 | 1.77 |
| 4a-RO2 → PC5a* | HO2-Elimination* | 21.56 | 3.82 × 10−3 | 1.46 × 10−3 | 0.38 | 1.31 | 3.02 |
| 2s-RO2 → 4s-RO2 | O2-Migration | 11.89 | 2.49 × 104 | 1.05 × 104 | 0.42 | 2.05 | 1.02 |
| 2s-RO2 → PC5s | HO2-Elimination | 19.17 | 0.328 | 0.145 | 0.44 | 2.40 | 2.46 |
| 4s-RO2 → 2s-RO2 | O2-Migration | 14.39 | 3.65 × 102 | 93.6 | 0.42 | 1.54 | 1.02 |
| 4s-RO2 → M7s | 1,5 H-shift | 20.50 | 8.37 × 10−3 | 2.83 × 10−3 | 0.34 | 0.38 | 3.75 |
| 4s-RO2 → PC5s* | HO2-Elimination* | 21.67 | 3.62 × 10−3 | 1.30 × 10−3 | 0.36 | 1.81 | 2.46 |
| M7s → M8s | β-Scission | 0.93 | 1.28 × 1012 | 9.88 × 1011 | 0.77 | 1.03 | 0.96** |
Significantly faster than other competing channels, the O2-migration reactions serve to rapidly establish equilibrium between the 2- and 4-RO2 isomer pairs, highly favoring the 4-RO2 isomers. Past point B in Fig. 2, i.e., after ∼1 ms most of the produced 2a-RO2 and 2s-RO2 radicals have been converted into their respective more stable 4a-RO2 and 4s-RO2 isomers. Due to these fast O2-migration steps, the 4-RO2 isomers also have prompt, indirect access to the HO2-elimination pathways available to the 2-RO2 isomers via TS5a and TS5s.
Equilibrium between the syn and anti 4-RO2 isomers is approached after around 1 s (Fig. 2(C)), with a portion of the 4s-RO2 species being converted into the slightly more stable (∼0.3 kcal mol−1) 4a-RO2, indicating that dissociation of the RO2 adducts back to the reactants (5-OH + O2) is significant. Some studies investigating the reaction of O2 with other resonance stabilized radicals reported a similar behaviour.99 Due to partial or complete loss of resonance stabilization, the RO2 radicals produced in these reactions correspond to relatively shallow wells, leading to faster back-reaction rates. In the absence of other fast RO2 sinks, which seems to be the case during the OH-initiated oxidation of imidazole, the R˙ + O2 ⇄ RO2˙ reaction may approach equilibrium on relatively short timescales. As a consequence, the calculated product yields have a low dependence on the uncertainty in the rate coefficients of the four O2-addition reactions, which were estimated as described in the Methods section.
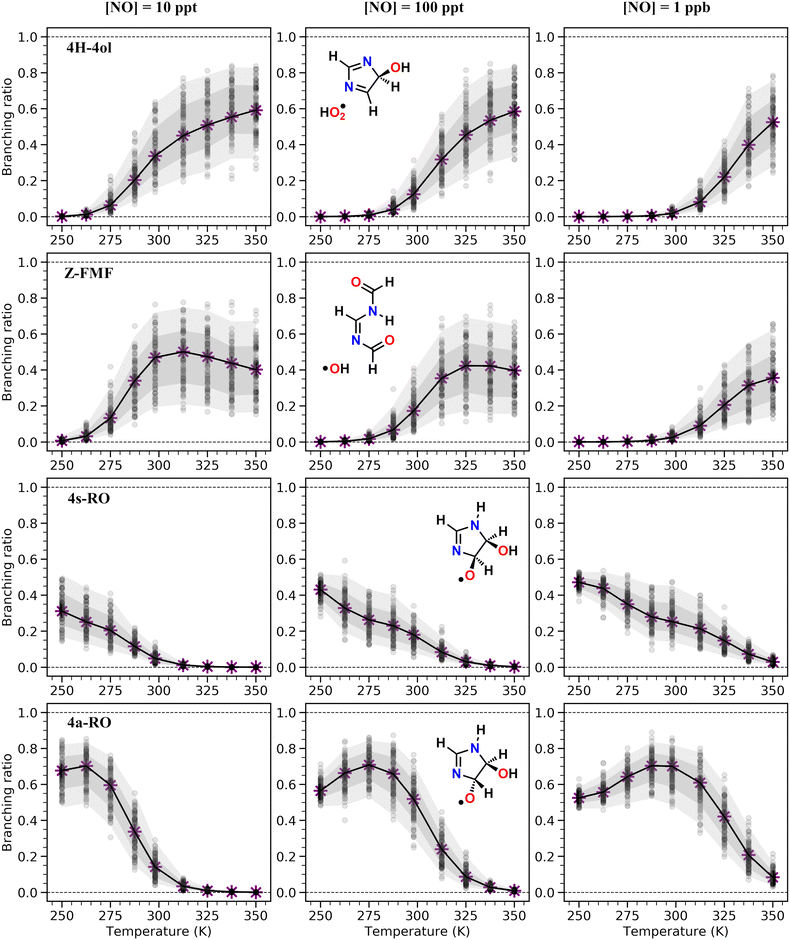
As seen in Table 2 and Fig. 3, results from RRKM-ME calculations show that unimolecular channels via TS5a, TS5s and TS7s, as well as bimolecular RO2 + NO → RO + NO2 channels involving the 4a-RO2 and 4s-RO2 isomers are all competitive at 298 K and 1 atm. The branching ratios of competitive channels are, however, strongly dependent on the NO concentration. We illustrate this effect in Fig. 3, where we show the branching fraction predictions and their uncertainty at various NO concentrations for the main channels. The only negligible channel under most conditions considered here is HO2-elimination via TS6a to produce 5-ol. This finding is in line with other studies indicating that this type of reaction (HO2-elimination involving H-shift from a C atom) is a negligible pathway in the Earth's atmosphere.48,51,59 Production of 5-ol via direct H-abstraction from 5-OH by O2 is also negligible, as confirmed by a test RRKM-ME calculation where this channel was included alongside the RO2 channels.
| Product | Yield (%) (±σ) | ||
|---|---|---|---|
| [NO] = 10 ppt | [NO] = 100 ppt | [NO] = 1 ppb | |
| 5-ol | 0.1 (+0.1−0.0) | 0.0 (+0.1−0.0) | 0.0 (+ 0.1−0.0) |
| 4H-4ol | 33.7 (+15.6−9.4) | 12.4 (+6.4−4.7) | 1.8 (+1.1−0.6) |
| Z-FMF | 47.0 (+11.3−16.6) | 17.3 (+9.2−7.2) | 2.4 (+1.8−1.0) |
| 4s-RO | 4.9 (+2.2−2.3) | 18.1 (+4.4−6.6) | 25.3 (+9.8−6.0) |
| 4a-RO | 14.2 (+5.0−5.9) | 51.9 (+9.9−11.4) | 70.1 (+6.0−11.1) |
| 2-RO | 0.1 (+0.0−0.0) | 0.3 (+0.1−0.1) | 0.4 (+0.1−0.1) |
Under more pristine conditions ([NO] = 10 ppt) unimolecular channels predominate, products 4H-4ol + HO2 and Z-FMF + OH showing yields of 33.7 (+15.6−9.4)% and 47.0 (+11.3−16.6)% respectively at 298 K, whereas bimolecular channels are minor, with products 4a-RO + NO2 and 4s-RO + NO2 showing yields of 14.2 (+5.0−5.9)% and 4.9 (+2.2−2.3)% respectively. Rising NO concentrations are accompanied by a sharp rise in the yield of alkoxyl radicals, which become the major products at intermediate (100 ppt) and high (1 ppb) NO concentration levels. Unlike with unimolecular channels, competition among the four bimolecular channels depends on the relative concentration of the RO2 reactants. Thus, the equilibrium established between the RO2 isomers is reflected on the relative yield of RO products: the yield of 4a-RO is about 3 times larger than that of 4s-RO, while 2a-RO and 2s-RO have a combined yield of only 0.4 (±0.1)% under high NO concentration (1 ppb).
Product yields from first-generation RO2 also display a strong temperature dependence. As expected, unimolecular channels are favored at higher temperatures, while the barrierless bimolecular RO2 + NO → RO + NO2 channels, whose rate coefficients have a weak negative temperature dependence, are favored at lower temperatures. Thus, rising temperatures counteract the effect of rising NO concentrations, as seen in Fig. 3. Also, upwards of 312 K at [NO] = 100 ppt, 4H-4ol becomes the major product, with a yield of 45.5%, surpassing that of Z-FMF (42.4%). While only one reaction channel leads to Z-FMF, two HO2-elimination channels can produce 4H-4ol, both with very similar energy barrier heights and loose transition states (see ratio of TS and reactant partition functions QTS/QR in Table 1). So, as the temperature rises, entropy favors formation of 4H-4ol. The equilibrium with the four RO2 isomers discussed previously is more clearly observed when comparing the RRKM-ME time evolution of concentrations calculated at different temperatures, shown in Fig. S5 (ESI†). Lower temperatures see a delay in the establishment of these equilibria, which is reflected in the ratio of RO stereoisomer yields. At 250 K, RO2 back-reactions are minor and only occur prior to thermalization of the RO2 adducts, seen by the slightly higher concentration of 4a-RO2 relative to 4s-RO2.
The dependence of product yields on pressure is weak, as seen from Table S7 (ESI†), with yields changing by a maximum of ∼0.5% in the 0.1–10 atm range, at 298 K. This possibly indicates that the kinetics for this part of the oxidation mechanism is close to the high-pressure limit, the regime at which TST is applicable.
3.2 Alkoxyl radical products
Given that the alkoxyl radicals 4a-RO and 4s-RO appear to be major products of imidazole oxidation by OH radicals, being competitive even under low NO concentrations, we also investigated their fate in the atmosphere, as illustrated by the PES in Fig. 4. The RO species were assumed to be produced via the following:| 4s-RO2˙ + NO˙ → 4s-ROONO ΔE = −24.8 kcal mol−1 | (13) |
| 4s-ROONO → 4s-RO˙ + NO2˙ ΔE = +12.7 kcal mol−1 | (14) |
| 4a-RO2˙ + NO˙ → 4a-ROONO ΔE = −24.5 kcal mol−1 | (15) |
| 4a-ROONO → 4a-RO˙ + NO2˙ ΔE = +13.4 kcal mol−1 | (16) |
Three initial unimolecular reaction pathways are available to both the syn isomer (via TS12s, TS13s and TS14s) and the anti isomer (via TS12a, TS13a and TS14a) of the major alkoxyl radical intermediate 4-RO. Each of these channels correspond to the cleavage of one of the RO˙ Cα–Xβ bonds (β-scissions), leading to the formation of a carbonyl group and a X-centered radical.
The RO channels involving cleavage of the C–C bond, via TS12a and TS12s, have the lowest associated reaction energy barriers (4.17 and 5.04 kcal mol−1 respectively), and initially lead to different products. In the syn RO isomer, the oxyl and alcohol groups interact with a weak H-bond, which is preserved (and perhaps strengthened) as the C–C bond is broken during reaction via TS12s, as revealed by IRC calculations. Further along the post-TS reaction coordinate, the alcohol hydrogen is spontaneously transferred to the carbonyl oxygen atom in a 1,7 H-shift, producing the C-centered radical M12s. On the other hand, no such intramolecular H-bond is present in the anti RO isomer, and C–C bond scission proceeds with no concerted rearrangements, leading to species M12a. However, torsion about the C˙–N bond in M12a (through transition state TS15a) brings the alcohol group in proximity of the carbonyl, allowing for the 1,7 H-shift to spontaneously occur, thus connecting M12a to M12s via a low torsional barrier (∼3.6 kcal mol−1).
Resonance brought by N-imino and N-amido substitution to the radical center makes species M12s especially stable, being almost 15 kcal mol−1 lower in energy than M12a. M12s is also completely planar and assumes a 8-membered ring-like structure, held together by an intramolecular H-bond. Planarity favors conjugation of the functional groups, but the ring-like conformation requires large bond angles, introducing strain to the system. The H-bond is lost with inversion at the conjugated C–N–C moiety (TS17s), producing species M17s, but it also leads to strain relief while maintaining the planar geometry. As a consequence, M17s is just slightly less stable than M12s, by about 0.6 kcal mol−1.
The channels involving cleavage of the C–N bond, via TS13a and TS13s, have slightly higher reaction energy barriers (9.57 and 7.37 kcal mol−1 respectively), both leading to the same product, the N-centered (amidinyl) radical M13. Similarly, cleavage of the C–H bond (H-elimination) in either RO stereoisomer via TS14a or TS14s leads to the same outcome, the closed-shell product imidazol-4-one (P4) plus an H atom, but crossing much higher reaction barriers (16.02 and 15.38 kcal mol−1 respectively).
All of the C–C and C–N bond scission transition states (TS12a, TS12s, TS13a, and TS13s) are stabilized by release of ring strain, which can explain the low energy barriers observed overall (<10 kcal mol−1). Additionally, TS12a and TS12s are further stabilized by a hyperconjugative interaction of the developing, singly-occupied pC-orbital with the hydroxyl O lone-pair (nO → pC), and to a lesser extent, with the amidine N(H) lone-pair (nN → pC). These interactions can explain the lower C–C bond scission energy barriers relative to C–N bond scissions. The effects underlying the observed difference in reactivity between stereoisomers is less clear, but a tentative explanation could be the presence of an intramolecular H-bond in 4s-RO and the maintenance of such bond in TS12s and TS13s. Similar to what is observed with 4s-RO2, an H-bond between the oxyl and hydroxyl groups in 4s-RO is possible but sub-optimal, due to a constraint imposed by the cyclic structure. This constraint is relaxed as the C–N bond is lengthened in TS13s, allowing for a stronger H-bond, which grants extra stabilization to the transition state. Thus, the energy barrier to C–N bond scission is ∼3 kcal mol−1 lower for 4s-RO than it is for 4a-RO, where no such H-bond is possible.
Subsequent reactions available to the two C-centered radicals (M12a and M12s) and the N-centered radical (M13) produced from the RO β-scission channels were also explored. Several of these reaction pathways were found during reaction search for M12a and M12s. However, most have high (>20 kcal mol−1) associated energy barriers, and are not expected to compete with O2-addition. Thus, for species M12a and M12s, we limited our analysis to the pathways whose reaction barriers are lower in energy than the original RO reactants 4a-RO and 4s-RO. These reactions are included in the PES in Fig. 4.
We also note here that, given the high degree of conjugation present in species M12s and M12a, it is not immediately obvious whether equilibrium between their respective conformations (or E–Z isomers) can be achieved, especially considering the short lifetime of C-centered radicals. For this reason, we treated M12a and M12s as single-conformer species, corresponding to the structures obtained from IRC end-points, connected to TS12a and TS12s respectively. An exhaustive search for reaction paths connecting E–Z isomers would go beyond the scope of this work, but a few critical torsional and inversion transition states were found, either accidentally by KinBot's algorithm (TS15a, TS17a, TS18a) or by manual search (TS17s). Thus, torsional isomerism in species M12a and M12s was treated explicitly, but including only the steps necessary to properly connect reaction channels to either M12a or M12s. For example, one of the reaction channels found is the one leading from species M12a to species M19a, involving a 1,5 H-shift. In order to react in this manner, species M12a must first undergo torsion about the imine C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond (TS17a), followed by torsion about the C˙–N bond (TS18a), leading to species M18a, which may then finally react via H-shift (TS19a) to yield product M19a. The N-inversion transition state TS17s was included in the analysis because, as shall be discussed further in Section 3.3, O2-addition to species M12s or M17s leads to different RO2 radicals which are not necessarily interconnected via low-barrier channels.
N bond (TS17a), followed by torsion about the C˙–N bond (TS18a), leading to species M18a, which may then finally react via H-shift (TS19a) to yield product M19a. The N-inversion transition state TS17s was included in the analysis because, as shall be discussed further in Section 3.3, O2-addition to species M12s or M17s leads to different RO2 radicals which are not necessarily interconnected via low-barrier channels.
Species M12a and M12s may also react by cyclization (via TS16a or TS16s), where the carbonyl O attacks the radical center, forming a 6-membered ring. A more detailed discussion on the cyclization and H-shift channels available to M12a or M12s is provided in Section S2 of the ESI.†
Species M13, the product of RO C–N bond scission, may react further via a 1,4 H-shift (TS20), where the hydrogen is transferred from the α-OH carbon to the imine N, or via a 1,5 H-shift (TS21), where the hydrogen is transferred from the aldehyde group instead.
The calculated reaction barrier heights and associated thermal rate coefficients for the unimolecular channels discussed in this section are shown in Table 3. Product yields obtained from ME calculations at 298.15 K and 1 atm are shown in Table 4. For the sake of limiting computational costs, a separate ME calculation was done for each RO stereoisomer, produced from their respective parent RO2 radical viareactions (13)–(16). Reaction of O2 with C-centered radicals M12a, M12s, M16a, M16s, M17s, M19a, M20, and M21 was treated as a simple bimolecular sink, with a rate coefficient value of kO2 (298 K) = 2 × 10−12 cm3 molecule−1 s−1. Typically, N-centered radicals formed in the atmosphere may also react with O2, NO or NO2 (Reactions (4) and (5)). Reaction of M13 with O2 is expected to lead to the formation of a nitrile plus HO2,100 whereas reaction with NO or NO2 may produce a nitrosamine or a nitramine. Only reaction with O2 was included in the ME modelling for bimolecular loss terms involving M13, but treated as a simple bimolecular sink leading to a single product with a rate coefficient value of 10−16 cm3 molecule−1 s−1, corresponding to an upper limit to rate coefficients typically observed for the reaction of N-centered radicals with O2.47
| Reaction step | Description | Δ‡Ev=0 (kcal mol−1) | k LC-TST (s−1) | k MC-TST (s−1) | k MC/kLC | Q TS/QR | κ |
|---|---|---|---|---|---|---|---|
| 4a-RO → M12a | β-Scission | 4.17 | 5.78 × 109 | 9.01 × 109 | 1.56 | 0.91 | 1.17 |
| 4a-RO → M13 | β-Scission | 9.57 | 6.24 × 105 | 3.90 × 105 | 0.63 | 0.73 | 1.40 |
| 4a-RO → P4 + H | H-Elimination | 16.02 | 6.93 | 5.61 | 0.81 | 0.62 | — |
| 4s-RO → M12s | β-Scission | 5.04 | 1.47 × 109 | 1.00 × 109 | 0.68 | 1.06 | 1.10 |
| 4s-RO → M13 | β-Scission | 7.37 | 2.32 × 107 | 1.58 × 107 | 0.68 | 0.70 | 1.35 |
| 4s-RO → P4 + H | H-Elimination | 15.38 | 48.8 | 33.3 | 0.68 | 1.47 | — |
| M12a → M16a | Cyclization | 7.05 | 6.66 × 106 | 7.43 × 106 | 1.12 | 0.14 | 1.10 |
| M12a → M17a | N-Inversion | 9.65 | 6.37 × 105 | — | 1 | 1.18 | 1.04 |
| M12a → M12s | C–N torsion | 3.58 | 1.35 × 1010 | — | 1 | 0.87 | 1.05 |
| M17a → M18a | C–N torsion | 6.13 | 3.52 × 108 | — | 1 | 1.55 | 1.14 |
| M12s → M16s | Cyclization | 17.30 | 0.212 | — | 1 | 0.13 | 1.29 |
| M12s → M17s | N-Inversion | 11.98 | 7.92 × 103 | — | 1 | 0.73 | 1.05 |
| M13 → M20 | 1,4 H-shift | 17.73 | 56.4 | 39.6 | 0.70 | 0.26 | 351.24 |
| M13 → M21 | 1,5 H-shift | 16.22 | 3.04 × 102 | 2.14 × 102 | 0.70 | 0.51 | 74.58 |
| Product | Yield (%) (±σ) | |
|---|---|---|
| Initial reactant: 4a-RO2 | Initial reactant: 4s-RO2 | |
| M12s-O2/M17s-O2* | 97.8 (+1.0−1.4) | 95.8 (+1.6−3.3) |
| M13-O2 | ∼ 0 | 1.5 (+1.5−0.8) |
| M16a-O2 | 0.4 (+0.3−0.1) | ∼ 0 |
| M19a-O2 | 1.9 (+1.3−0.8) | ∼ 0 |
| M20-O2 | ∼0 | 0.5 (+1.1−0.3) |
| M21-O2 | ∼0 | 2.4 (+1.8−1.4) |
Results from ME calculations revealed that both 4a-RO and 4s-RO react almost solely via their respective C–C bond scission channels, producing species M12a and M12s respectively. For 4s-RO, C–N bond scission (via TS13s) is slightly competitive, with a yield of ∼4.4% at 298 K, whereas it is a negligible channel for the anti isomer (via TS13a). The channels involving C–H bond scission via TS14a and TS14s, expected to be negligible due to their much higher energy barriers, were not included in the ME treatment.
As for the fate of the subsequently produced C-centered radicals, the major loss channel of species M12a is conversion to M12s via bond torsion/H-shift, as described above, with a yield of about 97.4% at 298 K. Thus, the great majority of the RO radicals (either syn or anti) produced from imidazole + OH reacts further leading to the same C-centered radical, M12s. Once formed, M12s can undergo fast N-inversion via TS17s to produce M17s. The only competitive loss channel for M12s and M17s is reaction with O2, yielding second-generation RO2 radicals. These RO2 are the major products from both RO isomers, with summed yields of about 95.7% and 97.4% from 4s-RO and 4a-RO respectively. About 85% of the second-generation RO2 is produced from O2-addition to M17s, whereas 15% is produced from O2-addition to M12s, a distribution which indicates that equilibrium between M12s and M17s is approached, favoring the latter. Due to a less rigid structure, M17s is ∼0.2 kcal mol−1 lower in free energy relative to M12s.
Cyclization constitutes a minor channel for M12a, with a yield of 0.4% at 298 K, and it is negligible for M12s. The H-shift channel initiated via the torsional transition state TS17a is also minor for M12a, but with a slightly higher yield (1.9% at 298 K), despite involving a reaction energy barrier ∼2.6 kcal mol−1 higher than cyclization. This observation, which may be explained by vibrationally hot molecules reacting at non-thermal rates, is further discussed in Section S2 of the ESI.†
Concerning the fate of the N-centered radical M13, results indicate that its reaction with O2 is a minor channel, with a maximum yield of only 1.5% at 298 K from the total 4s-RO, the 1,5 H-shift channel via TS21 being slightly more competitive, with a yield of 2.4%. Reaction of N-centered radicals with NO or NO2 can lead to nitrosamines (RN–NO) or nitramines (RN–NO2) respectively, compounds which are known to be toxic. However, these channels are expected to be negligible for 4s-RO, given that reaction of M13 with O2 is a barely competitive sink, even when assuming an upper limit to the rate coefficient. Under this assumption, reaction with O2 has a pseudo-first order rate coefficient of ∼500 s−1, which is 20 times faster than the upper limit for the rate of reaction with NO or NO2 (∼25 s−1, assuming collision-limit kNOx = 10−10 cm3 molecule−1 s−1 and [NOx] = 10 ppb).
In contrast to what was seen with first-generation RO2, the fate of alkoxyl radicals 4s-RO and 4a-RO shows a weak temperature dependence in the range analysed here (see Tables S3–S5 in the ESI†). Variation in product yields is, at most, just over 1% for 4a-RO, and ∼3% for 4s-RO.
3.3 Second generation peroxyl radicals
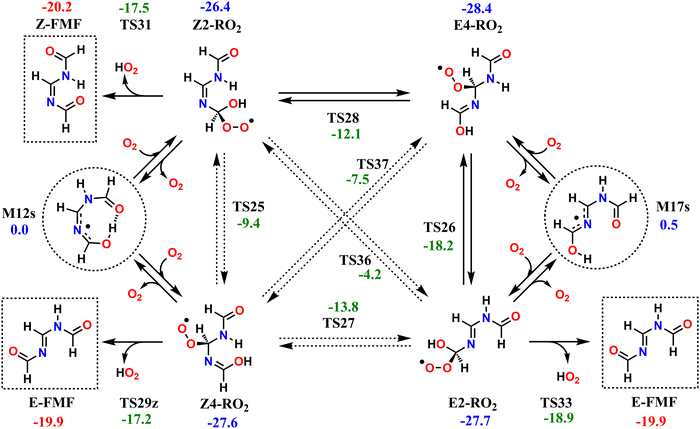
The reaction mechanisms which determine the fate of the second-generation RO2 radicals are seemingly rather complex; however, they all converge to the same outcome. The investigated second-generation RO2, as well as the unimolecular reactions available to these radicals are shown in Scheme 2. Reaction of M12s or M17s (circled in Scheme 2) with O2 may initially lead to two different RO2 products each, depending on which C atom of the conjugated C–N–C moiety O2-addition occurs. O2-addition to M12s may lead to Z2-RO2 or Z4-RO2, while O2-addition to M17s may lead to E2-RO2 or E4-RO2. Analogous to what is observed with the first-generation RO2, an O2-migration step connects the Z-RO2 isomer pair via transition state TS25 and another connects the E-RO2 isomer pair via TS26. Since the α-peroxyl carbon in these RO2 is sp3 hybridized, torsion about the adjacent C–N bond is possible, which allows for two additional connections by O2-migration: TS27 connects E2-RO2 to Z4-RO2 and TS28 connects Z2-RO2 to E4-RO2. Direct connection between E4-RO2 and Z4-RO2 or between E2-RO2 and Z2-RO2 is possible only via imine N-inversion channels (via TS36 and TS37), which have energy barriers too high (>22 kcal mol−1) to be important. KinBot's conformer sampling algorithm accounts for E–Z isomerism in alkenes, but the version used here does not separate those isomers in imines, and for this reason we chose to employ only the reaction search module of the code for second-generation RO2. Conformer sampling and high-level quantum chemistry calculations were done manually.The second-generation RO2 species correspond to significantly deeper wells than the first-generation ones, and most have access to decomposition channels with lower reaction barriers than their O2-migration steps, so rapid equilibrium between RO2 isomers is not achieved. Species Z2-RO2, E2-RO2 and Z4-RO2 can react via HO2-elimination with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double-bond formation, all yielding FMF, the first RO2 producing the (Z) isomer and the latter two producing the (E) isomer. While HO2-elimination in Z2-RO2 and E2-RO2 involves the typical concerted 1,4 H-shift/C–O bond scission, in Z4-RO2 this reaction occurs with a 1,6 span instead, which is possible due to the presence of an imine group between the reacting OH and OO groups. Species E4-RO2 cannot react in this manner, since the OH group is not accessible to the peroxyl group. However, E4-RO2 has access to a low-barrier (10.2 kcal mol−1, via TS26) O2-migration, connecting it to E2-RO2, and granting the former indirect access to the latter's HO2-elimination channel. Reaction channels involving HO2-elimination with C
O double-bond formation, all yielding FMF, the first RO2 producing the (Z) isomer and the latter two producing the (E) isomer. While HO2-elimination in Z2-RO2 and E2-RO2 involves the typical concerted 1,4 H-shift/C–O bond scission, in Z4-RO2 this reaction occurs with a 1,6 span instead, which is possible due to the presence of an imine group between the reacting OH and OO groups. Species E4-RO2 cannot react in this manner, since the OH group is not accessible to the peroxyl group. However, E4-RO2 has access to a low-barrier (10.2 kcal mol−1, via TS26) O2-migration, connecting it to E2-RO2, and granting the former indirect access to the latter's HO2-elimination channel. Reaction channels involving HO2-elimination with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double-bond formation were also found for Z2-RO2, E4-RO2 and Z4-RO2, but these have significantly higher reaction barriers (see Fig. S4, ESI†) and are therefore expected to be negligible.
N double-bond formation were also found for Z2-RO2, E4-RO2 and Z4-RO2, but these have significantly higher reaction barriers (see Fig. S4, ESI†) and are therefore expected to be negligible.
The reaction pathways available to the second-generation RO2 are included in the RRKM-ME modelling for alkoxyl radicals 4s-RO and 4a-RO, connecting the PESs in Fig. 4 and Scheme 2. Results from ME calculations, shown in Table 5, indicate that virtually all of the second-generation RO2 radicals formed in the atmosphere undergo HO2-elimination to yield FMF, about 91% of which formed as the (E) isomer and about 9% as the (Z) isomer. This ratio between E–Z isomers is largely insensitive to the temperature or to the stereochemistry of the precursor RO radical. Nevertheless, the energy barrier of imine N-inversion in FMF is ∼15 kcal mol−1, and inter-conversion between these isomers is relatively fast, with a rate coefficient of ∼100 s−1 at 298 K. Thus, under these conditions, an equilibrium favoring the more stable (Z)-FMF is expected to be established on the time-scales relevant to the fate of this product. A (Z)/(E) ratio of 57/43 is expected at equilibrium, at 298.15 K.
| Product | Yield (%) (±σ) | |
|---|---|---|
| Initial reactant: 4a-RO2 | Initial reactant: 4s-RO2 | |
| E-FMF | 91.2 (+3.4−7.0) | 91.2 (+4.3−7.4) |
| Z-FMF | 8.8 (+6.4−3.3) | 8.8 (+5.4−4.2) |
3.4 Multiple conformer effects
In comparison to the standard lowest-conformer TST, the inclusion of multiple-conformer effects with MC-TST lowers the estimated rate coefficients of most of the studied reactions by a similar factor, as seen from Tables 1, 3, and Table S6 (ESI†). Thus, relying on error cancellation, we expect that the neglect of multiple conformations in the RRKM-ME calculations introduces small errors, which are well within the variation ranges assumed during uncertainty analysis of product distributions. The exceptions to this trend are 4a-RO C–C bond scission (4a-RO → M12a), M12a cyclization (M12a → M16a), O2-migration via TS25 (Z2-RO2 → E2-RO2), and HO2-elimination via TS31. However, apart from cyclization, these reactions are either the only competitive channels for their respective reactants, or much slower than competing channels, so that a slight increase in rate coefficients is not expected to affect product yields. Treatment of multiple-conformations leads to a small increase in the rate coefficient for M12a cyclization (a factor of 1.12) and this reaction competes only with single-conformer channels.3.5 Uncertainties in product yields
Uncertainties in product yields are given as standard deviation ranges in Fig. 3 and Table 2 for first-generation RO2, in Table 4 for the alkoxyl radical products, and in Table 5 for second-generation RO2. The first stage of the oxidation mechanism, involving reactions with the first-generation RO2, is by far the most uncertain when it comes to predicting product yields. The largest sources of uncertainty are likely to be the rates of unimolecular reaction pathways, more specifically, the HO2-elimination steps via TS5a or TS5s and the 1,5 H-shift step via TS7s. The calculated energy barrier heights for these three reactions are very similar (0.8, 1.2 and 0.1 kcal mol−1, relative to 5-OH + O2, for TS5a, TS5s, and TS7s respectively), and therefore a variation of ±0.5 kcal mol−1 to the energy of their transition states can completely alter their order of importance. This is clearly observed from the broad product yield uncertainty ranges under conditions in which unimolecular channels dominate, such as low [NO] and high temperatures.Smaller, but still present, the uncertainty associated with bimolecular RO2 channels is mostly due to the ±0.25 kcal mol−1 variation in the energy of RO2 wells, altering their relative concentrations at equilibrium (or near-equilibrium), than it is to the variation in kNO rate coefficients. The rate coefficients for RO2 + NO reactions are not very sensitive to the identity of the R group,88 hence a small variation range was applied to kNO during the analysis (see Methods section). Surprisingly, variation in the rate coefficients of O2-addition reactions (kO2), which can have values spanning different orders of magnitude, and are unknown for the systems investigated here, had a minimal impact in the overall product yield uncertainty. As discussed in Section 3.1, the equilibrium established (or approached) between the four RO2 isomers nullifies the uncertainties associated with their formation rates. A test RRKM-ME uncertainty analysis at 298 K and [NO] = 100 ppt, applying random variations only to 5-OH + O2 kO2 values, produces negligible uncertainties in product yields, with a maximum standard deviation of +0.03%/−0.05%.
Concerning the latter stage of the oxidation mechanism, the fate of the alkoxyl radical products is much less uncertain, and largely independent of the ratio of stereoisomers produced – 97.8 (+1.0−1.4)% of the 4a-RO and 95.8 (+1.6−3.3)% of the 4s-RO formed react leading to M12s (and M17s), ∼100% of which produces FMF upon O2-addition/HO2-elimination. The ratio of E–Z isomers of FMF produced immediately after oxidative chain termination is somewhat uncertain, however, as discussed in Section 3.3, equilibrium between these isomers is expected to be rapidly established, favoring Z-FMF.
3.6 Comparison to oxidation of similar compounds
Similar to aliphatic N-containing heterocycles whose RO2 chemistry has been studied, such as pyrrolidine,59 piperazine,54 piperidine,101 and 1,2,3,6-tetrahydropyrazine (THP),48 HO2-elimination with imine formation is also an important reaction channel during imidazole OH-initiated gas-phase oxidation. However, unlike with these aliphatic species, this reaction is not the major channel for imidazole, due to a few structural and mechanistic differences, as outlined below.Relative to their respective α-amino RO2 reactants, the reaction barrier heights of HO2-elimination channels in the oxidation of imidazole, pyrrolidine, piperazine, piperidine and THP are all relatively low, with calculated Δ‡E values ranging from 14.4 to 19.2 kcal mol−1. As it seems, a more important factor controlling differences in reactivity here is the well depth of those RO2. The RO2 derivatives of saturated species (pyrrolidine, piperazine, and piperidine), and the β-N-imino RO2 derivative of THP correspond to deep wells (−33.9, −35.4, −35.1, and −33.3 kcal mol−1 respectively), and their respective HO2-elimination barriers are submerged far below the entrance energy level (R˙ + O2), meaning that excess energy imparted to the system during the preceding O2-addition step may propel these reactions to happen at non-thermal rates. On the other hand, since imidazole is an aromatic species whose oxidation is initiated preferentially via OH-addition, rather than via H-abstraction, subsequent O2-addition reactions are bound to be accompanied by loss of resonance stabilization, producing RO2 radicals corresponding to shallower wells. Thus, reaction barriers to HO2-elimination are not submerged for imidazole, albeit nearly so, and non-thermal reactions are less likely. THP is not completely saturated, bearing an endocyclic imine group, and its oxidation shares some characteristics with that of imidazole. The α-C-imino RO2 derivative of THP, whose parent alkyl radical is also resonance stabilized, corresponds to a shallow well (−14.8 kcal mol−1), with its available HO2-elimination channel having a slightly submerged barrier (−0.4 kcal mol−1).48
Another important factor is that O2 attack at the other available site in a parent resonance stabilized alkyl radical can compete with the α-amino substitution required for HO2-elimination. In imidazole, the effect of this competition is partly counteracted by the availability of fast O2-migration channels, which promote an equilibrium between the γ-amino RO2 (4-RO2) and the α-amino RO2 (2-RO2). This means that the γ-amino RO2 species also have access to the HO2-elimination channel, but surpassing a higher reaction energy barrier, since these RO2 correspond to deeper wells. In the oxidation of THP, however, no such competition is possible. In the α-C-imino alkyl radical, resonance occurs at a conjugated C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N moiety, and O2 attack on the nitrogen cannot compete with C-addition.
N moiety, and O2 attack on the nitrogen cannot compete with C-addition.
Finally, the reactivity of imidazole's RO2 derivatives is significantly affected by OH-substitution, which is absent from the aliphatic heterocycles considered in this comparison. The OH group not only grants access to a slightly faster reaction channel, the 1,5 H-shift via TS7s, but it can alter the energetics of competing pathways, via intramolecular H-bonds and steric effects, as discussed in Section 3.1. Moreover, OH-substitution adds further complexity to the oxidation mechanism by introducing stereoisomeric effects.
Many of the characteristics of imidazole's oxidation mechanism are also observed for homocyclic aromatics, such as a OH-addition-initiated oxidation, shallow RO2 wells, and stereoisomeric effects.102,103 The major differences displayed by oxidation of homocyclic aromatics, such as toluene102 and benzene,103 are the absence of competitive HO2-elimination channels, which are in general slower if involving H-shift from a C atom, and the predominance of endo-cyclization reactions leading to bicyclic endoperoxides. Endo-cyclization transition states were found for imidazole's RO2 derivatives during reaction search, but the corresponding energy barriers exceed the 20 kcal mol−1 cutoff at L1. Manual calculations at the L3//L2 level revealed that these reactions indeed cannot be competitive for imidazole's products (see Fig. S1 in the ESI†), with barriers >12 kcal mol−1 relative to 5-OH + O2. The high barriers may be due to the extra ring-strain brought to an already strained five-membered cycle, and the placement the radical center on the less-accommodating nitrogen bridge atom. That being said, a similarly high barrier was found for analogous reactions during the OH-initiated oxidation of THP, a less strained six-membered heterocycle,48 possibly indicating that the channel is unfavorable for N-containing RO2 mainly due to destabilization brought by formation of the N-centered radical.
Perhaps a unique mechanistic feature of the oxidation of imidazole is the availability of O2-migration channels. The molecular structure of the O2-migration transition state TS4a is depicted in Fig. 5. To the best of our knowledge, no such reaction channel has been reported before in mechanistic studies of atmospheric oxidation reactions. As of yet, it is unclear whether these reactions are possible for other N-containing aromatics, but the availability of O2-migrations for the second-generation RO2 studied here indicates that these reactions should only require the formation of α-N-imino RO2 radicals. In the OH-initiated oxidation of oxazole,104 for example, O2-migration is presumably possible and competitive. In the oxidation of pyrrole,105 however, a α-N-imino RO2 cannot be formed, and O2-migration may not be available. Despite this, drawing from knowledge of imidazole's oxidation mechanism, we would expect pyrrole's RO2 derivatives to react preferentially via similar unimolecular channels: HO2-elimination with imine formation and 1,5 H-shift from the alcohol group. A previous computational study105 has investigated the fate of the first-generation RO2 from pyrrole's OH-initiated oxidation, however, neither of these channels were reported. We speculate that these reactions do exist for pyrrole, and could very well be the major loss channels, alongside bimolecular RO2 + NO reactions.
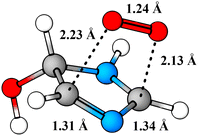 | ||
| Fig. 5 Structure of O2-migration transition state TS4a. C atoms in gray, H atoms in white, O atoms in red, and N atoms in blue. | ||
3.7 Atmospheric implications
Our calculations predict that over 95% of imidazole oxidized by OH radicals in the atmospheric gas-phase, via addition to position C5, leads to oxidative chain termination within two RO2 generations, producing two closed-shell products, the cyclic diimine 4H-4ol and the acyclic amidine FMF. A scheme depicting the overall mechanism of imidazole's OH-initiated oxidation via adduct 5-OH, simplified to include only important reaction steps, is shown in Scheme 3. Relative yields of 4H-4ol and FMF are relatively uncertain and sensitive to NOx concentrations, but the latter species is consistently predicted to be the major product, with ∼66%, ∼85%, and ∼95% yield under 10 ppt, 100 ppt and 1 ppb of NO respectively, at 298 K. The minor product 4H-4ol is predicted to be formed with ∼34%, ∼12%, and ∼2% yield under 10 ppt, 100 ppt and 1 ppb of NO respectively, at 298 K. The reaction channels leading to N-centered radical M13 are minor, with a maximum yield of ∼2% at 298 K and 1 ppb NO, considering the combined uncertainties in product yields. Moreover, subsequent unimolecular reactions available to M13 are fast, leading to C-centered radicals M20 and M21. Thus, we expect that formation of nitrosamines or nitramines via reaction of M13 with NO or NO2 to be negligible. Yield of autoxidation channels, leading to highly functionalized products, is also expected to be negligible. The C-centered radical with the highest yield (M19a), predicted to be formed with a maximum of ∼2% yield at 298 K and 1 ppb NO, has access to a potentially predominant O2-addition/HO2-elimination channel leading to FMF. It is apparent that no matter how complex imidazole's oxidation may be, reaction pathways seem to converge to the formation of the dicarbonyl amidine FMF. In fact, this compound was also proposed as a bio-degradation product of ornidazole,106 an imidazole derivative used as antibiotic.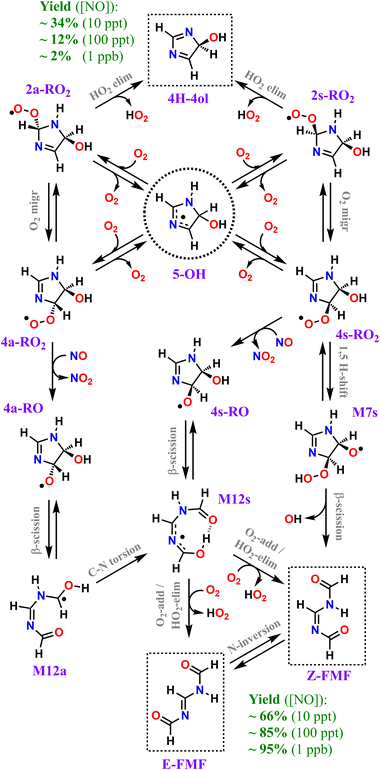 | ||
| Scheme 3 Overall mechanism of OH-initiated oxidation of imidazole via adduct 5-OH. Dashed boxes indicate major products. Minor products and less important reaction steps omitted for clarity. | ||
Concerning the atmospheric implications of the major product FMF, we speculate on its fate in the atmosphere. Upon reaction with another OH radical in the gas-phase, FMF could produce an isocyanate (R–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) via three different initial H-abstraction pathways. Initial H-abstraction by OH radicals from the amide (–NH–CH
O) via three different initial H-abstraction pathways. Initial H-abstraction by OH radicals from the amide (–NH–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) carbon107,108 or nitrogen, followed by O2-addition/HO2-elimination, could both lead to N-formylformimidoyl isocyanate (O
O) carbon107,108 or nitrogen, followed by O2-addition/HO2-elimination, could both lead to N-formylformimidoyl isocyanate (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–N
CH–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–NCO). Similarly, initial H-abstraction/O2-addition at the
CH–NCO). Similarly, initial H-abstraction/O2-addition at the ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–CH
N–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group could lead to the exact same isocyanate, but via a HO2-elimination transition state with a larger 1,6 span, like that observed for Z4-RO2 (TS29z). If, however, the amidine hydrogen is abstracted, and assuming HO2-elimination is both available and competitive for a R–N
O group could lead to the exact same isocyanate, but via a HO2-elimination transition state with a larger 1,6 span, like that observed for Z4-RO2 (TS29z). If, however, the amidine hydrogen is abstracted, and assuming HO2-elimination is both available and competitive for a R–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(OO)–NH–R type radical, it could lead to a carbodiimide (R–N
C(OO)–NH–R type radical, it could lead to a carbodiimide (R–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–R′). Nothing is known about carbodiimides in the atmosphere, however, formation of isocyanates has indeed been reported to be possible from the OH-oxidation of amides107,108 and imines.48 Given that isocyanates are typically toxic, their potential formation from FMF oxidation warrants further investigation. Nevertheless, FMF is likely to be highly water soluble due to a presence multiple H-bond acceptors in its structure, and therefore it may partition into aerosol particles efficiently. Assuming a condensation sink rate typical of more pristine environments (10−4 s−1), and an imidazole concentration of 183 ppt, we estimate a steady-state gas-phase concentration for FMF of up ∼46 ppt. In aerosols, FMF may participate in aqueous-phase reactions with potentially many outcomes. One such reaction, which is perhaps the most important, is amidine hydrolysis leading to formamide plus N-formylformamide. Speculating further, another possibility is the formation of 1,3,5-triazine, a six-membered aromatic compound with three alternated nitrogens, via a multi-step reaction analogous to imidazole's own proposed formation route in aerosols, from reaction of glyoxal with ammonia.19
N–R′). Nothing is known about carbodiimides in the atmosphere, however, formation of isocyanates has indeed been reported to be possible from the OH-oxidation of amides107,108 and imines.48 Given that isocyanates are typically toxic, their potential formation from FMF oxidation warrants further investigation. Nevertheless, FMF is likely to be highly water soluble due to a presence multiple H-bond acceptors in its structure, and therefore it may partition into aerosol particles efficiently. Assuming a condensation sink rate typical of more pristine environments (10−4 s−1), and an imidazole concentration of 183 ppt, we estimate a steady-state gas-phase concentration for FMF of up ∼46 ppt. In aerosols, FMF may participate in aqueous-phase reactions with potentially many outcomes. One such reaction, which is perhaps the most important, is amidine hydrolysis leading to formamide plus N-formylformamide. Speculating further, another possibility is the formation of 1,3,5-triazine, a six-membered aromatic compound with three alternated nitrogens, via a multi-step reaction analogous to imidazole's own proposed formation route in aerosols, from reaction of glyoxal with ammonia.19
4 Conclusions
In this work we used quantum chemistry and theoretical reaction kinetics to investigate the atmospheric gas-phase chemistry of imidazole. We employed an automated kinetics workflow code to explore and characterize the stationary points on the potential energy surface relevant for imidazole's atmospheric oxidation initated by OH-radical addition to position C5, and propagated onwards by RO2 chemistry. We estimated product distributions by assembling and solving a master equation under a range of different atmospheric conditions. The explored mechanism included pathways available to the alkoxyl radical products from RO2 + NO reactions, and the subsequently formed second-generation RO2 radicals. Our calculations predict a complex, branched oxidation mechanism, but with converging pathways leading to two major closed shell species, the cyclic diimine 4H-imidazol-4-ol (4H-4ol) and the acyclic N,N′-diformylformamidine (FMF). Relative yields of 4H-4ol and FMF are strongly dependent on NO concentrations, but the latter species consistently appears as the main product.Overall, we estimate the branching percentage for FMF and 4H-4ol formation from imidazole's oxidation initiated via OH-addition to position C5 to be 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34, 85
34, 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12, and 95
12, and 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 under 10 ppt, 100 ppt and 1 ppb of NO respectively, at 298 K. Under more pristine atmospheric conditions ([NO] = 10 ppt) and 298 K, major reaction channels for first-generation peroxyl radicals are HO2-elimination leading to 4H-4ol (∼34%), a 1,5 H-shift channel followed by β-scission and OH-elimination leading to FMF (∼47%), and RO2 + NO reactions leading to alkoxyl radicals (∼19%). Under more polluted conditions ([NO] = 1 ppb), however, bimolecular reactions with NO dominate (∼96%). The major alkoxyl radical products may further react, the majority (∼96–98%) of which undergoing C–C bond scission, followed by O2-addition/HO2-elimination to yield FMF.
2 under 10 ppt, 100 ppt and 1 ppb of NO respectively, at 298 K. Under more pristine atmospheric conditions ([NO] = 10 ppt) and 298 K, major reaction channels for first-generation peroxyl radicals are HO2-elimination leading to 4H-4ol (∼34%), a 1,5 H-shift channel followed by β-scission and OH-elimination leading to FMF (∼47%), and RO2 + NO reactions leading to alkoxyl radicals (∼19%). Under more polluted conditions ([NO] = 1 ppb), however, bimolecular reactions with NO dominate (∼96%). The major alkoxyl radical products may further react, the majority (∼96–98%) of which undergoing C–C bond scission, followed by O2-addition/HO2-elimination to yield FMF.
Our calculations also revealed the availability of O2-migration reaction pathways for α-N-imino peroxyl radicals. This type of reaction involves a concerted attack of the peroxyl group on the C-terminus of the imine and C–O(O) bond scission, exchanging the positions of the two groups:
RR′C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C(OO)R′′R′′′ ⇄ RR′(OO)C–N N–C(OO)R′′R′′′ ⇄ RR′(OO)C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR′′R′′′ CR′′R′′′ | (17) |
For imidazole's first-generation peroxyl radicals, these reactions are fast (102–105 s−1), and serve to establish equilibrium between the connected RO2 isomers. If available, this mechanism may be important in the atmospheric oxidation of other unsaturated organic nitrogen compounds.
This work provides a detailed description of imidazole chemistry in the atmospheric gas-phase, and may serve as a blueprint to understand the fate of important substituted imidazole compounds, as well as other N-containing aromatics.
Author contributions
Thomas Golin Almeida: conceptualization, methodology, software, validation, formal analysis, investigation, writing – original draft, visualization; Carles Martí: software, writing – review & editing; Theo Kurtén: funding acquisition, supervision, writing – review & editing; Judit Zádor: conceptualization, methodology, software, supervision, writing – review & editing; Sommer L. Johansen: conceptualization, supervision, funding acquisition, writing – review & editing.Data availability
Research data files are available in the CERN Zenodo repository: https://doi.org/10.5281/zenodo.13143561. The raw data (energies, cartesian coordinates, and vibrational frequencies), required to reproduce the results of this work, is available in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Arkke Eskola, Timo Pekkanen, Siddharth Iyer, and Rashid Valiev for insightful discussions on the topic of this work. The work of JZ and CM was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences under the Gas Phase Chemical Physics program. SLJ was supported by the Laboratory Directed Research and Development program at Sandia National Laboratories. The work of TGA and TK was funded by the University of Helsinki (CHEMS) and the Research Council of Finland (center of excellence VILMA, grant no. 346369). Computational resources were provided by CSC – IT Center for Science, in Finland. This article has been authored by employees of National Technology & Engineering Solutions of Sandia, LLC under contract no. DE-NA0003525 with the U.S. Department of Energy (DOE). The employees co-own right, title and interest in and to the article and are responsible for its contents. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this article or allow others to do so, for United States Government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan https://www.energy.gov/downloads/doe-public-access-plan.Notes and references
- X. Ge, A. S. Wexler and S. L. Clegg, Atmos. Environ., 2011, 45, 524–546 CrossRef CAS.
- E. D. Pusfitasari, J. Ruiz-Jimenez, I. Heiskanen, M. Jussila, K. Hartonen and M.-L. Riekkola, Sci. Total Environ., 2022, 808, 152011 CrossRef CAS PubMed.
- E. D. Pusfitasari, J. Ruiz-Jimenez, A. Tiusanen, M. Suuronen, J. Haataja, Y. Wu, J. Kangasluoma, K. Luoma, T. Petäjä, M. Jussila, K. Hartonen and M.-L. Riekkola, Atmos. Chem. Phys., 2023, 23, 5885–5904 CrossRef CAS.
- M. Teich, D. van Pinxteren, S. Kecorius, Z. Wang and H. Herrmann, Environ. Sci. Technol., 2016, 50, 1166–1173 CrossRef CAS PubMed.
- Y. Takao, T. Atarashi, T. Kubo, M. Nagae and T. Nakayama, Asian J. Atmos. Environ., 2019, 13, 259–265 CrossRef CAS.
- M. Teich, M. Schmidtpott, D. van Pinxteren, J. Chen and H. Herrmann, J. Sep. Sci., 2020, 43, 577–589 CrossRef CAS PubMed.
- C. He, H. Wang, D. Gong, S. Lv, G. Wu, R. Wang, Y. Chen, Y. Ding, Y. Li and B. Wang, Sci. Total Environ., 2022, 806, 150804 CrossRef CAS PubMed.
- M. T. Martins-Costa, J. M. Anglada, J. S. Francisco and M. F. Ruiz-López, Chem. Sci., 2022, 13, 2624–2631 RSC.
- M. Hallquist, J. C. Wenger, U. Baltensperger, Y. Rudich, D. Simpson, M. Claeys, J. Dommen, N. Donahue, C. George, A. Goldstein, J. F. Hamilton, H. Herrmann, T. Hoffmann, Y. Iinuma, M. Jang, M. E. Jenkin, J. L. Jimenez, A. Kiendler-Scharr, W. Maenhaut, G. McFiggans, Th. F. Mentel, A. Monod, A. S. H. Prévôt, J. H. Seinfeld, J. D. Surratt, R. Szmigielski and J. Wildt, Atmos. Chem. Phys., 2009, 9, 5155–5236 CrossRef CAS.
- T. Drugé, P. Nabat, M. Mallet, M. Michou, S. Rémy and O. Dubovik, Atmos. Chem. Phys., 2022, 22, 12167–12205 CrossRef.
- D. L. Nelson and M. M. Cox, Lehninger Principles of Biochemistry, W.H. Freeman, New York, NY, 4th edn, 2004 Search PubMed.
- V. B. Silva and E. S. Orth, Quím. Nova, 2021, 44, 318–333 CrossRef CAS.
- M. Galloway, P. Chhabra, A. Chan, J. Surratt, R. Flagan, J. Seinfeld and F. Keutsch, Atmos. Chem. Phys., 2009, 9, 3331–3345 CrossRef CAS.
- D. O. D. Haan, A. L. Corrigan, K. W. Smith, D. R. Stroik, J. J. Turley, F. E. Lee, M. A. Tolbert, J. L. Jimenez, K. E. Cordova and G. R. Ferrell, Environ. Sci. Technol., 2009, 43, 2818–2824 CrossRef PubMed.
- N. Sedehi, H. Takano, V. A. Blasic, K. A. Sullivan and D. O. De Haan, Atmos. Environ., 2013, 77, 656–663 CrossRef CAS.
- X. Lian, G. Zhang, Y. Yang, Q. Lin, Y. Fu, F. Jiang, L. Peng, X. Hu, D. Chen, X. Wang, P. Peng, G. Sheng and X. Bi, Environ. Sci. Technol. Lett., 2020, 8, 9–15 CrossRef.
- G. T. Drozd, K. S.-M. Brown and H. Q. Karp, ACS Earth Space Chem., 2022, 6, 1772–1781 CrossRef CAS.
- J. Kua, H. E. Krizner and D. O. De Haan, J. Phys. Chem. A, 2011, 115, 1667–1675 CrossRef CAS PubMed.
- V. P. Tuguldurova, A. V. Fateev, O. K. Poleshchuk and O. V. Vodyankina, Phys. Chem. Chem. Phys., 2019, 21, 9326–9334 RSC.
- H. Debus, Justus Liebigs Ann. Chem., 1858, 107, 199–208 CrossRef.
- A. Laskin, J. S. Smith and J. Laskin, Environ. Sci. Technol., 2009, 43, 3764–3771 CrossRef CAS PubMed.
- Y. Wang, H. Deng, P. Li, J. Xu, G. Loisel, H. Pang, X. Xu, X. Li and S. Gligorovski, Environ. Sci. Technol. Lett., 2022, 9, 493–500 CrossRef CAS.
- M. van Pinxteren, K. W. Fomba, D. van Pinxteren, N. Triesch, E. H. Hoffmann, C. H. Cree, M. F. Fitzsimons, W. von Tümpling and H. Herrmann, Atmos. Environ., 2019, 203, 183–195 CrossRef CAS.
- T. Moise, J. M. Flores and Y. Rudich, Chem. Rev., 2015, 115, 4400–4439 CrossRef CAS PubMed.
- A. Laskin, J. Laskin and S. A. Nizkorodov, Chem. Rev., 2015, 115, 4335–4382 CrossRef CAS PubMed.
- K. Z. Aregahegn, B. Nozière and C. George, Faraday Discuss., 2013, 165, 123–134 RSC.
- W.-Y. Li, X. Li, S. Jockusch, H. Wang, B. Xu, Y. Wu, W. G. Tsui, H.-L. Dai, V. F. McNeill and Y. Rao, J. Phys. Chem. A, 2016, 120, 9042–9048 CrossRef CAS PubMed.
- S. Szopa, V. Naik, B. Adhikary, P. Artaxo, T. Berntsen, W. Collins, S. Fuzzi, L. Gallardo, A. Kiendler-Scharr, Z. Klimont, H. Liao, N. Unger and P. Zanis, in Short-Lived Climate Forcers, ed. V. Masson-Delmotte, P. Zhai, A. Pirani, S. Connors, C. Péan, S. Berger, N. Caud, Y. Chen, L. Goldfarb, M. Gomis, M. Huang, K. Leitzell, E. Lonnoy, J. Matthews, T. Maycock, T. Waterfield, O. Yelekçi, R. Yu and B. Zhou, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2021, pp. 817–922 Search PubMed.
- D. Spracklen, J. Jimenez, K. Carslaw, D. Worsnop, M. Evans, G. Mann, Q. Zhang, M. Canagaratna, J. Allan, H. Coe, G. McFiggans, A. Rap and P. Forster, Atmos. Chem. Phys., 2011, 11, 12109–12136 CrossRef CAS.
- T. Felber, T. Schaefer and H. Herrmann, J. Phys. Chem. A, 2019, 123, 1505–1513 CrossRef CAS PubMed.
- F. Witte and C. Zetzsch, International Symposium on Gas Kinetics (9th) Held in Bordeaux, France on 20-25 July 1986. Abstracts, 1986.
- A. Samunl and P. Neta, J. Phys. Chem., 1973, 77, 1629–1635 CrossRef CAS.
- K. Bansal and R. Sellers, J. Phys. Chem., 1975, 79, 1775–1780 CrossRef CAS.
- G. Lassmann, L. A. Eriksson, F. Himo, F. Lendzian and W. Lubitz, J. Phys. Chem. A, 1999, 103, 1283–1290 CrossRef CAS.
- J. Llano and L. A. Eriksson, J. Phys. Chem. B, 1999, 103, 5598–5607 CrossRef CAS.
- Z. Safaei, A. Shiroudi, E. Zahedi and M. Sillanpää, Phys. Chem. Chem. Phys., 2019, 21, 8445–8456 RSC.
- T. V.-T. Mai and L. K. Huynh, Phys. Chem. Chem. Phys., 2019, 21, 21162–21165 RSC.
- J. J. Orlando and G. S. Tyndall, Chem. Soc. Rev., 2012, 41, 6294–6317 RSC.
- D. R. Glowacki and M. J. Pilling, ChemPhysChem, 2010, 11, 3836–3843 CrossRef CAS PubMed.
- J. Zádor, C. A. Taatjes and R. Fernandes, Prog. Energy Combust. Sci., 2011, 37, 371–421 CrossRef.
- S. Richters, M. Pfeifle, M. Olzmann and T. Berndt, Chem. Commun., 2017, 53, 4132–4135 RSC.
- J. D. Crounse, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard and P. O. Wennberg, J. Phys. Chem. Lett., 2013, 4, 3513–3520 CrossRef CAS.
- J. D. Savee, E. Papajak, B. Rotavera, H. Huang, A. J. Eskola, O. Welz, L. Sheps, C. A. Taatjes, J. Zádor and D. L. Osborn, Science, 2015, 347, 643–646 CrossRef CAS PubMed.
- F. Bianchi, T. Kurtén, M. Riva, C. Mohr, M. P. Rissanen, P. Roldin, T. Berndt, J. D. Crounse, P. O. Wennberg, T. F. Mentel, J. Wildt, H. Junninen, T. Jokinen, M. Kulmala, D. Worsnop, J. A. Thornton, N. Donahue, H. G. Kjaergaard and M. Ehn, Chem. Rev., 2019, 119, 3472–3509 CrossRef CAS PubMed.
- C. R. Lindley, J. G. Calvert and J. H. Shaw, Chem. Phys. Lett., 1979, 67, 57–62 CrossRef CAS.
- Y. Tang and C. J. Nielsen, Atmos. Environ., 2012, 55, 185–189 CrossRef CAS.
- C. Liu, F. Ma, J. Elm, Z. Fu, W. Tang, J. Chen and H.-B. Xie, Chemosphere, 2019, 237, 124411 CrossRef CAS PubMed.
- T. Golin Almeida and T. Kurtén, ACS Earth Space Chem., 2022, 6, 2453–2464 CrossRef.
- Y. G. Lazarou, K. G. Kambanis and P. Papagiannakopoulos, J. Phys. Chem., 1994, 98, 2110–2115 CrossRef CAS.
- S. Ravnum, E. Rundén-Pran, L. Fjellsbø and M. Dusinska, Regul. Toxicol. Pharmacol., 2014, 69, 250–255 CrossRef CAS PubMed.
- N. Hyttinen, H. C. Knap, M. P. Rissanen, S. Jørgensen, H. G. Kjaergaard and T. Kurten, J. Phys. Chem. A, 2016, 120, 3588–3595 CrossRef CAS PubMed.
- G. da Silva, B. B. Kirk, C. Lloyd, A. J. Trevitt and S. J. Blanksby, J. Phys. Chem. Lett., 2012, 3, 805–811 CrossRef CAS PubMed.
- M. P. Rissanen, A. J. Eskola, T. L. Nguyen, J. R. Barker, J. Liu, J. Liu, E. Halme and R. S. Timonen, J. Phys. Chem. A, 2014, 118, 2176–2186 CrossRef CAS PubMed.
- Z. Ren and G. da Silva, ACS Earth Space Chem., 2019, 3, 2510–2516 CrossRef CAS.
- C. T. Cheng, M. N. Chan and K. R. Wilson, J. Phys. Chem. A, 2016, 120, 5887–5896 CrossRef CAS PubMed.
- M. E. Jenkin, R. Valorso, B. Aumont and A. R. Rickard, Atmos. Chem. Phys., 2019, 19, 7691–7717 CrossRef CAS.
- J. J. Orlando, G. S. Tyndall and T. J. Wallington, Chem. Rev., 2003, 103, 4657–4690 CrossRef CAS PubMed.
- M. E. Jenkin, R. Valorso, B. Aumont, A. R. Rickard and T. J. Wallington, Atmos. Chem. Phys., 2018, 18, 9297–9328 CrossRef CAS.
- J. Zádor, C. Martí, R. Van de Vijver, S. L. Johansen, Y. Yang, H. A. Michelsen and H. N. Najm, J. Phys. Chem. A, 2023, 127, 565–588 CrossRef PubMed.
- M. E. Jenkin, R. Valorso, B. Aumont, A. R. Rickard and T. J. Wallington, Atmos. Chem. Phys., 2018, 18, 9329–9349 CrossRef CAS.
- A. W. Birdsall and M. J. Elrod, J. Phys. Chem. A, 2011, 115, 5397–5407 CrossRef CAS PubMed.
- R. Van de Vijver and J. Zádor, Comput. Phys. Commun., 2020, 248, 106947 CrossRef CAS.
- J. Zádor, R. Van de Vijver, A. Dewyer and C. Martí, KinBot, 2023, https://github.com/zadorlab/KinBot.git Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- K. H. Møller, R. V. Otkjær, N. Hyttinen, T. Kurtén and H. G. Kjaergaard, J. Phys. Chem. A, 2016, 120, 10072–10087 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.02, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- H.-J. Werner and P. J. Knowles, et al., MOLPRO, version 2022.2, a package of ab initio programs Search PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona and D. A. Kreplin, et al. , J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- Spartan'20, Wavefunction, Inc., Irvine, CA, 2020.
- T. A. Halgren, J. Comput. Chem., 1999, 20, 730–748 CrossRef CAS PubMed.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560 CrossRef CAS PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- J. W. Davies, N. J. B. Green and M. J. Pilling, Chem. Phys. Lett., 1986, 126, 373–379 CrossRef CAS.
- S. H. Robertson, M. J. Pilling, D. L. Baulch and N. J. B. Green, J. Phys. Chem., 1995, 99, 13452–13460 CrossRef CAS.
- M. E. Jenkin, R. Valorso, B. Aumont and A. R. Rickard, Atmos. Chem. Phys., 2019, 19, 7691–7717 CrossRef CAS.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- L. S. Tee, S. Gotoh and W. E. Stewart, Ind. Eng. Chem. Fundam., 1966, 5, 356–363 CrossRef.
- K. G. Joback and R. C. Reid, Chem. Eng. Commun., 1987, 57, 233–243 CrossRef CAS.
- L. Vereecken, T. L. Nguyen, I. Hermans and J. Peeters, Chem. Phys. Lett., 2004, 393, 432–436 CrossRef CAS.
- A. Karton, E. Rabinovich, J. M. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 114108 CrossRef PubMed.
- A. Karton, S. Daon and J. M. Martin, Chem. Phys. Lett., 2011, 510, 165–178 CrossRef CAS.
- K. Madajczyk, P. S. Żuchowski, F. Brzek, Ł. Rajchel, D. Kdziera, M. Modrzejewski and M. Hapka, J. Chem. Phys., 2021, 154, 134106 CrossRef CAS PubMed.
- A. V. Copan, H. F. Schaefer III and J. Agarwal, Mol. Phys., 2015, 113, 2992–2998 CrossRef CAS.
- R. R. Valiev and T. Kurten, R. Soc. Open Sci., 2020, 7, 200521 CrossRef CAS PubMed.
- H. S. Johnston and J. Heicklen, J. Phys. Chem., 1962, 66, 532–533 CrossRef.
- T. T. Pekkanen, G. Lendvay, M. Döntgen, R. S. Timonen and A. J. Eskola, Proc. Combust. Inst., 2023, 39, 189–197 CrossRef.
- A. J. C. Bunkan, Y. Tang, S. R. Sellevag and C. J. Nielsen, J. Phys. Chem. A, 2014, 118, 5279–5288 CrossRef CAS PubMed.
- W. Tan, L. Zhu, T. Mikoviny, C. J. Nielsen, A. Wisthaler, B. D’Anna, S. Antonsen, Y. Stenstrøm, N. J. Farren, J. F. Hamilton, G. A. Boustead, T. Ingham and D. E. Heard, J. Phys. Chem. A, 2024, 128, 2789–2814 CrossRef CAS PubMed.
- L. Xu, K. H. Møller, J. D. Crounse, H. G. Kjaergaard and P. O. Wennberg, Environ. Sci. Technol., 2020, 54, 13467–13477 CrossRef CAS PubMed.
- R. Wu, S. Pan, Y. Li and L. Wang, J. Phys. Chem. A, 2014, 118, 4533–4547 CrossRef CAS PubMed.
- A. Shiroudi, M. A. Abdel-Rahman, A. M. El-Nahas and M. Altarawneh, New J. Chem., 2021, 45, 2237–2248 RSC.
- T. V.-T. Mai, H. T. Nguyen and L. K. Huynh, Chemosphere, 2021, 263, 127850 CrossRef CAS PubMed.
- J. Zeng, S. Xu, K. Lin, S. Yao, B. Yang, Z. Peng, T. Hao, X. Yu, T. Zhu, F. Jiang and J. Sun, Water Res., 2024, 249, 120940 CrossRef CAS PubMed.
- N. Borduas, G. da Silva, J. G. Murphy and J. P. Abbatt, J. Phys. Chem. A, 2015, 119, 4298–4308 CrossRef CAS PubMed.
- N. Borduas, J. P. Abbatt, J. G. Murphy, S. So and G. da Silva, Environ. Sci. Technol., 2016, 50, 11723–11734 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational details and cartesian coordinates for optimized molecular geometries. See DOI: https://doi.org/10.1039/d4cp02103g |
| This journal is © the Owner Societies 2024 |