 Open Access Article
Open Access ArticleSpontaneous mirror symmetry breaking in benzil-based soft crystalline, cubic liquid crystalline and isotropic liquid phases†
Tino
Reppe
a,
Silvio
Poppe
a,
Xiaoqian
Cai
b,
Yu
Cao
b,
Feng
Liu
 *b and
Carsten
Tschierske
*b and
Carsten
Tschierske
 *a
*a
aInstitute of Chemistry, Martin Luther University Halle-Wittenberg, Kurt-Mothes-Straße 2, 06120 Halle, Germany. E-mail: carsten.tschierske@chemie.uni-halle.de
bState Key Laboratory for Mechanical Behaviour of Materials, Shaanxi International Research Center for Soft Matter, Xi'an Jiaotong University, Xi'an 710049, P. R. China. E-mail: feng.liu@xjtu.edu.cn
First published on 30th April 2020
Abstract
Benzil (diphenylethane-1,2-dione), which is a long known example for an achiral molecule crystallizing in a chiral space group, can also show mirror symmetry breaking in the fluid state if it is suitably functionalized. For some of the new benzil derivatives even three different subsequent mirror symmetry broken soft matter states with a chiral conglomerate structure can be observed. One is an isotropic liquid, the second one a cubic liquid crystal with a complex network structure and the third is a soft crystalline solid. Chirality develops by helical self-assembly combined with dynamic network formation, thus allowing macroscopic chirality synchronization. These achiral molecules, combining a transiently chiral bent core with multiple alkyl chains, provide a unique link between the mirror symmetry breaking phenomena observed for polycatenar and bent-core mesogens. The homogeneously chiral networks are of interest for application as chiral materials, and as templates for chiral recognition, separation and enantioselective catalysis.
Mirror symmetry breaking and development of uniform chirality is considered essential for the development of life. Understanding and controlling the formation of chirality is crucial across different disciplines. In biosystems the chirality of nucleic acids, sugars and amino acids enables the formation of the helical nanostructures of DNA and proteins.1 Enantioselective synthesis, catalysis and autocatalysis2 were successfully developed during recent decades for the synthesis of enantiopure molecules from achiral precursors. This requires expensive chiral reagents or catalysts, synthesized in multistep processes from the chiral pool of nature. However, there is a more economic approach to homochirality, because it can also emerge spontaneously as a result of physical processes such as crystallization,3 as for example shown for the Viedma ripening,4 where rapidly enantiomerizing racemic mixtures of chiral molecules, or even achiral molecules crystallizing in a chiral space group spontaneously form uniform chiral crystals with optical activity (OA). The combination of generation of chiral centers with deracemization by dynamic crystallization provides a new absolute asymmetric synthesis methodology.5 Likewise, spontaneous chirality can also emerge during the formation of liquid crystalline (LC) phases and even in liquids due to a dynamic process of chirality synchronization,6 which is the subject of this contribution.
One of the most prominent examples of achiral molecules crystallizing in a chiral space group is benzil (1, Fig. 1a), whose OA has been more closely studied than for any other organic crystal.7,8 In the chiral crystal structure the molecules assume a helical conformation with a torsion angle of the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of about α = 110°.7 This twisted (skewed) cisoid conformation is also found as a preferred conformation in the gas phase9 and in solution.10 However, the energy barrier for the rotation around the O
O bond of about α = 110°.7 This twisted (skewed) cisoid conformation is also found as a preferred conformation in the gas phase9 and in solution.10 However, the energy barrier for the rotation around the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is relatively low and in solution or in the melted state it leads to optical inactivity. Thus benzil is a typical transiently chiral molecule capable of mirror symmetry breaking in the crystalline state by Viedma ripening.11
O bond is relatively low and in solution or in the melted state it leads to optical inactivity. Thus benzil is a typical transiently chiral molecule capable of mirror symmetry breaking in the crystalline state by Viedma ripening.11
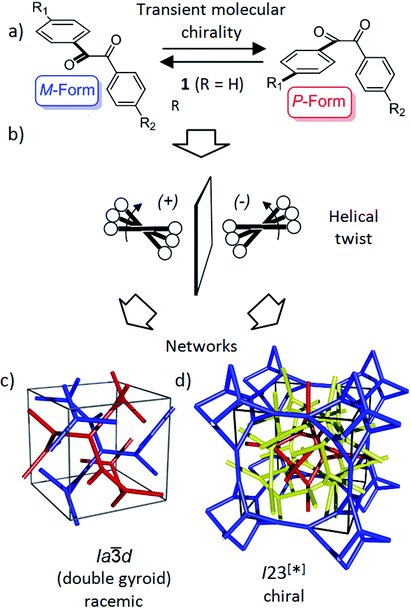 | ||
| Fig. 1 Schematics showing (a) the transient chirality of benzil derived molecules; and (b) the development of the helical twist by clashing of the bulky end groups attached to the cores and (c and d) the network structure of the Cubbi phases under discussion.25 The benzil based polyaromatic cores form the helical networks which are embedded in the continuum filled by the terminal chains. (c and d) were reproduced from ref. 25 by permission of The Royal Society of Chemistry. | ||
Recently, we have observed emergence of OA in bicontinuous cubic (Cubbi) LC phases12 (Fig. 1d) and even in isotropic liquids (Iso1[*]) by formation of conglomerates of chiral domains.13 This OA is related to the helical nano-scale organization of the molecules in these Cubbi and Iso1[*] phases.6 The question arises whether the transient chirality of the benzil unit can support the development of this spontaneous dissymmetry. Moreover, the twisted conformation leads to a non-linear bent shape of the aromatic core, providing some similarity to bent-core molecules, which are also known for their capability of showing mirror symmetry breaking.14–16 In this case besides helix formation the reduction of the phase symmetry to C2v, due to the organization of the tilted molecules with their bent direction parallel to the layer planes (see Fig. S16†), contributes to symmetry breaking.14
Besides the well-known case of lyotropic LCs,17 Cubbi phases are also known to be formed in solvent-free (thermotropic) systems by rod-like polyaromatic molecules with two18,19 or multiple alkyl end-chains (polycatenar compounds),20 branched chains (swallow tailed compounds)21 or other bulky end groups.22 In these Cubbi phases the rods form networks and the alkyl chains fill the space between them (Fig. 1c and d). Within the networks the orientation of the rods is perpendicular or slightly tilted with respect to the local network direction and the mismatch of the cross sectional areas of these cores with the cross sectional area of the terminally attached chains leads to the curvature of the aggregates, and simultaneously, to a helical twist along the networks (Fig. 1b).6,12a There are two major types of such thermotropic Cubbi phases, the double gyroid phase (space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d) and the triple network phase designated as Im
d) and the triple network phase designated as Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Fig. 1c and d).18,23,24 The Ia
m (Fig. 1c and d).18,23,24 The Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase involves two helical networks with opposite handedness (red, blue in Fig. 1c) and therefore it is achiral.12a However, in the Im
d phase involves two helical networks with opposite handedness (red, blue in Fig. 1c) and therefore it is achiral.12a However, in the Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase this degeneracy is broken by the presence of three networks24 and the synchronization of the helix sense between them.12a The chiral space group with the highest symmetry, derived from the achiral Im
m phase this degeneracy is broken by the presence of three networks24 and the synchronization of the helix sense between them.12a The chiral space group with the highest symmetry, derived from the achiral Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group would be I432,12 but the actual space group was recently identified as I23.25 In this new structural model of the “Im
m space group would be I432,12 but the actual space group was recently identified as I23.25 In this new structural model of the “Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m” type Cubbi phase there are three networks with all junctions being threefold, but with distances and twist angles between the junctions being slightly different from those in the Ia
m” type Cubbi phase there are three networks with all junctions being threefold, but with distances and twist angles between the junctions being slightly different from those in the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase (Fig. 1d).
d phase (Fig. 1d).
Herein we report the first mirror symmetry broken LC phases formed by a series of suitably designed multi-chain benzil derivatives (Tables 1 and 2). The decyloxy substituted compounds with a different number of chains are labelled as 2–6 according to their order in Table 1. Compounds 3 have three decyloxy chains at one end and either no chain (compound 3/H) or a single n-alkyloxy chain with a variable length at the other end (compounds 3/n); here the number n after the slash indicates the length of this chain (Table 2). The respective compounds were synthesized as described in Scheme S1† and the experimental procedures are given in the ESI.† Analysis of their self-assembly was performed by polarizing optical microscopy (POM), differential scanning calorimetry (DSC) and X-ray diffraction (XRD). As is obvious from Table 1, with the growing number of n-decyl chains a transition from lamellar (SmC, 2) via two different types of Cubbi phases (Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d, I23[*], 3/10, 4) to hexagonal columnar phases (Colhex, 4, 5) is observed. Only the hexaalkyl substituted compound 6 does not show any LC phase. The SmC and Colhex phases were indicated by their typical birefringent optical textures observed between crossed polarizers (Fig. 2e, h and S2–S5†) and were confirmed by XRD for compounds 2 and 5 (Table S6†). The transition from the isotropic liquid state (Iso) to the Cubbi phases was indicated by a small exotherm in the DSC scans, accompanied by an increase in the viscosity while the phase remained optically isotropic. The cubic phase types are distinguished by optical investigation between polarizers, rotated by a small angle (∼5°) out of the 90° crossed orientation, where only the I23 phase shows a conglomerate of optically active (dark and bright) domains (I23[*] phase), whereas Ia
d, I23[*], 3/10, 4) to hexagonal columnar phases (Colhex, 4, 5) is observed. Only the hexaalkyl substituted compound 6 does not show any LC phase. The SmC and Colhex phases were indicated by their typical birefringent optical textures observed between crossed polarizers (Fig. 2e, h and S2–S5†) and were confirmed by XRD for compounds 2 and 5 (Table S6†). The transition from the isotropic liquid state (Iso) to the Cubbi phases was indicated by a small exotherm in the DSC scans, accompanied by an increase in the viscosity while the phase remained optically isotropic. The cubic phase types are distinguished by optical investigation between polarizers, rotated by a small angle (∼5°) out of the 90° crossed orientation, where only the I23 phase shows a conglomerate of optically active (dark and bright) domains (I23[*] phase), whereas Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d is optically inactive (Fig. 2f and g).12 Interestingly, the Cubbi phase type depends on the chain distribution and the chain length (Tables 1 and 2); for the symmetric compound 4 the achiral Ia
d is optically inactive (Fig. 2f and g).12 Interestingly, the Cubbi phase type depends on the chain distribution and the chain length (Tables 1 and 2); for the symmetric compound 4 the achiral Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase occurs as a monotropic (metastable) phase below Colhex, whereas the non-symmetric compound 3/10 has exclusively a broad range of the mirror symmetry broken I23[*] phase. To the best of our knowledge, these are the first benzil derivatives forming cubic LC phases, whereas a few benzil based compounds involving amide groups were found to form exclusively columnar LC phases.26
d phase occurs as a monotropic (metastable) phase below Colhex, whereas the non-symmetric compound 3/10 has exclusively a broad range of the mirror symmetry broken I23[*] phase. To the best of our knowledge, these are the first benzil derivatives forming cubic LC phases, whereas a few benzil based compounds involving amide groups were found to form exclusively columnar LC phases.26
| Compd. | A | B | D | E | T/°C [ΔH kJ mol−1] |
|---|---|---|---|---|---|
a DSC peak temperatures at 10 K min−1; values in round parantheses indicate monotropic phases, only observed on cooling; abbreviations: Cr = crystalline solid, SmC = tilted lamellar phase, Cubbi/Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d = achiral Cubbi phase with the Ia d = achiral Cubbi phase with the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d space group, Cubbi/I23[*] = mirror symmetry broken Cubbi phase with the I23 space group; Iso = achiral isotropic liquid; Iso1[*] = mirror symmetry broken Iso phase; for DSC traces, see Fig. S1, and for textures, see Fig. S2–S5.
b
d = 3.66 nm.
c Enthalpies of both transitions.
d
a
hex = 4.39 nm. d space group, Cubbi/I23[*] = mirror symmetry broken Cubbi phase with the I23 space group; Iso = achiral isotropic liquid; Iso1[*] = mirror symmetry broken Iso phase; for DSC traces, see Fig. S1, and for textures, see Fig. S2–S5.
b
d = 3.66 nm.
c Enthalpies of both transitions.
d
a
hex = 4.39 nm.
|
|||||
| 2 | H | H | H | H | Cr 149 [27.0] SmCb 243 [12.0] Iso |
| 3/10 | R | R | H | H | Cr 97 [63.2] (CrIso[*] 90 [17.6]) Cubbi/I23[*] 131 [2.2] Iso1 138 [5.7] Iso |
| 4 | R | H | R | H | Cr 151 [69.5] (Cubbi/Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d 141 Colhex 143 [12.4]c) Iso d 141 Colhex 143 [12.4]c) Iso |
| 5 | R | R | R | H | Cr 92 [14.2] Colhexd 105 [7.1] Iso |
| 6 | R | R | R | R | Cr 84 [33.2] Iso |
| 3/n | T/°C [ΔH kJ mol−1] | a cub/nm | n raft | Φ/° | L mol/nm |
|---|---|---|---|---|---|
a DSC peak temperatures on heating/cooling (H/C) at 10 K min−1; nraft = ncell/(Lnet/0.45) with Lnet = 20.68aI23; and Lnet = 8.485aIa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d; Φ(Ia d; Φ(Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d) = 70.5°/[0.354acub/0.45 nm]; Φ(I23) = 90°/[0.290acub/0.45 nm];25Lmol = maximum molecular length as determined with space filling models assuming a molecular bend of 110° and all-trans alkyl chains, see Fig. S15; abbreviations: Iso1 = achiral cybotactic isotropic liquid (see Fig. 3d), Cr = birefringent crystalline solid; CrIso = optically isotropic crystalline mesophase; CrIso[*] = mirror symmetry broken CrIso forming a conglomerate of chiral domains; Ia d) = 70.5°/[0.354acub/0.45 nm]; Φ(I23) = 90°/[0.290acub/0.45 nm];25Lmol = maximum molecular length as determined with space filling models assuming a molecular bend of 110° and all-trans alkyl chains, see Fig. S15; abbreviations: Iso1 = achiral cybotactic isotropic liquid (see Fig. 3d), Cr = birefringent crystalline solid; CrIso = optically isotropic crystalline mesophase; CrIso[*] = mirror symmetry broken CrIso forming a conglomerate of chiral domains; Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) = short pitch Ia d(S) = short pitch Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase with a smaller number of molecules in the unit cell/rafts and a larger twist angle Φ than in Ia d phase with a smaller number of molecules in the unit cell/rafts and a larger twist angle Φ than in Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(L) = long pitch Ia d(L) = long pitch Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase with a larger number of molecules in the unit cell/rafts and a smaller twist angle Φ; for other abbreviations, see Table 1; chiral phases are shown in bold; because the transitions Iso–Iso1 are very broad (see Table S1) it is difficult to determine precise enthalpy values; for DSC traces, see Fig. S1 and for XRD data, see Tables S1–S7 and Fig. S7 and S10–S14. d phase with a larger number of molecules in the unit cell/rafts and a smaller twist angle Φ; for other abbreviations, see Table 1; chiral phases are shown in bold; because the transitions Iso–Iso1 are very broad (see Table S1) it is difficult to determine precise enthalpy values; for DSC traces, see Fig. S1 and for XRD data, see Tables S1–S7 and Fig. S7 and S10–S14.
|
|||||
| 3/H | H: Cr 126 [52.2] Iso | — | — | — | 4.2 |
| C: Iso 110 [27.3] Cr | |||||
| 3/1 | H: Cr 127 [36.3] Iso | — | — | — | 4.3 |
| C: Iso 115 [36.4] Cr | |||||
| 3/2 | H: Cr 120 [37.9] Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(L) 127 [1.8] Iso1 135 [2.8] Iso d(L) 127 [1.8] Iso1 135 [2.8] Iso |
12.9 | 5.0 | 6.9 | 4.4 |
C: Iso 133 [2.7] Iso1 121 [0.2] Iso1[*] 110 [0.3] Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(L) 105 [31.3] Cr d(L) 105 [31.3] Cr |
|||||
| 3/4 | H: Cr 128 [53.5] Iso | 18.4 | 4.0 | 7.6 | 4.6 |
| C: Iso 128 [4.5] Iso1 122 [0.4] Iso1[*] 116 [0.7] I23[*] 73 [21.2] Cr | |||||
| 3/6 | H: Cr 118 [64.6] (CrIso[*] 82 [17.3]) I23[*] 126 [2.2] Iso1 134 [5.7] Iso | 18.1 | 3.8 | 7.7 | 4.8 |
| C: Iso 130 [7.1] Iso1 123 [0.5] Iso1[*] 118 [1.1] I23[*] 61 [15.3] CrIso[*] | |||||
| 3/10 | H: Cr 97 [63.2] (CrIso[*] 90 [17.6]) I23[*] 131 [2.2] Iso1 138 [5.7] Iso | 18.4 | 3.7 | 7.6 | 5.2 |
| C: Iso 135 [5.9] Iso1 127 [0.3] Iso1[*] 122 [0.9] I23[*] 66 [17.8] CrIso[*] | |||||
| 3/12 | H: Cr 114 [47.0] Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) 135 [3.4] Iso1 139 [6.2] Iso d(S) 135 [3.4] Iso1 139 [6.2] Iso |
11.4 | 3.3 | 7.9 | 5.4 |
C: Iso 137 [8.9] Iso1 128 [0.3] Iso1[*] 122 [0.7] Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) 48 [17.9] CrIso < 20 Cr d(S) 48 [17.9] CrIso < 20 Cr |
|||||
| 3/14 | H: Cr 108 [44.1] Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) 135 [2.7] Iso1 138 [7.2] Iso d(S) 135 [2.7] Iso1 138 [7.2] Iso |
11.3 | 3.2 | 7.8 | 5.6 |
C: Iso 136 [9.2] Iso1 129 [1.4] Colhex 125 [0.5] Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) 42 [16.9] CrIso < 20 Cr d(S) 42 [16.9] CrIso < 20 Cr |
|||||
| 3/16 | H: Cr 80 [36.4] Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) 133 [3.1] Iso1139 [6.1] Iso d(S) 133 [3.1] Iso1139 [6.1] Iso |
11.5 | 3.2 | 7.8 | 5.8 |
C: Iso 136 [6.0] Iso1130 [2.3] Colhex 121 [0.5] Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) 45 [25.0] Cr d(S) 45 [25.0] Cr |
|||||
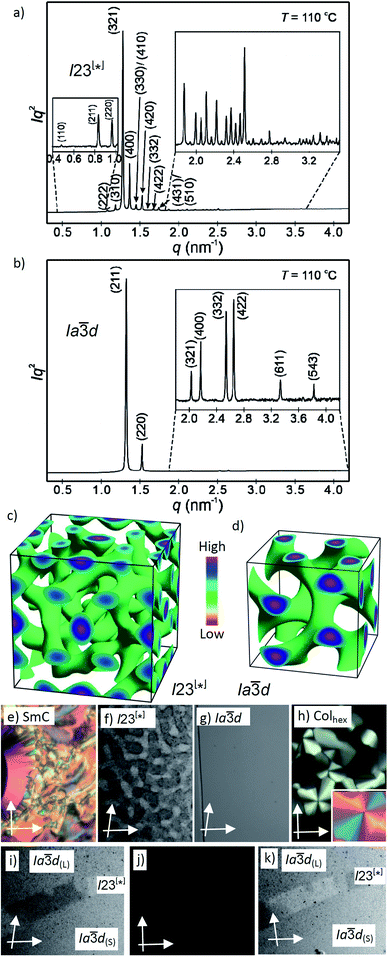 | ||
Fig. 2 (a and b) SAXS diffractograms of the I23[*] (3/4) and the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) (3/16) phases (for the synchrotron source and for numerical data, see Tables S4 and S5;† the full indexations of the I23[*] phase and the WAXS scans are shown in Fig. S7†); (c and d) reconstructed electron density maps of the I23[*] and Ia d(S) (3/16) phases (for the synchrotron source and for numerical data, see Tables S4 and S5;† the full indexations of the I23[*] phase and the WAXS scans are shown in Fig. S7†); (c and d) reconstructed electron density maps of the I23[*] and Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) phase; the aromatic cores are located in the networks formed by the green iso-surfaces, the space between is filled by the alkyl chains; for more details, see the ESI, and Fig. S8† for the individual networks; (e–h) the textures of the (e) SmC phase of 3/10 at 230 °C; (f) the Cubbi/I23[*] phase of 3/10 at 121 °C and (g) Cubbi/Ia d(S) phase; the aromatic cores are located in the networks formed by the green iso-surfaces, the space between is filled by the alkyl chains; for more details, see the ESI, and Fig. S8† for the individual networks; (e–h) the textures of the (e) SmC phase of 3/10 at 230 °C; (f) the Cubbi/I23[*] phase of 3/10 at 121 °C and (g) Cubbi/Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) phase of 3/12 at 120 °C, as observed between slightly uncrossed polarizers; (h) Colhex phase of 3/10 at 141 °C; the inset shows the texture with an additional λ-plate, indicating that the phase is optically negative, i.e. the orientation of the aromatic cores is perpendicular or only slightly tilted to the column long axis; (i–k) show the induced chiral I23[*] phase in the contact region between the achiral Ia d(S) phase of 3/12 at 120 °C, as observed between slightly uncrossed polarizers; (h) Colhex phase of 3/10 at 141 °C; the inset shows the texture with an additional λ-plate, indicating that the phase is optically negative, i.e. the orientation of the aromatic cores is perpendicular or only slightly tilted to the column long axis; (i–k) show the induced chiral I23[*] phase in the contact region between the achiral Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(L) phase of 3/2 (top) and the Ia d(L) phase of 3/2 (top) and the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) phase of 3/16 (bottom); the orientation of the polarizers is shown by white arrows; the width of the POM images in (e–k) is 200 μm, and in (f), (i) and (k) the contrast is enhanced; for additional textures, see also Fig. S2–S6.† d(S) phase of 3/16 (bottom); the orientation of the polarizers is shown by white arrows; the width of the POM images in (e–k) is 200 μm, and in (f), (i) and (k) the contrast is enhanced; for additional textures, see also Fig. S2–S6.† | ||
Here we focus on the homologous series of the non-symmetric tetracatenars 3/n where only 3/H and 3/1 are non-mesomorphic and all the following homologues form Cubbi phases (Table 2). In this series the Cubbi phase type changes from Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d (n = 2) via I23[*] (n = 4–10) to Ia
d (n = 2) via I23[*] (n = 4–10) to Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d again (n = 12–16), upon chain elongation. The high resolution diffraction patterns of the I23[*] phase of 3/4 and the Ia
d again (n = 12–16), upon chain elongation. The high resolution diffraction patterns of the I23[*] phase of 3/4 and the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase of 3/16, recorded with a synchrotron source, are shown as representative examples in Fig. 2a and b. Besides the diffuse wide angle scattering (Fig. S7b and c†), there are several sharp small angle scatterings, the strongest being indexed either to (211) and (220) of the Ia
d phase of 3/16, recorded with a synchrotron source, are shown as representative examples in Fig. 2a and b. Besides the diffuse wide angle scattering (Fig. S7b and c†), there are several sharp small angle scatterings, the strongest being indexed either to (211) and (220) of the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d lattice or (321), (400) and (420) reflections of the I23[*] lattice. The electron density maps (Fig. 2c, d and S9†) reconstructed from these patterns are in agreement with the proposed phase structures shown schematically in Fig. 1c and d. The method of selecting the correct phase combination is described in previous work.12,25,27 The cubic lattice parameter is around 11–13 nm for Ia
d lattice or (321), (400) and (420) reflections of the I23[*] lattice. The electron density maps (Fig. 2c, d and S9†) reconstructed from these patterns are in agreement with the proposed phase structures shown schematically in Fig. 1c and d. The method of selecting the correct phase combination is described in previous work.12,25,27 The cubic lattice parameter is around 11–13 nm for Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d and 18 nm for I23[*], in line with a double- and triple-network structure, respectively. Remarkably, the Ia
d and 18 nm for I23[*], in line with a double- and triple-network structure, respectively. Remarkably, the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d lattice is the largest for the smallest molecule 3/2 (Lmol = 4.4 nm; acub = 12.9 nm) and becomes smaller for the Ia
d lattice is the largest for the smallest molecule 3/2 (Lmol = 4.4 nm; acub = 12.9 nm) and becomes smaller for the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phases of the larger compounds 3/12–3/16 with much longer chains (Lmol = 5.8–6.3 nm; acub = 11.3–11.5 nm).28 In line with this, in the Ia
d phases of the larger compounds 3/12–3/16 with much longer chains (Lmol = 5.8–6.3 nm; acub = 11.3–11.5 nm).28 In line with this, in the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase of 3/2 about 5 molecules are arranged side-by-side in the cross section of the networks, whereas for 3/12–3/16 there are only 3.2 molecules (Tables 2 and S7†). The twist between the molecules in the adjacent rafts with a height of 0.45 nm (Φ) can be calculated as ∼7° in the long pitch Ia
d phase of 3/2 about 5 molecules are arranged side-by-side in the cross section of the networks, whereas for 3/12–3/16 there are only 3.2 molecules (Tables 2 and S7†). The twist between the molecules in the adjacent rafts with a height of 0.45 nm (Φ) can be calculated as ∼7° in the long pitch Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(L) phase of 3/2 and ∼8° for the short pitch Ia
d(L) phase of 3/2 and ∼8° for the short pitch Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) phase of compounds 3/12–3/16 (Table 2). The intermediate homologues 3/4–3/10 escape from forming the Ia
d(S) phase of compounds 3/12–3/16 (Table 2). The intermediate homologues 3/4–3/10 escape from forming the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase by assuming the triple network I23[*] structure instead. The twist in this network is almost constant 7.6–7.7° and between the angles in the Ia
d phase by assuming the triple network I23[*] structure instead. The twist in this network is almost constant 7.6–7.7° and between the angles in the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(L) and Ia
d(L) and Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) phases. The I23[*] phase obviously allows for these twist angles a better fit of the helical pitch length with junction distances and inter-junction twist angles than in the competing Ia
d(S) phases. The I23[*] phase obviously allows for these twist angles a better fit of the helical pitch length with junction distances and inter-junction twist angles than in the competing Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d lattices.12a,25 This phase sequence was also reported for the Cubbi phases of other rod-like molecules18a,19,29 and it is observed in the contact regions between the achiral Ia
d lattices.12a,25 This phase sequence was also reported for the Cubbi phases of other rod-like molecules18a,19,29 and it is observed in the contact regions between the achiral Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(L) and Ia
d(L) and Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) phases of 3/2 and 3/12–3/16, respectively, where a concentration gradient develops, and in a certain concentration range the chiral conglomerate of the I23[*] phase is induced (Fig. 2i–k).29,30
d(S) phases of 3/2 and 3/12–3/16, respectively, where a concentration gradient develops, and in a certain concentration range the chiral conglomerate of the I23[*] phase is induced (Fig. 2i–k).29,30
In addition to the cubic phases, for compounds 3/2–3/12 a mirror symmetry broken isotropic liquid (Iso1[*] phase) occurs as a metastable (monotropic) phase on cooling the achiral Iso phase and replaces a part of the Cubbi phase range (Table 2). The Iso1[*] phase disappears at the transition from n = 12 to 14 right after the transition from I23[*] to Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) occurring from n = 10 to 12. Hence, it can be concluded that the local structure in the Iso1[*] phase is likely to be related to that of the chiral I23[*] triple network (Fig. 1d). Remarkably, for 3/2–3/12 the transition Iso–Iso1[*] takes place in two separate steps, as indicated by the DSC trace of 3/12 (Fig. 3a). A very broad feature within the isotropic liquid range (with a maximum around 137 °C on cooling) indicates the transition from an ordinary isotropic liquid (Iso) to a kind of cybotactic isotropic liquid with a fluctuating local network structure (Iso1),31 which is still achiral (Tables 2 and S1†). With further decrease in the temperature the number of linkages between the clusters increases. Mirror symmetry breaking sets in at the next much sharper transition at 128 °C which we attribute to the transition from the cybotactic to a percolated liquid, after crossing a certain critical density of connectivity between the cybotactic clusters,6a,32 thus leading to a long range transmission of the helical twist, and hence, chirality (Iso1[*]). In the Iso1[*] range the connections are transient and at the next transition at 122 °C they become permanent with formation of the Ia
d(S) occurring from n = 10 to 12. Hence, it can be concluded that the local structure in the Iso1[*] phase is likely to be related to that of the chiral I23[*] triple network (Fig. 1d). Remarkably, for 3/2–3/12 the transition Iso–Iso1[*] takes place in two separate steps, as indicated by the DSC trace of 3/12 (Fig. 3a). A very broad feature within the isotropic liquid range (with a maximum around 137 °C on cooling) indicates the transition from an ordinary isotropic liquid (Iso) to a kind of cybotactic isotropic liquid with a fluctuating local network structure (Iso1),31 which is still achiral (Tables 2 and S1†). With further decrease in the temperature the number of linkages between the clusters increases. Mirror symmetry breaking sets in at the next much sharper transition at 128 °C which we attribute to the transition from the cybotactic to a percolated liquid, after crossing a certain critical density of connectivity between the cybotactic clusters,6a,32 thus leading to a long range transmission of the helical twist, and hence, chirality (Iso1[*]). In the Iso1[*] range the connections are transient and at the next transition at 122 °C they become permanent with formation of the Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d phase (or I23[*] for the shorter homologues, Fig. 3e). In the temperature range of the isotropic liquid phases there is an almost continuous increase in the line width of the small angle XRD scattering (Fig. 3c) and there is also no obvious discontinuity in the viscosity, as indicated by optical microscopy, where all three isotropic liquid phases flow under the influence of gravity. Only at the transition to the cubic phase the material suddenly becomes viscoelastic. The enthalpy of the Iso–Iso1 transition increases with the growing chain length with a distinct jump from n = 4 to 6 (Table 2), in line with improved rod-chain segregation, supporting the cluster formation.
d phase (or I23[*] for the shorter homologues, Fig. 3e). In the temperature range of the isotropic liquid phases there is an almost continuous increase in the line width of the small angle XRD scattering (Fig. 3c) and there is also no obvious discontinuity in the viscosity, as indicated by optical microscopy, where all three isotropic liquid phases flow under the influence of gravity. Only at the transition to the cubic phase the material suddenly becomes viscoelastic. The enthalpy of the Iso–Iso1 transition increases with the growing chain length with a distinct jump from n = 4 to 6 (Table 2), in line with improved rod-chain segregation, supporting the cluster formation.
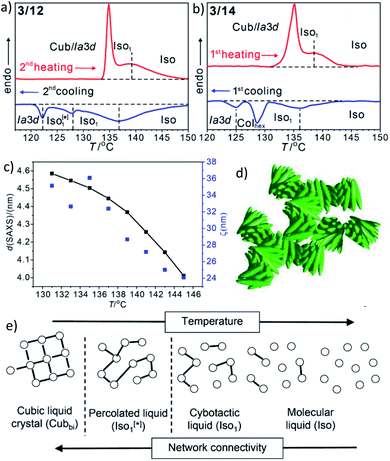 | ||
| Fig. 3 (a and b) sections of the DSC traces (10 K min−1) of compounds 3/12 and 3/14 (see Fig. S1† for complete traces); (c) plot of the d-values (black) and the correlation length (ζ, blue) of the small angle scattering of 3/12 in the isotropic liquid phases (see also Fig. S10 and S11†); (d) sketch of the fused helical clusters in the Iso1[*] phase; (e) schematic sketch showing the transition from Iso via a cybotactic and a percolated liquid to Cubbi by increasing the transient network connectivity; the dots represent locally ordered clusters, the lines indicate the connections between them, and the vertical dotted lines indicate phase transitions. | ||
For the longer homologues 3/14 and 3/16 the Iso1[*] phase is replaced by a Colhex phase (Fig. 3b). The growing chain length obviously disfavours the branching, thus leading to predominately linear aggregates which do not form networks, but assume long range order and transform to the achiral Colhex phase.
Another interesting feature of compounds 3/6–3/10 is that on further cooling from the Cubbi/I23[*] phase a transition to an optically isotropic crystalline mesophase is observed, in which, the conglomerate texture is retained (CrIso[*] phase, see Fig. 4c–f). Because this transition is associated with a change in the XRD pattern and a sharp transition with a significant transition enthalpy of 17–18 kJ mol−1 (Table 2 and Fig. 4g), it cannot be a glass transition. The XRD pattern of the CrIso[*] phase is characterized by a relatively broad small angle scattering, with a maximum at d = 5.38 nm for 3/6 (Fig. 4h) and 5.45 nm for 3/10, approximately corresponding to the lengths of the respective intercalated anti-parallel molecular pairs (5.5 nm, see Fig. S15†). In the wide angle range, there are three broad scatterings with very low intensity (Fig. 4i, S12 and S13†), which can tentatively be attributed to the mean alkyl chain distance (0.44 nm) and the edge-to-edge and face-to-face packing distances of the aromatics (0.56/0.37 nm). This diffraction pattern is similar to those typically recorded for the symmetry broken soft crystalline mesophases of bent-core mesogens, helical nano-filaments (HNFs),16,33a helical nano-crystallites (HNCs)34 and related helical phases,35 which in some respect can be considered as solvent free gels.16,36,37 A transition from the LC Cubbi phase to a soft crystalline network structure, where the polyaromatic rods and parts of the aliphatic chains assume a crystalline packing, appears likely. Similar to the bent-core mesogens, the directed packing of the twisted and bent 4,4′-diphenylbenzil units (Fig. S15†) is likely to contribute to the development of the helical packing modes in the liquid, LC and especially in the soft crystalline mesophases of compounds 3/n. For compounds 3/12 and 3/14, forming the achiral Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) cubic phase instead of I23[*], the isotropic crystalline phase appears to be achiral (CrIso, see Fig. S6†), though the XRD pattern (Fig. S14†) is almost the same as for 3/6 and 3/10. Whether this phase is intrinsically achiral, or the symmetry breaking at the transition from the achiral Ia
d(S) cubic phase instead of I23[*], the isotropic crystalline phase appears to be achiral (CrIso, see Fig. S6†), though the XRD pattern (Fig. S14†) is almost the same as for 3/6 and 3/10. Whether this phase is intrinsically achiral, or the symmetry breaking at the transition from the achiral Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d(S) to a CrIso[*] phase can only develop locally, as the OA domains are too small to be observable by optical investigation, cannot be decided at present.
d(S) to a CrIso[*] phase can only develop locally, as the OA domains are too small to be observable by optical investigation, cannot be decided at present.
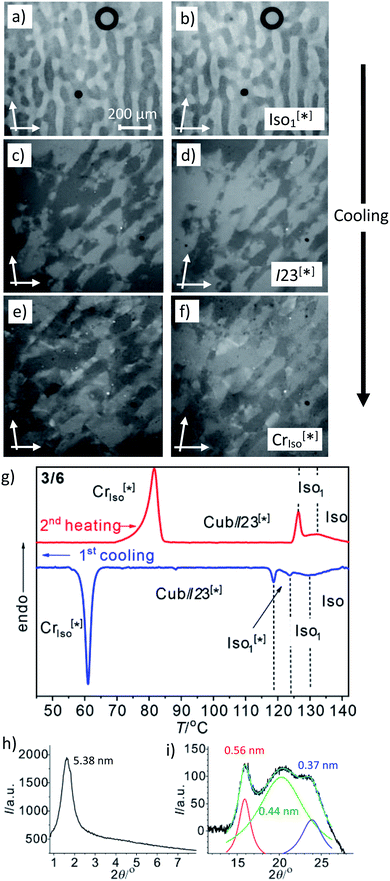 | ||
| Fig. 4 The mirror symmetry broken mesophases of compound 3/6. (a–f) Conglomerates of optically active domains: (a and b) in the liquid Iso1[*] phase at 120 °C; (c and d) in the LC Cubbi/I23[*] phase at 110 °C and (e and f) in the soft crystalline CrIso[*] phase at 60 °C, as observed on cooling between slightly uncrossed polarizers rotated by 5°; (a, c and e) in the anticlockwise and (b, d and f) in the clockwise direction (contrast enhanced). (g) DSC heating and cooling traces (10 K min−1); (h) small angle and (i) wide angle XRD pattern in the CrIso[*] phase at 50 °C (see also Fig. S12† for the complete diffraction pattern and Fig. S13† for the diffraction pattern of 3/10). | ||
In summary, first benzil derivatives forming a series of LC phases, ranging from lamellar via two types of Cubbi phases to columnar, have been obtained. Mirror symmetry breaking is observed in three of the soft matter phases, the isotropic liquid, the liquid crystalline Cubbi/I23[*] phase and in the soft crystalline phase (CrIso[*]). This work contributes to the understanding of the development of mirror symmetry breaking in isotropic liquids as a consequence of network formation and increasing network-connectivity (Fig. 3e). In addition, these molecules with a bend around the central O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond appear to provide the still missing link between the mirror symmetry broken modes of soft self-assembly observed in polycatenars and in bent-core LC systems,6,15,16,33,36b,38 bent mesogenic dimers6,16,36a and oligomers.39 Moreover, as the Iso1[*] and Cubbi/I23[*] phases can provide giant chirality amplification,6,13 the homogeneously chiral crystalline networks, once developed from these spontaneously mirror symmetry broken soft matter states, could be of interest as chiral templates for chiral recognition and separation, and the emerging field of dynamic enantioselective catalysis.37,39,40
O bond appear to provide the still missing link between the mirror symmetry broken modes of soft self-assembly observed in polycatenars and in bent-core LC systems,6,15,16,33,36b,38 bent mesogenic dimers6,16,36a and oligomers.39 Moreover, as the Iso1[*] and Cubbi/I23[*] phases can provide giant chirality amplification,6,13 the homogeneously chiral crystalline networks, once developed from these spontaneously mirror symmetry broken soft matter states, could be of interest as chiral templates for chiral recognition and separation, and the emerging field of dynamic enantioselective catalysis.37,39,40
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (Ts 39/24-2), the National Natural Science Foundation of China (No. 21761132033, 21774099 and 21374086) and the Science and Technology Agency of Shaanxi Province (2016KW-050 and 2018KWZ-03). The authors are grateful to Beamline BL16B1 at SSRF (Shanghai Synchrotron Radiation Facility, China) for providing the beamtime.References
-
A. Guijarro and M. Yus, The Origin of Chirality in the Molecules of Life, RSC, Publishing, Cambridge, 2009 Search PubMed
.
- K. Soai, T. Kawasaki and A. Matsumoto, Chem. Rec., 2014, 14, 70–83 CrossRef CAS
.
- D. B. Amabilino and R. M. Kellogg, Isr. J. Chem., 2011, 51, 1034–1040 CrossRef CAS
.
- C. Viedma, Phys. Rev. Lett., 2005, 94, 065504 CrossRef CAS
; P. Cintas and C. Viedma, Chirality, 2012, 24, 894–898 CrossRef PubMed
; J. E. Hein, B. H. Cao, C. Viedma, R. M. Kellogg and D. G. Blackmond, J. Am. Chem. Soc., 2012, 134, 12629–12636 CrossRef PubMed
.
- R. R. E. Steendam, J. M. M. Verkade, T. J. B. van Benthem, H. Meekes, W. J. P. van Enckevort, J. Raap, F. P. J. T. Rutjes and E. Vlieg, Nat. Commun., 2014, 5, 5543 CrossRef CAS PubMed
; N. Uemura, K. Sano, A. Matsumoto, Y. Yoshida, T. Mino and M. Sakamoto, Chem.–Asian J., 2019, 14, 4150–4153 CrossRef PubMed
.
-
(a) C. Tschierske, Liq. Cryst., 2018, 45, 2221–2252 CrossRef CAS
; (b) C. Tschierske and G. Ungar, ChemPhysChem, 2016, 17, 9–26 CrossRef CAS
.
- C. J. Brown and R. Sadanaga, Acta Crystallogr., 1965, 18, 158–164 CrossRef CAS
.
- T. Kawasaki, Y. Harada, K. Suzuki, T. Tobita, N. Florini, G. Palyi and K. Soai, Chem. Lett., 2008, 10, 4085–4088 CAS
.
- Q. Shen and K. Hagen, J. Phys. Chem., 1987, 91, 1357–1360 CrossRef CAS
.
- Z. Pawelka, A. Koll and T. Zeegers-Huyskens, J. Mol. Struct., 2001, 597, 57–66 CrossRef CAS
.
- D. T. McLaughlin, T. P. Thao Nguyen, L. Mengnjo, C. Bian, Y. H. Leung, E. Goodfellow, P. Ramrup, S. Woo and L. A. Cuccia, Cryst. Growth Des., 2014, 14, 1067–1076 CrossRef CAS
.
-
(a) C. Dressel, F. Liu, M. Prehm, X. B. Zeng, G. Ungar and C. Tschierske, Angew. Chem., Int. Ed., 2014, 126, 13331–13336 CrossRef
; (b) M. Alaasar, S. Poppe, Q. Dong, F. Liu and C. Tschierske, Chem. Commun., 2016, 52, 13869–13872 RSC
.
-
(a) C. Dressel, T. Reppe, M. Prehm, M. Brautzsch and C. Tschierske, Nat. Chem., 2014, 6, 971–977 CrossRef CAS
; (b) C. Dressel, W. Weissflog and C. Tschierske, Chem. Commun., 2015, 51, 15850–15853 RSC
; (c) M. Alaasar, M. Prehm, Y. Cao, F. Liu and C. Tschierske, Angew. Chem., Int. Ed., 2016, 55, 312–316 CrossRef CAS
; (d) M. Alaasar, S. Poppe, Q. Dong, F. Liu and C. Tschierske, Angew. Chem., Int. Ed., 2017, 56, 10801–10805 CrossRef CAS
.
- D. R. Link, G. Natale, R. Shao, J. E. Maclennan, N. A. Clark, E. Korblova and D. M. Walba, Science, 1997, 278, 1924–1927 CrossRef CAS PubMed
.
- R. A. Reddy and C. Tschierske, J. Mater. Chem., 2006, 16, 907–961 RSC
.
- K. V. Le, H. Takezoe and F. Araoka, Adv. Mater., 2017, 1602737 CrossRef
.
-
Bicontinuous Liquid Crystals, ed. M. L. Lynch and P. T. Spicer, CRC Press, Taylor & Francis Group, Boca Raton, FL, 2005 Search PubMed
.
-
(a) S. Kutsumizu, Isr. J. Chem., 2012, 52, 844–853 CrossRef CAS
; (b) G. Ungar, F. Liu and X. B. Zeng, in Handbook of Liquid Crystals, ed. J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. F. Gleeson and P. Raynes, Wiley-VCH, 2nd edn, 2014, vol. 5, pp. 363–436 Search PubMed
.
- Y. Yamamura, Y. Nakazawa, S. Kuzumizu and K. Saito, Phys. Chem. Chem. Phys., 2019, 21, 23705–23712 RSC
.
- H. T. Nguyen, C. Destrade and J. Malthete, Adv. Mater., 1997, 9, 375–388 CrossRef CAS
; D. W. Bruce, Acc. Chem. Res., 2000, 33, 831–840 CrossRef PubMed
.
- I. Nishiyama, Chem. Rec., 2009, 9, 340–355 CrossRef CAS PubMed
; M. Yoneya, Chem. Rec., 2011, 11, 66–76 CrossRef PubMed
.
- E. Nishikawa, J. Yamamoto and H. Yokoyma, J. Mater. Chem., 2003, 13, 1887–1893 RSC
; E. Nishikawa and E. T. Samulski, Liq. Cryst., 2000, 27, 1463–1471 CrossRef CAS
; A. Yoshizawa, Polym. J., 2012, 44, 490–502 CrossRef
; S. Kutsumizu, I. Tokiwa, A. Kawafuchi, Y. Miwa, Y. Yamamura and K. Saito, Phys. Chem. Chem. Phys., 2016, 18, 9013–9020 RSC
.
- A. M. Levelut and M. Clerc, Liq. Cryst., 1998, 24, 105–115 CrossRef CAS
.
- X. B. Zeng, G. Ungar and M. Imperor-Clerc, Nat. Mater., 2005, 4, 562–567 CrossRef CAS
.
- X. B. Zeng and G. Ungar, J. Mater. Chem. C, 2020, 8, 5389–5398 RSC
.
- S. Debnath, H. F. Srour, B. Donnio, M. Fourmigue and F. Camerel, RSC Adv., 2012, 2, 4453–4462 RSC
.
- X. B. Zeng, S. Poppe, A. Lehmann, M. Prehm, C. L. Chen, F. Liu, H. J. Lu, G. Ungar and C. Tschierske, Angew. Chem., Int. Ed., 2019, 58, 7375–7379 CrossRef CAS PubMed
.
- This is in contrast to a previous series of rod-like molecules with only two terminal chains, forming a similar sequence Ia
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d–I23[*]–Ia
d–I23[*]–Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d with the growing chain length, but with an increasing d-value.18a,19.
d with the growing chain length, but with an increasing d-value.18a,19. - T. Reppe, C. Dressel, S. Poppe and C. Tschierske, Chem. Commun., 2020, 56, 711–713 RSC
.
- S. Kutsumizu, S. Miisako, Y. Miwa, M. Kitagawa, Y. Yamamura and K. Saito, Phys. Chem. Chem. Phys., 2016, 18, 17341–17344 RSC
.
- J. W. Goodby, D. A. Dunmur and P. J. Collings, Liq. Cryst., 1995, 19, 703–709 CrossRef CAS
.
- H. R. Brand and H. Pleiner, Eur. Phys. J. E, 2017, 40, 34 CrossRef
.
-
(a) L. E. Hough, H. T. Jung, D. Krüerke, M. S. Heberling, M. Nakata, C. D. Jones, D. Chen, D. R. Link, J. Zasadzinski, G. Heppke, J. P. Rabe, W. Stocker, E. Körblova, D. M. Walba, M. A. Glaser and N. A. Clark, Science, 2009, 325, 456–460 CrossRef CAS
; (b) L. E. Hough, M. Spannuth, M. Nakata, D. A. Coleman, C. D. Jones, G. Dantlgraber, C. Tschierske, J. Watanabe, E. Körblova, D. M. Walba, J. E. Maclennan, M. A. Glaser and N. A. Clark, Science, 2009, 325, 452–456 CrossRef CAS PubMed
.
- M. Alaasar, M. Prehm and C. Tschierske, Chem.–Eur. J., 2016, 22, 6583–6597 CrossRef CAS
; M. Alaasar, M. Prehm, M. Brautzsch and C. Tschierske, J. Mater. Chem. C, 2014, 2, 5487–5501 RSC
; M. Alaasar, M. Prehm, M. Brautzsch and C. Tschierske, Soft Matter, 2014, 10, 7285–7296 RSC
; M. Alaasar, M. Prehm and C. Tschierske, Chem.–Eur. J., 2016, 22, 6583–6597 CrossRef PubMed
.
- S. Shadpour, A. Nemati, N. J. Boyd, L. Li, M. E. Prevot, S. L. Wakerlin, J. P. Vanegas, M. Salamonczyk, E. Hegmann, C. Zhu, M. R. Wilson, A. I. Jakli and T. Hegmann, Mater. Horiz., 2019, 6, 959–968 RSC
.
-
(a) A. Zep, M. Salamonczyk, N. Vaupotic, D. Pociecha and E. Gorecka, Chem. Commun., 2013, 49, 3119–3121 RSC
; (b) J. Matraszek, N. Topnani, N. Vaupotic, H. Takezoe, J. Mieczkowski, D. Pociecha and E. Gorecka, Angew. Chem., Int. Ed., 2016, 55, 3468–3472 CrossRef CAS
.
- Z. Shen, Y. Sang, T. Wang, J. Jiang, Y. Meng, Y. Jiang, K. Okuro, T. Aida and M. Liu, Nat. Commun., 2019, 10, 3976 CrossRef
.
- Cubic phases of bent core mesogens: R. A. Reddy, U. Baumeister, C. Keith, H. Hahn, H. Lang and C. Tschierske, Soft Matter, 2007, 3, 558–570 RSC
; S. Kang, M. Harada, X. Li, M. Tokita and J. Watanabe, Soft Matter, 2012, 8, 1916–1922 RSC
; J. Matraszek, J. Zapala, J. Mieczkowski, D. Pociecha and E. Gorecka, Chem. Commun., 2015, 51, 5048–5051 RSC
.
- A. Yoshizawa and M. Kurata, New J. Chem., 2019, 43, 8865–8868 RSC
.
- Y. Nagata, R. Takeda and M. Suginome, ACS Cent. Sci., 2019, 5, 1235 CrossRef CAS
; S. E. Denmark, ACS Cent. Sci., 2019, 5, 1117–1119 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01396j |
| This journal is © The Royal Society of Chemistry 2020 |


