Open Access Article
Open Access ArticleWhy heterogeneous single-atom catalysts preferentially produce CO in the electrochemical CO2 reduction reaction†
Yu
Wang‡
 ,
Tianyang
Liu‡
and
Yafei
Li
,
Tianyang
Liu‡
and
Yafei
Li
 *
*
Jiangsu Collaborative Innovation Centre of Biomedical Functional Materials, Jiangsu Key Laboratory for Numerical Simulation of Large Scale Complex Systems, School of Chemistry and Materials Science, Nanjing Normal University, Nanjing 210023, China. E-mail: yafeili@njnu.edu.cn
First published on 4th May 2022
Abstract
Formate and CO are competing products in the two-electron CO2 reduction reaction (2e CO2RR), and they are produced via *OCHO and *COOH intermediates, respectively. However, the factors governing CO/formate selectivity remain elusive, especially for metal–carbon–nitrogen (M–N–C) single-atom catalysts (SACs), most of which produce CO as their main product. Herein, we show computationally that the selectivity of M–N–C SACs is intrinsically associated with the CO2 adsorption mode by using bismuth (Bi) nanosheets and the Bi–N–C SAC as model catalysts. According to our results, the Bi–N–C SAC exhibits a strong thermodynamic preference toward *OCHO, but under working potentials, CO2 is preferentially chemisorbed first due to a charge accumulation effect, and subsequent protonation of chemisorbed CO2 to *COOH is kinetically much more favorable than formation of *OCHO. Consequently, the Bi–N–C SAC preferentially produces CO rather than formate. In contrast, the physisorption preference of CO2 on Bi nanosheets contributes to high formate selectivity. Remarkably, this CO2 adsorption-based mechanism also applies to other typical M–N–C SACs. This work not only resolves a long-standing puzzle in M–N–C SACs, but also presents simple, solid criteria (i.e., CO2 adsorption modes) for indicating CO/formate selectivity, which help strategic development of high-performance CO2RR catalysts.
Introduction
Electroreduction of CO2 to produce valuable chemicals via heterogeneous catalysis has emerged as an effective approach to alleviate the ongoing climate crisis caused by massive consumption of fossil fuels.1,2 During a typical CO2 reduction reaction (CO2RR), excess renewable electricity is utilized, and waste CO2 is converted into C1 products including CO, formate/HCOOH, CH4, CH3OH, and C2–C4 products.3–5 Generation of two-electron (2e) products, i.e., CO and formate, is considered a worthwhile endeavour since it proceeds with low overpotentials (e.g., 0.2–0.4 V) and high faradaic efficiencies (∼99%). Moreover, for a given electrical energy input, generating such products is relatively more profitable than the generation of the aforementioned multi-electron products.6,7 However, CO production and formate production are competitive, and there remains a scientific conundrum as to which factors determine the catalytic selectivity.8The issue regarding selectivity is particularly noticeable for a novel class of heterogeneous catalysts, namely metal–carbon–nitrogen (M–N–C) single-atom catalysts (SACs), which are inexpensive and earth-abundant, and they exhibit great potential for facilitating the 2e CO2RR.9 Intriguingly, almost all reported M–N–C SACs produce CO instead of formate as the major product in the 2e CO2RR.10–15 An extreme example is bismuth (Bi), a well-established formate-producing catalyst;16–19 however, when the Bi species is atomically dispersed, the as-prepared Bi–N–C SAC exhibits considerable selectivity toward CO formation.20 Similarly, bulk indium (In) has a high formate selectivity up to 99%,21 while the In–N–C SAC has been observed to produce CO predominantly.22 The apparent ambiguity in CO/formate selectivity seriously hampers strategic optimization of catalytic performance, which calls for a better understanding of the underlying mechanism.
In this work, we address this ambiguity via first-principles computations with explicit consideration of electrode potentials and solvent effects. The CO-producing Bi–N–C SAC and formate-producing Bi nanosheets were chosen as model catalysts with which we can explore the factors that determine the CO2RR selectivity of M–N–C SACs. It is found that the CO2 adsorption mode plays a key role in governing the CO/formate selectivity of the M–N–C catalysts. Under working potentials (U), CO2 displays typical chemisorption behaviour on the Bi–N–C SAC but prefers physisorption on Bi nanosheets. Comprehensive structural and kinetic analyses indicate that protonation of the chemisorbed CO2 (*CO2) preferentially generates the *COOH intermediate instead of the *OCHO intermediate, which makes the Bi–N–C SAC a CO-producing catalyst despite its higher thermodynamic affinity for OCHO*. By contrast, the physisorption preference of CO2 on Bi nanosheets contributes to high formate selectivity. Particularly, this CO2 adsorption-based mechanism is also applicable for other active M–N–C SACs, which rationalizes existing experimental observations.
Results and discussion
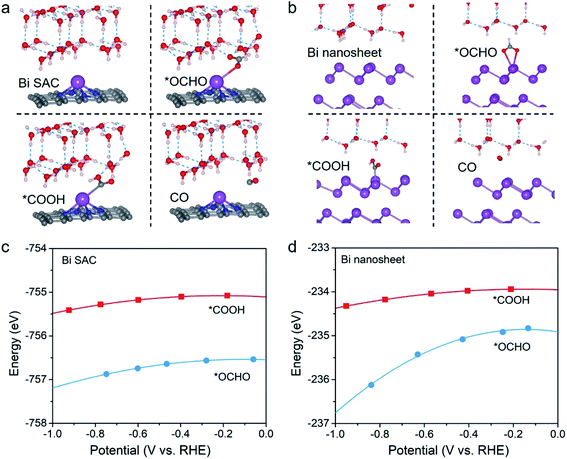
Potential-dependent thermodynamics of the 2e CO2RR on the Bi–N–C SAC and Bi nanosheets
In recent years, a consensus has been achieved for the electrochemical 2e CO2RR, which states that CO generation is associated with the *COOH intermediate, and formate production involves the *OCHO intermediate.23–27 The thermodynamics of *COOH and *OCHO formation have been studied intensively with conventional first-principles modelling (e.g., the constant-charge method), and they have been proposed as criteria to deduce the CO/formate selectivity. For example, it has been proposed that the high formate selectivity of Bi nanosheets can be attributed to their thermodynamic affinity for the key intermediate *OCHO rather than *COOH.28,29 To this end, we first studied the thermodynamics for formation of *COOH and *OCHO on the Bi–N–C SAC, and Bi nanosheets with three-layer thickness were also studied for comparison (Fig. S1†). It is found that *COOH and *COHO on the C and N sites of the Bi–N–C SAC spontaneously move to the Bi sites after structural optimization, and hence we focus on the Bi sites.Considering that the accuracy of the conventional constant-charge method is undermined because it neglects the surface charge effect, we employed a constant-potential/hybrid-solvent approach to explore the thermodynamics of *COOH and *OCHO formation at a solid–liquid interface (see Methods for details). The optimized structures are shown in Fig. 1a and b, while the total energies of *OCHO (E*OCHO) and *COOH (E*COOH) as a function of working potential for the Bi–N–C SAC and Bi nanosheets are shown in Fig. 1c and d, respectively. Please note that the Bi–N–C SAC exhibited good stability during the CO2RR as experimentally demonstrated.20 To obtain theoretical insight into the stability, we computed the dissolution potential (Udis) of the Bi–N–C SAC, defined as Udis = U0Bi + (EBi,bulk − EBi,SAC)/3e, where U0Bi is the standard dissolution potential, EBi,bulk is the energy of one Bi atom in the bulk, and EBi,SAC is the binding energy of one Bi atom in the Bi–N–C SAC. According to our calculations, the Udis of the Bi–N–C SAC is as high as 0.33 V, suggesting that the Bi species is stable under working potentials. In addition, the structural integrity of the Bi–N–C SAC can be well maintained throughout a 10 ps first-principles molecular dynamics simulation at 300 K (Fig. S2†), indicating its high structural stability.
Notably, for both the Bi–N–C SAC and Bi nanosheets, E*OCHO is always lower than E*COOH under working potentials, indicating that the Bi species in these two catalysts have a higher thermodynamic affinity toward *OCHO. The results for Bi nanosheets were consistent with previous experimental measurements16–19,28 and theoretical studies.28,29 However, due to the higher thermodynamic affinity for *OCHO, the Bi–N–C SAC is also thought to have formate selectivity, which contradicts the experimental result.20 Actually, this does not mean that either the theoretical or the experimental results are wrong, since thermodynamic criteria for the selectivity of 2e CO2RR often fail to give the rational indication. For example, silver (Ag)30 and gold (Au)31 are well-established CO-producing catalysts, but they both bind more strongly to *OCHO than to *COOH,23 analogous to the Bi–N–C SAC.
An important question then arises: why is a CO2RR catalyst with higher thermodynamic affinity for *OCHO not guaranteed to produce formate? To address this, we revisited previous thermodynamic computations and mechanistic schemes (Fig. S3†). A detailed examination of modelling results revealed that the thermodynamics of CO2 adsorption and the kinetics of CO2 protonation are usually overlooked or oversimplified. CO2 adsorption is crucial for the CO2RR because CO2 molecules are activated with a net charge on the catalyst surface under a negative working potential. In most thermodynamic calcualtions, the effect of this net charge on the CO2 molecule is neglected, and instead an isolated, inactivated CO2 molecule is studied. Indeed, it has been demonstrated that formation of the chemisorbed CO2 molecule (*CO2) plays a vital role in the CO2RR for numerous catalysts.32–35 Nevertheless, physisorbed CO2 may also contribute to the CO2RR. For example, the one-step reduction process in which physisorbed CO2 reacts with surface-bound *H has been established as the key pathway for formate production.36
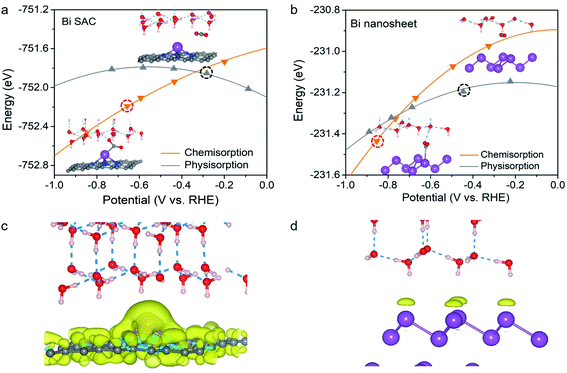
CO2 adsorption mode of the Bi–N–C SAC and Bi nanosheets under working potentials
Based on the above analysis, we shifted our focus to CO2 adsorption on the Bi–N–C SAC and Bi nanosheets at working potentials. Remarkably, the adsorption configuration for CO2 was found to be significantly dependent on the working potential. This is evident in Fig. 2a; at U > −0.33 V, the CO2 molecule maintains its original structure during physisorption on the Bi–N–C SAC, whereas chemisorption is energetically more favourable below a potential of −0.33 V. Therefore, CO2 can be activated on the Bi–N–C SAC to form *CO2 at the working potentials. The as-formed *CO2 would lead to subsequent *COOH formation rather than *OCHO formation. This can be understood intuitively by inspecting the geometric structures of the two intermediates (Fig. S4†). The structures of *CO2 and *COOH share a similar configuration for the O–C–O moiety (exhibiting a V-shaped pattern), suggesting that a transition from the former to the latter is much more likely to occur than the *CO2 to*OCHO transformation, during which the O–C–O moiety must be inverted from a V-shaped pattern to a Λ-shaped pattern. Please note that CO is physisorbed on the Bi–N–C SAC, and the chemisorbed CO state is unavailable at negative potentials (Fig. S5†), indicating that the generated CO species can be easily desorbed from the Bi–N–C SAC.Compared with that on the Bi–N–C SAC, the CO2 molecule on Bi nanosheets adopts a physisorption configuration preferentially, as it is energetically more favourable than the chemisorption configuration over a wide range of potentials (Fig. 2b). It seems that CO2 could also be chemisorbed on Bi nanosheets when the potential is below −0.74 V; however, at such potentials, the surface of the Bi nanosheets would be covered by *H instead of *CO2, and the production of formate proceeds through the surface hydrogenation mechanism.
Why is the adsorption behaviour of CO2 on the Bi–N–C SAC more sensitive to electrode potential than that on Bi nanosheets? In principle, a catalyst can gain net surface charge under negative working potential. For the Bi–N–C SAC, a considerable amount of additional charge is gained and largely located at the Bi site (Fig. 2c). For the Bi nanosheets, the amount of the additional charge is much smaller than that of the Bi–N–C SAC subjected to an equal potential change, and this charge is uniformly distributed on the Bi atoms at the surface (Fig. 2d). Therefore, the chemisorption preference for CO2 on the Bi–N–C SAC should be essentially attributed to the pronounced charge accumulation around the Bi site, which facilitates the adsorption and activation of CO2 to form *CO2.
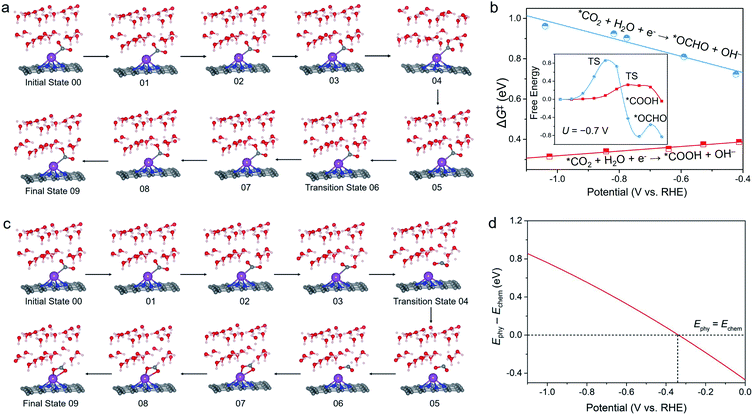
Potential-dependent kinetics analysis
To obtain more insight into the CO selectivity of the Bi–N–C SAC, we investigated the kinetics of *CO2 protonation. Snapshots of the path for protonation of *CO2 to *COOH are shown in Fig. 3a. In accordance with our expectations, the kinetic barrier (ΔG‡) of *COOH formation was found to be much smaller than that of *OCHO formation under working potentials (Fig. 3b). For example, at U = −0.70 V, the ΔG‡ of *COOH formation is only 0.35 eV, which is much lower than that of *OCHO formation (0.85 eV). As with many other electrochemical reactions,37,38 the ΔG‡ of *COOH formation also decreases with increasing negative potential, indicating that the formation of *COOH is kinetically more favourable at high working potentials.Unexpectedly, the ΔG‡ of *CO2-to-*OCHO conversion on the Bi–N–C SAC increases as U increases. This is because to form *OCHO, the chemisorbed CO2 (V-shaped pattern) should first desorb to adopt the physisorption configuration before bending to form an adsorbed O–C–O moiety with the Λ-shaped pattern (Fig. 3c), and specifically, the energy difference between the physisorbed CO2 configuration and chemisorbed CO2 configuration of the Bi–N–C SAC increases with the decrease of U (Fig. 3d). This situation implied that the chemisorbed CO2 configuration of the Bi–N–C SAC is more stable at lower potentials, and the structural conversion from the chemisorbed CO2 configuration to the physisorbed CO2 configuration is more energetically unfavourable, thereby leading to the increased ΔG‡ for *OCHO formation at lower potentials.
The above results vividly indicate that although the formation of *OCHO is thermodynamically favourable on the Bi–N–C SAC, it would be significantly suppressed by the formation of *COOH due to kinetic factors. In contrast, for Bi nanosheets, the kinetic results based on the surface hydrogenation mechanism reveal that *OCHO formation is kinetically more favourable than *COOH formation (Fig. S6†), which is consistent with the thermodynamic data (Fig. 1d). For instance, at U = −0.74 V, ΔG‡ of *OCHO formation is 0.65 eV, which is much lower than that of *COOH formation (0.94 eV). Overall, the above results demonstrate that the CO/formate selectivities of the Bi–N–C SAC and Bi nanosheets are intrinsically associated with the CO2 adsorption mode.
CO2 adsorption mode serving as the criteria for indicating the 2e selectivity of other typical M–N–C SACs
Although only the Bi–N–C SAC was explicitly investigated in the present study, the CO2 adsorption mode-based criteria are expected to be applicable to many other M–N–C SACs that show high CO selectivity. This is because that these M–N–C SACs should also exhibit charge accumulation effects under working potentials, which would promote CO2 chemisorption and, from a kinetic perspective, protonation of *CO2 to give *COOH. For this reason, we have evaluated the CO2 adsorption performance of four M–N–C SACs (M = Fe, Co, Ni, and In), which are the most commonly studied SACs for the CO2RR in the literature.12–15,22 As expected, the CO2 molecule adopts a chemisorption configuration on all of these M–N–C SACs under working potentials (Fig. 4), which should contribute to high CO selectivity in the 2e CO2RR.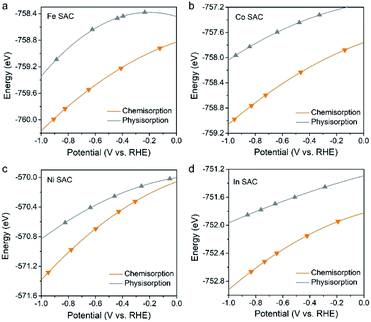 | ||
| Fig. 4 Calculated total energies of chemisorbed and physisorbed CO2 on the (a) Fe–N–C, (b) Co–N–C, (c) Ni–N–C, and (d) In–N–C SACs as a function of potential. | ||
Further kinetic results also reveal that protonation of the chemisorbed CO2 to *COOH is kinetically much more favourable than that to *OCHO, as shown in Fig. S7–S9,† where the Co–N–C SAC was explored as an example due to the high computational cost. Therefore, it is not surprising that almost all M–N–C SACs were observed to produce CO instead of formate as their main product in the 2e CO2RR. In contrast, the general criteria based on the thermodynamics of *COOH/*OCHO incorrectly indicate the selectivities of M–N–C SACs (M = Co, Ni, and In) (Fig. S10†).
To provide more insight into the CO2 adsorption mode-based criteria, we also explored the CO2 adsorption on the well-established Au and Ag catalysts of which the selectivity is incorrectly indicated by the thermodynamics of *COOH/*OCHO. As shown in Fig. S11,† Au and Ag preferentially adopt the CO2 chemisorption configuration under typical working potentials, indicating that the CO2 adsorption mode-based criteria also apply to Au and Ag.
Conclusions
To summarize, a fundamental understanding of the high CO selectivity of heterogeneous M–N–C SACs has been provided in this work by means of constant-potential first-principles computations. It was found that under working potentials, the metal sites of M–N–C SACs are subjected to a charge accumulation effect, which would facilitate chemisorption of CO2 molecules. Although the formation of *OCHO is thermodynamically favoured, the chemisorbed *CO2 tends to be protonated to form *COOH rather than *OCHO due to the more favourable kinetics, and this ultimately leads to high CO selectivity. Our work provides new mechanical insights into the selectivity of the 2e CO2RR, which resolves a long-standing puzzle in M–N–C SACs. We expect our findings to provide useful guidance for improving the selectivity of M–N–C SACs as well as other catalysts for the CO2RR.Methods
First-principles calculations
Spin-polarized first-principles calculations were performed using the projector-augmented wave approach,39 as implemented in the Vienna Ab initio Simulation Package (VASP).40,41 The electronic exchange–correlation energy was modelled using the BEEF-vdW functional,42 which provides a good description of the intermediate adsorption. A k-space sampling of 3 × 3 × 1 and a cutoff energy of 400 eV were adopted in all calculations. The convergence thresholds for energy and atomic forces were set as 5 × 10−5 eV and 0.01 eV Å−1, respectively. For M–N–C SACs (M = Bi, Fe, Co, and In), a typical MN4-embedded graphene slab was constructed, which contains 44 carbon atoms, 4 pyridine-type nitrogen atoms, and 1 metal atom. There is still a debate about the active moiety of the Ni–N–C SAC, and herein a pyrrole-type NiN4 moiety is adopted due to its favourable formation energy. For Bi nanosheets, according to previous studies,28,29 a (2 × 2) Bi trilayer slab was modelled; the top two layers plus adsorbates are allowed to relax freely, while the bottom layer is fixed. For Au and Ag, the typical (111) slabs with a (2 × 2 × 4) supercell were constructed, where bottom two layers were frozen during structural optimization. The vacuum space of the slabs was set as ∼30 Å to minimize interactions between periodic images. An explicit water bilayer was constructed to describe the solvation effect.Constant-potential computations
The Poisson–Boltzmann implicit solvation model was used to establish the relationship between charge (adding or removing extra electrons into the slab) and electrode potential (U).43,44 This method takes advantage of that the electro-static potential goes to zero in the electrolyte region. For each reaction species, independent calculations with five different system charges were performed. For a charged slab, the potential with respect to the standard hydrogen electrode (SHE) was calculated by:| USHE = Wf/e − 4.6 V |
Physisorbed and gas-phase CO2 (+0.33 eV) and H2 (+0.09 eV) have been corrected to account for the error in the description of the OCO backbone and H2 configuration.50 The free energy of each species, G(U), was determined by further considering the zero-point energy (EZPE) and entropy (−TS) contributions, which are derived from vibrational frequency analysis.
Kinetics computations
The transition states were obtained by using the climbing-image nudged elastic band (CI-NEB) approach.51 A set of CI-NEB calculations with different charges was performed to assess the potential-dependent barriers. All transition states were verified by vibrational frequency calculations (only one imaginary frequency).Data availability
The computational data supporting the findings can be found in the article and ESI,† and are available from the authors upon reasonable request.Author contributions
Y. L. designed the research. W. Y. and T. L. performed all the computations. All authors analysed the data and wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Liming You for productive discussions. The authors are grateful for funding support from the National Key R&D Program of China (2019YFA0308000), the Natural Science Foundation of China (No. 22173048) and the Priority Academic Program Development of Jiangsu Higher Education Institutions.References
- Y. Y. Birdja, E. Pérez-Gallent, M. C. Figueiredo, A. J. Göttle, F. Calle-Vallejo and M. T. Koper, Nat. Energy, 2019, 4, 732–745 CrossRef CAS.
- I. Sullivan, A. Goryachev, I. A. Digdaya, X. Li, H. A. Atwater, D. A. Vermaas and C. Xiang, Nat. Catal., 2021, 4, 952–958 CrossRef CAS.
- Y. Zheng, A. Vasileff, X. Zhou, Y. Jiao, M. Jaroniec and S.-Z. Qiao, J. Am. Chem. Soc., 2019, 141, 7646–7659 CrossRef CAS PubMed.
- X. Zhi, Y. Jiao, Y. Zheng, A. Vasileff and S.-Z. Qiao, Nano Energy, 2020, 71, 104601 CrossRef CAS.
- S. Agarwal and A. K. Singh, ACS Appl. Mater. Interfaces, 2022, 14, 11313–11321 CrossRef CAS PubMed.
- N. Han, P. Ding, L. He, Y. Li and Y. Li, Adv. Energy Mater., 2020, 10, 1902338 CrossRef CAS.
- M. G. Kibria, J. P. Edwards, C. M. Gabardo, C.-T. Dinh, A. Seifitokaldani, D. Sinton and E. H. Sargent, Adv. Mater., 2019, 31, 1807166 CrossRef PubMed.
- X. Zhi, A. Vasileff, Y. Zheng, Y. Jiao and S.-Z. Qiao, Energy Environ. Sci., 2021, 14, 3912–3930 RSC.
- A. S. Varela, W. Ju, A. Bagger, P. Franco, J. Rossmeisl and P. Strasser, ACS Catal., 2019, 9, 7270–7284 CrossRef CAS.
- Y. Cheng, S. Yang, S. P. Jiang and S. Wang, Small Methods, 2019, 3, 1800440 CrossRef.
- T. N. Nguyen, M. Salehi, Q. V. Le, A. Seifitokaldani and C. T. Dinh, ACS Catal., 2020, 10, 10068–10095 CrossRef.
- C. Zhao, Y. Wang, Z. Li, W. Chen, Q. Xu, D. He, D. Xi, Q. Zhang, T. Yuan and Y. Qu, Joule, 2019, 3, 584–594 CrossRef CAS.
- J. Gu, C.-S. Hsu, L. Bai, H. M. Chen and X. Hu, Science, 2019, 364, 1091–1094 CrossRef CAS PubMed.
- W. Ju, A. Bagger, G.-P. Hao, A. S. Varela, I. Sinev, V. Bon, B. R. Cuenya, S. Kaskel, J. Rossmeisl and P. Strasser, Nat. Commun., 2017, 8, 944 CrossRef PubMed.
- P. Hou, W. Song, X. Wang, Z. Hu and P. Kang, Small, 2020, 16, 2001896 CrossRef CAS PubMed.
- D. Yao, C. Tang, A. Vasileff, X. Zhi, Y. Jiao and S.-Z. Qiao, Angew. Chem., Int. Ed., 2021, 60, 18178–18184 CrossRef CAS PubMed.
- J. Fan, X. Zhao, X. Mao, J. Xu, N. Han, H. Yang, B. Pan, Y. Li, L. Wang and Y. Li, Adv. Mater., 2021, 33, 2100910 CrossRef CAS PubMed.
- S. He, F. Ni, Y. Ji, L. Wang, Y. Wen, H. Bai, G. Liu, Y. Zhang, Y. Li, B. Zhang and H. Peng, Angew. Chem., Int. Ed., 2018, 57, 16114–16119 CrossRef CAS PubMed.
- S. Kim, W. J. Dong, S. Gim, W. Sohn, J. Y. Park, C. J. Yoo, H. W. Jang and J.-L. Lee, Nano Energy, 2017, 39, 44–52 CrossRef CAS.
- E. Zhang, T. Wang, K. Yu, J. Liu, W. Chen, A. Li, H. Rong, R. Lin, S. Ji, X. Zheng, Y. Wang, L. Zheng, C. Chen, D. Wang, J. Zhang and Y. Li, J. Am. Chem. Soc., 2019, 141, 16569–16573 CrossRef CAS PubMed.
- J. Li, M. Zhu and Y.-F. Han, ChemCatChem, 2021, 13, 514–531 CrossRef CAS.
- W. Guo, X. Tan, J. Bi, L. Xu, D. Yang, C. Chen, Q. Zhu, J. Ma, A. Tayal, J. Ma, Y. Huang, X. Sun, S. Liu and B. Han, J. Am. Chem. Soc., 2021, 143, 6877–6885 CrossRef CAS PubMed.
- J. S. Yoo, R. Christensen, T. Vegge, J. K. Nørskov and F. Studt, ChemSusChem, 2016, 9, 358–363 CrossRef CAS PubMed.
- J. T. Feaster, C. Shi, E. R. Cave, T. Hatsukade, D. N. Abram, K. P. Kuhl, C. Hahn, J. K. Nørskov and T. F. Jaramillo, ACS Catal., 2017, 7, 4822–4827 CrossRef CAS.
- Q. Tang, Y. Lee, D.-Y. Li, W. Choi, C. W. Liu, D. Lee and D.-E. Jiang, J. Am. Chem. Soc., 2017, 139, 9728–9736 CrossRef CAS PubMed.
- S. Back, J. Lim, N.-Y. Kim, Y.-H. Kim and Y. Jung, Chem. Sci., 2017, 8, 1090–1096 RSC.
- H. Yuan and Z. Li, J. Phys. Chem. C, 2021, 125, 18180–18186 CrossRef CAS.
- N. Han, Y. Wang, H. Yang, J. Deng, J. Wu, Y. Li and Y. Li, Nat. Commun., 2018, 9, 1320 CrossRef PubMed.
- W. Oh, C. K. Rhee, J. W. Han and B. Shong, J. Phys. Chem. C, 2018, 122, 23084–23090 CrossRef CAS.
- Y. Chen, C. W. Li and M. W. Kanan, J. Am. Chem. Soc., 2012, 134, 19969–19972 CrossRef CAS PubMed.
- Q. Lu, J. Rosen, Y. Zhou, G. S. Hutchings, Y. C. Kimmel, J. G. Chen and F. Jiao, Nat. Commun., 2014, 5, 3242 CrossRef PubMed.
- S. Vijay, W. Ju, S. Brückner, S.-C. Tsang, P. Strasser and K. Chan, Nat. Catal., 2021, 4, 1024–1031 CrossRef CAS.
- Y. Wang, L. You and K. Zhou, Chem. Sci., 2021, 12, 14065–14073 RSC.
- X. Zhao and Y. Liu, J. Am. Chem. Soc., 2020, 142, 5773–5777 CrossRef CAS PubMed.
- J. A. Gauthier, M. Fields, M. Bajdich, L. D. Chen, R. B. Sandberg, K. Chan and J. K. Nørskov, J. Phys. Chem. C, 2019, 123, 29278–29283 CrossRef CAS.
- T. Cheng, H. Xiao and W. A. Goddard, J. Am. Chem. Soc., 2016, 138, 13802–13805 CrossRef CAS PubMed.
- K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2016, 7, 1686–1690 CrossRef CAS PubMed.
- J. Long, C. Guo, X. Fu, H. Jing, G. Qin, H. Li and J. Xiao, J. Phys. Chem. Lett., 2021, 12, 6988–6995 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligarrard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. A. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- K. Mathew, V. C. Kolluru and S. Mula, J. Chem. Phys., 2019, 151, 234101 CrossRef PubMed.
- C. D. Taylor, S. A. Wasileski, J.-S. Filhol and M. Neurock, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165402 CrossRef.
- J.-S. Filhol and M. Neurock, Angew. Chem., Int. Ed., 2006, 45, 402–406 CrossRef CAS PubMed.
- Y.-H. Fang and Z.-P. Liu, J. Am. Chem. Soc., 2010, 132, 18214–18222 CrossRef CAS PubMed.
- Z. Duan and G. Henkelman, ACS Catal., 2019, 9, 5567–5573 CrossRef CAS.
- T. Liu, Y. Jing and Y. Li, J. Phys. Chem. Lett., 2021, 12, 12230–12234 CrossRef CAS PubMed.
- F. Studt, F. Abild-Pedersen, J. B. Varley and J. K. Nørskov, Catal. Lett., 2013, 143, 71–73 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc01593e |
| ‡ Y. W. and T. L. contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |