Open Access Article
Open Access ArticleUltrafast coherent photoexcited dynamics in a trimeric dendrimer probed by X-ray stimulated-Raman signals†
Victor M.
Freixas‡
 a,
Daniel
Keefer‡
a,
Daniel
Keefer‡
 b,
Sergei
Tretiak
b,
Sergei
Tretiak
 c,
Sebastian
Fernandez-Alberti
c,
Sebastian
Fernandez-Alberti
 a and
Shaul
Mukamel
a and
Shaul
Mukamel
 *b
*b
aDepartamento de Ciencia y Tecnologia, Universidad Nacional de Quilmes/CONICET, B1876BXD, Bernal, Argentina
bDepartment of Chemistry and Physics and Astronomy, University of California, Irvine, California 92697-2025, USA. E-mail: smukamel@uci.edu
cTheoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
First published on 6th May 2022
Abstract
The photoinduced ultrafast coherent inter-chromophore energy redistribution in a triarylamine trimer is explored using nonadiabatic excited state molecular dynamics followed by simulations of X-ray Raman signals. The nitrogencentered system ensures strong interchromophore interactions and, thus, the presence of coherences. Nevertheless, the multitude of non-deterministic photoinduced pathways during the ultrafast inter-branch migration of the excitation results in random confinement on some branches and, therefore, spatial exciton scrambling and loss of phase information at long times. We show that the vibronic coherence dynamics evolving into the incoherent scrambling mechanism on ultrafast 50 fs timescale, is accurately probed by the TRUECARS X-ray stimulated Raman signal. In combination with previous results, where the technique has revealed long-lived coherences in a rigid heterodimer, the signal is most valuable for detecting ultrafast molecular coherences or their absence. We demonstrate that X-ray Raman spectroscopy is a useful tool in the chemical design of functional molecular building blocks.
Introduction
Dendrimers are highly branched multichromophoric conjugated macromolecules with well-defined structural arrangements.1–3 Their highly polarizable and spatially extended π-electron manifold controls their highly tunable photoexcited dynamics and potential applications. The efficiency of light harvesting and subsequent electronic and vibrational (vibronic) energy redistribution depends on the type of their constituent chromophore units, their structural organization in the connected branches, symmetry, and the energy funneling through different nonradiative relaxation channels.4The energy transfer between dendritic branches can involve coherent5 or incoherent6 hopping mechanisms. While coherent processes involve in-phase evolution of spatially delocalized electronic wavefunctions, incoherent hopping-like mechanisms ultimately lead to a random exciton self-trapping and spatial scrambling on different units.7–12 The competition between these two processes reflects the relative strengths of electronic couplings and thermal fluctuations.
Coherences can have either pure electronic or vibronic origin.13,14 Electronic coherences are evaluated through the calculation of the pure dephasing time,15,16i.e., the dephasing of the off-diagonal elements of the density matrix involving a mechanism which erodes the phase relationship between states without changing their population. On the other hand, vibronic coherences require the calculation of the full quantum wavefunction of electrons and nuclei as well as the corresponding nonadiabatic couplings between states.14 Often, vibronic dynamics funnel the energy transfer through specific vibrational modes that modulate the wavelike localized – delocalized motion of the electronic wavefunction.11 That is, the nonequilibrium dynamics of such selected excited vibrations is observed as ultrafast beatings of electronic populations.17–24
The choice of the dendrimer's branching unit allows a direct control of the inter-branch interactions and, therefore, the coherence between branches. This has significant effects on its spectroscopic properties. Nitrogen-centered dendrimers have been shown to induce stronger interactions and electronic delocalizations compared to benzene-centered ones.5,10,25 The fast decay observed in ultrafast fluorescence anisotropy measurements performed on a triarylamine trimer supports the fact that coherence processes must be taken into account.25 The photoexcitation and subsequent electronic and vibrational energy redistribution in large conjugated dendrimers involve dynamics in coupled excited states and multiple events like transient localization and delocalization of the wavefunction, coherent and incoherent inter-chromophore energy transfers, exciton self-trapping and internal conversion processes.26 Such dynamics imply the passages through conical intersections that require quantum methods beyond Born–Oppenheimer approximation.27,28
Understanding coherence in dendrimers is a crucial challenge toward utilization of underpinning physical process for tailored chemical design. Over the past decade, sophisticated 2D electronic spectroscopy techniques29,30 have been developed to provide time-resolved signatures of coherences.31 More recently, X-ray free electron laser (XFEL) beam sources that offered unprecedented spatial, temporal and spectral resolutions,32 making them novel probes of ultrafast chemical dynamics.33,34 Pioneering experimental probes such as stimulated Raman transitions between electronic states35 or (time-resolved) X-ray scattering-based measurements36,37 have been demonstrated.
The theoretical design of new signals, and the prediction of their capabilities on molecular systems with distinct dynamics, is an important step in ultrafast X-ray sciences due to the extremely high cost and difficulty of the corresponding experiments. One promising signal that has been put forward recently, is the Transient Redistribution of Ultrafast Electronic Coherences in Attosecond Raman Signals (TRUECARS).38,39 It uses a hybrid broadband + narrowband off-resonant X-ray probe field at delay time τ after the pump pulse that initiates a stimulated Raman process between two electronic states. The hybrid field – requiring precise phase control between the two pulses – can alternatively be substituted by a single stochastic XFEL pulse in a covariance-based measurement.40 In either case, the signal is free from the usually dominating population dynamics and is finite only when there is a nuclear wavepacket overlap between electronic states. At short times, these coherences can be unique signatures of passages through conical intersections, since they are created due to wavepacket bifurcation. The signal is also a good indicator of whether the coherences survive multiple nonadiabatic passages, or whether they are destroyed by decoherence processes. We have previously simulated TRUECARS for the photoinduced dynamics in a rigid heterodimer, demonstrating that the signal can adequately monitor the experimentally observed long-living coherence surviving multiple conical intersection passages for several hundred femtoseconds at room temperature.41
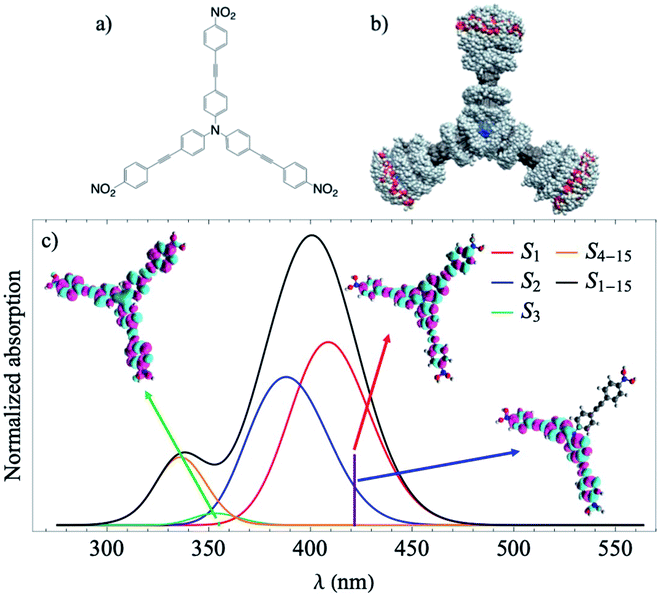
In the present study, we perform excited state nonadiabatic molecular dynamics simulations of the triarylamine trimer depicted in Fig. 1a using the ab initio multiple cloning approach (AIMC).42,43 The three equivalent branches of the dendrimer are connected by a nitrogen center that enhances the interaction and delocalization between states. According to previous ultrafast fluorescence anisotropy measurements, its fast decay cannot be reproduced using the Förster energy transfer model and coherences must be taken into account.25 This implies using sophisticated computational techniques that consider transient strong coupling regimes and wavefunction delocalizations. Using information from AIMC calculations, we then simulate the non-linear X-ray TRUECARS signal to monitor the interplay between coherent and incoherent inter-chromophore energy redistribution regimes. Due to the fast energy exchange between the three branches, it is expected that coherences only persist during a few tens of femtoseconds, making this dendrimer an ideal system to test the capacity of AIMC and the TRUECARS signal to monitor coherences.
Results
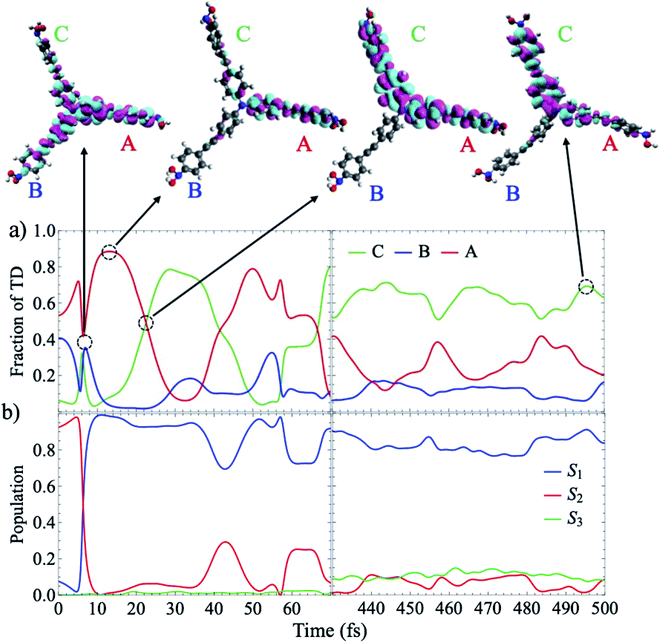
We start with conformational sampling of the triarylamine trimer using equilibrated ground state molecular dynamics. It shows that phenylene ethynylene units can freely rotate at room temperature (Fig. 1b). Fig. 1c displays the simulated absorption spectra with separated contributions from different excited states S1–S15. The energies and spatial distribution of electronic transition densities of S1, S2 and S3 reflect the 3-fold symmetry, that is, S1, S2 are degenerate at ground state minimum, while S3 is fully delocalized at higher energy as shown by the respective orbital plots in the insets of Fig. 1c. The validity of the electronic structure method for phenylene–ethynylene dendrimer in question is justified by a good agreement with the experimental absorption spectra25 and consistency with the Frenkel exciton Hamiltonian typically used for these systems.The time evolution of the expectation values of the electronic state populations42,44 are shown in Fig. 2a. According to Fig. 1c, an initial laser excitation at 388 nm populates the excited states S1 and S2 with a negligible contribution from S3. An efficient energy transfer to S1 then takes place within the first 100 fs. Different processes take place during that time. An exponential decay from S2 to S1 is concomitant with a damped oscillatory interchange between these states. These two behaviors of the population transfer are due to two different effects introduced by the energy transfer between these states. To analyze them, the increase of S1 population in time has been fitted to the equation:
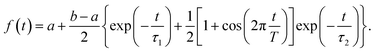 | (1) |
 | ||
| Fig. 2 (a) Time evolution of the electronic populations averaged over the ensemble of AIMC simulations according to the expectation values calculated according to (eqn S18†). The inset shows the oscillations of S1 and S2 at earlier times. The dashed black line is the fit to the f(t) function given by eqn (1); (b) time evolution of the mean fraction of electronic transition density localized on the different branches. For each trajectory we label the three branches as A, B, and C according to their decreasing order of fraction of transition density at t = 0. | ||
The parameters from this fitting are given in supplementary Table S1.† On one hand, after each crossing of the S2/S1 seam, the molecular system follows different pathways on either the S1 or S2 potential energy surfaces. The nuclear motion on the S1 state moves the molecular system away to regions of low coupling, while the nuclear motion on S2 keeps it lingering in the regions of strong coupling, which facilitates subsequent relaxation to S1. This behavior, previously reported in other branched dendritic molecules,45,46 leads to the ultimate exponential decay of the initial S2 electronic population to S1. It is represented by the pure decoherence time τ1 = 5.42 fs that corresponds to the decoherence time τ = 4.94 fs obtained from the pure dephasing rate D12 calculated using the autocorrelation function within linear response theory14,15 (eqn S14†). The corresponding curve is shown in supplemental Fig. S3.† On the other hand, the direction of energy transfer between S2 and S1, represented by the non adiabatic couplings (NACR), does not involve a random participation of all vibrational motions, but of a reduced set of vibrational modes with periods of ∼20 fs (see Fig. S4c†). This manifests in Fig. 2a as oscillation patterns of the S2 and S1 electronic populations with periods of ∼20 fs, which therefore are associated to vibronic coherences with the vibronic decoherence time τ2 = 23.31 fs.
Localization patterns of the transition densities associated with intra- and inter-branch energy transfers are mediated by thermal fluctuations at room temperature within the same electronic state or by energy transfers between different electronic states. Therefore, the time evolution of the electronic populations shown in Fig. 2a is not necessarily related to inter-branch energy transfer. This is evident from Fig. 2b that shows the average fraction of electronic transition density localized on the different branches. The formal definition of fraction of transition density is provided in the ESI (eqn S11†). In each trajectory we label the three branches as A, B, and C according to their decreasing order of fraction of transition density at t = 0. During the first ∼100 fs, the excess of electronic energy leads to an ultrafast inter-branch migration. The absence of an energy gradient leads to an ultrafast energy redistribution among isoenergetic branches. Thus, we observe a final scrambling of the spatial electronic transition density due to incoherent dynamic mechanisms governed by thermal fluctuations. This process competes with the concerted evolution of the nuclear wavepackets in S1 and S2 that modulates the strength and longevity of the vibronic coherence. Considering coupling as one third of the energy splitting between S1/S2 and S3 calculated at ground state minimum, a value of 1484 cm−1 was obtained. The strength of the thermal fluctuations, calculated as the full width at half maximum of the excitation energy, results in 2000 cm−1 and 2250 cm−1 for S1 and S2 respectively. That is, thermal fluctuations compete with coupling by randomly distorting the equivalent branches and breaking their symmetry, which leads to persistent interbranch exciton exchanges throughout the simulations. Despite that, the coupling is large enough to guarantee certain initial coherence.
It is worth pointing out that previous studies using the trajectory surface hopping protocol, in a similar system but with a benzene being the branching center, totally miss the oscillation patterns observed in this work.47 This difference is attributed to partially stronger couplings introduced by the nitrogen-center that increase the interaction and delocalization between states, as well as the superior AIMC method able to properly describe coherent dynamics in contrast with ad hoc nature of trajectory surface hopping method. In order to clarify this issue, surface hopping simulations of the triarylamine trimer were performed. Results are shown in supplemental Fig. S4.† The evolution in time of S1 and S2 populations do not reproduce the oscillation patterns shown in Fig. 2a, pointing out the limitation of this method to properly evidenciate vibronic coherences.
Our analysis of individual trajectories indicates that the spatial scrambling corresponding to the ensemble-average values shown in Fig. 2b is due to random transfers between linear branches rather than to a complete delocalization of the wavefunction across the entire molecule. This is clearly evident from Fig. 3 that shows results for AIMC trajectory 1, which is typical for the majority of trajectories in the ensemble. We observe that population exchanges between S1 and S2 states involve sudden changes in the transition density spatial localization. While transient delocalizations take place at the moments of energy transfer between states and induce energy transfer between different branches, the final result is a random exciton self-trapping on one or two branches, with the fraction of transition density not necessarily related to the initial order. Since the identity of the branches is defined at t = 0, the random exciton self-trapping reflects as a deceiving equivalence between the fraction of transition density on the branches at the end of the simulation, as shown in Fig. 2b. The electronic transition density matrices that correspond to the different snapshots indicated in Fig. 3a, are depicted in supplemental Fig. S5.† In agreement with Fig. 3a, we can observe a transient delocalization of the electronic transition density within the branches A and B at 6.4 fs, accompanied by a population exchange between S1 and S2. Subsequently, the transition density is localized on the branch A and a new transient delocalization between the branches A and C takes place at t = 22.6 fs. The excitation finally relaxed to S1 and becomes localized on the C branch.
Thus, the successive transient couplings between states through multitude of non-deterministic photoinduced pathways involve delocalizations of pairs of different branches that ultimately leads to an exciton self-trapping on one within a random molecular scrambling. Furthermore, as shown in supplemental Fig. S6,† these transient couplings driving the vibronic dynamics are assisted by a reduced set of high-frequency normal modes.
We next examine the possibility to probe the coherence dynamics of the triarylamine trimer with the TRUECARS X-ray stimulated Raman signal, given by:
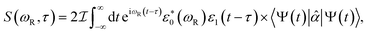 | (2) |
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) denotes the imaginary part. The time-dependent polarizability 〈α〉 is taken to be constant in the nuclear space, following the original formulation,38 so each matrix element factorizes into the wavepacket overlap between the involved electronic states given in eqn (5).
denotes the imaginary part. The time-dependent polarizability 〈α〉 is taken to be constant in the nuclear space, following the original formulation,38 so each matrix element factorizes into the wavepacket overlap between the involved electronic states given in eqn (5).
The probe fields are kept off-resonant with any real valence-to-core transitions. Otherwise the populations will start to contribute and dominate the coherences. We have previously found that an ideal scenario to maximize the experimental cross-section is to choose the central frequency near a valence-to-core resonance, while still staying off-resonant (pre resonant).40,41 Our molecule, shown in Fig. 1a, offers carbon, nitrogen and oxygen species as potential candidates. Another possibility to enhance the intrinsically weak coherence contribution and overcome potential loss channels like ionization or Auger–Meitner decay, is to use tailored light fields that steer the molecular wavepacket motion by coherent control.48
X-ray TRUECARS initiates a stimulated Raman process between electronic states, similar to Raman spectroscopy between vibrational levels in the visible domain.33 Only the ensemble average over all trajectories is experimentally observable. It is however useful to first discuss individual trajectories to gain insight about the underlying mechanisms. One example is depicted in Fig. 4 for a representative trajectory 2. Following an initial population transfer from S2 to S1, there is a free 100 fs evolution period. At 150 fs, the molecule again enters a region of strong nonadiabatic coupling, with population exchange between all three states (although S3 is only slightly affected). The transition density fractions in Fig. 4b exhibit the typical fluctuations, with the majority of excitation being located in branches B and C after a short redistribution period at the beginning of the dynamics.
 | ||
| Fig. 4 Dynamics and TRUECARS signal in trajectory 2. (a) Populations in the S1 (blue), S2 (red) and S3 (yellow) states. (b) Fraction of transition density in branch A (purple), B (yellow), C (red) and around the central nitrogen (blue). (c) Frequency-dispersed TRUECARS signal (eqn (2)) for the coherence ρ12 between S1 and S2. (d and e) same as (c) for ρ13 and ρ23. (f) Total TRUECARS signal for trajectory 2 given by the sum of (c–e). | ||
Since three electronic states are involved, there exist three coherences ρ12, ρ13 and ρ23. A TRUECARS signal according to eqn (2) can be calculated for each of these coherences, and their sum gives the total signal of the trajectory. According to Fig. 4, the contribution from the ρ12 coherence is the strongest. Interestingly, it is not only strong during the times when the molecule enters strong coupling regions – around 150–200 fs – but also in between. This suggests a concerted wavepacket evolution in the electronic states, where cloning events do not necessarily lead to decoherence. The signal contribution from the ρ13 coherence is only slightly weaker, and is located at the higher Raman shifts, in agreement with the larger S3–S1 energy difference compared to S2–S1. The ρ23 contribution is the weakest, as these two states are much less populated than S1 throughout the dynamics. The signal exhibits considerable magnitude only around 150 fs, where both S2 and S3 get significantly populated intermediately.
Trajectory 2 illustrates the characteristics of a large fraction of trajectories in the ensemble. The domination of the ρ12 contribution to the signal (given degeneracy of S1 and S2 states due to molecular symmetry), as well as the trapping of transition density in two of the three branches, is typical. Three additional trajectories shown in supplemental Fig. S7–S9† exhibit the largest differences to give insight about the variance within the ensemble. Individual features – like the magnitude of population transfer, the relative magnitude of the coherence contributions or the branches where the transition density is eventually trapped – may vary, but the qualitative structure persists.
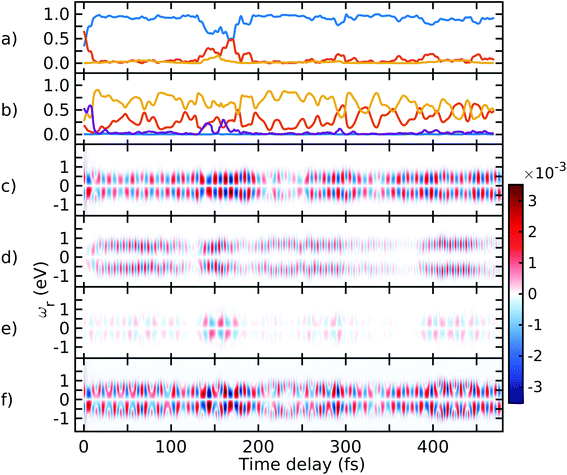
The spectrogram of the TRUECARS signal I(ωc, τ)39 (eqn (6)) gives the vibronic coherence distribution and corresponds to the energetic splitting of the adiabatic electronic states. I(ωc, τ) is depicted in Fig. 5 for trajectory 2, dissected into the three coherences similar to Fig. 4. The spectrogram of each contribution correctly reproduces the energy splitting of the involved adiabatic electronic states, with S2–S1 and S3–S2 oscillating between 0 and 0.4 eV, and S3–S1 oscillating between 0.4 and 0.8 eV. Both contributions are visible in the total spectrogram depicted in Fig. 5d, with the dominating feature around 0.3 eV and the weaker S3–S1 signal at higher ωc. The spectrograms along other trajectories (not shown) are very similar.
 | ||
| Fig. 5 Spectrogram of the TRUECARS signal (eqn (6)), dissected into the three contributions. (a) Spectrogram of the ρ12 coherence signal in Fig. 4c. (b) Spectrogram of the ρ13 coherence signal in Fig. 4d. (c) Spectrogram of the ρ23 coherence signal in Fig. 4e. The pink lines show the energy splitting between the corresponding adiabatic states as extracted from the AIMC simulations. (d) Spectrogram of the total signal in Fig. 4f. | ||
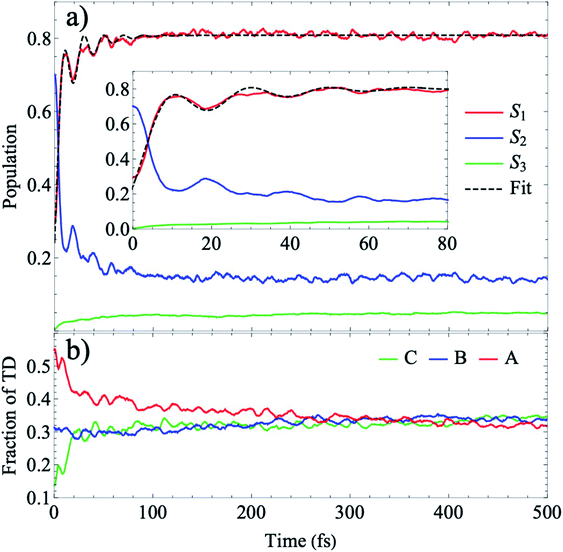
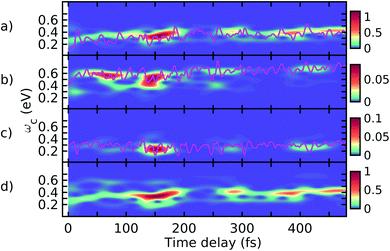
In Fig. 6, we present the total TRUECARS signal averaged over all 300 trajectories. Surprisingly, even though the individual trajectories exhibit persisting coherences throughout the dynamics, the total signal is strong only in the very beginning and rapidly decays. This is in agreement with Fig. 2, where the population transfer as well as the transition density relocalization complete over after 50–100 fs. The spectrogram shown in Fig. 6 exhibits the main feature centered around 0.3 eV, with additional weak features stemming mainly from the ρ13 coherence at higher Raman shifts. This dynamics is in a stark contrast to the rigid heterodimer previously investigated,41 where the experimentally observed long-living coherences are correctly reproduced in the ensemble-averaged TRUECARS signal. In the present molecule, we observe a rapid decay of the coherence, corresponding to the incoherent scrambling of the transition density across all three arms. This corroborates that TRUECARS can be a powerful tool in the molecular design of future optoelectronic devices on the basis of such dendritic or multi-chromophoric building blocks, where coherent electronic evolution is advantageous for conversion efficiencies. As demonstrated here, TRUECARS can directly monitor whether or not such coherence properties are present in a given molecule.
 | ||
| Fig. 6 (a) TRUECARS signal (eqn (2)) of the ensemble, obtained by averaging the over all 300 trajectories. (b) Spectrogram of the TRUECARS signal (eqn (6)). | ||
Conclusions
The photoexcitation and subsequent inter-branch energy redistribution of the triarylamine trimer shown in Fig. 1a have been simulated using AIMC that treats decoherences in a natural way beyond the Born–Oppenheimer dynamics on several excited states. The photophysics of this trimer results in a competition between coherent and incoherent energy transfers between branches. An initial ultrafast coherent dynamics is followed by incoherent mechanisms governed by thermal fluctuations that ultimately lead to a random molecular scrambling. Successive transient couplings creates multitude of non-deterministic photoinduced pathways involving delocalizations of pairs of different branches that ultimately leads to an exciton self-trapping on one within a random molecular scrambling. This is a consequence of the fact that thermal fluctuations compete with coupling differentially and randomly distorting the equivalent branches, which leads to persistent interbranch exciton exchanges throughout the simulations. Despite that, the coupling seems to be relatively large enough to guarantee certain initial coherence. Two distinct coherences, i.e., pure electronic and vibronic coherences, can be distinguished at earlier times. Vibronic couplings principally involve asymmetric motions in two of the three branches per time and are related to specific high-frequency bond-stretching vibrational modes (supplemental Fig. S6†).We have calculated the TRUECARS X-ray stimulated Raman signal for all individual trajectories as well as the ensemble average of the AIMC dynamics. TRUECARS is an unambiguous probe of molecular vibronic coherences as it is free from the usually dominating population background. The signal is strong only at the very beginning of the dynamics and rapidly decays within the first 50 femtoseconds, reproducing the incoherent scrambling dynamics of the photoexcited triarylamine trimer. This is different from previous results on a bichromophoric heterodimer,41 where TRUECARS has revealed long-living coherences that were also experimentally observed. This demonstrates the unique capability of near-future XFEL experiments in monitoring coherent molecular dynamics, and thereby help in the chemical design of molecular building blocks for optoelectronic materials that benefit from these coherences. While coherent TRUECARS, as calculated here, requires phase control of the two pulses in the hybrid probe field, the information is equally accessible by a covariance-based measurement with an existing single stochastic XFEL pulse.40
Methods
AIMC simulations
The ab initio multiple cloning (AIMC)42,43 technique is an extension of the Multiconfigurational Ehrenfest (MCE) method49–51 that uses trajectory-guided Gaussian basis functions (TBF). Independent Ehrenfest trajectories, i.e. configurations ψn(t) are used as a basis set to represent the full time-dependent quantum-mechanical wavefunction of electrons and nuclei: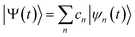 | (3) |
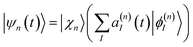 | (4) |
χ n (t) are coherent states52,53 given by frozen Gaussian functions centered in the Ehrenfest trajectories. In the original versions of MCE and AIMC,51ϕ(n)I are adiabatic states. However, photoinduced dynamics in large conjugated molecules like dendrimers can involve unavoided crossings between states whose nonadiabatic couplings have sharp peaks strongly localized in configurational space.54–56 In these situations, the adiabatic states change abruptly within the Gaussian width and the molecule should follow the diabatic pathways. Otherwise, unphysical intramolecular energy redistributions can occur. To address this issue, we use time-dependent diabatic electronic states, defined to coincide with adiabatic states in the center of each Gaussian,54–56 as detailed elsewhere.51
Ehrenfest trajectories evolve on an average potential energy surface that can lead to unphysical nuclear motions if the intramolecular energy redistribution follows different relaxation pathways dominated by several electronic states whose forces are very different. In these situations, the original wavefunction branches out into multiple parts, each following a specific pathway. AIMC quantifies them by using a set of cloning criteria.42,57 When these criteria are met, the original Ehrenfest trajectory splits into two new trajectories that continue their dynamics with the same nuclear wave function at the moment of cloning event but different electronic populations in order to be independently propagated on different potential energy surfaces. Such cloning events introduce decoherence in a natural way for wavefunctions moving on sufficiently different potential energy surfaces. More details and technical aspects of the AIMC method can be found elsewhere.42,43,57,58
The AIMC method is implemented within the nonadiabatic excited state molecular dynamics (NEXMD) framework.42,59,60 It is worth mentioning that the ab initio from AIMC comes from historical reasons and the method can be adapted either to TDDFT61 or semiempirical calculations as is the case of NEXMD. The NEXMD implementation has been specifically developed to deal with photoinduced dynamics in large multichormophoric conjugated molecules involving several coupled electronic excited states. Excited states energies,62–64 gradients65,66 and nonadiabatic couplings67–69 are calculated on-the-fly at the configuration interaction singles (CIS) level of theory using the semiempirical Austin Model 1 (AM1) Hamiltonian70 with the Collective Electronic Oscillator (CEO) approach.71–73 In our previous studies we have tested this approach for a number of dendritic chromophores, where we have found semi-quantitative agreement with experimental data and higher level electronic structure methodologies.45–47,59,62 Furthermore, the accuracy of this AIMC implementation has been previously tested on photoinduced nonadiabatic energy transfer pathways dynamics in poly(phenylene ethynylene) dendrimer building blocks.74
AIMC trajectories start by vertical excitation of 300 initial configurations equispaced in time obtained from a 1 ns equilibrated ground state molecular dynamics simulation. This simulation was performed at ambient conditions (T = 300 K) using the Langevin thermostat with a friction coefficient γ = 2.0 ps−1 and a time step of 0.5 fs starting from an initial structure that has been previously minimized using the generalized amber force field75 followed by a subsequent second minimization using AM1. The initial excited states were populated according to a Franck–Condon window given by gI(r, R) = fI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−T2(Elaser − EI)2] where fI and EI are the oscillator strength and energy of excited state I, and Elaser is the energy of a Gaussian laser pulse f(t) = exp(−t2/2T2), centered at 388 nm that corresponds to the maximum of the absorption for the S2 state, and T = 42.5 fs, i.e., a FWHM = 100 fs. AIMC trajectories were run at constant energy and with a 0.05 fs time step. Gaussian widths were taken from the optimized parameters reported by Thompson et al.76 Details on the cloning criteria and thresholds can be found in the ESI.†
exp[−T2(Elaser − EI)2] where fI and EI are the oscillator strength and energy of excited state I, and Elaser is the energy of a Gaussian laser pulse f(t) = exp(−t2/2T2), centered at 388 nm that corresponds to the maximum of the absorption for the S2 state, and T = 42.5 fs, i.e., a FWHM = 100 fs. AIMC trajectories were run at constant energy and with a 0.05 fs time step. Gaussian widths were taken from the optimized parameters reported by Thompson et al.76 Details on the cloning criteria and thresholds can be found in the ESI.†
The coherence between any two electronic states K and L can be extracted from AIMC simulations as:
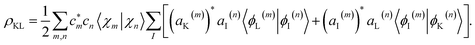 | (5) |
It includes coherences between the electronic and the nuclear subsystem, each carrying their own phases. Their joint information is required to obtain a TRUECARS signal, and their state is accounted for in the molecular wavefunction when calculating ρKL.
TRUECARS signal spectrogram
The TRUECARS signal given by eqn (2), was calculated with the broadband 500 attosecond pulse ε0 and the narrowband 3 fs pulse ε1. A powerful analysis tool that is experimentally available for the TRUECARS signal is its spectrogram I.39 This is a post-processing analysis using a gating function Egate convoluted with a TRUECARS signal trace S(t) at constant Raman shift ωR (integration over positive or negative ωR is also possible, while integration over the whole ωR range yields zero). It is given by: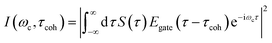 | (6) |
Data availability
The data that supports the findings of this study are available within the ESI† and from the corresponding author upon reasonable request.Author contributions
S. T., S. F.-A. and S. M. designed the project. V. M. F. and S. F.-A. performed AIMC simulations. D. K. calculated the signals and the Wigner spectrograms. All authors analyzed and interpreted the results. V. M. F. and D. K. prepared the figures. The manuscript was written with contributions from all authors. All authors were involved in the scientific discussion of the results of the paper. V. M. F. and D. K. contributed equally.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge support from the Chemical Sciences, Geosciences, and Bio-Sciences Division, Office of Basic Energy Sciences, Office of Science, US Department of Energy (DOE), through award DE-SC0019484 and under Triad National Security, LLC (“Triad”) contract grant # 89233218CNA000001 (FWP: LANLE3T1). The work at Los Alamos National Laboratory (LANL) was performed in part at the Center for Integrated Nanotechnologies (CINT), a U.S. DOE User Facility. This research used resources provided by the LANL Institutional Computing Program. D. K. gratefully acknowledges support from the Alexander von Humboldt foundation through the Feodor Lynen program. S. F.-A. and V. M. F acknowledge support of CONICET, UNQ and ANPCyT (PICT-2018-02360).References
- V. Balzani, P. Ceroni, M. Maestri and V. Vicinelli, Light-harvesting dendrimers, Curr. Opin. Chem. Biol., 2003, 7, 657–665 CrossRef CAS PubMed.
- A. Nantalaksakul, D. Reddy, C. Bardeen and S. Thayumanavan, Light Harvesting Dendrimers, Photosynth. Res., 2006, 87, 133–150 CrossRef CAS PubMed.
- A. De Sio, X. T. Nguyen and C. Lienau, A new approach to light-harvesting with dendritic antenna, Thin Solid Films, 1998, 331, 254–258 CrossRef.
- D. L. Andrews, Light harvesting in dendrimer materials: Designer photophysics and electrodynamics, J. Mater. Res., 2012, 27, 627–638 CrossRef CAS.
- J. M. Lupton, I. D. W. Samuel, P. L. Burn and S. Mukamel, Control of intrachromophore excitonic coherence in electroluminescent conjugated dendrimers, J. Phys. Chem. B, 2002, 106, 7647–7653 CrossRef CAS.
- T. Förster, Energiewanderung und fluoreszenz, Naturwissenschaften, 1946, 33, 166–175 CrossRef.
- J. Galindo, E. Atas, A. Altan, D. Kuroda, S. Fernandez-Alberti, S. Tretiak, A. Roitberg and V. Kleiman, Dynamics of Energy Transfer in a Conjugated Dendrimer Driven by Ultrafast Localization of Excitations, J. Am. Chem. Soc., 2015, 137, 11637–11644 CrossRef CAS PubMed.
- F. Ricci, T. Kim, W. Gao, Y. Lin, C.-Q. Ma and T. Goodson, Coherent energy and charge transport processes in oligothiophene dendrimers probed in solution and in the solid state with time-resolved spectroscopy and microscopy methods, J. Phys. Chem. C, 2019, 123, 23419–23426 CrossRef CAS.
- M. C. Aguilera, A. E. Roitberg, V. D. Kleiman, S. Fernandez-Alberti and J. F. Galindo, Unraveling Direct and Indirect Energy Transfer Pathways in a Light-Harvesting Dendrimer, J. Phys. Chem. C, 2020, 124, 22383–22391 CrossRef CAS.
- O. Varnavski, I. D. W. Samuel, L. O. Plsson, P. L. Burn and T. Goodson, Investigations of excitation energy transfer and intramolecular interactions in a nitrogen corded distyrylbenzene dendrimer system, J. Chem. Phys., 2002, 116, 8893–8903 CrossRef CAS.
- T. R. Nelson, D. Ondarse-Alvarez, N. Oldani, B. Rodriguez-Hernandez, L. Alfonso-Hernandez, J. F. Galindo, V. D. Kleiman, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Coherent exciton-vibrational dynamics and energy transfer in conjugated organics, Nat. Commun., 2018, 9, 2316 CrossRef PubMed.
- D. Ondarse-Alvarez, N. Oldani, A. E. Roitberg, V. D. Kleiman, S. Tretiak and S. Fernandez-Alberti, Energy transfer and spatial scrambling of an exciton in a conjugated dendrimer, Phys. Chem. Chem. Phys., 2018, 20, 29648–29660 RSC.
- T. Aida, D.-L. Jiang, E. Yashima and Y. Okamoto, Signatures of strong vibronic coupling mediating coherent charge transfer in two-dimensional electronic spectroscopy, Z. Naturforsch., A: Phys. Sci., 2019, 74, 721–737 CrossRef.
- V. M. Freixas, S. Tretiak, D. V. Makhov, D. Shalashilin and S. Fernandez-Alberti, Vibronic quantum beating between electronic excited states in a heterodimer, J. Phys. Chem. B, 2020, 124, 3992–4001 CrossRef CAS PubMed.
- S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University PressNew York, 1995, vol. 29 Search PubMed.
- R. Hildner, D. Brinks and N. F. van Hulst, Femtosecond coherence and quantum control of single molecules at room temperature, Nat. Phys., 2011, 7, 172–177 Search PubMed.
- A. Kolli, E. J. O'Reilly, G. D. Scholes and A. Olaya-Castro, The fundamental role of quantized vibrations in coherent light harvesting by cryptophyte algae, J. Chem. Phys., 2012, 137, 174109 CrossRef PubMed.
- E. J. O'Reilly and A. Olaya-Castro, Non-classicality of the molecular vibrations assisting exciton energy transfer at room temperature, Nat. Commun., 2014, 5, 3012 CrossRef PubMed.
- S. Siwiak-Jaszek and A. Olaya-Castro, Transient synchronisation and quantum coherence in a bio-inspired vibronic dimer, Faraday Discuss., 2019, 216, 38–56 RSC.
- H. Chen, X. Wang, C.-M. Han and H.-R. Li, Phonon-Mediated Excitation Energy Transfer in a Detuned Multi-Sites System, J. Phys. B: At., Mol. Opt. Phys., 2019, 52, 075501 CrossRef CAS.
- I. B. Juhász and Á. I. Csurgay, Impact of Undamped and Damped Intramolecular Vibrations on the Efficiency of Photosynthetic Exciton Energy Transfer, AIP Adv., 2018, 8, 045318 CrossRef.
- R. Stones and A. Olaya-Castro, Vibronic Coupling as a Design Principle to Optimize Photosynthetic Energy Transfer, Chem, 2016, 1, 822–824 CAS.
- Z. Zhang and J. Wang, Origin of Long-Lived Quantum Coherence and Excitation Dynamics in Pigment-Protein Complexes, Sci. Rep., 2016, 6, 37629 CrossRef CAS PubMed.
- H.-B. Chen, P.-Y. Chiu and Y.-N. Chen, Vibration-Induced Coherence Enhancement of the Performance of a Biological Quantum Heat Engine, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2016, 94, 052101 CrossRef PubMed.
- O. P. Varnavski, J. C. Ostrowski, L. Sukhomlinova, R. J. Twieg, G. C. Bazan and T. Goodson, Coherent Effects in Energy Transport in Model Dendritic Structures Investigated by Ultrafast Fluorescence Anisotropy Spectroscopy, J. Am. Chem. Soc., 2002, 124, 1736–1743 CrossRef CAS PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Nonadiabatic excited-state molecular dynamics: Modeling photophysics in organic conjugated materials, Acc. Chem. Res., 2014, 47, 1155–1164 CrossRef CAS PubMed.
- G. a. Worth and L. S. Cederbaum, Beyond Born-Oppenheimer: molecular dynamics through a conical intersection, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- W. Domcke and D. R. Yarkony, Role of conical intersections in molecular spectroscopy and photoinduced chemical dynamics, Annu. Rev. Phys. Chem., 2012, 63, 325–352 CrossRef CAS PubMed.
- S. Mukamel, Multidimensional femtosecond correlation spectroscopies of electronic and vibrational excitations, Annu. Rev. Phys. Chem., 2000, 51, 691–729 CrossRef CAS PubMed.
- D. M. Jonas, Two-dimensional femtosecond spectroscopy, Annu. Rev. Phys. Chem., 2003, 54, 425–463 CrossRef CAS PubMed.
- T. Brixner, J. Stenger, H. M. Vaswani, M. Cho, R. E. Blankenship and G. R. Fleming, Two-dimensional spectroscopy of electronic couplings in photosynthesis, Nature, 2005, 434, 625–628 CrossRef CAS PubMed.
- J. Duris, S. Li, T. Driver, E. G. Champenois, J. P. MacArthur, A. A. Lutman, Z. Zhang, P. Rosenberger, J. W. Aldrich and R. Coffee, et al. , Tunable isolated attosecond x-ray pulses with gigawatt peak power from a free-electron laser, Nat. Photonics, 2020, 14, 30–36 CrossRef CAS.
- S. Mukamel, D. Healion, Y. Zhang and J. D. Biggs, Multidimensional attosecond resonant x-ray spectroscopy of molecules: Lessons from the optical regime, Annu. Rev. Phys. Chem., 2013, 64, 101–127 CrossRef CAS PubMed.
- L. Young, K. Ueda, M. Gühr, P. H. Bucksbaum, M. Simon, S. Mukamel, N. Rohringer, K. C. Prince, C. Masciovecchio and M. Meyer, et al. , Roadmap of ultrafast x-ray atomic and molecular physics, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 032003 CrossRef.
- J. T. O'Neal, E. G. Champenois, S. Oberli, R. Obaid, A. Al-Haddad, J. Barnard, N. Berrah, R. Coffee, J. Duris and G. Galinis, et al. , Electronic population transfer via impulsive stimulated x-ray Raman scattering with attosecond soft-x-ray pulses, Phys. Rev. Lett., 2020, 125, 073203 CrossRef PubMed.
- J. Küpper, S. Stern, L. Holmegaard, F. Filsinger, A. Rouzée, A. Rudenko, P. Johnsson, A. V. Martin, M. Adolph and A. Aquila, et al. , X-ray diffraction from isolated and strongly aligned gas-phase molecules with a free-electron laser, Phys. Rev. Lett., 2014, 112, 083002 CrossRef.
- M. Minitti, J. Budarz, A. Kirrander, J. Robinson, D. Ratner, T. Lane, D. Zhu, J. Glownia, M. Kozina and H. Lemke, et al. , Imaging molecular motion: Femtosecond x-ray scattering of an electrocyclic chemical reaction, Phys. Rev. Lett., 2015, 114, 255501 CrossRef CAS PubMed.
- M. Kowalewski, K. Bennett, K. E. Dorfman and S. Mukamel, Catching conical intersections in the act: Monitoring transient electronic coherences by attosecond stimulated x-ray Raman signals, Phys. Rev. Lett., 2015, 115, 193003 CrossRef PubMed.
- D. Keefer, T. Schnappinger, R. de Vivie-Riedle and S. Mukamel, Visualizing conical intersection passages via vibronic coherence maps generated by stimulated ultrafast x-ray Raman signals, Proc. Natl. Acad. Sci., 2020, 117, 24069–24075 CrossRef CAS PubMed.
- S. M. Cavaletto, D. Keefer and S. Mukamel, High temporal and spectral resolution of stimulated x-ray Raman signals with stochastic free-electron-laser pulses, Phys. Rev. X, 2021, 11, 011029 CAS.
- D. Keefer, V. M. Freixas, H. Song, S. Tretiak, S. Fernandez-Alberti and S. Mukamel, Monitoring molecular vibronic coherences in a bichromophoric molecule by ultrafast x-ray spectroscopy, Chem. Sci., 2021, 12, 5286–5294 RSC.
- V. M. Freixas, S. Fernandez-Alberti, D. V. Makhov, S. Tretiak and D. Shalashilin, An ab initio multiple cloning approach for the simulation of photoinduced dynamics in conjugated molecules, Phys. Chem. Chem. Phys., 2018, 20, 17762–17772 RSC.
- D. V. Makhov, W. J. Glover, T. J. Martinez and D. V. Shalashilin, Ab initio multiple cloning algorithm for quantum nonadiabatic molecular dynamics, J. Chem. Phys., 2014, 141, 054110 CrossRef PubMed.
- S. Fernandez-Alberti, D. V. Makhov, S. Tretiak and D. V. Shalashilin, Non-adiabatic excited state molecular dynamics of phenylene ethynylene dendrimer using a multiconfigurational Ehrenfest approach, Phys. Chem. Chem. Phys., 2016, 18, 10028–10040 RSC.
- S. Fernandez-Alberti, A. E. Roitberg, V. D. Kleiman, T. Nelson and S. Tretiak, Shishiodoshi unidirectional energy transfer mechanism in phenylene ethynylene dendrimers, J. Chem. Phys., 2012, 137, 22A526 CrossRef CAS PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Electronic delocalization, vibrational dynamics, and energy transfer in organic chromophores, J. Phys. Chem. Lett., 2017, 8, 3020–3031 CrossRef CAS PubMed.
- D. Ondarse-Alvarez, S. Komurlu, A. E. Roitberg, G. Pierdominici-Sottile, S. Tretiak, S. Fernandez-Alberti and V. D. Kleiman, Ultrafast electronic energy relaxation in a conjugated dendrimer leading to inter-branch energy redistribution, Phys. Chem. Chem. Phys., 2016, 18, 25080–25089 RSC.
- D. Keefer and S. Mukamel, Selective enhancement of spectroscopic features by quantum optimal control, Phys. Rev. Lett., 2021, 126, 163202 CrossRef CAS PubMed.
- D. V. Shalashilin, Nonadiabatic dynamics with the help of multiconfigurational Ehrenfest method: Improved theory and fully quantum 24D simulation of pyrazine, J. Chem. Phys., 2010, 132, 244111 CrossRef PubMed.
- K. Saita and D. V. Shalashilin, On-the-fly ab initio molecular dynamics with multiconfigurational Ehrenfest method, J. Chem. Phys., 2012, 137, 22A506 CrossRef PubMed.
- D. V. Makhov, C. Symonds, S. Fernandez-Alberti and D. V. Shalashilin, Ab initio quantum direct dynamics simulations of ultrafast photochemistry with multiconfigurational Ehrenfest approach, Chem. Phys., 2017, 493, 200–218 CrossRef CAS.
- D. V. Shalashilin and M. S. Child, The phase space CCS approach to quantum and semiclassical molecular dynamics for high-dimensional systems, Chem. Phys., 2004, 304, 103–120 CrossRef CAS.
- D. V. Shalashilin, Multiconfigurational Ehrenfest approach to quantum coherent dynamics in large molecular systems, Faraday Discuss., 2011, 153, 105 RSC.
- M. V. Berry, Quantal phase factors accompanying adiabatic changes, Proc. R. Soc. London, Ser. A, 1984, 392, 103–120 Search PubMed.
- C. Mead and D. Truhlar, On the determination of born-Oppenheimer nuclear motion wave functions including complications due to conical intersections and identical nuclei, J. Chem. Phys., 1979, 70, 2284–2296 CrossRef CAS.
- S. Fernandez-Alberti, A. E. Roitberg, T. Nelson and S. Tretiak, Identification of unavoided crossings in nonadiabatic photoexcited dynamics involving multiple electronic states in polyatomic conjugated molecules, J. Chem. Phys., 2012, 137, 014512 CrossRef PubMed.
- V. M. Freixas, A. J. White, T. Nelson, H. Song, D. V. Makhov, D. Shalashilin, S. Fernandez-Alberti and S. Tretiak, Nonadiabatic excited-state molecular dynamics methodologies: Comparison and convergence, J. Phys. Chem. Lett., 2021, 12, 2970–2982 CrossRef CAS PubMed , pMID: 33730495..
- D. V. Makhov, K. Saita, T. J. Martinez and D. V. Shalashilin, Ab initio multiple cloning simulations of pyrrole photodissociation: Tker spectra and velocity map imaging, Phys. Chem. Chem. Phys., 2015, 17, 3316–3325 RSC.
- T. R. Nelson, A. J. White, J. A. Bjorgaard, A. E. Sifain, Y. Zhang, B. Nebgen, S. Fernandez-Alberti, D. Mozyrsky, A. E. Roitberg and S. Tretiak, Non-adiabatic excited-state molecular dynamics: Theory and applications for modeling photophysics in extended molecular materials, Chem. Rev., 2020, 120, 2215–2287 CrossRef CAS PubMed.
- W. Malone, B. Nebgen, A. White, Y. Zhang, H. Song, J. A. Bjorgaard, A. E. Sifain, B. Rodriguez-Hernandez, V. M. Freixas and S. Fernandez-Alberti, et al. , Nexmd software package for non-adiabatic excited state molecular dynamics simulations, J. Chem. Theory Comput., 2020, 16, 5771–5783 CrossRef CAS PubMed.
- H. Song, V. M. Freixas, S. Fernandez-Alberti, A. J. White, Y. Zhang, S. Mukamel, N. Govind and S. Tretiak, An ab initio multiple cloning method for non-adiabatic excited-state molecular dynamics in nwchem, J. Chem. Theory Comput., 2021, 17, 3629–3643 CrossRef CAS PubMed.
- S. Tretiak and S. Mukamel, Density matrix analysis and simulation of electronic excitations in conjugated and aggregated molecules, Chem. Rev., 2002, 102, 3171–3212 CrossRef CAS PubMed.
- V. Chernyak, M. F. Schulz, S. Mukamel, S. Tretiak and E. V. Tsiper, Krylov-space algorithms for time-dependent Hartree–Fock and density functional computations, J. Chem. Phys., 2000, 113, 36–43 CrossRef CAS.
- S. Tretiak, C. M. Isborn, A. M. Niklasson and M. Challacombe, Representation independent algorithms for molecular response calculations in time-dependent self-consistent field theories, J. Chem. Phys., 2009, 130, 054111 CrossRef PubMed.
- F. Furche and R. Ahlrichs, Adiabatic time-dependent density functional methods for excited state properties, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- S. Tretiak and V. Chernyak, Resonant nonlinear polarizabilities in the time-dependent density functional theory, J. Chem. Phys., 2003, 119, 8809–8823 CrossRef CAS.
- M. Tommasini, V. Chernyak and S. Mukamel, Electronic density-matrix algorithm for nonadiabatic couplings in molecular dynamics simulations, Int. J. Quantum Chem., 2001, 85, 225–238 CrossRef CAS.
- V. Chernyak and S. Mukamel, Density-matrix representation of nonadiabatic couplings in time-dependent density functional (tddft) theories, J. Chem. Phys., 2000, 112, 3572–3579 CrossRef CAS.
- R. Send and F. Furche, First-order nonadiabatic couplings from time-dependent hybrid density functional response theory: Consistent formalism, implementation, and performance, J. Chem. Phys., 2010, 132, 044107 CrossRef PubMed.
- M. J. Dewar, E. G. Zoebisch, E. F. Healy and J. J. Stewart, Development and use of quantum mechanical molecular models. 76. am1: a new general purpose quantum mechanical molecular model, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS.
- S. Mukamel, S. Tretiak, T. Wagersreiter and V. Chernyak, Electronic coherence and collective optical excitations of conjugated molecules, Science, 1997, 277, 781–787 CrossRef CAS.
- S. Tretiak, V. Chernyak and S. Mukamel, Recursive density-matrix-spectral-moment algorithm for molecular nonlinear polarizabilities, J. Chem. Phys., 1996, 105, 8914–8928 CrossRef CAS.
- S. Tretiak, W. M. Zhang, V. Chernyak and S. Mukamel, Excitonic couplings and electronic coherence in bridged naphthalene dimers, Proc. Natl. Acad. Sci., 1999, 96, 13003–13008 CrossRef CAS PubMed.
- V. M. Freixas, D. Ondarse-Alvarez, S. Tretiak, D. V. Makhov, D. V. Shalashilin and S. Fernandez-Alberti, Photoinduced non-adiabatic energy transfer pathways in dendrimer building blocks, J. Chem. Phys., 2019, 150, 124301 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- A. L. Thompson, C. Punwong and T. J. Martínez, Optimization of width parameters for quantum dynamics with frozen gaussian basis sets, Chem. Phys., 2010, 370, 70–77 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc00601d |
| ‡ These two authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |