A feasible approach for automatically differentiable unitary coupled-cluster on quantum computers†
Abstract
We develop computationally affordable and encoding independent gradient evaluation procedures for unitary coupled-cluster type operators, applicable on quantum computers. We show that, within our framework, the gradient of an expectation value with respect to a parameterized n-fold fermionic excitation can be evaluated by four expectation values of similar form and size, whereas most standard approaches, based on the direct application of the parameter-shift-rule, come with an associated cost of 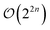 expectation values. For real wavefunctions, this cost can be further reduced to two expectation values. Our strategies are implemented within the open-source package Tequila and allow blackboard style construction of differentiable objective functions. We illustrate initial applications through extended adaptive approaches for electronic ground and excited states.
expectation values. For real wavefunctions, this cost can be further reduced to two expectation values. Our strategies are implemented within the open-source package Tequila and allow blackboard style construction of differentiable objective functions. We illustrate initial applications through extended adaptive approaches for electronic ground and excited states.



 Please wait while we load your content...
Please wait while we load your content...