Exploring the optical management and efficiency limit of luminescent solar concentrators based on advanced luminophores†
Qi
Nie
,
Wenqing
Li
,
Kuilin
Li
and
Xiao
Luo
 *
*
School of Optoelectronic Science and Engineering, University of Electronic Science and Technology of China (UESTC), Chengdu 610054, PR China. E-mail: luox@uestc.edu.cn
First published on 10th July 2024
Abstract
In the context of global warming, luminescent solar concentrators (LSCs) hold great promise as solar windows. Over nearly five decades of development, various suitable luminophores for LSCs, including dye molecules, perovskites and quantum dots, have seen significant advancements. However, the commercialization of LSCs is still immature, and achieving a balance between large area (∼1 m2) and high efficiency in laboratory-reported LSCs remains challenging. Consequently, it is important to find more promising luminophores with small reabsorption and high photoluminescence quantum yield (PLQY). In this work, we used Monte Carlo (MC) simulation and recognized calculation formulae to predict the LSCs efficiency of several advanced luminophores of our choice. According to our results, photon-multiplying (PM) LSCs, which include quantum-cutting (QC)-based luminophores and singlet-fission (SF)-based luminophores, hold a promising solution to overcome thermalization loss for high-energy photon excitation for coupled Si-PVs and reduce reabsorption loss. Under the condition of optimal PLQY, the external quantum efficiency of SF-LSCs is expected to exceed 18% even if the area of the LSCs reaches ∼1 m2. Considering the thermodynamic concentration limit, PM-LSCs may be better suited for operation under weaker light conditions. We also proposed that tandem LSCs remain an effective approach to maximize efficiency. By employing SF-LSCs as the top layer and CuInSe2/ZnS-based LSCs as the bottom layer, the power conversion efficiency (PCE) of tandem LSCs can reach 11% for an LSC length of 10 cm and 9% for an LSC length of 100 cm under optimal PLQY. Based on the existing material systems, we predict the efficiency bottlenecks in LSCs and provide reliable theoretical support for their commercialization.
Introduction
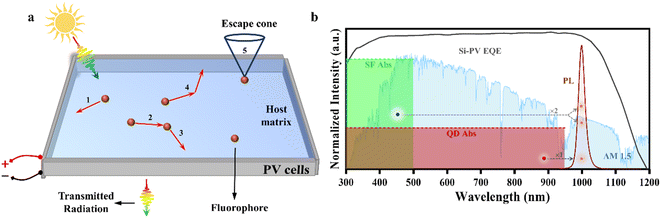
Global warming and the energy crisis are pressing issues around the world, and finding clean and renewable energy is critical. According to a reported work, 40% of global energy consumption and 28% of carbon emissions are contributed by buildings.1,2 The design concept of luminescent solar concentrators (LSCs) aligns well with building integrated photovoltaics (BIPVs). LSCs are considered one of the best choices of devices for solar windows, which are transparent (or semitransparent) and inexpensive. The schematic principle of the LSC-PV system is shown in Fig. 1a, and the system simply consists of luminophores, a waveguide medium, and four PV cells. The light concentrating process of LSCs can be divided into the following steps: when the incident photons reach an LSC, some photons are absorbed by luminophores and new photons are emitted, according to their emission spectra (step 1 in Fig. 1a), and the remaining photons that are not absorbed are transmitted out from the bottom surface. For the emitted photons in the waveguide medium, some of them enter the escape cone and then escape (step 5 in Fig. 1a), some of them are reabsorbed by the luminophores (step 2 in Fig. 1a), and the others may reach the LSC's edges directly. For the reabsorbed photons, the luminophores may re-emit new photons depending on their photoluminescent quantum yields (PLQYs) (step 3 in Fig. 1a). After going through the above processes, some of these photons reach the LSC's edges and are absorbed by coupled solar cells to produce energy.Since the LSC was proposed by Weber and Lambe in 1976 first,3 the luminophore system of LSCs grew dramatically within fifty years of development. The luminophores of LSCs contain dye molecules, colloidal quantum dots (QDs), various nanocrystals (NCs) and so on. Highly efficient PLQY and large Stokes shifts of light-emitting cluster materials are always the goals pursued by LSCs. From the initial use of rhodamine 6G or its derivatives as the luminophores4 to chalcogenide core/shell QDs,5 the advancement of LSCs has seen a gradual pace over the first three decades of development. However, for the last decade, LSCs have witnessed a vigorous burst and a vast amount of new materials have been reported. Many novel organic molecule-based LSCs, including thermally activated delayed fluorescence dye,6 aggregation-induced emission molecule7,8 and fluorescence resonance energy transfer complex,9–11 have achieved relatively excellent performance. Among molecule-based LSCs, a promising power conversion efficiency (PCE) of 2.6% was reported by Zhang et al., and the length of their large-area LSC was 20 cm.10 For perovskite NCs, despite their excellent luminescent properties, reabsorption remained a hindrance until quantum-cutting (QC) was first introduced for LSC applications by Luo et al.12 The CsPbCl3:Yb3+-based LSCs (25 cm2) had an internal quantum efficiency of up to 118%, but the weaker absorption efficiency affected their performance. Subsequently, Cohen et al. proposed that using CsPbClxBr3−x:Yb3+-based LSCs can further improve the absorption efficiency of QC-based LSCs.13 Due to the theoretically optimal PLQY of 200%, the QC luminophores can be considered one of the photon-multiplying (PM) materials. Recently, non-toxic luminophore materials, such as I–III–VI ternary QDs14 and carbon dots (CDs), have become the research hotspot. Wu et al. used CuInSe2/ZnS QDs as the luminophore of bottom layer LSCs of their tandem system and achieved 3.1% of PCE when their length of LSCs was 15.24 cm.15 Gungor et al. reported that their Zn-doped core/shell CuInSe2−xSx/CuInS2-based LSCs had an external quantum efficiency of 11.8% when the length of the LSC was 9.5 cm.16 It is the highest external quantum efficiency under the standard AM 1.5 solar spectrum reported so far. More recently, Park et al. introduced a new structure in CuInS2/ZnS based LSC where a patterned low-refractive-index medium acted as an optical ‘guard rail’ to reduce reabsorption loss.17 They achieved external quantum efficiencies of 45% for a 100 cm2 area under 405 nm excitation. CD-based LSCs have many advantages, such as being stable, nontoxic, earth-abundant and low-cost.18,19 However, we found that many of the reported CD-based LSCs with high efficiency are very small in size due to their relatively large reabsorption.20–25 To address this issue, Gong et al. proposed using barium-doped CDs with a Stokes shift of 0.68 eV and PLQY of 80.81% to build large-area LSC until very recently and achieved a breakthrough optical conversion efficiency of 7.16% and PCE of 6.87% under natural light irradiation (40 mW cm−2).26 We also observed some luminophore systems with great potential for LSCs, such as molecular triplet energy transfer (TET) to QDs or ions for luminescence. This system of singlet fission (SF) can be considered another PM material. Rao et al. proposed that using SF could improve efficiency by overcoming thermalization loss in applications of photovoltaics.27 Gray et al. achieved the TET from 6,11-bis[(triisopropylsilyl)ethynyl]tetracene-2-methylthiol to PbS QDs.28 The triplet yield from singlet fission was calculated as 130% ± 10%, and the internal triplet transfer efficiency was close to unity. In their subsequent work, they proposed the ligand-directed self-assembly of organic-QD blend films with an SF efficiency of 186% ± 18%, while the whole PLQY system was 24.5%.29 Very recently, Baikie et al. proposed PM technologies for LSCs,30 and they suggested that using PbS with tetracene ligands attached could provide considerable efficiency in the application of LSCs. However, for systems with tetracene-anchored PbS NCs, there is absorption competition between QDs and tetracene, making it challenging to control the concentration ratio between the components. This results in the relatively low PLQY of the whole system because the luminescence of the QDs comes partly from the intrinsic transition of QDs and partly from the molecular TET following the SF process. Interestingly, Han et al. achieved the energy transfer from the triplet of tetracene to Yb3+ of NaGdF4:Yb NCs for luminescence,31 but the PLQY was not reported. Because NaGdF4:Yb NCs have only a very small absorption in the range of the solar spectrum, the luminescence of Yb3+ is mainly dominated by the molecular SF process.
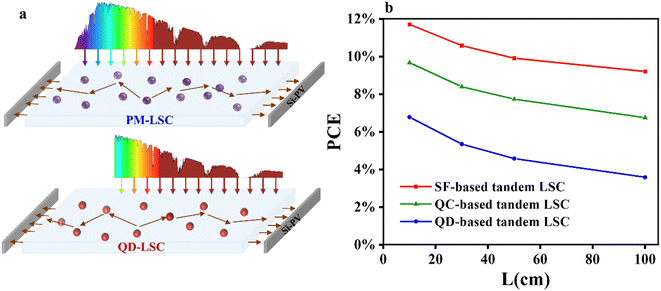
In the context of BIPVs, the LSC-PV system should be regarded as a whole device. Consequently, the efficiency and absorption regions of coupled solar cells are of vital importance. Given that silicon-based photovoltaic (Si-PV) cells have reached a mature and commercialized stage, and their high external quantum efficiency (EQE) region covers the wavelength ranging from 300 to 1100 nm (as indicated by the grey curve in Fig. 1b), we choose to focus on Si-PVs as the stationary component in our discussion.32 Considering the bandgap of silicon (∼1.1 eV), to maximize the conversion of solar energy, the PL emission of LSC luminophores should be close to ∼1000 nm. This ensures sufficient photon absorption and matches the high EQE range of Si-PV cells. However, for narrow bandgap luminophores, the process of absorbing high-energy photons and then emitting near-infrared light results in thermalization losses in the LSC-PV system. Given that SF materials exhibit effective sunlight absorption of up to ∼500 nm and can overcome thermalization losses by multiplying luminescence, we propose an optical management scheme for tandem LSCs (Fig. 1b), which effectively mitigates the contradiction between absorption efficiency and thermalization losses. These tandem LSCs are constructed by SF luminophore-based LSCs as the top layer (green region in Fig. 1b) and narrow bandgap luminophore-based LSCs as the bottom layer (red region in Fig. 1b).
In this work, we identify six representative materials that hold significant promise in the current stage of LSC research. These materials include CsPbCl3:Yb3+ NCs, CsPbClxBr3−x:Yb3+ NCs and NaGdF4:Yb–tetracene NCs, serving as the PM materials. Additionally, we analyze Mn2+-doped CdxZn1−xS/ZnS QDs with negligible reabsorption, CuInSe2/ZnS QDs with broad absorption and a larger Stokes shift, and non-toxic CDs. We use Monte Carlo (MC) simulation and recognized methods of calculation to predict the different LSC parameters, such as external quantum efficiency (ηext), internal quantum efficiency (ηint) and concentration factor (C). For luminophores with unavoidable reabsorption, such as CuInSe2/ZnS QDs and red CDs, the constructed LSCs by them exhibit competitiveness in small-size LSCs. For luminophores with negligible reabsorption, they are quite suitable for large-area LSCs. Under optimal PLQY, NaGdF4:Yb–tetracene-based LSCs can achieve a size-independent superior ηext of 18.8%, which is much higher than the efficiency reported so far. We adopt NaGdF4:Yb–tetracene-based LSCs and CuInSe2/ZnS QD-based LSCs to construct a system of tandem LSCs. The ηext of the tandem system reaches 27.6% for L = 10 cm, and the PCE exceeds 11% under optimal PLQY. In addition, the PCE reaches ∼9% when L = 100 cm due to the reabsorption of the bottom layer of tandem LSCs. In the context of commercialized silicon-based cells, our simulation results demonstrate the efficiency bottleneck of LSCs at this stage and provide reliable theoretical support for their commercialization.
Experimental
(I) Synthesis of NaGdF4:Yb NCs
NaGdF4:Yb NCs were synthesized by hot-injection following procedures reported by Han et al.31 A water solution (2 mL) containing Gd(Ac)3 (0.2 mmol) and Yb(Ac)3 (0.2 mmol) was mixed with oleic acid (3.5 mL) and 1-octadecene (10.5 mL) in a 50 mL flask, followed by heating at 150 °C for 2 h. Thereafter, the reactant was cooled to 50 °C, and a methanol solution (6 mL) containing NH4F (1.36 mmol) and NaOH (1 mmol) was added. The mixed solution was stirred for 30 min. The reaction temperature was then increased to 100 °C to remove the methanol from the reaction solution. After that, the reactant was heated at 270 °C under a nitrogen atmosphere for 1 h, followed by cooling to room temperature. The target product is obtained by centrifuging.(II) Synthesis of CsPbCl3:Yb3+ NCs
CsPbCl3:Yb3+ NCs were synthesized by hot-injection following the procedures reported by Luo et al.12 Briefly, 5.0 mL 1-octadecene, 0.5 mL oleyl amine, 1.0 mL oleic acid, 0.2 mmol Pb(OAc)2·3H2O, 280 μL of 1 M CsOAc in ethanol, and 0.16 mmol Yb(OAc)3·xH2O were loaded into a 50 mL flask. The solution was degassed at room temperature for 5 min and at 110 °C for 1 hour. The reaction was then switched to an N2 atmosphere and heated to 240 °C. At this temperature, 0.2 mL chlorotrimethylsilane (TMS-Cl) in 0.5 mL 1-octadecene was swiftly injected. The target product is obtained by cooling the flask rapidly and centrifuging.(III) Synthesis of CsPbClxBr3−x:Yb3+ NCs
CsPbClxBr3−x:Yb3+ NCs were obtained by anion exchange reported by Milstein et al.33 Briefly, the as-synthesized CsPbCl3:Yb3+ NCs were dissolved in hexane, and the bromotrimethylsilane (TMS-Br) was added to the reaction under nitrogen atmosphere until the onset of absorption of the sample reached 490 nm.(IV) Synthesis of CuInSe2/ZnS QDs
CuInSe2/ZnS QDs were synthesized by hot injection following procedures reported by Wu et al.15 0.6 mmol In(Ac)3, 0.6 mmol CuI, 6 mL oleyl amine and 6 mL 1-octadecene were loaded into a three-neck flask, heated to 100 °C and degassed for 30 min. The mixture was then heated to 210 °C under N2 atmosphere. Next, by dissolving 1.2 mmol Se pellets in 3 mL oleyl amine and 0.9 mL diphenylphosphine, the Se-solution was injected into the above mixture at 210 °C. The reaction was heated to 230 °C for ZnS shell growth. The ZnS-solution was prepared by dissolving 5 mmol Zn(St)2 in 10 mL 1-octadecene, 5 mL oleic acid and 5 mL dodecanethiol at 150 °C for 10 min. The solution was injected in the CuInSe2 core solution at 2 h intervals between each injection and 2 mL per injection. After the last injection, the reaction was kept at 230 °C for 4 h. The target product was obtained by cooling the flask rapidly and centrifuging.(V) Synthesis of CdxZn1−xS/ZnS QDs
5 mL dodecanethiol and 10 mL 1-octadecene were loaded into a three-neck flask and kept under vacuum at 40 °C for 1 h, which was then cooled to room temperature and changed to N2 atmosphere. 5 mL of the Zn-solution (1 mmol Zn(OAc)2·2H2O dissolved in 0.8 mL oleyl amine and 9.2 mL 1-octadecene), 5 mL of the Cd-solution (1 mmol CdO dissolved in 2 mL oleic acid and 8 mL 1-octadecene), 5 mL of the Mn-solution (0.05 mmol Mn(OAc)2·4H2O dissolved in 1 mL oleyl amine and 9 mL 1-octadecene) and 5 mL of the S-solution (4.0 mmol S powder dissolved in 10 mL 1-octadecene) were added to the flask and heated to 230 °C under N2 atmosphere. The mixture was kept at this temperature for 1 min. Then, 15 mL of the Zn-solution (4 mmol Zn(OAc)2·2H2O dissolved in 3 mL oleyl amine and 7 mL 1-octadecene) was added dropwise into the reaction mixture six times (2.5 mL per time) at 10 min intervals. The target product is obtained by cooling the flask rapidly after 10 min reaction and centrifuging.(VI) Synthesis of red CDs
Red CDs were prepared by solvothermal synthesis using the literature method.34 10 mg 1,3-dihydroxynaphthalene and 40 mg KIO4 were dissolved in ethanol (10 mL), and the solution was then transferred to a poly(tetrafluoroethylene) (Teflon)-lined autoclave (25 mL) and heated at 180 °C for 1 h. The target product is obtained by cooling naturally and purifying via silica column chromatography using a mixture of methyl alcohol and dichloromethane as the eluent.Results and discussion
(I) The luminophores of LSCs
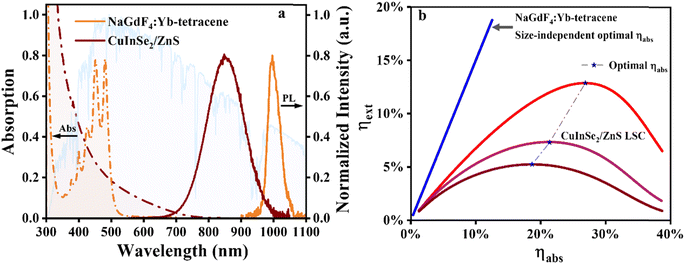
To explore the possible future optimal efficiency of LSCs in this field of solar windows, in this work, we select the following six highly promising materials for our analysis: CsPbCl3:Yb3+ NCs, CsPbClxBr3−x:Yb3+ NCs, CuInSe2/ZnS QDs, Mn2+-doped CdxZn1−xS/ZnS QDs, red CDs and NaGdF4:Yb–tetracene NCs. The absorption and emission spectra of NaGdF4:Yb–tetracene NCs and CuInSe2/ZnS QDs are shown in Fig. 2a. The absorption and emission spectrum of CsPbCl3:Yb3+ NCs, CsPbClxBr3−x:Yb3+ NCs, Mn2+-doped CdxZn1−xS/ZnS QDs and red CDs are shown in Fig. S1a–d,† respectively.For the Yb3+-doped luminophores, we categorize both QC-based LSCs and SF-based LSCs as PM-LSCs. The PM-LSCs imply that, under ideal conditions, these materials can absorb one high-energy photon and subsequently emit two low-energy photons, thereby increasing the theoretical limit of PLQY to 200%. These materials reduce thermalization losses, make the Stokes shift of the luminophores increase greatly in the process of energy transfer, and achieve negligible reabsorption. These advantages make PM materials one of the most promising candidates for LSCs. The emissive 2F5/2 → 2F7/2 f–f transition of Yb3+, which has an energy gap (Ef–f) of ∼1.25 eV, matches the high-efficiency region of commercialized silicon-based PV cells. The energy gaps (Eg) of CsPbCl3 NCs and CsPbBr3 NCs are ∼3.05 eV and ∼2.39 eV, respectively. According to the law of conservation of energy, the energy bandgap consistent with Eg > Ef–f of the CsPbClxBr3−x NCs can be used as carriers for QC.33 Therefore, based on our previous work in which we first introduced the QC materials into LSCs,12 we choose the CsPbCl3:Yb3+ NCs and CsPbClxBr3−x:Yb3+ NCs with the Eg of ∼2.53 eV for use in simulations to predict the optimal efficiency of LSCs.
For SF-based LSCs, we tend to choose NaGdF4:Yb–tetracene NCs as the luminophores for analysis. In the study by Han et al., they demonstrated that triplet energy can be transferred to Yb3+ luminescence based on NaGdF4:Yb–tetracene NCs.31 In the progress of SF, a photogenerated singlet exciton (S1) is converted into two triplet excitons (T1). Intriguingly, SF also proceeds very efficiently in endothermic systems, where E(S1) < 2 × E(T1), which overcomes energy barriers (Eb = 2E(T1) − E(S1)) of up to 200 meV.35 Therefore, the cutoff of the absorption spectrum of tetracene is close to 540 nm (as shown in Fig. 2a), which provides an appreciable absorption efficiency for its use as the LSC luminophores. In contrast, CsPbClxBr3−x:Yb3+ NCs can absorb only the solar photons before ∼490 nm. These results show that NaGdF4:Yb–tetracene NCs are very promising materials for LSC applications and are better than QC-based LSCs.
Excluding PM-LSCs, research in this field has predominantly focused on luminophores with minimal reabsorption. Mn2+-doped QDs are the solution used to increase the Stokes shift and achieve no reabsorption. Consequently, we chose Mn2+-doped CdxZn1−xS/ZnS QDs as an analytical sample, as reported by Wu et al.15 However, the efficiency of solar energy absorption leads to their limitation as the LSC luminophores. Instead, copper-based ternary QDs provide sufficient absorption efficiency. Although their reabsorption is rather small, the loss of reabsorption is unavoidable as the size of the LSCs increases. We selected CuInSe2/ZnS QDs, which have a large absorption efficiency of solar energy, for our evaluation. Recently, in light of the growing interest in environmentally friendly and sustainable materials within the scientific community, CDs have emerged as promising new materials without toxicity. Numerous studies have demonstrated that CDs can serve as efficient luminophores for LSCs. Consequently, we included red CDs as one of our predicted luminophores for use. The red CDs have an absorption onset of 700 nm and an emission center wavelength of 599 nm. Large reabsorption is an unavoidable problem for this class of materials.
(II) Optimal concentration of luminophores
The key parameters commonly associated with LSCs include ηint, ηext, C, and external quantum efficiency for PV-LSC systems (EQELSC-PV) and PCE. Klimov et al. derived expressions for each parameter of LSCs under ideal conditions of single-wavelength excitation.36 In this work, we discuss the theoretical efficiency that can be achieved by the LSCs under the conditions of practical application and the irradiation of the AM 1.5 solar spectrum (Sin(λ)). Therefore, we take the wide spectrum of conditions and the scattering coefficient (s) into consideration. The spectral averaging equations are expressed as follows: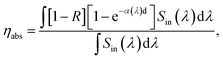 | (1) |
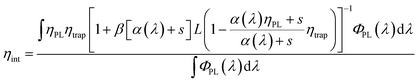 | (2) |
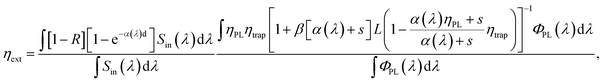 | (3) |
Liu et al. categorized LSCs according to their structure into full polymer LSCs, top-coated thin film LSCs, liquid LSCs and laminated LSCs.37 We can analyze the different structures of LSCs by calculating the effective absorption coefficient and transforming them into the structure of full polymer LSCs. Consequently, in this work, we use a full polymer LSC with a thickness of d = 0.5 cm as the model for the analysis. The L of LSCs varies from 5 to 150 cm. We emphasize that the LSCs with a special waveguide structure are not within the scope of discussion in this work.
Then, we calculated the spectral data of the six luminophores to determine the optimal concentration of different LSCs. Under optimal PLQY and ideal situation without scattering, we find that NaGdF4:Yb–tetracene-based LSCs have size-independent optimal ηabs due to their no reabsorption and ηext has a linear relationship with ηabs, which is shown as a blue line in Fig. 2b. The QC-LSCs and Mn2+-doped CdxZn1−xS/ZnS-based LSCs governed by the same rule and the results are shown in Fig. S2a–c.† Therefore, we choose the maximum ηabs of the four luminophores for use in this work. For CuInSe2/ZnS-based LSCs, as the value of L increases, the optimal ηabs decreases progressively (as depicted in Fig. 2b). This phenomenon arises because higher ηabs values lead to increased reabsorption losses in large-area LSCs, resulting in the existence of an optimal point for ηabs. Red CD-based LSCs have a similar tendency, as shown in Fig. S2d.† Our investigation reveals that the optimal ηabs for red CD-based LSCs exhibits a more rapid decline compared to CuInSe2/ZnS-based LSCs. Specifically, this trend indicates that as reabsorption increases, the size-dependent ηabs experiences a faster decrease. We also calculate the results under the situation that considers the scattering and unideal PLQY. According to the study of Wu et al., their LSCs have a scattering factor of 0.012 cm−1, which represents some of the possible shortcomings of existing preparation processes.15 Therefore, we set the scattering factor to be 0.012 cm−1, and the results are shown in Fig. S3 and S4.† The size-dependent ηext decreases as the L increases for the six materials. In particular, for NaGdF4:Yb–tetracene-based LSCs, the optimal ηext decreases from 16.15% to 10.95% when the L increases from 10 cm to 100 cm under the condition that the PLQY is 180% and the scattering factor is 0.012 cm−1. Moreover, QC-based LSCs and Mn2+-doped CdxZn1−xS/ZnS-based LSCs have a similar tendency. Hence, optimizing the PLQY of the luminophores and refining the fabrication processes are crucial for the practical application of LSCs.
(III) MC simulation results for LSCs
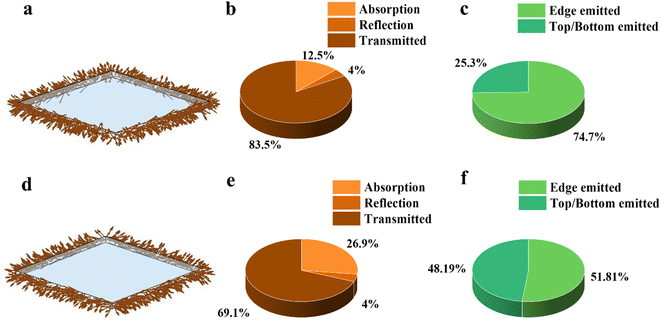
To estimate the performance of six luminophore-based LSCs, we build an appropriate MC simulation model for all the luminophores. We used the mentioned LSC model, and the details of the MC simulation are described in the ESI.† First, we simulate the ideal PLQY situation using optimal ηabs, and we set the number of incident photons to be 106, which is enough to get stabilized results. The simulation result plots of 10 cm-LSC, as well as the photon going statistics are displayed in Fig. 3 and S5,† respectively. The brown statistic graphs represent the destination of the incident photons, which can demonstrate the absorption capacity of different luminophores (Fig. 3b and e). The green statistic graphs represent the destination of the photons emitted by the luminophores, which demonstrates the efficiency of photon transfer to the edges (ηedge) (Fig. 3c and f). According to the density of outgoing photons at the edges of the ray tracing schematic of LSCs (Fig. 3a, d, S5a, d, g and j†), NaGdF4:Yb–tetracene-based LSCs and CuInSe2/ZnS-based LSCs have excellent ηext than other luminophores-based LSCs. The CuInSe2/ZnS-based LSCs and red CD-based LSCs have relatively low ηedge, which are 51.81% and 39.8% due to their reabsorption, respectively. Other luminophore-based LSCs have the ηedge approach of 75% due to their negligible reabsorption. Then, we simulate the 100 cm LSCs under an ideal situation, as shown in Fig. S6.† The ηedge of CuInSe2/ZnS-based LSCs decreases to 22.59%, and the ηedge of red CD-based LSCs decreases to 6.57%. For the other four luminophores without absorption, the efficiency remains unchanged when the L enlarges. Second, the unideal PLQY situation and scattering factor are included in the discussion. The MC simulation results are shown in Fig. S7 and S8,† and the trends in efficiency are consistent with the previous section. All the results demonstrate that the NaGdF4:Yb–tetracene-based LSCs are the most promising luminophores in the large-area LSCs, and CuInSe2/ZnS-based LSCs have excellent efficiency in relatively small-area LSCs.To better show the performance of each important parameter of LSCs under the situation of considering the scattering factor, we set the PLQY as 200%, 180% and 160% for three PM luminophores and the scattering factor as 0.012 cm−1. For the other three luminophores, we set the PLQY to be 100%, 80% and 60%. The results of ηint as well as the ηext of the LSCs of the six luminophores are shown in Fig. S9–S14.† The ηint and ηext of the LSCs of all the six luminophores decreases with increasing size, but the rate of decrease varies depending on the differences in luminophore's reabsorption. To visually describe the variation of ηint and ηext with L, we first obtain two predictive curves by changing the β and length in eqn (1) and (2). Based on the results obtained from the six luminophores (as depicted in Fig. S9–S14†), the two dashed lines in each case correspond to the calculated outcomes for β values of 1.4 and 1.8, respectively. Notably, we observed that all the MC simulation results fell within the range defined by these two dashed curves, but they did not precisely align with the calculated results. We then set the value of β as β = 1.4 + 0.5(L/150)1/2, and we obtained a new solid that can perfectly match our MC simulation results for all the six luminophores (Fig. S9–S14†). The PLQY plays a critical role in determining the ηint and ηext. For CuInSe2/ZnS-based LSCs (shown in Fig. S9†), as the value of PLQY increases from 60% to 100%, there is a substantial increase in ηint and ηext over the entire range of L. Notably, when the PLQY reaches 100%, both ηint and ηext are approximately twice as high as when the PLQY is 60%. For instance, at an L of 5 cm, the ηint is 52.92% and ηext is 14.56%. However, as the LSC size increases (e.g., L = 150 cm), the ηint decreases to 8.86%, and ηext reduces to 2.43%. These findings highlight that even for copper-based ternary quantum dots with relatively low reabsorption, efficiency decline remains significant in large LSCs. For red CD-based LSC (shown in Fig. S10†), the ηint and ηext decay at a faster rate than CuInSe2/ZnS-based LSCs with increasing L. We believe that this is because the reabsorption of red CDs is much greater than that of the CuInSe2/ZnS QDs. For luminophores without reabsorption losses, the L-dependence of the ηint and ηext are only related to the scattering factor. Even though the scattering factor is only 0.012 cm−1, the efficiency of these luminophore-based LSCs still decays very badly (Fig. S11–S14†). This means that the process is equally crucial for preparing large-area LSCs. All the results under optimal PLQY and a scattering factor of 0.012 cm−1 are shown in Fig. S15.†
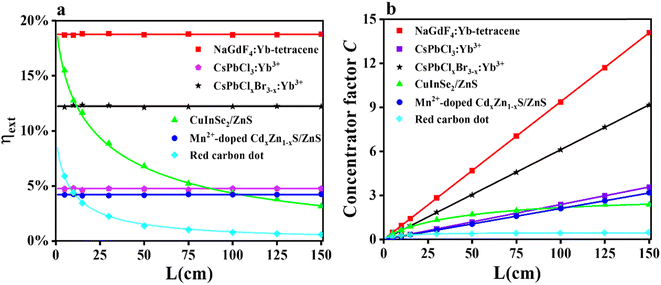
We summarized the MC simulation results and computational predictions for the six luminophores under the ideal case, as depicted in Fig. 4. For the ηext, we find that NaGdF4:Yb–tetracene-based LSCs have the best ηext of 18.8% in all the sizes of LSCs. It is much higher than the QC-based LSCs due to its excellent ability of absorption. We can emphasize that the NaGdF4:Yb–tetracene is a very promising luminophore for LSCs if we can optimize its PLQY to the limit. For the CuInSe2/ZnS-based LSCs, it is still an excellent material for luminophore at this stage due to its large Stokes shift and very strong light-absorbing capacity. In a relatively small area, the CuInSe2/ZnS-based LSCs can achieve higher ηext than the CsPbClxBr3−x:Yb3+-based LSCs.
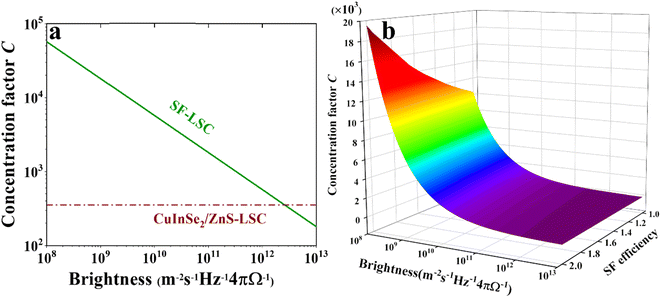
For the concentrating factor, we can observe from Fig. 4b that the CuInSe2/ZnS and red CDs with reabsorption loss show saturation with increasing LSC size. For the other four luminophores without reabsorption loss, none of them saturated in the range of LSC sizes we simulated. It is worth noting that C quantifies the real increase in the electrical power output compared to the original PV cell. If C > 1, we can assume that the current of the PV cells increases under the action of an LSC. Red CD-based LSCs show a small concentration factor that is smaller than 1 due to their large reabsorption. This means that the red CDs may not be suitable for constructing LSC. Moreover, CuInSe2/ZnS-based LSCs show their potential to achieve a concentration larger than 1 because of their high ηabs and relatively small reabsorption. Consequently, luminophores with reabsorption make it difficult to achieve a large concentration factor. The concentration factor of CsPbCl3:Yb3+ NC-based LSCs and Mn2+-doped CdxZn1−x/ZnS-based LSCs can reach ∼3 when the L is 150 cm due to their poor absorption of solar energy. If the scattering factor is considered, both of the two LSCs have a concentration factor of ∼1 when the L is 150 cm (Fig. S15b†). Notably, CsPbClxBr3−x:Yb3+ NC-based LSCs and NaGdF4:Yb–tetracene-based LSCs show their powerful potential to achieve large concentration factors in the large LSC devices. For NaGdF4:Yb–tetracene-based LSCs, factor C can exceed 10.
Next, we analyze the thermodynamic limits of the aforementioned LSCs. Based on the second law of thermodynamics, Eli Yablonovitch38 derived the formula of thermodynamic limit C as follows:
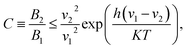 | (4) |
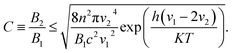 | (5) |
It is very exciting to find that the concentration factor is closely related to the intensity of the incident light. Subsequently, we bring our simulation objects, NaGdF4:Yb–tetracene-based LSCs and CuInSe2/ZnS-based LSCs, into eqn (4) and (5), respectively. If the emission of these luminophores is narrow enough, the NaGdF4:Yb–tetracene NCs have an emission at hν2 = 1.253 eV and CuInSe2/ZnS QDs have an emission at hν2 = 1.459 eV. For NaGdF4:Yb–tetracene-based LSCs, hν1 = 2 × 1.253 + 0.24 = 2.746 eV, where the value of 0.24 is the thermal loss. For CuInSe2/ZnS-based LSCs, hν1 = 1.459 + 0.16 = 1.619 eV, where the value of 0.16 eV represents the Stokes shift.
The results (Fig. 5) show a significant difference against our real simulations because the thermodynamic concentration limit can reach 103 to 105 for NaGdF4:Yb–tetracene-based LSCs and 353.5 for CuInSe2/ZnS-based LSCs. Achieving the thermodynamic concentration limit requires an ideal PLQY and an ideal LSC cavity. Moreover, this limiting value is derived under the ideal conditions of single-wavelength light incidence, and emission at the center wavelength, so its value is much larger than our simulation results. The three-dimensional coordinate plot in Fig. 5b further demonstrates the close correlation between the concentrating factor limit of NaGdF4:Yb–tetracene-based LSCs and the PLQY of the luminophores. Therefore, optimizing the efficiency of these luminophores is of paramount importance. Notably, PM-LSCs have a high light-concentration factor in low-brightness environments, whereas QD-based LSCs are not influenced. This remains an important reference for our study although it has not been experimentally confirmed.
(IV) Tandem LSCs
For single-layer LSCs, their efficiency is limited because luminophores with wide bandgaps face the limitation of the absorption efficiency of sunlight while those with narrow bandgaps face the unavoidable thermalization losses caused by the relaxation of high-energy photons to band-edge luminescence. Therefore, tandem LSCs are considered an effective solution for breaking through the efficiency limit. In this work, we choose the NaGdF4:Yb–tetracene-based LSCs as the top layer and CuInSe2/ZnS-based LSCs as the bottom layer (as shown in Fig. 6a). We emphasize that in practical applications, it is the entire system where LSCs are coupled to PVs that need to be investigated rather than just considering the performance of LSCs alone. Thus, EQELSC-PV and PCE should be studied, and they are strictly required to quantify all PV devices.40 If a high-performance LSC device is obtained, the alignment between the EQE curve of the PV cell and the PL emission spectrum of the LSC's luminophores significantly impacts the overall energy conversion efficiency. The EQELSC-PV can be written as follows: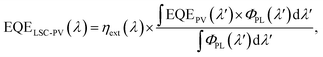 | (6) |
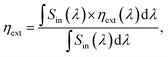 | (7) |
For the PCE of the LSC-PV system, due to the inconsistency of the spectrum emitted from the LSC edge with the solar spectrum, we introduce a spectral shaping factor, qLSC, which is defined as
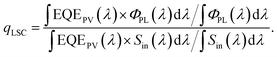 | (8) |
According to eqn (8), we can estimate the PCE of the system based on the following formula:
| PCE = qLSCηextηPV, | (9) |
We conducted MC simulations for different L values (10 cm, 30 cm, 50 cm, and 100 cm) under various conditions with optimal PLQY. The top layer luminophores varied from NaGdF4:Yb–tetracene and CsPbClxBr3−x:Yb3+ to Mn2+-doped CdxZn1−xS/ZnS. Notably, the choice of top layer luminophore significantly influences the optimal ηabs of the bottom layer. As the absorption capability of the top layer increases, leading to weaker light reaching the bottom layer, the optimal ηabs of the bottom layer decreases. Therefore, we change the ηabs of bottom LSCs when using different top layer LSCs according to the results shown in Fig. S16.† The results of PCE are shown in Fig. 6b, while those of ηext and EQELSC-PV are shown in Fig. S17.† If the top layer is Mn2+-doped CdxZn1−xS/ZnS-based LSCs, the PCE can reach 6.34% when L equals 10 cm, and it decreases to 3.35% when L equals 100 cm. In contrast, if the top layer is CsPbClxBr3−x:Yb3+-based LSCs, the PCE increases to 9% when L equals 10 cm and decreases to 6.28% when L equals 100 cm. The differences in ηabs between the two materials are marginal, and the enhancement in efficiency is attributed to photon multiplication. For NaGdF4:Yb–tetracene-based top-layer LSCs, the PCE of a tandem system can reach up to 10.9%, while the ηext reaches 27.55% for L = 10 cm. Even though when L equals 100 cm, the PCE can still reach ∼9%. If we can further shorten the half-height width of the emission spectra of the luminophores, the PCE can reach its limit of 11.7%. The tandem LSCs based on SF luminophore show great promise for commercialization, provided that we achieve the optimal PLQY of the luminophore. Our simulation results establish the efficiency limits of LSCs at this stage. Notably, these simulation data were calculated using the methodology assessed by Yang et al., authoritative experts in the field of LSCs.40
Conclusion
Through a combination of MC simulation and computational studies, we showed six promising luminophores of LSCs that are representative of the materials most likely to break through the efficiency limit of LSCs. For luminophores with large Stokes shift but still having reabsorption such as CuInSe2/ZnS QD, the constructed LSCs have competitiveness when the area is small. For luminophores without reabsorption, they are quite suitable for large-area LSCs even when L reaches 1 m. Absorption efficiency plays an important role in affecting the ηext of PM-LSCs. Consequently, NaGdF4:Yb–tetracene-based LSCs can achieve a superior ηext of 18.8%, which is much higher than the efficiency reported thus far. Intriguingly, the thermodynamic concentration limit demonstrates that PM-LSCs are more suitable for working in situations of lower incident light intensity. We emphasize that constructing PM-LSCs is one of the most promising ways to break through the efficiency bottleneck of LSCs due to their negligible reabsorption and their capability to multiply the emitted photons. Subsequently, we use NaGdF4:Yb–tetracene-based LSCs in combination with CuInSe2/ZnS-based LSCs to form the tandem LSCs. The ηext of the tandem system reaches 27.55% for L = 10 cm, and the PCE exceeds 11% under an ideal situation. Even when L equals 100 cm, the PCE could remain ∼9%. We believe that this tandem LSC system can reach the highest efficiency that can be achieved by LSCs based on existing materials. Consequently, it is crucial to work on improving the PLQY of these luminophores in future studies. To achieve excellent LSC performance under practical situations, the PLQY of the luminophores should be larger than 80%; meanwhile, the PLQY of PM luminophores should be larger than 160%. More luminophores with large Stokes shift and free absorption should be investigated, and the development of highly efficient, large-area LSCs is urgent.Data availability
The data are available from the corresponding author on reasonable request.Author contributions
Qi Nie: conceptualization, data curation, investigation, formal analysis, and writing original draft; Wenqing Li: investigation and data curation; Kuilin Li: formal analysis and validation; Xiao Luo: funding acquisition, supervision, and writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the National Natural Science Foundation of China (No. 62274024), Natural Science Foundation Program of Sichuan Province (No. 2024NSFSC0232), Key Teacher Start-Up Research Grant of UESTC (No. Y030202059018069) and Medical Engineering Innovations Program of UESTC.Notes and references
- J. Clarke and J. Searle, Nat. Energy, 2021, 6, 1087–1089 CrossRef.
- X. Zhu, M. Du, J. Feng, H. Wang, Z. Xu, L. Wang, S. Zuo, C. Wang, Z. Wang, C. Zhang, X. Ren, S. Priya, D. Yang and S. F. Liu, Angew Chem. Int. Ed. Engl., 2021, 60, 4238–4244 CrossRef CAS PubMed.
- W. H. Weber and J. Lambe, Appl. Opt., 1976, 15, 2299–2300 CrossRef CAS PubMed.
- R. Olson, R. F. Loring and M. Fayer, Appl. Opt., 1981, 20, 2934–2940 CrossRef CAS PubMed.
- K. Barnham, J. L. Marques, J. Hassard and P. O'Brien, Appl. Phys. Lett., 2000, 76, 1197–1199 CrossRef CAS.
- F. Mateen, S. Y. Lee and S.-K. Hong, J. Mater. Chem. A, 2020, 8, 3708–3716 RSC.
- J. L. Banal, B. Zhang, D. J. Jones, K. P. Ghiggino and W. W. Wong, Acc. Chem. Res., 2017, 50, 49–57 CrossRef CAS PubMed.
- X. Li, J. Qi, J. Zhu, Y. Jia, Y. Liu, Y. Li, H. Liu, G. Li and K. Wu, J. Phys. Chem. Lett., 2022, 13, 9177–9185 CrossRef CAS PubMed.
- C. Tummeltshammer, M. Portnoi, S. A. Mitchell, A.-T. Lee, A. J. Kenyon, A. B. Tabor and I. Papakonstantinou, Nano Energy, 2017, 32, 263–270 CrossRef CAS.
- B. Zhang, P. Zhao, L. J. Wilson, J. Subbiah, H. Yang, P. Mulvaney, D. J. Jones, K. P. Ghiggino and W. W. H. Wong, ACS Energy Lett., 2019, 4, 1839–1844 CrossRef CAS.
- B. Zhang, G. Lyu, E. A. Kelly and R. C. Evans, Adv. Sci., 2022, 9, e2201160 CrossRef PubMed.
- X. Luo, T. Ding, X. Liu, Y. Liu and K. Wu, Nano Lett., 2019, 19, 338–341 CrossRef CAS PubMed.
- T. A. Cohen, T. J. Milstein, D. M. Kroupa, J. D. MacKenzie, C. K. Luscombe and D. R. Gamelin, J. Mater. Chem. A, 2019, 7, 9279–9288 RSC.
- F. Meinardi, F. Bruni, C. Castellan, M. Meucci, A. M. Umair, M. La Rosa, J. Catani and S. Brovelli, Adv. Energy Mater., 2024, 14, 2304006 CrossRef CAS.
- K. Wu, H. Li and V. I. Klimov, Nat. Photonics, 2018, 12, 105–110 CrossRef CAS.
- K. Gungor, J. Du and V. I. Klimov, ACS Energy Lett., 2022, 7, 1741–1749 CrossRef CAS.
- K. Park, J. Yi, S.-Y. Yoon, S. M. Park, J. Kim, H.-B. Shin, S. Biswas, G. Y. Yoo, S.-H. Moon, J. Kim, M. S. Oh, A. Wedel, S. Jeong, H. Kim, S. J. Oh, H. K. Kang, H. Yang and C. J. Han, Nat. Photonics, 2024, 18, 177–185 CrossRef.
- S. Li, L. Li, H. Tu, H. Zhang, D. S. Silvester, C. E. Banks, G. Zou, H. Hou and X. Ji, Mater. Today, 2021, 51, 188–207 CrossRef CAS.
- A. Xu, G. Wang, Y. Li, H. Dong, S. Yang, P. He and G. Ding, Small, 2020, 16, e2004621 CrossRef PubMed.
- Y. Li, P. Miao, W. Zhou, X. Gong and X. Zhao, J. Mater. Chem. A, 2017, 5, 21452–21459 RSC.
- Z. Wang, X. Zhao, Z. Guo, P. Miao and X. Gong, Org. Electron., 2018, 62, 284–289 CrossRef CAS.
- X. Gong, W. Ma, Y. Li, L. Zhong, W. Li and X. Zhao, Org. Electron., 2018, 63, 237–243 CrossRef CAS.
- H. Y. Huang, M. J. Talite, K. B. Cai, R. J. Soebroto, S. H. Chang, W. R. Liu, W. C. Chou and C. T. Yuan, Nanoscale, 2020, 12, 23537–23545 RSC.
- J. Li, J. Chen, X. Zhao, A. Vomiero and X. Gong, Nano Energy, 2023, 115, 108674 CrossRef CAS.
- K. B. Cai, H. Y. Huang, M. L. Hsieh, P. W. Chen, S. E. Chiang, S. H. Chang, J. L. Shen, W. R. Liu and C. T. Yuan, ACS Nano, 2022, 16, 3994–4003 CrossRef CAS PubMed.
- J. Li, H. Zhao, X. Zhao and X. Gong, Adv. Funct. Mater., 2024, 34, 2404473 CrossRef.
- A. Rao and R. H. Friend, Nat. Rev. Mater., 2017, 2, 17063 CrossRef CAS.
- V. Gray, Z. Zhang, S. Dowland, J. R. Allardice, A. M. Alvertis, J. Xiao, N. C. Greenham, J. E. Anthony and A. Rao, J. Phys. Chem. Lett., 2020, 11, 7239–7244 CrossRef CAS PubMed.
- V. Gray, D. T. W. Toolan, S. Dowland, J. R. Allardice, M. P. Weir, Z. Zhang, J. Xiao, A. Klimash, J. F. Winkel, E. K. Holland, G. M. Fregoso, J. E. Anthony, H. Bronstein, R. Friend, A. J. Ryan, R. A. L. Jones, N. C. Greenham and A. Rao, J. Am. Chem. Soc., 2024, 146, 7763–7770 CrossRef CAS PubMed.
- T. K. Baikie, B. Daiber, E. Kensington, J. Xiao, N. C. Greenham, B. Ehrler and A. Rao, Joule, 2024, 8, 799–816 CrossRef CAS.
- S. Han, R. Deng, Q. Gu, L. Ni, U. Huynh, J. Zhang, Z. Yi, B. Zhao, H. Tamura, A. Pershin, H. Xu, Z. Huang, S. Ahmad, M. Abdi-Jalebi, A. Sadhanala, M. L. Tang, A. Bakulin, D. Beljonne, X. Liu and A. Rao, Nature, 2020, 587, 594–599 CrossRef CAS PubMed.
- K. Yoshikawa, H. Kawasaki, W. Yoshida, T. Irie, K. Konishi, K. Nakano, T. Uto, D. Adachi, M. Kanematsu, H. Uzu and K. Yamamoto, Nat. Energy, 2017, 2, 17032 CrossRef CAS.
- T. J. Milstein, K. T. Kluherz, D. M. Kroupa, C. S. Erickson, J. J. De Yoreo and D. R. Gamelin, Nano Lett., 2019, 19, 1931–1937 CrossRef CAS PubMed.
- Z. Wang, F. Yuan, X. Li, Y. Li, H. Zhong, L. Fan and S. Yang, Adv. Mater., 2017, 29, 1702910 CrossRef PubMed.
- H. L. Stern, A. Cheminal, S. R. Yost, K. Broch, S. L. Bayliss, K. Chen, M. Tabachnyk, K. Thorley, N. Greenham, J. M. Hodgkiss, J. Anthony, M. Head-Gordon, A. J. Musser, A. Rao and R. H. Friend, Nat. Chem., 2017, 9, 1205–1212 CrossRef CAS PubMed.
- V. I. Klimov, T. A. Baker, J. Lim, K. A. Velizhanin and H. McDaniel, ACS Photonics, 2016, 3, 1138–1148 CrossRef CAS.
- X. Liu, D. Benetti, J. Liu, L. Jin and F. Rosei, Nano Energy, 2023, 111, 108438 CrossRef CAS.
- E. Yablonovitch, J. Opt. Soc. Am., 1980, 70, 1362–1363 CrossRef.
- T. K. Baikie, A. Ashoka, A. Rao and N. C. Greenham, PRX Energy, 2022, 1, 033001 CrossRef.
- C. Yang, H. A. Atwater, M. A. Baldo, D. Baran, C. J. Barile, M. C. Barr, M. Bates, M. G. Bawendi, M. R. Bergren, B. Borhan, C. J. Brabec, S. Brovelli, V. Bulović, P. Ceroni, M. G. Debije, J.-M. Delgado-Sanchez, W.-J. Dong, P. M. Duxbury, R. C. Evans, S. R. Forrest, D. R. Gamelin, N. C. Giebink, X. Gong, G. Griffini, F. Guo, C. K. Herrera, A. W. Y. Ho-Baillie, R. J. Holmes, S.-K. Hong, T. Kirchartz, B. G. Levine, H. Li, Y. Li, D. Liu, M. A. Loi, C. K. Luscombe, N. S. Makarov, F. Mateen, R. Mazzaro, H. McDaniel, M. D. McGehee, F. Meinardi, A. Menéndez-Velázquez, J. Min, D. B. Mitzi, M. Moemeni, J. H. Moon, A. Nattestad, M. K. Nazeeruddin, A. F. Nogueira, U. W. Paetzold, D. L. Patrick, A. Pucci, B. P. Rand, E. Reichmanis, B. S. Richards, J. Roncali, F. Rosei, T. W. Schmidt, F. So, C.-C. Tu, A. Vahdani, W. G. J. H. M. van Sark, R. Verduzco, A. Vomiero, W. W. H. Wong, K. Wu, H.-L. Yip, X. Zhang, H. Zhao and R. R. Lunt, Joule, 2022, 6, 8–15 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta03247k |
| This journal is © The Royal Society of Chemistry 2024 |