Open Access Article
Open Access ArticleDetermination of collision mechanisms at low energies using four-vector correlations
P. G.
Jambrina
 *a,
J. F. E.
Croft
*a,
J. F. E.
Croft
 b,
N.
Balakrishnan
b,
N.
Balakrishnan
 c,
Hua
Guo
c,
Hua
Guo
 d and
F. J.
Aoiz
d and
F. J.
Aoiz
 e
e
aDepartamento de Química Física, Universidad de Salamanca, Salamanca 37008, Spain. E-mail: pjambrina@usal.es
bDepartment of Chemistry, Durham University, Durham, DH1 3LE, UK. E-mail: james.f.croft@durham.ac.uk
cDepartment of Chemistry and Biochemistry, University of Nevada, Las Vegas, Nevada 89154, USA. E-mail: naduvala@unlv.nevada.edu
dDepartment of Chemistry and Chemical Biology, University of New Mexico, Albuquerque, New Mexico 87131, USA. E-mail: hguo@unm.edu
eDepartamento de Química Física, Universidad Complutense, Madrid 28040, Spain. E-mail: aoiz@quim.ucm.es
First published on 20th February 2024
Abstract
In molecular dynamics, a fundamental question is how the outcome of a collision depends on the relative orientation of the collision partners before their interaction begins (the stereodynamics of the process). The preference for a particular orientation of the reactant complex is intimately related to the idea of a collision mechanism and the possibility of control, as revealed in recent experiments. Indeed, this preference holds not only for chemical reactions involving complex polyatomic molecules, but also for the simplest inelastic atom–diatom collisions at cold collision energies. In this work, we report how the outcome of rotationally inelastic collisions between two D2 molecules can be controlled by changing the alignment of their internuclear axes under the same or different polarization vectors. Our results demonstrate that a higher degree of control can be achieved when two internuclear axes are aligned, especially when both molecules are relaxed in the collision. The possibility of control extends to very low energies, even to the ultracold regime, when no control could be achieved just by the alignment of the internuclear axis of one of the colliding partners.
1 Introduction
The outcome of a bimolecular collision is determined by the chemical nature of the colliding partners, their internal states, the relative translational (collision) energy, as well as their relative orientation as they approach each other (the stereodynamics of the process). This statement holds for complex chemical reactions, where the dependence of the reactivity on the stereodynamics of the reaction is intimately related to the idea of a reaction mechanism and can be traced back to the anisotropy (direction) of the chemical bonds that are broken or formed,1–6 and also applies to simpler reactions between an atom and a diatomic molecule.7–11 On top of this, stereodynamics determines the properties of the products formed during chemical reactions, such as for example the propensity for given Λ-doublet states experimentally found in the O(3P) + D2 reaction.12–15For inelastic collisions no bonds are formed or broken, and the products of the collision differ from the reactants just in the rotational and/or vibrational energy levels, so it is not that obvious how (or if) the outcome of the collision will be modified by the stereodynamics of the collision. However, experiments have consistently found that the outcome of inelastic collisions is also strongly dependent on the relative orientation of the molecules before the collision (see for example ref. 16–30). Recent advances combining Stark-induced adiabatic Raman passage (SARP) with a co-expansion beam have made it possible to study the stereodynamics of inelastic collisions at cold energies (below 1 K).25–30 At these energies, scattering is dominated by quantum resonances, and calculations have proved that by selecting a suitable relative orientation of the reactants it is possible to modify (control) to a significant extent the integral (ICS) and differential cross sections (DCS).31–42
The stereodynamics of a process can be quantified in terms of correlations between the vector properties of the collision system.43–51 The simplest, the differential cross section, quantifies the correlation the initial (k) and final (k′) relative velocities of the collision partners. Three vector correlations involving the direction of the rotational angular momentum of one of the colliding partners (jA) as well as k and final k′ provides information about how the collision outcome will depend on the direction jA with respect to k. Analysis of this vector correlation is necessary to account for most of the experiments cited above, and to describe the collision mechanism for reactive or inelastic collisions between an atom and a diatomic molecule. Recent breakthrough experiments20,30 have been able to measure 4-vector correlations involving k, k′, jA, and either the direction of the angular momentum after the collision 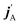 20 or the direction of the angular momentum of the other partner (jB).30 The latter measurements were successfully simulated from first principles, combining quantum scattering calculations on an accurate potential energy surface and a formalism that describes up to four vector correlations.41
20 or the direction of the angular momentum of the other partner (jB).30 The latter measurements were successfully simulated from first principles, combining quantum scattering calculations on an accurate potential energy surface and a formalism that describes up to four vector correlations.41
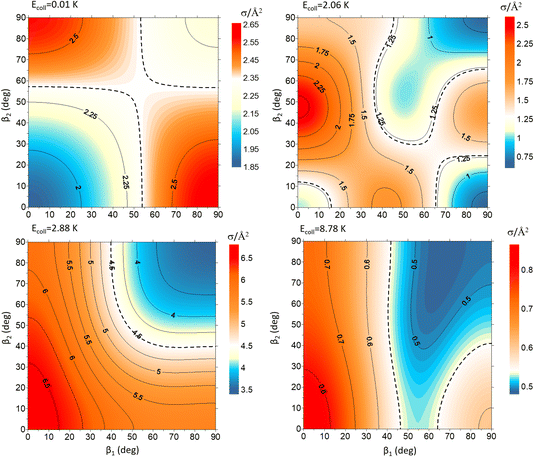
In this work, we go beyond the simulation of the experimental angular distributions and study how the collision mechanism for the inelastic collisions between two diatomic molecules can be determined through the analysis of the k–jA–jB–k′ 4-vector correlation, even for situations in which the polarisation of the two incoming molecules is different. Crossed molecular beam experiments in which the two collision partners are independently polarised, for instance using SARP schemes for the two beams, are conceivable. Of course, performing such experiments at cold energies entails additional difficulties. However, the successes achieved over the last decade with merged beams52–55 or Stark56–58 and Zeeman59 decelerators suggest that such experiments may be feasible in the near future. The system that we will study is the D2(v, j = 2) + D2(v, j = 2) at cold energies, as this was the system studied in ref. 30. In particular, we will focus on quantum effects such as resonances, their influence on the reaction mechanism, and how they are modified by the alignment and orientation of the collision complex. We will analyze three different scenarios:
| (a) D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 2) + D2(v = 2, j = 0) |
| (b) D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 0) + D2(v = 2, j = 0) |
| (c) D2(v = 2, j = 2) + D2(v = 2, j = 2) → D2(v = 2, j = 2) + D2(v = 2, j = 0) |
In cases (a) and (c) only one of the D2 molecules is relaxed from j = 2 to j = 0, with the difference that in case (a) we have two “distinguishable” molecules, while in case (c) we have two identical D2(v = 2) molecules. Case (b) corresponds to a situation in which both molecules are relaxed during the collision. Cases (a) and (b) involve the rotational excitation of one of the partners (pure rotational pumping), whilst case (c) involves the vibrational excitation of the two partners as in a recent work using SARP.30
The paper is organized as follows. The equations needed to calculate the 4-vector correlations and the details of the scattering calculations are shown in Section 2. Results for the three different cases are discussed in Section 3, while the main conclusions are summarized in Section 4.
2 Methods
2.1 Scattering calculations
Full dimension QM scattering calculations were performed using the time-independent close-coupling formalism and a modified version of the TwoBC code60 on the recent PES of Zuo et al.61 In these calculations, the two D2 molecules were treated as indistinguishable molecules, following the convention of Huo and Green.62 In the calculations, the close coupling equations were propagated using a log-derivative method from 3 to 103a0 with a step size of 0.05a0. Calculations were carried out for each parity and exchange permutation symmetry, up to a maximum value of the total angular momentum Jmax = 16.42The asymptotic scattering amplitude was obtained in the orbital angular momentum representation. However, for our purposes here it is more convenient to convert the scattering amplitudes into the helicity or body-fixed representation. The transformation of the T-matrix (T = I − S) from the space-fixed (SF) to the helicity representation is given by63
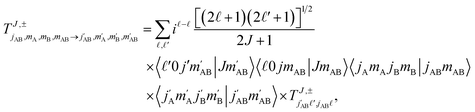 | (1) |
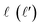 is the initial (final) orbital angular momentum, and jA, jB,
is the initial (final) orbital angular momentum, and jA, jB, 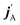 and
and 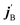 are the initial and final rotational angular momentum quantum numbers of A and B molecules. The quantum numbers mA/B and
are the initial and final rotational angular momentum quantum numbers of A and B molecules. The quantum numbers mA/B and 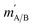 are the projections of jA/B and
are the projections of jA/B and 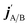 onto the initial relative velocity vector and jAB = jA + jB and
onto the initial relative velocity vector and jAB = jA + jB and 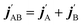 . The indices that denote the asymptotic channel (initial and final rovibrational states) have been omitted for clarity. In eqn (1) the ± index denotes the exchange permutation symmetry index of the molecules, and the last two Clebsch–Gordan coefficients guarantee that mAB = mA + mB and
. The indices that denote the asymptotic channel (initial and final rovibrational states) have been omitted for clarity. In eqn (1) the ± index denotes the exchange permutation symmetry index of the molecules, and the last two Clebsch–Gordan coefficients guarantee that mAB = mA + mB and 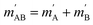 , so in what follows mAB and
, so in what follows mAB and 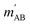 will be omitted for the sake of simplicity. From the S matrix in the helicity representation, the scattering amplitude can be calculated as:
will be omitted for the sake of simplicity. From the S matrix in the helicity representation, the scattering amplitude can be calculated as: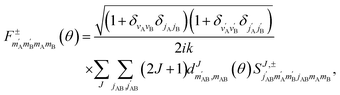 | (2) |
 is an element of the Wigner reduced rotation matrix. The
is an element of the Wigner reduced rotation matrix. The 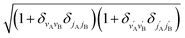 factor only applies for inelastic scattering between indistinguishable molecules. 64,65
factor only applies for inelastic scattering between indistinguishable molecules. 64,65
The exchange-permutation symmetrized differential cross section (DCS) is given in terms of the corresponding scattering amplitudes:
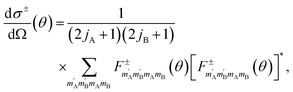 | (3) |
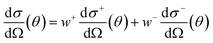 | (4) |
 | (5) |
2.2 4-Vector correlations
Miranda and Clary46,50 and Balint-Kurti and Vasyutinskii51 provided formalisms to calculate 4-vector correlations. The methodology presented here is an extension of the 3-vector correlations methodology used by Aoiz, Miranda and coworkers.47–49,67 It is based on the distinction between “intrinsic” and “extrinsic” polarization moments. The extrinsic polarization moments describe and quantify the actual preparation of the incoming molecules in a hypothetical (or real) experiment; they depend on the properties of the experiment rather than on the collision dynamics. In the scattering frame, the extrinsic polarization parameters, a(k)q, are given by| a(k)q = Ckq(β,α)A(k)0 | (6) |
The intrinsic polarization parameters (PDDCSs from Polarization Dependent Differential Cross Sections), in turn, do not depend on the experimental set-up but on the collision dynamics. They are intimately connected to the idea of collision mechanisms, with the difference that polarization parameters can be quantified. For the k–jA–jB–k′ four-vector correlation corresponding to the polarization of the two rotational angular momenta before the collision, the PDDCSs can be calculated in the uncoupled representation as:41
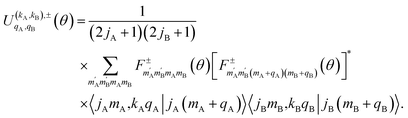 | (7) |
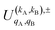 is the PDDCS with rank kA × kB and components (qA, qB). The possible values of kA, kB, qA, and qB are limited by the Clebsch–Gordan coefficients of eqn (7). Hence,
is the PDDCS with rank kA × kB and components (qA, qB). The possible values of kA, kB, qA, and qB are limited by the Clebsch–Gordan coefficients of eqn (7). Hence,| 0 ≤ kA ≤ 2jA, 0 ≤ kB ≤ 2jB | (8) |
| −kA ≤ qA ≤ kA, −kB ≤ qB ≤ kB. | (9) |
It should be noted that U0,0,±0,0(θ) is nothing but the isotropic (no preparation) DCS, and that if either kA or kB are zero, we recover the expression for the three vector correlations PDDCSs corresponding to the polarization of jB and jA, respectively. An equation similar to (4) holds for the calculation of the unsymmetrized 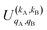 . Similarly, for distinguishable particles, the
. Similarly, for distinguishable particles, the 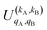 can be calculated straight from eqn (7).
can be calculated straight from eqn (7).
Once the 4-vector correlations have been calculated, the observable DCS can be evaluated as:
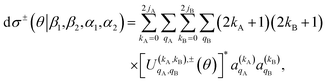 | (10) |
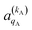 and
and 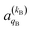 , which can be calculated following eqn (6).
, which can be calculated following eqn (6).
Similar to the PDDCSs corresponding to the three vector correlations, the 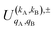 defined in eqn (7) are complex numbers. If kA + kB is even, the
defined in eqn (7) are complex numbers. If kA + kB is even, the 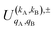 only have a real part, while if kA + kB is odd, they are purely imaginary. Moreover, in the particular case of qA = 0 and qB = 0 the only non-vanishing
only have a real part, while if kA + kB is odd, they are purely imaginary. Moreover, in the particular case of qA = 0 and qB = 0 the only non-vanishing 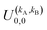 are those for which kA + kB is even.
are those for which kA + kB is even.
To quantify the effect of reactants polarization on the integral cross section, it is necessary to calculate the polarization moments, 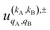 , which are defined as:
, which are defined as:
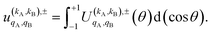 | (11) |
Eqn (11) is general but requires the calculation of 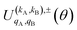 . For the particular case of qA = 0 and qB = 0 the
. For the particular case of qA = 0 and qB = 0 the 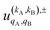 can also be calculated straight from the modulus of the scattering matrix elements, as:
can also be calculated straight from the modulus of the scattering matrix elements, as:
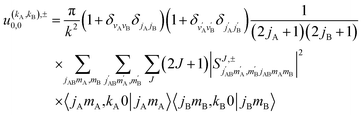 | (12) |
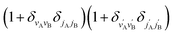 applies only to inelastic scattering between indistinguishable molecules. Note that u(0,0),±0,0 is the isotropic ICS.
applies only to inelastic scattering between indistinguishable molecules. Note that u(0,0),±0,0 is the isotropic ICS.
The observable ICS, i.e. the ICS for an experiment in which the two molecules are polarized, can be calculated from the integration of the observable DCS (eqn (10)) over the azimuthal, and the scattering angle. The resulting expression is:
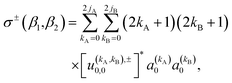 | (13) |
As just described, the intrinsic PDDCSs and PPs express how the DCS and ICS change with reactant polarization in absolute terms, as they are proportional to the isotropic DCS and ICS, respectively. Sometimes it is important to express them relative to the isotropic DCS or ICS so they can convey how important the effect of the polarization is for those observables. The normalized PPs, denoted as 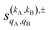 can be calculated as:
can be calculated as:
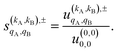 | (14) |
3 Results
3.1 D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 2) + D2(v = 2, j = 0)
We begin with a discussion of D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 2) + D2(v = 2, j = 0) collisions. The two molecules are treated as indistinguishable in the scattering calculations, but in the range of Ecoll considered here we find that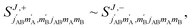 which indicates that the two collision partners are effectively distinguishable62 (the probability of going from v = 2 to v = 0 and simultaneously from v = 0 to v = 2 is negligible). According to this, we can describe this process as the rotational quenching from D2(v = 2, j = 2) to D2(v = 2, j = 0) induced by a collision with a D2(v = 0, j = 2) molecule that does not change its initial state.
which indicates that the two collision partners are effectively distinguishable62 (the probability of going from v = 2 to v = 0 and simultaneously from v = 0 to v = 2 is negligible). According to this, we can describe this process as the rotational quenching from D2(v = 2, j = 2) to D2(v = 2, j = 0) induced by a collision with a D2(v = 0, j = 2) molecule that does not change its initial state.
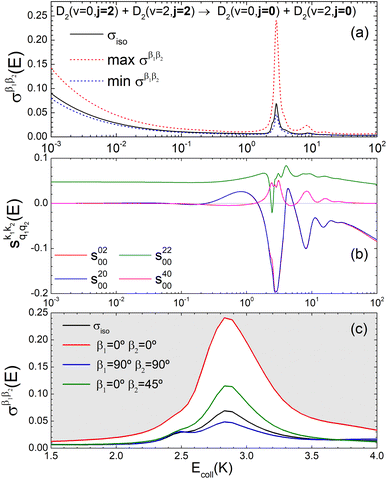
Panel (a) of Fig. 1 shows the isotropic (no polarization) excitation function, i.e. the cross section as a function of Ecoll in the 1 mK–100 K range. Along with the isotropic excitation function, we show the maximum and minimum values that could be obtained by changing independently the alignment of each of the two partners at each energy. These were calculated by scanning all of the possible values of β1 and β2 in eqn (13). It should be emphasised that the values of β1 and β2 that maximise/minimise the cross sections vary with the Ecoll, especially around the resonances.
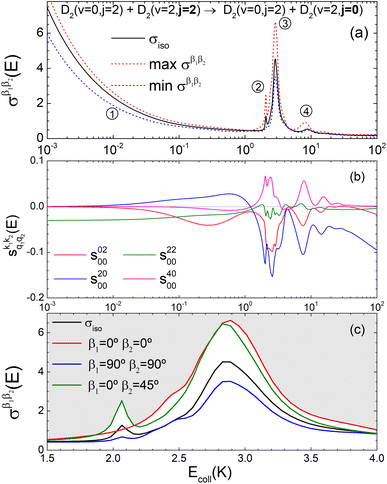 | ||
Fig. 1 Panel (a) shows the isotropic cross section (solid black line) as a function of Ecoll for D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 2) + D2(v = 2, j = 0) collisions along with the maximum (red dashed line) and minimum (blue dashed line) values of the cross sections that can be achieved by a given alignment of the internuclear axes of the two diatoms. The labels 1–4 indicate the values of Ecoll at which the dependence on σβ1β2 is shown in Fig. 3. Panel (b) shows the relevant polarization parameters, 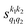 , as functions of Ecoll. Panel (c) shows the ICS σβ1β2 as functions of Ecoll for four different preparations. The region above the maximum value of the cross section that could be achieved is shaded in grey. , as functions of Ecoll. Panel (c) shows the ICS σβ1β2 as functions of Ecoll for four different preparations. The region above the maximum value of the cross section that could be achieved is shaded in grey. | ||
The isotropic excitation function at very low Ecoll is found to decrease with increasing energy, a behaviour that is predicted by the Wigner threshold laws (σ ∝ Ecoll−1/2).68 A specific preparation of the internuclear axes of the two D2 molecules makes it possible to enhance/suppress the cross sections at these low energies. As we will see below, this is unexpected as integral cross sections cannot be modified by the alignment of just one of the reactants in the limit of zero Ecoll.67 At higher Ecoll the most salient feature of the excitation function is the presence of sharp peaks around 2.0, 2.9 and 8.9 K, the first two associated to a 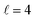 shape resonance, and the latter to a
shape resonance, and the latter to a 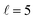 resonance. It is around these resonances where the cross sections could be controlled to a considerable extent.
resonance. It is around these resonances where the cross sections could be controlled to a considerable extent.
Some of the PPs that are responsible for the stereodynamical control are shown in panel (b) of Fig. 1 as a function of Ecoll. Only the PPs with even kA, and kB are shown since the corresponding extrinsic a0(kA/B) are different from zero only for even values for the simulated experiment (alignment). In the present notation, 1 corresponds to the D2(v = 0, j = 2), whose internal state is not modified during the collision, and 2 corresponds to the D2(v = 2, j = 2) which is rotationally relaxed. The respective PPs are denoted as 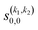 . It should be stressed that if one of the two ranks k of the moment is zero, this moment will be the same as that obtained for the corresponding 3-vector correlation. The physical meaning of the PPs represented here is:
. It should be stressed that if one of the two ranks k of the moment is zero, this moment will be the same as that obtained for the corresponding 3-vector correlation. The physical meaning of the PPs represented here is:
• Positive (negative) values of s(2,0)0,0 indicate that quenching of D2(v = 2, j = 2) is promoted when the internuclear axis of D2(v = 0, j = 2) is aligned perpendicular (parallel) to k, and hence increase the cross section for β1 ∼ 90° (β1 ∼ 0°).
• Positive (negative) values of s(4,0)0,0 indicate that quenching of D2(v = 2, j = 2) is promoted when the internuclear axis of D2(v = 0, j = 2) is aligned perpendicular or parallel (tilted) to k, and hence increase the cross section for β1 ∼ 90° or ∼0° (β1 ∼ 45°).
• Positive (negative) values of s(0,2)0,0 indicate that quenching of D2(v = 2, j = 2) is promoted when its internuclear axis is aligned perpendicular (parallel) to k, and hence increase the cross section for β2 ∼ 90° (β2 ∼ 0°).
• Positive values of s(2,2)0,0 indicate that quenching of D2(v = 2, j = 2) is promoted especially when the internuclear axis of both D2 molecules is aligned parallel to k and to a lesser extent when both are aligned perpendicular to k, and hence increase the cross section especially for β1 ∼ 0° and β2 ∼ 0°. Negative values of s(2,2)0,0 indicate that the quenching is promoted when one internuclear axis is aligned parallel to the initial relative velocity k whilst the other is perpendicular to k (i.e. either for β1 ∼ 0° and β2 ∼ 90° or for β1 ∼ 90° and β2 ∼ 0°).
According to Fig. 1(b), at low Ecoll the only relevant PP is s(2,2)0,0 which indicates that cross sections will be enhanced when the two internuclear axes are perpendicular to each other. With increasing Ecoll, s(2,0)0,0 and s(0,2)0,0 are also relevant, the former being positive and the latter negative, which favors the preference for collisions where the two internuclear axes are perpendicular to each other. Around the energies of the resonances the values of the PPs start oscillating and take larger absolute values, indicating the different collision mechanism at the resonance. Interestingly, for Ecoll above 20 K, the only relevant PP is s(2,0)0,0, which indicates that D2(v = 2, j = 2) quenching only depends on the alignment of the D2(v = 0, j = 2) internuclear axis, favoring a parallel alignment with k.
Panel (c) of Fig. 1 shows the excitation functions for different combinations of β1 and β2 around the energy of the 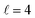 resonance, with the shaded region representing the cross sections above the maximum values that could be achieved by any preparation. In the vicinity of the resonance, collisions in which both internuclear axes are perpendicular to k minimise the cross section, while collisions for which D2(v = 0, j = 2) is aligned parallel to k and where D2(v = 2, j = 2) is aligned either parallel or tilted to k significantly enhances the cross section.
resonance, with the shaded region representing the cross sections above the maximum values that could be achieved by any preparation. In the vicinity of the resonance, collisions in which both internuclear axes are perpendicular to k minimise the cross section, while collisions for which D2(v = 0, j = 2) is aligned parallel to k and where D2(v = 2, j = 2) is aligned either parallel or tilted to k significantly enhances the cross section.
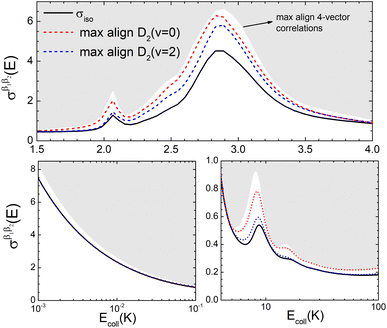
To appreciate the different extent of control that can be achieved by aligning both D2 molecules compared to that obtained when only one of the molecules is aligned, in Fig. 2 we show the isotropic excitation function along with the maximum value that can be obtained by aligning just one of the molecules, and the maximum value obtained when both molecules are aligned. Our results show that for Ecoll > 2.0 K higher cross sections can be obtained by aligning D2(v = 0, j = 2) rather than D2(v = 2, j = 2). Only around the 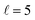 resonance (Ecoll ∼ 8 K) there is a clear gain in the degree of control achieved by aligning both molecules, and from 20 K, the alignment of D2(v = 2, j = 2) has almost no effect on the ICS.
resonance (Ecoll ∼ 8 K) there is a clear gain in the degree of control achieved by aligning both molecules, and from 20 K, the alignment of D2(v = 2, j = 2) has almost no effect on the ICS.
The behaviour at very low energies deserves a separate analysis. As demonstrated in ref. 67, it is not possible to modify the ICS at energies where only 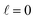 contributes by the polarization of just one of the molecules (i.e. three-vector correlations). Mathematically, it means that the only polarization parameter, u(k)0, that is different from zero is u(0)0. It does not mean that
contributes by the polarization of just one of the molecules (i.e. three-vector correlations). Mathematically, it means that the only polarization parameter, u(k)0, that is different from zero is u(0)0. It does not mean that 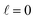 scattering is insensitive to an anisotropic preparation of the reactants, and indeed in the zero energy limit the DCS depends on the alignment,39,67 but simply these differences cancel out upon integration over the scattering angle. For the simpler case of an atom + diatom scattering, if
scattering is insensitive to an anisotropic preparation of the reactants, and indeed in the zero energy limit the DCS depends on the alignment,39,67 but simply these differences cancel out upon integration over the scattering angle. For the simpler case of an atom + diatom scattering, if 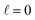 , J = j and eqn (12) reduces to
, J = j and eqn (12) reduces to
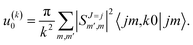 | (15) |
Irrespective of j and k, it is true that 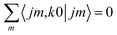 , so u(k)0 can only be zero if
, so u(k)0 can only be zero if 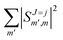 is independent of m. This behaviour could be generalized to diatom + diatom scattering and, in fact, it is systematically observed that there is no control of ICS for Ecoll → 0 when only one of the diatomic molecules is polarized.31,37 In the case of the alignment of two molecules the situation is different. On the one hand, in eqn (12) we have two different Clebsch–Gordan coefficients, and since
is independent of m. This behaviour could be generalized to diatom + diatom scattering and, in fact, it is systematically observed that there is no control of ICS for Ecoll → 0 when only one of the diatomic molecules is polarized.31,37 In the case of the alignment of two molecules the situation is different. On the one hand, in eqn (12) we have two different Clebsch–Gordan coefficients, and since 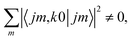 even if all the elements of the S matrix had the same values, the
even if all the elements of the S matrix had the same values, the 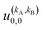 would be different from zero, which opens the possibility of control over the ICS. On the other hand, at least at 1 mK, we still observe differences in the values of the S matrix even though all three vector correlations are zero for Ecoll < 10 mK. In fact, the value (and even the sign) of the s(2,2)0,0 at Ecoll = 1 mK is different for the three systems studied.
would be different from zero, which opens the possibility of control over the ICS. On the other hand, at least at 1 mK, we still observe differences in the values of the S matrix even though all three vector correlations are zero for Ecoll < 10 mK. In fact, the value (and even the sign) of the s(2,2)0,0 at Ecoll = 1 mK is different for the three systems studied.
To exemplify the extent of control attainable through the alignment of the two diatoms, we will examine four different Ecoll values and demonstrate how changing β1 and β2 affects the cross section. These results are represented in Fig. 3 as contour maps where β1 is the angle that defines the direction of the internuclear axis D2(v = 0, j = 2), and β2 corresponds to the direction of D2(v = 2, j = 2). The color scale is shown in the side panels with red and yellow denoting values above that of the isotropic cross section, while blue indicates (β1, β2) regions for which the cross section is smaller. The value of the isotropic cross section is highlighted with dashed curves. To gain further insights into the collision mechanism, we combine this information with sketches of the probability density functions corresponding to the angles that maximise the cross section.
 | ||
| Fig. 3 Contour maps showing the ICS σβ1β2 for D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 2) + D2(v = 2, j = 0) collisions as a function of β1 and β2 for each of the four values of Ecoll indicated in Fig. 1. β1 is the angle that defines the direction of the internuclear axis of the D2(v = 0, j = 2), whose internal state does not change in the collision, whereas β2 refers to the D2(v = 2, j = 2) molecule that experiences the quenching of its rotational level. | ||
At Ecoll = 10 mK, within the cold regime, the contour map is symmetric with respect to the diagonal, which indicates that alignment of either partner yields equivalent results for the same alignment angle. The minimum value of the cross section corresponds to (β1 = 0°, β2 = 0°), while the maximum value is attained for (β1 = 0°, β2 = 90°) or (β1 = 90°, β2 = 0°), as expected for a collision dominated by the negative s(2,2)0,0 moment. The cross section for (β1 = 90°, β2 = 90°) is similar to the isotropic cross section. The sketch for the alignment that maximizes the cross section is represented in Fig. 4. Please note that we do not have information about the impact parameter, b, and in this sketch we have assumed a small b, as 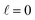 dominates at this Ecoll (b is represented in the figure as the horizontal separation between the blue and red portraits). It should be borne in mind that the direction of D2(v = 0, j = 2) internuclear axis has a significant influence in the cross section, even though this molecule does not change its rovibrational state in the collision.
dominates at this Ecoll (b is represented in the figure as the horizontal separation between the blue and red portraits). It should be borne in mind that the direction of D2(v = 0, j = 2) internuclear axis has a significant influence in the cross section, even though this molecule does not change its rovibrational state in the collision.
 | ||
| Fig. 4 Pictorial representation of the extrinsic stereodynamical portraits (distributions that graphically represent the dependence of the reaction dynamics on directions in space) showing the asymptotic spatial distributions of internuclear axes of the two partners which maximise the cross sections in D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 2) + D2(v = 2, j = 0) collisions at the Ecoll values indicated in Fig. 1. The portraits for D2(v = 0, j = 2) are shown in blue while those for the D2(v = 2, j = 2) collision partner are shown in red. In each case, the horizontal separation between the center-of-mass of the blue and red portraits qualitatively represents the value of the classical impact corresponding to the partial wave associated to the resonance that dominates scattering at each energy. | ||
The plot for Ecoll = 2.06 K corresponds to the energy at which the first resonance peak is observed (see Fig. 1). The contour map is no longer symmetric, and the maximum value is obtained for (β1 = 45°, β2 = 0°), whose sketch is represented in Fig. 4, where we have assumed a large impact parameter compatible with 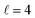 (b = 10.9 Å), the partial wave associated to the resonance. There are two minima corresponding to (β1 = 90°, β2 = 0, 90°). It is also worth noting that, in this case, the cross section could only be decreased to a small extent. Similar behaviour is observed at the two higher Ecoll considered.
(b = 10.9 Å), the partial wave associated to the resonance. There are two minima corresponding to (β1 = 90°, β2 = 0, 90°). It is also worth noting that, in this case, the cross section could only be decreased to a small extent. Similar behaviour is observed at the two higher Ecoll considered.
The PPs were found to vary around the Ecoll of the resonance, and at Ecoll = 2.88 K, where the sharpest resonance peak was observed, the relative orientation that maximises the cross section is (β1 = 0°, β2 = 0°), and in this case the contour map is again symmetric along the diagonal. The sketch of this relative polarisation is also displayed in Fig. 4, showing a preference for head-on collisions. The smallest values of the cross sections are obtained for (β1 = 90°, β2 = 90°). Finally, Ecoll = 8.78 K corresponds to the 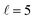 resonance, and at this energy the orientation that maximises the cross sections is again β1 = 0°, β2 = 0°, while β1 = 70°, β2 = 70–90° yields the smallest cross sections.
resonance, and at this energy the orientation that maximises the cross sections is again β1 = 0°, β2 = 0°, while β1 = 70°, β2 = 70–90° yields the smallest cross sections.
3.2 D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 0) + D2(v = 2, j = 0)
Now we examine the effect of the alignment of the two diatomic molecules in a process where both molecules are relaxed to their rotational ground state, D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 0) + D2(v = 2, j = 0). The excitation functions presented in panel (a) of Fig. 5 are qualitatively similar to those obtained when only one partner is quenched to j = 0 (Fig. 1). They feature two resonances, one associated with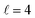 at 2.83 K, and another corresponding to
at 2.83 K, and another corresponding to 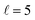 at 8.78 K. Quantitatively, the cross sections are significantly smaller, as expected for a double quenching process. Experimental detection of this channel would be hampered by the small value of the cross sections, particularly since D2(v = 2, j = 0) is generated through single-relaxation processes with significantly higher cross-sections. To detect this channel, a method would be required that is highly sensitive to the recoil velocity and can distinguish between the D2(v = 2, j = 0) produced by single and double quenching. The latter will imply a lower recoil energy in the center of mass equivalent to two rotational quanta. Despite this, the study of the double-quenching process illustrates the degree of control attainable through the alignment of the two diatomic molecules. In the present case, it exceeds significantly that of the single quenching process, resulting in an increase of up to a factor of three in the cross section around the resonances (a factor of 4 at 3.07 K), and an increase by a factor of two at the highest energies. At the lowest energies the increase is only 50%.
at 8.78 K. Quantitatively, the cross sections are significantly smaller, as expected for a double quenching process. Experimental detection of this channel would be hampered by the small value of the cross sections, particularly since D2(v = 2, j = 0) is generated through single-relaxation processes with significantly higher cross-sections. To detect this channel, a method would be required that is highly sensitive to the recoil velocity and can distinguish between the D2(v = 2, j = 0) produced by single and double quenching. The latter will imply a lower recoil energy in the center of mass equivalent to two rotational quanta. Despite this, the study of the double-quenching process illustrates the degree of control attainable through the alignment of the two diatomic molecules. In the present case, it exceeds significantly that of the single quenching process, resulting in an increase of up to a factor of three in the cross section around the resonances (a factor of 4 at 3.07 K), and an increase by a factor of two at the highest energies. At the lowest energies the increase is only 50%.
Panel (b) of Fig. 5 shows the PPs responsible for the stereodynamical control. Strikingly, we observe that 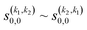 , and there are only very subtle differences between s(2,0)0,0 ∼ s(0,2)0,0 around 2 K and from 40 K. This suggests that in this process, the collision mechanism does not differentiate between the alignment of either partner, which evinces the spectator role of the vibrational quantum number at these Ecoll. At very low Ecoll, the value of s(2,2)0,0 is positive and significantly different from zero. This contrasts with the results obtained for the single relaxation process, where s(2,2)0,0 was negative at low energies. Hence, at low Ecoll the collision prefers preparations in which both internuclear axes are aligned parallel to k, i.e., corresponding to a (β1 = 0°, β2 = 0°) conformation. The s(2,2)0,0 remains nearly constant with Ecoll. This together with the s(2,0)0,0 ∼ s(0,2)0,0 values, causes the arrangement (β1 = 0°, β2 = 0°) to maximize the cross section for the whole Ecoll range.
, and there are only very subtle differences between s(2,0)0,0 ∼ s(0,2)0,0 around 2 K and from 40 K. This suggests that in this process, the collision mechanism does not differentiate between the alignment of either partner, which evinces the spectator role of the vibrational quantum number at these Ecoll. At very low Ecoll, the value of s(2,2)0,0 is positive and significantly different from zero. This contrasts with the results obtained for the single relaxation process, where s(2,2)0,0 was negative at low energies. Hence, at low Ecoll the collision prefers preparations in which both internuclear axes are aligned parallel to k, i.e., corresponding to a (β1 = 0°, β2 = 0°) conformation. The s(2,2)0,0 remains nearly constant with Ecoll. This together with the s(2,0)0,0 ∼ s(0,2)0,0 values, causes the arrangement (β1 = 0°, β2 = 0°) to maximize the cross section for the whole Ecoll range.
Panel (c) of Fig. 5 shows that the alignment of both partners leads to a substantial increase of the cross sections in the vicinity of the  resonance. In this case, there is only one resonance peak, and the cross section is significantly enhanced by a (β1 = 0°, β2 = 0°) alignment. (β1 = 0°, β2 = 45°) and (β1 = 45°, β2 = 0°) lead to a small increase in the cross section. The (β1 = 90°, β2 = 90°) alignment makes the cross section smaller than the isotropic one, implying that side-on collisions are less effective in double quenching processes.
resonance. In this case, there is only one resonance peak, and the cross section is significantly enhanced by a (β1 = 0°, β2 = 0°) alignment. (β1 = 0°, β2 = 45°) and (β1 = 45°, β2 = 0°) lead to a small increase in the cross section. The (β1 = 90°, β2 = 90°) alignment makes the cross section smaller than the isotropic one, implying that side-on collisions are less effective in double quenching processes.
Fig. 6 illustrates that the simultaneous alignment of both internuclear axes leads to cross sections that significantly exceed (on a relative basis compared to isotropic collisions) that obtained by the alignment of just one of the molecules in the whole Ecoll range considered here. In fact, by polarizing only one of the diatomic molecules, significant control is only achieved at the resonances, and even then, optimal alignment never results in more than an increase of 70% with respect to the isotropic cross section.
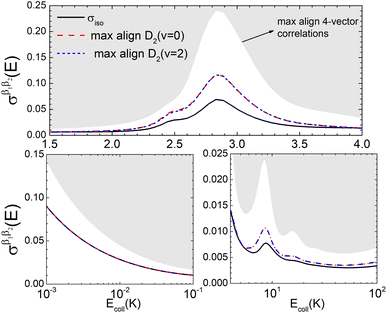 | ||
| Fig. 6 Same as Fig. 2 but for D2(v = 0, j = 2) + D2(v = 2, j = 2) → D2(v = 0, j = 0) + D2(v = 2, j = 0) collisions. | ||
3.3 D2(v = 2, j = 2) + D2(v = 2, j = 2) → D2(v = 2, j = 2) + D2(v = 2, j = 0)
The third case that we will examine is that in which two identical molecules collide, a D2(v = 2, j = 2) + D2(v = 2, j = 2) → D2(v = 2, j = 2) + D2(v = 2, j = 0) collision, which corresponds to that studied experimentally by Zhou et al.,30 and analyzed in ref. 41 under experimental conditions (same alignment for the two partners).In contrast to the previous cases, in this system the two molecules are truly indistinguishable, and accordingly we find that 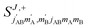 differs significantly from
differs significantly from 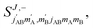 which makes impossible to discriminate the molecule that is relaxed to j = 0. Bearing that in mind, it makes no sense to attribute β1 and β2 to the alignment of one or the other partner, and although we will keep this notation, β1 and β2 are equivalent for this process.
which makes impossible to discriminate the molecule that is relaxed to j = 0. Bearing that in mind, it makes no sense to attribute β1 and β2 to the alignment of one or the other partner, and although we will keep this notation, β1 and β2 are equivalent for this process.
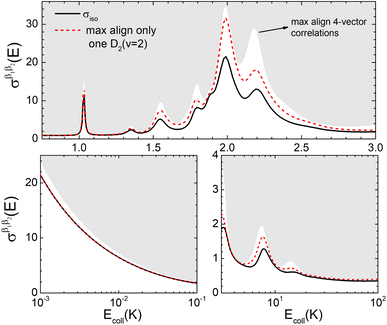
The isotropic excitation function for this process, displayed in panel (a) of Fig. 7, exhibits features similar to those of the previous processes, but differs in the splitting of the  resonance into six peaks, with the first three peaks also showing a significant contribution from
resonance into six peaks, with the first three peaks also showing a significant contribution from  The level of control that could be attainable via alignment of the two molecules is somewhat smaller to that obtained for the single quenching process of D2(v = 0, j = 2) + D2(v = 2, j = 2), and is very modest compared to that obtained for the double quenching process. Only in the vicinity of the resonances is the level of control significant and, as shown in Fig. 8, only for some of the peaks do their magnitudes differ significantly from those obtained by the alignment of just one of the molecules, especially for the Ecoll = 2.19 K peak.
The level of control that could be attainable via alignment of the two molecules is somewhat smaller to that obtained for the single quenching process of D2(v = 0, j = 2) + D2(v = 2, j = 2), and is very modest compared to that obtained for the double quenching process. Only in the vicinity of the resonances is the level of control significant and, as shown in Fig. 8, only for some of the peaks do their magnitudes differ significantly from those obtained by the alignment of just one of the molecules, especially for the Ecoll = 2.19 K peak.
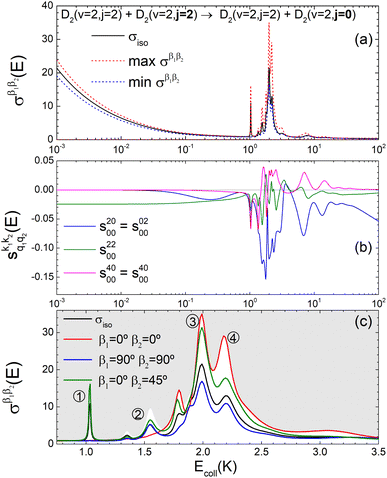 | ||
Fig. 7 (a) Isotropic cross section (solid black curve) as a function of Ecoll for D2(v = 2, j = 2) + D2(v = 2, j = 2) → D2(v = 2, j = 2) + D2(v = 2, j = 0) collisions. The maximum and minimum values of the cross sections that could be achieved by a given alignment of the two internuclear axes of the diatoms are shown as red and blue dashed curves, respectively. (b) The relevant polarization parameters, 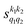 , are shown as a function of Ecoll. (c) σβ1β2 calculated as a function of Ecoll for three given preparations. The region above the maximum value of the cross section that could be achieved is shaded in grey. The labels 1–4 indicate the Ecoll at which the dependence on σβ1β2 is displayed in Fig. 9. , are shown as a function of Ecoll. (c) σβ1β2 calculated as a function of Ecoll for three given preparations. The region above the maximum value of the cross section that could be achieved is shaded in grey. The labels 1–4 indicate the Ecoll at which the dependence on σβ1β2 is displayed in Fig. 9. | ||
The PPs displayed in panel (b) of Fig. 7 are qualitatively similar to those obtained for the single quenching of D2(v = 0, j = 2) + D2(v = 2, j = 2), although their absolute values are slightly smaller, resulting in a lower degree of control. We attribute this to the indistinguishability of the two partners because the absolute value of 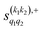 is different from that of the
is different from that of the 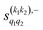 , the former prevailing at the lowest Ecoll due to the higher cross section associated with the + exchange parity symmetry.
, the former prevailing at the lowest Ecoll due to the higher cross section associated with the + exchange parity symmetry.
To assess the extent of control attainable in the vicinity of the 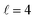 resonance, panel (c) of Fig. 7 shows the cross sections calculated at four different preparations (β1 = 0°, β2 = 0°), (β1 = 90°, β2 = 90°), and (β1 = 0°, β2 = 45°) ≡ (β1 = 45°, β2 = 0°). The combination of two partial waves (
resonance, panel (c) of Fig. 7 shows the cross sections calculated at four different preparations (β1 = 0°, β2 = 0°), (β1 = 90°, β2 = 90°), and (β1 = 0°, β2 = 45°) ≡ (β1 = 45°, β2 = 0°). The combination of two partial waves (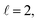 and
and 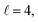 the latter being dominant) alongside two exchange symmetry parities enriches the stereodynamics at the resonance. For example, (β1 = 0°, β2 = 0°) alignment leads to the highest cross sections at the two dominant peaks at 1.99 K and 2.19 K, while it leads to the vanishing of the resonance peaks at 1.03 and 1.55 K. Interestingly, the 1.03 K peak also vanishes for the apparently opposite (β1 = 90°, β2 = 90°) alignment. However, the (β1 = 0°, β2 = 45°) alignment is capable of enhancing this resonance and almost maximises the cross sections at 1.99 K.
the latter being dominant) alongside two exchange symmetry parities enriches the stereodynamics at the resonance. For example, (β1 = 0°, β2 = 0°) alignment leads to the highest cross sections at the two dominant peaks at 1.99 K and 2.19 K, while it leads to the vanishing of the resonance peaks at 1.03 and 1.55 K. Interestingly, the 1.03 K peak also vanishes for the apparently opposite (β1 = 90°, β2 = 90°) alignment. However, the (β1 = 0°, β2 = 45°) alignment is capable of enhancing this resonance and almost maximises the cross sections at 1.99 K.
Fig. 9 shows how changing β1 and β2 affects the cross section at some of the resonances peaks. For the Ecoll = 1.03 K peak, the contour map is very symmetrical. Interestingly, this symmetry is missing if we restrict the results for either 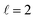 or
or 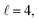 the former showing a maximum for (β1 = 0°, β2 = 90°). In fact, the cross sections for the different preparations are not only determined by
the former showing a maximum for (β1 = 0°, β2 = 90°). In fact, the cross sections for the different preparations are not only determined by  or their incoherent sum, but also for their interference (due to the distinguishability of the two D2 partners). At Ecoll = 1.55 K, the preparation (β1 = 0°, β2 = 0°) minimises the cross section, which also shrinks for (β1 = 60°, β2 = 90°) alignment. The cross section is maximised for (β1 = 90°, β2 = 0°). Also at this energy, the cross section for a specific alignment is given by the interference between the
or their incoherent sum, but also for their interference (due to the distinguishability of the two D2 partners). At Ecoll = 1.55 K, the preparation (β1 = 0°, β2 = 0°) minimises the cross section, which also shrinks for (β1 = 60°, β2 = 90°) alignment. The cross section is maximised for (β1 = 90°, β2 = 0°). Also at this energy, the cross section for a specific alignment is given by the interference between the  and the
and the  contributions. At the two main resonance peaks, Ecoll = 1.99 K, and 2.19 K, it is the (β1 = 0°, β2 = 0°) alignment that boosts the cross section, whereas the (β1 = 90°, β2 = 90°) alignment suppresses it.
contributions. At the two main resonance peaks, Ecoll = 1.99 K, and 2.19 K, it is the (β1 = 0°, β2 = 0°) alignment that boosts the cross section, whereas the (β1 = 90°, β2 = 90°) alignment suppresses it.
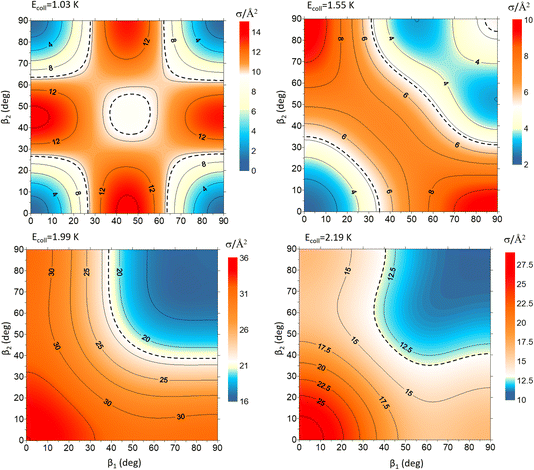 | ||
| Fig. 9 Contour maps showing the σβ1β2 for D2(v = 2, j = 2) + D2(v = 2, j = 2) → D2(v = 2, j = 2) + D2(v = 2, j = 0) collisions as a function of β1 and β2 for each of the four Ecoll highlighted in Fig. 7. Since both D2 molecules are indistinguishable β1 and β2 represent the angles that define the direction of the internuclear axis of any of the two diatoms. | ||
4 Conclusions
In this work we have investigated how the integral cross section of inelastic diatom–diatom collisions can be controlled by simultaneously changing the direction of the rotational angular momentum (and hence of the internuclear axis) of both diatoms. This requires the evaluation of the correlations between the following 4 vectors: the initial (k) and final (k′) relative velocities of the collision partners, and the directions of the angular momentum of the two molecules, jA and jB. The underlying quantum theory is presented in full-dimensions. As a case study, we have performed time-independent quantum scattering calculations for the rotational quenching of D2(v, j = 2) + D2(v, j = 2) collisions for three different scenarios: (a) v = 0 + v = 2, where the D2(v = 2, j = 2) molecule is quenched to (v = 2, j = 0); (b) v = 0 + v = 2, where both molecules are quenched to j = 0; (c) v = 2 + v = 2, where one of the two indistinguishable molecules is quenched to j = 0.For all cases, the cross section can be controlled over the entire range of collision energies considered, varying from the cold regime (1 mK) to 100 K. The degree of control that can be achieved is higher in the vicinity of the resonances, and especially for the quenching of both collision partners, where a suitable preparation can significantly enhance the cross section (up to a factor of four), or decrease the cross section, sometimes leading to the disappearance of the resonance. At very low energies, the alignment of only one rotational angular momentum could not lead to control of the integral cross section, whereas simultaneous alignment of both rotational angular momenta can provide some control, due to the behaviour of the s(2,2)0,0 moments which do not vanish in the ultracold energy regime.
At higher energies, our results show that the cross sections are typically maximised/minimised when the two internuclear axes have the same alignment. For the processes studied here, the cross section is maximised when the two molecules are aligned along the initial velocity, and is minimised when both are aligned almost perpendicular to the relative initial velocity. However, this behaviour changes in the vicinity of resonances and also for energies below 1 K, in which we have also observed cases where the cross sections are maximised when the two internuclear axes are aligned perpendicular to each other. These results can be generalised to other systems and, indeed, we expect that for chemical reactions or inelastic collisions between more complex molecules a greater degree of control could be achieved by the simultaneous alignment of two internuclear axes. We anticipate that the methods and results presented here will inform future experiments on 4-vector correlations at cold or hyperthermal energies.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work is supported in part by NSF grant no. PHY-2110227 (N. B.) and by a MURI grant from Army Office of Research (grant no. W911NF-19-1-0283 to H. G. and N. B.). F. J. A. acknowledges funding by the Spanish Ministry of Science and Innovation (grant PID2021-122839NB-I00). P. G. J. acknowledges grant no. PID2020-113147GA-I00 funded by MCIN/AEI/10.13039/501100011033 (Spanish Ministry of Science and Innovation).References
- F. Wang, J. S. Lin and K. Liu, Science, 2011, 331, 900–903 CrossRef CAS PubMed.
- F. Wang, K. Liu and T. P. Rakitzis, Nat. Chem., 2012, 4, 636–641 CrossRef CAS PubMed.
- F. Wang and K. Liu, J. Chem. Phys., 2016, 145, 144305 CrossRef PubMed.
- F. Wang and K. Liu, J. Chem. Phys., 2016, 145, 144306 CrossRef PubMed.
- H. Pan and K. Liu, Phys. Chem. Chem. Phys., 2020, 22, 10949–10956 RSC.
- H. Pan and K. Liu, Nat. Chem., 2022, 14, 545–549 CrossRef CAS PubMed.
- Z. Karny, R. C. Estler and R. N. Zare, J. Chem. Phys., 1978, 69, 5199 CrossRef CAS.
- M. G. Prisant, C. T. Rettner and R. N. Zare, Chem. Phys. Lett., 1982, 88, 271 CrossRef CAS.
- Y. Wang, J. Huang, W. Wang, T. Du, Y. Xie, Y. Ma, C. Xiao, Z. Zhang, D. H. Zhang and X. Yang, Science, 2023, 379, 191–195 CrossRef CAS PubMed.
- S. A. Kandel, A. J. Alexander, Z. H. Kim, R. N. Zare, F. J. Aoiz, L. Bañares, J. F. Castillo and V. Sáez-Rábanos, J. Chem. Phys., 2000, 112, 670–685 CrossRef CAS.
- H. J. Loesch and F. Stienkemeier, J. Chem. Phys., 1993, 98, 9570–9584 CrossRef CAS.
- S. A. Lahankar, J. Zhang, K. G. McKendrick and T. K. Minton, Nat. Chem., 2013, 5, 315 CrossRef CAS PubMed.
- S. A. Lahankar, J. Zhang, T. K. Minton and K. G. McKendrick, J. Am. Chem. Soc., 2014, 136, 12371–12384 CrossRef CAS PubMed.
- P. G. Jambrina, A. Zanchet, J. Aldegunde, M. Brouard and F. J. Aoiz, Nat. Commun., 2016, 7, 13439 CrossRef CAS PubMed.
- P. G. Jambrina, A. Zanchet, M. Menéndez, V. J. Herrero and F. J. Aoiz, Phys. Chem. Chem. Phys., 2019, 21, 25389 RSC.
- K. T. Lorenz, D. W. Chandler, J. W. Barr, W. Chen, G. L. Barnes and J. I. Cline, Science, 2001, 293, 2063–2066 CrossRef CAS PubMed.
- M. Brouard, H. Chadwick, C. J. Eyles, B. Hornung, B. Nichols, F. J. Aoiz, P. G. Jambrina and S. Stolte, J. Chem. Phys., 2013, 138, 104310 CrossRef CAS PubMed.
- M. Brouard, H. Chadwick, S. Gordon, B. Hornung, B. Nichols, F. J. Aoiz and S. Stolte, J. Phys. Chem. A, 2015, 119, 12404–12416 CrossRef CAS PubMed.
- J. Onvlee, S. D. S. Gordon, S. N. Vogels, T. Auth, T. Karman, B. Nichols, A. van der Avoird, G. C. Groenenboom, M. Brouard and S. Y. T. van de Meerakker, Nat. Chem., 2017, 9, 226–233 CrossRef CAS PubMed.
- T. R. Sharples, J. G. Leng, T. F. M. Luxford, K. G. McKendrick, P. G. Jambrina, F. J. Aoiz, D. W. Chandler and M. L. Costen, Nat. Chem., 2018, 10, 1148–1153 CrossRef CAS PubMed.
- C. G. Heid, I. P. Bentham, V. Walpole, P. G. Jambrina, F. J. Aoiz and M. Brouard, J. Phys. Chem. Lett., 2021, 12, 310 CrossRef CAS PubMed.
- C. G. Heid, V. Walpole, M. Brouard, P. G. Jambrina and F. J. Aoiz, Nat. Chem., 2019, 11, 662 CrossRef CAS PubMed.
- O. Ghafur, A. Rouzée, A. Gijsbertsen, W. Kiu Siu, S. Stolte and M. J. J. Vrakking, Nat. Phys., 2009, 5, 289 Search PubMed.
- A. Gijsbertsen, H. Linnartz, C. A. Taatjes and S. Stolte, J. Am. Chem. Soc., 2006, 128, 8777 CrossRef CAS PubMed.
- H. Zhou, W. E. Perreault, N. Mukherjee and R. N. Zare, J. Chem. Phys., 2021, 154, 104309 CrossRef CAS PubMed.
- H. Zhou, W. E. Perreault, N. Mukherjee and R. N. Zare, Science, 2021, 374, 960–964 CrossRef CAS PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, J. Chem. Phys., 2019, 150, 174301 CrossRef PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Science, 2017, 358, 356–359 CrossRef CAS PubMed.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Nat. Chem., 2018, 10, 561–567 CrossRef CAS PubMed.
- H. Zhou, W. E. Perreault, N. Mukherjee and R. N. Zare, Nat. Chem., 2022, 14, 658–663 CrossRef CAS PubMed.
- P. G. Jambrina, J. F. E. Croft, N. Balakrishnan and F. J. Aoiz, Phys. Chem. Chem. Phys., 2021, 23, 19364 RSC.
- M. Morita, Q. Yao, C. Xie, H. Guo and N. Balakrishnan, Phys. Rev. Res., 2020, 2, 032018(R) CrossRef.
- M. Morita and N. Balakrishnan, J. Chem. Phys., 2020, 153, 184307 CrossRef CAS PubMed.
- M. Morita and N. Balakrishnan, J. Chem. Phys., 2020, 153, 091101 CrossRef CAS PubMed.
- J. F. E. Croft, N. Balakrishnan, M. Huang and H. Guo, Phys. Rev. Lett., 2018, 121, 113401 CrossRef CAS PubMed.
- J. F. E. Croft and N. Balakrishnan, J. Chem. Phys., 2019, 150, 164302 CrossRef CAS PubMed.
- P. G. Jambrina, J. F. E. Croft, H. Guo, M. Brouard, N. Balakrishnan and F. J. Aoiz, Phys. Rev. Lett., 2019, 123, 043401 CrossRef CAS PubMed.
- P. G. Jambrina, L. González-Sánchez, M. Lara, M. Menéndez and F. J. Aoiz, Phys. Chem. Chem. Phys., 2020, 22, 24943–24950 RSC.
- P. G. Jambrina, M. Morita, J. F. E. Croft, F. J. Aoiz and N. Balakrishnan, J. Phys. Chem. Lett., 2022, 13, 4064–4072 CrossRef CAS PubMed.
- D. Yang, D. Xie and H. Guo, J. Phys. Chem. Lett., 2022, 13, 1777–1784 CrossRef CAS PubMed.
- P. G. Jambrina, J. F. E. Croft, J. Zuo, H. Guo, N. Balakrishnan and F. J. Aoiz, Phys. Rev. Lett., 2023, 130, 033002 CrossRef CAS PubMed.
- J. F. E. Croft, P. G. Jambrina, F. J. Aoiz, H. Guo and N. Balakrishnan, J. Phys. Chem. A, 2023, 127, 1619–1627 CrossRef CAS PubMed.
- D. Case and D. Herschbach, Mol. Phys., 1975, 30, 1537–1564 CrossRef CAS.
- D. A. Case and D. R. Herschbach, J. Chem. Phys., 1976, 64, 4212–4222 CrossRef CAS.
- A. J. Orr-Ewing and R. N. Zare, Annu. Rev. Phys. Chem., 1994, 45, 315–366 CrossRef CAS.
- M. P. de Miranda and D. C. Clary, J. Chem. Phys., 1997, 106, 4509–4521 CrossRef.
- M. P. de Miranda, F. J. Aoiz, L. Bañares and V. Saéz-Rábanos, J. Chem. Phys., 1999, 111, 5368 CrossRef CAS.
- F. J. Aoiz and M. P. de Miranda, in Tutorials in Molecular Reaction Dynamics, ed. M. Brouard and C. Vallance, RSC Publishing, 2010 Search PubMed.
- J. Aldegunde, M. P. de Miranda, J. M. Haigh, B. K. Kendrick, V. Saez-Rabanos and F. J. Aoiz, J. Phys. Chem. A, 2005, 109, 6200–6217 CrossRef CAS PubMed.
- S. K. de Miranda, M. P. Pogrebnya and D. C. Clary, Faraday Discuss., 1999, 113, 119–132 RSC.
- G. G. Balint-Kurti and O. S. Vasyutinskii, J. Phys. Chem. A, 2009, 113, 14281–14290 CrossRef CAS PubMed.
- M. Costes and C. Naulin, Chem. Sci., 2016, 7, 2462 RSC.
- A. B. Henson, S. Gersten, Y. Shagam, J. Narevicius and E. Narevicius, Science, 2012, 338, 234 CrossRef CAS PubMed.
- P. Paliwal, N. Deb, D. M. Reich, A. van der Avoird, C. P. Koch and E. Narevicius, Nat. Chem., 2021, 13, 94 CrossRef CAS PubMed.
- S. D. S. Gordon and A. Osterwalder, Int. Rev. Phys. Chem., 2020, 39, 109 Search PubMed.
- S. Y. T. van de Meeraker, H. L. Bethlem, N. Vanhaecke and G. Meijer, Chem. Rev., 2012, 112, 4828 CrossRef PubMed.
- A. Von Zastrow, J. Onvlee, S. N. Vogels, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meeraker, Nat. Chem., 2014, 6, 216 CrossRef CAS PubMed.
- S. N. Vogels, J. Onvlee, S. Chefdeville, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2015, 350, 787–790 CrossRef CAS PubMed.
- V. Plomp, X. Wang, F. Lique, J. Klos, J. Onvlee and S. Y. T. van de Meeraker, J. Phys. Chem. Lett., 2021, 12, 12210 CrossRef CAS PubMed.
- R. Krems, TwoBC – Quantum Scattering Program, University of British Columbia, Vancouver, Canada, 2006 Search PubMed.
- J. Zuo, J. F. E. Croft, Q. Yao, N. Balakrishnan and H. Guo, J. Chem. Theory Comput., 2021, 17, 6747–6756 CrossRef CAS PubMed.
- W. M. Huo and S. Green, J. Chem. Phys., 1996, 104, 7572–7589 CrossRef CAS.
- J. Z. H. Zhang, Theory and Application of Quantum Molecular Dynamics, World Scientific, 1998 Search PubMed.
- K. Takayanagi, Adv. At. Mol. Phys., 1965, 1, 149–194 Search PubMed.
- J. Pérez-Ríos, M. Bartolomei, M. I. Campos-Martínez and R. Hernández-Lamoneda, J. Phys. Chem. A, 2009, 113, 14952 CrossRef PubMed.
- D. L. Johnson, R. S. Grace and J. G. Skofronick, J. Chem. Phys., 1979, 71, 4554–4569 CrossRef CAS.
- J. Aldegunde, J. M. Alvariño, M. P. de Miranda, V. Sáez-Rábanos and F. J. Aoiz, J. Chem. Phys., 2006, 125, 133104 CrossRef CAS PubMed.
- H. R. Sadeghpour, J. L. Bohn, M. J. Cavagnero, B. D. Esry, I. I. Fabrikant, J. H. Macek and A. R. P. Rau, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, R93 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |