Freestanding carbon nanofoam papers with tunable porosity as lithium–sulfur battery cathodes†
Zachary G.
Neale
 a,
Matthew J.
Lefler
a,
Jeffrey W.
Long
a,
Matthew J.
Lefler
a,
Jeffrey W.
Long
 b,
Debra R.
Rolison
b,
Megan B.
Sassin
b and
Rachel
Carter
b,
Debra R.
Rolison
b,
Megan B.
Sassin
b and
Rachel
Carter
 *b
*b
aNational Research Council Postdoctoral Associate, U.S. Naval Research Laboratory, Washington, DC, USA
bSurface Chemistry Branch (Code 6170), U.S. Naval Research Laboratory, Washington, DC, USA. E-mail: Rachel.carter@nrl.navy.mil
First published on 11th August 2023
Abstract
To reach energy density demands greater than 3 mA h cm−2 for practical applications, the electrode structure of lithium–sulfur batteries must undergo an architectural redesign. Freestanding carbon nanofoam papers derived from resorcinol–formaldehyde aerogels provide a three-dimensional conductive mesoporous network while facilitating electrolyte transport. Vapor-phase sulfur infiltration fully penetrates >100 μm thick electrodes and conformally coats the carbon aerogel surface providing areal capacities up to 4.1 mA h cm−2 at sulfur loadings of 6.4 mg cm−2. Electrode performance can be optimized for energy density or power density by tuning sulfur loading, pore size, and electrode thickness.
1 Introduction
Sulfur is a naturally abundant, low-cost, nonstrategic resource to exploit for electrochemical energy-storage applications.1 Interest in sulfur-based batteries is further driven by the high theoretical specific capacity of 1675 mA h g−1 that derives from the 16-electron reduction of S8 to 8 S2−.2 Despite being investigated since the 1940s in high-temperature battery systems,3 the implementation of ambient-temperature sulfur-based batteries faces many remaining challenges before practical commercialization: intrinsically poor electronic conductivity, low sulfur utilization, limited cyclability, and redox shuttling of soluble polysulfides. The twenty-first century pursuit for battery cell chemistries delivering specific energy >500 W h kg−1 has kindled a renaissance of academic and commercial research in lithium–sulfur (Li–S) batteries aimed to solve these roadblocks.1For practical battery use, sulfur should be expressed in a conductive, porous matrix that contains and constrains the sulfur and its electrochemical byproducts (i.e., polysulfides).4 Numerous nanostructured carbons such as carbon nanotubes,5–10 graphene,11,12 and “yolk–shell” spheres13–15 have also been demonstrated as hosts for sulfur, providing polysulfide confinement, facile electronic conduction, and short ion transport pathways. While reports of porous carbon hosts for Li–S batteries are numerous, many lab-scale studies use electrodes comprising carbons with needlessly low density, insufficient sulfur weight loadings, or those made via processes that would otherwise be difficult to scale. Coupled with unrealistic electrochemical testing protocols that are sometimes employed, the results of such early-stage investigations often fail to yield results directly relevant to large-scale, real-world Li–S batteries.3,16
The design of sulfur–carbon composite electrodes must account for such performance metrics as gravimetric, volumetric, and geometric capacity, as well as high-rate capability. These metrics are, in turn, affected by such cathode-specific factors as pore size distribution, accessible surface area, local and macroscale electronic conductivity, sulfur distribution within the electrode, and porosity/tap density.17,18 High-surface-area microporous carbons offer better confinement of polysulfides but typically have lower sulfur loadings and correspondingly suboptimal capacity. Mesoporous, macroporous, and hierarchical porous structures allow more space for higher sulfur loadings and promote electrolyte transport to maximize sulfur utilization.1,19–24 Melt-infiltration is a common approach to load sulfur into these porous hosts, but such methods rely on capillary action and require time to produce uniform and conformal distributions of sulfur.5,12,17,20,25–29 These sulfur–carbon composites are often prepared in powder form and mixed with carbon black, binder, and solvent, then cast as a slurry onto a foil current collector.5,9,12,17,19,20,26–31 The resulting electrodes have suboptimal conductivity and mechanical strength, impeding rate capability and hindering the use of thicker electrodes to achieve high areal capacity.
Among mesoporous/macroporous scaffolds, carbon aerogels and related aerogel-like carbons (e.g., nanofoams) exhibit many desirable structural characteristics for serving as an effective sulfur host, including through-connected pore networks of tunable size (nm to μm), high specific surface area (100 s of m2 g−1), and moderately high electronic conductivity (10 s of S cm−1).32–36 Carbon aerogels have shown promising initial results in Li–S cells when the aerogel powder is infused with sulfur and then processed into a conventional composite electrode with polymer binder.26,31,37 Alternatively, we have demonstrated the electrochemical versatility of freestanding carbon nanofoam papers (CNFPs), in which porous aerogel-like carbon networks fill and span the macroscale voids of a supporting carbon-fiber paper.38–46 The CNFP requires no additional binders or conductive additives before incorporation into an electrochemical cell, and the continuity of intermingled networks of conductive carbon and void volume is not interrupted across the macroscale thickness of the electrode, as would be the case for most powder-composite constructions.
In order to take advantage of the freestanding nature of the CNFPs, we here utilize isothermal vapor infiltration7,8,47–49 to incorporate sulfur (forming “S@CNFP”) and then deploy the resulting S@CNFP object as a cathode in a Li–S cell without any additional processing. We examine the performance of Li–S cells with S@CNFPs while varying such structural parameters as pore size distribution, sulfur weight loading, and electrode thickness. Our findings illustrate the ability to balance pore size and weight loading to tune high capacity with respect to mass, volume, or footprint to optimize Li–S performance.
2 Experimental
2.1 Synthesis of carbon nanofoam papers
Freestanding CNFPs with tunable pore size distributions were synthesized via a resorcinol–formaldehyde (RF) sol–gel process described elsewhere.41 In brief, resorcinol (R) and formaldehyde (F) in a 1R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2F mole ratio were mixed in water with a Na2CO3 catalyst (C) and aged at room temperature for 3 h creating a sol precursor. The CNFP formulations are designated by their RF-water wt% and R
2F mole ratio were mixed in water with a Na2CO3 catalyst (C) and aged at room temperature for 3 h creating a sol precursor. The CNFP formulations are designated by their RF-water wt% and R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C molar ratio, herein labeled as “RF wt%/R
C molar ratio, herein labeled as “RF wt%/R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C”, with three formulations selected for testing: 40/300, 40/500, and 40/1000. Commercial carbon fiber papers (Lydall Technimat®, density 0.2 g cm−3, ∼90 μm thick) were cut to 4 × 4 cm2 and cleaned in an air/ice plasma for 45 min then soaked in the RF sol under vacuum. The RF-soaked carbon fiber papers were sandwiched between glass slides with excess sol added and clamped together with binder clips. Multi-ply CNFPs were made by stacking multiple sheets of sol-infused carbon fiber paper in between glass slides. The assemblies were wrapped in duct tape to prevent leaking of sol and packaged together in aluminum foil with a few milliliters of water added to maintain humidity, then aged at room temperature for an additional 21 h. The aluminum foil packages were then cured in a commercial pressure cooker (Nesco 3-in-1 pressure cooker) set to steam mode for 9.5 h on slow-cook setting (∼88–94 °C) followed by a 14.5 h warm cycle (∼80 °C). The RF-polymer@CNFP nanofoam composite sheets were soaked in water and then acetone for 1–2 h, followed by drying in air at room temperature. The dry polymer nanofoam papers were pyrolyzed into CNFPs under flowing argon, ramping at 1 °C min−1 and holding at 1000 °C for 2 h.
C”, with three formulations selected for testing: 40/300, 40/500, and 40/1000. Commercial carbon fiber papers (Lydall Technimat®, density 0.2 g cm−3, ∼90 μm thick) were cut to 4 × 4 cm2 and cleaned in an air/ice plasma for 45 min then soaked in the RF sol under vacuum. The RF-soaked carbon fiber papers were sandwiched between glass slides with excess sol added and clamped together with binder clips. Multi-ply CNFPs were made by stacking multiple sheets of sol-infused carbon fiber paper in between glass slides. The assemblies were wrapped in duct tape to prevent leaking of sol and packaged together in aluminum foil with a few milliliters of water added to maintain humidity, then aged at room temperature for an additional 21 h. The aluminum foil packages were then cured in a commercial pressure cooker (Nesco 3-in-1 pressure cooker) set to steam mode for 9.5 h on slow-cook setting (∼88–94 °C) followed by a 14.5 h warm cycle (∼80 °C). The RF-polymer@CNFP nanofoam composite sheets were soaked in water and then acetone for 1–2 h, followed by drying in air at room temperature. The dry polymer nanofoam papers were pyrolyzed into CNFPs under flowing argon, ramping at 1 °C min−1 and holding at 1000 °C for 2 h.
2.2 Synthesis of S@CNFPs
Based on our prior work,7,8,47,48 sulfur vapor deposition into CNFP was performed in a round chamber (∼3 cm tall with a 3.75 cm radius, inner volume ∼106 cm3) consisting of a PTFE body and cap with a Viton O-ring for sealing (Fig. S1†). The CNFP was punched into 15 mm diameter discs and placed onto a piece of stainless-steel mesh which sat on a ledge above a well containing 1 g of sulfur powder. The infiltration chamber was sealed and placed inside a muffle furnace preheated to 175 °C. Vapor infiltration time varied, and lasted for 2 h, 6 h, or 18 h depending on the experiment. After infiltration to the set time, the chamber was removed from the furnace and allowed to cool for ∼30 min. The S@CNFP were weighed before and after infiltration to determine the sulfur loading. A simplified schematic of the synthesis of S@CNFPs can be found in Fig. S2.†2.3 Structural characterization of carbon nanofoam papers
Scanning electron microscopy (SEM; Zeiss Supra 55) was performed on CNFP cross-sections prepared by fast fracturing samples soaked in liquid nitrogen with a fresh razor blade. Pore size distribution and specific surface area were determined by nitrogen physisorption (Micromeritics ASAP 2020 Plus) with samples degassed prior to testing for 10 h at 150 °C. Pore size distributions were calculated from the adsorption isotherm data using a density functional theory (DFT) model. Apparent porosities and total specific pore volumes were estimated by Archimedes principle using water.2.4 Electrochemical characterization
Coin cells (CR2032) were fabricated with the sulfur-infiltrated CNFP discs versus a Li chip electrode (MTI, 16 mm diameter, 0.6 mm thick), an Entek Gold LP separator (19 mm diameter), and ∼80 μL of electrolyte (1 M LiTFSI (Sigma-Aldrich, bis(trifluoro-methane)sulfonimide lithium salt, 99.95% trace metals basis) and 0.2 M LiNO3 (ACROS Organics, lithium nitrate salt, 99.999% trace metals basis) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of DOL (Sigma-Aldrich, 1,3-dioxolane, anhydrous, contains ∼75 ppm BHT as inhibitor, 99.8%) and DME (Sigma-Aldrich, 1,2-dimethoxyethane, anhydrous, 99.5%, inhibitor free). The coin cell components (can, spacer, and wave spring) were purchased through Hohsen Corp (Japan), and the cells were assembled using Hohsen Corp's automatic coin cell crimper for 2032 cells.
1 ratio of DOL (Sigma-Aldrich, 1,3-dioxolane, anhydrous, contains ∼75 ppm BHT as inhibitor, 99.8%) and DME (Sigma-Aldrich, 1,2-dimethoxyethane, anhydrous, 99.5%, inhibitor free). The coin cell components (can, spacer, and wave spring) were purchased through Hohsen Corp (Japan), and the cells were assembled using Hohsen Corp's automatic coin cell crimper for 2032 cells.
Cycling was performed at a C-rate of 0.1C (based on the theoretical capacity of the sulfur deposited on the specific electrode) between 1.8 V and 2.6 V on a Maccor model 4300 desktop automated test system. Rate studies were performed on an Ametek PARSTAT MC Multichannel Potentiostat using PMC-1000 modules. These symmetric rate studies utilized C-rates of 0.1C for 10 cycles, 0.2C for 5 cycles, 0.5C for 5 cycles, 1C for 5 cycles, and a return to 0.1C for 10 cycles.
3. Results and discussion
3.1 Carbon nanofoam paper
Three variants of CNFPs were prepared in which the pore size distribution within the CNF component is tuned by controlling the resorcinol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catalyst (Na2CO3) ratio in the precursor RF sols. Increasing the R
catalyst (Na2CO3) ratio in the precursor RF sols. Increasing the R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
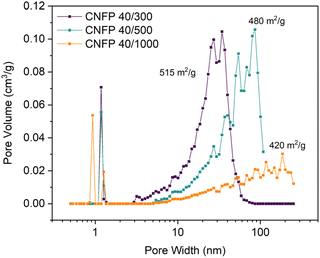
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio (decreasing catalyst concentration) results in larger RF particles and correspondingly larger pores in the polymer nanofoam, and ultimately in the pyrolyzed carbon form (Fig. 1).32,35 Consequently, the nitrogen adsorption isotherms change from mesoporous type IV to macroporous type II behavior (Fig. S3†) and pore size distributions broaden and shift to larger pore sizes (Fig. 2) while specific surface areas decrease from 515 m2 g−1 for CNFP-40/300 to 480 and 420 m2 g−1 for CNFP-40/500 and CNFP-40/1000, respectively (Table 1).
C ratio (decreasing catalyst concentration) results in larger RF particles and correspondingly larger pores in the polymer nanofoam, and ultimately in the pyrolyzed carbon form (Fig. 1).32,35 Consequently, the nitrogen adsorption isotherms change from mesoporous type IV to macroporous type II behavior (Fig. S3†) and pore size distributions broaden and shift to larger pore sizes (Fig. 2) while specific surface areas decrease from 515 m2 g−1 for CNFP-40/300 to 480 and 420 m2 g−1 for CNFP-40/500 and CNFP-40/1000, respectively (Table 1).
| CNFP | Total surface areaa (m2 g−1) | Micropore areab (m2 g−1) | Micropore volumeb (cm3 g−1) | Mesopore areac (m2 g−1) | Pore volumec (cm3 g−1) | Bulk densityd (g cm−3) | Bulk pore volumed (cm3 g−1) | Bulk porosityd (%) |
|---|---|---|---|---|---|---|---|---|
| a Total surface area determined by Brunauer–Emmett–Teller (BET) specific surface area. b Micropore surface area and volume estimated using t-plot method. c Mesopore surface area and pore volume determined by DFT. d Bulk properties determined by Archimedes Principle using water. | ||||||||
| 40/300 | 515 | 238 | 0.12 | 270 | 1.45 | 0.46 | 1.60 | 74.0 |
| 40/500 | 480 | 302 | 0.15 | 225 | 1.54 | 0.47 | 1.56 | 74.0 |
| 40/1000 | 420 | 338 | 0.17 | 198 | 0.70 | 0.42 | 1.80 | 76.5 |
The nitrogen physisorption-measured pore volume in CNFPs is dominated by mesopores (2–50 nm) and macropores (>50 nm), with micropores (<2 nm) contributing only a small fraction. CNFP-40/300 and CNFP-40/500 possess similar specific pore volumes of about 1.5 cm3 g−1; however, CNFP-40/1000 results in a drastically lower pore volume of 0.7 cm3 g−1 in mesopores and small macropores. This result reflects the limits of nitrogen physisorption to measure pores >100 nm, a size range that is prevalent in CNFP-40/1000, as evident in SEM images (see Fig. 1). In comparison to nitrogen physisorption, bulk density determined by the Archimedes Principle estimates the total pore volume of CNFPs to be between 1.6–1.8 cm3 g−1, which better demonstrates the contribution of pores >100 nm. All formulations should nominally have the same total pore volume because all derive from a 40 wt% RF sol.
The CNFPs provide higher volumetric surface areas between 168–259 m2 cm−3 compared to other as-synthesized high-surface area carbon aerogels with porosities over 90% due to the higher bulk density of the former.31 The bulk density of freestanding CNFP is also directly related to its electrode tap density without need for further processing.
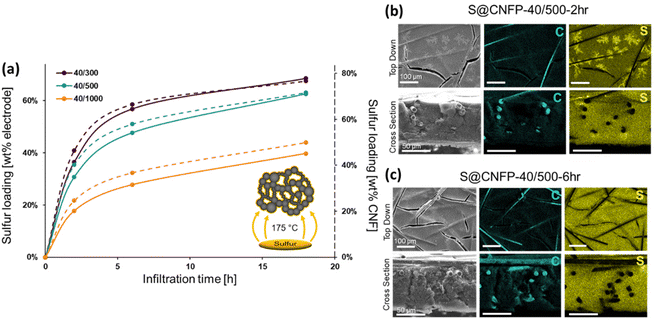
When employing mesoporous/macroporous materials that are expressed as unitary macroscale objects, self-limiting non-line-of-sight coating/modification schemes are essential to decorate interior surfaces without clogging the pore structure, as we previously demonstrated with CNFPs coated with nanoscale metal oxides44–46 and polymers.50 Thus, the present vapor-phase approach7,8,30,47–49 is ideally suited to incorporate sulfur within the device-ready CNFP architecture. When tracking the CNFP mass as a function of vapor-infiltration time, uptake is initially rapid, with weight loading correlating to the specific surface area of a CNFP (Fig. 3a). Beyond 6 h infiltration, the rate of weight gain for all CNFP formulations stabilizes at about 1 wt% h−1, reaching 69, 63, and 40 wt% sulfur loadings after 18 h for CNFP-40/300, CNFP-40/500, and CNFP-40/1000, respectively. The decrease in deposition rate beyond 6 h indicates that all nanostructured carbon surfaces are coated by sulfur, emphasizing the self-limiting nature of the vapor infiltration process, which prevents the formation of thick regions of sulfur.
Elemental mapping using EDS reveals uniform incorporation of sulfur throughout the CNF component but not along the supporting carbon fibers (Fig. 3b & c). The supporting carbon-fiber paper component contributes ∼34 wt% of the total mass of the CNFP and provides mechanical integrity and enhanced electrical conductivity, but the carbon fibers themselves contribute minimally to the charge-storage capacity.39 Thus, we also note sulfur loading as normalized to the mass of the CNF domains in the CNFP in Fig. 3a for fundamental comparison with other porous carbons.
Sulfur coating thicknesses derived mathematically based on BET surface area, sulfur mass loadings, and density of sulfur (∼2 g cm−3) result in coatings between 1–9 nm thick (Table S1†). In general, CNFPs with smaller pores obtain thicker coatings. The condensation of sulfur from the vapor phase is influenced by surface energy, whereby smaller pores of negative curvature have higher surface energies.8 In contrast, the supporting carbon fiber paper has larger positive curvature, along with a dense non-porous interior, that results in the low sulfur EDS signal.
Thicker sulfur coatings result in higher pore-volume occupation by sulfur and this relation is stronger for smaller pores (Table S2†). For example, after 18 h infiltration CNFPs nominally have 68, 53, and 18 vol% of pore-volume occupied by sulfur corresponding to 69, 63, and 40 wt% sulfur loading for CNFP-40/300, CNFP-40/500, and CNFP-40/1000, respectively. Comparing between CNFP-40/300 and CNFP-40/1000, the smaller pore CNFP-40/300 has 73% greater sulfur mass loading but corresponds to 278% greater pore-volume occupation due to the smaller pore radius. Remaining void space in S@CNFPs is important to facilitate volume expansion and electrolyte diffusion. If pore volume is insufficient the electrode will suffer from electrolyte starvation and high concentration overpotentials.
The porous carbon network with minimal dead volume grants high volumetric sulfur loadings up to 1 g cm−3 for 1-ply S@CNFP-40/300-18 h (Table S3†). However, areal sulfur loading is a more important metric to the design of practical Li–S battery cathodes. Average sulfur loadings for 1-ply CNFP samples are tabulated in Table 2, with the highest reaching 10.2 mg cm−2 for S@CNFP-40/300-18 h. Novel thin-film and composite electrodes may exhibit high gravimetric and volumetric capacities but lack practical applicability due to low areal weight loadings. Increasing sulfur loadings by producing thick-film composite electrodes are prone to cracking and separation from the current collector. In contrast, the interconnected mesoporous carbon framework and carbon fiber backbone of CNFPs act as an integrated current collector and allow for thick electrode structures without sacrificing electronic conductivity.
| Infiltration time (h) | Areal loading (mgsulfur/cm2CNFP) | ||
|---|---|---|---|
| 40/300 | 40/500 | 40/1000 | |
| 2 | 2.5 | 1.9 | 1.1 |
| 6 | 6.1 | 3.7 | 1.7 |
| 18 | 10.2 | 6.7 | 3.0 |
3.2 Li–S battery performance
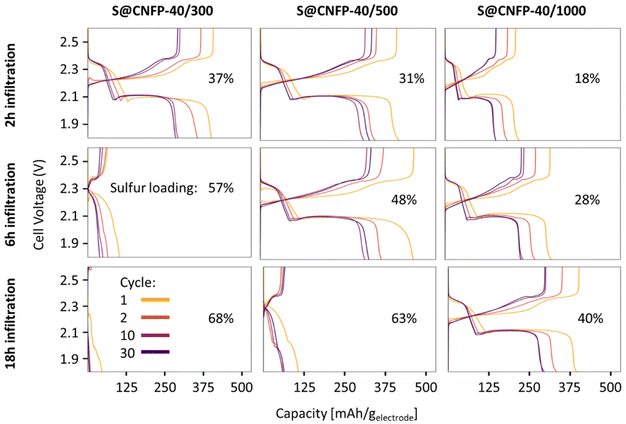
Multiple variants of sulfur-loaded CNFPs were incorporated into Li–S coin cells and electrochemically evaluated by galvanostatic charge–discharge. These cells show the two typical discharge plateaus associated with sulfur reduction to soluble, anionic polysulfides commencing at ∼2.4 V followed by reduction to insoluble Li2S at ∼2.1 V (Fig. 4). The re-dox activity at these voltages is further revealed with dQ/dV in Fig. S4.†Specific capacity metrics in sulfur-cathode studies are often reported in terms of mA h gsulfur−1, which only considers the mass of the active sulfur material. This method of calculation can often be misleading, sometimes overstating the capabilities of certain cathode materials that have efficient sulfur utilization but require significant additional mass from other electrode components. Here, we also tabulate specific capacity normalized to total weight of the CNFP-based electrode (mA h gelectrode−1), which includes the mass of the infiltrated sulfur, the carbon nanofoam domains, and the supporting carbon fibers (which themselves do not store significant sulfur, as noted above). Charge–discharge cycling at a 0.1C (0.167 A gsulfur−1) rate illustrates general trends in measured capacity as a function of CNFP pore structure and sulfur loading (Fig. 5a). For example, CNFPs with intermediate sulfur loadings at 35–50 wt% exhibit the best specific capacity values (up to 350 mA h gelectrode−1 at cycle 30 for S@CNFP-40/500-6 h at 48 wt% sulfur), while capacity rapidly decreases as loadings surpass ∼50%, as seen for S@CNFP-40/300-6 h and S@CNFP-40/500-18 h.
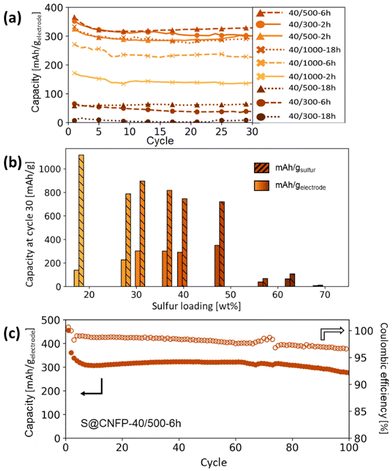 | ||
| Fig. 5 (a) Summary of Li–S cycling capacities at 0.1C for CNFPs using different sulfur infiltration durations and (b) their corresponding gravimetric capacities per weight sulfur and per total electrode weight after cycle 30 versus their sulfur weight loadings. (c) Long-term cycling of the S@CNFP-40/500-6 h sample to 100 cycles. Results are summarized in Table S4,† and cycling capacity normalized to sulfur mass is shown in Fig. S5.† | ||
Sulfur utilization, the fraction of sulfur that is redox active, is another important metric to track across this series. Fig. 5b shows that highest sulfur utilization is realized at low weight loadings (e.g., S@CNFP-40/1000-2 h), but at the expense of overall specific capacity. We find an optimal balance of utilization and electrode capacity with S@CNFP-40/500-6 h at 48% S loading and 719 mA h gsulfur−1 at cycle 30. We attribute decreasing sulfur utilization at high loadings to increased electronic resistance from thicker sulfur coatings, as evidenced by impedance spectroscopy (Fig. S6†). The decrease in both total capacity and sulfur utilization at the highest weight loadings is likely caused by impeded electrolyte transport from pore narrowing. Insufficient electrolyte flux results in local saturation of soluble polysulfide species during discharge, which increases overpotential due to reduced conductivity and increased viscosity (see S@CNFP-40/300-6 h, S@CNFP-40/300-18 h, and S@CNFP-40/500-18 h; Fig. 4).25,51 Our findings show that a balance of electrode pore volume and sulfur loading is needed to achieve optimal specific capacity for given electrochemical conditions. Prior studies with mesoporous carbons have shown that partial sulfur fillings lead to improved performance.27–29 Upon identifying S@CNFP-40/500-6 h as a pore-solid architecture that balances sulfur utilization and electrode specific capacity, we cycled additional cells for 100 cycles demonstrating good capacity retention and high coulombic efficiency (>95%).
The role of pore structure in transport and concentration polarization are further exacerbated at higher rates. In order to explore rate capability within varied pore structures, we selected CNFPs of similar sulfur loadings—S@CNFP-40/300-2 h (37 wt% S), S@CNFP-40/500-6 h (48 wt% S), and S@CNFP-40/1000-18 h (40 wt% S)—probing specific currents of 0.1, 0.2, 0.5, 1, 2, and 5 A gsulfur−1 (0.06, 0.12, 0.3, 0.6, 1.2, and 3C), followed by a return to 0.1 A gsulfur−1 (0.06C) to assess the damage issued as a result of high rate excursion; see Fig. 6a. At moderate rates, the intermediate pore-sized S@CNFP-40/500-6 h demonstrates superior specific capacity as observed in Fig. 5. Yet, sharp capacity loss is observed at 1 A gsulfur−1 where transport limitations dominate. Overall, we see that CNFPs with larger pores (mix of mesopores and macropores) support moderately lower capacity but better rate capability, while CNFPs that are primarily mesoporous (2–50 nm) deliver higher capacity at low rates but inferior rate performance. The Ragone plot in Fig. 6b summarizes the tradeoff in capacity and rate for this series, highlighting the high specific energy that can be achieved with S@CNFP cathodes at moderate power requirements, but also showcasing the ability for respectable energy density under high power conditions (i.e., 578 W h kgelectrode−1 at 166 W kg−1 and 388 W h kgelectrode−1 at 700 W kg−1).
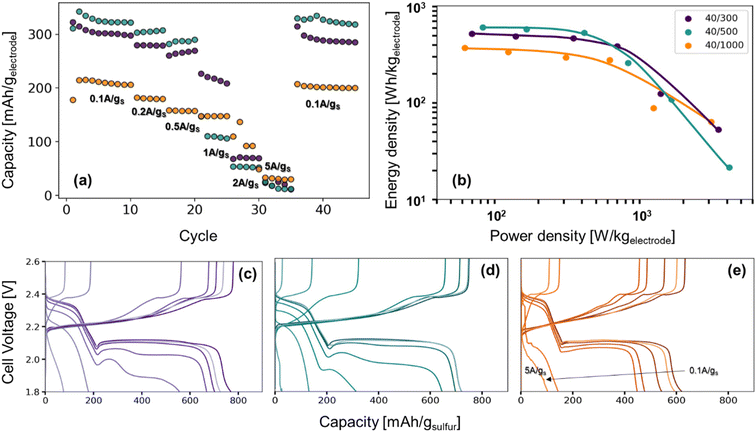 | ||
| Fig. 6 (a) Rate study of Li–S coin cells from 0.1 A gsulfur−1 to 5 A gsulfur−1, (b) the Ragone plot produced from the third cycle of each rate, and (c–e) their corresponding charge–discharge curves. | ||
Looking more closely at the charge–discharge voltage profiles, increasing polarization is evident as the discharge rate is increased for S@CNFP-40/300 and S@CNFP-40/500, as demonstrated by the decrease in the discharge voltage at higher rates, possibly arising from electrolyte starvation due to small pore volume (Fig. 6c–e). We calculated the moles of lithium ions residing in internal void volume and divided by the number of moles required to satisfy the specific capacity recorded at 0.1 A gsulfur−1, determining ratios of 0.11, 0.10, and 0.33 for S@CNFP-40/300-2 h, S@CNFP-40/500-6 h, and S@CNFP-40/1000-18 h, respectively. Significantly more lithium from outside the electrode must diffuse into the voids of S@CNFP-40/300 and S@CNFP-40/500 compared to S@CNFP-40/1000 with larger pore size, leading to poor sulfur utilization and low energy density at high power demand. The effect that pore size has on concentration polarization at high rate in CNFPs is analogously observed in aqueous lithium-ion electrochemical capacitors.43
In some discharge profiles we observe a dip in voltage between these two plateaus, a feature ascribed to the nucleation of solid lithium sulfide products, which is strongly influenced by kinetic transport limitations. At a modest rate of 0.5 A gsulfur−1 the voltage minima of this transition are 2.03, 2.00, and 2.06 V for S@CNFP-40/300-2 h, S@CNFP-40/500-6 h, and S@CNFP-40/1000-18 h, respectively. Prior studies conclude that sulfide nucleation is limited by mass transfer rather than electron transfer.51,52 Pore clogging in S@CNFP-40/500-6 h restricts ion transport to a greater extent and generates higher concentration polarization, in turn lowering specific energy more severely when diffusion limitations dominate at higher rate.
3.3 Multi-ply carbon nanofoam papers
The thickness of CNFPs can be varied based on the number of carbon fiber paper plies used during the RF-sol infiltration step in increments beyond the “1-ply” used for CNFPs discussed thus far.43 As a means to further increase areal-capacity metrics, we fabricate 2-ply and 3-ply CNFPs (Fig. 7a), which exhibit average thickness values of 210 and 290 μm, respectively, compared to 120 μm for 1-ply CNFP. The nonlinearity in thickness per ply results from increased clamping force on RF sheets during curing due to increased ply count. Subjecting these multi-ply CNFPs to vapor-phase sulfur infiltration for 6 h decreases sulfur loading as thickness increases (Table S5†). Non-constant weight loading suggests that sulfur loading depends on total surface area, not just specific surface area, thus longer vapor exposure times are required for thicker electrodes. Additionally, the 2- and 3-ply CNFPs have a larger mass fraction of inactive carbon fiber due to their smaller thicknesses.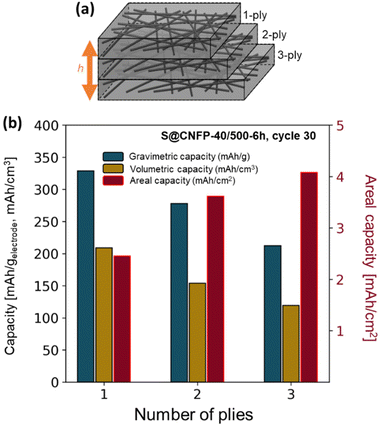 | ||
| Fig. 7 (a) Schematic of multi-ply CNFPs and (b) the gravimetric, volumetric, and areal capacities of these multi-ply papers. | ||
The areal discharge capacity of multi-ply S@CNFP-40/500-6 h at a rate of 0.1C (Fig. 7b) is highest for 3-ply S@CNFP-40/500-6 h at 4.1 mA h cm−2. Tradeoffs appear between gravimetric and volumetric capacity due to decreased sulfur loading and greater inactive carbon fiber content. This areal capacity is much higher compared to carbon-based powder composite cathodes with lower areal sulfur loadings (Table S6†). The scalable and tunable properties of the CNFP proves valuable to applications where footprint is the dominant constraint. We also note the impressive tap density of the device-ready 1-ply CNFP supports high volumetric capacity of 209 mA h cm−3.
4. Conclusions
Carbon nanofoam papers are efficacious cathode architectures for rechargeable Li–S cells. The adaptable nature of the CNFP synthesis permits pore structure tuning to optimize sulfur loading and ultimately balance such electrochemical performance metrics as gravimetric/volumetric/areal capacity and rate capability. In contrast with the ad hoc structures of most conventional Li–S cathodes, the CNFP provides the benefits of designer pore-solid architectures expressed in freestanding form factors that are device ready and require minimal additional processing or components. The ability to scale the CNFP in thickness while maintaining electronic and ionic continuity through the volume of the architecture electrode also enables high areal capacity, which is becoming an important performance metric for many energy-storage applications.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to thank Junghoon Yeom for SEM EDS analysis and Corey Love for use of laboratory equipment. This work was supported by Office of Naval Research, USA (N0001423WX00004).References
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 19–29 CrossRef CAS PubMed
.
- A. Fotouhi, D. J. Auger, L. O'Neill, T. Cleaver and S. Walus, Energies, 2017, 10, 1937 CrossRef
.
- K. Zhu, C. Wang, Z. Chi, F. Ke, Y. Yang, A. Wang, W. Wang and L. Miao, Front. Energy Res., 2019, 7, 123 CrossRef
.
- M. Wang, X. Xia, Y. Zhong, J. Wu, R. Xu, Z. Yao, D. Wang, W. Tang, X. Wang and J. Tu, Chem. – Eur. J., 2019, 25, 3710–3725 CrossRef CAS
.
- S. Xin, L. Gu, N.-H. Zhao, Y.-X. Yin, L.-J. Zhou, Y.-G. Guo and L.-J. Wan, J. Am. Chem. Soc., 2012, 134, 18510–18513 CrossRef CAS PubMed
.
- B. Zhang, X. Qin, G. R. Li and X. P. Gao, Energy Environ. Sci., 2010, 3, 1531–1537 RSC
.
- R. Carter, L. Oakes, N. Muralidharan, A. P. Cohn, A. Douglas and C. L. Pint, ACS Appl. Mater. Interfaces, 2017, 9, 7185–7192 CrossRef CAS
.
- M. Li, R. Carter, A. Douglas, L. Oakes and C. L. Pint, ACS Nano, 2017, 11, 4877–4884 CrossRef CAS
.
- M. Li, X. Zhou, X. Ma, L. Chen, D. Zhang, S. Xu, D. Duan, C. Chen, Q. Yuan and S. Liu, Chem. Eng. J., 2021, 409, 128164 CrossRef CAS
.
- Y.-J. Yen and S.-H. Chung, Chem. Commun., 2021, 57, 2009–2012 RSC
.
- J. Kim, Y. Kang, S.-W. Song and J. Suk, Electrochim. Acta, 2019, 299, 27–33 CrossRef CAS
.
- T. Wang, Q. Zhang, J. Zhong, M. Chen, H. Deng, J. Cao, L. Wang, L. Peng, J. Zhu and B. Lu, Adv. Energy Mater., 2021, 11, 2100448 CrossRef CAS
.
- A. Fu, C. Wang, F. Pei, J. Cui, X. Fang and N. Zheng, Small, 2019, 15, 1804786 CrossRef PubMed
.
- S. Li and Z. Fan, Energy Storage Mater., 2021, 34, 107–127 CrossRef
.
- Y. Xu, Y. Wen, Y. Zhu, K. Gaskell, K. A. Cychosz, B. Eichhorn, K. Xu and C. Wang, Adv. Funct. Mater., 2015, 25, 4312–4320 CrossRef CAS
.
- T. Cleaver, P. Kovacik, M. Marinescu, T. Zhang and G. Offer, J. Electrochem. Soc., 2018, 165, A6029 CrossRef CAS
.
- N. Kang, Y. Lin, L. Yang, D. Lu, J. Xiao, Y. Qi and M. Cai, Nat. Commun., 2019, 10, 4597 CrossRef PubMed
.
- Y.-T. Liu, S. Liu, G.-R. Li and X.-P. Gao, Adv. Mater., 2021, 33, 2003955 CrossRef CAS PubMed
.
- Q. Hu, H. Dong, B. Wang, C. Yang, X. Wang, J. Lu, Y. Hong and L. Zhang, Electrochim. Acta, 2021, 377, 138063 CrossRef CAS
.
- C. Kensy, D. Leistenschneider, S. Wang, H. Tanaka, S. Dörfler, K. Kaneko and S. Kaskel, Batteries Supercaps, 2021, 4, 612–622 CrossRef CAS
.
- E. Markevich, G. Salitra, S. Bretler, H. Yoshida, S. Sawada and D. Aurbach, J. Power Sources, 2022, 552, 232250 CrossRef CAS
.
- A. D. Dysart, J. C. Burgos, A. Mistry, C.-F. Chen, Z. Liu, C. Hong, P. B. Balbuena, P. P. Mukherjee and V. G. Pol, ECS Meet. Abstr., 2016, MA2016-03, 403 CrossRef
.
- C. Lv, H. Cao, W. Deng, M. Zhao, Y. Miao, C. Guo, P. Liu and Y. Wu, Dalton Trans., 2023, 52, 4700–4707 RSC
.
- C.-C. Wu and S.-H. Chung, J. Power Sources, 2023, 566, 232944 CrossRef CAS
.
- R. Carter, D. Ejorh, K. Share, A. P. Cohn, A. Douglas, N. Muralidharan, T. M. Tovar and C. L. Pint, J. Power Sources, 2016, 330, 70–77 CrossRef CAS
.
- M. M. Gaikwad, K. K. Sarode, A. D. Pathak and C. S. Sharma, Chem. Eng. J., 2021, 425, 131521 CrossRef CAS
.
- L. Li, Z. Ma and Y. Li, Carbon, 2022, 197, 200–208 CrossRef CAS
.
- X. Li, Y. Cao, W. Qi, L. V. Saraf, J. Xiao, Z. Nie, J. Mietek, J.-G. Zhang, B. Schwenzer and J. Liu, J. Mater. Chem., 2011, 21, 16603–16610 RSC
.
- S. Zhang, A. Ikoma, Z. Li, K. Ueno, X. Ma, K. Dokko and M. Watanabe, ACS Appl. Mater. Interfaces, 2016, 8, 27803–27813 CrossRef CAS PubMed
.
- R. Carter, L. Oakes, A. Douglas, N. Muralidharan, A. P. Cohn and C. L. Pint, Nano Lett., 2017, 17, 1863–1869 CrossRef CAS PubMed
.
- M. Nojabaee, B. Sievert, M. Schwan, J. Schettler, F. Warth, N. Wagner, B. Milow and K. A. Friedrich, J. Mater. Chem. A, 2021, 9, 6508–6519 RSC
.
- S. A. Al-Muhtaseb and J. A. Ritter, Adv. Mater., 2003, 15, 101–114 CrossRef CAS
.
- M. Antonietti, N. Fechler and T.-P. Fellinger, Chem. Mater., 2014, 26, 196–210 CrossRef CAS
.
- F. Li, L. Xie, G. Sun, Q. Kong, F. Su, Y. Cao, J. Wei, A. Ahmad, X. Guo and C.-M. Chen, Microporous Mesoporous Mater., 2019, 279, 293–315 CrossRef CAS
.
- A. M. ElKhatat and S. A. Al-Muhtaseb, Adv. Mater., 2011, 23, 2887–2903 CrossRef CAS PubMed
.
- A. Kausar, I. Ahmad, T. Zhao, M. H. Eisa and O. Aldaghri, Nanomanufacturing, 2023, 3, 37–56 CrossRef
.
- S.-Y. Chen and S.-H. Chung, Nanomaterials, 2021, 11, 2083 CrossRef CAS
.
- R. H. DeBlock, R. Carter, M. J. Lefler, M. B. Sassin, D. R. Rolison and J. W. Long, J. Electrochem. Soc., 2022, 169, 060514 CrossRef CAS
.
- R. H. DeBlock, J. S. Ko, M. B. Sassin, A. N. Hoffmaster, B. S. Dunn, D. R. Rolison and J. W. Long, Energy Storage Mater., 2019, 21, 481–486 CrossRef
.
- J. S. Ko, M. B. Sassin, J. F. Parker, D. R. Rolison and J. W. Long, Sustainable Energy Fuels, 2018, 2, 626–636 RSC
.
- J. C. Lytle, J. M. Wallace, M. B. Sassin, A. J. Barrow, J. W. Long, J. L. Dysart, C. H. Renninger, M. P. Saunders, N. L. Brandell and D. R. Rolison, Energy Environ. Sci., 2011, 4, 1913–1925 RSC
.
- M. B. Sassin, S. G. Greenbaum, P. E. Stallworth, A. N. Mansour, B. P. Hahn, K. A. Pettigrew, D. R. Rolison and J. W. Long, J. Mater. Chem. A, 2013, 1, 2431–2440 RSC
.
- M. B. Sassin, C. P. Hoag, B. T. Willis, N. W. Kucko, D. R. Rolison and J. W. Long, Nanoscale, 2013, 5, 1649–1657 RSC
.
- M. B. Sassin, A. N. Mansour, K. A. Pettigrew, D. R. Rolison and J. W. Long, ACS Nano, 2010, 4, 4505–4514 CrossRef CAS
.
- A. E. Fischer, K. A. Pettigrew, D. R. Rolison, R. M. Stroud and J. W. Long, Nano Lett., 2007, 7, 281–286 CrossRef CAS
.
- A. E. Fischer, M. P. Saunders, K. A. Pettigrew, D. R. Rolison and J. W. Long, J. Electrochem. Soc., 2008, 155, A246 CrossRef CAS
.
- R. Carter, B. Davis, L. Oakes, M. R. Maschmann and C. L. Pint, Nanoscale, 2017, 9, 15018–15026 RSC
.
- R. Carter, L. Oakes, N. Muralidharan and C. L. Pint, J. Phys. Chem. C, 2017, 121, 7718–7727 CrossRef CAS
.
- L. Oakes, R. Carter and C. L. Pint, Nanoscale, 2016, 8, 19368–19375 RSC
.
- A. E. Fischer, M. P. Saunders, J. C. Lytle, D. R. Rolison and J. Long, ECS Trans., 2008, 6, 159 CrossRef CAS
.
- F. Y. Fan and Y.-M. Chiang, J. Electrochem. Soc., 2017, 164, A917 CrossRef CAS
.
- T. Zhang, M. Marinescu, S. Walus, P. Kovacik and G. J. Offer, J. Electrochem. Soc., 2018, 165, A6001 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr02699j |
| This journal is © The Royal Society of Chemistry 2023 |