Open Access Article
Open Access ArticlePathways to enhance electrochemical CO2 reduction identified through direct pore-level modeling†
Evan F.
Johnson
 ,
Etienne
Boutin
,
Etienne
Boutin
 ,
Shuo
Liu
,
Shuo
Liu
 and
Sophia
Haussener
and
Sophia
Haussener
 *
*
Laboratory of Renewable Energy Science and Engineering, EPFL, Station 9, 1015 Lausanne, Switzerland. E-mail: sophia.haussener@epfl.ch; Tel: +41 21 693 3878
First published on 15th June 2023
Abstract
Electrochemical conversion of CO2 to fuels and valuable products is one pathway to reduce CO2 emissions. Electrolyzers using gas diffusion electrodes (GDEs) show much higher current densities than aqueous phase electrolyzers, yet models for multi-physical transport remain relatively undeveloped, often relying on volume-averaged approximations. Many physical phenomena interact inside the GDE, which is a multiphase environment (gaseous reactants and products, liquid electrolyte, and solid catalyst), and a multiscale problem, where “pore-scale” phenomena affect observations at the “macro-scale”. We present a direct (not volume-averaged) pore-level transport model featuring a liquid electrolyte domain and a gaseous domain coupled at the liquid–gas interface. Transport is resolved, in 2D, around individual nanoparticles comprising the catalyst layer, including the electric double layer and steric effects. The GDE behavior at the pore-level is studied in detail under various idealized catalyst geometries configurations, showing how the catalyst layer thickness, roughness, and liquid wetting behavior all contribute to (or restrict) the transport necessary for CO2 reduction. The analysis identifies several pathways to enhance GDE performance, opening the possibility for increasing the current density by an order of magnitude or more. The results also suggest that the typical liquid–gas interface in the GDE of experimental demonstrations form a filled front rather than a wetting film, the electrochemical reaction is not taking place at a triple-phase boundary but rather a thicker zone around the triple-phase boundary, the solubility reduction at high electrolyte concentrations is an important contributor to transport limitations, and there is considerable heterogeneity in the use of the catalyst. The model allows unprecedented visualization of the transport dynamics inside the GDE across multiple length scales, making it a key step forward on the path to understanding and enhancing GDEs for electrochemical CO2 reduction.
Broader contextA vast reduction in CO2 emissions is needed to limit climate change, and the conversion of CO2 into useful fuels and products is one pathway toward this goal. After capturing CO2 (either from a point source or directly from the air), it can be converted into a variety of fuels and chemicals using an electrolyzer powered by renewable electricity. Numerous products are under investigation, including ethylene, methane, formic acid, and carbon monoxide (used in “synthesis gas” for liquid fuels). Continuum-level computational models should provide useful insights and optimization strategies for fabricating electrolyzers. Though electrolyzers using “gas diffusion electrodes” (GDEs) have demonstrated high CO current densities, they are a challenge to model due their multi-physics nature, as the porous catalyst contacts both the liquid electrolyte and gaseous CO2 (the “triple-phase boundary”). Unlike previous GDE models using a volume-averaged approach, we present a modeling methodology resolving the physics down to the nanometer scale (“pore-level”), including effects from the electric double layer. Such detailed multi-physics modeling reveals useful conclusions for optimizing the catalyst layer thickness, roughness, and the local environment. The methodology may be useful beyond electrochemical CO2 reduction for modeling the GDE in other electrochemical devices. |
1 Introduction
Electrochemical synthesis provides one pathway towards atmospheric carbon neutrality by using renewable electricity and CO2 to produce useful chemicals or fuels. Various products are under research, including ethylene, methane, formic acid, and carbon monoxide (CO). CO is an important building block for numerous industrial chemicals currently produced with fossil fuels.1 Alternatively, CO combined with hydrogen (so-called synthesis gas) can be processed into a variety of liquid fuels through the Fischer–Tropsch process.2 Liquid fuels provide a dense energy storage medium to balance variable renewable electricity production and can be used to address sectors which are hard to electrify, such as aviation and ocean shipping. Early work on CO2 electrolyzers was done with planar electrodes immersed in an aqueous electrolyte, with CO2 supplied as a dissolved gas (an “H-cell”).3 Immersed, planar electrode configurations are well-suited for studying the catalysts and reaction mechanisms, with a well-defined geometric surface area and aqueous phase reactants. As electrochemical CO2 reduction (CO2R) is maturing, focus has shifted towards configurations using a gas diffusion electrode (GDE) for the cathode, which promises the high current densities needed for industry.3 GDEs are typically constructed by applying a catalyst onto a porous (often carbon) matrix, creating a porous catalyst layer. In this configuration, liquid electrolyte still flows in the space between the anode and the cathode, but gaseous CO2 is supplied from the outside of the GDE, with the interface of the liquid and gas (ideally) lying within the catalyst layer.4 The high CO2R current in GDE configurations is attributed to the short diffusion length from the CO2 gas phase to the catalyst surface5 and the high electrochemically active surface area (ECSA) of the porous catalyst.6 However, a thorough understanding of the multi-physical species transport inside the GDE is still lacking, as it is experimentally not (easily) accessible. Here, we focus on the GDE configuration in the presence of a liquid catholyte, though numerous different cell configurations are reported, including membrane electrolytes3 and “zero-gap”7 configurations.Continuum modeling approaches have been applied successfully to gain insight into the physical phenomena in CO2 electrolyzers, as reviewed by Bui et al.8 Configurations with planar, immersed electrodes have been modeled with a 1D approach, with the partial differential equations governing the species transport solved only in the normal direction with respect to the layers comprising the cathode and anode. Notable examples are Singh et al.9 and Zhu et al.10 who both used a 1D continuum model for the liquid electrolyte and a DFT-derived microkinetic model for the electrode surface reactions. Compared to immersed electrode configurations, far fewer studies have modeled GDE configurations. The studies to date have applied volume-averaging to model the catalyst layer as a porous medium using characteristic parameters including porosity, permeability, saturation, and specific surface area. Weng et al.11 modeled a GDE in 1D by assuming an idealized pore wetted with a thin liquid film covering the entire catalyst layer. Blake et al.12 pursued a similar model, adding the Sechenov relation for gas solubility in the liquid phase. Similar volume-averaged GDE models have recently been extended to 2D.13,14 These volume-averaged models typically do not consider effects at the nano- to micron-scale at the catalyst-electrolyte interface.
Most previous studies use the Nernst–Planck equation to model diffusion, convection, electrostatic migration, and homogeneous reactions in the liquid electrolyte. Either electroneutrality (no charge separation) is assumed, or the potential is solved by coupling with the Poisson equation, forming the Poisson–Nernst–Planck (PNP) formulation.8,15 Recently, several studies have added a new term to the PNP formulation to include steric effects, allowing for modeling the electric double layer (EDL) in more detail, which is termed the Generalized Modified Poisson–Nernst–Planck (GMPNP) formulation.16 The steric term is derived from a Langmuir-type activity coefficient under the assumption that a rigid, spherical hydration shell surrounds each ion. The steric limit (maximum concentration possible) is assumed to be reached when the spheres form a simple cubic packing structure, one layer thick, along the charged surface.16 Such an assumption leads to, for example, a steric limit of 5.73 M for K+ with a hydrated diameter of 0.662 nm.17 Without the steric term, the cation concentration computed near the cathode can reach unphysically high levels, as cations are attracted to the cathode, but they are allowed to pack tighter than is physically possible based on their hydrated size.17 Furthermore, the high cation concentration along the catalyst surface excludes other species (including CO2) from this area. The GMPNP formulation has been used in several recent 1D studies such as Bohra et al.,17,18 Ringe et al.,19 and Zhu et al.10 GMPNP has not been used extensively in higher dimensions.
The interacting phenomena inside the GDE are quite complex, with numerous species in the liquid undergoing transport from diffusion, electrostatic migration, and steric effects, through a porous 3D geometry. Gaseous reactants and products diffuse in opposite directions through the diffusion medium (DM), meeting the liquid electrolyte at the liquid–gas interface, where gaseous species dissolve into the liquid. Furthermore, homogeneous buffer reactions of CO2, bicarbonate, and carbonate occur in the electrolyte, depleting the CO2 available at the catalyst surface, especially at high current densities as hydroxide ions accumulate. The geometry of the catalyst particles and the surrounding liquid both affect these dynamics, as hydroxide must be able to diffuse through liquid pathways out to the bulk electrolyte, and open gas pathways must allow CO2 in and gaseous products out. All of these detailed geometric and transport effects are not captured in volume-averaged 1D continuum GDE models, making them of limited use for informing experimental work or improving actual GDEs.
The aim of the present work is to model these phenomena in much more detail by resolving the multiphase transport around numerous nanoparticles comprising the catalyst layer, without volume-averaging. This detailed nm-scale modeling approach is referred to by Bui et al. as Direct Numerical Simulation (DNS),8 and has been the subject of almost no research in CO2R. One of the few examples is from Suter et al.20 who optimized catalyst shapes in 3D using the reaction-diffusion equations (without electrostatic migration or steric effects), where the configuration modeled was an immersed electrode, not a GDE. Volume-averaged continuum models in 1D may provide an order of magnitude approximation to rationalize experimental findings, and as the technology matures they will be important for device-level modeling. However, as the phenomena inside the catalyst layer are not yet entirely understood, only DNS can provide the level of accuracy and detail to give quantitative and predictive insights into engineering a highly functional GDE. The chief drawback of DNS is the high computational cost compared to volume-averaged continuum models. The method developed here is able to perform detailed, insightful DNS simulations that are computationally tractable thanks to a scaling approach.
Ideally, the liquid–gas interface lies within the catalyst layer, providing a short diffusion path between the gas and the catalyst surface, however, the exact shape and location of the interface is not yet clear. Liu et al.21 studied GDEs to find water penetration and contact angles using both experimental and modeling techniques (Lattice Boltzmann method), though focus was on the carbon GDE comprising the DM, not the catalyst layer. Carbon is the most common DM material found in literature, which can have a hydrophobic PTFE coating to keep the electrolyte confined to the catalyst layer. However, Yang et al.4 show the liquid electrolyte can penetrate entirely through the catalyst layer and the DM within several hours, and they hypothesize the flooding is promoted by electro-wetting (a reduction in solid–liquid interfacial tension due to the applied potential). In addition, H2 is thought to be produced on the flooded carbon GDE, reducing the Faradaic efficiency to CO (FECO). GDEs featuring a DM made entirely of PTFE may alleviate some of the flooding drawbacks of carbon-based GDEs.22,23
The central aim of this work is to develop modeling methods to predict multi-physical transport in GDEs with much greater detail than previously possible, and subsequently, to explore ways to optimize GDE geometry and operating conditions for maximized performance using the newly developed tool. The model is applied to a CO selective catalyst as an example. The model contains numerous novel features. It resolves transport inside the catalyst layer at the pore-level in a GDE configuration, allowing for modeling specific catalyst shapes (e.g. nanoparticles, leaf-shapes), which is not possible when using a volume-averaged approach. The GMPNP formulation is used to capture the important physics of the EDL, which has not been included in previous GDE studies and has not been applied beyond 1D. Unlike previous models, the presented model uses two simulations coupled at the liquid–gas interface, where transport to and from the interface is modeled in detail down to the nm scale. Perhaps most important, the model connects the pore-scale to the macro-scale, yielding results that are directly comparable to experiments. Armed with this new model, we investigate various cathode design parameters, capturing the effects of wetting within the catalyst layer, catalyst surface roughness, and the catalyst layer thickness. With the modeling methodology developed, many possible GDE designs can be envisioned and investigated, making it a key step forward on the path to understanding and enhancing GDEs for CO2R.
2 Methodology
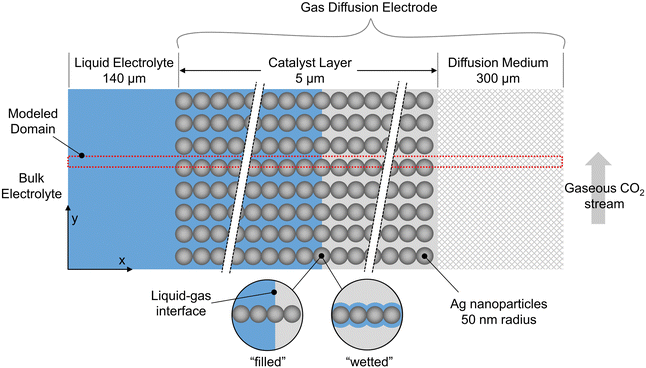
A schematic of the overall GDE is shown in Fig. 1, where the liquid electrolyte fills the space around spherical catalyst nanoparticles. Simulations are run in 2D, with red lines indicating the portion modeled after reducing by symmetry planes. To develop the methodology, we take the example of a catalyst layer composed of 50 spherical nanoparticles (each 50 nm in radius) spanning the 5 μm cathode layer width, consistent with previous modeling work,11 and within in the range found in experimental studies (0.3 to 15.1 μm24). The catalyst is silver, which is selective towards CO and hydrogen.25 The mass-transfer boundary layer thickness (from bulk electrolyte to catalyst layer) is 140 μm, in the range previously specified,11,26 and the DM thickness is 300 μm to match the commercially available GDE, Sigracet GDL 35 BA.27,28 All computations were performed using COMSOL 6.0, using the general partial differential equation solver for the aqueous domain and the predefined modules “Transport of Concentrated Species” and “Darcys Law” for the gaseous domain.We use the somewhat idealized catalyst layer composed of ordered spheres, as the results should yield useful trends and a reasonable accuracy compared to a real catalyst layer. Ideally, a catalyst layer with a realistic morphology could be modeled, and it could be compared with experimental data from the same exact catalyst for model validation. However, this would require accurate and representative 2D slices for the real catalyst geometry found through imaging (e.g. nano-tomography) along with the accompanying experimental results. Since no such data set is currently available in literature, the modeling methods are developed using the idealized catalyst layer geometry in anticipation of imaging becoming available in the near future.
The shape of the liquid inside the catalyst layer is still unclear in literature. Therefore, we start with the assumption that the liquid may (or may not) form a perfectly planar front, due to the combination of several factors that likely govern the fluid mechanics: the local surface tension, hydrophilicity, electrowetting, and gas releasing in the form of bubbles or more static streams. We neglect the fluid mechanics challenges for the time being by assuming several extreme, static geometries for the liquid phase (i.e. steady state conditions of the liquid–gas distribution). These include “filled” cases where the liquid–gas interface forms a perfectly planar front, and “wetted” cases where a thin film coats the particles, similar to the geometry assumed in volume-averaged models.11,12 Thus, dynamic bubble transport is not modeled explicitly, but the effect of gas evolution on the static liquid configuration is included implicitly given the various wetting configurations modeled. Bubbles are notoriously difficult to model and are generally excluded from previous CO2R models.10–12,18–20 Though idealized, the cases modeled represent the extremes in liquid wetting, chosen to encompass the range of possible wetting behaviors in a real GDE. As further experiments and modeling begin to give clarity on the location and shape of the liquid electrolyte, the modeling methods described here can be applied to even more realistic 2D or 3D geometries of the solid and liquid phases.
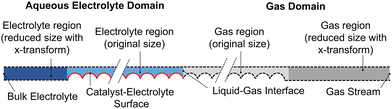
The computational model consists of a liquid electrolyte domain and a gaseous domain, coupled at the liquid–gas interface. The domains and boundaries are shown in Fig. 2 for the example of a filled (no wetting) electrolyte configuration. The domain is assumed to repeat in the y-direction, so symmetric (no-flux) boundaries are used on the top and bottom (dashed lines). For both domains, the governing equations and boundary conditions are described below.
2.1 Aqueous electrolyte domain: GMPNP
The GMPNP formulation is used to model the liquid domain, given by eqn (1)–(3), and as previously applied in 1D.10,16,17,19 This formulation models the electric double layer, including both steric effects and charge separation in the diffuse layer (see Section S8 for more details, ESI†).In eqn (1), Ci is the concentration of species i, ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) i is the species flux, and all simulations are run at steady state. Ri is the total source/sink term for each species due to the homogeneous reactions of water self-ionization (eqn (4)), carbonate formation (eqn (5)), and bicarbonate formation (eqn (6)), where a positive Ri value corresponds to an increase in species concentration (see Section S1 for all Ri expressions, ESI†). The species flux is given by eqn (2), where the first and second terms govern the diffusion and electrostatic migration. F is the Faraday constant, R is the universal gas constant, and T is the temperature. The potential with respect to the potential of zero charge (PZC) is ϕ. The third term accounts for steric effects, where NA is Avogadros number, and aj is the solvated diameter of species j. As assumed by Zhu et al.,10 K+ has by far the highest concentration near the catalyst surface, so it is assumed to be the only species contributing to the steric flux (i.e. the flux is applied to all species i, but the summation over the species of relevant steric size j contains only K+). However, we note that extending the equations to 2D can reveal some limitations of the GMPNP formulation under extreme conditions (see Results and Discussion).
i is the species flux, and all simulations are run at steady state. Ri is the total source/sink term for each species due to the homogeneous reactions of water self-ionization (eqn (4)), carbonate formation (eqn (5)), and bicarbonate formation (eqn (6)), where a positive Ri value corresponds to an increase in species concentration (see Section S1 for all Ri expressions, ESI†). The species flux is given by eqn (2), where the first and second terms govern the diffusion and electrostatic migration. F is the Faraday constant, R is the universal gas constant, and T is the temperature. The potential with respect to the potential of zero charge (PZC) is ϕ. The third term accounts for steric effects, where NA is Avogadros number, and aj is the solvated diameter of species j. As assumed by Zhu et al.,10 K+ has by far the highest concentration near the catalyst surface, so it is assumed to be the only species contributing to the steric flux (i.e. the flux is applied to all species i, but the summation over the species of relevant steric size j contains only K+). However, we note that extending the equations to 2D can reveal some limitations of the GMPNP formulation under extreme conditions (see Results and Discussion).
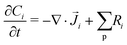 | (1) |
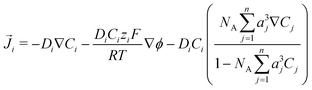 | (2) |
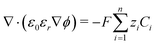 | (3) |
The potential and charge density are solved with the Poisson equation, eqn (3), where ε0 and εr are the permittivity of free space and the relative permittivity, respectively. The species modeled in the aqueous phase are K+, CO2, HCO3−, CO32−, OH−, H+, CO, and H2. The gaseous species (CO2, CO, and H2) are considered dissolved in liquid, with no bubbles modeled. All relevant parameters used are given in the Table S1 (ESI†), including reaction rate constants, steric sizes, and diffusivities.
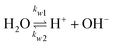 | (4) |
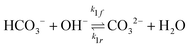 | (5) |
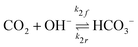 | (6) |
| ϕSHE = ϕRHE − 0.05916 pH | (7) |
| ϕ = ϕSHE + 0.70 | (8) |
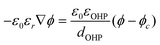 | (9) |
Regarding the boundary conditions for species transport, CO2 and H2O are reduced at the catalyst surface according to eqn (10) and (11), with CO being the only CO2R product considered. The CO2 to CO electrochemical reaction on an Ag electrode has been modeled previously considering both the anodic and cathodic processes,20,31 or by considering only the cathodic process.11,12 Since the potential range studied is much lower than the equilibrium potential, only the cathodic process is considered in the present model. Taking the concentration of CO2 at the reaction plane (OHP) into account, eqn (12) gives the mass transport corrected Tafel relation, where CCO2 and CCO2,ref are the concentration at the OHP and a reference concentration (taken as 1 mol m−3), ηCO is the overpotential, and i0,CO and αCO are fit from experimental data. In eqn (14), the overpotential ηCO is the difference between the applied potential vs. RHE and the apparent standard reduction potential for the reaction CO2(g) + 2H+ + 2e− ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) CO(g) + H2O which is −0.11 V vs. RHE,32 consistent with previous modeling literature.11,12 Since we are restricted to the cathodic part of the Tafel-type electron transfer model, and because the value of i0,CO is fitted from experimental data, the choice of the standard reduction potential has no influence on the accuracy of the model, as any additive constant on the overpotential term Δη will be compensated by a multiplication factor of exp
CO(g) + H2O which is −0.11 V vs. RHE,32 consistent with previous modeling literature.11,12 Since we are restricted to the cathodic part of the Tafel-type electron transfer model, and because the value of i0,CO is fitted from experimental data, the choice of the standard reduction potential has no influence on the accuracy of the model, as any additive constant on the overpotential term Δη will be compensated by a multiplication factor of exp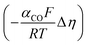 in the i0,CO term upon parameter fitting. For this reason, the i0,CO and αCO terms shall not be regarded as the actual exchange current density and charge transfer coefficient in the strict sense of the Bulter–Volmer theory.
in the i0,CO term upon parameter fitting. For this reason, the i0,CO and αCO terms shall not be regarded as the actual exchange current density and charge transfer coefficient in the strict sense of the Bulter–Volmer theory.
The same strategy is followed for modeling the hydrogen evolution reaction (HER) in eqn (13), but without the mass transport correction, as the reactant is assumed to be water in a neutral/basic medium. The acidic reaction pathway (2H+ + 2e− ⇌ H2(g)) is assumed negligible because of the scarcity of free protons. The overpotential term (eqn (15)) in this case is defined as the difference between the applied potential vs. RHE and the apparent standard reduction potential for the reaction 2H+ + 2e− ⇌ H2(g), which is 0.00 V vs. RHE. Some CO2R studies have included a pH-dependent HER term.33 Experimental data shows HER is suppressed at a higher pH in acidic media,34 but no such trend is visible above pH 7 (see Fig. S10, ESI†), matching the expectation that the acidic pathway is negligible, so no pH dependence at the reaction plane is considered in the present model. See Section S9 for more details (ESI†).
To find the Tafel parameters (i0,CO, αCO, i0,H2, αH2), the data set from Hatsukade et al.25 was used (similar to previous GDE models11,12), along with a 1D version of the GMPNP model for an immersed, planar cathode. Two distinct regions are evident (see Fig. S1, ESI†) indicating a change in reaction mechanism is likely, as the distinct change in slope cannot be attributed to mass transfer effects, since these are already included. Above −1.07 V vs. RHE, the Tafel slope is 120 mV dec−1, which is characteristic of a reaction limited by the first electron transfer,35 and at potentials more negative than −1.07 V the Tafel slope changes to 391 mV dec−1. This potential-dependent Tafel parameterization is an improvement upon 1D volume-averaged models with only a single Tafel slope,11,12 as parameterizing with only the higher region leads to overestimation of the CO current density by several orders of magnitude at the most negative potentials. All parameters are given in Table S1 (ESI†), and more details are available in Section S2 (ESI†).
The partial current densities (iCO, iH2) are used to find the molar flux boundary conditions at the catalyst-electrolyte surface for the GMPNP equations, with 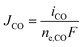 and
and 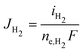 . ne,CO and ne,H2 are the number of electrons transferred per molecule of CO and H2 produced, which are both 2. Fluxes of CO2 and OH− are found from the stoichiometry of eqn (10) and (11): JCO2 = −JCO and JOH− = 2(JCO + JH2). The flux of all other species at the catalyst surface is zero.
. ne,CO and ne,H2 are the number of electrons transferred per molecule of CO and H2 produced, which are both 2. Fluxes of CO2 and OH− are found from the stoichiometry of eqn (10) and (11): JCO2 = −JCO and JOH− = 2(JCO + JH2). The flux of all other species at the catalyst surface is zero.
CO2(aq) + H2O + 2e− ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) CO(aq) + 2OH− CO(aq) + 2OH− | (10) |
2H2O + 2e− ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) H2(aq) + 2OH− H2(aq) + 2OH− | (11) |
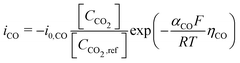 | (12) |
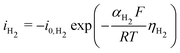 | (13) |
| ηCO = ϕc,RHE − U0,CO | (14) |
| ηH2 = ϕc,RHE − U0,H2 | (15) |
The two conditions are simultaneously enforced using the boundary condition in eqn (16), where Jint,i is the molar flux crossing the interface, i represents the gaseous species (CO2, CO, and H2), Ci,aq is the concentration on the liquid side of the interface, pi,gas is the partial pressure on the gaseous side of the interface, and Hi is Henry's constant. The partial pressure pi,gas is not a constant but is taken from the gaseous side of the simulation, forming the coupling between the two domains. The factor Mint is assigned a high value, such that Ci,aq very nearly equals Hi·pi,gas. Modeling shows a value of 100 m s−1 is adequately high to make the two quantities essentially equal. Note that though the equation appears similar to other studies,11,12 the critical differences are that the high value of Mint enforces a local equilibrium between the two sides of the interface, and the concentrations and pressures are the values at the interface itself (not at a distance “δ” away from the interface as is commonly done). The other aqueous species (K+, HCO3−, CO32−, OH−, H+) have no flux across the liquid–gas interface.
| Ji,int = Mint(Ci,aq − Hi·pi,gas) | (16) |
Henry's constant decreases with an increase in electrolyte concentration, an effect modeled using the Sechenov relation.37 Henry's constant is modified to include this effect with eqn 17, where i represents the gaseous species and j represents the ionic species. Hi,0 is the Henry's constant in pure water, Cj is the ion concentration at the liquid–gas interface, and hj and hg,i are the parameters for each ionic species and for the dissolved gas, respectively, fit by Weisenberger and Schumpe from experimental data.37 See Section S5 (ESI†) for a discussion of the various forms of this equation shown in CO2R literature. The effect is a significant reduction in CO2 solubility, as concentrations can greatly exceed the bulk concentrations in the catalyst layer due to the hydroxide produced in both CO2R and HER. Relevant parameters for CO2 and H2 are given in Table S3 (ESI†), however, no parameters are available for CO, so the nominal CO Henry's constant is not modified.
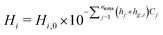 | (17) |
2.2 Gas domain: mixture averaged diffusion and darcy's law
The gaseous domain consists of the DM region and any of the catalyst region not occupied by liquid electrolyte (dark gray and light gray in Fig. 2), where the species modeled are CO2, CO, and H2. As previously done in GDE studies,11,14 multi-component diffusion is modeled with the Mixture-Average Diffusion (MAD) formulation, and Darcy's law models convection of the fluid mixture through a porous medium. See Section S3 (ESI†) for details.| ṁint = JCO2,intMCO2 + JCO,intMCO + JH2,intMH2 | (18) |
2.3 Size Reduction with x-coordinate transformation
Modeling transport around the catalyst nanoparticles requires resolving down to the nm scale, but the lengths of the DM and electrolyte are orders of magnitude larger (300 and 140 μm), making it computationally untenable to solve both regions simultaneously. In the current model, this is simplified by transforming the x-coordinate in the DM and the electrolyte region not containing catalyst particles (dark gray and dark blue in Fig. 2 and 3). A length reduction factor (FR) is chosen, and a substitution of variables is performed such that x → FRxt, where xt is the new coordinate. Applied to the GMPNP equations, this essentially means the length of the domain is reduced by a factor of FR and the diffusivity and reaction terms are adjusted to compensate for the size reduction (see Section S6 for more details, ESI†). The result is a model computing the same flux as the original problem though the length is reduced, making it much more computationally feasible to solve the entire geometry simultaneously. An FR value of 100 is used for both DM and electrolyte transformations, resulting in domain lengths of 3.0 and 1.4 μm, bringing them much closer to the width of the catalyst layer at 5 μm. For verification, simulations using the original and transformed domains are compared, showing identical results (Fig. S5 and S6, ESI†).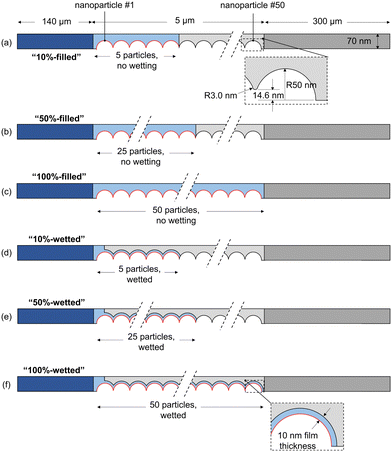 | ||
| Fig. 3 Geometry and wetting configuration for three filled (a–c) and three wetted (d–f) GDE cases, with abbreviated names in bold and the catalyst surface active for CO2R shown in red. | ||
3 Results and discussion
We first investigate the wetting behavior of the electrolyte in the catalyst layer by assuming several wetting configurations. This is followed by an analysis of some of the main factors GDE design: the role of parasitic reactions, gas solubility effects, and the catalyst layer properties including thickness, porosity, ECSA.To investigate the wetting behavior in the catalyst layer, six liquid geometries are modeled, shown in Fig. 3, including filled (a–c) and wetted (d–f) electrolyte configurations, each with 10%, 50% and 100% of catalyst particles submerged in a 0.1 M KHCO3 electrolyte. In the following discussion the abbreviated names are used, as given in the figure (e.g. “50%-filled” for 25 particles submerged, without any wetting by a film). The 50 catalyst particles (radius 50 nm) are arranged so they are just touching, and a 3 nm radius fillet is applied to avoid modeling the infinitesimally thin region between two spheres making a point contact (Fig. 3(a)). A gap of 40 nm between particles in the y-direction is assumed, giving the domain a height of 70 nm. For the wetted cases, the film thickness is 10 nm to match previous modeling studies.11
To visualize and interpret the many interconnecting phenomena, contour plots of the potential, concentrations, and partial pressures are shown in Fig. 4, for the 50%-filled configuration at a cathode potential of −1.1 V vs. RHE. Note that when analyzing these plots, the rectangular electrolyte region and DM subdomains are actually reduced in length by 100 times in the x-direction, whereas the area around the catalyst particles is the true, unmodified size. The potential field (vs. PZC) gradually decreases from the electrolyte bulk in the direction of the cathode, and a high negative gradient develops radially around each catalyst nanoparticle (−0.178 V nm−1 at particle 25) within several nm of the OHP (see close-ups), as expected inside the electric double layer.18 The potential only goes as low as −0.15 V as it is shown on the PZC scale, and the domain modeled only includes up to the OHP, not the additional potential drop between the OHP and the metal surface (see Fig. S7 for more details, ESI†). Similarly, the K+ concentration shows a rapid increase radially towards the nanoparticle, as predicted by 1D GMPNP modeling,17 reaching a peak value of 4.3 M and respecting the steric limit (5.73 M based on simple cubic packing of K+). The HCO3− concentration decreases from the bulk value, as it is readily consumed by the reaction with OH− (eqn (5)). CO2 is similarly consumed, with a low concentration in the electrolyte, but its concentration increases near the liquid–gas interface as dissolved gas enters the liquid. The CO2 concentration also decreases near the OHP due to steric effects. CO and H2 are each produced at the catalyst and diffuse to the liquid–gas interface as well as to the electrolyte bulk. Hydroxide is produced by both CO2R and HER, leading to a high concentration throughout the catalyst layer, and therefore a high rate of carbonate and bicarbonate formation is expected. This reduces the CO2 available at the catalyst surface, eventually restricting the CO current density. The homogeneous parasitic reaction rate for CO2 (from CO2 + OH− ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) HCO3−) is shown as well, with a strong depletion of CO2 (high in magnitude but negative) visible where both OH− and CO2 concentrations are high. Reducing this side reaction is one of the keys to designing an effective GDE, and its effects will be seen throughout the following results. The pH (−log[H+]) is quite high throughout the catalyst layer due to OH− production (note though that H+ and OH− are not in equilibrium near the catalyst surface, per Fig. S9, ESI†). The gas mixture is dominated by CO2, with H2 and CO diffusing towards the gas supply stream and CO2 diffusing towards the catalyst layer. Looking at the species concentrations, rates and the potential field at more negative applied potentials, the K+ concentration at the catalyst surface increases (though is still limited to 5.73 M by steric effects), OH− and CO32− concentrations increase, and the parasitic reaction rate RCO2 increases in magnitude. A similar set of plots for the 50%-wetted configuration is given in Fig. S2 (ESI†), showing the concentration of CO2 and most other species are much more homogeneous throughout the catalyst layer, as the liquid–gas interface runs along the entire length of the 10 nm thick film.
HCO3−) is shown as well, with a strong depletion of CO2 (high in magnitude but negative) visible where both OH− and CO2 concentrations are high. Reducing this side reaction is one of the keys to designing an effective GDE, and its effects will be seen throughout the following results. The pH (−log[H+]) is quite high throughout the catalyst layer due to OH− production (note though that H+ and OH− are not in equilibrium near the catalyst surface, per Fig. S9, ESI†). The gas mixture is dominated by CO2, with H2 and CO diffusing towards the gas supply stream and CO2 diffusing towards the catalyst layer. Looking at the species concentrations, rates and the potential field at more negative applied potentials, the K+ concentration at the catalyst surface increases (though is still limited to 5.73 M by steric effects), OH− and CO32− concentrations increase, and the parasitic reaction rate RCO2 increases in magnitude. A similar set of plots for the 50%-wetted configuration is given in Fig. S2 (ESI†), showing the concentration of CO2 and most other species are much more homogeneous throughout the catalyst layer, as the liquid–gas interface runs along the entire length of the 10 nm thick film.
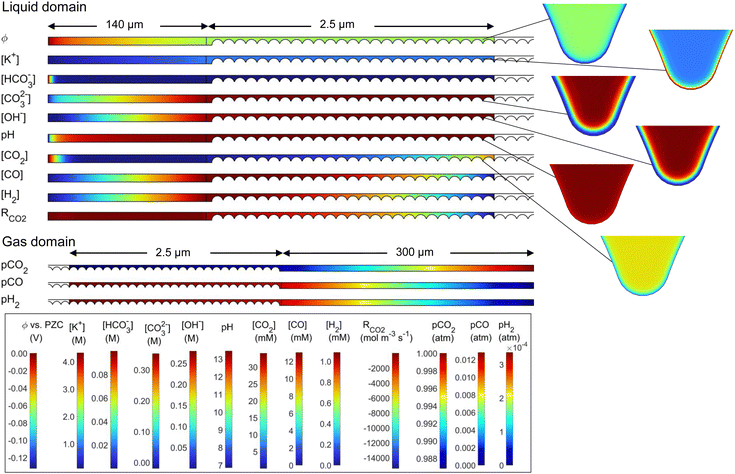 | ||
| Fig. 4 Potential, concentrations, and partial pressures for the 50%-filled case with a cathode potential of −1.1 V vs. RHE and a 0.1 M KHCO3 electrolyte. | ||
Such detailed pore-level transport modeling has been scarce in literature to date. One key development utilized by the present model is the steric effect term of the GMPNP formulation (eqn (2)), allowing for a more realistic description of the electric double layer. This has been implemented previously in several 1D boundary models10,17,19 but not extensively in higher dimensions or in GDE models. To demonstrate the importance of the steric term, a 1D aqueous model is run both with the steric term (GMPNP) and without the steric term (PNP). As shown in Fig. S8 (ESI†), if the steric term is not included, the cation concentration can quickly reach unreasonably high levels near the catalyst surface, showing the steric term is necessary to accurately model the EDL.
Results in terms of current density and FECO in the catalyst layer are shown first on a per-nanoparticle basis in Fig. 5 and 6, which allows for a detailed look at the inhomogeneity across the catalyst layer. In these results, the current density is calculated using the true surface area of catalyst-electrolyte contact. Then, the overall CO current density and FECO are shown in Fig. 7, where the current density is calculated using the “geometric” area, which is the area projected onto the catalyst layer plane (70 nm, Fig. 3), allowing for direct comparisons to experimental and modeling studies.
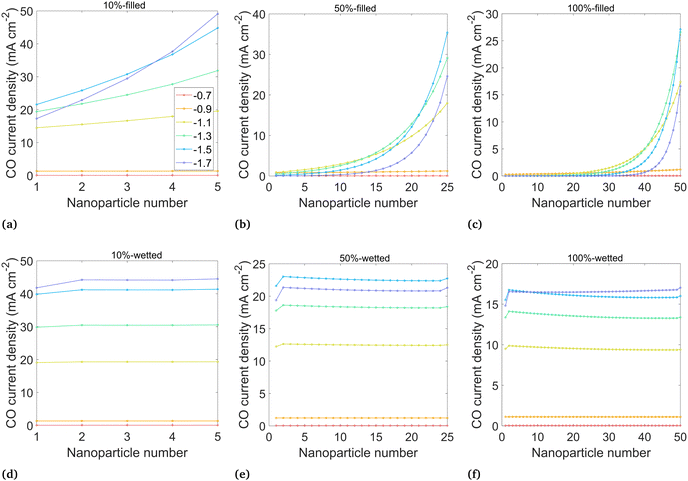 | ||
| Fig. 5 Average CO current density at the surface of each catalyst nanoparticle at potentials from −0.7 to −1.7 V vs. RHE, for the six wetting cases ((a)–(f) correspond directly to Fig. 3). Nanoparticles are numbered starting at 1 for the left-most (deepest) particle. Current density calculated using catalyst-electrolyte surface area. | ||
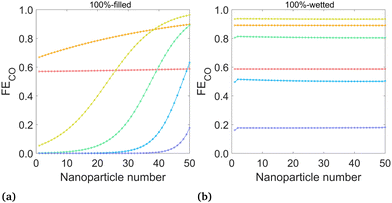 | ||
| Fig. 6 Mean FECO at the surface of each nanoparticle for (a) the 100%-filled case and (b) the 100%-wetted case, at various applied potentials. Nanoparticles are numbered starting at 1 for the left-most (deepest) particle. (Legend same as Fig. 5) | ||
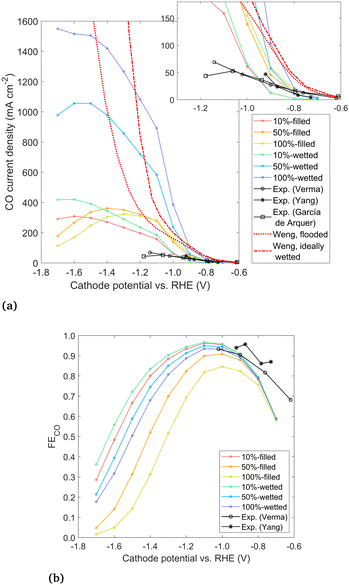 | ||
| Fig. 7 (a) Geometric CO current density for modeled cases and experimental data from Verma et al.,38 Yang et al.,4 and García de Arquer et al.24 and (b) overall Faradaic efficiency to CO. | ||
The CO partial current density, averaged over each nanoparticle, is shown in Fig. 5 for the six cases shown in Fig. 3. Nanoparticle numbering starts with 1 as the left-most particle (furthest from the liquid–gas interface). Analyzing the “filled” cases (a–c), the highest current density is nearest to the liquid–gas interface, where the highest CO2 concentrations in the catalyst layer are found. More negative potentials bring higher CO current densities and larger inhomogeneity among the particles. This inhomogeneity starts to be pronounced at around −1.5 V for the 10%-filled configuration and at −1.3 V for the 50%-filled and 100%-filled configurations, with the particles near the surface becoming highly active (reaching 30–50 mA cm−2), while the deeper particles are nearly inactive. This inactivity is due to OH− accumulation, which has two detrimental effects. First, an increase in OH− reduces the concentration of gas dissolved into the electrolyte at the liquid–gas interface (modeled with the Sechenov constant). At −1.5 V, the Henry's constant (averaged along the liquid–gas interface) is 63% of its nominal value in the 10%-filled configuration, vs. 54% for the 50%-filled and 43% for the 100%-filled configuration. (See Fig. S3 for a full comparison of solubilities, ESI.†) The effect is exacerbated at more negative potentials, where the OH− current density is highest. Furthermore, the accumulated negative charge from OH− causes the K+ concentration to increase as well, as the system strives for electroneutrality (which also contributes to the reduction in Henry's constant). Second, dissolved CO2 must diffuse from the interface to the catalyst particles, but parasitic carbonate reactions occurring along this path reduce the CO2 that can reach the catalyst surface. The effects of OH− are strong enough that at the most negative applied potentials, even the particles nearest to the liquid–gas interface become less effective. Note that OH− production keeps increasing at more negative potentials despite the CO partial current diminishing, as it is proportional to the total current (eqn (12)–(13)), not the CO partial current.
Comparing the 50%-filled and 100%-filled cases (Fig. 5(b) and (c)), they appear quite similar, as the deepest 25 particles in the 100%-filled configuration are mostly deprived of CO2 and contribute essentially no CO current. The 10%-filled case has slightly higher and more uniform current densities, as the geometry allows for easier diffusion of OH− out of the catalyst layer to the bulk, so less OH− accumulates. Though the CO current density in the 10%-filled case (calculated using the catalyst-electrolyte surface area) is higher than the in other configurations, it has only a fraction of the surface area compared to the others, leading to the lower geometric CO current density at moderate applied potentials, as shown in Fig. 7(a). However, at potentials more negative than −1.5 V the 10%-filled configuration outperforms the others, as the CO2 available to the catalyst surface is highly suppressed in the 50% and 100% configurations due to the long diffusion pathway and a strong accumulation of OH−.
The wetted cases (Fig. 5(d)–(f)) look remarkably different. The CO current density is nearly uniform along the entire catalyst layer due to the short diffusion length from the liquid–gas interface to the catalyst surface. The OH− produced along the catalyst surface diffuses towards the bulk, with the highest OH− concentrations found around the right-most particles, causing the slight decrease in CO current density for these particles (visible in the 25 and 50 particle configurations). The sharp downturn for particle 1 is because that particle is only wetted with the film on one side of the particle, while the other side faces the open electrolyte region (refer to Fig. 3(d–f)). Similarly, the slight uptick for the particle nearest the liquid–gas interface is due to the geometry of this particle, which does not have a fillet. The thin 10 nm film used in the wetted configurations is responsible for two opposing factors. The benefit is a short diffusion length from the liquid–gas interface to the catalyst, but the drawback is that all OH− produced must diffuse out through the thin, meandering path of the film, so OH− concentrations are high, promoting carbonate formation and decreasing gas solubility. With a high current density found throughout the catalyst layer, the benefit of the short diffusion length is shown to dominate in this trade-off. Comparing the filled and wetted configurations, the highest current densities are found in the filled cases, but the wetted versions show higher CO current density for the deeper particles leading to the much higher overall (geometric) current densities shown in Fig. 7.
The FECO (iCO/(iCO + iH2)) on each nanoparticle is plotted for the 100%-filled and 100%-wetted cases in Fig. 6 (results for all six cases given in Fig. S4, ESI†). These plots give detail into which particles promote high or low FECO, whereas the total FECO over all nanoparticles (Fig. 7(b)) corresponds to the metric given in experimental studies. The 100%-filled case shows the FECO is highest for the particles near the liquid–gas interface but quickly decreases for deeper particles, and the deepest 25 particles have a near-zero FECO at potentials of −1.3 V or lower. The CO production changes along the catalyst based on the concentration of CO2 at the OHP (accounted for with the [CCO2] term in the Tafel equation), but HER has no such dependence, so H2 is produced equally on all particles. Therefore, not only do the deepest 25 particles produce virtually no CO, they continue to produce H2, driving down the FECO overall. Therefore, a triple penalty is paid for the “extra” 25 particles in the 100%-filled configuration: they produce extra H2, reducing FECO, and they produce extra hydroxide, which both decreases the gas solubility and promotes carbonate formation, each reducing the CO2 available to the catalyst. Thus, if the catalyst layer is made thicker than necessary, this will only lead to more H2 and less CO production. Here, 25 particles (2.5 μm) is thick enough to produce all of the CO possible, though it likely depends on the catalyst geometry and electrolyte conditions. The wetted cases show nearly uniform FECO across all particles, as both the H2 and CO currents are essentially uniform. The 100%-wetted configuration has the highest FECO at −1.1 V, which can also be seen in the overall FECO in Fig. 7(b).
The geometric CO current density and overall FECO for the six modeled cases are given in Fig. 7, along with three experimental data sets for GDEs with Ag catalysts in a KHCO3 electrolyte run in a microfluidic (not zero-gap) device configuration. The conditions and cathode preparation vary slightly between the experiments. García de Arquer et al.24 use a catalyst layer of thickness 0.3 μm sputtered onto a PTFE substrate. Yang et al.4 use a catalyst layer of only 25 nm sputtered onto a porous carbon substrate, but neither study gives the loading. Both of these studies use sputtered catalysts, without any ionomer binder around the catalyst nanoparticles. Verma et al.38 apply the catalyst layer using an ionomer ink, where the ink is later removed (yielding the same results as with the ink left in place). They give a loading of 2 mg cm−2 but no catalyst layer thickness is reported. To make a rough estimate of the thickness, assuming a porosity of 0.5 leads to a thickness of 3.8 μm. Though the experimental conditions and preparation differ to some degree, the results are all quite similar. The modeled data is in the same order of magnitude, though the model overpredicts performance at more negative overpotentials. The discrepancy may be due to flooding under experimental conditions, where the electrolyte fills past the catalyst layer and extends into or entirely through the DM, which has been shown to be both common and detrimental to CO2R.4 The discrepancy may also be due to aggressive bubble formation at high current densities which is not modeled explicitly or due to the idealized 2D geometry assumed in this study. With a lack of detailed, quantitative information about the catalyst layer in the experimental studies, it is difficult to make exact comparisons to a particular study, but broadly, the modeled and experimental curves show similar trends and magnitudes for applied potentials down to −1.0 V vs. RHE.
Results from a 1D volume-averaged model by Weng et al.11 are also shown for both a flooded catalyst layer and an ideally wetted case, which reach over 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mA cm−2 and do not show a peak (see Fig. S11, ESI†). The vast overestimation of the CO current predicted by the 1D model likely has several causes. The reduction in solubility is not taken into account, which has been shown to cause a large decrease in the CO2 available at the reaction plane. Also, the study used a single-region Tafel parameterization, which may overpredict the CO current density by several orders of magnitude at the very negative potentials (Fig. S1, ESI†). Finally, the geometry of the 1D model assumes each catalyst nanoparticle is surrounded by a thin liquid film (∼10 nm). This “wetted film” assumption gives a very short diffusion length through the liquid to every catalyst nanoparticle, which is likely an overly optimistic assumption given that liquid will likely flood past at least some particles. The 2D modeling approach represents a significant enhancement in the accuracy and level of detail compared to such 1D volume-averaged models, with the chief drawback often cited for such detailed modeling being the high computational expense.8 However, computation times for the current model are not prohibitive, ranging from 1–10 hours using 10 processors, for the whole potential sweep from −0.7 to −1.7 V.
000 mA cm−2 and do not show a peak (see Fig. S11, ESI†). The vast overestimation of the CO current predicted by the 1D model likely has several causes. The reduction in solubility is not taken into account, which has been shown to cause a large decrease in the CO2 available at the reaction plane. Also, the study used a single-region Tafel parameterization, which may overpredict the CO current density by several orders of magnitude at the very negative potentials (Fig. S1, ESI†). Finally, the geometry of the 1D model assumes each catalyst nanoparticle is surrounded by a thin liquid film (∼10 nm). This “wetted film” assumption gives a very short diffusion length through the liquid to every catalyst nanoparticle, which is likely an overly optimistic assumption given that liquid will likely flood past at least some particles. The 2D modeling approach represents a significant enhancement in the accuracy and level of detail compared to such 1D volume-averaged models, with the chief drawback often cited for such detailed modeling being the high computational expense.8 However, computation times for the current model are not prohibitive, ranging from 1–10 hours using 10 processors, for the whole potential sweep from −0.7 to −1.7 V.
Comparing the experimental data to results of the present model in Fig. 7, two important conclusions can be drawn. First, the comparison of wetting vs. filled results points strongly towards the real electrolyte forming a planar front under experimental conditions. The wetted configurations seem too optimistic, reaching up to an order of magnitude higher current densities than the experimental data. Therefore, we conclude that current GDE experiments exhibit little wetting, with the liquid–gas interface forming a relatively planar front inside the catalyst layer. While the commonly noted benefit of a GDE is the short diffusion length from the gas phase to the catalyst surface, it appears that a diffusion length on the order of a few nm applies only to the particles nearest to the liquid–gas interface. This is in contrast with the high wetting behavior assumed in previous 1D models.11
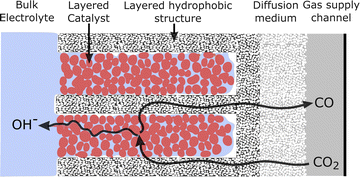
The second conclusion drawn from Fig. 7 is that by moving from the filled (planar front) regime to a highly wetted one, there is vast room for improvement in CO current density. CO current densities >1000 mA cm−2 are predicted by moving to highly wetted electrolyte configurations. Since the wetted configurations are likely not naturally formed, they may perhaps be induced by engineering the catalyst layer. One pathway may be to introduce alternating layers (in the y-direction) of hydrophobic porous material in between layers of catalyst particles. The electrolyte would wick into the space around the catalyst particles (due to hydrophilicity and electrowetting), but a gas channel would remain along/inside the hydrophobic layer, as shown in Fig. 8. Optimally, a configuration similar to the 100%-wetted case could be achieved. The filled configuration can be considered to have a 1D planar liquid–gas interface, whereas the layering would lead to a liquid–gas interface with a serpentine shape in 2 dimensions. Taking the concept to 3D, layers could be replaced by cylindrically shaped hydrophobic gas channels, which may lead to yet another order of magnitude increase in current density. Catalyst layering is being explored in the field of fuel cells to overcome similar transport challenges.39 Another approach in CO2R was recently shown by García de Arquer et al.,24 where an ionomer coating was added to the catalyst to enhance gas transport along the supporting fibers. The result is a large increase in current compared to an uncoated catalyst, similar to moving from the filled to wetted configurations in Fig. 7, as both methods relieve the bottleneck of dissolved gas transport. Undoubtedly there are other similar approaches, but the challenge appears clear: moving from a (nearly) planar liquid–gas interface to a 2D or 3D shaped interface – with a high interface surface area in close proximity to the catalyst surface – promises to increase the CO current density by many-fold.
Immersed, aqueous electrode experiments show a peak in CO current density at around −1.3 V vs. RHE,25 as CO2 is limited by the long diffusion path from the bulk electrolyte, and the homogeneous carbonate reactions reduce the CO2 reaching the catalyst surface.40 GDE experiments4,38 usually do not show such a peak, though experimental results in literature often proceed no lower than −1.2 V vs. RHE. However, results in Fig. 7 indicate a GDE configuration still features a peak at around −1.3 to −1.6 V vs. RHE. The origin of the peak could be attributed to diffusion (though diffusion lengths are short), plus the detrimental effects of either carbonate formation or the reduction in solubility. A comparison is made to show which phenomena are responsible, using the 100%-filled case, shown in Fig. 9. First, a simulation is run with both the homogeneous carbonate reactions and the solubility reduction from the Sechenov relation disabled (red), which can be considered an optimum scenario for a certain catalyst geometry if no OH− were allowed to accumulate. Since the CO2 reaching the catalyst surface is limited only by diffusion, the CO current is high, and no peak is seen. Turning on the homogeneous reactions with the Sechenov relation still disabled (orange), the CO current is reduced significantly, but no peak is found. Turning on the Sechenov relation with homogeneous reactions disabled (yellow) shows a diminished CO current and a distinct bell-shaped curve. Turning on both the Sechenov and homogeneous reactions results in the same 100%-filled curve shown previously (green). Comparing these curves, we conclude that the solubility is the primary driver of the bell-shaped curve, with the homogeneous reactions playing a significant but secondary role. While the Sechenov relation is not included in many CO2R modeling studies, this analysis shows it is necessary, as neglecting it results in a CO current that continues to increase at very negative applied potentials. Carefully designing the catalyst geometry to allow a robust diffusion pathway of OH− out of the porous structure is therefore another top priority for a GDE design. Though not modeled, this hints at an advantage of CO2R in acidic media, as both carbonate formation and gas solubility effects will be reduced if electrochemical reactions consume protons rather than producing OH−.
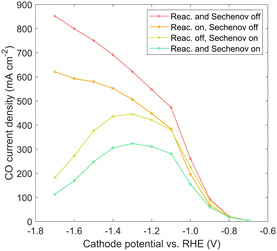 | ||
| Fig. 9 CO current density solved with and without the carbonate reactions and the solubility reduction from the Sechenov relation, for the 100%-filled case. | ||
The saturation parameter (S) has been used in 1D volume-averaged models to describe the degree to which liquid fills the catalyst layer, defined as the volume fraction of liquid in the pores.11 However, in 2D or 3D the same saturation value can lead to vastly different outcomes depending on the shape of the liquid. For example, S = 0.5 can be obtained with a filled configuration (Fig. 3(b)) or with a wetted configuration (similar to Fig. 3(f) with a thicker film), which give very different results. Thus, the saturation parameter is of little use unless the electrolyte shape is already well defined.
The triple-phase boundary has been suggested to account for the high current density of GDEs.3 Visualizing the liquid at the nm scale in two dimensions, the triple-phase boundary is the exact point where the liquid, gas, and catalyst surfaces all intersect. Since the physics exactly at this point are not yet established, the catalyst surface was set as inactive (zero flux boundary condition) within 1 nm of the triple-phase point. Our modeling shows that the CO current density increases near the triple-phase point, but it is spread among numerous particles near the liquid–gas interface. Consequently, the model shows that the reaction is not only taking place at the strict triple-phase boundary but in a “triple-phase region”, where all three phases are within close proximity. Since the CO current diminishes with the distance from the liquid–gas interface, we estimate the thickness for the triple-phase region by finding the region containing 90% of the total CO current. Under this definition and the data from Fig. 5(c), the triple-phase region extends 1.3 μm from the liquid–gas interface at −1.3 V vs. RHE. This can be taken as a “rule of thumb”, with the exact thickness changing slightly based on the applied potential and catalyst layer thickness, but all curves in Fig. 5(a)–(c) provide a similar estimate.
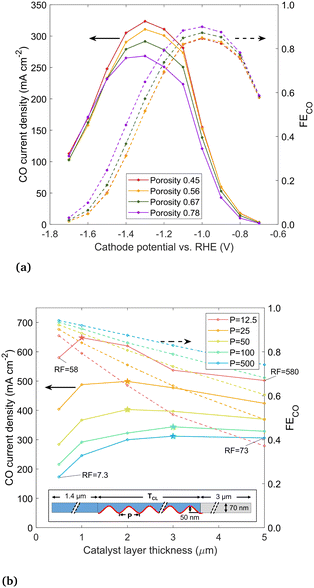
Next, the porosity of the catalyst layer is varied by evenly distributing 50 (the base case), 40, 30, and 20 nanoparticles throughout the 5 μm catalyst layer, corresponding to porosities of 0.45, 0.56, 0.67 and 0.78, respectively. The results in Fig. 10(a) show that as the porosity increases, the CO current density decreases, as there is simply less surface area for CO2R. FECO has the opposite trend, as a catalyst layer filled sparsely with nanoparticles produces less OH− and is subject to less detrimental effects. Thus, there is a clear trade-off but no single optimum porosity, as it depends if CO current density or FECO is desired to be maximized.
Lastly, we study the effect of GDEs with a high electrochemically active surface area (ECSA), and specifically, how the catalyst layer thickness and ECSA together affect the CO current. High ECSA is seen as one path towards higher CO currents, with recent studies focusing on unique, high surface area catalyst shapes (e.g. “nanoflowers”) instead of nanoparticles.6 In the current model, the ECSA is taken as the surface area of the catalyst in contact with the electrolyte, and the roughness factor (RF) is the ECSA divided by the geometric area. Again adopting an idealized geometry, the catalyst is shaped using a sine wave, with the period (P) varied between 12.5 and 500 nm and the catalyst layer thickness (TCL) varied between 0.5 and 5 μm, to achieve different RFs. The sinusoidal catalyst layer is shown in Fig. 10(b), with the domain mirrored along top and bottom symmetry planes (forming alternating channels in the y-direction of electrolyte and roughened catalyst material). The catalyst layer is flooded, with the liquid–gas interface at the boundary between the catalyst layer and the DM, to reflect the most likely wetting behavior of current GDEs as per our conclusion. The sine wave amplitude is 50 nm, matching the radius of the nanoparticles modeled previously. All other geometric parameters are the same as in the preceding simulations. For comparison to the circular nanoparticle geometry studied previously, the RF values are 94, 47, and 9.5 for the 100%, 50%, and 10% filled or wetted configurations (taking into account only catalyst surface in contact with liquid electrolyte).
The CO current density and FECO is shown in Fig. 10(b) for different sine wave periods and catalyst layer thicknesses, at a cathode potential of −1.2 V vs. RHE. The highest RF designs are those with the shortest period and highest catalyst layer thickness (as labeled on the figure). A shorter sine wave period generally leads to higher current density, however, for each period there is an optimum catalyst layer thickness. Similar to trends seen in the nanoparticle analysis, this peak is explained by the fact that as the catalyst layer thickness increases, the catalyst surface farthest from the liquid–gas interface becomes inactive due to limited CO2 but continues to produce OH−, driving down the solubility and promoting carbonate reactions. The peak current density for each sine wave is noted with a star, showing optimum catalyst layer thickness decreases as the period of the sine wave is shortened. The peak is around 3 μm for a long-period sine wave (P = 250 and 500). The highest CO current overall is found with a very short period (12.5 nm) and a catalyst layer of 1 μm with a RF of 116. The CO current density of 648 mA cm−2 is roughly twice that of a thick catalyst layer with low RF. The trends indicate that further decreasing the period would lead to even higher current densities, however, at some point the trend must stop as the thickness approaches the molecular scale. This comparison is for −1.2 V vs. RHE. More negative applied potentials will likely push the peak in CO current density towards thinner catalyst layers, as OH− accumulation suppresses the CO current more in catalyst geometries with a long diffusion pathway, as described near the beginning of this section. Thinner catalyst layers also lead to higher FECO, as thicker catalyst layers have more surface area far from the liquid–gas interface, which is less active for CO2R. In general, rougher the catalyst layers (lower P) have lower FECO, though the difference is moderate when the catalyst layer is thin. Though there is no optimum point in FECO, it appears very advantageous that both the current density and FECO are both high for thin catalyst layers.
From these trends, the general conclusions are, first, that a high ECSA does not necessarily translate to a high CO current, as the thickness of the catalyst layer affects how much of the catalyst surface is active for CO2R. The ECSA, similar to the saturation parameter, is an important metric, but it must be taken in the context of the rest of the catalyst geometry. Second, the highest (geometric) CO current densities can be achieved with an extremely rough catalyst surface and a thin (∼1 μm) catalyst layer, with the key being to maximize the catalyst surface area in close proximity to the gas phase.
Finally, we note some limitations of the GMPNP formulation to guide future work on model development. The current model does not take into account bubble formation. Results such as the contour plots in Fig. 4 show the aqueous CO concentration reaching 12 mM, well exceeding the solubility of 1 mM, so CO will likely form bubbles to reach the gas stream. Bubbles would disturb the static liquid geometry assumed, but it is beyond the scope of the current model to account for these (transient) effects. However, in the wetted configurations, the impact of bubbles is expected to be small, as the 10 nm film is orders of magnitude smaller than a typical bubble diameter leaving the surface of a planar catalyst (31 to 97 μm40). On the other hand, in the filled cases, a bubble formed deep within the liquid would have to bubble out to the interface to release. This may cause a blockage, hurting performance, which could be the root cause of the disagreement between the experimental and modeled results seen at very negative applied potentials (Fig. 7). Or, if designed specifically for the purpose, bubbles may present an opportunity to induce a higher mass flow and mixing, as already demonstrated for planar electrodes.40
This is the first work where the GMPNP formulation is applied extensively in 2D, and some conditions are reached which are never found in 1D. With a high CO current and a long, thin, and tortuous diffusion pathway towards the bulk, the OH− produced at the catalyst surface (and HCO3− and CO32− subsequently formed through homogeneous reactions) cannot readily escape to the bulk, and their concentrations in the area around the catalyst particles can build up to several molar, with K+ increasing as well to balance the charges. As modeled by GMPNP, the concentrations must always remain below the steric limit, which is enforced with the denominator of the steric term (eqn (2)) providing a near-infinite flux if the steric limit is approached. Under extreme conditions, the steric term can start to contribute a meaningful amount to the flux in the region around the catalyst nanoparticles. However, in reality, the steric limit can be exceeded, at least away from the catalyst surface, which is clear because the solubility limit is much higher than the steric limit for K2CO3: precipitation will not occur until the concentrations reach 16.06 M K+ and 8.03 M CO3−2,41 whereas the steric limit is reached at only 5.73 M K+. Thus, in GMPNP modeling, precipitation can never be reached. Therefore, precipitation cannot be investigated with the current GMPNP formulation, and under these conditions the steric term can be thought of as adding extra (erroneous) diffusion. The root cause behind this discrepancy is likely due to the “hard sphere” assumption used to derive the GMPNP equations. The steric term is based on the assumption of cations with hard, spherical solvation shells forming layers along the catalyst surface in a simple cubic packing structure. This assumption appears reasonable directly along the catalyst surface where K+ has by far the highest concentration, and nearly no anions are present due to electrostatic repulsion. However, the assumption of hard solvation shells must break down away from the catalyst surface, because in reality the steric limit can be passed to reach precipitation. Similarly, electrolytes at high concentration tend not to fully dissociate,42 which contradicts the GMPNP assumption that each ion is surrounded by a hard solvation shell. While it is beyond the scope of the current work, the GMPNP formulation may need to be adjusted to accurately model this situation and to simulate precipitation.
In the current implementation, K+ is the only ion considered to have a relevant steric size, which is done to reduce the impact of the steric flux away from the catalyst surface in the extreme cases where concentrations approach the steric limit. This means the steric limit will not be reached until K+ is 5.73 M, as opposed to a much lower concentration if all ions are considered to have a steric size. Very near the catalyst surface (within ∼2 nm), the K+ concentration is orders of magnitude higher than the other species, so neglecting their steric sizes has essentially no impact on the steric flux along the catalyst surface.
4 Conclusions
The central aim of this work was to develop the modeling methods to predict multi-physical transport in GDEs with much greater detail than previously possible, and subsequently, to explore ways to optimize GDE geometry and operating conditions for maximized performance using the newly developed tool. Providing much more detail than is possible with 1D volume-averaged models, the 2D results can be easily visualized, and a high degree of relevant information can be extracted. Several idealized 2D geometries were analyzed, but in future work, the same model can be applied to more realistic or novel 2D or 3D porous geometries. Results show similar trends and a reasonable accuracy compared with experimental data sets under similar conditions. Several analyses have been performed in the Results and Discussion to address some of the key questions in the field of CO2R. To generalize the results into tangible guidance for optimizing a GDE, the following recommendations are given as pathways towards higher performing GDEs.Modeling the electrolyte in a highly wetted configuration shows CO currents an in excess of above 1000 mA cm−2, indicating that the liquid–gas interface likely forms a roughly planar front with little wetting under the experimental conditions modeled. This indicates there is vast room for improvement by engineering the porous substrate and catalyst layer together to make the liquid–gas interface form a 2D serpentine shape, instead of a planar front. This would place much more catalyst surface area within a low diffusion length of the gas phase. Constructing such a device is undoubtedly challenging, but modeling predicts the CO current design would increase by several-fold.
Catalyst layers should be limited to 1.3 μm or less, as almost no CO2R occurs beyond 1.3 μm from the liquid–gas interface. We quantify this as an estimate of the dimension of the “triple-phase region” active for CO2 reduction. Some experiments have used thicker Ag catalyst layers,38,43 but the modeling predicts this is sub-optimal. A catalyst layer thicker than this active region will only be detrimental, as the deeper particles still produce H2, lowering the FECO, and the extra OH− produced decreases the CO current by reducing the gas solubility and promoting carbonate formation. In the ECSA analysis, this trade-off resulted in an optimum thickness dependent upon the roughness of the catalyst surface. Of the modeled cases, the highest CO current density was found for a highly rough, 1 μm thick catalyst layer, which is over twice that of a less rough, 5 μm thick catalyst. Conveniently, very thin catalyst layers also show the highest FECO. Thus, a highly rough catalyst layer with a thin, optimized thickness is one key pathway towards a high current density GDE.
Similar to planar electrodes, a bell-shaped curve is predicted in the current, indicating the CO2R reaction is transport-limited at large negative applied potentials. Unlike planar electrodes, this limitation is due to a reduction in CO2 gas solubility, with carbonate formation having a secondary influence. Both detrimental effects are promoted by OH− accumulation inside the catalyst layer, so a well-designed GDE must have robust diffusion pathways to allow OH− to escape to the bulk electrolyte. This is expected in a general sense, however, some of the few published nm-scale images43,44 indicate that sputtered catalyst layers can (depending on their preparation) have few diffusion pathways. Thus, an additional recommendation is that the catalyst layer morphology should be inspected carefully via nano-tomography or tested for permeability to ensure it does not prevent OH− from diffusing readily to the bulk.
With the modeling methodology established, future work may take numerous directions. This could include applying the model to realistic catalyst geometries made from digitally reproduced tomography images. The GMPNP formulation adds a steric term to enforce a packing limit, but it has been used in relatively few studies to date, and a detailed analysis or verification of the precise physics have yet to be performed. C2 products could also be investigated by implementing the kinetic parameters. Recent studies have shown CO2R in acidic media is possible,15 reducing the negative effects of the OH− which could be investigated more thoroughly. Layered catalyst and high ECSA designs may be investigated further to combine their strengths, aiming at exceptionally high current densities. In addition, the methodology developed here for CO2R could be applied to other devices with a triple-phase region, such as fuel cells and metal–air batteries. Finally, experimental corroboration of the predicted trends would lead to both a better validation of the modeling methodology, and optimally, to GDEs with higher current densities.
Author contributions
EJ: conceptualization, methodology, software, writing – original draft. EB: writing – review & editing. SL: software, writing – review & editing. SH: project administration, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication was created as part of NCCR Catalysis (grant number 180544), a National Centre of Competence in Research funded by the Swiss National Science Foundation. The work has been supported by the European Unions Horizon 2020 research and innovation programme (851441, project SELECT-CO2).References
- F. Ullmann, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH, 2003 Search PubMed.
- F. Fischer, Ind. Eng. Chem., 1925, 17, 574–576 CrossRef CAS.
- T. Burdyny and W. A. Smith, Energy Environ. Sci., 2019, 12, 1442–1453 RSC.
- K. Yang, R. Kas, W. A. Smith and T. Burdyny, ACS Energy Lett., 2021, 6, 33–40 CrossRef CAS.
- A. Senocrate and C. Battaglia, J. Energy Storage, 2021, 36, 102373 CrossRef.
- D. Corral, D. U. Lee, V. M. Ehlinger, S. Nitopi, J. E. Avilés Acosta, L. Wang, A. J. King, J. T. Feaster, Y.-R. Lin, A. Z. Weber, S. E. Baker, E. B. Duoss, V. A. Beck, C. Hahn and T. F. Jaramillo, Chem Catal., 2022, S2667109322005097 Search PubMed.
- B. Endrödi, E. Kecsenovity, A. Samu, T. Halmágyi, S. Rojas-Carbonell, L. Wang, Y. Yan and C. Janáky, Energy Environ. Sci., 2020, 13, 4098–4105 RSC.
- J. C. Bui, E. W. Lees, L. M. Pant, I. V. Zenyuk, A. T. Bell and A. Z. Weber, Chem. Rev., 2022, 122, 11022–11084 CrossRef CAS PubMed.
- M. R. Singh, J. D. Goodpaster, A. Z. Weber, M. Head-Gordon and A. T. Bell, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E8812–E8821 CrossRef CAS PubMed.
- X. Zhu, J. Huang and M. Eikerling, ACS Catal., 2021, 11, 14521–14532 CrossRef CAS.
- L.-C. Weng, A. T. Bell and A. Z. Weber, Phys. Chem. Chem. Phys., 2018, 20, 16973–16984 RSC.
- J. Blake, J. Padding and J. Haverkort, Electrochim. Acta, 2021, 393, 138987 CrossRef CAS.
- Z. Yang, D. Li, L. Xing, H. Xiang, J. Xuan, S. Cheng, E. H. Yu and A. Yang, ACS Sustainable Chem. Eng., 2021, 9, 351–361 CrossRef CAS.
- R. Kas, A. G. Star, K. Yang, T. Van Cleve, K. C. Neyerlin and W. A. Smith, ACS Sustainable Chem. Eng., 2021, 9, 1286–1296 CrossRef CAS.
- J. Gu, S. Liu, W. Ni, W. Ren, S. Haussener and X. Hu, Nat. Catal., 2022, 5, 268–276 CrossRef CAS.
- H. Wang, A. Thiele and L. Pilon, J. Phys. Chem. C, 2013, 117, 18286–18297 CrossRef CAS.
- D. Bohra, PhD thesis, Delft University of Technology, 2020.
- D. Bohra, J. H. Chaudhry, T. Burdyny, E. A. Pidko and W. A. Smith, Energy Environ. Sci., 2019, 12, 3380–3389 RSC.
- S. Ringe, C. G. Morales-Guio, L. D. Chen, M. Fields, T. F. Jaramillo, C. Hahn and K. Chan, Nat. Commun., 2020, 11, 33 CrossRef CAS PubMed.
- S. Suter and S. Haussener, Energy Environ. Sci., 2019, 12, 1668–1678 RSC.
- C. P. Liu, P. Saha, Y. Huang, S. Shimpalee, P. Satjaritanun and I. V. Zenyuk, ACS Appl. Mater. Interfaces, 2021, 13, 20002–20013 CrossRef CAS PubMed.
- D. Wakerley, S. Lamaison, J. Wicks, A. Clemens, J. Feaster, D. Corral, S. A. Jaffer, A. Sarkar, M. Fontecave, E. B. Duoss, S. Baker, E. H. Sargent, T. F. Jaramillo and C. Hahn, Nat. Energy, 2022, 7, 130–143 CrossRef CAS.
- A. Senocrate, F. Bernasconi, D. Rentsch, K. Kraft, M. Trottmann, A. Wichser, D. Bleiner and C. Battaglia, ACS Appl. Energy Mater., 2022, 5(11), 14504–14512 CrossRef CAS.
- F. P. García de Arquer, C.-T. Dinh, A. Ozden, J. Wicks, C. McCallum, A. R. Kirmani, D.-H. Nam, C. Gabardo, A. Seifitokaldani, X. Wang, Y. C. Li, F. Li, J. Edwards, L. J. Richter, S. J. Thorpe, D. Sinton and E. H. Sargent, Science, 2020, 367, 661–666 CrossRef PubMed.
- T. Hatsukade, K. P. Kuhl, E. R. Cave, D. N. Abram and T. F. Jaramillo, Phys. Chem. Chem. Phys., 2014, 16, 13814–13819 RSC.
- E. L. Clark, J. Resasco, A. Landers, J. Lin, L.-T. Chung, A. Walton, C. Hahn, T. F. Jaramillo and A. T. Bell, ACS Catal., 2018, 8, 6560–6570 CrossRef CAS.
- Sigracet Spec Sheet, GDL 34 & 35 Series Gas Diffusion Layer, https://www.fuelcellstore.com/spec-sheets/SGL-GDL_34-35.pdf.
- A. El-kharouf, T. J. Mason, D. J. Brett and B. G. Pollet, J. Power Sources, 2012, 218, 393–404 CrossRef CAS.
- S. Trasatti and E. Lust, in Modern Aspects of Electrochemistry, ed. R. E. White, J. O. Bockris and B. E. Conway, Springer, US, Boston, MA, 1999, pp. 1–215 Search PubMed.
- J. Newman and K. Thomas-Alyea, Electrochemical Systems, 3rd edn, 2004 Search PubMed.
- C. Delacourt, P. L. Ridgway and J. Newman, J. Electrochem. Soc., 2010, 157, B1902 CrossRef CAS.
- J.-M. Savéant, Chem. Rev., 2008, 108, 2348–2378 CrossRef PubMed.
- L.-C. Weng, A. T. Bell and A. Z. Weber, Energy Environ. Sci., 2019, 12, 1950–1968 RSC.
- J. Zheng, W. Sheng, Z. Zhuang, B. Xu and Y. Yan, Sci. Adv., 2016, 2, e1501602 CrossRef PubMed.
- W. Deng, P. Zhang, B. Seger and J. Gong, Nat. Commun., 2022, 13, 803 CrossRef CAS PubMed.
- E. Cussler, Diffusion, mass transfer in fluid systems, 3rd edn, 2007 Search PubMed.
- S. Weisenberger and A. Schumpe, AIChE J., 1996, 42, 298–300 CrossRef CAS.
- S. Verma, X. Lu, S. Ma, R. I. Masel and P. J. A. Kenis, Phys. Chem. Chem. Phys., 2016, 18, 7075–7084 RSC.
- A. Forner-Cuenca, J. Biesdorf, L. Gubler, P. M. Kristiansen, T. J. Schmidt and P. Boillat, Adv. Mater., 2015, 27, 6317–6322 CrossRef CAS PubMed.
- T. Burdyny, P. J. Graham, Y. Pang, C.-T. Dinh, M. Liu, E. H. Sargent and D. Sinton, ACS Sustainable Chem. Eng., 2017, 5, 4031–4040 CrossRef CAS.
- Y. Xu, J. P. Edwards, S. Liu, R. K. Miao, J. E. Huang, C. M. Gabardo, C. P. OBrien, J. Li, E. H. Sargent and D. Sinton, ACS Energy Lett., 2021, 6, 809–815 CrossRef CAS.
- O. Redlich, Chem. Rev., 1946, 39, 333–356 CrossRef CAS PubMed.
- D. McLaughlin, M. Bierling, R. Moroni, C. Vogl, G. Schmid and S. Thiele, Adv. Energy Mater., 2020, 10, 2000488 CrossRef CAS.
- E. Boutin, S. Liu, F. Lorenzutti and S. Haussener, SelectCO2, Deliverable 7.2, 2022.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ey00122a |
| This journal is © The Royal Society of Chemistry 2023 |