Defect-engineered MOF-801 for cycloaddition of CO₂ with epoxides

Abstract

Heterogeneous catalysts based on defective metal–organic frameworks (MOFs) have attracted wide attention due to their facile formation of defects during synthesis. Herein, two MOFs, MOF-801(D) and MOF-801(P), were synthesized by a solvothermal method using a modulation approach. The synthesized MOFs were characterized by using PXRD, N₂ BET, TGA, NH₃ and CO₂-TPD, CO₂ adsorption isotherms, XPS, FT-IR, FE-SEM, and HR-TEM. A computational characterization method was developed to approximate the degree of defects using a combination of molecular simulation and a linear programming approach. Master isotherm models for N₂ isotherms at 77 K were constructed to match the experimental isotherm data of MOF-801(D) and MOF-801(P), and the pore size distribution and the degree of defects were quantified based on the predicted N₂ isotherms at 77 K. MOF-801(D) showed a high conversion of epoxide with >99% selectivity toward cyclic carbonate and 92% conversion under mild and solvent-less reaction conditions. MOF-801(D) was easily separated using a centrifuge and can be recycled up to 5 times without any significant decrease in its initial performance. Density functional theory (DFT) calculations were carried out to corroborate that the increased acid sites, from the cluster defects, are responsible for the increased catalytic conversion of the catalyst.

---

Introduction

Due to the concerns over global climate change with the increasing CO₂ concentration in the atmosphere, the development of engineering and materials technologies that can efficiently capture, store, and utilize CO₂ into valuable chemicals is gaining momentum in a broad scientific community.^1–3 One such method of transforming CO₂ into valuable chemicals is the synthesis of cyclic carbonate from carbon dioxide and epoxides.^2,4,5 The main advantage of the cyclic carbonate synthesis by the cycloaddition reaction is that the reaction (Fig. 1) is more environmentally friendly than traditional carbonate synthesis routes⁵ with a 100% atom economy. According to a recent report, almost 80 kilotons of cyclic carbonates are produced per year, corresponding to the potential for 40 kilotons per year of direct CO₂ utilization.^5,6 The demand for cyclic carbonates has been growing rapidly due to their utilization as an electrolyte in Li-ion batteries,^7,8 and as intermediates in the synthesis of polyurethane, ethylene glycol, paints, and pharmaceutical products.^9–13 Additionally, the synthesis of cyclic carbonates using CO₂ as a feedstock leads to long-time CO₂ fixation compared to other CO₂-based products, such as urea and fertilizer.^14,15

Fig. 1 Cycloaddition reaction of epoxide and CO₂ to form a five-membered cyclic carbonate (Cat. represents catalyst).

Metal–organic frameworks (MOFs) typically consist of metal clusters and organic ligands and could have a very high surface area, porosity, and crystallinity, depending on the choice of the building blocks for the synthesis. In principle, the internal pore size of MOFs can be controlled by judiciously choosing the framework ligands while the pore surface chemistry can be modulated by introducing functional groups into these ligands.¹⁶ As such, MOFs have been investigated for their use in heterogeneous catalysts, sensors, biological and medical materials, proton conductors, gas separators, and adsorbent materials for selective gas capture.^13,17–20 MOFs have been developed as efficient catalysts for the synthesis of cyclic carbonates from CO₂ and epoxides.^21–27

One of the key drawbacks of MOFs for such applications is their chemical and thermal stability.²⁸ For example, many reported MOFs are not stable under humid conditions and at high temperatures because of the weak coordination bond between the metal node and organic ligands. For instance, Zn²⁺ based MOFs, including Zn-MOF-74, are easily dissociated in a typical atmosphere via water hydrolysis.^29,30 Due to the influence of water, the metal–oxygen bond of the MOFs is elongated, which leads to the framework collapsing. However, MOFs based on the Zr⁴⁺ node (i.e., Zr-MOFs) have shown to be water-stable and acid–gas resistant,^31–33 which makes them an ideal candidate for applications under high temperature and pressure conditions, such as thermal catalysis. More importantly, Zr-based MOFs, such as UiO-66 and MIL-140, were reported to be catalytically active and stable,^31,34–37 likely due to the high oxidation states of Zr-based MOFs that can readily activate the reaction substrates.³¹

The choice of synthesis methods for Zr-MOFs plays a critical role in the degree of defects and the crystallinity of the material. For example, Wißmann et al. reported the modulation approach,³¹ which consists of the addition of a monovalent modulator (monocarboxylic acid, e.g., acetic acid, formic acid, difluoroacetic acid, and trifluoroacetic acid) to the reaction blend. The modulation approach enhances the reproducibility of the catalyst synthesis, increases the crystallization of catalysts, and controls the crystal size and shape, as well as the degree of agglomeration/aggregation of the crystals.³⁸

During the crystallization, the modulator influences the crystal nucleation and growth by competing with the ligand for the coordination site at the metal ion or metal cluster, which leads to the creation of defect sites. However, only a few studies of the modulation approach have been reported in the literature.^39,40

Defects play a central role in heterogeneous catalysis and its utilization.^41–45 These defects can be formed from missing linkers clusters, or a combination of both.^46,47 Many studies have reported that the role of defect sites in MOFs has been continuously increased after Farrusseng et al.'s original work on the defect of MOF-5 in 2008.⁴⁸ The presence of defects can also tune the local atomic structure, optical properties, electronic structure, or electrical conductivity of materials, and thus further affect the physicochemical properties and adsorptive and catalytic performance.^49–54 Nevertheless, the presence of defects was considered as the primary reason for the unexpected, and sometimes significantly enhanced, catalytic properties of various MOFs, such as UiO-66,^55–60 UiO-67,⁶¹ MIL-101(Fe),⁶² MOF-5,⁶³ MOF-808,⁶⁴ HKUST-1,⁶⁵ and ZIF-8.⁶⁶ Among zirconium MOFs, the Zr-fumarate MOF (i.e., MOF-801(Zr)) has a fcu topology, with metal clusters interconnected by a nonlinear dicarboxylate ligand, which leads to a lowering of symmetry and slight tilting of the [Zr₆(μ₃-O)₄(μ₃-OH)₄]¹²⁺ clusters.⁶⁷ Recently, Zr-MOFs have attracted the attention of many researchers for their water stability, potential for green synthesis, and facile shaping using a direct monolith formation by a gel approach.⁶⁸

Defects and their associated property modulation in MOF-801(Zr) have been recently investigated by Iacomi et al. for the adsorption and separation of C3 hydrocarbons.⁶⁹ Two types of defects, missing linkers, and missing clusters, at various concentrations and conformations in the structure have been predicted. A combination of experimental and simulation methodology reveals that the equilibrium adsorption behavior of C3 hydrocarbons can best be described by a model where zirconium clusters are missing cluster defects.

In this work, we prepared pristine and defective MOF-801(Zr) using the modulation method. The catalytic performances of MOF-801(Zr) were characterized based on the experimental and simulated N₂ adsorption isotherms, and DFT calculations were carried out to provide a plausible reaction mechanism and an explanation for the increased catalytic activity for the cycloaddition of CO₂ and epoxides into cyclic carbonates.⁴⁸ From the analyses, we conclude that the presence of defects leads to increased catalytic conversion of CO₂ into cyclic carbonates by providing additional acid sites for reaction and a pathway for faster mass transfer of reactants.

Results and discussion

Characterization of the synthesized catalysts

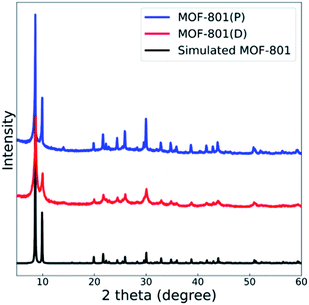
The powder X-ray diffraction (PXRD) spectra of the synthesized MOF-801(D, defective) and MOF-801(P, pristine) were compared with the theoretical single crystal spectrum (Fig. 2). Also, the crystal homogeneity, structural integrity, and degree of crystallinity of all the MOF-801 catalysts were confirmed through PXRD analysis. The PXRD peaks of both catalysts well fitted with the theoretical spectrum of the CCDC (Cambridge Crystallographic Data Center, Cambridge, United Kingdom) database, thereby verifying the good synthesis of all the catalysts (Fig. 2).

Fig. 2 XRD patterns of MOF-801(D) and MOF-801(P) with simulated MOF-801.

NH₃ and CO₂ temperature-programmed desorption (TPD) analyses (Fig. S1†) were carried out to investigate acid–base sites in the MOF-801 catalysts. As shown in Table 1, MOF-801(D) showed a higher amount of acidic sites than MOF-801(P). In contrast, MOF-801(P) had a higher amount of basic sites than MOF-801(D).

Table 1 Amount of acidic and basic sites in the MOF-801(Zr) catalysts

Catalyst	Acidic sites NH3-TPD (mmol g^−1)	Basic sites CO2-TPD (mmol g^−1)
MOF-801(D)	4.4	2.4
MOF-801(P)	3.8	3.0

---

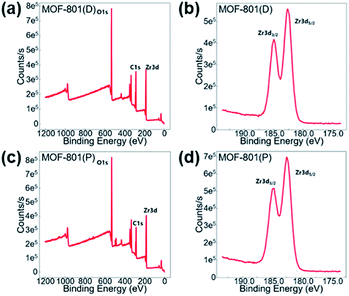
X-ray photoelectron spectroscopy (XPS) was carried out to verify the valence state of the Zr-MOF catalysts. The XPS spectra, as shown in Fig. 3, supports the existence of Zr, C, and O in the Zr-MOF catalysts. The Zr 3d peak located at a binding energy of around 182.68 eV and 184.98 eV can be assigned to Zr 3d_5/2 and Zr 3d_3/2, which is similar to previous Zr-based MOFs that some of us reported.⁷⁰

Fig. 3 XPS spectra (a) and (b) for MOF-801(D) and (c) and (d) for MOF-801(P).

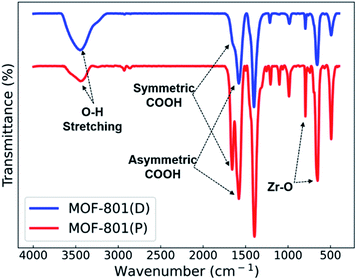
Fourier transform infrared spectroscopy (FT-IR) spectra of the MOF-801 catalysts are shown in Fig. 4. The wide peak in the range of 3400–3450 cm⁻¹ corresponds to the O–H stretching frequency of coordinated H₂O. The peaks observed at approximately 1670–1510 cm⁻¹ correspond to the symmetric and asymmetric stretching vibration of the carboxylic group (COOH) of the ligand. The symmetric stretching vibration of the Zr–O bond at 790 cm⁻¹ and 650 cm⁻¹ confirms the good coordination of the metal with the ligands.^13,34

Fig. 4 FT-IR spectra of MOF-801(D) and MOF-801(P).

From the thermogravimetric analysis (TGA), the thermal stability of MOF-801(P) and MOF-801(D) was confirmed to be as high as 200 °C, as shown in Fig. S2.† The TGA of MOF-801 mainly indicates three decaying steps in the temperature ranges of 40–130, 140–500, and 550–700 °C. The first continuous weight loss of 3–4 wt% corresponds to the loss of free water molecules, and the second and third steps can be ascribed to the successive decomposition of the 3D lattice network of the dehydrated catalyst [Zr₆O₆(O₂C-(CH)₂-CO₂)₆] to form (ZrO₂)₆. MOF-801(P) showed larger weight loss near 500 °C than MOF-801(D). Since MOF-801(P) contains more fumarate ligands in the framework, the weight loss originating from their decomposition could be higher than in MOF-801(D) containing smaller number of the ligands. The total weight loss in wt% between 100 °C (ligand containing state) and 500 °C (ligands are decomposed) for MOF-801(P) and MOF-801(D) was calculated to be 43.1% and 38.8%, respectively. If one of the six ligands in the formula of the dehydrated MOF-801 is missing to form a defect structure, Zr₆O₆(O₂C-(CH)₂-CO₂)₅ [M.W. = 1207.45], the estimated weight loss will be (1207.45–739.272)/1207.45 = 38.8%. Therefore, we can estimate that almost 1/6 ligand of its perfect crystal structure was missing in MOF-801(D). The detailed calculations are included in the ESI (Fig. S2†).

The morphology images of MOF-801 catalysts were obtained using field-emission scanning electron microscopy (FE-SEM), performed under vacuum conditions. FE-SEM images revealed the formation of crystalline solids (Fig. S3†). The image of defective MOF-801(D) was investigated using high-resolution transmission electron microscopy (HR-TEM), operated at 200 kV. The HR-TEM image (Fig. S4†) shows the presence of defects in the crystal structure of MOF-801(D).

Computational methods for defect characterization

There are two types of defects in zirconium MOFs: (1) the missing cluster (mc) defects and (2) the missing linker (ml) defects (Scheme 1). Computational structural analysis, which includes molecular grand canonical Monte Carlo (GCMC) simulations, linear programming, and 2D-NLDFT calculations, was carried out to predict the degree of defects and estimate the pore size distributions and BET area of MOF-801(D) and MOF-801(P). The porosity and isotherm analysis of both MOF-801 catalysts were analyzed by N₂ physical adsorption at 77 K. The BET areas of simulated and experimental MOF-801(D) and MOF-801(P) were calculated using the SESAMI 1.0 code⁷¹ which is an open-source python program that can automate the BET analyses. Four consistency criteria were satisfied when obtaining the BET areas.⁷² The simulated BET areas are given in Table S1.† The experimental BET area of MOF-801(P) and MOF-801(D) was 707 and 832 m² g⁻¹, respectively.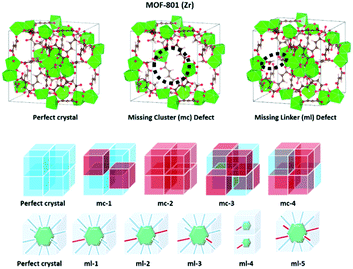

Scheme 1 Pristine MOF-801(Zr) and defective MOF-801(Zr). Red boxes represent the missing cluster defects (defective structure).

We constructed different master isotherm models composed of the various combinations of the missing linker (ml) and missing cluster (mc) (Table 2). The linear programming approach was used to estimate the BET area, and the results are shown in Table 3, Fig. S5, and S6.† Here, the BET areas of the structures based on the master isotherms were modelled as a minimization problem, and the proportion of different defects that led to the best agreement with the BET area obtained from the experimental isotherm data was selected based on the linear programming approach.

Table 2 Composition (%) of defects in different master models^a

Model	P	mc-1	mc-2	mc-3	mc-4	ml-1	ml-2	ml-3	ml-4	ml-5
a P: perfect crystal, mc: missing cluster, and ml: missing linker.
1	0	0	0	100	0	0	0	0	0	0
2	0	0	0	0	0	0	100	0	0	0
3	0	36	0	64	0	0	0	0	0	0
4	0	0	0	37	34	0	0	0	0	29
5	0	45	23	0	0	0	0	0	32	0
6	0	100	0	0	0	0	0	0	0	0
7	100	0	0	0	0	0	0	0	0	0
8	89	0	0	0	0	0	0	0	0	11
9	58	31	0	0	0	0	0	0	0	11
10	90	0	0	0	0	0	0	0	0	10

---

Table 3 Simulated and experimental BET areas of MOF-801(D) and MOF-801(P)

MOF-801(D)
Master model	1	2	3	4	5	Exp.
BET area (m^2 g^−1)	1125	684	1070	1077	963	832

---

MOF-801(P)
Master model	6	7	8	9	10	Exp.
BET area (m^2 g^−1)	966	686	784	667	707	707

---

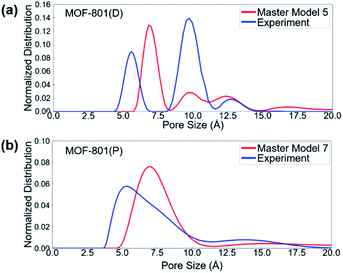
To first validate our approach, we used the method on the N₂ isotherm data for MOF-801(P) (Table 3 and Fig. S5†). We found that master model 7 was the best master isotherm model composed of 100% pristine crystals, which provides the basis for using the method to further characterize the defective MOF-801. We found that the best model for MOF-801(D) was master model 5 consisting of 45% mc-1, 23% mc-2, and 32% ml-4 (Table 3 and Fig. S6†). Note that mc-1 and mc-2 are the missing cluster defects which can provide more acid sites for the cycloaddition reaction of epichlorohydrin with CO₂.

The CO₂ adsorption experiments of these catalysts were additionally carried out at 298 K. For additional model validation, CO₂ isotherms were predicted from the suggested master model of defect composition from the N₂ isotherm (Fig. S7†). The similarity of the isotherm shape in the experimental and simulated cases further supports that the degree of defect estimated using the master isotherm is reasonable. Furthermore, since the CO₂ uptake in MOF-801(D) is lower than that in MOF-801(D), the high CO₂ uptake is not necessary for the high conversion in the cycloaddition reaction, and the presence of more active sites, as characterized by the master isotherm approach, is a more important feature for high-performance catalyst development.

Pore size distributions (PSDs)

The pore size distributions (PSDs) of defective and pristine MOFs were characterized based on the experimental and simulated N₂ adsorption isotherm data. PSDs of materials are typically characterized using different methods, depending on the size of the pores and the heterogeneity of pore surfaces. The 2D non-local density functional theory (2D-NLDFT) method,⁷³ as implemented in SAIEUS 3.0 software (Micromeritics, GA),⁷⁴ was used to evaluate the pore size distributions of pristine and defective MOFs. The 2D-NLDFT method requires the user to select a proper kernel. For the kernel selection, carbon and N₂ at 77 K kernel was chosen since this kernel provides the best agreement when compared with the geometric PSD result calculated using zeo++ (Fig. S8†).^75,76 All the simulated structures were first analyzed with the 2D-NLDFT method (Fig. S9 and S10†) to provide a basis for the comparison. Fig. 5 shows the 2D-NLDFT PSD result from the constructed master model and experimental isotherms. In general, the master model-based isotherms (i.e., simulated isotherms) provide reasonable agreement with experimental isotherms in terms of the location and number of peaks. For MOF-801(D), the PSD showed two peaks of larger pore sizes (∼10 and ∼12 angstrom) from the master model and experimental isotherms, whereas there was only a single small pore size (∼7 angstrom) in MOF-801(P). Note that the large pore allows for faster mass transfer of the reactants into the pore, which can subsequently lead to the higher catalytic performance of defective MOF-801(D).

Fig. 5 2D-NLDFT result for (a) MOF-801(D), and (b) MOF-801(P) with the master isotherm model.

Cycloaddition of epichlorohydrin with CO₂

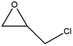
To evaluate the catalytic performances of MOF-801(D) and MOF-801(P), epichlorohydrin (ECH) was used as the reactant to perform the CO₂ cycloaddition reaction for the synthesis of chloropropene carbonate. At first, an appropriate weight of the synthesized MOF-801 catalyst was taken in an autoclave reactor, and the reaction conditions were changed suitably. Under the catalyst-less conditions, the CO₂ cycloaddition reaction did not occur even after 15 hours of reaction time at 80 °C and atmospheric CO₂ pressure (Table 4, entry 1). The homogeneous catalysts (metal salt and organic ligand) were tested for their respective catalytic activities and ECH converted much lower chloropropene carbonate as the final product (Table 4, entries 2–3). Without a co-catalyst, each MOF-801(D) and MOF-801(P) showed very low ECH conversion under the above conditions (Table 4, entries 4–5). We used tetrabutylammonium halide (TBAX, X = Cl⁻, Br⁻, I⁻) as the co-catalyst to increase the reactivity. The experiments using TBABr alone showed a relatively low conversion (38.9%), but when the catalysts and TBABr were used together, the conversion was significantly increased (Table 4, entries 7–10). This is likely due to the synergistic effect between the MOF catalyst and the co-catalysts in performing the reaction, which has been well-documented in the literature. Comparing the cycloaddition reactions using MOF-801(D) and MOF-801(P) as catalysts, MOF-801(D) leads to a higher conversion (Table 4, entry 7, 92.4%) due to the additional acidic sites (epoxide activation) from undercoordinated zirconium nodes, and pores with >10 angstrom diameter which allows for accelerated mass transfer of reactants. Among different tetrabutylammonium halide cocatalysts (TBABr, TBACl, and TBAI), showing the order of nucleophilicity of anions as I⁻ > Br⁻ > Cl⁻, bromine anions revealed higher catalytic performance than chloride and iodide anions. Because of the bulky structure of iodide anions, MOF-801(D) with tetrabutylammonium iodide (TBAI) showed lower ECH conversion (77%) than with TBABr due to the mass transfer limitation effect (Table 4, entries 10–12).

Table 4 Comparison of the catalytic activities for the cycloaddition reaction of ECH and CO₂^a

Entry	Catalysts	Conversion^c (%)	Selectivity^c (%)
a Reaction conditions: epichlorohydrin (ECH) = 19.2 mmol, catalyst amount = 0.6 mol%, TBAB = 0.5 mol%, pressure = 0.1 MPa CO2, temperature = 80 °C time = 15 h, semi-batch reaction. b Catalyst amount = 0.4 mol% and TBAB = 0.4 mol%. c Determined by GC.
1	None	—	—
2	Zirconium salt	1.52	94
3	Zr salt/fumaric acid	1.71	96
4	MOF-801(P)	2.13	>99
5	MOF-801(D)	3.08	>99
6	TBAB	38.9	>99
7	MOF-801(P)/TBABr^b	70.3	>99
8	MOF-801(D)/TBABr^b	78.8	>99
9	MOF-801(P)/TBABr	83.1	>99
10	MOF-801(D)/TBABr	92.4	>99
11	MOF-801(D)/TBACl	86.5	>99
12	MOF-801(D)/TBAI	77.0	>99

---

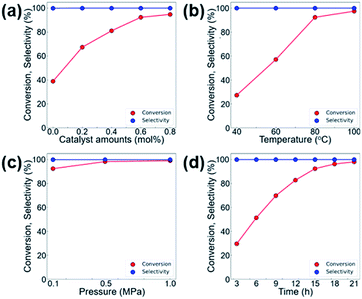
We further investigated the effects of various reaction parameters, such as the catalyst amount, temperature, reaction time, and CO₂ pressure that lead to higher conversion in the CO₂ cycloaddition reaction of CO₂ and ECH. As shown in Fig. 6, the conversion of ECH monotonically increases with increasing temperature, pressure, and reaction time, and no longer increases at certain points. Therefore, the optimum operating conditions are selected as 0.6 mol% of MOF-801(D) and 0.5 mol% of the TBABr co-catalyst, at a reaction temperature of 80 °C, under atmospheric CO₂ pressure (0.1 MPa), and with a reaction time of 15 hours.

Fig. 6 Effect of various reaction parameters on the cycloaddition of CO₂ and ECH with MOF-801(D) catalysts (a) catalyst amount (co-catalyst 0.5 mol%, 80 °C, 15 h, 0.1 MPa CO₂), (b) temperature (catalyst 0.6 mol%, co-catalyst 0.5 mol%, 15 h, 0.1 MPa CO₂), (c) CO₂ pressure (catalyst 0.6 mol%, co-catalyst 0.5 mol%, 80 °C, 15 h), and (d) time (catalyst 0.6 mol%, co-catalyst 0.5 mol%, 80 °C, 0.1 MPa CO₂).

Catalyst activity with different epoxides

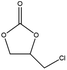
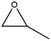
The activity of the MOF-801(D) catalyst was tested for several different epoxides for the cycloaddition reaction with CO₂ under the optimized reaction conditions. As shown in Table 5, the MOF-801(D) and TBABr co-catalyst system could transform all the epoxides (epichlorohydrin, propylene oxide, allyl glycidyl ether, styrene oxide, and cyclohexene oxide) to their corresponding cyclic carbonates. Good conversion of epoxide was observed for epichlorohydrin (92.4%), allyl glycidyl ether (82.3%), propylene oxide (70.8%), and styrene oxide (87.1%) with >99% selectivity of the carbonate product. However, cyclohexene oxide revealed relatively low conversion (14.3%), likely due to the presence of the sterically hindered cyclohexene ring, which prevents the approach of the substrate toward the catalytic acidic site of the catalyst,^77–79 and likely due to the small pore size of the material that prevents the reactant from diffusing through the internal surface of MOFs.

Table 5 Synthesis of cyclic carbonates from various epoxides^a

Entry	Reactant	Product	Yield^b (%)
a Reaction conditions: epoxides = 19.2 mmol, catalyst = 0.6 mol%, TBABr = 0.5 mol%, pressure = 0.1 MPa CO2, temperature = 80 °C, time = 15 h, semi-batch reaction. b Determined by GC.
1			92.4
2			90.8
3			82.3
4			87.1
5			17.7

---

Catalyst separation and reusability

After simple separation using a centrifuge (7000 rpm), the reusability of the MOF-801(D) catalyst was tested by repeating the same experiments five times with the same catalyst materials to verify the integrity of the catalyst under the optimized reaction conditions (0.6 mol% of MOF-801(D), 0.5 mol% of TBABr, 80 °C, 15 h, atmospheric CO₂ pressure). As shown in Fig. 7, there was no significant decrease in ECH conversion and chloropropene carbonate selectivity. The reused MOF-801(D) catalyst was subsequently analyzed through various physico-chemical analyses such as PXRD and FT-IR. The PXRD patterns and FT-IR spectra of MOF-801(D) show that the catalyst remains stable even after recycling up to five times (Fig. S11 and S12†).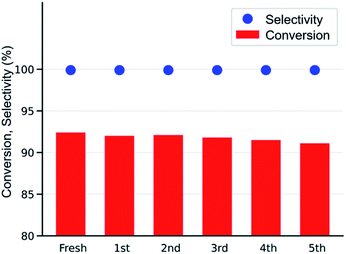

Fig. 7 Reusability test of the MOF-801(D) catalyst (ECH 19.2 mmol, catalysts 0.6 mol%, TBABr 0.5 mol%, 80 °C, 15 h, 0.1 MPa, semi-batch).

Reaction mechanism

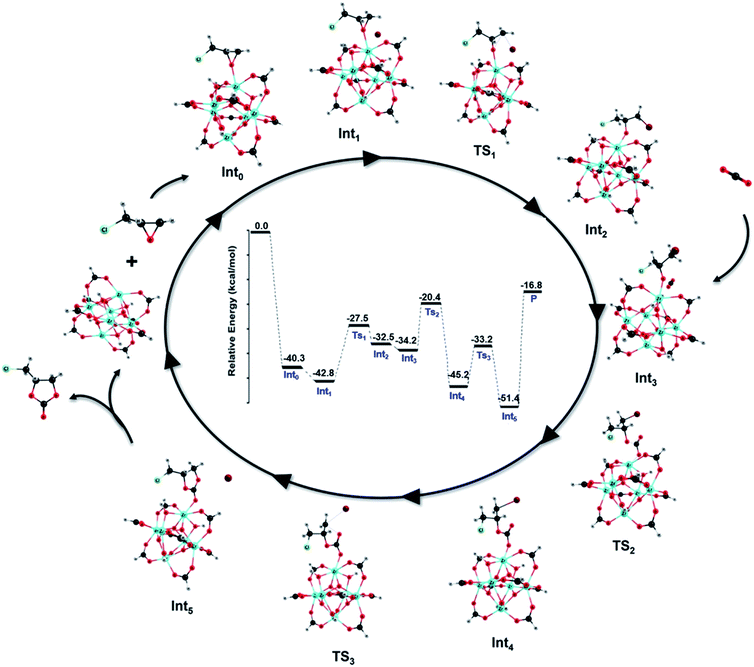
The cycloaddition reaction mechanism between CO₂ and epichlorohydrin (ECH) to form chloropropene carbonate catalyzed by defective MOF-801 and co-catalyzed by TBABr was investigated using density functional theory (DFT) calculations. Fig. 8 provides the relative potential energy profile along with the optimized structures of intermediates and transition states. Initially, the uncatalyzed reaction mechanism was performed (Fig. S13†). The uncatalyzed reaction has an activation barrier of 60.2 kcal mol⁻¹ which suggests the importance of the catalyst.

Fig. 8 Relative energy profile for the MOF-801/TBABr catalyzed cycloaddition reaction of CO₂ with ECH to form chloropropene carbonate and the DFT optimized structures of intermediates and transition states.

A plausible reaction mechanism for the cycloaddition of epoxides with CO₂ in the presence of MOF-801(D) and the co-catalyst TBABr was formulated based on the previous experimental and simulation studies.^13,78 According to our TPD results (Table 1), MOF-801(D) has strong acidic sites which served as active centers for the cycloaddition reaction. The reaction mechanism for the cycloaddition reaction typically involves three steps consisting of the epoxide ring-opening, CO₂ insertion and the carbonate ring-closure. TBABr provides a nucleophilic reagent, Br⁻ for the reaction. Fig. S14† shows the reaction mechanism with only TBABr as a comparison. In the first step, the oxygen atom of epoxides is activated by the unsaturated metal center of MOF-801(D). Here, ECH is coordinated on the unsaturated Zr site to generate a stable Int₀ (−40.3 kcal mol⁻¹). Consequently, the bromide anion of TBABr attacks the less hindered carbon atom to form a weak van der Waals complex (Int₁) with a relative energy of −42.8 kcal mol⁻¹.

The ring-opening occurs through TS₁ where the nucleophilic attack of bromide results in the epoxide ring opening (Int₂). The activation energy (E_a) for the ring-opening step is 15.3 kcal mol⁻¹ which is less than half of the activation energy required for the TBABr catalyzed step (Fig. S14,†E_a = 34.9 kcal mol⁻¹). Subsequently, the O⁻ of the opened ring attacks the carbon atom of the carbon dioxide molecule through TS₂, with an activation energy of 13.8 kcal mol⁻¹, whereas for the TBABr catalyzed CO₂ insertion barrier it is 20.4 kcal mol⁻¹ (Fig. S14†). The resulting intermediate, Int₃ has a relative energy of −45.2 kcal mol⁻¹. Finally, the ring closure occurs through TS₃ (E_a = 12.0 kcal mol⁻¹) where the formation of the O–C bond and consequent removal of the bromide anion happen leading to the formation of the product, chloropropene carbonate. The high activation energy (E_a = 39.1 kcal mol⁻¹) required for the typical ring closure step in the TBABr catalyzed reaction was significantly reduced using MOF-801(D) as a catalyst. The overall mechanism proves the efficacy of MOF-801 as an excellent catalyst in converting CO₂ and epoxide to cyclic carbonates.

Conclusions

A pristine zirconium-fumarate MOF (MOF-801(P)) and its defective analogue (MOF-801(D)) were synthesized and compared for their catalytic performance for the cycloaddition reaction of epichlorohydrin and CO₂. MOF-801(D) with the TBABr co-catalyst showed over 92% of ECH conversion with >99% of chloropropene carbonate selectivity at 80 °C under atmospheric pressure of CO₂ without using any solvent. The nature of defects was characterized through combined experimental and simulation methods. Among the two types of defects in Zr-MOFs, we found that the two types of missing cluster defect models best matched the experimental data. The higher catalytic performance of MOF-801(D) over MOF-801(P) comes from the high surface area, presence of dual pores and missing cluster defects, and higher amounts of acidic sites due to the presence of open metal sites.

Experimental

Chemicals

Zirconyl chloride octahydrate (ZrOCl₂·8H₂O, 98%, reagent grade), fumaric acid (≥99.0%, purum), formic acid (≥96%, ACS reagent), methanol (99.8%, anhydrous), epichlorohydrin (ECH, ≥99%, purum), propylene oxide (PO, ≥99.5%, puriss. p.a.), styrene oxide (SO, 97%), allyl glycidyl ether (AGE, ≥99%), and cyclohexene oxide (CHO, 98%) were obtained from Sigma-Aldrich. N,N′-Dimethylformamide (DMF, >99.5%) was purchased from Tokyo Chemical Industry (TCI). All synthesis materials and solvents were used without further purification.

Preparation of MOF-801(D, defective)

MOF-801(D) was prepared according to the reported synthesis method.⁶⁷ For the synthesis of MOF-801(D), 16 g of (50 mmol) ZrOCl₂·8H₂O and 5.8 g (50 mmol) of fumaric acid were dissolved in a blend of DMF/formic acid (200 mL/70 mL) in a 500 mL glass jar. The glass jar was sealed and heated at 130 °C for 6 h. Pure white crystals were obtained and rinsed 3 times with DMF after cooling to room temperature. The as formed MOF-801(D) was washed with DMF 3 times a day for 3 days and soaked in methanol for 3 days. Methanol was exchanged 3 times per day. The white crystal was dried under vacuum conditions at 120 °C for 24 h.

Preparation of MOF-801(P, pristine)

For the synthesis of MOF-801(P),⁶⁷ in a 60 mL glass jar, 0.23 g (0.7 mmol) of ZrOCl₂·8H₂O and 0.081 g (0.7 mmol) of fumaric acid were dissolved in a mixture of DMF/formic acid (35 mL/5.3 mL). The glass jar was fastened and placed in a 120 °C oven for 24 h. Pure white crystals were obtained and rinsed 3 times with DMF after cooling to room temperature. The synthesized MOF-801(P) was washed with DMF 3 times per day for 3 days and soaked in methanol for 3 days. Methanol was also exchanged 3 times per day. The white crystal was dried in a vacuum oven at 120 °C for 24 h.

Cycloaddition of CO₂ and epoxides

All the CO₂ cycloaddition reactions were carried out in a 25 mL stainless steel reactor filled with a suitable amount of the catalyst, the co-catalyst, and epoxides. The reactor was kept connected to a CO₂ tank and stirred at 600 rpm. After the reaction finished, the reactor was cooled to reach room temperature, and the remaining CO₂ was released into the atmosphere. The final products were analyzed using gas chromatography (GC, HP 7890A, Agilent technologies, flame ionization detector, HP-5 capillary column) to determine the conversion, selectivity, and yields. Dichloromethane was used as the internal standard.

Computational methods

Model construction and grand canonical Monte Carlo simulation. In this work, we developed a master isotherm approach to closely approximate the nature of defects in MOF-801(D) based on the simulated and experimental nitrogen adsorption isotherms. First, a total of nine MOF-801 defective CIF files were collected from the literature.⁶⁹ The partial atomic charges on all crystal structures were assigned by message passing neural networks (MPNNs) for partial charge assignment to metal–organic frameworks.⁸⁰ The initial MPNN method was not trained to predict the charges on zirconium atoms, so the Zr atoms were exchanged for Ti atoms, and the partial atomic charges predicted from Ti atoms were transferred to Zr atoms by substituting the coordinates of titanium with zirconium. This approach can be justified based on the similarity between the oxidation states of zirconium and titanium atoms, and the assigned average charge of Zr was 2.32 from the MPNN, while the partial atomic charge predicted from DDEC was 2.34.⁸¹

GCMC simulations were carried out to calculate the N₂ isotherms at 77 K and CO₂ adsorption at 298 K for pristine and defective structures. All the GCMC simulation pressure points were taken to the exact same points as in the experimental isotherm data. For N₂ isotherms, we calculated the uptake at 73 pressure points for the MOF-801(D) case (1.12 × 10⁻⁶ bar to 0.99 bar) and 68 pressure points for MOF-801(P) (from 9.7 × 10⁻⁷ bar up to 0.99 bar). The GCMC simulation consisted of 20 000 cycles for equilibration and 20 000 cycles for the ensemble averages. Translation, rotation, reinsertion, and swap Monte Carlo moves were set with equal probabilities for sampling. The TraPPE model was used to model N₂ and CO₂ molecules.⁸² For N₂ isotherm calculations, only the van der Waals interactions were accounted for in the simulations, while both electrostatic interactions and van der Waals interactions were considered for CO₂ isotherm calculations. For van der Waals interactions, the Lennard–Jones 12–6 potential function was used to model the interaction with 12.8 angstrom cutoffs for framework-adsorbate and adsorbate–adsorbate interactions. For electrostatic interactions, the famous Ewald summation methods were used with summation of both reciprocal and real space parts up to 10⁻⁵ precision. RASPA 2.0 open-source software was used to carry out all GCMC simulations.⁸³

Linear programming and master isotherm models. Two master model isotherms for MOF-801(D) and MOF-801(P) were derived to approximate the experimental N₂ and CO₂ isotherms of the pristine and defective structures using the linear programming method. The sum squared errors of the loadings at each pressure point were calculated between the simulated and experimental isotherm data up to the monolayer coverage points, as characterized by using the SESAMI code.⁸⁴ The calculated monolayer coverage pressure point was 0.7 bar for MOF-801(D) and 0.3 bar for MOF-801(P). The objective functions for the minimization problem were minimized with different constraints to obtain the master isotherm model. Five different methods of minimization with different constraints were explored and the details are provided in Table S2.† The analysis code was written in Python and the objective functions were optimized using the methods implemented in NumPy.⁸⁵

Density functional theory (DFT) calculations. All the simulations for the catalytic cycle were performed using the Gaussian 16 program⁸⁶ with the B3LYP functional.⁸⁷ The basis set used for all the atoms except Zr is 6-31+G(d,p), and for Zr the LANL2DZ effective core potential (ECP) is used.⁸⁷ The choices of functional and basis sets follow previous reported investigations into the cycloaddition reaction.⁸⁸ The geometric optimization was followed by vibrational frequency analysis, and the transition states (TS) were confirmed with only one imaginary frequency whereas all the reactants, intermediates (Int), and the product were confirmed with no imaginary frequencies. The transition states were confirmed using the intrinsic reaction coordinate (IRC) method. The potential energies are given relative to the energies of non-interacting systems.

Author contributions

Conceptualization, investigation, and methodology: Y. G., B. A. A., and Y. G. C.; writing – original draft preparation: Y. G.; investigation and data curation: S. Y.; writing, review and editing, Y. C., and Y. G .C.; supervision: Y. G. C., and D. W. P. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Research Foundation of Korea through the Basic Research Program (2019R1I1A3A01057644), and supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSTI) (No. 2020R1C1C1010373). This study has been conducted with the support of the Korea Institute of Industrial Technology (KITECH) as “Development of AI Platform Technology for Smart Chemical Preocess” (JH210005-01). This work was also partially supported by the Industrial Strategic Technology Development Program-Alchemist Project (20012383, Technical Development of Hydrogen Production from Green Ammonia) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea). The authors acknowledge the computational time provided by the Korea Institute of Science and Technology Information (KISTI) (KSC-2021-CRE-0066). The authors also thank to J. Cha for performing simulations.

Notes and references

1. K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724–781.
2. M. Aresta, A. Dibenedetto and A. Angelini, Chem. Rev., 2014, 114, 1709–1742.
3. P. Markewitz, W. Kuckshinrichs, W. Leitner, J. Linssen, P. Zapp, R. Bongartz, A. Schreiber and T. E. Müller, Energy Environ. Sci., 2012, 5, 7281–7305.
4. M. Cokoja, M. E. Wilhelm, M. H. Anthofer, W. A. Herrmann and F. E. Kühn, ChemSusChem, 2015, 8, 2436–2454.
5. A. Rehman, F. Saleem, F. Javed, A. Ikhlaq, S. W. Ahmad and A. Harvey, J. Environ. Chem. Eng., 2021, 9, 105113.
6. J. F. Kurisingal, Y. Rachuri, Y. Gu, G.-H. Kim and D.-W. Park, Appl. Catal., A, 2019, 571, 1–11.
7. B. Scrosati, J. Hassoun and Y.-K. Sun, Energy Environ. Sci., 2011, 4, 3287–3295.
8. K. D. Fulfer and D. G. Kuroda, J. Phys. Chem. C, 2016, 120, 24011–24022.
9. S. Gennen, B. Grignard, T. Tassaing, C. Jérôme and C. Detrembleur, Angew. Chem., 2017, 129, 10530–10534.
10. A. Pascual, J. P. Tan, A. Yuen, J. M. Chan, D. J. Coady, D. Mecerreyes, J. L. Hedrick, Y. Y. Yang and H. Sardon, Biomacromolecules, 2015, 16, 1169–1178.
11. F. Shi, Y. Deng, T. SiMa, J. Peng, Y. Gu and B. Qiao, Angew. Chem., 2003, 115, 3379–3382.
12. H. Xiong, X. Wei, D. Zhou, Y. Qi, Z. Xie, X. Chen, X. Jing and Y. Huang, Bioconjugate Chem., 2016, 27, 2214–2223.
13. J. F. Kurisingal, Y. Li, Y. Sagynbayeva, R. K. Chitumalla, S. Vuppala, Y. Rachuri, Y. Gu, J. Jang and D.-W. Park, Catal. Today, 2020, 352, 227–236.
14. E. Koohestanian, J. Sadeghi, D. Mohebbi-Kalhori, F. Shahraki and A. Samimi, Energy, 2018, 144, 279–285.
15. J. W. Lee and R. Li, Energy Convers. Manage., 2003, 44, 1535–1546.
16. J. F. Kurisingal, Y. Rachuri, R. S. Pillai, Y. Gu, Y. Choe and D.-W. Park, ChemSusChem, 2019, 12, 1033–1042.
17. H.-Y. Li, S.-N. Zhao, S.-Q. Zang and J. Li, Chem. Soc. Rev., 2020, 49, 6364–6401.
18. A. Bieniek, A. P. Terzyk, M. Wiśniewski, K. Roszek, P. Kowalczyk, L. Sarkisov, S. Keskin and K. Kaneko, Prog. Mater. Sci., 2020, 117, 100743.
19. Y.-S. Wei, X.-P. Hu, Z. Han, X.-Y. Dong, S.-Q. Zang and T. C. Mak, J. Am. Chem. Soc., 2017, 139, 3505–3512.
20. H. Bux, C. Chmelik, R. Krishna and J. Caro, J. Membr. Sci., 2011, 369, 284–289.
21. R. Zou, P. Z. Li, Y. F. Zeng, J. Liu, R. Zhao, H. Duan, Z. Luo, J. C. Wang, R. Zou and Y. Zhao, Small, 2016, 12, 2334–2343.
22. Y. H. han, Z. Y. Zhou, C. B. Tiana and S. W. Du, Green Chem., 2016, 18, 4086–4091.
23. L. Yang, L. Yu, G. Diao, M. Sun, G. Cheng and S. Chen, J. Mol. Catal. A: Chem., 2014, 392, 278–283.
24. J. Song, Z. Zhang, S. Hu, T. Wu, T. Jiang and B. Han, Green Chem., 2009, 3, 1031–1036.
25. J. Kim, S. Kim, H. Jang, G. Seo and W. S. Ahn, Appl. Catal., A, 2013, 453, 175–180.
26. D. A. Yang, H. Y. Cho, J. Kim, S. T. Yang and W. S. Ahn, Energy Environ. Sci., 2012, 5, 6465–6473.
27. Y. Ren, X. Cheng, S. Yang, C. Qi, H. Jiang and Q. Mao, Dalton Trans., 2013, 42, 9930–9937.
28. A. J. Howarth, Y. Liu, P. Li, Z. Li, T. C. Wang, J. T. Hupp and O. K. Fraha, Nat. Rev. Mater., 2016, 1, 15018.
29. Y. Gu, C.-H. Lee, D.-W. Park and D.-H. Lim, Nanosci. Nanotechnol. Lett., 2018, 10, 1088–1094.
30. S. Zuluaga, E. M. Fuentes-Fernandez, K. Tan, F. Xu, J. Li, Y. J. Chabal and T. Thonhauser, J. Mater. Chem. A, 2016, 4, 5176–5183.
31. G. Wißmann, A. Schaate, S. Lilienthal, I. Bremer, A. M. Schneider and P. Behrens, Microporous Mesoporous Mater., 2012, 152, 64–70.
32. L. Yang, K. B. Idrees, Z. Chen, J. Knapp, Y. Chen, X. Wang, R. Cao, X. Zhang, H. Xing and T. Islamoglu, ACS Appl. Nano Mater., 2021, 4, 4346–4350.
33. Z. Li, F. Liao, F. Jiang, B. Liu, S. Ban, G. Chen, C. Sun, P. Xiao and Y. Sun, Fluid Phase Equilib., 2016, 427, 259–267.
34. H.-M. Jeong, R. Roshan, R. Babu, H.-J. Kim and D.-W. Park, Korean J. Chem. Eng., 2018, 35, 438–444.
35. J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850–13851.
36. F. Vermoortele, B. Bueken, G. Le Bars, B. Van de Voorde, M. Vandichel, K. Houthoofd, A. Vimont, M. Daturi, M. Waroquier and V. Van Speybroeck, J. Am. Chem. Soc., 2013, 135, 11465–11468.
37. M. Pander, M. Janeta and W. Bury, ACS Appl. Mater. Interfaces, 2021, 13, 8344–8352.
38. S. Diring, S. Furukawa, Y. Takashima, T. Tsuruoka and S. Kitagawa, Chem. Mater., 2010, 22, 4531–4538.
39. T. Tsuruoka, S. Furukawa, Y. Takashima, K. Yoshida, S. Isoda and S. Kitagawa, Angew. Chem., Int. Ed., 2009, 121, 4833–4837.
40. A. Schaate, P. Roy, A. Godt, J. Lippke, F. Waltz, M. Wiebcke and P. Behrens, Chem.–Eur. J., 2011, 17, 6643–6651.
41. C. Xie, D. Yan, S. Du, W. Chen, Y. Wang, Y. Zou, R. Chen and S. Wang, ACS Catal., 2020, 10, 11082–11098.
42. S. M. J. Rogge, J. Wieme, L. Vanduyfhuys, S. Vandenbrande, G. Maurin, T. Verstraelen, M. Waroquier and V. Van Speybroeck, Chem. Mater., 2016, 28, 5721–5732.
43. J. Canivet, M. Vandichel and D. Farrusseng, Dalton Trans., 2016, 45, 4090–4099.
44. Y. Liu, R. C. Klet, J. T. Hupp and O. K. Farha, Chem. Commun., 2016, 52, 7806–7809.
45. C. A. Trickett, K. J. Gagnon, S. Lee, G. Gandara, H. B. Buergi and O. M. Yagi, Angew. Chem., Int. Ed., 2015, 54, 1162–1167.
46. M. Taddei, Coord. Chem. Rev., 2017, 343, 1–24.
47. L. Liu, Z. Chen, J. Wang, D. Zhang, Y. Zhu, S. ling, K. W. Hwang, Y. Belmabkhout, K. Adil, Y. Zhang, B. Slater, M. Eddaoudi and Y. Han, Nat. Chem., 2019, 11, 622–628.
48. U. Ravon, M. E. Domine, C. Gaudillere, A. Desmartin-Chomel and D. Farrusseng, New J. Chem., 2008, 32, 937–940.
49. J. T. Ren, Y. Yali and Z. Y. Yuan, Green Energy Environ., 2021, 6, 620–643.
50. Z. Xu, J. Gao, L. Shi and Z. Bian, Trans. Tianjin Univ., 2021, 27, 147–154.
51. M. Y. Gao, B. Q. Song, D. Sensharma and M. J. Zaworotko, SmartMat, 2021, 2, 38–55.
52. K. Tan, H. Pandey, H. Wang, E. Velasco, K. Y. Wang, H. C. Zhou, J. Li and T. Thonhauser, J. Am. Chem. Soc., 2021, 143, 6328–6332.
53. M. Vandichel, J. Hajek, F. Vermoortele, M. Waroquier, D. E. De Vos and V. Van Speybroeck, CrystEngComm, 2015, 17, 395–406.
54. S. L. Ling and B. Slater, Chem. Sci., 2016, 7, 4706–4712.
55. F. Vermoortele, M. Vandichel, B. Van de Voorde, R. Ameloot, M. Waroquier, V. Van Speybroeck and D. E. De Vos, Angew. Chem., Int. Ed., 2012, 51, 4887–4890.
56. J. B. DeCoste, G. W. Peterson, H. Jasuja, T. G. Glover, Y.-g. Huang and K. S. Walton, J. Mater. Chem. A, 2013, 1, 5642–5650.
57. G. C. Shearer, S. Chavan, S. Bordiga, S. Svelle, U. Olsbye and K. P. Lillerud, Chem. Mater., 2016, 28, 3749–3761.
58. F. C. Firth, M. J. Cliffe, D. Vulpe, M. Aragones-Anglada, P. Z. Moghadam, D. Fairen-Jimenez, B. Slater and C. P. Grey, J. Mater. Chem. A, 2019, 7, 7459–7469.
59. J. Winarta, B. Shan, S. M. Mcintyre, L. Ye, C. Wang, J. Liu and B. Mu, Cryst. Growth Des., 2019, 20, 1347–1362.
60. H. Wu, Y. S. Chua, V. Krungleviciute, M. Tyagi, P. Chen, T. Yildirim and W. Zhou, J. Am. Chem. Soc., 2013, 135, 10525–10532.
61. O. V. Gutov, M. G. Hevia, E. C. Escudero-Adan and A. Shafir, Inorg. Chem., 2015, 54, 8396–8400.
62. P. Horcajada, S. Surblé, C. Serre, D.-Y. Hong, Y.-K. Seo, J.-S. Chang, J.-M. Grenèche, I. Margiolaki and G. Férey, Chem. Commun., 2007, 2820–2822.
63. L. Huang, H. Wang, J. Chen, Z. Wang, J. Sun, D. Zhao and Y. Yan, Microporous Mesoporous Mater., 2003, 58, 105–114.
64. H.-H. Mautschke, F. Drache, I. Senkovska, S. Kaskel and F. L. i. Xamena, Catal. Sci. Technol., 2018, 8, 3610–3616.
65. S. Marx, W. Kleist and A. Baiker, J. Catal., 2011, 281, 76–87.
66. L. H. Wee, T. Lescouet, J. Ethiraj, F. Bonino, R. Vidruk, E. Garrier, D. Packet, S. Bordiga, D. Farrusseng and M. Herskowitz, ChemCatChem, 2013, 5, 3562–3566.
67. H. Furukawa, F. Gandara, Y.-B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, J. Am. Chem. Soc., 2014, 136, 4369–4381.
68. J. Koo, I.-C. Hwang, X. Yu, S. Saha, Y. Kim and K. Kim, Chem. Sci., 2017, 8, 6799–6803.
69. P. Iacomi, F. Formalik, J. Marreiros, J. Shang, J. Rogacka, A. Mohmeyer, P. Behrens, R. Ameloot, B. Kuchta and P. L. Llewellyn, Chem. Mater., 2019, 31, 8413–8423.
70. F. Ke, C. Peng, T. Zhang, M. Zhang, C. Zhou, H. Cai, J. Zhu and X. Wan, Sci. Rep., 2018, 8, 1–11.
71. A. Datar, Y. G. Chung and L.-C. Lin, J. Phys. Chem. Lett., 2020, 11, 5412–5417.
72. J. Rouquerol, P. Llewellyn and F. Rouquerol, Stud. Surf. Sci. Catal., 2007, 160, 49–56.
73. J. Jagiello and J. P. Olivier, Carbon, 2013, 55, 70–80.
74. J. Jagiello, Langmuir, 1994, 10, 2778–2785.
75. T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141.
76. M. Pinheiro, R. L. Martin, C. H. Rycroft, A. Jones, E. Iglesia and M. Haranczyk, J. Mol. Graphics, 2013, 44, 208–219.
77. J. F. Kurisingal, Y. Rachuri, Y. Gu, Y. Choe and D.-W. Park, Chem. Eng. J., 2020, 386, 121700.
78. J. F. Kurisingal, Y. Rachuri, Y. Gu, R. K. Chitumalla, S. Vuppala, J. Jang, K. K. Bisht, E. Suresh and D.-W. Park, ACS Sustainable Chem. Eng., 2020, 8, 10822–10832.
79. X. Yan, R. Fu, F. Liu, Y. Pan, X. Ding and G. He, Ind. Eng. Chem. Res., 2018, 57, 3195–3203.
80. A. Raza, A. Sturluson, C. M. Simon and X. Fern, J. Phys. Chem. C, 2020, 124, 19070–19082.
81. N. Prasetyo and F. I. Pambudi, Int. J. Hydrogen Energy, 2021, 46, 4222–4228.
82. J. J. Potoff and J. I. Siepmann, AIChE J., 2001, 47, 1676–1682.
83. D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, Mol. Simul., 2016, 42, 81–101.
84. P. Sinha, A. Datar, C. Jeong, X. Deng, Y. G. Chung and L.-C. Lin, J. Phys. Chem. C, 2019, 123, 20195–20209.
85. C. R. Harris, K. J. Millman, S. J. Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. Kerkwijk, M. Brett, A. Haldane, J. F. Rio, M. Wiebe, P. Peterson, P. G. Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362.
86. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich; A. D. Daniels, O. Farkas, J. B. Foresman; J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision A.03, Gaussian Inc, Wallingford, CT, 2016.
87. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
88. Y. Rachuri, J. F. Kurisingal, R. K. Chitumalla, S. Vuppala, Y. Gu, J. Jang, Y. Choe, E. Suresh and D.-W. Park, Inorg. Chem., 2019, 58, 11389–11403.

---

Footnote

† Electronic supplementary information (ESI) available: NH₃ and CO₂-TPD curves, FE-SEM images, HR-TEM images, TGA data, BET analysis, 2D-NLDFT and zeo++ PSD results, recycle characterization, and DFT results. See DOI: 10.1039/d2ta00503d

---