Open Access Article
Open Access ArticleInfluence of Fe-clustering on the water oxidation performance of two-dimensional layered double hydroxides†
Alvaro
Seijas-Da Silva‡
 ,
Víctor
Oestreicher‡
,
Víctor
Oestreicher‡
 ,
Eugenio
Coronado
,
Eugenio
Coronado
 and
Gonzalo
Abellán
and
Gonzalo
Abellán
 *
*
Instituto de Ciencia Molecular (ICMol), Universitat de València, Catedrático José Beltrán 2, 46980, Paterna, Valencia, Spain. E-mail: gonzalo.abellan@uv.es
First published on 21st February 2022
Abstract
Among the two-dimensional (2D) materials family, layered double hydroxides (LDHs) represent a key member due to their unparalleled chemical versatility. In particular, Fe-based LDHs are distinguished candidates due to their high efficiency as oxygen evolution reaction (OER) electrocatalysts. Herein, we have selected MgFe-based LDH phases as model systems in order to decipher whether Fe-clustering exerts an effect on the OER performance. For that, we have optimized hydrothermal synthesis by using triethanolamine (TEA) as the chelating agent. The magnetic characterisation allows us to identify the Fe-clustering degree by following both magnetic susceptibility as well as magnetization values at 2 K. Thanks to this, we demonstrated that TEA induces an increment in Fe-clustering. Electrochemical OER measurements show that both samples behave identically by using glassy carbon electrodes. Interestingly, when the samples are tested in the most commonly employed electrode, nickel foam, striking differences arise. The sample exhibiting a lower Fe-clustering behaves as a better electrocatalyst with a reduction of the overpotential values of more than 50 mV to reach 100 mA cm−2, as a consequence of a favoured surface transformation of MgFe-LDHs phases into more reactive oxyhydroxide NiFe-based phases during the electrochemical tests. Hence, this work alerts about the importance of the electrocatalyst–electrode collector interactions which can induce misinterpretations in the OER performance.
Introduction
In recent years, concerns related to global energy demand and its pollution consequences have led to the search for environmentally friendly solutions in the fields of energy storage and conversion. In this context, and in line with the European Green Deal policy, water splitting technologies represent the main strategy towards the transformation of sustainable resources into chemical energy; thus, hydrogen stands up as the fuel of the future allowing a promising transition to a clean and circular economy.1 The water splitting process is a thermodynamically uphill reaction (ΔG = 286 kJ mol−1 at environmental conditions: room temperature and atmospheric pressure) which requires the employment of specific electrocatalysts to be carried out efficiently. In addition, the oxygen evolution reaction (OER) is reckoned as the limiting step of the energy process, suffering slow kinetics (>10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lower than the hydrogen evolution reaction), and therefore requiring high overpotentials, which trigger the main energy losses.2 For this reason, currently much of the efforts of the scientific community are focused on the design and development of earth-abundant electrocatalysts for the OER;3–5 in particular, considering that nowadays precious metal oxides such as ruthenium oxide (RuO2) or iridium oxide (IrO2) are utilized as state-of-the-art electrocatalysts for the OER under alkaline conditions.6,7
000 lower than the hydrogen evolution reaction), and therefore requiring high overpotentials, which trigger the main energy losses.2 For this reason, currently much of the efforts of the scientific community are focused on the design and development of earth-abundant electrocatalysts for the OER;3–5 in particular, considering that nowadays precious metal oxides such as ruthenium oxide (RuO2) or iridium oxide (IrO2) are utilized as state-of-the-art electrocatalysts for the OER under alkaline conditions.6,7
In this front, iron is one of the most attractive earth-abundant electrocatalytic elements for water splitting technologies. Its huge abundance in the Earth's crust, low toxicity, and high efficiency for O2 activation distinguish it from other transition metals. Interestingly, many reports focused on Fe-based materials (metal oxides, layered hydroxides or MOFs, among others) have demonstrated a synergistic effect between Fe centres and other transition metal cations.8–12 In fact, the synergy with the nearest neighbour (3d cations) sites through the formation of O-bridges, induces an increment in the electrical conductivity of Fe-based catalysts favouring their performance.13
Among the Fe-based materials, layered double hydroxides (LDHs) represent a key family of catalyst for OER. These layered structures are composed of divalent (MII) and trivalent (MIII) cations located in octahedral environments, where the two dimensional (2D) positively charged layers stack by the incorporation of the anion (An− inorganic, organic, macromolecules, etc.) and solvent molecules into the interlayer space.14–16 These highly tunable structures, defined by the formula MII1−xMIIIx(OH)2An/xn−·m(H2O), represent a perfect platform to design Fe-based materials with interesting properties for use in several fields such as anion exchange, water cleaning, magnetism, catalysis, energy storage, anticorrosion, drug delivery, among others.17–20
Currently, 2D NiFe-LDHs have attracted increasing attention due to their outstanding performance in OER in basic media.21–23 In this sense, different approximations have been carried out to understand and enhance their electrocatalytic behaviour: exfoliation,24,25 doping with other metal cations,26,27 defect engineering (cations and/or oxygen vacancies),28 formation of hybrid materials,29 or increment of the interlayer space,30 to name few. Moreover, in situ techniques such as X-ray absorption (XAS), Raman, and Mössbauer spectroscopy have demonstrated that Fe cations act as catalytic centres.31 However, despite all these considerable efforts, there is a lack of information related to the specific role of the atomic distribution of Fe centres along the LDH sheets towards the OER activity. Cation clustering has been an important matter of study in LDHs for many years including both Al- and Fe-based materials.32–34 Remarkably, as reported by Kawabata et al. for MgAlFe LDH samples, those exhibiting higher amounts of Fe–O–Fe moieties are catalytically more active in terms of the Baeyer–Villiger oxidation/reaction.35
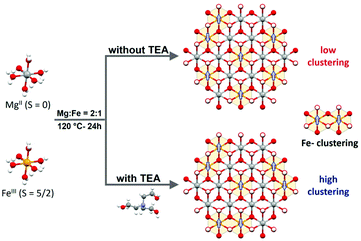
Therefore, to shed light on the influence of Fe clustering on OER performance, we have selected as a model system MgFe-based LDHs due to the non-electrocatalytic role of Mg as divalent cation. This will permit to evaluate exclusively the role of Fe centres; at the same time, the diamagnetic Mg cations will allow us to assess Fe distribution by using conventional magnetic characterization (i.e.: Fe-clustering versus Fe-isolated distribution). For that, we have optimized the hydrothermal synthesis of MgFe-based LDHs by employing TEA as a chelating agent (MgFe-TEA), previously introduced by us as an effective synthetic route for the synthesis of pure (spinel-free) hexagonal NiFe-based LDHs showing high crystallinity.36 Since the formation of Fe-TEA complexes prevents the precipitation of insoluble iron hydroxides,37 this approach could serve as a tool for controlling Fe-clustering. Indeed, the magnetic characterization supports our hypothesis. The sample obtained through the TEA approach depicts higher antiferromagnetic ordering and lower magnetization values (Ms) at 2 K, suggesting a higher proportion of antiferromagnetic (AF) Fe-pairs, i.e.: higher Fe-clustering. However, in terms of water splitting reaction, both MgFe-LDH samples exhibit the same OER performance when glassy carbon collector electrodes are used. Remarkably, the OER performance on nickel foam (the most widely used electrode collector) displays clear differences. The MgFe sample containing the lower Fe-clustering exhibits a better OER performance in comparison with the highly clustered one, which linearly increases with the current density: less than 50 mV of overpotential to reach 100 mA cm−2. These results suggest that the interaction between the electrocatalytic material and the electrode collector can drive changes in the nature of the pristine electrocatalyst modifying its inherent reactivity, i.e.: formation of highly reactive NiFe (oxo)hydroxides during the activation process and electrochemical tests in the case of Ni-foam electrode collectors. Hence, these results suggest that rational chemical improvements such as cationic doping, vacancy incorporation or defect engineering38–40 performed to boost the OER performance of LDHs should be measured employing inert electrode collectors in order to avoid misinterpretation.
Results and discussion
To address the role of Fe-clustering on OER performance, we decided to employ the MgFe = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 LDH phase as a model system. This choice is based on three main reasons: (i) the Mg
1 LDH phase as a model system. This choice is based on three main reasons: (i) the Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe = 2
Fe = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio represents the highest possible value for a LDH structure, (ii) Mg(II) is a non-electrocatalytic cation that allows us to explore the role of the electrocatalytic Fe-centres, exclusively; in addition, (iii) diamagnetic Mg(II) permits to track Fe-clustering by conventional magnetic measurements (Scheme 1).
1 ratio represents the highest possible value for a LDH structure, (ii) Mg(II) is a non-electrocatalytic cation that allows us to explore the role of the electrocatalytic Fe-centres, exclusively; in addition, (iii) diamagnetic Mg(II) permits to track Fe-clustering by conventional magnetic measurements (Scheme 1).
The MgFe-based LDHs were hydrothermally synthesized at 120 °C for 24 h by employing ammonia as the alkalinisation reagent. Due to the higher solubility of Mg-based LDHs, the initial pH needs to be adjusted to 10.5 to ensure the complete precipitation of both cations.41,42 Specifically, triethanolamine (TEA) is added to the solution as a chelating agent (atrane route), where Fe-TEA complex formation could be used to modulate the Fe-clustering. The formation of Fe-TEA complexes can be easily evidenced by the change in the colour of the solution (Fig. 1C – inset) and confirmed by UV-vis spectroscopy (see Fig. S1†).
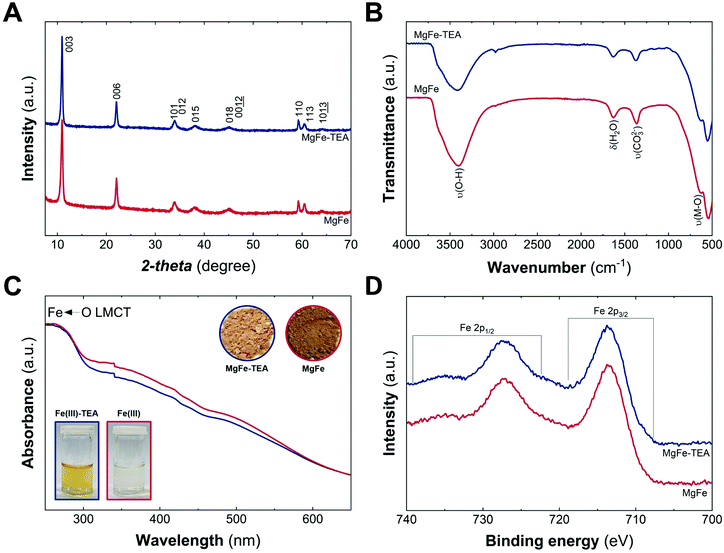
Fig. 1A depicts the PXRD patterns of MgFe-based LDHs samples, where crystalline materials obtained in both cases, with and without TEA, are denoted as MgFe-TEA and MgFe, respectively. The two main peaks at low 2-theta values, ca. 11° and 22°, ascribed to interlayer reflections, exhibit a basal space distance (dBS) value of around 8 Å. On the other hand, the signal centred around 2-theta = 59.2° is associated with the intralayer distance (d110). The calculated structural parameters and the crystallite size along both cell axes (L00l and L110) evidence similar values, suggesting no marked changes in the aging process as a function of TEA concentration (see Table S1†). Furthermore, attenuated total reflectance Fourier-transform infrared spectroscopy (ATR-FTIR) confirms the partial incorporation of carbonate as interlayer anion, according to the signal around 1365 cm−1. Signals at ca. 3400 and 1630 cm−1 are assigned to water molecules, while those ones below 750 cm−1 correspond to M–O vibrations, as shown in Fig. 1B. In addition, UV-vis diffuse reflectance spectroscopy (UV-vis) gives an initial clue of the possibility of having different Fe-arrangements, considering that the MgFe solid sample is slightly darker than the MgFe-TEA one (Fig. 1C – inset). The absorption band below 300 nm could be ascribed to the ligand-to-metal charge transfer (from the hydroxyl ligands to Fe(III) cations), while the shoulders centred in the range 300–400 nm and around 500 nm might be associated with oligomeric and aggregated large-sized iron clusters, respectively.43–45 Sample MgFe depicts slightly larger shoulders in both regions, that could be interpreted as the first evidence of the role of TEA on the Fe-clustering modulation. Moreover, X-ray photoelectron (XPS) spectroscopy was performed to evaluate the chemical composition and oxidation state of iron. Fig. 1D depicts the XPS spectra where the main peaks centred at 713.7 (2p3/2) and 727.3 eV (2p1/2) confirm the presence of Fe(III), as expected.46 In addition, the XPS spectra of magnesium and chloride display slight differences which could also be related to Fe-clustering (see Fig. S2 and S3†). In both samples, the presence of chloride was observed in a Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cl ratio of 0.7. Finally, and in combination with EDS and ICP-MS measurements, Mg
Cl ratio of 0.7. Finally, and in combination with EDS and ICP-MS measurements, Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe and Cl
Fe and Cl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe have been estimated to be 2.0 ± 0.1 and 0.6 ± 0.1 for both samples (see Table S1†).
Fe have been estimated to be 2.0 ± 0.1 and 0.6 ± 0.1 for both samples (see Table S1†).
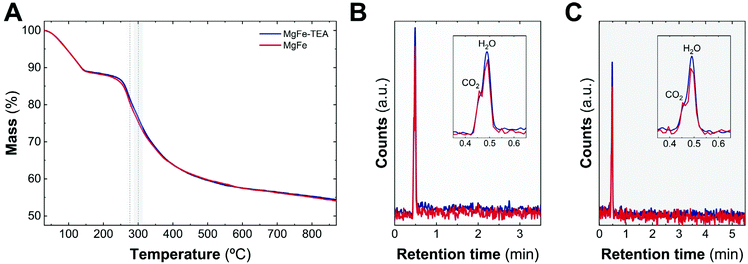
As a complement experiment to discard the presence of TEA molecules on an MgFe-TEA sample, which may affect either the magnetic properties and could alter the electrochemistry characterization,47 we have performed thermogravimetric analysis coupled with gas chromatography and mass spectrometry (TG–GC–MS) under an inert atmosphere of helium. This technique arises as a powerful way to analyse the presence of ligands, impurities, and track the thermal evolution of LDH samples.48,49Fig. 2A shows the thermogravimetric analysis of both samples. The indistinguishable decomposition profiles suggest the lack of coordinated TEA molecules in MgFe-TEA samples. In addition, the elugrams for the injections at 270 and 300 °C (figures B and C, respectively) confirm the presence of the CO2 and H2O molecules during the LDH phase decomposition, exclusively. Therefore, we can satisfactorily conclude the obtaining of free-TEA MgFe-LDHs samples.
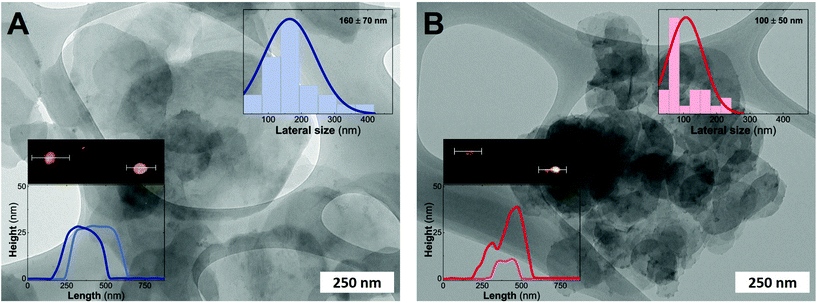
Fig. 3 depicts the electron microscopy characterization performed with TEM. The presence of platelets displaying rounded edges with a diameter of around 100–160 nm is observed for the entire MgFe-LDH family, without any evidence of spinel impurities. In addition, AFM measurements confirm the anisotropy of the samples with thicknesses lower than 25 nm for both samples (aspect ratios 5–10) highlighting the inherent 2D growth of layered hydroxides.50
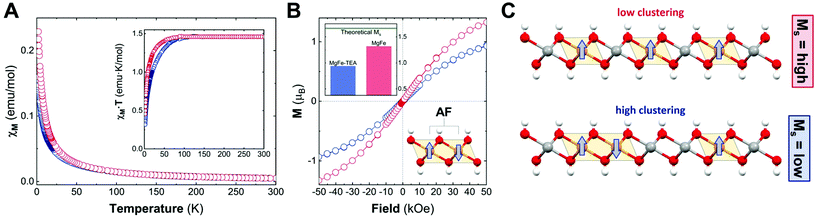
After confirming the synthesis of crystalline 2D platelets of MgFe LDHs, we decided to evaluate the role played by TEA on Fe-clustering by performing conventional magnetic characterization. Specifically, the magnetic behaviour of the LDH phases is controlled by two main contributions: on the one hand, the intralayer (in-plane) magnetic superexchange between magnetic centres through the OH bridges, representing the main factor; on the other hand, the less intense interlayer (out-of-plane) dipolar interactions.15 Considering the diamagnetic behaviour of Mg cations (S = 0), the magnetic response of the MgFe-based LDH samples is exclusively governed by Fe(III) cations (S = 5/2) and their distribution; thus, in the case of neighbouring iron cations, an antiferromagnetic (AF) coupling is expected, i.e.: Fe–OH–Fe moieties. Hence, conventional magnetic characterization allows us to evaluate this process for the whole sample.33,51,52
To begin with, we analysed the temperature-dependent magnetic susceptibility measurements (χMvs. T plot) in order to exclude the presence of electroactive iron oxide impurities.53Fig. 4A depicts the temperature-independent component in χMvs. T at high temperature for both cases, thus confirming the purity of the MgFe-based LDH samples. It is worth mentioning that the Fe-oxide spinel phases are hard to identify with conventional techniques (PXRD, TEM, etc.). Therefore, magnetic characterization emerges as a very useful technique for Fe-based LDHs.53 In addition, the MgFe-TEA sample depicts lower values in the χMvs. T plot, in comparison with the MgFe one, suggesting more AF behaviour. In the case of the χM·T vs. T plot (see Fig. 4A-inset), the signal for the MgFe-TEA sample decays at higher temperatures (ca. 80 vs. 50 K) suggesting stronger AF couplings, which can be understood as an increment in the Fe–OH–Fe AF interactions, i.e.: a higher Fe-clustering. In accordance with this, applying the Curie–Weiss law above 150 K (see Fig. S4†), the Weiss constant (Θ) presents a more negative value for the MgFe-TEA sample, which reflects higher AF contribution (see Table S2†).
To finally confirm the differences in the degree of Fe-clustering in MgFe-based samples, isothermal magnetization at 2 K was recorded as a function of the magnetic field, Ms (Fig. 4B). For MgFe-based LDH without Fe-clustering, this value can be estimated at ca. 1.67μB. Thus, any decrease from this value should be ascribed to Fe-clustering, as the AF Fe–OH–Fe pairs do not contribute to the magnetic moment at this temperature (2 K).54 The experimental Ms values for the MgFe and MgFe-TEA samples are 1.32 and 0.94μB, respectively, confirming the presence of Fe-clustering. By comparing with the theoretical Ms value, we can estimate a deviation of 21% and 44% for MgFe and MgFe-TEA samples, respectively. In brief, the tendency of magnetic parameters evidence a higher degree of Fe-clustering in the MgFe-TEA sample compared to the MgFe one (Fig. 4C).
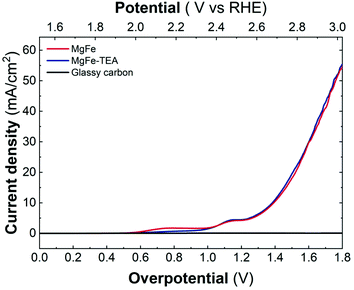
Upon confirming the role of TEA in Fe-clustering, we decided to evaluate whether different degrees of clustering have a role in the electrocatalytic behaviour, specifically on the oxygen evolution reaction (OER) performance in basic media by employing glassy carbon collectors (GC). In this case, the electrocatalytic activity can be directly studied from linear sweep voltammetry (LSV) recorded at 5 mV s−1 up to 3.2 V vs. RHE. The electrocatalytic behaviour of both the MgFe-LDH samples in comparison with bare GC electrodes is depicted in Fig. 5. As it is clearly observed, Fe-based LDHs display a significant catalytic behaviour, highlighting the role of Fe as the catalytic center.55–58 However, judging from the LSVs, the OER performance is not affected by the degree of clustering in the MgFe LDH samples.
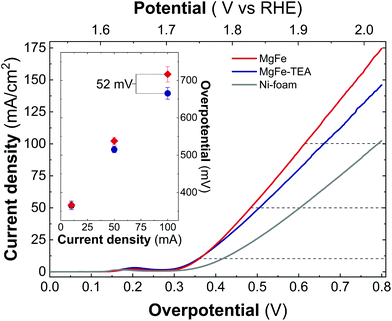
In addition, both samples were also tested on Ni-foam collectors—the most employed OER electrode—by measuring LSV at 5 mV s−1 up to 2.0 V vs. RHE (Fig. 6). As expected, the electrocatalytic behaviour of both MgFe LDHs samples is much better than the ones recorded on GC electrodes showing lower OP values, mainly due to the inherent conductivity of Ni-foam. However, striking differences between both samples arise: In contrast to GC electrodes, the MgFe sample exhibiting the lower Fe-clustering degree considerably outperformed the MgFe-TEA one. To quantify these differences, the overpotential at different current densities (Fig. 6 – inset) and the differences in the OP for both samples (OPMgFe–OPMgFe-TEA) as a function of the current density were calculated (Fig. S5†). Remarkably, a difference of ca. 52 mV at 100 mA cm−2 can be measured. It is worth to mention that the OP values have been extracted from at least three LSV measurements. Furthermore, in order to discard the possibility of assigning these changes to different electrolyte accessibilities as a consequence of structural modifications during the surface reconstruction of the catalysts, we measured the electrochemical surface area (ECSA) (see Fig. S6† for further details). Overall, the observed tendencies indicate that the MgFe sample behaves as a better electrocatalyst when Ni-foam electrodes are employed.
Taking into account the identical OER performance of GC electrodes (Fig. 5), these results alert about some interaction between the electrocatalytic LDH materials and the Ni-foam electrode surface. To shed light on this, cyclic-voltammetry (CV) at 5 mV s−1 for bare Ni-foam, MgFe@Ni-foam, MgFe-TEA@Ni-foam after an activation process of 20 cycles was conducted (see Fig. S7†). In all of them, it is possible to observe the redox couple Ni(II)/Ni(III) with a peak in the range of 1.2–1.5 V vs. RHE (Fig. 7). It is worth noting that this redox signal is attributed to the presence of the surface oxidation of the collector, Ni(II)-based (oxo)hydroxides, as reported for commercially available Ni-foams.59 However, the CV of the electrodes containing the MgFe-LDH material shows a clear shift to a higher oxidation potential (>25 mV), which is attributed to the incorporation of Fe cations on the Ni-foam.60 By analysing the difference between the maximum oxidation and reduction peaks, we can confirm that the MgFe sample behaves as the most reversible and conductive electrode. Therefore, this MgFe-LDH material exhibiting the lower Fe-clustering might work as a better OER catalyst. Indeed, these changes in the OER performance as a function of the electrode collector can be understood as the transformation of MgFe-LDHs into NiFe-oxyhydroxide phases due to the higher stability of Ni-based LDHs in comparison with the Mg-based ones, as demonstrated by solubility constants.41,61,62 In addition, ex situ XPS measurements were recorded over the Ni-foam electrodes after OER activity (Fig. 8). While the Fe 2p3/2 peaks centred at 713.7 eV shift by 1.44 eV to lower binding energy values for both samples, the Fe 2p1/2 peaks positioned at 727.3 eV are shifted 2.08 and 2.65 eV for the MgFe-TEA and MgFe samples, respectively. In the case of the MgFe sample containing the lower Fe-clustering, this pronounced shift is associated with highly reactive Fe-sites.63
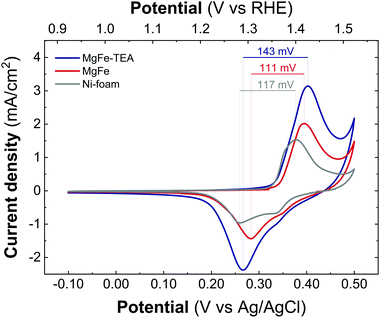 | ||
| Fig. 7 Cyclic voltammetry recorded at 5 mV s−1 between −0.1 V and 0.4 V versus Ag/AgCl for the samples MgFe-TEA (blue) and MgFe (red) and Ni-foam (gray) after 20 cycles of the activation process. | ||
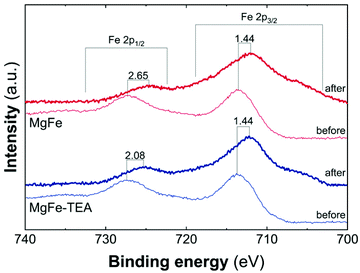 | ||
| Fig. 8 High resolution Fe 2p XPS spectra in the range of 740–700 eV for samples MgFe-TEA (blue) and MgFe (red) deposited on Ni-foam before and after the OER catalyst. | ||
In summary, while the MgFe LDH samples containing different Fe-clustering behave identically in terms of OER performance on glassy carbon electrode collectors, the samples with lower Fe-clustering exhibit better OP values on Ni-foam collectors, with the OPMgFe–OPMgFe-TEA differences exceeding 50 mV at 100 mA cm−2. These marked changes are attributed to the surface reconstruction effects along with the electrochemical tests, which are more pronounced for the most ordered catalysts (lower cation clustering) leading to highly reactive Fe-sites.
Experimental
Chemicals
Magnesium chloride hexahydrate (MgCl2·6H2O), iron chloride hexahydrate (FeCl3·6H2O), ammonium hydroxide solution, triethanolamine (TEA, C6H15NO3), acetylene black, and polytetrafluoroethylene (PTFE) were purchased from Sigma-Aldrich. Potassium hydroxide (KOH, 99.99%) and ethanol absolute (EtOH) were purchased from Panreac. All chemicals were used as received. Milli-Q water was obtained from Millipore Milli-Q equipment.Synthesis of MgFe-LDHs
MgFe-LDH was synthesized with an Mg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe ratio of 2
Fe ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 using a hydrothermal method. In a typical procedure, the chloride salts of the metals were dissolved in 90 mL of a 1
1 using a hydrothermal method. In a typical procedure, the chloride salts of the metals were dissolved in 90 mL of a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) ethanol/water Milli-Q mixture without or with TEA (in a TEA
1 (v/v) ethanol/water Milli-Q mixture without or with TEA (in a TEA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe ratio of 23 according to the previous report)30,64 reaching in both cases a total concentration of metal cations of 20 mM. Afterward, under an argon atmosphere, ammonium hydroxide solution was added until the pH was set at 10.5. The resulting solution was mixed thoroughly and transferred to a Teflon-lined stainless steel autoclave. The autoclave was placed in a preheated oven at 120 °C for 24 h. Finally, it was cooled to room temperature, and the final powder was filtered and washed with H2O and EtOH several times and dried for 24 h under vacuum. The samples were labelled as MgFe-TEA (synthesis with TEA) and MgFe (synthesis without TEA).
Fe ratio of 23 according to the previous report)30,64 reaching in both cases a total concentration of metal cations of 20 mM. Afterward, under an argon atmosphere, ammonium hydroxide solution was added until the pH was set at 10.5. The resulting solution was mixed thoroughly and transferred to a Teflon-lined stainless steel autoclave. The autoclave was placed in a preheated oven at 120 °C for 24 h. Finally, it was cooled to room temperature, and the final powder was filtered and washed with H2O and EtOH several times and dried for 24 h under vacuum. The samples were labelled as MgFe-TEA (synthesis with TEA) and MgFe (synthesis without TEA).
Chemical and structural characterization
Powder X-ray powder diffraction (PXRD) patterns were obtained by employing a PANalytical Empyrean X-ray platform with a capillary platform and copper radiation (Cu Kα = 1.541 78 Å). Measurements were carried out in triplicate in the 2-theta range 2–70° by employing a step size of 0.02° per step with an integration time of 1 s. The attenuated total reflectance-Fourier transform infrared spectroscopy (ATR-FTIR) spectra were recorded using a Bruker alpha II FTIR spectrometer in the 4000–400 cm−1 range. The UV-vis absorption spectra of the solid samples were recorded in the reflectance mode by using a Jasco V-670 spectrometer. X-ray photoelectron spectroscopy (XPS) spectra were recorded using a Thermo Scientific™ K-Alpha X-ray Photoelectron Spectrometer. Al Kα X-ray radiation was employed as the X-ray source. For all the elements, more than 100 spectra were recorded by employing a step of 0.1 eV with a focused spot higher than 400 μm. XPS data were analysed with the Thermo Avantage v5.9912 software.Magnetic data were collected over the bulk material using a Quantum Design superconducting quantum interference device (SQUID) MPMS-XL-5. The magnetic susceptibility of the samples was corrected considering the diamagnetic contributions of their atomic constituents as deduced from Pascal's constant tables and the sample holder. In addition, a small TIP term (χM = C/(T − θ) + χTIP) was applied as previously reported for the hydroxide samples.65 The DC data were recorded under an externally applied field of 1000 Oe in the 2–300 K temperature range. All magnetic measurements were carried out in eicosane, as this diamagnetic material allows for better immobilization of these small anisotropic crystals, precluding any artefact in the magnetic measurements.
Electrode preparation
For electrochemical measurements using glassy carbon, an initial suspension was prepared by adding 25 μL of 5% Nafion solution to 5 mg of LDH powder and 2.5 mg of graphitized carbon and then dispersed in 1.25 mL of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v) EtOH/H2O and sonicated for 20 min. Then, 5 μL of this dispersion was dropcasted onto a previously polished (sequentially with 1.0, 0.3, and 0.05 μm alumina powder) 3 mm diameter RDE and dried at room temperature for 30 min.
1 (v/v) EtOH/H2O and sonicated for 20 min. Then, 5 μL of this dispersion was dropcasted onto a previously polished (sequentially with 1.0, 0.3, and 0.05 μm alumina powder) 3 mm diameter RDE and dried at room temperature for 30 min.
For the electrochemical measurements using Ni-foam, firstly a mixture of the LDHs, acetylene black and PTFE in ethanol in a mass ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 was prepared and deposited on a nickel foam electrode. The as-prepared electrode was let dry for 2 h at 80 °C. Each working electrode contained around 0.4 mg of the LDH sample and a square-like shape with edges of 1 cm. The geometrical area of electrodes was determined as 1 cm2 × 1 cm2 and thus electrode mass loading achieved was 0.4 mg cm−2.
10 was prepared and deposited on a nickel foam electrode. The as-prepared electrode was let dry for 2 h at 80 °C. Each working electrode contained around 0.4 mg of the LDH sample and a square-like shape with edges of 1 cm. The geometrical area of electrodes was determined as 1 cm2 × 1 cm2 and thus electrode mass loading achieved was 0.4 mg cm−2.
Electrochemical characterization
A typical three-electrode cell equipped with a steel sheet as the counter electrode and a Metrohm Ag/AgCl (3 M KCl) as the reference electrode was used for the electrochemical characterization of the nanocomposite material trapped by the working electrodes, while an aqueous solution of 1 M KOH (99.99%) was employed as the electrolyte. The glassy carbon measurements were performed with an Autolab rotating disc electrode (RDE) and analysed with an Autolab PGSTAT 128N potentiostat/galvanostat, while Ni-foam characterization was performed using a Gamry Interface 1000E potentiostat/galvanostat controlled by Gamry's Global Software. All the electrochemical experiments were performed at room temperature. Prior to OER experiments, an activation process of the prepared electrode (consisting of 20 voltammetric cycles between −0.1 V and 0.5 V versus Ag/AgCl at 100 mV s−1) was performed. Cyclic voltammetry curves (CVs) were obtained in the range of −0.1 to 0.5 V versus Ag/AgCl at 5 mV s−1 to evaluate the redox behaviour of the materials. Linear sweep voltammetry (LSV) measurements were performed at 5 mV s−1 in a previously N2-purged 1 M KOH aqueous solution. All electrochemical experiments were done without iR correction, to make a fair comparison of the intrinsic electrocatalytic behaviour of each sample instead of searching for the best performance of the electrode.Electrochemical surface area (ECSA) was acquired by measuring the current associated with the double-layer capacitance from the scan rate dependence of CVs. ECSA was measured on the working electrode after LSV measurements. The potential range used for the CVs was −0.1–0.1 V versus Ag/AgCl (3 M KCl). The scan rates were 10, 20, 50, and 100 mV s−1. The double-layer capacitance was calculated by plotting the (ja − jc)/2 (anodic versus cathodic currents) at 0 V versus Ag/AgCl (3 M KCl) against the scan rate. ECSA measurements were obtained using an Autolab PGSTAT 128N potentiostat/galvanostat.
Conclusions
In this work, we have reported the modulation of the degree of Fe-clustering in 2D MgFe-based LDHs by employing TEA during hydrothermal synthesis. The diamagnetic behaviour of Mg(II) as a divalent cation allows having a platform to follow Fe-clustering by magnetic characterization. At the same time, the non-catalytic activity of Mg(II) for OER allows us to study the possible influence of Fe-clustering in OER performance. In this line, we observed that the Fe-TEA complex formation drives a higher degree of Fe-clustering in MgFe-LDHs, as demonstrated by the magnetic susceptibility and spontaneous magnetization measurements. Concerning OER performance, both samples are indistinguishable when measured using inert glassy carbon electrodes. Surprisingly, upon using nickel foam collectors, the MgFe sample containing the lower Fe-clustering degree exhibits a reduction in the overpotential values of more than 50 mV to reach 100 mA cm−2. These results, can be understood as the surface transformation of the MgFe-LDH phases into more reactive oxyhydroxide NiFe-based phases during the electrochemical tests. This work highlights the importance of the hidden electrocatalyst–electrode collector interactions during OER performance. An aspect that should be analyzed with care as it can lead to erroneous interpretations in the behavior of new electrocatalysts. In this sense, the use of inert electrode collectors in combination with nickel foams is recommended in order to reliably design new electrocatalytic materials based on LDHs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Research Council (ERC Starting Grant No. 2D-PnictoChem 804110 to G. A. and ERC Advanced Grant Mol-2D 788222 to E. C.), the Spanish MICINN (PID2019-111742GA-I00 to G. A., Unit of Excellence “Maria de Maeztu” CEX2019-000919-M, PDC2021-121106-I00 and project PID2020-117152RB-I00 co-financed by FEDER) and the Generalitat Valenciana (CIDEGENT/2018/001 to G. A., Prometeo/2021/022, and iDiFEDER/2018/061 co-financed by FEDER). A. S.-D thanks the Universidad de Valencia, for an ‘Atracción del talento’ predoctoral grant. The authors thank Ana Alemany-Domenech and Christian Olivares-Martínez for their assistance with the experimental work, Dr G. Agustí and Dr J. M. Martínez for the magnetic measurements and Dr M. D. Jordán-Martín for her kind assistance with the XPS measurements. V. O. is an ALN fellow.Notes and references
- J. A. Turner, Science, 2004, 305, 972–974 CrossRef CAS PubMed.
- I. Roger, M. A. Shipman and M. D. Symes, Nat. Rev. Chem., 2017, 1, 003 CrossRef CAS.
- H. N. Nong, L. Gan, E. Willinger, D. Teschner and P. Strasser, Chem. Sci., 2014, 5, 2955–2963 RSC.
- Z.-P. Wu, X. F. Lu, S.-Q. Zang and X. W. Lou, Adv. Funct. Mater., 2020, 30, 1910274 CrossRef CAS.
- F. Lyu, Q. Wang, S. M. Choi and Y. Yin, Small, 2019, 15, 1804201 CrossRef PubMed.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed.
- Y. Lee, J. Suntivich, K. J. May, E. E. Perry and Y. Shao-Horn, J. Phys. Chem. Lett., 2012, 3, 399–404 CrossRef CAS PubMed.
- C. Feng, M. B. Faheem, J. Fu, Y. Xiao, C. Li and Y. Li, ACS Catal., 2020, 10, 4019–4047 CrossRef CAS.
- H. Bandal, K. K. Reddy, A. Chaugule and H. Kim, J. Power Sources, 2018, 395, 106–127 CrossRef CAS.
- F. Song, M. M. Busch, B. Lassalle-Kaiser, C.-S. Hsu, E. Petkucheva, M. Bensimon, H. M. Chen, C. Corminboeuf and X. Hu, ACS Cent. Sci., 2019, 5, 558–568 CrossRef CAS PubMed.
- S. Zou, M. S. Burke, M. G. Kast, J. Fan, N. Danilovic and S. W. Boettcher, Chem. Mater., 2015, 27, 8011–8020 CrossRef CAS.
- M. Gong and H. Dai, Nano Res., 2015, 8, 23–39 CrossRef CAS.
- F. Dionigi, Z. Zeng, I. Sinev, T. Merzdorf, S. Deshpande, M. B. Lopez, S. Kunze, I. Zegkinoglou, H. Sarodnik, D. Fan, A. Bergmann, J. Drnec, J. F. de Araujo, M. Gliech, D. Teschner, J. Zhu, W.-X. Li, J. Greeley, B. R. Cuenya and P. Strasser, Nat. Commun., 2020, 11, 1–10 Search PubMed.
- Layered double hydroxides, ed. X. Duan and D. G. Evans, Springer, Berlin, New York, 2005 Search PubMed.
- G. Abellán, C. Martí-Gastaldo, A. Ribera and E. Coronado, Acc. Chem. Res., 2015, 48, 1601–1611 CrossRef PubMed.
- G. Abellán, J. A. Carrasco and E. Coronado, Layered double hydroxide nanocomposites based on carbon nanoforms, in Layered Double Hydroxide Polymer Nanocomposites, ed. S. Thomas and S. Daniel, Woodhead Publishing, Elsevier, Kidlington, 2020, pp. 411–460 Search PubMed.
- A. Gomes, D. Cocke, D. Tran and A. Baksi, in Energy Technology 2015: Carbon Dioxide Management and Other Technologies, ed. A. Jha, C. Wang, N. R. Neelameggham, D. P. Guillen, L. Li, C. K. Belt, R. Kirchain, J. S. Spangenberger, F. Johnson, A. J. Gomes, A. Pandey and P. Hosemann, Springer International Publishing, Cham, 2016, pp. 309–316 Search PubMed.
- F. Li and X. Duan, Aplications of layered double hydroxides, in Layered Double Hydroxides, ed. X. Duan and D. G. Evans, Springer, Berlin, New York, 2005 Search PubMed.
- Q. Wang and D. O'Hare, Chem. Rev., 2012, 112, 4124–4155 CrossRef CAS PubMed.
- A. Seijas-Da Silva, R. Sanchis-Gual, J. A. Carrasco, V. Oestreicher, G. Abellán and E. Coronado, Batteries Supercaps, 2020, 3, 499–509 CrossRef CAS.
- F. Dionigi and P. Strasser, Adv. Energy Mater., 2016, 6, 1600621 CrossRef.
- Y. Wang, D. Yan, S. El Hankari, Y. Zou and S. Wang, Adv. Sci., 2018, 5, 1800064 CrossRef PubMed.
- H. Yi, S. Liu, C. Lai, G. Zeng, M. Li, X. Liu, B. Li, X. Huo, L. Qin, L. Li, M. Zhang, Y. Fu, Z. An and L. Chen, Adv. Energy Mater., 2021, 11, 2002863 CrossRef CAS.
- F. Song and X. Hu, Nat. Commun., 2014, 5, 4477 CrossRef CAS PubMed.
- J. A. Carrasco, A. Harvey, D. Hanlon, V. Lloret, D. McAteer, R. Sanchis-Gual, A. Hirsch, F. Hauke, G. Abellán, J. N. Coleman and E. Coronado, Chem. Commun., 2019, 55, 3315–3318 RSC.
- J. M. Gonçalves, P. R. Martins, L. Angnes and K. Araki, New J. Chem., 2020, 44, 9981–9997 RSC.
- P. Li, X. Duan, Y. Kuang, Y. Li, G. Zhang, W. Liu and X. Sun, Adv. Energy Mater., 2018, 8, 1703341 CrossRef.
- X. Zhang, Y. Zhao, Y. Zhao, R. Shi, G. I. N. Waterhouse and T. Zhang, Adv. Energy Mater., 2019, 9, 1900881 CrossRef.
- J. A. Carrasco, A. S. Da Silva, V. Oestreicher, J. Romero, B. G. Márkus, F. Simon, B. J. C. Vieira, J. C. Waerenborgh, G. Abellán and E. Coronado, Chem. – Eur. J., 2020, 26, 6504–6517 CrossRef CAS PubMed.
- J. A. Carrasco, R. Sanchis-Gual, A. Seijas-Da Silva, G. Abellán and E. Coronado, Chem. Mater., 2019, 31, 6798–6807 CrossRef CAS.
- D. Zhou, P. Li, X. Lin, A. McKinley, Y. Kuang, W. Liu, W.-F. Lin, X. Sun and X. Duan, Chem. Soc. Rev., 2021, 50, 8790–8817 RSC.
- P. J. Sideris, F. Blanc, Z. Gan and C. P. Grey, Chem. Mater., 2012, 24, 2449–2461 CrossRef CAS.
- G. Abellán, E. Coronado, C. Martí-Gastaldo, J. Waerenborgh and A. Ribera, Inorg. Chem., 2013, 52, 10147–10157 CrossRef PubMed.
- S. S. C. Pushparaj, C. Forano, V. Prevot, A. S. Lipton, G. J. Rees, J. V. Hanna and U. G. Nielsen, J. Phys. Chem. C, 2015, 119, 27695–27707 CrossRef CAS.
- T. Kawabata, N. Fujisaki, T. Shishido, K. Nomura, T. Sano and K. Takehira, J. Mol. Catal. A: Chem., 2006, 253, 279–289 CrossRef CAS.
- G. Abellán, E. Coronado, C. Martí-Gastaldo, E. Pinilla-Cienfuegos and A. Ribera, J. Mater. Chem., 2010, 20, 7451 RSC.
- S. Jaśkaniec, C. Hobbs, A. Seral-Ascaso, J. Coelho, M. P. Browne, D. Tyndall, T. Sasaki and V. Nicolosi, Sci. Rep., 2018, 8, 1–8 Search PubMed.
- R. L. Doyle, I. J. Godwin, M. P. Brandon and M. E. G. Lyons, Phys. Chem. Chem. Phys., 2013, 15, 13737–13783 RSC.
- Y. Gorlin, C.-J. Chung, J. D. Benck, D. Nordlund, L. Seitz, T.-C. Weng, D. Sokaras, B. M. Clemens and T. F. Jaramillo, J. Am. Chem. Soc., 2014, 136, 4920–4926 CrossRef CAS PubMed.
- M. Görlin, P. Chernev, J. Ferreira de Araújo, T. Reier, S. Dresp, B. Paul, R. Krähnert, H. Dau and P. Strasser, J. Am. Chem. Soc., 2016, 138, 5603–5614 CrossRef PubMed.
- V. Oestreicher and M. Jobbágy, Chem. – Eur. J., 2019, 25, 12611–12619 CrossRef CAS PubMed.
- V. Oestreicher, I. Fábregas and M. Jobbágy, J. Phys. Chem. C, 2014, 115, 30274–30281 CrossRef.
- G. Centi and F. Vazzana, Catal. Today, 1999, 53, 683–693 CrossRef CAS.
- M. Schwidder, M. Kumar, K. Klementiev, M. Pohl, A. Bruckner and W. Grunert, J. Catal., 2005, 231, 314–330 CrossRef CAS.
- A. C. Heredia, M. I. Oliva, U. Agú, C. I. Zandalazini, S. G. Marchetti, E. R. Herrero and M. E. Crivello, J. Magn. Magn. Mater., 2013, 342, 38–46 CrossRef CAS.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson, R. St. and C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- Y. H. Wen, H. M. Zhang, P. Qian, H. T. Zhou, P. Zhao, B. L. Yi and Y. S. Yang, Electrochim. Acta, 2006, 51, 3769–3775 CrossRef CAS.
- V. Oestreicher, D. Hunt, R. Torres-Cavanillas, G. Abellán, D. A. Scherlis and M. Jobbágy, Inorg. Chem., 2019, 58, 9414–9424 CrossRef CAS PubMed.
- V. Oestreicher, G. Abellán and E. Coronado, Phys. Status Solidi RRL, 2020, 14, 2000380 CrossRef CAS.
- V. Oestreicher, C. Dolle, D. Hunt, M. Fickert and G. Abellán, Nano Mater. Sci., 2020 DOI:10.1016/j.nanoms.2020.12.004.
- J. A. Carrasco, G. Abellán and E. Coronado, J. Mater. Chem. C, 2018, 6, 1187–1198 RSC.
- G. Abellán, E. Coronado, C. J. Gómez-García, C. Martí-Gastaldo and A. Ribera, Polyhedron, 2012, 52, 216–221217 CrossRef.
- G. Abellán, J. A. Carrasco and E. Coronado, Inorg. Chem., 2013, 52, 7828–7830 CrossRef PubMed.
- Y. Du and D. O'Hare, J. Phys. Chem. Solids, 2008, 69, 1040–1043 CrossRef CAS.
- B. Wu, Z. Yang, X. Dai, X. Yin, Y. Gan, F. Nie, Z. Ren, Y. Cao, Z. Li and X. Zhang, Dalton Trans., 2021, 50, 12547–12554 RSC.
- Y. Qiu, Q. Jia, S. Yan, B. Liu, J. Liu and X. Ji, ChemSusChem, 2020, 13, 4911–4915 CrossRef CAS PubMed.
- W. Huo, L. Li, Y. Zhang, J. Li, Q. Xu, B. Zhang, L. Zhang and X. Li, Front. Mater., 2019, 6, 154 CrossRef.
- B.-J. Kim, E. Fabbri, D. F. Abbott, X. Cheng, A. H. Clark, M. Nachtegaal, M. Borlaf, I. E. Castelli, T. Graule and T. J. Schmidt, J. Am. Chem. Soc., 2019, 541, 5231–5240 CrossRef PubMed.
- M. Grdeń, M. Alsabet and G. Jerkiewicz, ACS Appl. Mater. Interfaces, 2012, 4, 3012–3021 CrossRef PubMed.
- L. Trotochaud, S. L. Young, J. K. Ranney and S. W. Boettcher, J. Am. Chem. Soc., 2014, 136, 6744–6753 CrossRef CAS PubMed.
- J. J. Bravo-Suárez, E. A. Páez-Mozo and S. T. Oyama, Quím. Nova, 2004, 27, 601–614 Search PubMed.
- V. Oestreicher, I. Fábregas and M. Jobbágy, J. Phys. Chem. C, 2014, 118, 30274–30281 CrossRef CAS.
- Z. Wang, P. Fang, P. Kumar, W. Wang, B. Liu and J. Li, Nanomaterials, 2019, 9, 807 CrossRef CAS PubMed.
- L. Dang, H. Liang, J. Zhuo, B. K. Lamb, H. Sheng, Y. Yang and S. Jin, Chem. Mater., 2018, 30, 4321–4330 CrossRef CAS.
- C. J. Wang, Y. A. Wu, R. M. J. Jacobs, J. H. Warner, G. R. Williams and D. O'Hare, Chem. Mater., 2011, 23, 171–180 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1dt03737d |
| ‡ Both authors contribute equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |