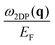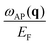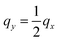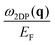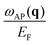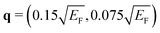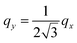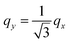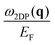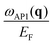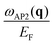Impact of the energy dispersion anisotropy on the plasmonic structure in a two-dimensional electron system
Unai
Muniain
*a and
Vyacheslav M.
Silkin
 abc
abc
aDonostia International Physics Center (DIPC), P. de Manuel Lardizabal 4, 20018 San Sebastián/Donostia, Basque Country, Spain. E-mail: waxslavas@ehu.es; Fax: +34 943 015 600; Tel: +34 943 018 284
bDepartamento de Polímeros y Materiales Avanzados: Física, Química y Tecnología, Facultad de Ciencias Químicas, Universidad del País Vasco UPV/EHU, Apartado 1072, 20080 San Sebastián/Donostia, Basque Country, Spain
cIKERBASQUE, Basque Foundation for Science, 48009 Bilbao, Basque Country, Spain
First published on 5th July 2022
Abstract
The effect of the band structure anisotropy (triangular, square, and hexagonal wrapping) on the electronic collective excitations (plasmons) in a two-dimensional electron gas (2DEG) is studied in the framework of the random-phase approximation. We show that the dynamical dielectric response in these systems strongly depends on the direction of the in-plane momentum transfer q. The effect is so pronounced that it results in a different number of electronic collective excitations in some q regions, both with 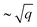 - and ∼q-like energy dispersions. This finding is in striking contrast to the conventional 2DEG case with isotropic energy band dispersion where only a single plasmon with
- and ∼q-like energy dispersions. This finding is in striking contrast to the conventional 2DEG case with isotropic energy band dispersion where only a single plasmon with 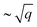 dispersion can exist. Our prediction of acoustic modes (with the ∼q dispersion) in a one-energy-band electron system expands the previous knowledge that such kind of plasmon can be realized only in two-component systems.
dispersion can exist. Our prediction of acoustic modes (with the ∼q dispersion) in a one-energy-band electron system expands the previous knowledge that such kind of plasmon can be realized only in two-component systems.
1 Introduction
The field of plasmonics has progressed rapidly over the last few decades, motivated by the ability of plasmonic resonances to control light in the nanoscale.1–3 Plasmons are collective oscillations of valence electrons that originate from long-range Coulomb interactions. In bulk metals, these resonances are polarized longitudinally and, therefore, they cannot interact with light. However, metal–dielectric boundaries support additional plasmonic modes with a transverse polarization, which enables the interaction with electromagnetic radiation and the creation of surface plasmon polaritons. These light–matter hybrid quasiparticles enhance the electromagnetic field by many orders of magnitude by concentrating light on a scale much smaller than the wavelength.Many works in the field of plasmonics have been devoted to the analysis of the effects of the geometry of the system on the plasmonic properties.4 For instance, considering a Drude metal with the bulk plasmon frequency ωP,5 the frequency of the surface plasmon (SP) that can be excited at the interface between this metal and vacuum is 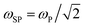 in the long-wavelength limit.6 The localized plasmons (LP) that are supported by nanostructures further shift the plasmon frequency to
in the long-wavelength limit.6 The localized plasmons (LP) that are supported by nanostructures further shift the plasmon frequency to 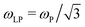 for spherical particles.7 Therefore, by choosing appropriate materials, the plasmon frequency can be engineered by fabricating devices. However, in three-dimensional (3D) materials, the plasmon frequency tends to a finite value, and the use of two-dimensional (2D) materials has been a promising alternative since Stern predicted8 that in these systems the plasmon frequency ω disperses as
for spherical particles.7 Therefore, by choosing appropriate materials, the plasmon frequency can be engineered by fabricating devices. However, in three-dimensional (3D) materials, the plasmon frequency tends to a finite value, and the use of two-dimensional (2D) materials has been a promising alternative since Stern predicted8 that in these systems the plasmon frequency ω disperses as 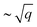 in the q → 0 limit (the symbol q denotes the amplitude of the in-plane momentum q). Therefore, 2D materials can support plasmons of arbitrarily small frequencies, even in the mid-infrared and THz parts of the spectrum. This prediction has been confirmed in metals by further calculations and experiments on metallic layers9 and graphene.10
in the q → 0 limit (the symbol q denotes the amplitude of the in-plane momentum q). Therefore, 2D materials can support plasmons of arbitrarily small frequencies, even in the mid-infrared and THz parts of the spectrum. This prediction has been confirmed in metals by further calculations and experiments on metallic layers9 and graphene.10
Recently, plasmons have been extensively studied in 2D materials including graphene11–15 and in systems exploiting electronic surface states like those at surfaces of metals and topological insulators.16–18 In many 2D systems the dispersion of energy bands may be very different from the free-electron-like behavior. Thus, it was found that the in-plane anisotropy in the electronic structure leads to the anisotropic 2D plasmon dispersion in graphene,10,19 borophene,20,21 and black phosphorous.22–24 Some previous works have analyzed the effect of anisotropy on the conventional 2D and 3D plasmons,25–27 considering materials with an elliptical band dispersion, but no additional plasmon mode has been found there.
In the two-component electron systems, another kind of electronic collective excitation can appear if two groups of carriers with different Fermi velocities reside in the vicinity of the Fermi surface.28 This excitation is characterized by a linear sound-like dispersion and is, therefore, called acoustic plasmon (AP). Due to such dispersion those plasmons can concentrate light on an even smaller scale. A similar excitation called acoustic surface plasmon was predicted29,30 and measured on simple,31 noble,32–35 and transition36 metal surfaces where the slow electrons in a partially filled Shockley state are dynamically screened by the fast electrons of the metallic substrate. It has also been predicted that in graphene the presence of carriers moving with different Fermi velocities in the same energy band (namely in two valleys) can also lead to an AP.19 Such a mode was predicted by first-principles calculations in alkali-doped graphene as well.37,38
Since there have been measurements of band dispersions with other types of anisotropy, such as that of the triangular form in borophene,39 diamond-like in the topological nodal semimetal ZrSeS,40–42 or hexagonal in the topological insulator Bi2Se3,43 in this work we analyze the plasmon dispersions of materials with such anisotropies. In particular, we study the excitation spectra in a free electron gas that has a distorted Fermi surface with triangular, square, or hexagonal shapes. The calculations of the dielectric properties of these systems allow us, on the one hand, to analyze how the dispersion of the conventional 2D plasmon is altered depending on the anisotropy, and, on the other hand, to perform a systematical study of the properties of additional plasmons with a sound-like dispersion.
2 Calculation methods
Here we calculate the excitation spectra of 2D anisotropic materials by random phase approximation (RPA). In this approach, we start modelling their electronic systems with the Hamiltonian44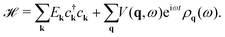 | (1) |
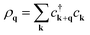 .
.
The potential V(q, ω) includes the contribution due to external perturbation Vext(q, ω) and due to the screening charge Vsc(q, ω): V(q, ω) = Vext(q, ω) + Vsc(q, ω). According to the linear response theory, the response of the system to an external perturbation is encoded in the linear response function χ0, so that 〈ρq(ω)〉 = χ0(q, ω)V(q, ω). χ0 reads
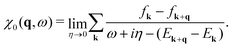 | (2) |
We note that eqn (2) is the response function of a non-interacting system because in the RPA the interactions between the electrons are considered to be external to the system and are included in the total potential V(q, ω). However, the response function χ(q, ω) of the interacting system describes the reaction solely with respect to the external potential Vext(q, ω) without the screening potential Vsc(q, ω), i.e., 〈ρq(ω)〉 = χ(q, ω)Vext(q, ω). In the RPA, χ(q, ω) can be calculated from the non-interacting response function χ0(q, ω), as45
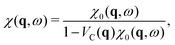 | (3) |
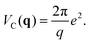 | (4) |
A key parameter for determining the dielectric function ε is the energy band dispersion Ek of the system. In this work, we consider anisotropic free-electron gases with different geometries of the Fermi surfaces, and in all the systems the dispersion can generally be expressed as
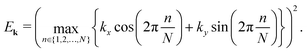 | (5) |
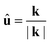 in the k-space the dispersion is free-electron-like, Ek ∝ |k|2, but the effective mass depends on the direction û, the minimum being in the normal direction to the sides of the Fermi surface (indicated by brown dashed lines in the band dispersions of the figures) and the maximum in the direction of the edges (indicated by green dashed lines).
in the k-space the dispersion is free-electron-like, Ek ∝ |k|2, but the effective mass depends on the direction û, the minimum being in the normal direction to the sides of the Fermi surface (indicated by brown dashed lines in the band dispersions of the figures) and the maximum in the direction of the edges (indicated by green dashed lines).
3 Results and discussion
3.1 Triangular anisotropy
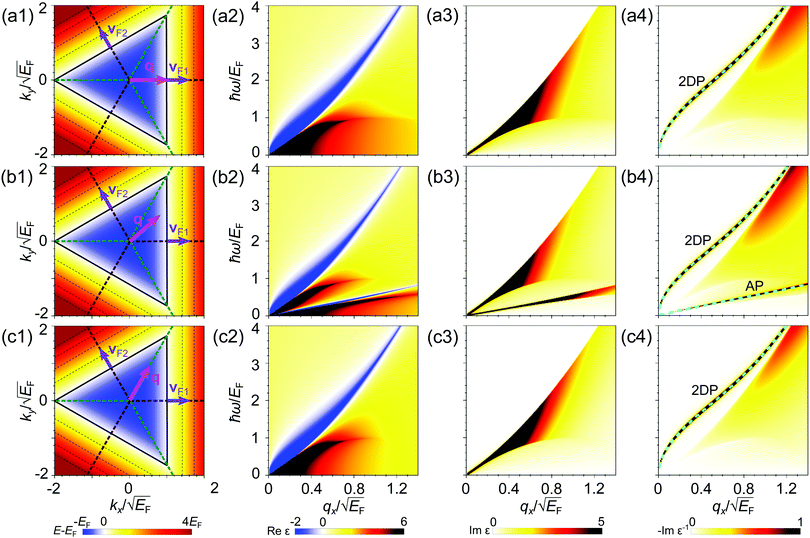
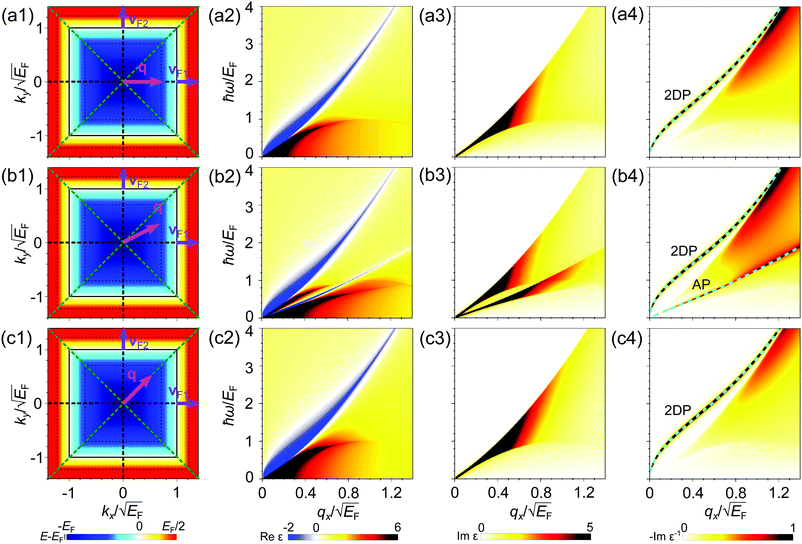
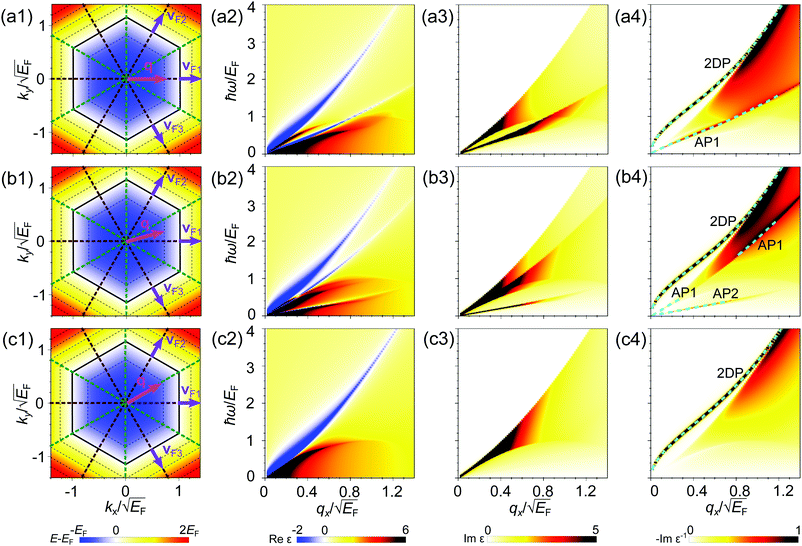
The dielectric function ε(q, ω) and the loss function −Im[ε−1(q, ω)] for the electronic system with a triangular anisotropy (where the band dispersion is given by eqn (5) with N = 3) are reported in Fig. 1. We calculate the dielectric properties as a function of the x component of the momentum, qx, for three different directions of the q vector given by the equations qy = 0,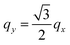 , and
, and 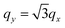 . The momentum transfer qs along these three directions are indicated by magenta arrows in panels (a1), (b1), and (c1) of Fig. 1, respectively. In each of these panels, the energy band dispersion Ek is indicated by the contour plot.
. The momentum transfer qs along these three directions are indicated by magenta arrows in panels (a1), (b1), and (c1) of Fig. 1, respectively. In each of these panels, the energy band dispersion Ek is indicated by the contour plot.
The collective excitations characterized by the momentum q and energy ω are extracted from the positions of the sharp peaks in the loss function. When the momentum of the perturbation lies in the qy = 0 direction we observe in Fig. 1(a4) a continuum of electron–hole excitations in the area delimited by 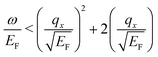 . This condition corresponds to the range of energies where intra-band transitions can occur for a given qx, as also occurs for systems with an isotropic 2D band dispersion.8 An additional peak corresponding to the 2D plasmon (2DP) can be observed in the loss function, highlighted by a dashed line. This excitation lies outside the electron–hole continuum, so the plasmon has an infinite lifetime since there is no decay into electron–hole pairs. The finite thickness of the plasmon peak seen in Fig. 1(a4) is solely due to the finite parameter η introduced in numerical calculations employing eqn (2). Interestingly, the dispersion of the 2D plasmon is similar to that in an isotropic free electron gas predicted by Stern,8 with a
. This condition corresponds to the range of energies where intra-band transitions can occur for a given qx, as also occurs for systems with an isotropic 2D band dispersion.8 An additional peak corresponding to the 2D plasmon (2DP) can be observed in the loss function, highlighted by a dashed line. This excitation lies outside the electron–hole continuum, so the plasmon has an infinite lifetime since there is no decay into electron–hole pairs. The finite thickness of the plasmon peak seen in Fig. 1(a4) is solely due to the finite parameter η introduced in numerical calculations employing eqn (2). Interestingly, the dispersion of the 2D plasmon is similar to that in an isotropic free electron gas predicted by Stern,8 with a 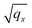 -like dependence at small momentum transfers. The triangular energy anisotropy only causes a weak distortion in the dispersion of the plasmon in this symmetry direction because most of the dielectric properties of isotropic materials appear also in the anisotropic case.
-like dependence at small momentum transfers. The triangular energy anisotropy only causes a weak distortion in the dispersion of the plasmon in this symmetry direction because most of the dielectric properties of isotropic materials appear also in the anisotropic case.
At momentum transfers in the line 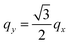 (indicated by the magenta arrow in Fig. 1(b1)), the excitation spectrum of the system with the triangular anisotropy is richer than that in the qy = 0 case, as can be observed in ε1, ε2, and −Im[ε−1] reported in Fig. 1(b2), (b3), and (b4), respectively. While the upper border for the electron–hole continuum in ε2 of Fig. 1(b3) appears at almost the same position as in Fig. 1(a3), an additional sharp peak is seen in ε2 at small energy transfers. The presence of the clear two-peak structure in ε2 is explained by the fact that the intraband transitions close to the Fermi surface occur mainly around two energies. Here we take into account that in this system the Fermi velocity vF of all electrons is of the same magnitude vF = |vF|, but there are three groups of carriers with the Fermi vector pointing in different directions: vF1 = vF(1,0),
(indicated by the magenta arrow in Fig. 1(b1)), the excitation spectrum of the system with the triangular anisotropy is richer than that in the qy = 0 case, as can be observed in ε1, ε2, and −Im[ε−1] reported in Fig. 1(b2), (b3), and (b4), respectively. While the upper border for the electron–hole continuum in ε2 of Fig. 1(b3) appears at almost the same position as in Fig. 1(a3), an additional sharp peak is seen in ε2 at small energy transfers. The presence of the clear two-peak structure in ε2 is explained by the fact that the intraband transitions close to the Fermi surface occur mainly around two energies. Here we take into account that in this system the Fermi velocity vF of all electrons is of the same magnitude vF = |vF|, but there are three groups of carriers with the Fermi vector pointing in different directions: vF1 = vF(1,0), 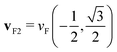 , and
, and 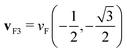 . These vectors point in the directions of the three brown dashed lines shown in Fig. 2(b1). Each group of electrons is on one side of the triangle of the Fermi surface (indicated by the thick black line in Fig. 1(b1)). Considering that the carriers at the Fermi energy level, Ek = EF, are excited to the states with energy Ek+q = EF + q2 + q·vF, the energies of the excited states are different for electrons with Fermi velocities vF1 and vF2 as indicated in Fig. 1(b1) [we note that for qy = 0 (the case reported in the upper row of Fig. 1) only the carriers with the Fermi velocity vF1 are excited]. The consequence of the existence of these two different excitation channels is seen in ε2 of Fig. 1(b3), where there are two separate regions with large values of ε2. The presence of two groups of carriers moving mainly with two different velocity components along the direction of q results in the existence of two different modes, in which both groups of carriers oscillate in phase and out of phase. The former collective excitation is the 2D plasmon that has also been observed for the momentum transfers with the zero qy component. The dispersion of this plasmon seen in Fig. 1(b4) is very similar to that reported in Fig. 1(a4). The out-of-phase46 collective oscillation represented by a peak in the loss function of Fig. 1(b4) comes from an additional zero crossing of ε1 detectable in the low-energy part of Fig. 1(b2). We attribute this peak to an AP since its dispersion is linear and is similar to that of the sound waves. However, as opposed to the 2D plasmon case, the AP is located inside the electron–hole continuum, where ε2 does not vanish for the respective moments and energies and has a local minimum just above the lower-energy peak. Hence, the acoustic plasmon is predicted to have a finite lifetime even in a free-electron model. Upon the momentum increase the width of the AP peak in the loss function gradually increases with the respective lifetime decreasing.
. These vectors point in the directions of the three brown dashed lines shown in Fig. 2(b1). Each group of electrons is on one side of the triangle of the Fermi surface (indicated by the thick black line in Fig. 1(b1)). Considering that the carriers at the Fermi energy level, Ek = EF, are excited to the states with energy Ek+q = EF + q2 + q·vF, the energies of the excited states are different for electrons with Fermi velocities vF1 and vF2 as indicated in Fig. 1(b1) [we note that for qy = 0 (the case reported in the upper row of Fig. 1) only the carriers with the Fermi velocity vF1 are excited]. The consequence of the existence of these two different excitation channels is seen in ε2 of Fig. 1(b3), where there are two separate regions with large values of ε2. The presence of two groups of carriers moving mainly with two different velocity components along the direction of q results in the existence of two different modes, in which both groups of carriers oscillate in phase and out of phase. The former collective excitation is the 2D plasmon that has also been observed for the momentum transfers with the zero qy component. The dispersion of this plasmon seen in Fig. 1(b4) is very similar to that reported in Fig. 1(a4). The out-of-phase46 collective oscillation represented by a peak in the loss function of Fig. 1(b4) comes from an additional zero crossing of ε1 detectable in the low-energy part of Fig. 1(b2). We attribute this peak to an AP since its dispersion is linear and is similar to that of the sound waves. However, as opposed to the 2D plasmon case, the AP is located inside the electron–hole continuum, where ε2 does not vanish for the respective moments and energies and has a local minimum just above the lower-energy peak. Hence, the acoustic plasmon is predicted to have a finite lifetime even in a free-electron model. Upon the momentum increase the width of the AP peak in the loss function gradually increases with the respective lifetime decreasing.
Furthermore, at the momentum transfer along the line 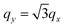 (the panels (c1)–(c4) in Fig. 1), the acoustic plasmon does not appear. Although along this symmetry direction of the system two groups of carriers with different Fermi velocities vF1 and vF2 can be excited (as highlighted by purple arrows in Fig. 1(c1)), these two velocities have the same component q·vF along the direction of the momentum q, preventing the appearance of two well separated peaks in ε2, which is a necessary condition for the existence of an acoustic plasmon. This is related to the fact that the vector q is pointing in a symmetry direction of the band structure (green dashed line in Fig. 1(c1)), as also happens in the case of qy = 0 (brown dashed line in Fig. 1(a1)). Therefore, these results suggest that in order to excite an AP in an anisotropic electron system, the momentum transferred by the perturbation should not follow the symmetry directions in the energy band structure.
(the panels (c1)–(c4) in Fig. 1), the acoustic plasmon does not appear. Although along this symmetry direction of the system two groups of carriers with different Fermi velocities vF1 and vF2 can be excited (as highlighted by purple arrows in Fig. 1(c1)), these two velocities have the same component q·vF along the direction of the momentum q, preventing the appearance of two well separated peaks in ε2, which is a necessary condition for the existence of an acoustic plasmon. This is related to the fact that the vector q is pointing in a symmetry direction of the band structure (green dashed line in Fig. 1(c1)), as also happens in the case of qy = 0 (brown dashed line in Fig. 1(a1)). Therefore, these results suggest that in order to excite an AP in an anisotropic electron system, the momentum transferred by the perturbation should not follow the symmetry directions in the energy band structure.
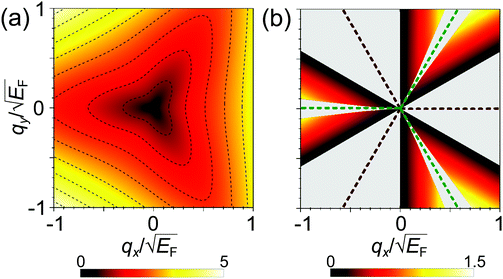
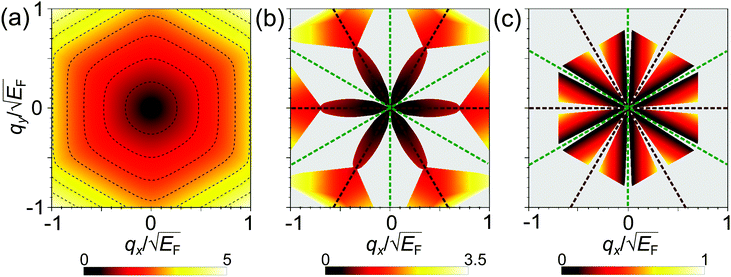
Having discussed the dielectric properties in three different directions for the momentum transfer, let us generalize the discussion to any direction of q. In Fig. 2 we present the plots with the energies of the two plasmons normalized to the Fermi energy, 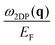 and
and 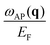 , as a function of q. The dispersion of the 2D plasmon is plotted in Fig. 2(a), where the dashed lines highlight the curves of constant energies of this plasmon. As expected for the system geometry, the 2D plasmon dispersion is positive in any radial direction of q and follows the triangular symmetry of the energy band dispersion. For large values of q, the curves of constant plasmon energy ω2DP have a very similar triangular shape as the curves of constant energy in the band dispersion (first column in Fig. 1). However, at small q the shape of the curves with constant plasmon energy ω2DP becomes significantly distorted from the characteristic triangular shape of the band dispersion, leading to a more complex dependence on the direction of the momentum transfer.
, as a function of q. The dispersion of the 2D plasmon is plotted in Fig. 2(a), where the dashed lines highlight the curves of constant energies of this plasmon. As expected for the system geometry, the 2D plasmon dispersion is positive in any radial direction of q and follows the triangular symmetry of the energy band dispersion. For large values of q, the curves of constant plasmon energy ω2DP have a very similar triangular shape as the curves of constant energy in the band dispersion (first column in Fig. 1). However, at small q the shape of the curves with constant plasmon energy ω2DP becomes significantly distorted from the characteristic triangular shape of the band dispersion, leading to a more complex dependence on the direction of the momentum transfer.
The dispersion of the acoustic plasmon energy 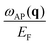 is reported in Fig. 2(b). As already observed in Fig. 1, this plasmon cannot exist at certain momentum transfers, and these regions of q are represented in Fig. 2(b) by the gray areas. The energy of the acoustic plasmon can be written approximately as ωAP ≃ q·vF, where vF corresponds to the lowest Fermi velocity among the two groups of carriers. Taking into account that in the system with triangular anisotropy electrons have three different velocity vectors, for some momentum transfers only one group of carriers has a positive value for q·vF, and, therefore, the condition for the appearance of an acoustic plasmon cannot be satisfied. This happens in the gray areas of Fig. 2(b) around qy = 0 and positive qx or in the equivalent symmetry directions (around brown dashed lines). In the
is reported in Fig. 2(b). As already observed in Fig. 1, this plasmon cannot exist at certain momentum transfers, and these regions of q are represented in Fig. 2(b) by the gray areas. The energy of the acoustic plasmon can be written approximately as ωAP ≃ q·vF, where vF corresponds to the lowest Fermi velocity among the two groups of carriers. Taking into account that in the system with triangular anisotropy electrons have three different velocity vectors, for some momentum transfers only one group of carriers has a positive value for q·vF, and, therefore, the condition for the appearance of an acoustic plasmon cannot be satisfied. This happens in the gray areas of Fig. 2(b) around qy = 0 and positive qx or in the equivalent symmetry directions (around brown dashed lines). In the 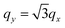 direction and the symmetry equivalent ones (shown by green dashed lines), although two groups of carriers have a positive value of q·vF, both values are the same. Although the AP is forbidden by symmetry in these particular directions it cannot appear in the extended regions around the brown dashed lines. This is because the electron–hole transitions involving the states with different Fermi velocities generate two peaks with a finite linewidth in ε2 around q·vF. As a result, if the two Fermi velocity components are close enough, these peaks in ε2 overlap and an AP cannot realize. That is, for the appearance of the AP it is necessary to have a range of energies with ε2(ω) ≃ 0 between the two peaks, and thus both velocity components along q must be sufficiently different. The linewidth of the two electron–hole peaks in ε2 increases with increasing amplitude of q with the respective increase of the overlap between these two peaks. Therefore at small q the acoustic plasmon can exist in more directions than at larger q.
direction and the symmetry equivalent ones (shown by green dashed lines), although two groups of carriers have a positive value of q·vF, both values are the same. Although the AP is forbidden by symmetry in these particular directions it cannot appear in the extended regions around the brown dashed lines. This is because the electron–hole transitions involving the states with different Fermi velocities generate two peaks with a finite linewidth in ε2 around q·vF. As a result, if the two Fermi velocity components are close enough, these peaks in ε2 overlap and an AP cannot realize. That is, for the appearance of the AP it is necessary to have a range of energies with ε2(ω) ≃ 0 between the two peaks, and thus both velocity components along q must be sufficiently different. The linewidth of the two electron–hole peaks in ε2 increases with increasing amplitude of q with the respective increase of the overlap between these two peaks. Therefore at small q the acoustic plasmon can exist in more directions than at larger q.
3.2 Square anisotropy
After analyzing in detail the dielectric function and the excitation spectra of the system with triangular anisotropy, we now consider the case when the shape of the Fermi surface takes a square form, which corresponds to the band dispersion parameterized by eqn (5) for N = 4. The dielectric function and the loss function for such a system are plotted in Fig. 3 as a function of qx for q with (a) qy = 0, (b)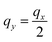 , and (c) qy = qx. The line qy = 0 is the symmetry direction with the lowest effective mass (these directions are indicated by brown dashed lines in the first column of Fig. 3), while along the line qy = qx (or qy = −qx) the system has the largest effective mass. These directions are indicated by green dashed lines. The results shown in Fig. 3 confirm the observations that we have made for the case with the triangular band dispersion. In the N = 4 case we also find that the conventional 2D plasmon exists at momentum transfers in all directions, while the phase space where the AP can appear is more restrictive. This is because in order for this plasmon to exist at a certain q, two groups of carriers with different Fermi velocity components along the same direction should be presented. By symmetry, this does not occur for qy = 0 (row (a) in Fig. 3) and qy = qx (row (c) in the same figure). The conditions for the existence of the AP can be fulfilled only at q other than the lines of high symmetry.
, and (c) qy = qx. The line qy = 0 is the symmetry direction with the lowest effective mass (these directions are indicated by brown dashed lines in the first column of Fig. 3), while along the line qy = qx (or qy = −qx) the system has the largest effective mass. These directions are indicated by green dashed lines. The results shown in Fig. 3 confirm the observations that we have made for the case with the triangular band dispersion. In the N = 4 case we also find that the conventional 2D plasmon exists at momentum transfers in all directions, while the phase space where the AP can appear is more restrictive. This is because in order for this plasmon to exist at a certain q, two groups of carriers with different Fermi velocity components along the same direction should be presented. By symmetry, this does not occur for qy = 0 (row (a) in Fig. 3) and qy = qx (row (c) in the same figure). The conditions for the existence of the AP can be fulfilled only at q other than the lines of high symmetry.
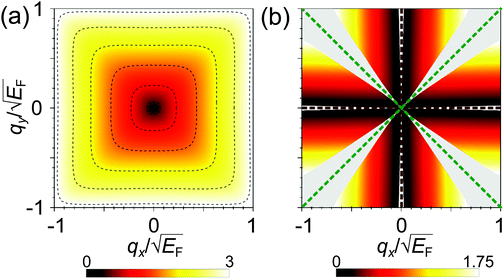
In Fig. 4 we report the full dispersion in the qx − qy plane of both plasmons that can exist in materials with the band structure having a square shape. In Fig. 4(a) the dispersion of the 2D plasmon 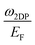 is presented. This dispersion is very isotropic at small q while at larger distances from q = 0 the anisotropy increases and acquires the same shape as the energy band. This behavior is different from the 2D plasmon dispersion observed in a system with the triangular symmetry where, as discussed before, the dispersion
is presented. This dispersion is very isotropic at small q while at larger distances from q = 0 the anisotropy increases and acquires the same shape as the energy band. This behavior is different from the 2D plasmon dispersion observed in a system with the triangular symmetry where, as discussed before, the dispersion 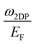 is highly anisotropic even at small momentum transfers.
is highly anisotropic even at small momentum transfers.
The dispersion of the AP, 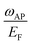 , is reported in Fig. 4(b). In principle, the origin of the AP in the system with a four-fold symmetry is the same as in the previously studied triangular system. It resides in the existence of two groups of carriers moving in a given direction with different group velocities. As pointed out before, in the case of the square band structure, there are only two particular directions (here we do not distinguish the directions connected by the symmetry operations of the system) where this does not occur. However, as seen in Fig. 4(b) the regions around each symmetry line where this plasmon does not appear have different extensions. At q close to the directions with the lowest effective mass (indicated by brown dashed lines), the AP emerges very quickly upon breaking the symmetry. In contrast, in the regions close to the directions with the largest effective mass (green dashed lines), the space with no AP is substantially more extended. This can be related to the fact that in the former case the AP energy is minimal (with a low damping rate) close to the symmetry directions marked by brown dashed lines, whereas in the latter case the AP energy becomes maximal (accompanied by a heavy decay into the electron–hole pairs) upon approaching the green dashed lines.
, is reported in Fig. 4(b). In principle, the origin of the AP in the system with a four-fold symmetry is the same as in the previously studied triangular system. It resides in the existence of two groups of carriers moving in a given direction with different group velocities. As pointed out before, in the case of the square band structure, there are only two particular directions (here we do not distinguish the directions connected by the symmetry operations of the system) where this does not occur. However, as seen in Fig. 4(b) the regions around each symmetry line where this plasmon does not appear have different extensions. At q close to the directions with the lowest effective mass (indicated by brown dashed lines), the AP emerges very quickly upon breaking the symmetry. In contrast, in the regions close to the directions with the largest effective mass (green dashed lines), the space with no AP is substantially more extended. This can be related to the fact that in the former case the AP energy is minimal (with a low damping rate) close to the symmetry directions marked by brown dashed lines, whereas in the latter case the AP energy becomes maximal (accompanied by a heavy decay into the electron–hole pairs) upon approaching the green dashed lines.
Up to this point, we have analyzed systems having ideal band dispersions, where the Fermi surfaces are perfect regular polygons. However, even though the anisotropy of different symmetries has been measured in several materials,25 the Fermi surface geometry differs from such an ideal shape. In order to establish whether our analysis realized for the ideal systems can also be valid in non-ideal realistic cases, here we study how the dielectric properties and the excitation spectra depend on the level of the anisotropy in a system with a four-fold band structure. For that, we consider the following band dispersion,
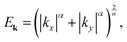 | (6) |
The dependence of the dielectric properties on the anisotropy index can be seen in Fig. 5. Here we show ε1, ε2, and −Im[ε−1] as a function of ω for different values of α and at 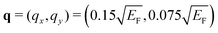 . As expected, in the isotropic case (α = 2) we observe that the electron–hole continuum (orange line) in ε2 of Fig. 5(b) is spread up to the energy
. As expected, in the isotropic case (α = 2) we observe that the electron–hole continuum (orange line) in ε2 of Fig. 5(b) is spread up to the energy 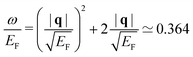 . By increasing α, the density of states with the Fermi velocities in the qx and qy directions increases, favouring intraband transitions with energies around ω = qxvF = 0.3EF and ω = qyvF = 0.15EF. Therefore two peaks in ε2 grow at these two energies with increasing α, as observed in Fig. 5(b). The emergence of these two peaks in ε2 causes dramatic modifications in ε1 (Fig. 5(a)) around ω = 0.15EF, where it reaches zero at α exceeding 4. We attribute the appearance of the AP to this situation when ε1 approaches zero, with the respective emergence of a well-defined peak in the loss function of Fig. 5(c) at slightly larger energies. This confirms that even though we are mainly focused here on the 2D systems with the band dispersions being ideal polygons, our results can be applied to more realistic systems.
. By increasing α, the density of states with the Fermi velocities in the qx and qy directions increases, favouring intraband transitions with energies around ω = qxvF = 0.3EF and ω = qyvF = 0.15EF. Therefore two peaks in ε2 grow at these two energies with increasing α, as observed in Fig. 5(b). The emergence of these two peaks in ε2 causes dramatic modifications in ε1 (Fig. 5(a)) around ω = 0.15EF, where it reaches zero at α exceeding 4. We attribute the appearance of the AP to this situation when ε1 approaches zero, with the respective emergence of a well-defined peak in the loss function of Fig. 5(c) at slightly larger energies. This confirms that even though we are mainly focused here on the 2D systems with the band dispersions being ideal polygons, our results can be applied to more realistic systems.
3.3 Hexagonal anisotropy
Here we consider the dielectric properties of 2DEG with the energy band having hexagonal anisotropy (corresponding to N = 6 in eqn (5)). The respective dielectric functions and the loss function are reported in Fig. 6 as a function of the energy and the momentum transfer component qx. The qy component of vector q in the top, middle, and bottom rows is fixed as qy = 0,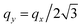 , and
, and 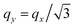 , respectively. The respective directions are shown by magenta arrows in the first column. As opposed to the materials with the triangular and square anisotropic band structures, in the loss function at q = (qx, 0) of Fig. 6(a4) one can observe two clear peaks. Namely, besides the conventional 2D plasmon, which exists in 2D electron gases with any anisotropy, an additional mode with a linear dispersion at lower energies appears along this symmetry direction. We denote this acoustic branch as AP1. The emergence of the AP1 can be explained by the existence of three different groups of carriers at the Fermi surface. Those residing at the Fermi surface edge with the Fermi velocity vF1 constitute a fast moving group. The intraband transitions involving these carriers generate in ε2 of Fig. 6(a3) a well defined peak on the upper side of the electron–hole continuum. The carriers at the edges with the Fermi velocities vF2 and vF3 are moving with equal velocities in the direction of vector q. These velocities at the Fermi level are lower than vF1 by a factor of 2. The transitions related to these slow carriers result in the appearance of a second clear peak in ε2 at lower energies. The initial dispersion slope of this peak is lower by exactly the same factor 2 than that of the upper peak. At small qx these peaks in ε2 are very sharp. Upon increasing the momentum the thickness of these peaks increases in accordance with the incorporation of the states with the velocities increasingly deviating from the Fermi surface values. This is accompanied by an increase in the linewidth of the AP1 peak in the loss function of Fig. 6(a4). At qx larger than
, respectively. The respective directions are shown by magenta arrows in the first column. As opposed to the materials with the triangular and square anisotropic band structures, in the loss function at q = (qx, 0) of Fig. 6(a4) one can observe two clear peaks. Namely, besides the conventional 2D plasmon, which exists in 2D electron gases with any anisotropy, an additional mode with a linear dispersion at lower energies appears along this symmetry direction. We denote this acoustic branch as AP1. The emergence of the AP1 can be explained by the existence of three different groups of carriers at the Fermi surface. Those residing at the Fermi surface edge with the Fermi velocity vF1 constitute a fast moving group. The intraband transitions involving these carriers generate in ε2 of Fig. 6(a3) a well defined peak on the upper side of the electron–hole continuum. The carriers at the edges with the Fermi velocities vF2 and vF3 are moving with equal velocities in the direction of vector q. These velocities at the Fermi level are lower than vF1 by a factor of 2. The transitions related to these slow carriers result in the appearance of a second clear peak in ε2 at lower energies. The initial dispersion slope of this peak is lower by exactly the same factor 2 than that of the upper peak. At small qx these peaks in ε2 are very sharp. Upon increasing the momentum the thickness of these peaks increases in accordance with the incorporation of the states with the velocities increasingly deviating from the Fermi surface values. This is accompanied by an increase in the linewidth of the AP1 peak in the loss function of Fig. 6(a4). At qx larger than 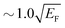 this mode ceases to exist.
this mode ceases to exist.
When the q vector points as shown in Fig. 6(b1), the respective components of vF2 and vF3 become different. Taking into account the states with vF1, now in the system there are three groups of carriers moving with different group velocities. As a result, the lower energy peak in ε2 splits into two well-separated ones as seen in Fig. 6(b3). The presence of three well separated peaks in ε2 at small qs makes the real part of ε cross the zero line six times. In turn, this produces three clear peaks in the loss function of Fig. 6(b4), namely, the upper-energy optical branch 2DP and two acoustic ones, denoted as AP1 and AP2. The lower-dispersing AP2 mode corresponds to the out-of-phase oscillation of the carriers residing at the Fermi surface edges with vF2 and vF3. The AP1 mode with a larger group velocity presents the out-of-phase movement of the carriers with vF1 and vF2.
One can notice that the AP2 peak in Fig. 6(b4) appears at larger qx in comparison to the AP1 one. However, after its disappearance, the AP1 peak reappears again and can be traced up to 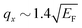 . Nevertheless, the exact limit for the dispersion of these two modes is rather difficult to establish because of the gradual evolution of all the quantities with the variation of q. Moreover, at every qx beyond
. Nevertheless, the exact limit for the dispersion of these two modes is rather difficult to establish because of the gradual evolution of all the quantities with the variation of q. Moreover, at every qx beyond 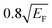 the AP1 peak has a strongly asymmetric shape. This is explained by the almost constant value of ε2 at the energies exceeding the AP1 energy at a fixed qx. Additionally, by varying the q direction the low-energy excitation spectra change rather quickly, which presents some difficulties in the determination of the whole picture.
the AP1 peak has a strongly asymmetric shape. This is explained by the almost constant value of ε2 at the energies exceeding the AP1 energy at a fixed qx. Additionally, by varying the q direction the low-energy excitation spectra change rather quickly, which presents some difficulties in the determination of the whole picture.
When the q vector points along the green dashed line, as shown in Fig. 6(c1), the only transitions involving the states close to the borders with vF1 and vF2 are allowed. Moreover, the respective group velocity components are equal, i.e., both groups of carriers are moving with the same velocities and are indistinguishable. This results in a single peak in ε2 of Fig. 6(c3), i.e., the situation is similar to the conventional one-component electron gas case.8 In consequence, the electron–hole continuum in the loss function shown in Fig. 6(c4) is not altered, and a single 2D plasmon peak is presented only at upper energies. By changing the direction of q, the two acoustic plasmons AP1 and AP2 have an opposite dispersion and their energies get closer while q approaches the brown dashed line.
The dispersion of the conventional 2D plasmon for momentum transfers q in any direction is shown in Fig. 7(a). At small q its dispersion is highly isotropic, while at large momentums the dispersion acquires the hexagonal form characteristic of electron dispersion. This same behavior has been observed for the system with square anisotropy. However, for the system with a square-shaped band structure, the anisotropic behavior of the 2D plasmon dispersion appears at smaller q than in the hexagonal case. This is expected because the hexagonal form is closer to the isotropic case than the square symmetry. Only for the triangular case, which is the regular polygon that strongly differs from the circle, an anisotropic dispersion for very small wavevectors is observed.
The dispersions of the two acoustic plasmons AP1 and AP2 observed in the system with hexagonal anisotropy are plotted in Fig. 7(b) and (c), respectively. For both of them, the initial dispersion is linear in any radial direction of q, and the slopes are defined by the two lowest values of the velocity components q·vF among the three groups of electrons that are excited by the perturbation. Directions of high symmetry in the band dispersion do not allow the existence of one or two acoustic plasmons because there are no three different velocity components q·vF there. The importance of the direction has already been discussed in the previously analyzed cases of the triangular and square forms, but in comparison to them, the acoustic plasmons are more strongly damped for the hexagonal form. That is, although the number of plasmons with a sound-like dispersion increases for the hexagonal system, the overall strength of such modes reduces.
We can generalize the existence of the acoustic plasmons for materials with a band structure in the form of any regular polygon (that is, given by eqn (5) with any value of N). For any q, the number of acoustic plasmons that can be excited is given by the number of different Fermi velocity components in the q direction, that is, q·vF. This can be obtained by increasing N, where the Fermi surface contains a larger number of linear sides and therefore the Fermi velocities of the electrons point in a larger number of different directions, with at most N/2 different positive values of q·vF. But, on the other hand, the q·vF components become closer to each other and the density of electrons decreases for each vF. Therefore different groups overlap with each other and the damping increases. This means that at the cost of having more acoustic plasmons, each of them becomes more efficiently damped. This is easily seen in the limit N → ∞, where we recover the circle or the isotropic case. Here, each electron of the Fermi surface has a different value q·vF, but since there is no group of electrons with a particular Fermi velocity, there is no acoustic plasmon.
4 Conclusions
Here we have shown that the dielectric properties in a two-dimensional free electron gas can be profoundly modified by the variation of the shape of the energy band. Considering the systems with a single band having triangular, square, and hexagonal shapes, we found anisotropy in the dispersion of a conventional two-dimensional plasmon with characteristic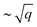 behaviour. In the case of the triangular system the strong distortion of the plasmon dispersion from the isotropic behavior is observed on any momentum transfer. In the cases of higher symmetry at small momentum transfers, the plasmon dispersion becomes almost isotropic. The respective symmetry becomes visible at larger momentum transfers. The threshold for the transition from the isotropic to the anisotropic dispersion increases with increasing symmetry in the systems.
behaviour. In the case of the triangular system the strong distortion of the plasmon dispersion from the isotropic behavior is observed on any momentum transfer. In the cases of higher symmetry at small momentum transfers, the plasmon dispersion becomes almost isotropic. The respective symmetry becomes visible at larger momentum transfers. The threshold for the transition from the isotropic to the anisotropic dispersion increases with increasing symmetry in the systems.
Additionally, we have found that in the momentum-energy-phase-space regions which in the isotropic case are dominated by electron–hole pairs, strong inhomogeneity in the Fermi velocities of the carriers causes strong variations in the dielectric function. As a result, additional plasmon modes with characteristic sound-like dispersion can emerge. In the case of the systems with the triangle and square symmetries, one acoustic plasmon is found and its dispersion in the whole momentum space is determined. In the hexagonal case the number of acoustic plasmons increases to two. Thus, it is possible to have acoustic plasmons in a one-component 2D system just due to energy-band dispersion anisotropy which enlarges the class of systems in which acoustic plasmons might arise with respect to what has been known so far. We predict that at higher symmetries the number of such plasmons should increase even more. However, this process is accompanied by a quick reduction of the spectral weight of such modes, which eventually leads to the well-known result that such kind of mode cannot be realized in an isotropic two-dimensional electron gas.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
U. M. acknowledges financial support by Grant No. PID2019-107432GB-I00 funded by MCIN/AEI/10.13039/501100011033/. V. M. S. acknowledges financial support by Grant No. PID2019-105488GB-I00 funded by MCIN/AEI/10.13039/501100011033/.Notes and references
- M. Rocca, Surf. Sci. Rep., 1995, 22, 1–71 CrossRef CAS.
- W. L. Barnes, A. Dereux and T. W. Ebbesen, Nature, 2003, 424, 824–830 CrossRef CAS PubMed.
- J. M. Pitarke, V. M. Silkin, E. V. Chulkov and P. M. Echenique, Rep. Prog. Phys., 2006, 70, 1–87 CrossRef.
- W. L. Barnes, Am. J. Phys., 2016, 84, 593–601 CrossRef CAS.
- D. Pines and D. Bohm, Phys. Rev., 1952, 85, 338–353 CrossRef CAS.
- R. H. Ritchie, Phys. Rev., 1957, 106, 874–881 CrossRef CAS.
- G. Mie, Ann. Phys., 1908, 25, 377–445 CrossRef CAS.
- F. Stern, Phys. Rev. Lett., 1967, 18, 546–548 CrossRef CAS.
- T. Nagao, T. Hildebrandt, M. Henzler and S. Hasegawa, Phys. Rev. Lett., 2001, 86, 5747–5750 CrossRef CAS PubMed.
- A. Hill, S. A. Mikhailov and K. Ziegler, EPL, 2009, 87, 27005 CrossRef.
- M. Jablan, H. Buljan and M. Soljačić, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245435 CrossRef.
- F. H. L. Koppens, D. E. Chang and F. J. García de Abajo, Nano Lett., 2011, 11, 3370–3377 CrossRef CAS PubMed.
- C. Tegenkamp, H. Pfnür, T. Langer, J. Baringhaus and H. W. Schumacher, J. Phys.: Condens. Matter, 2011, 23, 012001 CrossRef CAS PubMed.
- F. J. García de Abajo, ACS Photon., 2014, 1, 135–152 CrossRef.
- A. Cupolillo, A. Politano, N. Ligato, D. M. C. Perez, G. Chiarello and L. S. Caputi, Surf. Sci., 2015, 634, 76–80 CrossRef CAS.
- T. Stauber, J. Phys.: Condens. Matter, 2014, 26, 123201 CrossRef PubMed.
- A. Politano, V. M. Silkin, I. A. Nechaev, M. Vitiello, L. Vitti, Z. Aliev, M. Babanly, G. Chiarello, P. M. Echenique and E. V. Chulkov, Phys. Rev. Lett., 2015, 115, 216802 CrossRef CAS PubMed.
- A. Kogar, S. Vig, A. Thaler, M. Wang, Y. Xiao, D. Reig-i Plessis, G. Cho, T. Valla and Z. Pan, Phys. Rev. Lett., 2015, 115, 257402 CrossRef CAS PubMed.
- M. Pisarra, A. Sindona, P. Riccardi, V. M. Silkin and J. M. Pitarke, New J. Phys., 2014, 16, 083003 CrossRef CAS.
- K. Sadhukhan and A. Agarwal, Phys. Rev. B, 2017, 96, 035410 CrossRef.
- Z. Torbatian, D. Novko and R. Asgari, Phys. Rev. B, 2021, 104, 075432 CrossRef CAS.
- J. S. Gomez-Diaz and A. Alú, ACS Photonics, 2016, 3, 2211 CrossRef CAS.
- Z. Torbatian and R. Asgari, Phys. Rev. B, 2018, 98, 205407 CrossRef CAS.
- E. van Veen, A. Nemilentsau, A. Kumar, R. Roldán, M. I. Katsnelson, T. Low and S. Yuan, Phys. Rev. Appl., 2019, 12, 014011 CrossRef CAS.
- J. A. Budagosky and E. E. Krasovskii, Phys. Rev. B, 2019, 99, 245149 CrossRef CAS.
- S. Ahn and S. Das Sarma, Phys. Rev. B, 2021, 103, L041303 CrossRef CAS.
- R. Hayn, T. Wei, V. M. Silkin and J. van den Brink, Phys. Rev. Mater., 2021, 5, 024201 CrossRef CAS.
- D. Pines, Can. J. Phys., 1956, 34, 1379–1394 CrossRef CAS.
- V. M. Silkin, A. García-Lekue, J. M. Pitarke, E. V. Chulkov, E. Zaremba and P. M. Echenique, Europhys. Lett., 2004, 66, 260–264 CrossRef CAS.
- V. M. Silkin, J. M. Pitarke, E. V. Chulkov and P. M. Echenique, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 115435 CrossRef.
- B. Diaconescu, K. Pohl, L. Vattuone, L. Savio, P. Hofmann, V. M. Silkin, J. M. Pitarke, E. V. Chulkov, P. M. Echenique, D. Farías and M. Rocca, Nature, 2007, 448, 57–59 CrossRef CAS PubMed.
- S. J. Park and R. E. Palmer, Phys. Rev. Lett., 2010, 105, 016801 CrossRef PubMed.
- L. Vattuone, M. Smerieri, T. Langer, C. Tegenkamp, H. Pfnür, V. M. Silkin, E. V. Chulkov, P. M. Echenique and M. Rocca, Phys. Rev. Lett., 2013, 110, 127405 CrossRef CAS PubMed.
- J. Pischel, E. Welsch, O. Skibe and A. Pucci, J. Phys. Chem. C, 2013, 117, 26964–26968 CrossRef CAS.
- G. Bracco, L. Vattuone, M. Smerieri, G. Carraro, L. Savio, G. Paolini, G. Benedek, P. M. Echenique and M. Rocca, J. Phys. Chem. Lett., 2021, 12, 9894–9898 CrossRef CAS PubMed.
- G. Benedek, M. Bernasconi, D. Campi, I. V. Silkin, I. P. Chernov, V. M. Silkin, E. V. Chulkov, P. M. Echenique, J. P. Toennies, G. Anemone, A. Al Taleb, R. Miranda and D. Farías, Sci. Rep., 2021, 11, 1506 CrossRef CAS PubMed.
- L. Marušić and V. Despoja, Phys. Rev. B, 2017, 95, 201408 CrossRef.
- V. Despoja, D. Novko, I. Lončarić, N. Golenić, L. Marušić and V. M. Silkin, Phys. Rev. B, 2019, 100, 195401 CrossRef CAS.
- B. Feng, J. Zhang, S. Ito, M. Arita, C. Cheng, L. Chen, K. Wu, F. Komori, O. Sugino, K. Miyamoto, T. Okuda, S. Meng and I. Matsuda, Adv. Mater., 2018, 30, 1704025 CrossRef PubMed.
- M. Neupane, I. Belopolski, M. Mofazzel Hosen, D. S. Sanchez, R. Sankar, M. Szlawska, S.-Y. Xu, K. Dimitri, N. Dhakal, P. Maldonado, P. M. Oppeneer, D. Kaczorowski, F. Chou, M. Zahid Hasan and T. Durakiewicz, Phys. Rev. B, 2016, 93, 201104(R) CrossRef.
- L. M. Schoop, M. N. Ali, C. Strasser, A. Topp, A. Varykhalov, D. Marchenko, V. Duppel, S. S. P. Parkin, B. V. Lotsch and C. R. Ast, Nat. Commun., 2016, 7, 11696 CrossRef CAS PubMed.
- S. Xue, M. Wang, Y. Li, S. Zhang, X. Jia, J. Zhou, Y. Shi, X. Zhu, Y. Yao and J. Guo, Phys. Rev. Lett., 2021, 127, 186802 CrossRef CAS PubMed.
- K. Kuroda, M. Arita, K. Miyamoto, M. Ye, J. Yiang, A. Kimura, E. E. Krasovskii, E. V. Chulkov, H. Iwasawa, T. Okuda, K. Shimada, Y. Ueda, H. Namatame and M. Taniguchi, Phys. Rev. Lett., 2010, 105, 076802 CrossRef CAS PubMed.
- D. Pines and P. Nozières, The Theory of Quantum Liquids: Normal Fermi Liquids, W. A. Benjamin, New York, 1966, vol. 1 Search PubMed.
- G. D. Mahan, Many-Particle Physics, Kluwer Academic/Plenum Publishers, New York, 2000 Search PubMed.
- V. M. Silkin, I. A. Nechaev, E. V. Chulkov and P. M. Echenique, Surf. Sci., 2006, 600, 3875–3878 CrossRef CAS.
| This journal is © the Owner Societies 2022 |