Dynamical time scales of friction dynamics in active microrheology of a model glass
A.
Madanchi†
a,
Ji Woong
Yu†
b,
Won Bo
Lee
 *b,
M. R.
Rahimi Tabar
*cd and
S. H. E.
Rahbari
*b,
M. R.
Rahimi Tabar
*cd and
S. H. E.
Rahbari
 *be
*be
aDepartment of Physics, McGill University, H3A2T8, Montreal, Canada
bSchool of Chemical and Biological Engineering, Institute of Chemical Processes, Seoul National University, Seoul 08826, Korea
cDepartment of Physics, Sharif University of Technology, Tehran, 11155-9161, Iran
dInstitute of Physics and ForWind, Carl von Ossietzky University, 26111, Oldenburg, Germany
eSchool of Physics, Korea Institute for Advanced Study, Seoul 02455, Korea
First published on 22nd March 2021
Abstract
Owing to the local/heterogeneous structures in supercooled liquids, after several decades of research, it is now clear that supercooled liquids are structurally different from their conventional liquid counterparts. Accordingly, an approach based on a local probe should provide a better understanding about the local mechanical properties as well as heterogeneous structures. Recently, the superiority of active microrheology over global rheology has been demonstrated [Yu et al., Sci. Adv., 2020, 6, 8766]. Here, we elaborate this new avenue of research and provide more evidence for such superiority. We report on the results of an extensive molecular dynamics simulation of active microrheology of a model glass. We identify several time scales in time series of friction, and detect a transition in dynamical behavior of friction. We discuss the possible relation to structural heterogeneities—a subject of considerable interest in glass physics.
1 Introduction
When a liquid is cooled rapidly below its melting temperature, its dynamics drastically slows down, and its viscosity increases more than fifteen orders of magnitude.1 The structure of a supercooled liquid, explored by conventional measures such as structure factor or two-point density correlation function, shows no dramatic change upon the transition into the glass phase. As a result, it was believed that liquids and glasses are structurally equivalent. Two main key discoveries proved that there exist intimate, previously unnoticed, structural differences between glasses and liquids: (1) dynamic heterogeneities (DH),1 and (2) hierarchical static structures—Tanaka et al. provide an excellent recent review of this subject.2In a supercooled liquid, particles transiently trap in cages formed by their neighbors. The dynamics of a supercooled liquid is thus described by two main relaxation processes, which is mathematically described by a two-step relaxation function C(t), (1) a fast exponential relaxation, known as β process with C(t) ∼ e−(t/τβ), and (2) a slow stretched-exponential relaxation, known as α process with C(t) ∼ e−(t/τα)b where b < 1. In the β process, a particle rattles within the cage created by its neighbors. This back and forth movement terminates when the particle eventually escapes the cage, and this results in the final α relaxation. Below the melting temperature, cages become permanent and the α process, within accessible laboratory time scales, becomes unattainable. This picture may suggest a homogeneous relaxation dynamics in a supercooled liquid. In contrast, it was revealed that in a supercooled liquid, particles displaced, let's say longer than the average particle displacement, form clusters; This is known as DH. As a result of DH, the dynamics in a supercooled liquid is heterogeneous.1,3 This is in contrast to liquids that are widely considered homogeneous. Even though its name suggests a dynamic scenario, it is not clear whether the origin of DH is static or dynamic. Unveiling the origin of DH is important, because it will help to understand whether glass transition is a phase transition (the static origin) or a dynamic phenomenon (the dynamic origin). There are conflicting reports regarding the origin of DHs: some researchers advocate a static origin,4–7 while others suggest a dynamic origin.8 For example, Kawasaki and Tanaka identified clusters of medium-range crystalline order (MCRO), and demonstrated that MCROs are slower than the rest of the particles. The size of these clusters grows upon approaching the glass transition temperature. This suggests a possible link between MCRO and DH, and the authors concluded that MCRO may be the origin of DHs. Tanaka and co-workers pioneered this line of research and identified many other static structures;2 These results demonstrate the existence of a hierarchical order in supercooled liquids. Most of these structures provide length scales that grow upon cooling. However, these length scales never become macroscopic. This is perhaps because of the the dramatic slowing down of the dynamics near the glass transition temperature.
Interestingly, the mechanical properties of a glass are very different from those of liquids, and share many similarities with conventional solids; though glasses have some special features such as the existence of excess vibrations, known as the boson peak. These similarities can be summarized into one main feature: both glasses and solids are rigid. These mechanical properties are investigated via global deformations, or shearing. However, a global deformation would only render an average response, and the local properties due to typical structural heterogeneities of supercooled liquids cannot be explored by a global deformation. A remedy for this problem is an approach based on local deformation: active microrheology. In this technique, local mechanical and transport properties can be obtained via the investigation of dynamics of a single-out probe particle driven into host medium.9 This technique, active microrheology, has been widely used for investigations on biological materials, complex fluids,10 and hard spheres as model systems for colloids.11–14
Three of us have previously investigated active microrheology of model glasses in a recent paper.15 In this paper, a probe particle moves with a constant velocity, U, and the local response of the medium is obtained via friction force experienced by the probe particle. It was revealed that the time series of friction contains blueprints of the structural relaxations of the host medium. The study had three major outcomes:
First, the probe particle exhibited a second-order delocalization transition when the temperature was varied across the glass transition temperature. As a result, the friction, F, satisfied a scaling ansatz of the form:
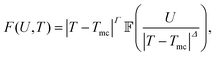 | (1) |
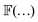 is a scaling function, Γ is a parameter-dependent exponent, and Δ is a universal gap exponent. At T = Tmc, scale invariance requires F ∝ Uq, in which q is a critical exponent, and eqn (1) grants q = Γ/Δ. Via a systematic critical scaling analysis, we found out that the critical delocalization temperature was Tmc = 0.36875 ± 0.0062, which was approximately 23% higher than the thermodynamic glass transition temperature, at TK = 0.3, and the critical exponents associated with this transition were q = 0.17303 ± 0.0248, with the crossover exponents Γ = 0.475 ± 0.068 and Δ = 2.75.
is a scaling function, Γ is a parameter-dependent exponent, and Δ is a universal gap exponent. At T = Tmc, scale invariance requires F ∝ Uq, in which q is a critical exponent, and eqn (1) grants q = Γ/Δ. Via a systematic critical scaling analysis, we found out that the critical delocalization temperature was Tmc = 0.36875 ± 0.0062, which was approximately 23% higher than the thermodynamic glass transition temperature, at TK = 0.3, and the critical exponents associated with this transition were q = 0.17303 ± 0.0248, with the crossover exponents Γ = 0.475 ± 0.068 and Δ = 2.75.
Second, auto-correlation of the friction showed a two-step relaxation, described by a compressed exponential C(t) ∼ e−(t/τα)b where b > 1. Third, the study provided the first glance into the spatial distribution of micro-viscosity, ηm. The distribution was bell-shaped, and the skewness of the distribution function of ηm increased as the temperature was lowered. A possible connection to DH was discussed in ref. 15. We further elaborate this in the current manuscript and provide more clues about the dynamical behavior of the friction in this system.
We notice that the delocalization transition is related to a larger class of far-from equilibrium phase transitions of driven particles over random or periodic substrates; dubbed depinning transition. At low temperatures, where the thermal motion of the medium is seized, active microrheology resembles a probe particle driven over a random substrate. The depinning transition has far more ramifications in a much broader context of vortices in type-II superconductors, and skyrmions, and many other examples are given in a recent review at ref. 16.
In this work, we look at more clues in time series of friction. We will follow a usual practice in time series analysis to investigate fluctuations and the corresponding scaling behaviors across all characteristic time scales. We will ask whether time series of friction are stationary. By stationarity, we mean a time series in which two point correlation function decays as a function of the time lag, similar to the behavior of a correlation function in an equilibrium system. Another possibility is a reverse behavior in which the correlation increases as a function of time lag; this is similar to fractional Brownian Motion (fBM). This corresponds to a non-stationary time series, and results in the persistency of the underlying fluctuations. For this purpose, we will not directly use correlation functions owing to the inadequacy of the correlation functions for non-stationary processes. Instead, we will use a standard method, known as multifractal detrended fluctuation analysis,17 for the time series of friction. We will show a transition in time series from stationary to non-stationary in the dynamics of friction. This will help us to identify a length scale that grows by lowering the temperature.
2 Method
We performed large scale Molecular Dynamics (MD) simulations using LAMMPS. We simulated a singled-out probe particle moving with constant velocity U embedded in a host medium at temperature T. A Nose–Hoover thermostat is used for constant-temperature molecular dynamics. The host is a binary mixture widely used as a model glass. For each U and T, we obtained an ensemble of 500 different independent realizations by starting from different initial conditions. We recorded the force acting on the probe particle, friction, and each simulation provided a time series of friction. Below, we describe details of simulations; more details can be found in our previous work.152.1 Kob–Andersen mixture
We used a binary system known as the Kob–Andersen (KA) mixture.18,19 In KA model, atoms interact via a Lennard-Jones potential, and there are atoms of type-A and -B. The interaction potential between a pair is given by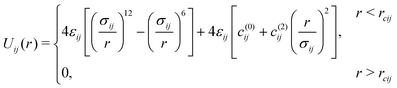 | (2) |
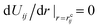 . These parameters are invariant under a swap of subscripts i and j. The εij and σij parameters are given by εAA = 1.0ε, εAB = 1.5ε, εBB = 0.5ε, and σAA = 1.0σ, σAB = 0.88σ, σBB = 0.8σ. For all particles we set mass to unity. For the simplicity, length, energy, mass and time are represented in dimensionless unit σ, ε, m,
. These parameters are invariant under a swap of subscripts i and j. The εij and σij parameters are given by εAA = 1.0ε, εAB = 1.5ε, εBB = 0.5ε, and σAA = 1.0σ, σAB = 0.88σ, σBB = 0.8σ. For all particles we set mass to unity. For the simplicity, length, energy, mass and time are represented in dimensionless unit σ, ε, m, 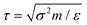 respectively. The number density ρ = 1.20σ−3, and in all simulations, the time step, Δt, is 0.01τ. The simulation box is a cube. Two parallel hard walls are placed along the vertical axis, and periodic boundary conditions are applied to otherwise directions. Particles in the medium interact with walls via a Weeks–Chandler–Andersen (WCA) potential, Uwall(d) = 4ε[(σ/d)12 − (σ/d)6 + 1/4], d ≤ dc = 21/6σ where d is the shortest distance between wall and a particle.
respectively. The number density ρ = 1.20σ−3, and in all simulations, the time step, Δt, is 0.01τ. The simulation box is a cube. Two parallel hard walls are placed along the vertical axis, and periodic boundary conditions are applied to otherwise directions. Particles in the medium interact with walls via a Weeks–Chandler–Andersen (WCA) potential, Uwall(d) = 4ε[(σ/d)12 − (σ/d)6 + 1/4], d ≤ dc = 21/6σ where d is the shortest distance between wall and a particle.
We used a state-of-the-art method, known as shear annealing, to stabilize the host medium.20,21 In this method, the system is periodically sheared, and below a threshold yielding amplitude, the system settles down into deeper basins in the energy landscape. The more the system is annealed, the more stable it becomes, and the fewer fluctuations happen. This step is crucial to reduce the fluctuations of the system when we perform active microrheology.
2.2 Active microrheology
A probe particle with a prescribed constant velocity is driven into the host medium. The interaction potential of the probe particle with the host medium is given by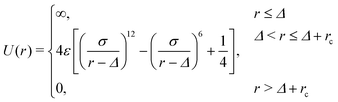 | (3) |
2.3 Methodology of analysis
Apart from the auto-correlation function and power spectrum of friction fluctuations, we will analyse the corresponding time series using detrended fluctuation analysis (DFA). Here, we provide a brief summary of this methodology, which we have used to investigate the scaling properties of fluctuations of the friction time series. This method enables us to eliminate possible biases due to trends in the time series, therefore will provide precise scaling exponents. Below, we describe the steps for DFA and its connection to the stationary and non-stationary behavior of friction time series.17For the given time series x(ti) ≡ x(i) (here friction time series) for {I = 1,…,N}, we define the mean of x series as:
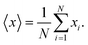 | (4) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) i, is defined as
i, is defined as![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) i = xi − 〈x〉. i = xi − 〈x〉. | (5) |
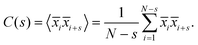 | (6) |
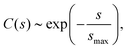 | (7) |
| C(s) ∼ s−γ, | (8) |
(i) Integration: compute integral of the original time series
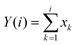 | (9) |
(ii) Division: the time series (with the length of N) is then divided into 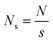 non-overlapping segments, where s is the box size. Because N/s has normally a non-zero remainder, especially when s is large, the remaining part of the time series is discarded. To prevent any bias as a result of division, the time-series is first divided from the beginning to end, and the remaining part is left, and second time the division is performed in the opposite direction. As a result 2Ns segments are produced. Now, one can perform the detrending step.
non-overlapping segments, where s is the box size. Because N/s has normally a non-zero remainder, especially when s is large, the remaining part of the time series is discarded. To prevent any bias as a result of division, the time-series is first divided from the beginning to end, and the remaining part is left, and second time the division is performed in the opposite direction. As a result 2Ns segments are produced. Now, one can perform the detrending step.
(iii) Detrending: for each segment s, a linear, or higher-order, regression is performed using least square algorithm. For a linear dependence, the resulting function is Ps(i) = as + bsi, where as and bs are constants obtained from the regression, and i is time. The detrending is performed by a simple subtraction from each data point within the interval:
| Ydet.s(i) = Y(i) − Ps(i). | (10) |
(iv) Scaling of fluctuations: variance of an interval of length s is defined as
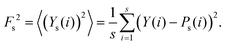 | (11) |
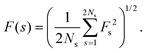 | (12) |
| F(s) ∼ sh, | (13) |
| γ = 2 − 2h. | (14) |
 | (15) |
 | (16) |
The implementation of DFA has been done by the MFDFA package in python provided by LRydin/MFDFA.
3 Results
In Fig. 1, time series of friction for three different probe velocities U = 1, 0.223 and 0.018 are depicted versus the probe displacement, t × U. The temperature is T = 0.45, which is above the delocalization temperature, Tmc = 0.36875.15 We will show that the corresponding generalized Hurst exponent for U = 1 is h < 1 at all time scales, indicating that the time series is stationary. However, for U = 0.018, in some time scales we obtain h > 1, which indicates that the time series is non-stationary. The case for U = 0.223, depicted by green and red curves, exhibits a mixed nature; for one case h > 1 and for the other h < 1. Therefore, U = 0.223 presents the boundary between the stationary and non-stationary dynamics in the detected time intervals.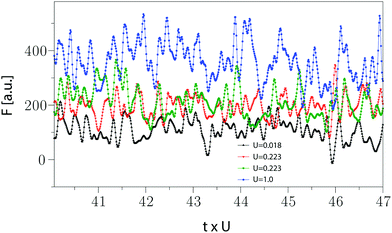 | ||
| Fig. 1 Friction time series. The magnitude of the total force exerted by the medium to the probe particle, friction, is depicted versus the probe displacement, t × U, for different probe velocities. The medium is in the liquid state with temperature T = 0.45, which is above the delocalization transition temperature Tmc = 0.36875.15 The stochastic characteristics of the times series of friction depends on temperature and velocity. We will show that for U = 1 and 0.018, the corresponding generalized Hurst exponents are h < 1 and h > 1, respectively. However, for U = 0.223, some of simulated time series are stationary and some others are non-stationary. This represents a transition as a function of the control parameter U in the behavior of time series. | ||
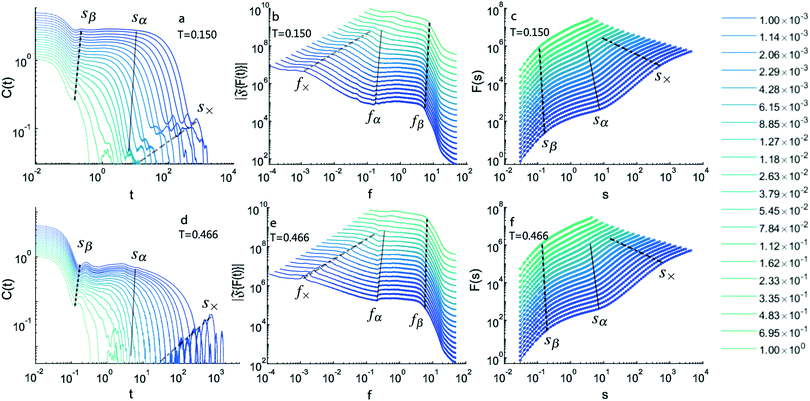
In order to gain more insight about the dynamical nature of friction time series, similar to our previous work,15 we present auto-correlation of time series of friction, C(t) = 〈F(0)F(t)〉, in Fig. 2a and d, for T = 0.15 and 0.466, respectively. Each curve has a different color which corresponds to different probe velocity U whose values are given in the legend. One can see that C(t) faithfully represents the typical two-step structural relaxation of a supercooled liquid: (1) an exponential decay as a result of ballistic motion, followed by a plateau representing the cage effect akin to the β relaxation with time scale τβ, and (2) final relaxation due to escape of a particle from the surrounding cage akin to the α relaxation with τα. These time scales can be obtained by a model-fitting function of the form:
| C(t) = (1 − A)e−(t/τβ) + Ae−(t/τα)b | (17) |
We have previously shown that by rescaling C(t) versus x = t × Uν, where ν = 1 − q = 0.95 being the force-thinning exponent, all curves collapse into a master curve given by a compressed exponential function e−(x/τα)b with b > 1, resembling a time-force superposition similar to time-shear superposition principle predicted by mode-coupling theory31 and spin glass theory.32 These results established the fact that friction time series contains blueprint of structural relaxations in supercooled liquids.
An interesting point is the appearance of a second small plateau for low-temperature and glass phase and small enough probe velocities in panel-a, which might be related to the fBm nature of friction dynamics in those scales and propagation of waves in the system as a result of the probe motion. This secondary plateau does not exist in the liquid state in panel-d. Therefore, active microrheology reveals many more interesting time scales that are not visible for globally averaged quantities, such as the self part of the scattering function. These time scales cannot be obtained by a simple fitting procedure using eqn (17), and more elaborate techniques should be used. To distinguish these cross overs, we compute the magnitude of Fourier transform of time series, ![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) {F(t)}, depicted in Fig. 2 panel-b and -e. The existence of many cross overs at different time scales becomes much more clear in the frequency domain, f = 1/t. Below a frequency f×, curves nearly level off at f → 0. For f > f×, a scaling regime is observed. In panel-f in liquid phase, we observe a ripple mode on fx line (zoom in required).33 This scaling region levels off at fα, which is followed by another plateau, similar to the corresponding plateau in the time domain in C(t), then there is another scaling regime at the end of this region for f > fβ. We use these plots to identify cross over frequencies f×, fα and fβ for every curve individually. These cross overs are marked by dashed lines. The boundaries between these cross overs become blurred at large probe velocities for U > 2.33 × 10−1.
{F(t)}, depicted in Fig. 2 panel-b and -e. The existence of many cross overs at different time scales becomes much more clear in the frequency domain, f = 1/t. Below a frequency f×, curves nearly level off at f → 0. For f > f×, a scaling regime is observed. In panel-f in liquid phase, we observe a ripple mode on fx line (zoom in required).33 This scaling region levels off at fα, which is followed by another plateau, similar to the corresponding plateau in the time domain in C(t), then there is another scaling regime at the end of this region for f > fβ. We use these plots to identify cross over frequencies f×, fα and fβ for every curve individually. These cross overs are marked by dashed lines. The boundaries between these cross overs become blurred at large probe velocities for U > 2.33 × 10−1.
We are now ready to perform DFA. This is done in Fig. 2 panel-c and -f. One can see that each curve crosses over to various scaling regimes. Generally, DFA provides more clean scaling behavior with respect to other methods. The corresponding cross overs can be found using both DFA or power spectrum analysis. Using the results of the Fourier transform analysis, we can determine cross overs in these curves as, sβ = 1/fβ, sα = 1/fα and s× = 1/f×. Using linear regressions for the ranges sβ < s < sα and sα < s < sx in double logarithmic scale, we examine the following scaling behaviors
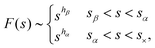 | (18) |
![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) {F(t)} ∼ f−β, via Wiener–Khinchin theorem according to β = 2h − 1. Note that the similarity between names of exponent β and hβ is just a coincidence. We use this relationship to cross check our results, and we found plausible agreement between them. One can see that some of the curves in Fig. 2c and f have strong correction-to-scaling near the crossover region marked by sα. This means that eqn (18) cannot capture the full behavior of the data, and new terms, such as sh(1 + ksh1), must be added. To prevent this, we use compensated plots to compute the corresponding asymptotic exponent h for each respective region.34 An example of a compensated plot is given in Appendix A.
{F(t)} ∼ f−β, via Wiener–Khinchin theorem according to β = 2h − 1. Note that the similarity between names of exponent β and hβ is just a coincidence. We use this relationship to cross check our results, and we found plausible agreement between them. One can see that some of the curves in Fig. 2c and f have strong correction-to-scaling near the crossover region marked by sα. This means that eqn (18) cannot capture the full behavior of the data, and new terms, such as sh(1 + ksh1), must be added. To prevent this, we use compensated plots to compute the corresponding asymptotic exponent h for each respective region.34 An example of a compensated plot is given in Appendix A.
3.1 Scaling behavior of the friction dynamics
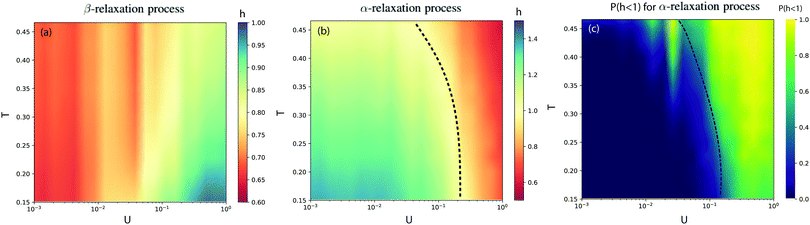
We construct diagrams showing dynamics of friction in T–U plane using hβ and hα. Fig. 3a and b show diagrams for β and α regions, respectively. The color code is given by the corresponding exponents, hβ and hα. One can see that for all T and U, in β region of relaxation functions, we obtain hβ < 1, which indicates the stationarity of the process. Moreover, the exponent satisfies inequality 0.5 < hβ < 1, which refers to the persistency of friction over this time scale. By persistency we mean that an increase of friction will be followed by an increase, and similarly, a decrease will be followed by a decrease.More interesting behavior is found in panel-b for α region. Here, we discover that hα crosses over from a region with h > 1 to h < 1. A transition boundary can be drawn at h = 1; this is marked by a dashed line. The area inside the cone represents the non-stationary regime. The non-stationary region expands as temperature is lowered. The area outside the cone represents the stationary region. To gain a better insight about the nature of this “stationary to non-stationary” transition, we look individually at each trajectory within our ensemble, and we calculate the ratio of cases where h < 1 to the total number of trajectories, or probability P(hα < 1) in panel-c. It can be seen that deep inside the non-stationary region near the origin of the plot, almost all trajectories are non-stationary P(hα < 1) ≃ 0; however, near the transition boundary almost half of trajectories are stationary. This may imply that the transition is second-order-type.
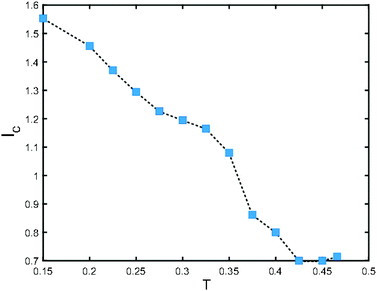
The transition boundary at h = 1 for a given T occurs at a critical probe velocity U = Uc. We define a critical length scale, lc, given by lc = (tx − tα)Uc. We plot this length scale as a function of temperature in Fig. 4. One can see that lc increases as T is lowered. The largest gap in lc happens near the delocalization transition temperature at Tmc = 0.36875. In the liquids phase, lc is almost zero. Similar to many other length scales that are proposed for supercooled liquids, this length scale remains microscopic across all temperatures. However, to gain a better understanding of this length scale, a finite size scaling is required to see how lc grows with the system size. This is out of reach for the present work, but we will address it in near future.
4 Discussion and conclusion
In this paper, using extensive molecular dynamics simulations of active microrheology of a model glass combined with various statistical methods of time series analyses, we unveiled that friction time series undergoes a dynamical transition from stationary (h < 1) to non-stationary (h > 1) behavior in α region. The non-stationary behavior is akin to fBM in which correlations grow as a function of time. This is in contrast to conventional equilibrium-like systems where correlations decay as a function of time. We also computed diagrams using the generalized Hurst exponent, h, in T–U plane for both β and α regions. Whereas β region is always stationary, we showed that the non-stationary region in α domain grows as the temperature is lowered. As a result, for a given T, there exists a critical probe velocity Uc at which the dynamics crosses over.Previous studies on the rheology of supercooled liquids by Berthier-Barrat,35 and Varnik36 demonstrated that, even though a supercooled liquid falls out of equilibrium near the melting temperature, however, the application of a shear flow into the system settles down the system into a dynamical stationary state akin to an equilibrium system. Here, active microrheology demonstrates that there exists a stationary state only above a critical threshold, U > Uc. Note that, we previously have shown that the probe velocity U is akin to a global flow rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) via
via ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) =U/D, where D is the probe diameter. It is possible that the onion structure in T–U plane is smeared out in macrorheology. This demonstrates once again the superiority of active microrheology with respect to macrorheology.
=U/D, where D is the probe diameter. It is possible that the onion structure in T–U plane is smeared out in macrorheology. This demonstrates once again the superiority of active microrheology with respect to macrorheology.
Our analysis allowed us to extract a length scale, lc, from our data, which is defined based on the cross over probe velocity Uc, and the corresponding time scale, tx − tα. We found that this length scale is almost zero in the liquid phase. Near Tmc, the critical delocalization temperature, lc has a sharp increase, and then grows monotonically as the temperature is lowered. Similar growth of a length scale has been also observed in dynamic heterogeneities and hierarchal structures.2 Our next goal is to find a relationship between this length scale and other known length scales in the literature. It will also be very interesting to see whether lc will grow with the system size. This requires a systematic finite size scaling. We will address these questions in near future.
Microrheology is known to exhibit pronounced finite-size effects due to the finite size of system and the size of tracer. In its passive version, when the external drive on the tracer is switched off, results of simulations showed satisfactory quantitative agreement with continuum theories when the tracer size was about five times larger than that of the embedding medium particles.37,38 A recent study on active microrheology found good agreement between the hydrodynamic theory and simulations for the dependence of viscosity as a function of system size only at intermediate system sizes,39 and the the subject requires further investigation. Our scaling approach offers a sound framework for this problem, because the system size, L, can be cast as a relevant perturbation to the scaling ansatz proposed in our previous work.15 Because the delocalization transition in this system suggests a critical point at which the correlation length diverges, b = ξ ∝ δT−ν, and the friction scales as a function of distance from the critical temperature, F ∝ δTy, near the critical temperature δT → 0 a standard critical scaling can be written as
F = b−y/ν![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) 0(Ubz,bL−1), 0(Ubz,bL−1), | (19) |
F = L−y/ν![[Fraktur F]](https://www.rsc.org/images/entities/char_e183.gif) 1(ULz), 1(ULz), | (20) |
Conflicts of interest
There are no conflicts to declare.A Appendix
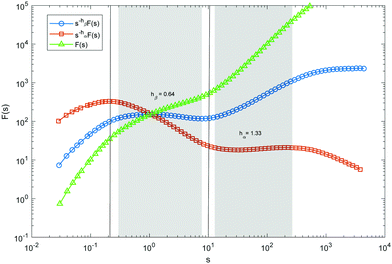
Here, we explain how we carried out a compensated plot. The goal of a compensated plot is to derive an asymptotic exponent, like hα and hβ in eqn (18), from the behavior of the data. For this purpose, a plot of s−hF(s) versus s is depicted. Then the exponent h is varied over an interval and the genuine asymptotic exponent is the one by which the compensated plot becomes flat over the region of interest. In Fig. 5, we plot F(s) versus s for U = 0.001 and T = 0.15. The original data are given by the green triangles. We would like to derive hβ and hα over β and α regions, respectively, from the original data. These regions are highlighted by two grey columns. We find that s−hβF(s) versus s becomes flat over the β region if we choose hβ = 0.64. This is given by the blue circles. Similarly, hα = 1.33 makes s−hαF(s) versus s flat over α region. This is shown by the brown squares.Acknowledgements
S. H. E. R. deeply appreciates enlightening discussions with Takeshi Kawasaki. W. B. L. acknowledges grant No. NRF-2018M3D1A1058633, Creative Material Discovery Project under NRF.Notes and references
- C. A. Angell, Science, 1995, 267, 1924–1935 CrossRef CAS PubMed.
- H. Tanaka, H. Tong, R. Shi and J. Russo, Nat. Rev. Phys., 2019, 1, 333–348 CrossRef.
- L. Janssen, Front. Phys., 2018, 6, 97 CrossRef.
- A. Widmer-Cooper and P. Harrowell, Phys. Rev. Lett., 2006, 96, 185701 CrossRef PubMed.
- H. Shintani and H. Tanaka, Nat. Phys., 2006, 2, 200 Search PubMed.
- T. Kawasaki, T. Araki and H. Tanaka, Phys. Rev. Lett., 2007, 99, 215701 CrossRef PubMed.
- T. Kawasaki and H. Tanaka, J. Phys.: Condens. Matter, 2010, 22, 232102 CrossRef PubMed.
- L. O. Hedges, R. L. Jack, J. P. Garrahan and D. Chandler, Science, 2009, 323, 1309–1313 CrossRef CAS PubMed.
- A. M. Puertas and T. Voigtmann, J. Phys.: Condens. Matter, 2014, 26, 243101 CrossRef CAS PubMed.
- T. A. Waigh, Rep. Prog. Phys., 2005, 68, 685 CrossRef.
- P. Habdas, D. Schaar, A. C. Levitt and E. R. Weeks, Europhys. Lett., 2004, 67, 477 CrossRef CAS.
- I. C. Carpen and J. F. Brady, J. Rheol., 2005, 49, 1483–1502 CrossRef CAS.
- A. S. Khair and J. F. Brady, J. Fluid Mech., 2006, 557, 73 CrossRef.
- L. G. Wilson, A. W. Harrison, A. B. Schofield, J. Arlt and W. C. K. Poon, J. Phys. Chem. B, 2009, 113, 3806–3812 CrossRef CAS PubMed.
- J. W. Yu, S. H. E. Rahbari, T. Kawasaki, H. Park and W. B. Lee, Sci. Adv., 2020, 6, eaba8766 CrossRef PubMed.
- C. Reichhardt and C. J. O. Reichhardt, Rep. Prog. Phys., 2016, 80, 026501 CrossRef PubMed.
- S. V. Buldyrev, A. L. Goldberger, S. Havlin, R. N. Mantegna, M. E. Matsa, C. K. Peng, M. Simons and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1995, 51, 5084 CrossRef CAS PubMed.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 4364 CrossRef CAS PubMed.
- W. Kob and H. C. Andersen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 4626 CrossRef CAS PubMed.
- P. Das, A. D. S. Parmar and S. Sastry, 2018, arXiv preprint arXiv:1805.12476.
- D. J. Lacks and M. J. Osborne, Phys. Rev. Lett., 2004, 93, 255501 CrossRef PubMed.
- J. Feder, Fractals, Springer Science & Business Media, 2013 Search PubMed.
- P. C. Ivanov, M. G. Rosenblum, C. K. Peng, J. E. Mietus, S. Havlin, H. E. Stanley and A. L. Goldberger, Phys. A, 1998, 249, 587–593 CrossRef PubMed.
- A. Bunde, S. Havlin, J. W. Kantelhardt, T. Penzel, J. H. Peter and K. Voigt, Phys. Rev. Lett., 2000, 85, 3736 CrossRef CAS PubMed.
- M. S. Movahed, F. Ghasemi, S. Rahvar and M. R. R. Tabar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 021103 CrossRef PubMed.
- A. Madanchi, M. Absalan, G. Lohmann, M. Anvari and M. R. R. Tabar, Sol. Energy, 2017, 144, 1–9 CrossRef.
- A. Madanchi, F. Taghavi-Shahri, S. M. Taghavi-Shahri and M. R. R. Tabar, Eur. Phys. J. B, 2020, 93, 1–8 CrossRef.
- P. C. Ivanov, L. A. N. Amaral, A. L. Goldberger, S. Havlin, M. G. Rosenblum, Z. R. Struzik and H. E. Stanley, Nature, 1999, 399, 461–465 CrossRef CAS PubMed.
- M. S. Movahed, G. R. Jafari, F. Ghasemi, S. Rahvar and M. R. R. Tabar, J. Stat. Mech. Theor. Exp., 2006, 2006, P02003 Search PubMed.
- S. Sengupta, S. Karmakar, C. Dasgupta and S. Sastry, J. Chem. Phys., 2013, 138, 12A548 CrossRef PubMed.
- W. Gotze and L. Sjogren, Rep. Prog. Phys., 1992, 55, 241 CrossRef.
- L. Berthier and G. Biroli, Glasses and Aging, A Statistical Mechanics Perspective on, 2009 Search PubMed.
- N. Abedpour, R. Asgari and M. R. R. Tabar, Phys. Rev. Lett., 2010, 104, 196804 CrossRef CAS PubMed.
- M. R. R. Tabar, M. Anvari, G. Lohmann, D. Heinemann, M. Wächter, P. Milan, E. Lorenz and J. Peinke, Eur. Phys. J.-Spec. Top., 2014, 223, 2637–2644 CrossRef.
- L. Berthier and J. L. Barrat, J. Chem. Phys., 2002, 116, 6228–6242 CrossRef CAS.
- F. Varnik, J. Chem. Phys., 2006, 125, 164514 CrossRef CAS PubMed.
- I. C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS.
- R. O. Sokolovskii, M. Thachuk and G. N. Patey, J. Chem. Phys., 2006, 125, 204502 CrossRef CAS PubMed.
- F. Orts, G. Ortega, E. M. Garzón and A. M. Puertas, Comput. Phys. Commun., 2019, 236, 8–14 CrossRef CAS.
Footnote |
| † Madanchi and Yu have equal contribution. |
| This journal is © The Royal Society of Chemistry 2021 |