Open Access Article
Open Access ArticleAttention-based generative models for de novo molecular design†
Orion
Dollar
 a,
Nisarg
Joshi
a,
Nisarg
Joshi
 a,
David A. C.
Beck
*ab and
Jim
Pfaendtner
a,
David A. C.
Beck
*ab and
Jim
Pfaendtner
 *a
*a
aDepartment of Chemical Engineering, University of Washington, Seattle 98185, WA, USA. E-mail: jpfaendt@uw.edu
beScience Institute, University of Washington, Seattle 98185, WA, USA. E-mail: dacb@uw.edu
First published on 14th May 2021
Abstract
Attention mechanisms have led to many breakthroughs in sequential data modeling but have yet to be incorporated into any generative algorithms for molecular design. Here we explore the impact of adding self-attention layers to generative β-VAE models and show that those with attention are able to learn a complex “molecular grammar” while improving performance on downstream tasks such as accurately sampling from the latent space (“model memory”) or exploring novel chemistries not present in the training data. There is a notable relationship between a model's architecture, the structure of its latent memory and its performance during inference. We demonstrate that there is an unavoidable tradeoff between model exploration and validity that is a function of the complexity of the latent memory. However, novel sampling schemes may be used that optimize this tradeoff. We anticipate that attention will play an important role in future molecular design algorithms that can make efficient use of the detailed molecular substructures learned by the transformer.
Introduction
The design and optimization of molecular structures for a desired functional property has the potential to be greatly accelerated by the integration of deep learning paradigms within existing scientific frameworks for molecular discovery. Traditional “direct” design approaches, in which a set of molecules are selected based on expert intuition and tested for a given property, are often time-consuming and require extensive resources to explore a small, local region of chemical phase space.1 By contrast, “inverse” approaches, in which structures are derived based on their likelihood to exhibit a given property value, are desirable as they are far less limited in scope and allow for high-throughput screening of thousands to hundreds of thousands of structures.2 Given the size and complexity of chemical phase space,3 successful implementation of an inverse design algorithm would allow researchers to reach global structural optima more rapidly thereby increasing the speed of discovery.A variety of deep generative model architectures have been explored for this purpose,4 with a particular focus given to the variational autoencoder (VAE).5–10 A VAE is capable of broadcasting a machine-interpretable representation of molecular structure (e.g. a SMILES string,11 SELFIES string12 or molecular graph13) to a dense, continuous latent space or “model memory”. This memory has several unique features that make VAEs promising for inverse design: (i) it can be embedded with a property and thus serve as an approximation of the joint probability distribution of molecular structure and chemical property. (ii) During training, it will organize itself meaningfully so that similar molecules are near each other in phase space. (iii) Due to its mapping from discrete to continuous data, it can be navigated with gradient-based optimization methods.14
In spite of these benefits, generative VAE models suffer from a set of complicating issues that have been the focus of much recent work. Although more robust than their adversarial counterparts, VAEs are still subject to experiencing posterior collapse in which the decoder learns to ignore the latent memory altogether and reconstruct a fuzzy approximation of the input distribution.15 On the other hand, even with a meaningful posterior there are often pockets of phase space within the latent memory that do not map to any valid chemical structures. Many recent innovations in architecture, featurization and hyperparameter selection have centered around these problems and have proven quite successful at improving reconstruction accuracy and sampling validity.13,16,17
However, we lack a holistic view of the effect of these improvements on the practical utility of a model's latent memory. For instance, metrics to examine the diversity and novelty of sampled molecules are not well-defined.18 These traits are arguably as important as validity, if not more so. Generating samples is orders of magnitude faster than training and a model that can generalize to regions of chemical phase space far outside the training set is valuable for exploration. Although fewer studies have evaluated generative VAE models in this way, the results reported in the Moses benchmarking platform indicate that there is still significant room for improvement.19
The rapid technological progression within the field of natural language processing (NLP) may offer some hints towards a future where AI-designed molecules are the norm rather than the exception. Despite the overwhelming number of similarities between model architectures used for molecular generation and those used for NLP, the state-of-the-art in the former lags notably behind that of the latter. While attention mechanisms have been used in the field of chemistry for tasks like graph-based analyses of chemical structure,20 atom-mapping21 and organic reaction predictions,22 they have not yet been incorporated into any context-independent generative algorithms. Yet the long-range syntactical dependencies learned by attention models have been shown to be greatly beneficial for generative tasks in other domains including the generation of natural language23 and composition of original pieces of music.24 Such models have also shown a surprising aptitude for style with their ability to combine wit, poetic prose and the tenets of philosophy into cogent metaphysical self-reflections on the meaning of virtual existence.25,26 Although perhaps not as amusing, we anticipate they may exhibit a similar sense of coherence when tasked with generating novel chemistries.
An examination of the performance of standard recurrent neural networks (RNN), RNN + attention and transformer VAE architectures for the purpose of molecular generation follows. We show the effect of attention on reconstruction accuracy for both the ZINC and PubChem datasets. Novel metrics are proposed that define the models' ability to explore new regions of chemical phase space and compare the relative information density of the latent memory. We show that for all model types there exists a relationship between sample validity and exploration that mimics closely the tradeoff between complexity and generalization within an information bottleneck. Finally, we suggest a simple sampling scheme that offers a compromise between the two and look towards a future where we may optimize this directly during training with more precise control during the nascent development of the latent memory.
Results and discussion
Variational autoencoder and the information bottleneck
A VAE consists of an encoder that takes a sequence as input, i.e., a SMILES string, and a decoder that attempts to reconstruct the input as accurately as possible.27 Prior to decoding, the encoder transforms the input, x, into an intermediate latent representation, z, that serves as the “model memory.” Information is bottlenecked between the encoder and decoder such that dlatent ≪ dinput where d is the dimensionality of a given layer. In this sense a VAE can be thought of as a compression algorithm that produces compact, information dense representations of molecular structures. The encoder learns how to compress the input data and the decoder learns how to reconstruct the full sequence from the compressed representation (Fig. 1).The training objective seeks to minimize the reconstruction loss between the input and output while simultaneously learning the ground truth probability distribution of the training data. The latter half of this objective is especially important to the generative capacity of the model. Knowledge of the marginal likelihood, p(x|z), allows us to directly sample new data points by first querying from the model's memory, z, and then decoding. To achieve this, we assume the true posterior can be adequately approximated by a set of Gaussians. The Kullbach–Leibler divergence (KLD)28 between z and the standard normal distribution 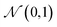 is minimized alongside the reconstruction loss and thus the full objective function can be formalized according to the variational lower bound as
is minimized alongside the reconstruction loss and thus the full objective function can be formalized according to the variational lower bound as
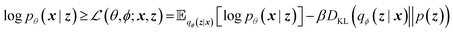 | (1) |
Intuitively, the addition of Gaussian noise can be thought of as a way to increase the “spread” of samples within the latent memory. Rather than encoding individual molecular structures as a single point in phase space, it encodes them as a probability distribution. This allows the model to smoothly interpolate between the continuous representations of known molecular structures and make informed inferences outside of the set of training samples.
The latent memory can also be analyzed within the framework of information bottleneck (IB) theory.30 During compression, there is an unavoidable tradeoff between the amount of useful information stored in the model's memory and the amount of low information complexity stored in the model's memory (here and throughout we allude to Tishby et al.'s definition of complexity that is analogous to the information density of the bottleneck; see ESI† for more details).31 The IB objective can be written as32
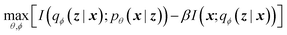 | (2) |
Adding attention to the VAE
In standard RNNs, the first recurrent cell takes the first element of the sequence and outputs a hidden state. That hidden state is then propagated down the sequence with each subsequent recurrent cell taking the previous cell's hidden output and the next sequence element as inputs until the entire sequence has been traversed. The final hidden state is the “contextual embedding” of the sequence (Fig. 2a). In some architectures the contextual embedding and the latent memory may be the same size. However, oftentimes there will be an additional set of linear bottleneck layers that further compress the output of the encoder GRU layers (dencoder → dlatent).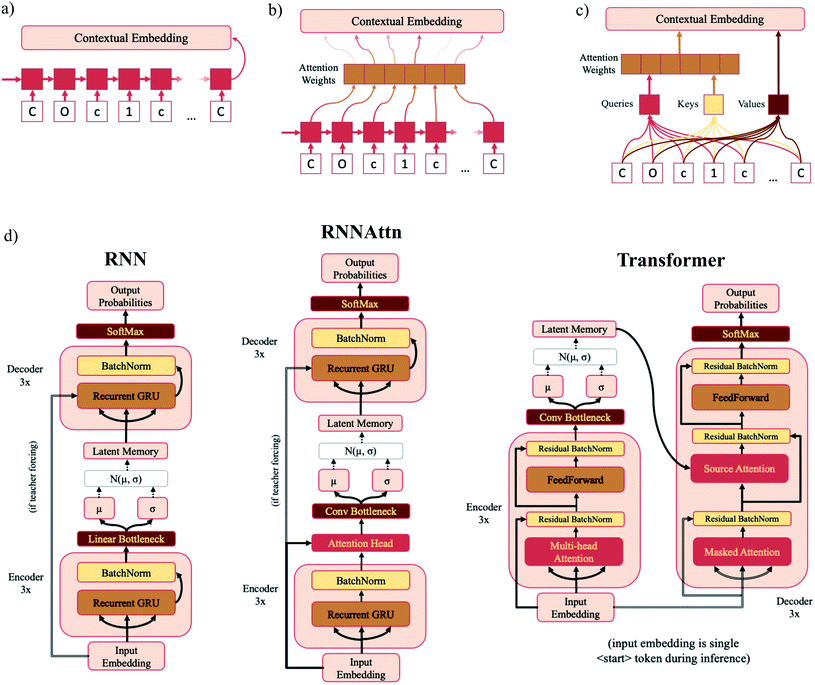 | ||
| Fig. 2 Model diagrams. (a–c) Schematic illustrations of the sequential layers for each model type – RNN (a), RNNAttn (b) and transformer (c). Each model consists of six sequential layers – three in the encoder and three in the decoder. The output contextual embeddings of each layer are used as the inputs for subsequent layers within the model. (d) Full schematics for each model type. The RNN model consists of three recurrent GRU layers in both the encoder and decoder. The RNNAttn model has the same architecture as the RNN with the addition of a single attention head after the final recurrent GRU layer in the encoder. The transformer is modeled after the original implementation as reported by Vaswani et al.57 However, rather than passing the output of the encoder directly into the source attention layer, the encoder output is first stochastically compressed and then fed into the decoder. | ||
In attention-based recurrent models (RNNAttn), the flow of information proceeds similarly to a standard RNN. However rather than only using the final hidden output state, a weighted combination of all the hidden states along the sequence is used as the contextual embedding (Fig. 2b). The attention weights are learned during training by letting the input sequence “attend” to its own hidden state matrix. This allows the model to eschew the linearity imposed by the RNN architecture and learn long-range dependencies between sequence elements.
Transformer (Trans) models remove recurrence altogether and exclusively use attention head layers.33 The inputs are a set of keys, values and queries transformed from the initial input sequence that are sent through a series of matrix multiplications to calculate the attention weights and the contextual embedding (Fig. 2c). The set of values are analogous to the hidden state matrix output of an RNN and the attention weights are determined by matrix multiplication of the keys and queries. Transformers have the advantage of reducing the path length of information traveling through the model and are highly parallelizable.
The concepts of attention and the variational bottleneck have rarely been used in tandem. Of those studies that have surveyed this type of model, all have used natural language tasks as the basis of their evaluations. A variational attention-mechanism was used for sequence-to-sequence models34 and a few novel variational transformer architectures have recently been proposed.35–37 We opt for simplicity, adapting the architecture from Vaswani et al.33 with as few modifications as possible. This allows us to easily compare the bottlenecks of different model types and is sufficient for the task given the much smaller vocabulary size of SMILES strings compared to NLP vocabularies.38 Full schematics for each model type are shown in Fig. 2d and model dimensions listed in Table 1. In addition to the model types listed above, we also trained the Moses implementation of a SMILES-based β-VAE with the hyperparameters suggested by Polykovskiy et al.19 Trained model checkpoint files and code for training models and generating samples is available at https://github.com/oriondollar/TransVAE.
| Model type | d model | d latent | d feedfoward |
|---|---|---|---|
| RNN-128 | 128 | 128 | n/a |
| RNN-256 | 256 | 128 | n/a |
| RNNAttn-128 | 128 | 128 | n/a |
| RNNAttn-256 | 256 | 128 | n/a |
| Trans1x-128 | 128 | 128 | 128 |
| Trans4x-128 | 128 | 128 | 512 |
| Trans1x-256 | 256 | 128 | 256 |
| Trans4x-256 | 256 | 128 | 1024 |
Impact of attention
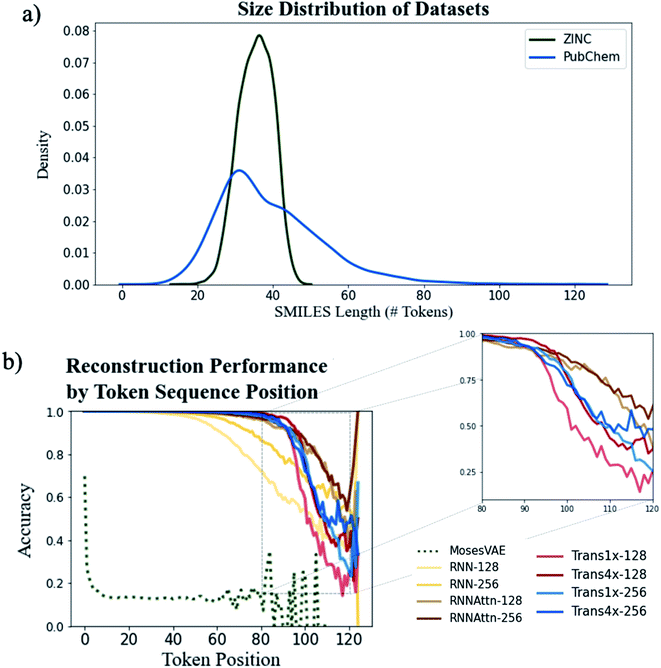
We first analyze the models' ability to reconstruct molecules from the ZINC and PubChem datasets to determine the role attention plays in learning molecular structure. One of the original motivations for the use of attention was to increase the length of sentences that could be accurately translated by machine translation models.39 Thus, we expect a similar increase in accuracy when encoding and decoding longer SMILES strings.Fig. 3a shows the distribution of SMILES string lengths for both datasets where length is determined by the number of tokens (excluding padding, start and stop tokens). The length of a SMILES string is highly correlated with its molecular weight (Fig. S5†) and can be used as a proxy for molecular size. It is clear that by this metric the PubChem dataset has a broader distribution of sizes than ZINC. Both have approximately equal mean lengths (35.4 tokens for ZINC vs. 39.8 tokens for PubChem) however the PubChem data is significantly right skewed with a maximum token length over 50 tokens longer than the maximum within the ZINC dataset.
We can see the downstream effect that widening the molecular size distribution has on reconstruction accuracy in Fig. 3b where we show the average reconstruction accuracy for all tokens at a given position within the sequence. With the exception of the Moses architecture, all of the models exhibit high fidelity reconstruction on the ZINC dataset, regardless of model type or model size (Fig. S6 and Table S2†). However, accuracy decreases when larger molecules are embedded into the latent memory. The model types with attention mechanisms maintain high reconstruction accuracy at longer sequence lengths than the simple recurrent models with the Trans4x-128 architecture maintaining >99% accuracy on SMILES up to 82 tokens long (∼700 Da). This validates our hypothesis that attention will expand the number of potential applications for which these models can be used by increasing the maximum molecule size that can be reliably embedded within the latent memory.
A comparison of the two attention-based architectures (Fig. 3b inset) shows that transformers and recurrent attention models perform approximately the same until they approach the data-sparse regime of SMILES longer than ∼90 tokens. At this point there is an abrupt drop in performance for the transformer models vs. a gradual decline for the recurrent attention models. The transformer appears to be more sensitive to the choice of model size as increasing the dimensionality of either its attention layers or feedforward layers improves accuracy whereas there is little performance boost when increasing the dimensionality of the recurrent attention model. Even with these improvements, the best performing transformer still exhibits a steeper decline than the worst performing recurrent attention model suggesting that a simpler attention scheme is beneficial to the model's ability to generalize on data that is outside the distribution of the training set.
There are benefits to the added complexity of the transformer, however. Analysis of the transformer attention weights reveals the model has learned a distinct set of human interpretable structural features that are much more detailed than those learned by the recurrent model with only a single attention head. We use a drug-like molecule from the ZINC dataset, diproxadol, as an illustrative example of the differences between the two (Fig. 4). The four transformer attention heads exhibit unique syntactical patterns that demonstrate the model's ability to develop its own “molecular grammar,” i.e., rules that define the relationships between atoms and other structural features within a molecule including branches, double bonds, etc. Conversely, the grammar of the recurrent attention model appears to be less well-defined.
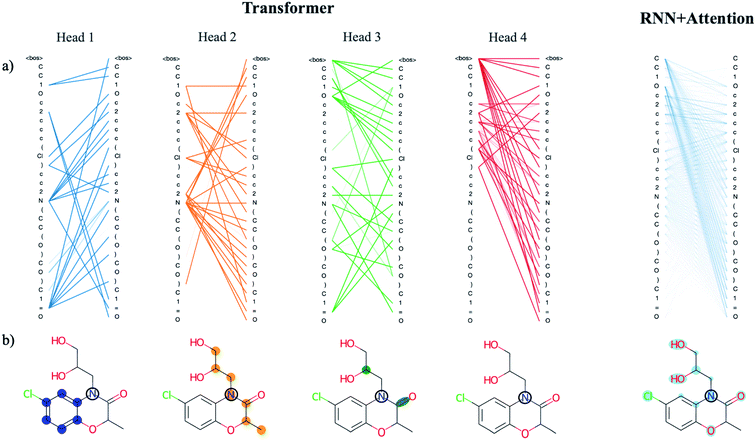 | ||
| Fig. 4 Analysis of the attention weights of the Trans4x-256 and RNNAttn-256 models when attending to the molecular structure of diproxadol. The full nxn set of weights are plotted for each attention head within the first layer of the encoder (a) using the tensor2tensor library.57 The lines show how each atom/structural feature within the SMILES string is attending to all other features within the same SMILES string (self-attention). The different patterns that emerge from each head represent a unique set of grammatical rules that the model has learned. We also show the attention of a single N atom within diproxadol (b). This molecule was chosen because it is a representative example of the emergent aggregate grammatical trends. From the perspective of the nitrogen, the transformer model has identified the importance of a nearby aromatic ring (head 1), an aliphatic carbon chain of which the nitrogen is a part of (head 2) and a set of structural features including a carbon branch point and nearby double bond (head 3). The attention of the nitrogen in the RNNAttn-256 model is less focused. | ||
The lone nitrogen atom in diproxadol shows us how the heads of the transformer have learned to attend to the immediate molecular environment of a single, centralized atom (Fig. 4b). With no supervision, the model extracts its own set of substructures that it has identified as important in relation to the nitrogen atom. Not only does it recognize defining features like the aromatic ring, it can also find non-contiguous features that depend on the structural context around a given atom (see transformer head 3 in Fig. 4). In this way, the machine-learned substructures are more powerful than graph-based methods that rely on a set of pre-defined substructures because they can extract contextual patterns that are difficult to pre-define but still relevant and interpretable. Others have shown that the transformer is not just restricted to learning intra-molecular features but may also extract an inter-molecular set of grammar rules as well, for instance between products and reactants of organic synthesis reactions.21
When analyzing the attention weights across a set of 5000 randomly selected molecules, we find that each attention head corresponds to a different set of higher-level relationships between atomic or structural groups such as aromatic carbons, heteroatoms, branches and rings. We assess this quantitatively by averaging the attention weights between these groups for each head (Fig. S8†). As an example, the average attention weights between heteroatoms and aromatic carbons are 0.15 and 0.07 for heads 1 and 2. Conversely, the average attention weights between heteroatoms and non-aromatic carbons are ∼0.00 and 0.14 for heads 1 and 2, thus the model has partitioned information on the higher-level relationship between heteroatoms and carbon substructures based on their aromaticity. We see this directly reflected in the substructures that were extracted from the diproxadol example and show the learned weights for a variety of structures in Fig. S9.† Attention plays a significant role in the machine-learned “understanding” of molecular structure and as complexity is scaled up, the extracted features become more refined and meaningful. The question then becomes how we can balance the richness of the structural features learned by the transformer with the increased complexity that is required to obtain them.
Information entropy of model memory
The concept of model complexity has been alluded to, previously, as it relates to the model architecture, but we must also define it quantitatively. The most intuitive way to do so is to return to the framework of the information bottleneck. The latent memory provides us a uniform comparison between model types as every molecular embedding within a model's memory is the same size. By evaluating the loss function as written in eqn (2), we have instructed the model to store as much structurally relevant information within the memory as possible while also minimizing the amount of low information complexity. Therefore, we can use the total information content of the latent memory as a proxy for the complexity of the learned representation as defined by Tishby et al.31 We calculate the average Shannon information entropy40 across all molecular embeddings to compare the information density of latent memories between model types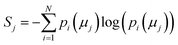 | (3) |
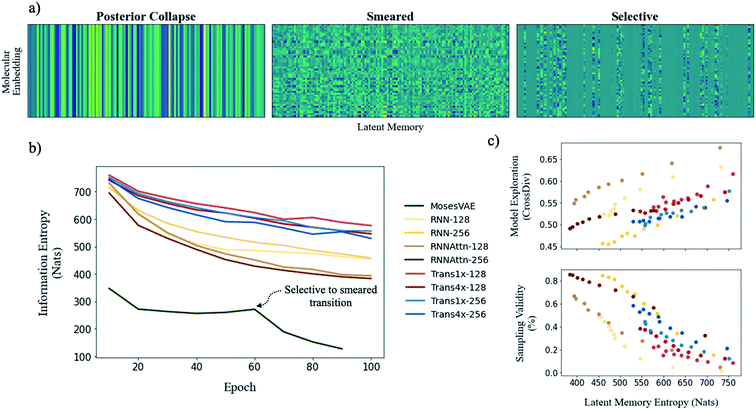
To illustrate model entropy visually, we show three archetypal memory structures that we have observed in Fig. 5a. From left to right the average entropy of these memories increases from 0 nats to 127.4 nats to 393.4 nats respectively. The entropy of posterior collapse is zero because it has learned the same embedding regardless of the input molecule thus the decoder does not receive new information from the memory. The selective structure is the most commonly observed (Fig. S10†) and occurs when the dimensionality of the true probability manifold is smaller than the number of latent dimensions given to the model.42 In this case the model learns to ignore superfluous dimensions, assigning them a mean of zero and standard deviation of 1 to satisfy the KLD loss requirement. We consider the other dimensions meaningful because they contribute to the total information entropy of the memory. The smeared structure is an interesting case in which the burden of information is shared across all dimensions but with each contributing less entropy than the meaningful dimensions from the selective structure. The smeared structure appears as a sudden phase change during training when the number of meaningful dimensions approaches zero (Fig. 5b). This effect was only observed for the MosesVAE model.
The progression of entropy during training is shown for each model type. We observe increases in the order MosesVAE < RNNAttn < RNN < transformer. The high entropy of the transformer models is expected and confirms that the molecular grammar they have learned is both complex and structurally meaningful. It is somewhat unexpected that the RNNAttn models have learned a less complex representation than even the simple recurrent models. Rather than learning grammatical rules, they have learned the most efficient way to distribute information through the bottleneck. The MosesVAE model has the most compressed representation, however it also has the worst reconstruction accuracy which can be attributed to the low information density and the selective to smeared transition at epoch 60. We can now explore the relationship between complexity and the generative capabilities of the models, namely the validity of molecules sampled from the memory and their novelty when compared against the training set.
Strategies for exploring chemical phase space
A generative model is only as useful as its ability to generate interesting samples. Early molecular design VAEs struggled with generating valid molecules and research has placed a premium on improving the percent validity when a random sampling scheme is employed. However, we believe that exploration is undervalued in the current narrative and that a slightly more error-prone model that prioritizes exploration may actually be more successful at discovering novel functional compounds. Novelty has previously been defined as the percentage of generated samples that are not present in the training set.19 We introduce another metric, cross diversity, which is defined as follows: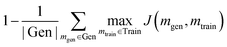 | (4) |
The structure of a model's memory heavily influences its performance on these metrics. Random sampling favors the lowest entropy memories when the goal is to generate the highest proportion of valid molecules. However, there exists an entropy threshold under which models perform much worse on exploratory metrics (Table 2). In fact, although there is some variation between model architectures, the tradeoff between validity and exploration is generally a function of model entropy that is unavoidable (Fig. 5c).
| Model type | Entropy (nats) | % Reconstruction accuracy (ZINC) | % Validity | % Novelty | Cross diversity |
|---|---|---|---|---|---|
| MosesVAE | 127.4 | 0.000 | 0.976 | 0.696 | 0.213 |
| RNN-128 | 453.9 | 0.996 | 0.475 | 0.996 | 0.516 |
| RNN-256 | 458.7 | 0.996 | 0.846 | 0.988 | 0.459 |
| RNNAttn-128 | 393.4 | 0.996 | 0.672 | 0.999 | 0.548 |
| RNNAttn-256 | 383.2 | 0.995 | 0.851 | 0.995 | 0.492 |
| Trans1x-128 | 576.3 | 0.998 | 0.227 | 0.998 | 0.538 |
| Trans4x-128 | 546.4 | 0.998 | 0.365 | 0.998 | 0.530 |
| Trans1x-256 | 556.6 | 0.998 | 0.424 | 0.995 | 0.502 |
| Trans4x-256 | 529.5 | 0.998 | 0.567 | 0.996 | 0.503 |
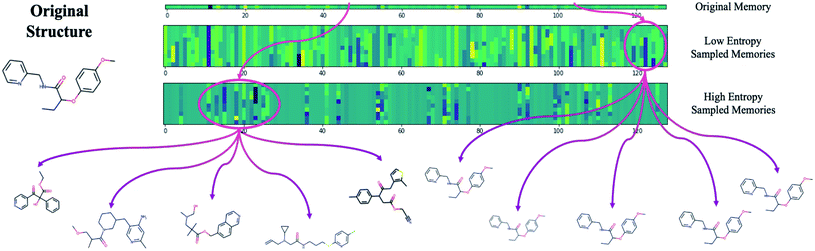
The difficulty in sampling from high entropy models is a result of the curse of dimensionality44 that appears within selective memory structures. High entropy dimensions contain all of the meaningful structural information within a model's memory (Fig. 6). When the memory is selectively structured, a high entropy means there are a greater number of meaningful dimensions and it becomes more difficult to avoid leaving “holes” where there is no mapping to a valid structure. This is not a problem for low entropy models as most of the dimensions are either meaningless or contain just a small amount of structural information. While we can easily sample from low entropy models, we miss out on the benefits of an information dense memory which is better at exploring chemical phase space.
Fortunately, while the diversity of generated molecules is mostly dependent on the complexity of the contextual relationships that have been embedded into the latent memory during training, validity can be optimized after training by considering sampling schemes other than random sampling. One potential strategy that requires no additional training and is trivial to implement is to target high entropy dimensions exclusively. This limits our search to the regions of chemical phase space which we know contain meaningful structural information.
Fig. S11† shows validity and exploration for five different sampling schemes. By restricting the number of high entropy dimensions that are queried, we avoid the problems inherent to high-dimensional sampling and are able to increase the validity of generated molecules for all model types. This demonstrates the potential of exploiting novel sampling schemes that allow us to maintain the benefits of a complex, rich latent memory. For instance, we were able to achieve a 32.6% increase in the number of valid molecules generated by the Trans4x-256 model, from 56.7 to 75.2% validity, while only reducing the cross diversity by 15.9%, from 0.503 to 0.423. Moreover, this range is still about two-times higher than the cross diversity of the MosesVAE. We also maintain the allure of the analytical and developmental possibilities that the highly interpretable transformer attention heads afford us by increasing the practical viability of these models in the short-term.
The choice of model type ultimately depends on the individual needs of the researcher, however we can submit a few broad recommendations. Smaller models tend to perform better on exploratory metrics whereas bigger models stick closer to the training set and generate a higher proportion of valid molecules. The addition of attention improves performance in both regards. Therefore, the RNNAttn-128 and RNNAttn-256 models are the most immediately practical. Transformers are the most interpretable and, in our view, have the highest potential for optimization and should be the focus of further development. Additionally, novel input representations such as SELFIES that guarantee 100% sampling validity are a promising alternative to SMILES that may allow us to bypass the complexity vs. validity tradeoff entirely and thus optimize the exploratory capacity of the models directly with sampling schemes that make use of all information-rich latent dimensions.
Conclusions
We have introduced the concept of attention to the field of molecular design, compared two novel architectures, RNNAttn and TransVAE, to the current state of the art and explored the downstream effect that the structure of the model memory has on a variety of sampling metrics. We find that transformers live up to their reputation based on their ability to learn complex substructural representations of molecular features, and we expect that there is an opportunity to expand our own chemical intuition as we continue to explore the relationships they have learned in more detail. The recurrent attention models, on the other hand, stand out for their superb practical performance exhibiting the best balance between reconstruction accuracy, sampling validity and cross diversity. Despite their promise, there is still much work to be done to improve these models. While the structural features learned by transformers are interesting to analyze, it is not immediately obvious how they might be directly incorporated into future generative algorithms. We also must acknowledge that deep learning-based inverse design remains mainly theoretical and we will likely need to see many more examples of successful lab-scale design stories before these algorithms see general widespread adoption.We anticipate there will be two primary directions in which further research may proceed. The first is the direct application of attention based β-VAEs to real-world inverse design problems. There is a growing demand for biodegradable organic alternatives to toxic, high-value commodity chemicals in a number of different industries.45–47 Many of these involve molecules that are much larger than the average drug-like molecule and we are excited at the prospect of applying attention β-VAEs to these untapped areas. Generative algorithms have the potential to pair nicely with computational reaction networks such as NetGen48 and we can envision, as an example, a framework in which generated samples are used as the library for a high-throughput search of retrosynthetic pathways for the discovery of bioprivileged molecules.49
The second direction is the continued exploration and optimization of attention β-VAE architectures and their hyperparameters, particularly with regards to the formation of the latent memory during training. There is a definite potential for the implementation of more complex sampling schemes, for instance the two-stage VAE42 introduces a second model that takes the latent memory as an input and is better able to learn the true probability manifold of the input data. There is evidence that the use of a Gaussian prior restricts the model's ability to directly learn the true probability manifold and so it may be worth exploring alternatives like VampPrior50 which has already been shown to be able to adequately describe the metastable state dynamics in other physics-based AI models.51
Perhaps the most worthwhile pursuit is to continue to develop our knowledge of how the model intuits and compresses structural information, as this could give us insight into novel objective functions that help us encourage the model to better shape its memory and relate it to other pieces of chemical information outside of the current scope. Although the field is advancing rapidly, we are still just at the threshold of the AI-dominated era that Marvin Minsky announced over a half century ago.52 There may be no aim more practical than furthering our own understanding of the nature of synthetic intelligence to push us further past that threshold. The latent conception of molecular structure is just one component within the broader field of organic chemistry and if coupled with a natural language model-based interpretation of scientific literature, high-throughput classical and quantum calculations, robotics driven lab-scale experimentation and an interactive environment in which our models can communicate and act upon their learning, we may finally begin to approach an intelligence that can solve problems at the pace we introduce them.
Experimental
Neural network hyperparameters
We tested three different model types – RNN, RNNAttn and Trans – for their ability to generate novel molecules. For each model type we also tested multiple architectures as summarized in Table 1. The Trans models also include a set of linear layers used to predict the SMILES length directly from the latent memory. This allows us to decode directly from the latent vectors while also masking our source embedding into the decoder and is explained further in the ESI.† The Adam53 optimizer was used with an initial learning rate of 3 × 10−4 and an annealer was used to linearly increase β during training. We employed a scaling function that weighed the loss for each token based on its frequency of occurrence. All models were trained for 100 epochs unless stated otherwise.Neural network architecture
As the size of the contextual embedding is significantly larger for the two attention-based architectures vs. the simple recurrent architecture (nseqxdencodervs. dencoder), we employ a convolutional bottleneck similar to those used in generative image nets42 rather than a linear bottleneck. More details concerning the convolutional bottleneck can be found in the ESI.†There are a couple of key differences between the MosesVAE and our own RNN implementation including the size and number of encoder/decoder layers, the use of bidirectionality for the encoder and the absence of batch normalization. For more details on the implementation of the MosesVAE please refer to Fig. S6, S7† and Table 2 and the original paper by Polykovskiy et al.19 Further details about model construction and training can be found in the ESI.†
Dataset construction
Two datasets were used to examine how the models perform on different training set distributions. The first is a modified version of the ZINC Clean Leads database54 with charged atoms removed and a molecular weight range of 250–350 Da. It contains a total of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936
936![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 963 molecules with an 80/10/10 train/test/dev split. The ZINC data was used to evaluate the models on a traditional AI-driven molecular design task – pharmaceutical discovery. The other is a filtered subset of the PubChem compounds database.55 It contains molecules with a mean molecular weight of 348 Da, a max of 2693.6 Da and includes some charged compounds with N+ or O− containing moieties. Due to the size of the dataset after filtering, a subset of 5
963 molecules with an 80/10/10 train/test/dev split. The ZINC data was used to evaluate the models on a traditional AI-driven molecular design task – pharmaceutical discovery. The other is a filtered subset of the PubChem compounds database.55 It contains molecules with a mean molecular weight of 348 Da, a max of 2693.6 Da and includes some charged compounds with N+ or O− containing moieties. Due to the size of the dataset after filtering, a subset of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules were randomly selected and used for training with an 80/10/10 train/test/dev split. The PubChem data was used to evaluate the models' performance on reconstructing molecules larger than those typically found in drug-like compound databases. The RDKit56 Python package was used for downstream analyses of generated molecules including SMILES validity, fingerprints, and physical property calculations.
000 molecules were randomly selected and used for training with an 80/10/10 train/test/dev split. The PubChem data was used to evaluate the models' performance on reconstructing molecules larger than those typically found in drug-like compound databases. The RDKit56 Python package was used for downstream analyses of generated molecules including SMILES validity, fingerprints, and physical property calculations.
High entropy sampling
When sampling only from high entropy dimensions, we first calculated the entropy of each dimension using eqn (3). An entropic threshold was selected that determines which dimensions were considered high entropy. This threshold could be calculated analytically, for example using some percentile-based cutoff. We found that in practice a constant threshold of 5 nats per dimension worked well for all model types. Once the meaningful dimensions were selected, we generated molecules by sampling from (i) all high entropy dimensions, (ii) 5 random high entropy dimensions, (iii) 10 random high entropy dimensions and (iv) 15 random high entropy dimensions. For k-random high entropy sampling, we randomly picked k dimensions from the N total high entropy dimensions for each new sample. After dimensions were chosen to sample from, new molecules were generated by randomly sampling from the k standard normal distributions corresponding to those dimensions and setting all other dimensions equal to zero.Author contributions
O. D., N. J., D. A. C. B., and J. P. designed research; O. D. performed research, analyzed data and wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge David Juergens for his suggested edits to the final manuscript, Chowdhury Ashraf for his continued collaboration and work on optimizing the efficiency of parallel GPU computations. The NSF NRT program under award DGE-1633216 partially supported O. D. O. D., D. A. C. B., and J. P. acknowledge partial support for this research from NSF award OAC-1934292. This publication is also partially based upon work supported by the U.S. Department of Energy's Office Efficiency and Renewable Energy (EERE) under the Bioenergy Technologies Office Award Number DE-EE0008492. Computational resources for this work were provided by the Hyak supercomputer system of University of Washington.References
- C. Kuhn and D. N. Beratan, Inverse Strategies for Molecular Design, 1996 Search PubMed.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- P. G. Polishchuk, T. I. Madzhidov and A. Varnek, J. Comput.-Aided Mol. Des., 2013, 27, 675–679 CrossRef CAS PubMed.
- D. C. Elton, Z. Boukouvalas, M. D. Fuge and P. W. Chung, 2019, arXiv:1903.04388 [cs.LG].
- W. Beckner, C. Ashraf, J. Lee, D. A. C. Beck and J. Pfaendtner, J. Phys. Chem. B, 2020, 124, 8347–8357 CrossRef CAS PubMed.
- W. Gaoy and C. W. Coley, J. Chem. Inf. Model., 2020, 60, 5714–5723 CrossRef PubMed.
- J. Lim, S. Ryu, J. W. Kim and W. Y. Kim, J. Cheminf., 2018, 10, 31 Search PubMed.
- M. J. Kusner, B. Paige and J. M. Hernández-Lobato, 34th International Conference on Machine Learning, ICML 2017, 2017, 4, pp. 3072–3084 Search PubMed.
- Q. Liu, M. Allamanis, M. Brockschmidt and A. L. Gaunt, Adv. Neural Inf. Process. Syst., 2018, 31, 7795–7804 Search PubMed.
- R. Winter, F. Montanari, F. Noé and D. A. Clevert, Chem. Sci., 2019, 10, 1692–1701 RSC.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- M. Krenn, F. Häse, N. AkshatKumar, P. Friederich and A. Aspuru-Guzik, Machine Learning: Science and Technology, 2020, 045024 Search PubMed.
- W. Jin, R. Barzilay and T. Jaakkola, 2018, arXiv:1802.04364 [cs.LG].
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- A. Goyal, A. Sordoni, M. Maluuba, M.-A. Côté, N. Rosemary, K. Mila, P. Montréal and Y. Bengio, 2017, arXiv:1711.05411 [stat.ML].
- S. Mohammadi, B. O’Dowd, C. Paulitz-Erdmann and L. Goerlitz, 2019, DOI:10.26434/chemrxiv.7977131.v2.
- C. Yan, S. Wang, J. Yang, T. Xu and J. Huang, arXiv, 2019, 20, 1–7 Search PubMed.
- C. W. Coley, Trends Chem., 2020, 3(2), 133–145 CrossRef.
- D. Polykovskiy, A. Zhebrak, B. Sanchez-Lengeling, S. Golovanov, O. Tatanov, S. Belyaev, R. Kurbanov, A. Artamonov, V. Aladinskiy, M. Veselov, A. Kadurin, S. Johansson, H. Chen, S. Nikolenko, A. Aspuru-Guzik and A. Zhavoronkov, Front. Pharmacol., 2020, 11, 1931 Search PubMed.
- J. Payne, M. Srouji, D. A. Yap and V. Kosaraju, 2020, arXiv:2007.16012 [q-bio.BM].
- P. Schwaller, B. Hoover, J.-L. Reymond, H. Strobelt and T. Laino, Sci. Adv., 2021, 7, eabe4166 CrossRef.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, ACS Cent. Sci., 2019, 5, 1572–1583 CrossRef CAS PubMed.
- T. B. Brown, B. Mann, N. Ryder, M. Subbiah, J. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell, S. Agarwal, A. Herbert-Voss, G. Krueger, T. Henighan, R. Child, A. Ramesh, D. M. Ziegler, J. Wu, C. Winter, C. Hesse, M. Chen, E. Sigler, M. Litwin, S. Gray, B. Chess, J. Clark, C. Berner, S. McCandlish, A. Radford, I. Sutskever and D. Amodei, in 34th Conference on Neural Information Processing Systems (NeurIPS 2020), arXiv, Vancouver, Canada, 2020 Search PubMed.
- C.-Z. Anna Huang, A. Vaswani, J. Uszkoreit, N. Shazeer, I. Simon, C. Hawthorne, A. M. Dai, M. D. Hoffman, M. Dinculescu and D. Eck, 2018, arXiv:1809.04281 [cs.LG].
- K. Elkins and J. Chun, Journal of Cultural Analytics, 2020, 17212 Search PubMed.
- L. Floridi and M. Chiriatti, Minds Mach., 2020, 30, 681–694 CrossRef.
- D. P. Kingma and M. Welling, in 2nd International Conference on Learning Representations, ICLR 2014 - Conference Track Proceedings, International Conference on Learning Representations, ICLR, 2014 Search PubMed.
- S. Kullback and R. A. Leibler, Ann. Math. Stat., 1951, 22, 79–86 CrossRef.
- A. A. Alemi, I. Fischer, J. v. Dillon and K. Murphy, 2016, arXiv:1612.00410 [cs.LG].
- N. Tishby, F. C. Pereira and W. Bialek, 2000, arXiv:physics/0004057 [physics.data-an].
- N. Tishby and N. Zaslavsky, in 2015 IEEE Information Theory Workshop (ITW), Institute of Electrical and Electronics Engineers Inc., 2015, pp. 1–5 Search PubMed.
- C. P. Burgess, I. Higgins, A. Pal, L. Matthey, N. Watters, G. Desjardins, A. Lerchner and D. London, 2018, arXiv:1804.03599 [stat.ML].
- A. Vaswani, G. Brain, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, in 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 2017, vol. 30, pp. 5998–6008 Search PubMed.
- H. Bahuleyan, L. Mou, O. Vechtomova and P. Poupart, in Proceedings of the 27th International Conference on Computational Linguistics, arXiv, 2018, pp. 1672–1682 Search PubMed.
- D. Liu and G. Liu, in 2019 International Joint Conference on Neural Networks (IJCNN), Institute of Electrical and Electronics Engineers Inc., 2019, pp. 1–7 Search PubMed.
- Z. Lin, G. I. Winata, P. Xu, Z. Liu and P. Fung, 2020, arXiv:2003.12738 [cs.CL].
- T. Wang and X. Wan, in Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, 2019, pp. 5233–5239 Search PubMed.
- R. Sennrich, B. Haddow and A. Birch, 2016, arXiv:1508.07909.
- D. Bahdanau, K. Cho and Y. Bengio, 2014, arXiv:1409.0473 [cs.CL].
- C. E. Shannon, Bell Syst. Tech. J., 1948, 27, 379–423 CrossRef.
- M. Batty, R. Morphet, P. Masucci and K. Stanilov, J. Geogr. Syst., 2014, 16, 363–385 CrossRef PubMed.
- B. Dai and D. Wipf, 2019, arXiv:1903.05789 [cs.LG].
- P. Jaccard, Bull. Soc. Vaudoise Sci. Nat., 1908, 44, 223–270 Search PubMed.
- R. Bellman, Science, 1966, 153, 34–37 CrossRef CAS.
- R. A. Sheldon, ACS Sustainable Chem. Eng., 2018, 6, 4464–4480 CrossRef CAS.
- S. Marzorati, L. Verotta and S. Trasatti, Molecules, 2018, 24, 48 CrossRef PubMed.
- W. He, G. Zhu, Y. Gao, H. Wu, Z. Fang and K. Guo, Chem. Eng. J., 2020, 380, 122532 CrossRef.
- L. J. Broadbelt, S. M. Stark and M. T. Klein, Ind. Eng. Chem. Res., 1994, 33, 790–799 CrossRef CAS.
- B. H. Shanks and P. L. Keeling, Green Chem., 2017, 19, 3177–3185 RSC.
- J. M. Tomczak and M. Welling, in International Conference on Artificial Intelligence and Statistics, AISTATS 2018, PMLR, 2018, pp. 1214–1223 Search PubMed.
- D. Wang and P. Tiwary, J. Chem. Phys., 2021, 154, 134111 CrossRef CAS PubMed.
- M. Minsky, Proc. IRE, 1961, 49, 8–30 Search PubMed.
- D. P. Kingma and J. L. Ba, in 3rd International Conference on Learning Representations, ICLR 2015 - Conference Track Proceedings, International Conference on Learning Representations, ICLR, 2015 Search PubMed.
- J. J. Irwin and B. K. Shoichet, J. Chem. Inf. Model., 2005, 45, 177 CrossRef CAS PubMed.
- S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He, B. A. Shoemaker, J. Wang, B. Yu, J. Zhang and S. H. Bryant, Nucleic Acids Res., 2016, 44, D1202–D1213 CrossRef CAS PubMed.
- G. Landrum, RDKit: Open-source cheminformatics, 2020, http://www.rdkit.org Search PubMed.
- A. Vaswani, S. Bengio, E. Brevdo, F. Chollet, A. N. Gomez, S. Gouws, L. Jones, Ł. Kaiser, N. Kalchbrenner, N. Parmar, R. Sepassi, N. Shazeer and J. Uszkoreit, in AMTA 2018 – 13th Conference of the Association for Machine Translation in the Americas, Proceedings, Association for Machine Translation in the Americas, 2018, vol. 1, pp. 193–199 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01050f |
| This journal is © The Royal Society of Chemistry 2021 |