Accurate crystal structures and chemical properties from NoSpherA2

Abstract

The relationship between the structure and the properties of a drug or material is a key concept of chemistry. Knowledge of the three-dimensional structure is considered to be of such importance that almost every report of a new chemical compound is accompanied by an X-ray crystal structure – at least since the 1970s when diffraction equipment became widely available. Crystallographic software of that time was restricted to very limited computing power, and therefore drastic simplifications had to be made. It is these simplifications that make the determination of the correct structure, especially when it comes to hydrogen atoms, virtually impossible. We have devised a robust and fast system where modern chemical structure models replace the old assumptions, leading to correct structures from the model refinement against standard in-house diffraction data using no more than widely available software and desktop computing power. We call this system NoSpherA2 (Non-Spherical Atoms in Olex2). We explain the theoretical background of this technique and demonstrate the far-reaching effects that the improved structure quality that is now routinely available can have on the interpretation of chemical problems exemplified by five selected examples.

---

1. Introduction

1.1 The importance of crystallography for science

Single-crystal X-ray structure determination is arguably the most important analytical technique available to chemists since it alone can reveal the three-dimensional structure of matter cheaply, routinely and – above all – unambiguously. The impact of this technique on the scientific developments in chemistry, biology, materials science, engineering, and physics cannot be overstated. To date, 26 Nobel Prizes in medicine, chemistry, and physics have been awarded to more than 50 researchers directly associated with crystallography.¹ Some of the milestones of science are based on single-crystal X-ray diffraction, including the elucidation of the structures of DNA² and graphene.³ Large investments are made to push diffraction techniques for three-dimensional structure determination to new limits. These include the construction of X-ray synchrotron facilities and X-ray free-electron lasers⁴ as well as the exploration of possibilities to employ other radiation types like from neutron spallation sources⁵ and electron diffractometers.⁶

Unfortunately, crystallographic methods and software development have not kept up with hardware development. The vast majority of structure refinements are still based on techniques that make use of one crucial simplification that was introduced in the early days of crystallographic refinement: the Independent Atom Model (IAM), in which atoms are assumed to be separate, non-interacting spherical entities.⁷ Here, we show how an accessible generalized procedure in which quantum chemical calculations coupled with modern crystallographic software can solve a variety of chemical problems using single-crystal diffraction data of any kind.

1.2 How it used to work

X-rays interact with the electrons in a crystalline material, and this interaction gives rise to measurable diffraction. While most of the electrons are centered on the atoms themselves, some electrons are involved in chemical bonding and are therefore not located where they would be in non-interacting, spherical atoms, which are assumed in any standard refinement. This means that the diffraction pattern obtained from the experiment is due to the real distribution of the electrons in the compound of interest, not due to spherical distributions.

The diffraction pattern consists of thousands of unintelligible spots on hundreds of images. To make sense of it, it is necessary to resort to a model of the molecule that will give rise to the measured diffraction pattern. This model building is central to any technique based on diffraction, and it is this final model that we call a ‘crystal structure’. Calculating the expected diffraction pattern from this model requires a certain amount of computing power – and this is where the approximation comes in. Calculations are a lot easier if a spherical distribution of electron density around each atom is assumed. This IAM approximation works very well since most of the diffraction is due to the electrons on the atoms themselves – and the quality of diffraction data that could be obtained in the early days of the field was itself rather limited.

Today, X-ray crystallography finds itself in the strange position where the real diffraction pattern arising from the interaction of X-rays with electrons in their real positions can be measured with high precision and accuracy, and yet we still use an approximation in our models that leads to assuming the wrong positions of these electrons.

1.3 What we gain when we leave the century-old spherical approximation behind

In every chemical compound, electrons are involved in bonding of one kind or another – and in traditional X-ray crystallography, this has been ignored. Only if we model this non-sphericity we can gain deep insights into intra- and intermolecular chemical bonding. Detailed and accurate information on chemical bonding from the diffraction experiment is of major importance, for example, for materials design,⁸ catalysis,⁹ drug design,¹⁰ and chemical textbook education.¹¹ Non-spherical atomic electron density features are highly significant for hydrogen atoms, which have only a single valence electron, and therefore the relative error caused by a spherical core approximation is most severe. Using X-rays, hydrogen atom positions can be obtained with the same accuracy and precision as afforded by neutron diffraction experiments, but only if the non-spherical nature of the electron distribution can be accounted for.¹² Improved structural information is important in many areas, including the understanding of thermodynamic properties such as heat capacities,¹³ interaction or lattice energies,^14,15 or the development of force fields.¹⁶

1.4 Non-spherical structure refinement

There are two strategies by which we can introduce atomic non-sphericity: either we actually refine the electron density (experimental electron density determination) or we find theoretical ways of introducing the shape of the electron cloud that is associated with each atom and then use that shape when we refine the structure against the diffraction pattern.‡ This is what this work is about; and to avoid any possible confusion with electron density refinements, we will use the term ‘non-spherical structure refinement’ when referring to using calculated non-spherical atomic form factors.

In a standard structure refinement, where atoms are treated as independent of each other (IAM), the atomic form factors have been calculated theoretically from the spherical electron-density distribution of isolated atoms in the past and are now available in tabulated form.²⁵ Hence, refinements are fast and convenient, but they neglect chemical bonding, as discussed above. Non-spherical structure refinements are either based on approximate pre-calculated and averaged multipole populations or theoretical wavefunctions, which are tailor-made for the compound under investigation. In both cases, non-spherical bonded-atom electron densities are calculated and are then Fourier-transformed to produce non-spherical atomic form factors. However, only in the latter case, the theoretical chemical-bonding information is readily available after the refinement and can be chemically interpreted.

1.4.1 Multipole-based databank approaches. Multipole parameters can be calculated theoretically from synthetic structure factors of model compounds and stored in tables according to the atom type defined in its chemical environment (Invarioms²⁶ or UBDB²⁷). Alternatively, such multipole databanks can be constructed from averaged experimental electron densities (ELMAM²⁸). Multipole parameters are then transferred from the databank to the compound under investigation, and non-spherical atomic form factors are calculated for use in the refinement on the fly from the transferred multipole populations. Although such refinements produce, e.g., better structural parameters for hydrogen atoms,²⁹ they are currently restricted to organic and bio-organic compounds, for which the number of atom types is manageable. A simplification to only dipole level for chemical bonds is now also implemented in the ShelXL software.³⁰

1.4.2 Hirshfeld atom refinement. The non-spherical structure refinement method called Hirshfeld atom refinement (HAR)^31,32 is central to this study. Starting from the atomic positions obtained from a standard X-ray structure, a molecular wavefunction is calculated using quantum mechanical methods and then dissected into atomic electron density functions (the Hirshfeld atoms, see Fig. 1) using Hirshfeld's stockholder partitioning scheme.³³ The resulting Hirshfeld atoms are never stored in tables, but a Fourier-transformation of their electron density is carried out on the fly to produce the related atomic form factors used in the least-squares refinement. This will produce an improved structure, and the procedure is then repeated – a new wavefunction and new atomic form factors are calculated after each refinement cycle – until convergence is reached. This makes HAR the most accurate of the non-spherical structure refinement methods.³⁴

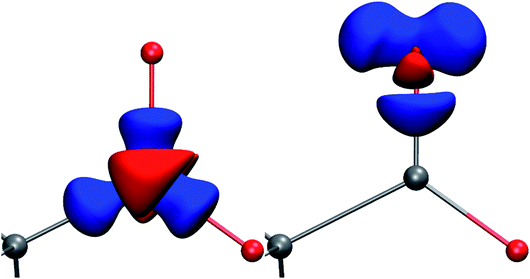Fig. 1 Deformation Hirshfeld densities¹² for the carbon (left) and oxygen (right) atoms in the carboxylate group of Gly-L-Ala, i.e. difference between the spherical atomic electron density used in the IAM and the non-spherical Hirshfeld atom density used in HAR (IAM minus HAR). Red = negative, blue = positive. Isovalue = 0.17 eÅ⁻³.

1.4.3 Current implementations of HAR and their limitations

The first implementation of HAR was based on the software Tonto,³⁵ and at least two early interfaces to the procedure have been built: lamaGOET³⁶ and HARt in conjunction with Olex2.³⁷ Both tools are limited by the capabilities of Tonto. Hirshfeld atoms in Tonto are not optimized for elements heavier than Kr, which can introduce large numerical errors for heavy elements. They also rely on Tonto as the actual crystallographic refinement engine, which it was not primarily designed to be. Vital features such as restraints, treatment of special positions, partial occupancies, twinning, solvent masking, and reliable CIF output are missing.

HAR requires the repeated calculation of a molecular wavefunction, which restricts its applications even further. The overall process can be slow because of the repeated quantum-mechanical step. One approach is to combine HAR with libraries of extremely localized molecular orbitals (ELMOs),³⁸ which has resulted in the HAR-ELMO method.³⁹ While this is very fast, it relies on the availability of pre-calculated molecular orbitals and is therefore not suitable for general use, but is highly relevant for the refinement of proteins which consist of a fixed subset of 20 amino acid building blocks.

Periodic network compounds could not be handled previously because molecular wavefunctions are used – a problem discussed in ref. 40 by analyzing periodic wavefunctions in combination with stockholder partitioning.

Disordered compounds cannot be handled by Tonto, and there are no apparent plans that this feature will be implemented in Tonto in the foreseeable future.

1.5 NoSpherA2 enables new possibilities for HAR

In this work, we present a new implementation of HAR in Olex2: NoSpherA2 (Non-Spherical Atoms in Olex2). It decouples HAR from Tonto and instead makes use of the Olex2 Graphical User Interface (GUI) as well as of the fully-featured olex2.refine least-squares refinement engine. All modeling options (including restraints, constraints, disorder modeling, solvent masking, etc.) thus become accessible to HAR. Besides, the NoSpherA2 development also focussed on the accurate description of core electrons and spin states for heavy elements. This opens HAR to all those researchers already familiar with standard structure determination procedures and extends its use to include almost all classes of compounds, so that they can be routinely determined.

We present here three different compound classes that could not previously have been refined with HAR – but exhibit important chemical-bonding questions:

• Disordered structures (both occupational and conformational disorder).

• Structures in highly symmetric space groups with special positions.

• Structures with heavy elements next to very light elements.

We have refined representative structures of each class using NoSpherA2 as summarized in Table 1.

Table 1 Summary of problems solved by the NoSpherA2 implementation of HAR and the exemplary structures shown in this work. Additionally, possible fields of application that benefit from this are given

Problem	Example	Field of Application
Occupational disorder	(C6H6O2)(CO2)0.854	Supramolecular chemistry, host–guest systems, MOFs/COFs
Conformational disorder	C10H10N4F2	Protein crystallography, solvent disorder, macromolecular crystallography
High symmetry network compounds	CaF2/(NH4)2B6H6	Network compounds, crystal design, inorganic structure refinement
Compounds containing heavy metals	OsH6(PC12H19)2	Inorganic and metalorganic compounds, catalytic complex understanding, metal–metal interactions

---

1.5.1 Disordered structures. A search in the Cambridge Structural Database⁴¹ shows that 27% of all crystal structures are affected by disorder. Hence, it is of utmost importance to be able to extend HAR toward the treatment of disordered compounds. Here, we distinguish between occupational and conformational disorder.
Occupational disorder. Occupational disorder relates to a part of the crystalline compound not being present in every unit cell. This happens regularly in host–guest systems,⁴²e.g. in loaded metal–organic⁴³ or covalent-organic frameworks.⁴⁴ In the crystalline sponge method,⁴⁵ the host framework is well known, but it is the structure of the mostly disordered guest which is to be elucidated. Understanding host–guest interactions in such systems widely used as storage or analysis tools for smaller molecules relies on an accurate description of the location and geometry of both the host and the, very likely disordered, guest molecule. We have chosen the CO₂-hydroquinone clathrate as an example of how the guest-molecule position and partial occupation can be refined accurately in HAR.^46,47
Conformational disorder. In biological macromolecular crystallography, disorder is omnipresent in the main molecules as well as in the solvation sphere. This kind of disorder consists of different conformations being spatially overlaid. For their description, it does not matter if they are caused by dynamic effects or are static. However, dynamic disorder is the most frequent in protein crystallography and could imply many different conformations that need to be modeled. Therefore, an extension of HAR to macromolecular chemistry crucially depends on the ability to treat the complex disorder in different disorder groups.³⁹ Here, we demonstrate how non-spherical atomic form factors from different molecular wavefunctions corresponding to different molecular conformations can be combined for an accurate HAR of a tetrahydropyrido[2,3-b]pyrazine derivative, a compound class of interest for drug development.⁴⁸

1.5.2 Structures in highly symmetric space groups with special positions. Inorganic materials often consist of solid ionic network compounds. Until now, this entire compound class has been excluded from HAR. We have chosen a textbook ionic salt (fluorite, fluorspar, CaF₂) and the molecular salt ammonium hexahydrohexaborate (NH₄)₂B₆H₆ to demonstrate the ability of NoSpherA2 in Olex2 to refine such compound classes using HAR for the first time. We show that, even for such simple compounds, an analysis of improved geometrical parameters plus a theoretical wavefunction perturbed by the respective crystal field yields deep and perhaps even surprising insights into bonding phenomena.

The textbook notion that species such as CaF₂ consist of spherical ions has rarely been questioned, although there is evidence that either a multipole or a neutral-atom model may describe such compounds better than the conventional ionic model.^49,50 Electron and γ-ray diffraction have shown that there is non-sphericity of the valence electron density in KCl, LiF, and MgO.^51,52 Specifically for Ca²⁺, the formally empty d-orbitals can be partially populated to add substantial covalent bonding character to the cation–anion interactions, as, for example, in the putative Zintl-phase of CaSi⁵³ or the calcocenes.⁵⁴ Here, utilizing HAR, we show that there is significant bond-directed non-spherical valence density present in the crystal structure of CaF₂.⁴⁹

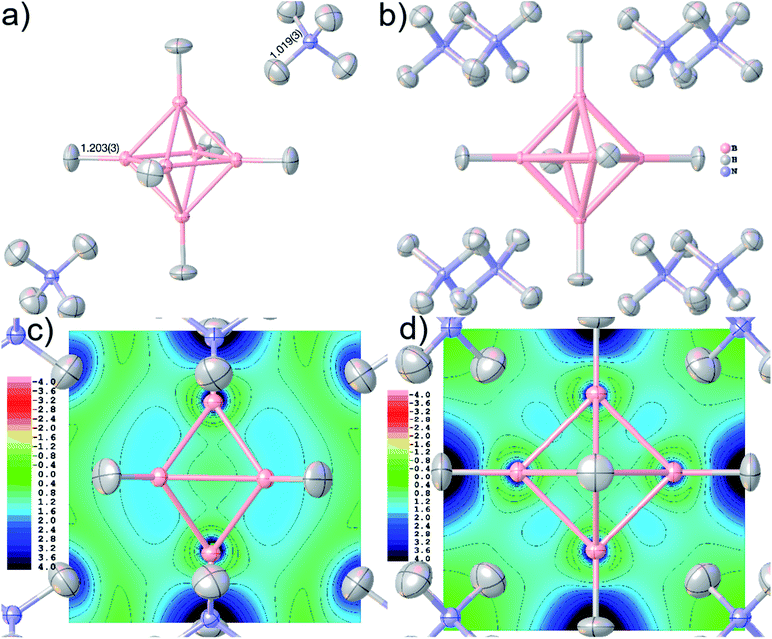
The bonding in polyhedral boranes and borates cannot be explained by 2-center-2-electron Lewis models, but various other concepts such as three-dimensional aromaticity must be invoked.⁵⁵ Therefore, there are many diffraction- and electron-density-based studies on borates.⁵⁶ Here, we have chosen (NH₄)₂B₆H₆ because of its fundamental character and symmetric crystal packing, but also because in previous studies the quantum-crystallographic description involving the hydrogen atoms was ambiguous.⁵⁷ However, if the potential of closo-hexaborates for hydrogen-storage applications⁵⁸ is to be fully exploited, the hydrogen atom geometric and bonding parameters must be determined accurately and precisely, which will be demonstrated in this paper.

1.5.3 Structures with heavy elements. Another area where the accurate determination of hydrogen atom parameters is of tremendous importance is transition-metal catalyzed hydrogen activation and hydrogenation.⁵⁹ Specifically, the structures of heavy atom hydrides are of interest, but it is extremely challenging to determine parameters of hydrogen atoms bonded to heavy elements accurately by X-ray crystallography.¹² Already by itself, the description of the heavy element in heavy-element containing species is challenging enough from both the crystallographic and the quantum-chemical point of view.^39,60,61

Here, we report how the methodological progress manifested in NoSpherA2 allows the successful non-spherical refinement of the osmium atom and the accurate determination of hydrogen atom parameters in bis(diisopropylphenylphosphine) hexahydridoosmium, OsH₆(PC₁₂H₁₉)₂,⁶² referenced against results from neutron diffraction of the same compound.⁶³ Limits of the X-ray diffraction experiment and its resolution truncation are also revealed and discussed.

2 NoSpherA2

NoSpherA2 brings wavefunction calculations, non-spherical atom partitioning, subsequent atomic form factor calculation, and finally least-squares refinement together under the umbrella of the freely available Olex2 software.⁶⁴ It is presented here utilizing the HAR non-spherical structure refinement method, but it is compatible with other flavors of (X-ray and electron) non-spherical structure refinement as well.

Besides the NoSpherA2 method developments discussed below, the advantages gained within HAR by switching from the Tonto to the olex2.refine refinement engine are manifold and significant. It allows HAR to access the use of restraints and constraints, hydrogen atom riding models, correct crystallographic description of special positions, refinement of partial occupancies, twinning models, solvent disorder treatment via BYPASS, different choices of weighting schemes, and many more options. In olex2.refine, refinements are carried out in F², not in F as previously done in Tonto. Advantages of the use of the Olex2 GUI include the automatic generation and validation of crystallographic information files (CIFs), the generation of maps and plots, and the straightforward generation of completed molecules or clusters of symmetry-related molecules on the screen, which are then used in the refinement as input.

2.1 Fundamental concepts

The diffraction pattern and the electron density associated with the geometry of the measured crystal are related via a mathematical method, the Fourier transform. More precisely, the Fourier transform of the electron-density distribution ρ_xyz in the unit cell is the structure factor F_hkl depending on the Miller indices hkl (eqn (1)). The F_hkl are complex numbers, and the square of their amplitudes is proportional to the measured Bragg-reflection intensities identified by Miller indices hkl representing vectors h⃑ in the reciprocal lattice. The structure factor is obtained as a finite sum involving the atomic form factors (also known as ‘atomic scattering factors’) f_hkl,_j of each atom j in the unit cell. The atomic form factors are, in turn, derived from the atomic electron density distributions via a Fourier transform. N_atoms is the number of atoms in the unit cell, r⃑_j is the position vector of atom j, and T_j is the Debye–Waller factor of atom j, that is, an exponential function involving the atomic displacement parameters of atom j. 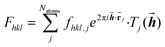These values appear in the equation describing the crystallographic model (eqn (1)):

In the classical Independent Atom Model (IAM), the atoms are considered independent non-interacting entities, and their electron densities are spherical functions depending only on the atomic type. The resulting form factors are listed in tables.²⁵ In a model that takes interatomic interactions into account, the atomic electron densities – translated to the origin – are no longer spherical functions and are dependent on the geometry of the whole molecule. Therefore, the corresponding atomic form factors are no longer real, but complex-valued functions of the Miller indices.

The idea behind the flexible approach to non-spherical structure refinement that underlies NoSpherA2 is to provide these complex-valued form factors of each atom within the unit cell via a table given in a file provided from plugin software (.tsc-file).⁶⁵ The underlying total electron density can be provided by quantum-mechanical calculations or other sources.

For molecules that are related by symmetry within the unit cell, only the form factors of atoms within the asymmetric unit are required, since the geometric transformation from an atom in this asymmetric unit to an equivalent atom in the unit cell corresponds to a transformation of the Miller indices of the corresponding non-spherical atomic form factor. Therefore, it is necessary to pay attention that all Miller indices resulting from transformations for all equivalent atoms are provided in the .tsc-file.

Moreover, the least-squares minimization used in non-spherical structure refinement requires not only information about the non-spherical form factors themselves but also about their partial derivatives. To avoid the time-consuming process of additional .tsc-files at close-by configurations, for which the numerical densities of the individual atoms vary only very little under tiny changes of their atom positions, we neglect these small variations in our calculations of the partial derivatives. The validity of this approximation will be discussed in more detail in a forthcoming publication.⁶⁶ The mathematical details of this general and flexible approach as well as the precise format of the .tsc-files are discussed in the ESI.†

2.2 NoSpherA2 GUI and interface

Fig. 2 summarizes the interplay of different steps of the non-spherical structure refinement and related software programs interfaced by NoSpherA2. At first, the input for the refinement is selected in the Olex2 GUI (Fig. 2) from a grown structure if necessary. The atomic coordinates of this structure are then transferred to the chosen quantum-mechanical software in form of a .cif or .xyz file. At present, ORCA,⁶⁷Gaussian,⁶⁸ and Tonto³⁵ are interfaced. The software ORCA, which is free of charge for academic use, has been tested most extensively here and has been used for all the examples in this work. The wavefunction output (.wfn or .wfx formats) is transferred to the program of choice that performs the Hirshfeld atom partitioning and the subsequent atomic form factor calculation. Supported programs for this are Tonto or NoSpherA2 itself, whereby Tonto is only used for validation purposes in this study, and all the examples are based on NoSpherA2. Finally, the atomic form factors are handed to olex2.refine in .tsc format (see the previous subsection and ESI†) for regular least-squares refinement in Olex2. The entire cycle visualized in Fig. 2 can be iterated manually or automatically until convergence in all refined parameters within less than 1% of their standard uncertainties is reached. This automatically iterated refinement is consistent with the standard definition of Hirshfeld Atom Refinement (HAR).³²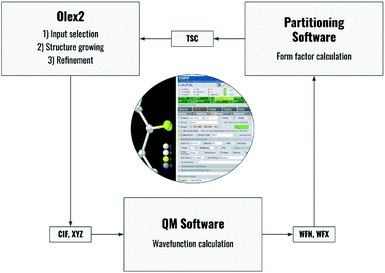

Fig. 2 Flowchart of the process behind HAR controlled by NoSpherA2 and a visual representation of the GUI for NoSpherA2 inside Olex2.

Every aspect of the entire process can be controlled directly from within the Olex2 GUI. Depending on the quantum mechanical package used, different choices affecting the molecular wavefunction calculation will be available. The required basis sets are provided by Olex2 and contain all relevant elements of the periodic table. A detailed description of the available options is provided in Section 5.

2.3 Dealing with disorder

For compounds including occupational disorder, the only methodological difference to previous HARs in Tonto is that olex2.refine allows the refinement of partial occupancy parameters. For conformational disorder, NoSpherA2 recognizes disorder parts previously defined inside the Olex2 GUI. Subsequently, individual molecular wavefunctions are calculated separately for every conformer and individual _part.tsc files are written for every wavefunction, which will in the end be combined to a single _total.tsc file for refinement. If there are more than two disorder parts, they can be grouped so that in each group the parts add up to 100% occupancy (in a semicolon-separated list in the Olex2 interface). Molecular wavefunctions are then calculated for every combination of parts between the disorder groups. This tool is essential for protein crystallography, which we will test in a separate forthcoming study.

2.4 Open-shell wavefunctions: multiplicity

The handling of open-shell wavefunctions was introduced in NoSpherA2, so that non-spherical atomic form factor calculations become possible for any spin state as found, for example, in high- or low-spin transition metal complexes. As long as the unrestricted or even multi-configurational wavefunction, e.g. after a CASSCF calculation, is presented in .wfn or .wfx format, NoSpherA2 will read the information and calculate the electron density based on all fully or partially occupied molecular orbitals and produce the .tsc file accordingly.

2.5 Dealing with heavy elements

To address the heavier elements of the periodic table, the inclusion of all-electron basis sets covering such atoms was necessary (x2c basis sets of Pollak and Weigend⁶⁹). Also, the DKH2-relativistic 2-component Hamiltonian approach⁷⁰ was made accessible in combination with any HF or DFT method selected (the DKH2 method should only be used with the x2c basis sets).

The calculation of atomic form factors is different from previous HAR implementations, and this has the biggest impact on heavy elements. Integrable grids are calculated with an adaption of numgrid⁷¹ which uses a Lindh–Malmqvist–Gagliardi radial description⁷² and a modern implementation of the spherical Lebedev quadrature procedure.^73,74 Becke partitioning⁷⁵ with a hardness factor of 3 is applied; and for the Hirshfeld partitioning³³ spherical atomic electron densities calculated from Thakkar densities,⁷⁶ represented by Slater-type functions, are used. More details are provided in Section 5.

2.6 Visualization of derived properties and functions

Olex2 natively includes engines for the generation of two- and three-dimensional maps and plots for the representation of residual electron densities. In the course of the implementation of the NoSpherA2 software, we have significantly extended the plotting options from dynamic and static deformation electron density and Laplacian of electron density maps to properties that can only be obtained with wavefunction information. This includes the electron localizability indicator ELI,⁷⁷ electrostatic potentials, molecular orbitals, and the non-covalent interaction NCI index.⁷⁸ Therefore, all pictures in this paper except for Fig. 1 and 4(b) are generated with the Olex2 software.

3 Validation of HAR in NoSpherA2

The multi-temperature X-ray and neutron-diffraction data sets of L-Ala and Gly-L-Ala represent a well-established benchmark set of structures already used in previous tests and validations of HAR.^32,39,79 Here, five X-ray datasets of Gly-L-Ala and three X-ray datasets of L-Ala were refined at HF/6-311G(d,p) using six different refinement techniques each (Table 2).

Table 2 Models used during validation with combinations of selected software and parameters

ID	Type	Program	QM	Partitioning	Weighting scheme
i	IAM	olex2.refine	—	—	1/σ^2(F^2)
ii	HAR	Tonto	Tonto	Tonto	1/σ(F)
iii	HAR	NoSpherA2	Tonto	Tonto	1/σ^2(F^2)
iv	HAR	NoSpherA2	ORCA	Tonto	1/σ^2(F^2)
v	HAR	NoSpherA2	ORCA	Tonto	Shelxl-type
vi	HAR	NoSpherA2	ORCA	NoSpherA2	1/σ^2(F^2)

---

In all models and datasets, the hydrogen atom positions and displacement parameters were freely refined. In all HAR models, hydrogen atoms were refined anisotropically. Fig. 3 shows an indicative comparison between the residual density distributions after a standard (IAM) refinement and a HAR with model vi. After IAM, distinctive positive residual densities remain on the covalent bonds and in the lone pairs of the oxygen atoms. After HAR, the bonding and lone-pair densities have been fully accounted for by the non-spherical atomic form factors (compare deformation Hirshfeld density representations in Fig. 1).

Fig. 3 Visualizations of the residual density distribution of the carboxylate group in L-Ala after IAM (a) and HAR, model vi (b). The residual density was calculated with Olex2 from fcf files and plotted on a grid of 0.05 Å with an iso-value of 0.10 eÅ⁻³ (green = positive, red = negative). In the IAM plot, residual density regions of a different functional group that obstructed the view onto the carboxylate were manually removed.

The tested models iii to vi introduce an increasing amount and combination of parameters that distinguish the new NoSpherA2 HARs from the traditional Tonto HARs (model ii). Summarizing the validation results (Tables S2–33 and Fig. S5–10, ESI†), all HARs present the same accuracy and precision relative to the neutron-diffraction results regardless of the way the model was generated. The exchange of the least-squares refinement in Tonto with olex2.refine through the .tsc files provides statistically identical results, with all differences being far below the measurement uncertainty. However, the results cannot be numerically identical because of the differences in the procedure discussed in Section 2 (such as refinement in F² instead of F, different Becke grids used, etc.). We find that the iteratively updated ShelXL-type weighting scheme is advantageous concerning the derivation of ADPs when compared to neutron-diffraction results. The combination of ORCA and NoSpherA2 also seems to produce a slightly closer agreement with the neutron-diffraction results for all parameters compared to the Tonto-derived results. Certainly, the results are produced much faster with ORCA and NoSpherA2 (183 seconds) relative to Tonto (884 seconds, Gly-L-Ala at 23 K, 6 CPUs), and additionally, the grid density is higher in NoSpherA2. The final refinements used for producing the results shown in Section 4 are based on model vi as this is indicated as the most promising combination of settings: HAR in NoSpherA2 using ORCA-wavefunctions and NoSpherA2-partitioning with a Shelxl-type weighting scheme.

4 Results and discussion

Table 3 provides an overview of the different nature of all five compounds discussed in Section 4 concerning symmetry, resolution and data/parameter ratios. It further describes the data quality as well as the extent and success of the refinements, focusing on a comparison of the IAM with the HAR results. There are two general observations:

Table 3 Refinement indicators using IAM and HAR. More details are given in the ESI, Table S1

Selected parameters	(C6H6O2) (CO2)0.854	C10H10N4F2	CaF2	(NH4)2(B6H6)	OsH6(PC12H19)2
Space group	R3̄ (trigonal)	P21/n (monoclinic)	Fm3̄m (cubic)	Fm3̄m (cubic)	P21/n (monoclinic)
No. of unique reflections	857	2975	96	364	13 109
d min/Å (radiation source)	0.58 (Mo)	0.70 (Mo)	0.40 (Ag)	0.40 (Mo)	0.58 (Mo)
# param's (const/rest), IAM vs. HAR	51(3/0) vs. 70(1/0)	204(7/0) vs. 258(1/4)	3(0/0) vs. 3(0/0)	11(0/0) vs. 11(0/0)	421(0/0) vs. 636(0/6)
Level of theory	PBE/def2-TZVPP	PBE/def2-TZVPP	PBE/def2-TZVPP	PBE/def2-TZVPP	PBE-DKH2/x2c-TZVPP
Charge/multiplicity	0/1	0/1	+18/1	+6/1	0/1
R int/%	1.73	5.36	6.73	2.41	5.82
R1 (IAM)/%	3.26	3.89	1.31	1.84	2.11
R1 (HAR)/%	1.45	2.14	1.14	0.95	1.92
Δρ (IAM)/eÅ^−3	0.581/−0.179	0.402/−0.313	0.690/−0.476	0.179/−0.216	1.128/−1.093
Δρ (HAR)/eÅ^−3	0.227/−0.254	0.175/−0.216	0.686/−0.415	0.119/−0.066	1.167/−0.938

---

• R-factors and residual densities are significantly lower for HAR in comparison to IAM refinements.

• R-factors after HAR are very low, regardless of R_int values, space group, resolution of measured data or the presence of disorder.

4.1 Disordered structures

4.1.1. Occupational disorder in (C₆H₆O₂)(CO₂)_0.854 (HQ-CO₂). The central motif in the hydroquinone crystal structure is a void encapsulated by hydrogen-bonded rings of hexagonal topology. These voids are normally filled with guest molecules forming clathrate structures; in fact, it is difficult to keep hydroquinone guest-free.⁸⁰ Various guest molecules can be trapped and then be transported through the host structure, which leads to various applications of hydroquinone clathrates.^46,47,81,82

Many studies focus on carbon dioxide inside the hydroquinone voids for fuel and energy science, but the occupancy (or filling ratio) of the voids is unclear.^46,47,80,82 In the example of the HQ-CO₂ compound shown here, the occupancy of the entity in the void was refined in HAR to be precisely 0.854(2) (Fig. 4(a)). The experimental details are provided in Section 5.

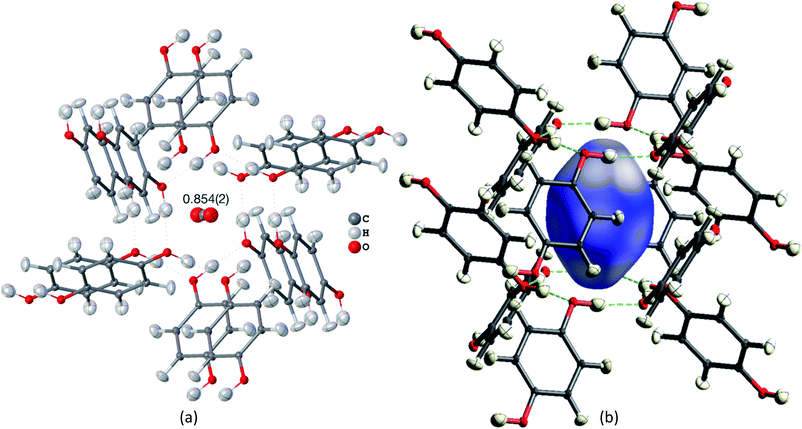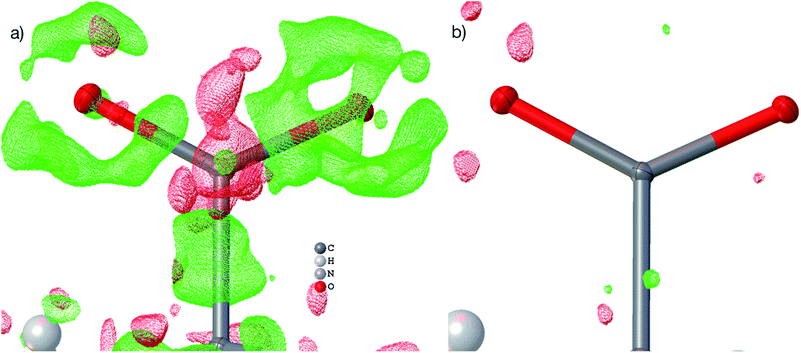
Fig. 4 HAR-refined hydroquinone-CO₂ clathrate structure (HQ-CO₂) with anisotropic displacement parameters depicted at 80% probability level. The cluster of the guest CO₂ molecule with the 12 surrounding HQ molecules encapsulating CO₂ inside a void is shown as used in the wavefunction calculation underlying the non-spherical form factor generation. (a) Final refined geometry and partial occupation number of CO₂. (b) Hirshfeld surface representation of CO₂ inside the void mapped with the property d_norm. Color scale from 0.08 (white) to 0.77 (blue). Generated with CrystalExplorer.⁸³

Not only was it possible to determine the occupancy of CO₂ precisely, but all hydrogen-atom positions and anisotropic displacement parameters were obtained accurately and precisely. There is one symmetry-independent hydrogen bond that closes (by symmetry) the two six-membered rings that encapsulate the void (Fig. 4). HAR-refined geometric details of this hydrogen bond identify it as short and strong: d(O⋯O) = 2.6805(3) Å, d(O–H) = 0.963(6) Å, d(H⋯O) = 1.724(6), a(O–H⋯O) = 171.7(6)°. Three void channels are intersecting the unit cell (see Fig. S1†). Having accurate and precise hydrogen-atom positions from HAR, the volume of each void could be estimated with the software CrystalExplorer⁸³ to be 68.5 ų.⁸⁴ In total, 16% of the unit cell are guest-accessible void volumes. The Hirshfeld surface⁸⁵ of the CO₂ molecule encloses a volume of 44.4 ų, which means that the CO₂ molecule fits into this particular void but is presumably not closely bound. Further analysis of the Hirshfeld surface using the property d_norm mapped onto it (Fig. 4(b)) reveals that there are no contacts closer than the sum of the van-der-Waals radii of the atoms in CO₂ and the atoms of the host structure; in fact, d_norm is positive throughout the entire range. This implies that there are only weak van-der-Waals and dispersion forces between host and guest, enabling the guest molecule to travel through the void channels. Nevertheless, the CO₂ molecule is not dynamically disordered in this crystal structure – it is just not always present in the void.

4.1.2 Conformational disorder in C₁₀H₁₀N₄F₂ (THPP). The THPP crystal structure⁴⁸ provides an example of a conformational disorder where two different disorder parts are present within the same disorder group (compare Section 2.3). In HAR, the disorder could not only be resolved unambiguously, but the hydrogen atoms in the major disorder component (88.2(5)%) could even be refined anisotropically (Fig. 5(a)). The THPP molecule was split into two disorder parts, i.e. different conformers, including the two nitrogen atoms next to the methylene CH₂ groups to allow for the calculation of different atomic form factors of these nitrogen atoms in different chemical environments while fixing their positions to be the same. Some angle and ADP restraints had to be used on the methylene groups of the minor disorder component (11.8(5)%) and the hydrogen atoms of this minor part were refined isotropically with bond length constraints to the major part.

Fig. 5 (a) Final HAR geometry after disorder treatment of THPP. (b) Dynamic deformation density distribution in the main molecular plane of the molecule. Color scale legend in eÅ⁻³. Atomic anisotropic and isotropic displacement parameters at 80% probability level.

Fig. 5(b) shows a dynamic deformation density map in the main molecular plane, i.e. the difference electron density of the HAR and the IAM including the effect of refined atomic displacement parameters. The map confirms that all the details of chemical bonding can be analyzed from this HAR disorder refinement, also in the disordered region where several displacement ellipsoids overlap. Moreover, the lone pair regions at nitrogen and fluorine atoms are accurately shaped.

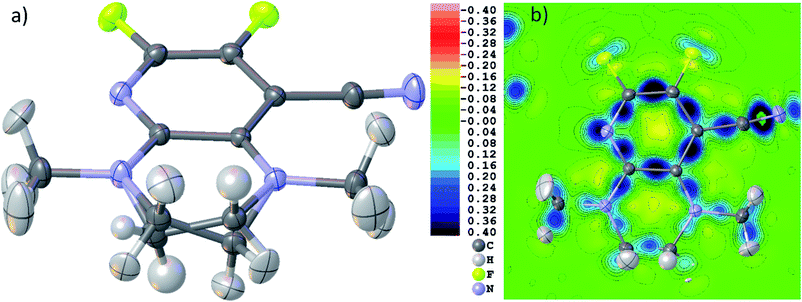
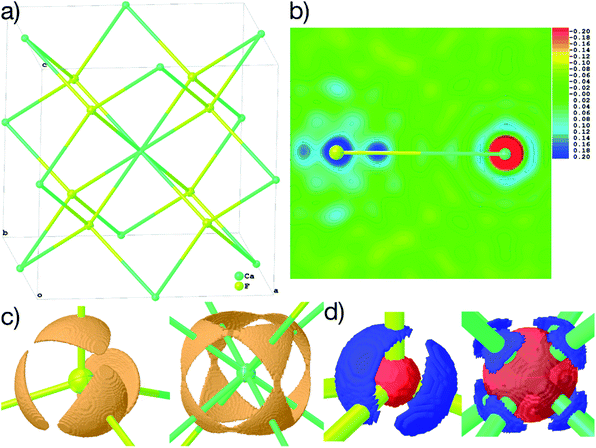
4.2 Structures in highly symmetric space groups with special positions

4.2.1 Fluorite CaF₂. Since periodic-boundary conditions of solid-state quantum mechanical programs are not yet available in NoSpherA2, we tested many explicit clusters of Ca²⁺ and F⁻ ions for the wavefunction calculations in ORCA, up to several hundred ions large, to ensure a proper description of the network polarizing the asymmetric unit. In comparison to the large clusters, it turned out that the minimal cluster, which consists of the completed coordination sphere (cube) of a central calcium ion and of the completed coordination spheres (tetrahedra) of the eight adjacent fluoride ions (Fig. 6(a)), is sufficient to accurately determine the displacement parameters and the properties of the ions obeying the symmetry of the system. The cluster consists of 21 ions, a total charge of +18, and multiplicity 1. Both ions Ca²⁺ and F⁻ are located on special positions in such a way that all their coordinates are fixed (distance = 2.3603 Å) and only two displacement parameters and the scale factor are refinable (see Table 3). This also means that in this case, the wavefunction for HAR does not need to be updated during the refinement since the atomic positions do not change.

Fig. 6 (a) Structure of the explicit cluster used for the calculation of the wavefunction of CaF₂ during HAR, coinciding with a unit cell. (b) 2D-plane of dynamic deformation density, color scale in steps of 0.02 eÅ⁻³. (c) 3D-isosurfaces of the ELI-D with iso-values of 1.835 (F) and 1.910 (Ca). (d) 3D-isosurfaces of the atomic deformation Hirshfeld densities at isovalues of ±0.411 (F) and ±0.088 (Ca) eÅ⁻³. All maps are calculated on a 0.01 Å grid and plotted using Olex2. Displacement parameters at 80% probability level.

Fig. 6(b)–(d) show unambiguously that the description of CaF₂ as an ionic salt with spherical ions is incorrect. There are significant charge concentrations in the deformation density maps (Fig. 6(b) and (d)) and charge localization in the electron localizability (ELI-D) map (Fig. 6(c)) directed along the Ca–F interactions. Hence, non-spherical, bond-directed valence electron density distribution caused by polarization, charge transfer, and electron-density deformation play a significant role in the bonding in CaF₂. In an analysis of the wavefunction within the framework of QTAIM⁸⁶ the atomic charges imply significant charge transfer from F⁻ to Ca²⁺ (+1.74 e (Ca) and −0.87 e (F)), there is a Ca–F bond critical point with an electron-density value of 0.22 eÅ⁻³ and a Laplacian value of 4.43 eÅ⁻⁵, as well as a delocalization index⁸⁷ of 0.14, which can be interpreted as the partial bond order.⁴⁹ It remains to be clarified by more detailed follow-up studies to which extent covalency, d-orbital population, or core deformation interplay to support the ionic framework of the crystal structure. However, we note that covalency and ionicity are not necessarily opposing forces but might be two sides of the same coin.^88,89

The maps in Fig. 6(b)–(d) are based on the theoretical cluster wavefunction, and represent the input for the non-spherical structure refinement, most directly represented by the deformation Hirshfeld density plots in Fig. 6(d), the difference between the IAM and HAR densities used in the refinement. This information can be used according to ref. 90 to directly show the significance of the non-spherical signal in the X-ray diffraction data, supporting similar findings by electron and γ-ray diffraction.^51,52 For this purpose, in Fig. 7 the difference between the calculated F_c and the measured F_o structure factor magnitudes in both models IAM and HAR is plotted relative to their resolution; weighted by their standard uncertainty σ in Fig. 7(a) and (b), or by their absolute magnitude in Fig. 7(c) and (d). The non-spherical valence density signal is expected to be more relevant for the low-order reflections. Consequently, for a compound such as alanine with many strongly covalent bonds, the IAM shows large discrepancies between the measured and modeled structure factor magnitudes below ca. 0.8 Å resolution, whereas HAR does not show such model insufficiencies probed by the experiment (Fig. 7(b) and (d)). For CaF₂, the same systematic effect is not as strongly pronounced, but it is clearly present for the 8 to 10 lowest-order reflections out of a total of 96 reflections in this data set. This shows that HAR can reveal the degree of non-sphericity by model comparison with the X-ray diffraction experiment directly, which was so far believed to be only possible for the more precise convergent-beam electron diffraction experiment. In turn, the model of spherical ions is not suited to describe the ions in CaF₂.^49,50

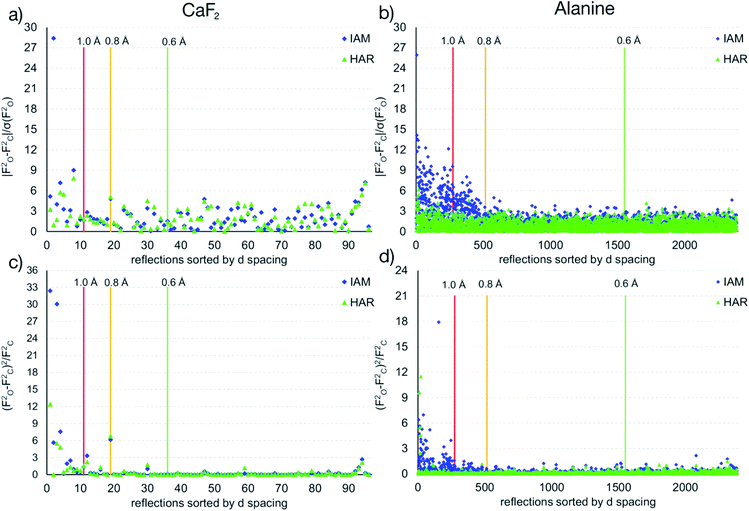Fig. 7 Differences of observed and calculated structure factors versus resolution for CaF₂ and L-Ala for the IAM and the HAR models.

The shortcomings of the IAM model impact on the refined parameters because the neglected non-sphericity must be absorbed by the weighting scheme and the atomic displacement parameters. The coefficients of the weighting scheme are a = 0.0217 and b = 0.3133 in the IAM, while the coefficients in HAR are reduced to a = 0.0175 and b = 0.0607. This trend of significantly smaller weighting scheme factors is observed for all other refinements, too. The two refinable U_iso values are 0.00337(5)/0.00495(9) Ų for Ca/F in the IAM, which change to 0.00325(7)/0.00488(9) Ų if the simple 1/σ² weighting scheme is used. The differences in HAR are slightly smaller: 0.00334(4)/0.00505(6) Ųvs. 0.00328(5)/0.00502(7) Ų.

4.2.2 Ammonium hexahydrohexaborate (NH₄)₂B₆H₆. For (NH₄)₂B₆H₆, many different symmetric and asymmetric, large and small clusters were tested for the wavefunction calculation. As for CaF₂, a minimal cluster that obeys the crystallographic symmetry is sufficient for an accurate and precise HAR of the borate anion of interest. Here, a six-fold positively charged cluster with the central borate octahedron neighbored by all 8 ammonium ions in the first coordination sphere was used (Fig. 8(b)). Preliminary tests with single-zeta basis sets resulted in inferior residual densities and X–H distances (X = N,B); only after using a triple-zeta basis set the refinement improved considerably compared to IAM. The refinement using PBE/def2-TZVPP resulted in a significant drop in R-value and residual density (see Table 3) and gave accurate N/B–H distances of 1.019(3) Å and 1.203(3) Å, respectively (Fig. 8(a)). Reported values for N–H distances in ammonium ions from neutron diffraction have an average value of 1.021 Å and a standard deviation of 0.037 Å.⁹¹ For any borane or borate clusters, we find only two single-crystal neutron diffraction studies in the literature yielding an average terminal B–H bond distance of 1.195 Å with a standard deviation of 0.009 Å over 14 symmetry-independent B–H bonds.^92,93 For comparison, the IAM fails to produce similar X–H distances: N–H 0.836(7)/B–H 1.078(6) Å.

Fig. 8 Final geometry and anisotropic displacement parameters at 80% probability level of ammonium borate (NH₄)₂B₆H₆ after HAR, showing (a) the formula unit with the two symmetry-independent refined bond distances in Å, and (b) the molecular cluster used in the wavefunction calculation. Electron localizability indicator ELI-D at contour intervals of 0.4 in a cut-plane (c) intersecting two pairs of opposite BBB faces, and (d) in the central boron square.

Accurate X–H distances are crucial for the derivation of properties such as charge concentrations and localizations related to the special bonding situation in boranes and borates. As an example of possibilities inside Olex2 for bonding analysis after HAR, Fig. 8(c) and (d) show two different ELI-D maps as cut-planes intersecting the B–B–B faces and in the central B–B–B–B square. The ELI-D maxima are clearly outside the bond axes and are delocalized around the boron polyhedron, which is in line with previous theoretical calculations that show the ELF/ELI polyhedron being dual/complementary to the structural B₆H₆²⁻ polyhedron, within the theory of three-dimensional aromaticity.^57,94,95

4.3 Structures with heavy elements

The refinement of hydrogen atom parameters in heavy metal hydrides is one of the most challenging aspects of X-ray crystallography. In fact, not only is the diffraction pattern dominated by the heavy element,⁹⁶ but truncation errors of the Fourier series of the structure factors that are limited by resolution also spatially occur in regions where the hydrogen atoms are located. Therefore, to overcome these drawbacks, it is necessary to collect both very high-quality low-order data to capture the hydrogen-atom signal and high-resolution data to reduce truncation errors.⁹⁷ However, the experimental X-ray diffraction data of compounds containing heavy elements are very often affected by systematic problems such as significant absorption and radiation-damage effects.^39,98 Here, we test to which extent a very sophisticated theoretical electron-density model underlying the refinement (see Section 2.5) can help to interpret the diffraction pattern of the osmium hexahydride OsH₆(PC₁₂H₁₉)₂.

In all HARs reported in Table 4, the Os–H distances were refined freely, while some restraints on the hydrogen atom anisotropic displacement parameters were applied, and one hydrogen atom was refined isotropically. Extinction correction was also applied during the refinements. Calculations were performed using the B3LYP, M06-2X, and PBE DFT functionals,⁹⁹ always with the DKH2 relativistic extension and the basis set x2c-TZVPP. This series was repeated for a subset of the reflections (pruned at d = 0.7 Å), as there is a significant rise in R_int for data beyond this resolution. In Table 4, the R-value, the residual density minimum and maximum values, and the timing for the QM step are compared. More details and model differences are deposited as CIFs with the paper.

Table 4 Comparison of HARs of OsH₆(PC₁₂H₁₉)₂ using different DFT functionals and different resolution cut-offs. The functionals are extended with the DKH2 relativistic method and the basis set x2c-TZVPP

	B3LYP full	B3LYP 0.7 Å	M06-2X full	M06-2X 0.7 Å	PBE full	PBE 0.7 Å
R1/%	1.94	1.20	1.93	1.19	1.92	1.19
Δρ/eÅ^−3	1.210/−0.708	0.592/−0.317	1.210/−0.681	0.581/−0.318	1.167/−0.686	0.583/−0.317
t of QM step/s	639		1335		579

---

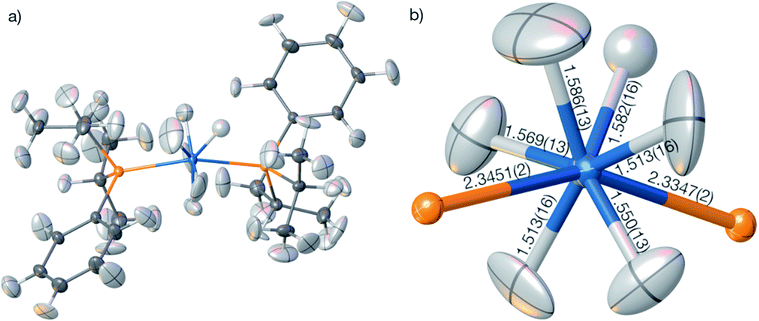
The geometry and the displacement parameters of the refinement using the full resolution are shown in Fig. 9. The sum of covalent radii¹⁰⁰ of Os and H is 1.61 Å, which is significantly longer than the distances resulting from the HAR refinement (Fig. 7(b), average 1.554 Å, average standard uncertainty 0.014 Å). However, the corresponding neutron-diffraction experiment yielded longer Os–H bonds, on average 1.649 Å.⁶² The isotropic IAM refinement, in turn, yielded much shorter Os–H bond lengths (1.510 Å). When the resolution cut-off from 0.58 to 0.7 Å was used, the average HAR-derived bond distance and the average standard uncertainty remain constant at 1.555 Å and 0.015 Å. This means that the significant difference in R-value and maximum residual-density value located at the Os core between the two resolutions (Table 4) are unrelated to the Fourier truncation error and do not impact on the hydrogen atom treatment. It is unclear whether the advantage of having more information from higher resolution data or the disadvantage of compromising on the overall data quality by including more high-resolution data prevail over the other.

Fig. 9 (a) HAR-refined molecular structure of OsH₆(PC₁₂H₁₉)₂ with the PBE-DKH2/x2c-TZVPP model at full resolution. (b) Coordination geometry of the Os atom with the freely refined distances to the six nearest hydrogen and two nearest phosphorus atoms. All displacement parameters are displayed at 80% probability level.

In summary, the HAR results for those hydrogen atom parameters in OsH₆(PC₁₂H₁₉)₂ that are bonded directly to the Os atom are improved relative to the IAM results but are still significantly less accurate and less precise than those for compounds involving only lighter elements. To understand whether the insufficient match with the neutron-diffraction derived Os–H bond lengths is caused by problems in the HAR methodology or complications of X-ray diffraction experiments on heavy-element containing species, we calculated and refined a theoretical structure factor set of OsH₆(PC₁₂H₁₉)₂ based on the neutron-derived geometry at the same level of theory as used in HAR. A dynamic set of structure factors was obtained by a combination of ORCA, the .tsc routine in NoSpherA2, and the .fcf routine in Olex2 up to the same resolution (0.58 Å) as the experimental structure factor file. In addition to the information on the displacement parameters, the theoretical structure factors include information on anomalous dispersion based on the Sasaki table.¹⁰¹ Uncertainties were set to 0.001 of the calculated intensities.

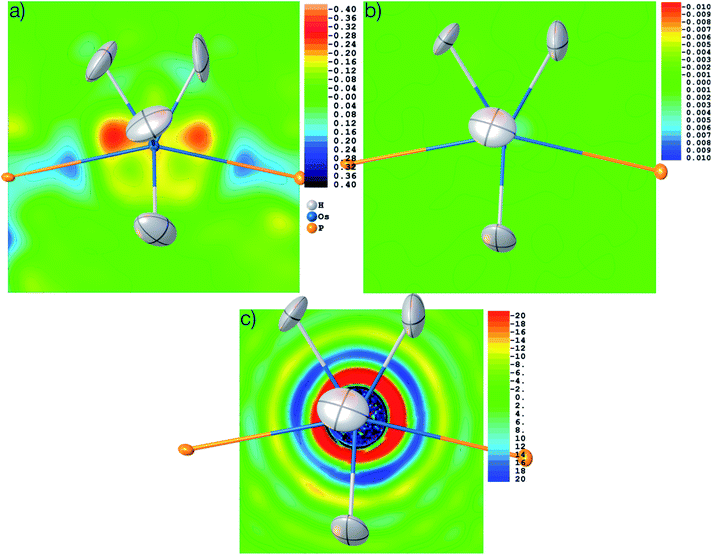
The structure was solved from scratch on the basis of the theoretical structure factors. A subsequent IAM refinement resulted in shortened Os–H distances (av. 1.574 Å) in comparison to the input structure (av. 1.649 Å). This means that the IAM model is insufficient and cannot produce the input parameters even for theoretical data. This is reflected in the residual density distributions depicted in Fig. 10(a) where unmodelled Os–H bonding density and overestimated Os core density is visible at levels as high as 0.58 and −0.26 eÅ⁻³. After HAR at PBE-DKH2/x2c-TZVPP with high integration accuracy, coordinates and atomic displacement parameters agree exactly to the last digit with the input values (see CIFs deposited as ESI†), and the residual electron density has vanished (0.003 eÅ⁻³, see Fig. 10(b)). These results imply that the experimental X-ray diffraction data and not the HAR model are the reason for the inaccurate determination of the Os–H bond lengths discussed above.

Fig. 10 Residual electron density after refinement against theoretical structure factors in (a) IAM model and (b) HAR model. (c) Electron density as the Fourier transform of the theoretical structure factors in the vicinity of the Os atom, showing Fourier truncation ripples. Three different contour intervals (see text). Color scale in eÅ⁻³. Displacement parameters at 80% probability level.

It is worth noting that the OsH₆(PC₁₂H₁₉)₂ measurement used here is not of especially inferior quality, but rather represents a standard measurement as it is nowadays routinely obtained for service measurements of coordination and organometallic compounds. Therefore, we use this example to have a closer look at the problem of truncation effects caused by limited resolution because it was shown recently in ref. 97 that even at resolutions as high as d = 0.20 Å, core and outer-core electron-density distributions of a mercury hydride cannot be reproduced at all from structure factors, regardless of the sophistication of the quantum-crystallographic model. Fig. 10(c) shows a detailed view of the electron-density map obtained by the Fourier transform of the structure factor set calculated for the Os hydride at d = 0.58 Å resolution. The area around the nucleus is highly positive (in fact so highly positive that the values cause some trouble for the color mapping). Further out, two shells of highly negative electron density values (red and yellow) are separated by another highly positive shell (blue). These are the so-called Fourier truncation ripples, and it is worth remembering how severe the effect is, with highly significant physically meaningless negative electron-density areas near the core of the heavy element. The third shell of positive electron-density values (light blue) is still as high as 5 to 10 eÅ⁻³. It is located at a distance of about 1.5 Å from the Os nucleus and therefore overlaps with the hydrogen atom electron densities, which makes the localization of hydrogen atoms bonded to heavy elements and the refinement of their parameters so difficult.

These truncation ripples cannot be avoided because of the nature of the X-ray diffraction experiment and its resolution limitation. They can only be mitigated by extremely high resolution which is not available at home sources so far; and at synchrotron sources, radiation damage becomes much more likely to occur. Whenever there are small errors in the Fourier series of the calculated structure factors, the steep gradients between the highly positive and negative electron density regions cause huge errors and consequently large residual electron density effects. Therefore, a much better understanding of the physical background of effects such as absorption, fluorescence, radiation damage, anharmonic motion, thermal diffuse scattering, and other systematic effects impacting on heavy elements is needed, leading to more sophisticated correction procedures^39,96,102 and improved diffractometer hardware and software technology.

5 Settings/experimental part

5.1 Software details

To make the refinements convenient, a NoSpherA2 GUI (Fig. 2) was added to the “Refine” tab inside the Olex2 GUI which appears once the NoSpherA2 tick-box is activated. “Update Table” asks for the source of the .tsc file. For HAR, this means that either the QM software for the .tsc generation or an existing .tsc file must be chosen to be used in the least-squares refinement. The remaining user-specified options concern settings for all of the three major job steps. Basis sets and methods are pre-selected according to the QM software choice. PBE/def2-SVP is the minimal level for quick and yet reliable results. Most results in this paper are based on PBE/def2-TZVPP, because the PBE-GGA density seems to be well suited for the HARs,⁹⁹ whereas higher basis sets seem to be necessary for accurate atomic displacement parameters.³⁷ Hartree-Fock or hybrid methods such as B3LYP are also available. In principle, all kinds of levels of theory are possible in the input section of the QM code if the resulting electron density can still be evaluated on a Becke grid. The accuracy of Becke grids, both in the QM step and in the Hirshfeld atom partitioning, can be set. The application of a relativistic Hamiltonian is possible when activating the “REL” tick-box. More details on the treatment of heavy elements are discussed in Section 2.5.

The final refinement result is independent of the QM software used, but different QM programs provide different sets of features. If Tonto is chosen, a cluster of self-consistent Hirshfeld point charges and dipoles can be used to simulate the crystal field, and the radius of this cluster can be specified in the GUI. If ORCA is chosen, the resolution of identity (RI) and chain of spheres (COSX) approximations in meta-GGA functionals speed up the calculations without loss of accuracy of the refinement results. They are set by default, but the convergence threshold and convergence strategy can be controlled. Computational resources (number of CPUs and memory) can be allocated and might result in different gains of calculation speed in the different QM codes. In the future, we envisage the possibility to send calculations from the NoSpherA2 GUI to a supercomputer infrastructure for further speed gains.

Crystallographic options concerning the hydrogen atom treatment in the refinement are only convenient switches since the least-squares procedure is controlled via the Olex2 GUI in the same way an IAM Shelxl or olex2.refine refinement is controlled, including all the options such as riding models or restraints. Here, the tick boxes “H Aniso” will set all the hydrogen atoms to anisotropic displacement parameters at the start of the refinement, and “No Afix” removes all the previously fixed hydrogen atom parameters to ensure that HAR refines all parameters freely. “DISP” automatically adds Δf′ and Δf′′ values for the anomalous dispersion correction from the Sasaki table¹⁰¹ according to the wavelength specified in the input .ins or .cif files.

The calculation of grids is based on preselected levels of accuracy (low, normal, high, max; tick-box “Integr. Accuracy”), of which “normal” is usually sufficient, but “high” was used to reproduce the atomic electron density of the isolated osmium atom (Z = 76) with an integrated accuracy of better than 0.0001 e. According to the choice of integration accuracy used here for the atomic form factor calculation, a corresponding accuracy will also be selected for the wavefunction calculation in the QM software.

All HARs presented in the Results and Discussion part (Section 4) were carried out with the following settings: source of .tsc: ORCA; basis set: def2-TZVPP (except Os where x2c-TZVPP was used); method: PBE; relativistics: not used (except for Os); SCF Conv. Thresh.: NormalSCF; SCF Conv. Strategy: NormalConv; H Aniso: activated (if not mentioned otherwise); No Afix: activated; updated Shelxl-type weighting scheme: activated; automatic HAR; Integr. Accuracy: high; EXTI: not activated; DISP: activated. Cluster charges were not used for the simulation of the crystal field. Only for validation purposes and for the Os-containing compound, settings were varied. Other refinement details are shown in Table 3 as well as in the Crystallographic Information Files (CIFs) deposited with the Cambridge Structural and Inorganic Crystal Structure Database (CCDC-2034385 to 2034389, 2035147 to 2035148).

The setup for benchmarking the heavy element refinements was a 4-core 2.81 GHz hyperthreaded laptop with 16 GB RAM and no solid-state drives using 7 threads for ORCA. A significant part of the calculation was the evaluation and saving of relativistic integrals, which is similar for all functionals (approx. 125 s in these calculations). Apart from that, the PBE calculation was significantly faster than the MO6-2X calculation (161% longer), and still faster than the B3LYP calculation (13% longer). Furthermore, the results of the refinement using PBE are very similar to those of the more sophisticated functionals, so the use of PBE for all-purpose refinements is suggested, even when heavy elements are involved. In contrast, the application of relativistic corrections is imperative, and all-electron x2c basis sets lower than triple-zeta are not recommended. Therefore, all results discussed in Section 4.3 refer to PBE-DKH2/x2c-TZVPP HARs.

5.2 Origin of datasets and synthesis of compounds

For the validation part (Section 3), previously published X-ray structure factors of L-alanine (L-Ala)¹⁰³ and glycyl-L-alanine (Gly-L-Ala)³² were used. For comparison, the results of neutron-diffraction studies at the respective same temperatures were used, from ref. 39 for L-Ala, and from ref. 104 for Gly-L-Ala. X-ray structure factors of the CO₂-hydroquinone clathrate (HQ-CO₂) were taken as deposited in the Cambridge Structural Database belonging to ref. 46, whereas those of the tetrahydropyrido[2,3-b]pyrazine derivative (THPP) stem from ref. 48.

The CO₂ molecule in HQ-CO₂ is located in a special crystallographic position. For the wavefunction calculations, we constructed a cluster of 12 hydroquinone molecules around the trapped CO₂ molecule enclosing the void (Fig. 4), but only a fraction of that cluster was refined as the crystallographic asymmetric unit, which consists of half a molecule of hydroquinone and half a CO₂ molecule (Z = 9, Z′ = 0.5 formula units).

A high-resolution X-ray diffraction experiment of CaF₂, obtained as a small single-crystal from a fluorite mineralogical sample, was performed in-house on a Rigaku Synergy-S diffractometer equipped with a Hypix6000 detector at 100 K using Ag-K_α radiation. A single-crystal of ammonium hexahydrohexaborate (NH₄)₂B₆H₆ was synthesized for this study according to the procedure described in ref. 105 to yield the hexaborate anion as a sodium salt and subsequently yielding (NH₄)₂B₆H₆ after aqueous workup at pH 10 with ammonium chloride in solution. Single crystals were obtained by evaporation of the solvent after filtration. It was measured to high resolution using a Rigaku Synergy diffractometer equipped with a Pilatus 300 K detector at 100 K using Mo-K_α radiation.

The compound bis(diisopropylphenylphosphine) hexahydridoosmium, OsH₆(PC₁₂H₁₉)₂, was synthesized according to ref. 106 a suitable single crystal was measured to medium resolution on a Rigaku SuperNova EosS2 diffractometer with a CCD detector at 120 K using Mo-K_α radiation. Further crystallographic and measurement details are given in Tables 2 and S1.†

6 Conclusions and outlook

In this work, we have generalized ‘non-spherical structure refinement’ so that any flavor of quantum-crystallographic crystal-structure treatment can be linked with the established and modern free software Olex2, and specifically with its comprehensive refinement engine olex2.refine. The capabilities of NoSpherA2 are demonstrated here for the example of Hirshfeld Atom Refinement, which can now be applied to disordered structures, inorganic periodic network compounds including salts, and compounds containing heavy elements. These developments also open HAR to the fields of protein crystallography, as well as inorganic and metal–organic materials. In this respect, as a core chemical result, we demonstrate that there is a strong directional dependence of bonding and non-sphericity of electron density in fluorite CaF₂, although it is generally assumed that it consists of spherical ions. We will investigate this point further by applying non-spherical refinements to other ionic species.

HARs in NoSpherA2 are significantly faster than previous implementations of HAR and often more accurate. In principle, any modern quantum-mechanical software can now be used for the theoretical steps, demonstrated here by the use of ORCA, which is a QM software freely available for academic use. The PBE DFT method with triple-zeta basis sets is recommended for a good balance between accuracy and speed. This is even true for heavy transition metals, where relativistic extensions are necessary. NoSpherA2 also enabled us to pin down the problems in the crystallographic refinement of heavy elements and show pathways for further developments in the field.

Since the format file underlying NoSpherA2 is entirely general, interfacing Olex2 with other flavors of X-ray non-spherical structure refinement is simple and straightforward. First tests have been made for the HAR-ELMO method³⁹ and the multipole databank software Discamb.²⁹ Moreover, any of these kinds of non-spherical structure refinement are not restricted to X-radiation. First tests towards the non-spherical refinement of electron-diffraction data have been made inside and outside¹⁰⁷NoSpherA2.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge much feedback of testers and users of NoSpherA2 alpha versions leading to optimization of the GUI and code and many bug-fixes. We thank Professor Hans-Beat Bürgi for continuous constructive criticism during the development of NoSpherA2, and Dr Georgia Cametti for the crystal of CaF₂. We gratefully acknowledge the support for LM through the Intensive Industrial Innovation Programme run by Durham University and funded by the European Regional Development Fund (ERDF).

Notes and references

1. M. Jaskolski, Z. Dauter and A. Wlodawer, FEBS J., 2014, 281, 3985–4009.
2. J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737–738.
3. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
4. E. Cartlidge, Science, 2016, 354, 22–23.
5. T. E. Mason, D. Abernathy, I. Anderson, J. Ankner, T. Egami, G. Ehlers, A. Ekkebus, G. Granroth, M. Hagen, K. Herwig, J. Hodges, C. Hoffmann, C. Horak, L. Horton, F. Klose, J. Larese, A. Mesecar, D. Myles, J. Neuefeind, M. Ohl, C. Tulka, X.-L. Wang and J. Zhao, Phys. B, 2006, 385–386, 955–960.
6. T. Gruene, J. T. C. Wennmacher, C. Zaubitzer, J. J. Holstein, J. Heidler, A. Fecteau-Lefebvre, S. De Carlo, E. Müller, K. N. Goldie, I. Regeni, T. Li, G. Santiso-Quinones, G. Steinfeld, S. Handschin, E. van Genderen, J. A. van Bokhoven, G. H. Clever and R. Pantelic, Angew. Chem., Int. Ed., 2018, 57, 16313–16317.
7. A. H. Compton, Nature, 1915, 95, 343–344.
8. H. Kasai, K. Tolborg, M. Sist, J. Zhang, V. R. Hathwar, M. Ø. Filsø, S. Cenedese, K. Sugimoto, J. Overgaard, E. Nishibori and B. B. Iversen, Nat. Mater., 2018, 17, 249–252.
9. H. Keil, M. Hellström, C. Stückl, R. Herbst-Irmer, J. Behler and D. Stalke, Chem. – Eur. J., 2019, 25, 15786–15794.
10. C. Jelsch, M. M. Teeter, V. Lamzin, V. Pichon-Pesme, R. H. Blessing and C. Lecomte, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 3171–3176.
11. M. Fugel, L. A. Malaspina, R. Pal, S. P. Thomas, M. W. Shi, M. A. Spackman, K. Sugimoto and S. Grabowsky, Chem. – Eur. J., 2019, 25, 6523–6532.
12. M. Woińska, S. Grabowsky, P. M. Dominiak, K. Woźniak and D. Jayatilaka, Sci. Adv., 2016, 2, e1600192.
13. A. A. Hoser and A. Ø. Madsen, Acta Crystallogr., Sect. A: Found. Adv., 2017, 73, 102–114.
14. M. J. Turner, S. Grabowsky, D. Jayatilaka and M. A. Spackman, J. Phys. Chem. Lett., 2014, 5, 4249–4255.
15. S. P. Thomas, P. R. Spackman, D. Jayatilaka and M. A. Spackman, J. Chem. Theory Comput., 2018, 14, 1614–1623.
16. F. Kleemiss, A. Justies, D. Duvinage, P. Watermann, E. Ehrke, K. Sugimoto, M. Fugel, L. A. Malaspina, A. Dittmer, T. Kleemiss, P. Puylaert, N. R. King, A. Staubitz, T. M. Tzschentke, R. Dringen, S. Grabowsky and J. Beckmann, J. Med. Chem., 2020, 63, 12614–12622.
17. C. Gatti and P. Macchi, Modern Charge-Density Analysis, Springer, Dordrecht, 2012, ISBN: 978-90-481-3835-7.
18. D. Stalke, Electron Density and Chemical Bonding I: Experimental Charge Density Studies, in Structure and Bonding, vol 146, Springer, Dordrecht, 2012.
19. R. F. Stewart, J. Chem. Phys., 1969, 51, 4569–4577.
20. N. K. Hansen and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 909–921.
21. (a) D. M. Collins, Nature, 1982, 298, 49–51; (b) M. Sakata and M. Sato, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 263–270.
22. M. Woińska, D. Jayatilaka, B. Dittrich, R. Flaig, P. Luger, K. Woźniak, P. M. Dominiak and S. Grabowsky, ChemPhysChem, 2017, 18, 3334–3351.
23. S. Grabowsky, A. Genoni and H.-B. Bürgi, Chem. Sci., 2017, 8, 4159–4176.
24. A. Genoni, L. Bučinský, N. Claiser, J. Contreras-García, B. Dittrich, P. M. Dominiak, E. Espinosa, C. Gatti, P. Giannozzi, J.-M. Gillet, D. Jayatilaka, P. Macchi, A. Ø. Madsen, L. Massa, C. F. Matta, K. M. Merz Jr, P. N. H. Nakashima, H. Ott, U. Ryde, K. Schwarz, M. Sierka and S. Grabowsky, Chem. – Eur. J., 2018, 24, 10881–10905.
25. (a) D. T. Cromer and J. B. Mann, Los Alamos Scientific Laboratory report LA-3816, 1968; (b) D. T. Cromer and J. T. Waber, International tables for X-ray crystallography, 1974, vol. IV, 71.
26. B. Dittrich, C. B. Hübschle, K. Pröpper, F. Dietrich, T. Stolper and J. J. Holstein, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 91–104.
27. K. N. Jarzembska and P. M. Dominiak, Acta Crystallogr., Sect. A: Found. Crystallogr., 2012, 68, 139–147.
28. S. Domagała, B. Fournier, D. Liebschner, B. Guillot and C. Jelsch, Acta Crystallogr., Sect. A: Found. Crystallogr., 2012, 68, 337–351.
29. K. K. Jha, B. Gruza, P. Kumar, M. L. Chodkiewicz and P. M. Dominiak, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2020, 76, 296–306.
30. J. Lübben, C. M. Wandtke, C. B. Hübschle, M. Ruf, G. M. Sheldrick and B. Dittrich, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 50–62.
31. B. Dittrich and D. Jayatilaka, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 383–393.
32. S. C. Capelli, H.-B. Bürgi, B. Dittrich, S. Grabowsky and D. Jayatilaka, IUCrJ, 2014, 1, 361–379.
33. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
34. W. F. Sanjuan-Szklarz, M. Woińska, S. Domagała, P. M. Dominiak, S. Grabowsky, D. Jayatilaka, M. Gutmann and K. Woźniak, IUCrJ, 2020, 7, 920–933.
35. D. Jayatilaka and D. J. Grimwood, in Computational Science — ICCS 2003, Springer, Berlin, Heidelberg, 2003, pp. 142–151.
36. L. A. Malaspina, A. Genoni and S. Grabowsky, J. Appl. Crystallogr., 2021 , under revision.
37. M. Fugel, D. Jayatilaka, E. Hupf, J. Overgaard, V. R. Hathwar, P. Macchi, M. J. Turner, J. A. K. Howard, O. V. Dolomanov, H. Puschmann, B. B. Iversen, H.-B. Bürgi and S. Grabowsky, IUCrJ, 2018, 5, 32–44.
38. B. Meyer and A. Genoni, J. Phys. Chem. A, 2018, 122, 8965–8981.
39. L. A. Malaspina, E. K. Wieduwilt, J. Bergmann, F. Kleemiss, B. Meyer, M. F. Ruiz-López, R. Pal, E. Hupf, J. Beckmann, R. O. Piltz, A. J. Edwards, S. Grabowsky and A. Genoni, J. Phys. Chem. Lett., 2019, 10, 6973–6982.
40. M. E. Wall, IUCrJ, 2016, 3, 237–246.
41. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 . Cambridge Structural Database accessed June 18th, 2020.
42. J. J. Lee, A. N. Sobolev, M. J. Turner, R. O. Fuller, B. B. Iversen, G. A. Koutsantonis and M. A. Spackman, Cryst. Growth Des., 2014, 14, 1296–1306.
43. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444.
44. P. J. Waller, F. Gándara and O. M. Yaghi, Acc. Chem. Res., 2015, 48, 3053–3063.
45. M. Hoshino, A. Khutia, H. Xing, Y. Inokuma and M. Fujita, IUCrJ, 2016, 3, 139–151.
46. J.-P. Torré, R. Coupan, M. Chabod, E. Pere, S. Labat, A. Khoukh, R. Brown, J.-M. Sotiropoulos and H. Gornitzka, Cryst. Growth Des., 2016, 16, 5330–5338.
47. J.-P. Torré, H. Gornitzka, R. Coupan, C. Dicharry, M. Pérez-Rodríguez, A. Comesaña and M. M. Piñeiro, J. Phys. Chem. C, 2019, 123, 14582–14590.
48. C. A. Hargreaves, G. Sandford, R. Slater, D. S. Yufit, J. A. K. Howard and A. Vong, Tetrahedron, 2007, 63, 5204–5211.
49. M. Stachowicz, M. Malinska, J. Parafiniuk and K. Woźniak, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 643–653.
50. (a) P. Seiler and J. D. Dunitz, Helv. Chim. Acta, 1986, 69, 1107–1112; (b) M. G. Trefry, E. N. Maslen and M. A. Spackman, J. Phys. C: Solid State Phys., 1987, 20, 19–28.
51. M. C. Schmidt, R. Colella and D. R. Yoder-Short, Acta Crystallogr., Sect. A: Found. Crystallogr., 1985, 41, 171–175.
52. J. M. Zuo, M. O'Keeffe, P. Rez and J. C. H. Spence, Phys. Rev. Lett., 1997, 78, 4777–4780.
53. I. M. Kurylyshyn, T. F. Fässler, A. Fischer, C. Hauf, G. Eickerling, M. Presnitz and W. Scherer, Angew. Chem., Int. Ed., 2014, 53, 3029–3032.
54. R. Pal, S. Mebs, M. W. Shi, D. Jayatilaka, J. M. Krzeszczakowska, L. A. Malaspina, M. Wiecko, P. Luger, M. Hesse, Y.-S. Chen, J. Beckmann and S. Grabowsky, Inorg. Chem., 2018, 57, 4906–4920.
55. R. B. King, Chem. Rev., 2001, 101, 1119–1152.
56. S. Mebs, R. Kalinowski, S. Grabowsky, D. F. Förster, R. Kickbusch, E. Justus, W. Morgenroth, C. Paulmann, P. Luger, D. Gabel and D. Lentz, Inorg. Chem., 2011, 50, 90–103.
57. S. Mebs, J. Henn, P. Luger and D. Lentz, Z. Anorg. Allg. Chem., 2013, 639, 2057–2064.
58. Q. L. Lu, J. W. Meng, W. J. Song and J. G. Wan, Int. J. Hydrogen Energy, 2013, 38, 13328–13334.
59. G. J. Kubas, Metal Dihydrogen and σ-Bond Complexes in Modern Inorganic Chemistry, Kluwer Academic/Plenum Publishers, New York, 2001.
60. L. Bučinský, D. Jayatilaka and S. Grabowsky, J. Phys. Chem. A, 2016, 120, 6650–6669.
61. C. Gao, A. Genoni, S. Gao, S. Jiang, A. Soncini and J. Overgaard, Nat. Chem., 2020, 12, 213–219.
62. P. W. Frost, J. A. K. Howard and J. L. Spencer, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 946–949.
63. J. A. K. Howard, O. Johnson, T. F. Koetzle and J. L. Spencer, Inorg. Chem., 1987, 26, 2930–2933.
64. (a) GUI: O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341; (b) Refinement engine olex2.refine: L. J. Bourhis, O. V. Dolomanov, R. J. Gildea, J. A. K. Howard and H. Puschmann, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 59–75.
65. L. Midgley, L. J. Bourhis, O. V. Dolomanov, N. Peyerimhoff and H. Puschmann, 2019, arXiv:1911.08847.
66. L. Midgley, L. J. Bourhis, O. V. Dolomanov, S. Grabowsky, F. Kleemiss, H. Puschmann, N. Peyerimhoff, in preparation.
67. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 . For Version 4.0 and above also: F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
68. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 09, Revision D.03, Gaussian, Inc., Wallingford C. T., 2016.
69. P. Pollak and F. Weigend, J. Chem. Theory Comput., 2017, 13, 3696–3705.
70. A. Wolf, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 9215.
71. R. Bast, Numgrid: Numerical integration grid for molecules, 2020,  DOI:10.5281/zenodo.3746461.
72. R. Lindh, P.-Å. Malmqvist and L. Gagliardi, Theor. Chem. Acc., 2001, 106, 178–187.
73. L. Lebedev, Russian Academy of Sciences Doklady Mathematics, 1999, 59, 477–481.
74. J. Burkardt SPHERE_LEBEDEV_RULE: Quadrature Rules for the Unit Sphere 2010, https://people.sc.fsu.edu/%7Ejburkardt/cpp_src/sphere_lebedev_rule/sphere_lebedev_rule.html.
75. A. D. Becke, J. Chem. Phys., 1988, 88, 2547–2553.
76. For Z=1 to Z=36: T. Koga, K. Kanayama, S. Watanabe and A. J. Thakkar, Int. J. Quantum Chem., 1999, 71, 491–497 . For Z = 37 to Z = 86: T. Koga, K. Kanayama, T. Watanabe, T. Imai and A. J. Thakkar, Theor. Chem. Acc., 2000, 104, 411–413.
77. M. Kohout, Int. J. Quantum Chem., 2004, 97, 651–658.
78. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
79. E. K. Wieduwilt, G. Macetti, L. A. Malaspina, D. Jayatilaka, S. Grabowsky and A. Genoni, J. Mol. Struct., 2020, 1209, 127934.
80. Y.-J. Lee, K. W. Han, J. S. Jang, T.-I. Jeon, J. Park, T. Kawamura, Y. Yamamoto, T. Sugahara, T. Vogt, J.-W. Lee, Y. Lee and J.-H. Yoon, ChemPhysChem, 2011, 12, 1056–1059.
81. A. Nemkevich, M. A. Spackman and B. Corry, Chem. – Eur. J., 2013, 19, 2676–2684.
82. J.-W. Lee, J. Poudel, M. Cha, S. J. Yoon and J.-H. Yoon, Energy Fuels, 2016, 30, 7604–7609.
83. M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, P. R. Spackman, D. Jayatilaka and M. A. Spackman, CrystalExplorer17, The University of Western Australia, 2017.
84. M. J. Turner, J. J. McKinnon, D. Jayatilaka and M. A. Spackman, CrystEngComm, 2011, 13, 1804–1813.
85. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
86. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1994.
87. R. F. W. Bader and M. E. Stephens, J. Am. Chem. Soc., 1975, 97, 7391–7399.
88. M. Kaupp, Angew. Chem., Int. Ed., 2001, 40, 3534–3565.
89. M. Fugel, M. F. Hesse, R. Pal, J. Beckmann, D. Jayatilaka, M. J. Turner, A. Karton, P. Bultinck, G. S. Chandler and S. Grabowsky, Chem. – Eur. J., 2018, 24, 15275–15286.
90. V. G. Tsirelson, A. S. Avilov, G. G. Lepeshov, A. K. Kulygin, J. Stahn, U. Pietsch and J. C. H. Spence, J. Phys. Chem. B, 2001, 105, 5068–5074.
91. Search in the Cambridge Structural Database for ammonium ions determined by single-crystal neutron diffraction (June 22nd, 2020). The value given is an average of 11 entries.
92. M. A. Fox, A. E. Goeta, J. A. K. Howard, A. K. Hughes, A. L. Johnson, D. A. Keen, K. Wade and C. C. Wilson, Inorg. Chem., 2001, 40, 173–175.
93. R. Brill, H. Dietrich and H. Dierks, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 2003–2018.
94. A. Burkhardt, U. Wedig, H. G. von Schnering and A. Savin, Z. Anorg. Allg. Chem., 1993, 619, 437–441.
95. C. Börrnert, Y. Grin and F. R. Wagner, Z. Anorg. Allg. Chem., 2013, 639, 2013–2024.
96. L. Bučinský, D. Jayatilaka and S. Grabowsky, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 705–717.
97. M. Podhorský, L. Bučinský, D. Jayatilaka and S. Grabowsky, Acta Crystallogr., Sect. A: Found. Adv., 2021, 77 DOI:10.1107/S2053273320014837.
98. J. Christensen, P. N. Horton, C. S. Bury, J. L. Dickerson, H. Taberman, E. F. Garman and S. J. Coles, IUCrJ, 2019, 6, 703–713.
99. M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Science, 2017, 355, 49–52.
100. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Reves, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 21, 2832–2838.
101. S. Sasaki, Report No. KEK–88-14, National Lab. for High Energy Physics, 1989.
102. B. Niepötter, R. Herbst-Irmer and D. Stalke, J. Appl. Crystallogr., 2015, 48, 1485–1497.
103. R. Destro, R. E. Marsh and R. Bianchi, J. Phys. Chem., 1988, 92, 966–973.
104. S. C. Capelli, H.-B. Bürgi, S. A. Mason and D. Jayatilaka, Acta Crystallogr., Sect. C: Struct. Chem., 2014, 70, 949–952.
105. R. M. Kabbani, Polyhedron, 1996, 15, 1951–1955.
106. N. G. Connelly, J. A. K. Howard, J. L. Spencer and P. K. Woodley, Dalton Trans., 1984, 2003–2009.
107. B. Gruza, M. L. Chodkiewicz, J. Krzeszczakowska and P. M. Dominiak, Acta Crystallogr., Sect. A: Found. Adv., 2020, 76, 92–109.

---

Footnotes

† Electronic supplementary information (ESI) available: CIFs of all refinements, further electron-density analysis of compound HQ-CO₂, theoretical background of non-spherical refinements in NoSpherA2 and the tsc file format, graphs and tables documenting the validation procedure described in Section 3. CCDC 2034385–2034389, 2035147 and 2035148. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc05526c

‡ Three main theories can each be used for both strategies:^17,18 multipole modelling,^19,20 maximum entropy methods²¹ and X-ray wavefunction refinement.²² The latter is part of the original definition of quantum crystallography (QCr),²³ whereas all theories are discussed in the generalized field of QCr.²⁴

---