Exciton delocalization length in chlorosomes investigated by lineshape dynamics of two-dimensional electronic spectra
Sunhong
Jun
ab,
Cheolhee
Yang
ab,
Seungjoo
Choi
c,
Megumi
Isaji
d,
Hitoshi
Tamiaki
 d,
Hyotcherl
Ihee
d,
Hyotcherl
Ihee
 *ab and
Jeongho
Kim
*ab and
Jeongho
Kim
 *c
*c
aDepartment of Chemistry and KI for the BioCentury, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Republic of Korea. E-mail: hyotcherl.ihee@kaist.ac.kr
bCenter for Nanomaterials and Chemical Reactions, Institute for Basic Science (IBS), Daejeon 34141, Republic of Korea
cDepartment of Chemistry, Inha University, 100 Inha-ro, Michuhol-gu, Incheon 22212, Republic of Korea. E-mail: jkim@inha.ac.kr
dGraduate School of Life Sciences, Ritsumeikan University, Kusatsu, Shiga 525-8577, Japan
First published on 9th September 2021
Abstract
A chlorosome, a photosynthetic light-harvesting complex found in green sulfur bacteria, is an aggregate of self-assembled pigments and is optimized for efficient light harvesting and energy transfer under dim-light conditions. In this highly-disordered aggregate, the absorption and transfer of photoexcitation energy are governed by the degree of disorder. To describe the disorder, the number of molecules forming excitons, which is termed exciton delocalization length (EDL), is a relevant parameter because the EDL sensitively changes with the disorder of the constituent molecules. In this work, we determined the EDL in chlorosomes using two-dimensional electronic spectroscopy (2D-ES). Since spectral features correlated with EDL are spread out in the two-dimensional (2D) electronic spectra, we were able to determine the EDL accurately without the effects of homogeneous and inhomogeneous line broadening. In particular, by taking advantage of the multi-dimensionality and the time evolution of 2D spectra, we not only determined the excitation frequency dependence of EDL but also monitored the temporal change of EDL. We found that the EDL is ∼7 at 77 K and ∼6 at 298 K and increases with the excitation frequency, with the maximum located well above the maximum of the absorption spectrum of chlorosomes. The spectral profile of EDL changes rapidly within 100 fs and becomes flat over time due to dephasing of initial exciton coherence. From the coherent oscillations superimposed on the decay of EDL, it was learned that high-frequency phonons are more activated at 298 K than at 77 K.
Introduction
A chlorosome is a photosynthetic light-harvesting antenna system found in green sulfur bacteria and has been considered as an excellent light-harvester with potential application for artificial photosynthesis. A chlorosome consists of hundreds of thousands of bacteriochlorophyll (BChl) molecules that are self-assembled to form an aggregate through non-covalent bonding and are thus highly disordered.1–4 Since green sulfur bacteria live under dim-light conditions, chlorosomes must be optimized to harvest solar energy with maximum efficiency,5 in contrast to light-harvesting systems found in higher plants and algae equipped with mechanisms of self-protection from intense sunlight. In chlorosomes of highly-disordered aggregate structure, the degree of disorder would be a key factor for maximizing the efficiencies of absorption and transfer of photoexcitation energy because it dictates the number of molecules forming excitons and eventually modulates the bandwidth of the absorption band. As the number of molecules forming an exciton increases, the absorption band becomes narrower due to exchange narrowing, which averages out inhomogeneities of individual molecules involved in a delocalized exciton.6,7 As a result, the spectral range for light absorption becomes narrowed, and the diversity of states needed for energy funneling is reduced, thus deteriorating the light-harvesting efficiency. The energy transfer efficiency of chlorosomes at ambient temperature is exceptionally high, close to unity,8–10 despite the increased degree of disorder at a higher temperature, indicating that the disorder of the chlorosomal aggregate is optimized for achieving high light-harvesting efficiency.When considering the relationship between the degree of disorder and the light-harvesting efficiency, exciton delocalization length (EDL), which refers to the number of molecules forming excitons, is a relevant parameter to describe the disorder because the EDL sensitively changes with the disorder of the constituent molecules. Since a chlorosome consists of hundreds of thousands of BChl molecules strongly coupled to each other in local regions, photoexcitation would create local excitons of various EDLs. The EDL of an aggregate of chromophores can be determined from the collective effects manifested in the optical response, for example, exciton superradiance11 and exchange narrowing.12 However, the measurement of superradiance requires the knowledge of the fluorescence quantum yield, which is generally not known very well, and determining exchange narrowing requires the knowledge of the disorder distribution experienced by a single molecule in the aggregate, which is also not easily obtainable. Thus, both methods have high uncertainties in determining the EDL. Another method of determining the EDL is transient absorption (TA) spectroscopy.13 While various time-resolved techniques have been developed to investigate the optical, electronic, and structural properties of photoinduced transient states,14–24 TA spectroscopy has served as a workhorse tool for characterizing the excitons formed by electronic transitions. A TA spectrum contains (i) a positive contribution arising from ground state bleaching (GSB) and stimulated emission (SE) of the singly-excited states generated by the pump pulse and (ii) a negative contribution arising from excited state absorption (ESA) from the singly-excited to highly-excited states. The degree of shift between the positive and negative features shows a strong correlation with the degree of exciton delocalization, making TA spectroscopy a more accurate and more practical method of determining the EDL than the measurement of exciton superradiance or exchange narrowing, with less uncertainty.
While TA spectroscopy has been commonly used to estimate the EDL in previous studies,25–28 it gives only the average EDL over the entire excitation spectrum. Also, because homogeneous and inhomogeneous line broadenings are mixed in the TA spectrum, it is difficult to determine the EDL accurately from the TA spectrum. In this regard, two-dimensional electronic spectroscopy (2D-ES) is a more appropriate method to determine the EDL because the added dimension in the two-dimensional (2D) spectrum allows us to distinguish homogeneous and inhomogeneous broadening and resolve the GSB/SE and the ESA features more clearly. Besides, since the 2D spectra give information on the correlation between the excitation and emission frequencies and they are measured at various population times, the dependence of EDL on the excitation frequency as well as the time evolution of EDL can be determined. Thus, in this work, we used 2D-ES to investigate the EDL in chlorosomes. In particular, we not only determined the distribution of EDL depending on the excitation frequency but also measured the temporal change of EDL after photoexcitation. Also, we examined the effect of the degree of disorder on the EDL by performing 2D-ES measurements at two different temperatures, 77 K and 298 K.
Experimental
The 2D-ES measurements were performed using the diffractive-optic based setup.29 Briefly, 800 nm pulses of 50 fs duration were generated from a 1 kHz regenerative amplified Ti:sapphire laser (Coherent Legend Elite seeded by Vitesse) and were converted to visible pulses of 720 nm center wavelength and 60 nm bandwidth using a home-built, noncollinear optical parametric amplifier (NOPA) based on all-reflective optics design. A prism-pair compressor was used to compensate for the dispersion of the transmissive optics in the NOPA and the 2D-ES setup, giving a pulse duration of 17 fs at the sample position. The output from NOPA was focused on a diffractive optical element (DOE; Holoeye DE228) and split into four beams, which are ±1 orders of the diffracted light, in a BOXCARS geometry. The four beams were then focused into the sample using a concave spherical mirror. Three beams (beams 1–3) were used to induce the 3rd-order polarization signal, and the fourth beam (beam 4) was attenuated by a neutral density filter and used as the local oscillator (LO). The time delays between pulses 1, 2 and 3 (beam 1–3) were controlled using a pair of wedges inserted in an antiparallel orientation. By translating only one of the pair of wedges using a motorized stage, the time delay can be changed with a 2.7 attosecond resolution. For the 2D-ES measurements, the third-order photon echo signal was detected in the ks = −k1 + k2 + k3 phase-matched direction, one corner of the BOXCARS geometry. The LO field (beam 4), which was collinear with the third-order signal field, was mixed with the signal, enabling the phase-sensitive heterodyne detection using the spectral interferometry. The spectral interference fringes between the signal and the LO fields were recorded using a spectrometer and a CCD while scanning the time delay between pulses 1 and 2 (coherence time, τ) and the delay between pulses 2 and 3 (population time, T). Fourier transform of the measured signal along the τ axis gives the absorption frequency of ωτ, while the emission frequency of ωt is directly obtained by dispersed detection using CCD, thus giving a 2D spectrum. The coherence time τ was varied from −125 fs to +125 fs in 0.25 fs increments, and the population time T was varied from 0 to 480 fs in 5 fs increments. The third-order signal at each τ was collected with a CCD integration time of 300 ms, and we repeated the scan in the entire τ and T ranges four times to check the reproducibility of the signal. The time resolution of the measurement was determined to be 15 fs at the sample position from a non-resonant transient grating measurement of pure solvent (carbon tetrachloride). The frequency-resolved pump–probe spectra were separately measured at various population times using pulses 1 and 2 as pump and probe pulses, respectively. The 2D spectra were phased by comparing the pump–probe spectra and the projection of 2D spectra onto the ωt-axis at each T. Chlorosomes were extracted from Chl. phaeobacteroides, which consists of BChl e molecules, and the diluted solution of chlorosomes in 50 mM Tris–HCl buffer and glycerol 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 v/v mixture with Na2S2O4 added as the reductant was used as the sample for the 2D-ES measurements. The optical density of the sample solution was 0.3 in a sandwich-type sapphire cell of 0.2 mm optical path length. For the low-temperature measurement, a cryostat (JANIS VPF-100) with liquid nitrogen as the coolant was used to keep the sample at 77 K.
70 v/v mixture with Na2S2O4 added as the reductant was used as the sample for the 2D-ES measurements. The optical density of the sample solution was 0.3 in a sandwich-type sapphire cell of 0.2 mm optical path length. For the low-temperature measurement, a cryostat (JANIS VPF-100) with liquid nitrogen as the coolant was used to keep the sample at 77 K.
Results and discussion
A. Energy-resolved EDL obtained from the 2D spectra of chlorosomes
In the conventional femtosecond TA spectroscopic measurement, pump pulses of broad bandwidths are often used. Therefore, only an average EDL value for a broad range of excitation frequencies is obtained from the TA measurement, with no information on the excitation frequency dependence of EDL. In principle, two-color TA spectroscopy employing narrowband pump pulses at various excitation frequencies can be used to obtain the excitation frequency dependence of EDL. In a previous two-color TA study on molecular aggregates,30 it was found that the EDL increases with the excitation frequency. Also, the excitation frequency dependence of EDL in molecular aggregates was predicted theoretically.31–33 For example, according to a theoretical study on J-aggregates,33 the EDL increases with the excitation frequency, and the excitation frequency profile of EDL has the maximum at an energy higher than the absorption maximum and matches well with the density of states (DOS) distribution, indicating that the dark states also contribute to the EDL.33,34From the 2D electronic spectra measured with 2D-ES employing broadband light sources, the correlation between absorption and emission energies can be obtained at once, and thus the EDL at a specific excitation frequency of interest can be readily determined.35 Since a cross-section of an absorptive contribution (that is, real part) of a 2D spectrum at an excitation frequency, ωτ, is equivalent to a TA spectrum measured with narrowband pump pulses of ωτ frequency, we can estimate the EDL from the cross-section of the 2D spectrum using the following equation:
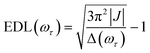 | (1) |
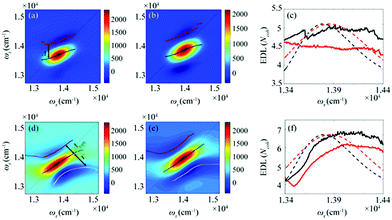
From the 2D spectra at T = 0 measured at 77 K and 298 K shown in Fig. 1a and b, respectively, we determined Δ at each ωτ by taking the energy difference between the ωt positions of the maximum (GSB and SE) and the minimum (ESA) amplitudes in a cross-section of the 2D spectrum (that corresponds to a TA spectrum). With the J value determined from the energy difference between the peaks in the absorption spectra of chlorosomes and BChl monomers,31,36 the EDLs at various ωτ values were calculated from the determined Δ values, as shown in Fig. 1c. In other words, we obtained the excitation frequency dependence of EDL from the 2D spectra. First of all, it can be seen that the ωτ-profile of EDL is nearly flat over the entire absorption spectrum, which is in contrast to the EDL profile of J-aggregates with EDL increasing sharply with the increase of excitation frequency near the absorption maximum.34 When comparing the ωτ-profiles of EDL at 77 K and 298 K, it can be seen that the EDL is higher at 77 K than at 298 K, indicating a lower degree of disorder at a lower temperature. Here we note that, while the 2D spectrum allows us to distinguish the positive and negative features more clearly, with a minimal overlap between those features, than the TA spectrum, there still remains uncertainty about the exact positions of those spectral features (and thus uncertainty about the EDL) due to the finite bandwidth of the laser spectrum. Also, there is a possibility that the overlap between the positive GSB/SE and negative ESA features may change with ωτ, thus affecting the Δ value and EDL. For example, considering that the positive 2D peak is tilted down from the diagonal, the Δ value might be overestimated as ωτ increases, resulting in the underestimation of EDL.
To determine the EDL more accurately, we decomposed a 2D spectrum into the rephasing and non-rephasing spectra by separately processing the data collected at τ > 0 and τ < 0, respectively. The rephasing spectrum contains contributions from rephasing of induced dipoles in an inhomogeneous distribution of transition energies (that is, photon echo signals) and is elongated along the diagonal direction. In contrast, the non-rephasing spectrum contains contributions from free induction decay signals and is elongated along the antidiagonal direction. The spectral lineshape of the 2D spectrum sensitively changes with various parameters of a molecular ensemble. For example, in the 2D spectra of chlorosomes, homogeneous broadening, inhomogeneous broadening, and exchange narrowing can be considered as the main factors that affect the lineshape. We note that the lineshape changes induced by such line-broadening mechanisms are manifested in orthogonal directions in the 2D rephasing and 2D non-rephasing spectra. For example, the inhomogeneous broadening increases the bandwidth of a peak along the diagonal in the rephasing spectrum but in the antidiagonal direction in the non-rephasing spectrum. The exchange narrowing reduces the bandwidth of a peak along the diagonal in the rephasing spectrum and in the antidiagonal direction in the non-rephasing spectrum. Since the measured 2D spectrum corresponds to the sum of rephasing and non-rephasing spectra, to estimate the effects of those line-broadening mechanisms on the lineshape of 2D spectra and ultimately determine the EDL accurately, it would be desirable to separate the 2D spectrum into rephasing and non-rephasing spectra. In a theoretical study on J-aggregates,34 it was shown that the 2D rephasing spectrum provides a more effective means of determining the EDL than the 2D total spectrum and only the rephasing spectrum can be used for determining the EDL because the exchange narrowing and the homogeneous broadening cannot be separated in the non-rephasing spectrum. Thus, we used only the 2D rephasing spectra for the determination of EDL.
According to a theoretical study on J-aggregates,34 as J increases, the negative ESA feature on the higher-energy side in the 2D rephasing spectrum becomes stronger and red-shifted, resulting in a decrease of the energy difference, termed Δreph in Fig. 1d and e, between the positive GSB/SE feature and the negative ESA feature on the higher-energy side. Therefore, the same theoretical study suggested that Δreph in the 2D rephasing spectrum can serve as a sensitive measure of EDL,34 as Δ in the TA spectrum can be used for determining the EDL. From the 2D rephasing spectra measured at T = 0 at 77 K and 298 K shown in Fig. 1d and 1e, respectively, we determined Δreph at each ωτ by taking the energy difference between the positive feature and the higher-energy negative feature in the antidiagonal direction. From the determined Δreph values, the EDLs were calculated as a function of ωτ, as shown in Fig. 1f. When comparing the ωτ-profiles of EDL shown in Fig. 1c and f, it can be seen that the EDL determined from the 2D rephasing spectra is higher than the one determined from the 2D total spectra (that is, the sum of rephasing and non-rephasing contributions). Specifically, from the 2D total spectra, the EDL is estimated to be ∼5 at 77 K and ∼4.5 at 298 K. In contrast, from the 2D rephasing spectra, the EDL is estimated to be ∼7 at 77 K and ∼6 at 298 K. The larger EDL at 77 K confirms the lower degree of disorder at the lower temperature as expected. These estimated EDLs are similar to the values determined in previous studies on molecular aggregates.37–41 In a recent theoretical study on molecular aggregates, the EDL was determined to be smaller than ten at low temperatures.42 From a TA study on a natural antenna structure composed of Bchl a or Bchl c, the EDL was determined to be 2–6 at 298 K and 5–12 at low temperatures. The higher EDL value determined from the 2D rephasing spectra can be ascribed to the more effective elimination of inhomogeneous broadening and the more sensitive manifestation of exchange narrowing in the 2D rephasing spectra than in the 2D total spectra. Also, in agreement with the theoretical prediction, the EDL determined from the 2D rephasing spectra increases with the excitation frequency, showing a peak at an energy higher than the peak of the absorption spectrum, as can be seen from Fig. 1f.
B. Time evolution of EDL in chlorosomes
After the photoexcitation initially creates excitons in chlorosomes, excitons would evolve over time, leading to the temporal change of EDL. Although such evolution of EDL has never been monitored previously, in principle, the EDL43 and its temporal change44 can be determined from the 0–0 to 0–1 peak ratio in the fluorescence spectrum.35 The 2D-ES measurement allows us to measure the temporal change of EDL because the 2D spectrum can be measured at various population times, and the EDL can be determined for each 2D spectrum. To monitor the temporal change of EDL relevantly using the 2D spectra, the effect of homogeneous broadening on the spectral linewidth needs to be corrected because the dephasing occurs to influence the spectral linewidth of the 2D spectrum. To do so, we can make use of the ESA feature on the lower-energy side in the 2D rephasing spectrum. According to the theoretical study on J-aggregates,34 the negative ESA feature on the lower-energy side in the 2D rephasing spectrum is barely affected by the change of intermolecular coupling strength (J) that governs exchange narrowing. According to the same theoretical study,34 the energy difference, termed γ in Fig. 1d and e, between the positive GSB/SE feature and the negative ESA feature on the lower-energy side in the 2D rephasing spectrum is a damping parameter related to the dephasing and can serve as a selective measure of homogeneous broadening without the effect of exchange narrowing. Specifically, the same theoretical study showed that the ratio, γ/Δreph, is directly correlated with the EDL, with the effect of homogeneous broadening eliminated from Δreph by dividing by γ.34 Specifically, when considering that Δreph is inversely proportional to the EDL as can be seen from eqn (1), the ratio, γ/Δreph, can serve as a quantity that is directly proportional to the EDL without the effect of homogeneous broadening.The temporal evolutions of spectrally resolved γ/Δreph at 77 K and 298 K are shown in Fig. 2a and b, respectively. It can be seen that, at early population times, the EDL is low at low excitation energies (∼13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1) and high at high excitation energies (∼14
600 cm−1) and high at high excitation energies (∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1). Subsequently, the ωτ-profile of EDL becomes nearly flat at later population times. The ωτ-profiles of γ/Δreph at the time delays of T = 0 and 480 fs are compared in Fig. 2c (77 K) and Fig. 2d (298 K). Compared with the ωτ-profile of EDL calculated from Δreph shown in Fig. 1c and f, γ/Δreph at T = 0 increases more sharply with the increase of excitation frequency. Also, it is noted that γ/Δreph keeps increasing with excitation frequency in the spectral window covering the absorption spectrum, indicating that the maximum of γ/Δreph is located at a much higher frequency than the absorption peak of chlorosomes. Such a significant change of γ/Δreph with the excitation frequency is in better agreement with the ωτ-profiles of EDL from the previous theoretical study on a J-aggregate, compared with the EDL determined from only Δreph shown in Fig. 1f. The location of the maximum EDL at a higher energy than the absorption maximum of the J-aggregate indicates that the center of DOS distribution is located at a much higher energy than the absorption maximum, probably because there exist many electronic states of BChl monomers in that spectral range. Therefore, γ/Δreph seems to better reflect the excitation frequency dependence of EDL than the EDL calculated from Δreph only, probably because of the correction of homogeneous broadening. The spectral profile of EDL changes rapidly within 100 fs, and, at T = 480 fs, the ωτ-profile of EDL is nearly flat over the entire spectral range. Such flattening of the EDL over time can be ascribed to (i) the localization of excitations that are initially generated at high-energy states and (ii) the population relaxation from high-energy states to low-energy states.
300 cm−1). Subsequently, the ωτ-profile of EDL becomes nearly flat at later population times. The ωτ-profiles of γ/Δreph at the time delays of T = 0 and 480 fs are compared in Fig. 2c (77 K) and Fig. 2d (298 K). Compared with the ωτ-profile of EDL calculated from Δreph shown in Fig. 1c and f, γ/Δreph at T = 0 increases more sharply with the increase of excitation frequency. Also, it is noted that γ/Δreph keeps increasing with excitation frequency in the spectral window covering the absorption spectrum, indicating that the maximum of γ/Δreph is located at a much higher frequency than the absorption peak of chlorosomes. Such a significant change of γ/Δreph with the excitation frequency is in better agreement with the ωτ-profiles of EDL from the previous theoretical study on a J-aggregate, compared with the EDL determined from only Δreph shown in Fig. 1f. The location of the maximum EDL at a higher energy than the absorption maximum of the J-aggregate indicates that the center of DOS distribution is located at a much higher energy than the absorption maximum, probably because there exist many electronic states of BChl monomers in that spectral range. Therefore, γ/Δreph seems to better reflect the excitation frequency dependence of EDL than the EDL calculated from Δreph only, probably because of the correction of homogeneous broadening. The spectral profile of EDL changes rapidly within 100 fs, and, at T = 480 fs, the ωτ-profile of EDL is nearly flat over the entire spectral range. Such flattening of the EDL over time can be ascribed to (i) the localization of excitations that are initially generated at high-energy states and (ii) the population relaxation from high-energy states to low-energy states.
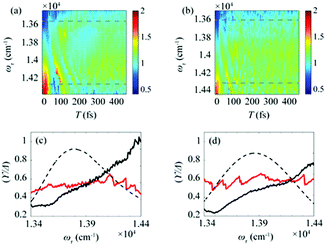 | ||
| Fig. 2 Time evolution of the bandwidth ratio, γ/Δreph, obtained from the rephasing 2D spectra at (a) 77 K and (b) 298 K. The dashed lines indicate two representative energy points, at which time-dependent changes of γ/Δreph are shown in Fig. 3. (c and d) The ωτ-profiles of γ/Δreph at T = 0 fs (solid black line) and T = 480 fs (solid red line) at (c) 77 K and (d) 298 K. The normalized absorption spectrum (dashed black line) at each temperature is shown together. | ||
To gain more insights into the decay dynamics of EDL, we compared the time evolution of EDL at two representative energy points, one on the high-energy side and the other on the low-energy side from the absorption maximum, as indicated by dashed lines in Fig. 2a and b. As the population time after excitation increases, γ/Δreph shows different time-dependent behaviors at the low-energy and high-energy points as shown in Fig. 3; that is, γ/Δreph increases at the low-energy point and decreases at the high-energy point, eventually converging into a common value at both points. This anti-correlated time dependence at the two different energies is in agreement with the flattening of the spectral profile of EDL over time, as shown in Fig. 2a and b, and such time dependence is observed at both 77 K and 298 K, although it is somewhat obscured at 77 K by strong coherent oscillations superimposed on the decay or the rise. To separate the decay or rise from the oscillations, the time-dependent change of γ/Δreph was fit with a single exponential decay combined with two damping sinusoidal functions, and the fitted parameters are shown in Table 1. The time constants of the decay and rise components are determined to be 55 fs on average at 77 K and 26 fs on average at 298 K. These dynamics would correspond to the localization of initially generated excitations as well as population relaxation from higher- to lower-energy states and are faster at a higher temperature as expected.
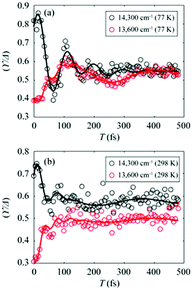 | ||
Fig. 3 (a and b) Temporal evolution of γ/Δreph at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 (black empty dots) and 13 300 cm−1 (black empty dots) and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 (red empty dots), which correspond to dashed lines in Fig. 2a and b, and their fits using two damped cosine functions and an exponential decay (solid lines of their corresponding colors) at (a) 77 K and (b) 298 K. 600 cm−1 (red empty dots), which correspond to dashed lines in Fig. 2a and b, and their fits using two damped cosine functions and an exponential decay (solid lines of their corresponding colors) at (a) 77 K and (b) 298 K. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 and 13
300 cm−1 and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 were fit by the sum of two damping cosine functions and an exponential decay
600 cm−1 were fit by the sum of two damping cosine functions and an exponential decay
| 1st oscillation | 2nd oscillation | Exponential decay | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Frequency (cm−1) | Amplitude | Phase (degrees) | Damping time (fs) | Frequency (cm−1) | Amplitude | Phase (degrees) | Damping time (fs) | Decay time (fs) | Amplitude | |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 77 K 300 cm−1 77 K |
159 | 0.09 | 316 | 101 | 364 | 0.24 | −2 | 96 | 55 | 0.20 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 77 K 600 cm−1 77 K |
118 | 0.09 | 53 | 312 | 704 | 0.03 | 35 | 79 | 55 | −0.09 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 298 K 300 cm−1 298 K |
114 | 0.02 | −1 | 527 | 505 | 0.14 | 67 | 35 | 24 | 0.12 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1 298 K 600 cm−1 298 K |
105 | 0.01 | −1 | 1.0 × 106 | 689 | 0.05 | 25 | 52 | 28 | –0.21 |
The coherent oscillations superimposed on the exponential decays may reflect the phonon modes associated with the evolution of excitons. In particular, according to the fitting analysis of the time-dependent change of γ/Δreph shown in Table 1, the amplitude ratio of the high-frequency and low-frequency oscillations is much higher at 298 K than at 77 K. While it has been reported that low-frequency molecular vibrations mediate the efficient energy transfer in natural light-harvesting complexes,45 high-frequency molecular vibrations tend to weaken the intermolecular coupling among pigments.6,46 Since the EDL is proportional to the intermolecular coupling strength as can be seen from eqn (1), the attenuated intermolecular coupling would reduce EDL at a higher temperature. However, the weakening of intermolecular coupling would reduce the exchange narrowing as well, resulting in the broadening (or less narrowing) of the absorption spectrum, which would be beneficial for light harvesting in the dim-light environment.1 Overall, the light-harvesting efficiency would be maintained at an optimum level, irrespective of the activation of high-frequency modes at ambient temperature.
Conclusions
In this study, we investigated the properties of exciton delocalization in chlorosomes by applying 2D-ES. In particular, we determined the EDL accurately without the effects of homogeneous and inhomogeneous line broadening by taking advantage of the 2D spectra, where the spectral features correlated with EDL are spread out in two dimensions. In addition, by taking advantage of the multi-dimensionality of 2D spectrum, we determined the excitation frequency dependence of EDL and, by measuring the 2D spectra at various population times, we monitored the temporal change of EDL. The EDL increases with excitation frequency, with the maximum located well above the maximum of the absorption spectrum of chlorosomes. The spectral profile of EDL changes rapidly within 100 fs and becomes flat over time, due to dephasing of initial exciton coherence. The analysis of coherent oscillations superimposed on the decay of EDL indicates that high-frequency phonons are more activated at 298 K than at 77 K, but the activated high-frequency modes are expected to influence the light-harvesting efficiency only minimally. This work demonstrates that the 2D-ES is an effective technique for studying the spectral and temporal properties of EDL.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Institute for Basic Science (IBS-R004). This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (No. 2016R1E1A1A01941978 and No. 2021R1F1A1048431).References
- G. T. Oostergetel, H. van Amerongen and E. J. Boekema, Photosynth. Res., 2010, 104, 245–255 CrossRef CAS PubMed.
- J. M. Linnanto and J. E. I. Korppi-Tommola, J. Phys. Chem. B, 2013, 117, 11144–11161 CrossRef CAS PubMed.
- J. Harada, T. Mizoguchi, Y. Tsukatani, M. Noguchi and H. Tamiaki, Sci. Rep., 2012, 2, 671 CrossRef PubMed.
- N.-U. Frigaard and D. A. Bryant, in Complex Intracellular Structures in Prokaryotes, ed. J. M. Shively, Springer, Berlin, Germany, 2006, vol. 2, pp. 79–114 Search PubMed.
- A. K. Manske, J. Glaeser, M. M. Kuypers and J. Overmann, Appl. Environ. Microbiol., 2005, 71, 8049–8060 CrossRef CAS PubMed.
- E. W. Knapp, Chem. Phys., 2005, 85, 73–82 CrossRef.
- P. B. Walczak, A. Eisfeld and J. S. Briggs, J. Chem. Phys., 2008, 128, 044505 CrossRef CAS PubMed.
- H. Vasmel, R. J. v. Dorssen, G. J. D. Vos and J. Amesz, Photosynth. Res., 1986, 7, 281–294 CrossRef CAS PubMed.
- R. J. v. Dorssen, H. Vasmel and J. Amesz, Photosynth. Res., 1986, 9, 33–45 CrossRef PubMed.
- J. Wang, D. C. Brune and R. E. Blankenship, Biochim. Biophys. Acta, 1990, 1015, 457–463 CrossRef CAS.
- S. de Boer, K. J. Vink and D. A. Wiersma, Chem. Phys. Lett., 1987, 137, 99–106 CrossRef CAS.
- E. W. Knapp, Chem. Phys., 1984, 85, 73–82 CrossRef CAS.
- L. D. Bakalis and J. Knoester, J. Phys. Chem. B, 1999, 103, 6620–6628 CrossRef CAS.
- T. R. Barends, L. Foucar, A. Ardevol, K. Nass, A. Aquila, S. Botha, R. B. Doak, K. Falahati, E. Hartmann, M. Hilpert, M. Heinz, M. C. Hoffmann, J. Köfinger, J. E. Koglin, G. Kovacsova, M. Liang, D. Milathianaki, H. T. Lemke, J. Reinstein, C. M. Roome, R. L. Shoeman, G. J. Williams, I. Burghardt, G. Hummer, S. Boutet and I. Schlichting, Science, 2015, 350, 445–450 CrossRef CAS PubMed.
- F. Bencivenga, R. Cucini, F. Capotondi, A. Battistoni, R. Mincigrucci, E. Giangrisostomi, A. Gessini, M. Manfredda, I. P. Nikolov, E. Pedersoli, E. Principi, C. Svetina, P. Parisse, F. Casolari, M. B. Danailov, M. Kiskinova and C. Masciovecchio, Nature, 2015, 520, 205–208 CrossRef CAS.
- H. Ihee, M. Lorenc, T. K. Kim, Q. Y. Kong, M. Cammarata, J. H. Lee, S. Bratos and M. Wulff, Science, 2005, 309, 1223–1227 CrossRef CAS PubMed.
- H. Ihee, Acc. Chem. Res., 2009, 42, 356–366 CrossRef CAS PubMed.
- J. G. Kim, S. Nozawa, H. Kim, E. H. Choi, T. Sato, T. W. Kim, K. H. Kim, H. Ki, J. Kim, M. Choi, Y. Lee, J. Heo, K. Y. Oang, K. Ichiyanagi, R. Fukaya, J. H. Lee, J. Park, I. Eom, S. H. Chun, S. Kim, M. Kim, T. Katayama, T. Togashi, S. Owada, M. Yabashi, S. J. Lee, S. Lee, C. W. Ahn, D. S. Ahn, J. Moon, S. Choi, T. Joo, S. I. Adachi and H. Ihee, Nature, 2020, 582, 520–524 CrossRef CAS PubMed.
- P. Kukura, D. W. McCamant and R. A. Mathies, Annu. Rev. Phys. Chem., 2007, 58, 461–488 CrossRef CAS PubMed.
- S. Jun, J. H. Lee, J. Kim, K. H. Kim, Q. Kong, T. K. Kim, M. Lo Russo, M. Wulff and H. Ihee, Phys. Chem. Chem. Phys., 2010, 12, 11536–11547 RSC.
- C. Bressler, C. Milne, V. T. Pham, A. Elnahhas, R. M. van der Veen, W. Gawelda, S. Johnson, P. Beaud, D. Grolimund, M. Kaiser, C. N. Borca, G. Ingold, R. Abela and M. Chergui, Science, 2009, 323, 489–492 CrossRef CAS PubMed.
- G. Lambert, B. Vodungbo, J. Gautier, B. Mahieu, V. Malka, S. Sebban, P. Zeitoun, J. Luning, J. Perron, A. Andreev, S. Stremoukhov, F. Ardana-Lamas, A. Dax, C. P. Hauri, A. Sardinha and M. Fajardo, Nat. Commun., 2015, 6, 6167 CrossRef CAS PubMed.
- C. Stamm, T. Kachel, N. Pontius, R. Mitzner, T. Quast, K. Holldack, S. Khan, C. Lupulescu, E. F. Aziz, M. Wietstruk, H. A. Dürr and W. Eberhardt, Nat. Mater., 2007, 6, 740–743 CrossRef CAS PubMed.
- K. Pande, C. D. Hutchison, G. Groenhof, A. Aquila, J. S. Robinson, J. Tenboer, S. Basu, S. Boutet, D. P. DePonte, M. Liang, T. A. White, N. A. Zatsepin, O. Yefanov, D. Morozov, D. Oberthuer, C. Gati, G. Subramanian, D. James, Y. Zhao, J. Koralek, J. Brayshaw, C. Kupitz, C. Conrad, S. Roy-Chowdhury, J. D. Coe, M. Metz, P. L. Xavier, T. D. Grant, J. E. Koglin, G. Ketawala, R. Fromme, V. Šrajer, R. Henning, J. C. Spence, A. Ourmazd, P. Schwander, U. Weierstall, M. Frank, P. Fromme, A. Barty, H. N. Chapman, K. Moffat, J. J. van Thor and M. Schmidt, Science, 2016, 352, 725–729 CrossRef CAS PubMed.
- G. Juzeliūnas, ZPhys-e.D: At., Mol. Clusters, 1988, 8, 379–384 Search PubMed.
- T. Meier, V. Chernyak and S. Mukamel, J. Phys. Chem. B, 1997, 101, 7332–7342 CrossRef CAS.
- M. van Burgel, D. A. Wiersma and K. Duppen, J. Chem. Phys., 1995, 102, 20–33 CrossRef CAS.
- Y. Hamanaka, H. Kurasawa, A. Nakamura, Y. Uchiyama, K. Marumoto and S. Kuroda, Chem. Phys. Lett., 2002, 363, 233–240 CrossRef CAS.
- S. Jun, C. Yang, M. Isaji, H. Tamiaki, J. Kim and H. Ihee, J. Phys. Chem. Lett., 2014, 5, 1386–1392 CrossRef CAS PubMed.
- J. R. Durrant, J. Knoester and D. A. Wiersma, Chem. Phys. Lett., 1994, 222, 450–456 CrossRef CAS.
- H. Fidder, J. Knoester and D. A. Wiersma, J. Chem. Phys., 1991, 95, 7880–7890 CrossRef CAS.
- M. Schreiber and Y. Toyozawa, J. Phys. Soc. Jpn., 1982, 51, 1537–1543 CrossRef CAS.
- A. G. Dijkstra, T. la Cour Jansen and J. Knoester, J. Chem. Phys., 2008, 128, 164511 CrossRef PubMed.
- J. Han, H. Zhang and D. Abramavicius, J. Chem. Phys., 2013, 139, 034313 CrossRef PubMed.
- I. Stiopkin, T. Brixner, M. Yang and G. R. Fleming, J. Phys. Chem. B, 2006, 110, 20032–20037 CrossRef CAS PubMed.
- N.-U. Frigaard, K. L. Larsen and R. P. Cox, FEMS Microbiol. Ecol., 1996, 20, 69–77 CrossRef CAS.
- T. Pullerits, M. Chachisvilis and V. Sundström, J. Phys. Chem., 1996, 100, 10787–10792 CrossRef CAS.
- V. Novoderezhkin, R. Monshouwer and R. van Grondelle, Biophys. J., 1999, 77, 666–681 CrossRef CAS PubMed.
- V. Novoderezhkin and Z. Fetisova, Biophys. J., 1999, 77, 424–430 CrossRef CAS PubMed.
- A. Yakovlev, V. Novoderezhkin, A. Taisova and Z. Fetisova, Photosynth. Res., 2002, 71, 19–32 CrossRef CAS PubMed.
- V. I. Prokhorenko, D. B. Steensgaard and A. R. Holzwarth, Biophys. J., 2000, 79, 2105–2120 CrossRef CAS PubMed.
- G. D. Scholes, Faraday Discuss., 2019, 221, 265–280 RSC.
- F. C. Spano and H. Yamagata, J. Phys. Chem. B, 2011, 115, 5133–5143 CrossRef CAS PubMed.
- R. Tempelaar, F. C. Spano, J. Knoester and T. L. Jansen, J. Phys. Chem. Lett., 2014, 5, 1505–1510 CrossRef CAS PubMed.
- V. Tiwari, W. K. Peters and D. M. Jonas, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1203–1208 CrossRef CAS PubMed.
- J. Moll, S. Daehne, J. R. Durrant and D. A. Wiersma, J. Chem. Phys., 1995, 102, 6362 CrossRef CAS.
| This journal is © the Owner Societies 2021 |