Investigation of nonadiabatic dynamics in the photolysis of methyl nitrate (CH3ONO2) by on-the-fly surface hopping simulation†
Juanjuan
Zhang
 ab,
Jiawei
Peng
ab,
Deping
Hu
ab,
Jiawei
Peng
ab,
Deping
Hu
 *ab and
Zhenggang
Lan
*ab and
Zhenggang
Lan
 *ab
*ab
aSCNU Environmental Research Institute, Guangdong Provincial Key Laboratory of Chemical Pollution and Environmental Safety & MOE Key Laboratory of Environmental Theoretical Chemistry, South China Normal University, Guangzhou 510006, China. E-mail: hudp1990@gmail.com; zhenggang.lan@m.scnu.edu.cn; zhenggang.lan@gmail.com
bSchool of Environment, South China Normal University, Guangzhou 510006, China
First published on 1st September 2021
Abstract
The photolysis mechanism of methyl nitrate (CH3ONO2) was studied using the on-the-fly surface hopping dynamics at the XMS-CASPT2 level. Several critical geometries, including electronic state minima and conical intersections, were obtained, which play essential roles in the nonadiabatic dynamics of CH3ONO2. The ultrafast nonadiabatic decay dynamics to the ground state were simulated, which gives a proper explanation on the broad and structureless absorption spectra of CH3ONO2. The photodissociation channels, including CH3O + NO2, CH3O + NO + O, and others, as well as their branching ratios, were identified. When the dynamics starts from the lowest two electronic states (S1 and S2), the CH3O + NO2 channel is the dominant photolysis pathway, although we observed the minor contributions of other channels. In contrast, when the trajectories start from the third excited state S3, both CH3O + NO2 and CH3O + NO + O channels become important. Here the CH3O–NO2 bond dissociation takes place first, and then for some trajectories, the N–O bond of the NO2 part breaks successively. The quasi-degeneracy of electronic states may exist in the dissociation limits of both CH3O + NO2 and CH3O + NO + O channels. The current work provides valuable information in the understanding of experimental findings of the wavelength-dependent photolysis mechanism of CH3ONO2.
1. Introduction
Alkyl nitrates (RONO2, R = CH3, C2H5, etc) have received considerable research attention because they play an essential role in the NOx-involved chemical reactions in the atmosphere.1–11 The oxidation and photoinduced reactions of reactive nitrogen oxides cause significant impacts on our atmospheric environments, such as affecting air quality, changing climates, and modifying nutrient cycles.1–4,7–13 A group of stable organic nitrates involved in the atmospheric NOx reactions are RONO2. On one side, this series of compounds are generated by the photo-oxidation of hydrocarbons in the presence of NOx or reactions of NO3 with alkenes.1,2,6,11–16 Due to the thermal stability of RONO2, they may survive in the atmosphere for a sufficiently long time and may be transferred to regions far from where they are produced. Therefore, several studies tried to explore their potential roles as NOx reservoirs in the troposphere.2 On the other side, RONO2 experience photolysis and give NO2 again after UV radiation.1,2,17–35 Therefore, the study of RONO2 photoreaction at the atomic level is certainly important.As the simplest alkyl nitrate, methyl nitrate (CH3ONO2) was found in marine boundary layer of the South Pacific, which was related to 20–80% of the reactive nitrogen (NOx).16 The UV absorption spectra of CH3ONO26,19,24,27,28,33,35–37 display an intense band around 190–220 nm, along with a much weaker diffusion band extending to around 330 nm. In fact, both are rather broad and structureless, namely, lack of vibronic progression. The broadness of the absorption band strongly indicates that the lifetime of the excited states should be extremely short.38,39 Therefore, after UV absorption, the wavepacket should quickly move out of the Franck–Condon (FC) region on the excited-state surfaces, and even decay via conical intersections (CIs). This implies that ultrafast excited-state dynamics in principle should take place.
Several experimental studies focused on the photolysis dynamics of CH3ONO2 and other alkyl nitrates.6,20,22–24,27,28,31,32,35,40 In particular, these works demonstrated that different photolysis products may be formed with laser excitation at different wavelengths. Yang et al.20 found that the photolysis of CH3ONO2 at 248 and 193 nm results in different dissociation products. The photolysis at 248 nm mainly gives CH3O + NO2 with a rather high quantum yield. At 193 nm two different channels were observed after the CH3O–NO2 bond breaking, in which the low-energy channel gives CH3O + NO2 products and the high-energy channel induces a further dissociation of the N–O bond in NO2, giving the CH3O + NO + O reaction. An additional channel CH3ONO + O was also identified. The UV photolysis of CH3ONO2 was examined by Talukdar et al.,35 who suggested that the CH3ONO2 photodissociation at long wavelengths, namely 248 nm and 308 nm, is dominated by the CH3O + NO2 channel. At a much shorter wavelength of 193 nm, a visible quantum yield of the O atom was observed, which may come from the further dissociation of the NO2 fragment. The photolysis of CH3ONO2 at a long wavelength (>300 nm) closing to the low-energy absorption tail always results in the CH3O + NO2 photoproducts. Derro et al.24 examined the photolysis dynamics of CH3ONO2 at 193 nm. They suggested that the excitation of CH3ONO2 at 193 nm causes the local excitation of the −NO2 moiety, and most available energy is thus partitioned to the NO2 fragment during dissociation. As a consequence, after the CH3O + NO2 photoproducts are generated by the laser excitation at 193 nm, the highly excited NO2 fragment may experience the further N–O bond dissociation, resulting in the CH3O + NO + O channel. Other alkyl nitrates and derivatives were also studied experimentally,6,17,21–24,27,28,31,32,35,40 which indicates a similar tendency.
Several theoretical efforts were made to examine the reactions of alkyl nitrates and similar compounds.5,18,25,26,41–49 The ground-state reactivity and the dissociation dynamics of CH3ONO2 were examined by electronic structure calculations and Born–Oppenheimer dynamics simulations.25 One of the early theoretical studies on the excited states of alkyl nitrates was performed by Harris18,49 at the semi-empirical level, who provided the excitation energies and oscillator strengths of the low-lying excited states for the initial assignment of the absorption spectra of these species. Recently, Soto, Arenas and coworkers performed systematic studies on the photoreactions of CH3ONO2 and derivatives.26,41,43,48,50–52 At the multi-state complete active space second order perturbation theory (MS-CASPT2) level, they built the highly accurate potential energy surfaces (PESs) of several excited states along the CH3O–NO2 dissociative coordinate.26 The pathways towards different products were constructed. Several key geometries including the minimum-energy geometries and CIs were located. We noticed that the quasi-degeneracy of the low-lying electronic states exists in the dissociation limit due to the symmetry property of the photoproducts. This provides an important starting point to address the photolysis mechanism of CH3ONO2.
From the theoretical point of view, the direct simulation of the excited-state dynamics of CH3ONO2 should provide valuable information for the understanding of the CH3ONO2 photolysis mechanism. Therefore, we tried to employ the on-the-fly trajectory surface hopping (TSH) dynamics with the extended multi-state complete active space second order perturbation theory (XMS-CASPT2)53–55 to study the excited-state nonadiabatic dynamics of CH3ONO2. Several key geometries, including the minima of electronic states and CIs, were located. The nonadiabatic dynamics including low-lying excited states was simulated. The results showed that the ultrafast nonadiabatic dynamics takes place after photoexcitation, followed by the successive dissociation dynamics. Different photoproducts were identified when dynamics starts from different excited states. The simulated results were in qualitative agreement with available experimental studies. This work deepens our understanding of the photochemistry of alkyl nitrates. In addition, we clearly demonstrate that both nonadiabatic internal conversion and photodissociation dynamics of CH3ONO2 take place within the ultrafast time scale. This indicates that such a system may become an interesting candidate in future experimental studies of ultrafast spectroscopy. At the same time, the theoretical treatment of photodynamics of volatile organic compounds (VOCs) becomes more and more attractive in recent years.1,2,56–60 We believe that the on-the-fly nonadiabatic dynamics56,58–67 may provide an indispensable simulation tool in the explanation of the photochemistry of VOCs.56,58–60,68,69
2. Computational details
Scheme 1 shows the molecular structure of CH3ONO2 and atomic labels. The critical internal coordinates are listed in Table 1, in which the O–N, O–Oa, and O–Ob distances are described by ra, rb, and rc, respectively. The distances of N–Oa and N–Ob are shown as rd and re, respectively. The angle Oa–N–Ob (θa) describes the bending motion of the NO2 fragment. The dihedral angle O–Oa–Ob–N (τa) describes the pyramidalization at the N atom.| Label | Internal coordinate |
|---|---|
| r a | Distance O–N |
| r b | Distance O–Oa |
| r c | Distance O–Ob |
| r d | Distance N–Oa |
| r e | Distance N–Ob |
| θ a | Angle Oa–N–Ob |
| τ a | Dihedral angle O–Oa–Ob–N |
The geometry optimization of the ground-state minimum (S0-min) and the vibrational analysis of methyl nitrate were performed at the B3LYP/6-311+G* level with the Gaussian 16 package.70 The optimized S0-min geometry was used to calculate excited states using the XMS-CASPT2 with the def2-SVPD basis set. The XMS-CASPT2 calculations employed the active space of 12 electrons in 9 orbitals and four states were averaged, namely, XMS(4)-CASPT2(12,9). The active space contains three π, one σ and one n orbital, as well as one antibonding π* orbital, two antibonding σ* orbitals, one n/σ mixed orbital. The orbitals in the active space are given in Fig. S1 in ESI.† The optimization of the S1 minimum (S1-min) was also performed by the XMS(4)-CASPT2/def2-SVPD method with the same active space.
The ultrafast nonadiabatic decay dynamics simulations of CH3ONO2 were studied by the on-the-fly TSH method with Tully's fewest-switches algorithm71 at the XMS(4)-CASPT2(12,9)/def2-SVPD level. The initial geometries and velocities were sampled from the Wigner distribution function72 of the lowest vibrational state at the S0-min. After the generation of many geometries by the Wigner sampling, their vertical excitation energies and oscillator strengths were calculated at the XMS(4)-CASPT2(12,9)/def2-SVPD level. The absorption spectrum was calculated by the nuclear ensemble approach (NEA),73 in which 500 snapshots were taken, and the stick spectra were broadened by the Gaussian line shape with the phenomenological broadening parameter as 0.10 eV.
In the on-the-fly nonadiabatic dynamics simulation, the nuclear motion was propagated with a time step of 0.5 fs with the velocity-Verlet algorithm, and 100 steps of electronic motion were integrated within each step of nuclear motion. The decoherence correction approach proposed by Granucci et al.74 was taken, and the parameter was set to 0.1 hartree.75 Finally, 100, 99, and 98 trajectories were performed for the dynamics initialized from S1, S2, and S3, respectively. All dynamics calculations were performed with the JADE-NAMD package.67,76,77 We developed the Python interface between the TSH dynamics in the JADE-NAMD package and the XMS-CASPT2 calculations in the BAGEL package.78,79 In the dynamics propagation process, the PESs, nuclear gradients, and nonadiabatic coupling vectors were calculated directly at the XMS-CASPT2 level using the BAGEL package.
The S1–S0 (CI10), S2–S1 (CI21), and S3–S2 (CI32) minimum-energy CIs (MECIs) were optimized at the state-averaged complete active space self-consistent field,80,81 SA(4)-CASSCF(12,9)/cc-pVDZ using the OpenMolcas package,82 in which the initial geometries were taken from hopping geometries in nonadiabatic dynamics. The single-point calculations were performed at those optimized CIs using the XMS(4)-CASPT2(12,9)/def2-SVPD level with the same setup as other XMS-CASPT2 calculations. We constructed the excited-state potential energy curves by the linear interpolation in internal coordinates (LIIC) approach from S0-min to S1–S0 MECIs at the XMS(4)-CASPT2(12,9)/def2-SVPD level.
Furthermore, the S1–S0 CI seams (CI10-seams) along the O–N distance (ra) were also built at the SA(2)-CASSCF(12,9)/def2-SVPD level by the constrained optimization using the MOLPRO package.83–85 For convergence, only two-state averaged calculations were employed in the CI10-seam construction. Although this only provided a preliminary view, the obtained CI-seam structure information is reasonable enough for our analysis purpose because we mainly focused on the CI10 here.
3. Results
3.1. S0-min and S1-min
The molecular structures at the S0 and S1 minima of CH3ONO2 are shown in Fig. 1. The important geometrical parameters and excited-state energies at S0-min and S1-min are displayed in Tables S1 and S2 in ESI.† The geometrical structure of S0-min shows Cs symmetry, where C, O, N, Oa, and Ob atoms are located in the same plane (τa = 0°). The distances of N–Oa (rd) and N–Ob (re) are 1.21 Å and 1.20 Å, respectively. This geometry is similar to previous work.86 At S0-min, the XMS(4)-CASPT2(12,9)/def2-SVPD calculations show that the vertical energies of S1 and S2 are 4.84 and 5.76 eV, respectively. S1 and S2 correspond to the n (HOMO−1) → π* (LUMO) and n/σ (HOMO) → π* (LUMO) transition, respectively. Here the electronic character of the HOMO displays the mixture of n and σ, see Fig. S1 in ESI.† The orbitals involved in the electronic transition of S1 are shown in Fig. S2(a) in ESI.† Both S1 and S2 show very weak oscillator strengths, while S3 is a bright state. The vertical excitation energy of S3 is 6.54 eV, which is dominated by the π (HOMO−2) → π* (LUMO) transition. The excitation energies of these states are similar to those of previous theoretical studies.26,28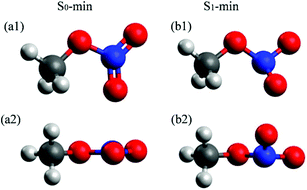 | ||
| Fig. 1 Optimized S0-min (B3LYP/6-311+G*) and S1-min [XMS(4)-CASPT2(12,9)/def2-SVPD] geometries of CH3ONO2. The top and side views are shown up and down, respectively. | ||
We calculated the absolute crossing section of the theoretical absorption spectra, including all individual contributions to different excited states using the NEA.73 The absorption spectra in the broad energy range (from 180 nm to 320 nm) and in the long-wavelength domain (from 240 nm to 320 nm) are given in Fig. 2(a) and (b), respectively, along with the experimental ones.6,27 Please notice that all available experimental works only gave the absorption spectra above 190 nm.87
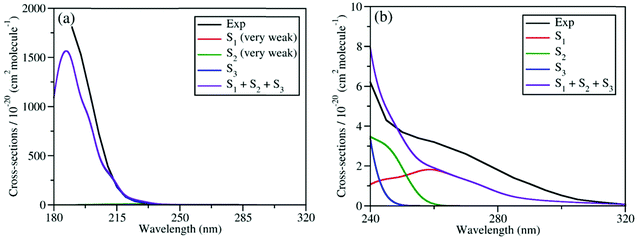 | ||
| Fig. 2 Comparison of experimental and simulated UV absorption spectra of CH3ONO2: (a) from 180 nm to 320 nm; (b) from 240 nm to 320 nm. The theoretical spectra were simulated at XMS(4)-CASPT2(12,9)/def2-SVPD level. The experimental spectra in (a) and (b) were taken from previous works.6,27 The intensities of absorption bands shown in (a) and (b) differ by several magnitudes. | ||
As shown in Fig. 2(a), the theoretical and experimental absorption spectra agree well in the whole energy domain. The short-wavelength absorption band is dominant by the S3 transition with very high oscillator strength. The profiles of theoretical and experimental bands near 190 nm are highly consistent, except that the theoretical peak intensity is a little lower. The electronic transitions to both S1 and S2 are much weaker, and their absorption intensities are several magnitudes lower than the transition to S3. Thus, the contribution of the former two components cannot be seen directly in Fig. 2(a). If we examine the long-wavelength region (from 240 nm to 320 nm) in Fig. 2(b), the very weak long tail of the whole absorption band is attributed to the summation of the transitions to both S1 and S2. Their overall contribution basically agrees well with the experimental data, except that the theoretical band is slightly weaker.
Overall, the simulated spectra agree well with the experimental one in the broad energy domain, including peak position, intensity, and profile. In particular, the transition amplitudes to different excited states differ by several magnitudes, while the absolute crossing sections in theoretical spectra agree well with available experimental data in all relevant energy domains. This confirms that the XMS-CASPT2 gives a reliable description of these low-lying excited states of the current system in the FC region. In addition, this also indicates that the initial sampling of nuclear conditions used in the further TSH dynamics are reasonable.
In contrast to the S0-min geometry, the S1-min geometry displays a significant pyramidalization at the N atom (τa = 26.8°). With the pyramidal movement of the N atom, we observed the elongation of the N–Oa (rd = 1.27 Å) bond and the N–Ob (re = 1.32 Å) bond, as well as the bending motion of the Oa–N–Ob (θa = 109.0°) angle. This geometry deformation implies that the hybridization status of the N atom changes from sp2 to sp3 when the geometry changes from S0-min to S1-min. At S1-min, the relative energies of S0, S1, S2, and S3 with respect to the S0 energy of S0-min are 2.06, 3.74, 5.54, and 7.27 eV, respectively. The transition of the S1 state is n (HOMO) → π* (LUMO), and the orbitals are shown in Fig. S2(b) in ESI.† We noticed that HOMO−1 at S0-min becomes HOMO at S1-min, and the same occupied orbital is always involved in the electronic transitions of S1, indicating that its electronic character remains unchanged from S0-min to S1-min.
3.2. Conical intersections
Fig. 3 shows all optimized MECIs, and Table S2 (ESI†) gives their corresponding energies. Normally, it is better to perform the dynamics simulation and the CI optimation at the same level of theories. However, several test CI optimization tasks at the XMS-CASPT2 level did not give us the converged results. To give a comprehensive picture of all involved MECIs and CI-seams, we took the CASSCF method to perform the CI optimization, since it is easier to obtain the converged results. To make sure that all obtained MECIs are reasonable, the single-point calculations at the XMS-CASPT2 level were conducted again. The results in Table S2 (ESI†) show that these MECIs optimized at the CASSCF level are reasonable because the energy gaps of electronic states involved in the state degeneracy are very small at the XMS-CASPT2 level.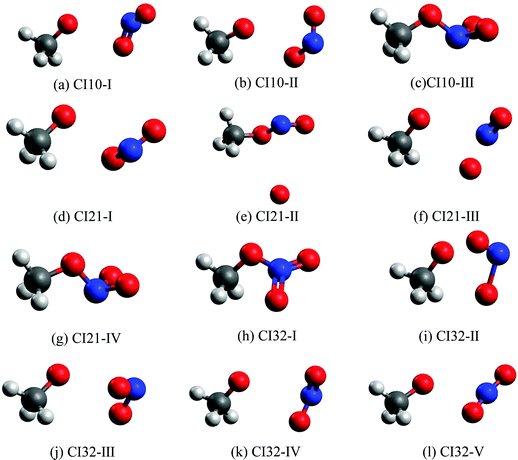 | ||
| Fig. 3 The MECIs optimized at the SA(4)-CASSCF(12,9)/cc-pVDZ level: (a)–(c): S1–S0 CIs; (d)–(g): S2–S1 CIs; (h)–(l): S3–S2 CIs. | ||
The first minimum-energy CI10 is CI10-I (1.91 eV) characterized by the significant CH3O–NO2 stretching motion (ra = 3.11 Å) with respect to the S0-min geometry. The Oa–N–Ob bond angle (θa = 133.5°) at this CI is very close to that (130.0°) at the S0-min geometry. At CI10-I, the system is roughly viewed as two radical fragments, CH3O and NO2. The important frontier orbitals are composed of the p orbital located at the O atom of the CH3O radical and the π orbital at the NO2 side. Here the later π orbital is a delocalized one, which is the linear combination of p orbitals at Oa and Ob atoms in the NO2 part, as shown in Fig. 4(a).
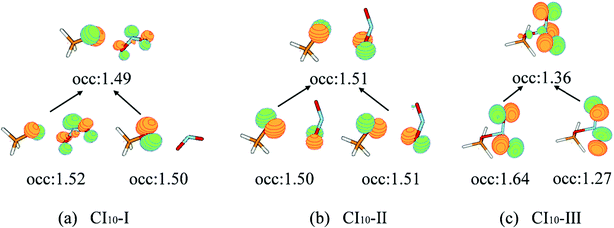 | ||
| Fig. 4 The natural transition orbitals along with their fractional occupation numbers at the S1–S0 MECIs optimized at the SA(4)-CASSCF(12,9)/cc-pVDZ level. | ||
The second minimum-energy CI10 (CI10-II) lies at a higher energy domain (3.92 eV). At CI10-II, both the large CH3O–NO2 stretching and the Ob–N–Oa bond angle bending motion were observed, which are characterized by 3.19 Å and 110.3°, respectively. Here the frontier orbitals are still composed of the p orbital located at the O atom of the CH3O radical and the p orbital at the Ob atom of the NO2 side. Different from the CI10-I, the frontier orbitals of the NO2 side become fully localized at the Ob atom, shown in Fig. 4(b). The underlying reason is easy to understand; the distances of N–Oa and N–Ob are very similar at CI10-I. Two localized p orbitals associated with the Oa and Ob atoms show similar energies; thus, their electronic coupling results in the delocalized molecular orbitals, see Fig. 4(a). In contrast, the bond rd and re of the NO2 radical are quite different at CI10-II. Therefore, the frontier orbitals become localized at the Ob atom, see Fig. 4(b).
At the third minimum-energy CI10, labeled as CI10-III, the O–N bond is in a bonded status and the strong pyramidalization at the N atom exists (τa = 34.8°). Different from CI10-I and CI10-II, as shown in Fig. 4(c), the frontier orbitals are localized in the NO2 fragment.
We noticed that a previous study once localized a CI10 that is close to the CI10-II here.26 Another study showed that a similar system CH3NO2 has a CI that displays the bonded O–N bond and the pyramidalization at the N atom.52 This is similar to the CI10-III in the current work.
We also located the MECIs between different excited states, namely CI21 and CI32, and all obtained CI geometries are given in Fig. 3. The CI21-IV and CI32-I display the obvious pyramidalization at the N atom, and no bond breaking is observed at these two CIs, while the bond cleavage is observed at other CI21 and CI32. More information about other CIs is listed in Tables S2 and S3 (ESI†).
3.3. Nonadiabatic dynamics
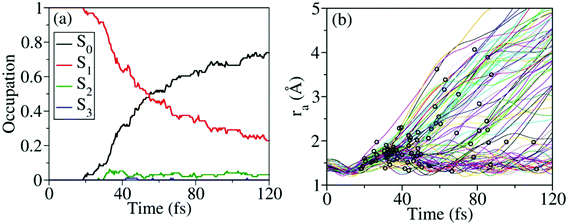
Nonadiabatic excited-state dynamics of CH3ONO2 were simulated using the on-the-fly TSH dynamics at the XMS-CASPT2 level. We first considered the dynamics starting from S1. After excitation to S1, the ultrafast S1 → S0 population decay was observed, see Fig. 5(a). Within the first 18 fs, almost all trajectories were propagating on S1, and no decay was observed. After 53 fs, 50% of the trajectories jumped back to S0. At 120 fs, the S1 population decayed to 23%. In the whole decay dynamics, both S2 and S3 did not play important roles here.The current population dynamics indicates that most trajectories go back to the ground state and only a few trajectories stay on the excited state. Thus it is necessary to identify which molecular motion is essential to drive the S1 → S0 decay dynamics. From the trajectory propagation from the FC region to the S1 → S0 hops, the obvious elongation of the CH3O–NO2 (ra = 1.31–4.24 Å) bond and the significant pyramidalization at the N atom (τa = 7.2–170.1°) were noticed. After the S1 → S0 internal conversion, most trajectories continue moving towards the dissociation limit, which results in the CH3O–NO2 bond cleavage, as shown in Fig. 5(b).
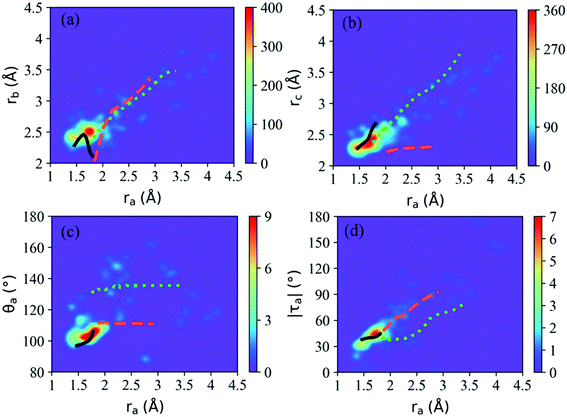
According to Fig. 5(b), most hops take place at geometries with a long CH3O–NO2 distance, while the system is still not fully broken. Thus the CH3O–NO2 bond strengthening motion should be one of the key degrees of freedom in the nonadiabatic dynamics. The S1–S0 CI seams along the CH3O–NO2 bond length were built with the constrained optimization by freezing the CH3O–NO2 distance, as shown in Fig. 6. The energies of three CI10-seams as a function of ra are shown in Fig. S3 (ESI†).
Both the CI10-seam-I and CI10-seam-II exist extensively in both short CH3O–NO2 distance and long CH3O–NO2 distance regions. We only obtained a small part of the CI10-seam-III, and the other optimization jobs did not give the converged results. From the geometrical distribution at hops within 120 fs, many hops are governed by the CI10-seam-III (∼72% of hops). Therefore, these hopping geometries do not show the full cleavage of the CH3O–NO2 bond. Instead, the strong pyramidalization at the N atom is observed. The other two CI10 seams result in the hop geometries displaying the longer CH3O–NO2 distances, and the ratio of hops around CI10-seam-I and CI10-seam-II is about 13% and 11% of all hops, respectively, assigned by the Oa–N–Ob bond angles of these hops.
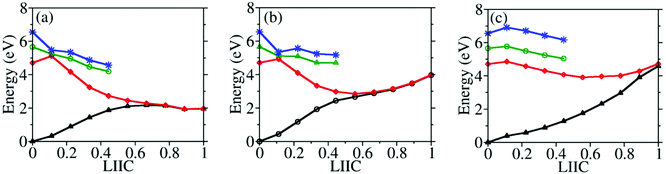
To understand why CI10-III is the leading channel in the S1 to S0 nonadiabatic decay dynamics, the linear-interpolated PESs from S0-min to S1–S0 CIs were constructed, as shown in Fig. 7. At the SA(4)-CASSCF(12,9) optimized MECI geometries, the single point calculations at the XMS-CASPT2 level also indicated that the lowest two states remain nearly degenerated. Thus the SA(4)-CASSCF(12,9) optimized CI geometries are reasonable. Although the energy of CI10-III is higher, the reaction pathway from S0–min to it shows a minor barrier on the S1 PES. Although CI10-I and CI10-II lie in the low-energy region, the pathways towards them display obvious barriers that may be caused by the existence of the CIs between different excited-states. In addition, the CI10-III geometry is close to the FC region; this also means that the system may easily access the CI10-III without undergoing drastic structural deformation.
After the analysis of the first S1 → S0 hops, the next task is to examine the final photoreaction products. In fact, most trajectories follow the CH3O + NO2 dissociation pathway, no matter via which CI. Only for a few of the trajectories passing CI10-III, the CH3O + NO + O channel was found, as shown in Table 2.
| Initial state | Final products | Ratio (%) |
|---|---|---|
| S1 | CH3O + NO2 | 83 |
| CH3O + NO + O | 5 | |
| CH3ONO2 (no breaking) | 12 | |
| S2 | CH3O + NO2 | 87 |
| CH3O + NO + O | 3 | |
| CH3ONO + O | 3 | |
| CH3ONO2 (no breaking) | 7 | |
| S3 | CH3O + NO2 | 53 |
| CH3O + NO + O | 42 | |
| CH3ONO + O | 5 | |
The typical trajectories towards different dissociation channels are given in Fig. S4–S7(a) (ESI†), along with the state degeneracy in the dissociation limit. These trajectories start from S1, experience the S1–S0 hop via CI10-I (Fig. S4, ESI†), CI10-II (Fig. S5, ESI†), and CI10-III (Fig. S6, ESI†), and move to the CH3O + NO2 channel at the end. No matter which CI is passed, the CH3O + NO2 dissociation limit always displays the quasi-degeneracy of two lowest states S0 and S1. Although the trajectory starting from S1 may generate the CH3O + NO + O channel, this channel becomes important in the dynamics initialized from the S3 state. Thus the typical trajectory towards this channel in Fig. S7 (ESI†) starts from S3, in which all four lowest electronic states included in the state-averaged calculations become nearly degenerated in the CH3O + NO + O dissociation limit. The underlying reasons for the state degeneracy are relevant to the symmetries of molecular geometries and the degeneracy of frontier orbitals, and more details are given in the below section.
In a short summary, the ultrafast decay dynamics (the lifetime ∼53 fs) was observed for CH3ONO2 when the trajectories start from S1, which is governed by three S1–S0 CIs (CI10-I, CI10-II, and CI10-III). Among them, CI10-III plays a crucial role in the S1 to S0 hops. Most trajectories passing CI10-III finally move towards two dissociation channels, in which the major channel is CH3O + NO2, and the minor channel is CH3O + NO + O. The trajectories decaying via the other S1–S0 CIs (CI10-I and CI10-II) give dissociation products CH3O + NO2. Overall, the primary photolysis channel is CH3O + NO2 and the ratio towards this channel is 83%. The minor channel gives the CH3O + NO + O products with a ratio ∼5%.
Please notice that the above ratio is only a rough estimation of the probabilities of photolysis product channels. The reason is as follows. When trajectories jump back to the ground state, the high kinetic energy results in distorted geometries. At some of these geometries, the electronic structure calculations become unstable, giving either the non-convergence results or the sudden flip of state energies. Therefore, we only considered the trajectory propagation before these questionable events. However, the geometries at these events may not be easily assigned as the dissociative or bonded status. For instance, the N–O bond in the NO2 fragment may become quite long while it is still not fully dissociated. In this case, our assignment of the photolysis channels according to the N–O bond distance was highly approximated. In this sense, the current estimation of the photolysis products ratio is rather qualitative, while such information should still be quite useful to understand the CH3ONO2 photodynamics.
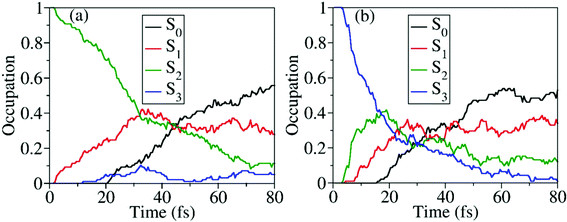
When the dynamics starts from S2 and S3, the time-dependent occupations of electronic states are shown in Fig. 8(a) and (b). No matter whether the trajectory starts from S2 or S3, the ultrafast nonadiabatic dynamics was observed, as shown in Fig. 8(a) and (b). Even in the early time of dynamics, the excited-state population decays were observed, and the S0 population started to increase quickly. As expected, when the higher excited states are prepared, the S0 population rises more quickly.
Starting from the S2, all three S1–S0 CIs play essential roles in the nonadiabatic decay to the ground state, as shown in Fig. S8 (ESI†). It is hard to distinguish their precise contributions here because more distorted hopping geometries appear. More than 93% trajectories move to the dissociation limit, giving three different reaction channels, CH3O + NO2 (∼87%), CH3O + NO + O (∼3%), and CH3ONO + O (∼3%). When the dynamics starts from S3, the final photoproducts are CH3O + NO2 (∼53%), CH3O + NO + O (∼42%), and CH3ONO + O (∼5%), as shown in Table 2.
4. Discussion
The theoretical study of the nonadiabatic dynamics of CH3ONO2 represents a great challenging task due to its rather complicated electronic configurations in the photolysis dynamics. First, the different types of complicated multi-state quasi-degeneracy may appear from time to time along the CH3O–NO2 dissociation pathway, which brings difficulty in electronic treatments. Second, the photochemistry of CH3ONO2 involves high-lying excited states, while their theoretical description by currently available electronic structure approaches may not be accurate enough. Third, after the internal conversion, the excessive energy could lead to highly distorted geometries at which the electronic structure calculations become non-converged or state energies may change suddenly. Because we can only trust the trajectory propagation before these improper events, the estimation of the branching ratio of the final photoproducts is rather qualitative. One question is whether it is possible to use some tricks to improve the numerical stability in the trajectory propagation after hops, for instance using some more robust theories, such as the algebraic diagrammatic construction method to the second order [ADC(2)] or density functional theory (DFT), to restart our propagation after S1–S0 hops. However, we do not prefer this approach because the quasi-degeneracy of the two-lowest electronic states (S1 and S0), even the multi-state degeneracy, exists in the dissociation limit. At the same time, the shorter time step may also not solve the numerical instability problem. In the current system, many orbitals may show very similar energies and start to highly mix due to orbital symmetry in the dissociation limit. In this case, the orbitals inside and outside of the active space are easily mixed, and this brings the discontinuities of the electronic wavefunctions. When the strong geometry distortion exists, this orbital mixture becomes even more pronounced. Therefore, the employment of the smaller-time step does not alleviate this problem.However, considering the computational facilities and available theoretical approaches currently, the current treatment represents a state-of-the-art approach that in principle provides valuable information to address the major reaction channels and relevant key molecular motion of the excited-state dynamics of CH3ONO2. Previous computational work demonstrated the existence of visible barriers along the direct CH3O–NO2 bond-breaking pathway when no additional nuclear motions are involved.26 In the current work, we demonstrated that the pyramidalization at the N atom along with the CH3O–NO2 bond stretching can drive the system accessing an S1–S0 CI (CI10-III) and induce the ultrafast internal conversion dynamics. Even when the inclusion of other relevant degrees of freedom modifies the barrier height for the direct excited-state CH3O–NO2 dissociation channel (Fig. 7), the pathways towards the CI10-I and CI10-II still display visible barriers. Thus these two CIs only act as the secondary channels in the internal conversion dynamics of CH3ONO2 starting from S1. When the trajectories start from high-lying excited states (S2 and S3), the barriers towards CI10-I and CI10-II may be overcome more easily, and thus they start to play more important roles here.
No matter which CI is passed, most trajectories finally move to dissociation limits. One major dissociation channel gives the products CH3O + NO2. At this dissociation limit, the ground state CH3O radical geometry is very close to the C3v symmetry and the two lowest electronic states of the CH3O radical become almost degenerated. This explains the existence of the state degeneracy in the dissociation limit of this channel. In fact, such state degeneracy was also noticed by previous work.26 In principle, the existence of the 3-fold rotational axis of the CH3O may give the high symmetry structure,88,89 and this is the origin of the state degeneracy.38,39 Such a symmetric geometry is easily destroyed by the Jahn–Teller effects.38,39 For CH3O, previous theoretical discussions clearly demonstrated that such Jahn–Teller distortion is very weak.88,89 As a consequence, the energy gap between the two lowest electronic states remains extremely small after considering the geometry distortion due to the symmetry breaking. Therefore, when the trajectories following the CH3O + NO2 channel move to the dissociation limit, we observed the state degeneracy.
In fact, the state degeneracy may also exist for the NO2 part.90–92 As shown in previous studies, the two lowest electronic states of the NO2 part may become close to each other when the O–N–O bond angle approaches ∼106° or ∼180°.90,92 In our calculations, we seldom saw that the Oa–N–Ob bond angle accesses these values in the CH3O + NO2 dissociation limit when the trajectory starts from S1. When the higher excited electronic state is excited initially, the excessive energy may drive the strong bending motion to nearly 106° during the dynamics and push the system close to such degeneracy. If so, many states become nearly degenerated, and one of such typical trajectories is shown in Fig. S9 (ESI†).
Some trajectories give the CH3O + NO + O photolysis channel. The resulting O atom has three p orbitals with the same energies. When two lowest quasi-degenerated states of the CH3O radical were taken into account, a much higher state degeneracy situation should exist. In this situation, electronic characters become extremely complicated in the dissociation limit. Our current calculation setup cannot provide the perfect description of this highly degenerated situation involving many electronic states. However, the current calculations still roughly captured the existence of this channel. Here we also showed that the ratio of this channel increases when the high-lying electronic state is excited. This feature shows a qualitative agreement with experimental works.20,24,27,35
Although the current calculations face many limitations, we still can get a valuable explanation of available experimental works. First, we provided a clear interpretation of the absorption spectra of CH3ONO2. The ultrafast nonadiabatic decay dynamics in the current simulation indicated that the excited-state lifetime is extremely short. This gives an excellent explanation of why the low-lying bands in the absorption spectra of CH3ONO2 are quite broad and diffusive.6,27 Considering the existence of ultrafast nonadiabatic dynamics, the further ultrafast-spectroscopy experimental studies of such dynamics of CH3ONO2 and derivatives should be highly interesting. Second, the current simulation gives some valuable data to explain the photolysis dynamics. In experimental works,20,27,35,37 the photolysis dynamics at the long wavelength, ∼250 nm or > 300 nm, always gives the CH3O + NO2 channel. In our calculations, the dynamics starting from both S1 and S2 show that this channel is always dominant. Although we obtained other channels possibly due to the limitation of current calculations, their branching ratios of the minor channels are rather low. We also observed that some trajectories starting from S1 do not show dissociation, and this may explain why the quantum yield of the CH3O + NO2 photolysis channel is not unity in low-pressure long-wavelength (>300 nm) experimental work. Only when the trajectories started from S3, did we observe that both CH3O + NO2 and CH3O + NO + O channels become important. The system first breaks into CH3O + NO2, and then the N–O bond of NO2 breaks. These features are consistent with experimental works.20,24,30 In the end, the CH3ONO + O is observed when the trajectories start from S3. This channel was confirmed by previous experimental studies with short-wavelength laser excitation.20,24,35
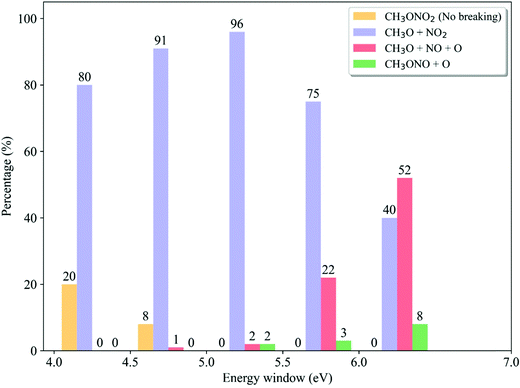
We analyzed the dependence of the ratios of dissociation channels on the excitation energy. In each energy window, the reaction probability of each channel is determined by the destination of trajectory propagation starting from such a window and the transition probability of each initial sample.58 As shown in Fig. 9, only in the low-energy domain (4.0–4.5 eV and 4.5–5.0 eV), the non-dissociative channel appears while it vanishes quickly with the increase of photolysis excitation energy. At the same time, the CH3O + NO2 channel is always dominant when the low excitation energy is taken. Above 5.0–5.5 eV, the ratio of the CH3O + NO2 channel decreases monotonically with the higher photolysis excitation energy, 75% at 5.5–6.0 eV and 40% at 6.0–7.0 eV. As contrast, the CH3O + NO + O channel does not appear at all in the very low-energy domain (4.0–4.5 eV) and is basically neglectable (≤2% at 4.5–5.0 eV). This channel starts to be important with the increase of the photolysis excitation energy, giving 22% at 5.5–6.0 eV and even more than half in the high-energy domain (52% at 6.0–7.0 eV). The CH3ONO + O channel only appears in the high-energy domain. This observation is even more consistent with the experimental results,6,24,27,28 compared to the data obtained by considering the photolysis from different excited states only. All experimental observations indicated that the CH3O + NO2 channel is dominant in the low-energy excitation, while both CH3O + NO2 and CH3O + NO + O channels may become equally important in the high-energy photolysis excitation situations.
As discussed in ref. 93 and 94, the excitations of sunlight, short-pulse laser fields, and continuum-wave laser fields in principle should give rather different initial conditions for photoreactions. Using more advanced theoretical approaches suggested by these works, the proper initial conditions can be defined in the nonadiabatic dynamics simulation. In principle, these theoretical treatments should be important because the dynamics simulation results may be dependent on the selection of initial conditions. In the current work, we still keep the original ways of the initial sampling in nonadiabatic dynamics simulations. As discussed in our manuscript several times, this work represents our initial efforts to treat the photolysis dynamics of alkyl nitrate systems. In the current stage, we only wish to provide some initial understanding of the photolysis dynamics of these compounds qualitatively, instead of the accurate description at the quantitative level. In particular, the nonadiabatic dynamics simulation of these systems is still rare. Our calculations of both PES and nonadiabatic dynamics indicate that the photolysis reaction of CH3ONO2 is extremely fast. We also get the branching ratios of photolysis channels vs. the excitation wavelengths, which agrees well with the experimental observations. Therefore, the main purpose of the current research is basically achieved. For the precise lifetime, we still do not have any available experimental data for comparison. As our current simulation gives the primary results on the ultrafast excited-state lifetime, this result certainly should be verified by further experimental and theoretical works. The new time-resolved ultrafast pump–probe experiments may be helpful to address the ultrafast photolysis dynamics. At the same time, additional efforts should be made to give a better representation of the initial conditions in the nonadiabatic dynamics simulation of similar systems, in order to give better descriptions of the experimental setups and even sunlight. We believe that such a challenging study should be an important research topic in the future. On one side, this provides the direct bridge to link the experimental observations and theoretical simulations. On another side, this helps us to get a deep understanding of the realistic photochemistry of these alkyl nitrates in the atmosphere, which are environmentally significant.
It is well known that the nitro- and nitrate- compounds may undergo intersystem crossing, as shown by several previous works.95–97 In the current system, the intersystem crossing dynamics may not play an essential role here. The current photolysis dynamics takes place extremely fast, less than 60 fs. Within such a short time scale, the contribution of the intersystem crossing dynamics should not be significant, because in principle the weak spin-orbital coupling should exist in such molecules due to the missing heavy atom. On the other hand, the investigation of the possible role of the intersystem crossing dynamics should be an interesting topic in the future.
In the simulation of excited-state dynamics, the selection of suitable electronic state methods and dynamics approaches is not a trivial task. In the electronic-structure treatments, it is well known that all excited-state electronic-structure approaches have their own advantages and shortcomings. Among them, the CASPT2 approaches display reasonable accuracy in many benchmark calculations.58,98,99 In this sense, this approach can more or less be viewed as the “accurate approach” in the excited-state electronic-structure calculations, while its shortcoming is also well known.100 In the current work, the XMS-CASPT2 method is an extended MS-CASPT2 approach, while it essentially provides a similar computational accuracy with higher efficiency.54,55 On the other hand, some other high-level approaches, such as multireference configuration interaction (MRCI),101 may also be the possible choice. In recent years, we noticed that there is a huge development in other advanced excited-state calculation approaches, such as multireference coupled cluster (MRCC),102 and full configuration-interaction quantum Monte Carlo (FCI-QMC) methods.103 If these methods can be used to simulate the excited state dynamics, we expect that more fruitful insights can be generated. However, there is still a long way to employ them in the excite-state dynamics.
In the choice of the dynamics approaches, a similar situation is held. The on-the-fly TSH is a practical choice that gives a reasonable description of the excited-state nonadiabatic dynamics with the balance of computational accuracy and efficiency. However, its shortcoming is also widely known, for instance, its overcoherence problems.74,104,105 Other more advanced approaches, such as ab initio multiple spawning,62 multi-configurational Ehrenfest,106 variational multiconfiguration Gaussian (vMCG),107,108 different on-the-fly semiclassical dynamics based on the mapping Hamiltonian,77,109 and coupled-trajectory surface-hopping dynamics based on exact factorization,110–112 may become possible choices in the future. If we find a suitable electronic structure method that shows enough accuracy in the treatment of the excited state, it would be highly interesting to take it and try to benchmark the performance of different on-the-fly mixed-quantum-classical and semiclassical dynamics approaches. This should provide important evidence to help us select the proper dynamics approaches in the treatment of realistic polyatomic systems with full dimensionality.
5. Conclusion
In this work, we studied the excited-state nonadiabatic dynamics of CH3ONO2 using the on-the-fly TSH simulation at the XMS(4)-CASPT2(12,9)/def2-SVPD level. We mainly paid close attention to the nonadiabatic decay dynamics and the successive photolysis channels.Three S1–S0 MECIs were located at the SA(4)-CASSCF(12,9)/cc-pVDZ level. Both CI10-I and CI10-II display significant CH3O–NO2 elongation, while the Oa–N–Ob bond angle bending motion is observed at CI10-II. The CI10-III shows strong pyramidalization at the N atom, as well as a much shorter CH3O–NO2 distance with respect to CI10-I and CI10-II.
The ultrafast decay processes from different initial excited states were simulated using the on-the-fly TSH simulations. A majority of trajectories starting from S1 jump back to S0via the CI10-III geometries with the weakness of the CH3O–NO2 bond and the pyramidalization at the N atom. When the trajectories start from high-lying excited states (S2 and S3), the internal conversion dynamics becomes faster as expected, and all three CI10 become essential in the nonadiabatic decay.
Starting from both S1 and S2, most trajectories show the photodissociation and follow the CH3O + NO2 photolysis channel. In the dissociation limit, the state degeneracy exists between S1 and S0 due to the 3-fold rotational symmetric geometry of CH3O. The other channels only play a minor role here. When the trajectories start from S3, we still observed that the CH3O + NO2 channel is the major one, while the secondary channel CH3O + NO + O also becomes important. For the latter one, the CH3O–NO2 bond first breaks and the cleavage of the N–O bond in the NO2 fragment then occurs. A third photolysis channel CH3ONO + O also appears. The dependence of the photoproduct channels on the UV excitation wavelength is qualitatively in agreement with available experimental studies.
The current work presents a primary study of our understanding of organic nitrate photochemistry. It should be highly interesting to simulate these processes with highly accurate electronic structure methods, treat the highly-excited state dynamics with more proper dynamics approaches, simulate the experimental signals and study the chemical substitution effects on the photolysis. At the same time, in recent years we witness that great experimental efforts were made to study the ultrafast nonadiabatic dissociation dynamics of VOC systems.113–118 On the basis of the current theoretical work, the CH3ONO2 and derivatives may be a group of interesting prototype VOC systems in experimental ultrafast spectroscopy studies. These works will help us understand more thoroughly the photochemistry of VOCs and this represents a great challenging task in future studies.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by NSFC projects (No. 21933011 and 21873112). The authors thank the Supercomputing Center, Computer Network Information Center, Chinese Academy of Sciences; National Supercomputing Center in Shenzhen for providing computational resources.References
- R. Atkinson and J. Arey, Atmospheric degradation of volatile organic compounds, Chem. Rev., 2003, 103(12), 4605–4638 CrossRef CAS PubMed
.
- A. E. Perring, S. E. Pusede and R. C. Cohen, An observational perspective on the atmospheric impacts of alkyl and multifunctional nitrates on ozone and secondary organic aerosol, Chem. Rev., 2013, 113(8), 5848–5870 CrossRef CAS PubMed
.
- A. L. Chuck, S. M. Turner and P. S. Liss, Direct evidence for a marine source of C1 and C2 alkyl nitrates, Science, 2002, 297(5584), 1151–1154 CrossRef CAS PubMed
.
- Y. Miller, B. J. Finlayson-Pitts and R. B. Gerber, Ionization of N2O4 in contact with water: mechanism, time scales and atmospheric implications, J. Am. Chem. Soc., 2009, 131(34), 12180–12185 CrossRef CAS PubMed
.
- H. Xiao, S. Maeda and K. Morokuma, Excited-state roaming dynamics in photolysis of a nitrate radical. J. Phys, Chem. Lett., 2011, 2(9), 934–938 CAS
.
- M. P. Turberg, D. M. Giolando, C. Tilt, T. Soper, S. Mason, M. Davies, P. Klingensmith and G. A. Takacs, Atmospheric photochemistry of alkyl nitrates, J. Photochem. Photobiol., 1990, 51(3), 281–292 CrossRef CAS
.
- J. E. Williams, G. Le Bras, A. Kukui, H. Ziereis and C. A. M. Brenninkmeijer, The impact of the chemical production of methyl nitrate from the NO + CH3O2 reaction on the global distributions of alkyl nitrates, nitrogen oxides and tropospheric ozone: a global modelling study, Atmos. Chem. Phys., 2014, 14(5), 2363–2382 CrossRef
.
- C. Reed, M. J. Evans, P. Di Carlo, J. D. Lee and L. J. Carpenter, Interferences in photolytic NO2 measurements: explanation for an apparent missing oxidant?, Atmos. Chem. Phys., 2016, 16(7), 4707–4724 CrossRef CAS
.
- F. Keshavarz, J. A. Thornton, H. Vehkamäki and T. Kurtén, Reaction mechanisms underlying unfunctionalized alkyl nitrate hydrolysis in aqueous aerosols, ACS Earth Space Chem., 2021, 5(2), 210–225 CrossRef CAS
.
- J. M. Roberts, The atmospheric chemistry of organic nitrates, Atmos. Environ., Part A, 1990, 24(2), 243–287 CrossRef
.
- S. M. Aschmann, J. Arey and R. Atkinson, Products of the OH radical-initiated reactions of 2- and 3-hexyl nitrate, Atmos. Environ., 2012, 46, 264–270 CrossRef CAS
.
- R. Atkinson, S. M. Aschmann, W. P. L. Carter, A. M. Winer and J. N. Pitts, Alkyl nitrate formation from the NOx-air photooxidations of C2-C8 n-alkanes, J. Phys. Chem., 1982, 86(23), 4563–4569 CrossRef CAS
.
- S. He, Z. Chen and X. Zhang, Photochemical reactions of methyl and ethyl nitrate: a dual role for alkyl nitrates in the nitrogen cycle, Environ. Chem., 2011, 8(6), 529–542 CrossRef CAS
.
- A. Lesar, M. Hodošček, E. Drougas and A. M. Kosmas, Quantum mechanical investigation of the atmospheric reaction CH3O2 + NO, J. Phys. Chem. A, 2006, 110(25), 7898–7903 CrossRef CAS PubMed
.
- J. R. Barker, L. L. Lohr, R. M. Shroll and S. Reading, Modeling the organic nitrate yields in the reaction of alkyl peroxy radicals with nitric oxide. 2. reaction simulations, J. Phys. Chem. A, 2003, 107(38), 7434–7444 CrossRef CAS
.
- R. M. Moore and N. V. Blough, A marine source of methyl nitrate, Geophys. Res. Lett., 2002, 29(15), 27-1–27-4 CrossRef
.
- R. E. Rebbert, Primary processes in the photolysis of ethyl nitrate, J. Phys. Chem., 1963, 67(9), 1923–1925 CrossRef CAS
.
- L. E. Harris, The lower electronic states of nitrite and nitrate ion, nitromethane, nitramide, nitric acid, and nitrate esters, J. Chem. Phys., 1973, 58(12), 5615–5626 CrossRef CAS
.
- W. D. Taylor, T. D. Allston, M. J. Moscato, G. B. Fazekas, R. Kozlowski and G. A. Takacs, Atmospheric photodissociation lifetimes for nitromethane, methyl nitrite, and methyl nitrate, Int. J. Chem.
Kinet., 1980, 12(4), 231–240 CrossRef CAS
.
- X. Yang, P. Felder and J. R. Huber, Photodissociation of methyl nitrate in a molecular beam, J. Phys. Chem., 1993, 97(42), 10903–10910 CrossRef CAS
.
- K. C. Clemitshaw, J. Williams, O. V. Rattigan, D. E. Shallcross and K. S. Law, Anthony Cox, R., Gas-phase ultraviolet absorption cross-sections and atmospheric lifetimes of several C2-C5 alkyl nitrates, J. Photochem. Photobiol., 1997, 102(2), 117–126 CrossRef
.
- L. Zhu and C.-F. Ding, Temperature dependence of the near UV absorption spectra and photolysis products of ethyl nitrate, Chem. Phys. Lett., 1997, 265(1), 177–184 CrossRef CAS
.
- L. Zhu and D. Kellis, Temperature dependence of the UV absorption cross sections and photodissociation products of C3-C5 nitrates, Chem. Phys. Lett., 1997, 278(1), 41–48 CrossRef CAS
.
- E. L. Derro, C. Murray, M. I. Lester and M. D. Marshall, Photodissociation dynamics of methyl nitrate at 193 nm: energy disposal in methoxy and nitrogen dioxide products, Phys. Chem. Chem. Phys., 2007, 9(2), 262–271 RSC
.
- I. V. Schweigert and B. I. Dunlap, Electronic structure and molecular dynamics of breaking the RO–NO2 bond, J. Chem. Phys., 2009, 130(24), 244110 CrossRef PubMed
.
- J. Soto, D. Peláez, J. C. Otero, F. J. Avila and J. F. Arenas, Photodissociation mechanism of methyl nitrate. A study with the multistate second-order multiconfigurational perturbation theory, Phys. Chem. Chem. Phys., 2009, 11(15), 2631–2639 RSC
.
- P. G. Carbajo and A. J. Orr-Ewing, NO2 quantum yields from ultraviolet photodissociation of methyl and isopropyl nitrate, Phys. Chem. Chem. Phys., 2010, 12(23), 6084–6091 RSC
.
- C. M. Higgins, L. A. Evans, G. C. Lloyd-Jones, D. E. Shallcross, D. P. Tew and A. J. Orr-Ewing, Quantum yields for photochemical production of NO2 from organic nitrates at tropospherically relevant wavelengths, J. Phys. Chem. A, 2014, 118(15), 2756–2764 CrossRef CAS PubMed
.
- J. A. Gray and D. W. G. Style, The photolysis of ethyl nitrate, Trans. Faraday Soc., 1953, 49, 52–57 RSC
.
- P. Gray and G. T. Rogers, The explosion and decomposition of methyl nitrate in the gas phase, Trans. Faraday Soc., 1954, 50(0), 28–36 RSC
.
- W. T. Luke and R. R. Dickerson, Direct measurements of the photolysis rate coefficient of ethyl nitrate, Geophys. Res. Lett., 1988, 15(11), 1181–1184 CrossRef CAS
.
- W. T. Luke, R. R. Dickerson and L. J. Nunnermacker, Direct measurements of the photolysis rate coefficients and Henry's law constants of several alkyl nitrates, J. Geophys. Res.: Atmos., 1989, 94(D12), 14905–14921 CrossRef CAS
.
- I. Barnes, K. H. Becker and T. Zhu, Near UV absorption spectra and photolysis products of difunctional organic nitrates: Possible importance as NOx reservoirs, J. Atmos. Chem., 1993, 17(4), 353–373 CrossRef CAS
.
- R. K. Talukdar, S. C. Herndon, J. B. Burkholder, J. M. Roberts and A. R. Ravishankara, Atmospheric fate of several alkyl nitrates Part 1 Rate coefficients of the reactions of alkyl nitrates with isotopically labelled hydroxyl radicals, J. Chem. Soc., Faraday Trans., 1997, 93(16), 2787–2796 RSC
.
- R. K. Talukdar, J. B. Burkholder, M. Hunter, M. K. Gilles, J. M. Roberts and A. R. Ravishankara, Atmospheric fate of several alkyl nitrates Part 2 UV absorption cross-sectionsand photodissociation quantum yields, J. Chem. Soc., Faraday Trans., 1997, 93, 2797–2805 RSC
.
- J. M. Roberts and R. W. Fajer, UV absorption cross sections of organic nitrates of potential atmospheric importance and estimation of atmospheric lifetimes, Environ. Sci. Technol., 1989, 23(8), 945–951 CrossRef CAS
.
- O. Rattigan, E. Lutman, R. L. Jones, R. A. Cox, K. Clemitshaw and J. Williams, Temperature-dependent absorption cross-sections of gaseous nitric acid and methyl nitrate. J, Photochem. Photobiol., 1992, 66(3), 313–326 CrossRef CAS
.
-
Conical Intersections I: Electronic Structure, Dynamics and Spectroscopy, ed. W. Domcke, D. R. Yarkony and H. Köppel, World Scientic, Singapore, 2004 Search PubMed
.
-
Conical Intersections II: Theory, Computation and Experiment, ed. W. Domcke, D. R. Yarkony and H. Köppel, World Scientific, Singapore, 2011 Search PubMed
.
- R. Atkinson, W. P. L. Carter and A. M. Winer, Effects of temperature and pressure on alkyl nitrate yields in the NOx photooxidations of n-pentane and n-heptane, J. Phys. Chem., 1983, 87(11), 2012–2018 CrossRef CAS
.
- J. F. Arenas, F. J. Avila, J. C. Otero, D. Peláez and J. Soto, Approach to the atmospheric chemistry of methyl nitrate and methylperoxy nitrite. Chemical mechanisms of their formation and decomposition reactions in the gas phase, J. Phys. Chem. A, 2008, 112(2), 249–255 CrossRef CAS PubMed
.
- Z. Homayoon and J. M. Bowman, Quasiclassical trajectory study of CH3NO2 decomposition via roaming mediated isomerization using a global potential energy surface, J. Phys. Chem. A, 2013, 117(46), 11665–11672 CrossRef CAS PubMed
.
- J. F. Arenas, J. C. Otero, D. Peláez and J. Soto, The ground and excited state potential energy surfaces of nitromethane related to its dissociation dynamics after excitation at 193 nm, J. Chem. Phys., 2003, 119(15), 7814–7823 CrossRef CAS
.
- J. Zhang, T. Dransfield and N. M. Donahue, On the mechanism for nitrate formation via the peroxy radical + NO reaction, J. Phys. Chem. A, 2004, 108(42), 9082–9095 CrossRef CAS
.
- A. G. Sage, T. A. Oliver, D. Murdock, M. B. Crow, G. A. Ritchie, J. N. Harvey and M. N. Ashfold, nσ* and πσ* excited states in aryl halide photochemistry: a comprehensive study of the UV photodissociation dynamics of iodobenzene, Phys. Chem. Chem. Phys., 2011, 13(18), 8075–8093 RSC
.
- M. Isegawa, F. Liu, S. Maeda and K. Morokuma, Ab initio reaction pathways for photodissociation and isomerization of nitromethane on four singlet potential energy surfaces with three roaming paths, J. Chem. Phys., 2014, 140(24), 244310 CrossRef PubMed
.
- D. Aranda, F. J. Avila, I. López-Tocón, J. F. Arenas, J. C. Otero and J. Soto, An MS-CASPT2 study of the photodecomposition of 4-methoxyphenyl azide: role of internal conversion and intersystem crossing, Phys. Chem. Chem. Phys., 2018, 20(11), 7764–7771 RSC
.
- J. Soto, D. Peláez and J. C. Otero, A SA-CASSCF and MS-CASPT2 study on the electronic structure of nitrosobenzene and its relation to its dissociation dynamics, J. Chem. Phys., 2021, 154(4), 044307 CrossRef CAS PubMed
.
- L. E. Harris, Lower electronic states of nitric acid and esters, Nature, 1973, 243(128), 103–104 CAS
.
- J. Soto, J. F. Arenas, J. C. Otero and D. Peláez, Effect of an S1/S0 conical intersection on the chemistry of nitramide in its ground state. A comparative CASPT2 study of the nitro-nitrite isomerization reactions in nitramide and nitromethane, J. Phys. Chem. A, 2006, 110(26), 8221–8226 CrossRef CAS PubMed
.
- J. Soto, F. J. Avila, J. C. Otero, D. Peláez and J. F. Arenas, A molecular mechanism for direct generation of nitric oxide, peroxynitrite and superoxide in the reaction of nitroglycerin with a cysteil-cysteine derivative, Theor. Chem. Acc., 2010, 128(4-6), 593–599 Search PubMed
.
- J. F. Arenas, J. C. Otero, D. Peláez and J. Soto, Role of surface crossings in the photochemistry of nitromethane, J. Chem. Phys., 2005, 122(8), 084324 CrossRef PubMed
.
- J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, The multi-state CASPT2 method, Chem. Phys. Lett., 1998, 288, 299 CrossRef CAS
.
- A. A. Granovsky, Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory, J. Chem. Phys., 2011, 134(21), 214113 CrossRef PubMed
.
- T. Shiozaki, W. Győrffy, P. Celani and H.-J. Werner, Communication: extended multi-state complete active space second-order perturbation theory: energy and nuclear gradients, J. Chem. Phys., 2011, 135(8), 081106 CrossRef PubMed
.
- P. Cattaneo, G. Granucci and M. Persico, Simulations of condensed phase photochemistry:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cage effect and internal conversion in azoalkanes and nitrosamines, J. Phys. Chem. A, 1999, 103(18), 3364–3371 CrossRef CAS
cage effect and internal conversion in azoalkanes and nitrosamines, J. Phys. Chem. A, 1999, 103(18), 3364–3371 CrossRef CAS .
- H. Lignell, S. A. Epstein, M. R. Marvin, D. Shemesh, B. Gerber and S. Nizkorodov, Experimental and Theoretical Study of Aqueous cis-Pinonic Acid Photolysis, J. Phys. Chem. A, 2013, 117(48), 12930–12945 CrossRef CAS PubMed
.
- A. Prlj, L. M. Ibele, E. Marsili and B. F. E. Curchod, On the theoretical determination of photolysis properties for atmospheric volatile organic compounds. J. Phys, Chem. Lett., 2020, 11(14), 5418–5425 CAS
.
- D. Shemesh, S. A. Nizkorodov and R. B. Gerber, Photochemical Reactions of Cyclohexanone: Mechanisms and Dynamics, J. Phys. Chem. A, 2016, 120(36), 7112–7120 CrossRef CAS PubMed
.
- D. Shemesh, Z. Lan and R. B. Gerber, Dynamics of Triplet-State Photochemistry of Pentanal: Mechanisms of Norrish I, Norrish II, and H Abstraction Reactions, J. Phys. Chem. A, 2013, 117(46), 11711–11724 CrossRef CAS PubMed
.
- M. Persico and G. Granucci, An overview of nonadiabatic dynamics simulations methods, with focus on the direct approach versus the fitting of potential energy surfaces, Theor. Chem. Acc., 2014, 133(9), 1526 Search PubMed
.
- B. F. E. Curchod and T. J. Martínez, Ab initio nonadiabatic quantum molecular dynamics, Chem. Rev., 2018, 118(7), 3305–3336 CrossRef CAS PubMed
.
-
M. Persico and G. Granucci, Photochemistry: A Modern Theoretical Perspective, Berlin, Springer, 2018 Search PubMed
.
- M. Ben-Nun and T. J. Martínez, Ab initio quantum molecular dynamics, Adv. Chem. Phys., 2002, 121, 439–512 CrossRef CAS
.
- S.-H. Xia, G. Cui, W.-H. Fang and W. Thiel, How photoisomerization drives peptide folding and unfolding: insights from QM/MM and MM dynamics simulations, Angew. Chem., Int. Ed., 2016, 55(6), 2067–2072 CrossRef CAS PubMed
.
- G. Cui, Z. Lan and W. Thiel, Intramolecular Hydrogen Bonding Plays a Crucial Role in the Photophysics and Photochemistry of the GFP Chromophore, J. Am. Chem. Soc., 2012, 134(3), 1662–1672 CrossRef CAS PubMed
.
- L. Du and Z. Lan, An on-the-fly surface-hopping program JADE for nonadiabatic molecular dynamics of polyatomic systems: implementation and applications, J. Chem. Theory Comput., 2015, 11(9), 4522–4523 CrossRef CAS PubMed
.
- C. Xu, F. L. Gu and C. Zhu, Ultrafast intersystem crossing for nitrophenols: ab initio nonadiabatic molecular dynamics simulation, Phys. Chem. Chem. Phys., 2018, 20(8), 5606–5616 RSC
.
- K. Lin, D. Hu, J. Peng, C. Xu, F. L. Gu and Z. Lan, Prediction of the excited-state reaction channels in photo-induced processes of nitrofurantoin using first-principle calculations and dynamics simulations, Chemosphere, 2021, 281, 130831 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed
.
- J. C. Tully, Molecular dynamics with electronic transitions, J. Chem. Phys., 1990, 93(2), 1061–1071 CrossRef CAS
.
- E. Wigner, On the quantum correction for thermodynamic equilibrium, Phys. Rev., 1932, 40(5), 749–759 CrossRef CAS
.
- R. Crespo-Otero and M. Barbatti, Spectrum simulation and decomposition with nuclear ensemble: formal derivation and application to benzene, furan and 2-phenylfuran, Theor. Chem. Acc., 2012, 131(6), 1237 Search PubMed
.
- G. Granucci and M. Persico, Critical appraisal of the fewest switches algorithm for surface hopping, J. Chem. Phys., 2007, 126(13), 134114 CrossRef PubMed
.
- C. Zhu, S. Nangia, A. W. Jasper and D. G. Truhlar, Coherent switching with decay of mixing: An improved treatment of electronic coherence for non-Born–Oppenheimer trajectories, J. Chem. Phys., 2004, 121(16), 7658–7670 CrossRef CAS PubMed
.
- D. Hu, Y. F. Liu, A. L. Sobolewski and Z. Lan, Nonadiabatic dynamics simulation of keto isocytosine: a comparison of dynamical performance of different electronic-structure methods, Phys. Chem. Chem. Phys., 2017, 19(29), 19168–19177 RSC
.
- D. Hu, Y. Xie, J. Peng and Z. Lan, On-the-fly symmetrical quasi-classical dynamics with Meyer–Miller mapping Hamiltonian for the treatment of nonadiabatic dynamics at conical intersections, J. Chem. Theory Comput., 2021, 17(6), 3267–3279 CrossRef CAS PubMed
.
- BAGEL, Brilliantly Advanced General Electronic-structure Library, (http://www.nubakery.org).
- T. Shiozaki, BAGEL: Brilliantly Advanced General Electronic-structure Library, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), e1331 Search PubMed
.
- P. J. Knowles and N. C. Handy, A determinant based full configuration interaction program, Cornp. Phys. Commun., 1989, 54(1), 75–83 CrossRef CAS
.
- H.-J. Werner and P. J. Knowles, A second order multiconfiguration SCF procedure with optimum convergence, J. Chem. Phys., 1985, 82(11), 5053–5063 CrossRef CAS
.
- I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, OpenMolcas: From Source Code to Insight, J. Chem. Theory Comput., 2019, 15(11), 5925–5964 CrossRef PubMed
.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: a general-purpose quantum chemistry program package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(2), 242–253 CAS
.
- Q. Ma and H.-J. Werner, Explicitly correlated local coupled-cluster methods using pair natural orbitals, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(6), e1371 Search PubMed
.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, T. F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, The Molpro quantum chemistry package, J. Chem. Phys., 2020, 152(14), 144107 CrossRef CAS PubMed
.
- A. M. Launder, J. Agarwal and H. F. Schaefer III, Exploring mechanisms of a tropospheric archetype: CH3O2 + NO, J. Chem. Phys., 2015, 143(23), 234302 CrossRef PubMed
.
- http://satellite.mpic.de/spectral_atlas/cross_sections .
- T. A. Barckholtz and T. A. Miller, The Calculation of spectroscopic Jahn–Teller parameters by ab initio methods, J. Phys. Chem. A, 1999, 103(14), 2321–2336 CrossRef CAS
.
- C. F. Jackels, A theoretical potential energy surface study of several states of the methoxy radical, J. Chem. Phys., 1982, 76(1), 505–515 CrossRef CAS
.
- G. D. Gillispie, A. U. Khan, A. C. Wahl, R. P. Hosteny and M. Krauss, The electronic structure of nitrogen dioxide. I. Multiconfiguration self-consistent-field calculation of the low-lying electronic states, J. Chem. Phys., 1975, 63(8), 3425–3444 CrossRef CAS
.
- V. Kurkal, P. Fleurat-Lessard and R. Schinke, NO2: Global potential energy surfaces of the ground (12A1) and the first excited (12B2) electronic states, J. Chem. Phys., 2003, 119(3), 1489–1501 CrossRef CAS
.
- C. F. Jackels and E. R. Davidson, An ab initio potential-energy surface study of several electronic states of NO2, J. Chem. Phys., 1976, 65(8), 2941–2957 CrossRef CAS
.
- J. Suchan, D. Hollas, B. F. E. Curchod and P. Slavíček, On the importance of initial conditions for excited-state dynamics, Faraday Discuss., 2018, 212(0), 307–330 RSC
.
- M. Barbatti, Simulation of excitation by sunlight in mixed quantum-classical dynamics, J. Chem. Theory Comput., 2020, 16(8), 4849–4856 CrossRef CAS PubMed
.
- M. Richter, S. Mai, P. Marquetand and L. González, Ultrafast intersystem crossing dynamics in uracil unravelled by ab initio molecular dynamics, Phys. Chem. Chem. Phys., 2014, 16(44), 24423–24436 RSC
.
- S. Bai and M. Barbatti, Why Replacing Different Oxygens of Thymine with Sulfur Causes Distinct Absorption and Intersystem Crossing, J. Phys. Chem. A, 2016, 120(32), 6342–6350 CrossRef CAS PubMed
.
- B. F. Curchod, C. Rauer, P. Marquetand, L. González and T. J. Martínez, Communication: GAIMS—Generalized Ab Initio Multiple Spawning for both internal conversion and intersystem crossing processes, J. Chem. Phys., 2016, 144(10), 101102 CrossRef PubMed
.
- M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, Benchmarks for electronically excited states: CASPT2, CC2, CCSD, and CC3, J. Chem. Phys., 2008, 128(13), 134110 CrossRef PubMed
.
- J. W. Park, R. Al-Saadon, M. K. MacLeod, T. Shiozaki and B. Vlaisavljevich, Multireference Electron Correlation Methods: Journeys along Potential Energy Surfaces, Chem. Rev., 2020, 120(13), 5878–5909 CrossRef CAS PubMed
.
- N. Forsberg and P.-Å. Malmqvist, Multiconfiguration perturbation theory with imaginary level shift, Chem. Phys. Lett., 1997, 274(1-3), 196–204 CrossRef CAS
.
- H. Lischka, D. Nachtigallová, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Multireference Approaches for Excited States of Molecules, Chem. Rev., 2018, 118(15), 7293–7361 CrossRef CAS PubMed
.
- D. I. Lyakh, M. Musiał, V. F. Lotrich and R. J. Bartlett, Multireference Nature of Chemistry: The Coupled-Cluster View, Chem. Rev., 2012, 112(1), 182–243 CrossRef CAS PubMed
.
- G. H. Booth, A. J. W. Thom and A. Alavi, Fermion Monte Carlo without fixed nodes: A game of life, death, and annihilation in Slater determinant space, J. Chem. Phys., 2009, 131(5), 054106 CrossRef PubMed
.
- J. E. Subotnik, A. Jain, B. Landry, A. Petit, W. Ouyang and N. Bellonzi, Understanding the Surface Hopping View of Electronic Transitions and Decoherence, Annu. Rev. Phys. Chem., 2016, 67(1), 387–417 CrossRef CAS PubMed
.
- L. Wang, A. Akimov and O. V. Prezhdo, Recent Progress in Surface Hopping: 2011–2015. J. Phys, Chem. Lett., 2016, 7(11), 2100–2112 CAS
.
- S. Fernandez-Alberti, D. V. Makhov, S. Tretiak and D. V. Shalashilin, Non-adiabatic excited state molecular dynamics of phenylene ethynylene dendrimer using a multiconfigurational Ehrenfest approach, Phys. Chem. Chem. Phys., 2016, 18(15), 10028–10040 RSC
.
- I. Burghardt, H.-D. Meyer and L. S. Cederbaum, Approaches to the approximate treatment of complex molecular systems by the multiconfiguration time-dependent Hartree method, J. Chem. Phys., 1999, 111(7), 2927–2939 CrossRef CAS
.
- G. A. Worth and I. Burghardt, Full quantum mechanical molecular dynamics using Gaussian wavepackets, Chem. Phys. Lett., 2003, 368(3), 502–508 CrossRef CAS
.
- W. Zhou, A. Mandal and P. Huo, Quasi-Diabatic Scheme for Nonadiabatic On-the-Fly Simulations. J. Phys, Chem. Lett., 2019, 10(22), 7062–7070 CAS
.
- A. Abedi, N. T. Maitra and E. K. U. Gross, Exact Factorization of the Time-Dependent Electron-Nuclear Wave Function, Phys. Rev. Lett., 2010, 105(12), 123002 CrossRef PubMed
.
- J.-K. Ha, I. S. Lee and S. K. Min, Surface Hopping Dynamics beyond Nonadiabatic Couplings for Quantum Coherence, J. Phys. Chem. Lett., 2018, 9(5), 1097–1104 CrossRef CAS PubMed
.
- B. F. E. Curchod, F. Agostini and E. K. U. Gross, An exact factorization perspective on quantum interferences in nonadiabatic dynamics, J. Chem. Phys., 2016, 145(3), 034103 CrossRef PubMed
.
- V. G. Stavros, A bright future for sunscreens, Nat. Chem., 2014, 6(11), 955–956 CrossRef CAS PubMed
.
- G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, Direct observation of hydrogen tunneling dynamics in photoexcited phenol. J. Phys, Chem. Lett., 2012, 3(3), 348–352 CAS
.
- K. I. Hilsabeck, J. L. Meiser, M. Sneha, J. A. Harrison and R. N. Zare, Nonresonant photons catalyze photodissociation of phenol, J. Am. Chem. Soc., 2019, 141(2), 1067–1073 CrossRef CAS PubMed
.
- L. A. Baker, M. D. Horbury, S. E. Greenough, P. M. Coulter, T. N. V. Karsili, G. M. Roberts, A. J. Orr-Ewing, M. N. R. Ashfold and V. G. Stavros, Probing the ultrafast energy dissipation mechanism of the sunscreen oxybenzone after UVA irradiation, J. Phys. Chem. Lett., 2015, 6(8), 1363–1368 CrossRef CAS PubMed
.
- L. A. Baker, B. Marchetti, T. N. Karsili, V. G. Stavros and M. N. Ashfold, Photoprotection:
extending lessons learned from studying natural sunscreens to the design of artificial sunscreen constituents, Chem. Soc. Rev., 2017, 46(12), 3770–3791 RSC
.
- M. N. Ashfold, D. Murdock and T. A. Oliver, Molecular photofragmentation dynamics in the gas and condensed phases, Annu. Rev. Phys. Chem., 2017, 68, 63–82 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: I: Relevant information: the active space and transition orbitals, the geometrical parameters and state energies at S0-min, S1-min, and all CIs mentioned in this work, CI10–seams, typical trajectories via different decay channels, and distribution of geometric parameters at S1 to S0 hops. II: The Cartesian coordinates of all critical geometries. See DOI: 10.1039/d1cp03226g |
| This journal is © the Owner Societies 2021 |