Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Self-absorption corrected non-invasive transmission Raman spectroscopy (of biological tissue)†
Benjamin
Gardner
 ab,
Pavel
Matousek
ab,
Pavel
Matousek
 *c and
Nicholas
Stone
*c and
Nicholas
Stone
 *ab
*ab
aSchool of Physics and Astronomy, University of Exeter, Exeter, EX4 4QL, UK. E-mail: N.Stone@exeter.ac.uk
bRoyal Devon and Exeter NHS Foundation Trust, Barrack Road, Exeter, Devon EX2 5DW, UK
cCentral Laser Facility, Research Complex at Harwell, STFC Rutherford Appleton Laboratory, Harwell Oxford, OX11 0QX, UK. E-mail: Pavel.Matousek@stfc.ac.uk
First published on 8th December 2020
Abstract
The first near infrared window in biological tissue (λ ∼ 700–950 nm) is of great interest for its potential to safely deliver light based diagnosis and therapeutic interventions, especially in the burgeoning field of nano-theranostics. In this context, Raman spectroscopy is increasingly being used to provide rapid non-invasive chemical molecular analysis, including bulk tissue analysis by exploiting the near infrared window, with transmission Raman spectroscopy (TRS). The disadvantage of this approach, is that when probing depths of several centimetres self-attenuation artefacts are typically exhibited, whereby TRS spectra can suffer from relative changes in the “spectral features” due to differential absorption of Raman photons by the various constituents of biological tissues. Simply put, for a homogenous substance with increasing thickness, spectral variances occur due to the optical properties of the material and not through changes in the chemical environment. This can lead to misinterpretation of data, or features of interest become obscured due to the unwanted variance. Here we demonstrate a method to correct TRS data for this effect, which estimates the pathlengths derived from peak attenuation and uses expected optical properties to transform the data. In a validation experiment, the method reduced total Raman spectral intensity variances >5 fold, and improved specific peak ratio distortions 35×. This is an important development for TRS, Spatially Offset Raman Spectroscopy (SORS) and related techniques operating at depth in the near IR window; applicable to samples where there is large sample thickness and inter- and intra-sample thickness is variable i.e. clinical specimens from surgical procedures such as breast cancer. This solution is expected to yield lower detection limits and larger depths in future applications such as non-invasive breast cancer diagnosis in vivo.
Introduction
The biological near infrared (NIR) window is a spectral region within biological materials where the optical properties exhibit lower scattering (μs) and absorption (μa), as well as lower levels of auto florescence,1,2 compared with the visible spectral region. This window is often broken down into two sub regions, NIR-I (700–950 nm) and NIR-II (1000–1700 nm). The NIR windows are especially important for a number of biomedical imaging modalities including fluorescence imaging, and spectroscopy techniques including Raman spectroscopy. Raman spectroscopy is of particular interest as it is at a new frontier of novel theranostics,3i.e. the combination of optical diagnostics and photothermal therapies mediated by nanostructures.3 These techniques aim to complement existing tomographic techniques e.g. MRI, CT and PET where there are either safety concerns (ionising radiation), or they yield limited temporal, spatial or chemical information.Deep Raman spectroscopy (DRS) is a group term for closely related innovative techniques for non-invasive and non-destructive probing deep into samples using Raman spectroscopy, the principal techniques are spatially offset Raman spectroscopy (SORS)4 and transmission Raman spectroscopy (TRS).5 What these techniques share is a separation between laser illumination and collection zones on the sample surface. In SORS the two zones are generally on the same side of the sample surface, while TRS illumination and collection is separated by the sample itself, i.e. being on opposite sides of the sample. These approaches exploit diffuse scattering of light in the material being probed and allow a retrieval of chemical signals up to several cm in depth. There are continuously new and sophisticated ways of carrying out DRS,6–9 yet the basic premise remains the same. DRS has seen a broad range of applications in a number of fields including pharmaceutical analysis and security,10 cultural heritage11 as well as extensive biomedical applications.12–14
Over time the sophistication of signal retrieval has increased from identifying a single compound,5,15 to multiplexed signal recovery,13 physical property signal recovery16 and depth localisation.17–21 A number of publications have demonstrated how differential optical properties in a scattering medium, i.e. tissue, between different Raman components can also be exploited for depth localisation. These examples have been demonstrated in well-controlled samples, wherein the sample has typically a uniform thickness in transmission geometry.19–21 However, in the real world there is often little control of the sample thickness, when performing deep Raman on biological samples. This variation can arise undesirably in two key ways, firstly with thickness variation within a sample during Raman mapping, secondly due to differences in thickness between different samples. Both of these phenomena can lead to differences in the Raman spectra as a function of thickness and composition, due to the optical properties experienced by Raman photons propagating through the material as a function of wavelength. For example, two Raman bands sufficiently separated in wavelength might experience significantly different optical properties therefore one can be more attenuated than another over increasingly large propagation distances. Previous DRS studies have noted this phenomena,22–24 having been highlighted in one TRS experiment at λex 830 nm, with Raman spectra having shown significant loss of signal above 1250 cm−1 when the sample thickness increased from 20 mm to around 50 mm.22 While, other work specifically noticed the relative loss of the amide I signal23,24 in their spectra, and had to remove this region entirely from the subsequent multivariate data analysis. However, these works lacked extensive signal collection, i.e. multiple spatial locations over a sample with varying thickness. Therefore, the mechanism of how changes in thickness in samples vary with complex attenuation profiles and thus affect the collected Raman spectra was not fully realised and otherwise useful data could not be utilised.
Moreover, self-attenuation of conventional Raman signal has been observed in solution based surface enhanced Raman spectroscopy (SERS), where there was competition between extinction due to absorption of light mediated by nanoparticles and the SERS enhancement these provide.25,26 Previous work has also addressed some limitations of Raman spectroscopy and factors which can distort its quantitative capabilities, when applied to measurements in diffusely scattering media.27–31 The work of Reble et al.29 demonstrated absolute Raman scattering coefficients were restored under back scattered Raman geometry. While the work of Barman et al.30 also investigated distortions arising from multiple scattering events. In addition, studies using both SORS31 and TRS,32 discussed how the optical properties can affect sampling depth and recovered signal distributions respectively. However, these studies have not addressed the influence of sample geometry or how the optical properties can distort the recovered spectra themselves.
This perturbation to the spectra can often overwhelm and easily mask many other, more subtle, changes to Raman spectral signatures of biological relevance, e.g. the presence or absence of disease and represent a fundamental limitation of DRS. The spectral distortions are particularly problematic for common analytical tools used in spectroscopic analysis such as Principal Component Analysis (PCA), which is often used as an important initial step to reduce data complexity prior to application of more advanced machine learning algorithms/regression techniques. In PCA for example, these distortions give rise to high ranked contributions (eigenvectors), or the distortion features are mixed with other eigenvectors that relate to chemical features of interest. This acts to complicate and confound development of robust numerical models, thereby reducing overall sensitivity and the maximal depth DRS can probe.
A useful term for describing the combined influence of the optical properties of a medium is effective transport coefficient (μeff), where 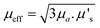 .33–35 This term describes the combined influence of both absorption coefficient μa and the reduced scattering coefficient μ′s, where μ′s = μs(1 − g) and g is the measure of anisotropy i.e. the mean cosine of scattering angles. Therefore, having an approximate knowledge of μeff (λ) of the material being investigated alongside the sample thickness, one can consider how significant, if at all, the spectral distortions are likely to be. Some materials will exhibit a flat profile i.e. uniform attenuation across a spectral window, while others contain a gradient, or worse a complex profile, which gives arise to distortions in relative peak intensities.
.33–35 This term describes the combined influence of both absorption coefficient μa and the reduced scattering coefficient μ′s, where μ′s = μs(1 − g) and g is the measure of anisotropy i.e. the mean cosine of scattering angles. Therefore, having an approximate knowledge of μeff (λ) of the material being investigated alongside the sample thickness, one can consider how significant, if at all, the spectral distortions are likely to be. Some materials will exhibit a flat profile i.e. uniform attenuation across a spectral window, while others contain a gradient, or worse a complex profile, which gives arise to distortions in relative peak intensities.
Here we demonstrate the effect that variation in sample thickness has on the Raman spectra measured with TRS and how this is dependent on the optical properties of the medium being probed, rather than solely the chemical composition. Moreover, the severity of the distortions, as expected, differ between common biological materials i.e. protein-rich, lipid-rich. Finally, we demonstrate that with limited a priori information i.e. approximate optical properties, the Raman spectrum can be restored, thereby reducing spectral variation due exclusively to material thickness and therefore enhancing the underlying differences arising in the chemistry that could otherwise be obscured. This effect can be observed, even in materials with homogenous chemistry. This work builds on previous studies that have noticed similar phenomena.22,25,26
Materials and methods
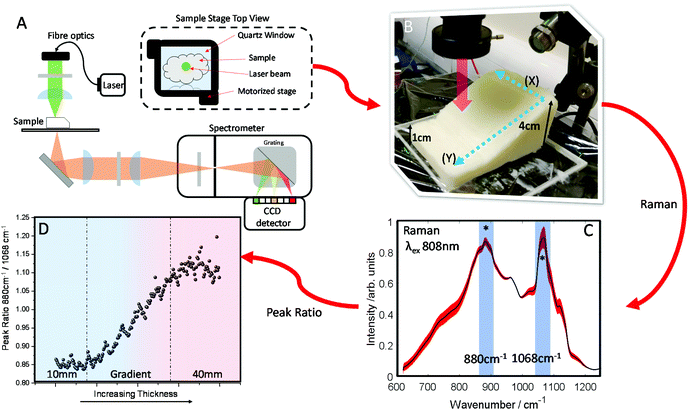
Transmission Raman measurements were carried out on a custom built system, of which a similar system has been previously described.36,37 In summary, an 808 nm solid state laser (Innovative Photonic Solutions, Monmouth Junction, NJ, US) was coupled to illumination optics via an optical fibre. Two 808 nm laser clean up filters (LL01-808-25, Semrock, Rochester, New York, US) filtered the laser output prior to focusing into a ∼15 mm diameter beam on the sample surface. The sample stage platform consisted of a fused quartz window (2 mm thickness), sitting on a motorized stage (8MTF, Standa), providing full XY positioning control with a range of 102 mm in both directions. The collected signal was filtered by 3 edge filters, and focused into a Holospec 1.8i (Kaiser Optical Systems, Ann Arbor, Michigan, USA). The spectrometer contains a custom high dispersion grating providing a spectral range of ∼600–1200 cm−1 and a 1 mm slit, providing an effective spectral resolution of ∼15 cm−1. The spectrometer was coupled to a deep depletion CCD detector (Andor BR-DD iDus 420) to record the Raman signals.Sample preparation included cutting commercially available blocks of lard (pork fat) into either flat segments of a uniform thickness, or cutting these into an approximate wedge shape. Additionally, we used calcium hydroxyapatite (HAP) (Sigma Aldrich) contained in a quartz cell (Starna Scientific) as a target chemical component placed on top of lard samples, on the surface with the laser beam incident upon it. This has previously been used in studies as a substitute for in vivo breast calcifications.37,38 For all Raman measurements a laser power of 2 W was used, delivering a power density at the sample surface of ∼12 mW mm−2. We performed TRS mapping experiments, i.e. spectra were gathered from multiple spatial points across the sample, under the following parameters; each spatial location was probed with 3 TRS spectra consisting each of (0.05 s × 20) accumulations, while for static measurements 20 spectra of (0.05 s × 20) accumulations were acquired.
All data was processed in Matlab 2017a undergoing the following pre-processing steps. Firstly a median filter was applied to the data to remove the presence of cosmic rays, and the data was then averaged to leave one mean spectrum per spatial location. A linear baseline was then subtracted from the data prior to vector normalisation.
Results and discussion
The optical properties of fat (μa and μ′s) for the near-IR spectral window ∼700–950 nm (Fig. 1A), show that while scattering has an inverse relationship with wavelength i.e. decreases monotonically as a function of increasing wavelength, the absorption conversely has a more complex profile, which varies across the spectrum.39 Therefore, undertaking transmission Raman measurements in a sample containing a high proportion of fat, it is important to take the absorption profile into account. Looking at the approximate Raman spectral range of the 808 nm system described within this paper (Fig. 1B), it is clear there is a significant change in the wavelength dependent optical properties. Moreover, as is shown (Fig. 1C), when the Raman spectrum of lard is overlaid with the combined optical properties term μeff, it is clear to see how different regions of the TRS spectrum will be experiencing significantly different attenuation especially if sample thickness changes.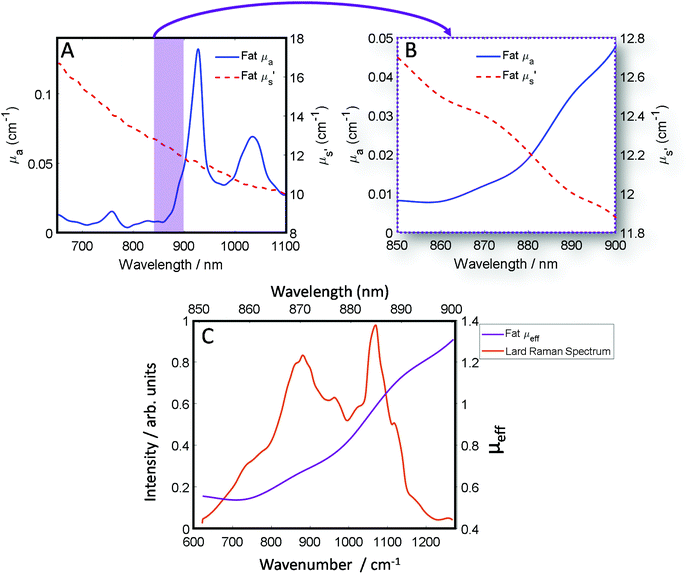 | ||
| Fig. 1 (A) Optical properties (μa and μ′s) of fat between 650 nm and 1100 nm. (B) Optical properties (μa and μ′s) of fat between 850 nm and 900 nm, equivalent to the spectral range of 600–1250 cm−1 using an λex 808 nm and our high dispersion Raman grating. (C) The combined optical properties contribution of μa and μ′s of fat termed μ effective (μeff) over the Raman spectral range (purple) while in orange a transmission Raman spectrum of lard (1 cm thick). Optical properties data (A and B) was adapted with permission from the work of Mosca et al.40 | ||
A block of lard was shaped so that it had a varied thickness (1–4 cm), while being reasonably homogenous in the overall chemical composition (Fig. 2B). Transmission Raman spectra were acquired in a grid map over the block of lard, with 200 spatial points recorded in total (Fig. 2C). As can be seen, even post processing and normalising the TRS data, a major difference in variance remains in the spectra. Most notable exhibited by the relative intensity variation between the two peaks highlighted with (*) as a function of sample thickness. These two bands are assigned to C–C bending modes of the lipid skeleton,41,42 and relative changes would not be expected normally within a relatively homogeneous sample.
This is evidenced clearly by plotting the peak intensity ratios as a function of sample thickness. As the thickness increases the intensity of the 1068 cm−1 decreases relative to the 880 cm−1 peak (Fig. 2D).
In contrast, low variation in the peak ratio is observed when scanning across as denoted by directional arrow X (Fig. 2B) with no sample thickness variation, with a similar standard deviation in the intensity of ∼0.011 seen for each subsequent line. This is also seen in Fig. S1A,† where each box and whisker plot contains the data measured in each row, with all showing similar variance as the ratio changes. However, scanning up and down (as denoted by directional arrow Y, Fig. 2B), through lesser or greater thicknesses of material shows a great variance in the intensity along the line, the standard deviation is ∼0.08, i.e. approximately 8× larger (Fig. S1B†) and here there is a consistent spread of data in the box and whisker plot. In summary this indicates a low level of contributions from Raman spectral noise and sample spatial chemical heterogeneity, and the dominant changes attributable to sample thickness. This is in agreement with what might be expected when considering the optical properties of the sample i.e. the μeff.
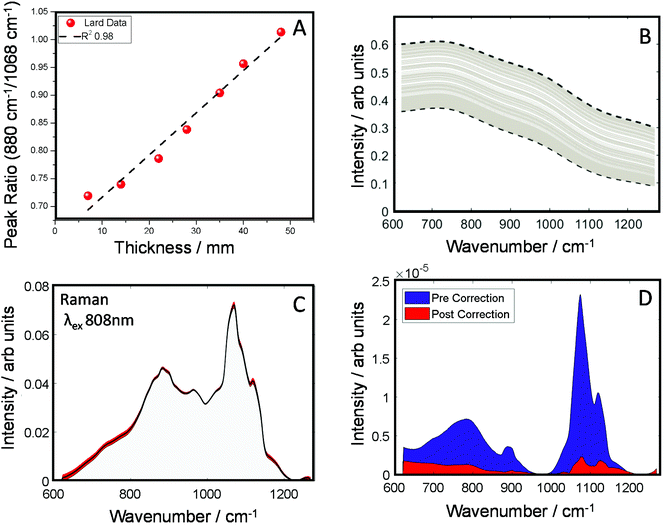
In the next set of experiments, we measured the TRS spectra of a series of lard slices of uniform thickness. The sections were stacked on top of each other so to create an increasingly thick transmission pathway. The ratio of two main Raman peaks previously discussed (880/1068 cm−1) are plotted against the overall sample thickness and shown in Fig. 3A. A clear linear relationship (in the central zone of the sample) can be established between the peak ratio and overall thickness of the sample, this data was then used as a simple calibration set for predicting thickness based on this ratiometric change. There was little variance within each measurement at a given thickness, <0.5% around the average. From this we were able to estimate sample thickness for all the TRS spectra from the mapping experiment (Fig. 2B).
Knowing the thickness for each TRS spectrum, we were then able to properly apply a correction function utilising μeff for the spectral range of the measurements (Fig. 3B) to correct for the spectral distortion. For this we used μeff as our attenuation coefficient, and pathlength ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , is half the sample thickness. The spectrum arising from TRS is comprised of multiple phenomena, firstly the excitation beam attenuates as it travels through the sample, usually in a exponential decay fashion. Therefore, the amount of Raman events decrease the further from the illumination point (deeper) with the sample. The Raman spectra generated are then attenuated to differing degrees depending on the total propagation distance, and the wavelength dependent optical properties have a varying influence. In short, the most Raman events occurs at the sample surface, however these Raman photons are the most likely to be maximally distorted. Conversely, Raman photons generated at the exit surface are most likely to be undistorted, however there will be significantly fewer (thickness depending). However, a simplification to account for the assumed bulk transmission Raman signal origin,43 can be utilised. Therefore, rearranging the transmittance equation T = e−μeff
, is half the sample thickness. The spectrum arising from TRS is comprised of multiple phenomena, firstly the excitation beam attenuates as it travels through the sample, usually in a exponential decay fashion. Therefore, the amount of Raman events decrease the further from the illumination point (deeper) with the sample. The Raman spectra generated are then attenuated to differing degrees depending on the total propagation distance, and the wavelength dependent optical properties have a varying influence. In short, the most Raman events occurs at the sample surface, however these Raman photons are the most likely to be maximally distorted. Conversely, Raman photons generated at the exit surface are most likely to be undistorted, however there will be significantly fewer (thickness depending). However, a simplification to account for the assumed bulk transmission Raman signal origin,43 can be utilised. Therefore, rearranging the transmittance equation T = e−μeff![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) allowing us to create a correction function that relates the sample thickness and the optical properties.
allowing us to create a correction function that relates the sample thickness and the optical properties.
The corrected spectra (Fig. 3C) show considerably less variance than present originally. This is further demonstrated in plots of spectral variance (Fig. 3D) in the data before (blue) and after correction (red). While some peak variance remains, as expected, it has greatly been diminished across the whole spectrum. Overall, full spectral intensity variance is reduced by a factor of ∼5.5. Moreover, specifically looking at the peak ratio of interest (880/1068 cm−1) this itself has been reduced 35 times. The reduction of this spectral distortion, due to physical properties of the sample, now enables a more accurate characterisation of any underlying chemical properties, provided by the Raman scattered signal, which might previously be masked by the interfering spectral distortions. This, in practical terms, is expected to enable TRS to detect with higher sensitivity more subtle spectral changes, e.g. those associated with a medical condition. While less variance is observed in the corrected spectra (Fig. 3C), no prior information of the pure spectrum is used in the reconstruction, therefore over or under correction can occur. Therefore, the corrected spectrum might not necessarily match that of the pure, undistorted Raman spectrum. It is noted that the goal of the correction procedure is to minimise variance in the Raman data set rather than recovering a ‘perfect’ undistorted Raman spectrum one would have obtained when measuring, for example, a very thin sample with negligible signal self-absorption.
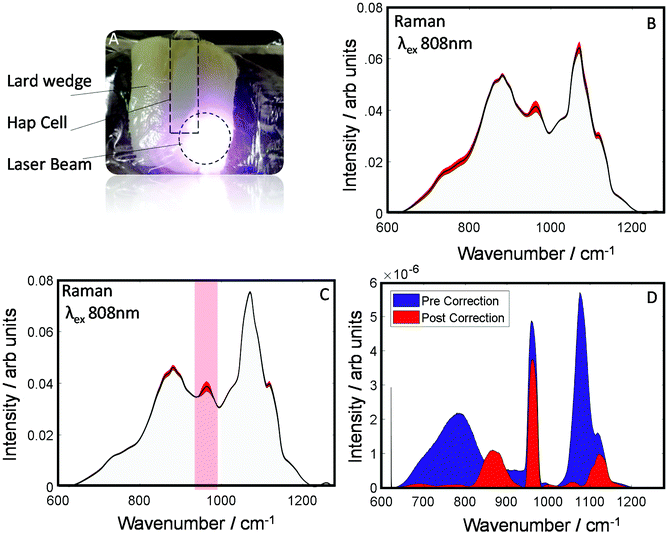
To evaluate the robustness of this approach to derive more accurately the chemical information about the sample an additional dataset was investigated as is shown (Fig. 4A). This dataset was collected from a smaller wedge-shaped block of lard (with a maximal thickness of 3 cm) that had a quartz cell containing HAP placed upon it (representing a detected spectral component – e.g. calcification associated with a breast cancer lesion). TRS spectra of the maps are shown pre- and post-correction (Fig. 4B and C). As can be seen visually, post-correction acts to limit the spectral variability of the lard particularly in the region where you would expect to see the main HAP peak (PO4 symmetric stretch), centered at ∼960 cm−1. Furthermore, when comparing the variance (Fig. 4D), the pre-correction spectral features (blue) are dominated by distortions due to optical properties; while, post correction (Fig. 4D red) HAP dominates the variance plot relative to the attenuation distortions, indicating a considerably enhanced sensitivity to detect such desirable chemical signatures.
When a common analytical tool used in spectroscopy such as principal component analysis (PCA) is applied to the datasets, the principal component (PC) loadings (Fig. S2A†), which are weighted for the variance explained, you can see the correction decreases considerably the influence of the background distortions and increases the relative presence of HAP in PCs 1 & 2. Moreover, looking at the variance explained in the PCs, the correction increases HAP's relative importance from 16% to 43% (Fig. S2B†).
Conclusions
Here we have demonstrated within the first NIR spectroscopy optical window, a general region of lower absorption and scattering within biological tissue, TRS spectra are susceptible to distortions due to the optical properties of the bulk sample and Raman photons achieve differential transmittance across the detected spectral range. In a homogenous sample of fat over a range of 1–4 cm, large Raman spectral distortions are observed as thickness increases. By the application of a correction function that utilises the effective attenuation co-efficient μeff and the approximate optical properties of fat, the spectral distortions could be significantly reduced (35×). This finding is vitally important for the general applicability of TRS, in situations where inter- and intra-sample thickness can differ, as it considerably increases the sensitivity of TRS in these circumstances. Relevant deep Raman applications include non-invasive disease diagnosis44,45 such as cancer detection in vivo, non-invasive neurotransmitter quantification,46,47 glucose sensing48 and blood sensing,49 to name but a few.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Optical properties data was accessed from the following sources: S. Mosca and P. Lanka, https://doi.org/10.6084/m9.figshare.11844789 & https://doi.org/10.6084/m9.figshare.11482923. EPSRC grant EP/P012442/1 and EP/R020965/1 funded the work presented here. We would like to acknowledge Dr R. Edginton, for invaluable feedback of visual elements of the work presented here.References
- S. He, J. Song, J. Qu and Z. Cheng, Chem. Soc. Rev., 2018, 47, 4258–4278 RSC.
- J. Zhao, D. Zhong and S. Zhou, J. Mater. Chem. B, 2018, 6, 349–365 RSC.
- T. A. Tabish, P. Dey, S. Mosca, M. Salimi, F. Palombo, P. Matousek and N. Stone, Adv. Sci., 2020, 1–28 Search PubMed , In press.
- P. Matousek, I. P. Clark, E. R. C. Draper, M. D. Morris, A. E. Goodship, N. Everall, M. Towrie, W. F. Finney and A. W. Parker, Appl. Spectrosc., 2005, 59, 393–400 CrossRef CAS.
- N. Stone and P. Matousek, Cancer Res., 2008, 68, 4424–4430 CrossRef CAS.
- P. Matousek, Appl. Spectrosc., 2006, 60, 1341–1347 CrossRef CAS.
- Z. Liao, F. Sinjab, G. Gibson, M. Padgett and I. Notingher, Opt. Express, 2016, 24, 12701–12712 CrossRef CAS.
- K. M. Khan, S. K. Majumder and P. K. Gupta, J. Biophotonics, 2015, 8, 889–896 CrossRef.
- P. Matousek, C. Conti, M. Realini and C. Colombo, Analyst, 2016, 141, 731–739 RSC.
- P. Matousek, TrAC, Trends Anal. Chem., 2018, 103, 209–214 CrossRef CAS.
- C. Conti, C. Colombo, M. Realini and P. Matousek, J. Raman Spectrosc., 2015, 46, 476–482 CrossRef CAS.
- F. Nicolson, B. Andreiuk, C. Andreou, H. T. Hsu, S. Rudder and M. F. Kircher, Theranostics, 2019, 9, 5899–5913 CrossRef CAS.
- H. N. Xie, R. Stevenson, N. Stone, A. Hernandez-Santana, K. Faulds and D. Graham, Angew. Chem., Int. Ed., 2012, 51, 8509–8511 CrossRef CAS.
- A. S. Moody, P. C. Baghernejad, K. R. Webb and B. Sharma, Anal. Chem., 2017, 89, 5688–5692 CrossRef CAS.
- P. Matousek and N. Stone, Analyst, 2009, 134, 1058 RSC.
- B. Gardner, P. Matousek and N. Stone, Analyst, 2019, 144, 3552–3555 RSC.
- S. K. V. Sekar, S. Mosca, A. Farina, F. Martelli, P. Taroni, G. Valentini, R. Cubeddu and A. Pifferi, Opt. Express, 2017, 25, 4585 CrossRef.
- M. Z. Vardaki, H. Sheridan, N. Stone and P. Matousek, Appl. Spectrosc., 2017, 71, 1849–1855 CrossRef CAS.
- S. Mosca, P. Dey, T. A. Tabish, F. Palombo, N. Stone and P. Matousek, Anal. Chem., 2019, 91, 8994–9000 CrossRef CAS.
- B. Gardner, N. Stone and P. Matousek, J. Raman Spectrosc., 2020, 51, 1078–1082 CrossRef CAS.
- B. Gardner, N. Stone and P. Matousek, Anal. Chem., 2017, 89, 9730–9733 CrossRef CAS.
- N. Stone, M. Kerssens, G. R. Lloyd, K. Faulds, D. Graham and P. Matousek, Chem. Sci., 2011, 2, 776–780 RSC.
- K. Buckley, J. G. Kerns, J. Vinton, P. D. Gikas, C. Smith, A. W. Parker, P. Matousek and A. E. Goodship, J. Raman Spectrosc., 2015, 46, 610–618 CrossRef CAS.
- K. Buckley, J. G. Kerns, A. W. Parker, A. E. Goodship and P. Matousek, J. Raman Spectrosc., 2014, 45, 188–192 CrossRef CAS.
- S. T. Sivapalan, B. M. DeVetter, T. K. Yang, T. van Dijk, M. V. Schulmerich, P. S. Carney, R. Bhargava and C. J. Murphy, ACS Nano, 2013, 7, 2099–2105 CrossRef CAS.
- T. van Dijk, S. T. Sivapalan, B. M. DeVetter, T. K. Yang, M. V. Schulmerich, C. J. Murphy, R. Bhargava and P. S. Carney, J. Phys. Chem. Lett., 2013, 4, 1193–1196 CrossRef CAS.
- W.-C. Shih, K. L. Bechtel and M. S. Feld, Opt. Express, 2008, 16, 12726 CrossRef CAS.
- K. L. Bechtel, W.-C. Shih and M. S. Feld, Opt. Express, 2008, 16, 12737 CrossRef CAS.
- C. Reble, I. Gersonde, S. Andree, H. J. Eichler and J. Helfmann, J. Biomed. Opt., 2010, 15, 037016 CrossRef.
- I. Barman, G. P. Singh, R. R. Dasari and M. S. Feld, Anal. Chem., 2009, 81, 4233–4240 CrossRef CAS.
- C. Reble, I. Gersonde, C. A. Lieber and J. Helfmann, Biomed. Opt. Express, 2011, 2, 520 CrossRef.
- M. Z. Vardaki, B. Gardner, N. Stone and P. Matousek, Analyst, 2015, 140, 5112–5119 RSC.
- B. Gardner, P. Matousek and N. Stone, Analyst, 2019, 144, 3552–3555 RSC.
- F. Martelli, S. Del Bianco, A. Ismaelli and G. Zaccanti, Light Propagation through Biological Tissue and Other Diffusive Media: Theory, Solutions, and Software, SPIE, 2009 Search PubMed.
- I. J. Bigio and S. Fantini, Quantitative Biomedical Optics, Cambridge University Press, 2016 Search PubMed.
- A. Ghita, P. Matousek and N. Stone, Sci. Rep., 2018, 8, 8379 CrossRef.
- A. Ghita, P. Matousek and N. Stone, J. Biophotonics, 2018, 11, e201600260 CrossRef.
- P. Matousek and N. Stone, J. Biomed. Opt., 2007, 12, 24008 CrossRef.
- S. Mosca, P. Lanka, N. Stone, S. Konugolu Venkata Sekar, P. Matousek, G. Valentini and A. Pifferi, Biomed. Opt. Express, 2020, 11, 1697 CrossRef.
- S. Mosca, P. Lanka, N. Stone, S. K. V. Sekar, P. Matousek, G. Valentini and A. Pifferi, Biomed. Opt. Express, 2020, 11, 1697–1706 CrossRef.
- P. Meksiarun, B. B. Andriana, H. Matsuyoshi and H. Sato, Sci. Rep., 2016, 6, 37068 CrossRef CAS.
- K. Sowoidnich and H.-D. Kronfeldt, ISRN Spectrosc., 2012, 2012, 256326 Search PubMed.
- P. Matousek, N. Everall, D. Littlejohn, A. Nordon and M. Bloomfield, Appl. Spectrosc., 2011, 65, 724–733 CrossRef CAS.
- T. J. Moore, A. S. Moody, T. D. Payne, G. M. Sarabia, A. R. Daniel and B. Sharma, Biosensors, 2018, 8(2), 46 CrossRef.
- S. Pahlow, K. Weber, J. Popp, B. R. Wood, K. Kochan, A. Rüther, D. Perez-Guaita, P. Heraud, N. Stone, A. Dudgeon, B. Gardner, R. Reddy, D. Mayerich and R. Bhargava, Appl. Spectrosc., 2018, 72(S1), 52–84 CrossRef CAS.
- A. S. Moody and B. Sharma, ACS Chem. Neurosci., 2018, 9, 1380–1387 CrossRef CAS.
- R. A. Odion, P. Storbbia, B. M. Crawford and T. Vo-Dinh, J. Raman Spectrosc., 2018, 1–9 Search PubMed.
- J. M. Yuen, N. C. Shah, J. T. Walsh, M. R. Glucksberg and R. P. Van Duyne, Anal. Chem., 2010, 82, 8382–8385 CrossRef CAS.
- M. Z. Vardaki, C. G. Atkins, H. G. Schulze, D. V. Devine, K. Serrano, M. W. Blades and R. F. B. Turner, Analyst, 2018, 143, 6006–6013 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0an01940b |
| This journal is © The Royal Society of Chemistry 2021 |