Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New insights into phenazine-based organic redox flow batteries by using high-throughput DFT modelling†
Carlos
de la Cruz
 ,
Antonio
Molina
,
Nagaraj
Patil
,
Antonio
Molina
,
Nagaraj
Patil
 ,
Edgar
Ventosa
,
Edgar
Ventosa
 ,
Rebeca
Marcilla
,
Rebeca
Marcilla
 * and
Andreas
Mavrandonakis
* and
Andreas
Mavrandonakis
 *
*
Electrochemical Processes Unit, IMDEA Energy, Avda. Ramón de la Sagra 3, 28935 Móstoles, Madrid, Spain. E-mail: rebeca.marcilla@imdea.org; andreas.mavrantonakis@imdea.org
First published on 3rd August 2020
Abstract
Identification of new redox compounds is essential for the design of new improved redox-flow batteries. Phenazines are a new class of organic compounds that have been recently used in electrochemical energy storage applications. By applying high-throughput density functional theory calculations, we investigated the redox-potentials of 200 phenazine derivatives in non-aqueous media containing various electron-donating or -withdrawing groups at different positions. We identified promising candidates for both the negative and positive sides of organic-based flow batteries. By adding an appropriate number of functional groups at the specific targeted positions, the redox potentials can be modified up to −0.65 V (for the electron-donating amino groups) and to +2.25 V (for the electron-withdrawing cyano groups) compared to the parent phenazine. The analysis of the results revealed the effect of both the functional groups and their position on the redox potential. By strategically partially functionalizing with EDGs at the appropriate positions, a redox potential equal to or even more negative than that of full functionalization can be obtained. To further accelerate the design of new improved batteries, a computational approach was used in order to assess their structural stability. The results show that the proposed compounds are predicted to have similar stabilities to other organic molecules that are used in redox-flow batteries.
Introduction
Climate change and rising global energy demands have prompted an urgent search for new renewable energy solutions. While great technological advances in accessing sustainable forms of energy such as wind and solar power have been made, the storage of these energies for on-demand usage and transport remains a major challenge.1,2Electrical energy storage and conversion is vital to a clean, sustainable, and secure energy future. Rechargeable batteries, based mainly on lithium, have attracted great attention due to their high energy density for portable (electronics), mobile (electrical vehicles), and stationary (micro-grids) applications.3 Despite their high energy densities, lithium-ion batteries exhibit several limitations, such as the use of critical elements and associated safety issues that eventually might cause a battery explosion. Therefore, new and improved technologies for energy storage are urgently required to make a more efficient use of our finite supply of fossil fuels, and to enable the effective and safe use of renewable energy sources. In this scenario, Redox-Flow Batteries (RFBs) are considered an interesting alternative energy storage technology, which can exhibit high potential, high efficiency, room temperature operation, and long charge/discharge cycle life.4,5 The main advantage of the RFBs is that power is independent of the energy density, thus allowing for independent power and energy sizing, which can be tailored according to each desired application.6 The energy density of RFBs depends on the concentration (solubility) of the active species in the electrolytes, the number of electrons involved in the redox reaction and the operation voltage, given by the potential difference between the redox reaction at the catholyte and anolyte (E ∝ nCV). Therefore, species with high solubilities and highly separated redox potentials are required in order to maximize the energy density of RFBs. Currently, most of the RFB systems are based on dissolved metallic redox species including vanadium, iron and chromium, with the aqueous all-vanadium technology (VRFB) being the one employed in most commercial available RFBs.7 However, the main disadvantages of VRFBs are associated with the toxicity, high cost and scarcity of vanadium salts.5
During the last few years there has been a boom in the field of organic redox flow batteries triggered by the research on abundant, environment friendly and cheaper redox active organic materials as substitutes of vanadium compounds.8,9 Moreover, non-aqueous solvents are also being investigated due to their wider electrochemical window enabling larger cell voltage that might boost the energy density of RFBs.10
Many different molecules and specially those based on quinones,11,12 viologens,13 nitroxides14 and methoxybenzenes,15,16 have been proposed and investigated in both aqueous and non-aqueous organic redox flow batteries. Among all candidates, the quinoyl family has been the most widely investigated due to their structural diversity and broad tunability, permitting the engineering of solubility, redox potential, kinetics, and stability.12,17–19 As an inspiring example, Yang et al. exploited the tunable redox potential of the quinoyl family to develop the first all-quinone aqueous RFB in which active species in both catholyte and anolyte were quinones having different functionalities.20 Recently, our group reported the first example of a membrane-free battery, in which the same molecule, p-benzoquinone, was used as the active material in both immiscible electrolytes.21 In that work, we took advantage of the different redox mechanisms undergone by quinones in electrolytes with different nature; in protic electrolytes the reduction proceeds via a 2e−/2H+ proton-coupled electron transfer (PCET) mechanism in one single step whereas in aprotic electrolytes quinones are reduced in successive one-electron steps (ET) to form the radical anion and dianion.22
Computational modeling has been proved to be a useful tool to explain the electrochemical properties of redox-active materials and also predict new molecules with improved properties. High-throughput computational screening offers the possibility of exploring thousands of molecules for desirable properties without the need for experimental trial and error.23–25 The computational results can provide key insights into structure–activity properties that may be used in the design and tuning of new molecules for electrochemical energy storage. The majority of theoretical studies have been conducted on the quinone family (benzoquinone, naphthoquinone, and anthraquinone) whose redox potential and solvation free energies strongly depend on the chemical nature of electron donating groups (EDGs) and electron withdrawing groups (EWGs) attached to the basic quinoyl skeleton.24,26,27 Though solubilities higher than 2 M have been reported, the reversible capacities achieved in those reports are still substantially lower than their theoretical values. Moreover, parasitic side reactions in quinoid-based compounds and relatively high redox potentials in most anolyte materials are still an issue in the development of organic redox flow batteries.28–30 Therefore, there is still a need for discovering new redox-active molecules to fulfill the exigent requirements of redox flow batteries, and computational chemistry can undoubtedly accelerate this task.
Phenazines comprise a large group of redox-active nitrogen-containing heterocyclic anthracene skeletons, sharing similar chemical, electrochemical and physical properties to those of the quinone family. They are structural analogues to anthraquinones and their reduction mechanism also depends on the media, occurring either via a 2-electron reduction (ET) in two steps in aprotic solvents, or via a 2e−/2H+ proton-coupled electron transfer (PCET) mechanism in a single step in protic media.31–33 Moreover, similar to quinones, some properties of phenazines such as their redox potential strongly depend on the nature of functional groups in the molecular structure.34 However, there are only a few examples where phenazine compounds have been used for redox flow batteries.35–37 In the first example, a bipolar redox active molecule containing phenazine and TEMPO moieties acting as anolyte and catholyte redox centers, respectively, was synthesized and employed in a symmetric RFB.35 Following a similar strategy to the quinone family,24,38 Hollas et al. performed a virtual screening on several phenazine derivatives with hydroxo, carboxylate and sulfonate groups in aqueous solutions and modified the molecular structure of the pristine phenazine with hydroxo and sulfonate groups to increase the solubility and tune the redox potential.36 In a similar fashion, Wang et al. characterized phenazines containing amino and hydroxo groups in aqueous RFBs with experimental and computational techniques.37 They also performed a systematic computational investigation of various multi-hydroxyl substituted phenazines and showed how the redox potentials depend on the number and position of the hydroxo groups. However, a systematic computational screening of phenazine derivatives with functional groups of different nature is still highly needed, considering that more than 100 different phenazine structural derivatives have been identified in nature, and over 6000 compounds that contain phenazine as a central unit have been synthesized.39,40
Here, we provide a systematic computational study to fill the existing gap in knowledge on how the relevant electrochemical properties of phenazines change by systematic insertion of different functional groups (FGs). The main objective is to determine the effects of the: (i) addition of FGs with different electronic behaviors, (ii) position of the FG, and (iii) degree of functionalization (i.e. single versus multiple FGs), on the redox potentials of phenazine-derivatives. To achieve this, we analyzed ∼200 phenazine compounds containing 22 FGs with different electronic behaviors like electron donating groups (EDGs) and electron withdrawing groups (EWGs). As a result, new insights into the phenazine structure–activity relationships in non-aqueous electrolytes are disclosed for the first time. Additionally, we performed a theoretical assessment of their stability based on structural criteria and we determined how the different FGs affect this stability. This computational–experimental research aims to contribute to the rational design of appropriate redox molecules and to accelerate the development of phenazine compounds as high performing anolytes for RFBs.
Methodology
Experimental details
Phenazine (98% purity) was purchased from Sigma Aldrich and used as received. The redox behavior of phenazine was determined by cyclic voltammetry (CV) of 5 mM of phenazine in 1,2-dimethoxyethane (DME) with 0.5 M TBAPF6 as the supporting salt. CV was carried out at room temperature in a three-electrode cell using 3 mm diameter glassy carbon and a Pt wire as working and counter electrodes, respectively. A silver wire in a frit tube filled with electrolyte solution was used as the pseudo-reference electrode. Ferrocene was used as an internal standard for electrochemical measurements. CV at different scan rates was conducted in a Biologic VMP multichannel potentiostat inside a glove box (O2 < 0.1 ppm, H2 ≤ 0.1 ppm).Computational details
| G0(i,sol) = G0therm(i,gas) + EM06-2X(i,sol) | (1) |
All DFT calculations were performed with the Gaussian 16 software package.51 An example of an input file with DME as the solvent for the SMD calculation is given in section A of the ESI,† since the DME solvent needs to be defined explicitly via its descriptors.
The reduction potentials of the functionalized compounds (RPZ) were calculated using the isodesmic reaction: [PZ]− + [RPZ] → [PZ] + [RPZ]−, relative to the corresponding values for the reference species, the parent phenazine (PZ). The following equation was used:
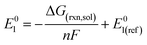 | (2) |
Two properties that can be related to the structural stability are (i) the reorganization energy (λ) and (ii) the root-mean-square deviation (RMSD) between the optimized coordinates of the neutral and reduced state of the phenazine species. The reorganization energy (λ) of a molecule during the reduction and oxidation process was computed from the geometries of the neutral and anionic states using the Vertical Electron Affinity (VEA), the Vertical Detachment Energy (VDE) and the Adiabatic Electron Affinity (AEA) energies. The total reorganization energy (λtot) is defined as the sum of the reorganization energy during oxidation (λox) and reduction (λred).
Results and discussion
Accuracy of the computational approach
The reduction potentials of the phenazine derivatives were calculated according to eqn (1) and (2) using DFT, the standard thermodynamic relations and the reference value for the parent phenazine. The redox potential of the parent phenazine was determined experimentally by cyclic voltammetry as presented in Fig. S1 in the ESI.†In order to assess the accuracy of the proposed computational approach, the redox potentials calculated by this methodology were benchmarked against reported experimental values for several trifluoro-methylated derivatives of phenazine.34Table 1 shows that the calculated values for these phenazine derivatives are in very good agreement with the experimental redox potentials, thus validating the choice of the density-functional and basis set.
| Compound | Computed E01 (V) | Experimental E01a (V) |
|---|---|---|
| a Obtained from ref. 34. | ||
| 1,3,9-Phenazine–(CF3)3 | −1.14 | −1.07 |
| 1,4,6-Phenazine–(CF3)3 | −1.13 | −1.12 |
| 1,4,6,9-Phenazine–(CF3)4 | −0.92 | −0.97 |
| 1,2,4,6,9-Phenazine–(CF3)5 | −0.67 | −0.71 |
| 1,2,4,6,7,9-Phenazine–(CF3)6 | −0.42 | −0.46 |
| 1,3,4,6,7,9-Phenazine–(CF3)6 | −0.44 | −0.46 |
Influence of the dielectric constant on the redox potential
Initially, the effect of the dielectric constant (εr) of the solvent on the redox potential of the parent phenazine was investigated. Several solvents with values of the dielectric constant ranging from 2 up to 109 were selected for the calculations. Fig. 1 shows that the change in the redox potential of the parent phenazine is very pronounced among solvents with low values (εr < 20), where the potential increases rapidly from −2.3 V in 1,4-dioxane (εr = 2.20) to −1.6 V in 1,2-dichloroethane (εr = 10.12). For solvents with higher values of the dielectric constant, the potential increases very slowly reaching a plateau at −1.4 V. A similar trend is expected for the other phenazine derivatives.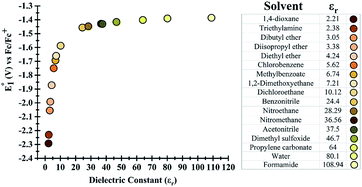 | ||
| Fig. 1 (Left) Dependence of the redox potential of the parent phenazine on the dielectric constant of the solvent. (Right) List of solvents considered and their dielectric constants. | ||
Influence of the incorporated functional group on the redox potential
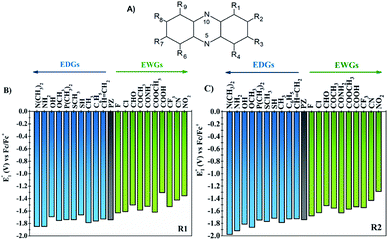
One of the main objectives of this study is to understand the effect of the chemical nature of the functional groups (FGs) and their position on the redox potential of phenazines. Due to the symmetry of the phenazine molecule (see Fig. 2A), there are only two possible positions to introduce those substituents: the R1-position, adjacent to nitrogen and the R2-position. As depicted in Fig. 2A, the R4, R6, and R9 positions are equivalent to R1, while R3, R7 and R8 are equivalent to R2.As a first step, the effect of adding one functional group into the R1 or R2 positions was studied. We investigated the following functional groups (FGs) that were ordered by the electron donating ability; –N(CH3)2, –NH2, –OH, –OCH3, –P(CH3)2, –SCH3, –SH, –CH3, –C6H5, –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, –F, –Cl, –CHO, –COCH3, –CONH2, –COOCH3, –COOH, –CF3, –CN and –NO2. The calculated values of the first reduction potential of the phenazine derivatives after incorporating one functional group either in R1 or R2 positions are presented in Fig. 2B and C, respectively.
CH2, –F, –Cl, –CHO, –COCH3, –CONH2, –COOCH3, –COOH, –CF3, –CN and –NO2. The calculated values of the first reduction potential of the phenazine derivatives after incorporating one functional group either in R1 or R2 positions are presented in Fig. 2B and C, respectively.
Fig. 2 suggests that EDGs, such as –OH and –NH2, shift the redox potential (E01) to lower values, whereas functionalization with EWGs, such as –NO2 and –CN, lead to higher E01 values. For example, compared to the parent molecule, the –N(CH3)2 group shifts the E01 by −107 and −239 mV when incorporated in R1 and R2 positions, respectively. In contrast, the incorporation of the –NO2 group shifts the E01 by +386 and +454 mV at the R1 and R2 positions, respectively. Therefore, it is clearly shown in Fig. 2 that the electronic behavior of the FGs plays a key role in the redox potential of phenazine derivatives. For compounds negatively charged, such as the anion or dianion of a reduced molecule, the presence of FGs with electron withdrawing behavior tends to stabilize the effect of the negative charge on the whole molecule. Consequently, the Gibbs free energy of the reaction of phenazines with EWGs present more positive values resulting in the redox potential shifting towards more positive values than for the parent phenazine. In contrast, the presence of EDGs tends to destabilize the reduced phenazine, shifting the potential towards more negative values. These results are in good agreement with the trends observed in both computational and experimental studies reported for quinones and other heteroatom-doped organic redox compounds with 5- and 6-membered rings.26,27,34,55–57
Influence of the position of added functional groups on the redox potential
In order to clearly identify the influence of the position of functional groups on the E01 of the phenazine derivative, Fig. 3 presents the difference between the two calculated redox potentials (ΔE01(R2, R1) = E01(R2) − E01(R1)). The presence of negative values in the y-axis indicates that the functionalization in the R2 position shifts the redox potential to more negative values compared to that calculated for the R1 position.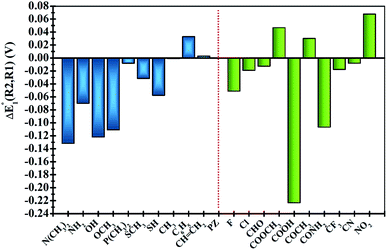 | ||
| Fig. 3 Plots of the relative changes in the redox potential ΔE01(R2, R1) = E01(R2) − E01(R1) (in V). Vertical blue and green bars indicate the EDGs and the EWGs, respectively. | ||
Significant changes are calculated for the ΔE01(R2,R1) values of the –N(CH3)2, –NH2, –OH, –OCH3, –SH, –COOH and –CONH2 FGs as shown in Fig. 3. In these cases, the hydrogen atoms from the FGs are in proximity to the nitrogen atom of the phenazine when the FG is attached to the R1 position, and intramolecular interactions are present. The main geometric characteristics of the above mentioned examples are shown in Fig. S2 in the ESI.† In the cases of –NH2, –OH, –SH, –COOH and –CONH2, the interactions are attributed to weak hydrogen bonds between the proton and the nitrogen atom based on the analysis of the main geometrical features (see Fig. S2 in the ESI†). In the reduced form, the negative charge stabilizes even more the hydrogen-bond, therefore the RPs for the FGs at R1 are shifted to more positive values compared to those for R2.
It is also observed that in the case of EWGs (green bars in Fig. 3), there is not a clear trend with the position of the FG and the ΔE01(R2,R1) seem to have a random distribution with negative and positive values. However, most of the derivatives with EDGs (blue bars in Fig. 3) show E01 shifted to more negative values when the FG is incorporated in the R2 position. The best examples are the –N(CH3)2 and –OH groups, where the R2-derivatives have a more negative potential by −132 and −122 mV respectively, compared to the R1-derivatives. Although there is only one exception, we can conclude that functionalization with EDGs in the R2 position is highly desirable to design new anolytes for RFBs, where more negative potentials are required. It is important to remark that this unique trend of phenazines is revealed for the first time in organic redox molecules. Compared to their quinone analogues, anthraquinones showed the opposite effect, i.e. functionalization of the 9,10-AQ with EDGs always produced positive values for the ΔE01(R2,R1).24
Effect of multiple substitutions
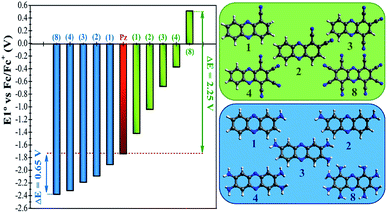
In a more detailed computational study we investigated the effect of adding more than one FG on the redox potential of phenazine. Amino (–NH2) and cyano (–CN) groups were selected as two representative examples of EDGs and EWGs, respectively. Two, three, four and eight amino or cyano FGs were introduced on different positions and the redox potentials were calculated. Although the synthesis of phenazines with eight FGs is a challenging task,58 we computationally explored these fully substituted derivatives to identify the upper and lower limits for the redox potential. All possible combinations were investigated, although only the redox potential of the derivative showing the largest shift in E01 is shown for each group in Fig. 4. A more extended table with all the results is reported in the ESI (see Table S2†).Fig. 4 shows that after the insertion of the second amino group, the redox potential (E01) decreases from −1.92 V to −2.09 V. This represents a redox potential shift of −0.17 V with respect to the addition of only one amino group. As mentioned in the previous section, the insertion of the first amino group induces the same redox potential shift of −0.17 V compared to the parent phenazine. For the successive addition of the third and fourth amino functionality, the redox potential shift is reduced to −0.11 V and −0.14 V for the tri-amino-phenazine and tetra-amino-phenazine (TAPZ) respectively, while between four and eight groups the potential changes only by −0.05 V. Thus, the lowest limit of the redox potential after functionalization with eight amino groups is calculated to be −2.39 V for the octa-amino-phenazine (OAPZ). The marginal difference of the potentials between TAPZ and OAPZ suggests that full functionalization with amino groups is not necessary to achieve the most negative potential. By strategically functionalizing at the appropriate positions with EDGs, a derivative with four amino groups is able to achieve an almost equally negative potential as a derivative with eight groups. This is a unique property of phenazines that has not been shown to exist for quinones. This effect is not dependent on the EDG, since the same trend is computed for functionalization with hydroxo groups (see Table S2 in the ESI†). Regarding the functionalization with EWGs, Fig. 4 shows that the effect of increasing the degree of functionalization is clearly more pronounced with cyano groups. It can be observed that the consecutive addition of one cyano group shifts the potential by an almost constant value of +0.35 V per group up to four substitutions. With eight cyano groups the redox potential can reach a value as high as +0.51 V for the octa-cyano-phenazine (OCPZ), which represents an increment of +1.23 V with respect to the phenazine with four cyano groups. This effect is also not dependent on the EWG, since the same trend is observed for functionalization with nitro groups (see Table S2 in the ESI†). Interestingly, this huge shift of redox potential towards more positive values might pave the way towards the design of phenazine derivatives to be used not only as anolytes but also as catholytes in RFBs.
Comparison of phenazines with other common anolytes and catholytes
Fig. 5 presents the redox potentials of the most promising phenazines computed in this work in comparison with those of other redox-active candidates reported for non-aqueous RFBs.34,59,60 Since not all reported molecules were tested on the same electrolyte, for a fair comparison, the first redox potentials of all compounds were recalculated in the same DME media and plotted together with the best phenazine candidates obtained in this work. Fig. 5 shows that the redox potential of TAPZ is 140 mV more negative than that of N-methylphthalimide (MePht), having one of the most negative redox potentials reported so far.60 This evidences the potential of phenazine derivatives, in particular amino-phenazines, as anolytes for non-aqueous RFBs.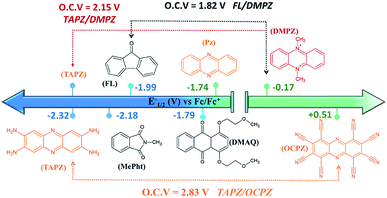 | ||
| Fig. 5 Redox potential of most promising anolytes/catholytes reported so far for non-aqueous RFBs and redox potential of selected candidates from this work. Abbreviations and related references from left to right: TAPZ = Tetra-AminoPhenaZine (this work), MePht = N-Methyl-Phthalimide,60FL = 9-FLuoroenone,59,61DMAQ = 1,4-bis(2-methoxyethoxy)-anthraquinone-9,10,62PZ = phenazine (this work and ref. 34), DMPZ = N,N-dimethyl-phenazine,59 and OCPZ = octa-cyanophenazine (this work). | ||
Fig. 5 shows that the high theoretical voltage calculated in DME for a battery using 9-FLuoroenone (FL) as the anolyte and N,N-dimethyl-phenazine (DMPZ) as the catholyte59 (its first oxidation peak at 1.82 V) might be further increased by 330 mV until 2.15 V, if the FL anolyte is substituted by the TAPZ reported here. In such an example, the voltage for the battery is associated with the first-redox peak of the DMPZ catholyte at a positive potential.59 Interestingly, due to the huge effect of the functional groups on the redox potential of the phenazine family, it was possible to envisage the first theoretical example of the all-phenazine battery having a meritorious 2.83 V by combining the phenazine functionalized with four amino groups (TAPZ) as the anolyte with the phenazine functionalized with cyano groups (OCPZ) as the catholyte.
Stability-performance prediction
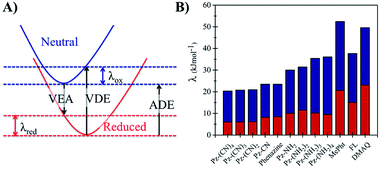
The long-term performance of a RFB depends on the stability of the redox organic molecules used as the anolyte and catholyte. Stability is a multifaceted issue that can be further categorized into: (i) chemical stability, which is associated with the decomposition of the redox molecule upon reaction with its reduced/oxidized species or solvent molecules, (ii) electrochemical stability, which is related to the decomposition reactions at very negative/positive potentials and (iii) structural stability, which is associated with the geometric strain between the oxidized and the reduced form of the redox molecule. From the computational perspective, predicting the chemical stability of a molecule is challenging because of the many possible decomposition reactions and products. When the kinetic aspects are taken into account on top of thermodynamics, this task becomes even more cumbersome because the reaction barriers for the decomposition reactions need to be calculated. While the degradation mechanisms can be calculated by applying heuristically aided quantum chemistry approaches to modeling complex chemical reactions,63 this is out of the scope of the current work. However, a preliminary assessment of their structural stability can be performed based on the structural differences between the neutral and reduced forms of the phenazine compounds, as it was reported previously in the case of methoxy-benzene catholytes.64Fig. 6 shows the reorganization energy (λ) of a molecule during the reduction and oxidation process computed using the geometries of the neutral and anionic states using the Vertical Electron Affinity (VEA), the Vertical Detachment Energy (VDE) and the Adiabatic Electron Affinity (AEA) energies. The total reorganization energy (λtot) is defined as the sum of the reorganization energy during oxidation (λox) and reduction (λred) as presented on the right side of Fig. 6. The results for all compounds with one functional group at the R1 and R2 position are shown in Fig. S3 and S4 in the ESI.†
Based on the calculations, phenazine and its amino- and cyano-derivatives have lower (oxidation and total) reorganization energies than commonly reported anolytes such as the FL, MePht or DMAQ. The lower reorganization energies suggest that the anionic molecular species after the VEA is closer to the minimum energy of the reduced state, thus it can reach the reduced state faster.
The second structural stability criterion is associated with the geometric changes upon reduction. Molecules with larger geometric distortions after the reduction are more prone to decomposition reactions.65 The root-mean-square deviation (RMSD) between the optimized coordinates of the neutral and reduced state can also serve as an indicator for the geometric distortion, thus large RMSD values are not desired. The computed RMSD values (see Table S1, Fig. S5 and S6 in the ESI†) suggest that the majority of the phenazine compounds have values in the same range as the FL and MePht compounds as can be seen in the ESI (Table S1†). While the parent phenazine and the cyano-derivatives show lower RMSD values, the corresponding values for the amino-derivatives are slightly higher. However, the values remain small, and do not exceed 0.05 Å. Summarizing, all the above results suggest that the structural stability of the amino- and cyano-phenazine compounds from this work is predicted to be similar to that of the FL and MePht and better than that of the DMAQ.
Conclusions
With the use of DFT calculations, the redox potentials of ∼200 phenazine-derivatives were computed and structure–property relationships were revealed. After analysis of the results, the main conclusions are drawn:(1) The use of EDGs shifts the potential toward negatives values, whereas the use of EWGs increases the potential toward positive values.
(2) The calculations have identified an unprecedented effect of the position (R1 versus R2) of functional groups on the redox potential. Functionalization with EDGs in the R2 position shifts the potential to more negative values compared to the R1 position. This is a highly desirable property for the newly designed anolytes for RFBs, where more negative potentials are required. Surprisingly, this is a unique feature exhibited by phenazines that has never been observed in the quinone family.
(3) The shift in the redox potential of phenazines functionalized with the electron withdrawing cyano groups was found to be proportional to the number of cyano groups. Therefore, the functionalization with EWGs has an additive effect on the reduction potential of phenazine derivatives. In contrast, the amino groups do not show such a pronounced additive effect. It was observed that by functionalization at the appropriate positions with four groups, a potential equal to or even more negative than that of the full functionalization was obtained.
(4) Phenazines can be a promising substitute for anthraquinones in RFBs, due to their higher ability of modifying the redox potential. The changes in their redox potential are significantly higher than in their anthraquinone analogues after the introduction of multiple functional groups. For example, introduction of four cyano groups in the phenazine increases the potential by 1.3 V, whereas in the anthraquinones by ∼0.5 V.27
(5) Based on the reorganization energies and the RMSD values between the geometries of oxidized and reduced states of the phenazines, the new derivatives are predicted to have similar or even improved structural stabilities than the commonly reported anolytes.
(6) The first theoretical example of an all-phenazine battery having a meritorious voltage of 2.83 V was envisaged by combining the TAPZ and OCPZ as the anolyte and catholyte, respectively.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement no. 726217), the Spanish Ministry of Science, Innovation and Universities through the Juan de la Cierva-formation fellowship (FJC2018-037781-I) and the SUSBAT project (Ref. RTI2018-101049-B-I00) (MINECO/FEDER, UE), and the TALENTO grant (2017-T1/AMB-5264) from Comunidad de Madrid for financial support. The results reflect only the authors' view and the Agency is not responsible for any use that may be made of the information they contain. The authors acknowledge the computing facilities of CSUC for providing resources that contributed to the research results reported within this paper.Notes and references
- Z. Yang, J. Zhang, M. C. W. Kintner-Meyer, X. Lu, D. Choi, J. P. Lemmon and J. Liu, Chem. Rev., 2011, 111, 3577–3613 CrossRef CAS PubMed.
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed.
- B. Dunn, H. Kamath and J. M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- M. Park, J. Ryu, W. Wang and J. Cho, Nat. Rev. Mater., 2016, 2, 16080 CrossRef.
- A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. Liu, J. Appl. Electrochem., 2011, 41, 1137–1164 CrossRef CAS.
- P. Alotto, M. Guarnieri and F. Moro, Renewable Sustainable Energy Rev., 2014, 29, 325–335 CrossRef CAS.
- M. Skyllas-Kazacos, J. Electrochem. Soc., 1987, 134, 2950–2953 CrossRef CAS.
- J. Winsberg, T. Hagemann, T. Janoschka, M. D. Hager and U. S. Schubert, Angew. Chem., Int. Ed., 2017, 56, 686–711 CrossRef CAS PubMed.
- T. B. Schon, B. T. McAllister, P. F. Li and D. S. Seferos, Chem. Soc. Rev., 2016, 45, 6345–6404 RSC.
- K. Gong, Q. Fang, S. Gu, S. F. Y. Li and Y. Yan, Energy Environ. Sci., 2015, 8, 3515–3530 RSC.
- D. G. Kwabi, K. Lin, Y. Ji, E. F. Kerr, M. A. Goulet, D. De Porcellinis, D. P. Tabor, D. A. Pollack, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Joule, 2018, 2, 1894–1906 CrossRef CAS.
- B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. R. Gerhardt, C. J. Galvin, X. Chen, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Nature, 2014, 505, 195–198 CrossRef CAS PubMed.
- T. Liu, X. Wei, Z. Nie, V. Sprenkle and W. Wang, Adv. Energy Mater., 2016, 6, 1501449 CrossRef.
- X. Wei, W. Xu, M. Vijayakumar, L. Cosimbescu, T. Liu, V. Sprenkle and W. Wang, Adv. Mater., 2014, 26, 7649–7653 CrossRef CAS PubMed.
- X. Wei, W. Duan, J. Huang, L. Zhang, B. Li, D. Reed, W. Xu, V. Sprenkle and W. Wang, ACS Energy Lett., 2016, 1, 705–711 CrossRef CAS.
- J. Huang, L. Cheng, R. S. Assary, P. Wang, Z. Xue, A. K. Burrell, L. A. Curtiss and L. Zhang, Adv. Energy Mater., 2015, 5, 1–6 CAS.
- Z. Yang, L. Tong, D. P. Tabor, E. S. Beh, M. A. Goulet, D. De Porcellinis, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Adv. Energy Mater., 2018, 8, 1702056 CrossRef.
- M.-A. Goulet, L. Tong, D. A. Pollack, D. P. Tabor, S. A. Odom, A. Aspuru-Guzik, E. E. Kwan, R. G. Gordon and M. J. Aziz, J. Am. Chem. Soc., 2019, 141, 8014–8019 CAS.
- C. Wang, Z. Yang, Y. Wang, P. Zhao, W. Yan, G. Zhu, L. Ma, B. Yu, L. Wang, G. Li, J. Liu and Z. Jin, ACS Energy Lett., 2018, 3, 2404–2409 CrossRef CAS.
- B. Yang, L. Hoober-Burkhardt, F. Wang, G. K. Surya Prakash and S. R. Narayanan, J. Electrochem. Soc., 2014, 161, A1371–A1380 CrossRef CAS.
- P. Navalpotro, J. Palma, M. Anderson and R. Marcilla, Angew. Chem., Int. Ed., 2017, 56, 12460–12465 CrossRef CAS PubMed.
- P. S. Guin, S. Das and P. C. Mandal, Int. J. Electrochem., 2011, 2011, 81602 Search PubMed.
- K. M. Pelzer, L. Cheng and L. A. Curtiss, J. Phys. Chem. C, 2017, 121, 237–245 CrossRef CAS.
- S. Er, C. Suh, M. P. Marshak and A. Aspuru-Guzik, Chem. Sci., 2015, 6, 885–893 RSC.
- J. F. Kucharyson, L. Cheng, S. O. Tung, L. A. Curtiss and L. T. Thompson, J. Mater. Chem. A, 2017, 5, 13700–13709 RSC.
- M. T. Huynh, C. W. Anson, A. C. Cavell, S. S. Stahl and S. Hammes-Schiffer, J. Am. Chem. Soc., 2016, 138, 15903–15910 CrossRef CAS PubMed.
- J. E. Bachman, L. A. Curtiss and R. S. Assary, J. Phys. Chem. A, 2014, 118, 8852–8860 CrossRef CAS PubMed.
- T. J. Carney, S. J. Collins, J. S. Moore and F. R. Brushett, Chem. Mater., 2017, 29, 4801–4810 CrossRef CAS.
- K. Lin, R. Gómez-Bombarelli, E. S. Beh, L. Tong, Q. Chen, A. Valle, A. Aspuru-Guzik, M. J. Aziz and R. G. Gordon, Nat. Energy, 2016, 1, 16102 CrossRef CAS.
- A. Orita, M. G. Verde, M. Sakai and Y. S. Meng, Nat. Commun., 2016, 7, 13230 CrossRef CAS.
- D. T. Sawyer and R. Y. Komai, Anal. Chem., 1972, 44, 715–721 CrossRef CAS PubMed.
- E. Laviron and L. Roullier, J. Electroanal. Chem. Interfacial Electrochem., 1983, 157, 7–18 CAS.
- Y. Mugnier, L. Roullier and E. Laviron, Electrochim. Acta, 1991, 36, 803–809 CrossRef CAS.
- K. P. Castro, T. T. Clikeman, N. J. Deweerd, E. V. Bukovsky, K. C. Rippy, I. V. Kuvychko, G. L. Hou, Y. S. Chen, X. Bin Wang, S. H. Strauss and O. V. Boltalina, Chem.–Eur. J., 2016, 22, 3930–3936 CrossRef CAS PubMed.
- J. Winsberg, C. Stolze, S. Muench, F. Liedl, M. D. Hager and U. S. Schubert, ACS Energy Lett., 2016, 1, 976–980 CrossRef CAS.
- A. Hollas, X. Wei, V. Murugesan, Z. Nie, B. Li, D. Reed, J. Liu, V. Sprenkle and W. Wang, Nat. Energy, 2018, 3, 508–514 CrossRef CAS.
- C. Wang, X. Li, B. Yu, Y. Wang, Z. Yang, H. Wang, H. Lin, J. Ma, G. Li and J. Zhong, ACS Energy Lett., 2020, 5, 411–417 CrossRef CAS.
- D. P. Tabor, R. Gómez-Bombarelli, L. Tong, R. G. Gordon, M. J. Aziz and A. Aspuru-Guzik, J. Mater. Chem. A, 2019, 7, 12833–12841 RSC.
- L. S. Pierson and E. A. Pierson, Appl. Microbiol. Biotechnol., 2010, 86, 1659–1670 CrossRef CAS PubMed.
- J. B. Laursen and J. Nielsen, Chem. Rev., 2004, 104, 1663–1686 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeerschd, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 616–641 CrossRef CAS.
- T. A. Halgren, J. Comput. Chem., 1999, 20, 720–729 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2008, 4, 297–306 CrossRef CAS PubMed.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- E. Papajak and D. G. Thrular, J. Chem. Theory Comput., 2010, 6, 597–601 CrossRef CAS PubMed.
- N. Treitel, R. Shenhar, I. Aprahamian, T. Sheradsky and M. Rabinovitz, Phys. Chem. Chem. Phys., 2004, 6, 1113–1121 RSC.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- E. J. Bylaska, A. J. Salter-Blanc and P. G. Tratnyek, in ACS Symposium Series, ed. S. B. Haderlein, T. J. Grundl and P. G. Tratnyek, 2011, vol. 1071, pp. 37–64 Search PubMed.
- A. V. Marenich, J. Ho, M. L. Coote, C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2014, 16, 15068–15106 RSC.
- M. Namazian, H. A. Almodarresieh, M. R. Noorbala and H. R. Zare, Chem. Phys. Lett., 2004, 396, 424–428 CrossRef CAS.
- R. S. Assary, F. R. Brushett and L. A. Curtiss, RSC Adv., 2014, 4, 57442–57451 RSC.
- Y. Liang, Y. Jing, S. Gheytani, K. Y. Lee, P. Liu, A. Facchetti and Y. Yao, Nat. Mater., 2017, 16, 841–848 CrossRef CAS PubMed.
- R. B. Araujo, A. Banerjee, P. Panigrahi, L. Yang, M. Strømme, M. Sjödin, C. M. Araujo and R. Ahuja, J. Mater. Chem. A, 2017, 5, 4430–4454 RSC.
- S. Miao, C. G. Bangcuyo, M. D. Smith and U. H. F. Bunz, Angew. Chem., Int. Ed., 2006, 45, 661–665 CrossRef CAS PubMed.
- G. Kwon, S. Lee, J. Hwang, H. S. Shim, B. Lee, M. H. Lee, Y. Ko, S. K. Jung, K. Ku, J. Hong and K. Kang, Joule, 2018, 2, 1771–1782 CrossRef CAS.
- C. Zhang, Z. Niu, Y. Ding, L. Zhang, Y. Zhou, X. Guo, X. Zhang, Y. Zhao and G. Yu, Chem, 2018, 4, 2814–2825 CAS.
- G. Kwon, K. Lee, M. H. Lee, B. Lee, S. Lee, S.-K. Jung, K. Ku, J. Kim, S. Y. Park, J. E. Kwon and K. Kang, Chem, 2019, 5, 2642–2656 CAS.
- J. Huang, Z. Yang, M. Vijayakumar, W. Duan, A. Hollas, B. Pan, W. Wang, X. Wei and L. Zhang, Adv. Sustainable Syst., 2018, 2, 1700131 CrossRef.
- D. Rappoport and A. Aspuru-Guzik, J. Chem. Theory Comput., 2019, 15, 4099–4112 CrossRef CAS PubMed.
- R. S. Assary, L. Zhang, J. Huang and L. A. Curtiss, J. Phys. Chem. C, 2016, 120, 14531–14538 CrossRef CAS.
- L. Cheng, R. S. Assary, X. Qu, A. Jain, S. P. Ong, N. N. Rajput, K. Persson and L. A. Curtiss, J. Phys. Chem. Lett., 2015, 6, 283–291 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental CVs, tables with all computed values and Cartesian coordinates of all structures. See DOI: 10.1039/d0se00687d |
| This journal is © The Royal Society of Chemistry 2020 |