Open Access Article
Open Access ArticleMutation effects on charge transport through the p58c iron–sulfur protein†
Ruijie D.
Teo
 a,
Agostino
Migliore
a,
Agostino
Migliore
 *a and
David N.
Beratan
*a and
David N.
Beratan
 *abc
*abc
aDepartment of Chemistry, Duke University, Durham, North Carolina 27708, USA. E-mail: agostino.migliore@duke.edu; david.beratan@duke.du
bDepartment of Physics, Duke University, Durham, North Carolina 27708, USA
cDepartment of Biochemistry, Duke University, Durham, North Carolina 27710, USA
First published on 17th June 2020
Abstract
Growing experimental evidence indicates that iron–sulfur proteins play key roles in DNA repair and replication. In particular, charge transport between [Fe4S4] clusters, mediated by proteins and DNA, may convey signals to coordinate enzyme action. Human primase is a well studied [Fe4S4] protein, and its p58c domain (which contains an [Fe4S4] cluster) plays a role in the initiation of DNA replication. The Y345C mutation in p58c is linked to gastric tumors and may influence the protein-mediated charge transport. The complexity of protein–DNA systems, and the intricate electronic structure of [Fe4S4] clusters, have impeded progress into understanding functional charge transport in these systems. In this study, we built force fields to describe the high potential [Fe4S4] cluster in both oxidation states. The parameterization is compatible with AMBER force fields and enabled well-balanced molecular dynamics simulations of the p58c–RNA/DNA complex relevant to the initiation of DNA replication. Using the molecular mechanics Poisson–Boltzmann and surface area solvation method on the molecular dynamics trajectories, we find that the p58c mutation induces a modest change in the p58c–duplex binding free energy in agreement with recent experiments. Through kinetic modeling and analysis, we identify key features of the main charge transport pathways in p58c. In particular, we find that the Y345C mutation partially changes the composition and frequency of the most efficient (and potentially relevant to the biological function) charge transport pathways between the [Fe4S4] cluster and the duplex. Moreover, our approach sets the stage for a deeper understanding of functional charge transfer in [Fe4S4] protein–DNA complexes.
1 Introduction
The past decade has witnessed remarkable progress towards understanding the structural and functional properties of [Fe4S4] proteins involved in DNA repair and replication.1–12 One of these proteins is human primase (containing a [Fe4S4] cluster in its p58c domain), which synthesizes the RNA primer required for the DNA synthesis. The DNA template/RNA primer duplex needs to be handed off to the DNA polymerase α for DNA synthesis. Recent experiments show that the DNA-binding affinity of the primase p58c domain is significantly increased when the [Fe4S4] cluster is oxidized.9 This property was proposed to establish a redox signaling mechanism between iron–sulfur proteins that might be responsible for the duplex handoff.9 A mechanism of this kind implicates protein-mediated charge transfer between the [Fe4S4] cluster and DNA, as well as DNA-mediated charge transport between the two [Fe4S4] proteins. The charge transport mechanism is the subject of ongoing debate,9,10,13,14 with questions surrounding the amino acid residues involved in the charge transfer (CT) routes through the p58c protein.9,13–15 In particular, Y345 has emerged as one of the p58c residues receiving attention in the debate. The functional relevance of Y345 is certainly indicated by the fact that the Y345C mutation is linked to gastric tumors,16 and ref. 9 proposes a CT role for Y345. The aim of this study is to use the tools of modeling and simulation to examine the role of Y345 in the protein-mediated charge transport between the [Fe4S4] cluster of p58c and the RNA/DNA duplex. Assessment of the charge transport characteristics requires a comprehensive campaign of electronic structure analysis, force field development, and tunneling kinetic analysis.Experimental studies of [Fe4S4]2+-p58c oxidation by bulk electrolysis and subsequent reduction by cyclic voltammetry9 indicate that the speed of the protein charge transport is reduced by a number of mutations, including the Y345C mutation, even though the mutations do not significantly alter the protein–DNA binding affinity. The experiments did not directly measure the decrease in the rate of the protein-mediated charge transport between the [Fe4S4] cluster and the DNA, but the experimental results can be interpreted in terms of a decrease of this kind. In particular, assuming that p58c diffusion is a property of the whole p58c protein that is not affected by mutations, the decrease in the bulk electrolysis yield may be interpreted as arising from the competition between two timescales: the time spent by p58c in sufficient proximity to the nucleic acid to enable [Fe4S4]2+ oxidation by protein-mediated charge transport, and the time required for the charge transport to occur. These two time scales can differ for the wild-type (WT) and Y345C proteins. This difference would translate into different probabilities of charging the single p58c proteins, and thus in a different electrolysis yield.
Given the unidirectional character of electron and hole transport between protein bound [Fe4S4] clusters and RNA/DNA duplexes,10 we focus on hole transport from an initially oxidized duplex to [Fe4S4]2+ that causes oxidation of the cluster and tightening of p58c binding to DNA. One cannot rule out the possibility that the non-biological context of the experiments reported in ref. 9 (in particular, the DNA proximity to an electrode and the application of an external voltage) may enable charge transport mechanisms that are different from the unidirectional processes studied in ref. 10. This uncertainty surrounding the CT mechanisms in the experimental context does not diminish the value of the present analysis, which aims to explore the protein-mediated hole transport and possible effects of the Y345C mutation on the pertinent kinetics.
One way to study hole transport in the p58c–RNA/DNA complex is to simulate its structural fluctuations using classical molecular dynamics (MD) and to analyze the fluctuations in its associated charge transport properties, including the composition and charge-transport rate of the CT chain. Among the advantages that this approach affords is its ability to access long time scales. However, two issues need to be addressed in order to pursue this strategy.
First, suitable force field (FF) parameters are required to describe the high potential [Fe4S4] cluster in both oxidation states. The complexity of the cluster's electronic structure, with large spin-polarization effects and other intricacies,17 makes the generation of this FF a challenge. An AMBER compatible FF for the [Fe4S4]2+ cluster was provided in a prior study.17 Here, we produced a FF for the [Fe4S4]3+ cluster using the approach described in Section 2.2. We used the same approach to build a new FF for the [Fe4S4]2+ cluster. Both FFs are compatible with the AMBER FFs that we used to describe the other molecular components (Section 2.3).
A second issue in simulating the p58–RNA/DNA duplex system (as well as other [Fe4S4] protein–nucleic acid complexes) arises from the fact that the complex is more stable when the [Fe4S4] cluster is oxidized than when it is reduced,9 while the hole transport starts with the reduced [Fe4S4] cluster. Our analysis (Section 3.1) and kinetic modeling (Section 2.5) suggest strategies to tackle this issue and to enable the comparison of the WT and Y345C systems in terms of duplex-binding energies and protein charge transport properties (Section 3.2).
2 Methods
2.1 System modeling
We studied the charge transport between the [Fe4S4] cluster bound to p58c (p58c is the C-terminal domain of the human primase large subunit) and a nucleic acid duplex consisting of a DNA template and a RNA primer. The coordinates of the protein–nucleic acid complex were taken from the crystal structure with PDB ID 5F0Q.7 We used the [Fe4S4(SCH3)4]1− molecular moiety, corresponding to [Fe4S4]3+, to build the FF. We pruned the Cys ligands to obtain this moiety, and saturated the dangling bonds with hydrogen atoms, using the Maestro Molecular Modeling Suite.18 Then, we relaxed the positions of the saturating H atoms by DFT geometry optimization at the B3LYP19/6-31g* level. We used the structure resulting from this procedure as the starting point for all other geometry optimizations needed to obtain the [Fe4S4]2+/3+ FF parameters.2.2 Force field derivation
The antiferromagnetic coupling between two Fe2S2 layers in [Fe4S4]3+ produces a total spin of S = 1/2. One layer is a mixed-valence pair with total spin S1 = 9/2 and a formal charge of +2.5 on each Fe. The other layer is a ferric pair with formal charge +3 on each ion and S2 = 4.20–22 A 2D NMR study of the high potential iron–sulfur protein from Chromatium vinosum assigned the first two Cys ligands in the sequence (Cys 43 and Cys 46) to the more oxidized layer and the other two Cys ligands (Cys 61 and Cys 75) to the less oxidized layer.23 However, this assignment cannot be generalized to other iron–sulfur proteins.24 We expect that the geometry of the cluster (including its frequent departure from tetrahedral symmetry) and its division into distinct spin layers are influenced by the potential of the nearby environment. Thus, depending on the strength of the structural constraints and the interactions of the [Fe4S4] cluster with the protein, structural fluctuations may induce changes in the spin layer partitioning of the cluster during the molecular motion. A continuous reassignment of the spin-layers in the cluster during the MD simulation of an iron–sulfur protein is computationally unfeasible. In addition, we lack information about the appropriate spin-layer partitioning in the [Fe4S4]3+ cluster of p58c, even for the crystal structure. Therefore, in our first step to construct the FF, we optimized the geometry of the pruned system with all six possible redox-layer assignments for [Fe4S4]3+. We proceeded similarly for the three possible redox layer assignments in the [Fe4S4]2+ cluster, which consists of two antiferromagnetically coupled layers each with spin S = 9/2 (zero total spin).For each layer assignment, we optimized the geometry of the model system comprising the cluster and the truncated Cys ligands using the broken symmetry (BS) DFT approach,24–27 with the B3LYP density functional, the 6-31g** basis set, an extra fine integration grid, Grimme's DFT-D3 dispersion correction,28 and the COSMO solvation model29–32 (with ε = 4 (ref. 33)) in order to model the effect of the protein dielectric environment on the geometry of the iron–sulfur cluster.17 The DFT computations were performed using NWChem.34
Consistent with the [Fe4S4] cluster structures found in previous studies,24,35 the cluster geometries from our DFT optimizations deviate from an ideal cube and from concentric interlocking regular tetrahedra36 (Fig. 1). For each geometry, we computed the Hessian matrix and used the VFFDT program37 to extract the force constants corresponding to bond stretching and angle bending. We did not calculate the dihedral parameters since the torsion barriers for the dihedral angles are smaller than the thermal energy kBT.37,38 The six sets of force constants, bond distances and bond angles for each optimized [Fe4S4]3+ geometry, as well as their averages, are presented in ESI Tables S1–S4.† Similarly, the three sets of parameters pertaining to [Fe4S4]2+ and their average values are reported in ESI Tables S6–S9.†
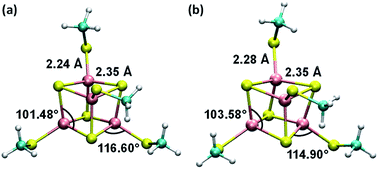 | ||
| Fig. 1 Average geometries of the iron–sulfur cluster that result from (a) the six redox-layer assignments for [Fe4S4]3+ and (b) the three assignments for [Fe4S4]2+. For each oxidation state of the cluster, the averaging over the different structures (ESI Fig. S1†) was performed using the Z-matrices, which were built with the help of the newzmat utility in the Gaussian package.39 | ||
ESI Tables S5 and S10† report the restrained electrostatic potential (RESP) charges for the atoms of the model system in the two oxidation states. For compatibility of the RESP charges with the charges on the deprotonated Cys (CYM) in AMBER ff14SB,40 we constrained the charge on the saturating H atom of each Cys to 0.0987e, i.e., the charge in the missing portion of the amino acid residue.
We obtained FFs A3+ and A2+ for the [Fe4S4(SCH3)4]1− and [Fe4S4(SCH3)4]2− model systems, respectively, averaging the force constants, distances, angles, and atomic charges over the 4 Fe atoms, S atoms, and Cys fragments. The partial atomic charges in the 4 Cys fragments were averaged to have the same charge on the corresponding atoms.
Since the oxidized cluster consists of Fe3+–Fe3+ and Fe2.5+–Fe2.5+ layers, the average formal charge on each Fe ion is +2.75e. With this consideration, we obtained the values of the 12–6 Lennard-Jones (LJ) parameters Rmin (the atomic distance at the potential minimum) and ε (the well depth) by linear interpolation of the values obtained for Fe2+ and Fe3+ in TIP3P water41 in ref. 42 and 43, respectively. Therefore, we assigned the values Rmin/2 = 1.3778 Å and ε = 0.0125 kcal mol−1 to each Fe ion in [Fe4S4]3+. A similar interpolation was used for the four Fe ions with formal charge +2.5e in [Fe4S4]2+, thus obtaining Rmin/2 = 1.3695 Å and ε = 0.0115 kcal mol−1 (all FF parameters are reported in the ESI†). We expect that our simple recipe to evaluate the LJ parameters is a very good approximation to describe non-bonded van der Waals interactions with surrounding water molecules, a reasonably good approximation for the description of the interactions with O and N atoms in the protein, and a reasonable approximation to describe the interactions with other atoms.
Tables S11 and S12† show that, for each oxidation state of the iron–sulfur cluster, the different spin-layer assignments lead to optimized structures of the parameterized model system that have similar energies. In fact, the energies of the six structures with an oxidized cluster differ by less than ∼4 kBT and the three structures with a reduced cluster differ by less than 1.5 kBT. These energy variations are much smaller than the energy fluctuations that the same model system can experience within the protein environment, as is easily appreciated even within the dielectric continuum model of the protein environment used to construct the FFs (see ESI Tables S11 and S12†). We therefore averaged the FF parameters without using Boltzmann weighting factors to obtain an “unbiased” FF to simulate the cluster dynamics in the macromolecular complex.
We also performed MD simulations of the macromolecular complex using the FF corresponding to one of the six spin-layer assignments (33+; see details in the next section). For this FF, we assigned the Fe3+ LJ parameters43 to two Fe ions, while the other two Fe ions were assigned Fe2.5+ LJ parameters by linear interpolation. The other FF parameters were averaged over homologous atoms in each Fe2S2 redox layer.
2.3 MD simulations
We performed MD simulations of the p58c–RNA/DNA complex using the NAMD 2.11 program,44 with the A3+, 33+ and A2+ FFs. 33+ is one of the six specific FFs produced for the oxidized cluster using the different spin-layer assignments (see ESI†). We selected this specific FF because it corresponds to the cluster geometry with the smallest deviation from the crystal structure of the cluster, with an RMSD of 0.258 Å. It is worth noting that a similar comparison with the crystal structure was not addressed for the three structures involved in the derivation of the A2+ FF because the crystal structure is expected to correspond to [Fe4S4]3+, since the aerobic sitting-drop vapor diffusion protocol was used and generated needle-like prisms over 2–4 days.7We used the ff14SB parameters (parm10) for all molecular components beyond the two model systems. In particular, we used the CYM parameters for the atomic charges, bonds and angles that involved atoms of the Cys ligands excluded from the models. The AMBER parameters for the N-terminal GTP of the DNA/RNA duplex were taken from ref. 45. Protein and duplex were parameterized as in AMBER FFs ff14SB40 and ff99-bsc0,46,47 respectively. The molecular complex was neutralized with Na+ ions and solvated with TIP3P water that extended 10 Å on each side of the system. The size of the unit cell was 66 × 88 × 74 Å3. The H–O and H–H distances in the water molecules were constrained using the SHAKE algorithm.48 Full calculation of the electrostatic interaction energy was performed every 2 time steps using the particle mesh Ewald summation method49 with a grid spacing of 1 Å and scaling factor of 0.833333 for the 1–4 interactions. Non-bonded atomic pairs within 14 Å were counted for the periodic interaction energy calculation, while van der Waals interactions were truncated at 12 Å.
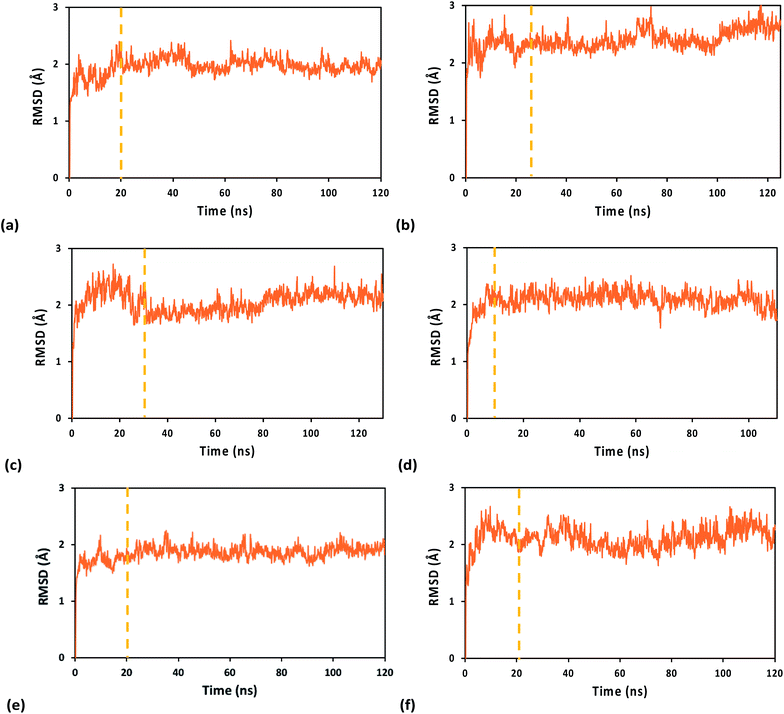
The system geometry was relaxed through 8 × 104 steps of energy minimization, followed by solvent equilibration (using a Langevin thermostat with damping coefficient of 1.0 ps−1) at 295 K (the crystallization temperature of the structure in PDB file 5F0Q) for 150 ps, with fixed protein–nucleic acid complex. Next, we carried out 75 ps of equilibration for the full system at 295 K and an additional 50 ps at 298 K, followed by equilibration at constant temperature (298 K) and pressure (1 atm) for 1.0 ns, using the Nosé–Hoover Langevin piston pressure control50,51 with a piston period of 100 fs, a damping coefficient of 2.0 ps−1 and a barostat damping time scale of 50 fs. During such equilibration, the backbone of the RNA/DNA duplex, the iron–sulfur cluster, and the sulfur atoms of the coordinated Cys residues were fixed. The constraints on these atoms were released in further 0.5 ns of NPT equilibration at the same temperature and pressure. The MD production runs for the systems with the WT protein and its Y345C mutant, containing either the oxidized or the reduced [Fe4S4] cluster, lasted between 110 and 130 ns, with a time step of 0.5 fs, in order to collect 100 ns of MD simulation with stable RMSD for each system (Fig. 2). This time window was used for the analysis of the nucleic acid-binding free energy and the charge transport pathways between the [Fe4S4] cluster and the duplex.
2.4 Protein–nucleic acid binding free energies
We used the MMPBSA.py program52,53 to calculate the protein–duplex binding free energies using the molecular mechanics with Poisson–Boltzmann and surface area solvation (MM/PBSA)54–56 method. We performed the PB calculations with the AMBER default atomic radii57 and we used the CPPTRAJ software58 to ensure that the input MD trajectories (which were sampled every 1 ns) were compatible with MMPBSA.py.2.5 Kinetic modeling
We focused our analysis on hole transport from an initially oxidized RNA/DNA duplex to an initially reduced [Fe4S4] cluster, using two models with a birth and death master equation59–61 (BDME) that differ in their boundary conditions (Fig. 3). The use of the two models aims to examine the robustness of the conclusions concerning the relative speed of charge transport through the WT and Y345C proteins irrespective of model approximations. We first analyzed hole transport from the elementary perspective of ref. 10, in which one electron charge travels from the cluster to the DNA through the protein (model 1). Then, considering the experiments in ref. 9 (which emphasize the role of the cluster oxidation in the protein binding to DNA and suggest that the electron–hole remains on [Fe4S4], unless cyclic voltammetry is used to reduce the cluster), we applied the standard BDME to describe the hole transport, with the cluster behaving as a hole absorber (model 2). The treatment of the cluster as an absorber is a good approximation based on previous calculations of the hole transfer rate constants using the crystal structure of the p58c–cluster interface.10 Consistently with this choice, and differently from the analysis of ref. 10 (in which the emphasis was primarily on the duplex-mediated inter-[Fe4S4] protein communication), we considered both forward and backward CT processes across the p58c–duplex interface (Fig. 3). The BDME of model 2 is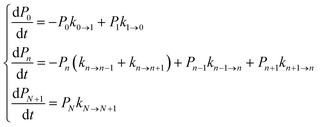 | (1) |
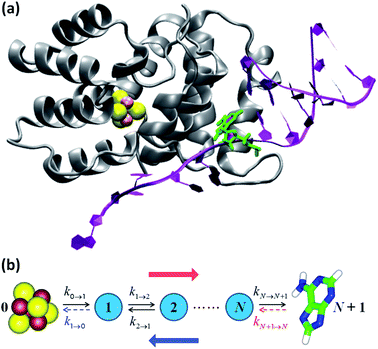 | ||
| Fig. 3 (a) p58c complexed with the DNA template/RNA primer (the coordinates were drawn from PDB file 5F0Q7). The DA7 nucleobase is highlighted in green. (b) Kinetic models. The hole transport (blue arrow) proceeds from DA7 to the [Fe4S4] cluster. Therefore, the electron charge moves in the opposite direction (red arrow). The rate constants refer to either electron transfer processes in the directions indicated by the black arrows or hole transfer steps in opposite directions. k1→0 is included in model 1, where kN+1→N is, instead, neglected or irrelevant.10 Model 2 directly describes the hole motion; hence, DA7 and the cluster become sites 0 and N + 1, respectively (not shown). This model includes both kN→N+1 and kN+1→N, while neglecting k1→0. | ||
Hole occupation probabilities are used, and there is no approximation made concerning the number of active particles in the model system, since a single hole is expected to transfer in the real system. Note that, in model 2, the hole moves from the nucleic acid duplex to the [Fe4S4] cluster, as in model 1 (or as in the model of ref. 10). The absence of a charge drain in this standard BDME model,61 compared to the model of ref. 10, does not affect the expression for the average time τ to transit the complex in terms of the rate constants for the individual CT steps.10,60,62 Therefore, the transit time can be written as10,62
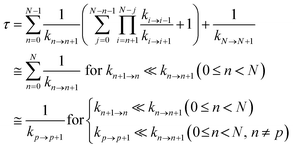 | (2) |
Ref. 62 shows that the conditions in the last line of eqn (2) are sufficient.
The analysis of ref. 10, and the evaluation through model 1 of the CT routes during the MD simulations, identify purine nucleobase DA7 (ref. 10) as the hole donor to be used in model 2. For both kinetic models, we used the EHPath.py code63 (setting the reorganization energy scaling parameter α to unity63) to find the fastest charge hopping pathways and to calculate the corresponding τ value in the MD snapshots of the WT and Y345C systems selected each ns over the time windows indicated in Fig. 2. Then, we averaged τ over the snapshots. Although the system structure relevant to a hopping route can change on the τ time scale, we assumed that the averaging approximatively accounts for the set of hopping paths that would emerge from longer MD simulations by updating the path search after each CT step.
The study of charge transport dynamics through the [Fe4S4] protein–duplex complex is challenging. The crystal structure used here7 is expected to correspond to an oxidized cluster and, more generally, experiments show that cluster oxidation leads to tighter protein binding to the duplex.9 These observations suggest that MD simulations should be carried out using a FF for the oxidized cluster. However, when electron–hole transport occurs, the cluster cannot start in the oxidized state. In fact, the hole can travel from an initially oxidized nucleic acid to a reduced cluster, but not from an initially oxidized cluster to neutral nucleic acid.10 This unidirectionality of CT suggests that the kinetic analysis should be performed on MD simulations for the complex with the reduced cluster. Ideally, the MD should be updated in terms of FFs as the hole proceeds from the duplex to the cluster, by transiently localizing on different sites in the macromolecular complex. More approximately, MD using A2+ should be more appropriate when the hole is closer to the nucleic acid, while MD using A3+, or 33+, would better describe the complex when the charge is on the cluster or is sufficiently close to it, especially since the use of these FF corresponds to the correct total charge in the molecular complex. To mitigate the dilemma of the FF choice, we note that charge transport is kinetically feasible if the protein is in a pose relative to the RNA/DNA duplex that enables the occurrence of the interfacial CT, even though the [Fe4S4] cluster is initially in a reduced state. Moreover, the protein and duplex should maintain a similar relative positioning over sufficiently short time scales preceding and following the hole transfer that oxidizes the [Fe4S4] cluster. This suggests that MD simulations using A3+ and A2+ might both be used to analyze the hole transport routes and should lead to similar results. Based on all of these arguments, and on the availability of a crystal structure in which the [Fe4S4] cluster is presumably oxidized,7 we analyzed the hole transport routes using both A2+ and A3+, 33+ MD simulations.
3 Results and discussion
3.1 FF performance, MD simulations, and binding free energy
Table 1 reports the average value and amplitude of fluctuation (as described by the standard deviation) of the RMSD for the WT and Y345C protein complex using the A3+, 33+ and A2+ FFs. While the mean RMSD value only depends on the transient evolution of the systems prior to final structural stabilization, the standard deviation of the RMSD provides a measure for the flexibility of each system. However, this is a global measure of flexibility that, in general, cannot distinguish structural fluctuations inherent in the chemical–physical properties of the system from unphysical effects related to the FF ability to maintain the system structural integrity and stability. The amplitude of structural fluctuations certainly is within the range typically found for biomolecular systems in all MD simulations of this study. Nonetheless, both A3+ and A2+ FFs, compared to 33+, produce a smoother transient evolution of the RMSD, as well as smaller equilibrium structural fluctuations, for the WT system (compare Fig. 2a and e with Fig. 2c). Furthermore, the RMSD of the [Fe4S4]3+ cluster, together with either the Cys ligand portions used in the derivation of the FFs or the full Cys ligands, shows a larger initial structural adjustment on a sub-nanosecond timescale when the 33+ FF, rather than A3+, is used (ESI Fig. S2†). Such RMSD difference can account for most of the difference in the average RMSD values for the full system listed in Table 1. The MD simulations using the A3+ FF, compared to the ones using the 33+ FF, lead to results more consistent with the expectation9 that the protein–duplex complex is more tightly bound when the [Fe4S4] cluster is oxidized. In particular, Table 2 shows that the MD using A3+ produces a smaller average distance between the cluster and the nucleic acid than the MD using A2+ (as expected due to the binding affinity dependence on the oxidation state of the cluster8,9), while 33+ fails to do so.| FF | WT protein complex | Y345C protein complex |
|---|---|---|
| A3+ | 2.00 ± 0.11 | 2.43 ± 0.16 |
| 33+ | 2.03 ± 0.17 | 2.11 ± 0.14 |
| A2+ | 1.88 ± 0.10 | 2.10 ± 0.18 |
| FF | WT protein complex | Y345C protein complex |
|---|---|---|
| A3+ | 19.2 ± 0.9 | 19.7 ± 0.4 |
| 33+ | 19.8 ± 0.3 | 20.1 ± 0.5 |
| A2+ | 19.7 ± 0.4 | 20.1 ± 0.8 |
The analysis above leads us to hypothesize that the A3+ FF performs slightly better than the 33+ FF. Yet, for the mutated system, the 33+ MD simulation produces slightly smaller RMSD fluctuations than the A3+ simulation. While the comparison between the two FFs merits further analysis, we can assert that A3+ describes the anchoring of [Fe4S4]3+ to the protein domain without the restraints that result from a specific redox layer pre-assignment, and this may be responsible for the results in ESI Fig. S2.† Consequently, we expect the transferability of the A3+ FF to iron–sulfur clusters in other proteins.
The MD trajectories using the A3+ and A2+ FFs produce RMSDs with similar fluctuations (quantified by their standard deviations). This observation suggests that the protein–DNA complexes with oxidized and reduced clusters may have similar structural properties over the 0.1 μs timescale that is sampled. This hypothesis is consistent with the fact that the protein and nucleic acid duplex need to achieve an optimal configuration to enable the charge transfer, and this configuration should mainly depend on the structural properties of the protein and duplex near the docking region, although the stability of the docked structure will depend, on a longer time scale, upon the cluster redox state.9
Both A3+ and A2+ produce a larger RMSD for the mutated protein–RNA/DNA complex than for the WT system. This outcome agrees with our estimate of the binding free energy difference of 1.7 kcal mol−1 (∼3 kBT) between the WT and Y345C systems using the MM/PBSA method. Using an average force constant of ∼100 kcal mol−1 Å−2 for the bonds and considering that the nuclear modes coupled to the duplex binding may involve between ∼10 atoms (size of an amino acid residue or of the iron–sulfur cluster) and ∼1000 atoms (order of magnitude of the total number of atoms in the complex), this binding free energy difference may be associated with an average excess atomic displacement on the 0.01 Å length scale. This agrees with the RMSD difference between WT and mutant systems shown in Table 1. Nevertheless, such differences in RMSD and in binding free energy are quite small, indicating accordingly small perturbations to the protein–nucleic acid complex by the mutation on the timescale studied. Our results agree with recent experiments9 that find mutations such as Y345C do not significantly influence the p58c binding to DNA.
Finally, we note that a FF for the [Fe4S4]2+ cluster is available in the literature.17 However, here we adopted a consistent strategy to obtain the FFs for both reduced and oxidized [Fe4S4] clusters, which enables an appropriate comparison between the corresponding complexes. Furthermore, we expect that the A2+ and A3+ FFs are both transferable to [Fe4S4] clusters of other proteins. The comparison of A2+ (as well as 32+) with the previously available FF for the reduced [Fe4S4] cluster17 shows comparable bond stretching force constants but larger angle bending force constants (assuming that the same units for the bending parameters are used in ref. 17), although the equilibrium values of the angles in the two FFs are comparable.
3.2 Charge transport in the [Fe4S4]–protein–nucleic acid complex
Table 3 and 4 show the results of our charge transport analysis for the WT and Y345 [Fe4S4] proteins in complex with the RNA/DNA duplex. The data in Table 3 were obtained using model 1, where the initially oxidized duplex acts as an electron trap. The proximity of an electrode and/or other surroundings may endow one of the purine nucleobases in the duplex with an electron trapping property. In this case, kN+1→N is zero, while the final occupation probability of site N + 1 is 1. Alternatively, the boundary conditions on the side of the nucleic acid might be better described by including a charge drain in the model (as in ref. 10), and thus assuming that the occupation probability of site N + 1 is always zero. We need not, indeed, make a choice between these two models, since they lead to the same results in terms of residence times62 and because the main focus of our analysis is the protein-mediated charge transport and its sensitivity to the Y345C mutation. Model 2 was used to compute the data in Table 4. In the hopping pathways of Tables 3 and 4, the [Fe4S4] cluster and the DA7 base (which are not shown) are, respectively, on the left and right of the reported sequences of amino acid residues.| FF | System | τ (μs) | Residues in route | % |
|---|---|---|---|---|
| A3+ | WT | 4.8 ± 2.4 | M307 | 37 |
| Y309-W327 | 28 | |||
| Y309-W327-M307 | 27 | |||
| Y309-M307 | 8 | |||
| Y345C | 7.1 ± 6.0 | M307 | 53 | |
| Y309-W327-M307 | 37 | |||
| Y309-M307 | 10 | |||
| 33+ | WT | 5.1 ± 2.6 | M307 | 52 |
| Y309-W327-M307 | 43 | |||
| Y309-M307 | 5 | |||
| Y345C | 9 ± 11 | M307 | 59 | |
| Y309-W327-M307 | 31 | |||
| Y309-M307 | 10 | |||
| A2+ | WT | 9.2 ± 7.0 | M307 | 91 |
| Y309-W327-M307 | 6 | |||
| Y309-M307 | 3 | |||
| Y345C | 5.1 ± 2.3 | Y309-W327-M307 | 60 | |
| M307 | 35 | |||
| Y309-M307 | 5 |
| FF | System | τ (μs) | Residues in route | % |
|---|---|---|---|---|
| A3+ | WT | 34 ± 47 | Y309-W327 | 95 |
| Y309-W327-Y345 | 4 | |||
| Direct | 1 | |||
| Y345C | 260 ± 190 | Y309-W327 | 71 | |
| Direct | 23 | |||
| Y309-W327-C345 | 6 | |||
| 33+ | WT | 72 ± 48 | Y309-W327 | 95 |
| Direct | 5 | |||
| Y345C | 210 ± 260 | Y309-W327 | 89 | |
| Direct | 9 | |||
| Y309-W327-C345 | 1 | |||
| Y309-W327-M307 | 1 | |||
| A2+ | WT | 200 ± 160 | Y309-W327 | 65 |
| Y309-W327-Y345 | 18 | |||
| Direct | 16 | |||
| Y309-W327-M307 | 1 | |||
| Y345C | 110 ± 160 | Y309-W327 | 90 | |
| Direct | 10 |
The predominant roles of the [Fe4S4]-M307-DA7 and [Fe4S4]-Y309-W327-M307-DA7 charge hopping paths in Table 3 confirm the findings of ref. 10 that were based on analysis of the complex crystal structure. The significance of these CT pathways is preserved by the Y345C mutation (Table 3). [Fe4S4]-Y309-M307-DA7 also contributes appreciably to the charge transport in both the WT and Y345C systems.
[Fe4S4]-Y309-W327-DA7 (where W327, rather than M307, is the amino acid residue engaged in CT to the DNA) is one of the predominant CT routes in the WT system when the A3+ FF is used to describe the [Fe4S4] cluster (Table 3). Y309, W327 and M307 are found to be the residues most responsible for charge transport in both the WT and Y345C systems, irrespective of the FF used for the cluster.
The MD simulations for the complex with the oxidized iron–sulfur cluster (which also give information about the structural fluctuations of the crystalized duplex–protein complex, since the latter is expected to contain an oxidized cluster) show that the W327-DA7 base pair experiences the largest distance change upon the Y345C mutation compared to all other redox pairs involved in the protein-mediated charge transport. In the A3+ simulations, the W327-DA7 distance increases by 1.56 Å upon mutation, while a more moderate increase of 0.52 Å results in the 33+ simulation. This structural change favors faster CT through the WT protein, as indicated by the data of Table 3, although other distances (ESI Tables S13 and S14†) influence the τ values.
In kinetic model 2 (Table 4), the rate constant for the hole transfer back to DA7 (namely, electron transfer back to the iron–sulfur protein), which is missing in model 1, changes the set of dominant hopping routes. In fact, the redox potential landscape shown in Fig. 2 of ref. 10 indicates that this backward CT step is energetically favorable when M307 and DA7 are involved, thus considerably increasing the charge propagation time in the forward direction. In contrast, the backward hole transfer from W327 to DA7 is energetically unfavorable, although it remains kinetically accessible. This behavior enhances the role of the W327 residue in the protein-mediated charge transport compared to the prediction of model 1. As a result, model 2 also predicts that Y345 or C345 participate in some of the fastest hopping routes. This amino acid residue plays a secondary role when the iron–sulfur cluster is oxidized (upper and central panels of Table 4), while its CT role seems to be more appreciable in the WT protein with a reduced cluster (bottom panel of Table 4).
The results of Tables 3 and 4 provide new insights into the controversial role of Y347 and Y345 in the protein-mediated electron transport to DNA.9,13–15 Y347 is not involved in any of the predominant CT routes, while Y345 is involved in some routes mediated by W327.
In the MD simulations with the [Fe4S4]3+ cluster, the average value of the travel time τ grows with protein mutation. That is, charge transport is faster through the WT protein. The opposite trend is seen for the simulations with the [Fe4S4]2+ cluster: the charge transport is faster through the mutant. Thus, based on the mean values of τ, we conclude that the Y345C mutation reduces the efficiency of the protein-mediated CT only if the system adopts poses that are typical of the tightly bound duplex–[Fe4S4]3+ protein complex. However, for each FF choice, the τ variation following the Y345C mutation is comparable to (or smaller than) the widths of the τ value distributions in the WT and mutated systems. Therefore, future investigations of the two systems over longer timescales (at least μs) would be useful to deepen the comparison between the two systems.
We also explored excess electron transfer from a negatively charged DA7 nucleobase to an oxidized [Fe4S4] cluster, using theoretical estimates of relevant reduction potentials drawn from previous studies.10,64 However, the direct electron transfer between DNA and the cluster was the fastest CT pathway in all A3+ MD snapshots of the WT system. The process occurs deeply in the Marcus inverted region, leading to an average value of τ around 2s. Overestimation of the reduction potentials may be responsible for this finding, but experimental measurements of the reduction potentials (and of the reorganization energies for excess electron transfer) are lacking. Therefore, the analysis of excess electron transfer was not pursued.
4 Conclusions
We have built FFs for oxidized and reduced [Fe4S4] clusters and used the FFs to conduct MD simulation of the [Fe4S4]-containing p58c domain of human primosome. In both cluster oxidation states, variations in the local potential produced by protein structure and environment fluctuations may determine switching of the redox layer partition (and therefore of the spin distribution) in the cluster. Our study indicates that averaging the FF parameters that correspond to different spin-layer assignments provides a practical strategy to produce a FF that (i) yields an appropriate description of the [Fe4S4] cluster during the biomolecular dynamics and (ii) is transferable to [Fe4S4] clusters in other proteins.The developed FFs, in combination with AMBER FFs for the macromolecular system, allowed study of molecular dynamics and functional charge transport in the native p58c–RNA/DNA duplex complex, as well as in a complex with a protein mutation relevant to research on gastric tumors.16 We found that the mutation has a weak effect on the p58c binding to the duplex, consistent with recent experiments.9 These experiments (which were criticized because of the use of a mutated I271S p58c protein and of biologically irrelevant DNA substrates13) are thus supported by our theoretical analysis, which uses the native protein7 and a biologically relevant7,13,14 RNA/DNA substrate.
Our study suggests that the reduced [Fe4S4] p58c and the RNA/DNA duplex may adopt poses that are similar to those typical of the oxidized complex on the CT timescale. This similarity would also account for the necessary hole transfer between cluster and duplex, and the related functional role of the [Fe4S4] redox switching,9 without being in contrast with the increase in p58c DNA-binding affinity upon [Fe4S4] cluster oxidation that would be observed over longer timescales.
Our analysis of hole transport through the WT and mutated protein systems based on 0.1 μs MD simulations does not reveal a clear difference in charge transport rates between the WT and mutated systems, but does show a clear change in the population of the fastest charge hopping routes in the protein ensemble upon mutation. However, based on the wide ranges of charge transit times in the native and mutant systems caused by structural fluctuations, the effect of the mutation on the protein charge transport might emerge from simulations on the 1 μs to 100 μs timescales. Our comprehensive theoretical-computational approach provides a toolbox for future investigation of the p58c–RNA/DNA system on these timescales and sets the stage for a deeper understanding of functional charge transport in nucleic acid–[Fe4S4] protein complexes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computations were performed, in part, with the Duke Compute Cluster. We acknowledge Dr Victor Anisimov for helpful discussion and the support of our research by the National Institutes of Health (Grant GM-48043) and the Blue Waters sustained-petascale computing project (R. D. T.), which is funded by the National Science Foundation (Awards OCI-0725070 and ACI-1238993) and the State of Illinois.Notes and references
- A. K. Boal, J. C. Genereux, P. A. Sontz, J. A. Gralnick, D. K. Newman and J. K. Barton, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15237–15242 CrossRef CAS PubMed.
- M. A. Grodick, H. M. Segal, T. J. Zwang and J. K. Barton, J. Am. Chem. Soc., 2014, 136, 6470–6478 CrossRef CAS PubMed.
- B. Roche, L. Aussel, B. Ezraty, P. Mandin, B. Py and F. Barras, Biochim. Biophys. Acta, Bioenerg., 2013, 1827, 455–469 CrossRef CAS PubMed.
- T. A. Rouault, Nat. Rev. Mol. Cell Biol., 2015, 16, 45–55 CrossRef CAS PubMed.
- J. O. Fuss, C.-L. Tsai, J. P. Ishida and J. A. Tainer, Biochim. Biophys. Acta, Mol. Cell Res., 2015, 1853, 1253–1271 CrossRef CAS PubMed.
- D. J. A. Netz, C. M. Stith, M. Stümpfig, G. Köpf, D. Vogel, H. M. Genau, J. L. Stodola, R. Lill, P. M. J. Burgers and A. J. Pierik, Nat. Chem. Biol., 2012, 8, 125–132 CrossRef CAS PubMed.
- A. G. Baranovskiy, N. D. Babayeva, Y. Zhang, J. Gu, Y. Suwa, Y. I. Pavlov and T. H. Tahirov, J. Biol. Chem., 2016, 291, 10006–10020 CrossRef CAS PubMed.
- E. C. M. Tse, T. J. Zwang and J. K. Barton, J. Am. Chem. Soc., 2017, 139, 12784–12792 CrossRef CAS PubMed.
- E. O'Brien, M. E. Holt, M. K. Thompson, L. E. Salay, A. C. Ehlinger, W. J. Chazin and J. K. Barton, Science, 2017, 355, eaag1789 CrossRef PubMed.
- R. D. Teo, B. J. G. Rousseau, E. R. Smithwick, R. Di Felice, D. N. Beratan and A. Migliore, Chem, 2019, 5, 122–137 CAS.
- J. K. Barton, R. M. B. Silva and E. O'Brien, Annu. Rev. Biochem., 2019, 88, 163–190 CrossRef CAS PubMed.
- A. G. Baranovskiy, H. M. Siebler, Y. I. Pavlov and T. H. Tahirov, Methods Enzymol., 2018, 599, 1–20 CAS.
- A. G. Baranovskiy, N. D. Babayeva, Y. Zhang, L. Blanco, Y. I. Pavlov and T. H. Tahirov, Science, 2017, 357, eaan2396 CrossRef PubMed.
- L. Pellegrini, Science, 2017, 357, eaan2954 CrossRef PubMed.
- E. O'Brien, M. E. Holt, M. K. Thompson, L. E. Salay, A. C. Ehlinger, W. J. Chazin and J. K. Barton, Science, 2017, 357, eaan2762 CrossRef PubMed.
- S. A. Forbes, N. Bindal, S. Bamford, C. Cole, C. Y. Kok, D. Beare, M. M. Jia, R. Shepherd, K. Leung, A. Menzies, J. W. Teague, P. J. Campbell, M. R. Stratton and P. A. Futreal, Nucleic Acids Res., 2011, 39, D945–D950 CrossRef CAS PubMed.
- A. T. P. Carvalho and M. Swart, J. Chem. Inf. Model., 2014, 54, 613–620 CrossRef CAS PubMed.
- Schrödinger Release 2018-1: Maestro, LLC, New York, NY, 2018.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- G. Hanson and L. Berliner, High resolution EPR: applications to metalloenzymes and metals in medicine, Springer Science & Business Media, 2009 Search PubMed.
- I. Bertini, F. Briganti, C. Luchinat, A. Scozzafava and M. Sola, J. Am. Chem. Soc., 1991, 113, 1237–1245 CrossRef CAS.
- S. G. Tabrizi, V. Pelmenschikov, L. Noodleman and M. Kaupp, J. Chem. Theory Comput., 2016, 12, 174–187 CrossRef CAS PubMed.
- I. Bertini, F. Capozzi, S. Ciurli, C. Luchinat, L. Messori and M. Piccioli, J. Am. Chem. Soc., 1992, 114, 3332–3340 CrossRef CAS.
- B. S. Perrin, S. Niu and T. Ichiye, J. Comput. Chem., 2013, 34, 576–582 CrossRef CAS PubMed.
- M.-L. Tan, B. S. Perrin, S. Niu, Q. Huang and T. Ichiye, Protein Sci., 2016, 25, 12–18 CrossRef CAS PubMed.
- X.-B. Wang, S. Niu, X. Yang, S. K. Ibrahim, C. J. Pickett, T. Ichiye and L.-S. Wang, J. Am. Chem. Soc., 2003, 125, 14072–14081 CrossRef CAS PubMed.
- S. Niu, X.-B. Wang, X. Yang, L.-S. Wang and T. Ichiye, J. Phys. Chem. A, 2004, 108, 6750–6757 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt, V. Jonas, T. Burger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- D. M. York and M. Karplus, J. Phys. Chem. A, 1999, 103, 11060–11079 CrossRef CAS.
- M. K. Gilson and B. Honig, Proteins, 1988, 4, 7–18 CrossRef CAS PubMed.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- S. Niu and T. Ichiye, J. Phys. Chem. A, 2009, 113, 5710–5717 CrossRef CAS PubMed.
- L. L. Tan, R. H. Holm and S. C. Lee, Polyhedron, 2013, 58, 206–217 CrossRef CAS PubMed.
- S. Zheng, Q. Tang, J. He, S. Du, S. Xu, C. Wang, Y. Xu and F. Lin, J. Chem. Inf. Model., 2016, 56, 811–818 CrossRef CAS PubMed.
- P. Li and K. M. Merz, J. Chem. Inf. Model., 2016, 56, 599–604 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- P. Li, B. P. Roberts, D. K. Chakravorty and K. M. Merz Jr, J. Chem. Theory Comput., 2013, 9, 2733–2748 CrossRef CAS PubMed.
- P. Li, L. F. Song and K. M. Merz, J. Phys. Chem. B, 2015, 119, 883–895 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- K. L. Meagher, L. T. Redman and H. A. Carlson, J. Comput. Chem., 2003, 24, 1016–1025 CrossRef CAS PubMed.
- J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- A. Pérez, I. Marchán, D. Svozil, J. Sponer, T. E. Cheatham, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829 CrossRef PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- S. E. Feller, Y. H. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621 CrossRef CAS.
- B. R. Miller, T. D. McGee, J. M. Swails, N. Homeyer, H. Gohlke and A. E. Roitberg, J. Chem. Theory Comput., 2012, 8, 3314–3321 CrossRef CAS PubMed.
- D. A. Case, T. A. Darden, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, R. C. Walker, W. Zhang, K. M. Merz, B. Roberts, S. Hayik, A. Roitberg, G. Seabra, J. Swails, A. W. Götz, I. Kolossváry, K. F. Wong, F. Paesani, J. Vanicek, R. M. Wolf, J. Liu, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, Q. Cai, X. Ye, J. Wang, M.-J. Hsieh, G. Cui, D. R. Roe, D. H. Mathews, M. G. Seetin, R. Salomon-Ferrer, C. Sagui, V. Babin, T. Luchko, S. Gusarov, A. Kovalenko and P. A. Kollman, AMBER 12, University of California, San Francisco, 2012 Search PubMed.
- J. Srinivasan, T. E. Cheatham, P. Cieplak, P. A. Kollman and D. A. Case, J. Am. Chem. Soc., 1998, 120, 9401–9409 CrossRef CAS.
- P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. H. Huo, L. Chong, M. Lee, T. Lee, Y. Duan, W. Wang, O. Donini, P. Cieplak, J. Srinivasan, D. A. Case and T. E. Cheatham, Acc. Chem. Res., 2000, 33, 889–897 CrossRef CAS PubMed.
- S. Genheden and U. Ryde, Expert Opin. Drug Discovery, 2015, 10, 449–461 CrossRef CAS PubMed.
- C. Wang, P. H. Nguyen, K. Pham, D. Huynh, T.-B. N. Le, H. Wang, P. Ren and R. Luo, J. Comput. Chem., 2016, 37, 2436–2446 CrossRef CAS PubMed.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- I. Oppenheim, K. E. Shuler and G. H. Weiss, Physica A, 1977, 88, 191–214 CrossRef.
- I. Procaccia, S. Mukamel and J. Ross, J. Chem. Phys., 1978, 68, 3244–3253 CrossRef CAS.
- A. Bar-Haim and J. Klafter, J. Chem. Phys., 1998, 109, 5187–5193 CrossRef CAS.
- R. D. Teo, E. R. Smithwick and A. Migliore, Phys. Chem. Chem. Phys., 2019, 21, 22869–22878 RSC.
- R. D. Teo, R. Wang, E. R. Smithwick, A. Migliore, M. Therien and D. N. Beratan, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 15811–15816 CrossRef CAS PubMed.
- C. E. Crespo-Hernández, D. M. Close, L. Gorb and J. Leszczynski, J. Phys. Chem. B, 2007, 111, 5386–5395 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02245d |
| This journal is © The Royal Society of Chemistry 2020 |