Open Access Article
Open Access ArticleEfficient and selective alkene hydrosilation promoted by weak, double Si–H activation at an iron center†
Patrick W.
Smith‡
 ,
Yuyang
Dong§
,
Yuyang
Dong§
 and
T. Don
Tilley
and
T. Don
Tilley
 *
*
Department of Chemistry, University of California, Berkeley, Berkeley, California 94720-1460, USA. E-mail: tdtilley@berkeley.edu
First published on 18th June 2020
Abstract
Cationic iron complexes [Cp*(iPr2MeP)FeH2SiHR]+, generated and characterized in solution, are very efficient catalysts for the hydrosilation of terminal alkenes and internal alkynes by primary silanes at low catalyst loading (0.1 mol%) and ambient temperature. These reactions yield only the corresponding secondary silane product, even with SiH4 as the substrate. Mechanistic experiments and DFT calculations indicate that the high rate of hydrosilation is associated with an inherently low barrier for dissociative silane exchange (product release).
Introduction
Olefin hydrosilation is one of the most commercially important reactions, used to produce various silicon-containing materials and fine chemicals.1,2 As practiced, this reaction mainly employs Pt-based catalysts3,4 which, given the limited supply and high demand for platinum, creates a strong motivation for development of alternative catalysts based on more earth-abundant metals such as Fe, Co, and Ni.5–22 There are profound differences between the chemical properties of Pt and those of the base metals; most notably the lighter 3d metals have a higher propensity for one-electron reaction steps, which may preclude the oxidative addition/reductive elimination cycles associated with noble metal catalysis. For this reason, the search for base metal hydrosilation catalysts must include discovery of alternative mechanistic pathways suitable for the 3d metals.23Previous work in this laboratory identified a new mechanism for hydrosilation24,25 associated with cationic silylene complexes of Ru24,26 and Ir.27 Unique to this mechanism is the Si–C bond forming step, in which a Si–H bond in a silylene ligand directly adds across the olefin.2,28 This process is attractive for the design of new hydrosilation catalysts based on 3d metals such as iron, as this critical bond formation does not rely on a metal-centered redox process. Hydrosilation reactions catalyzed by cationic silylene complexes form secondary silane products with linear regioselectivity for the Si–H addition. This selectivity represents an advantage over the more conventional Chalk–Harrod mechanism, which can result in a mixture of linear and branched products due to its reliance on reversible olefin insertion into a metal hydride.
Another aspect of a silylene-based mechanism is the double Si–H bond activation that occurs at the metal center.25,30 Double Si–H activations of this type occur to varying degrees, from moderate activation to give η3-silane complexes (A, Scheme 1),30–32 to more strongly activated cases that have undergone a double oxidative addition to form a silylene dihydride (B, C).26,33–35 Structures along this continuum exhibit high electrophilicity at silicon and greater reactivity for the terminal Si–H bond.
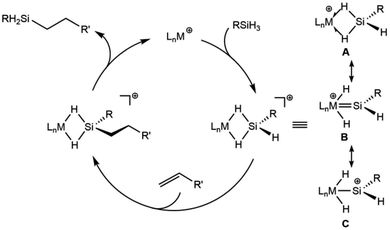 | ||
| Scheme 1 Representation of the cationic silylene mechanism for hydrosilation with three selected resonance structures for the cationic complexes. | ||
Since the silylene-based mechanism is well established for ruthenium complexes of the type [Cp*(iPr3P)Ru(H)2SiHR]+, catalytic transformations with analogous iron complexes could provide increased activity due to the enhanced lability of metal–ligand bonds in 3d complexes. This report describes the utility of Cp*(iPr2MeP)FeH(N2)36 (1) as a precatalyst for alkene hydrosilation via generation of a cationic iron intermediate. This Fe system is associated with higher rates of conversion for many substrates, and a marked selectivity toward terminal olefins that underscores fundamental mechanistic differences with the related Ru catalyst.
Results and discussion
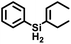
Precursors to the catalytic species of interest are neutral iron complexes of the type Cp*(iPr2MeP)Fe(H)2SiH2R. Compound 1 reacts with primary silanes (RSiH3, R = Trip,37 Ph, p-Tol, Mes; Trip = 2,4,6-triisopropylphenyl) by oxidative addition of an Si–H bond to form the corresponding dihydrides Cp*(iPr2MeP)Fe(H)2SiH2R (2R, eqn (1)). Note that related half-sandwich complexes have been reported previously.36,38,39 These silyl dihydride complexes do not promote hydrosilations up to 80 °C, but they are converted to active cationic catalysts by hydride abstraction.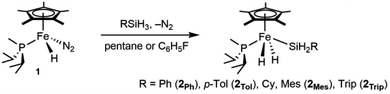 | (1) |
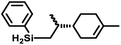
The cationic complex [Cp*(iPr2MeP)FeH2SiHPh][BArF4] (3Ph; BArF4 = tetrakis(pentafluorophenyl)borate) was generated by treatment of 1 with 1000 equiv. of PhSiH3 followed by 1 equiv. [Ph3C][BArF4] in fluorobenzene at −35 °C. After warming to ambient temperature, treatment with 1100 equiv. of 1-octene resulted in quantitative conversion of the silane substrate over 6 h to the linear product Ph(nOct)SiH2 (eqn (2)), corresponding to a turnover frequency (TOF) of at least 170 h−1. This selectivity toward primary silanes is reminiscent of the cationic Ru silylene hydrosilation catalyst, but other selectivities (vide infra) suggest that there are fundamental differences in the mechanistic pathways.24,26,28,29 For this reaction the iron catalyst is more active, as the ruthenium catalyst required a higher loading (1 mol%) and elevated temperature (80 °C) to achieve a comparable conversion.26 This activity is in the range of the most active iron catalysts for the hydrosilation of olefins by primary silanes (Table S1†).22,40–43
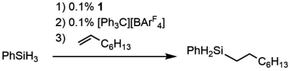 | (2) |
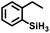
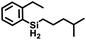
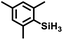
Aryl- and alkyl-substituted primary silanes are suitable substrates for this catalysis (Table 1), but steric factors play an important role. While (o-ethylphenyl)silane is a competent substrate, hydrosilation of 4-methylpentene with mesitylsilane did not proceed even at 80 °C. No hydrosilation products were observed with secondary or tertiary silanes (e.g. PhMeSiH2 and Et3SiH) up to 1 mol% catalyst loading over 20 h at ambient temperature. Unlike the Ru silylenes, the Fe catalysts are highly selective toward hydrosilation of terminal olefins (Table 2). This difference in substrate tolerance may arise from the size difference between ruthenium and iron, resulting in greater steric demands from the Fe ancillary ligands in the hydrosilation transition state, and is most dramatically illustrated by the hydrosilation of limonene (entry k) which resulted in complete selectivity for the terminal double bond.
The iron catalysts selectively give cis-hydrosilation of internal alkyne substrates (entries l and m; Table 2, by 1H NMR spectroscopy), which is consistent with direct Si–H addition. No conversion was observed for diphenylacetylene (entry n), presumably due to steric factors, and further evidence that catalyst selectivity is driven by steric factors is seen with propynyltrimethylsilane as substrate, to predominantly form 2-phenylsilyl-1-trimethylsilylpropene (∼90% selectivity). The intolerance for the terminal acetylenic substrate (entry o) is most likely due to side reactions with the acetylenic C–H bond.
The selectivity of this catalyst system suggested the use of SiH4 to form secondary silanes (eqn (3)). For this reaction, the catalyst was generated by reaction of 2Mes with [Ph3C][BArF4] in fluorobenzene, which was then treated with 400 equiv. of 4-methylpentene and exposed to 1 atm of 15% silane in nitrogen. While the yield of (4-Me-pentyl)2SiH2 was only 2.6% after 18 h (based on olefin; TON = 52), the reaction is highly selective in that only the secondary silane was observed as product (by 1H NMR spectroscopy and TLC). The low yield is attributed to the low concentration of SiH4; higher pressures of silane and longer reaction times would likely give greater turnover.
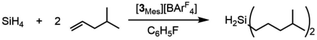 | (3) |
Attempts to isolate the activated catalysts as crystalline solids were not successful; in all cases, crystallization attempts produced impure oils, prompting characterization in situ by NMR spectroscopy. Complex 2Tol was treated with 1 equiv. of [Ph3C][BArF4] at −35 °C in fluorobenzene in an attempt to generate [Cp*(iPr2MeP)FeH2SiH(p-Tol)]+ (3Tol, eqn (4)), which resulted in a color change to blue. Integration against a C6Me6 internal standard indicated that 3Tol was formed in >99% yield. The 1H NMR spectrum at room temperature did not contain obvious Fe–H–Si or Si–H resonances, suggesting the possibility of exchange between such positions. Upon cooling a solution of 3Tol in fluorobenzene-d5 to −30 °C, Fe–H (−15.12 ppm, JHP = 20.9 Hz, JSi(μ-H) = 90 Hz) and Si–H (6.74 ppm, JSiH = 180 Hz) resonances were observed. These resonances display cross peaks to a downfield 29Si resonance at 188 ppm in the HMBC spectrum (JSi(μ-H) 90 Hz).
 | (4) |
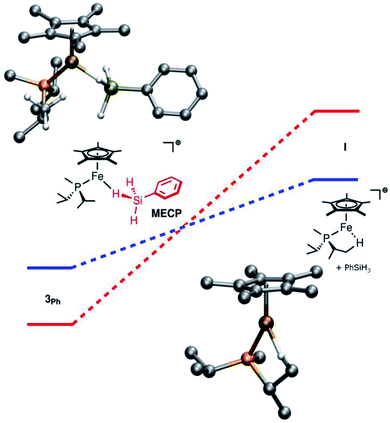
Computations on the structure of 3Ph were found to be highly dependent upon the choice of functional, particularly with respect to the extent of Si–H activation at the Fe center. The experimentally determined structure of the related Ru complex, [Cp*(iPr3P)Ru(H)2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si(H)Mes]+, was used to calibrate the choice of functional, and the range-separated-hybrid functional ωB97X-D3 was found to be in best agreement with this structure. For the Fe complex, calculations at the ωB97X-D3/def2-TZVP/SVP level of theory are consistent with the interpretation that Si–H activation at Fe is modest. The geometry of the molecule resembles an η3-silane structure (Fig. 1), with the hydrides symmetrically bridging the Fe and Si atoms and minimal Si–H activation relative to free silane (dFeSi = 2.20 Å; FSR = 0.95). The Si–H(bridge) distances are slightly longer than the terminal Si–H distance (1.59 vs. 1.47 Å) and the Fe–H distances average to 1.68 Å (FSR = 1.14). The FeH2Si unit is planar (Σ∠ = 358°). In contrast, [Cp*(iPr2MeP)RuH2SiHPh]+ (3RuPh) is computed to have proceeded significantly further along the double Si–H activation continuum, and toward a structure that may be regarded as a silylene dihydride. To wit, 3RuPh is computed to possess an extremely short Ru–Si distance (2.25 Å; FSR = 0.93), Si–H(bridge) distances which are elongated relative to those in 3Ph (1.67 Å), and short Ru–H interactions (1.75 Å; FSR = 1.11).
Si(H)Mes]+, was used to calibrate the choice of functional, and the range-separated-hybrid functional ωB97X-D3 was found to be in best agreement with this structure. For the Fe complex, calculations at the ωB97X-D3/def2-TZVP/SVP level of theory are consistent with the interpretation that Si–H activation at Fe is modest. The geometry of the molecule resembles an η3-silane structure (Fig. 1), with the hydrides symmetrically bridging the Fe and Si atoms and minimal Si–H activation relative to free silane (dFeSi = 2.20 Å; FSR = 0.95). The Si–H(bridge) distances are slightly longer than the terminal Si–H distance (1.59 vs. 1.47 Å) and the Fe–H distances average to 1.68 Å (FSR = 1.14). The FeH2Si unit is planar (Σ∠ = 358°). In contrast, [Cp*(iPr2MeP)RuH2SiHPh]+ (3RuPh) is computed to have proceeded significantly further along the double Si–H activation continuum, and toward a structure that may be regarded as a silylene dihydride. To wit, 3RuPh is computed to possess an extremely short Ru–Si distance (2.25 Å; FSR = 0.93), Si–H(bridge) distances which are elongated relative to those in 3Ph (1.67 Å), and short Ru–H interactions (1.75 Å; FSR = 1.11).
 | ||
| Fig. 1 Computed energy profile for addition of propylene to 3Ph (blue) or 3RuPh (red). Bottom left: computed structure of 3Ph. Top right: computed structure of TSFe. | ||
The selectivity of the Fe catalysts with respect to the olefin substrates prompted an investigation into the hydrosilation mechanism. For [Cp*(iPr3P)RuH2SiHR]+, the rate-limiting step in catalysis is the dissociative exchange of the product silane with silane substrate.26 For the corresponding osmium complexes, catalytic activity was not observed, even though stoichiometric Si–H addition to olefins proceeds rapidly.24,44 This suggests that dissociative silane exchange is even less favorable for Os. In light of this trend toward lower barriers to silane exchange from Os to Ru, a reasonable hypothesis is that the barrier to silane exchange for Fe is even lower, to the extent that the rate of direct Si–H addition to the olefin may become competitive. This would explain both the increased activity of the Fe catalysts for unhindered substrates and the sterically-based selectivity for terminal olefins.
This hypothesis is supported by computational investigations of the catalytic cycle using geometries calculated at the ωB97X-D3/def2-TZVP/SVP level of theory, with single point energies corrected at the DLPNO-CCSD(T)/def2-TZVP level of theory. The computed energy profile for the olefin addition (Fig. 1) indicates that the transition state for Si–H addition to the olefin (TS) is at a higher energy than that for the Ru system (ΔG‡ = 19.1 kcal mol−1 for Fe vs. 11.7 kcal mol−1 for Ru; previous computations indicated a 8–15 kcal mol−1 barrier for Ru).28,29 Importantly, this barrier height is comparable to that of silane exchange (vide infra), and a consequence is that the rate-determining step for catalysis is substrate dependent. Thus, in at least some cases the Si–H addition is slow enough (e.g., due to steric factors) to render this step rate-determining. This substrate-dependent reactivity could explain the novel selectivity of this Fe system.
Notably, while the 3Ph ground state involves bridging Fe–H–Si interactions, the Si–H interactions are considerably weaker in transition state TSFe, manifested in elongation of the Si–HFe interactions from 1.59 to 1.89 Å, and shortening of the Fe–H (from 1.68 to 1.52 Å; ΔFSR = −0.11) and Fe–Si (from 2.20 to 2.15 Å; ΔFSR = −0.02) distances, consistent with generation of an electrophilic silylene in this transition state by a “double α-migration”.45
A dissociative mechanism for silane exchange is supported by VT NMR spectroscopy. The complex [Cp*(iPr2MeP)FeH2SiH(p-Tol)][BArF4] (3Tol) was generated in fluorobenzene solution in the presence of 1 equiv. of p-tolylsilane, and the tolyl CH3 and silane SiH31H NMR resonances were monitored from 246 to 330 K. Above 290 K, the resonances attributed to free and bound p-TolSiH3 broaden and coalesce, consistent with chemical exchange between the two species. Rate constants for the exchange between p-tolylsilane and 3Tol were determined based on lineshape analyses of the p-CH3 resonances; an Eyring plot gave the activation parameters ΔH‡ = 27.0(4) kcal mol−1 and ΔS‡ = 34(1) cal mol−1 K−1 ( at 298 K; see ESI†). These activation parameters are consistent with a dissociative exchange mechanism similar to that proposed for the Ru silylene system (ΔH‡ = 32(2) kcal mol−1 and ΔS‡ = 19(1) cal mol−1 K−1,
at 298 K; see ESI†). These activation parameters are consistent with a dissociative exchange mechanism similar to that proposed for the Ru silylene system (ΔH‡ = 32(2) kcal mol−1 and ΔS‡ = 19(1) cal mol−1 K−1,  ). The somewhat lower enthalpy of activation for Fe likely reflects the weaker bonding of the η3-H3SiR ligand to the metal, and the lower activation of the Si–H bonds in the Fe system relative to Ru.
). The somewhat lower enthalpy of activation for Fe likely reflects the weaker bonding of the η3-H3SiR ligand to the metal, and the lower activation of the Si–H bonds in the Fe system relative to Ru.
Computationally, the dissociative mechanism for silane exchange involving the coordinatively unsaturated intermediate Cp*(iPr2MeP)Fe+ (I, Fig. 2) is reasonable. This structure includes an agostic interaction with one of the phosphine iPr substituents, as evidenced by a close contact with a C-bound H atom (dFeH = 1.943 Å). Additionally, the triplet state for I is lower in energy than the singlet state by 12.5 kcal mol−1 suggesting a two-state mechanism for dissociative silane exchange at Fe in this system. In the triplet structure, the Fe–H distance in the agostic interaction is shorter (dFeH = 1.893 Å). Notably, this situation is not observed computationally for [Cp*(iPr2MeP)Ru]+, for which the triplet state is higher in energy than the singlet state by 18.1 kcal mol−1. A minimum energy crossing point (MECP) was found along the reaction coordinate for silane dissociation from 3Ph. Note that the MECP computed using the ωB97X-D3 functional most likely does not reproduce either the energy or geometry of the MECP well, as this functional overstabilizes triplet states in both the present and related systems.37 Thus, using the B3LYP functional (for which the singlet-triplet gap of I agrees much better with DLPNO-CCSD(T)) the MECP is found to be 4.6 kcal mol−1 above 3Ph, and still lower in energy than the fully dissociated triplet species. In this structure, the Fe–Si bond has lengthened by ca. 0.2 Å, and one of the iPr-Me groups from the phosphine has approached the Fe center.
While we were unable to fully optimize a transition state structure for silane dissociation, nudged elastic band (NEB) calculations of the silane dissociation coordinate indicate a very late transition state for the triplet state of I (Table S4†). Thus, the energetics of this intermediate can be used as a proxy for activation energies for silane dissociation; these energies are summarized in Table S3.† For dissociation to the triplet state of I, ΔH = 22.7 kcal mol−1 and ΔS is extremely positive (52.7 cal mol K−1). However, since the true transition state for dissociation likely involves a closely-associated silane⋯I pair, all the translational and rotational entropy from dissociation will not have manifested in the Eyring analysis. Additionally, MECPs prior to the transition state can result in inefficient spin crossover, which should lead to a decrease in the rate relative to that of an analogous one-state process. These factors would result in a less positive experimental ΔS‡ in an Eyring analysis.
Conclusions
The cationic Fe catalysts described here are highly active in the hydrosilation of unhindered olefins with primary silanes. This discovery provides the foundation for new catalyst design strategies involving the first-row transition metals. Importantly, the mechanistic pathway for these catalysts is non-oxidative in character, in that distinct oxidative additions are not required. The observed rate accelerations and enhanced selectivities relative to a related Ru system highlight the distinctly different catalysis that is possible for the 3d metals. In this case, mechanistic studies suggest that the promising characteristics of the iron catalysts relate to a modest degree of Si–H bond activation in the silane substrate, and therefore weaker metal–silane binding and a faster dissociative exchange of the product silane for the silane substrate. The lower cost and greater sustainability of Fe makes the present system highly attractive for the synthesis of unsymmetrical secondary silanes, and multiply-substituted silicon centers derived therefrom.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the US National Science Foundation under grant no. CHE-1566538 and CHE-1954808. The UC Berkeley Molecular Graphics and Computation Facility is supported by the National Institutes of Health under grant no. S10-OD023532. We thank Boulder Scientific Co. for a generous donation of chemicals.Notes and references
- B. Marciniec, Catalysis of Hydrosilylation of Carbon-Carbon Multiple Bonds: Recent Progress, Silicon Chem., 2003, 1, 155–175 CrossRef.
- M. A. Brook, Silicon in Organic, Organometallic, and Polymer Chemistry, A Wiley-Interscience Publication, Wiley, 2000 Search PubMed.
- L. N. Lewis, J. Stein, Y. Gao, R. E. Colborn and G. Hutchins, Platinum Catalysts Used in the Silicone Industry, Platinum Met. Rev., 1997, 41, 66–75 CAS.
- A. J. Holwell, Global Release Liner Industry Conference 2008, Platinum Met. Rev., 2008, 52, 243–246 CrossRef.
- X. Du and Z. Huang, Advances in Base-Metal-Catalyzed Alkene Hydrosilylation, ACS Catal., 2017, 7, 1227–1243 CrossRef CAS.
- M. D. Greenhalgh, A. S. Jones and S. P. Thomas, Iron-Catalysed Hydrofunctionalisation of Alkenes and Alkynes, ChemCatChem, 2015, 7, 190–222 CrossRef CAS.
- J. Y. Wu, B. N. Stanzl and T. A. Ritter, Strategy for the Synthesis of Well-Defined Iron Catalysts and Application to Regioselective Diene Hydrosilylation, J. Am. Chem. Soc., 2010, 132, 13214–13216 CrossRef CAS PubMed.
- A. M. Tondreau, C. C. H. Atienza, K. J. Weller, S. A. Nye, K. M. Lewis, J. G. P. Delis and P. J. Chirik, Iron Catalysts for Selective Anti-Markovnikov Alkene Hydrosilylation Using Tertiary Silanes, Science, 2012, 335, 567–571 CrossRef CAS PubMed.
- K. Kamata, A. Suzuki, Y. Nakai and H. Nakazawa, Catalytic Hydrosilylation of Alkenes by Iron Complexes Containing Terpyridine Derivatives as Ancillary Ligands, Organometallics, 2012, 31, 3825–3828 CrossRef CAS.
- A. M. Tondreau, C. C. H. Atienza, J. M. Darmon, C. Milsmann, H. M. Hoyt, K. J. Weller, S. A. Nye, K. M. Lewis, J. Boyer, J. G. P. Delis, E. Lobkovsky and P. J. Chirik, Synthesis, Electronic Structure, and Alkene Hydrosilylation Activity of Terpyridine and Bis(Imino)Pyridine Iron Dialkyl Complexes, Organometallics, 2012, 31, 4886–4893 CrossRef CAS.
- M. D. Greenhalgh, D. J. Frank and S. P. Thomas, Iron-Catalysed Chemo-, Regio-, and Stereoselective Hydrosilylation of Alkenes and Alkynes Using a Bench-Stable Iron(II) Pre-Catalyst, Adv. Synth. Catal., 2014, 356, 584–590 CrossRef CAS.
- M.-Y. Hu, Q. He, S.-J. Fan, Z.-C. Wang, L.-Y. Liu, Y.-J. Mu, Q. Peng and S.-F. Zhu, Ligands with 1,10-Phenanthroline Scaffold for Highly Regioselective Iron-Catalyzed Alkene Hydrosilylation, Nat. Commun., 2018, 9, 221 CrossRef PubMed.
- J. Sun and L. Deng, Cobalt Complex-Catalyzed Hydrosilylation of Alkenes and Alkynes, ACS Catal., 2016, 6, 290–300 CrossRef CAS.
- B. Cheng, P. Lu, H. Zhang, X. Cheng and Z. Lu, Highly Enantioselective Cobalt-Catalyzed Hydrosilylation of Alkenes, J. Am. Chem. Soc., 2017, 139, 9439–9442 CrossRef CAS PubMed.
- C. Wang, W. J. Teo and S. Ge, Cobalt-Catalyzed Regiodivergent Hydrosilylation of Vinylarenes and Aliphatic Alkenes: Ligand- and Silane-Dependent Regioselectivities, ACS Catal., 2017, 7, 855–863 CrossRef CAS.
- X. Du, W. Hou, Y. Zhang and Z. Huang, Pincer Cobalt Complex-Catalyzed Z-Selective Hydrosilylation of Terminal Alkynes, Org. Chem. Front., 2017, 4, 1517–1521 RSC.
- I. Buslov, J. Becouse, S. Mazza, M. Montandon-Clerc and X. Hu, Chemoselective Alkene Hydrosilylation Catalyzed by Nickel Pincer Complexes, Angew. Chem., Int. Ed., 2015, 54, 14523–14526 CrossRef CAS PubMed.
- M. I. Lipschutz and T. D. Tilley, Synthesis and Reactivity of a Conveniently Prepared Two-Coordinate Bis(Amido) Nickel(II) Complex, Chem. Commun., 2012, 48, 7146–7148 RSC.
- I. Buslov, F. Song and X. Hu, An Easily Accessed Nickel Nanoparticle Catalyst for Alkene Hydrosilylation with Tertiary Silanes, Angew. Chem., Int. Ed., 2016, 55, 12295–12299 CrossRef CAS PubMed.
- Y. Nakajima, K. Sato and S. Shimada, Development of Nickel Hydrosilylation Catalysts, Chem. Rec., 2016, 16, 2379–2387 CrossRef CAS PubMed.
- I. Pappas, S. Treacy and P. J. Chirik, Alkene Hydrosilylation Using Tertiary Silanes with α-Diimine Nickel Catalysts. Redox-Active Ligands Promote a Distinct Mechanistic Pathway from Platinum Catalysts, ACS Catal., 2016, 6, 4105–4109 CrossRef CAS.
- Chirik's (iPrPDI)Fe(N2)2 catalyst shows slightly higher activities (TOF for 1-hexene: 364 mol h−1), but lower selectivity for terminal olefins. See: S. C. Bart, E. Lobkovsky and P. J. Chirik, Preparation and Molecular and Electronic Structures of Iron(0) Dinitrogen and Silane Complexes and Their Application to Catalytic Hydrogenation and Hydrosilation, J. Am. Chem. Soc., 2004, 126, 13794–13807 CrossRef CAS PubMed.
- H. A. Brunner, New Hydrosilylation Mechanism - New Preparative Opportunities, Angew. Chem., Int. Ed., 2004, 43, 2749–2750 CrossRef CAS PubMed.
- P. B. Glaser and T. D. Tilley, Catalytic Hydrosilylation of Alkenes by a Ruthenium Silylene Complex. Evidence for a New Hydrosilylation Mechanism, J. Am. Chem. Soc., 2003, 125, 13640–13641 CrossRef CAS PubMed.
- R. Waterman, P. G. Hayes and T. D. Tilley, Synthetic Development and Chemical Reactivity of Transition-Metal Silylene Complexes, Acc. Chem. Res., 2007, 40, 712–719 CrossRef CAS PubMed.
- M. E. Fasulo, M. C. Lipke and T. D. Tilley, Structural and Mechanistic Investigation of a Cationic Hydrogen-Substituted Ruthenium Silylene Catalyst for Alkene Hydrosilation, Chem. Sci., 2013, 4, 3882–3887 RSC.
- E. Calimano and T. D. Tilley, Synthesis and Structure of PNP-Supported Iridium Silyl and Silylene Complexes: Catalytic Hydrosilation of Alkenes, J. Am. Chem. Soc., 2009, 131, 11161–11173 CrossRef CAS PubMed.
- C. Beddie and M. B. Hall, A Theoretical Investigation of Ruthenium-Catalyzed Alkene Hydrosilation: Evidence to Support an Exciting New Mechanistic Proposal, J. Am. Chem. Soc., 2004, 126, 13564–13565 CrossRef CAS PubMed.
- C. Beddie, M. B. Hall and M. B. Do, B3LYP and CCSD(T) Predict Different Hydrosilylation Mechanisms? Influences of Theoretical Methods and Basis Sets on Relative Energies in Ruthenium-Silylene-Catalyzed Ethylene Hydrosilylation, J. Phys. Chem. A, 2006, 110, 1416–1425 CrossRef CAS PubMed.
- M. C. Lipke, A. L. Liberman-Martin and T. D. Tilley, Electrophilic Activation of Silicon-Hydrogen Bonds in Catalytic Hydrosilations, Angew. Chem., Int. Ed., 2017, 56, 2260–2294 CrossRef CAS PubMed.
- M. C. Lipke and T. D. Tilley, Hypercoordinate Ketone Adducts of Electrophilic η3-H2SiRR′ Ligands on Ruthenium as Key Intermediates for Efficient and Robust Catalytic Hydrosilation, J. Am. Chem. Soc., 2014, 136, 16387–16398 CrossRef CAS PubMed.
- M. C. Lipke and T. D. Tilley, High Electrophilicity at Silicon in η3-Silane σ-Complexes: Lewis Base Adducts of a Silane Ligand, Featuring Octahedral Silicon and Three Ru-H-Si Interactions, J. Am. Chem. Soc., 2011, 133, 16374–16377 CrossRef CAS PubMed.
- B. V. Mork and T. D. Tilley, Synthons for Coordinatively Unsaturated Complexes of Tungsten, and Their Use for the Synthesis of High Oxidation-State Silylene Complexes, J. Am. Chem. Soc., 2004, 126, 4375–4385 CrossRef CAS PubMed.
- P. B. Glaser and T. D. Tilley, Synthesis and Reactivity of Silyl and Silylene Ligands in the Coordination Sphere of the 14-Electron Fragment Cp*(iPr3P)Os+, Organometallics, 2004, 23, 5799–5812 CrossRef CAS.
- M. E. Fasulo, P. B. Glaser and T. D. Tilley, Cp*(PiPr3)RuOTf: A Reagent for Access to Ruthenium Silylene Complexes, Organometallics, 2011, 30, 5524–5531 CrossRef CAS.
- P. W. Smith and T. D. Tilley, Silane-Allyl Coupling Reactions of Cp*(iPr2MeP)Fe(η3-allyl)} and Synthetic Access to the Hydrido-Dinitrogen Complex Cp*(iPr2MeP)FeH(N2), Organometallics, 2015, 34, 2134–2138 CrossRef CAS.
- P. W. Smith and T. D. Tilley, Base-Free Iron Hydrosilylene Complexes via an α-Hydride Migration That Induces Spin Pairing, J. Am. Chem. Soc., 2018, 140, 3880–3883 CrossRef CAS PubMed.
- T. Hatanaka, Y. Ohki and K. Tatsumi, Synthesis of Coordinatively Unsaturated Half-Sandwich Iron-Silyl Complexes with an N-Heterocyclic Carbene Ligand and Their Reactions with H2, Eur. J. Inorg. Chem., 2013, 3966–3971 CrossRef CAS.
- D. V. Gutsulyak, L. G. Kuzmina, J. A. K. Howard, S. F. Vyboishchikov and G. I. Nikonov, Cp(Pri2MeP)FeH2SiR3: Nonclassical Iron Silyl Dihydride, J. Am. Chem. Soc., 2008, 130, 3732–3733 CrossRef CAS PubMed.
- X. Du, Y. Zhang, D. Peng and Z. Huang, Base-Metal-Catalyzed Regiodivergent Alkene Hydrosilylations, Angew. Chem., Int. Ed., 2016, 55, 6671–6675 CrossRef CAS PubMed.
- B. Cheng, W. Liu and Z. Lu, Iron-Catalyzed Highly Enantioselective Hydrosilylation of Unactivated Terminal Alkenes, J. Am. Chem. Soc., 2018, 140, 5014–5017 CrossRef CAS PubMed.
- A. J. Challinor, M. Calin, G. S. Nichol, N. B. Carter and S. P. Thomas, Amine-Activated Iron Catalysis: Air- and Moisture-Stable Alkene and Alkyne Hydrofunctionalization, Adv. Synth. Catal., 2016, 358, 2404–2409 CrossRef CAS.
- D. Peng, Y. Zhang, X. Du, L. Zhang, X. Leng, M. D. Walter and Z. Huang, Phosphinite-Iminopyridine Iron Catalysts for Chemoselective Alkene Hydrosilylation, J. Am. Chem. Soc., 2013, 135, 19154–19166 CrossRef CAS PubMed.
- P. G. Hayes, C. Beddie, M. B. Hall, R. Waterman and T. D. Tilley, Hydrogen-Substituted Osmium Silylene Complexes: Effect of Charge Localization on Catalytic Hydrosilation, J. Am. Chem. Soc., 2006, 128, 428–429 CrossRef CAS PubMed.
- M. A. Rankin, D. F. MacLean, G. Schatte, R. McDonald and M. Stradiotto, Silylene Extrusion from Organosilanes via Double Geminal Si–H Bond Activation by a Cp*Ru(κ2-P,N)+ Complex: Observation of a Key Stoichiometric Step in the Glaser-Tilley Alkene Hydrosilylation Mechanism, J. Am. Chem. Soc., 2007, 129, 15855–15864 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details, characterization data, and computational details (PDF). See DOI: 10.1039/d0sc01749c |
| ‡ Current address: Department of Chemistry, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA. |
| § Current address: Department of Chemistry and Chemical Biology, Harvard University, 12 Oxford Street, Cambridge, Massachusetts 02138, USA. |
| This journal is © The Royal Society of Chemistry 2020 |