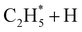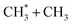Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultraviolet photochemistry of ethane: implications for the atmospheric chemistry of the gas giants†
Yao
Chang
a,
Jiayue
Yang
a,
Zhichao
Chen
a,
Zhiguo
Zhang
ab,
Yong
Yu
a,
Qingming
Li
a,
Zhigang
He
a,
Weiqing
Zhang
a,
Guorong
Wu
 a,
Rebecca A.
Ingle
a,
Rebecca A.
Ingle
 c,
Matthew
Bain
d,
Michael N. R.
Ashfold
c,
Matthew
Bain
d,
Michael N. R.
Ashfold
 *d,
Kaijun
Yuan
*d,
Kaijun
Yuan
 *a,
Xueming
Yang
*a,
Xueming
Yang
 *ae and
Christopher S.
Hansen
*ae and
Christopher S.
Hansen
 *f
*f
aState Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, 457 Zhongshan Road, Dalian, 116023, China. E-mail: kjyuan@dicp.ac.cn; xmyang@dicp.ac.cn
bKey Laboratory of Functional Materials and Devices for Informatics of Anhui Higher Education Institutions, School of Physics and Electronic Engineering, Fuyang Normal University, Fuyang, Anhui 236041, China
cDepartment of Chemistry, University College London, London, WC1H 0AJ, UK
dSchool of Chemistry, University of Bristol, Bristol, BS8 1TS, UK. E-mail: mike.ashfold@bristol.ac.uk
eDepartment of Chemistry, Southern University of Science and Technology, Shenzhen 518055, China
fSchool of Chemistry, University of New South Wales, Sydney, NSW 2052, Australia. E-mail: christopher.hansen@unsw.edu.au
First published on 29th April 2020
Abstract
Chemical processing in the stratospheres of the gas giants is driven by incident vacuum ultraviolet (VUV) light. Ethane is an important constituent in the atmospheres of the gas giants in our solar system. The present work describes translational spectroscopy studies of the VUV photochemistry of ethane using tuneable radiation in the wavelength range 112 ≤ λ ≤ 126 nm from a free electron laser and event-triggered, fast-framing, multi-mass imaging detection methods. Contributions from at least five primary photofragmentation pathways yielding CH2, CH3 and/or H atom products are demonstrated and interpreted in terms of unimolecular decay following rapid non-adiabatic coupling to the ground state potential energy surface. These data serve to highlight parallels with methane photochemistry and limitations in contemporary models of the photoinduced stratospheric chemistry of the gas giants. The work identifies additional photochemical reactions that require incorporation into next generation extraterrestrial atmospheric chemistry models which should help rationalise hitherto unexplained aspects of the atmospheric ethane/acetylene ratios revealed by the Cassini–Huygens fly-by of Jupiter.
Introduction
Understanding, and perhaps one day exploiting, the environment of extraterrestrial bodies is a central objective of planetary science. The gas giants in our solar system (Jupiter, Saturn, Uranus and Neptune) are rich in molecular chemistry and remain targets of intense scientific study. Like Earth, each of these planets orbits the sun with its own eccentricity and obliquity leading to seasonal variations in incident solar radiation and thus a cycling chemical composition with latitudinal and altitudinal variations in the abundances of the various molecular constituents.1 Absorption of near-infrared solar radiation by methane (CH4) makes important contributions to heating the upper atmospheres (stratospheres) of these planets.1–3 Methane contributes less to stratospheric cooling, however, which is more reliant on emission from ethane (C2H6) and acetylene (C2H2).1 Understanding the balance and interplay between CH4 and C2H6/C2H2 is central to understanding the atmospheric dynamics of the gas giants.Chemical processing in the stratospheres of the gas giants is driven by incident vacuum ultraviolet (VUV) light,4 even in the distant, gas-poor giants Uranus and Neptune.5 Numerous possible reactions merit consideration, but common photochemical models for these planetary atmospheres necessarily employ a reduced set pruned from a much larger library of reactions, along with their corresponding rates/branching fractions. These models describe many aspects of the atmospheres of Saturn and Jupiter reasonably well1–3 but have recognised shortcomings. For example, the dominant C2H6 and C2H2 generation mechanisms are assumed to involve secondary reactions following photolysis of CH4.6–8 But both the Cassini–Huygens fly-by of Jupiter and terrestrial measurements reveal very different meridional and latitudinal distributions for C2H6 and C2H2. Such would be surprising if both species are tightly coupled to methane photolysis.3,9,10 Neglect of ion-molecule chemistry has been suggested as one possible explanation for this discrepancy,3,11,12 but it is also appropriate to question the inputs to the commonly used photochemical schemes. These draw on data8 from a range of (often indirect) sources, including predictions, wherein chemical pathways have been included or removed on the basis of how well the model fits the measurements. Ethane is an important participant in these models and, whilst VUV photolysis is accepted as its main destruction route,13,14 the dominant fragmentation pathways and photoproducts are not well determined.
Early laboratory studies of C2H6 photolysis at the resonance wavelengths emitted by a xenon lamp (λ = 147.0 and 129.5 nm) deduced the involvement of (at least) three fragmentation pathways. Two involve loss of H2 or two H atoms, the other yields CH4 + CH2 products.15 Subsequent studies using Kr and Ar resonance lamps (λ = 123.6 and 106.7/104.8 nm, respectively) suggested additional primary fragmentation channels, to CH3 + CH3 and, particularly, H + C2H5 products.16–18 These studies all involved careful end-product analysis but could not distinguish primary photofragmentation processes from secondary reactions following photolysis, nor yield any dynamical information. More recent imaging studies showed formation of H atoms following C2H6 photolysis at the Lyman-α wavelength (λ = 121.6 nm, the most intense VUV wavelength in the solar spectrum), with an isotropic velocity distribution peaking at low kinetic energies and a weak tail extending to higher energies. The form of this distribution was attributed to initial C–H bond fission, yielding a fast H atom and an electronically excited 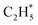 fragment, followed by a second (slow) H atom from unimolecular decay of the latter.19
fragment, followed by a second (slow) H atom from unimolecular decay of the latter.19
The present study employs two cutting-edge technologies – the intense, pulsed VUV free electron laser (FEL) at the Dalian Coherent Light Source (DCLS)20 and an event-triggered, fast framing, Pixel Imaging Mass Spectrometry (PImMS2) sensor21 – to advance understanding of C2H6 photochemistry and to identify similarities and differences with the photochemistry of both lighter (i.e. CH4) and heavier (e.g. propane (C3H8)) alkanes. The reported data derive from two sets of collision-free experiments: (i) multi-mass velocity-map ion imaging (PImMS2 detected)22 studies following one-color VUV photolysis of ethane and ‘universal’ (i.e. not quantum state selected) photoionisation of CH2 and CH3 photoproducts at four (FEL-produced) wavelengths in the range 112.0 ≤ λ ≤ 125.6 nm, and (ii) VUV photolysis at λ = 121.6 nm (using photons generated by four wave mixing outputs from a tabletop pulsed laser) and subsequent detection of H atom products using the high resolution H-atom Rydberg tagging technique.23,24 The experimental procedures have all been described previously and are thus confined to the ESI.†
Results and discussion
(a) Ethane absorption and the energetics of its various dissociation channels
Fig. 1 shows the chosen photolysis wavelengths superimposed on the electronic absorption spectrum of ethane.25,26 As with the other alkanes, the absorption of C2H6 lies in the VUV region but, uniquely amongst the alkanes, its room temperature absorption spectrum displays resolved vibronic structure. This structure is attributed to transitions from the near degenerate highest occupied 3a1g and 1eg valence orbitals to orbitals with dominant 3p Rydberg character. One or more of these are suggested to have significant antibonding valence σ* character also.27 Excitations to the 3s Rydberg orbital in C2H6 are predicted at lower energies, but to be weak – as a result of the molecular center of symmetry – thus distinguishing the 3s Rydberg excitations of ethane from those in CH4 and the heavier alkanes which all show large absorption cross-sections. This seemingly simple description hides a wealth of potential complexity, however. The degeneracy of the ground (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Eg) state of the C2H6+ cation is lifted by Jahn–Teller distortion, and the structure and dynamics of the resulting cation states are further complicated by the energetic proximity of the low lying Ã2A1g excited state – with the result that even a full interpretation of the threshold photoelectron spectrum of C2H6 remains elusive.28 Such interactions must also affect the Rydberg states of current interest – since they share the same ion core(s) – and thus affect the absorption spectrum shown in Fig. 1.
2Eg) state of the C2H6+ cation is lifted by Jahn–Teller distortion, and the structure and dynamics of the resulting cation states are further complicated by the energetic proximity of the low lying Ã2A1g excited state – with the result that even a full interpretation of the threshold photoelectron spectrum of C2H6 remains elusive.28 Such interactions must also affect the Rydberg states of current interest – since they share the same ion core(s) – and thus affect the absorption spectrum shown in Fig. 1.
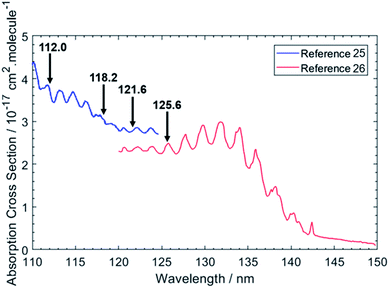 | ||
| Fig. 1 VUV absorption spectrum of C2H6 from ref. 25 and 26. The data from ref. 26 were extracted manually, while the data from ref. 25 were retrieved from ref. 48. The black arrows indicate the photolysis wavelengths (in nm) used in the present study. | ||
Contemporary computational chemistry methods have enabled global investigations of the ground (S0) state potential energy surfaces (PESs) for species involved in the early stages of the pyrolysis of ethane and other C1–C3 hydrocarbons29 but have yet to be directed at the excited state photochemistry of any but the very simplest alkanes. Fig. 2 shows the lower-lying dissociation limits of C2H6. The predicted minimum energy conical intersections were located using the global reaction route mapping (GRRM) method and are discussed later. The S0 state correlates adiabatically with the ground state products from either C–C or C–H bond fission (i.e. ground state CH3 + CH3 and H + C2H5 fragments). The former is the weaker bond, and the formation of 1CH2 + CH4 products is attributed to an (essentially barrierless) H atom transfer between the incipient CH3 radicals.29 The energetic thresholds for these three processes are all lower than the calculated barrier to H2 elimination on the S0 PES (∼5.1 eV).29 As Fig. 2 also shows, many more spin-allowed fragmentation channels are energetically accessible following electronic excitation of ethane. Table 1 lists no fewer than 17 chemically intuitive channels that require less than the 10.2 eV of energy provided by a Lyman-α photon. Of these, 8, 7, 6 and 5 of the channels yield, respectively, H atoms, H2 molecules, CH2 and CH3 radicals amongst the dissociation products. Such commonalities provide a major challenge for quantitative studies of the primary photochemistry of ethane (and larger alkanes). Of particular relevance to the present study, the reduced models currently used to describe the atmospheric chemistry of Jupiter and Saturn1–3 recognise just reactions (1)–(5) in Table 1.
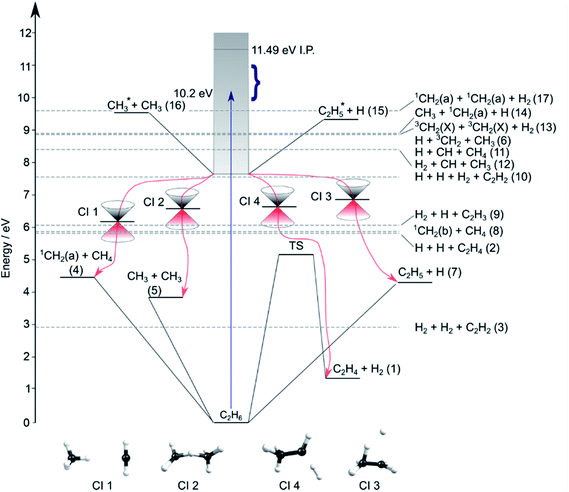 | ||
| Fig. 2 Energy diagram depicting the excited states of ethane, the thresholds for forming various product combinations (as labelled in Table 1) and illustrative members of families of low-lying CIs (labelled CI1–CI4, identified using the GRRM method) that could facilitate non-adiabatic coupling of excited state population to the S0 PES and thence to the various dissociation products. Representative structures of these CIs are shown at the foot of the figure. The shaded region indicates the energies spanned by excited electronic states of C2H6, the density of which increases as the ionisation potential (IP) is approached. The vertical arrow shows the energy of a Lyman-α photon and the bracket indicates the range of photolysis photon energies explored in this study. | ||
(b) Ion imaging studies
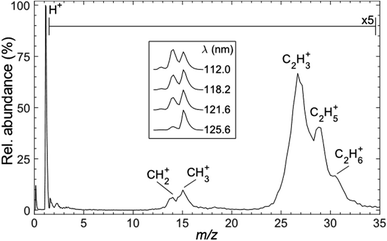
Fig. 3 shows a representative time-of-flight mass spectrum (TOF-MS) of the ions formed following FEL excitation (at λ = 121.6 nm) of a jet-cooled sample of C2H6 in helium. The spectrum is dominated by a peak associated with H+ ions. This is unsurprising, given that this wavelength is resonant with the Lyman-α transition from the ground (n = 1) state of the H atom. The remainder of the TOF-MS, displayed on a 5× expanded vertical scale, reveals two clumps of partially-resolved peaks corresponding to CHx+ (x = 2, 3) and C2Hy+ (y = 3–6) ions. The most intense features in the latter are associated with C2H3+ and C2H5+ ions. Tables S1 and S2 in the ESI† list relevant adiabatic ionisation and dissociative ionisation thresholds, respectively, and show that four of the neutral products of particular interest (i.e. CH2, CH3, C2H3 and C2H5) are amenable to single photon ionisation at 10.2 eV, with dissociative ionisation only a (potential) concern if any of these species carry high levels of internal excitation. Note, however, that the observation of some parent C2H6+ ion signal highlights the difficulty of completely excluding multiphoton processes even when operating at threshold FEL pulse intensities (<100 nJ).The inset to Fig. 3 shows that the relative intensity of the CH2+ signal increases as the excitation wavelength is decreased. Note that the data shown in the inset were recorded with the detector sensitivity raised for just the relevant narrow range of mass/charge (m/z) ratios, thus allowing averaging over many more acquisitions and improved signal-to-noise ratios. The λ-dependent trend in the CH2+ signal is also recognisable in spectra recorded using higher FEL pulse energies but, as shown in Fig. S1,† the relative peak intensities are also pulse energy dependent. Such variations are not unexpected, given the inevitable differences in the wavelength and internal energy dependent photoionisation cross-sections for CH3, 1CH2 and 3CH2 radicals.
Use of the PImMS2 sensor affords not just TOF mass spectra such as those presented in Fig. 3, but also an ion image for each mass channel, in a single acquisition. This provides velocity distributions for each ion peak in Fig. 3. Since C–C bond rupture processes are likely to be pivotal in the cycling of ethane and methane and thus to have a major effect on the atmospheric dynamics, we first present kinetic energy distributions of CH2 and CH3 fragments (monitored via the corresponding ions) from the photofragmentation of ethane.
Fig. 4 presents the total kinetic energy release P(TKER) distributions (calculated on the basis that the partner to the observed fragment carries all of the remaining mass) and TKER-dependent best-fit recoil anisotropy (β) parameters30 obtained from analysing the ion images retrieved from the central time slice of the TOF-MS peaks corresponding to (A, B) CH2+ and (C, D) CH3+ ions recorded at FEL wavelengths λ = 125.6 nm (9.87 eV), 121.6 nm (10.19 eV), 118.2 nm (10.49 eV) and 112.0 nm (11.07 eV). Note that the signal intensities at TKER > 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 are too low for recoil anisotropy parameters to be fitted satisfactorily. Fig. 4A and C also show the corresponding [P(TKER)]1/2 plots (dotted lines) to allow better visualisation of the high TKER data. The raw ion images are shown in Fig. S2 of the ESI.†
000 cm−1 are too low for recoil anisotropy parameters to be fitted satisfactorily. Fig. 4A and C also show the corresponding [P(TKER)]1/2 plots (dotted lines) to allow better visualisation of the high TKER data. The raw ion images are shown in Fig. S2 of the ESI.†
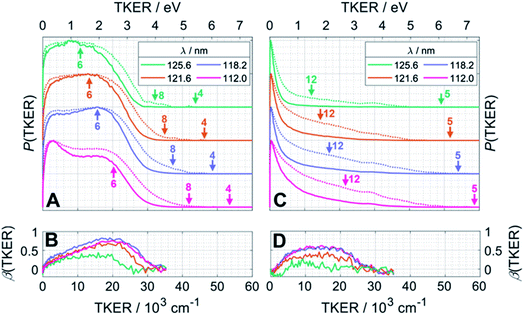 | ||
| Fig. 4 P(TKER) and β(TKER) distributions derived from the analysis of ion images (Fig. S2†) for (A and B) CH2 and (C,D) CH3 fragments from photolysis of a jet-cooled C2H6 sample, with the TKER shown in both cm−1 and eV (bottom and top axes, respectively). The distributions for each photolysis wavelength are offset vertically for display purposes and the dotted lines in plots (A) and (C) show the square root of P(TKER) – normalised to the same maximum value – in order to accentuate the high TKER tails. The TKERmax values associated with the two-body fragmentation channels (4), (5) and (8) as well as the most exoergic three body fragmentations yielding CH2 and/or CH3 fragments (channels (12) and (6)) are also indicated by vertical arrows in panels (A) and (C). TKERmax values for other many-body fragmentation channels can be derived from Table 1 but, as noted in the text, given the assumed TOF to TKER conversion scheme it is likely that the products from such many-body fragmentations would appear at TKER values well below TKERmax. | ||
The distributions derived from the CH2+ ion images (Fig. 4A) assume that the co-fragments are CH4 (i.e. that the CH2 fragments derive from reaction (4) in Table 1). This assumption must be correct for the more translationally excited CH2 products, which display an anisotropic velocity distribution characterised by a positive recoil anisotropy parameter, β ∼ +0.5–0.7 (Fig. 4B), i.e. the CH2 fragments recoil preferentially along the axis parallel to the polarisation vector ε of the photolysis laser photons. But the P(TKER) distributions extend to TKER ∼0 – implying substantial internal excitation of some of the CH2 and/or CH4 fragments. Indeed, as Table 1 shows, the chosen photon energies exceed the thresholds for several three-body fragmentation processes that yield CH2 products. Some or all of channels (6), (13), (14) and (17) in Table 1 could contribute to the increased low-TKER product yield observed at the two shortest excitation wavelengths – a point to which we return later. Thus the precise form of the P(TKER) distribution at low TKER is ill-defined, since the momentum conservation arguments used to convert a measured CH2 fragment velocity (derived from the image radius) into a TKER value are likely not to apply in a three-body dissociation. But this does not negate the conclusions that (i) the relative yield of slow fragments in the CH2+ images increases with increasing photon energy and (ii) the slower fragments, which display minimal recoil anisotropy (β ∼ 0), likely arise via one or more of the three-body fragmentation processes.
The distributions derived from the CH3+ ion images (Fig. 4C) peak at TKER ∼0 and show a tail extending to higher TKER that becomes more anisotropic (to positive β) and relatively more intense as the photolysis wavelength is reduced. As can be deduced from Table 1, the maximum possible TKER of CH3 fragments formed via reaction (5) following excitation at λ = 121.6 nm (Fig. 4C) would be ∼6.38 eV (∼51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1); the high-TKER tails of the P(TKER) distributions shown in Fig. 4C (derived assuming C–C bond fission) extend to values for which the direct C–C bond fission channel (5) is the only possible one photon induced CH3 fragment formation pathway. Most of the imaged CH3 fragments appear with much lower TKER, however. Table 1 shows several potential sources of slow CH3 radicals, including three-body dissociations (6), (12) and (14) and the production of an electronically excited CH3 partner (channel (16)), the relative likelihoods of which are discussed below.
500 cm−1); the high-TKER tails of the P(TKER) distributions shown in Fig. 4C (derived assuming C–C bond fission) extend to values for which the direct C–C bond fission channel (5) is the only possible one photon induced CH3 fragment formation pathway. Most of the imaged CH3 fragments appear with much lower TKER, however. Table 1 shows several potential sources of slow CH3 radicals, including three-body dissociations (6), (12) and (14) and the production of an electronically excited CH3 partner (channel (16)), the relative likelihoods of which are discussed below.
(c) H atom photofragment time-of-flight (TOF) spectra
H atom TOF spectra were recorded following photolysis of a jet-cooled ethane sample in He at λ = 121.6 nm with ε aligned at, respectively, ϕ = 0, 54.7 and 90° to the detection axis and converted to the corresponding P(TKER) and β(TKER) distributions, shown in Fig. 5A and B, by assuming C2H5 as the co-fragment. The fastest products have TKER ∼35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (∼4.3 eV). This TKER value is greater than that reported in the earlier imaging study at this wavelength19 but still well below the maximum allowed by energy conservation assuming single C–H bond fission in ethane (channel (7), for which TKERmax ∼ 6.5 eV). In contrast to the case of CH4, however, the H atom recoil velocity distribution is essentially isotropic.
000 cm−1 (∼4.3 eV). This TKER value is greater than that reported in the earlier imaging study at this wavelength19 but still well below the maximum allowed by energy conservation assuming single C–H bond fission in ethane (channel (7), for which TKERmax ∼ 6.5 eV). In contrast to the case of CH4, however, the H atom recoil velocity distribution is essentially isotropic.
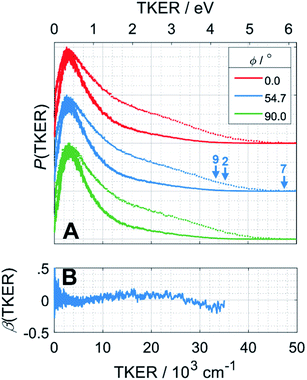 | ||
| Fig. 5 (A) P(TKER) distribution distributions derived from H atom TOF spectra recorded following photolysis of a jet-cooled C2H6 sample at λ = 121.6 nm with the ε vector aligned at ϕ = 0, 54.7 and 90° to the detection axis and (B) the β(TKER) distribution derived therefrom. As in Fig. 4, the individual data sets are offset vertically for display purposes and the high TKER part of the data are accentuated by also plotting [P(TKER)]1/2 distributions (dotted lines). The TKERmax values associated with primary C–H bond fission (channel (7)) and the two lowest energy three-body dissociation channels (2) and (9) from Table 1 are indicated by vertical arrows. | ||
(d) Active photofragmentation channels
The present work identifies fragments formed by VUV photolysis of C2H6, assures that these arise via collision-free unimolecular dissociation and affords insights into the fragmentation dynamics. The translational spectroscopy data for the CH2, CH3 and H atom products hint at similarities in the fragmentation mechanisms following VUV photoexcitation of C2H6 and CH4 and it is useful to summarise current knowledge of the photofragmentation dynamics of CH4 to provide context for the discussion that follows.Only the ground (S0) state and a repulsive triplet excited state of CH4 correlate with the lowest energy C–H bond fission limit (associated with H + CH3 products). The first excited singlet (S1) state of CH4 correlates adiabatically with 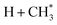 products; the electronically excited
products; the electronically excited 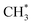 fragments predissociate rapidly to H + 1CH2(ã) products.31 (Here and henceforth, we use superscript * and # symbols to indicate, respectively, electronically and rovibrationally excited products). Nonetheless, experiments find a substantial quantum yield of ground state C–H bond fission products following VUV photoexcitation of CH4, and the H atom products display anisotropic recoil velocity distributions – implying that the photoexcited molecules dissociate on a time scale that is much shorter than the rotational period of the parent molecule (which is estimated to be a few picoseconds).30,32–34 These findings highlight the importance of non-adiabatic couplings via conical intersection (CIs) between the S1 and S0 PESs.35,36 Theory shows that, to form H + CH3 products, one C–H bond in the photoexcited CH4 must start stretching and sweep through the plane defined by the other atoms to access the S0 PES and dissociate. Angular momentum conservation requires that the resulting CH3 products are highly rotationally excited; indeed, some of these CH3(
fragments predissociate rapidly to H + 1CH2(ã) products.31 (Here and henceforth, we use superscript * and # symbols to indicate, respectively, electronically and rovibrationally excited products). Nonetheless, experiments find a substantial quantum yield of ground state C–H bond fission products following VUV photoexcitation of CH4, and the H atom products display anisotropic recoil velocity distributions – implying that the photoexcited molecules dissociate on a time scale that is much shorter than the rotational period of the parent molecule (which is estimated to be a few picoseconds).30,32–34 These findings highlight the importance of non-adiabatic couplings via conical intersection (CIs) between the S1 and S0 PESs.35,36 Theory shows that, to form H + CH3 products, one C–H bond in the photoexcited CH4 must start stretching and sweep through the plane defined by the other atoms to access the S0 PES and dissociate. Angular momentum conservation requires that the resulting CH3 products are highly rotationally excited; indeed, some of these CH3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) )# fragments are formed with so much internal energy that they dissociate further – to H + CH2 and/or H2 + CH products. Rival distortions have also been identified, whereby photoexcited CH4 molecules dissociate by eliminating H2. Theory suggests that the partner CH2 fragments in this case are formed in the ã1A1 state (for dissociations occurring after non-adiabatic coupling to the parent S0 PES) and the
)# fragments are formed with so much internal energy that they dissociate further – to H + CH2 and/or H2 + CH products. Rival distortions have also been identified, whereby photoexcited CH4 molecules dissociate by eliminating H2. Theory suggests that the partner CH2 fragments in this case are formed in the ã1A1 state (for dissociations occurring after non-adiabatic coupling to the parent S0 PES) and the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 state (if dissociation occurs adiabatically on the excited state PES).36
1B1 state (if dissociation occurs adiabatically on the excited state PES).36
Quantitative simulations of the early time nuclear motions following photoexcitation of C2H6 remain challenging but global reaction route mapping (GRRM)37,38 calculations (summarised in the ESI†) can offer important insights by predicting low-lying conical intersections (CIs) between the PESs for the S0 and S1 states. The present VUV photoexcitations will populate one or more Sn (n > 1) states of ethane, but we henceforth assume that molecules excited to these higher Sn states undergo efficient non-radiative coupling to the S1 state. As Fig. 2 showed, the S1 state of ethane correlates with 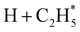 and
and 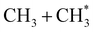 products (channels (15) and (16) in Table 1). The
products (channels (15) and (16) in Table 1). The 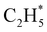 and
and 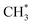 species are both unstable and dissociate to give, respectively, H + C2H4 (ref. 39–41) and H + 1CH2(ã) (ref. 31) products. As in CH4, C2H6(S1) molecules can also decompose after non-adiabatic coupling to the S0 PES. The nuclear distortions required to access the predicted CIs between the S1 and S0 PESs (shown in Fig. 2) correlate well with 1CH2 elimination once an H atom has inserted between the two C atoms, with C–C or C–H bond fissions and with loss of H2. The present study is sensitive to the first three fragmentation processes, which are considered in turn. Given the photon energies involved and the multi-dimensional nature of many of these distortions, we can anticipate that (as in the case of CH4 (ref. 30, 33 and 34)) many of the polyatomic products will be formed with sufficient internal energy that they will fragment further.
species are both unstable and dissociate to give, respectively, H + C2H4 (ref. 39–41) and H + 1CH2(ã) (ref. 31) products. As in CH4, C2H6(S1) molecules can also decompose after non-adiabatic coupling to the S0 PES. The nuclear distortions required to access the predicted CIs between the S1 and S0 PESs (shown in Fig. 2) correlate well with 1CH2 elimination once an H atom has inserted between the two C atoms, with C–C or C–H bond fissions and with loss of H2. The present study is sensitive to the first three fragmentation processes, which are considered in turn. Given the photon energies involved and the multi-dimensional nature of many of these distortions, we can anticipate that (as in the case of CH4 (ref. 30, 33 and 34)) many of the polyatomic products will be formed with sufficient internal energy that they will fragment further.
![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) 1B1 state (for dissociation on the S1 PES). But the distributions also extend to TKER ∼0, showing that one or other or both fragments are formed with a broad spread of internal energies. The photoexcitation energies are sufficient to induce three-body fragmentations and, simply on energetic grounds, any of channels (6), (13), (14) and (17) in Table 1 could contribute to signal in the CH2+ ion images. Of these, unimolecular decay of any sufficiently internally excited CH#4 partner would be expected to contribute to the yield of (slow) H and CH3 products, i.e. the net reaction (14) in Table 1.
1B1 state (for dissociation on the S1 PES). But the distributions also extend to TKER ∼0, showing that one or other or both fragments are formed with a broad spread of internal energies. The photoexcitation energies are sufficient to induce three-body fragmentations and, simply on energetic grounds, any of channels (6), (13), (14) and (17) in Table 1 could contribute to signal in the CH2+ ion images. Of these, unimolecular decay of any sufficiently internally excited CH#4 partner would be expected to contribute to the yield of (slow) H and CH3 products, i.e. the net reaction (14) in Table 1.
Fig. 4A shows an additional feature at low TKER in the distributions derived from the CH2+ images measured at the two shorter wavelengths. This might signify the opening of a new (three-body) route to 1CH2 products, but this feature more likely indicates the presence of 3CH2 photoproducts: The ground states of the 3CH2 radical and the CH2+ cation have very similar geometries. Photoionisation of 3CH2 thus tends to be vibrationally adiabatic (i.e. to favour Δv = 0 transitions)42–44 and, from Table S1,† should only be expected at Ephot >10.39 eV (i.e. at λ < 119.3 nm). Note that the feature at low TKER in the P(TKER) distributions shown in Fig. 4A appears to ‘turn on’ and become more prominent as the photon energy is tuned above this threshold. Several possible routes to forming 3CH2 products can be envisaged, including the unimolecular decay of highly internally excited CH#3 fragments (from initial C–C bond fission) or of C2H#5 fragments (following primary C–H bond fission) after non-adiabatic coupling to the S0 state – as discussed below. Both would contribute to net process (6) in Table 1, though not necessarily exhibit similar energy disposals.
In principle, the entire P(TKER) distribution derived from the CH3 image could be attributed to channel (5) if the fragmentation dynamics were heavily biased towards forming very highly internally excited CH#3 products. The unimolecular decay of these CH#3 fragments would be a source of the 3CH2 products inferred above (reaction (6)), and these 3CH2 products would be expected to display a similar translational energy distribution to that of the CH#3 products (since the light H atom partner would take the bulk of any excess energy released in the secondary fragmentation). Such expectations are consistent with the experimental data and, as noted above, the non-observation of a peak attributable to 3CH2 products at longer wavelengths (e.g. at λ = 121.6 nm) need not imply that CH#3 fragments are not formed but simply that the 3CH2 products from their decay are not amenable to photoionisation at the longer wavelengths.
The dominance of translationally ‘cold’ (i.e. internally ‘hot’) CH3 products in the P(TKER) distributions is striking, however. Table 1 suggests several other potential sources of slow CH3 products. Adiabatic dissociation on the S1 PES to 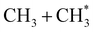 products is an interesting contender. This process is exoergic at all wavelengths studied, though the adiabatic S1 PES will likely exhibit a barrier at short RC–C bond extensions as the Rydberg function acquires increasing σ* antibonding valence character.6 The
products is an interesting contender. This process is exoergic at all wavelengths studied, though the adiabatic S1 PES will likely exhibit a barrier at short RC–C bond extensions as the Rydberg function acquires increasing σ* antibonding valence character.6 The 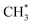 radicals would be unstable with respect to H + 1CH2(ã) products.31 Again, the H atoms would carry most of any kinetic energy release, so the translational energy distributions of any 1CH2(ã) fragments formed in this way should broadly mirror that of their
radicals would be unstable with respect to H + 1CH2(ã) products.31 Again, the H atoms would carry most of any kinetic energy release, so the translational energy distributions of any 1CH2(ã) fragments formed in this way should broadly mirror that of their 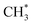 precursor. 1CH2(ã) fragments are amenable to photoionisation at all wavelengths investigated in the present work, but the TKER distributions derived from the CH2+ images measured at the longer excitation wavelengths show no ‘spike’ at low TKER – suggesting that any contribution to the 1CH2(ã) yield from adiabatic dissociation to
precursor. 1CH2(ã) fragments are amenable to photoionisation at all wavelengths investigated in the present work, but the TKER distributions derived from the CH2+ images measured at the longer excitation wavelengths show no ‘spike’ at low TKER – suggesting that any contribution to the 1CH2(ã) yield from adiabatic dissociation to 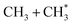 products on the S1 PES must be small compared to that from reaction (4).
products on the S1 PES must be small compared to that from reaction (4).
C–H bond fission
The P(TKER) distribution derived from the H atom TOF measurements (Fig. 5A) extends to TKER values that can only be attributed to prompt C–H bond fission following VUV photoexcitation of C2H6, i.e. to reaction (7) in Table 1. The C2H5 co-fragments are formed with a very broad spread of internal energies. Analogy with CH4 suggests that this energy disposal is a consequence of the nuclear motions that promote C–H bond fission by non-adiabatic coupling to the S0 PES.6,35 Most of the ‘C2H5’ products assumed in deriving the P(TKER) distribution have sufficient internal energy to dissociate further – by loss of another H atom (net reaction (2)), or H2 (net process (9)), or both (net channel (10)), or to two CHx species (e.g. via net channels (6) or (11) in Table 1).42 However, the smoothly varying P(TKER) distributions shown in Fig. 5A suggest that such overall three- (or more-) body dissociations occur sequentially, i.e. via a prompt C–H bond fission and subsequent unimolecular decay of the resulting C2H#5 radicals. The low-TKER peak in Fig. 5A could also indicate an adiabatic contribution to the overall dissociation, yielding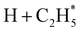 as primary products – as suggested in the earlier imaging study at λ = 121.6 nm.19 Any
as primary products – as suggested in the earlier imaging study at λ = 121.6 nm.19 Any 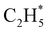 fragments would dissociate, yielding H + C2H4 products with a spread of translational energies39,45 (i.e. net reaction (2)). Many of the C2H4 products formed by decay of C2H#5 or
fragments would dissociate, yielding H + C2H4 products with a spread of translational energies39,45 (i.e. net reaction (2)). Many of the C2H4 products formed by decay of C2H#5 or 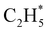 species may well be formed with sufficient internal energy to decay yet further, to H + C2H3 (vinyl) radical products, or by eliminating H2 to yield C2H2. The former products are observed in the present study, via the C2H3+ peak in the TOF-MS in Fig. 3 and corresponding small ion image shown in Fig. S3 of the ESI,† but the current work is blind to C2H2 products – which were identified by end-product analysis in the early VUV photolysis studies of C2H6 under collisional conditions.16–18 For completeness, we note that C2H2 products could also arise via sequential H2 eliminations from, first, C2H#6 (formed by non-adiabatic coupling to the S0 state) and then from the resulting C2H#4 intermediates (i.e. net reaction (3) in Table 1). C2H2 formation by loss of four H atoms from C2H6 is energetically forbidden at the VUV wavelengths of current interest.
species may well be formed with sufficient internal energy to decay yet further, to H + C2H3 (vinyl) radical products, or by eliminating H2 to yield C2H2. The former products are observed in the present study, via the C2H3+ peak in the TOF-MS in Fig. 3 and corresponding small ion image shown in Fig. S3 of the ESI,† but the current work is blind to C2H2 products – which were identified by end-product analysis in the early VUV photolysis studies of C2H6 under collisional conditions.16–18 For completeness, we note that C2H2 products could also arise via sequential H2 eliminations from, first, C2H#6 (formed by non-adiabatic coupling to the S0 state) and then from the resulting C2H#4 intermediates (i.e. net reaction (3) in Table 1). C2H2 formation by loss of four H atoms from C2H6 is energetically forbidden at the VUV wavelengths of current interest.
The present study does not return quantum yields and, as noted above, is silent regarding some molecular elimination channels. But it certainly identifies several active fragmentation channels and provides new insights into the likely fragmentation dynamics. The present analysis finds no compelling evidence for adiabatic dissociation on an excited state PES – implying efficient non-adiabatic coupling between excited states of C2H6 and to the S0 PES. Many of the present interpretations align with the results of recent quasi-classical trajectory surface hopping calculations for the next larger alkane, propane (C3H8), following excitation at λ = 157 nm, wherein it was concluded that most dissociations occur after internal conversion to the S0 PES, that the energy disposal in the resulting fragments is governed by dynamical rather than statistical factors, and that the three-body fragmentation processes occur sequentially.46
(e) Implications for modelling the atmospheres of the gas giants
This work provides detailed new insights into the VUV photochemistry of ethane. The results discussed in detail in the above subsections are summarised below in terms of their implications for modelling the atmospheres of the gas giants. These new results must influence future models:(i) The HRA-PTS studies reveal kinetic energy distributions extending to values that, on energetic grounds, can only be attributed to prompt C–H bond fission, confirming primary C–H bond fission yielding H + C2H5 products (reaction (7) in Table 1). This reaction does not feature in current models used to describe the chemical processing in the stratospheres of the gas giants. Most of the C2H5 species are formed with enough internal energy to decay further, almost certainly yielding some H + C2H4 products. The present study thus supports inclusion of reaction (2) in the modelling and implies that the two H atoms in that case are lost sequentially.
(ii) The kinetic energy distributions derived from the CH3+ ion images extend to TKER values that can only be attributed to C–C bond fission yielding two CH3 radicals, confirming that the C–C bond fission channel (reaction (5)) is active and supporting its inclusion in the modelling. The finding that the P(TKER) distributions peak at TKER ∼0 implies that one of the CH3 fragments is generally formed with sufficient internal energy to decay further. If C–C bond fission completes after non-adiabatic coupling to the S0 PES, the resulting CH#3 fragments most likely decay to H + 3CH2(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) ) products (i.e. net reaction (6)). This reaction is not included in the current model and, according to the present analysis, will have significantly higher quantum yield than reaction (5).
) products (i.e. net reaction (6)). This reaction is not included in the current model and, according to the present analysis, will have significantly higher quantum yield than reaction (5).
(iii) The imaging studies confirm formation of CH2 fragments, with a smooth P(TKER) distribution that extends to TKER values such that the partner fragment can only be CH4. Spin-conservation arguments and the deduced efficiency of non-adiabatic coupling to the S0 PES suggest that these faster CH2 fragments are formed in the ã1A1 state. The inclusion of reaction (4) in the photochemical modelling is vindicated.
(iv) The primary fragmentations and resulting product energy disposals following VUV photoexcitation of ethane are shown to be governed by dynamical rather than statistical factors; three-body dissociations are commonplace and occur sequentially. Clearly, quantitative branching ratios for the various active channels are still needed, but the present work offers several clear pointers. Reaction (7) and, particularly, the three-body fragmentation (6) are active and require incorporation in future modelling. The yield of (currently neglected) reaction (6) is deduced to be larger than that of reaction (5). The processes revealed in this study all involve relatively ‘prompt’ C–H or C–C bond fission, after non-adiabatic coupling to the S0 PES. As Fig. 2 shows, the respective bond energies are lower than the energy barriers to C2H4 formation by H2 elimination on the S0 PES. Analogy with CH4 suggests that any H2 and C2H4 products formed via process (1) will be both translationally and vibrationally excited. The likelihood that the C2H#4 species would have sufficient internal energy to surmount the barrier to eliminating a further H2 (to yield C2H2 or H2CC) is unclear. We further note that the substantial (∼60%) branching into C2Hx species following VUV photoexcitation of C2H6 assumed in the current planetary atmospheric photochemistry models derives from indirect measurements made more than half a century ago, and is predicated on an assumption that the decomposition of the internally excited C2H#4 species formed via reaction (1) would mimic that deduced following VUV photoexcitation of strategically deuterated ethene (CH2CD2) molecules.16,17 Such an assumption must be questionable, given the differences in available energy and the recognised importance of dynamics (i.e. the topographies of, and non-adiabatic couplings between, the PESs sampled in the two cases) in determining the product branching and energy disposal. It seems likely that the current models overestimate the relative yield of C2Hx (particularly C2H2) photoproducts.
Conclusions
Translational spectroscopy methods employing two cutting-edge technologies – the Dalian Coherent Light Source (DCLS) Free Electron Laser (FEL) and a fast-framing PImMS2 camera – have revealed many new insights into the rich (and hitherto largely impenetrable) VUV photochemistry of ethane. The present findings should serve to stimulate ab initio molecular dynamics simulations of this prototypical alkane following photoexcitation at VUV wavelengths and substantial refinements of the models currently used to describe the atmospheric photochemistry of the gas giants. This study (i) concludes that, as in CH4, the VUV photochemistry of ethane is driven by efficient non-adiabatic coupling to, and subsequent direct (and sequential) dissociations on the S0 PES, (ii) highlights the need to revise current photochemical models of the stratospheric photochemistry of the gas giants – by incorporating the hitherto neglected C–H bond fission channel (7) and the three-body decomposition (6) to CH3 + 3CH2 + H products and down-grading the relative yield of primary C2Hx photoproducts – and (iii) emphasises the pressing need for quantitative product branching fractions. Stratospheric C2H6 production in the gas giants is driven by VUV photodissociation of CH4, but the present analysis implies that the subsequent photochemical coupling between C2H6 and C2H2 is likely to be weaker than currently assumed.Data and materials availability
The raw ion event lists, H-atom TOF spectra and calculation log files are available from the authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC Center for Chemical Dynamics (Grant No. 21688102)), the National Natural Science Foundation of China (Grant No. 21673232, 21922306, and 21873099), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB17000000), and the international partnership program of Chinese Academy of Sciences (No. 121421KYSB20170012). CSH is grateful for funding from the Australian Research Council (ARC, DE200100549), MNRA is grateful for funding from the Engineering and Physical Sciences Research Council (EPSRC, EP/L005913) and both CSH and MNRA are grateful to the NSFC Center for Chemical Dynamics for the award of Visiting Fellowships. The authors thank the FEL staff (Lei Shi, Hongli Ding, Kai Tao, Yuhuan Tian, Guanglei Wang, Dongxu Dai) for technical support, and Professor Satoshi Maeda and Dr Yu Harabuchi (Hokkaido University) for use of the GRRM software and computational resources.References
- V. Hue, T. Cavalié, M. Dobrijevic, F. Hersant and T. K. Greathouse, Icarus, 2015, 257, 163–184 CrossRef CAS.
- V. Hue, T. K. Greathouse, T. Cavalié, M. Dobrijevic and F. Hersant, Icarus, 2016, 267, 334–343 CrossRef CAS.
- V. Hue, F. Hersant, T. Cavalié, M. Dobrijevic and J. A. Sinclair, Icarus, 2018, 307, 106–123 CrossRef CAS.
- Y. L. Yung and W. B. DeMore, in Photochemistry of Planetary Atmospheres, Oxford University Press, 1999 Search PubMed.
- J. I. Moses, L. N. Fletcher, T. K. Greathouse, G. S. Orton and V. Hue, Icarus, 2018, 307, 124–145 CrossRef CAS PubMed.
- M. N. R. Ashfold, R. A. Ingle, T. N. V. Karsili and J. S. Zhang, Phys. Chem. Chem. Phys., 2019, 21, 13880–13901 RSC.
- G. R. Gladstone, M. Allen and Y. L. Yung, Icarus, 1996, 119, 1–52 CrossRef CAS PubMed.
- E. Hébrard, M. Dobrijevic, Y. Bénilan and F. Raulin, J. Photochem. Photobiol., C, 2006, 7, 211–230 CrossRef.
- H. Melin, L. N. Fletcher, P. T. Donnelly, T. K. Greathouse, J. H. Lacy, G. S. Orton, R. S. Giles, J. A. Sinclair and P. G. J. Irwin, Icarus, 2018, 305, 301–313 CrossRef CAS.
- N. A. Lombardo, C. A. Nixon, M. Sylvestre, D. E. Jennings, N. Teanby, P. J. G. Irwin and F. M. Flasar, Astron. J., 2019, 157, 160 CrossRef CAS.
- J. A. Sinclair, G. S. Orton, T. K. Greathouse, L. N. Fletcher, J. I. Moses, V. Hue and P. G. J. Irwin, Icarus, 2017, 292, 182–207 CrossRef CAS.
- J. A. Sinclair, J. I. Moses, V. Hue, T. K. Greathouse, G. S. Orton, L. N. Fletcher and P. G. J. Irwin, Icarus, 2019, 328, 176–193 CrossRef CAS.
- J. C. Loison, E. Hébrard, M. Dobrijevic, K. M. Hickson, F. Caralp, V. Hue, G. Gronoff, O. Venot and Y. Bénilan, Icarus, 2015, 247, 218–247 CrossRef CAS.
- J. L. Moses and A. R. Pope, Icarus, 2017, 297, 33–58 CrossRef CAS PubMed.
- H. Okabe and J. R. McNesby, J. Chem. Phys., 1961, 34, 668–669 CrossRef CAS.
- J. R. Hampson-Jr, J. R. McNesby, H. Akimoto and I. Tanaka, J. Chem. Phys., 1964, 40, 1099–1105 CrossRef.
- H. Akimoto, K. Obi and I. Tanaka, J. Chem. Phys., 1965, 42, 3864–3868 CrossRef CAS.
- S. G. Lias, G. J. Collin, R. E. Rebbert and P. Ausloos, J. Chem. Phys., 1970, 52, 1841–1851 CrossRef CAS.
- W. M. Jackson, R. J. P. II, D. D. Xu, J. D. Wrobel, M. Ahmed, D. S. Peterka and A. G. Suits, J. Chem. Phys., 1998, 109, 4703–4706 CrossRef CAS.
- Y. Chang, S. Yu, Q. Li, Y. Yu, H. Wang, S. Su, Z. Chen, L. Che, X. Wang, W. Zhang, D. Dai, G. Wu, K. Yuan and X. Yang, Rev. Sci. Instrum., 2018, 89, 063113 CrossRef PubMed.
- J. J. John, M. Brouard, A. Clark, J. Crooks, E. Halford, L. Hill, J. W. L. Lee, A. Nomerotski, R. Pisarczyk, I. Sedgwick, C. S. Slater, R. Turchetta, C. Vallance, E. Wilman, B. Winter and W. H. Yuen, J. Instrum., 2012, 7, C08001 Search PubMed.
- R. A. Ingle, C. S. Hansen, E. Elsdon, M. Bain, J. W. L. Lee, M. Brouard, C. Vallance, R. Turchetta and M. N. R. Ashfold, J. Chem. Phys., 2017, 147, 013914 CrossRef CAS PubMed.
- L. Schnieder, W. Meier, K. H. Welge and M. N. R. A. C. M. Western, J. Chem. Phys., 1990, 92, 7027–7037 CrossRef CAS.
- M. N. R. Ashfold, K. J. Yuan and X. M. Yang, J. Chem. Phys., 2018, 149, 080901 CrossRef PubMed.
- K. Kameta, S. Machida, M. Kitajima, M. Ukai, N. Kouchi, Y. Hatano and K. Ito, J. Electron Spectrosc. Relat. Phenom., 1996, 79, 391–393 CrossRef CAS.
- F. Z. Chen and C. Y. R. Wu, J. Quant. Spectrosc. Radiat. Transfer, 2004, 85, 195–209 CrossRef CAS.
- R. J. Buenker and S. D. Peverimhoff, Chem. Phys., 1975, 8, 56–67 CrossRef CAS.
- U. Jacovella, C. J. Stein, M. Grütter, L. Freitag, C. Lauzin, M. Reiher and F. Merkt, Phys. Chem. Chem. Phys., 2018, 20, 1072–1081 RSC.
- M. N. Ryazantsev, A. Jamal, S. Maeda and K. Morokuma, Phys. Chem. Chem. Phys., 2015, 17, 27789–27805 RSC.
- P. A. Cook, M. N. R. Ashfold, Y. J. Lee, K. H. Jung, S. Harich and X. Yang, Phys. Chem. Chem. Phys., 2001, 3, 1848–1860 RSC.
- S. H. S. Wilson, J. D. Howe, K. N. Rosser, M. N. R. Ashfold and R. N. Dixon, Chem. Phys. Lett., 1994, 227, 456–460 CrossRef CAS.
- D. H. Mordaunt, I. R. Lambert, G. P. Morley, M. N. R. Ashfold, R. N. Dixon, L. Schnieder and K. H. Welge, J. Chem. Phys., 1993, 98, 2054–2065 CrossRef CAS.
- J. H. Wang, K. Liu, Z. Y. Min, H. M. Su, R. Bersohn, J. Preses and J. Z. Larese, J. Chem. Phys., 2000, 113, 4146–4152 CrossRef CAS.
- Y. W. Zhang, K. J. Yuan, S. R. Yu and X. M. Yang, J. Phys. Chem. Lett., 2010, 1, 475–479 CrossRef CAS.
- R. van Harrevelt, J. Chem. Phys., 2006, 125, 124302 CrossRef PubMed.
- B. M. D. Lodriguito, G. Lendvay and G. C. Schatz, J. Chem. Phys., 2009, 131, 224320 CrossRef PubMed.
- S. Maeda, K. Ohno and K. Morokuma, Phys. Chem. Chem. Phys., 2013, 15, 3683–3701 RSC.
- S. Maeda, Y. Osada, Y. Harabuchi, T. Taketsugu, K. Morokuma and K. Ohno, GRRM, a developmental version, Hokkaido University, Sapporo, 2015 Search PubMed.
- G. Amaral, K. S. Xu and J. S. Zhang, J. Chem. Phys., 2001, 114, 5164–5169 CrossRef CAS.
- J. M. Hostettler, A. Bach and P. Chen, J. Chem. Phys., 2009, 130, 034303 CrossRef PubMed.
- M. Steinbauer, J. Giegerich, K. H. Fischer and I. Fischer, J. Chem. Phys., 2012, 137, 014303 CrossRef PubMed.
- M. Litorja and B. Ruscic, J. Chem. Phys., 1998, 108, 6748–6755 CrossRef CAS.
- B. Gans, S. Boye-Péronne, M. Broquier, M. Delsaut, S. Douin, C. E. Fellows, P. Halvick, J.-C. Loison, R. R. Lucchese and D. Gauyacq, Phys. Chem. Chem. Phys., 2011, 13, 8140–8152 RSC.
- L. H. Coudert, B. Gans, F. Holzmeier, J.-C. Loison, G. A. Garcia, C. Alcaraz, A. Lopes and A. Roder, J. Chem. Phys., 2018, 149, 224304 CrossRef CAS PubMed.
- S. M. Poullain, D. V. Chicharro, A. Zanchet, L. Rubio-Lago, A. Garcia-Vela and L. Banares, Phys. Chem. Chem. Phys., 2019, 21, 23017–23025 RSC.
- A. K. Rauta and B. Maiti, J. Chem. Phys., 2018, 149, 044308 CrossRef PubMed.
- B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.122g of the Thermochemical Network, 2019, available at http://ATcT.anl.gov) Search PubMed.
- H. Keller-Rudek, G. K. Moortgat, R. Sander and R. Sörensen, Earth Syst. Sci. Data, 2013, 5, 365–373 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the experimental and computational methods used in this study; ionisation energies and dissociative ionisation thresholds for various CxHy (x = 1, 2, y ≤ 6) species of present interest; mass spectra showing CH2 (m/z 14) and CH3 (m/z 15) products from photolysis of C2H6 at λ = 125.6, 121.6, 118.2 and 112.0 nm using two different FEL pulse energies; CH2+ and CH3+ ion images analysed to prepare the P(TKER) and β(TKER) distributions shown in Fig. 4 and a representative C2H3+ ion image acquired following λ = 121.6 nm photolysis of a jet-cooled C2H6 sample. See DOI: 10.1039/d0sc01746a |
| This journal is © The Royal Society of Chemistry 2020 |