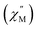Open Access Article
Open Access ArticleTrends in trigonal prismatic Ln-[1]ferrocenophane complexes and discovery of a Ho3+ single-molecule magnet†
Trevor P.
Latendresse
a,
Veacheslav
Vieru
 bc,
Apoorva
Upadhyay
ad,
Nattamai S.
Bhuvanesh
a,
Liviu F.
Chibotaru
*b and
Michael
Nippe
bc,
Apoorva
Upadhyay
ad,
Nattamai S.
Bhuvanesh
a,
Liviu F.
Chibotaru
*b and
Michael
Nippe
 *a
*a
aDepartment of Chemistry, Texas A&M University, 3255 TAMU, College Station, Texas 77843, USA. E-mail: nippe@chem.tamu.edu
bTheory of Nanomaterials Group, Katholieke Universiteit Leuven, Celestijnenlaan 200F, 3001 Leuven, Belgium. E-mail: Liviu.Chibotaru@chem.kuleuven.be
cMaastricht Science Programme, Faculty of Science and Engineering, Maastricht University, Maastricht, Netherlands
dDepartment of Chemistry, Wayne State University, 5101 Cass Ave, Detroit, MI 48202, USA
First published on 24th March 2020
Abstract
Lanthanide metallocenophanes are an intriguing class of organometallic complexes that feature rare six-coordinate trigonal prismatic coordination environments of 4f elements with close intramolecular proximity to transition metal ions. Herein, we present a systematic study of the structural and magnetic properties of the ferrocenophanes, [LnFc3(THF)2Li2]−, of the late trivalent lanthanide ions (Ln = Gd (1), Ho (2), Er (3), Tm (4), Yb (5), Lu (6)). One major structural trend within this class of complexes is the increasing diferrocenyl (Fc2−) average twist angle with decreasing ionic radius (rion) of the central Ln ion, resulting in the largest average Fc2− twist angles for the Lu3+ compound 6. Such high sensitivity of the twist angle to changes in rion is unique to the here presented ferrocenophane complexes and likely due to the large trigonal plane separation enforced by the ligand (>3.2 Å). This geometry also allows the non-Kramers ion Ho3+ to exhibit slow magnetic relaxation in the absence of applied dc fields, rendering compound 2 a rare example of a Ho-based single-molecule magnet (SMM) with barriers to magnetization reversal (U) of 110–131 cm−1. In contrast, compounds featuring Ln ions with prolate electron density (3–5) don't show slow magnetization dynamics under the same conditions. The observed trends in magnetic properties of 2–5 are supported by state-of-the-art ab initio calculations. Finally, the magneto-structural relationship of the trigonal prismatic Ho-[1]ferrocenophane motif was further investigated by axial ligand (THF in 2) exchange to yield [HoFc3(THF*)2Li2]− (2-THF*) and [HoFc3(py)2Li2]− (2-py) motifs. We find that larger average Fc2− twist angles (in 2-THF* and 2-py as compared to in 2) result in faster magnetic relaxation times at a given temperature.
Introduction
Single-molecule magnets (SMMs) are discrete molecules having a bistable magnetic ground state and a sufficient energy barrier to magnetization reversal (U) which can lead to magnetic hysteresis of purely molecular origin.1 SMMs represent the smallest magnetic units that can be predictively modified with synthetic chemistry. This renders SMMs highly attractive research targets and highlights their potential utility as memory components in future data processing and data storage devices.2,3 In recent years, SMM design has largely involved exploiting the magnetic anisotropy of a single metal ion with a finely tuned ligand-field environment. In contrast to the traditional “giant spin” approach in multinuclear metal complexes, designing SMMs with only a single paramagnetic ion offers the inherent advantage of simplified control of the molecular magnetic anisotropy thereby allowing the magnetic anisotropy of a single-ion to be maximized when it resides in an optimal ligand coordination environment. Although significant progress is being reported for transition metal based mononuclear SMMs,4–6 the majority of mononuclear SMMs aim to exploit the intrinsically large single-ion magnetic anisotropy of lanthanide ions which is due to their unquenched orbital angular momentum and can lead to large magnetic moments, especially in the latter half of the lanthanide series.7–11 Indeed, lanthanide-based SMMs can be considered the best performing SMMs to-date, especially given the family of bis-cyclopentadienyl lanthanide based cations, which led most recently to molecules that exhibit magnetic hysteresis at temperatures as high as 80 K.12–18SMM performance is highly dependent on the geometry enforced by the ligands surrounding the central ion. The ligand coordination environment dictates the height of the energy barrier to magnetization reversal (U) as well as influences the rate of quantum tunneling of the magnetization (QTM). For lanthanide ions, the crystal field potential acts as a perturbation on the ground spin–orbit coupled, J, term (within the 2S+1LJ coupling scheme) thereby determining the energy spacing between ground and excited mj projections. In the optimal case of spin relaxation occurring by an “over-the-barrier” Orbach mechanism, the value of U will be proportional to the energy gap of the ground and higher excited mj states.19,20 Molecular symmetry also has direct bearing on the probability of QTM between resonating mj projections. In some ligand field geometries transverse anisotropy terms will be included in the crystal-field Hamiltonian, thereby resulting in rapid QTM.21
With this in mind, understanding how various coordination geometries affect the magnetic anisotropy a Ln3+ ion is crucial in the continued development of high-performance SMMs. Many of the early examples of Ln-based SMMs featured multi-dentate oxygen and/or nitrogen-based donor ligands which naturally resulted in SMMs with high coordination numbers.22–24 Of the “classical” Ln-SMM geometries, those featuring axially elongated square antiprismatic (D4d),11,25–27 axially compressed square antiprismatic (D4d),28,29 or compressed pentagonal bipyramidal (D5h)8,10,30,31 geometries have been some of the most thoroughly investigated. More recently, unique and lower coordinate structural motifs for Ln3+ compounds have been achieved by incorporating organic based ligand scaffolds in SMM design.32–35 Modern organometallic lanthanide chemistry has led to structurally and magnetically important molecules such as the C8 symmetric lanthanide bis-cyclooctatetraene, [Ln(COT)2]−,32–35 and the aforementioned pseudo and strictly linear lanthanide metallocenium, [Ln(CpR)2]+1/0, complexes.
Lanthanide-based SMMs featuring six-coordinate ligand field geometries have been relatively unexplored in terms of relating molecular geometry to the magnetic behavior of various Ln3+ ions.9,36–40 This is most likely due to the relatively low number of six-coordinate lanthanide complexes reported in the literature as compared to those having higher coordination numbers. Of the cubic and trigonal coordination environments for six-coordinate lanthanide compounds, a trigonal ligand field is expected to be more suitable for SMM behavior.41 For a Ln3+ ion residing in an idealized octahedral (Oh) environment, slow magnetic relaxation is not expected, as the absence of the second-order uniaxial anisotropy parameter, B02, from the crystal-field Hamiltonian should exclude the possibility of easy-axis magnetic anisotropy.37,42,43 In contrast, an ideal trigonal prismatic ligand field (D3h) is predicted to stabilize a highly axial ±mj ground state which could result in dynamic SMM behavior. Indeed, recent reports have shown that a trigonal prismatic geometry can support SMM behavior of Dy3+ and Tb3+ ions.36,37,39,40,44,45
Recently, our group utilized the organometallic chemistry of the 1,1'- diferrocenyl (Fc2−) metallo-ligand to synthesize the first Ln-[1]ferrocenophane molecules, [DyFc3(THF)2Li2]− and [TbFc3(THF)2Li2]−, which feature a rare trigonal prismatic arrangement of the six C1 carbons of the three dianionic Fc2− ligands.44,45 [DyFc3(THF)2Li2]− and [TbFc3(THF)2Li2]− both exhibit zero applied field SMM behavior, with magnetic anisotropy energy barriers of U = 110 cm−1 and U = 274 cm−1, respectively. It is important to note that, to the best of our knowledge, [TbFc3(THF)2Li2]− features the largest zero-field magnetization energy barrier for a Ln–SMM with trigonal prismatic geometry. We recognized the [LnFc3(THF)2Li2]− structural motif as an ideal template for investigating the relationship between trigonal prismatic molecular geometry and the magnetic anisotropy of the rest of the late Ln3+ ions. The homoleptic coordination environment of [LnFc3(THF)2Li2]− leads to higher symmetry compared to many of the previously reported trigonal prismatic SMMs which contain hetero-ligand donor atoms.
Herein, we report the synthesis, structural, and magnetic characterization of the late Ln-[1]ferrocenophane complexes, [Li(THF)4][LnFc3(THF)2Li2] (Ln = Gd (1), Ho (2), Er (3), Tm (4), Yb (5), Lu (6)). Of the compounds reported, the Ho-[1]ferrocenophane compound [HoFc3(THF)2Li2]− exhibits slow magnetic relaxation in the absence of externally applied dc fields which renders it a rare example of a non-Kramers Ho3+ SMM. Furthermore, we show how small distortions in the trigonal prismatic ligand field can lead to dramatic differences in magnetization dynamics of the Ho-[1]ferrocenophane structural motif by synthesizing and magnetically characterizing the pyridine (py) and 2-methyl THF (THF*) solvent adducts, [Li(py)4][HoFc3(py)2Li2] (2-py) and [Li(THF*)4][HoFc3(THF*)2Li2] (2-THF*), respectively. Compounds 1–6 were also investigated by ab initio computational methods which provided further insight into the electronic structure of the Ln3+ ions residing in a trigonal prismatic ligand field geometry and their observed static and dynamic magnetic properties.
Results and discussion
Synthesis
The late Ln-[1]ferrocenophane compounds [Li(THF)4][LnFc3Li(THF)2] (Ln = Gd (1), Ho (2), Er (3), Tm (4), Yb (5), or Lu (6)) were prepared using a previously reported protocol via the salt elimination reaction of anhydrous LnCl3 with excess Li6Fc3(TMEDA)2 (TMEDA = tetramethylethylenediamine) in THF (Fig. 1).44,45 Crude 1–6 are moderately soluble in Et2O which allows for their facile separation from insoluble unreacted starting materials and/or biproducts. Following an Et2O extraction, crude 1–6 are recrystallized by slow diffusion of pentane into their concentrated THF solutions, forming highly air and moisture sensitive plate crystals of 1–6 in yields between 21–91% (based on Ln). The relatively high yield of the Tm-[1]ferrocenophane compound 4 (91%), is an outlier and could be a result of the Tm3+ six-coordinate ionic radii (0.880 Å) being the optimal size for the [LnFc3]3− coordination environment. Compound 1 can also be synthesized using anhydrous GdI3 but in lower yields due to difficult separation of (THF)xLiI or [(TMEDA)2LiI]2 salt biproducts. Furthermore, depending on the crystallinity of the LnCl3 salt, higher yields are obtained for compounds 1–6 by forming the LnCl3(THF)x solvate prior to addition to Li6Fc3(TMEDA)2.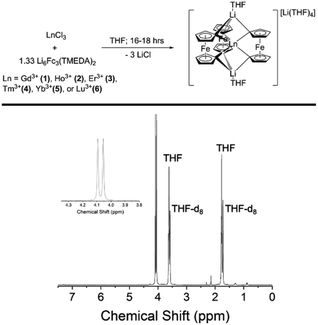 | ||
| Fig. 1 (Top) Preparation of late Ln-[1]ferrocenophane compounds. (Bottom) 1H NMR (400 MHz, THF-d8) of the Lu-[1]ferrocenophane compound 6. | ||
The low temperature crystallization of the heaviest Yb- and Lu-[1]ferrocenophane complexes 5 and 6 resulted in a mixture of crystals with two habits: crystals of plate and rod-like shapes could easily be identified. Analysis of both morphologies via single-crystal X-ray diffraction (vide infra) determined the rod-shaped crystals to contain structurally unique solvate of the [LnFc3(THF)2Li2]− anion (hereon denoted as 5Iso and 6Iso) whereas the plate crystals are isostructural to 1–4. The crystalline structure of 5Iso and 6Iso differs from 5 and 6 by means of an extra THF solvate molecule located in the crystal lattice. The formation of multiple solvates is unique to the preparation of 5 and 6 and could be a consequence of the ionic radii of Yb3+ and Lu3+ being the smallest of the 4f series.
The diamagnetic nature of the 4f14 electron configuration of the Lu3+ ion allows for facile analysis of the solution phase structure of 6 and 6Iso by 1H-NMR spectroscopy. The 1H-NMR spectrum of a mixture of 6 and 6Iso in THF-d8 shows nearly identical chemical shifts as the previously reported [Li(THF)4][YFc3(THF)2Li2] compound, with two downfield resonances at 4.05 ppm and 4.09 ppm corresponding to the two sets magnetically inequivalent protons of the diferrocenyl ligands (Fig. 1). The presence of only two resonances corresponding to the Fc2− ligand protons suggest the solution phase structures of 6 and 6Iso are similar on the NMR measurement timescale.
Once crystalized, compounds 1–6 are highly insoluble in nonpolar alkanes and ethers such as pentane, diethyl ether, and 1,4-dioxane as well as weakly or non-coordinating polar solvents, such as difluorobenzene. In contrast, 1–6 are highly soluble in polar coordinating solvents such as THF, 2-methyl THF (THF*) and pyridine (py). The solubility properties of 1–6 suggest that dissolution could involve coordination of the polar coordinating solvent to the Li+ ions within the lattice of 1–6. Therefore, we hypothesized that various solvent adducts of the general formula [Li(sol)x][LnFc3(sol)2Li2], where sol is a polar coordinating solvent, could be synthesized. Indeed, the synthesis of the Ho-[1]ferrocenophane solvent adducts, [Li(py)4][HoFc3(py)2Li2] (2-py) and [Li(THF*)4][HoFc3(THF*)2Li2] (2-THF*), was achieved by slow diffusion of pentanes into pyridine and 2-methyl THF solutions of [Li(THF)4][HoFc3(THF)2Li2], respectively. Single crystal X-ray diffraction studies of 2-py and 2-THF* (vide infra) reveal that for 2-py all coordinated THF molecules have been replaced by pyridine molecules. On the other hand, the structure of 2-THF* indicates significant disorder in the THF* solvate molecules which could suggest a statistical mixture of [Li–THF]+ and [Li–THF*]+ units within the same crystal lattice.
Solid state structural determination
The unit cells of 1–6 contain two structurally unique Ln-[1]ferrocenophane molecules per asymmetric unit (Ln(1) and Ln(2)), each having similar bonding parameters (Table 1). Across the series the average Ln–C bond distances decrease from 2.572[8] Å and 2.569[8] Å for 1 (Gd(1) and Gd(2), respectively) to 2.501[11] Å and 2.497[11] Å for compound 6 (Lu(1) and Lu(2), respectively). The observed decrease in Ln–C bond distance with increase in atomic number is most likely due to the increased Lewis acidity and/or the smaller ionic radii of the heaviest Ln3+ ions. The intramolecular Ln⋯Fe distances show a more subtle change across the period decreasing from 3.2281[12] Å and 3.2300[12] Å for 1 (Gd(1) and Gd(2), respectively) to 3.2108[16] Å and 3.2068[16] Å for 6 (Lu(1) and Lu(2), respectively). The average Ln⋯Fe distances between 3.2300[12] to 3.2068[16] Å are some of the closest reported for any heterometallic Ln–Fe species, but lie just outside the sum of the covalent radii of the Fe2+ and Ln3+ ions.46
| Compound | 1 (Gd) | 2 (Ho) | 3 (Er) | 4 (Tm) | 5 (Yb) | 6 (Lu) |
|---|---|---|---|---|---|---|
| Ln(1)–C, Å | 2.572[8] | 2.532[13] | 2.521[9] | 2.520[5] | 2.499[17] | 2.501[11] |
| Ln(2)–C, Å | 2.569[8] | 2.539[12] | 2.522[9] | 2.517[5] | 2.503[16] | 2.497[11] |
| Ln(1)⋯Fe, Å | 3.2281[12] | 3.229[8] | 3.2196[14] | 3.214[8] | 3.213[2] | 3.2108[16] |
| Ln(2)⋯Fe, Å | 3.2300[12] | 3.221[13] | 3.2172[14] | 3.212[8] | 3.209[2] | 3.2068[16] |
| Ln(1) C1–Fe–C1, ° | 105.3[3] | 103.5[5] | 102.9[4] | 103.1[2] | 102.1[7] | 102.2[4] |
| Ln(2) C1–Fe–C1, ° | 104.9[3] | 103.8[5] | 103.1[4] | 103.0[2] | 102.3[7] | 102.1[1] |
| C–Ln(1)–C, ° | 80.9[3] | 81.3[4] | 80.7[3] | 80.9[2] | 81.0[6] | 80.8[4] |
| C–Ln(2)–C, ° | 81.0[3] | 81.3[4] | 80.8[3] | 81.0[2] | 81.1[6] | 81.1[4] |
| Ln(1), Fc2− twist, ° | 8.16 | 10.67 | 11.57 | 12.76 | 13.18 | 14.24 |
| Ln(2), Fc2− twist, ° | 9.64 | 12.67 | 14.49 | 16.23 | 16.65 | 18.56 |
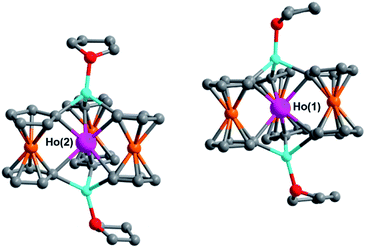
Despite miniscule differences in the average bonding parameters between the distinct Ln(1) and Ln(2) molecules within each unit cell of 1–6, each molecule shows significant differences of the average Fc2− ligand twist angle. Here, the ligand twist angle is defined by the torsion of the two C1 donor atoms of a single diferrocenyl ligand with respect to the centroids (previously described) of the trianionic pockets located above and below equatorial plane of the molecule (see Fig. 3 left inset). A ligand twist angle greater than 0° would indicate distortion of the molecular geometry away from ideal trigonal prismatic geometry. For the Ho(1) and Ho(2) molecules of compound 2, the average ligand twist angles are 10.67° and 12.67°, respectively. It is important to note here that such small differences in the ligand field geometry can greatly influence the spectroscopic and magnetic characteristics of a Ln3+ ion.47,48 Considering the Ln(2) molecules across the heavy lanthanide series, the average diferrocenyl twist angle has an inversely proportional relationship to the 6-coordinate ionic radius of the Ln3+ ion, increasing from 9.64° for Gd(2) (rGd3+ = 0.938 Å) to 18.56° for Lu(2) (rLu3+ = 0.861 Å). The Ln(1) molecules across the period show an identical trend. This inverse relationship between twist angle and ionic radius can be explained by the increased steric hindrance of the [Fc3]6− ligand field as the Ln3+ ionic radius decreases and the needed ‘twist’ of the Fc2− ligands to stabilize the smaller Ln3+ center.
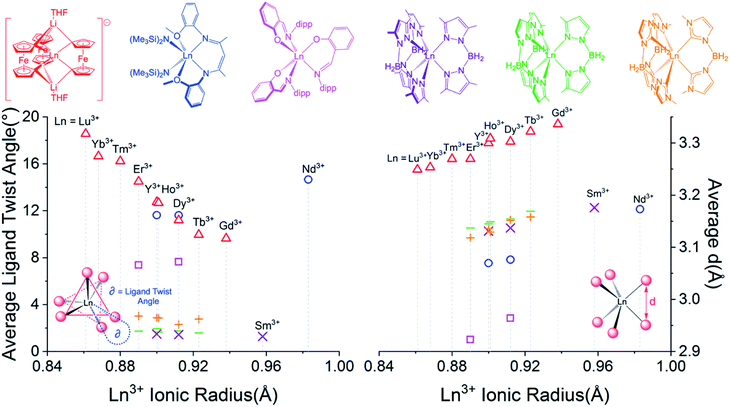 | ||
| Fig. 3 (Left) Ligand twist angle dependence on Ln3+ ionic radius of Ln(2) molecules of [LnFc3(THF)2Li2]− and selected previously reported trigonal prismatic lanthanide complexes. (Right) Dependence of average ligand donor distance, d (defined in right inset), on the Ln3+ ionic radius. Triangles = Ln(2) of 1–6 ([YFc3(THF)2Li2]− included from ref. 51), squares = [Ln(L)3], circles = [(LCO)Ln(N(SiMe3)2)2], crosses = Ln(BcMe)3, lines = Ln(BpMe)3, and X = Ln(Bp2Me)3 (Y3+ compounds included for selected examples). | ||
For the trigonal prismatic geometry, comparison of the distance, d, between eclipsed ligand donor atoms or pseudo eclipsed donors (in the case of a ligand twist angle > 0) for a series of similar complexes can indicate the degree of ligand rigidity as well as the axiality trigonal ligand field of the central Ln3+ ion. In the case of [LnFc3(THF)2Li2]−, d would be the distance between the two C1 donors of a single Fc2− ligand (see Fig. 3 right inset) and is proportional to the C–Ln–C bite angle. For the Ln(2) molecules of 1–6, the largest average d value of the three Fc2− ligands is 3.336 Å for 1 which features the largest Gd3+ ion. Upon moving across the row, the average C1⋯C1 distance of the Fc2− ligand decreases to a value of 3.249 Å for 6 (Fig. 3 right). The decrease in average Fc2− C1⋯C1 distance with decrease in Ln3+ ionic radii is accompanied by a decrease in the average C1–Fe–C1 angle of the Fc2− ligand from 104.9°[3] for the Gd(2) in 1 to 102.1°[1] for Lu(2) in 6.
In order to gain a more comprehensive picture of the geometric trends in trigonal prismatic lanthanide compounds, we compared the average ligand twist angle and d values of 1–6 with the same parameters of selected previously reported trigonal prismatic lanthanide complexes [(LCO)Ln(N(SiMe3)2)2] (HLCO = {N-[(2-MeO)–C6H5]}N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(Me)CH
C(Me)CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(Me)N(H){N'-[(2-MeO)C6H5]}; Ln = Nd3+, Dy3+, or Y3+),37,49, [Ln(L)3] (HL = 2-(((2,6-diisopropylphenyl)imino)methyl)-phenol; Ln = Dy3+ or Er3+),36 Ln(BpMe2)3 ([BpMe2]− = dihydrobis(dimethylpyrazole)borate; Ln = Sm3+, Dy3+, or Y3+),39,50 Ln(BpMe)3 ([BpMe]− = dihydrobis(methylpyrazole)borate; Ln = Tb3+, Dy3+, Y3+, Ho3+, or Er3+), and Ln(BcMe)3 ([BcMe]− = dihydrobis(methylimidazolyl)borate; Ln = Tb3+, Dy3+, Y3+, Ho3+, or Er3+)40 (Fig. 3). Of the compared complexes, 1–6, Ln(BpMe2)3, Ln(BpMe), and Ln(BcMe)3 feature a homo-ligand donor environment around the central Ln3+ ions. To this end, for the tris-pyrazolyl and tris-imidazolyl borate complexes, the possibility of HB–H⋯Ln agostic interactions complicate a complete structural comparison with these compounds. Upon inspection of Fig. 3 (Left), it is apparent that the Ln-[1]ferrocenophane complexes, 1–6, feature the greatest susceptibility of ligand twist angle with a change in ionic radius. Furthermore, in contrast to the Ln-[1]ferrocenophane series, [(LCO)Ln(N(SiMe3)2)2], [Ln(L)3], Ln(BpMe2)3, Ln(BpMe)3, and Ln(BcMe)3 feature an increase of the average ligand twist angle with Ln3+ ionic radius or do not show a significant correlation at all (in the case of the tris–borate complexes).
C(Me)N(H){N'-[(2-MeO)C6H5]}; Ln = Nd3+, Dy3+, or Y3+),37,49, [Ln(L)3] (HL = 2-(((2,6-diisopropylphenyl)imino)methyl)-phenol; Ln = Dy3+ or Er3+),36 Ln(BpMe2)3 ([BpMe2]− = dihydrobis(dimethylpyrazole)borate; Ln = Sm3+, Dy3+, or Y3+),39,50 Ln(BpMe)3 ([BpMe]− = dihydrobis(methylpyrazole)borate; Ln = Tb3+, Dy3+, Y3+, Ho3+, or Er3+), and Ln(BcMe)3 ([BcMe]− = dihydrobis(methylimidazolyl)borate; Ln = Tb3+, Dy3+, Y3+, Ho3+, or Er3+)40 (Fig. 3). Of the compared complexes, 1–6, Ln(BpMe2)3, Ln(BpMe), and Ln(BcMe)3 feature a homo-ligand donor environment around the central Ln3+ ions. To this end, for the tris-pyrazolyl and tris-imidazolyl borate complexes, the possibility of HB–H⋯Ln agostic interactions complicate a complete structural comparison with these compounds. Upon inspection of Fig. 3 (Left), it is apparent that the Ln-[1]ferrocenophane complexes, 1–6, feature the greatest susceptibility of ligand twist angle with a change in ionic radius. Furthermore, in contrast to the Ln-[1]ferrocenophane series, [(LCO)Ln(N(SiMe3)2)2], [Ln(L)3], Ln(BpMe2)3, Ln(BpMe)3, and Ln(BcMe)3 feature an increase of the average ligand twist angle with Ln3+ ionic radius or do not show a significant correlation at all (in the case of the tris–borate complexes).
In general, all five sets of compared trigonal prismatic lanthanide complexes exhibit an increase in the average eclipsed/pseudo eclipsed ligand donor distanced, with an increase in Ln3+ ionic radii (Fig. 3, right). Despite this similar trend, the Ln-[1]ferrocenophane complexes, 1–6, feature the largest average d values of the compared complexes. This distinction is significant and could suggest the Fc2− donor ligands of 1–6 might interact more strongly with f-orbitals of z-character, which in turn would have a significant influence of the magnetism of these compounds.
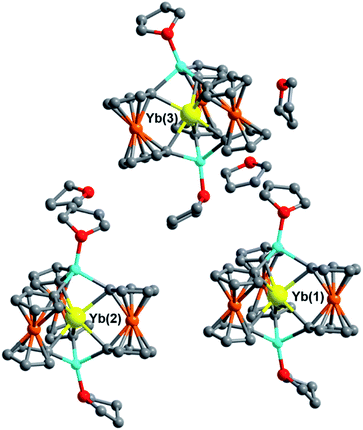
The single-crystal X-ray structures for the Yb3+ and Lu3+ solvates, 5Iso and 6Iso, were solved in the monoclinic space group Ia and Cc, respectively, inside a unit cell with lengths between 20–33 Å. Though solved in different space groups, 5Iso and 6Iso are most likely isostructural given the almost identical unit cell volumes of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 344(3) Å3 (for 5Iso) and 16
344(3) Å3 (for 5Iso) and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419(4) Å3 (for 6Iso) (see ESI† for details). Both 5Iso and 6Iso contain three structurally unique [Li(THF)4][LnFc3(THF)2Li2] molecules per unit cell along with an uncoordinated THF lattice solvate per Ln-[1]ferrocenophane molecule which is not present in compounds 5 and 6 (Fig. 4). The average Ln–C and Ln⋯Fe distances for the three independent molecules of 5Iso and 6Iso are close to the corresponding distances for the two independent molecules of compound 5 and 6, respectively (Table S12†). To this end, the average Fc2− twist angles vary significantly between corresponding solvates. The most distorted molecules of the THF solvated molecules, 5Iso and 6Iso, exhibit a 3.3° and a 2.4° increase in twist angle when compared to the most highly distorted molecules of 5 and 6, respectively. This result is significant as it highlights how crystal packing effects can greatly influence the geometry of the inner coordination sphere of the individual molecules in the solid state.
419(4) Å3 (for 6Iso) (see ESI† for details). Both 5Iso and 6Iso contain three structurally unique [Li(THF)4][LnFc3(THF)2Li2] molecules per unit cell along with an uncoordinated THF lattice solvate per Ln-[1]ferrocenophane molecule which is not present in compounds 5 and 6 (Fig. 4). The average Ln–C and Ln⋯Fe distances for the three independent molecules of 5Iso and 6Iso are close to the corresponding distances for the two independent molecules of compound 5 and 6, respectively (Table S12†). To this end, the average Fc2− twist angles vary significantly between corresponding solvates. The most distorted molecules of the THF solvated molecules, 5Iso and 6Iso, exhibit a 3.3° and a 2.4° increase in twist angle when compared to the most highly distorted molecules of 5 and 6, respectively. This result is significant as it highlights how crystal packing effects can greatly influence the geometry of the inner coordination sphere of the individual molecules in the solid state.
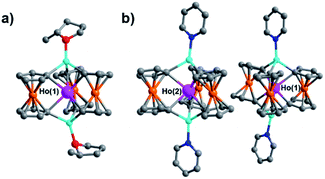
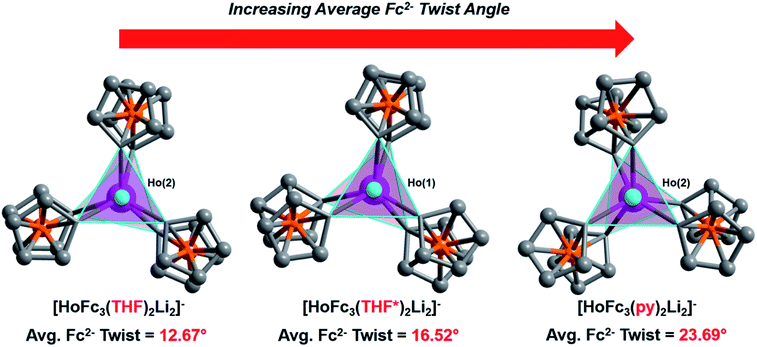
Though little variation is observed in the interatomic Ho–C distances between 2, 2-THF*, and 2-py, the average Fc2− twist angle varies significantly upon changing the identity of the axial [Li-sol]+ moiety. Considering the most highly distorted molecule within each of the unit cells, the average Fc2− twist angle increases from 12.67° (for 2), to 16.52° (for 2-THF*), to 23.69° (for 2-py) (Fig. 6). The average Fc2− twist angle for 2-py represents the largest of any of the Ln-[1]ferrocenophane compounds reported herein. As shown previously with the structural variation between the corresponding solvates of the Yb- and Lu-[1]ferrocenophane complexes, crystal packing can greatly influence the geometry of the [LnFc3(THF)2Li2]− inner coordination sphere. The variation in the crystal packing for 2, 2-THF*, and 2-py is also emphasized by the changes in the closest intermolecular distances between Ho3+ sites of 10.586 Å (for 2), 11.069 Å (for 2-THF*), and 8.941 Å (for 2-py) (Table S14†). The varying electronic donor strengths of the solvent molecules likely plays an additional role in the geometric variation between 2, 2-THF*, and 2-py though similar Li–C and Li⋯Ho interatomic distance between the molecules precludes any further discussion here.
Magnetic properties
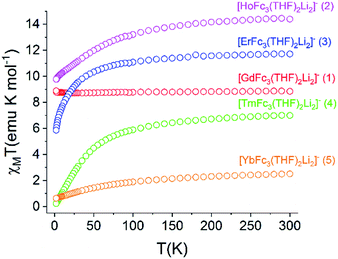
The static magnetic behavior of 1–5 was further investigated by measuring the field dependence of the magnetization between 2–8 K (Fig. S12†). For compounds 2–5, the 2 K magnetization values at the 7 T field limit are 5.11 μB (for 2), 6.16 μB (for 3), 1.28 μB (for 4), and 1.36 μB (for 5), respectively, and are much lower than the expected single ion Ms values of 10 μB (for Ho3+), 9 μB (for Er3+), 7 μB (for Tm3+), and 4 μB (for Yb3+). This discrepancy suggests anisotropy of the lowest energy J multiplets of the respective Ln3+ ion which results in non-degenerate mj microstates. The inherent magnetic anisotropy of 2–5 is further supported by the non-superposition of the M vs. H/T curves between 2–8 K (Fig. S13†). For compound 1, the 2 K magnetization curve reaches a maximum value of 7.78 μB at 7 T which corresponds nicely to the expected value of 7 μB for a single Gd3+ ion. This data along with the superposition of the M vs. H/T curves between 2–8 K supports the isotropic nature of an isolated S = 7/2 ground state in 1.
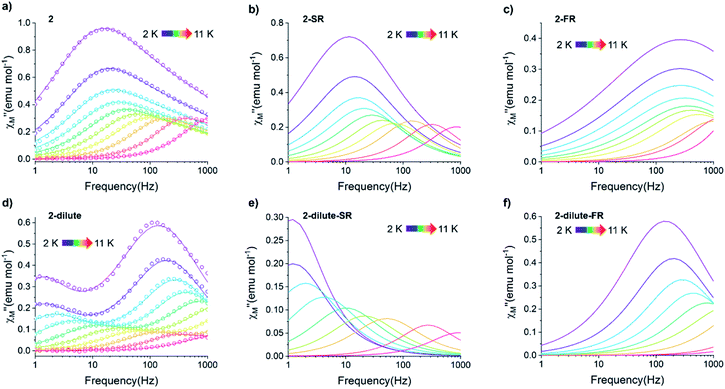
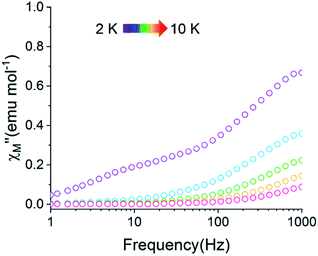
A common characteristic among the few reported Ho-based SMMs is a highly symmetric axial ligand field environment which stabilizes a suitably anisotropic mj ground state of the oblate Ho3+ ion. Previous ab initio studies of the Dy- and Tb-[1]ferrocenophane compounds suggest the three diferrocenyl ligands of [LnFc3(THF)2Li2]− promote a largely axial ligand field that stabilizes large mj ground states in the oblate Dy3+ and Tb3+ ions. Based on these results, we hypothesized that the trigonal prismatic [Fc3]6− ligand field could be suitable to promote a highly anisotropic ground state in the oblate Ho3+ ion resulting in SMM behavior in the [HoFc3(THF)2Li2]− complex. In order to probe the SMM behavior in 2, the variable temperature alternating current (ac) magnetic susceptibility was measured in the absence of an external magnetic field. The presence of a broad temperature dependent signal in the molar out-of-phase component 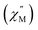 of the ac magnetic susceptibility versus frequency plot indicates 2 is indeed a rare example of zero applied field Ho3+ SMM (Fig. 8a). Between 2–5 K, the
of the ac magnetic susceptibility versus frequency plot indicates 2 is indeed a rare example of zero applied field Ho3+ SMM (Fig. 8a). Between 2–5 K, the 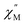 signal maximum is slightly temperature dependent, shifting to higher frequencies upon increasing the temperature. This slight variation of the
signal maximum is slightly temperature dependent, shifting to higher frequencies upon increasing the temperature. This slight variation of the 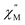 maximum with temperature is significant as it suggests contributions to the spin relaxation from thermally assisted Raman and/or Orbach mechanisms even at the lowest temperatures. Increasing the temperature above 5 K, the
maximum with temperature is significant as it suggests contributions to the spin relaxation from thermally assisted Raman and/or Orbach mechanisms even at the lowest temperatures. Increasing the temperature above 5 K, the 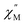 maximum becomes increasingly temperature dependent, moving outside the 1000 Hz frequency limit at 11 K.
maximum becomes increasingly temperature dependent, moving outside the 1000 Hz frequency limit at 11 K.
The exceptionally broad nature of the 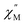 signal of 2 indicates multiple spin relaxation processes are occurring at similar ac frequencies.61 It is likely that this observation is predominately a result of the two structurally unique Ho(1) and Ho(2) sites in the solid state structure of 2 having slightly different magnetization dynamics. However, the complexity of the spin dynamics of Ln–SMMs has recently been emphasized and the simultaneous contribution from Raman, Orbach, and QTM processes to the spin relaxation of a single Ho3+ ion cannot be excluded.62 The molar in-phase
signal of 2 indicates multiple spin relaxation processes are occurring at similar ac frequencies.61 It is likely that this observation is predominately a result of the two structurally unique Ho(1) and Ho(2) sites in the solid state structure of 2 having slightly different magnetization dynamics. However, the complexity of the spin dynamics of Ln–SMMs has recently been emphasized and the simultaneous contribution from Raman, Orbach, and QTM processes to the spin relaxation of a single Ho3+ ion cannot be excluded.62 The molar in-phase 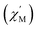 and the out-of-phase
and the out-of-phase 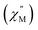 components of the ac magnetic susceptibility of 2 were used to construct Cole–Cole plots
components of the ac magnetic susceptibility of 2 were used to construct Cole–Cole plots 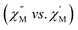 at each temperature which were subsequently fit with eqn (1):
at each temperature which were subsequently fit with eqn (1):
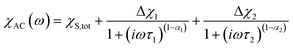 | (1) |
(Cole–Cole parameters defined in ESI†). Eqn (1) represents the sum of two modified Debye functions and describes two magnetic relaxation processes each having a characteristic magnetic relaxation time, τ1 and τ2, at each temperature.
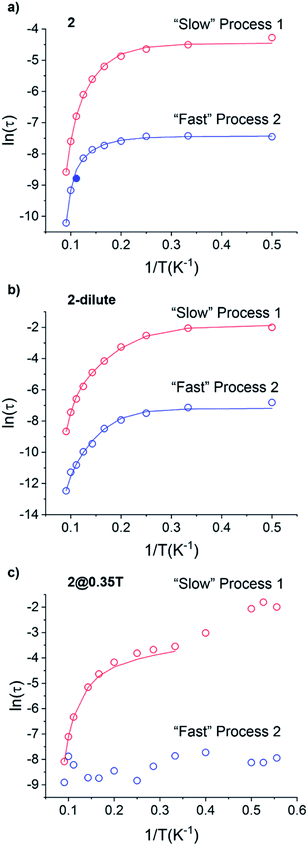
Using the extracted Cole–Cole parameters at each temperature, a “slow” (SR) and a “fast” (FR) relaxation process could be resolved in the 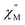 versus frequency plot of 2, where the 2 K
versus frequency plot of 2, where the 2 K 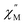 signal maxima of SR and FR appear at 11.6 and 262.5 Hz, respectively (Fig. 8b and c). For FR, the shorter 2 K magnetic relaxation time of τ2 = 0.00058 s (as compared to τ1 = 0.014 s for SR) and the temperature independence of the
signal maxima of SR and FR appear at 11.6 and 262.5 Hz, respectively (Fig. 8b and c). For FR, the shorter 2 K magnetic relaxation time of τ2 = 0.00058 s (as compared to τ1 = 0.014 s for SR) and the temperature independence of the 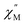 signal maximum suggests significant contribution of QTM to the spin relaxation. The origin of the increased QTM contribution for FR is most likely due to transverse fields arising from intermolecular interactions between neighboring spin centers or nuclear hyperfine interactions.
signal maximum suggests significant contribution of QTM to the spin relaxation. The origin of the increased QTM contribution for FR is most likely due to transverse fields arising from intermolecular interactions between neighboring spin centers or nuclear hyperfine interactions.
To further investigate the origin of QTM in 2, the magnetically dilute species, [Li(THF)4][Y0.94Ho0.06Fc3(THF)2Li2] (2-dilute), was prepared and magnetically characterized. Similar to 2, the zero-field ac magnetic susceptibility data of 2-dilute provides evidence of multiple spin relaxation processes, with two distinct maxima appearing at 1.2 Hz and 107.8 Hz in the 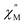 vs. Frequency plot at 2 K (Fig. 8d). As previously described, a FR and SR process were resolved by fitting the ac magnetic susceptibility of 2-dilute with eqn (1) (Fig. 8e amd f). The 2 K magnetic relaxation times of τ1 = 0.14 s (for SR) and τ2 = 0.0011 s (for FR) are at least half of an order of magnitude longer than the corresponding SR and FR processes for non-dilute 2 at the same temperature. This result is significant as it suggests that intermolecular magnetic interactions are playing a non-negligible role in the low temperature magnetization dynamics of compound 2. To this end, the
vs. Frequency plot at 2 K (Fig. 8d). As previously described, a FR and SR process were resolved by fitting the ac magnetic susceptibility of 2-dilute with eqn (1) (Fig. 8e amd f). The 2 K magnetic relaxation times of τ1 = 0.14 s (for SR) and τ2 = 0.0011 s (for FR) are at least half of an order of magnitude longer than the corresponding SR and FR processes for non-dilute 2 at the same temperature. This result is significant as it suggests that intermolecular magnetic interactions are playing a non-negligible role in the low temperature magnetization dynamics of compound 2. To this end, the 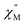 maximum of the SR processes of 2-dilute at low temperatures is still only marginally temperature dependent which might indicate intramolecular phenomenon such as nuclear hyperfine interactions are contributing to the QTM of 2.
maximum of the SR processes of 2-dilute at low temperatures is still only marginally temperature dependent which might indicate intramolecular phenomenon such as nuclear hyperfine interactions are contributing to the QTM of 2.
QTM pathways can also be mitigated by creating a field bias upon the application of an external magnetic field which breaks the degeneracy of the ±mj crystal field states thereby lowering the probability of spin relaxation through tunneling mechanisms. The temperature dependence of the ac magnetic susceptibility of compound 2 was measured under an optimal 0.35 T magnetic field (Fig. S31†) from 1.8–11 K. In an external field, the 2 K 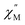 signal of 2@0.35T remains broad but shows a significant shift of the maximum to lower frequencies suggesting an increase in the magnetic relaxation time (Fig. 9). Heating the sample to 5 K results in a high frequency shift of the
signal of 2@0.35T remains broad but shows a significant shift of the maximum to lower frequencies suggesting an increase in the magnetic relaxation time (Fig. 9). Heating the sample to 5 K results in a high frequency shift of the 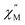 maximum as well as an increase in the magnitude of the signal. Interestingly, heating past 5 K results in an increase in symmetry of the
maximum as well as an increase in the magnitude of the signal. Interestingly, heating past 5 K results in an increase in symmetry of the 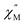 signal and indicates the spin dynamics of 2@0.35T is shifting towards a single relaxation process at higher temperatures. The 2@0.35T magnetic relaxation time for the SR process at 2 K of τ1 = 0.13 s (determined using eqn (1)) is close to the corresponding SR process relaxation time for 2-dilute at the same temperature. This observation suggests application of an external field and magnetic dilution have similar effects on the magnetization dynamics of 2, at least when considering only the SR process.
signal and indicates the spin dynamics of 2@0.35T is shifting towards a single relaxation process at higher temperatures. The 2@0.35T magnetic relaxation time for the SR process at 2 K of τ1 = 0.13 s (determined using eqn (1)) is close to the corresponding SR process relaxation time for 2-dilute at the same temperature. This observation suggests application of an external field and magnetic dilution have similar effects on the magnetization dynamics of 2, at least when considering only the SR process.
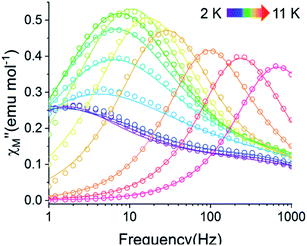 | ||
Fig. 9 Temperature dependence of the out-of-phase component of the molar ac magnetic susceptibility 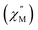 of 2@0.35T (H = 0.35 T, T = 2–11 K). Lines represent fits to the experimental data (circles). of 2@0.35T (H = 0.35 T, T = 2–11 K). Lines represent fits to the experimental data (circles). | ||
The magnetic relaxation times extracted using eqn (1) were used to construct Arrhenius plots (ln(τ) vs. 1/T) for each of the SR and FR processes of 2, 2-dilute, and 2@0.35T (Fig. 10). Each Arrhenius plot was fit using eqn (2), which accounts for spin relaxation through direct, QTM, Raman, and Orbach relaxation processes.63
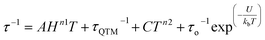 | (2) |
In the case of 2 and 2-dilute where H = 0 T, the direct term AHn1T becomes zero and was therefore disregarded. For 2@0.35T, the direct term A = 114 S−1 T−2 K−1 was determined by fitting the field dependence of the magnetic relaxation time (Fig. S31†). Due to the complicated nature of the 2@0.35T ac magnetic susceptibility, the low temperature regime (1.8–2.5 K) could not be fit accurately and only the higher temperature regime (3–11 K) of the SR process was considered in the Arrhenius fitting procedure. The best fit parameters obtained using this fitting procedure for 2, 2-dilute, and 2@0.35T are given in Table 2. It is important to note that the fitting parameters for the FR process of 2 and 2-dilute should only be considered as rough estimates, as the 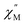 maximum of the resolved signal lies outside of the measured frequency range at higher temperatures. For all fits, the obtained Raman coefficients (n2) are close to the expected range of n2 = 5–7 for a non-Kramers ion.63 For the FR and SR processes of 2, 2-dilute, and 2@0.35T energy barrier values between U = 110–131 cm−1 were obtained.
maximum of the resolved signal lies outside of the measured frequency range at higher temperatures. For all fits, the obtained Raman coefficients (n2) are close to the expected range of n2 = 5–7 for a non-Kramers ion.63 For the FR and SR processes of 2, 2-dilute, and 2@0.35T energy barrier values between U = 110–131 cm−1 were obtained.
| Compound | 2 | 2@0.35T | 2-dilute |
|---|---|---|---|
| Relaxation process 1 | |||
| A (S−1 T−2 K−1) | 114 | ||
| τ QTM (s) | 0.0116 | 0 | 0.157 |
| C (s−1 K−n) | 0.00132 | 0.000261 | 0.00432 |
| n | 4.92 | 6.47 | 5.29 |
| τ o (s) | 1.56 × 10−10 | 2.88 × 10−11 | 2.88 × 10−11 |
| U (cm−1) | 110 | 129 | 121 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Relaxation process 2 | |||
| A (S−1 T−2 K−1) | |||
| τ QTM (s) | 0.000593 | 0.000755 | |
| C (s−1 K−n) | 0.251 | 0.00679 | |
| n | 4.25 | 6.08 | |
| τ o (s) | 2.02 × 10−12 | 6.21 × 10−13 | |
| U (cm−1) | 131 | 126 | |
The static magnetic behavior of 2-py is nearly identical to that of compound 2 (Fig. S11†). Interestingly, the dynamic magnetic properties of 2-py are markedly different from that of compound 2 (Fig. 11). Compound 2-py features extremely broad signals in the 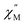 vs. frequency plot but does not feature any discernable signal maxima within the measured 1–1000 Hz frequency range. This qualitative observation readily suggests that the magnetic relaxation times for the more geometrically distorted Ho-[1]ferrocenophane molecules in 2-py, are much faster than the magnetic relaxation times observed for the Ho-[1]ferrocenophane molecules in 2, which features a low frequency
vs. frequency plot but does not feature any discernable signal maxima within the measured 1–1000 Hz frequency range. This qualitative observation readily suggests that the magnetic relaxation times for the more geometrically distorted Ho-[1]ferrocenophane molecules in 2-py, are much faster than the magnetic relaxation times observed for the Ho-[1]ferrocenophane molecules in 2, which features a low frequency 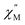 signal maximum at 18.2 Hz at 2 K. Upon increasing the temperature above 2 K, the
signal maximum at 18.2 Hz at 2 K. Upon increasing the temperature above 2 K, the 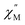 signal of 2-py moves out of the high frequency limit and almost completely disappears at 10 K. Out-of-phase signals at only the highest frequencies without signal maxima within the frequency range could suggest QTM is a major contributor to the spin relaxation in 2-py. Although the magnetic relaxation of 2-py is too fast to allow the extraction of an energy barrier of magnetization reversal, the presented data suggests that the deviation from idealized trigonal prismatic geometry (increase in torsion angle) increases relaxation times.
signal of 2-py moves out of the high frequency limit and almost completely disappears at 10 K. Out-of-phase signals at only the highest frequencies without signal maxima within the frequency range could suggest QTM is a major contributor to the spin relaxation in 2-py. Although the magnetic relaxation of 2-py is too fast to allow the extraction of an energy barrier of magnetization reversal, the presented data suggests that the deviation from idealized trigonal prismatic geometry (increase in torsion angle) increases relaxation times.
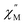 vs. Frequency plot in the absence of an external magnetic field. This result is not surprising as the axial [LnFc3]3− ligand field likely destabilizes the largest mj = ±15/2, ±6, and ±7/2 projections of the prolate Er3+, Tm3+, and Yb3+ ions, respectively. These results are also consistent with dc magnetization data for the Tm3+ compounds, 4, which suggest the lowest energy mj = 0 ground state for 4.
vs. Frequency plot in the absence of an external magnetic field. This result is not surprising as the axial [LnFc3]3− ligand field likely destabilizes the largest mj = ±15/2, ±6, and ±7/2 projections of the prolate Er3+, Tm3+, and Yb3+ ions, respectively. These results are also consistent with dc magnetization data for the Tm3+ compounds, 4, which suggest the lowest energy mj = 0 ground state for 4.
For the Yb3+ compound 5/5Iso, application of an optimal 0.2 T external magnetic field results in slow magnetic relaxation behavior as evidenced by a narrow temperature dependent signal in 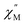 vs. Frequency plot (Fig. 12a). Between 1.8–2 K, the magnitude of the
vs. Frequency plot (Fig. 12a). Between 1.8–2 K, the magnitude of the  signal increases which could suggest that the spin relaxation is occurring through multiple relaxation mechanisms at the lowest temperatures and subsequently shifting towards a single mechanism upon heating. Heating results in an increased temperature dependence of the
signal increases which could suggest that the spin relaxation is occurring through multiple relaxation mechanisms at the lowest temperatures and subsequently shifting towards a single mechanism upon heating. Heating results in an increased temperature dependence of the  single maximum which eventually moves outside of the measured frequency range at 3.5 K.
single maximum which eventually moves outside of the measured frequency range at 3.5 K.
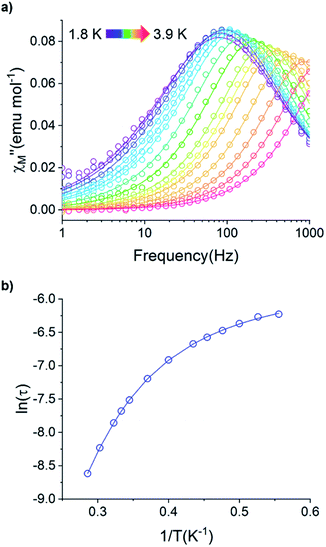 | ||
Fig. 12 (a) Temperature dependence of the out-of-phase component of the molar ac magnetic susceptibility 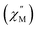 of 5. (H = 0.2 T, T = 1.8–3.9 K). (b) Arrhenius plot of the magnetic relaxation time of 5. of 5. (H = 0.2 T, T = 1.8–3.9 K). (b) Arrhenius plot of the magnetic relaxation time of 5. | ||
Using the ac magnetic susceptibility of compound 5/5Iso, Cole–Cole curves were constructed and were fitted using general Debye equation which considers only one spin relaxation process. The extracted magnetic relaxation times were then used to construct an Arrhenius plot between 1.8–3.5 K (Fig. 12b). Analyzing the Arrhenius plot for compound 5 shows the magnetic relaxation times for 5 are temperature dependent across the full temperature range suggesting low contribution from quantum tunneling processes. Between 2.5–3.5 K, the magnetic relaxation times become increasingly temperature dependent but never become fully linear on the logarithmic scale. This indicates significant contributions to the spin relaxation from second-order Raman and/or direct processes even at the highest temperature regime. Similar behavior has been observed in the trigonal Yb3+ SMM, Yb[trensal], where it was reported that considering solely an Orbach relaxation mechanism was insufficient in describing the anisotropy energy barrier of the system.64 As previously described, the Arrhenius plot for 5/5Iso was fit using eqn (2). The direct exponent, n1, was held constant at n1 = 4 and the direct term, A, was allowed to freely refine along with the other Arrhenius parameters due to the inability in acquiring a reasonable fit of the τ vs. H plot for compound 5/5Iso (Fig. S49†). Using this fitting procedure, values of Arrhenius parameters of A = 0.304 S−1 T−2 K−1, τQTM = 0.00269 s, C = 0.00812 s−1 K−4,25n2 = 4.25, τo = 9.04 × 10−5 s, and U = 6 cm−1 were obtained.
Electronic structure determination of compounds 1–5
To further investigate the electronic structure of the late lanthanide ions in the trigonal prismatic geometry and the observed magnetic properties of 2–5, multi-configurational ab initio calculations were performed using the Molcas 8.2 package within the CASSCF/SO-RASSI and XMS-CASPT2/SO-RASSI level of theory.65 For the two independent Ln(1) and Ln(2) molecules of 2–5, there are only small differences of the energies of the spin–orbit states and corresponding g-tensors, therefore only the results obtained for Ln(1) within the XMS-CASPT2 level of theory will be discussed here (Tables S21–S27†) (Table 3).| Compound | |||
|---|---|---|---|
| 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 |
| 0.1325 | 52.3575 | 86.9322 | 122.7001 |
| 137.0824 | 133.0082 | 115.6344 | 475.9593 |
| 137.1925 | 151.2557 | 348.8809 | 1208.0192 |
| 227.7217 | 372.2061 | 359.4642 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 479.2524 479.2524 |
| 228.2524 | 433.3370 | 614.8964 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 636.9361 636.9361 |
| 389.3542 | 603.7203 | 628.4261 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490.9949 490.9949 |
| 390.5907 | — | 793.9510 | |
| 424.9725 | 794.4556 | ||
| 433.2938 | 912.2663 | ||
| 447.0406 | 912.3256 | ||
| 504.8665 | 1196.5839 | ||
| 516.2164 | 1196.5971 | ||
| 522.8741 | 6103.0014 | ||
| 537.9741 | 6106.8661 | ||
| 540.7899 | |||
| 565.8972 | |||
| — | |||
The ground state electronic structures for 2–5 are shown in Fig. 13. The axial nature of the trigonal prismatic ligand field is expected to be least suitable for stabilizing the largest mj projections in the latest prolate lanthanide ions (Er3+, Tm3+, and Yb3+). The Er-[1]ferrocenophane compound, 3, shows highly mixed ground doublets containing mj = ±1/2 (24%), ±5/2 (23%), and ±7/2 (18.7%) character. The first and second excited mj states for 3 reside only 28 cm−1 and 52 cm−1 above the ground doublets which contributes to the highly mixed mj composition and large transverse g-tensors (gx and gy) of 3 (Table 4). These factors contribute to the lack of axial magnetic anisotropy of the ground state and explain the lack of SMM behavior for 3. For compound 4, a non-magnetic, mj = 0, ground state is observed and therefore it does not exhibit any magnetic anisotropy. This corresponds well with the direct current magnetic susceptibility data in which the molar magnetic susceptibility temperature product drops to near zero at 2 K. The composition of the ground doublet of the Yb-[1]ferrocenophane compound, 5, is mostly mj = ±7/2 (51%) and ±3/2 (11%) character and exhibits large transversal g-tensors which leads to a magnetic anisotropy axis which is nearly perpendicular to the principal C3 axis of the [LnFc3(THF)2Li2]− motif. Therefore, the lack of SMM behavior of 5 in the absence of an external magnetic field is not surprising as fast spin relaxation through QTM processes is expected. To this end, the observed slow relaxation under an applied magnetic field suggests that the ground mj = ±7/2 doublet becomes purer under an applied field and therefore QTM is at least partially shut down. For 5, the first excited mj state lies 121 cm−1 above the ground doublet, therefore if the spin relaxation of 5 under an applied field proceeds via an Orbach mechanism through the first excited state, and energy barrier ∼120 cm−1 is likely to be observed under an applied magnetic field. The experimentally extracted spin reversal barrier of 6 cm−1 is significantly lower than the energy gap between the ground and first excited state and suggest that spin relaxation proceeds mainly through a second-order Raman and/or direct mechanism.
| Doublet | Compound | ||||
|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | ||
| 1 | g x | 0 | 9.997 | — | 1.847 |
| g y | 0 | 7.516 | — | 2.645 | |
| g z | 17.400 | 0.150 | — | 4.920 | |
| 2 | g x | 0 | 2.156 | — | 0.425 |
| g y | 0 | 4.736 | — | 0.677 | |
| g z | 15.025 | 8.965 | — | 6.893 | |
| 3 | g x | 0 | 4.983 | — | 0.042 |
| g y | 0 | 3.382 | — | 0.336 | |
| g z | 17.774 | 0.736 | — | 5.298 | |
| 4 | g x | 0 | 10.797 | — | 0.084 |
| g y | 0 | 6.514 | — | 0.087 | |
| g z | 14.354 | 1.797 | — | 7.987 | |
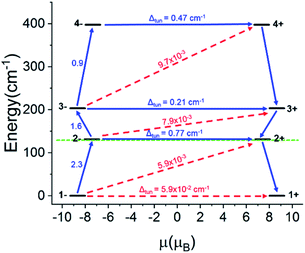
For the Ho-[1]ferrocenophane compound, 2, an almost pure mj = ±7 ground state is observed and is well stabilized from the first and second excited states by 137 cm−1 and 228 cm−1, respectively. The highly anisotropic ground state leads to an axial magnetic moment vector that resides along the principal {LnFc3} C3 axis explaining the observed SMM behavior of 2. The magnetic blocking barrier of the Ho(2) molecule of 2 was further investigated by following the methodology described in ref. 66 (Fig. 14). The tunneling gaps between the ground doublets are small which suggests ground state QTM is minimal. Spin relaxation is expected to proceed through the first excited state given the large tunneling gap of 0.77 cm−1. The energy of the first excited state (137 cm−1) corresponds remarkably well with the experimentally extracted energy barriers of 2, 2-dilute, and 2@0.35T (110–131 cm−1).
Conclusions
We present a detailed analysis of trends in structure and magnetic properties of the remaining members of the family of late Ln-[1]ferrocenophane complexes which all feature exclusively carbon-donors coordinated to trigonal prismatic lanthanide ions. The observed trend of increasing Fc2− twist angle with decreasing ionic radii of the Ln3+ ions can be rationalized by simple geometric arguments and considering the structural rigidity of the Fc2− units. The Ho3+ complex 2 exhibits slow magnetic relaxation in the absence of applied dc fields, rendering it a rare example of a Ho3+-based SMM. Structural modification of the approximate trigonal prismatic coordination environment can be achieved remotely via substitution of coordinating solvent molecules to the terminating Li+ ions. Specifically, an increase in Fc2− twist angle and deviation from ideal trigonal prismatic geometry is observed in the series 2, 2-THF*, and 2-py which is accompanied by a decrease in magnetic relaxation times at a given temperature for the pyridine solvated molecule 2-py. Taken together our results emphasize the sensitivity of the magnetic structure of Ln3+ ions in trigonal prismatic coordination environments to the twist angle and provide design guidelines for six-coordinate SMMs.Experimental section
General materials and methods
All syntheses and magnetic sample preparation were carried out under the rigorous exclusion of air and moisture using an ultra-high purity Ar filled glovebox (Vigor) in which the O2 and H2O levels were generally held under 2 ppm and 0.1 ppm, respectively. Tetrahydrofuran, diethyl ether, hexanes, and n-pentane were all dried and deoxygenated using a solvent purification system (JC Meyer or Innovative Technologies SPS) and were stored over molecular sieves (3a, 8 to 12 mesh) prior to use. Pyridine was dried by stirring over CaH2 for 24 hours and deoxygenated using freeze–pump–thaw methods. Prior to use 2-methyl tetrahydrofuran (THF*) was passed through a basic alumina column to remove the butylated hydroxytoluene (BHT) stabilizer. Stabilizer free THF* was deoxygenated by purging N2 gas through the solvent and was dried by refluxing over Na/benzophenone. Anhydrous THF* and pyridine were stored over molecular sieves (3a, 8 to 12 mesh). Anhydrous GdCl3, HoCl3, and ErCl3 were received as a generous gift from Dr Timothy Hughbanks. Anhydrous TmCl3 (Millipore Sigma), YbCl3 (Alfa Aesar), and LuCl3 (Alfa Aesar) were purchased from commercial sources and were used as received. Li6(Fe(η5-C5H4)2)3(TMEDA)2 (ref. 67) and [Li(THF)4][YFc3(THF)2Li2]44 were prepared as previously described. Carbon and hydrogen elemental analysis were performed on compounds 1–6, and 2-py by Midwest Microlab Inc.X-ray crystallography
Details regarding the structural determination of compounds 1–6, 5Iso, 6Iso, 2-THF*, and 2-py can be found in the ESI.†Magnetic characterization
Samples used for magnetic characterization were prepared by thoroughly crushing the respective paramagnetic species into a microcrystalline powder and subsequently adding between 20–40 mg to the bottom of a high purity glass NMR tube along with solid n-eicosane (∼27–65 mg). The NMR tube containing the paramagnetic species/n-eicosane mixture was equipped with a gas line adaptor, removed from the glovebox, and was sealed under vacuum on a Schlenk line. To prevent torqueing of small crystallites under high magnetic fields, the solid n-eicosane in the sealed sample was melted by heating the sealed tube between 40–43 °C in a hot water bath, forming a solid matrix upon cooling to room temperature.Magnetic characterization was carried out using a Quantum Design MPMS 3 SQUID magnetometer. The direct current (dc) magnetic susceptibility was measured under a 0.1 T magnetic field between 2–300 K. A diamagnetic correction (calculated using Pascal's constants) was included in the calculation of the dc molar magnetic susceptibility and considers the diamagnetic response of eicosane and the complex core electrons.68 The variable temperature magnetization was measured between 2–8 K up to external magnetic field strengths of 7 T. The alternating current (ac) magnetic susceptibly was measured using a 0.2 mT alternating field between 1–1000 Hz using external field strengths of either 0 T, 0.2 T, or 0.35 T.
Synthesis
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. N. is grateful for support of this project by the National Science Foundation (CHE-1753014) and general financial support through The Welch Foundation (A-1880). V. V. acknowledges the postdoctoral fellowships from the Fonds Wetenschappelijk Onderzoek Vlaanderen (FWO, Flemish Science Foundation). A. U. is grateful to SERB/IUSSTF (India) for a postdoctoral fellowship. We thank Dr Timothy Hughbanks for the generous gift of anhydrous lanthanide salt starting materials.Notes and references
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford Univ. Press., 2006 Search PubMed.
- M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M. A. Arrio, E. Otero, L. Joly, J. C. Cezar, A. Cornia and R. Sessoli, Nature, 2010, 468, 417–421 CrossRef CAS PubMed.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M. A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197 CrossRef CAS PubMed.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, eaat7319 CrossRef CAS PubMed.
- X. Yao, J. Du, Y. Zhang, X. Leng, M. Yang, S. Jiang, Z. Wang, Z. Ouyang, L. Deng, B. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380 CrossRef CAS PubMed.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581 CrossRef CAS PubMed.
- K. L. M. Harriman, J. L. Brosmer, L. Ungur, P. L. Diaconescu and M. Murugesu, J. Am. Chem. Soc., 2017, 139, 1420–1423 CrossRef CAS PubMed.
- Y. Ding, N. F. Chilton, R. E. P. Winpenny and Y. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed.
- M. Gregson, N. F. Chilton, A. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155–165 RSC.
- Y. Chen, J. Liu, L. Ungur, J. Liu, Q. Li, L. Wang, Z. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- P. Evans, D. Reta, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2019, 141, 19935–19940 CrossRef CAS PubMed.
- C. A. Gould, K. R. McClain, J. Yu, T. J. Groshens, F. Furche, J. R. Long and B. G. Harvey, J. Am. Chem. Soc., 2019, 141, 12967–12973 CrossRef CAS PubMed.
- K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503 RSC.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamaki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- B. M. Day, F.-S. Guo and R. A. Layfield, Acc. Chem. Res., 2018, 51, 1880–1889 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamaki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS PubMed.
- J. Wu, J. Jung, P. Zhang, H. Zhang, J. Tang and B. L. Guennic, Chem. Sci., 2016, 7, 3632–3639 RSC.
- A. Watanabe, A. Yamashita, M. Nakano, T. Yamamura and T. Kajiwara, Chem.–Eur. J., 2011, 17, 7428–7432 CrossRef CAS PubMed.
- S. Jiang, B. Wang, G. Su, Z. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448–7451 CrossRef CAS PubMed.
- Y. Chen, F. Ma, X. Chen, B. Dong, K. Wang, S. Jiang, C. Wang, X. Chen, D. Qi, H. Sun, B. Wang, S. Gao and J. Jiang, J. Inorg. Chem., 2017, 56, 13889–13896 CrossRef CAS PubMed.
- C. R. Ganivet, B. Balleseros, G. de la Torre, J. M. Clemente-Juan, E. Coronado and T. Torres, Chem.–Eur. J., 2012, 19, 1457–1465 CrossRef PubMed.
- S. Takamatsu, T. Ishikawa, S. Koshihara and N. Ishikawa, Inorg. Chem., 2007, 46, 7250–7252 CrossRef CAS PubMed.
- M. A. AlDaman, S. Cardonna-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, C. Martí-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467–3479 CrossRef PubMed.
- M. A. AlDaman, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875 CrossRef PubMed.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181–5191 RSC.
- J. Liu, Y. Chen, J. Liu, V. Vieru, L. Ungur, J. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X. Chen and M. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed.
- Y. S. Meng, C. H. Wang, T. Q. Zhang, X. B. Leng, B. W. Wang, Y. F. Chen and S. Gao, Inorg. Chem. Front., 2016, 3, 828–835 RSC.
- J. J. Le Roy, I. Korobkov and M. Murugesu, Chem. Commun., 2014, 50, 1602–1604 RSC.
- K. R. Miehaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957 CrossRef PubMed.
- S. Jiang, B. Wang, H. Sun, X. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733 CrossRef CAS PubMed.
- M. Guo and J. Tang, Inorganics, 2018, 6, 16 CrossRef.
- S. Liu, Y. Meng, Y. Zhang, Z. Meng, K. Lang, Z. Zhu, C. Shang, B. Wang and S. Gao, Inorg. Chem., 2017, 56, 7320–7323 CrossRef CAS PubMed.
- B. Na, X. Zhang, W. Shi, Y. Zhang, B. Wang, X. Gao, S. Gao and P. Cheng, Chem.–Eur. J., 2014, 20, 15975–15980 CrossRef CAS PubMed.
- K. R. Miehaus, J. D. Rinehart and J. R. Long, Inorg. Chem., 2011, 50, 8484–8489 CrossRef PubMed.
- K. R. Miehaus, S. G. Minasian, W. W. Lukens Jr, S. A. Kozimor, D. K. Shuh, T. Tyliszczak and J. R. Long, J. Am. Chem. Soc., 2014, 136, 6056–6068 CrossRef PubMed.
- L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043–10056 CrossRef CAS PubMed.
- R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, John Wiley & Sons, Weinheim, Germany, 2015 Search PubMed.
- J. J. Baldoví, S. Cardonna-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, Inorg. Chem., 2012, 51, 12565–12574 CrossRef PubMed.
- T. P. Latendresse, N. S. Bhuvanesh and M. Nippe, J. Am. Chem. Soc., 2017, 139, 8058–8061 CrossRef CAS PubMed.
- T. P. Latendresse, V. Vieru, B. O. Wilkins, N. S. Bhuvanesh, L. F. Chibortaru and M. Nippe, Angew. Chem., Int. Ed., 2018, 57, 8164–8169 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- N. F. Chilton, Inorg. Chem., 2015, 54, 2097–2099 CrossRef CAS PubMed.
- R. Olejník, Z. Padělková, A. Fridrichová, M. Horáček, J. Merna and A. Růžička, J. Organomet. Chem., 2014, 759, 1–10 CrossRef.
- A. Caralho, A. Domingos, P. Gaspar, N. Marques, A. Piresde Matos and I. Santos, Polyhedron, 1992, 11, 1481–1488 CrossRef.
- Unpublished results.
- Y. Chen, J. Liu, W. Wernsdorfer, D. Liu, L. F. Chibotaru, X. Chen and M. Tong, Angew. Chem., Int. Ed., 2017, 56, 4996–5000 CrossRef CAS PubMed.
- J. Dreiser, R. Westerström, Y. Zhang, A. A. Popov, L. Dunsch, K. Krämer, X. Liu, S. Decurtins and T. Greber, Chem.–Eur. J., 2014, 20, 13536–13540 CrossRef CAS PubMed.
- S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, A. Camón, M. Evangelisti, F. Luis, M. J. Martínez-Pérez and J. Sesé, J. Am. Chem. Soc., 2012, 134, 14982–14990 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS PubMed.
- R. J. Blagg, F. Tuna, E. J. L. McInnes and R. E. P. Winpenny, Chem. Commun., 2011, 47, 10587–10589 RSC.
- N. Isikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650–3651 CrossRef PubMed.
- C. A. P. Goodwin, D. Reta, F. Ortu, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2017, 139, 18714–18724 CrossRef CAS PubMed.
- S. Jiang, S. Liu, L. Zhou, B. Wang, Z. Wang and S. Gao, Inorg. Chem., 2012, 51, 3079–3087 CrossRef CAS PubMed.
- F. Pointillart, O. Cador, B. Le Guennic and L. Ouahab, Coord. Chem. Rev., 2017, 346, 150–175 CrossRef CAS.
- Y. Guo, G. Xu, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 9953–9963 RSC.
- L. T. A. Ho and L. F. Chibotaru, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 104422 CrossRef.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sørensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Inorg. Chem., 2015, 54, 7600–7606 CrossRef CAS PubMed.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov and R. K. Carlson, et al., OpenMolcas: From Source Code to Insight, J. Chem. Theory Comput., 2019, 15(11), 5925–5964 CrossRef PubMed.
- L. Ungur, M. Thewissen, J. P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328–6337 CrossRef CAS PubMed.
- J. J. Bishop, A. Davison, M. L. Katcher, D. W. Lichtenberg, R. E. Merrill and J. C. Smart, J. Organomet. Chem., 1971, 27, 241–249 CrossRef CAS.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: CCDC 1986607 (1), 1986530 (2), 1986548 (2-py), 1986581 (2-THF*), 1986886 (3), 1986808 (4), 1986810 (5), 1986941 (5iso), 1986815 (6), 1986828 (6iso). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc01197e |
| This journal is © The Royal Society of Chemistry 2020 |