Open Access Article
Open Access ArticleCatalytic resonance theory: parallel reaction pathway control†
M. Alexander
Ardagh
 ab,
Manish
Shetty
ab,
Manish
Shetty
 a,
Anatoliy
Kuznetsov
a,
Anatoliy
Kuznetsov
 a,
Qi
Zhang
a,
Qi
Zhang
 a,
Phillip
Christopher
a,
Phillip
Christopher
 bc,
Dionisios G.
Vlachos
bc,
Dionisios G.
Vlachos
 be,
Omar A.
Abdelrahman
be,
Omar A.
Abdelrahman
 bd and
Paul J.
Dauenhauer
bd and
Paul J.
Dauenhauer
 *ab
*ab
aDepartment of Chemical Engineering and Materials Science, University of Minnesota, 421 Washington Ave. SE, Minneapolis, MN 55455, USA. E-mail: hauer@umn.edu
bCatalysis Center for Energy Innovation, University of Delaware, 221 Academy Street, Newark, DE 19716, USA
cDepartment of Chemical Engineering, University of California Santa Barbara, Engineering II Building, Santa Barbara, CA 93106, USA
dDepartment of Chemical Engineering, University of Massachusetts Amherst, 686 N. Pleasant Street, Amherst, MA 01003, USA
eDepartment of Chemical and Biomolecular Engineering, University of Delaware, 150 Academy Street, Newark, DE 19716, USA
First published on 3rd March 2020
Abstract
Catalytic enhancement of chemical reactions via heterogeneous materials occurs through stabilization of transition states at designed active sites, but dramatically greater rate acceleration on that same active site can be achieved when the surface intermediates oscillate in binding energy. The applied oscillation amplitude and frequency can accelerate reactions orders of magnitude above the catalytic rates of static systems, provided the active site dynamics are tuned to the natural frequencies of the surface chemistry. In this work, differences in the characteristics of parallel reactions are exploited via selective application of active site dynamics (0 < ΔU < 1.0 eV amplitude, 10−6 < f < 104 Hz frequency) to control the extent of competing reactions occurring on the shared catalytic surface. Simulation of multiple parallel reaction systems with broad range of variation in chemical parameters revealed that parallel chemistries are highly tunable in selectivity between either pure product, even when specific products are not selectively produced under static conditions. Two mechanisms leading to dynamic selectivity control were identified: (i) surface thermodynamic control of one product species under strong binding conditions, or (ii) catalytic resonance of the kinetics of one reaction over the other. These dynamic parallel pathway control strategies applied to a host of simulated chemical conditions indicate significant potential for improving the catalytic performance of many important industrial chemical reactions beyond their existing static performance.
1. Introduction
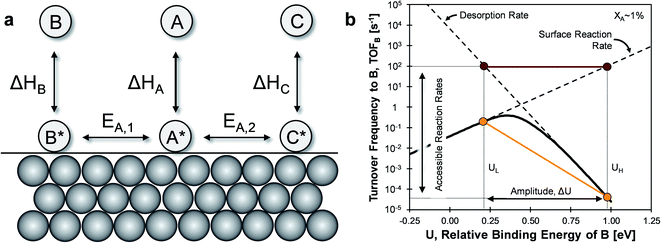
The core capability of catalysis is the controlled steering of molecules through preferred chemical pathways via manipulation of surface intermediates and transition state energies.1 The complex reaction networks of even small-molecule chemistries (e.g. methanol synthesis, ethylene epoxidation) contain energetically similar pathways to side products such as CO2, which devalue chemical processes and contribute to climate change.2–6 Traditional design aims for specific catalyst structures which preferentially lower the transition states of preferred pathways; catalyst binding strength and configuration are tuned in the structural shape (e.g. pores, pockets) and active site of materials.7–10 The limit of this strategy derives from the differences in competing pathway transition states, for which competitive stabilization in many important static catalytic systems has already achieved maximum capability.11,12An alternative strategy for catalytic reaction control proposes a dynamic catalytic surface, whereby the binding energy (i.e., heat of adsorption) of surface intermediates and associated transition state energies oscillate on the time scale of the catalytic turnover frequency.13 The heat of adsorption of hydrocarbons on metals and metal oxides can be altered by several methods14,15 including electric and magnetic fields,16–19 photocatalysis,20 surface strain,21,22 solid electrolytes,23–27 catalytic diodes,28–30 and back-gated field effect modulation.31–33 For each combination of catalyst material, chemical mechanism, and method of external stimulus, the dynamic variables including imposed surface binding energy frequency f and amplitude ΔU comprise a narrow set of conditions which can potentially achieve catalytic turnover frequencies which are orders of magnitude above the static Sabatier maximum (i.e., Balandin–Sabatier volcano peak).34
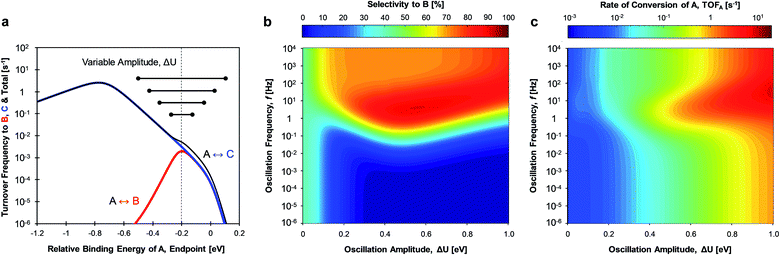
The mechanism of ‘catalytic resonance’ for enhanced catalytic turnover occurs by matching the frequency of oscillating binding energies to the natural frequencies of catalytic surface reactions. As depicted in Fig. 1a, a reaction is generally comprised of three parts (adsorption, surface reaction, and desorption), any one of which can be rate determining. In Fig. 1b, the Balandin–Sabatier volcano curve depicts the system turnover frequency as a function of a system descriptor; the maximum observed turnover frequency delineates the transition from one rate-limiting elementary step to another.35–37 An interpretation of catalytic resonance is that the oscillation between surface binding states on either side of the volcano peak permits each elementary step of the catalytic sequence to occur under conditions optimized for that particular step. The amplitude ΔU of the imposed surface binding energy oscillation connects the two conditions as drawn in maroon in Fig. 1b: low binding energy, UL, and high binding energy, UH. As the frequency of the imposed surface binding energy oscillation increases approaching the surface reaction frequencies, the maximum overall turnover frequency is achieved.
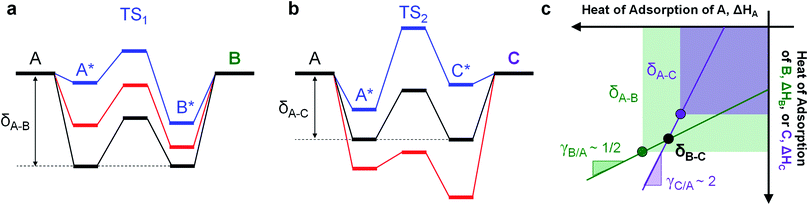
The introduction of two competing parallel surface reactions raises the question of whether selectivity to specific chemical products can be controlled by prescribed tuning of the imposed surface binding energy oscillation. Parallel reversible reactions of A-to-B and A-to-C as shown in Fig. 1a can have different transition states and different linear scaling relations. The transition state energy of an elementary reaction is linearly proportional to the surface energy by parameter α and offset by parameter β (kJ mol−1).38–40 Additionally, the binding energies of surface species B* and C* will exhibit different extents of change relative to changes in the binding energy of A*. A linear relationship between the binding energies of any two species has proportionality parameter γB/A (for the A-to-B reaction) and δB–A for the energy offset (kJ mol−1).34 It remains to identify parameter space from these operating and chemical reaction variations that preferentially enhance the rate of one elementary reaction over another.
In this work, the parallel reversible elementary reactions of A-to-B and A-to-C with thermoneutral free energy (ΔHA–B = ΔHA–C = 0 kJ mol−1) are evaluated via simulation under dynamic binding energy oscillation of all three intermediate species with the goal of assessing the parameter space leading to selective pathway control (i.e., more B than C, or more C than B). Parallel reactions are simulated in a continuous flow mixed reactor with varying parameters of γB–A and γC–A, as well as δB–A and δC–A in combination with different applied frequencies and amplitudes of surface binding energy oscillation to understand the conditions leading to pathway tunability.
2. Results and discussion
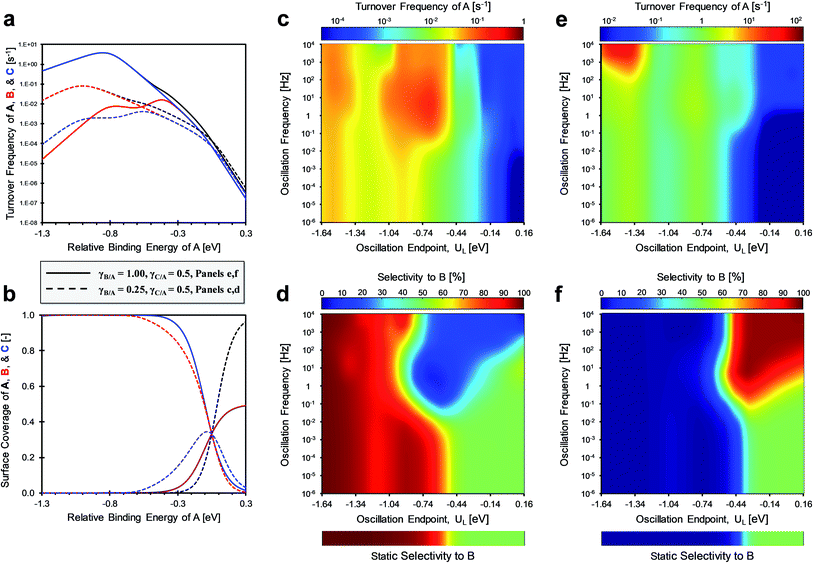
The competition between parallel catalytic surface reactions under dynamic conditions is most unique when the product surface species vary differently in binding energy. As depicted in Fig. 2, competing reactions of A-to-B and A-to-C are depicted with inverse gamma parameters. The reaction to produce B with γB/A of 0.5 has a multi-state energy profile in Fig. 2a, whereby B* changes only half as much in binding energy relative to A*. In contrast, the reaction to produce C with γC/A ∼ 2.0 has a multi-state energy profile in Fig. 2b, in which C* changes twice as much in binding energy as A*.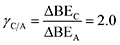 | (1) |
These two systems are depicted in the gamma–delta plot of Fig. 2c, with the values of slopes γ and point of common binding energy δ between surface reactant and surface product for each elementary reaction. The state whereby B* and C* have the same surface adsorption enthalpy occurs in the gamma–delta plot of Fig. 2c at the intersection of the two reaction lines and is identified as δB–C.
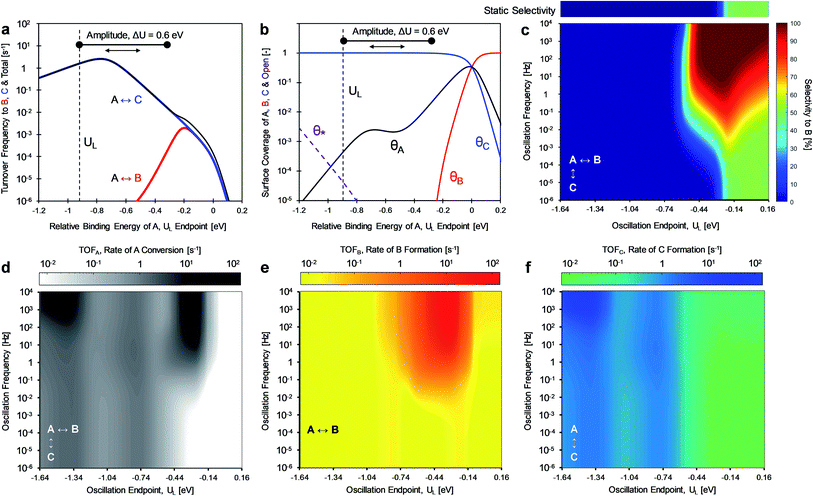
For the case of inverse (2.0 and 0.5) gamma parameters depicted in Fig. 2, the reaction kinetics were evaluated for identical reaction conditions (δB–A = 1.4 eV, δC–A = 1.4 eV). As depicted in Fig. 3a, variation of gamma (γB/A = 2.0, γC/A = 0.5) produces distinct volcano peak positions and reaction activity. The low γC/A of 0.5 produces a volcano peak of ∼5 s−1, while the high γB/A of 2.0 volcano peak maximum is significantly lower (5 × 10−3 s−1). The key transition in surface coverage of the system occurs at zero relative binding energy of A, at which the surface transitions between high coverage of C and B as the relative binding energy of A increases (Fig. 3b).
Oscillation of the binding energy of A (ΔUA) by 0.6 eV was simulated over ten decades of frequencies (10−6 < f < 104 Hz) and variation of the amplitude position is denoted by the position of the weakest binding energy (i.e., left oscillation endpoint, UL). As depicted in the results of Fig. 3c, the selectivity is fully tunable to either product B or C depending on the applied dynamic conditions. At low oscillation frequencies (f < 10−3 Hz), the catalytic system achieves nearly perfect selectivity to product C (blue) until about −0.2 eV relative binding energy of A, after which selectivity to both products is the same (SB ∼ SC ∼ 50%, green). This low frequency behavior is consistent with the activity predicted by the volcano plots of Fig. 3a; product C is dominant until UL of −0.2 eV, after which both products are produced at equal rate. This is consistent with the selectivity to B under static catalyst conditions described in the bar above Fig. 3c. As the oscillation frequency increases, a dramatic shift in product selectivity occurs at ∼10−2 Hz. As depicted in Fig. 3c, the transition from high selectivity to C (blue) to high selectivity to B (red) occurs in the range of −0.4 to −0.2 eV of UL (lower oscillation endpoint). Notably, there is a switch to ∼100% selectivity towards product B at these conditions that are not attainable under static conditions or under low oscillation frequencies (<10−3 Hz).
The transition between selective production of B or C in Fig. 3c is associated with dynamic rate enhancement of either product. See Fig. S0† for a detailed diagram with resonance frequencies and attainable rates for each product using dynamic catalysis. Fig. 3d–f depict the rates of total conversion of A (TOFA), total production rate of B (TOFB), and total formation rate of C (TOFC), respectively. As shown, TOFA exhibits two regions of high activity: (i) above 100 Hz and oscillation endpoint UL < −1.10 eV, and (ii) above 10 Hz and the oscillation endpoint range of −0.5 < UL < −0.2 eV. By comparison with the rates of the independent reactions (TOFB in Fig. 3e and TOFC in Fig. 3f), the regions of high activity of conversion of A can be associated with acceleration of the independent reactions to produce B and C, respectively.
The formation rate of C is enhanced at oscillation amplitude endpoints of UL < −1.10 eV (Fig. 3f), while the formation rate of B is enhanced in the oscillation amplitude endpoint range of −0.5 < UL < −0.2 eV. The enhanced formation of C occurs in the region of weak binding and a surface mostly covered in C*. In this region under dynamic conditions, the reaction is in resonance with the desorption of C, and the overall formation rate is enhanced over an order of magnitude. Alternatively, the nearly 100% selectivity towards B in the oscillation endpoint range of −0.5 < UL < 0.2 eV can be partially attributed to both the higher surface coverage of species B (especially above a UL value of 0 eV) and the resonance-enhanced rate of the reaction to form product B.
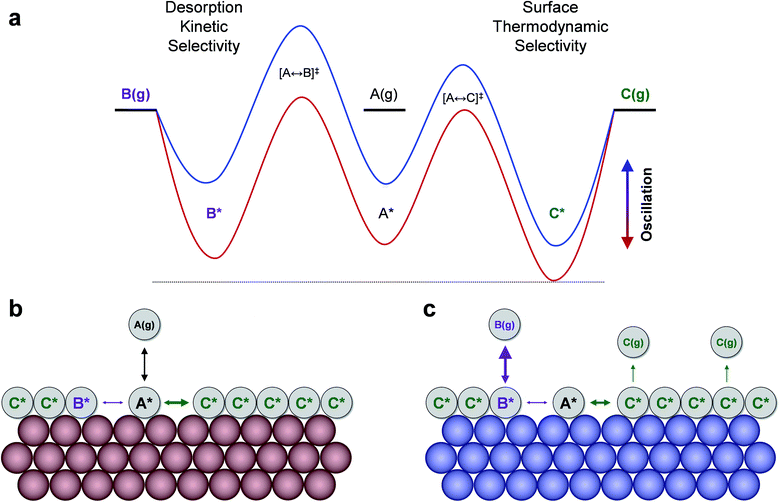
The product selectivity results of Fig. 3 indicate that there are at least two mechanisms for selectivity control in a parallel reaction system: (i) resonance rate enhancement with the individual reaction pathways, and (ii) control of surface coverage. These mechanisms are depicted in Fig. 4a where conditions have been selected to indicate both mechanisms. Surface species C* is thermodynamically preferred, since it has lower energy (i.e. stronger binding) than A* or B* in the stronger binding (red) state. As shown in Fig. 4b, A* preferentially converts to C* resulting in a surface covered in C*. The key transition determining surface coverage dominance is captured in the quantity, δB–C, which is the energy whereby B* and C* have the same surface adsorption enthalpy (identified in Fig. 2c). Alternatively, product B is kinetically favored, since the desorption of B proceeds quickly relative to C in the weaker binding (blue) state. As depicted in Fig. 4c, B* exhibits faster desorption kinetics. The ultimately favored product in this scenario depends on the overall balance of these two mechanisms (thermodynamic versus kinetic), which can shift as the binding energy of A* changes over the range of the volcano plot.
The two mechanisms enhancing selectivity are observed in the formation of product B in Fig. 3c. At stronger binding energies (oscillation endpoint UL > 0 eV), the product B is produced due to dominance of the surface coverage by B*. However, the kinetic mechanism exists at relative binding energies below 0 eV in the region of −0.5 < UL < 0 eV. In this range the oscillation amplitude (ΔUA = 0.6 eV) extends across the A-to-B reaction volcano, and this reaction is kinetically resonance enhanced. The reaction to form B increases from 10−3 s−1 under the static catalytic condition at the volcano peak (Fig. 3a) to a formation rate of 102 s−1 under dynamic conditions, even with the existence of the parallel A-to-C reaction. This 105-fold rate enhancement leads to high selectivity to B even when B* does not dominate the surface coverage.
More complicated behavior is observed when oscillation amplitude becomes a variable. In Fig. 3, the oscillation amplitude of A was fixed at ΔUA of 0.6 eV. This amplitude was permitted to vary between 0 < ΔUA < 1.0 eV as depicted in Fig. 5a for the same parallel reaction system (γB–A ∼ 2.0, γC–A ∼ 0.5, and δB–A ∼ 1.4 eV, δC–A ∼ 1.4 eV). As previously stated, this reaction system does not select for product B in excess of 50% under any condition when operated with a static catalyst, but high selectivity to B becomes possible under dynamic conditions. To assess the role of amplitude in dynamic catalytic operation, the oscillation amplitude was centered around the volcano peak for the A-to-B reaction (−0.2 eV relative binding energy of A); the reaction to form B transitions between surface reaction (A*-to-B*) control and desorption rate limitation (C*-to-C or B*-to-B) at the peak. Here, the consumption of A is limited by the desorption of C at the left oscillation amplitude endpoint and the desorption of B at the right amplitude endpoint.
The catalytic resonance of reaction A-to-B under variable amplitude (0 < ΔUA < 1.0 eV) and frequency (10−6 < f < 104 Hz) is depicted in Fig. 5b. As expected, the selectivity to B at low oscillation frequencies is minimal due to the relatively high production rate of C (the surface coverage dominating species). Preferential selectivity to B (>50% B) is only achieved once the oscillation frequency increases beyond ∼0.01 Hz, with a maximum selectivity of 93% achieved at moderate oscillation amplitudes of 0.5–0.6 eV. Generally, the consumption of A (Fig. 5c) increases with the oscillation amplitude, since the lower amplitude endpoint, UL, rises to higher TOFs as oscillation amplitude increases. However, a larger oscillation amplitude is not more favorable for selectivity enhancement, due to the tradeoff between enhancing the production of B versus C. Desorption of C proceeds quickly (1 < TOFC < 100 s−1) for all oscillation amplitudes, and higher frequencies above 10 Hz begin to reduce selectivity to product B. In addition, the consumption of A decreases at higher oscillation frequencies as the rate of B production decreases. Oscillation frequencies above 10 Hz are too fast for the desorption of B, which leads to incomplete emptying of surface B* at the left oscillation endpoint. Instead, C is produced but with minimal rate enhancement as these oscillations do not reach weak enough binding energies.
The linear scaling relationships of surface intermediates A*, B* and C* strongly impact the selectivity behavior of dynamic catalytic systems. Throughout Fig. 3 and 5, the linear scaling relationships between the adsorbates were held constant with γB–A of 2.0 and γC–A of 0.5. However, studies of gas phase reactions over periodic metals show that each adsorbate pair has quite different γ and δ values, with γ ranging between −20 to 20 and δ being −10 to 10 eV.40–43 In addition, density functional theory (DFT) calculations of adsorbates bound to common catalysts such as Pt(111) or Ni(111) reveal that the linear scaling relationships (γ and δ) for periodic metals can potentially vary for different external stimuli (i.e. stress/strain, electric field, lasers/light) applied to a single metal.43–46 To account for these variations in catalyst-stimulating methods, the effects of changing linear scaling relationships were evaluated for product selectivity and rate enhancement.
In two case studies, γB–A was decreased by a factor of 2× and 8× to evaluate the impact on selectivity trends if the ratio of γ between parallel surface catalytic reactions (e.g. γB/A/γC/A) was greater or less than one. Fig. 6a and b depict the volcano plots for the consumption of A (TOFA), production of B (TOFB), production of C (TOFC), and the surface coverage under static catalytic operation. In these two systems, the surface coverage transition occurs at δB–C = δA–C = δA–B = 1.4 eV (which is 0 eV relative binding energy of A in Fig. 6). Generally, the product with a lower γ dominates the surface coverage and production until a UL of about −0.5 eV and −0.4 eV for Fig. 6d and f, respectively. This occurs due to a shift in the rate determining step from surface reaction to desorption for the product with the higher γ. This indicates that the selectivity challenge for dynamic catalytic operation is to stimulate the rate of production of the surface species more sensitive to external stimuli (i.e., higher γ).
Fig. 6c and d present heat maps for the TOF for the consumption of A and selectivity to B when γB–A < γC–A (0.25 and 0.50, respectively) as a function of applied frequency (10−6 < f < 104 Hz) and oscillation endpoint (UL) at fixed total amplitude (ΔUA = 0.6 eV). In this scenario, the selectivity to B is high only when its desorption is enhanced at weak binding conditions (relative binding energies of −1.64 to −1.0 eV). Once the amplitude achieves an appreciable binding energy (UL > −1.0 eV), the product C is heavily favored over B for frequencies above ∼1 Hz. However, overall consumption rates of A do not increase when both products exhibit γ < 1.0, due to the lack of significant surface coverage for A* over a wide range of binding energies. This is further exacerbated by the stronger binding of both B* and C* at the low γB–A and γC–A values that limit the desorption rates of the products.
In the second scenario of Fig. 6, γB–A is increased to 1.0 revealing similar behavior to the scenario in Fig. 3 where γB–A was 2.0. Once γB–A is higher than γC–A, selectivity to B is low (<10%) across most binding energies less than −0.44 eV, and rate enhancement can only be achieved at weak binding (UL < −1.25 eV) and high frequencies (>100 Hz). This indicates that the ratio of γ between reaction pathways (γB/C = γB/A/γC/A) is critical to strategically controlling catalyst dynamics for specific products. High selectivity with a γB/C ratio less than one is readily achievable, while values greater than one require a precise selection of the amplitude and frequency.
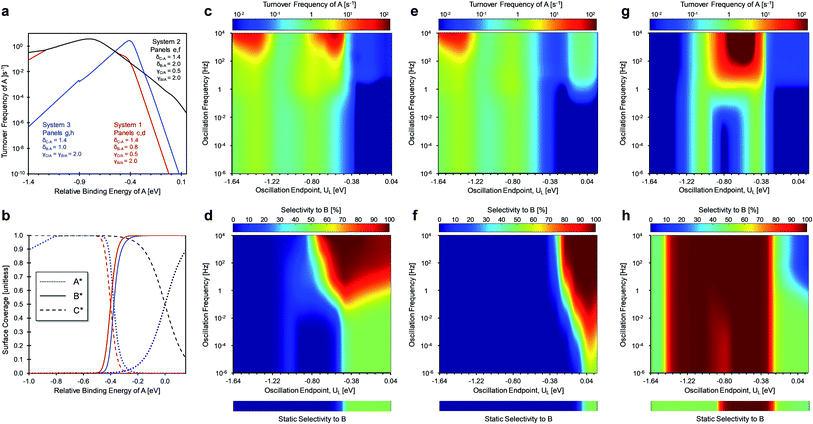
The other key surface chemistry parameter controlling dynamic selectivity is δ (depicted in Fig. 2a–c), which identifies the conditions of common binding energy between surface species. In the three scenarios of Fig. 7, the offset for the linear scaling relationship, δB–C, was varied (by selecting δA–B and δA–C) to determine its effect on catalytic selectivity to products under static and dynamic conditions with a fixed amplitude (ΔU = 0.6 eV) and varying oscillation frequency (10−6 < f < 104 Hz). The three scenarios are depicted in Fig. 7a as volcano plots of the turnover frequency of A and as the associated surface coverages in Fig. 7b. Systems 1 and 2 both have the same gamma ratios (γC/A = 0.5, γB/A = 2.0) and delta for the reaction of A-to-C (δA–C = 1.4 eV), but the delta for the reaction of A-to-B differs (δA–B of 0.8 eV for system 1 and δA–B of 2.0 eV for system 2). The third system considers the case of similar delta values (δA–C = 1.4 eV, δA–B = 1.0 eV) and identical gamma values (γC/A = γB/A = 2.0).
System 1 of Fig. 7c–d only selects for product C (UL < −0.4 eV) or an equimolar product mixture of B and C under static catalyst conditions. However, dynamic catalyst operation as square waves of 0.6 eV amplitude leads to parameter space with significant overall rate acceleration in addition to a third selectivity regime which overwhelmingly favors species B at higher frequencies. When δB–A is 0.8 eV in system 1 as shown in Fig. 7c, TOFA exhibits two regimes of ∼100× rate enhancement as compared to the static optima (Fig. 7a). At −1.64 < UL < −1.22 eV, C* is the dominant surface species under static conditions (Fig. 7b), and resonance with the desorption of C is achieved at oscillation frequencies >100 Hz with ∼100% selectivity towards C. Alternatively, the selectivity towards B is enhanced to nearly 100% at −0.75 < UL < 0 eV. This regime is partially attributed to the enhanced formation of B between −0.75 < UL < −0.4 eV, where the system achieves resonance with the pathway to B. At stronger binding energies above δB–C = −0.4 eV, high selectivity to B is attributed to the dominant surface coverage of B*. This transition, δB–C, can be predicted from the intersecting binding energy lines of a gamma–delta plot comparable to Fig. 2c or from the following equation based on the parameters of the independent elementary reactions.
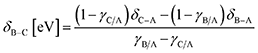 | (2) |
Similar selectivity behavior is observed for system 2 (Fig. 7e and f). When δB–A increases to 2.0 eV, the kinetic regime of high selectivity to B shifts to stronger binding energies (UL > −0.4 eV) and extends to lower oscillation frequencies (f > 10−2 Hz). This occurs due to the dominant surface coverage transition at UL of 0 eV from species C* to A* as the relative binding energy of A increases. The surface coverage transition of the two products only occurs at stronger binding energies associated with δB–C of +0.4 eV (not shown). Additionally, the enhancement in TOFA at weaker binding energies due to resonance with the desorption of C is almost identical to the behavior of system 1.
System 3 of Fig. 7g and h exhibited unique behavior when γB/A and γC/A were both equal to 2.0 and δB–A and δC–A were 1.0 eV and 1.4 eV, respectively. For static catalyst operation (Fig. 7h), most conditions of amplitude position (UL) produced equimolar selectivity to B and C; high selectivity to B existed only for −0.9 < UL < −0.3 eV. For square waveform oscillations at ΔUA of 0.6 eV, the region of high selectivity to B expands to −1.4 < UL < −0.4 eV where the surface coverage of B* dominates. In this region, significant rate enhancements of ∼10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000× can be achieved at oscillation frequencies greater than 100 Hz, as shown in Fig. 7g. With nearly 100% selectivity to B, this kinetic regime resembles a single A-to-B reaction whereby the system achieves ‘surface resonance’ at these UL ranges. This particular system is singular; because γB/A and γC/A are the same, the quantity δB–C does not exist (eqn (2)), and C* never exhibits high surface coverage. When depicted as a gamma–delta plot similar to Fig. 2c, this system would have two parallel reaction lines that never cross. Notably, selectivity of C is only enhanced at higher frequencies (f > 1 Hz) and strong binding energy (UL > 0 eV) where desorption rates to C are higher.
000× can be achieved at oscillation frequencies greater than 100 Hz, as shown in Fig. 7g. With nearly 100% selectivity to B, this kinetic regime resembles a single A-to-B reaction whereby the system achieves ‘surface resonance’ at these UL ranges. This particular system is singular; because γB/A and γC/A are the same, the quantity δB–C does not exist (eqn (2)), and C* never exhibits high surface coverage. When depicted as a gamma–delta plot similar to Fig. 2c, this system would have two parallel reaction lines that never cross. Notably, selectivity of C is only enhanced at higher frequencies (f > 1 Hz) and strong binding energy (UL > 0 eV) where desorption rates to C are higher.
3. Conclusions
The catalytic conversion of A via parallel pathways to products B and C was evaluated by simulation for selectivity control via applied oscillation of the surface binding energy of A in the form of square waves with variable amplitude and frequency. Implementation of surface dynamics leading to variation in the surface binding energies of all surface species (A*, B*, and C*) required definition of linear scaling parameters (γ and δ) and Brønsted–Evans–Polanyi parameters (α and β) that define the extent of variation of surface intermediate and transition state binding energies. Comparison of kinetically different parallel reactions with broad variation in scaling parameters indicated significant capability for targeting specific products by selection of the dynamic criteria (frequency, amplitude, etc.), even when targeted chemical products (B or C) were not possible to selectively produce under static catalyst operation. Two mechanisms were identified leading to dynamic operation for product selectivity: (i) dominant surface coverage of a single species in the strong binding state of the oscillation, and (ii) catalytic resonance of one elementary pathway to rates greater than the competing pathway. Sampling of several disparate combinations of chemical and dynamic parameters indicates significant potential for controlling a wide range of chemistries towards favorable products beyond existing static catalytic methods.4. Computational methods
Parallel A-to-B and A-to-C and single A-to-B or A-to-C reaction network numerical simulations were conducted in Matlab 2019a/b. Continuously stirred tank reactor (CSTR) model equations were used and appropriate model equations were implemented for three gas-phase (A, B, and C) and surface species (A*, B*, and C*). The conversion of the reactant A was held at 1% throughout the static and dynamic calculations. Pre-exponential factors for adsorption and surface reaction/desorption were taken from collision and transition state theory, respectively.47,48 Adsorption steps were assigned a pre-exponential of 106 (bar s)−1 and all other steps were assigned 1013 s−1. Example differential equations are shown below for the reactant A and its adsorbed state A*. For either parallel or single reaction systems, adsorption/desorption was described as a mass balance: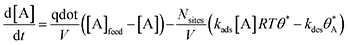 | (3) |
In parallel reaction systems, surface reaction/desorption was described:
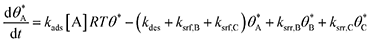 | (4) |
In single reaction systems, surface reaction/desorption was:
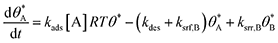 | (5) |
Activation energies for the surface reactions were calculated using Brønsted–Evans–Polanyi (BEP) relationships. The parameter α was set to a typical value of 0.6, and β was set to a moderate value of 100 kJ mol−1 based on literature of calculated BEP relationships.39,46,49 Binding energies at each oscillation endpoint were calculated using linear scaling relationships (LSRs) between the surface adsorbates. Previously defined parameters including γi/j and δi–j were used to fully specify the binding energies of B* and C* relative to the binding energy of A. The values of γi/j between 0.25–2.0 and δi–j between 0.8–2.0 eV were selected to evaluate their effects on static and dynamic reaction behavior. All binding energies were restricted to positive values to avoid nonphysical negative binding energies. Selectivity was defined as the ratio of the rate of production for one product (B or C) over the rate of consumption for the reactant (A).
Volcano plots and surface coverage were calculated for a given set of BEP and LSR parameters at 1% conversion of A. The reaction rates and coverage were sampled at intervals of 0.005 eV, and the built-in ‘fsolve’ function in Matlab was used to obtain values that most closely obtained 1% conversion of A. This calculation was repeated across a binding energy span of 1.0–2.0 eV, and extrapolation was performed using logarithmic extrapolation of rates and coverage.
Dynamic catalysis was implemented using dynamic parameters including oscillation amplitude (ΔUA), frequency (f), endpoints (UL, UH), and waveform type (square waves). All simulations in this manuscript were conducted using a symmetric square waveform with assigned endpoints and frequency. For each endpoint, a set of adsorption, surface reaction, and desorption rate constants were calculated. Then, the oscillation frequency was used to allow the simulation to run for an allotted amount of time at each endpoint. Time-averaged conversion and turnover frequency were calculated using the built in ‘trapz’ function in Matlab over the final and one intermediate oscillation period. The simulation was converged if it met two criteria: (i) time-averaged conversion of A of 1.00 ± 0.01% and (ii) <1.0% differences in the time-averaged conversion of A sampled at the end and middle of the simulation trial.
Heat maps were generated for the TOF of the consumption of A and the selectivity towards B production using the built in ‘heatmap’ function in Matlab. Data was obtained at 175–650 discrete data points and then subdivided by 80–130× to generate a 2080 × 2080 grid. The makima (modified Akima piecewise cubic Hermite interpolation) spline fitting procedure was used to construct curves over the discrete data points. A moving average smoothing function was fitted to the data to remove any fitting artifacts and outliers from the data set with a smoothing factor between 0.00–0.25. The jet color scheme was selected in most heat maps to indicate low selectivity or TOF (dark blue) and high selectivity or TOF (dark red). Raw data for all heat maps are provided in the ESI.†
Conflicts of interest
Authors M. Alexander Ardagh and Paul J. Dauenhauer have a patent pending on the ideas presented in this manuscript. All other authors have no conflicts to declare.Note added after first publication
This version replaces the manuscript published on 11th March 2020. Due to errors inadvertently added during the proofing, equations 2 and 3 contained errors that have now been corrected. The RSC apologies for any confusion.Acknowledgements
We acknowledge financial support of the Catalysis Center for Energy Innovation, a U.S. Department of Energy – Energy Frontier Research Center under Grant DE-SC0001004. The authors acknowledge the Minnesota Supercomputing Institute (MSI) at the University of Minnesota for providing resources that contributed to the research results reported within this paper. URL: http://www.msi.umn.edu/.References
- Report of the Basic Energy Sciences Workshop on Basic Research needs for Catalysis Science to Transform Energy Technologies, 2017 Search PubMed.
- S. Kuld, M. Thorhauge, H. Falsig, C. F. Elkjaer, S. Helveg, I. Chorkendorff and J. Sehested, Quantifying the promotion of Cu catalysts by ZnO for methanol synthesis, Science, 2016, 352(6288), 969–974 CrossRef CAS PubMed.
- S. Raynes, M. A. Shah and R. A. Taylor, Direct conversion of methane to methanol with zeolites: towards understanding the role of extra-framework d-block metal and zeolite framework type, Dalton Trans., 2019, 48, 10364–10384 RSC.
- E. A. Carbonio, T. C. R. Rocha, A. Y. Klyushin, I. Pis, E. Magnano, S. Nappini, S. Piccinin, A. Knop-Gericke, R. Schlogl and T. E. Johnson, Are multiple oxygen species selective in ethylene epoxidation on silver?, Chem. Sci., 2018, 9, 990 RSC.
- S. Linic and M. A. Barteau, Formation of a stable surface oxametallacycle that produces ethylene oxide, J. Appl. Chem. Sci., 2002, 124(2), 310–317 CAS.
- P. Tomkins, A. Mansouri, V. L. Sushkevich, L. I. van der Wal, S. E. Bozbag, F. Krumeich, M. Ranocchiari and J. A. van Bokhoven, Chem. Sci., 2019, 10, 167–171 RSC.
- C. J. Hofer, R. N. Grass, E. M. Schneider, L. Hendriks, A. F. Herzog, M. Zeltner, D. Gunther and W. J. Stark, Water dispersible surface-functionalized platinum/carbon nanorattles for size-selective catalysis, Chem. Sci., 2018, 9, 362–367 RSC.
- X. Liu, W. Zhou, Y. Yang, K. Cheng, J. Kang, L. Zhang, G. Zhang, X. Min, Q. Zhang and Y. Wang, Design of efficient bifunctional catalysts for direct conversion of syngas into lower olefins via methanol/dimethyl ether intermediates, Chem. Sci., 2018, 9, 4708–4718 RSC.
- B. R. Goldsmith, J. Esterhuizen, J.-X. Liu, C. J. Bartel and C. Sutton, Machine learning for heterogeneous catalyst design and discovery, AIChE J., 2018, 64(7), 2311–2323 CrossRef CAS.
- A. H. Motagamwala, M. R. Ball and J. A. Dumesic, Microkinetic analysis and scaling relations for catalyst design, Annu. Rev. Chem. Biomol. Eng., 2018, 9, 413–450 CrossRef PubMed.
- J. A. Labinger, Oxidative coupling of methane: An inherent limit to selectivity?, Catal. Lett., 1988, 1(11), 371–375 CrossRef CAS.
- R. Horn and R. Schlogl, Methane activation by heterogeneous catalysis, Catal. Lett., 2015, 145(1), 23–39 CrossRef CAS.
- M. Alexander Ardagh, O. A. Abdelrahman and P. J. Dauenhauer, Principles of Dynamic Heterogeneous Catalysis: Surface Resonance and Turnover Frequency Response, ACS Catal., 2019, 9(8), 6929–6937 CrossRef.
- J. Perez-Ramirez and N. Lopez, Strategies to break linear scaling relationships, Nat. Catal., 2019, 2, 971–976 CrossRef.
- M. J. Hulsey, C. W. Lim and N. Yan, Promoting heterogeneous catalysis beyond catalyst design, Chem. Sci., 2020, 11, 1456–1468 RSC.
- J. G. Patrow, S. A. Sorenson and J. M. Dawlaty, Direct spectroscopic measurement of interfacial electric fields near an electrode under polarizing or current-carrying conditions, J. Phys. Chem. C, 2017, 121, 11585–11592 CrossRef CAS.
- S. Linic and M. A. Barteau, On the mechanism of Cs promotion in ethylene epoxidation on Ag, J. Am. Chem. Soc., 2004, 126, 8086–8087 CrossRef CAS PubMed.
- F. Che, S. Ha and J.-S. McEwen, Elucidating the field influence on the energetics of the methane steam reforming reaction: A density functional theory study, Appl. Catal., B, 2016, 195, 7–89 CrossRef.
- F. A. Garces-Pineda, M. Blasco-Ahicart, D. Nieto-Castro, N. Lopez and J. R. Galan-Mascaros, Direct magnetic enhancement of electrocatalytic water oxidation in alkaline media, Nat. Energy, 2019, 4, 519–525 CrossRef CAS.
- M. J. Kale, T. Avanesian, H. Xin, J. Yan and P. Christopher, Controlling catalytic selectivity on metal nanoparticles by direct photoexcitation of adsorbate-metal bonds, Nano Lett., 2014, 14(9), 5405–5412 CrossRef CAS PubMed.
- L. Wang, Z. Zeng, W. Gao, T. Maxson, D. Raciti, M. Giroux, X. Pan, C. Wang and J. Greeley, Tunable Intrinsic Strain in Two Dimensional Transition Metal Electrocatalysts, Science, 2019, 363, 870–874 CrossRef CAS PubMed.
- M. F. Francis and W. A. Curtin, Mechanical Stress Combined with Alloying May Allow Continuous Control over Reactivity: Strain Effects on CO Dissociation and Subsequent Methanation Catalysis over Ni(211), Ni3Fe(211), and NiFe(112), J. Phys. Chem. C, 2017, 121, 6113–6119 CrossRef CAS.
- R. Imbihl, Electrochemical Promotion of Catalytic Reactions, Prog. Surf. Sci., 2010, 85, 241 CrossRef CAS.
- S. G. Neophytides and C. G. Vayenas, TPD and Cyclic Voltammetric Investigation of the Origin of Electrochemical Promotion in Catalysis, J. Phys. Chem., 1995, 99, 17063 CrossRef CAS.
- S. Ladas, S. Kennou, S. Bebelis and C. G. Vayenas, Origin of NonFaradaic Electrochemical Modification of Catalytic Activity, J. Phys. Chem., 1993, 97, 8845 CrossRef CAS.
- L. Basini, C. A. Cavalca and G. L. J. Haller, Electrochemical Promotion of Oxygen Atom Back-Spillover from Yttria-Stabilized Zirconia onto a Porous Platinum Electrode: Detection of SERS Signals, J. Phys. Chem., 1994, 98, 10853 CrossRef CAS.
- S. Ladas, S. Bebelis and C. G. Vayenas, Work Function Measurements on Catalyst Films Subject to in situ Electrochemical Promotion, Surf. Sci., 1991, 251–252, 1062 CrossRef CAS.
- A. Hervier, J. R. Renzas, J. Y. Park and G. A. Somorjai, Hydrogen Oxidation-Driven Hot Electron Flow Detected by Catalytic Nanodiodes, Nano Lett., 2009, 9(11), 3930–3933 CrossRef CAS PubMed.
- P. Deshlahra, W. F. Schneider, G. H. Bernstein and E. E. Wolf, Direct control of electron transfer to the surface-CO bond on a Pt/TiO2 catalytic diode, J. Am. Chem. Soc., 2011, 133, 16459–16467 CrossRef CAS PubMed.
- S. N. Maximoff and M. P. Head-Gordon, Chemistry of Fast Electrons, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(28), 11460–11465 CrossRef CAS PubMed.
- Y. Wang, C. H. Kim, Y. Yoo, J. E. Johns and C. D. Frisbie, Field Effect Modulation of Heterogeneous Charge Transfer Kinetics at Back-Gated Two-Dimensional MoS2 Electrodes, Nano Lett., 2017, 17, 7586–7592 CrossRef CAS PubMed.
- C. H. Kim and C. D. Frisbie, Field Effect Modulation of Outer Sphere Electrochemistry at Back-Gated, Ultrathin ZnO Electrodes, J. Am. Chem. Soc., 2016, 138, 7220–7223 CrossRef CAS PubMed.
- C. H. Kim, Y. Wang and C. D. Frisbie, Continuous and Reversible Tuning of Electrochemical Reaction Kinetics on Back-Gated 2D Semiconductor Electrodes: Steady-State Analysis Using a Hydrodynamic Method, Anal. Chem., 2019, 91, 1627–1635 CrossRef CAS PubMed.
- M. Alexander Ardagh, T. Birol, Q. Zhang, O. Abdelrahman and P. J. Dauenhauer, Catalytic Resonance Theory: Super Volcanoes, Catalytic Molecular Pumps, and Oscillatory Steady State, Catal. Sci. Technol., 2019, 9, 5058–5076 RSC.
- A. A. Balandin, The Multiplet Theory of Catalysis. Energy Factors in Catalysis, Russ. Chem. Rev., 1964, 33, 549–579 CAS.
- A. K. Vijh, Sabatier-Balandin Interpretation of the Catalytic Decomposition of Nitrous Oxide on Metal-Oxide Semiconductors, J. Catal., 1973, 31, 51–54 CrossRef CAS.
- S. Ichikawa, Volcano-Shaped Curves in Heterogeneous Catalysis, Chem. Eng. Sci., 1990, 45, 529–535 CrossRef CAS.
- M. A. Barteau, Linear Free Energy Relationships for C1- Oxygenate Decomposition on Transition Metal Surfaces, Catal. Lett., 1991, 8, 175–184 CrossRef CAS.
- J. E. Sutton and D. G. Vlachos, A Theoretical and Computational Analysis of Linear Free Energy Relations for the Estimation of Activation Energies, ACS Catal., 2012, 2, 1624–1634 CrossRef CAS.
- A. J. Medford, A. Vojvodic, J. S. Hummelshoj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the Sabatier Principle to a Predictive Theory of Transition-Metal Heterogeneous Catalysis, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- J. Greeley, Theoretical Heterogeneous Catalysis: Scaling Relationships and Computational Catalyst Design, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 605–635 CrossRef PubMed.
- M. M. Montemore and J. W. Medlin, Scaling relations between adsorption energies for computational screening and design of catalysts, Catal. Sci. Technol., 2014, 4, 3748–3761 RSC.
- G. Jones, J. G. Jakobsen, S. S. Shim, J. Kleis, M. P. Andersson, J. Rossmeisl, F. Abild-Pedersen, T. Bligaard, S. Helveg, B. Hinnemann, J. R. Rostrup-Nielsen, I. Chorkendorff, J. Sehested and J. K. Nørskov, First principles calculations and experimental insight into methane steam reforming over transition metal catalysts, J. Catal., 2008, 259(1), 147–160 CrossRef CAS.
- P. Mehta, P. Barboun, D. B. Go, J. C. Hicks and W. F. Schneider, Catalysis Enabled by Plasma Activation of Strong Chemical Bonds: A Review, ACS Energy Lett., 2019, 4(5), 1115–1133 CrossRef CAS.
- A. Khorshidi, J. Violet, J. Hashemi and A. A. Peterson, How strain can break the scaling relations of catalysis, Nat. Catal., 2018, 1, 263–268 CrossRef.
- F. Che, J. T. Gray, S. Ha and J.-S. McEwen, Improving Ni Catalysts Using Electric Fields: A DFT and Experimental Study of the Methane Steam Reforming Reaction, ACS Catal., 2017, 7(1), 551–562 CrossRef CAS.
- V. P. Zhdanov, J. Pavlicek and Z. Knor, Preexponential Factors for Elementary Surface Processes, Catal. Rev.: Sci. Eng., 2006, 30(4), 501–517 CrossRef.
- R. C. Baetzold and G. A. Somorjai, Preexponential factors in surface reactions, J. Catal., 1976, 45(1), 94–105 CrossRef CAS.
- S. A. Akhade, R. M. Nidzyn, G. Rostamikia and M. J. Janik, Using Brønsted-Evans-Polanyi relations to predict electrode potential-dependent activation energies, Catal. Today, 2018, 312, 82–91 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information including computer code, time-on-stream data, and simulation methods. See DOI: 10.1039/c9sc06140a |
| This journal is © The Royal Society of Chemistry 2020 |