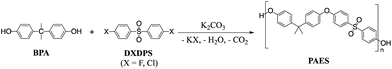Kinetics and mechanisms of polycondensation reactions between aryl halides and bisphenol A†
Yi
Yang
,
Christopher L.
Muhich
and
Matthew D.
Green
 *
*
Department of Chemical Engineering; School for Engineering of Matter, Transport and Energy, Arizona State University, Tempe, AZ 85287, USA. E-mail: mdgreen8@asu.edu
First published on 9th July 2020
Abstract
Aryl chlorides (ArCl) or aryl fluorides (ArF) were used in polycondensation reactions to form poly(arylene ether sulfone)s (PAES). Interestingly, the kinetics of the ArF reaction fit a third-order rate law, which is attributed to the activation of the carbon–fluorine bond by two potassium cations (at least one bound to phenolate), which form a three-body complex. The ArCl monomer follows a second-order rate law, where a two-body complex forms at the initial state of the aromatic nucleophilic substitution (SNAr) pathway. These metal cation-activated complexes act as intermediates during the attack by the nucleophile. This finding was reproduced with either the potassium or the sodium counterion (introduced via potassium carbonate or sodium carbonate). Through a combination of experimental analysis of reaction kinetics and computational calculations with density functional theory (DFT) methods, the present work extends the fundamental understanding of polycondensation mechanisms for two aryl halides and highlights the importance of the CX–metal interaction(s) in the SNAr reaction, which is translational to other ion-activated substitution reactions.
Introduction
The most widely used synthetic method to produce poly(arylene ether sulfone)s (PAES) for industrial and research purposes1–12 consists of polycondensation reactions of bisphenols with 4,4′-dichlorodiphenyl sulfone (DCDPS) or with 4,4′-difluorodiphenyl sulfone (DFDPS) in an aprotic polar solvent such as dimethyl sulfoxide (DMSO) using potassium carbonate (K2CO3) as the base (Scheme 1).13–15 The reaction typically begins with the deprotonation of bisphenols (pKa = 9.6–11.3) by a slight excess of K2CO3 (conjugate acid pKa = 10.25) to produce (1) phenolate compounds, which act as the electron withdrawing group in the subsequent polycondensation reaction with the aryl halide; and (2) side products, including water and carbon dioxide from the further decomposition of the protonated bicarbonate ion under the reaction heat. The mechanism behind this polycondensation reaction is widely accepted as a classical SNAr, in which the aryl halide is activated toward nucleophilic attack by an electron withdrawing group.16,17 In aromatic nucleophilic substitution (SNAr) reactions, the rate limiting step is typically the formation of the resonance-stabilized anionic intermediate, the Meisenheimer complex18 (Schemes 2 and 3), for which the reactivity of the aryl halide decreases in the order F ≫ Cl > Br > I based on the electronegativity of the halogen.16 Thus, it is rational to assume that the SNAr reaction for any aryl dihalide monomer and bisphenol-based nucleophile would follow a second order rate law.17Interestingly, in our present work, the order of the reaction for the aryl fluoride monomer (i.e., DFDPS) was different than that for the aryl chloride monomer (i.e., DCDPS). As expected, the reaction rate of the polymerization using the DFDPS monomer was significantly higher than that of the DCDPS monomer under identical experimental conditions. Ross and coworkers studied the base-catalyzed SNAr mechanism in the reaction of 1-chloro-2,4-dinitrobenzene and allylamine, which was self-catalyzed by both the amine and aromatic nitro groups.19–21 They showed that the reaction kinetics fit a third-order rate expression. A computational study22 related to the synthesis of polysulfones showed that the Meisenheimer complex formed via the formation of a two-body complex with a strong interaction between the metal cation and the aryl fluoride. However, the influence of the monomer interactions with the base on the rate law order in polycondensation reactions of different aryl halides has not been systematically studied using both experimental and computational techniques. In the present work, we systematically compared the kinetics of DFDPS/bisphenol-A (BPA) and DCDPS/BPA reactions during PAES synthesis and revealed surprising insights into the activity of the metal ion and its effect on the reaction kinetics in the two aryl halide systems. While we utilized BPA in order to prepare model PAES macromolecules, we predict that the findings will translate to PAESs prepared using other bisphenol monomers (e.g., 4,4′-biphenol, bisphenol F, etc.). The commercial relevance of polysulfones and the widespread use of SNAr reactions suggest these findings would be of interest to the greater organic chemistry and polymer science communities.
Experimental section
Materials and reagents
4,4′-Dichlorodiphenyl sulfone (DCDPS, 98%) was purchased from Sigma-Aldrich and recrystallized from diethyl ether before use. 4,4′-Difluorodiphenyl sulfone (DFDPS, >98%) was purchase from ThermoFisher Scientific Chemical and recrystallized from diethyl ether before use. Bisphenol A (BPA, ≥99%) was purchased from BDH® VMR analytical and recrystallized from acetic acid/water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) before use. THF and toluene (99.8%) were purchased from Sigma-Aldrich and used after passing through M. Braun SPS-800 solvent purification system. Dimethyl sulfoxide (DMSO, anhydrous, ≥99.9%) was purchased from Sigma-Aldrich and used as received. Potassium carbonate (K2CO3, ≥98%) and sodium carbonate (Na2CO3, ≥98%) were purchased from Sigma-Aldrich and vacuum dried overnight before use. Deuterated chloroform (CDCl3, 99.8 atom% D, 0.03% (v/v) TMS) was purchased from BDH® VMR analytical and used as received.
1 v/v) before use. THF and toluene (99.8%) were purchased from Sigma-Aldrich and used after passing through M. Braun SPS-800 solvent purification system. Dimethyl sulfoxide (DMSO, anhydrous, ≥99.9%) was purchased from Sigma-Aldrich and used as received. Potassium carbonate (K2CO3, ≥98%) and sodium carbonate (Na2CO3, ≥98%) were purchased from Sigma-Aldrich and vacuum dried overnight before use. Deuterated chloroform (CDCl3, 99.8 atom% D, 0.03% (v/v) TMS) was purchased from BDH® VMR analytical and used as received.
Synthesis of poly(arylene ether sulfone)s
The poly(arylene ether sulfone)s (PAES) were synthesized using traditional polycondensation reaction conditions. One reaction protocol for a DCDPS/BPA reaction is provided as an example. It is worth noting that different reaction temperatures and aryl halide monomers (DFDPS vs. DCDPS) were utilized for various studies performed herein (e.g., the stoichiometry study vs. the kinetics study). BPA (1.049 g, 4.605 mmol), DCDPS (1.406 g, 4.899 mmol), K2CO3 (0.667 g, 4.835 mmol) were added to a three-neck, 250 mL flask equipped with a condenser, Dean Stark trap, nitrogen inlet/outlet, and a mechanical stirrer. DMSO (24 mL) and toluene (6 mL) were added to the flask to dissolve the monomers. The solution was heated to 140 °C and refluxed for 1–6 h to remove the azeotropic mixture of toluene and water using the Dean Stark trap. The reaction continued for 48 h at 140 °C. Again, this protocol is provided as an example, the specific reaction temperatures and times utilized are noted in the figures and discussion below for each individual study. After the reaction, the mixture was cooled to room temperature and filtered to remove the precipitated salt. Then the clear solution was diluted with THF, passed through a 0.45 μm Teflon® filter, and precipitated by addition to stirring DI water. The polymer was filtered and dried under vacuum at 100 °C for 24 h. The yields of the final purified polymer products were all more than 95% by weight.Synthesis of potassium phenolate precursor
The potassium phenolate precursor was prepared by mixing potassium carbonate (1 g, 7.246 mmol) and bisphenol-A (1.652 g, 7.246 mmol) in 50 mL of DI water at 40 °C for at least 20 h until the solution became homogeneous. Then the potassium phenolate salt was obtained by evaporating water out of the aqueous solution completely via a rotary evaporator and then vacuum dried at 80 °C for 48 h.Characterizations of polymers and precursor
1H-NMR spectroscopy was performed on a Varian 400 MHz spectrometer using CDCl3 to analyze the polymer's chemical structure. Samples contained 20 mg of dried polymer dissolved in CDCl3. The chemical shifts are given in ppm downfield from tetramethylsilane (TMS), as shown in Fig. S1.†1H NMR (CDCl3 with 0.05% v/v TMS, 400 MHz): δ = 7.85 (4Ha, m, J = 9 Hz), 7.24 (4Hb, m, J = 9 Hz), 7.01 (4Hc, m, J = 9 Hz), 6.94 (4Hd, m, J = 9 Hz), 1.69 (6He, s).In order to determine the molecular weight of the copolymers, size exclusion chromatography (SEC) was performed using a Waters Alliance e2695 HPLC system, with Styragel® HR5 and HR4 7.8 × 300 mm (THF) columns in series, interfaced to a light scattering detector (miniDAWN TREOS) and an Optilab T-rEX differential refractive index (dRI) detector. The mobile phase was THF Optima (inhibitor-free) at a flow rate of 1.0 mL min−1, and samples were calibrated against Pressure Chemical Company low dispersity polystyrene standards of 30 kDa and 200 kDa using Astra v6.1 software. Then, ∼1.0 mg mL−1 filtered solutions of polymer in THF were prepared for SEC.
Density functional theory calculations
Density functional theory (DFT) calculations, as implemented in GAMESS23,24 using the M06-2X functional,25 a 6-311G**(+) basis set, and DMSO implicit solvent were used to calculate the reaction mechanism of the aryl halide condensation reaction through both second- and third-order mechanisms. Truncated monomers were used to represent the polymer, as shown in Fig. 3, with Na+ rather than K+ to save computational time. Experimental results validated no change in reaction order was caused by interchanging Na+ and K+ (discussed below).Results and discussion
In a polycondensation reaction between bifunctional A–A and B–B monomers where the stoichiometric ratio ([BPA]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [DXDPS], r) is 1
[DXDPS], r) is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the Carothers equation predicts an infinite degree of polymerization and molecular weight.26–28 However, in the present work, high molecular weight was not achieved at a 1
1, the Carothers equation predicts an infinite degree of polymerization and molecular weight.26–28 However, in the present work, high molecular weight was not achieved at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry. To determine the optimal non-stoichiometric ratio to achieve high molar mass polymers, therefore, we first conducted a series of polycondensations of BPA and DCDPS, as well as BPA and DFDPS at various molar ratios (Scheme 1). Initial reactions were performed with DCDPS and BPA and are shown in Fig. 1a. When DCDPS and BPA reacted at 180 °C for 48 h with a stoichiometric ratio of r = BPA
1 stoichiometry. To determine the optimal non-stoichiometric ratio to achieve high molar mass polymers, therefore, we first conducted a series of polycondensations of BPA and DCDPS, as well as BPA and DFDPS at various molar ratios (Scheme 1). Initial reactions were performed with DCDPS and BPA and are shown in Fig. 1a. When DCDPS and BPA reacted at 180 °C for 48 h with a stoichiometric ratio of r = BPA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCDPS = 1, a number-averaged molecular weight (Mn) of 17.3 kDa and molecular weight distribution (Đ) of 1.21 were obtained, which is much lower than the Đ of 2.0 predicted for a polycondensation product at full conversion. Then, a moderate excess of DCDPS was used in new reactions under identical reaction conditions (i.e., solvent/monomer concentration, temperature), and the highest molecular weights were observed at r = 0.94–0.97. In this case, an excess of DCDPS means that low conversion oligomers have two ArCl end groups. We predict that a fraction of the excess –Cl group is hydrolyzed to a –OH group, which achieves a 1
DCDPS = 1, a number-averaged molecular weight (Mn) of 17.3 kDa and molecular weight distribution (Đ) of 1.21 were obtained, which is much lower than the Đ of 2.0 predicted for a polycondensation product at full conversion. Then, a moderate excess of DCDPS was used in new reactions under identical reaction conditions (i.e., solvent/monomer concentration, temperature), and the highest molecular weights were observed at r = 0.94–0.97. In this case, an excess of DCDPS means that low conversion oligomers have two ArCl end groups. We predict that a fraction of the excess –Cl group is hydrolyzed to a –OH group, which achieves a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry in situ. Thus, an optimum conversion and a high molecular weight are obtained during the reaction. It is worth noting that the DCDPS/BPA polymerization exhibited an optimum Đ of ∼1.6 at the offset r = 0.94, which suggests that low molecular weight oligomers are still present. Thus, the reaction could be further improved (e.g., increased time, temperature, concentration, etc.) in order to obtain complete conversion. The same phenomenon, an increased Xnvia stoichiometric imbalance, was observed in the polymerization with DFDPS (Fig. 1b, at 140 °C for 4 h), where the highest Mn (33 kDa) and Đ (1.93) were observed at r = 0.94. Thus, an optimal stoichiometric ratio of 1
1 stoichiometry in situ. Thus, an optimum conversion and a high molecular weight are obtained during the reaction. It is worth noting that the DCDPS/BPA polymerization exhibited an optimum Đ of ∼1.6 at the offset r = 0.94, which suggests that low molecular weight oligomers are still present. Thus, the reaction could be further improved (e.g., increased time, temperature, concentration, etc.) in order to obtain complete conversion. The same phenomenon, an increased Xnvia stoichiometric imbalance, was observed in the polymerization with DFDPS (Fig. 1b, at 140 °C for 4 h), where the highest Mn (33 kDa) and Đ (1.93) were observed at r = 0.94. Thus, an optimal stoichiometric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.94 DXDPS
0.94 DXDPS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BPA was utilized for all subsequent reactions discussed. However, the complete conversion obtained for the DFDPS/BPA reaction prompted a subsequent kinetic study to better understand the polymerization behavior of the two aryl halides.
BPA was utilized for all subsequent reactions discussed. However, the complete conversion obtained for the DFDPS/BPA reaction prompted a subsequent kinetic study to better understand the polymerization behavior of the two aryl halides.
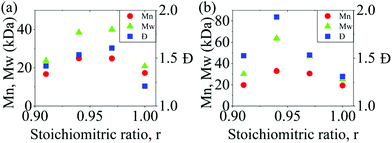 | ||
Fig. 1 The effect of BPA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DXDPS stoichiometry (r) on the molecular weight and Đ obtained during polycondensation reactions of (a) DCDPS/BPA at 180 °C for 48 h and (b) DFDPS/BPA at 140 °C for 4 h. DXDPS stoichiometry (r) on the molecular weight and Đ obtained during polycondensation reactions of (a) DCDPS/BPA at 180 °C for 48 h and (b) DFDPS/BPA at 140 °C for 4 h. | ||
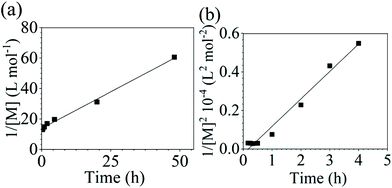
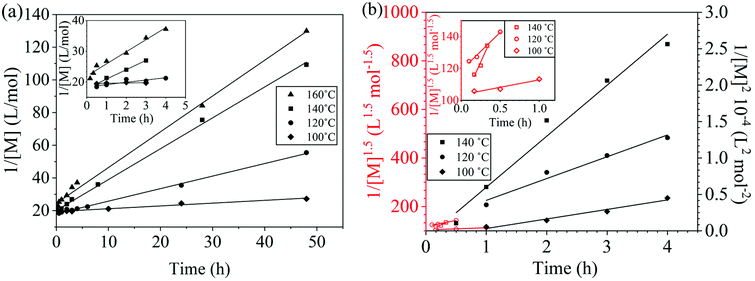
The reaction conversion for the polycondensations utilizing both aryl halides was monitored as a function of time (Fig. 2). Aliquots were collected from the reactor until the reaction reached completion. Importantly, it took around 4 h for the DFDPS/BPA polycondensation to reach the high conversion plateau, while the DCDPS/BPA reaction took up to 48 h under identical experimental conditions. Next, the conversion data was linearized using integer rate law expressions. The DCDPS/BPA polymerization showed linearity when fit with a second order rate expression, as seen in Fig. 3a. This corroborates previous literature17 that describes the mechanism of the condensation polymerization to form PAES via the SNAr mechanism. In the DFDPS/BPA reaction, the reaction rate constant is significantly higher than that of the DCDPS/BPA reaction under identical experimental conditions due to the relatively higher electronegativity and smaller size of fluorine.16 Interestingly, the DFDPS/BPA polymerization has a reaction order higher than second order (Fig. 3b). Specifically, the data are described fairly well with a third-order rate expression, suggesting that the reaction is second order with respect to either DFDPS or BPA. We hypothesize that the relatively higher electronegativity of the fluorine attracts two phenolate salts to make the reaction second order with respect to BPA and first order with respect to DFDPS. This hypothesis was tested using computational and experimental means. As a final note, overall, the third-order rate expression describes the reaction progression well, but deviations were observed at lower reaction times. This phenomenon was further examined and is discussed below.
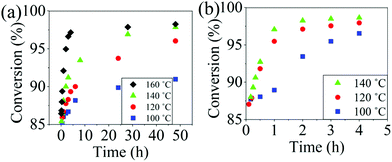 | ||
| Fig. 2 Plots of reaction conversion versus time for the polymerization of: (a) DCDPS and BPA, and (b) DFDPS and BPA at various temperatures with K2CO3. | ||
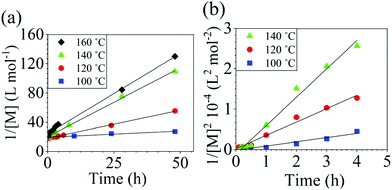 | ||
| Fig. 3 Linearized kinetic plots of: (a) second-order reaction for the DCDPS/BPA polycondensation, and (b) third-order reaction for the DFDPS/BPA polycondensation at various temperatures with K2CO3. | ||
Viswanathan and McGrath29 studied the reaction of DCDPS/BPA in N,N-dimethylacetamide (DMAc) and toluene (at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volumetric ratio) and catalyzed by K2CO3. They observed non-linear kinetics when plotting conversion versus the inverse of concentration with an apparent reaction order less than two. They attributed this deviation to the partially heterogeneous nature of the reaction (i.e., the K2CO3 is only partially soluble). In the present work, however, DMSO and toluene (at a 4
1 volumetric ratio) and catalyzed by K2CO3. They observed non-linear kinetics when plotting conversion versus the inverse of concentration with an apparent reaction order less than two. They attributed this deviation to the partially heterogeneous nature of the reaction (i.e., the K2CO3 is only partially soluble). In the present work, however, DMSO and toluene (at a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volumetric ratio) was used as the solvent, which improved the solubility of K2CO3 and also the overall dielectric constant of the reaction medium, thus a linear second order kinetic plot was observed in the DCDPS/BPA reaction. The DFDPS/BPA reaction, however, displayed a reaction order greater than two. Therefore, the mechanism for the DFDPS/BPA polycondensation is independent of the limited solubility of K2CO3 and is different than the classical SNAr mechanism.
1 volumetric ratio) was used as the solvent, which improved the solubility of K2CO3 and also the overall dielectric constant of the reaction medium, thus a linear second order kinetic plot was observed in the DCDPS/BPA reaction. The DFDPS/BPA reaction, however, displayed a reaction order greater than two. Therefore, the mechanism for the DFDPS/BPA polycondensation is independent of the limited solubility of K2CO3 and is different than the classical SNAr mechanism.
Additionally, polycondensation reactions with sodium carbonate (Na2CO3) as the base were also performed for combinations of both DCDPS/BPA and DFDPS/BPA. A steady increase in molecular weight was observed, though at a slower reaction rate, as expected. Two factors that contribute to the slower reaction are the relatively lower solubility of Na2CO3 in DMSO and the lower reactivity of the sodium phenolate compared to potassium phenolate. The SEC elution traces and time-dependent plots of conversion are seen in Fig. S5 and S6.† The conversion data were linearized (Fig. 4) and a good fit to a second-order rate law for the DCDPS/BPA reaction was observed with Na2CO3 whereas the DFDPS/BPA reaction followed a third order rate expression. These observations match the polymerizations performed using K2CO3 as a base and eliminate the possibility that the counterion influenced the reaction order.
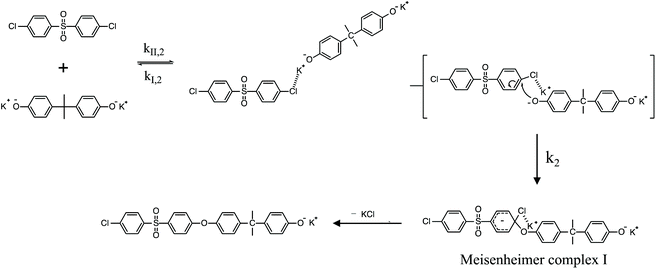
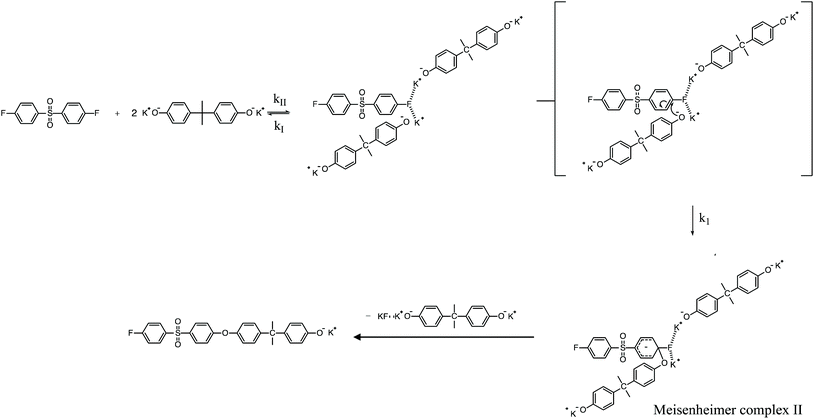
To review, the mechanism for the classical SNAr reaction is shown in Scheme 2. Following the formation of the phenolate ion a complex between the cation and the aryl halide forms. The phenolate then attacks the aryl halide to form the Meisenheimer complex, which then goes on to form the arylene ether. However, the observations above suggest a higher order reaction pathway when the aryl halide contains a fluorine. Therefore, a mechanism for the third-order reaction between DFDPS and BPA is proposed in Scheme 3. In this reaction pathway, the main difference is the formation of a three-body complex wherein two phenolates are interacting with the ArF. One of the phenolates continues activating the ArF while the other attacks causing the formation of the Meisenheimer complex. Then, aromaticity is reformed as the arylene ether is created. Importantly, though not captured in Scheme 3, the potassium ion can exist as either a free ion or as a part of the phenolate complex shown in Schemes 2 and 3. For the sake of clarity, the potassium ion, in either form, is referred to as “B” in the subsequent discussions.
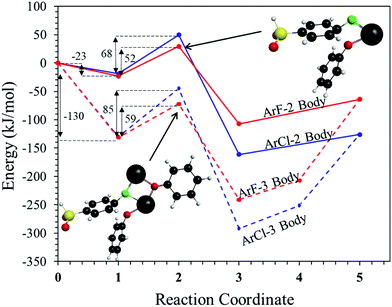
To probe the plausibility of this reaction pathway, DFT calculations were used to study the reaction. The kinetic data using potassium and sodium counterions suggested that sodium could be used to save computational time. Thus, the “B” noted above is used to denote a sodium ion in the DFT discussion below. Interestingly, previous computational work30,31 showed that potassium cresolate formed a two-body complex with an ArF as an intermediate of the nucleophilic substitution reaction. However, the possibility of a three-body complex was not considered or reported. The DFT calculations of the relative formation energies of the intermediate complexes and final products in the DFDPS/BPA and DCDPS/BPA reactions suggest that the formation of a single three-body ArX⋯2B complex (−131 kJ mol−1) is strongly favorable over forming a two-body ArX⋯B complex (−23 kJ mol−1, Fig. 5). The DFT results go on to show that the activation barrier to form the Meisenheimer transition state for the three-body ArCl⋯2B reaction is 85 kJ mol−1, which is significantly higher than that of the two-body ArCl⋯B complex (68.3 kJ mol−1). For the ArF monomer, the activation barriers are similar (52 and 59 kJ mol−1 for the two-body and three-body complexes, respectively). Together, this predicts that the ArCl reaction will proceed through the energetically more favorable two-body path (Scheme 2, in agreement with the experimental second-order kinetics) and the ArF reaction will proceed through the three-body pathway (Scheme 3). The three-body SNAr pathway has therefore been termed the cation-activated SNAr pathway.
The energetics of the complex formation and the reaction calculated using DFT were compared to the experimental data. Performing the polycondensation reactions at varying temperatures enabled the creation of Arrhenius plots for the DFDPS/BPA and DCDPS/BPA reactions (Fig. 6). The activation energy (Ea) for the DFDPS/BPA reaction was 6.0 kJ mol−1 lower than the DCDPS/BPA reaction. Also, the pre-exponential factor for the DFDPS/BPA reaction was nearly three orders of magnitude higher than that for the DCDPS/BPA reaction. Finally, the data revealed that the rate constant was significantly higher for the ArF reaction, as also evidenced by the shorter reaction time need to achieve complete conversion. Together, the DFT calculations, the proposed mechanism (Scheme 3), the activation energies, and the pre-exponential factors suggest that the reactions are driven by changes in both enthalpy and entropy. Moreover, the activation energies from the experimental data match in both the order of magnitude and the trend predicted by the DFT calculations. Table 1 summarizes the relevant kinetic data for the series of polymerizations.
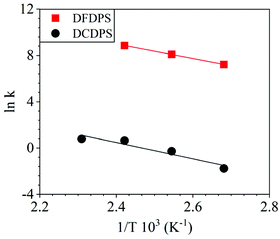 | ||
| Fig. 6 Arrhenius plots for the rate constants of polycondensation reactions of DFDPS/BPA (red square) and DCDPS/BPA (black circle) with K2CO3 as the base. | ||
| Monomers | Temperature (°C) | Reaction time (h) | Conversion (%) | k | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A A |
E a (kJ mol−1) | E a, DFT (kJ mol−1) | |
|---|---|---|---|---|---|---|---|---|
| a Activation energy obtained through DFT calculation. | ||||||||
| DFDPS + BPA | 140 | 4 | 98.7 | 7023 | L2 mol−2 h−1 | 24 | 52 | 59 |
| 120 | 97.9 | 3289 | ||||||
| 100 | 96.5 | 1366 | ||||||
| DCDPS + BPA | 160 | 48 | 98.2 | 2.2 | L mol−1 h−1 | 17 | 58 | 69 |
| 140 | 97.9 | 1.9 | ||||||
| 120 | 96.0 | 0.8 | ||||||
| 100 | 93.2 | 0.2 | ||||||
The following discussion details an in-depth analysis of the reaction kinetics for the DFDPS/BPA and DCDPS/BPA polymerizations. The energetic analyses from DFT and experimental data indicate that the ArF/BPA reaction proceeds via the formation of a three-body complex (ArF⋯2B), which is in equilibrium with ArF and two Bs (at least one of the two Bs is a K+PhO−). Whereas, the ArCl/BPA reaction proceeds through a two-body complex (ArCl⋯B) via the classical SNAr mechanism. The equilibrium constants, Ka,1 and Ka,2, for the formation of a three-body complex and two-body complex are expressed in eqn (1) and (2), respectively:
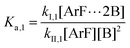 | (1) |
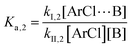 | (2) |
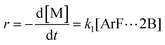 | (3) |
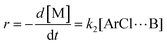 | (4) |
Combining eqn (1) and (3) yields:
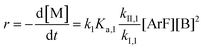 | (5) |
Similarly, combining eqn (2) and (4) yields:
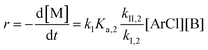 | (6) |
It is important to note a deviation from the third-order rate law fit was observed in the DFDPS/BPA polymerization at conversions <90%. However, the DCDPS/BPA polymerization fits the second-order rate law over the whole course of the reaction (Fig. 7a). Since the reaction proceeds exponentially with time, this the low-conversion region of DFDPS/BPA polymerization is captured by a relatively small period of time (Fig. 7b). According to Flory,32 the failure to fit the data over the low-conversion region is attributed to the large decrease in the polarity of the reaction medium as the phenolate groups are replaced by the arylene ether groups and the simultaneous removal of water at the initial stage of the reaction. The decrease in polarity alone can induce a change in the order of reaction, which is corroborated by the experimental data shown in Fig. 3b. Specifically, the reaction order changes from 2.5 in the low conversion region (Fig. 7b) to a reaction order of three in the high conversion region, which corresponds to a change in the composition of the three-body complex from [K+][K+PhO−][ArF] in the high polarity medium to [K+PhO−][K+PhO−][ArF] in the relatively lower polarity medium. This suggests that the free potassium cation is a more effective activator than the paired K+PhO− salt in the high polarity, low conversion region, where the concentration of free potassium cation ([K+]) is also relatively high. [K+] is given by:
| [K+] = (KK+PhO− [K+PhO−])1/2 | (7) |
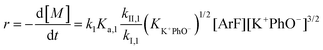 | (8) |
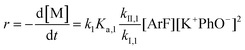 | (9) |
That this phenomenon was only observed for the DFDPS/BPA polymerization, and not the DCDPS/BPA polymerization, provides further evidence for K⋯F or Na⋯F interaction as well as the reaction mechanism proposed in Scheme 3.
The aryl fluoride–potassium interaction was further investigated using NMR spectroscopy. Specifically, K+PhO− was prepared and mixed with DFDPS at varying molar ratios under anhydrous conditions, and the chemical shifts of the 19F resonances were observed. The ArF strongly interacted with the potassium ion(s), as seen in Fig. 8. The 19F NMR spectra revealed that the chemical shift of fluorine increased monotonically as the DFDPS/K+PhO− ratio increased. This trend is further supportive that the rate expression is second order with respect to B since the trend continues linearly at stoichiometric ratios less than one. Changes in the chemical shift are the result of a combination of the effects from electron density changes (i.e., diamagnetic) and overlap/interactions between molecular orbitals (i.e., paramagnetic) effects.33 If the diamagnetic contributions only were analyzed, the increase in chemical shift would suggest a reduction in electron density at the ArF, which is counterintuitive and dissimilar to the proposed cation-activated SNAr reaction mechanism. Therefore, DFT calculations were utilized again to predict the changes in the charge state of the ArF upon complexation with the Na+PhO− (Table S1†). Note again that the counterion (Na+versus K+) will not affect the phenomenon observed, simply the magnitude of the effect. The negative charge of the fluorine is calculated to increase slightly (0.02 electron) upon the introduction of Na+PhO− at ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, based on Bader charge analysis.34 Although the amount gained is small, we note that the subtlety of electron density change is mirrored in the NMR which also shows only a slight shifts. For the sake of clarity, it is important to note that Bader charge does not necessarily correlate directly with formal charge, as electron sharing is explicitly included; however, it does show that additional electron density localizes on the fluorine of the ArF as each Na+ complexes with the DFDPS molecule. This additional electron localization on the fluorine of the ArF is consistent with the relative electronegativity of the F and Na as well as the additional charge attraction from the Na+ it would experience during the formation of the three-body complex in the cation-activated SNAr reaction. The results of this calculation are consistent with intuition. Thus, the 19F NMR spectroscopy and DFT calculations suggest that a significant paramagnetic effect occurs in the DFDPS/K+PhO− complex, which will be the subject of future investigations. In summary, the 19F NMR results (Fig. 8) and the DFT calculations of electron density distribution confirm the presence of the ArF⋯K+ interaction as well as provide strong support for the cation-activated SNAr mechanism.
2, based on Bader charge analysis.34 Although the amount gained is small, we note that the subtlety of electron density change is mirrored in the NMR which also shows only a slight shifts. For the sake of clarity, it is important to note that Bader charge does not necessarily correlate directly with formal charge, as electron sharing is explicitly included; however, it does show that additional electron density localizes on the fluorine of the ArF as each Na+ complexes with the DFDPS molecule. This additional electron localization on the fluorine of the ArF is consistent with the relative electronegativity of the F and Na as well as the additional charge attraction from the Na+ it would experience during the formation of the three-body complex in the cation-activated SNAr reaction. The results of this calculation are consistent with intuition. Thus, the 19F NMR spectroscopy and DFT calculations suggest that a significant paramagnetic effect occurs in the DFDPS/K+PhO− complex, which will be the subject of future investigations. In summary, the 19F NMR results (Fig. 8) and the DFT calculations of electron density distribution confirm the presence of the ArF⋯K+ interaction as well as provide strong support for the cation-activated SNAr mechanism.
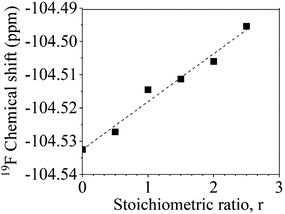 | ||
Fig. 8 Chemical shifts of the 19F nuclear magnetic resonance upon ArF interactions with K+PhO− at various stoichiometric ratios (r, K+PhO−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ArF). ArF). | ||
Collectively, this finding, that the mechanism of the SNAr reaction is dependent on the composition of the aryl halide is quite compelling. First, the findings are relevant to commercially relevant PAESs despite the recent move away from BPA-based macromolecules due to concerns over mutagenicity, endocrine disruption, and environmental accumulation; this sustained relevance is due to the effect of the aryl halide on the reaction pathway, not the bisphenol monomer. Moreover, we anticipate that this work could create interest and future endeavors in designing reaction catalysts and optimizing reaction conditions for SNAr reactions. The polymerization of PAES requires deprotonation of the phenol to produce a good nucleophile, which makes the use of carbonate salts fairly practical. Similarly, the desire to produce polymers of high molecular weight necessitate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometries (in situ). However, the opportunity to optimize analogous SNAr reactions using the outcomes of this work is possible. For example, other potassium salts, such as KPF6 and K(CF3SO2)N, are highly soluble in various organic solvents but are only weakly ion paired compared to K2CO3. Thus, the ion pairing in the salt and the improved solubility could be used to tune or optimize the reaction rate and improve reaction kinetics in organic solvents like DMSO. We note above that the reaction polarity affects the form of the salt and the reaction order; therefore, ion pairing strength can be used as a functional handle to tune the reaction kinetics.
1 stoichiometries (in situ). However, the opportunity to optimize analogous SNAr reactions using the outcomes of this work is possible. For example, other potassium salts, such as KPF6 and K(CF3SO2)N, are highly soluble in various organic solvents but are only weakly ion paired compared to K2CO3. Thus, the ion pairing in the salt and the improved solubility could be used to tune or optimize the reaction rate and improve reaction kinetics in organic solvents like DMSO. We note above that the reaction polarity affects the form of the salt and the reaction order; therefore, ion pairing strength can be used as a functional handle to tune the reaction kinetics.
Conclusions
In conclusion, we report the kinetics and mechanisms of SNAr of a classic polymer system: PAES prepared using DFDPS and DCDPS with BPA. As expected, the ArCl monomer follows a second-order rate law; however, the SNAr of ArF follows a third-order rate law. The C–F bond is activated by free alkali cations or alkali–phenolates within energetically favorable three-body [ArF⋯2B] complexes, producing a third-order rate law and alternate cation-activated SNAr mechanism. The C–Cl bond is activated by an alkali–phenolate that favors a two-body [ArCl⋯B] complex, producing a second-order rate law following the classical SNAr mechanism. This conclusion is supported by experimental observation and computational calculation for both potassium-activated reactions and sodium-activated reactions. Our results provide additional understanding of polycondensation mechanisms for aryl halide monomers as well as support the importance of C–X interactions with dissociated alkali ions and alkali-containing charge complexes. Further exploration of the polycondensation medium effects on the overall reaction behavior as well as the applications of this discovery to the synthesis of other arylene ethers is under investigation.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors acknowledge Prof. Jeffery L. Yarger, Dr Brian R. Cherry, and Dr Stephen K. Davidowski at ASU for helpful discussions. This work was financially supported by NSF CBET 1836719, NASA ECF (80NSSC18K1508), and ARPA-E (DE- AR0001103). This work used the Extreme Science and Engineering Discovery Environment (XSEDE) through allocation ECD190001.References
- H. R. Kricheldorf, What Does Polycondensation Mean?, in Macromolecular Symposia, 2003, vol. 199, pp. 1–13. DOI:10.1002/masy.200350901.
- A. Noshay and L. M. Robeson, Sulfonated Polysulfone, J. Appl. Polym. Sci., 1976, 20(7), 1885–1903, DOI:10.1002/app.1976.070200717.
- C. Zhao, J. Xue, F. Ran and S. Sun, Modification of Polyethersulfone Membranes - A Review of Methods, Prog. Mater. Sci., 2013, 58(1), 76–150, DOI:10.1016/j.pmatsci.2012.07.002.
- H. R. Kricheldorf, L. Vakhtangishvili and D. Fritsch, Synthesis and Functionalization of Poly(Ether Sulfone)s Based on 1,1,1-Tris(4-Hydroxyphenyl)Ethane, J. Polym. Sci., Part A: Polym. Chem., 2002, 40(17), 2967–2978, DOI:10.1002/pola.10372.
- J. Ren, B. O'Grady, G. deJesus and J. R. McCutcheon, Sulfonated Polysulfone Supported High Performance Thin Film Composite Membranes for Forward Osmosis, Polymer, 2016, 103, 486–497, DOI:10.1016/j.polymer.2016.02.058.
- F. Wang, T. Glass, X. Li, M. Hickner, Y. S. Kim and J. McGrath, Synthesis and Characterization of Controlled Molecular Weight Poly(Arylene Ether Sulfone) Copolymers Bearing Sulfonate Groups by Endgroup Analysis, in American Chemical Society, Polymer Preprints, Division of Polymer Chemistry, 2002, vol. 43, pp. 492–493 Search PubMed.
- W. L. Harrison, K. O'Connor, N. Arnett and J. E. McGrath, Homogeneous Synthesis and Characterization of Sulfonated Poly(Arylene Ether Sulfone)s via Chlorosulfonic Acid, in American Chemical Society, Polymer Preprints, Division of Polymer Chemistry, 2002, vol. 43, pp. 1159 Search PubMed.
- B. C. Johnson, İ. Yilgör, C. Tran, M. Iqbal, J. P. Wightman, D. R. Lloyd and J. E. McGrath, Synthesis and Characterization of Sulfonated Poly(Acrylene Ether Sulfones), J. Polym. Sci., Polym. Chem. Ed., 1984, 22(3), 721–737, DOI:10.1002/pol.1984.170220320.
- L. M. Robeson, A. G. Farnham and J. E. McGrath, Synthesis and Dynamic Mechanical Characteristics of Poly(Aryl Ethers), Appl. Polym. Symp., 1975, 26(polym. polycondensat), 375–385 Search PubMed.
- J. M. Dennis, G. B. Fahs, R. B. Moore, S. R. Turner and T. E. Long, Synthesis and Characterization of Polysulfone-Containing Poly(Butylene Terephthalate) Segmented Block Copolymers, Macromolecules, 2014, 47(23), 8171–8177, DOI:10.1021/ma501903h.
- A. J. Duncan, J. M. Layman, M. P. Cashion, D. J. Leo and T. E. Long, Oligomeric A2 + B3synthesis of Highly Branched Polysulfone Ionomers: Novel Candidates for Ionic Polymer Transducers, Polym. Int., 2010, 59(1), 25–35, DOI:10.1002/pi.2684.
- T. Suga, S. Wi and T. E. Long, Synthesis of Diazocine-Containing Poly(Arylene Ether Sulfone)s for Tailored Mechanical and Electrochemical Performance, Macromolecules, 2009, 42(5), 1526–1532, DOI:10.1021/ma802249a.
- H. R. Kricheldorf, S. Böhme, G. Schwarz, R. P. Krüger and G. Schulz, Macrocycles. 18. The Role of Cyclization in Syntheses of Poly(Ether-Sulfone)S, Macromolecules, 2001, 34(26), 8886–8893, DOI:10.1021/ma010218l.
- K. Sahre, T. Hoffmann, D. Pospiech, K. J. Eichhorn, D. Fischer and B. Voit, Monitoring of the Polycondensation Reaction of Bisphenol A and 4,4′-Dichlorodiphenylsulfone towards Polysulfone (PSU) by Real-Time ATR-FTIR Spectroscopy, Eur. Polym. J., 2006, 42(10), 2292–2301, DOI:10.1016/j.eurpolymj.2006.05.025.
- B. E. Jennings, M. E. B. Jones and J. B. Rose, Synthesis of Poly(Arylene Sulfones) and Poly(Arylene Ketones) by Reactions Involving Substitution at Aromatic Nuclei, J. Polym. Sci., Polym. Symp., 1967, 16(Pt. 2), 715–724, DOI:10.1002/polc.5070160212.
- J. F. Bunnett, Aromatic Substitution by the SRN1 Mechanism, Acc. Chem. Res., 1978, 11(11), 413–420, DOI:10.1021/ar50131a003.
- J. F. Bunnett and R. E. Zahler, Aromatic Nucleophilic Substitution Reactions, Chem. Rev., 1951, 49(2), 273–412, DOI:10.1021/cr60153a002.
- S. Ganguly and H. W. Gibson, Synthesis of a Novel Macrocyclic Arylene Ether Sulfone, Macromolecules, 1993, 26(10), 2408–2412, DOI:10.1021/ma00062a003.
- S. D. Ross, Nucleophilic Aromatic Substitution Reactions, in Progress in Physical Organic Chemistry, 2007, vol. 1, pp. 31–74. DOI:10.1002/9780470171806.ch2.
- S. D. Ross, Catalysis of Intermediate Formation in Nucleophilic Aromatic Substitution, Tetrahedron, 1969, 25(18), 4427–4436, DOI:10.1016/S0040-4020(01)82984-7.
- S. D. Ross, M. Finkelstein and R. C. Petersen, Nucleophilic Displacement Reactions in Aromatic Systems. V. The Mechanism of the Reaction of 2,4-Dinitrochlorobenzene with Primary Amines in Chloroform, J. Am. Chem. Soc., 1959, 81(20), 5336–5342, DOI:10.1021/ja01529a024.
- G. O. Jones, A. Al Somaa, J. M. O'Brien, H. Albishi, H. A. Al-Megren, A. M. Alabdulrahman, F. D. Alsewailem, J. L. Hedrick, J. E. Rice and H. W. Horn, Computational Investigations on Base-Catalyzed Diaryl Ether Formation, J. Org. Chem., 2013, 78, 5436–5443, DOI:10.1021/jo400550c.
- M. S. Gordon and M. W. Schmidt, Chapter 41 - Advances in Electronic Structure Theory: GAMESS a Decade Later, Theory and Applications of Computational Chemistry, The First Forty Years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. B. T.-T. Scuseria and A. of C. C., Elsevier, Amsterdam, 2005, pp. 1167–1189. DOI:10.1016/B978-044451719-7/50084-6.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis, J. A. Montgomery Jr., M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, General Atomic and Molecular Electronic Structure System, J. Comput. Chem., 1993, 14(11), 1347–1363, DOI:10.1002/jcc.540141112.
- D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function, in Theoretical chemistry accounts, Berlin, 2008, pp. 215–241 Search PubMed.
- V. V. Severnyi, Y. I. Minsker and N. A. Ovechkina, Processes Occurring in Organosilicon Compositions Undergoing Vulcanization by Atmospheric Moisture, Polym. Sci. U.S.S.R., 1977, 19(1), 42–49, DOI:10.1016/0032-3950(77)90146-0.
- N. Nomura, K. Tsurugi, T. V. RajanBabu and T. Kondo, Homogeneous Two-Component Polycondensation without Strict Stoichiometric Balance via the Tsuji-Trost Reaction: Remote Control of Two Reaction Sites by Catalysis, J. Am. Chem. Soc., 2004, 126(17), 5354–5355, DOI:10.1021/ja0492743.
- A. P. Dove and M. A. R. Meier, Step-Growth Polymerization in the 21st Century, in Macromolecular Chemistry and Physics, 2014, pp. 2135–2137. DOI:10.1002/macp.201400512.
- R. Viswanathan, B. C. Johnson and J. E. McGrath, Synthesis, Kinetic Observations and Characteristics of Polyarylene Ether Sulphones Prepared via a Potassium Carbonate DMAC Process, Polymer, 1984, 25, 1827–1836, DOI:10.1016/0032-3861(84)90258-1.
- H. Plenio, The Coordination Chemistry of the CF Unit in Fluorocarbons, Chem. Rev., 1997, 97(8), 3363–3384, DOI:10.1021/cr970465g.
- C. A. Costello and T. J. McCarthy, Surface-Selective Introduction of Specific Functionalities onto Poly (Tetrafluoroethylene, Macromolecules, 1987, 20(11), 2819–2828, DOI:10.1021/ma00177a030.
- G. Odian, Principles of Polymerization, 4th edn, 2004. DOI:10.1016/B978-1-85617-803-7.50022-5.
- J. N. Dahanayake, C. Kasireddy, J. P. Karnes, R. Verma, R. M. Steinert, D. Hildebrandt, O. A. Hull, J. M. Ellis and K. R. Mitchell-Koch, Progress in Our Understanding of 19F Chemical Shifts, in Annual Reports on NMR Spectroscopy, 2018. DOI:10.1016/bs.arnmr.2017.08.002.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36(3), 354–360 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details regarding characterization tools and procedures, 1H NMR spectra, size exclusion chromatography traces, off-set stoichiometry study, DFT calculation protocols, and kinetic data for polycondensation reactions in the presence of sodium carbonate. See DOI: 10.1039/d0py00740d |
| This journal is © The Royal Society of Chemistry 2020 |