Open Access Article
Open Access ArticleSurface specificity and mechanistic pathway of de-fluorination of C60F48 on coinage metals†
Rogger
Palacios-Rivera
 a,
David C.
Malaspina
a,
Nir
Tessler
a,
David C.
Malaspina
a,
Nir
Tessler
 b,
Olga
Solomeshch
b,
Jordi
Faraudo
b,
Olga
Solomeshch
b,
Jordi
Faraudo
 *a,
Esther
Barrena
*a,
Esther
Barrena
 *a and
Carmen
Ocal
*a and
Carmen
Ocal
 a
a
aInstitut de Ciència de Materials de Barcelona (ICMAB-CSIC), Campus UAB, Bellaterra, E-08193, Barcelona, Spain. E-mail: ebarrena@icmab.es; jfaraudo@icmab.es
bElectrical Engineering Department, Nanoelectronic Center, Technion, Haifa 32000, Israel
First published on 10th September 2020
Abstract
We provide experimental and theoretical understanding on fundamental processes taking place at room temperature when a fluorinated fullerene dopant gets close to a metal surface. By employing scanning tunneling microscopy and photoelectron spectroscopies, we demonstrate that the on-surface integrity of C60F48 depends on the interaction with the particular metal it approaches. Whereas on Au(111) the molecule preserves its chemical structure, on more reactive surfaces such as Cu(111) and Ni(111), molecules interacting with the bare metal surface lose the halogen atoms and transform to C60. Though fluorine–metal bonding can be detected depending on the molecular surface density, no ordered fluorine structures are observed. We show the implications of the metal-dependent de-fluorination in the electronic structure of the molecules and the energy alignment at the molecule–metal interface. Molecular dynamics simulations with ReaxFF reactive force field corroborate the experimental facts and provide a detailed mechanistic picture of the surface-induced de-fluorination, which involves the rotation of the molecule on the surface. Outstandingly, a thermodynamic analysis indicates that the effect of the metal surface is lowering and diminishing the energy barrier for C–F cleave, demonstrating the catalytic role of the surface. The present study contributes to in-depth knowledge of the mechanisms that affect the degree of stability of chemical species on surfaces, which is essential to advance our understanding of the chemical reactivity of metals and their role in on-surface chemical reactions.
Introduction
Understanding the mechanistic aspects of fundamental processes that take place between organic molecules and metal surfaces is a challenging topic with important implications in many interdisciplinary fields of nanoscience. Examples include on-surface synthesis1–5 (which allows one to obtain novel nanostructures difficult to obtain by solution chemistry methods), supramolecular organization and self-assembly6 (as a key bottom-up fabrication method with the lowest energy consumption) and charge transfer between molecules and metals7,8 (essential for charge injection/extraction in organic electronic devices, such as organic solar cells or field effect transistors). These processes depend on a delicate balance between inter and intramolecular interactions and molecule–surface interactions which are highly system-dependent. For example, density functional theory (DFT) calculations show that C60 makes covalent bonds with Pt(111) and the metal is able to dissociate the molecule whereas the interaction with Cu(111), Ag(111) and Au(111) is ionic and these metals are unable to induce C60 dissociation.9 The reasons cannot be traced back to the substrate electronic structure but to thermally activated local surface reconstructions.Tackling the problem from a theoretical perspective presents significant challenges. In principle, an accurate description of the involved interactions (intermolecular, intramolecular and molecule–surface) at the desired temperatures is possible using first-principles molecular dynamics simulations10 in which the motion of the atoms is computed using the interactions between atoms described by quantum mechanical (QM) methods. This technique has been employed to study the mechanisms of synthesis of C60 in gas phase11 and its decomposition over a Cu(111) surface12 at different temperatures from first principles electronic structure theory. However, the high computational costs associated to QM limit their use to simulations with a relatively small number of atoms and very short times (∼100 atoms and ∼1 ps in ref. 12). A useful alternative is to consider MD simulations based on a reactive force field for the calculation of atomic interactions.11 In a reactive force field, the interactions between atoms are described including a bond-order formalism, trained from QM calculations, which is able to model bond formation and breaking during chemical reactions. Reactive force-fields (ReaxFF)13 is probably the most popular reactive force field, and it has been successfully employed to simulate on-surface reactions14 including transition metal catalyzed reactions of formation of carbon and fluorinated compounds and their thermal and mechanical properties.15–17
The interest in understanding processes between organic molecules and metal surfaces for technological applications is evident, since development of all types of organic electronic devices involves molecular species in contact with metallic electrodes and any possible metal-mediated chemical modification of the molecules would be detrimental. In particular, among the different strategies to improve device performances, the use of high electron affinity molecules facilitates a decrease in the injection barrier at the interface between the organic film and the electrodes, resulting as well in a contact resistance lowering. Within this scenario, fluorinated fullerenes (C60Fx) are of particular interest as electron acceptor materials due to their large electron affinity and good chemical and thermal stability.18–21 The increase in fluorine content being accompanied by a rise in the depletion of the π/π* states and in the HOMO–LUMO gap.22 Thus, we select for our study the fluorofullerene with maximum number of fluorine, C60F48, a promising electron acceptor in organic devices20,23,24 with high thermal stability (up to 350 °C).21 Despite their practical importance, only few works exist on the adsorption of fluorinated fullerenes on metals. Among them, for the present study it is worth noting the supramolecular order reported for unperturbed C60F36 on Au(111)25 or the gradual and long lasting loss of halogen atoms taking place for C60F18, a tortoise-shaped molecule with far fewer fluorine atoms than the allotrope studied here, on Cu(100).26–28
In this work, different C60F48 coverages are deposited onto diverse transition metal surfaces to unveil the role that the organic–metal interactions have on the chemical stability of this molecule at room temperature (RT) and give insight into the pathway of surface-induced de-fluorination of the molecules. By combining scanning tunneling microscopy (STM), frequency modulation atomic force microscopy (FM-AFM) X-ray photoelectron spectroscopy (XPS) and ultra-violet photoelectron spectroscopy (UPS), we demonstrate that whereas on Au(111) the molecule preserves its chemical structure, the C–F bonds of C60F48 are cleaved when approaching more reactive surfaces such as Cu(111) or Ni(111) transforming into C60 at room temperature. By molecular dynamics (MD) with ReaxFF we examine the full dynamic evolution of the molecules on the surface, on timescales beyond what is accessible with quantum level calculations, and provide a realistic description of the catalytic role played by the metal surface. The joint experimental and theoretical information leads to a detailed mechanistic picture of the process.
Methods
Experimental details
Fluorinated fullerene C60F48 molecules were synthesized as described in ref. 29 at the Josef Stefan Institute (Slovenia). The product was characterized by chemical analysis, electron-ionization mass spectrometry and infrared spectroscopy. The purity was estimated to be 95%. The experiments were carried out in two separate (AFM/STM and XPS/UPS) ultrahigh vacuum (UHV) systems with a base pressure of 1 × 10−10 mbar. The molecules were deposited in both cases employing the same Knudsen cell (180 °C) onto in situ cleaned substrates kept at RT. The Au(111), Cu(111) and Ni(111) single crystals were cleaned by repeated cycles of Ar+ sputtering (0.8–1.0 keV) plus annealing (at 550 °C, 650 °C and 750 °C, respectively) in a preparation chamber equipped with Low Energy Electron Diffraction (LEED) optics and diverse evaporators connected to the STM characterization chamber. After this procedure, the observation by STM of large terraces separated by monoatomic steps and the sharpness of the LEED pattern confirmed a well-ordered clean surface. The azimuth orientation determined from LEED and the herringbone (HB) reconstruction in the case of Au(111) were employed throughout the present work as crystallographic references. The C60F48 molecules were in situ deposited from the vapour phase at deposition rates of about 2–3 Å min−1 using a Knudsen cell. The different molecular coverages (θ) at the surface have been estimated either from topographic STM images or from the relative intensity of element specific core level peaks as measured by XPS (see Fig. S4 in the ESI†). The shift of the XPS peaks was calculated from peak position obtained from the fits with a Pseudo Voigt function (Shirley type background subtracted).The STM measurements were performed at RT using a commercial Aarhus SPM 150 with KolibriSensor™ probes (f0 ∼ 1 MHz, Q ∼ 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and a Nanonis Control System (SPECS Surface Nano Analysis GmbH). The sharp metallic tip was cleaned in situ via Ar+ sputtering and, during STM measurements, was maintained oscillating at a constant amplitude (A = 200 pm) so that the tip–sample interaction was reflected in a frequency shift (Δf) from f0.30 Topographic STM was conducted in the constant current mode and the simultaneous Δf was recorded. Typical tunnelling parameters were: sample bias voltages of 1–2 V and currents of 100–200 pA. The in-plane lattice constant, in high resolution images, and step heights, in large-scale images of in situ cleaned Au(111) and Cu(111) single crystals were employed for calibration of the STM piezo scanner. All STM images were analysed by using the WSxM freeware.31 For XPS/UPS experiments, a system equipped with a SPECS Phoibos 150 hemispherical energy analyzer was used with Al-Kα (hν = 1486.6 eV) for XPS, and a ultra-violet source with monochromator selecting He I (21.2 eV) for UPS. UPS spectra were taken with the sample biased at −10 V to have access to the work function of the sample from secondary electrons cutoff (SECO). The electron binding energy is referenced to the Fermi level of the sample, in contact with the spectrometer and previously calibrated using a Au(111) reference sample.
000) and a Nanonis Control System (SPECS Surface Nano Analysis GmbH). The sharp metallic tip was cleaned in situ via Ar+ sputtering and, during STM measurements, was maintained oscillating at a constant amplitude (A = 200 pm) so that the tip–sample interaction was reflected in a frequency shift (Δf) from f0.30 Topographic STM was conducted in the constant current mode and the simultaneous Δf was recorded. Typical tunnelling parameters were: sample bias voltages of 1–2 V and currents of 100–200 pA. The in-plane lattice constant, in high resolution images, and step heights, in large-scale images of in situ cleaned Au(111) and Cu(111) single crystals were employed for calibration of the STM piezo scanner. All STM images were analysed by using the WSxM freeware.31 For XPS/UPS experiments, a system equipped with a SPECS Phoibos 150 hemispherical energy analyzer was used with Al-Kα (hν = 1486.6 eV) for XPS, and a ultra-violet source with monochromator selecting He I (21.2 eV) for UPS. UPS spectra were taken with the sample biased at −10 V to have access to the work function of the sample from secondary electrons cutoff (SECO). The electron binding energy is referenced to the Fermi level of the sample, in contact with the spectrometer and previously calibrated using a Au(111) reference sample.
Methodology for molecular dynamics simulations
We have performed all-atomic molecular dynamics (MD) simulations of the deposition of C60F48 onto a selected surface among those used in our experiments, namely Ni(111). We have also performed free energy calculations of the thermodynamic stability of C–F bonds in C60F48 in the absence or presence of a Ni(111) surface employing the Adaptive Biasing Force (ABF) method coupled to MD simulations.32 We model all atomic interactions using the ReaxFF force field. ReaxFF is a semi-empirical bond-order reactive force field parameterized from DFT calculations that allow to simulate chemical reactions in MD.13 The set of ReaxFF force field parameters was chosen from previous works on fluorinated carbon compounds16 and reactions onto transition metals surfaces.15 We have verified that ReaxFF gives an adsorption energy for F onto Ni(111) in perfect agreement with previous DFT calculations.33 All the simulations were performed employing the LAMMPS simulation engine for MD simulations34 which has an implementation of ReaxFF and other reactive force fields.35 The simulated MD trajectory was processed combining the Visual Molecular Dynamics (VMD) software for the snapshot analysis and movies and custom scripts for data analysis.36 Our choice of simulation time step and thermostat was taken from a previous systematic study of the effect of time step and thermostat in ReaxFF MD simulations with carbon compounds.17 We employed a simulation time step of 0.5 fs and a Langevin thermostat with a time constant of 10 fs. The thermostat at 300 K was coupled to the Ni atoms during all the simulation.The MD simulations were performed initially placing a C60F48 molecule at a distance of ∼6 Å from a Ni(111) surface (measured as the distance between the nearest C and Ni atoms). The employed Ni(111) structure was made by 840 atoms arranged in 5 atomic layers with an area of 9.6 nm2. Periodic boundary conditions were employed in all directions, with a large simulation box of size 31.08 × 30.89 × 180.0 Å3. The detailed protocol for the generation of the initial coordinates in our MD simulations is given in the ESI.† The simulation was performed during 3300 ps, which allowed us to follow in detail the adsorption process. Additionally, in order to be able to observe the relatively slow process of molecule rotation and diffusion we have performed further non-equilibrium MD simulations in the following way. Starting from the final configuration obtained in the MD simulations of adsorption of C60F48 onto a Ni(111) surface, we thermally excite the adsorbed molecule maintaining it with a thermostat at 1000 K while the surface and F atoms are maintained always at 300 K. In this way, we stimulate a faster motion for the adsorbed molecule. This nonequilibrium simulation run was performed for 10 ns until substantial rotation was observed.
For the thermodynamic study of the stability of the C–F bonds near a surface we have employed the Adaptive Bias Force (MD-ABF) method as included in the “colvars” module of the LAMMPS package.37 In these simulations, all atoms are thermalized at 300 K and they move as in an unbiased ordinary MD simulation except for a selected F atom, which is forced to change slowly its separation from its bonded C atom. During this process, the (reversible) work done as a function of the C–F separation (reaction coordinate) is evaluated and the free energy profile of the C–F bond is obtained. We performed the simulations for three different cases involving one C60F48 molecule at 300 K: (a) in absence of any surface, (b) at a distance of 7.0 Å from Ni(111) and (c) at 5.45 Å from Ni(111) (distances measured between the nearest C and Ni surface atoms). In (b and c) the selected F atom was the one closest to the surface.
The exploration of the reaction coordinate was made using very small bins of 0.01 Å width and a force constant of 4 × 105 kcal mol−1 Å−2 for (a and b) (which was necessary in order to study covalent bond breaking) and 4 × 104 kcal mol−1 Å−2 for the case (c). In cases (b and c), all other F atoms were also frozen at their positions at the molecule to avoid processes which will make difficult to compare with the results in (a), such as the molecule adsorbing to the surface or de-fluorination of other C atoms of the molecule. The simulations were performed until smooth free energy profiles were obtained, requiring ∼106 to 107 time steps for each case.
Results and discussion
Experimental results
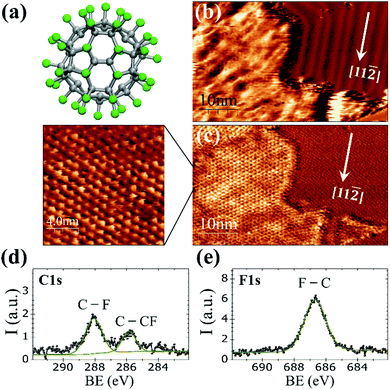
At room temperature on Au(111), the C60F48 molecule (Fig. 1a) initially nucleates at the step edges and pinched elbows of the herringbone (HB) reconstruction, followed by the formation of two-dimensional (2D) islands that grow in size with increasing coverage (Fig. S1 and S2 in the ESI†). As seen in Fig. 1b for θ ≈ 0.45 ML, the molecular islands exhibit an extremely wrinkled topographic appearance which contrasts to the highly ordered HB reconstruction of the surrounding Au(111) terraces. Despite the inhomogeneous contrast in the topographic image, the striking resolution of frequency shift (Δf) on the island top (Fig. 1c) reveals an almost perfect buckyballs packing. The nearest neighbor (NN) distance of ∼1.19 ± 0.05 nm measured for the hexagonal packing in the high resolution Δf image of Fig. 1c is compatible with the structure determined by X-ray diffraction for C60F48 powder samples38,39 and close to the reported distance between adjacent C60F36 (with lower F content) deposited at RT on the HB reconstructed Au(111).25 The relative orientation of the molecular lattice respect to the substrate is not unique but varies among different islands (Fig. S2c and d in ESI†). The height of the islands appears modulated by a quite large corrugation of up to ≈0.2 nm that causes the blurred aspect of the STM topography. This variation may be a consequence of the interaction between neighboring C60F48 leading to assorted orientations, with phenyl rings from one molecule interacting with fluorine atoms from the other.To confirm the chemical composition of the 2D islands formed on the gold surface, XPS measurements were performed immediately after deposition of the molecules at RT. As reported for powder samples, the C 1s core-level spectrum (Fig. 1d) of the deposited C60F48 exhibits two peaks at well distinct binding energy (BE) differing in ∼2 eV (ref. 22 and 29) as corresponds to the two chemical environments of carbon atoms within the fluorinated molecules that constitute their chemical signature.
The peak at BE = 288.1 eV is attributed to fluorinated sp3 carbons (C–F) and the one at BE = 285.8 eV to C atoms bound only to other C atoms (C–CF). The F 1s core level spectra (Fig. 1e) shows a single peak centered at 686.7 eV originated from F atoms bound to C (F–C)29 with none indication of fluorine–metal bonding, which would otherwise lead to a signal at lower BE (684 eV).
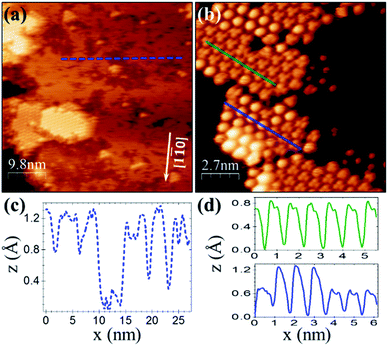
For a similar coverage (θ ≈ 0.4 ML), deposition of C60F48 on Cu(111) results as well in the formation of 2D islands. However, from the comparison with Au(111) (Fig. 1b), significant differences stand out. On Cu(111) the islands display a remarkable flatness and well-resolved hexagonal order in the STM topography (Fig. 2a and b). The lattice unit cell is ≈0.90 ± 0.05 nm, smaller than for C60F48 on Au(111) and very close to the reported lattice parameter (1.02 nm) of the close-packed (4 × 4)R0° structure of C60 on Cu(111).40–43
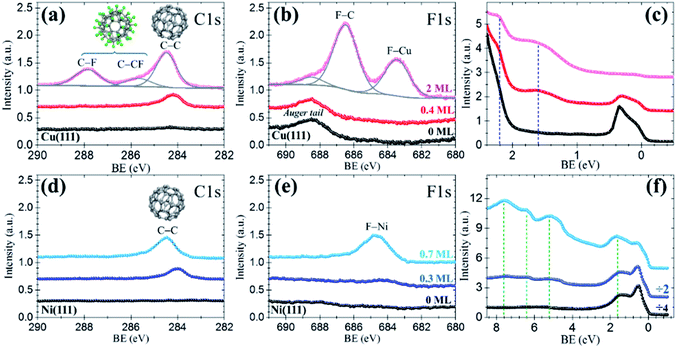
The resemblance with C60 is evident and straightforward. The islands consist of molecules exhibiting sub-molecular details in the form of clover-like (three-lobed) patterns or a smooth hemispherical shape with a distinct apparent height (green and blue profiles in Fig. 2d), which are commonly attributed to a different adsorption geometry of C60 with a hexagon (h-C60) or a pentagon (p-C60) facing up, respectively.41–44 This observation cannot be understood in terms of unperturbed C60F48 molecules. Remarkably, surrounding the highly ordered molecular islands (Fig. 2a) the copper surface has a perceptible frizzing appearance and a roughness arising from patches with apparent depth from 0.7 to 1.2 Å (Fig. 2c) which are indicative of mass transport and suggest a pit-etching process. These unexpected results suggest that the interaction between the fluorinated fullerene and the Cu(111) strongly affect both, the chemical nature of the molecule and the flatness of the copper substrate surface, at least for the first stages of the C60F48 deposition. At this coverage, the C 1s core-level spectra present a single peak (red data in Fig. 3a) at a BE ≈ 284.2 eV, lower than those shown for C60F48 on gold, which is characteristic for C60 on Cu(111). Such low BE is typical of non-fluorinated fullerene species adsorbed onto metallic surfaces.45
As remarkably seen, the photoelectron intensity in the F 1s region (red data in Fig. 3b) coincides in magnitude and shape with that of the pristine Cu(111) substrate (black data), where only the Cu Auger tail is visible. The lack of F signal indicates that fluorine atoms detached from the fullerene might go to the gas phase during the approach or after a short term at the surface. In spite of it, the interaction of fluorine with the metal surface seems, in any case, to be responsible of the observed surface pit-etching (Fig. 2a). These XPS data constitute an irrefutable proof certifying that due to the interaction with the copper surface the C60F48 molecules de-fluorinate and adsorb as C60, as also indicated by the spotlighted fingerprints typical of C60 seen in the STM data (Fig. 2b). These results are in contrast with the non-reactive adsorption described above for C60F48 on Au(111). Interestingly, despite the similar adsorption energy for F chemisorption on Cu(111) and Cu(100),33 the fast de-fluorination taking place on Cu(111) contrasts with the long lasting process reported for Cu(100).26 It is likely that full de-fluorination would imply molecular rotation (see simulations below), therefore this difference may arise from differences in the energy barrier for surface diffusion the molecules, lower on (111) than on (100) surfaces.46
In principle, only C60F48 interacting with uncovered copper turns into C60 and, therefore, as the substrate surface is being covered the reaction would cease. This hypothesis was verified by elemental sensitive XPS. As it can be seen in Fig. 3a, the C 1s spectrum corresponding to ≈2 ML of C60F48 (pink data) exhibits diverse peaks interpreted as follows. First, there is a considerable increase of the C–C peak attributed to C60 (BE ≈ 284.5 eV) with respect to that observed for ≈0.4 ML (red data). This intensity rise is expected for the ongoing de-fluorination of C60F48 until the copper surface becomes completely covered. As concluded from the appearance of a F 1s peak at BE ≈ 683.4 eV (Fig. 3b), at this stage, some fluorine atoms at the surface lead to the formation of metal fluoride species (F–Cu). We estimate that ≈35% of the fluorine atoms detached per molecule remain on the surface upon de-fluorination (Table 1). Secondly, the emergence of the two other C 1s peaks, at BE ≈ 287.9 eV and BE ≈ 285.4 eV, identified as C–F and C–CF, respectively, plus the F 1s peak at BE ≈ 686.5 eV corresponding to F–C bonds, are clear proof that above the first layer completion additional C60F48 retain their chemical structure (as shown in Fig. 1d and e for gold). These conclusive data confirm that, in the absence of bare copper, landing C60F48 molecules maintain their integrity.
| Surface | Cu(111) | Ni(111) | ||
|---|---|---|---|---|
| C60F48 coverage | 0.4 ML | 2 ML | 0.3 ML | 0.7 ML |
| I(F–metal)/I(C–C) | — | 1.76 | 0.50 | 2.17 |
| F on surface per molecule | — | 35% | 10% | 43% |
Motivated by the results obtained for the extreme cases of Au(111) and Cu(111), the study was extended to a third metal, Ni(111). To achieve a maximum number of molecules undergoing the surface-induced reaction, the coverage was restricted below the monolayer. As inferred from the unique C 1s peak at low BE (C–C) observed in the spectrum of Fig. 3d (dark blue data), small deposits of C60F48 (≈0.3 ML) convert to C60, on nickel as on copper. A faint hump hardly distinguished around a BE ≈ 684–685 eV in the F 1s region (Fig. 3e), is a subtle indication of fluorine on the surface (see MD simulations below). Indeed, for ≈0.7 ML (cyan data) an increase of the C–C peak (with no trace of C–F) and the neat development of a F–Ni peak (≈684.6 eV) support that fluorine rests at the surface after C60F48 de-fluorination. From the intensity ratio between F–Cu and C–C peaks, the percentage of detached fluorine atoms remaining on the Ni(111) surface is estimated (Table 1). It can be observed that the amount of F per molecule that remains on the surface depends on the coverage and is larger on Ni(111) than on Cu(111).
The dependence of the on-surface reaction on the substrate is also shown up by differences in the near Fermi-edge valence band (VB) density of states (DOS) and the secondary electron cutoff (SECO), both as measured by UPS. For simplicity, we discuss here the VB spectra for Cu(111) and Ni(111) whereas the results for Au(111) and all SECO data are presented in the Fig. S3 of the ESI.† Consistent with the deep-lying HOMO level of C60F48,22,23,47 its adsorption on Au(111) does not induce any extra feature close to the Fermi level with respect of that of the clean Au(111). On the other hand, despite the strong copper d-band emission at BE > 2 eV, already for low C60F48 deposition on Cu(111), two occupied molecular orbitals at ≈1.8 eV and ≈ 2.2 eV (Fig. 3c), assigned to frontier orbitals of the C60 are seen. In the case of Ni(111), the density of states near the Fermi level is dominated by the Ni d-band (black in Fig. 3f). The increase of intensity at this region upon deposition is ascribed to the highest occupied molecular orbital (HOMO) of C60, reported at ∼2 eV on diverse substrates including Ni,45 shifted to ≈1.7 eV due to the Ni 3d contribution. In addition, there is a clear observation of C60 deeper occupied molecular orbitals (up to HOMO−5) (light blue in Fig. 3f). As it can be seen from the shifts in the SECO spectra of Fig. S3,† upon deposition the surface work function is modified respect to the initial value of the bare metallic substrates. An irrefutable interpretation of the measured values is complicated since diverse contributions exits depending on coverage, degree of C60F48 de-fluorination and particular metal. In any case, the changes in work function indicate the formation of an interface dipole, with contribution from fluorine atoms bound to the surface and charge transfer between the metal and the acceptor molecules (see simulations below).
Molecular dynamics results
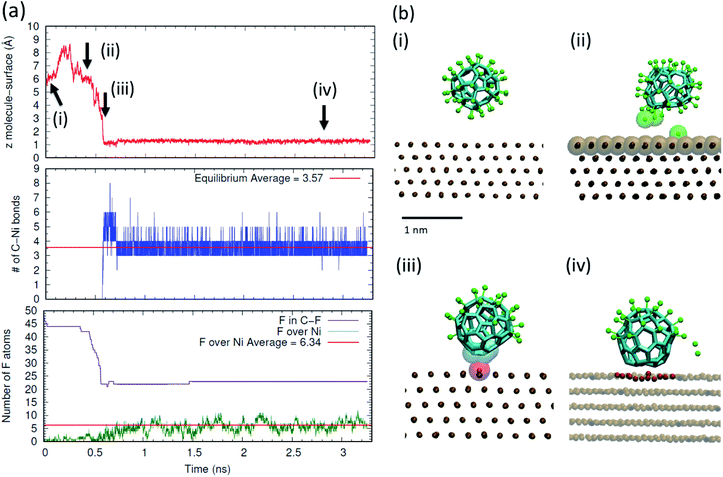
In order to obtain an atomistic insight on the mechanisms underlying the on-surface de-fluorination of C60F48 molecules observed experimentally at RT, we have performed all atomic reactive MD simulations. Also, we performed free energy calculations of the stability of the C–F bond in presence and absence of a metal surface. In the simulations, we focused on the case of deposition of C60F48 onto the Ni(111). Full technical details are given in the Methods section and in the ESI.†We have first considered the process of deposition of a C60F48 molecule from the gas phase to a Ni(111) thermostated at 300 K. The results are summarized in Fig. 4 (see also a movie of the adsorption process in the ESI†). In order to illustrate the changes occurring when a C60F48 molecule approaches the Ni surface, we show the evolution in time of the (nearest) distance between a C atom of C60F48 and a Ni surface atom, the number of formed C–Ni bonds and the number of F atoms bonded to C atoms or adsorbed at the surface. As seen in Fig. 4a, the molecule–surface separation evolves with a Brownian motion until the molecule reaches the surface. During the approaching process, we observe partial de-fluorination of C60F48 which takes place when the center-to-center separation between the nearest carbon atom and a surface Ni atom is ∼4.6 Å (which corresponds to a gap of ∼1.1 Å between the C60F48 and the surface). F atoms reaching this separation to the surface are seen to be released either to the surface or to the gas phase, as illustrated in the snapshots (Fig. 4b). The strong interaction between the nearest Ni atom and the de-fluorinated C atoms induces a displacement of that Ni atom from the surface towards the molecule. Subsequent chemisorption of the molecule involves a slight deformation of the surface, with about 5–7 atoms being clearly displaced from the top atomic layer (analogous reconstruction of the surface upon adsorption of C60 onto Ni(111) has been reported).48 In that way, the carbons of the adsorbed molecule increase as much as possible their interaction with Ni atoms. As seen in the middle panel of Fig. 4a, the chemisorption of the molecule onto the surface involves the formation of 3.6 bonds on average between carbon atoms of the molecule and Ni atoms of the surface. After chemisorption, we do not observe molecular desorption during all the remaining simulation time. As shown in the bottom panel of Fig. 4a, F atoms are seen to adsorb and desorb continuously, as corresponds to adsorption in thermodynamic equilibrium. The average number of adsorbed F onto Ni is about 6 (∼12% of F per molecule), consistent with the experimental 10% shown in Table 1 for very low coverage.
In the discussion of the experimental UPS data, we suggested that the observed change in the system work function upon molecular adsorption (Fig. S3 in the ESI†) may arise from charge transfer between the adsorbed molecules and the metal as well as from polarization of the adsorbed F atoms. This interpretation is supported by the simulations discussed here. As shown in Fig. 5, the chemisorption leads to charge transfer from the nickel surface to the molecule, which in average is charged by −1.5e.
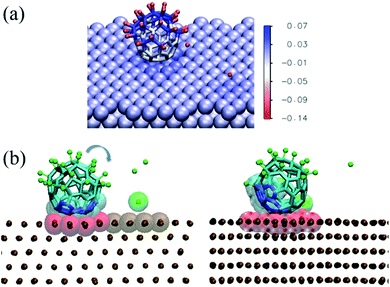 | ||
| Fig. 5 (a) Charge transfer in the adsorbed configuration of C60F48 on the Ni(111) surface at 300 K. The image shows the same snapshot as in Fig. 4a(ii), colored according to the partial charge of each atom (color scale in units of e). (b) Snapshots showing the on-surface rotation of a thermally excited adsorbed molecule. The time elapsed between the two snapshots is 2.3 ns. To better visualize the change in position due to molecular rotation, the carbon atoms initially in contact with the surface are indicated in blue and highlighted as van der Waals translucent spheres. The atoms of the surface in contact with the molecule at each instant are highlighted as red van der Waals spheres. The rest of the atoms are represented as in Fig. 4. | ||
In addition, F atoms adsorbed onto the Ni(111) surface are polarized with a partial charge of −0.13e, whereas de-fluorinated C atoms and C atoms in C–F bonds have nearly zero and positive partial charges, respectively. It can also be seen that the charge in the Ni(111) surface is distributed in a nearly homogeneous way, with only a slightly higher partial charge for the Ni atoms nearby each type of adsorbate.
The results shown in Fig. 4 and 5 indicate a partial de-fluorination of C60F48 at the time scales of some nanoseconds analyzed in the simulations. However, as suggested above, it is possible that mechanisms operating at longer time scales, such as rotation of the molecule over the surface,26,27 contribute to the complete de-fluorination of the molecule as implied by our experimental results (Fig. 3). In order to account for the possible rotation of the molecule over the Ni(111) surface, we have accelerated this process by considering a nonequilibrium simulation in which the molecule is thermally excited while the surface is maintained at 300 K. Indeed, a random rotation of the molecule over the surface is observed (Fig. 5b). The thermally excited rotation proceeds by “jumps” which also involve lateral drift of the molecule and rearrangement of surface atoms (see a movie of this rotation process in the ESI†). The C positions closest to the surface become replaced by others than the initial ones in about 2 ns. During this rotation process of a thermally excited molecule, unperturbed C–F bonds approach the surface and further fluorine atoms are detached from the molecule. For example, between the two snapshots shown in Fig. 5b (separated by 2.3 ns), five F atoms were released.
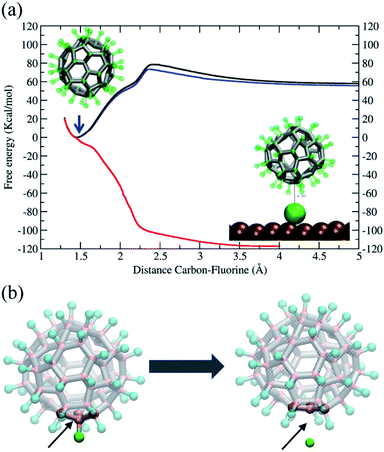
In conclusion, our simulations support and are consistent with the rotation mechanism proposed for full de-fluorination. The findings discussed above demonstrate that the C–F bond of the C60F48 molecule is unstable in the presence of the Ni(111) surface, but a detailed thermodynamic analysis of the C–F bond in absence or presence of the surface at 300 K would help to further understand the issue. To this end, we have performed free energy calculations using the Adaptive Biasing Force (MD-ABF) methodology (see Methods). This combination of ABF-MD and the reactive ReaxFF force field has been successfully employed in recent works to study the thermodynamics of chemical bonds49 and chemical reactions onto surfaces.14 In these MD-ABF simulations, all atoms are thermalized at 300 K and they move as in an ordinary MD simulation except a selected F atom, which is forced to slowly separate from its bonded C atom. During this process, the (reversible) work done as a function of the separation is evaluated and the free energy profile of the C–F bond is obtained. Fig. 6a shows the results for the C60F48 molecule obtained both in absence of any surface and in presence of a Ni(111) surface at two different molecule–surface distances. In the absence of surface (black line), there is a free energy minimum at a C–F separation of ∼1.46 Å corresponding to the bond equilibrium distance (consistent with the covalent radius of 0.77 Å and 0.72 Å of C and F, respectively, and consistent with typical C–F bond distances in fluoroalkanes).16 The free energy associated to the bond is ∼60 kcal mol−1, which is about half of bond energies of C–F bonds in fluoroalkanes.16 Note also the presence of a barrier of 15 kcal mol−1 at ∼2.4 Å separation between C and F, which corresponds to a change in the local geometry of the molecule as the F atom is released with the de-fluorinated C atom moving to a more planar conformation, as illustrated from left to right of Fig. 6b.
We now consider the effect of including a Ni(111) surface in the free energy profile. First, we consider the C60F48 molecule at a distance such that the separation between the center of the closest metal atom of the surface and the nearest C atom is ∼7 Å (Fig. 6, blue line). The F atom bonded to this C atom closest to the surface is slowly extracted from the molecule until becomes detached and adsorbed at the surface (Fig. 4 and 5). Note that the free energy profile (blue) is very similar to that obtained in the absence of surface (black), with the only difference of a small reduction in free energy of F after release due to the adsorption to the surface (which includes also an entropy penalty due to localization at the surface). The result is completely different when considering a situation in which the C60F48 molecule is closer to the surface. In the particular case shown, the distance between the center of the closest metal atom of the surface and the nearest F atom is now ∼4 Å (5.45 Å from the nearest C atom) and the free energy profile (Fig. 6, red line) changes completely. The minimum of the C–F free energy curve as well as the energy barrier disappear. The presence of the Ni(111) surface changes the nature of the C–C bonds in the molecule from that depicted in Fig. 5b to that shown in Fig. 5c and consequently the F atom is released spontaneously before reaching contact with the surface.
The whole series of atomistic simulations using MD with ReaxFF employed allows us to corroborate the experimental facts reported here. We demonstrate the decisive role of the molecule–metal interactions to provide a detailed mechanistic picture of surface-induced physicochemical processes determining the molecule–metal interfacial structure.
Conclusions
By means of scanning tunneling microscopy plus core level and valence band analysis, we provide experimental structural, chemical and electronic evidence of the dramatically different consequences that different metal substrates have on the promoted de-fluorination of C60F48, a powerful electron acceptor. Conversely to a non-reactive adsorption on Au(111) where molecules keep intact their chemical structure, the fluorinated fullerene with maximum fluorine content transforms at room temperature into C60 on other more reactive metals as Cu(111) and Ni(111). Interestingly though, the amount of fluorine atoms remaining at the surface depends on the coverage and is higher for nickel than for copper. The low deposition rates employed permit neglecting intermolecular interactions and point to an on-surface induced de-fluorination of the molecules. We prove the significance of the metal-dependent chemical transformation, from C60F48 to C60, in the electronic structure of the molecules and the energy alignment at the molecule–metal interface. We also verify experimentally that, as expected, de-fluorination ceases when impinging molecules arrive once the metal surface has been fully covered by a molecular monolayer.Reactive ReaxFF molecular dynamic simulations for C60F48 on Ni(111) demonstrate that the organic–metal interactions play an essential role on the chemical stability of C60F48 and provide an atomistic picture of the surface-induced reaction at different length scales. Outstandingly, the detailed thermodynamic analysis shows that the effect of the metal surface is lowering and diminishing the energy barrier for C–F cleave, demonstrating a catalytic role of the surface. Both molecule and surface become affected. On the one hand, the partial de-fluorination of C60F48 implies a slight distortion of the molecular cage. On the other hand, the subsequent adsorption of the molecule on Ni(111) involves deformation of the topmost surface. The whole process includes charge transfer between molecule and surface as well as between the strongly electronegative fluorine atoms that detached from the molecules remain bound to the metal. The overall charge rearrangements would contribute to a surface dipole as indeed manifested by changes in the measured work function. As a plausible scenario for the complete molecular de-halogenation observed for submonolayer coverages, we propose the rotation of the highly mobile molecules on the surface, adopting successive adsorption configurations until losing their whole fluorine content. MD simulations, where the molecules are thermally excited to reduce the time scale of the process, support this conjecture.
This study provides an unprecedented look at the mechanistic pathway of de-fluorination of C60F48 on some coinage metals and offers opportunities to advance our understanding of “chemical reactivity” of a metal surface and surface reactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Spanish Government under projects PID2019-110907GB-I00, MAT2016-77852-C2-1-R (AEI/FEDER, UE), RTI2018-096273-B-I00, the “Severo Ochoa” Program for Centers of Excellence in R&D (SEV-2015-0496) and the Generalitat de Catalunya 2017-SGR668. R. P. R. has been developing this work as part of his doctorate in Materials Science at the Universitat Autònoma de Barcelona (UAB). D. C. M. is supported by the European Union's Horizon 2020 Research and Innovation Programme under Marie Sklodowska-Curie grant agreement No. 6655919. O. S. is grateful for the support by the Center for Absorption in Science of the Ministry of Immigrant Absorption and the Committee for Planning and Budgeting of the Council for Higher Education in Israel under the framework of the KAMEA Program. We thank CESGA Supercomputing center for technical support and computer time at the supercomputer Finisterrae II. We are indebted to G. Sauthier from the ICN2 Photoemission Spectroscopy Facility. We are grateful to M. Paradinas and A. Mugarza from ICN2 for providing the Ni(111) crystal.References
- Q. Sun, R. Zhang, J. Qiu, R. Liu and W. Xu, Adv. Mater., 2018, 30, 1705630 CrossRef.
- C. Moreno, M. Vilas-Varela, B. Kretz, A. Garcia-Lekue, M. V. Costache, M. Paradinas, M. Panighel, G. Ceballos, S. O. Valenzuela, D. Peña and A. Mugarza, Science, 2018, 360, 199–203 CrossRef CAS.
- C. Moreno, M. Panighel, M. Vilas-Varela, G. Sauthier, M. Tenorio, G. Ceballos, D. Peña and A. Mugarza, Chem. Mater., 2019, 31, 331–341 CrossRef CAS.
- M. Lackinger, Chem. Commun., 2017, 53, 7872–7885 RSC.
- B. Cirera, N. Giménez-Agulló, J. Björk, F. Martínez-Peña, A. Martin-Jimenez, J. Rodriguez-Fernandez, A. M. Pizarro, R. Otero, J. M. Gallego, P. Ballester, J. R. Galan-Mascaros and D. Ecija, Nat. Commun., 2016, 7, 11002 CrossRef CAS.
- C.-A. Palma, M. Cecchini and P. Samorì, Chem. Soc. Rev., 2012, 41, 3713 RSC.
- N. Koch, S. Duhm, J. P. Rabe, A. Vollmer and R. L. Johnson, Phys. Rev. Lett., 2005, 95, 237601 CrossRef.
- S. Braun, W. R. Salaneck and M. Fahlman, Adv. Mater., 2009, 21, 1450–1472 CrossRef CAS.
- X. Q. Shi, M. A. Van Hove and R. Q. Zhang, J. Mater. Sci., 2012, 47, 7341–7355 CrossRef CAS.
- J. H. Jensen, Molecular Modeling Basics, CRC Press, 2010 Search PubMed.
- S. Irle, G. Zheng, Z. Wang and K. Morokuma, J. Phys. Chem. B, 2006, 110, 14531–14545 CrossRef CAS.
- R. Tatti, L. Aversa, R. Verucchi, E. Cavaliere, G. Garberoglio, N. M. Pugno, G. Speranza and S. Taioli, RSC Adv., 2016, 6, 37982–37993 RSC.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, npj Comput. Mater., 2016, 2, 15011 CrossRef CAS.
- S. Liu, J. Comer, A. C. T. van Duin, D. M. van Duin, B. Liu and J. H. Edgar, Nanoscale, 2019, 11, 5607–5616 RSC.
- K. D. Nielson, A. C. T. van Duin, J. Oxgaard, W.-Q. Deng and W. A. Goddard, J. Phys. Chem. A, 2005, 109, 493–499 CrossRef CAS.
- S. K. Singh, S. G. Srinivasan, M. Neek-Amal, S. Costamagna, A. C. T. van Duin and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104114 CrossRef.
- B. D. Jensen, K. E. Wise and G. M. Odegard, J. Comput. Chem., 2015, 36, 1587–1596 CrossRef CAS.
- M. L. Tietze, P. Pahner, K. Schmidt, K. Leo and B. Lüssem, Adv. Funct. Mater., 2015, 25, 2701–2707 CrossRef CAS.
- R. Meerheim, S. Olthof, M. Hermenau, S. Scholz, A. Petrich, N. Tessler, O. Solomeshch, B. Lüssem, M. Riede and K. Leo, J. Appl. Phys., 2011, 109, 103102 CrossRef.
- B. Nell, K. Ortstein, O. V. Boltalina and K. Vandewal, J. Phys. Chem. C, 2018, 122, 11730–11735 CrossRef CAS.
- W. Zhang, M. Dubois, K. Guérin, P. Bonnet, H. Kharbache, F. Masin, A. P. Kharitonov and A. Hamwi, Phys. Chem. Chem. Phys., 2010, 12, 1388–1398 RSC.
- R. Mitsumoto, T. Araki, E. Ito, Y. Ouchi, K. Seki, K. Kikuchi, Y. Achiba, H. Kurosaki, T. Sonoda, H. Kobayashi, O. V. Boltalina, V. K. Pavlovich, L. N. Sidorov, Y. Hattori, N. Liu, S. Yajima, S. Kawasaki, F. Okino and H. Touhara, J. Phys. Chem. A, 1998, 102, 552–560 CrossRef CAS.
- Y. Smets, C. B. Stark, S. Lach, F. Schmitt, C. A. Wright, M. Wanke, L. Ley, C. Ziegler and C. I. Pakes, J. Chem. Phys., 2013, 139, 44703 CrossRef CAS.
- A. F. Paterson, N. D. Treat, W. Zhang, Z. Fei, G. Wyatt-Moon, H. Faber, G. Vourlias, P. A. Patsalas, O. Solomeshch, N. Tessler, M. Heeney and T. D. Anthopoulos, Adv. Mater., 2016, 28, 7791–7798 CrossRef CAS.
- T. K. Shimizu, J. Jung, T. Otani, Y.-K. Han, M. Kawai and Y. Kim, ACS Nano, 2012, 6, 2679–2685 CrossRef CAS.
- A. I. Oreshkin, D. A. Muzychenko, S. I. Oreshkin, V. I. Panov, R. Z. Bakhtizin and M. N. Petukhov, J. Phys. Chem. C, 2018, 122, 24454–24458 CrossRef CAS.
- A. I. Oreshkin, D. A. Muzychenko, S. I. Oreshkin, V. A. Yakovlev, P. Murugan, S. S. Chandrasekaran, V. Kumar and R. Z. Bakhtizin, Nano Res., 2018, 11, 2069–2082 CrossRef CAS.
- R. Z. Bakhtizin, A. I. Oreshkin, D. A. Muzychenko, S. I. Oreshkin and V. A. Yakovlev, J. Surf. Invest.: X-Ray, Synchrotron Neutron Tech., 2019, 13, 14–22 CrossRef CAS.
- A. V. Kepman, V. F. Sukhoverkhov, A. Tressaud, C. Labrugere, E. Durand, N. S. Chilingarov and L. N. Sidorov, J. Fluorine Chem., 2006, 127, 832–836 CrossRef CAS.
- T. R. Albrecht, P. Grütter, D. Horne and D. Rugar, J. Appl. Phys., 1991, 69, 668–673 CrossRef.
- I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 13705 CrossRef CAS.
- J. Hénin and C. Chipot, J. Chem. Phys., 2004, 121, 2904–2914 CrossRef.
- A. Migani and F. Illas, J. Phys. Chem. B, 2006, 110, 11894–11906 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. J. Plimpton and A. P. Thompson, MRS Bull., 2012, 37, 513–521 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- G. Fiorin, M. L. Klein and J. Hénin, Mol. Phys., 2013, 111, 3345–3362 CrossRef CAS.
- S. Kawasaki, T. Aketa, H. Touhara, F. Okino, O. V. Boltalina, I. V. Gol'd, S. I. Troyanov and R. Taylor, J. Phys. Chem. B, 1999, 103, 1223–1225 CrossRef CAS.
- A. Yao, Y. Matsuoka, S. Komiyama, I. Yamada, K. Suito, S. Kawasaki, F. Okino and H. Touhara, Solid State Sci., 2002, 4, 1443–1447 CrossRef CAS.
- A. Fartash, J. Appl. Phys., 1996, 79, 742 CrossRef CAS.
- T. Hashizume, K. Motai, X. D. Wang, H. Shinohara, H. W. Pickering and T. Sakurai, J. Vac. Sci. Technol., A, 1994, 12, 2097–2100 CrossRef CAS.
- W. W. Pai, C.-L. Hsu, M. C. Lin, K. C. Lin and T. B. Tang, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 125405 CrossRef.
- K. Motai, T. Hashizume, H. Shinohara, Y. Saito, H. W. Pickering, Y. Nishina and T. Sakurai, Jpn. J. Appl. Phys., 1993, 32, L450–L453 CrossRef CAS.
- N. Hauptmann, F. Mohn, L. Gross, G. Meyer, T. Frederiksen and R. Berndt, New J. Phys., 2012, 14, 73032 CrossRef.
- M. Pedio, K. Hevesi, N. Zema, M. Capozi, P. Perfetti, R. Gouttebaron, J.-J. Pireaux, R. Caudano and P. Rudolf, Surf. Sci., 1999, 437, 249–260 CrossRef CAS.
- C. R. Bernard Rodríguez and J. A. Santana, J. Chem. Phys., 2018, 149, 204701 CrossRef.
- V. M. Mikoushkin, V. V. Shnitov, V. V. Bryzgalov, Y. S. Gordeev, O. V. Boltalina, I. V. Goldt, S. L. Molodtsov and D. V. Vyalikh, Tech. Phys. Lett., 2009, 35, 256–259 CrossRef CAS.
- C. H. Lin, K. C. Lin, T. B. Tang and W. W. Pai, J. Nanosci. Nanotechnol., 2008, 8, 602–607 CrossRef CAS.
- P. O. Hubin, D. Jacquemin, L. Leherte and D. P. Vercauteren, Theor. Chem. Acc., 2016, 135, 1–10 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Technical details of the molecular dynamics methodology; analysis for estimation of fluorine content on each metal surface for diverse coverages, including original C 1s and F 1s XPS data and fits; additional constant current STM and frequency shift images; full set of secondary electron cutoff (SECO) and valence band spectra for diverse coverages on Au(111), Cu(111) and Ni(111), accompanied by the corresponding energy levels diagram. Two movies showing reactive MD simulations for molecular de-fluorination plus adsorption (Movie 1) and excited rotation of a molecule on the surface (Movie 2) both in the case of Ni(111) surface. See DOI: 10.1039/d0na00513d |
| This journal is © The Royal Society of Chemistry 2020 |