 Open Access Article
Open Access ArticleNanoporous carbon for electrochemical capacitive energy storage
Hui
Shao†
ab,
Yih-Chyng
Wu†
ab,
Zifeng
Lin
 *c,
Pierre-Louis
Taberna
ab and
Patrice
Simon
*c,
Pierre-Louis
Taberna
ab and
Patrice
Simon
 *abd
*abd
aUniversité Paul Sabatier, CIRIMAT UMR CNRS 5085, 118 route de Narbonne, 31062 Toulouse, France. E-mail: simon@chimie.ups-tlse.fr
bRéseau sur le Stockage Electrochimique de l'Energie (RS2E), FR CNRS 3459, France
cCollege of Materials Science and Engineering, Sichuan University, Chengdu 610065, P. R. China. E-mail: linzifeng@scu.edu.cn
dInstitut Universitaire de France, 1, Rue des Ecoles, 75005 Paris, France
First published on 14th April 2020
Abstract
The urgent need for efficient energy storage devices has stimulated a great deal of research on electrochemical double layer capacitors (EDLCs). This review aims at summarizing the recent progress in nanoporous carbons, as the most commonly used EDLC electrode materials in the field of capacitive energy storage, from the viewpoint of materials science and characterization techniques. We discuss the key advances in the fundamental understanding of the charge storage mechanism in nanoporous carbon-based electrodes, including the double layer formation in confined nanopores. Special attention will be also paid to the important development of advanced in situ analytical techniques as well as theoretical studies to better understand the carbon pore structure, electrolyte ion environment and ion fluxes in these confined pores. We also highlight the recent progress in advanced electrolytes for EDLCs. The better understanding of the charge storage mechanism of nanoporous carbon-based electrodes and the rational design of electrolytes should shed light on developing the next-generation of EDLCs.
1. Introduction
Reducing the consumption of fossil fuels and developing renewable and sustainable energy sources have been considered to be effective strategies to tackle the climate change crisis. To address such issues, more efficient electrical energy conversion and storage devices are required.1 The most commonly used electrochemical energy storage technologies today are batteries and supercapacitors. Batteries store energy through faradaic reactions of electrode materials with electrolytes, usually along with chemical interconversions and phase changes, providing high energy supplement, with energy densities of a few hundreds of W h kg−1. However, these battery-type faradaic reactions undergo sluggish kinetics and material irreversible processes, leading to limited power performance and lifetime.2 By contrast, supercapacitors store the charge at the electrode/electrolyte interface, via physical ion adsorption/desorption process, for electrochemical double-layer capacitors (EDLCs); through fast and non-diffusion limited faradaic reactions for pseudocapacitive materials.3,4 These fast and highly reversible storage mechanisms make supercapacitors promising candidates for energy storage devices with high power density and a long cycling life,5 which are nowadays used in a broad range of applications where high power delivery and/or uptake is needed, such as energy harvesting.6,7 However, the energy density (∼10 W h kg−1 for the best commercial devices) still hampers the spread of this technology over a wider range of applications.1.1 Basic operating principles of EDLCs
As mentioned above, EDLCs are capacitive energy storage devices that store energy through a non-faradaic mechanism. Like batteries, a supercapacitor device contains two electrodes immersed in an electrolyte (see Fig. 1), with an ionically conducting, porous separator placed in-between to prevent electrical short circuits. Basically, when an external voltage is applied between the EDLC electrodes, the electronic charge that accumulates at electrode surfaces is balanced by the adsorption of the ions of opposite ionic charge from the electrolyte. The capacitance C created by this charge separation at the electrode/electrolyte interface, resulting from electrostatic charge separation, is given by8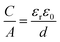 | (1) |
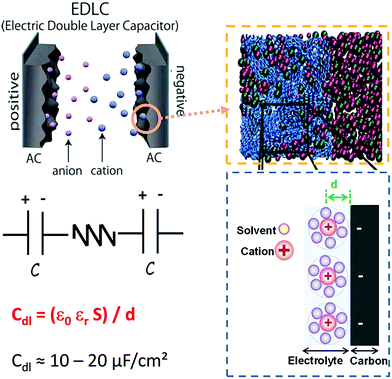 | ||
| Fig. 1 The upper left panel gives the schematic representation of an electric double layer capacitor (EDLC) using porous carbon materials as electrode materials. The upper right panel shows the simulation EDL cell consisting of a porous electrode filled with an ionic liquid (blue: carbon atoms, red: cation, and green: anion). The bottom left panel gives the equivalent circuit of an EDLC and the bottom right panel gives a schematic representation of EDL formation of a negative electrode. Adapted from ref. 23 with permission from Royal Society of Chemistry (copyright 2012). | ||
Tremendous efforts had been focused initially on the fabrication of high SSA carbons (such as activated carbons) since eqn (1) suggested that higher SSA leads to higher specific capacitance. In 2006, several groups observed an unexpected capacitance increase by using nanoporous carbons with tunable pore structures in the subnanometer range,14,15 revealing that not only the SSA but also the carbon pore structures, such as average pore size and pore size distribution,16,17 have significant impacts on the carbon electrode performance. The discovery of a drastic capacitance increase when the ions were confined in sub-nanopores (<1 nm) of porous carbon materials, that is in pores less than the size of the solvated ions, has not only resulted in a two-times increase of the energy density of commercial devices but has also led to revisit the fundamental concepts of the EDL charging in confined carbon nanopores. Since then, alternative EDL theories and models have been proposed and developed to understand the charge storage mechanisms in nanoporous carbons. This has been made possible by the important development of theoretical studies as well as analytical techniques to better understand the ion environment and ion fluxes in these confined pores.
This review aims at summarizing the recent progress in the field of capacitive energy storage using nanoporous carbon materials, from the viewpoint of materials science and the characterization techniques. In particular, we will focus on the charge storage mechanisms of the nanoporous carbon-based electrode in EDLCs, from classical theories to the most recent models. Simulations and advanced in situ techniques have been since then extensively developed and will be reviewed in the following. Finally, perspectives will be given as a guideline for building supercapacitors with improved performance.
1.2 Key characteristics of EDLCs
As mentioned earlier, a supercapacitor cell contains two parallel electrodes, in which the positive and negative electrodes are equivalent to two capacitors assembled in series (see Fig. 1); therefore, the capacitance Ccell of the device is expressed as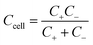 | (2) |
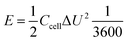 | (3) |
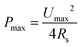 | (4) |
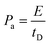 | (5) |
From a practical point of view, the energy and power of EDLCs can be presented and compared on a gravimetric (per weight), volumetric (per volume), or areal (per area) basis. It is worth noting that selecting suitable performance characteristics is essential for reporting new materials and electrode architectures, and the reader can refer to several papers recently published reporting best practices for interpreting the performances of electrochemical energy storage systems.18–21 To summarize, energy and power densities based on cell stack volume or total cell weight should be reported in Ragone plots instead of values normalized to the active material weight.18,19 In the case of microdevices and some flexible electronics which have a negligible mass loading (tens of μg) or an extremely thin film (hundreds of nm), the volumetric or areal energy density is more appropriate than gravimetric parameters.18,22
The key challenge EDLCs are facing is their energy density improvement to increase their operating time beyond one minute. This results in finding strategies to improve the cell voltage and/or the capacitance, such as shown in eqn (3). Basically, the capacitance of porous carbon electrodes is controlled by the carbon/electrolyte interface, and this will be the core of the present paper and extensively discussed in the next sections. The cell voltage of EDLCs is limited by the electrochemical stability of the electrolyte, as well as the presence of impurities (surface groups) on the carbon electrode. With the operating voltage in aqueous-based electrolytes being limited to about 1.23 V, because of water electrolysis, non-aqueous electrolytes are preferentially used since they can provide cell voltage beyond 3 V.24,25 Advanced electrolytes which have been recently proposed for EDLC devices will be briefly described in Section 4 at the end of this paper, but the reader will find more detailed information on the electrolytes from other literature.26–28
To sum up, choosing the suitable electrode material and electrolyte matrix remains the core issue to enhance the performance of EDLC devices.
2. EDL capacitance at the porous carbon/electrolyte interface
2.1 EDL models based on 2D electrodes
The first EDL model proposed by Helmholtz8 described the charge separation at the electrode/electrolyte interface considering a planar electrode surface. In this model (Fig. 2a), the charges accumulated at the electrode surface are balanced by electrostatic adsorption from the electrolyte of a counterion monolayer, resulting in two layers of opposite charges at the interface. This model is analogous to the conventional parallel-plate dielectric capacitors, and the Helmholtz layer capacitance can be therefore expressed as eqn (1).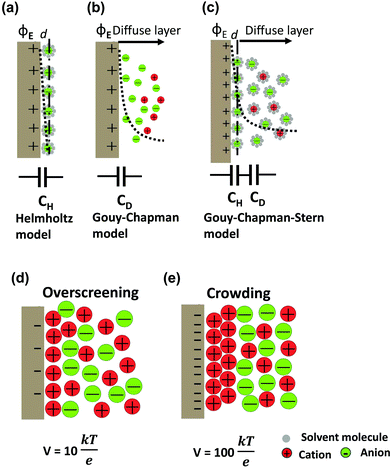 | ||
| Fig. 2 Schematic diagrams of EDL models based on the positive polarized (ϕE) 2D electrodes in an electrolyte with solvent: (a) Helmholtz model, (b) Gouy–Chapman model, and (c) Gouy–Chapman–Stern model. The dashed lines indicate the potential drop (ϕ) in each model. The bottom insets present the simplified equivalent circuits. DEL formation of ionic liquid electrolytes by a simple phenomenological theory: (d) overscreening effect at a moderate voltage, V = 10kBT/e (0.26 V) and (e) crowding effect at a high voltage, V = 100kBT/e (2.6 V). Adopted from ref. 38 with permission from American Physical Society (copyright 2011). | ||
The areal capacitance (per cm2) of the Helmholtz layer (CH) can be normalized by εr the electrolyte dielectric constant and d the thickness of the Helmholtz layer, both of them depending on the selected electrolytes. The dielectric constant value of bulk water is around 78,29 and it falls in the range of 1 to 100 at room temperature for most of the solvents used in EDLC applications.25,29,30 However, one should note that the dielectric constant would be arguably nonvalid at such scale (sub-nanometer) and it has been found to be smaller than that of the electrolyte bulk.29 The Helmholtz model suggests a linear potential drop within the Helmholtz layer. However, the surface excess charges of the electrode are unlikely to be entirely counterbalanced by the Helmholtz layer, especially in the case of low concentration solutions.25 Also, the counterion layer from the electrolyte side cannot be formed as a single static compact layer due to the ion movement from thermal fluctuation. The Gouy–Chapman model,31,32 as presented in Fig. 2b, includes a diffuse layer between the electrode and bulk electrolyte to take into account the thermal fluctuation according to the Poisson–Boltzmann equation.12 The ion distribution of the diffuse layer highly depends on the distance since the electrostatic attractions decrease from the electrode surface to the electrolyte bulk. The average thickness of the diffuse layer (also called Debye length, λD) for monovalent electrolytes is defined as
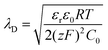 | (6) |
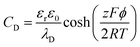 | (7) |
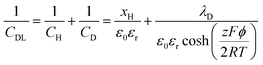 | (8) |
The EDL formation at planar electrodes in solvent-free ionic liquid electrolytes deviates from predictions of classical models based on dilute-solution approximation.36 Unlike solvent-containing electrolytes, the absence of solvent molecules for screening the charge between cations and anions in ionic liquids results in strong ion–ion correlations. The orientations and rearrangements of non-spherical shaped ion chains triggered by the polarization and complex force fields make it even more difficult to depict the electrode/ionic liquid interface structure.25 Kornyshev's group predicted the existence of a differential capacitance–potential curve with bell-like and camel-like shapes based on mean-field theory,36 which was further confirmed by experimental and simulation studies.39–43 For potential below the potential of zero charge (PZC) range, an over-screening effect is proposed due to the ion–ion correlations (see Fig. 2d), leading to the formation of a first counterion layer with an excess charge compared to the electrode. For even larger polarization below PZC, a crowding effect is predicted at higher voltage (vs. PZC), when the increased polarization suppresses the over-screening and leads to the formation of counterions approaching the inner layer (Fig. 2e).36,38 On a flat electrode, the global view is now that the EDL is formed by a stacking of multilayers of ions, as evidenced from both experimental and modeling observations.41,43–47 Monolayered interfacial structures48,49 and a controversial dilute electrolyte-like picture50 have also been proposed. Using molecular dynamics simulation based on coarse grained models, Kirchner et al. suggested a structural transition from multiple alternating layers of counter- and co-ions to a surface-frozen monolayer of counterions at certain charge densities.51
2.2 High surface area carbons for EDLC electrodes
According to IUPAC,52 pores can be classified into three categories, namely micropores (0.2 to 2 nm), mesopores (2 to 50 nm), and macropores (>50 nm). The smallest pores – micropores – can be sub-divided into super- (>0.7 nm) and ultra-micropores (<0.7 nm). Micropores are then nanosized. For the sake of clarity, in the next sections, we will refer to nanopores as pore size of nanoporous and sub-nanoporous dimensions.As mentioned above, nanoporous carbons have been widely used as EDLC electrode materials. First, an extremely high specific surface area (beyond 2000 m2 g−1) as well as tunable average pore size and pore size distribution can be achieved using various processes, including activation, carbonization, etc.5 Carbon materials also have excellent electrochemical stability in both aqueous and non-aqueous systems. The operating voltage windows of carbon-based EDLCs were usually limited by the decomposition potential of electrolytes instead of the carbon electrodes. Their electrical conductivity allows for a limited ohmic drop during electrochemical polarization. Finally, they can be prepared from low cost, abundant bio-sourced precursors using cheap processes.11
Fig. 3 shows that various kinds of carbon materials with several dimensionalities can be used for EDLC applications, from 0-dimensional (0D) non-porous carbon onions, to 1D (carbon nanotubes and carbon fibers), 2D (graphene), and 3D porous carbons (activated carbons, templated carbons, carbide-derived carbons). A few examples of various carbons used in EDLCs are summarized in Table 1.
 | ||
| Fig. 3 Transmission electron micrographs (TEM) of various carbons with several dimensionalities for EDLCs: (a) OLCs,94 (b) CNTs,76 (c) graphene,92 (d) ACs,95 (e) CDCs,65 and (f) TCs,96 with permission from Elsevier (copyright 2015), 2011 American Chemical Society, Springer Nature (copyright 2014), Elsevier (copyright 2019), Elsevier (copyright 2006), and Royal Society of Chemistry (copyright 2009), respectively. | ||
| Carbon | Electrode materials | SSAa (m2 g−1) | Electrolyte (mol l−1) | C g (F g−1) Cv (F cm−3) | Voltage (V) | Test conditions | High-rate test cgb (F g−1), cv (F cm−3) | Ref. |
|---|---|---|---|---|---|---|---|---|
| a B and D represent SSA obtained from the BET and DFT method, respectively. b g and v give the specific gravimetric and volumetric capacitance, respectively. | ||||||||
| ACs | PICACTIF SC | 2315 (B) | TEAMS (1.7) | 125 (g) | 2 | 10 mA cm−2 (2el) | — | 53 |
| Ppy-AC | 3432 (B) | EMIBF4 | 256 (g) | 2.3 | 1 mV s−1 (2el) | 150 (g) | 55 | |
| 2244 (D) | 100 mV s−1 | |||||||
| AC-W800 | 3967 (B) | TEABF4 (1) | 236 (g) | 2.3 | 1 mV s−1 (2el) | 173 (g) | 54 | |
| 2387 (D) | 100 (v) | 100 mV s−1 | ||||||
| B-AC | 2841 (B) | KOH (2) | 330 (g) | 1 | 1 A g−1 (3el) | 238 (g) | 57 | |
| 10 A g−1 | ||||||||
| CDCs | TiC-CDC | 1270 (B) | TEABF4 (1.5) | 145 (g) | 2.3 | 5 mA cm−2 (2el) | 128 (g) | 14 |
| 80 (v) | 100 mA cm−2 | |||||||
| TiC-CDC | 1270 (B) | EMITFSI | 160 (g) | 3 | 5 mA cm−2 (2el) | — | 60 | |
| 85 (v) | ||||||||
| OM-CDC | 2364 (B) | H2SO4 (1) | 188 (g) | 0.6 | 0.1 A g−1 (2el) | 140 (g) | 64 | |
| 20 A g−1 | ||||||||
| Mesoporous-CDC | 2250 (B) | TEA BF4 (1) | 170 (g) | 2 | 0.1 A g−1 (2el) | 150 (g) | 62 | |
| 17 A g−1 | ||||||||
| TCs | ZTC | 2940 (B) | TEA BF4 (1) | 168 (g) | 2 | 0.05 A g−1 (3el) | 153 (g) | 67 |
| 2 A g−1 | ||||||||
| ZTC-L | 2910 (B) | TEABF4 (1) | 75 (v) | 2 | 1 A g−1 (3el) | 60 (v) | 68 | |
| 20 A g−1 | ||||||||
| MCNAs | 1266 (B) | TEABF4 (1) | 152 (g) | 2.5 | 5 mV s−1 (2el) | — | 97 | |
| Z-900 | 1075 (B) | H2SO4 (0.5) | 214 (g) | 1.2 | 5 mV s−1 (3el) | 115 (g) | 98 | |
| 100 mV s−1 | ||||||||
| OCLs | ND-1200 | 500 (B) | TEABF4 (1.5) | 38 (g) | 2.3 | 5 mA cm−2 (2el) | 30 (g) | 73 |
| 200 mA cm−2 | ||||||||
| 1700-VAC | 364 (B) | TEABF4 (1) | 20 (g) | 2.7 | 1 mV s−1 (2el) | 18 (g) | 94 | |
| 340 (D) | 1 V s−1 | |||||||
| CNTs | MWCNT | 200 (B) | TEABF4 (1.5) | 18 (g) | 2.3 | 5 mA cm−2 (2el) | 16 (g) | 73 |
| 200 mA cm−2 | ||||||||
| Graphene | a-MEGO | 2400 (B) | BMIMBF4 (1) | 165 (g) | 3.5 | 1.4 A g−1 (2el) | 164 (g) | 90 |
| 60 (v) | 5.7 A g−1 | |||||||
| HGF | 830 (B) | EMIBF4 (1) | 262 (g) | 3.5 | 1 A g−1 (2el) | 190 (g) | 92 | |
| 186 (v) | 20 A g−1 | |||||||
| EM-CCG | 167 (B) | EMIBF4 (1) | 167 (g) | 3.5 | 1 A g−1 (2el) | 135 (g) | 89 | |
| 10 A g−1 | ||||||||
Activated carbons (ACs) are amorphous porous carbons containing mainly sp2 carbon atoms. They are prepared from physical (thermal) and/or chemical activation of various types of natural or synthetic organic precursors.11 In general, pre-carbonization is required before the activation process when natural precursors are used as carbon precursors. Physical activation takes place in the high temperature range of 600–1200 °C under oxidizing atmospheres (such as steam and CO2), while chemical activation requires a lower temperature range of 300–600 °C using chemical reagents (such as KOH, ZnCl2, etc.). ACs are highly porous with a broad range of pore sizes from a few tens of nanometers to a few nanometers, resulting in high SSA, mainly ranging from 1000 to 2000 m2 g−1. The SSA and pore size distribution are predominantly determined by carbon precursors and the activation process. Owing to their relatively good electrical properties and high SSA, and especially the low cost compared to other carbon materials, ACs have been widely used as supercapacitor electrode materials. AC based supercapacitors show a long cycle life span (>106 cycles), making ACs the best option as supercapacitor electrodes in commercial devices. The electrochemical performances of AC based electrodes have been significantly improved during the past few years, exceeding 200 F g−1 in nonaqueous based electrolytes.16,53–55 This has been mainly achieved by tuning the mean pore size and pore size distribution in the micropore range, below 1.5 nm (see below). In aqueous electrolytes, AC electrodes enable the delivery of capacitance ranging from 100 to 300 F g−1 depending on pore size distribution and surface chemistry, but the penalty is the low energy density associated with the limited voltage window.56,57
Carbide-derived carbons (CDCs) are produced by selective etching of metals from various metal carbides, with TiC being the most used.58 CDCs offer the key advantage of fine-tuning their pore size (below 2 nm) and pore size distribution by adjusting the synthesis parameters such as temperature and time; the carbon structures and particle size are defined by the carbide precursors.59 Generally, CDCs exhibit high BET SSA ranging from 1000 to 2000 m2 g−1 and a narrow pore size distribution in the nanometer and sub-nanometer range. Taking TiC-CDCs as an example, their average pore sizes vary from 0.68 to 1.1 nm which can be tunable with 0.05 nm accuracy by changing the chlorination temperature in the range of 500 to 1000 °C.14 Owing to their controlled, narrow pore size distribution in the micropore range, CDCs have been extensively used as model materials to understand the fundamental of EDL formation in porous materials14,60 and have helped in identifying the capacitance increase in nanopores (see later). TiC-CDCs showing a specific capacitance value of 160 F g−1 were reported in an ionic liquid, which showed a high volumetric capacitance of 85 F cm−3, higher than standard ACs at that time.60 Later on, several approaches have been proposed to design CDCs with high EDL capacitance and high-rate performance, including reducing the CDC particle size61 and adding mesopores.62–64 Interestingly, CDCs have moved into real products since they are now used in commercial EDLCs.65
Templated carbons (TCs) are obtained by template-assisted carbonization of carbon precursors and subsequent removal of the templates. This approach leads to carbon materials with precise control of the pore size in the mesopore range, which is of great significance for electrode materials of supercapacitors.66 The pore structures of TCs can be controlled by using two kinds of templates, namely hard template (such as zeolites, mesoporous silicas, and metal oxides) and soft template (such as metal–organic frameworks and block copolymer surfactants).10 Numerous publications based on TCs have been published during the last decade; here we provide a few examples. Zeolite templated carbons (ZTC) produced by acetylene CVD can achieve a high capacitance of 140 to 190 F g−1 (70 to 85 F cm−3) in organic-based electrolytes.67,68 Such materials are interesting for conducting basic studies of ion transfer and adsorption in nanopores. However, the commercial development is limited by the cost of production.
Carbon onions, also called onion-like carbons (OLCs), are spherical or polyhedral carbon nanoparticles, consisting of concentric defective sp2-hybridized carbon multiple shells, with a small size around a few tens of nanometers. Among a number of synthetic routes for preparing OLCs, thermal treatment of detonation nanodiamond powders is the most practical method.69–71 Since OLC particles are non-porous, they exhibit a limited external SSA of 300–600 m2 g−1, together with a high interparticle pore volume around 1 cm3 g−1.72 The pore structure of OLC electrodes consists predominantly of micro and mesopores existing between the OLC particles. However, due to the non-porous particles, the whole surface is highly accessible to electrolyte ions. As a result, OLC-based electrodes can achieve a limited capacitance of 50 F g−1,73,74 with an excellent power ability due to the highly accessible external surface area. In summary, OLCs are not good candidates to increase the capacitance of EDLC electrodes but can deliver high power.75,76 Besides, OLCs with a particle size around 10 nm are also employed as conductive additives for EDLCs.77,78
Carbon nanotubes (CNTs) are large cylindrical carbon materials consisting of a hexagonal arrangement of sp2 hybridized carbon atoms, which are formed by rolling up a single sheet of graphene (single-walled carbon nanotubes, SWCNTs) or by rolling up multiple sheets of graphene (multiwalled carbon nanotubes, MWCNTs).79 To date, the commonly used synthesis techniques for CNTs are arc discharge, laser ablation, and chemical vapor deposition (CVD).80 The SSA of CNTs ranges from 100 to 1000 m2 g−1.81 CNTs can exhibit narrow pore size distribution, but the internal pores are unlikely to contribute to EDL capacitance due to the ion diffusion limitation inside the carbon walls and because of the absence of the inner electric field in regular operating conditions. Instead, similar to OLCs, the external surface of CNTs can be used to form exohedral capacitors, leading to a moderate capacitance below 100 F g−1.59 However, the highly accessible external surface and excellent electric conductivity make CNTs suitable candidates for high power devices,59 even under extreme climatic conditions.76 In addition, CNTs have been used as model materials in simulation experiments to study the double layer formation inside or outside the tube.82–84
Graphene, one of the most studied two-dimensional materials, can be synthesized by (1) “bottom-up” approaches, such as CVD, epitaxial growth and chemical synthesis, and (2) “top-down” methods, including the micromechanical and liquid-phase exfoliation of graphite and the reduction of graphene oxide (rGO).85 A single graphene sheet has a high theoretical SSA of 2630 m2 g−1 and a high intrinsic capacitance of about 21 μF cm−2.86,87 However, these excellent properties at the single layer graphene scale do not translate at large macroscopic scale due to the restacking issue.85 In order to enhance the performance of graphene-based EDLCs, extensive efforts have been made to address such a restacking issue. One promising approach is to pre-insert molecules between the graphene layers or build 3D structures based on 2D rGO.88–91 For example, porous holey graphene (HGF) material showed an impressive capacitance beyond 200 F g−1 and high gravimetric and volumetric stack energy densities92 owing to the creation of 3D ionic pathways, but the synthesis process has to be carefully controlled to prepare porous graphene with suitable structure and surface composition. In summary, graphene and graphene-based materials show some interesting performance at the lab level, but the cost issue and the lack of techniques for industrial-scale high-quality graphene electrode production still hamper their commercial development. However, as an ideal 2D carbon surface, graphene offers great opportunities as a model surface material to develop some fundamental studies on the understanding of EDL formation in real and simulation experiments.93
2.3 Capacitance in nanoporous carbon-based electrodes
There are numerous parameters that affect the electrochemical performance of nanoporous carbon material-based EDLC electrodes, such as conductivity, the presence of surface groups, and most importantly, SSA, pore size, and PSD. Although most of the carbons can achieve high conductivity owing to their high density of electronic states at the Fermi level, still a few carbons exhibit semiconducting properties, such as SWCNTs with certain diameter and helicity99 or bilayer graphene.100 This semiconducting character was suggested to account for the observed current drop near the potential of zero charge (PZC) in a cyclic voltammogram (CV), resulting in a butterfly-shaped CV in a three electrode system and a trapezoid-shaped CV in a two electrode device, indicating that EDL capacitance in some carbon-based electrodes was not independent of the charging state.29 In addition, Xie et al. identified that the quantum capacitance versus gate potential has a symmetric V-shape with a minimum at the Dirac point in single- and bilayer graphene.87 Efforts have been made to modify the quantum capacitance of graphene by increasing its charge carrier density via N-doping approach, leading to an enhanced interfacial capacitance.101 However, more evidence on how the quantum capacitance quantitatively affects the electrode capacitance is needed. Besides, the presence of surface groups has strong impacts on the electrochemical performance of carbon-based electrodes, especially in aqueous systems. The surface groups such as –O and –OH are frequently present as impurities in activated carbons or rGO materials, coming from the synthesis and/or activated process. In addition, –N groups are used as the dopant to improve the electrochemical performance of carbons. These surface groups contribute to the capacitance in aqueous electrolytes by adding a pseudocapacitive contribution, which is beyond the scope of this review. Most importantly, the capacitance of carbon-based electrodes in the EDLC system is strongly correlated to the SSA and pore structures.A comprehensive characterization of the surface and textural properties is crucial to understand how the SSA and pore structures affect the electrochemical performance of porous carbon-based EDLCs since SSA is strongly connected to the pore structures. However, porous carbons are complex materials with various structures, including local graphitized and/or disorder carbon arrangements, that it is unrealistic to completely depict their real local- and long-range structures.102,103 Nevertheless, many experimental techniques, including gas sorption, electron microscopy, Raman spectroscopy, nuclear magnetic resonance spectroscopy, X-ray scattering, neutron scattering, and recently developed in situ techniques, have made sound progress in this way.104 In addition, complementary simulation techniques (such as the Monte Carlo method and density functional theory) and analysis models (pair distribution function) were also proposed to unravel the pore structures of porous carbons.104 Among these techniques, the gas sorption technique is the most commonly used one owing to its non-destructive nature and relatively low cost. Importantly, it can be used to characterize the textural properties of porous materials with a wide range of SSA and pore size distributions.105 The next section will focus on the surface area and pore structure characterization based on the gas sorption technique; other advanced techniques mentioned above will be presented in Section 3.
Once the adsorption isotherm has been made, one should select the appropriate model to fit the isotherm to get the SSA, pore volume and PSD. The Brunauer–Emmett–Teller (BET) equation was considered as the standard model to evaluate the surface area, denoted as SBET, for decades.109 However, now it is well known that this simplified model cannot clearly distinguish between monolayer–multilayer adsorption and micropore filling in microporous materials, leading to significant inaccuracies in the SSA and pore size distributions.110 Various classical macroscopic methods including models based on the Kelvin equation and Dubinin–Radushkevitch related approaches were also applied to interpret the gas isotherm, but the lack of description of molecular packing at the local level limits their applicability. DFT-based models and simulation from the microscopic level are now considered as more effective methods to analyze the data of gas sorption experiments.111 Non-local density functional theory (NLDFT)-based models firstly proposed by Lastoskie et al. to characterize nanoporous carbons have led to significantly improved accuracies.102,112,113 Thommes et al. proposed the quenched solid density functional theory (QSDFT) that takes into account the effects of surface heterogeneity, leading to a more reliable evaluation of porosity in nanoporous carbons.105,110,114
Although the description of the “real” surface of nanoporous carbon still remains challenging as outlined above, reliable porous carbon characteristics such as SSA, pore volume and PSD can be assessed by gas adsorption with a carefully selected gas probe and analysis model. Also, porosity obtained from other techniques (such as scattering methods) showed a good agreement with gas adsorption.115,116 This makes reasonable the comparison of the textural parameters of different porous carbons obtained from gas adsorption measurements, to further understand the correlation between electrochemical performance and porosity.
As a result, no direct clear trend could be established between SSA and capacitance.
However, several groups reported high capacitance by using microporous carbons with sub-nanometer pores in various electrolyte systems.14,15,122,123 Taking advantage of the tunable pore structure of CDCs, Chmiola et al. reported in 2006 high gravimetric and volumetric capacitance for CDC pore size below 1 nm.14 The specific gravimetric capacitance normalized by BET SSA (C/SBET) obtained from Ar gas sorption (see Fig. 4a) revealed a capacitance increase for carbon pore size smaller than 1 nm. In addition, DFT SSA-normalized capacitance was also calculated at that time and the same capacitance increase was obtained, which indicated that the underestimation of SSA of microporous carbons by the BET model was not the cause of the increasing trend of C/SBET.14 Raymundo-Pinero et al. reported a similar increasing trend of capacitance using microporous ACs in both aqueous and non-aqueous electrolytes. They suggested that pore filling was more efficient for EDL formation when the pore size is around 0.7 nm in aqueous and 0.8 nm in organic electrolytes, respectively.15 The EDL capacitance increase in sub-nanometer pores was defying the traditional views of ion adsorption and EDL formation in carbon electrodes.5 Partial ion desolvation was proposed to explain the enhanced capacitance in sub-nanometer pores: owing to the distortion of the solvation when entering nanosized pores, the ion could get closer to the carbon wall so that the d in eqn (1) is decreased (Fig. 4c), confirming previous experimental observations made on nanoporous carbons under polarization.17,124–126 Later on, by monitoring the potential change of each electrode of a symmetric system using a silver quasi-reference electrode, a different EDL capacitance behavior at negative and positive electrodes was reported by Chmiola et al.,127 which confirmed partial desolvation during the charge/discharge process.
 | ||
| Fig. 4 Plots of specific capacitance normalized by SSA vs. average pore size obtained for various CDC electrodes in 1.5 M TEABF4 in ACN (a) and (b), and in neat EMITFSI ionic liquid (d). Please note: SSA was obtained from the BET method for (a) and (d), and from the DFT method for (b). (c) Plots of normalized capacitance vs. the average distance from the charge ion center to the pore wall of various CDCs. Plots of specific gravimetric and volumetric capacitance vs. pore size of CDC electrodes in 1.5 M TEABF4 in ACN (e) and in neat EMITFSI ionic liquid (f). Panels (a, b, c, and e) are reproduced from ref. 14 with permission from American Association for the Advancement of Science (copyright 2006), panel (d) is reproduced from ref. 5 with permission from Springer Nature (copyright 2008), and panel (f) is reproduced from ref. 60 with permission from American Chemical Society (copyright 2008). | ||
The desolvation effect was further studied by using advanced in situ techniques and simulation approaches, and this is the focus of Section 3. All the sets of results make this ion desolvation a universal phenomenon for virtually all nanoporous carbons because of the pore size dispersion and presence of ultranarrow (sub-nanometer) pores.128
However, because of the presence of the solvation shell that affects the effective ion size, it was not clear whether an optimum pore size could be achieved to maximize the capacitance. To this end, CDCs with various controlled pore sizes and PSD were characterized in a solvent-free electrolyte, ethyl-methylimidazolium-bis(trifluoromethane-sulfonyl)imide (EMITFSI).60 Solvent-free electrolytes rule out the solvation effect, and EMI+ and TFSI− have similar ion sizes (0.79 and 0.76 nm in the longest dimension for TFSI and EMI ions, respectively).60,127Fig. 4d shows the change of the normalized capacitance of various CDC electrodes vs. pore size in the EMITFSI electrolyte. The same trend was also reported for the change of the specific gravimetric and volumetric capacitance vs. the carbon pore size. The capacitance reaches a maximum when the ion size is close to the carbon mean pore size. This result was a major finding since (i) it shows that high capacitance could be achieved when the ion was confined in pores of the same dimension, and (ii) it evidences that the conventional way to describe the EDL formation using the Gouy–Chapman model in these confined nanopores was not valid anymore. This has led to an important work from both experimental and modelling point of view to explain this behavior, which will be discussed in Section 3.
Although numerous experimental and modeling studies confirmed the capacitance increase in nanopores, Centeno et al. reported a “regular pattern”, depicting a constant specific capacitance contribution of all micro- and mesopores in porous carbon-based EDLCs.129,130 The constant capacitance claimed by Centeno et al. was the capacitance normalized by surface area (S), where S was determined by using different probe molecules.129,130 In ref. 129, Centeno et al. attributed the increase of surface-related capacitance (C/S) reported by Chmiola et al.14 to the shortcoming of the BET method for SSA determination, despite the fact that similar capacitance increase in the sub-nanometer range pores was also observed by using NLDFT SSA.14
Nevertheless, this controversy raised a very important discussion about the trend of C/S vs. pore size, and it is important to define the limitations of the approach. To begin with, the commonly used pore size in the literature is average pore size, since porous carbon with ideal monodisperse pore size distribution does not yet exist. The mean pore size is generally defined as the pore size where the value of 50% of cumulative porous volume is reached.131 Moreover, most of the porous carbons exhibit a dispersed, broad PSD, which makes the use of average pore size to describe the porosity inaccurate unless these carbons have unimodal pore size distribution.132 Therefore, porous carbons with a narrow unimodal pore size distribution such as CDCs are preferred to be used for the experimental verification of C/S vs. pore size. Then, unlike SSA which can only be obtained based on the use of a gas probe with finite dimension and modeling, the specific gravimetric or volumetric capacitance C can be accurately measured by electrochemical experiments by measuring the capacitance, the weight, and the volume of carbon films. As shown in Fig. 4e and f, there is a similar correlation between the specific gravimetric capacitance and pore size, as well as specific volumetric capacitance.14,60 Also, some works specifically designed to address this question confirmed the increasing trend of capacitance in micropores (see also Section 3). For instance, Galhena et al. confirmed the correlation between capacitance and pore size by in situ tuning the interlayer constrictions (measured by XRD) of a graphene oxide paper in an organic electrolyte, eliminating any potential interference factors that may originate from the complex porosity evaluations.133 A similar increasing trend of capacitance in the sub-nanometer pore size (referred to as interlayer spacing in this case) range was reported by the same group and the maximum capacitance was obtained when the pore size matched the desolvated ion size.133
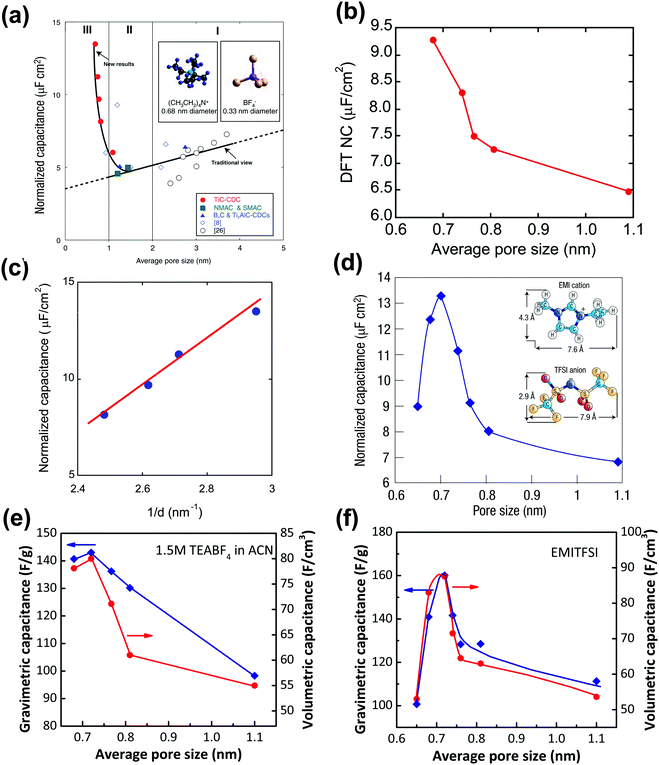
Although gravimetric and volumetric capacitances are better to be used since they are based on reliable experimental measurements, the use of SSA-normalized capacitance is interesting for fundamental studies of the EDL formation at porous carbon electrodes. As mentioned above, the porosity is determined by the size of the molecular probe used, and there is no doubt that this affects the SSA value used to normalize the capacitance. In ref. 130, Centeno et al. investigated three microporous carbon monoliths – average pore size in the micropore range – in 1 M solution of TEABF4 in ACN. They selected a cut-off at S>0.63 (that is the surface of pores above 0.63 nm, around 75% of the Stotal) to determine the SSA-normalized capacitance, which subsequently leads to the absence of capacitance change with the average carbon pore size.130 Note that, the computed neat ion size of TEA cation and BF4 anion is around 0.68 and 0.44 nm, respectively,134 and the specific value of 0.63 nm is the size of carbon tetrachloride used as a molecular probe in the porosity evaluation. S>0.63 was then interpreted as the accessible surface area of the carbon monoliths for both TEA+ cation and BF4− anion. However, this might be misleading since experimental evidence suggested that cations could be distorted when entering small pores under electric polarization.135 For instance, Ania et al. studied a microporous carbon with an average pore size centered at 0.58 nm with about 60% of pores smaller than the neat TEA cation in the same electrolyte as ref. 130; still, a high capacitance of 92 F g−1 was obtained.135 As illustrated in Fig. 5a, pores with a size of about 0.6 nm could allow distorted desolvated TEA+ to be squeezed inside, which at least indicated that pores smaller than 0.63 nm could be accessible for TEA+ to contribute to EDL capacitance. This is even more true when using BF4−, since its computed size is around 0.44 nm and it is assumed that such ions can access pores less than 0.63 nm, which makes the absence of any capacitance dependence on the pore size highly questionable.129,130,136 Instead, Jackel et al. proposed another model to investigate the capacitance of microporous carbons in organic electrolyte systems.137 DFT kernels were used to extract the porosity of several porous carbons from N2 and CO2 adsorption isotherms. Instead of collecting the total capacitance of the cell, the differential capacitances at both positive and negative electrodes during polarization, which reflect the contribution to EDL capacitance from the anions and cations, were used to understand the correlation between C/S and pore size. Importantly, the surface area accessible to anions and cations was also defined differently, with the cutoff pore size of 0.4 (S>0.4) and 0.6 (S>0.6) nm being selected for BF4− and TEA+, respectively, to take into account the difference in ion size. The pore sizes of d25 and d75 (representing the pore width at 25 and 75% of the total pore volume, respectively) were also added in complement to d50 (the pore width at 50% of the total pore volume) to capture a more reliable picture of the porosity than the mean diameter.137Fig. 5b shows the differential specific capacitance of porous carbons normalized by the accessible DFT SSA vs. pore size in both ACN and PC based electrolytes: a similar increasing trend of surface-normalized capacitance in the sub-nanometer range pores was observed.137
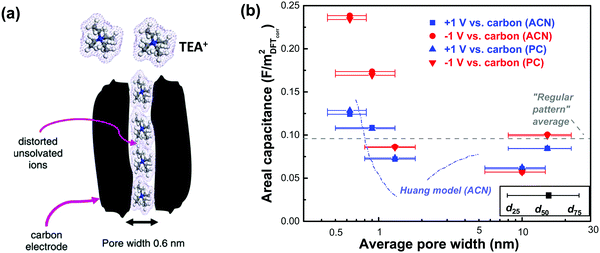 | ||
| Fig. 5 (a) Illustration of the polarization-induced distortion of TEA+ ions in pores with a size of 0.6 nm. Reprinted from ref. 135, with permission from Elsevier (copyright 2009). (b) Plot of differential specific surface-normalized capacitance vs. pore size of various carbons in organic electrolytes of 1 M TEABF4 in ACN and PC. The plot is reproduced from ref. 137 with permission from 2016 American Chemical Society; the grey dashed line representing the regular pattern is from ref. 129, and the blue dashed line representing the Huang model is from ref. 134. | ||
Finally, the capacitance increase in the sub-nanometer pore range was also studied from a theoretical point of view using DFT and molecular dynamics simulations, with various carbon structures and electrolyte combinations, and the details are presented in Section 3. Instead, Section 2.4 is focused on analytical analysis of the charge compensation process in cylindrical shaped pores, which has been proposed to depict the EDL charging in non-planar electrodes to represent the confined pores.
2.4 EDL models with surface curvature effects
The observed increase in specific capacitance in carbon nanopores has caught the interest of theoreticians to help in understanding the EDL formation in confined nanopores via advanced in situ techniques and simulation methods. Classical EDL models based on a 2D planar electrode were insufficient to describe the EDL formation in carbon nanopores since these 2D models do not take into account curvature and porous effects. Nanoporous carbons have pores of various shapes, including endohedral pores (cylindrical, slit, and spherical) and exohedral pores between the carbon nanoparticles (CNTs, OLCs).29 Depending on different pore shapes, endohedral capacitors – when the electrolyte ions enter inside the pores (see Fig. 6a, b, and f) – and exohedral capacitors – ions located on the outer surfaces of carbons (see Fig. 6d and e) – were proposed.29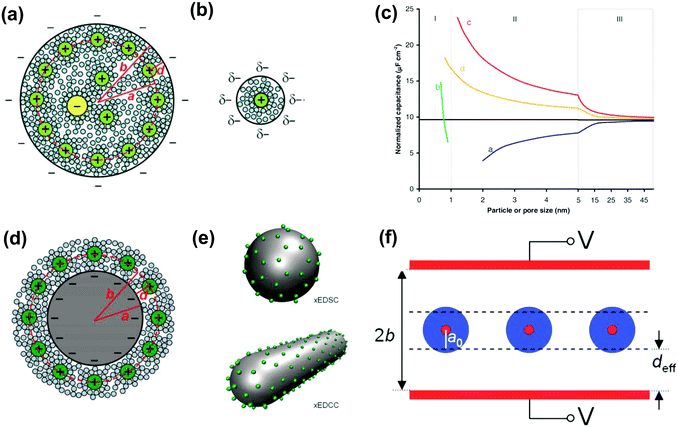 | ||
| Fig. 6 Schematic illustrations (top views) of (a) an electric double-cylinder capacitor based on mesopores and (b) an electric wire-in-cylinder capacitor based on micropores. Reprinted from ref. 134, with permission from Wiley (copyright 2008). (c) Plot of specific surface-normalized capacitance vs. particle/pore size for endohedral capacitors (curves a and b for mesoporous and microporous carbons, respectively) and exohedral capacitors (curves c and d for 0D spheres and 1D tubes, respectively). The black line represents a parallel-plate capacitor. Schematic illustrations of (d) cross-section of an exohedral capacitor, and (e) steric views of 0D spheres (top) and 1D tubes (down) with counterions approaching the outer surface, respectively. Reproduced from ref. 140, Copyright 2010, Materials Research Society. (f) Schematic of a sandwich capacitor. Reproduced from ref. 139, Copyright 2010, American Chemical Society. | ||
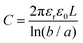 | (9) |
The capacitance normalized by the surface area A is given as
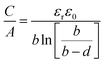 | (10) |
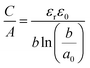 | (11) |
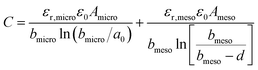 | (12) |
The EDCC/EWCC model was based on two assumptions: (i) the total charges of the carbon wall can be screened by the counterions inside the cylinder pore and (ii) the space charge capacitance of the carbon walls can be neglected owing to the high conductivity of carbon materials.29Eqn (10) and (11) indicate that the surface normalized capacitance depends on both the pore size of nanoporous carbon and electrolyte ion size. The linear C vs. A relationship suggested by the classical 2D model is not expected in the present EDCC/EWCC model, because of the curvature effects. Besides, the change of capacitance with carbon pore size predicted by the EDCC/EWCC model for various porous carbons in both aqueous and organic electrolyte systems (see Fig. 6c) agrees well with the experimental results (see Fig. 5b).134,138
Another sandwich capacitor model was proposed by Feng et al. by assuming the presence of slit-shaped pores.139 Using MD simulation, K+ ion distribution in the slit-shaped micropores was investigated by considering ion hydration and water–water interactions. As presented in Fig. 6f, the sandwich capacitor was formed by one layer of counterions located in the middle of two carbon walls with the same polarity, and the corresponding capacitance is given by
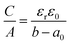 | (13) |
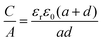 | (14) |
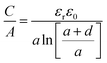 | (15) |
The C/A was calculated based on these two exohedral capacitor models by using a similar parameter as in the previously mentioned EDCC model, and the results are presented in Fig. 6c.140 Interestingly, a similar increasing trend of capacitance was observed along with the decrease in carbon particle size for both exohedral capacitor models; the capacitance of the xEDSC is increased faster than that of the xEDCC. Moreover, the results obtained for the xEDCC were similar to experimental results obtained with CNTs.141 The larger capacitance predicted from the xEDSC model compared to the experimental results obtained with OLCs73 was explained by particle agglomeration during electrode preparation.29
Reasonable prediction can then be made using these simple xEDCC and xEDSC models. However, they consider the electrode charge to be entirely screened by a single layer of counterions on the carbon surface so that the electrolyte contribution to the EDL beyond the counterion single layer is negligible. This situation is unlikely to occur in solvent-free ionic liquid electrolytes where an overscreening effect arises due to the strong ion–ion correlations in such concentrated electrolytes36 leading to the formation of extra layers of counterions/co-ions, and improved models were proposed.84
Finally, although these models correctly depict the capacitance trend in carbon nanopores, the cylindrical and slit-shaped pores considered in these models are too simplistic to depict the electrode/electrolyte interface in amorphous, nanoporous carbons. To push further our understanding of the EDL formation in carbon nanopores, the combination of in situ, advanced experimental techniques together with modeling has been successfully proposed; this is described in the next section.
3. Understanding the charge storage mechanisms in nanoporous carbons
In this section, we broadly review the advanced in situ techniques and computational tools used to characterize the interfaces between carbon material and electrolyte, specially dedicated to the topic of ion confinement in nanoporous carbons during the last ten years. The in situ techniques include in situ nuclear magnetic resonance (NMR) spectroscopy, in situ small-angle X-ray scattering (SAXS), in situ infrared (IR) spectroscopy, gravimetric and dissipative electrochemical quartz crystal microbalance (EQCM) and other in situ and advanced ex situ techniques. Besides the experimental methods, simulation is an alternative and complementary approach. Here, we will simply introduce the use of some classic simulation methods, such as ab initio, Monte Carlo and Molecular Dynamics simulations which, in combination with experimental techniques, have pushed further the fundamental understanding of the carbon/electrolyte interface and the charging mechanisms of electrochemical double layer capacitors.3.1 Electrochemical quartz crystal microbalance (EQCM)
EQCM is a powerful technique for monitoring the electrode/electrolyte interface and was developed by Sauerbrey in the 1950s.142 EQCM is composed of a thin piezoelectric quartz crystal sandwiched between two metal electrodes used to apply an alternating electric field across the crystal, causing vibrational motion of the crystal at its resonance frequency. Under gravimetric mode (linear behavior), the shift of the quartz resonance frequency (Δf) can be converted into mass change (Δm) on the quartz crystal and electrodes by applying Sauerbrey's equation:| Δm = −CfΔf | (16) |
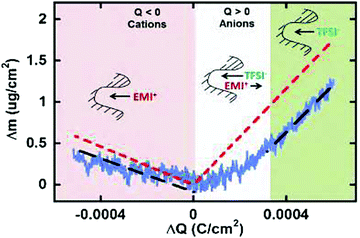 | ||
| Fig. 7 Scheme of neat ionic liquid EMITFSI transport in CDC-1 nm pores during different charging states based on EQCM results. The blue solid lines represent the measured mass change (EQCM), and the red dashed lines represent the theoretical mass change of neat ions calculated from Faraday's law. The black dashed line shows the linear fitting of the measured mass change. Reproduced from ref. 150 with permission from American Chemical Society (copyright 2008). | ||
Since the EQCM technique appeared to be a powerful tool to characterize the electrode/electrolyte interface during operation, several improvements have been made during the past few years. The disadvantage of this technique is the drop of the quartz quality factor – because viscoelasticity – because of active material deposit, an important step is expected through the improvement of the deposition process. With this aim, recently a work has been published dealing with the development of a deposition process of different active materials onto a quartz crystal resonator. Instead of typical drop coating or spray coating, a new method by using vacuum filtration has been developed to prepare homogeneous coatings on the Au coated quartz.155 The roughness and the homogeneity of the deposit being greatly improved, more accurate measurements are obtained with a lot less frequency noise.
Besides gravimetric EQCM, other advanced EQCM modes have been developed over the years. One of them is called EQCM with dissipation monitoring (EQCM-D). EQCM-D takes into account the mechanical properties of the film present on the quartz surface.156–160 Basically, the mechanical properties of the deposited film on the quartz can lead to a change in the resonance frequency not in relation to a weight change of the film; as a result, Sauerbrey's equation does not apply anymore in such a situation. The dissipation factor D is the reciprocal of the quality factor and is defined by the following equation:161–163
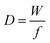 | (17) |
Despite the fact additional mechanical information can be extracted by monitoring the dissipation, EQCM used in gravimetric and dissipation modes has still some limitations. For instance, since an electrolyte is a mixture, it is difficult to break down clearly the respective contribution of each single species: individual ions, solvent molecules. For this aspect, ac-electrogravimetry (ac-EQCM) has been shown to be a great tool to help deconvolute the role of each involved species in the charge exchange process; interestingly such a technique gives access to rate constants.172–176 Escobar-Teran et al. used ac-EQCM to study the electrochemical behavior of carbon nanotubes in complex aqueous electrolytes.173 In this work, the authors first established charge/potential and electrogravimetric transfer functions considering all ionic species involved. Then, the transfer functions were used to fit the experimental results by playing with two kinetic parameters: Ki and Gi, respectively, accounting for ion and solvent molecule transfer at the interface and conductance. Fig. 8a and b present the experimental transfer functions 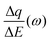 and
and 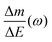 fitted by theoretical equations. With the change of frequency, as shown in Fig. 8b, the different ionic species can be distinguished. From Fig. 8c, the result shows that the hydrated Na+ ion mass transfer is surprisingly faster than that of protons, i.e. Ki (Na+·H2O) > Ki (H+). Moreover, the relative concentration change of individual species can be estimated by ac-EQCM which allows distinguishing between the contributions of the different ionic species to charge storage in nanoporous carbon (Fig. 8d). Although this technique is complex to set up and use, the ionic fluxes in carbon nanopores during the charge/discharge process can be analyzed in detail.
fitted by theoretical equations. With the change of frequency, as shown in Fig. 8b, the different ionic species can be distinguished. From Fig. 8c, the result shows that the hydrated Na+ ion mass transfer is surprisingly faster than that of protons, i.e. Ki (Na+·H2O) > Ki (H+). Moreover, the relative concentration change of individual species can be estimated by ac-EQCM which allows distinguishing between the contributions of the different ionic species to charge storage in nanoporous carbon (Fig. 8d). Although this technique is complex to set up and use, the ionic fluxes in carbon nanopores during the charge/discharge process can be analyzed in detail.
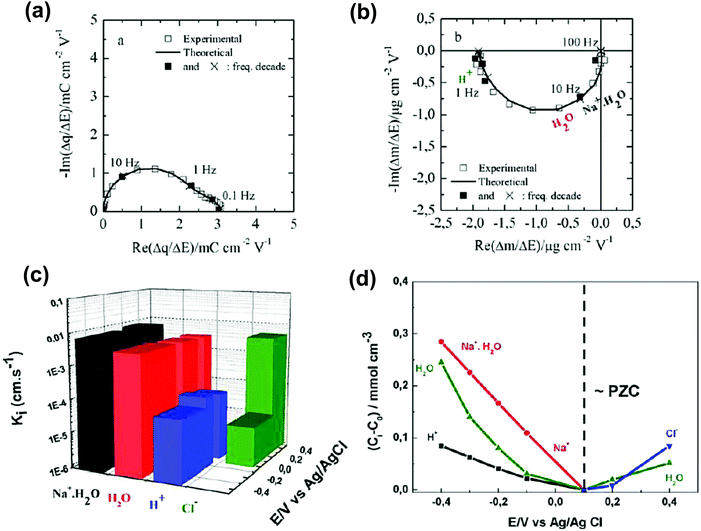 | ||
Fig. 8 (a) and (b) The transfer functions 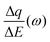 and and 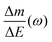 at −0.4 V vs. Ag/AgCl, respectively. (c) The kinetic parameters Ki (cm s−1) for each ion at different applied potentials. (d) Relative concentration variation of each ion in SWCNT based thin films as a function of potential in 0.5 M NaCl at pH = 7. Reproduced from ref. 173 with permission from Elsevier (copyright 2016). at −0.4 V vs. Ag/AgCl, respectively. (c) The kinetic parameters Ki (cm s−1) for each ion at different applied potentials. (d) Relative concentration variation of each ion in SWCNT based thin films as a function of potential in 0.5 M NaCl at pH = 7. Reproduced from ref. 173 with permission from Elsevier (copyright 2016). | ||
3.2 Nuclear magnetic resonance spectroscopy (NMR)
To observe and quantify the ion environments in porous carbons, nuclear magnetic resonance spectroscopy (NMR) is one of the promising techniques to work with.177–180 The working principle of NMR dedicated to the ion confinement in nanopores is based on the shift of resonance of the target electrolyte ions to lower frequency because of the delocalized electron distribution present at the carbon surface that shields the signal. The chemical shift difference between the resonances of ions confined inside nanopores and the neat electrolyte is defined as Δδ. With the help of density functional theory (DFT) calculations, Δδ is found to be related to the intrinsic electronic structures of carbon, carbon structure and pore size distribution.103,181,182 Studies show that this so-called nucleus-independent chemical shift (NICS) allows for distinguishing the ion confined within carbon pores, as well as the ion population.181–185In 2006, Lee et al. used ex situ magic angle spinning (MAS) NMR to study ion adsorption in porous carbon in organic electrolytes.186 Solid state 11B NMR spectra could distinguish between the BF4− anions located outside and inside the pores at the open-circuit voltage (OCP), charged, and discharged stages. The same technique was used to obtain the relative concentrations of cations, anions, and solvents inside or outside the carbon porosity. Moreover, the exchange of ions from the adsorption site to the free state of the electrolyte can be characterized using two-dimensional 12C and 11B NMR exchange spectra.187 To avoid cell dismantling needed for ex situ NMR analysis, in situ NMR has been developed by Grey's group which allows tracking the change of the local environment in porous carbon in real-time as well as the charge storage mechanisms operando.180,188,189 A detailed work aiming at understanding the electric double layer structure in microporous carbon YP50F in tetraethylphosphonium tetrafluoroborate (PEt4BF4) with acetonitrile has been published by combining in situ NMR and EQCM.185In situ NMR results showed the evolution of the absolute ion population of cations and anions confined in carbon nanopores at various states of charge. Two charging mechanisms were identified, depending on the electrode polarity. During negative polarization, the charge is stored by counter-ion (cation) adsorption, while ion exchange was the charge storage mechanism during positive polarization. On the other hand, similar results were obtained by EQCM which suggests a concomitant solvent reorganization in the pores, with no net solvent flux in and out of the porous network. This combination provided a direct insight into the molecular level of the charging process in carbon micropores.
Another microporous carbon material TiC-CDC has also been studied by ex situ NMR, in 1 M NEt4–BF4 in an acetonitrile organic electrolyte. The NMR results show in-pore and ex-pore features of ions in NMR spectra.182Fig. 9a and b show the experimental results with the signals corresponding to in-pore NEt4 and BF4 ions highlighted in red. Furthermore, the structural characterization of TiC-CDC nanoporous carbons was realized by combining ex situ NMR and Raman techniques.103
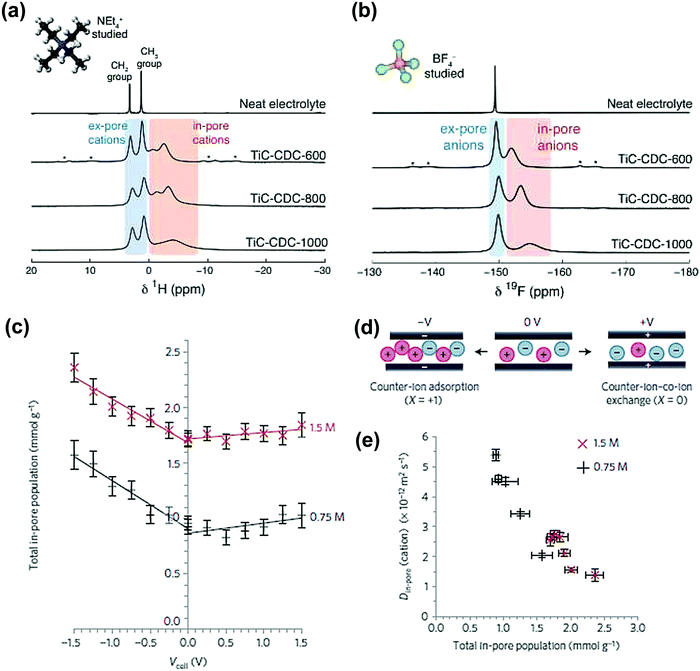 | ||
| Fig. 9 (a) 1H and (b) 19F MAS (5 kHz) NMR spectra of cations and anions filled pores TiC-CDC soaked with NEt4–BF4 in acetonitrile. The figure is reproduced from ref. 182 with permission from Elsevier (copyright 2014). (c) Calculated total in-pore ion population of the YP-50F electrode in 1.5 M PEt4BF4 in ACN at different potentials. (d) Scheme of the charge storage mechanism at positive, 0 V and negative charge. At 0 V, there is an equal number of cations and anions in the pores of the carbon electrodes. (e) Correlation between Din-pore (cations) and total in-pore ion population. The figure is reproduced from ref. 190 with permission from Springer Nature (copyright 2017). | ||
Lately, in situ pulsed field gradient NMR has been introduced to explore the ionic transport in porous carbon electrodes.190 As can be seen from Fig. 9c, the total in-pore ion population increased from 0 V to negative potential while the in-pore diffusion coefficients (Din-pore) decreased significantly for both cations and anions (Fig. 9d). In addition, the difference of electrolyte concentrations indicates that with less ions confined in nanopores, Din-pore will increase because of the reduced ion–ion interactions. This study emphasizes the strong correlation existing between the charging mechanisms and ion dynamics for microporous carbon electrodes.
3.3 Small angle scattering (SAS) techniques
SAS techniques are well-known to be efficient techniques for characterizing three-dimensional structures at the micro- and mesoscopic scale,191–196 using X-rays or thermal neutrons. Small angle X-ray scattering (SAXS) has been widely used for porosity characterization for carbon materials.197–199 Iiyama et al. firstly operated advanced in situ SAXS to study the formation of cluster-like water molecules adsorbed in activated carbon fiber micropores.200 Further on, SAXS also demonstrated its ability to study the adsorption of gas molecules in nanoporous carbon.201Since then, lots of studies based on in situ SAXS have revealed interesting facts during polarization of the nanoporous carbon electrode. For instance, some inaccessible micropores at OCP can be filled with the electrolyte under polarization, when the carbon electrode overpotential was large enough.197,202 This mechanism was proposed since the electron density contrast decreased greatly and was barely reversible. Besides, ion confinement in carbon micropores has also been studied with SAXS.203 By combining in situ SAXS and Monte Carlo simulation the degree of confinement (DoC) of ions in micropores has been reported for an aqueous-based electrolyte.128Fig. 10a shows an illustration of an example of a different DoC. The calculated DoC is based on Monte Carlo simulated in situ SAXS data. For carbon with different pore sizes, the ion number and shape of the histogram at different DoC vary (see Fig. 10b). We can observe that at the positive or negative charge, more charge-induced ions were confined in smaller pores (with higher DoC). The influence of a confined environment on in-pore ion concentration was pointed out. From Fig. 10c, at higher DoC sites, the surface charge density is higher (red). Thus, comparing the dashed circles in Fig. 10c for AC1 and CDC samples, the counterions are more localized at higher DoC and higher charge density sites (darker red) for 0.65 nm pore size CDC. If more counterions moved to higher DoC sites during charging, the repulsion of counterions can be minimized reducing the energy cost. With DoC, the degree of desolvation of ions (DoDS) can also be obtained (from the first solvation shell). In this article, they summarized that pore size is not the only factor impacting the capacitance for carbon-based supercapacitors, and that DoC, DoDS and the size dispersity of the carbon electrode are required to be considered thoroughly.
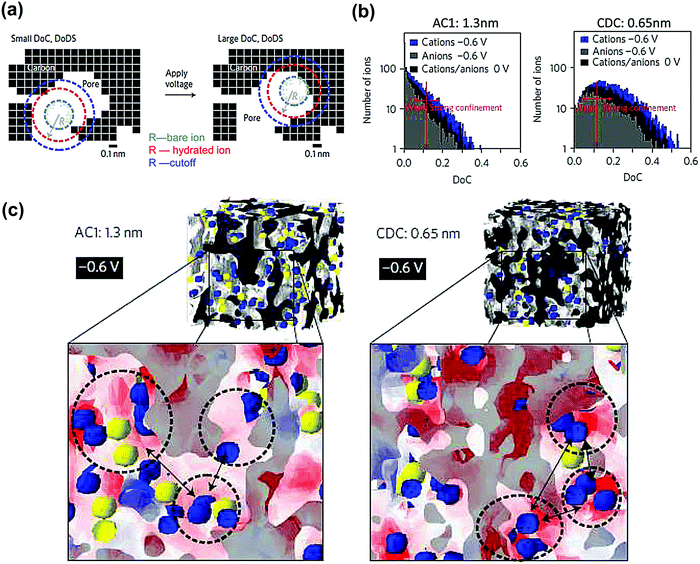 | ||
| Fig. 10 (a) A 2-D cross-section drawing demonstrating the concept of degree of confinement (DoC) and degree of desolvation (DoDS) in 3-D micropores. (b) Histograms of ion number corresponding to selected DoC at different charge state for AC1 and CDC samples in 1 M CsCl. (c) A 3-D view of the distribution of cations (blue) and anions (yellow) at −0.6 V for AC1 and CDC samples. The red and white areas indicate high negative surface charge density and zero electric fields, respectively. The figure is reproduced from ref. 128 with permission from Springer Nature (copyright 2017). | ||
Ionic liquids have been found to have a higher density of cations and anions confined at the center of the pore. With the help of molecular dynamics simulations, the authors concluded that the interaction between ionic liquid and carbon walls is stronger than the bonding of the ion pairs, resulting in a denser and less coordinated ions packed in the micropores. With the same methodology as the previous study, Futamura et al. revealed the structure of ionic liquids confined in TiC-CDC nanopores with the confirmation of a superionic state for EMIFSI and EMIBF4 ionic liquids confined in small 0.7 nm nanopores.204 The coulombic ordering was preserved in larger 1 nm nanopores under ion confinement. The partial breaking of the coulombic ordering – superionic state – was observed when monolayer confinement occurred due to the existence of image charges in the carbon walls that partially screen the repulsive electrostatic interaction between co-ions.
SAXS also provides information about the carbon structure and the electrolyte organization. Prehal et al. studied the structural and concentration change of ions confined in micropores during polarization, by acquiring the electron density profiles in various aqueous electrolytes, such as NaCl, KCl and CsCl.205 They first evidenced three regions from SAXS curves, shown in Fig. 11a. At the small value of scattering vector modulus Q (<0.7 nm−1), a part of the decay of the SAXS intensity is due to large pores between the activated particles. The second region between 0.7 and 5 nm−1 indicates the scattering from disordered micropores, which is described by the Debye–Anderson–Burmberger (DAB) model.206 At a larger Q value (>5 nm−1), the molecular structural factors of carbon and electrolyte govern. The intensity of the SAXS signal represents micropores filled with the electrolyte (blue line) is lower than that corresponding to empty pores (black line) until a large Q value is reached (WAXS signal). This result agrees with the literature: the SAXS contrast decreases once the micropores are filled with the electrolyte.207 On the other hand, the increase of electron density contrast at higher Q values for the blue line is the consequence of the addition of the electrolyte molecular structure factor to the carbon structure factor. Since the value of the electrolyte structure factor depends on the type of ions and their concentration,208 the intensities of different composition of ions in the three aqueous electrolytes are expected to vary at a larger Q value as shown in Fig. 11b. All aqueous electrolytes show a maximum intensity at positive and negative potentials (Fig. 11c–e). With the radius of gyration (Rg) obtained from Guinier analysis of the SAXS data and the average electrolyte electron density (ρel) measured by X-ray transmission, a model was proposed to fit the SAXS intensity changes versus potential which corresponds to the change of the electrolyte local environment near the micropore wall. At low charge density, ion swapping dominates the charge storage mechanism, while at higher charge density, not only counterion adsorption was involved in the charging process, but also local in-pore ion rearrangement took part. Counterions stay closer to the pore wall, resulting in a denser layer of ions and solvents.
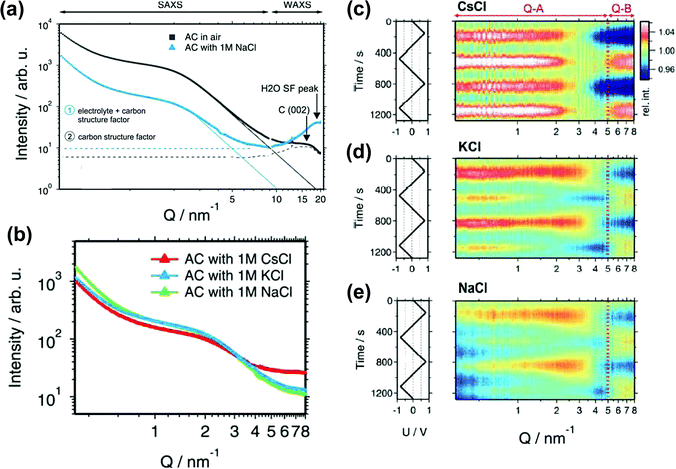 | ||
| Fig. 11 (a) SAXS and WAXS intensity for the activated carbon in air (black) and filled with a 1 M NaCl electrolyte (blue). (b) SAXS intensity for the AC filled with three different electrolytes: 1 M CsCl, KCl and NaCl. (c)–(e) In situ SAXS results for various electrolytes. The left rows show the applied voltage signal as a function of time. The right rows are the scattering intensity normalized to the intensity at 0 V as a function of time and the scattering vector length Q. The figure is reproduced from ref. 205 with permission from Royal Society of Chemistry (copyright 2015). | ||
The SAXS technique has also been useful to study the influence of the porous carbon texture and structure on the capacitive performance, especially the volume fraction of inaccessible pores, the shape of pores and the pore organization, which are key parameters controlling the ion confinement in nanopores.209 In addition, Koczwara et al. proposed an advanced SAXS technique called in situ anomalous small angle X-ray scattering (ASAXS), for characterizing both the structural change of pores and the concentration change of the in-pore ions at the same time.210 However, more equipment and theory are required to develop this technique for further electrolyte systems.
Small angle neutron scattering (SANS) involves scattering nuclei which may result in different scattering signals, especially the presence of micropores in carbon materials.211 Compared with other scattering techniques, SANS is easier to use “contrast-matching” to detect the closed porosity inaccessible to electrolytes.212,213 Some works have shown its ability to characterize microporous carbon materials.116,192,196 The variation of contrast was also observed when the micropores of carbon nanotubes were filled with a liquid.214 Yushin's group pioneered in situ SANS to reveal the electroadsorption of organic electrolyte ions in carbon pores of different sizes in aqueous and organic systems.215,216 They observed electrowetting – enhanced ion sorption in subnanometer pores under an applied potential – counterbalancing the high interfacial energy of the carbon/electrolyte interface in small pores.
In summary, the development of experimental in situ SAS techniques has been a key for pushing further our basic understanding of ion confinement in carbon nanopores and charging mechanisms of EDLCs.
3.4 Other ex situ and in situ characterization techniques
X-ray diffraction (XRD) is commonly used to describe the structural features of carbon materials.217–221 Kaneko's group firstly demonstrated the use of XRD to study C2H5OH gas sorption in slit-shaped micropores of activated carbon.222 Later, they used the same methodology to analyze organic electrolytes (TEABF4 in propylene carbonate) confined in the micropores of CDC and activated carbon fiber (ACF).223Fig. 12a shows the synchrotron XRD patterns of porous carbons and porous carbons impregnated with the electrolyte. Fig. 12b represents the corrected XRD patterns, obtained by removing the contribution from the carbon in Fig. 12a. By comparing the bulk and the confined electrolyte signals and with the help of Monte Carlo simulations, a visual view of the ions confined in micropores was obtained. The simulated XRD patterns are comparable to the experimental results, as shown in Fig. 12c. This study shows the interest of synchrotron XRD to study the electrolyte confinement in microporous carbons.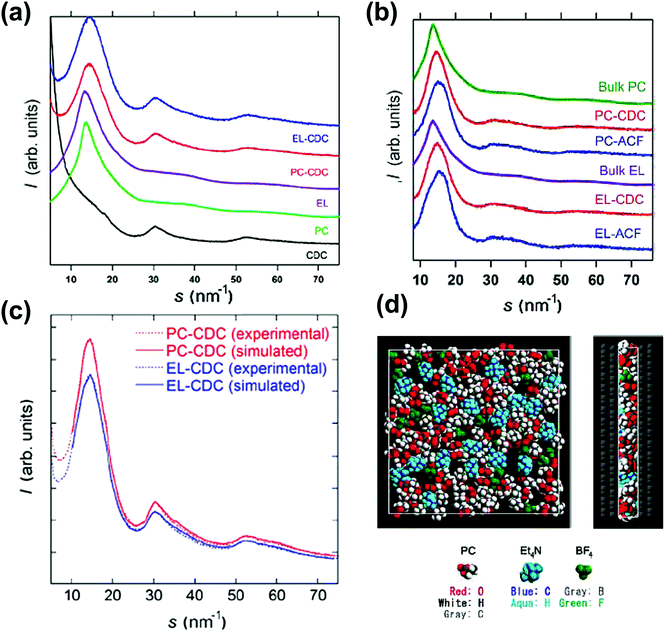 | ||
| Fig. 12 (a) XRD patterns of CDCs, PC, EL, PC-impregnated carbon (PC-carbon), and TEABF4–PC-impregnated carbon (EL-carbon). (b) Corrected XRD patterns of PC and TEABF4–PC confined in the pores of CDC and ACF and the XRD pattern of bulk PC at 303 K. The same for EL carbons. (c) Experimental and RMC-simulated XRD patterns. (d) Top and side views of the snapshot of TEABF4–PC confined in the pores of CDC from RMC simulation. The figure is reproduced from ref. 223 with permission from American Chemical Society (copyright 2008). | ||
In situ infrared spectroelectrochemistry, also known as attenuated total reflectance-surface-enhanced infrared adsorption spectroscopy (ATR-SEIRAS), has also delivered some key insights into the ion dynamics in porous carbon materials. This technique was first introduced by Richey et al. to study the interface between ionic liquid EMITFSI and pseudocapacitive RuO2 electrode, for probing the ion dynamics during the charging process.224 The technique is based on the infrared adsorption of the molecules at the solid/liquid interface, which is called surface enhanced infrared adsorption (SEIRA).225 This results in a local increase of the electromagnetic field, so the chemical changes at the surface of the material can be detected.226
Carbon materials such as carbon onions, CDCs and nanoporous carbon nanofibers were studied in ionic liquid systems by combining electrochemical measurement and in situ infrared spectroelectrochemistry.224,227,228 This technique allows for tracking the ion concentration change in the porous network. Infrared spectra were collected at different concentrations of cations and anions (Fig. 13a). This allows the calibration of the concentration of cations and anions, which can be plotted with the absorbance of infrared (Fig. 13b). As a result, the concentration of cations and anions can then be extracted from the infrared spectra during polarization. For example, from Fig. 13c, while the carbon nanotubes were charged from −0.5 to 1.5 V, the number of anions increases drastically compared with that of cations. As a result, it proposes that a larger concentration of anions is located in the nanopores of the nanofibers at higher voltage, although both ions are still present.
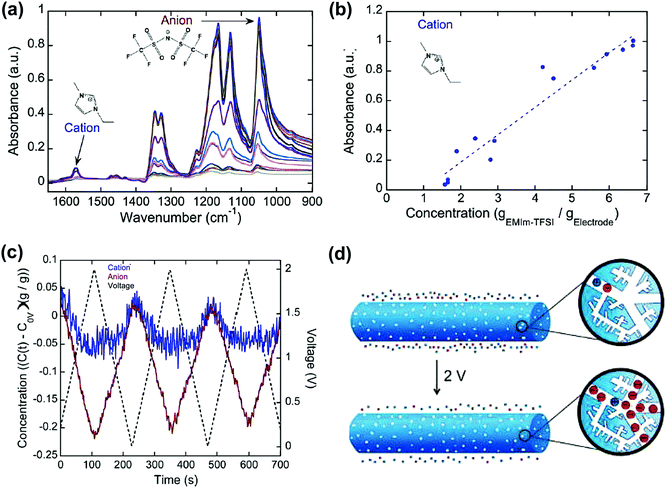 | ||
| Fig. 13 (a) Infrared spectra of the NCNF electrodes with varying concentrations of the EMITFSI electrolyte (1.6 to 8.8 gEMIm–TFSI gelectrode−1). (b) Concentration–absorbance calibrations of the cation. The dotted lines represent linear regressions. (c) Operando infrared spectroelectrochemical results show the initialized time-resolved concentration (gEMI–TFSI gelectrode−1) of EMI+ cations and TFSI− anions in NCNFs from 0 to 2 V at 20 mV s−1. (d) Illustration showing that a larger concentration of TFSI− anions than EMI+ cations is in the nanopores of the positively charged NCNF nanopores. The figure is reproduced from ref. 228 with permission from American Chemical Society (copyright 2008). | ||
Another in situ technique that was recently used to characterize ion confinement in nanopores is in situ dilatometry. Hantel et al. pioneered the technique to study the pore expansion/extraction and ion sieving effect during cycling of different carbon materials.229–231 They observed that the strain change at positive and negative polarization was asymmetric.229,232 A study combining in situ SAXS and dilatometry showed that the strain increased with the increasing amount of micropores. This result is related to the combination of total ion concentration (cations and anions) change during charging with a higher amount of micropores and the electron/hole doping causing the elongation of C–C bonding.233 A further study showed that in the ionic liquid system, with a different size of anions, the organization of ions confined in nanopores varies.234 This can be observed by dilatometry because the strain of pores is sensitive to ion adsorption/desorption, orientation, and transportation. Also, this technique evidenced the importance of the ion valence state during electrosorption in carbon nanopores from aqueous electrolytes.235 Rochefort's group used in situ dilatometry combined with solid state NMR to study ion fluxes in porous materials in biredox electrolytes.236 In these experiments, the dilatometry measurements helped in resolving the charge storage mechanism in carbon pores, in the presence of redox moieties in the electrolyte. They confirmed the ion exchange mechanism at low potential and counterion adsorption at high potentials at the positive electrode, while only counterion adsorption occurred at the negative electrode.
During the recent past year, new in situ techniques were introduced to the community. In situ electrochemical atomic force microscopy (AFM) has shown the transition of layering of ionic liquids and the orientation of cations and anions from zero volt to the applied voltage on graphite materials.237 Several studies carried out by in situ scanning tunneling microscopy (STM) demonstrated the interaction and structural change of ionic liquids at the surface of a polarized metal electrode.238–240 These techniques are useful for investigating the electrode/electrolyte interface. To understand the EDL changes during polarization, in situ vibrational spectroscopy measurements were made in an organic electrolyte system.241 Combined with MD simulation, the solvation shell of charged ions and the compositional change of the EDL were observed. This technique can serve to establish modern EDL models for ionic liquid and concentrated electrolyte systems. To study the ion dynamics, in complement to EQCM and classic in situ NMR techniques, in situ nuclear magnetic resonance imaging (MRI) has been proposed, pioneered by Grey's group for energy storage study.242 A 1-dimensional ion concentration profile was recorded during the charge/discharge of a supercapacitor cell.243 This approach gives a visual and realistic view of the interactions of ions and carbon electrodes inside the electrode and in the cell, which can be also useful for industrial purposes.
3.5 Modeling and simulation
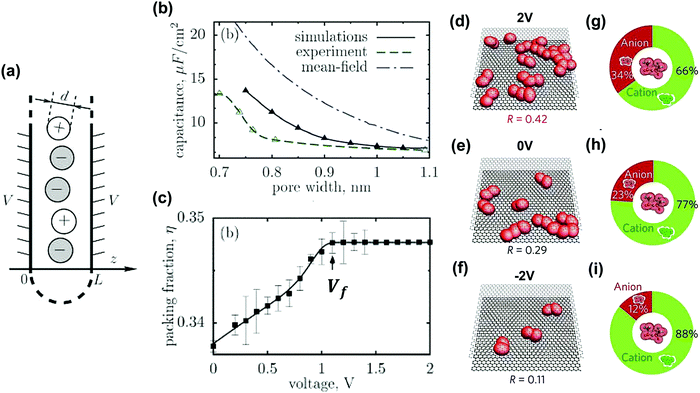
A lot of work has been dedicated to modeling the interface of electrode materials and electrolytes. We will highlight in this section some works focusing on ion confinement in nanoporous carbon-based materials.After the experimental discovery of the capacitance increase in carbon nanopores smaller than the solvated ion size, various nanoporous carbon structures and electrolytes have been used for modeling not only to improve the theoretical EDL models but also to resolve the underlying theory and predict optimized carbon structures.36,82,83,138,139,244–249 For example, in aqueous electrolytes, the desolvation process of ions in nanopores has proven to be crucial to explain their transport properties using molecular dynamics (MD).246,250,251 However, the origin for such a phenomenon was not yet clear until the group of Kornyshev brought up the “superionic state” of ions confined in nanopores.252 A schematic overview is shown in Fig. 14a. The superionic state, recently confirmed by experimental SAXS measurements as mentioned before,204 is attributed to two effects. Firstly, the metallic properties of carbon materials weaken the electrostatic interactions of ions, resulting in breaking the Coulombic ordering of ions in the nanopores, by the creation of image charges. Second, the negative free energy of ions entering the pores from the bulk due to the desolvation of ions favors the increase of ion density inside the pores. They applied mean field theory on a slit-shaped pore model and reproduced the capacitance increase versus pore width. The comparison results are displayed in Fig. 14b. In addition, the transition from ion-rich- to ion-deficient nanopores was observed when reaching a threshold voltage Vf as shown in Fig. 14c.252 Further on, they modified and investigated deeply the same model using Monte Carlo simulation for ionic liquid systems and ended up with simulation results closer to experiments.14,253 Experiments had proven the superionic state of ions in nanopores.204Fig. 14d–f shows different anion–anion pair ratios (R) at different applied potentials. In the first coordination shell of the TFSI− anion, there was also an existence of anions as calculated from Fig. 14g–i. For slit-shaped pores like carbon models, a fundamental work was proposed by Palmer et al. using quenched MD simulation.254 They built up a realistic carbon model in which the carbon structure changes with chlorination temperature such as observed for TiC-CDC materials. This establishment pushed further the modeling closer to reality.
 | ||
| Fig. 14 (a) The cross-section of a single, laterally infinite, slit-like narrow pore as a part of a porous electrode (L: pore width; V: applied voltage; d: diameter of ions). (b) Differential capacitance per surface area versus pore width. Evidence of capacitance increase in carbon nanopores by using different approaches: (c) the packing ratio at different voltage. At Vf, the total ion density reaches its maximum. (d–f) Visual views of co-ion pairs of anions of EMITFSI (R is the anion–anion pair ratio) and (g–i) the population in the first coordination shell around a TFSI anion in the 0.7 nm pores under 2, 0 and −2 V. Reproduced from ref. 204, 252 and 253 with permission from IOP Publishing (copyright 2010), Royal Society of Chemistry (copyright 2011), and Springer Nature (copyright 2017), respectively. | ||
Differently from the slit-shaped pore structure of porous carbon, another model based on cylindrical micropores was one of the first models proposed to mimic the ion confinement effect in carbon nanopores.138 Huang et al. simulated a series of organic electrolytes and their results aligned with the experimental results showing that the optimal capacitance was obtained when the ion size is close to the nanopore size. For both slit-shaped pore and cylindrical pore models, overscreening and crowding are not considered to happen in the ionic liquid system, such as can be observed when using a classic double layer model at planar electrodes.38,138
In a cylindrical model, the curvature of the electrode is an important difference compared to the slip-pore model. A few modeling works have mentioned the effect of curvature over the years.84,140,255–257 Merlet et al. used MD simulation to characterize different sites with various morphology of CDC materials (edge, plane, hollow and pocket) and calculate the degree of confinement of the adsorbed ions.256 The results showed that at the edge, plane, hollow and pocket sites (with the increased degree of confinement) of CDC samples, the degree of desolvation of anions varies compared to the bulk. Electrowetting of the smallest pores at high potential was also observed. This study not only raises the idea of a better way to confine ions in nanopores but also establishes the importance of how the carbon structure influences the ion confined environment, for further experimental and simulation works. To characterize precisely the porous structure of carbon materials, the DFT method is frequently used to estimate the pore size distribution and accessible surface area from gas sorption experiments.111,258–260 For carbon materials, which are relatively rough and contain more functional groups on the surface, QSDFT is found to be preferable to characterize microporous and mesoporous carbons.261–263 Classic DFT and molecular DFT (MDFT) can be used to calculate the free energy of solvent which is very useful information while discussing the desolvation of ions, especially for aqueous and organic electrolyte systems, confined in nanopores.264–273 Following on, we will introduce in the next section a few simulation methods which are frequently used for modeling the ion confinement in nanopores, starting with Monte Carle simulations.
The working principle of MC is based on the statistic of the ion movements and sampling the probability of an organization based on anion and cation number, ion-pair number and potential energy of the system at the molecular level.274–277 The potential energy considers the interaction between ions, ion and electrode, and electrodes. The movements of ions in this simulation include ion exchange, migration, insertion in electrodes, and also charge balance and transfer between anode and cathode. MC simulations run for million steps to reach the equilibrium of the system. Different electrode setups (planar to porous) and electrolyte systems have been studied by MC simulation.204,252,253,275,278–281 As mentioned before, the superionic state of ionic liquids has been studied by this method, which was also used to evidence the oscillation of capacitance in the ionic liquid system.282 Later on, Kornyshev's group used MC to discuss the effect of ionophilicity and ionophobicity of slit-like nanopores on the improvement of the energy density for supercapacitors.281 Unlike DFT, the MC method can simulate three-dimensional porous carbon, leading to a better view of the electrode/electrolyte interface.283–286
Another method also achieved at the molecular level is MD simulation. For EDLC related topics, MD simulation models the system by simulating the ion movements according to Newton's second law.287,288 There are two different ways to build up polarized electrodes. In the earlier time, most of the work based on MD simulations applied fixed charges to each carbon atom.83,84,245,246,250,251,289 However, in 2012, Salanne's group pointed out that the electrolyte responses to constant charge and constant potential applied to an electrode are distinct.290 Applying a constant potential, especially for porous carbon materials, results in a more realistic way to model the system by limiting energy dissipation (temperature increase is limited) and does not stray from equilibrium.290–292 However, the cost remains an issue for further applications. After discovering the anomalous increase of capacitance with sub-nanometer-sized pores, MD simulation was used to provide an insight at the molecular level into the electrolyte organization in carbon pores. The ionic structure of an ionic liquid confined in disordered microporous carbon was shown by MD simulation in 2012.293 Afterwards, the arrangement of ions in carbon micropores and mesopores was studied with various combinations of ionic liquids.43,203,294–298 The greatest advantage of MD simulation is the possibility of modeling the charging dynamics in nanopores. As shown in the previous section, there are mainly three charging mechanisms: counter-ion adsorption, co-ion desorption, and ion exchange. Over the years, MD simulation has proven that ion dynamics and transport properties of ions play an important role in improving the performance of supercapacitors. The origin of the increase of capacitance in nanopores and further improvement (fast ion transport) is not only due to the structure and texture of the carbon but also due to the combination of ion exchange and ion adsorption mechanisms during charging.293,299,300 The diffusion coefficients of the in-pore ions have also been related to the power performance of charging nanoporous carbon.301–305 Interestingly, Kornyshev et al. suggested an accelerating charging dynamics of ionic liquids in subnanometer ionophobic pores,301 and a recent simulation study observed a similar charging behavior.304 This enhanced charging dynamics in pores smaller than 1 nm was innovative compared to the conventional views that larger pores provide faster charging, and offered an exciting opportunity for designing ionophobic porous materials with both high energy and high power performance.
Classical coarse-grained simulation methods at the molecular level (MC and MD) share the disadvantage of considering ions as spheres, most of the time, for the sake of simplicity and cost. For a deeper investigation of the interaction between ions and carbons at the electrode/electrolyte interface, especially during polarization, more realistic atomistic approaches are required, such as ab initio simulations, which can capture molecular geometry and polarization. Ab initio simulation takes into account not only all the atoms or ions or molecules but also the electronic structure of carbon materials. During polarization, the screening potential and structure of the EDL are affected by the change of the electronic structure of the carbon electrode and the electrostatic interactions between ions. Classic DFT and other advanced DFT methods are mostly used for ab initio simulation. As mentioned above, DFT is useful to probe the porous carbon structure and texture. It also explains the origin of the capacitance increase in nanopores in terms of the positive curvature of carbon nanopores.84,140 Apart from the morphology of porous carbon, during the last decade, DFT calculations were utilized to study the EDL structure and electrode/electrolyte interface and detailed reviews can be found in more specialized papers.277,283
Interestingly, a new mesoscopic model called lattice model has been recently used to predict the structural, dynamical and capacitive properties of electrochemical double layer capacitors.300 A key advantage is that it is approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times faster than common molecular simulations. The model combines input from molecular and experimental results and has been used to study the effects of solvation and pore size on the quantity of adsorbed ions and capacitive properties in neat and solvated ionic liquid electrolytes. This approach has predicted the quantity of adsorbed ions, capacitances and diffusion coefficients in an efficient manner. Such type of model should rapidly develop in the near future.
000 times faster than common molecular simulations. The model combines input from molecular and experimental results and has been used to study the effects of solvation and pore size on the quantity of adsorbed ions and capacitive properties in neat and solvated ionic liquid electrolytes. This approach has predicted the quantity of adsorbed ions, capacitances and diffusion coefficients in an efficient manner. Such type of model should rapidly develop in the near future.
Finally, an alternative way to predict the capacitance of carbon-based electrodes via artificial neural network and machine learning methods was proposed very recently.306,307 By using the published data and adjusting several variables (such as SSA, PSD, voltage window, etc.), the machine learning approach can provide an acceptable prediction that is likely to benefit researchers in the selection of carbon materials for EDLC systems.
In summary, in academic research, experiments and simulations complement each other. Various advanced in situ techniques for experimental use and simulation methods at different time scales have been reviewed in this section. Owing to the advanced in situ techniques and simulations, the exploration of the insights into charge storage in porous carbon materials has stepped up over the years. We believe that the development of the present or new techniques will push further our basic understanding of ion dynamics and adsorption in porous carbon electrodes as well as the electrolyte structure in the porous networks. These results will be the key to boost the performance of the EDL cells or even create a new generation of supercapacitors with higher energy and power density.
4. Advanced electrolytes
The electrolyte is one of the most critical factors that determine the performance of EDLCs. Eqn (3) and (4) indicate the two main properties of the electrolytes used for EDLCs: (1) electrochemical stability, defining the voltage window, which is essential for energy density; (2) ionic conductivity related to the ESR, which limits the power performance. Electrolytes for supercapacitors can be classified into three main categories, depending on their nature: aqueous- and organic-based electrolytes and ionic liquids. For aqueous electrolytes, safety and low cost are key advantages from the industrial point of view. However, the operating voltage window for such electrolytes is limited by water electrolysis (1–1.2 V).308 As a result, the energy density of aqueous-based EDLCs is still one magnitude smaller compared to devices operating in non-aqueous electrolytes.309 To tackle the restriction of the limited voltage window of aqueous electrolytes, several approaches have been developed over the years. By combining a pseudocapacitive material (transition metal oxides or conducting polymers) as a positive electrode and carbon-based materials as a negative electrode, the potential of hydrogen evolution shifts which results in a wider potential window. Such asymmetric or hybrid configurations can enlarge the full cell voltage window up to 1.6–2 V.310–313 For conventional carbon-based configuration, with optimized electrode mass balance operating in neutral aqueous electrolytes such as Na2SO4 or Li2SO4, the voltage window can be improved as well.314–316In 2015, Suo et al. introduced the concept of “water-in-salt” electrolytes (WIS) for lithium-ion batteries where cell voltage beyond 2 V could be reached owing to the limited amount of free water molecules.317 As a result, the stability of water molecules toward oxidation is higher compared to conventional salt-in-water electrolytes. Using 21 M LiTFSI electrolytes and activated carbon as electrodes, the operating voltage window broadens to 2.4 V.318 Although the existing LiTFSI shows decent performance, the cost, high viscosity and limiting operating temperature of this kind of electrolyte still need to be solved. Some alternative salts to LiTFSI have been reported in recent years, such as NaTFSI or NaClO4.319,320 In addition, an idea of introducing a co-solvent is shown to be effective for improving the power performance of such electrolytes.321 The charging mechanism at the interface was demonstrated by MD simulation.322 The behavior of ions depending on the change of potential acted like ionic liquid, instead of solvated aqueous or organic electrolytes. The differences in the charging mechanisms are mentioned in the previous section. Although the approach sounds interesting, the WIS concept did not result in a major breakthrough in the energy storage field. Also, for supercapacitors, the porous structure of the electrode makes the ion exchange and transfer at the electrolyte/electrode interface even more complex compared to conventional battery materials.
Generally speaking, organic-based electrolytes have a wider voltage window compared with aqueous electrolytes, which results in a great improvement of energy density. Most of the supercapacitors available on the market are using organic electrolytes, and their energy density can reach up to 10 W h kg−1.323 However, the drawbacks of these electrolytes are the flammable property, high requirement for purification and lower conductivity compared to aqueous electrolytes. For carbon-based supercapacitors, the most frequent formulation for industrial use is TEABF4 in PC or ACN solvent.324,325 Several works have focused on the degradation of organic electrolytes and the aging of carbon materials in such a system, for improving safety.324,326–330 Although the reactions are complex, there is useful knowledge today about the degradation mechanisms and their impact on supercapacitor performance. On the other hand, to enhance the performance of supercapacitors in such an electrolyte system, the ionic dynamics and ion confinement in micropores have also been investigated,128,150,190 including the effect of solvent and desolvation of ions while entering micropores.127,286,331–334
Recently, a computational method was proposed to boost the process to discover new organic solvents in an efficient and systematic way.335,336 By screening the desirable properties of the solvent, such as voltage window, viscosity, and ion solubility, several combinations of new solvents (cyano ester-based and nitrile-based) and salts were proposed as alternative electrolytes.336–339Fig. 15 first shows the screening procedures, then an example of discovering new solvents.
 | ||
| Fig. 15 (a) The screening strategy based on computational methods. (b) An illustration abstract for selecting a new solvent for supercapacitor applications. The figure is reproduced from ref. 336 with permission from 2008 American Chemical Society. | ||
In combination with the conventional TEABF4 salt, an operating cell voltage up to 3.2 V was achieved which confirms the potential of the method and justifies further use of machine learning and artificial intelligence, owing to the large variety of combinations possible.131 The same computation method was also applied for investigating new ionic liquids. In addition to organic electrolytes, ionic liquids are also a compatible choice that can exhibit a high energy density. Ionic liquids are solvent-free electrolytes which only contain cations and anions. The general properties of ionic liquids are good chemical stability, wide electrochemical voltage window, but low to moderate ionic conductivity and limited low temperature operation.340–342 In the past decade, a lot of works have shown ionic liquids are safe and perform relatively well in a large range of temperature (80 to −50 °C).76,91,343–345 Although the energy density has met the requirement for industrial use, because of their high viscosity (relatively low ionic conductivity compared to other electrolytes), the improvement of power density for such systems is a challenge.346 A large amount of experimental and simulation works over the years have shown that with a mixture of different solvents and ionic liquids or ionic liquids with different viscosities, the general properties (viscosity, ionic conductivity, diffusion coefficient and so on) are improved; also the interaction of ionic liquids at an electrified surface can be modified.347–356 As a kind of solvent in the salt approach, the wettability of ionic liquids with a small addition of solvent has been improved for porous materials.357 Although this work did not yet result in a major breakthrough in terms of performance, it led to important advances in the scientific understanding of the ionic/carbon interaction in porous carbon electrodes. Recently, DFT calculation has been applied to predict the electrochemical potential windows for ionic liquids to accelerate the process for experimental selection.358 Theoretical and experimental works have shown that unlike solvated electrolytes, the EDL structure of ionic liquids does not align with the classic EDL models (for details of the model see Section 2.1).36,41,359 In ionic liquids, the existence of ion pairs and compact packing of ions result in a short- to long-range of electrostatic force based on the applied voltage.38,44,245,360–363 Apart from the development of the classic two dimensional EDL models for ionic liquids, the ion confinement and dynamics in nanoporous materials are also the main topic. Some experimental works, including basic electrochemical analysis and in situ techniques, such as in situ EQCM, in situ NMR, in situ SAXS, and simulation method at the molecular level, delivered some insights such as mentioned earlier.203,228,284,294,296,332,364–366 The information of how ions are packed inside nanopores, the selectivity of ions, and the charging mechanisms in such an electrolyte system will hopefully help to develop porous materials with the optimized structure to boost the performance of EDLCs.
In addition, to store the charge at the surface of porous materials, a new strategy has been recently proposed to enhance energy density by involving redox species in the electrolyte, which is called the redox electrolyte. Electrons can be injected/removed into/from redox species dissolved in the electrolyte, then adding an additional faradaic contribution to the double layer capacitance and transforming the electrolyte into an active material.131,367–371 The advantage of reactions occurring in an electrolyte medium is that the ion transport in solid materials is slower than that in liquids. In this case, the power performance will not be sacrificed while improving energy density. This concept was first applied for supercapacitors in aqueous-based electrolytes, including halide ions, quinones, and VOSO4.372–378 During these two years, some new strategies are proposed, for example, applying redox additive electrolytes for hybrid supercapacitors or choosing suitable supporting electrolytes.379 However, because of their high diffusivity of ions in aqueous electrolytes, the self-discharge remains a great issue.380
A new concept proposed by Rochefort's381 and Fontaine's group382 uses a biredox ionic liquid as salt in an electrolyte to achieve bulk-like redox density with liquid-like fast kinetics. The cation and anion of these biredox ionic liquids bear moieties that undergo very fast reversible redox reactions. Mourad et al. synthesized an ionic liquid with two different redox active species anthraquinone (AQ) and 2,2,6,6-tetramethylpiperidinyl-1-oxyl (TEMPO) attached on perfluorosulfonate anions (PFS−) and methyl imidazolium cations (MIm+), respectively.382 The structure and charge storage mechanisms are shown in Fig. 16. The capacitance in this biredox electrolyte was twice that of the biredox-free BMImTFSI ionic liquid electrolyte and remained stable for 2000 cycles. The power performance was similar in both electrolytes. Importantly, the leakage current measured for the biredox IL was two to three times lower than that for the biredox-free IL, which means a decreased self-discharge. This was explained by specific interactions inside the porous carbon network.
 | ||
| Fig. 16 (a) Structure of the biredox ionic liquid mentioned above. (b) and (c) Illustrations of the charge storage for pure IL and biredox IL, respectively. Reproduced from ref. 382 with permission from Springer Nature (copyright 2017). | ||
The biredox concept is certainly an interesting approach.383–386 These redox-active electrolytes offer opportunities for improving the energy density of EDLC devices and there is little doubt that more work will appear in the next years to exploit this concept.
Differently from conventional supercapacitors, micro-supercapacitors and flexible supercapacitors are currently fast developing to meet the requirements for diverse applications such as the internet of things (IoT). In this field, work has been dedicated to the development of solid-state electrolytes (SSEs) to prevent the leakage of liquid electrolytes.387–392 Like in batteries, a SSE acts as an electrolyte and a separator in the device. As a result, it requires high mechanical strength and wide operating temperature. Differently from batteries, a SSE cannot be prepared from ceramic (oxides or sulfur) because of the high surface area of the porous carbons used. Alternatively, SSEs for supercapacitors contain liquid electrolytes embedded inside the polymer or non-organic matrix (such as silica). For instance, a zwitterionic-type of polymer matrix has been proposed as an aqueous-based gel electrolyte, with high water content and fast ion migration, which result in decent volumetric capacitance for graphene-based supercapacitors (300 F cm−3 at 0.8 A cm−3).393 Ionogels, which combine an ionic liquid electrolyte entrapped in an inorganic silica matrix, have been successfully developed for this application.391,394,395 A key feature of these SSEs is the possibility of the IL to diffuse by capillarity, and by hydrophobic interaction, to impregnate the nanoporous network of the carbon electrode.396 As a result, the capacitance is close to that of IL electrolytes.
Another family of SSEs for supercapacitors deal with polymers. Polymers have been used as proton conducting electrolytes as well as gel polymer electrolytes (GPEs). There has been a huge amount of work on these systems so that we will not go into the details and will refer to review papers where all key information can be found.28,390,397 Basically, polymers offer interesting properties for designing proton conducting electrolytes and aqueous-based GPEs, but still fall short to provide a voltage window beyond 1.5 V with decent stability. As a result, the energy density is still low, but the absence of electrolyte leakage is an added value for micro-devices.
Last, a recent study proposed the design of an “all-in-gel” supercapacitor.398 The idea is to produce gel-like electrodes by mixing carbon nanotubes, an ionic liquid and some additives so that the contact issue at the electrode/electrolyte interface can be solved. The mechanical strength of this type of electrolyte is high and it is easy to shape it in different forms so that this approach could be interesting to follow for solid state micro-devices.
5. Summary and perspectives
Electrochemical capacitors are currently key energy storage devices for high-power applications. The recent decade has witnessed the booming of novel electrode materials, for instance metal oxides or metal carbides/nitrides, and electrolyte concepts; yet porous carbon-based electrodes are still the leading materials in real applications. This review is dedicated to covering the recent progress in nanoporous carbon electrodes for electrochemical capacitive energy storage.It has started up with detailing the fundamental basics of EDL formation from the view point of ion–electrode correlations at planar, 2D electrodes. However, this model falls short to describe correctly the charge mechanism in nanoporous carbons, for which a good picture of the porous structure is required. The refinement of gas sorption techniques turned out to be crucial to push further our basic understanding of the charge storage mechanism in porous carbon-based EDLCs. Ar and CO2 gas probes are the ones to be recommended instead of N2 for measuring the SSA and PSD of nanoporous carbons. Although high SSA is always beneficial for increasing capacitance, no direct trend has been established so far. Instead, it has been found that small pore size matters the most and leads to a capacitance increase for nanoporous carbons with pore size below 1 nm, due to the ion desolvation. Some authors, using simple analytical models, have succeeded in showing that, by means of ideal endo- and exo-hedral carbon, the local curvature of the carbon surface in nanopores can explain the capacitance increase in carbon nanopores.
Since then, new advanced in situ experimental setups and computational tools have been proposed to gain insights into the charge storage mechanisms. In situ EQCM is reviewed as a powerful tool for tracking ion and solvent molecule transfer across the porous carbon material/electrolyte interface, during the polarization of the electrode. This technique has been nicely complemented with in situ NMR, to obtain information on the ion environments in nanopores. In situ SAS techniques and other techniques like in situ XRD, in situ infrared spectroelectrochemistry, etc., have turned out to be useful for investigating ion adsorption in nanoporous carbon. When coupled with advanced characterization techniques, modeling and simulation demonstrate great potential in resolving the underlying theory and predicting optimized carbon structures. For instance, MD simulation and DFT approach are capable of illustrating the origin of the capacitance increase in nanopores in terms of positive curvature of carbon nanopores.
Even though lots of efforts have been made on the carbon side, there has been still recent progress in developing advanced electrolytes. The “water-in-salt” electrolytes have made possible the obtention of aqueous-based electrolytes exhibiting an operating voltage as high as 2.4 V. In the meantime, an appealing class of ionic liquids has been given birth: the biredox ionic liquids with great potential in bringing redox reaction on the nanoporous carbon surface, which may highly enhance the capacitance. There is still room for improvement of this aspect, and computational approaches have been recently proposed to boost the process to discover new organic solvents in an efficient and systematic way.
Despite the aforementioned impressive progress, carbon-based supercapacitors are still limited by relatively low energy density. The design of nanoporous carbon with finely tuned, controlled pore size below 1 nm is still highly challenging. Therefore, new strategies for producing high-quality nanoporous carbon with controlled pore size in a more cost-effective and efficient way are needed. Alternatively, carbon with ionophobic pores was predicted to achieve high energy density without compensation of power performance, and this could be an effective way to improve the performance; however, the preparation of these ionophobic carbons remains highly challenging. Progress can also be made by optimizing the electrode composition, which goes beyond the limitation of carbon materials to enhance the performance of EDLCs. For instance, while electrochemically inactive binders and conducting additives are used for electrode preparation, recent works suggested that these components can be replaced with graphene or MXene materials, which can contribute to EDL capacitance.399,400
The fundamental understanding of the charge storage mechanism in nanopores has achieved considerable progress; however, the full picture remains unclear, especially when a complex pore structure is considered, or a redox reaction is involved. More advanced techniques are essential to gain more information about the electrolyte/electrode interface interaction. As many techniques are claimed as in situ or operando techniques, attention should be paid to the possible change of the electrochemical process that may be induced by the measurements themselves, and therefore, non-destructive techniques are recommended. The combination with simulation or modeling is another effective tool for digging extra information, such as ion distribution and population.
Developing new electrolytes is one of the most effective routes to push EDLCs to higher energy density. Aqueous electrolytes with a large operating potential range as well as redox electrolytes are promising. More related electrolytes with low cost, high stability, and good safety should be designed with the assistance of computational methods. Considering the booming advancement of machine learning and artificial intelligence, there is no doubt that the computational methods will play a very important role in this field in the upcoming years.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
HS was supported by a grant from the China Scholarship Council (no. 201608370077). PS, PLT, YCW and HS thank the Agence Nationale de la Recherche (Labex STORE-EX) for financial support. ZL is supported by the Fundamental Research Funds for the Central Universities (YJ201886) and the National Natural Science Foundation of China (Grant No. 501902215).References
- S. Chu and A. Majumdar, Nature, 2012, 488, 294 CrossRef CAS PubMed.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- V. Augustyn, P. Simon and B. Dunn, Energy Environ. Sci., 2014, 7, 1597–1614 RSC.
- C. Choi, D. S. Ashby, D. M. Butts, R. H. DeBlock, Q. Wei, J. Lau and B. Dunn, Nat. Rev. Mater., 2019, 1–15 Search PubMed.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845–854 CrossRef CAS PubMed.
- M. Salanne, B. Rotenberg, K. Naoi, K. Kaneko, P.-L. Taberna, C. P. Grey, B. Dunn and P. Simon, Nat. Energy, 2016, 1, 16070 CrossRef CAS.
- J. R. Miller and P. Simon, Science, 2008, 321, 651–652 CrossRef CAS PubMed.
- H. v. Helmholtz, Ann. Phys., 1853, 165, 353–377 CrossRef.
- G. P. Wang, L. Zhang and J. J. Zhang, Chem. Soc. Rev., 2012, 41, 797–828 RSC.
- Y. Zhai, Y. Dou, D. Zhao, P. F. Fulvio, R. T. Mayes and S. Dai, Adv. Mater., 2011, 23, 4828–4850 CrossRef CAS PubMed.
- L. L. Zhang and X. Zhao, Chem. Soc. Rev., 2009, 38, 2520–2531 RSC.
- B. E. Conway, Electrochemical supercapacitors: scientific fundamentals and technological applications, Kluwer Academic/Plenum, New York, 1999 Search PubMed.
- J. Schindall, IEEE Spectrum, 2007, 44, 42–46 Search PubMed.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P.-L. Taberna, Science, 2006, 313, 1760–1763 CrossRef CAS PubMed.
- E. Raymundo-Pinero, K. Kierzek, J. Machnikowski and F. Béguin, Carbon, 2006, 44, 2498–2507 CrossRef CAS.
- H. Shi, Electrochim. Acta, 1996, 41, 1633–1639 CrossRef CAS.
- G. Salitra, A. Soffer, L. Eliad, Y. Cohen and D. Aurbach, J. Electrochem. Soc., 2000, 147, 2486–2493 CrossRef CAS.
- Y. Gogotsi and P. Simon, Science, 2011, 334, 917–918 CrossRef CAS PubMed.
- S. Zhang and N. Pan, Adv. Energy Mater., 2015, 5, 1401401 CrossRef.
- A. Noori, M. F. El-Kady, M. S. Rahmanifar, R. B. Kaner and M. F. Mousavi, Chem. Soc. Rev., 2019, 48, 1272–1341 RSC.
- A. Balducci, D. Belanger, T. Brousse, J. Long and W. Sugimoto, J. Electrochem. Soc., 2017, 164, A1487–A1488 CrossRef CAS.
- T. S. Mathis, N. Kurra, X. Wang, D. Pinto, P. Simon and Y. Gogotsi, Adv. Energy Mater., 2019, 1902007 CrossRef CAS.
- K. Naoi, S. Ishimoto, J.-I. Miyamoto and W. Naoi, Energy Environ. Sci., 2012, 5, 9363–9373 RSC.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed.
- J. Le Bideau, L. Viau and A. Vioux, Chem. Soc. Rev., 2011, 40, 907–925 RSC.
- D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250 RSC.
- C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, Chem. Soc. Rev., 2015, 44, 7484–7539 RSC.
- M. Lu, Supercapacitors: materials, systems, and applications, John Wiley & Sons, 2013 Search PubMed.
- M.-M. Huang, Y. Jiang, P. Sasisanker, G. W. Driver and H. Weingärtner, J. Chem. Eng. Data, 2011, 56, 1494–1499 CrossRef CAS.
- M. Gouy, J. Phys. Theor. Appl., 1910, 9, 457–468 CrossRef.
- D. L. Chapman, London, Edinburgh Dublin Philos. Mag. J. Sci., 1913, 25, 475–481 CrossRef.
- D. C. Grahame, Chem. Rev., 1947, 41, 441–501 CrossRef CAS PubMed.
- A. J. Bard, L. R. Faulkner, J. Leddy and C. G. Zoski, Electrochemical methods: fundamentals and applications, Wiley, New York, 1980 Search PubMed.
- O. Stern, Z. Elektrochem., 1924, 30, 1014–1020 Search PubMed.
- A. A. Kornyshev, J. Phys. Chem. B, 2007, 111, 5545–5557 CrossRef CAS PubMed.
- W. Fawcett, Isr. J. Chem., 1979, 18, 3–16 CrossRef CAS.
- M. Z. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
- M. M. Islam, M. T. Alam and T. Ohsaka, J. Phys. Chem. C, 2008, 112, 16568–16574 CrossRef CAS.
- V. Lockett, R. Sedev, J. Ralston, M. Horne and T. Rodopoulos, J. Phys. Chem. C, 2008, 112, 7486–7495 CrossRef CAS.
- M. V. Fedorov and A. A. Kornyshev, J. Phys. Chem. B, 2008, 112, 11868–11872 CrossRef CAS PubMed.
- M. Trulsson, J. Algotsson, J. Forsman and C. E. Woodward, J. Phys. Chem. Lett., 2010, 1, 1191–1195 CrossRef CAS.
- C. Merlet, B. Rotenberg, P. A. Madden and M. Salanne, Phys. Chem. Chem. Phys., 2013, 15, 15781–15792 RSC.
- M. Mezger, H. Schröder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schöder, V. Honkimäki, M. Deutsch, B. M. Ocko and J. Ralston, Science, 2008, 322, 424–428 CrossRef CAS PubMed.
- X. Mao, P. Brown, C. Červinka, G. Hazell, H. Li, Y. Ren, D. Chen, R. Atkin, J. Eastoe and I. Grillo, Nat. Mater., 2019, 1–8 Search PubMed.
- C. Merlet, M. Salanne, B. Rotenberg and P. A. Madden, J. Phys. Chem. C, 2011, 115, 16613–16618 CrossRef CAS.
- J. Vatamanu, O. Borodin and G. D. Smith, J. Am. Chem. Soc., 2010, 132, 14825–14833 CrossRef CAS PubMed.
- S. Baldelli, J. Phys. Chem. Lett., 2012, 4, 244–252 CrossRef PubMed.
- S. Baldelli, Acc. Chem. Res., 2008, 41, 421–431 CrossRef CAS PubMed.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed.
- K. Kirchner, T. Kirchner, V. Ivaništšev and M. V. Fedorov, Electrochim. Acta, 2013, 110, 762–771 CrossRef CAS.
- K. S. Sing, Pure Appl. Chem., 1985, 57, 603–619 CAS.
- J. Gamby, P. L. Taberna, P. Simon, J. F. Fauvarque and M. Chesneau, J. Power Sources, 2001, 101, 109–116 CrossRef CAS.
- L. Wei, M. Sevilla, A. B. Fuertes, R. Mokaya and G. Yushin, Adv. Energy Mater., 2011, 1, 356–361 CrossRef CAS.
- L. Wei, M. Sevilla, A. B. Fuertes, R. Mokaya and G. Yushin, Adv. Funct. Mater., 2012, 22, 827–834 CrossRef CAS.
- J. Yan, Q. Wang, T. Wei and Z. Fan, Adv. Energy Mater., 2014, 4, 1300816 CrossRef.
- C. Peng, X.-B. Yan, R.-T. Wang, J.-W. Lang, Y.-J. Ou and Q.-J. Xue, Electrochim. Acta, 2013, 87, 401–408 CrossRef CAS.
- Y. Gogotsi, A. Nikitin, H. Ye, W. Zhou, J. E. Fischer, B. Yi, H. C. Foley and M. W. Barsoum, Nat. Mater., 2003, 2, 591 CrossRef CAS PubMed.
- P. Simon and Y. Gogotsi, Acc. Chem. Res., 2012, 46, 1094–1103 CrossRef PubMed.
- C. Largeot, C. Portet, J. Chmiola, P.-L. Taberna, Y. Gogotsi and P. Simon, J. Am. Chem. Soc., 2008, 130, 2730–2731 CrossRef CAS PubMed.
- C. Portet, G. Yushin and Y. Gogotsi, J. Electrochem. Soc., 2008, 155, A531–A536 CrossRef CAS.
- Y. Korenblit, M. Rose, E. Kockrick, L. Borchardt, A. Kvit, S. Kaskel and G. Yushin, ACS Nano, 2010, 4, 1337–1344 CrossRef CAS PubMed.
- H. J. Liu, J. Wang, C. X. Wang and Y. Y. Xia, Adv. Energy Mater., 2011, 1, 1101–1108 CrossRef CAS.
- M. Rose, Y. Korenblit, E. Kockrick, L. Borchardt, M. Oschatz, S. Kaskel and G. Yushin, Small, 2011, 7, 1108–1117 CrossRef CAS PubMed.
- J. Chmiola, G. Yushin, R. Dash and Y. Gogotsi, J. Power Sources, 2006, 158, 765–772 CrossRef CAS.
- H. Nishihara and T. Kyotani, Adv. Mater., 2012, 24, 4473–4498 CrossRef CAS PubMed.
- H. Nishihara, H. Itoi, T. Kogure, P.-X. Hou, H. Touhara, F. Okino and T. Kyotani, Chem. – Eur. J., 2009, 15, 5355–5363 CrossRef CAS PubMed.
- H. Itoi, H. Nishihara, T. Kogure and T. Kyotani, J. Am. Chem. Soc., 2011, 133, 1165–1167 CrossRef CAS PubMed.
- V. L. Kuznetsov, A. L. Chuvilin, Y. V. Butenko, I. Y. Mal'kov and V. M. Titov, Chem. Phys. Lett., 1994, 222, 343–348 CrossRef CAS.
- M. Zeiger, N. Jäckel, V. N. Mochalin and V. Presser, J. Mater. Chem. A, 2016, 4, 3172–3196 RSC.
- J. K. McDonough and Y. Gogotsi, Electrochem. Soc. Interface, 2013, 22, 61–66 CrossRef CAS.
- M. Zeiger, N. Jäckel, M. Aslan, D. Weingarth and V. Presser, Carbon, 2015, 84, 584–598 CrossRef CAS.
- C. Portet, G. Yushin and Y. Gogotsi, Carbon, 2007, 45, 2511–2518 CrossRef CAS.
- E. Bushueva, P. Galkin, A. Okotrub, L. Bulusheva, N. Gavrilov, V. Kuznetsov and S. Moiseekov, Phys. Status Solidi B, 2008, 245, 2296–2299 CrossRef CAS.
- D. Pech, M. Brunet, H. Durou, P. Huang, V. Mochalin, Y. Gogotsi, P.-L. Taberna and P. Simon, Nat. Nanotechnol., 2010, 5, 651 CrossRef CAS PubMed.
- R. Lin, P.-L. Taberna, S. Fantini, V. Presser, C. R. Pérez, F. Malbosc, N. L. Rupesinghe, K. B. Teo, Y. Gogotsi and P. Simon, J. Phys. Chem. Lett., 2011, 2, 2396–2401 CrossRef CAS.
- K. Jost, C. R. Perez, J. K. McDonough, V. Presser, M. Heon, G. Dion and Y. Gogotsi, Energy Environ. Sci., 2011, 4, 5060–5067 RSC.
- N. Jäckel, D. Weingarth, M. Zeiger, M. Aslan, I. Grobelsek and V. Presser, J. Power Sources, 2014, 272, 1122–1133 CrossRef.
- R. H. Baughman, A. A. Zakhidov and W. A. De Heer, Science, 2002, 297, 787–792 CrossRef CAS PubMed.
- Z. Yang, J. Tian, Z. Yin, C. Cui, W. Qian and F. Wei, Carbon, 2019, 141, 467–480 CrossRef CAS.
- A. Peigney, C. Laurent, E. Flahaut, R. Bacsa and A. Rousset, Carbon, 2001, 39, 507–514 CrossRef CAS.
- Y. Shim and H. J. Kim, ACS Nano, 2010, 4, 2345–2355 CrossRef CAS PubMed.
- L. Yang, B. H. Fishbine, A. Migliori and L. R. Pratt, J. Am. Chem. Soc., 2009, 131, 12373–12376 CrossRef CAS PubMed.
- G. Feng, R. Qiao, J. Huang, S. Dai, B. G. Sumpter and V. Meunier, Phys. Chem. Chem. Phys., 2011, 13, 1152–1161 RSC.
- M. F. El-Kady, Y. Shao and R. B. Kaner, Nat. Rev. Mater., 2016, 1, 16033 CrossRef CAS.
- F. Bonaccorso, L. Colombo, G. Yu, M. Stoller, V. Tozzini, A. C. Ferrari, R. S. Ruoff and V. Pellegrini, Science, 2015, 347, 1246501 CrossRef PubMed.
- J. Xia, F. Chen, J. Li and N. Tao, Nat. Nanotechnol., 2009, 4, 505 CrossRef CAS PubMed.
- H. Banda, S. Périé, B. Daffos, P.-L. Taberna, L. Dubois, O. Crosnier, P. Simon, D. Lee, G. De Paëpe and F. Duclairoir, ACS Nano, 2019, 13, 1443–1453 CrossRef CAS PubMed.
- X. Yang, C. Cheng, Y. Wang, L. Qiu and D. Li, Science, 2013, 341, 534–537 CrossRef CAS PubMed.
- Y. Zhu, S. Murali, M. D. Stoller, K. Ganesh, W. Cai, P. J. Ferreira, A. Pirkle, R. M. Wallace, K. A. Cychosz and M. Thommes, Science, 2011, 332, 1537–1541 CrossRef CAS PubMed.
- W. Y. Tsai, R. Y. Lin, S. Murali, L. L. Zhang, J. K. McDonough, R. S. Ruoff, P. L. Taberna, Y. Gogotsi and P. Simon, Nano Energy, 2013, 2, 403–411 CrossRef CAS.
- Y. Xu, Z. Lin, X. Zhong, X. Huang, N. O. Weiss, Y. Huang and X. Duan, Nat. Commun., 2014, 5, 4554 CrossRef CAS PubMed.
- L. A. Jurado and R. M. Espinosa-Marzal, Sci. Rep., 2017, 7, 1–12 CrossRef CAS PubMed.
- M. Zeiger, N. Jäckel, D. Weingarth and V. Presser, Carbon, 2015, 94, 507–517 CrossRef CAS.
- J. Xu, N. Yuan, J. M. Razal, Y. Zheng, X. Zhou, J. Ding, K. Cho, S. Ge, R. Zhang, Y. Gogotsi and R. H. Baughman, Energy Storage Mater., 2019, 22, 323–329 CrossRef.
- H.-J. Liu, W.-J. Cui, L.-H. Jin, C.-X. Wang and Y.-Y. Xia, J. Mater. Chem., 2009, 19, 3661–3667 RSC.
- H.-J. Liu, X.-M. Wang, W.-J. Cui, Y.-Q. Dou, D.-Y. Zhao and Y.-Y. Xia, J. Mater. Chem., 2010, 20, 4223–4230 RSC.
- W. Chaikittisilp, M. Hu, H. Wang, H.-S. Huang, T. Fujita, K. C.-W. Wu, L.-C. Chen, Y. Yamauchi and K. Ariga, Chem. Commun., 2012, 48, 7259–7261 RSC.
- O. Kimizuka, O. Tanaike, J. Yamashita, T. Hiraoka, D. N. Futaba, K. Hata, K. Machida, S. Suematsu, K. Tamamitsu and S. Saeki, Carbon, 2008, 46, 1999–2001 CrossRef CAS.
- A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191 CrossRef CAS PubMed.
- L. L. Zhang, X. Zhao, H. Ji, M. D. Stoller, L. Lai, S. Murali, S. Mcdonnell, B. Cleveger, R. M. Wallace and R. S. Ruoff, Energy Environ. Sci., 2012, 5, 9618–9625 RSC.
- J. Jagiello and J. P. Olivier, Carbon, 2013, 55, 70–80 CrossRef CAS.
- A. C. Forse, C. Merlet, P. K. Allan, E. K. Humphreys, J. M. Griffin, M. Aslan, M. Zeiger, V. Presser, Y. Gogotsi and C. P. Grey, Chem. Mater., 2015, 27, 6848–6857 CrossRef CAS.
- K. A. Cychosz, R. Guillet-Nicolas, J. Garcia-Martinez and M. Thommes, Chem. Soc. Rev., 2017, 46, 389–414 RSC.
- M. Thommes and K. A. Cychosz, Adsorption, 2014, 20, 233–250 CrossRef CAS.
- S. Lowell, J. E. Shields, M. A. Thomas and M. Thommes, Characterization of porous solids and powders: surface area, pore size and density, Springer Science & Business Media, 2012 Search PubMed.
- J. Rouquerol, F. Rouquerol, P. Llewellyn, G. Maurin and K. S. Sing, Adsorption by powders and porous solids: principles, methodology and applications, Academic Press, 2013 Search PubMed.
- D. Cazorla-Amorós, J. Alcaniz-Monge and A. Linares-Solano, Langmuir, 1996, 12, 2820–2824 CrossRef.
- J. Rouquerol, P. Llewellyn and F. Rouquerol, Stud. Surf. Sci. Catal., 2007, 160, 49–56 CrossRef CAS.
- M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. Sing, Pure Appl. Chem., 2015, 87, 1051–1069 CAS.
- J. Landers, G. Y. Gor and A. V. Neimark, Colloids Surf., A, 2013, 437, 3–32 CrossRef CAS.
- C. Lastoskie, K. E. Gubbins and N. Quirke, J. Phys. Chem., 1993, 97, 4786–4796 CrossRef CAS.
- P. A. Monson, Microporous Mesoporous Mater., 2012, 160, 47–66 CrossRef CAS.
- A. V. Neimark, Y. Lin, P. I. Ravikovitch and M. Thommes, Carbon, 2009, 47, 1617–1628 CrossRef CAS.
- G. Laudisio, R. K. Dash, J. P. Singer, G. Yushin, Y. Gogotsi and J. E. Fischer, Langmuir, 2006, 22, 8945–8950 CrossRef CAS PubMed.
- L. He, S. M. Chathoth, Y. B. Melnichenko, V. Presser, J. McDonough and Y. Gogotsi, Microporous Mesoporous Mater., 2012, 149, 46–54 CrossRef CAS.
- M. Endo, T. Maeda, T. Takeda, Y. J. Kim, K. Koshiba, H. Hara and M. S. Dresselhaus, J. Electrochem. Soc., 2001, 148, A910 CrossRef CAS.
- O. Barbieri, M. Hahn, A. Herzog and R. Kötz, Carbon, 2005, 43, 1303–1310 CrossRef CAS.
- H. X. Ji, X. Zhao, Z. H. Qiao, J. Jung, Y. W. Zhu, Y. L. Lu, L. L. Zhang, A. H. MacDonald and R. S. Ruoff, Nat. Commun., 2014, 5, 3317 CrossRef PubMed.
- C. Lin, J. A. Ritter and B. N. Popov, J. Electrochem. Soc., 1999, 146, 3639–3643 CrossRef CAS.
- D. Lozano-Castello, D. Cazorla-Amorós, A. Linares-Solano, S. Shiraishi, H. Kurihara and A. Oya, Carbon, 2003, 41, 1765–1775 CrossRef CAS.
- L. Eliad, G. Salitra, A. Soffer and D. Aurbach, J. Phys. Chem. B, 2001, 105, 6880–6887 CrossRef CAS.
- L. Eliad, G. Salitra, A. Soffer and D. Aurbach, Langmuir, 2005, 21, 3198–3202 CrossRef CAS PubMed.
- B. Kastening and S. Spinzig, J. Electroanal. Chem. Interfacial Electrochem., 1986, 214, 295–302 CrossRef CAS.
- C. Vix-Guterl, E. Frackowiak, K. Jurewicz, M. Friebe, J. Parmentier and F. Béguin, Carbon, 2005, 43, 1293–1302 CrossRef CAS.
- T. Ohkubo, T. Konishi, Y. Hattori, H. Kanoh, T. Fujikawa and K. Kaneko, J. Am. Chem. Soc., 2002, 124, 11860–11861 CrossRef CAS PubMed.
- J. Chmiola, C. Largeot, P. L. Taberna, P. Simon and Y. Gogotsi, Angew. Chem., 2008, 120, 3440–3443 CrossRef.
- C. Prehal, C. Koczwara, N. Jäckel, A. Schreiber, M. Burian, H. Amenitsch, M. A. Hartmann, V. Presser and O. Paris, Nat. Energy, 2017, 2, 16215 CrossRef CAS.
- T. A. Centeno, O. Sereda and F. Stoeckli, Phys. Chem. Chem. Phys., 2011, 13, 12403–12406 RSC.
- A. García-Gómez, G. Moreno-Fernández, B. Lobato and T. A. Centeno, Phys. Chem. Chem. Phys., 2015, 17, 15687–15690 RSC.
- F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Adv. Mater., 2014, 26, 2219–2251 CrossRef PubMed.
- S. Kondrat, C. Perez, V. Presser, Y. Gogotsi and A. Kornyshev, Energy Environ. Sci., 2012, 5, 6474–6479 RSC.
- D. T. Galhena, B. C. Bayer, S. Hofmann and G. A. Amaratunga, ACS Nano, 2015, 10, 747–754 CrossRef PubMed.
- J. Huang, B. G. Sumpter and V. Meunier, Chem. – Eur. J., 2008, 14, 6614–6626 CrossRef CAS PubMed.
- C. O. Ania, J. Pernak, F. Stefaniak, E. Raymundo-Piñero and F. Béguin, Carbon, 2009, 47, 3158–3166 CrossRef CAS.
- B. Lobato, L. Suárez, L. Guardia and T. A. Centeno, Carbon, 2017, 122, 434–445 CrossRef CAS.
- N. Jackel, P. Simon, Y. Gogotsi and V. Presser, ACS Energy Lett., 2016, 1, 1262–1265 CrossRef.
- J. Huang, B. G. Sumpter and V. Meunier, Angew. Chem., Int. Ed., 2008, 47, 520–524 CrossRef CAS PubMed.
- G. Feng, R. Qiao, J. Huang, B. G. Sumpter and V. Meunier, ACS Nano, 2010, 4, 2382–2390 CrossRef CAS PubMed.
- J. Huang, B. G. Sumpter, V. Meunier, G. Yushin, C. Portet and Y. Gogotsi, J. Mater. Res., 2010, 25, 1525–1531 CrossRef CAS.
- Y. Honda, T. Haramoto, M. Takeshige, H. Shiozaki, T. Kitamura, K. Yoshikawa and M. Ishikawa, J. Electrochem. Soc., 2008, 155, A930–A935 CrossRef CAS.
- G. Sauerbrey, Z. Phys., 1959, 155, 206–212 CrossRef CAS.
- R. Etchenique and E. Calvo, Electrochem. Commun., 1999, 1, 167–170 CrossRef CAS.
- C. Eickes, J. Rosenmund, S. Wasle, K. Doblhofer, K. Wang and K. Weil, Electrochim. Acta, 2000, 45, 3623–3628 CrossRef CAS.
- M. Moshkovich, M. Cojocaru, H. Gottlieb and D. Aurbach, J. Electroanal. Chem., 2001, 497, 84–96 CrossRef CAS.
- H. Stadler, M. Mondon and C. Ziegler, Anal. Bioanal. Chem., 2003, 375, 53–61 CrossRef CAS PubMed.
- M. D. Levi, G. Salitra, N. Levy, D. Aurbach and J. Maier, Nat. Mater., 2009, 8, 872 CrossRef CAS PubMed.
- M. D. Levi, N. Levy, S. Sigalov, G. Salitra, D. Aurbach and J. Maier, J. Am. Chem. Soc., 2010, 132, 13220–13222 CrossRef CAS PubMed.
- M. D. Levi, S. Sigalov, D. Aurbach and L. Daikhin, J. Phys. Chem. C, 2013, 117, 14876–14889 CrossRef CAS.
- W.-Y. Tsai, P.-L. Taberna and P. Simon, J. Am. Chem. Soc., 2014, 136, 8722–8728 CrossRef CAS PubMed.
- M. D. Levi, S. Sigalov, G. Salitra, R. Elazari and D. Aurbach, J. Phys. Chem. Lett., 2011, 2, 120–124 CrossRef CAS PubMed.
- Y.-C. Wu, P.-L. Taberna and P. Simon, Electrochem. Commun., 2018, 93, 119–122 CrossRef CAS.
- J. Ye, Y.-C. W, K. Xu, K. Ni, N. Shu, P.-L. Taberna, Y. Zhu and P. Simon, J. Am. Chem. Soc., 2019, 141, 16559–16563 CrossRef CAS PubMed.
- R. Yan, M. Antonietti and M. Oschatz, Adv. Energy Mater., 2018, 8, 1800026 CrossRef.
- Q. Zhang, M. D. Levi, Y. Chai, X. Zhang, D. Xiao, Q. Dou, P. Ma, H. Ji and X. Yan, Small Methods, 2019, 1900246 CrossRef CAS.
- Z. Yang, M. C. Dixon, R. A. Erck and L. Trahey, ACS Appl. Mater. Interfaces, 2015, 7, 26585–26594 CrossRef CAS PubMed.
- N. Shpigel, M. D. Levi, S. Sigalov, D. Aurbach, L. Daikhin and V. Presser, J. Phys.: Condens. Matter, 2016, 28, 114001 CrossRef PubMed.
- M. D. Levi, N. Shpigel, S. Sigalov, V. Dargel, L. Daikhin and D. Aurbach, Electrochim. Acta, 2017, 232, 271–284 CrossRef CAS.
- M. D. Levi, M. R. Lukatskaya, S. Sigalov, M. Beidaghi, N. Shpigel, L. Daikhin, D. Aurbach, M. W. Barsoum and Y. Gogotsi, Adv. Energy Mater., 2015, 5, 1400815 CrossRef.
- N. Shpigel, M. D. Levi and D. Aurbach, Energy Storage Mater., 2019, 21, 399–413 CrossRef.
- A. Arnau, Sensors, 2008, 8, 370–411 CrossRef PubMed.
- M. C. Dixon, J. Biomol. Tech., 2008, 19, 151 Search PubMed.
- N. B. Eisele, F. I. Andersson, S. Frey and R. P. Richter, Biomacromolecules, 2012, 13, 2322–2332 CrossRef CAS PubMed.
- A. R. Hillman, M. A. Mohamoud and I. Efimov, Anal. Chem., 2011, 83, 5696–5707 CrossRef CAS PubMed.
- D. Johannsmann, Fundamentals and modeling, Springer International Publishing, Switzerland, 2015 Search PubMed.
- A. R. Hillman, I. Efimov and M. Skompska, Faraday Discuss., 2002, 121, 423–439 RSC.
- F. Höök, B. Kasemo, T. Nylander, C. Fant, K. Sott and H. Elwing, Anal. Chem., 2001, 73, 5796–5804 CrossRef PubMed.
- N. Shpigel, M. D. Levi, S. Sigalov, O. Girshevitz, D. Aurbach, L. Daikhin, P. Pikma, M. Marandi, A. Jänes and E. Lust, Nat. Mater., 2016, 15, 570 CrossRef CAS PubMed.
- N. Shpigel, S. Sigalov, M. D. Levi, T. Mathis, L. Daikhin, A. Janes, E. Lust, Y. Gogotsi and D. Aurbach, Joule, 2018, 2, 988–1003 CrossRef CAS.
- N. Jäckel, V. Dargel, N. Shpigel, S. Sigalov, M. D. Levi, L. Daikhin, D. Aurbach and V. Presser, J. Power Sources, 2017, 371, 162–166 CrossRef.
- N. Shpigel, M. R. Lukatskaya, S. Sigalov, C. E. Ren, P. Nayak, M. D. Levi, L. Daikhin, D. Aurbach and Y. Gogotsi, ACS Energy Lett., 2017, 2, 1407–1415 CrossRef CAS.
- S. Bourkane, C. Gabrielli and M. Keddam, Electrochim. Acta, 1989, 34, 1081–1092 CrossRef.
- F. Escobar-Teran, A. Arnau, J. Garcia, Y. Jiménez, H. Perrot and O. Sel, Electrochem. Commun., 2016, 70, 73–77 CrossRef CAS.
- C. Gabrielli, J. J. García-Jareño, M. Keddam, H. Perrot and F. Vicente, J. Phys. Chem. B, 2002, 106, 3182–3191 CrossRef CAS.
- C. Gabrielli, M. Keddam, N. Nadi and H. Perrot, J. Electroanal. Chem., 2000, 485, 101–113 CrossRef CAS.
- T. Le, D. Aradilla, G. Bidan, F. Billon, M. Delaunay, J.-M. Gérard, H. Perrot and O. Sel, Electrochem. Commun., 2018, 93, 5–9 CrossRef CAS.
- R. K. Harris, T. V. Thompson, P. R. Norman, C. Pottage and A. N. Trethewey, J. Chem. Soc., Faraday Trans., 1995, 91, 1795–1799 RSC.
- R. K. Harris, T. V. Thompson, P. R. Norman and C. Pottage, J. Chem. Soc., Faraday Trans., 1996, 92, 2615–2618 RSC.
- R. K. Harris, T. V. Thompson, P. R. Norman and C. Pottage, Carbon, 1999, 37, 1425–1430 CrossRef CAS.
- H. Wang, T. K. J. Köster, N. M. Trease, J. Ségalini, P.-L. Taberna, P. Simon, Y. Gogotsi and C. P. Grey, J. Am. Chem. Soc., 2011, 133, 19270–19273 CrossRef CAS PubMed.
- P. Ren, A. Zheng, X. Pan, X. Han and X. Bao, J. Phys. Chem. C, 2013, 117, 23418–23424 CrossRef CAS.
- A. C. Forse, J. M. Griffin, V. Presser, Y. Gogotsi and C. P. Grey, J. Phys. Chem. C, 2014, 118, 7508–7514 CrossRef CAS.
- D. Sebastiani, ChemPhysChem, 2006, 7, 164–175 CrossRef CAS PubMed.
- M. Kibalchenko, M. C. Payne and J. R. Yates, ACS Nano, 2010, 5, 537–545 CrossRef PubMed.
- J. M. Griffin, A. C. Forse, W.-Y. Tsai, P.-L. Taberna, P. Simon and C. P. Grey, Nat. Mater., 2015, 14, 812–819 CrossRef CAS PubMed.
- S.-I. Lee, K. Saito, K. Kanehashi, M. Hatakeyama, S. Mitani, S.-H. Yoon, Y. Korai and I. Mochida, Carbon, 2006, 44, 2578–2586 CrossRef CAS.
- M. Deschamps, E. Gilbert, P. Azais, E. Raymundo-Piñero, M. R. Ammar, P. Simon, D. Massiot and F. Béguin, Nat. Mater., 2013, 12, 351 CrossRef CAS PubMed.
- F. Blanc, M. Leskes and C. P. Grey, Acc. Chem. Res., 2013, 46, 1952–1963 CrossRef CAS PubMed.
- H. Wang, A. C. Forse, J. M. Griffin, N. M. Trease, L. Trognko, P.-L. Taberna, P. Simon and C. P. Grey, J. Am. Chem. Soc., 2013, 135, 18968–18980 CrossRef CAS PubMed.
- A. C. Forse, J. M. Griffin, C. Merlet, J. Carretero-Gonzalez, A.-R. O. Raji, N. M. Trease and C. P. Grey, Nat. Energy, 2017, 2, 16216 CrossRef.
- H. D. Bale and P. W. Schmidt, Phys. Rev. Lett., 1984, 53, 596 CrossRef CAS.
- L. Feigin and D. I. Svergun, Structure analysis by small-angle X-ray and neutron scattering, Springer, 1987 Search PubMed.
- M. Gardner, A. North, J. C. Dore, C. S.-M. de Lecea and D. Cazorla-Amoros, Studies in Surface Science and Catalysis, Elsevier, 1994, vol. 87, pp. 273–281 Search PubMed.
- D. Lozano-Castelló, E. Raymundo-Piñero, D. Cazorla-Amorós, A. Linares-Solano, M. Müller and C. Riekel, Carbon, 2002, 40, 2727–2735 CrossRef.
- D. Lozano-Castelló, D. Cazorla-Amorós, A. Linares-Solano, P. J. Hall, D. Gascon and C. Galan, Carbon, 2001, 39, 1343–1354 CrossRef.
- J. Calo and P. Hall, Carbon, 2004, 42, 1299–1304 CrossRef CAS.
- D. Stevens and J. Dahn, J. Electrochem. Soc., 2000, 147, 4428–4431 CrossRef CAS.
- F. Ehrburger-Dolle, I. Morfin, E. Geissler, F. Bley, F. Livet, C. Vix-Guterl, S. Saadallah, J. Parmentier, M. Reda and J. Patarin, Langmuir, 2003, 19, 4303–4308 CrossRef CAS.
- R. Kyutt, E. Smorgonskaya, A. Danishevskii, S. Gordeev and A. Grechinskaya, Phys. Solid State, 1999, 41, 1359–1363 CrossRef CAS.
- T. Iiyama, Y. Kobayashi, K. Kaneko and S. Ozeki, Colloids Surf., A, 2004, 241, 207–213 CrossRef CAS.
- T. Ohba, T. Omori, H. Kanoh and K. Kaneko, J. Phys. Chem. B, 2004, 108, 27–30 CrossRef CAS.
- P. Ruch, M. Hahn, D. Cericola, A. Menzel, R. Kötz and A. Wokaun, Carbon, 2010, 48, 1880–1888 CrossRef CAS.
- J. L. Bañuelos, G. Feng, P. F. Fulvio, S. Li, G. Rother, S. Dai, P. T. Cummings and D. J. Wesolowski, Chem. Mater., 2013, 26, 1144–1153 CrossRef.
- R. Futamura, T. Iiyama, Y. Takasaki, Y. Gogotsi, M. J. Biggs, M. Salanne, J. Ségalini, P. Simon and K. Kaneko, Nat. Mater., 2017, 1225–1232 CrossRef CAS PubMed.
- C. Prehal, D. Weingarth, E. Perre, R. T. Lechner, H. Amenitsch, O. Paris and V. Presser, Energy Environ. Sci., 2015, 8, 1725–1735 RSC.
- P. Debye, H. Anderson Jr and H. Brumberger, J. Appl. Phys., 1957, 28, 679–683 CrossRef CAS.
- O. Glatter and O. Kratky, Small angle X-ray scattering, Academic Press, 1982 Search PubMed.
- C. Pings and J. Waser, J. Chem. Phys., 1968, 48, 3016–3018 CrossRef CAS.
- D. Saurel, J. Segalini, M. Jauregui, A. Pendashteh, B. Daffos, P. Simon and M. Casas-Cabanas, Energy Storage Mater., 2019, 21, 162–173 CrossRef.
- C. Koczwara, C. Prehal, S. Haas, P. Boesecke, N. Huesing and O. Paris, ACS Appl. Mater. Interfaces, 2019, 11, 42214–42220 CrossRef CAS PubMed.
- P. J. Hall, S. Brown, J. Fernandez and J. Calo, Carbon, 2000, 38, 1257 CrossRef CAS.
- J. S. Gethner, J. Appl. Phys., 1986, 59, 1068–1085 CrossRef CAS.
- H. B. Stuhrmann, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 181–191 CrossRef CAS PubMed.
- K. Yurekli, C. A. Mitchell and R. Krishnamoorti, J. Am. Chem. Soc., 2004, 126, 9902–9903 CrossRef CAS PubMed.
- S. Boukhalfa, L. He, Y. B. Melnichenko and G. Yushin, Angew. Chem., Int. Ed., 2013, 52, 4618–4622 CrossRef CAS PubMed.
- S. Boukhalfa, D. Gordon, L. He, Y. B. Melnichenko, N. Nitta, A. Magasinski and G. Yushin, ACS Nano, 2014, 8, 2495–2503 CrossRef CAS PubMed.
- A. Sharma, T. Kyotani and A. Tomita, Carbon, 2000, 38, 1977–1984 CrossRef CAS.
- H. Takagi, K. Maruyama, N. Yoshizawa, Y. Yamada and Y. Sato, Fuel, 2004, 83, 2427–2433 CrossRef CAS.
- K. Xia, Q. Gao, J. Jiang and J. Hu, Carbon, 2008, 46, 1718–1726 CrossRef CAS.
- F. Fina, S. K. Callear, G. M. Carins and J. T. Irvine, Chem. Mater., 2015, 27, 2612–2618 CrossRef CAS.
- A. Thess, R. Lee, P. Nikolaev, H. Dai, P. Petit, J. Robert, C. Xu, Y. H. Lee, S. G. Kim and A. G. Rinzler, Science, 1996, 273, 483–487 CrossRef CAS PubMed.
- T. Ohkubo, T. Iiyama, K. Nishikawa, T. Suzuki and K. Kaneko, J. Phys. Chem. B, 1999, 103, 1859–1863 CrossRef CAS.
- M. Fukano, T. Fujimori, J. Segalini, E. Iwama, P.-L. Taberna, T. Iiyama, T. Ohba, H. Kanoh, Y. Gogotsi and P. Simon, J. Phys. Chem. C, 2013, 117, 5752–5757 CrossRef CAS.
- F. W. Richey and Y. A. Elabd, J. Phys. Chem. Lett., 2012, 3, 3297–3301 CrossRef CAS.
- M. Osawa and M. Ikeda, J. Phys. Chem., 1991, 95, 9914–9919 CrossRef CAS.
- M. Osawa, K.-I. Ataka, K. Yoshii and Y. Nishikawa, Appl. Spectrosc., 1993, 47, 1497–1502 CrossRef CAS.
- F. W. Richey, B. Dyatkin, Y. Gogotsi and Y. A. Elabd, J. Am. Chem. Soc., 2013, 135, 12818–12826 CrossRef CAS PubMed.
- F. W. Richey, C. Tran, V. Kalra and Y. A. Elabd, J. Phys. Chem. C, 2014, 118, 21846–21855 CrossRef CAS.
- M. Hantel, V. Presser, R. Kötz and Y. Gogotsi, Electrochem. Commun., 2011, 13, 1221–1224 CrossRef CAS.
- M. M. Hantel, V. Presser, J. K. McDonough, G. Feng, P. T. Cummings, Y. Gogotsi and R. Kötz, J. Electrochem. Soc., 2012, 159, A1897–A1903 CrossRef CAS.
- M. Hantel, D. Weingarth and R. Kötz, Carbon, 2014, 69, 275–286 CrossRef CAS.
- L.-H. Shao, J. Biener, D. Kramer, R. N. Viswanath, T. F. Baumann, A. V. Hamza and J. Weissmüller, Phys. Chem. Chem. Phys., 2010, 12, 7580–7587 RSC.
- C. Koczwara, S. Rumswinkel, C. Prehal, N. Jäckel, M. S. Elsässer, H. Amenitsch, V. Presser, N. Hüsing and O. Paris, ACS Appl. Mater. Interfaces, 2017, 9, 23319–23324 CrossRef CAS PubMed.
- N. Jäckel, S. Patrick Emge, B. Krüner, B. Roling and V. Presser, J. Phys. Chem. C, 2017, 121, 19120–19128 CrossRef.
- D. Moreno, Y. Bootwala, W.-Y. Tsai, Q. Gao, F. Shen, N. Balke, K. B. Hatzell and M. C. Hatzell, Environ. Sci. Technol. Lett., 2018, 5, 745–749 CrossRef CAS.
- J. Ming, Z. Cao, Q. Li, W. Wahyudi, W. Wang, L. Cavallo, K.-J. Park, Y.-K. Sun and H. N. Alshareef, ACS Energy Lett., 2019, 4, 1584–1593 CrossRef CAS.
- W.-Y. Tsai, J. Come, W. Zhao, R. Wang, G. Feng, B. P. Thapaliya, S. Dai, L. Collins and N. Balke, Nano Energy, 2019, 60, 886–893 CrossRef CAS.
- S. Liu, J. Peng, L. Chen, P. Sebastián, J. M. Feliu, J. Yan and B. Mao, Electrochim. Acta, 2019, 309, 11–17 CrossRef CAS.
- Y. Fu and A. V. Rudnev, Curr. Opin. Electrochem., 2017, 1, 59–65 CrossRef CAS.
- R. Wen, B. Rahn and O. M. Magnussen, Angew. Chem., Int. Ed., 2015, 54, 6062–6066 CrossRef CAS PubMed.
- J. H. Raberg, J. Vatamanu, S. J. Harris, C. H. M. van Oversteeg, A. Ramos, O. Borodin and T. Cuk, J. Phys. Chem. Lett., 2019, 10, 3381–3389 CrossRef CAS PubMed.
- A. J. Ilott, M. Mohammadi, H. J. Chang, C. P. Grey and A. Jerschow, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10779–10784 CrossRef CAS PubMed.
- G. Oukali, E. Salager, M. R. Ammar, C.-E. Dutoit, V. Sarou-Kanian, P. Simon, E. Raymundo-Piñero and M. Deschamps, ACS Nano, 2019, 13, 12810–12815 CrossRef CAS PubMed.
- J. Martí, G. Nagy, E. Guàrdia and M. C. Gordillo, J. Phys. Chem. B, 2006, 110, 23987–23994 CrossRef PubMed.
- S. A. Kislenko, I. S. Samoylov and R. H. Amirov, Phys. Chem. Chem. Phys., 2009, 11, 5584–5590 RSC.
- H. Liu, C. J. Jameson and S. Murad, Mol. Simul., 2008, 34, 169–175 CrossRef CAS.
- J. Vatamanu, Z. Hu, D. Bedrov, C. Perez and Y. Gogotsi, J. Phys. Chem. Lett., 2013, 4, 2829–2837 CrossRef CAS.
- J. Vatamanu, M. Vatamanu and D. Bedrov, ACS Nano, 2015, 9, 5999–6017 CrossRef CAS PubMed.
- J. Vatamanu, O. Borodin, M. Olguin, G. Yushin and D. Bedrov, J. Mater. Chem. A, 2017, 5, 21049–21076 RSC.
- Q. Shao, L. Huang, J. Zhou, L. Lu, L. Zhang, X. Lu, S. Jiang, K. E. Gubbins and W. Shen, Phys. Chem. Chem. Phys., 2008, 10, 1896–1906 RSC.
- R. K. Kalluri, D. Konatham and A. Striolo, J. Phys. Chem. C, 2011, 115, 13786–13795 CrossRef CAS.
- S. Kondrat and A. Kornyshev, J. Phys.: Condens. Matter, 2010, 23, 022201 CrossRef PubMed.
- S. Kondrat, N. Georgi, M. V. Fedorov and A. A. Kornyshev, Phys. Chem. Chem. Phys., 2011, 13, 11359–11366 RSC.
- J. Palmer, A. Llobet, S.-H. Yeon, J. Fischer, Y. Shi, Y. Gogotsi and K. Gubbins, Carbon, 2010, 48, 1116–1123 CrossRef CAS.
- H. Wang and L. Pilon, J. Power Sources, 2013, 221, 252–260 CrossRef CAS.
- C. Merlet, C. Péan, B. Rotenberg, P. A. Madden, B. Daffos, P. L. Taberna, P. Simon and M. Salanne, Nat. Commun., 2013, 4, 2701 CrossRef CAS PubMed.
- J. Seebeck, P. Schiffels, S. Schweizer, J.-R. Hill and R. H. Meissner, J. Phys. Chem. C, 2020, 124, 5515–5521 CrossRef CAS.
- Z. Ryu, J. Zheng, M. Wang and B. Zhang, Carbon, 1999, 37, 1257–1264 CrossRef CAS.
- J. Jagiello and M. Thommes, Carbon, 2004, 42, 1227–1232 CrossRef CAS.
- T. Centeno and F. Stoeckli, Carbon, 2010, 48, 2478–2486 CrossRef CAS.
- X. Hu, M. Radosz, K. A. Cychosz and M. Thommes, Environ. Sci. Technol., 2011, 45, 7068–7074 CrossRef CAS PubMed.
- M. Sevilla, J. B. Parra and A. B. Fuertes, ACS Appl. Mater. Interfaces, 2013, 5, 6360–6368 CrossRef CAS PubMed.
- K. T. Klasson, M. Uchimiya and I. M. Lima, Chemosphere, 2014, 111, 129–134 CrossRef PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of simple liquids: with applications to soft matter, Academic Press, 2013 Search PubMed.
- G. Jeanmairet, M. Levesque and D. Borgis, J. Chem. Phys., 2013, 139, 154101 CrossRef PubMed.
- Y. Liu, S. Zhao and J. Wu, J. Chem. Theory Comput., 2013, 9, 1896–1908 CrossRef CAS PubMed.
- R. Ramirez, R. Gebauer, M. Mareschal and D. Borgis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 031206 CrossRef PubMed.
- R. Ramirez and D. Borgis, J. Phys. Chem. B, 2005, 109, 6754–6763 CrossRef CAS PubMed.
- L. Gendre, R. Ramirez and D. Borgis, Chem. Phys. Lett., 2009, 474, 366–370 CrossRef CAS.
- S. Zhao, R. Ramirez, R. Vuilleumier and D. Borgis, J. Chem. Phys., 2011, 134, 194102 CrossRef PubMed.
- M. Levesque, R. Vuilleumier and D. Borgis, J. Chem. Phys., 2012, 137, 034115 CrossRef PubMed.
- G. Jeanmairet, M. Levesque, R. Vuilleumier and D. Borgis, J. Phys. Chem. Lett., 2013, 4, 619–624 CrossRef CAS PubMed.
- C. Zhan, M. R. Ceron, S. A. Hawks, M. Otani, B. C. Wood, T. A. Pham, M. Stadermann and P. G. Campbell, Nat. Commun., 2019, 10, 4858 CrossRef PubMed.
- The Monte Carlo Method, ed. Y. A. Shreider, N. P. Buslenko, D. I. Golenko, I. M. Sobol and V. G. Sragovich, Pergamon, 1966, pp. 1–90 Search PubMed.
- K. Kiyohara and K. Asaka, J. Chem. Phys., 2007, 126, 214704 CrossRef PubMed.
- R. Burt, G. Birkett and X. Zhao, Phys. Chem. Chem. Phys., 2014, 16, 6519–6538 RSC.
- Y. Bu, T. Sun, Y. Cai, L. Du, O. Zhuo, L. Yang, Q. Wu, X. Wang and Z. Hu, Adv. Mater., 2017, 29, 1700470 CrossRef PubMed.
- K.-L. Yang, S. Yiacoumi and C. Tsouris, J. Chem. Phys., 2002, 117, 8499–8507 CrossRef CAS.
- K. Kiyohara and K. Asaka, J. Phys. Chem. C, 2007, 111, 15903–15909 CrossRef CAS.
- T. Ohba, S. Yamamoto, A. Takase, M. Yudasaka and S. Iijima, Carbon, 2015, 88, 133–138 CrossRef CAS.
- S. Kondrat and A. A. Kornyshev, Nanoscale Horiz., 2016, 1, 45–52 RSC.
- S. R. Varanasi, A. H. Farmahini and S. K. Bhatia, J. Phys. Chem. C, 2015, 119, 28809–28818 CrossRef CAS.
- A. Hartel, J. Phys.: Condens. Matter, 2017, 29, 423002 CrossRef PubMed.
- M. Dudka, S. Kondrat, A. Kornyshev and G. Oshanin, J. Phys.: Condens. Matter, 2016, 28, 464007 CrossRef.
- D.-E. Jiang, Z. Jin and J. Wu, Nano Lett., 2011, 11, 5373–5377 CrossRef CAS PubMed.
- T. Ohba and K. Kaneko, J. Phys. Chem. C, 2013, 117, 17092–17098 CrossRef CAS.
- J. M. Haile, Molecular dynamics simulation: elementary methods, Wiley, New York, 1992 Search PubMed.
- F.-R. C. Chang, N. Skipper and G. Sposito, Langmuir, 1998, 14, 1201–1207 CrossRef CAS.
- G. Feng and P. T. Cummings, J. Phys. Chem. Lett., 2011, 2, 2859–2864 CrossRef CAS.
- C. Merlet, C. Péan, B. Rotenberg, P. A. Madden, P. Simon and M. Salanne, J. Phys. Chem. Lett., 2012, 4, 264–268 CrossRef.
- P. M. Vora, P. Gopu, M. Rosario-Canales, C. R. Pérez, Y. Gogotsi, J. J. Santiago-Avilés and J. M. Kikkawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155114 CrossRef.
- A. C. Forse, C. l. Merlet, J. M. Griffin and C. P. Grey, J. Am. Chem. Soc., 2016, 138, 5731–5744 CrossRef CAS PubMed.
- C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, Nat. Mater., 2012, 11, 306–310 CrossRef CAS PubMed.
- N. N. Rajput, J. Monk, R. Singh and F. R. Hung, J. Phys. Chem. C, 2012, 116, 5169–5181 CrossRef CAS.
- S. Li, K. S. Han, G. Feng, E. W. Hagaman, L. Vlcek and P. T. Cummings, Langmuir, 2013, 29, 9744–9749 CrossRef CAS PubMed.
- L. Xing, J. Vatamanu, O. Borodin and D. Bedrov, J. Phys. Chem. Lett., 2013, 4, 132–140 CrossRef CAS PubMed.
- J. N. Neal, K. L. Van Aken, Y. Gogotsi, D. J. Wesolowski and J. Wu, Phys. Rev. Appl., 2017, 8, 34018 CrossRef.
- K. Xu, Z. Lin, C. Merlet, P. L. Taberna, L. Miao, J. Jiang and P. Simon, ChemSusChem, 2018, 11, 1892–1899 CrossRef CAS PubMed.
- Y. M. Liu, C. Merlet and B. Smit, ACS Cent. Sci., 2019, 5, 1813–1823 CrossRef CAS PubMed.
- A. Belhboub, E. H. Lahrar, P. Simon and C. Merlet, Electrochim. Acta, 2019, 327, 135022 CrossRef CAS.
- S. Kondrat, P. Wu, R. Qiao and A. A. Kornyshev, Nat. Mater., 2014, 13, 387 CrossRef CAS PubMed.
- O. N. Kalugin, V. V. Chaban, V. V. Loskutov and O. V. Prezhdo, Nano Lett., 2008, 8, 2126–2130 CrossRef CAS PubMed.
- C. Péan, B. Rotenberg, P. Simon and M. Salanne, J. Power Sources, 2016, 326, 680–685 CrossRef.
- T. Mo, S. Bi, Y. Zhang, V. Presser, X. Wang, Y. Gogotsi and G. Feng, ACS Nano, 2020, 14, 2395–2403 CrossRef CAS PubMed.
- S. Delmerico and J. G. McDaniel, Carbon, 2020, 161, 550–561 CrossRef CAS.
- S. Zhu, J. Li, L. Ma, C. He, E. Liu, F. He, C. Shi and N. Zhao, Mater. Lett., 2018, 233, 294–297 CrossRef CAS.
- H. Su, S. Lin, S. Deng, C. Lian, Y. Shang and H. Liu, Nanoscale Adv., 2019, 1, 2162–2166 RSC.
- X. Zhang, X. Wang, L. Jiang, H. Wu, C. Wu and J. Su, J. Power Sources, 2012, 216, 290–296 CrossRef CAS.
- A. Lewandowski, A. Olejniczak, M. Galinski and I. Stepniak, J. Power Sources, 2010, 195, 5814–5819 CrossRef CAS.
- T. Cottineau, M. Toupin, T. Delahaye, T. Brousse and D. Bélanger, Appl. Phys. A: Solids Surf., 2005, 82, 599–606 CrossRef.
- J. Suárez-Guevara, V. Ruiz and P. Gomez-Romero, J. Mater. Chem. A, 2014, 2, 1014–1021 RSC.
- V. Khomenko, E. Raymundo-Pinero, E. Frackowiak and F. Beguin, Appl. Phys. A: Solids Surf., 2006, 82, 567–573 CrossRef CAS.
- F. Wang, S. Xiao, Y. Hou, C. Hu, L. Liu and Y. Wu, RSC Adv., 2013, 3, 13059 RSC.
- V. Khomenko, E. Raymundo-Piñero and F. Béguin, J. Power Sources, 2010, 195, 4234–4241 CrossRef CAS.
- L. Demarconnay, E. Raymundo-Piñero and F. Béguin, Electrochem. Commun., 2010, 12, 1275–1278 CrossRef CAS.
- K. Fic, G. Lota, M. Meller and E. Frackowiak, Energy Environ. Sci., 2012, 5, 5842–5850 RSC.
- L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943 CrossRef CAS PubMed.
- G. Hasegawa, K. Kanamori, T. Kiyomura, H. Kurata, T. Abe and K. Nakanishi, Chem. Mater., 2016, 28, 3944–3950 CrossRef CAS.
- D. Reber, R.-S. Kühnel and C. Battaglia, Sustainable Energy Fuels, 2017, 1, 2155–2161 RSC.
- X. Bu, L. Su, Q. Dou, S. Lei and X. Yan, J. Mater. Chem. A, 2019, 7, 7541–7547 RSC.
- Q. Dou, S. Lei, D.-W. Wang, Q. Zhang, D. Xiao, H. Guo, A. Wang, H. Yang, Y. Li, S. Shi and X. Yan, Energy Environ. Sci., 2018, 11, 3212–3219 RSC.
- C. Cheng, G. Jiang, G. P. Simon, J. Z. Liu and D. Li, Nat. Nanotechnol., 2018, 13, 685 CrossRef CAS PubMed.
- B. Pal, S. Yang, S. Ramesh, V. Thangadurai and R. Jose, Nanoscale Adv., 2019, 1, 3807–3835 RSC.
- P. Azaïs, L. Duclaux, P. Florian, D. Massiot, M.-A. Lillo-Rodenas, A. Linares-Solano, J.-P. Peres, C. Jehoulet and F. Béguin, J. Power Sources, 2007, 171, 1046–1053 CrossRef.
- M. Conte, Fuel Cells, 2010, 10, 806–818 CrossRef CAS.
- B. Ricketts and C. Ton-That, J. Power Sources, 2000, 89, 64–69 CrossRef CAS.
- P. Kurzweil and M. Chwistek, J. Power Sources, 2008, 176, 555–567 CrossRef CAS.
- H. Gualous, R. Gallay, G. Alcicek, B. Tala-Ighil, A. Oukaour, B. Boudart and P. Makany, Microelectron. Reliab., 2010, 50, 1783–1788 CrossRef CAS.
- D. Cericola, R. Kötz and A. Wokaun, J. Power Sources, 2011, 196, 3114–3118 CrossRef CAS.
- Y. Liu, B. Réty, C. M. Ghimbeu, B. Soucaze-Guillous, P.-L. Taberna and P. Simon, J. Power Sources, 2019, 434, 226734 CrossRef CAS.
- D. E. Jiang, Z. Jin, D. Henderson and J. Wu, J. Phys. Chem. Lett., 2012, 3, 1727–1731 CrossRef CAS PubMed.
- R. Lin, P. Huang, J. Segalini, C. Largeot, P.-L. Taberna, J. Chmiola, Y. Gogotsi and P. Simon, Electrochim. Acta, 2009, 54, 7025–7032 CrossRef CAS.
- R. Lin, P. L. Taberna, J. Chmiola, D. Guay, Y. Gogotsi and P. Simon, J. Electrochem. Soc., 2009, 156, A7–A12 CrossRef CAS.
- C. Decaux, C. M. Ghimbeu, M. Dahbi, M. Anouti, D. Lemordant, F. Beguin, C. Vix-Guterl and E. Raymundo-Pinero, J. Power Sources, 2014, 263, 130–140 CrossRef CAS.
- T. Husch, N. D. Yilmazer, A. Balducci and M. Korth, Phys. Chem. Chem. Phys., 2015, 17, 3394–3401 RSC.
- C. Schütter, T. Husch, M. Korth and A. Balducci, J. Phys. Chem. C, 2015, 119, 13413–13424 CrossRef.
- C. Schütter, T. Husch, V. Viswanathan, S. Passerini, A. Balducci and M. Korth, J. Power Sources, 2016, 326, 541–548 CrossRef.
- J. Krummacher, C. Schütter, S. Passerini and A. Balducci, ChemElectroChem, 2017, 4, 353–361 CrossRef CAS.
- C. Schütter, S. Passerini, M. Korth and A. Balducci, Electrochim. Acta, 2017, 224, 278–284 CrossRef.
- K. R. Seddon, J. Chem. Technol. Biotechnol., 1997, 68, 351–356 CrossRef CAS.
- M. Ue and M. Takeda, J. Korean Electrochem. Soc., 2002, 5, 192–196 CrossRef CAS.
- M. Galiński, A. Lewandowski and I. Stępniak, Electrochim. Acta, 2006, 51, 5567–5580 CrossRef.
- K. Yuyama, G. Masuda, H. Yoshida and T. Sato, J. Power Sources, 2006, 162, 1401–1408 CrossRef CAS.
- A. Balducci, R. Dugas, P.-L. Taberna, P. Simon, D. Plee, M. Mastragostino and S. Passerini, J. Power Sources, 2007, 165, 922–927 CrossRef CAS.
- C. Arbizzani, M. Biso, D. Cericola, M. Lazzari, F. Soavi and M. Mastragostino, J. Power Sources, 2008, 185, 1575–1579 CrossRef CAS.
- A. Brandt and A. Balducci, J. Power Sources, 2014, 250, 343–351 CrossRef CAS.
- V. Ruiz, T. Huynh, S. R. Sivakkumar and A. G. Pandolfo, RSC Adv., 2012, 2, 5591 RSC.
- J. Wang, H. Tang, L. Zhang, H. Ren, R. Yu, Q. Jin, J. Qi, D. Mao, M. Yang, Y. Wang, P. Liu, Y. Zhang, Y. Wen, L. Gu, G. Ma, Z. Su, Z. Tang, H. Zhao and D. Wang, Nat. Energy, 2016, 1, 16050 CrossRef CAS.
- E. Frackowiak, G. Lota and J. Pernak, Appl. Phys. Lett., 2005, 86, 164104 CrossRef.
- A. Krause and A. Balducci, Electrochem. Commun., 2011, 13, 814–817 CrossRef CAS.
- A. Brandt, C. Ramirez-Castro, M. Anouti and A. Balducci, J. Mater. Chem. A, 2013, 1, 12669 RSC.
- K. N. Marsh, J. A. Boxall and R. Lichtenthaler, Fluid Phase Equilib., 2004, 219, 93–98 CrossRef CAS.
- H. Kurig, M. Vestli, A. Jänes and E. Lust, Electrochem. Solid-State Lett., 2011, 14, A120 CrossRef CAS.
- H. Lu, L. He, X. Li, W. Zhang, J. Che, X. Liu, Z. Hou, H. Du and Y. Qu, J. Mater. Sci.: Mater. Electron., 2019, 30, 13933–13938 CrossRef CAS.
- C. Lian, K. Liu, K. L. Van Aken, Y. Gogotsi, D. J. Wesolowski, H. L. Liu, D. E. Jiang and J. Z. Wu, ACS Energy Lett., 2016, 1, 21–26 CrossRef CAS.
- M. W. Thompson, R. Matsumoto, R. L. Sacci, N. C. Sanders and P. T. Cummings, J. Phys. Chem. B, 2019, 123, 1340–1347 CrossRef CAS PubMed.
- R.-S. Kühnel, S. Obeidi, M. Lübke, A. Lex-Balducci and A. Balducci, J. Appl. Electrochem., 2013, 43, 697–704 CrossRef.
- C. Lian, H. Liu, C. Li and J. Wu, AIChE J., 2019, 65, 804–810 CrossRef CAS.
- S. Perkin, M. Salanne, P. Madden and R. Lynden-Bell, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E4121–E4121 CrossRef CAS PubMed.
- B. Skinner, M. Loth and B. Shklovskii, Phys. Rev. Lett., 2010, 104, 128302 CrossRef PubMed.
- Z. A. Goodwin and A. A. Kornyshev, Electrochem. Commun., 2017, 82, 129–133 CrossRef CAS.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224 RSC.
- K. Ma, C. Lian, C. E. Woodward and B. Qin, Chem. Phys. Lett., 2020, 739, 137001 CrossRef.
- A. C. Forse, J. M. Griffin, C. L. Merlet, P. M. Bayley, H. Wang, P. Simon and C. P. Grey, J. Am. Chem. Soc., 2015, 137, 7231–7242 CrossRef CAS PubMed.
- X. Wang, H. Zhou, E. Sheridan, J. C. Walmsley, D. Ren and D. Chen, Energy Environ. Sci., 2016, 9, 232–239 RSC.
- J. N. Neal, D. J. Wesolowski, D. Henderson and J. Wu, J. Chem. Phys., 2017, 146, 174701 CrossRef PubMed.
- T. Brousse, D. Bélanger and J. W. Long, J. Electrochem. Soc., 2015, 162, A5185–A5189 CrossRef CAS.
- P. Simon, Y. Gogotsi and B. Dunn, Science, 2014, 343, 1210–1211 CrossRef CAS PubMed.
- B. E. Conway, J. Electrochem. Soc., 1991, 138, 1539–1548 CrossRef CAS.
- K. Fic, E. Frackowiak and F. Béguin, J. Mater. Chem., 2012, 22, 24213–24223 RSC.
- B. Akinwolemiwa, C. Peng and G. Z. Chen, J. Electrochem. Soc., 2015, 162, A5054–A5059 CrossRef CAS.
- G. Lota, K. Fic and E. Frackowiak, Electrochem. Commun., 2011, 13, 38–41 CrossRef CAS.
- G. Lota and E. Frackowiak, Electrochem. Commun., 2009, 11, 87–90 CrossRef CAS.
- S. Roldán, M. Granda, R. Menéndez, R. Santamaría and C. Blanco, J. Phys. Chem. C, 2011, 115, 17606–17611 CrossRef.
- S. Roldán, C. Blanco, M. Granda, R. Menéndez and R. Santamaría, Angew. Chem., Int. Ed., 2011, 50, 1699–1701 CrossRef PubMed.
- S. Senthilkumar, R. K. Selvan and J. Melo, J. Mater. Chem. A, 2013, 1, 12386–12394 RSC.
- S. Senthilkumar, R. K. Selvan, N. Ponpandian, J. Melo and Y. Lee, J. Mater. Chem. A, 2013, 1, 7913–7919 RSC.
- S. Senthilkumar, R. K. Selvan, Y. Lee and J. Melo, J. Mater. Chem. A, 2013, 1, 1086–1095 RSC.
- B. Gorska, E. Frackowiak and F. Beguin, Curr. Opin. Electrochem., 2018, 9, 95–105 CrossRef CAS.
- S. Sathyamoorthi, V. Suryanarayanan and D. Velayutham, J. Power Sources, 2015, 274, 1135–1139 CrossRef CAS.
- H. J. Xie, B. Gélinas and D. Rochefort, Electrochem. Commun., 2016, 66, 42–45 CrossRef CAS.
- E. Mourad, L. Coustan, P. Lannelongue, D. Zigah, A. Mehdi, A. Vioux, S. A. Freunberger, F. Favier and O. Fontaine, Nat. Mater., 2017, 16, 446–453 CrossRef CAS PubMed.
- E. Mourad, L. Coustan, S. A. Freunberger, A. Mehdi, A. Vioux, F. Favier and O. Fontaine, Electrochim. Acta, 2016, 206, 513–523 CrossRef CAS.
- O. Fontaine, Energy Storage Mater., 2019, 21, 240–245 CrossRef.
- C. Bodin, E. Mourad, D. Zigah, S. Le Vot, S. A. Freunberger, F. Favier and O. Fontaine, Faraday Discuss., 2018, 206, 393–404 RSC.
- K. Wang, J. Wang, S. Zhao, Z. Wang and S. Wang, J. Power Sources, 2019, 434, 226745 CrossRef CAS.
- Y. Yoon, W. Cho, J. Lim and D. J. Choi, J. Power Sources, 2001, 101, 126–129 CrossRef CAS.
- P. Sivaraman, V. Hande, V. Mishra, C. S. Rao and A. Samui, J. Power Sources, 2003, 124, 351–354 CrossRef CAS.
- K. Wang, W. Zou, B. Quan, A. Yu, H. Wu, P. Jiang and Z. Wei, Adv. Energy Mater., 2011, 1, 1068–1072 CrossRef CAS.
- H. Gao and K. Lian, RSC Adv., 2014, 4, 33091–33113 RSC.
- L. Nègre, B. Daffos, P.-L. Taberna and P. Simon, J. Electrochem. Soc., 2015, 162, A5037–A5040 CrossRef.
- A. A. Łatoszyńska, G. Z. Żukowska, I. A. Rutkowska, P.-L. Taberna, P. Simon, P. J. Kulesza and W. Wieczorek, J. Power Sources, 2015, 274, 1147–1154 CrossRef.
- X. Peng, H. Liu, Q. Yin, J. Wu, P. Chen, G. Zhang, G. Liu, C. Wu and Y. Xie, Nat. Commun., 2016, 7, 11782 CrossRef CAS PubMed.
- B. Hsia, S. Wang, M.-S. Kim, C. Carraro and R. Maboudian, All solid-state micro-supercapacitors using ionogel electrolyte, 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS, XXVII), Barcelona, 2013, pp. 1328–1331.
- L. Yu and G. Z. Chen, Front. Chem., 2019, 7, 272 CrossRef CAS PubMed.
- L. Nègre, B. Daffos, V. Turq, P.-L. Taberna and P. Simon, Electrochim. Acta, 2016, 206, 490–495 CrossRef.
- S. Alipoori, S. Mazinani, S. H. Aboutalebi and F. Sharif, J. Energy Storage, 2020, 27, 101072 CrossRef.
- C. Yin, X. Liu, J. Wei, R. Tan, J. Zhou, M. Ouyang, H. Wang, S. J. Cooper, B. Wu, C. George and Q. Wang, J. Mater. Chem. A, 2019, 7, 8826–8831 RSC.
- B. Xu, H. Wang, Q. Zhu, N. Sun, B. Anasori, L. Hu, F. Wang, Y. Guan and Y. Gogotsi, Energy Storage Mater., 2018, 12, 128–136 CrossRef.
- L. Yu, L. Hu, B. Anasori, Y.-T. Liu, Q. Zhu, P. Zhang, Y. Gogotsi and B. Xu, ACS Energy Lett., 2018, 3, 1597–1603 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |





