Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rhodium(II)-catalyzed C–H aminations using N-mesyloxycarbamates: reaction pathway and by-product formation†
Emna
Azek
,
Maroua
Khalifa
,
Johan
Bartholoméüs
,
Matthias
Ernzerhof
and
Hélène
Lebel
 *
*
Département de Chimie, Université de Montréal, C.P. 6128, Succursale Centre-ville, Montréal, Québec, Canada H3C3J7. E-mail: helene.lebel@umontreal.ca
First published on 22nd October 2018
Abstract
N-Mesyloxycarbamates are practical nitrene precursors that undergo C–H amination reactions in the presence of rhodium dimer catalysts. Under these conditions, both oxazolidinones and chiral amines have been prepared in a highly efficient manner. Given the elevated reactivity of the intermediates involved in the catalytic cycle, mechanistic details have remained hypothetical, relying on indirect experiments. Herein a density functional theory (DFT) study is presented to validate the catalytic cycle of the rhodium-catalyzed C–H amination with N-mesyloxycarbamates. A concerted pathway involving Rh–nitrene species that undergoes C–H insertion is found to be favored over a stepwise C–N bond formation manifold. Density functional calculations and kinetic studies suggest that the rate-limiting step is the C–H insertion process rather than the formation of Rh–nitrene species. In addition, these studies provide mechanistic details about competitive by-product formation, resulting from an intermolecular reaction between the Rh–nitrene species and the N-mesyloxycarbamate anion.
Introduction
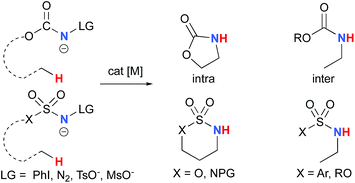
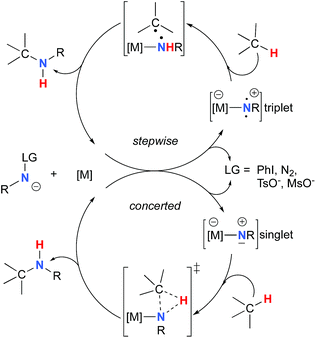
The synthesis of amines by the functionalization of C–H bonds has emerged as an efficient strategy to prepare molecules of relevance to many chemical areas, including the pharmaceutical industry.1–4 Significant advantages are associated with metal-catalyzed C–H amination via nitrene insertion, including mild reaction conditions as well as high chemo- and stereoselectivities.5,6 Among these processes, intramolecular metal-catalyzed C–H aminations with carbamate derivatives afford oxazolidinones in good to excellent yields,7–12 whereas intermolecular reactions produce amines bearing readily removable carbamate protecting groups (Scheme 1).13–16 Very recently, the synthesis of γ-lactams via C–H amidation was reported using tailored iridium catalysts.17 Alternatively, intramolecular cyclization with sulfamate derivatives has furnished the corresponding 6-membered oxathiazinane heterocycle intramolecularly.18–31The synthesis of sulfonyl-protected amines has also been achieved via intermolecular C–H amination processes.32–42 More recently, aryl and alkyl azides have been reported in metal-catalyzed intra- and intermolecular processes to afford various heterocyclic and amine products.43–54 Rhodium dimer complexes7,10–15,18–20,33–37,43–46 are the most reported catalysts, although Co,16,28–30,48–51 Cu,38–41,49 Ir,17,31 Fe,24,25,47,53,54 Mn,27,32 Ru21–23,32,42 and Ag8,9,26-catalyzed C–H amination processes have also been delineated. Most commonly used nitrene precursors include iminoiodinanes,7–9,18–27,32–41 azides,16,28–31,42–54 and N-sulfonyloxycarbamates.10–15 The generally accepted mechanism involves the formation of a metal nitrene species, which undergoes C–H insertion to form the observed product (Scheme 2).1–6 Two different mechanisms have been proposed for the C–H insertion/C–N formation step: a concerted C–H insertion, proceeding via a hydride transfer/C–N formation transition state and a stepwise process of hydrogen atom abstraction, followed by radical recombination. Due to their high reactivity, only a limited number of discrete metal−nitrene intermediates have been isolated.28,55–58 Consequently, in addition to various experimental analyses, density functional theory (DFT) studies have been instrumental in establishing the exact mechanism of metal nitrene C–H insertion reactions. With rhodium(II) dimer complexes, such as Rh2(OAc)4, using carbamate- and sulfamate-derived iminoiodinane reagents, a concerted asynchronous insertion of a singlet Rh(II)–nitrene has been found in previous computational studies,59,60 in agreement with what was observed experimentally.33,58,61 For Rh2(esp)2, an alternative one-electron mechanism involving Rh(II)–Rh(III) intermediates has been proposed with a concerted C–H insertion step.62–64 Conversely, computational and experimental data have established a stepwise mechanism for the C–H amination catalyzed by a diruthenium complex involving a short-lived diradical species.23,65
Calculations have suggested a substrate-based mechanism for Ru(II)–porphyrin66–69 and –pybox70 complexes, as the C–H insertion can also proceed via a concerted or a stepwise mechanism. In the case of first row metal complexes reacting with azide reagents, experimental and computational studies imply an open-shell electronic state of the metal nitrene (Co,49–51,71–73 Cu,40,74,75 Fe,25,76,77 Ni57), which reacts via a stepwise sequence.78 The first step involves a H-abstraction transition state and affords a radical intermediate that undergoes the C–N bond formation, which in some cases is a barrier-free process.74
Most computational studies had focused on the structure and reactivity of the metal nitrene species. As a result, little attention has been devoted to the formation of the metal nitrene species, and the type of nitrene precursors applied in C–H amination reactions. Namely, the rate-determining step is unknown for pre-oxidized metal nitrene precursors, such as N-sulfonyloxycarbamates. Furthermore, no studies have been conducted to establish the mechanism by which some particular substrates afforded ketones as by-products. Understanding the pathway producing these products may lead to ways to control the reaction to avoid their formation. Herein, the results of an in-depth mechanistic study with N-sulfonyloxycarbamates, known to produce oxazolidinones10–12 and carbamate-protected amines13–15 in high yields and selectivities (eqn (1) and(2)), are reported. The nature of the active amination reagent (metal nitrenoid vs. metal nitrene), the resting state of the catalyst, the rate-determining step, the mechanism (stepwise or concerted) and the pathway responsible for the formation of the by-products will be addressed in this computational study.
Results and discussion
Computational methods
A number of approximations were tested to determine their accuracy in reproducing the Rh2(OAc)4 crystal structure,79,80 the catalyst chosen for the DFT study (vide infra) (Table 1). The pure Perdew–Burke–Ernzerhof (PBE) functional81 was shown to best approximate the known X-ray data.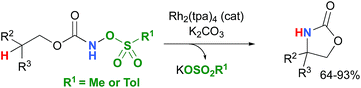 | (1) |
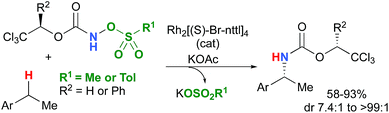 | (2) |
| Parameter °/Å | HF | LDA | BPW91 | BLYP | PBE | PBE1 | B3LYP | X-Ray |
|---|---|---|---|---|---|---|---|---|
| a See the ESI for the basis sets. | ||||||||
| Rh–Rh | 2.355 | 2.349 | 2.380 | 2.404 | 2.380 | 2.355 | 2.378 | 2.385 |
| Rh–O | 2.054 | 1.996 | 2.051 | 2.051 | 2.047 | 2.028 | 2.050 | 2.039 |
| C–O | 1.249 | 1.276 | 1.276 | 1.286 | 1.286 | 1.269 | 1.274 | 1.269 |
| C–C(CH3) | 1.504 | 1.489 | 1.489 | 1.521 | 1.511 | 1.502 | 1.510 | 1.499 |
| O–Rh–Rh | 87.9 | 88.8 | 88.7 | 88.6 | 88.7 | 88.6 | 88.4 | 88.1 |
| O–C–O | 124.6 | 125.6 | 125.6 | 125.9 | 126.0 | 125.7 | 125.5 | 124.8 |
The singlet–triplet energy difference (ΔEst) of the dirhodium–nitrene species ((HO(O)C)4Rh2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH) was calculated to be 1.4 kcal mol−1 with the Coupled-cluster (with) Single (and) Double (and Perturbative) Triple (excitations) (CCSD(T)) method,59 the most accurate level of computation. In comparison, the pure PBE functional method provided a value of 1.2 kcal mol−1, the closest among all other computational methods studied. Conversely, hybrid functional methods afforded singlet–triplet energy difference values superior to 10 kcal mol−1.82 Explicit relativistic effects treatment was also tested, but provided a less accurate value (0.8 kcal mol−1 with PBE-DKH/BS3).82 The reaction and activation energies were thus calculated using Kohn–Sham density functional theory (DFT) with the PBE approximation for the exchange–correlation energy. To evaluate the effect of solvent polarity on the energetics of the investigated reactions, single-point energy calculations were performed with the polarizable continuum model (PCM) in EtOAc (ε = 5.98) on the gas-phase optimized geometries.
NH) was calculated to be 1.4 kcal mol−1 with the Coupled-cluster (with) Single (and) Double (and Perturbative) Triple (excitations) (CCSD(T)) method,59 the most accurate level of computation. In comparison, the pure PBE functional method provided a value of 1.2 kcal mol−1, the closest among all other computational methods studied. Conversely, hybrid functional methods afforded singlet–triplet energy difference values superior to 10 kcal mol−1.82 Explicit relativistic effects treatment was also tested, but provided a less accurate value (0.8 kcal mol−1 with PBE-DKH/BS3).82 The reaction and activation energies were thus calculated using Kohn–Sham density functional theory (DFT) with the PBE approximation for the exchange–correlation energy. To evaluate the effect of solvent polarity on the energetics of the investigated reactions, single-point energy calculations were performed with the polarizable continuum model (PCM) in EtOAc (ε = 5.98) on the gas-phase optimized geometries.
Chemical models
In the interest of computational tractability, Rh2(OAc)4 was chosen as the model for dirhodiumtetracarboxylate complexes. Although experimentally it was not the most active catalyst for the C–H amination reaction with N-mesyloxycarbamates due to poor solubility, the catalyst provides the desired product with acceptable yields.10–15 Both intramolecular and intermolecular benzylic and aliphatic C–H insertion reactions were studied by DFT, with 2-phenylethyl N-mesyloxycarbamate (A) and n-hexyl N-mesyloxycarbamate (B) as the respective substrates (eqn (3) and (4)). The formation of the primary carbamate and the corresponding carbonyl compound was also studied, as these are known by-products identified namely in reactions with secondary N-mesyloxycarbamates (vide infra). (R)-Phenyl 2,2,2-trichloroethyl N-mesyloxycarbamate (C) is known to undergo C–H amination with 2-phenylethane and was selected to model the intermolecular pathway (eqn (5)). | (3) |
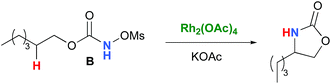 | (4) |
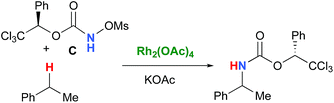 | (5) |
Formation of the N-mesyloxycarbamate anion
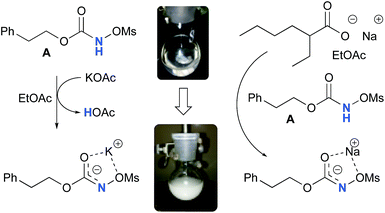
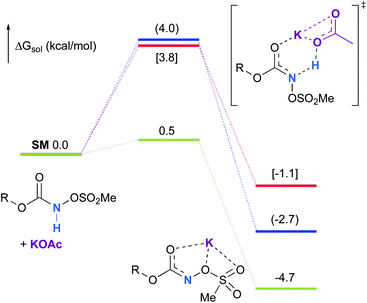
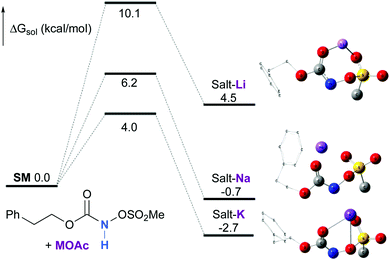
Experimentally, the reaction between N-mesyloxycarbamate A and potassium acetate or sodium 2-ethylhexanoate (known to be soluble in organic solvents) produced the potassium or sodium N-mesyloxycarbamate salt as a white precipitate (Scheme 3).12 The rhodium catalyst was not necessary for salt generation to occur. When the deprotonation with potassium acetate was studied in silico, all three models afforded potassium N-mesyloxycarbamate salts (Salt-K) with a small energy barrier of 0.5 to 4.0 kcal mol−1 (Fig. 1). All potassium salts were more stable than the corresponding N-mesyloxycarbamate starting material. The inner anion is doubly stabilized by the potassium cation, where the negative charge is distributed over the N–C–O moiety. The N–H of N-mesyloxycarbamate C is the most acidic (due to the electron withdrawing Cl3C group), leading to the most favoured TS and stable Salt-K. Similar results were obtained with sodium acetate and A with slightly higher values for the deprotonation TS (6.2 kcal mol−1), affording the sodium salt (−0.7 kcal mol−1). Of note, it is known that lithium bases afford only trace quantities of the desired amination product, likely due to the poor solubility of these reagents. In addition, DFT calculations showed that the energy barrier for the deprotonation TS with lithium acetate and A was substantially higher than that with sodium acetate (10.1 vs. 6.2 kcal mol−1), confirming the experimental observations, a 7-membered ring coordinated lithium salt (+4.5 kcal mol−1) was observed (Fig. 2).Formation of the rhodium nitrene species
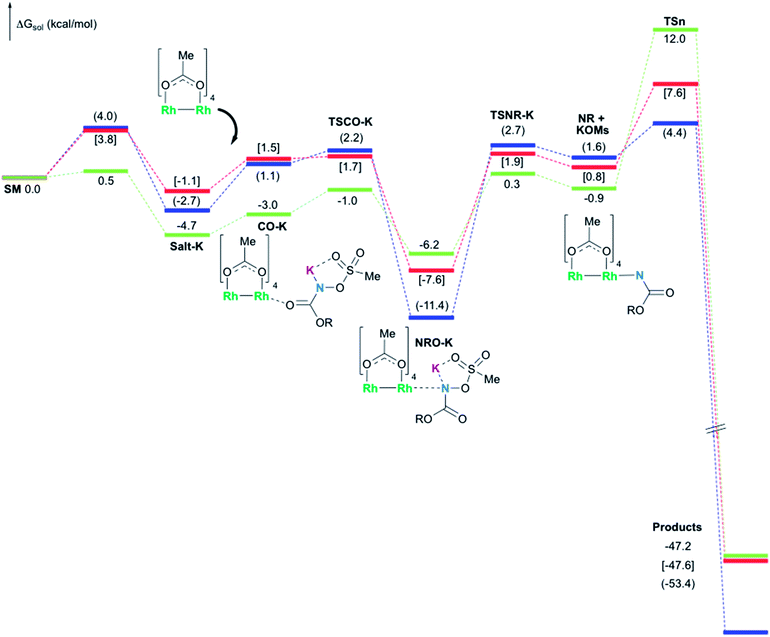
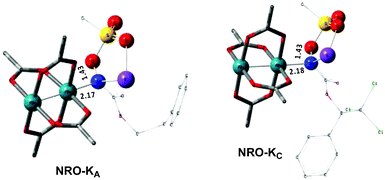
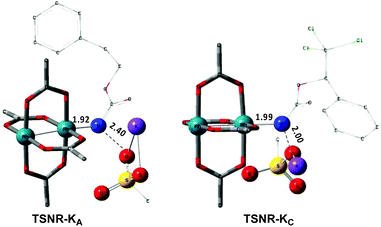
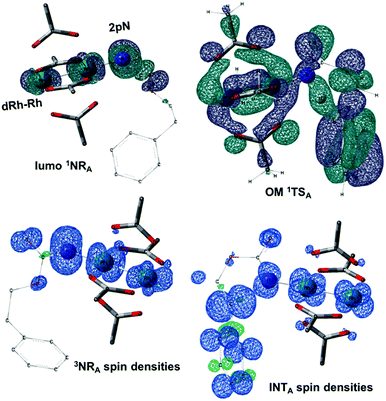
In the presence of Rh2(OAc)4, the potassium N-mesyloxycarbamate salt first forms a coordination complex (CO-K), in which the carbonyl of the carbamate is coordinated to the apical position of the rhodium complex (Fig. 3).83 The same relative stability order between the three models as previously seen for Salt-K is observed, indicating that CO-K complexes resemble their corresponding free potassium anions (Salt-K). The CO-K complex affords the stable nitrenoid species (NRO-K) via the transition state TSCO-K, where both carbamate carbonyl and nitrogen are coordinated to rhodium. The calculated activation barrier is lower than the one for the deprotonation transition state. NRO-K is the most stable metal intermediate, displaying a strong interaction between the nitrogen atom and the rhodium center, with the leaving group (MsOK) still bound to nitrogen. The Rh–nitrogen bond length of NRO-K is calculated to be 2.17–2.18 Å (Fig. 4). Conformations in which Me(Ms) and unbound O(Ms) are interchanged were also explored, but no further stabilization was observed. Compared to the less basic Salt-KC, Salt-K derived from A and B displays a stronger coordination with the Lewis acid rhodium, affording more stable NRO-K. In addition, a cation π-interaction between the phenyl group and potassium appears to stabilize NRO-KA (Fig. 4). Such an interaction is not present in model C, probably because of the sterically hindered trichloromethyl group. As the most stable rhodium intermediate, rhodium nitrenoid species is likely the resting state of the catalyst in the catalytic cycle. Rhodium nitrenoid species subsequently undergoes an endergonic concerted elimination of the mesylate group affording reactive Rh–nitrene species (NR, Fig. 3). The departure of the mesylate ion is assisted by the counter anion (K), resulting in the stretching of the N–OMs bond and shortening of the N–Rh bond in the transition state (Fig. 5). All three rhodium nitrene species were computed to be higher in energy compared to their corresponding rhodium nitrenoid complexes. As a result, rhodium nitrenes are the most reactive intermediates, and may serve as the active species for delivery of the NR group. This is in contrast with previous reports, as the metal nitrene species were either as stable as the nitrenoid intermediate when using iminoiodinanes59 or more stable than the nitrenoid complex when using azide reagents.69,76,84 Rhodium nitrenes have three reactive centers localized in the Rh–Rh–N moiety as depicted in the analysis of frontier molecular orbitals of the singlet and triplet nitrene species (vide infra, Fig. 7). The endothermicity of the formation of rhodium nitrenes from rhodium nitrenoids (ΔHr = +25.7, +22.6, and +21.3 kcal mol−1 for NRA, NRB and NRC, respectively) is due to the cleavage of the N–O(Ms) bond to release the mesylate salt. Consequently, the formation of NR from NRO is entropy driven and the positive ΔG value (+13.0, +8.4, and +5.3 kcal mol−1 for NRA, NRB and NRC, respectively) is a consequence of an increase of the enthalpy. Experimentally, we observed the precipitation of KOMs, which prevented the reversibility of the conversion of NRO-K to NR. The rhodium nitrene derived from N-mesyloxycarbamate C is the most stable, possibly due to a positive electronic effect of the trichloromethyl group.C–H insertion with triplet vs. singlet rhodium nitrene species
The relative thermodynamic stability of singlet (1NR) and triplet (3NR) rhodium nitrenes for all three models (A, B and C) has been calculated (Table 2). All values are within 1.0 kcal mol−1, indicating that both 1NR and 3NR could be present at similar concentrations. An additional electronic state that could be present is the open-shell singlet biradical. Despite attempts using the broken-symmetry DFT approach with a correction for triplet spin-contamination,85 these species could not be detected, only closed shell singlet states were observed.| PBE/BS2(PCM) | NRA | NRB | NRC |
|---|---|---|---|
| a E st= Esinglet − Etriplet. | |||
| ΔEst (kcal mol−1) | −0.8 | −0.6 | 0.9 |
| ΔGst (kcal mol−1) | 1.4 | 0.6 | 1.4 |
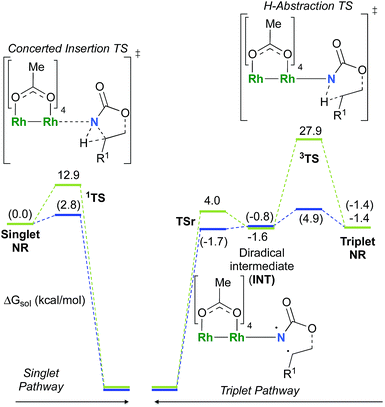
As the 1NR and 3NR species are close in energy, it is necessary to explore the insertion of the rhodium nitrene species into the C–H bond through the two known competitive pathways (see Scheme 2). The reaction pathways were examined through the location of the transition states and the product complexes associated with 1NR and 3NR on the potential-energy surfaces for A and C (Fig. 6). For both intramolecular and intermolecular processes, the singlet pathways were favoured over the triplet pathways.86
The reaction barrier for 1NR insertion into a benzylic C–H bond is 2.1 kcal mol−1 and 15.0 kcal mol−1, respectively, lower than the corresponding triplet pathway for the intramolecular and intermolecular reactions. Upon examination of MO coefficients, the LUMOs of 1NR have a large contribution from the nitrogen 2p orbital, making the N atom of 1NR strongly electrophilic (Fig. 7). The LUMO extends mainly over the two rhodium atoms as well as nitrogen. The σ C–H bonding electrons are attracted by the vacant nitrogen 2p orbital; as a result, the total charge of the –CH2– moiety increases from 0.01 for 1NRA to 0.10 for 1TSA and from −0.00 for 1NRC to 0.06 for 1TSC, while the total charge of the –Rh2NCO- moiety decreases from 0.53 for 1NRA to 0.43 for 1TSA and from 0.55 for 1NRC to 0.49 for 1TSC, overall indicating a hydride transfer. The hydride transfer is accompanied by simultaneous formation of the C–N bond as revealed by the orbitals of 1TS (Fig. 7). There is a strong orbital interaction between the carbon and nitrogen atoms, with a trigonal transition state structure, featuring a N–H–C angle of 144.14° for 1TSA and a N–H–C angle of 154.92° for 1TSC; as a result, both hydride transfer and C–N formation take place in a concerted manner (Fig. 8). Triplet nitrene species A (3NRA) has two singly occupied MOs and the two unpaired electrons are mainly localized on the Rh–Rh–N moiety (Fig. 7). The formation of the σ-N–H bond would require one electron from the approaching hydrogen atom to form a bond with an electron of a SOMO of the rhodium–nitrene complex, thus leading to a homolytic rather than a heterolytic cleavage of the C–H bond. The homolysis of the C–H bond leads to one unpaired electron residing on the C atom and the other residing in the remaining SOMO. In addition, the spin-density analysis supports these hypotheses.87 As the hydrogen atom approaches the nitrogen atom, the σ C–H bond undergoes a homolytic cleavage. As 3TS proceeds to INT, the spin density of carbon increased to 0.705 (A) and 0.778 (C), and the configuration of the carbon atom changed from a pyramidal to a planar structure to produce INT. The result of the spin-density analysis shows that INT is a diradical (Fig. 7). As INT proceeds to the recombination transition state (TSr), the spin density of C decreases to 0.671 (A) and 0.766 (C). The configuration of the C atom returns to pyramidal with a shortening of the C–N interaction to produce TSr. The relative reaction rates for the singlet pathways over the triplet may be estimated according to the transition-state theory (eqn (6)).
| ksinglet/ktriplet ≈ exp[(ΔGtriplet‡ − ΔGsinglet‡ + ΔGst)]/RT | (6) |
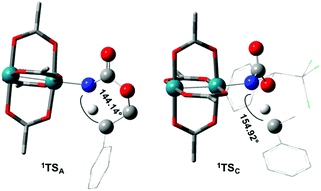 | ||
| Fig. 8 Optimized structures of the singlet C–H insertion TS for A and C. (Oxygen atom: red; nitrogen atom: blue; rhodium atom: aqua.) (Different atom styles are used for clarity.) | ||
The relative reaction rates ksinglet/ktriplet for the amidation of benzylic intramolecular and intermolecular C–H bonds are 33.7 and 8.4 × 1010, respectively. Consequently, it appears that the singlet-concerted pathway is predominant and responsible for the formation of oxazolidinone and carbamate products.
Nitrogen-atom insertion into C–H bonds with singlet rhodium nitrene species
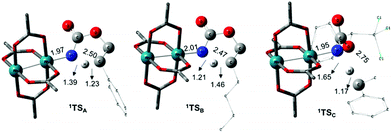
The C–H insertion of the singlet rhodium nitrene was studied with all models (A, B & C) (Fig. 3). The intramolecular C–H bond insertions (A & B) are more facile than the intermolecular C–H bond insertion (C) by 7.6 and 4.4 kcal mol−1, respectively, as a result of a favourable entropy. TSC is however an early, thus accessible transition state (Fig. 9). Among the examined intramolecular C–H bond insertions, the TSn for the benzylic C–H bond insertion (A) was determined to be 3.2 kcal mol−1 lower than the TSn for the singlet aliphatic intramolecular C–H insertion (B), in agreement with experimental results reported. The structural analysis of the corresponding transition states shows that the Rh–N(R) and C–H bonds are 0.04 Å and 0.23 Å, respectively, longer in TSB than TSA, whereas (H)C–N and N–H(C) bonds are 0.03 Å and 0.18 Å shorter, respectively (Fig. 9). TSB is thus a late transition state with larger geometry differences from the starting material, suggesting a higher activation energy barrier compared to TSA. As mentioned earlier, for all three models, the rhodium nitrenoid complex (NRO-K) is the resting state of the catalyst, i.e. the turnover frequency (TOF)-determining intermediate (TDI). The energetic span model was used to assess the kinetics of the catalytic cycle.88–90 In addition to confirming NRO-K as the TDI, the transition state of the C–H insertion (TSn) was established as the TOF-determining transition state (TDTS) or the transition state involved in the rate-limiting step. An energy range of 15.8 and 18.2 kcal mol−1 (ΔΔG = ΔGTSn − ΔGNRO), corresponding to the apparent activation energies of the full cycle, was determined for, respectively, the intramolecular amination of benzylic C–H bonds (A) and the intermolecular amination of C–H benzylic bonds (C). The experimental and calculated kinetic isotopic effect also confirms TSn as the rate limiting step (Table 3). The proposed catalytic cycle summarizing all mechanistic information is shown in Scheme 4.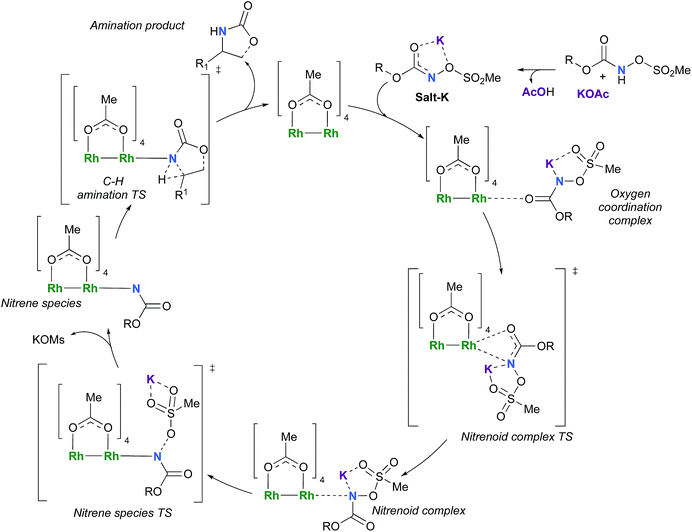 | ||
| Scheme 4 Proposed catalytic cycle for the rhodium-catalyzed C–H amination with N-mesyloxycarbamates. | ||
Primary carbamates and carbonyl derivatives as by-products in intramolecular C–H amination reactions
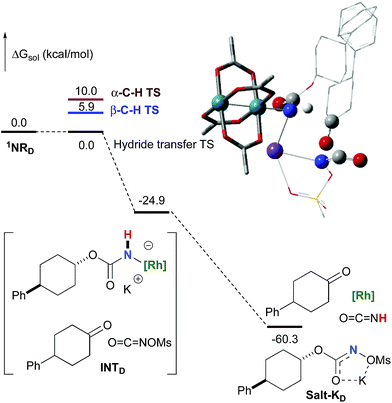
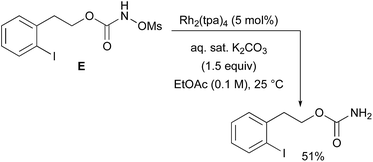
With a few substrates, namely N-sulfonyloxycarbamates derived from secondary alcohols, the corresponding primary carbamate and carbonyl derivatives became the major products. For example, the reaction with trans-4-phenylcyclohexyl-N-tosyloxycarbamate D afforded the ketone and the corresponding primary carbamate in respectively 58% and 15% yields (eqn (7)). The formation of ketones has also been observed in rhodium-catalyzed C–H amination reactions using iminoiodinanes as metal nitrene precursors.92–95 The formation of this by-product was postulated to be the result of an α-C–H insertion reaction producing a strained 4-membered intermediate that decomposes to afford the observed ketone.92 No experimental or in silico data are available to support this hypothesis. With orthohalogenated N-mesyloxycarbamates such as substrate E, only the corresponding primary carbamate was isolated (eqn (8)). Primary carbamates have been observed in other catalyzed C–H amination reactions. Initially, it was postulated that they arose from the homolytic cleavage of the [M]–N bond, as they appeared only when the metal–nitrene species are not rapidly intercepted by the substrate.33 However, DFT calculations involving porphyrin–cobalt-catalyzed C–H amination reactions using azides as metal nitrene precursors revealed that primary carbamates were formed via hydrogen atom abstraction processes from the substrate.72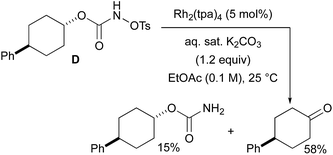 | (7) |
 | (8) |
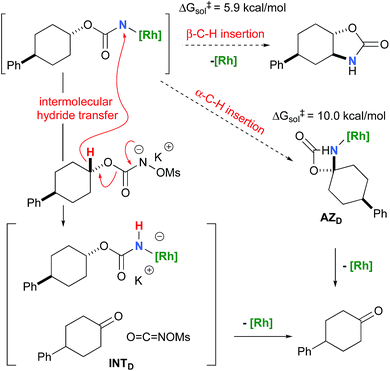
To further investigate the origin of the side reactions in rhodium-catalyzed aminations, we considered the formation of the ketone and primary carbamate as by-products from A, but also from substrates D&E.96 We first ruled out a number of hypotheses, including competitive reactivity of the triplet Rh–nitrene species (namely homolytic cleavage of the [M]–N bond) and α-intramolecular C–H amination, as those were found to have inaccessible activation energies at room temperature. For instance, the β-C–H amination 1TSD is 4.1 kcal mol−1 more favourable than the α-C–H amination 1TSD, leading to the formation of the corresponding ketone (Scheme 5). Conversely, we ascertained that a bimolecular α-hydride transfer from Salt-K to the electrophilic singlet Rh–nitrene species could compete with an intramolecular β-C–H insertion process.
In addition to the ketone, a rhodium imido species is also formed that is either protonated to afford the corresponding primary carbamate or reacted with O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NOMs to regenerate Salt-KD.97 For substrate D, this pathway displays an overall free activation barrier (Fig. 10). Steric hindrance plays a role in decelerating the intramolecular amination of substrate D. The transition state for the hydride bimolecular transfer has an intramolecular character with the potassium cation coordinating the two interacting molecules favouring the formation of the ketone by-product. The side-reaction is also enthalpy-driven, considering the high stability of the produced ketone.
NOMs to regenerate Salt-KD.97 For substrate D, this pathway displays an overall free activation barrier (Fig. 10). Steric hindrance plays a role in decelerating the intramolecular amination of substrate D. The transition state for the hydride bimolecular transfer has an intramolecular character with the potassium cation coordinating the two interacting molecules favouring the formation of the ketone by-product. The side-reaction is also enthalpy-driven, considering the high stability of the produced ketone.
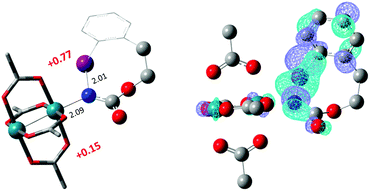
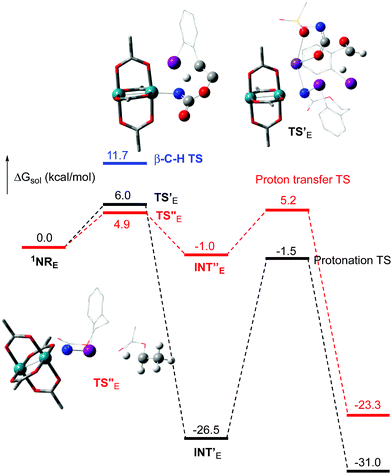
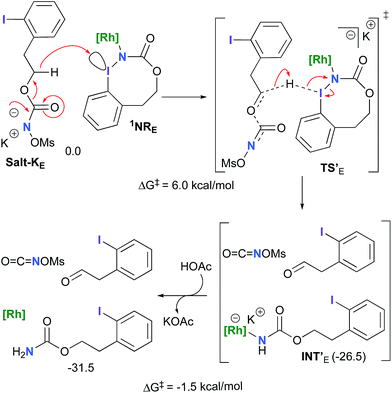
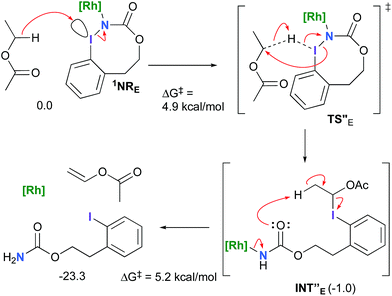
The hydride transfer hypothesis between Salt-K and 1NR cannot account for the reactivity of substrate E which formed exclusively the corresponding primary carbamate with no ketone. When we computed the rhodium nitrene derived from substrate E, we found a cyclic species, in which the iodine is coordinated to the nitrogen of the rhodium nitrene, with the N–I bond (2.01 Å) shorter than the Rh–N bond (2.09 Å) (Fig. 11). Donation from the p-halogen (5p–I) to the vacant 2p orbital of nitrogen is observed at the LUMO of the Rh–nitrene species E. This frontier orbital is thus mostly localized on the iodine resulting in a less electrophilic nitrogen. The charge analysis shows that the Rh2NCO moiety has a total charge of +0.15, whereas the iodine atom is highly electrophilic with a partial charge of +0.77. Because of a crowded iodine intra-coordinated 1NRE with a less electrophilic nitrogen, the calculated intramolecular β-C–H amination energy barrier is significantly higher (8.9 kcal mol−1) than the one calculated for A (Fig. 12). It was also discovered that hydride transfer processes proceed via the Rh–Rh–N–I π* orbital of iodine instead of the nitrogen. A barrier of 6.0 kcal mol−1 (TS′E) was calculated for a hydride transfer from Salt-KE, forming INT′E (Scheme 6).
However, if such a process is operative, the aldehyde would have been isolated experimentally. Ethyl acetate (solvent) was then suspected as the hydride source. The transfer to the 1NRE potential energy surface revealed an energy barrier of only +4.9 kcal mol−1 leading to a less stable imido intermediate INT′′E with a new C–I (C⋯I = 2.22 Å) bond formed (Scheme 7). The proton transfer is performed via the oxygen of the carbamate moiety simultaneously with the C–I cleavage (C⋯I = 2.67 Å) and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C formation of the alkene.
C formation of the alkene.
Proton tautomerization affords the primary carbamate. The overall ΔGsol for the formation of the primary carbamate from 1NRE and EtOAc is −23.3 kcal mol−1. When compared to the hydride transfer pathway with Salt-KE, the kinetic process is 3.8× faster with EtOAc. Given that EtOAc is also the solvent of the reaction, the pathway shown in Scheme 7 appears as the most plausible explanation to account for the exclusive isolation of primary carbamate 4 (with no aldehyde) experimentally.
Conclusions
A computational study of the rhodium-catalyzed C–H amination with N-mesyloxycarbamates was presented, where we consider the concerted C–H amination from a closed shell singlet Rh–nitrene species and a stepwise radical mechanism starting from an open-shell triplet Rh–nitrene species. The overall reaction is favoured by ≈−50.0 kcal mol−1. The coordination of the anion of the N-mesyloxycarbamate with the catalyst takes place in an associative way, chelating the carbonyl function of the substrate to the catalyst. Upon coordination, the O–Rh bond is substituted by the N–Rh bond through a low activation barrier. With the inner nitrenoid complex identified as the TOF-determining intermediate, potassium plays a relevant role as the coordinative cation holding together the leaving group and the nitrene moiety giving rise to a stable nitrenoid complex. The potassium mesylate leaves the imido-complex through a late transition state where the barrier is reachable at room temperature. After the loss of the salt, the two spin states of nitrene species (singlet and triplet) are both capable of performing the C–H insertion through two competitive paths. A concerted insertion through a singlet rhodium–nitrene species is computed to have a smaller activation barrier, rather than a H-abstraction from the triplet nitrene species, affording the amine product and releasing the catalyst. Along with the kinetic isotopic effect, this computational study has clearly identified the C–H insertion transition state as the one involved in the rate-limiting step. The rhodium catalyst is qualified as a more efficient catalyst for the C–H intramolecular amination reaction under these conditions with a calculated TOF value of 2.3 × 102 h−1 compared to a calculated TOF value of 21 h−1 for the analogous intermolecular C–H amination.Furthermore, the DFT study has ruled out homolytic cleavage of the [M]–N bond and α-intramolecular C–H amination as pathways responsible for the formation of ketones and primary carbamates as by-products. There is instead a competitive intermolecular reaction of the singlet rhodium nitrene species with a hydride source (either the N-sulfonyloxycarbamate anion or ethyl acetate) affording the primary carbamate with or without the corresponding carbonyl by-product. Now that the pathway leading to their formation has been established, one can envision that the control of the reaction conditions (more diluted reaction conditions, solvent change) may in some cases minimize the formation of these undesired products. Given that ketones had also been identified as by-products in other rhodium-catalyzed nitrene C–H insertions,92–95 namely with iminoiodinanes, the identified pathway may also be operational in these systems (with the iminoiodinane as the hydride source). Finally, we also established that iodine, through intramolecular coordination of the rhodium nitrene, may in some substrates strongly impede the electrophilic nature of the nitrogen.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the NSERC (Canada), the Canadian Foundation for Innovation, the Canada Research Chair Program, the Université de Montréal and the Ministry of Higher Education and Scientific Research of Tunisia. Computations were performed with the supercomputers Briarée and Cottos from Université de Montréal, Guillimin from McGill University, Cedar from Simon Fraser University, Graham from University of Waterloo and Mammouth-Série 2 from Université de Sherbrooke managed by Calcul Québec (https://www.calculquebec.ca) and Compute Canada (https://www.computecanada.ca). The operation of these supercomputers is funded by the Canada Foundation for Innovation (CFI), le Ministère de l’Économie, des Sciences et de l’Innovation du Québec (MESI) and le Fonds de recherche du Québec – Nature et technologies (FRQ-NT). We would like to thank Carl Trudel for the synthesis of N-tosyloxycarbamate D, Prof. Claude Legault and Dr James J. Mousseau for fruitful discussions.Notes and references
- Y. Park, Y. Kim and S. Chang, Chem. Rev., 2017, 117, 9247 CrossRef CAS PubMed.
- B. Darses, R. Rodrigues, L. Neuville, M. Mazurais and P. Dauban, Chem. Commun., 2017, 53, 493 RSC.
- D. Intrieri, P. Zardi, A. Caselli and E. Gallo, Chem. Commun., 2014, 50, 11440 RSC.
- J. L. Jeffrey and R. Sarpong, Chem. Sci., 2013, 4, 4092 RSC.
- T. Uchida and T. Katsuki, Chem. Rec., 2014, 14, 117 CrossRef CAS PubMed.
- F. Collet, C. Lescot and P. Dauban, Chem. Soc. Rev., 2011, 40, 1926 RSC.
- C. G. Espino and J. Du Bois, Angew. Chem., Int. Ed., 2001, 40, 598 CrossRef CAS PubMed.
- Y. Cui and C. He, Angew.Chem., Int. Ed., 2004, 43, 4210 CrossRef CAS PubMed.
- J. W. Rigoli, C. D. Weatherly, J. M. Alderson, B. T. Vo and J. M. Schomaker, J. Am. Chem. Soc., 2013, 135, 17238 CrossRef CAS PubMed.
- H. Lebel, K. Huard and S. Lectard, J. Am. Chem. Soc., 2005, 127, 14198 CrossRef CAS PubMed.
- K. Huard and H. Lebel, Chem.–Eur. J., 2008, 14, 6222 CrossRef CAS PubMed.
- H. Lebel, L. MamaniLaparra, M. Khalifa, C. Trudel, C. Audubert, M. Szponarski, C. Dicaire Leduc, E. Azek and M. Ernzerhof, Org. Biomol. Chem., 2017, 15, 4144 RSC.
- H. Lebel and K. Huard, Org. Lett., 2007, 9, 639 CrossRef CAS PubMed.
- H. Lebel, C. Spitz, O. Leogane, C. Trudel and M. Parmentier, Org. Lett., 2011, 13, 5460 CrossRef CAS PubMed.
- H. Lebel, C. Trudel and C. Spitz, Chem. Commun., 2012, 48, 7799 RSC.
- H. J. Lu, V. Subbarayan, J. R. Tao and X. P. Zhang, Organometallics, 2010, 29, 389 CrossRef CAS.
- S. Y. Hong, Y. Park, Y. Hwang, Y. B. Kim, M.-H. Baik and S. Chang, Science, 2018, 359, 1016 CrossRef CAS PubMed.
- C. G. Espino, P. M. Wehn, J. Chow and J. Du Bois, J. Am. Chem. Soc., 2001, 123, 6935 CrossRef CAS.
- C. G. Espino, K. W. Fiori, M. Kim and J. Du Bois, J. Am. Chem. Soc., 2004, 126, 15378 CrossRef CAS PubMed.
- D. N. Zalatan and J. Du Bois, J. Am. Chem. Soc., 2008, 130, 9220 CrossRef CAS PubMed.
- J. L. Liang, S. X. Yuan, J. S. Huang, W. Y. Yu and C. M. Che, Angew. Chem., Int. Ed., 2002, 41, 3465 CrossRef CAS PubMed.
- E. Milczek, N. Boudet and S. Blakey, Angew. Chem., Int. Ed., 2008, 47, 6825 CrossRef CAS PubMed.
- M. E. Harvey, D. G. Musaev and J. Du Bois, J. Am. Chem. Soc., 2011, 133, 17207 CrossRef CAS PubMed.
- S. M. Paradine and M. C. White, J. Am. Chem. Soc., 2012, 134, 2036 CrossRef CAS PubMed.
- Y. Liu, X. Guan, E. L.-M. Wong, P. Liu, J.-S. Huang and C.-M. Che, J. Am. Chem. Soc., 2013, 135, 7194 CrossRef CAS PubMed.
- J. M. Alderson, A. M. Phelps, R. J. Scamp, N. S. Dolan and J. M. Schomaker, J. Am. Chem. Soc., 2014, 136, 16720 CrossRef CAS PubMed.
- S. M. Paradine, J. R. Griffin, J. Zhao, A. L. Petronico, S. M. Miller and M. Christina White, Nat. Chem., 2015, 7, 987 CrossRef CAS PubMed.
- H. J. Lu, H. L. Jiang, L. Wojtas and X. P. Zhang, Angew. Chem., Int. Ed., 2010, 49, 10192 CrossRef CAS PubMed.
- H. Lu, Y. Hu, H. Jiang, L. Wojtas and X. P. Zhang, Org. Lett., 2012, 14, 5158 CrossRef CAS PubMed.
- H. Lu, C. Li, H. Jiang, C. L. Lizardi and X. P. Zhang, Angew. Chem., Int. Ed., 2014, 53, 7028 CrossRef CAS PubMed.
- M. Ichinose, H. Suematsu, Y. Yasutomi, Y. Nishioka, T. Uchida and T. Katsuki, Angew. Chem., Int. Ed., 2011, 50, 9884 CrossRef CAS PubMed.
- J. L. Liang, J. S. Huang, X. Q. Yu, N. Y. Zhu and C. M. Che, Chem.–Eur. J., 2002, 8, 1563 CrossRef CAS.
- K. W. Fiori and J. Du Bois, J. Am. Chem. Soc., 2007, 129, 562 CrossRef CAS PubMed.
- C. Liang, F. Collet, F. Robert-Peillard, P. Müller, R. H. Dodd and P. Dauban, J. Am. Chem. Soc., 2008, 130, 343 CrossRef CAS PubMed.
- J. L. Roizen, D. N. Zalatan and J. Du Bois, Angew. Chem., Int. Ed., 2013, 52, 11343 CrossRef CAS PubMed.
- E. N. Bess, R. J. DeLuca, D. J. Tindall, M. S. Oderinde, J. L. Roizen, J. Du Bois and M. S. Sigman, J. Am. Chem. Soc., 2014, 136, 5783 CrossRef CAS PubMed.
- N. D. Chiappini, J. B. C. Mack and J. Du Bois, Angew. Chem., Int. Ed., 2018, 57, 4956 CrossRef CAS PubMed.
- M. M. Diaz-Requejo, T. R. Belderrain, M. C. Nicasio, S. Trofimenko and P. J. Perez, J. Am. Chem. Soc., 2003, 125, 12078 CrossRef CAS PubMed.
- M. R. Fructos, S. Trofimenko, M. M. Diaz-Requejo and P. J. Perez, J. Am. Chem. Soc., 2006, 128, 11784 CrossRef CAS PubMed.
- V. Bagchi, P. Paraskevopoulou, P. Das, L. Chi, Q. Wang, A. Choudhury, J. S. Mathieson, L. Cronin, D. B. Pardue, T. R. Cundari, G. Mitrikas, Y. Sanakis and P. Stavropoulos, J. Am. Chem. Soc., 2014, 136, 11362 CrossRef CAS PubMed.
- T. M. U. Ton, C. Tejo, D. L. Y. Tiong and P. W. H. Chan, J. Am. Chem. Soc., 2012, 134, 7344 CrossRef CAS PubMed.
- Y. Nishioka, T. Uchida and T. Katsuki, Angew. Chem., Int. Ed., 2013, 52, 1739 CrossRef CAS PubMed.
- B. J. Stokes, H. J. Dong, B. E. Leslie, A. L. Pumphrey and T. G. Driver, J. Am. Chem. Soc., 2007, 129, 7500 CrossRef CAS PubMed.
- M. H. Shen, B. E. Leslie and T. G. Driver, Angew. Chem., Int. Ed., 2008, 47, 5056 CrossRef CAS PubMed.
- Q. Nguyen, K. Sun and T. G. Driver, J. Am. Chem. Soc., 2012, 134, 7262 CrossRef CAS PubMed.
- A. L. Pumphrey, H. Dong and T. G. Driver, Angew. Chem., Int. Ed., 2012, 51, 5920 CrossRef CAS PubMed.
- Q. Nguyen, T. Nguyen and T. G. Driver, J. Am. Chem. Soc., 2013, 135, 620 CrossRef CAS PubMed.
- O. Villanueva, N. M. Weldy, S. B. Blakey and C. E. MacBeth, Chem. Sci., 2015, 6, 6672 RSC.
- P. F. Kuijpers, M. J. Tiekink, W. B. Breukelaar, D. L. J. Broere, N. P. van Leest, J. I. vanderVlugt, J. N. H. Reek and B. deBruin, Chem.–Eur. J., 2017, 23, 7945 CrossRef CAS PubMed.
- P. F. Kuijpers, J. I. van der Vlugt, S. Schneider and B. de Bruin, Chem.–Eur. J., 2017, 23, 13819 CrossRef CAS PubMed.
- M. Goswami, P. Geuijen, J. N. H. Reek and B. de Bruin, Eur. J. Inorg. Chem., 2018, 2018, 617 CrossRef CAS.
- Y. M. Badiei, A. Dinescu, X. Dai, R. M. Palomino, F. W. Heinemann, T. R. Cundari and T. H. Warren, Angew. Chem., Int. Ed., 2008, 47, 9961 CrossRef CAS PubMed.
- E. T. Hennessy and T. A. Betley, Science, 2013, 340, 591 CrossRef CAS PubMed.
- A. Sharma and J. F. Hartwig, Nature, 2015, 517, 600 CrossRef CAS PubMed.
- S. M. Au, J. S. Huang, W. Y. Yu, W. H. Fung and C. M. Che, J. Am. Chem. Soc., 1999, 121, 9120 CrossRef CAS.
- S. Fantauzzi, E. Gallo, A. Caselli, F. Ragaini, N. Casati, P. Macchi and S. Cenini, Chem. Commun., 2009, 3952 RSC.
- S. Wiese, J. L. McAfee, D. R. Pahls, C. L. McMullin, T. R. Cundari and T. H. Warren, J. Am. Chem. Soc., 2012, 134, 10114 CrossRef CAS PubMed.
- DESI mass spectroscopy has also been employed to characterize the reactive metalnitrene intermediate: R. H. Perry, T. J. Cahill III, J. L. Roizen, J. Du Bois and R. N. Zare, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18295 CrossRef CAS PubMed.
- X. F. Lin, C. Y. Zhao, C. M. Che, Z. F. Ke and D. L. Phillips, Chem.–Asian J., 2007, 2, 1101 CrossRef CAS PubMed.
- X. Zhang, H. Xu and C. Zhao, J. Org. Chem., 2014, 79, 9799 CrossRef CAS PubMed.
- K. W. Fiori, C. G. Espino, B. H. Brodsky and J. Du Bois, Tetrahedron, 2009, 65, 3042 CrossRef CAS.
- K. P. Kornecki and J. F. Berry, Chem.–Eur. J., 2011, 17, 5827 CrossRef CAS PubMed.
- A. Varela-Alvarez, T. Yang, H. Jennings, K. P. Kornecki, S. N. Macmillan, K. M. Lancaster, J. B. C. Mack, J. Du Bois, J. F. Berry and D. G. Musaev, J. Am. Chem. Soc., 2016, 138, 2327 CrossRef CAS PubMed.
- X. Zhang, Z. Ke, N. J. DeYonker, H. Xu, Z.-F. Li, X. Xu, X. Zhang, C.-Y. Su, D. L. Phillips and C. Zhao, J. Org. Chem., 2013, 78, 12460 CrossRef CAS PubMed.
- X. Zhang, H. Xu, X. Liu, D. L. Phillips and C. Zhao, Chem.–Eur. J., 2016, 22, 7288 CrossRef CAS PubMed.
- S. K.-Y. Leung, W.-M. Tsui, J.-S. Huang, C.-M. Che, J.-L. Liang and N. Zhu, J. Am. Chem. Soc., 2005, 127, 16629 CrossRef CAS PubMed.
- X. Lin, C. M. Che and D. L. Phillips, J. Org. Chem., 2008, 73, 529 CrossRef CAS PubMed.
- Z. Guo, X. Guan, J.-S. Huang, W.-M. Tsui, Z. Lin and C.-M. Che, Chem.–Eur. J., 2013, 19, 11320 CrossRef CAS PubMed.
- G. Manca, E. Gallo, D. Intrieri and C. Mealli, ACS Catal., 2014, 4, 823 CrossRef CAS.
- D. G. Musaev and S. B. Blakey, Organometallics, 2012, 31, 4950 CrossRef CAS.
- F. Ragaini, A. Penoni, E. Gallo, S. Tollari, C. L. Gotti, M. Lapadula, E. Mangioni and S. Cenini, Chem.–Eur. J., 2003, 9, 249 CrossRef CAS PubMed.
- V. Lyaskovskyy, A. I. O. Suarez, H. Lu, H. Jiang, X. P. Zhang and B. de Bruin, J. Am. Chem. Soc., 2011, 133, 12264 CrossRef CAS PubMed.
- M. Goswami, V. Lyaskovskyy, S. R. Domingos, W. J. Buma, S. Woutersen, O. Troeppner, I. Ivanovic-Burmazovic, H. Lu, X. Cui, X. P. Zhang, E. J. Reijerse, S. DeBeer, M. M. van Schooneveld, F. F. Pfaff, K. Ray and B. de Bruin, J. Am. Chem. Soc., 2015, 137, 5468 CrossRef CAS PubMed.
- D. N. Barman, P. Liu, K. N. Houk and K. M. Nicholas, Organometallics, 2010, 29, 3404 CrossRef CAS.
- M. J. B. Aguila, Y. M. Badiei and T. H. Warren, J. Am. Chem. Soc., 2013, 135, 9399 CrossRef CAS PubMed.
- R. E. Cowley, N. J. DeYonker, N. A. Eckert, T. R. Cundari, S. DeBeer, E. Bill, X. Ottenwaelder, C. Flaschenriem and P. L. Holland, Inorg. Chem., 2010, 49, 6172 CrossRef CAS PubMed.
- J. Li, C. Wu, Q. Zhang and B. Yan, Dalton Trans., 2013, 42, 14369 RSC.
- Similar results were obtained for silver complexes, see: N. S. Dolan, R. J. Scamp, T. Yang, J. F. Berry and J. M. Schomaker, J. Am. Chem. Soc., 2016, 138, 14658 CrossRef CAS PubMed.
- F. A. Cotton, B. G. Deboer, M. D. Laprade, J. R. Pipal and D. A. Ucko, ActaCrystallogr., 1971, B27, 1664 CrossRef.
- E. Nakamura, N. Yoshikai and M. Yamanaka, J. Am. Chem. Soc., 2002, 124, 7181 CrossRef CAS PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS.
- See also Table S2-1 in the ESI.†.
- The formation of the free nitrene from Salt-K required >20 kcal/mol and was thus ruled out as a possible pathway..
- T. R. Cundari and G. R. Morello, J. Org. Chem., 2009, 74, 5711 CrossRef CAS PubMed.
- V. Sinha, B. Pribanic, B. de Bruin, M. Trincado and H. Grützmacher, Chem.–Eur. J., 2018, 24, 5513 CrossRef CAS PubMed.
- We have also calculated the singlet and triplet pathways for model A, using the hybrid functional B3LYP (that overestimates the triplet stability), and the singlet pathway was still the lowest in energy, see Table S2-2 in the ESI.†.
- See Table S2-3 in the ESI.†.
- S. Kozuch, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2, 795 CAS.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101 CrossRef CAS PubMed.
- A. Uhe, S. Kozuch and S. Shaik, J. Comput. Chem., 2011, 32, 978 CrossRef CAS PubMed.
- M. Saunders, K. E. Laidig and M. Wolfsberg, J. Am. Chem. Soc., 1989, 111, 8989 CrossRef CAS.
- C. G. Espino and J. Du Bois, in Modern Rhodium-Catalyzed Organic Reactions, ed. P. A.Evans, Wiley-VCHVerlag GmbH & Co. KGaA, Weinheim, 2005, p. 379 Search PubMed.
- T. Yakura, S. Sato and Y. Yoshimoto, Chem. Pharm. Bull., 2007, 55, 1284 CrossRef CAS PubMed.
- D. P. Uccello, S. M. Miller, N. A. Dieterich, A. F. Stepan, S. W. Chung, K. A. Farley, B. Samas, J. Chen and J. I. Montgomery, Tetrahedron Lett., 2011, 52, 4247 CrossRef CAS.
- B. Hurlocker, N. C. Abascal, L. M. Repka, E. Santizo-Deleon, A. L. Smenton, V. Baranov, R. Gupta, S. E. Bernard, S. Chowdhury and C. M. Rojas, J. Org. Chem., 2011, 76, 2240 CrossRef CAS PubMed.
- See the ESI† for preliminary studies with A.
- The regeneration of SaltD is favoured over the protonation, see the ESI† for details.
Footnote |
| † Electronic supplementary information (ESI) available: DFT-optimized geometries; tables containing ΔE, EZPE, imaginary frequencies, ΔH, and ΔG values for all of the DFT-optimized geometries. See DOI: 10.1039/c8sc03153c |
| This journal is © The Royal Society of Chemistry 2019 |