Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solar-driven co-thermolysis of CO2 and H2O promoted by in situ oxygen removal across a non-stoichiometric ceria membrane†
Maria
Tou
 a,
Jian
Jin
bc,
Yong
Hao
bc,
Aldo
Steinfeld
a,
Jian
Jin
bc,
Yong
Hao
bc,
Aldo
Steinfeld
 a and
Ronald
Michalsky
a and
Ronald
Michalsky
 *a
*a
aDepartment of Mechanical and Process Engineering, ETH Zürich, 8092 Zürich, Switzerland. E-mail: michalskyr@ethz.ch
bInstitute of Engineering Thermophysics, Chinese Academy of Sciences, 11 Beisihuanxi Rd., Beijing 100190, P. R. China
cUniversity of Chinese Academy of Sciences, No.19A Yuquan Rd., Beijing 100049, P. R. China
First published on 14th March 2019
Abstract
We report on the first ever experimental demonstration of simultaneous thermolysis of CO2 and H2O with in situ separation of fuel and oxygen in a solar-driven membrane reactor. Gaseous CO2/H2O mixtures at molar ratios from 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 to 2
4 to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were fed to a mixed ionic–electronic conducting non-stoichiometric ceria (CeO2−δ) membrane enclosed in a solar cavity receiver and exposed to simulated concentrated solar radiation of up to 4200 suns. Reaction rates were measured under isothermal and isobaric conditions in the range of 1723–1873 K and 0.2–1.7 Pa O2, yielding a maximum combined CO and H2 fuel production rate of 2.3 μmol cm−2 min−1 at 1873 K and 0.2 Pa O2 at steady state, which corresponded to a conversion of reactants of 0.7%. Under all conditions tested, CO production was favored over H2 production, as expected from theory. Experimental results followed the same trends as the thermodynamic equilibrium limits of membrane-assisted thermochemical fuel production.
1 were fed to a mixed ionic–electronic conducting non-stoichiometric ceria (CeO2−δ) membrane enclosed in a solar cavity receiver and exposed to simulated concentrated solar radiation of up to 4200 suns. Reaction rates were measured under isothermal and isobaric conditions in the range of 1723–1873 K and 0.2–1.7 Pa O2, yielding a maximum combined CO and H2 fuel production rate of 2.3 μmol cm−2 min−1 at 1873 K and 0.2 Pa O2 at steady state, which corresponded to a conversion of reactants of 0.7%. Under all conditions tested, CO production was favored over H2 production, as expected from theory. Experimental results followed the same trends as the thermodynamic equilibrium limits of membrane-assisted thermochemical fuel production.
Introduction
The utilization of the vast solar energy resource for electricity, heat, and fuels has become a key objective in research and development.1 The conversion and storage of solar energy in fuels is especially appealing as a means to transition from fossil fuels to a “CO2 economy”.2 With this, a solar refinery needs to be developed where solar energy is collected and used to convert CO2 and H2O to fuels by some method. Existing research spans solar-driven electrochemical, photo-electrochemical, and photocatalytic paths for direct conversion, as well as indirect routes via the solar thermochemical production of syngas (H2 and CO).3Solar thermochemical redox cycles utilize the entire spectrum of solar radiation concentrated to high-temperature process heat to drive the splitting of CO2 and H2O and produce CO and H2 at high rates, selectivity, mass conversions, and efficiencies.4–6 However, the temperature swing required between the redox steps induces significant material stresses and energy irreversibility, which prompted the search for alternative isothermal processes.7–9 One promising approach is the use of a dense, ceramic, mixed ionic–electronic conducting (MIEC) membrane for the continuous separation of oxygen and fuel (H2 and/or CO) derived from the thermolysis of CO2 and H2O at high temperatures, as pioneered for solar water splitting by Fletcher and co-workers.10,11 We recently demonstrated the proof-of-concept utilization of a solar-driven membrane reactor for splitting of CO2.12 Other investigations of thermochemical membrane reactors, both theoretical and experimental, have also only focused on either CO2- or H2O-splitting.10,13–18 This work goes further and demonstrates the feasibility of co-feeding both CO2 and H2O and assesses the relative favorability between the two thermolysis reactions occurring simultaneously. The desired dissociations are chemical equilibrium reactions in the gas phase described by:
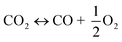 | (1) |
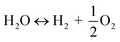 | (2) |
The reactions are analogous; that is, both are endothermic and thermolytic, but their reaction energetics differ. This is described by the standard Gibbs free energy changes at equilibrium (ΔG = 0):
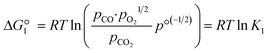 | (3) |
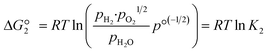 | (4) |
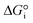 is related to the equilibrium constant Ki which in turn is a function of temperature only. Fig. 1a shows T − pO2 equilibrium contours of the separate thermolysis of CO2 and H2O for various mole fractions of CO or H2 in the product gas, respectively. For both CO2 and H2O thermolysis, products are favored with increasing T and decreasing pO2, i.e. higher mole fractions of fuel are possible towards the upper-left corner of Fig. 1a. At such high T, dissociation of CO2 is more thermodynamically favorable than that of H2O under equal conditions.19,20 A decrease in pO2 can be achieved without the use of high-value electrical energy by removal of O2 utilizing a dense membrane made of an oxygen-selective MIEC material.21pO2 is controlled to a low value on the opposite side of the membrane. For each of the separate thermolysis reactions, if pO2 ≥ 1/2 pCO or pO2 ≥ 1/2 pH2, the membrane provides no benefit.
is related to the equilibrium constant Ki which in turn is a function of temperature only. Fig. 1a shows T − pO2 equilibrium contours of the separate thermolysis of CO2 and H2O for various mole fractions of CO or H2 in the product gas, respectively. For both CO2 and H2O thermolysis, products are favored with increasing T and decreasing pO2, i.e. higher mole fractions of fuel are possible towards the upper-left corner of Fig. 1a. At such high T, dissociation of CO2 is more thermodynamically favorable than that of H2O under equal conditions.19,20 A decrease in pO2 can be achieved without the use of high-value electrical energy by removal of O2 utilizing a dense membrane made of an oxygen-selective MIEC material.21pO2 is controlled to a low value on the opposite side of the membrane. For each of the separate thermolysis reactions, if pO2 ≥ 1/2 pCO or pO2 ≥ 1/2 pH2, the membrane provides no benefit.
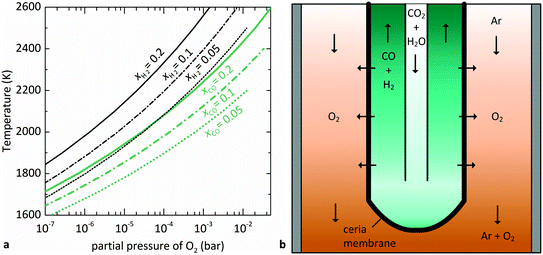 | ||
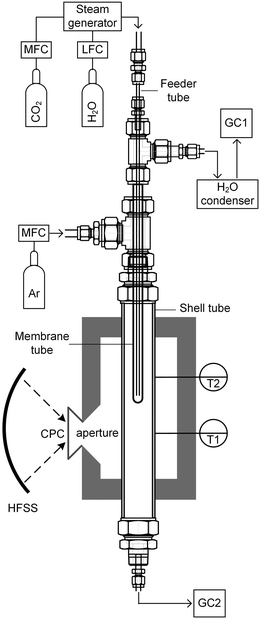
| Fig. 1 (a) Equilibrium contours for separate thermolysis of CO2 (light-colored) or H2O (dark-colored) at 1 bar total pressure as a function of T and pO2 (according to eqn (3) and (4)) for various mole fractions of CO or H2, respectively. Contours extend until pCO or pH2 = 2pO2, and increasing pO2 beyond this point no longer provides benefit over unperturbed thermolysis. (b) Schematic of the tubular redox membrane reactor for splitting of CO2 and H2O. CO2 and H2O are fed to the inner side of the membrane and dissociate into fuel and O2, with the latter selectively crossing the membrane into the Ar sweep gas. | ||
The membrane reactor concept used in this work for the co-thermolysis of H2O and CO2 is shown schematically in Fig. 1b. CO2 and H2O are fed to the inner side of a capped tubular non-stoichiometric ceria membrane. Ceria has become the benchmark material for oxygen-cycling applications due to its stability and fast kinetics.22–24 In our previous work it was also found to be an effective material for oxygen-conducting membranes.12 The supply of concentrated solar process heat at high temperatures drives the thermolysis, producing CO, H2, and O2. The latter adsorbs on the inner membrane surface, dissociates, and is transported across the membrane in an ionic form along a chemical potential gradient. O2− then associates into O2 at the outer membrane surface and desorbs into an inert sweep gas contained in a shell tube. This in situ removal of one of the reaction products drives the reactions forward towards dissociation and avoids downstream recombination. The counter-flow configuration of the reactant and product gases favorably maximizes the gradient of pO2 along the length of the membrane. By placing this reactor in a solar cavity receiver, the high-temperature heat for the reactions is provided by concentrated solar radiation incident on the shell tube.
Typical operating conditions require temperatures around 1773 K and partial pressures of O2 down to 1 Pa. These high temperatures eliminate the need for catalysts but pose significant constraints on the construction materials which must withstand these conditions over extended periods of time. Materials must also resist thermal shock that may occur due to cooling overnight, unless the reactor is equipped with an alternative heat source such as a high-temperature thermal energy storage system.25 A modular tubular membrane design could avoid costly maintenance by allowing for simple replacement of degraded membranes. Maintaining low partial pressures of oxygen is crucial, requiring additional energy for vacuum pumping or gas separation to regenerate the inert sweep gas (such as N2, though here we use Ar for gas analytic considerations).26,27 Alternatively, some studies have reported solar-driven production of pure O2 and inert gas with low partial pressures of oxygen using thermochemical oxygen pumps driven by low-grade process heat.27–29
Experimental
Materials
Cerium(IV) oxide (ceria, CeO2, powder, particle size <5 μm, 99.9% purity), poly(oxy-1,4-phenylene sulfonyl-1,4-phenylene) (PES, (C12H8O3S)n, pellets), polyvinylpyrrolidone (PVP, (C6H9NO)n, powder, average M.W. 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), and 1-methyl-2-pyrrolidinone (NMP, C5H9NO, liquid, ≥99.0% purity) were from Sigma Aldrich. Al2O3 membranes (Alsint 99.7, 7 mm outer diameter (OD), 5 mm inner diameter (ID), 250 mm length) were from Intertechno-Firag AG. High-purity alumina adhesive (Aremco Ceramabond 569) and glass-filled sealant (Aremco-Seal 617) were from Kager Industrieprodukte GmbH. CO2 (99.998%), Ar (99.996%, 99.999%), He (99.999%), and calibration gas mixtures, i.e., 1000 mol ppm H2 (99.999%) and 500 mol ppm CO (99.997%) in Ar (99.999%), and 1000 mol ppm CO (99.997%), 500 mol ppm CO2 (99.995%), 500 mol ppm N2 (99.999%), and 100 mol ppm O2 (99.999%) in Ar (99.999%) were from Messer Schweiz AG. According to the manufacturer, Ar (99.996%) contained <5 ppm O2 on a volume basis, equivalent to a limiting pO2 < 0.5 Pa.
000), and 1-methyl-2-pyrrolidinone (NMP, C5H9NO, liquid, ≥99.0% purity) were from Sigma Aldrich. Al2O3 membranes (Alsint 99.7, 7 mm outer diameter (OD), 5 mm inner diameter (ID), 250 mm length) were from Intertechno-Firag AG. High-purity alumina adhesive (Aremco Ceramabond 569) and glass-filled sealant (Aremco-Seal 617) were from Kager Industrieprodukte GmbH. CO2 (99.998%), Ar (99.996%, 99.999%), He (99.999%), and calibration gas mixtures, i.e., 1000 mol ppm H2 (99.999%) and 500 mol ppm CO (99.997%) in Ar (99.999%), and 1000 mol ppm CO (99.997%), 500 mol ppm CO2 (99.995%), 500 mol ppm N2 (99.999%), and 100 mol ppm O2 (99.999%) in Ar (99.999%) were from Messer Schweiz AG. According to the manufacturer, Ar (99.996%) contained <5 ppm O2 on a volume basis, equivalent to a limiting pO2 < 0.5 Pa.
Membrane fabrication
Capped tubular ceria membranes were produced as reported previously.12 Briefly, membranes were fabricated using a phase-inversion/sintering method.30,31 Two polymers, namely PES (5.7 wt%) and PVP (0.5 wt%), were dissolved in NMP (22.0 wt%). Ceria powder (71.8 wt%) was suspended in the polymer solution. The ceria slurry was coated onto membrane templates (highly flexible silicone tubing, 3 mm ID, 7 mm OD, RCT Reichelt Chemietechnik GMbH & Co.), which were placed in a water bath for phase inversion (unfiltered tap water coagulant under ambient conditions). The silicone templates were removed, and the dried membrane precursors were then sintered for 8 hours at 1873 K (oven model HTL 20/17, ThermConcept). The sintered membranes were 6–7 mm OD, 5–6 mm ID, and 150–250 mm in length. Typically, the membrane walls were about 0.5 mm thick. In-depth solid-state characterization of ceria membranes before and after use in the reactor was performed previously.12 SEM analysis shown in Fig. S1† shows that ceria membranes exposed to both CO2 and H2O in thermolysis experiments do not change morphologically, consistent with membranes used in pure-CO2 experiments.Experimental setup
The solar membrane reactor system is depicted schematically in Fig. 2. CO2 and/or H2O was fed through a feeder tube into the inner side of the membrane while Ar sweep gas was fed into the reactor shell tube in a counter-current flow. This assembly was placed in a thermally insulated solar cavity receiver with an aperture of 4 cm in diameter. A compound parabolic concentrator (CPC) was incorporated into the aperture to boost the solar flux concentration and generate a more uniform directional distribution of concentrated radiation entering the cavity.32 Experimentation was performed using the high-flux solar simulator (HFSS) of ETH Zurich: an array of seven Xe arcs, close-coupled to truncated ellipsoidal reflectors, provided an external source of intense thermal radiation that closely approximated the heat transfer characteristics of highly concentrating solar energy facilities. The radiative flux distribution at the focal plane was measured optically using a calibrated CCD camera focused on a Lambertian (diffusely reflecting) target. The solar radiative power input to the cavity was calculated by integration of the radiative flux over the aperture area and verified with a water calorimeter. Temperatures were measured at the outer surface of the reactor shell at two heights along the tube (indicated in Fig. 2) using B-type thermocouples. Gas flow rates were regulated using electronic mass flow controllers (MFC, Bronkhorst F-201 C, accuracy 0.5% Rd + 0.1% FS), whereas steam flow was generated using a liquid flow controller (LFC, Bronkhorst Liqui-Flow L23-AAD-33-K-305, accuracy 1% FS) and steam generator (Bronkhorst CEM W-202A-333-K). The product gas composition in each stream was monitored on-line by gas chromatography (GC, Agilent 490 MicroGC).Experimental runs
All volumetric flow rates are given under standard conditions (1 bar and 273 K). The HFSS heated the reactor to the desired temperatures in the range of 1723–1873 K with a radiative power input of 2.5–3.0 kW. For water-splitting experiments, steam was fed to the inner side of the membrane at a rate of 104 mL min−1 (5 g h−1 water to steam generator), carried in by 80–100 mL min−1 Ar. For co-feed experiments, the same flow of steam was carried by 75–200 mL min−1 CO2. At the outer side of the membrane, the reactor shell was purged with 200–1000 mL min−1 Ar. The compositions of both gas streams exiting the solar reactor were analyzed simultaneously using two gas chromatographs (GC). Steady state was defined as the condition at which the measured gas concentration was within 2% of the mean over the previous five consecutive measurements collected at a frequency of one every two minutes: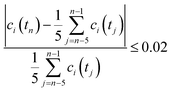 | (5) |
Thermodynamic analysis
We calculated the thermodynamic equilibrium limits of thermolysis of CO2 and H2O in a membrane reactor to compare to experimental results. Relatively fast rates are expected for each reaction step: gas-phase thermolysis, heterogeneous surface reaction, and oxygen bulk diffusion. When each of these serial processes is sufficiently fast, global kinetics are fast, and thermodynamics govern the net reaction. In this case, kinetics can be neglected.Previous observations with a solar cavity receiver containing a porous ceria structure directly exposed to high-flux irradiation reported that the overall kinetics are not controlled by solid-state diffusion within the crystal lattice.33 This is also expected for a ceria membrane because the measured values of ambipolar diffusion coefficients of oxygen in ceria (1.5 × 10−5–4 × 10−4 cm2 s−1 in the range of 1673–1823 K22) translate to diffusion times in the order of seconds for the length scales across the 0.5 mm-thick membrane. Thus, as far as solid-state diffusion is concerned, the transport of oxygen vacancies through the membrane is almost instantaneous compared with the time scales of data collection.
Reaction rates have an exponential dependence on temperature, scaling with exp(−EA/RT), as seen in the Arrhenius equation. The high temperature in the range of 1723–1873 K and consequent high activity of reactive oxygen vacancies at the surface of the membrane are expected to lead to fast surface exchange of oxygen from the gas into the solid phase.19 While studies of non-isothermal processes show that the heating rate limits the oxygen release rate, heat transfer should not be limiting in this isothermal process because the heat of the reaction is much lower than the heat input.23,33 Likewise, the high temperature, along with the catalytic effect of ceria, implies very fast thermolysis reactions in the gas phase.34 Therefore, a purely thermodynamic model is expected to adequately predict reactor performance.
However, to reach the thermodynamic limit in the countercurrent-flow reactor, there must be a sufficient membrane area and sweep gas flow rate relative to the flow rate of the reactant. To account for the oxygen capacity in a given flow of sweep gas, a thermodynamic model described by Bulfin was applied, which is specific to countercurrent-flow reactors.35 This approach guarantees compliance with the second law of thermodynamics and conservation of mass along the entire reactor by means of a dimensionless oxygen exchange coordinate, κ, defined as the number of moles of O2 crossing the membrane up to a certain point along the length, x, per mole of oxidant fed:
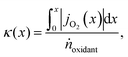 | (6) |
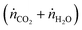 , and jO2(x) is the molar flux of O2 from the oxidant flow to the sweep gas as a function of the length along the membrane. Then pO2 in each flow can be formulated as a function of κ, and pO2,oxidant is determined by the thermodynamic equilibrium of thermolysis, as described by eqn (3) and (4) in the introduction. For O2 to spontaneously flow from the oxidant flow to the sweep gas, partial pressures must satisfy pO2,oxidant(κ) > pO2,sweep(κ), and equilibrium is reached if there exists a value of κ in [0, κtotal] where pO2,oxidant(κ) = pO2,sweep(κ). Bulfin detailed the full methodology in an example tailored to thermolysis in a membrane reactor with a counter-current sweep flow.35
, and jO2(x) is the molar flux of O2 from the oxidant flow to the sweep gas as a function of the length along the membrane. Then pO2 in each flow can be formulated as a function of κ, and pO2,oxidant is determined by the thermodynamic equilibrium of thermolysis, as described by eqn (3) and (4) in the introduction. For O2 to spontaneously flow from the oxidant flow to the sweep gas, partial pressures must satisfy pO2,oxidant(κ) > pO2,sweep(κ), and equilibrium is reached if there exists a value of κ in [0, κtotal] where pO2,oxidant(κ) = pO2,sweep(κ). Bulfin detailed the full methodology in an example tailored to thermolysis in a membrane reactor with a counter-current sweep flow.35
The countercurrent-flow thermodynamic model was implemented and solved numerically with Matlab using thermodynamic data from NIST JANAF.36 The model input parameters are T, p, pO2, the relative flow of sweep to oxidant (ṅsweep/ṅoxidant), and the relative flow rates of CO2 and H2O 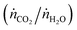 . Note that pO2 refers to the O2 impurity at the inlet of the sweep gas. The values were generally chosen to match experimental conditions as determined from mass flow controller, thermocouple, and GC measurements. For example, the reactor operated at ambient pressure and 1 bar total pressure was set on both sides of the membrane. It was not possible to measure the reaction temperature of the gas inside the membrane. Instead, the measured temperature at the outer wall of the shell tube (certainly greater than the reaction temperature) and a simple heat transfer model were used to estimate the reaction temperature. Consequently, this analysis presents the thermodynamic limits as a shaded region, where the upper and lower bounds are the limits at the maximum measured shell temperature and the estimated reaction temperature, respectively. In the range of operation, the difference between these temperatures is approximately 50 K. The simple heat transfer model used to calculate this temperature difference is described in the ESI.† The outputs of the thermodynamic model are the partial pressures of the products and conversion of the reactants at equilibrium.
. Note that pO2 refers to the O2 impurity at the inlet of the sweep gas. The values were generally chosen to match experimental conditions as determined from mass flow controller, thermocouple, and GC measurements. For example, the reactor operated at ambient pressure and 1 bar total pressure was set on both sides of the membrane. It was not possible to measure the reaction temperature of the gas inside the membrane. Instead, the measured temperature at the outer wall of the shell tube (certainly greater than the reaction temperature) and a simple heat transfer model were used to estimate the reaction temperature. Consequently, this analysis presents the thermodynamic limits as a shaded region, where the upper and lower bounds are the limits at the maximum measured shell temperature and the estimated reaction temperature, respectively. In the range of operation, the difference between these temperatures is approximately 50 K. The simple heat transfer model used to calculate this temperature difference is described in the ESI.† The outputs of the thermodynamic model are the partial pressures of the products and conversion of the reactants at equilibrium.
Results and discussion
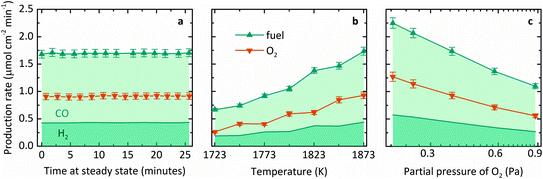
Fig. 3 summarizes the steady-state specific production rates measured experimentally for fuel, comprising CO (light shading) and H2 (dark shading), and O2 as a function of three process variables: (a) time, (b) T, and (c) pO2. These experiments used a roughly equimolar feed of CO2 and H2O and produced fuel with a relatively higher fraction of CO than H2. This product proportion is consistent with the more favorable change in Gibbs free energy for thermolysis of CO2 at high temperatures, as seen in Fig. 1a. The average molar ratio O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fuel over 19 experiments was 0.53 ± 0.07, corroborating a closed mass balance. Furthermore, no other by-products were detected, indicating the absence of undesired side reactions. Specifically, Fig. 3a shows production rates over time at steady state at a nominal T of 1873 K and pO2 of 0.4 Pa. Note that T refers to the maximum measured shell temperature and pO2 refers to the partial pressure of O2 at the Ar inlet, which is the minimum pO2 in the system and determined by the impurity in the sweep gas. Gas evolution rates leveled off at a constant incident radiative flux of about 3500 suns (1 sun = 1 kW m−2) over the cavity's aperture, and thus the reactor demonstrated continuous, steady-state operation under isothermal conditions. Fig. 3b shows the steady-state average production rates as a function of T in the range of 1723–1873 K. Mass flow rates were kept constant at 5 g h−1 H2O with 100 mL min−1 CO2 to the inner side and 500 mL min−1 Ar to the outer side of the membrane (L denotes standard liters). The measured pO2 ranged from 0.4–1.7 Pa due to variation in the small amount of air leakage into the reactor during different experimental runs. The specific fuel and O2 production rates at steady state increased with temperature, in accordance with the thermodynamic dependence on exp(−ΔG°/RT). Finally, Fig. 3c shows the steady-state average production rates as a function of pO2 in the range of 0.2–0.9 Pa at 1873 K. Although the range of pO2 tested was small, the gas production rates indeed decreased at higher pO2, as expected from the equilibrium relationship for the thermolysis of CO2 and H2O described in eqn (3) and (4). However, to achieve this range of pO2, the flow rate of Ar was adjusted, thus changing the relative flow of sweep gas, ṅsweep/ṅoxidant, which is also a key thermodynamic parameter in this reactor system.
fuel over 19 experiments was 0.53 ± 0.07, corroborating a closed mass balance. Furthermore, no other by-products were detected, indicating the absence of undesired side reactions. Specifically, Fig. 3a shows production rates over time at steady state at a nominal T of 1873 K and pO2 of 0.4 Pa. Note that T refers to the maximum measured shell temperature and pO2 refers to the partial pressure of O2 at the Ar inlet, which is the minimum pO2 in the system and determined by the impurity in the sweep gas. Gas evolution rates leveled off at a constant incident radiative flux of about 3500 suns (1 sun = 1 kW m−2) over the cavity's aperture, and thus the reactor demonstrated continuous, steady-state operation under isothermal conditions. Fig. 3b shows the steady-state average production rates as a function of T in the range of 1723–1873 K. Mass flow rates were kept constant at 5 g h−1 H2O with 100 mL min−1 CO2 to the inner side and 500 mL min−1 Ar to the outer side of the membrane (L denotes standard liters). The measured pO2 ranged from 0.4–1.7 Pa due to variation in the small amount of air leakage into the reactor during different experimental runs. The specific fuel and O2 production rates at steady state increased with temperature, in accordance with the thermodynamic dependence on exp(−ΔG°/RT). Finally, Fig. 3c shows the steady-state average production rates as a function of pO2 in the range of 0.2–0.9 Pa at 1873 K. Although the range of pO2 tested was small, the gas production rates indeed decreased at higher pO2, as expected from the equilibrium relationship for the thermolysis of CO2 and H2O described in eqn (3) and (4). However, to achieve this range of pO2, the flow rate of Ar was adjusted, thus changing the relative flow of sweep gas, ṅsweep/ṅoxidant, which is also a key thermodynamic parameter in this reactor system.
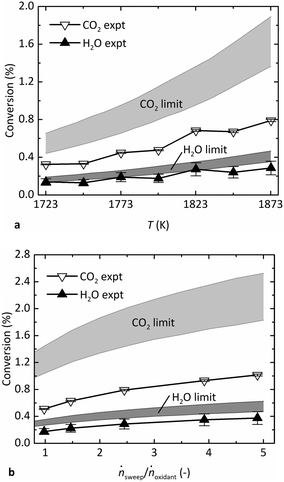
Fig. 4 shows the experimental steady-state conversion of CO2 to CO and H2O to H2 as a function of (a) T in the range of 1723–1873 K at pO2 = 1 Pa, ṅsweep/ṅoxidant = 2.4, and (b) ṅsweep/ṅoxidant ranging from 1–5 at T = 1873 K, pO2 = 0.5 Pa. The thermodynamic limits are also indicated, denoted by a band whose upper and lower bounds are calculated as described above at Tshell and the estimated reaction temperature, Tshell − 50 K, respectively. The band is wider for CO2 than that for H2O because its reaction favorability changes more steeply with T. Like the gas production rates, the conversion of reactants shown in Fig. 4a increased with T, as expected. The conversion also increased at higher relative sweep rates shown in Fig. 4b, because ṅsweep/ṅoxidant determines the total amount of O2 that can be removed across the membrane at equilibrium. In fact, the thermodynamic analysis reveals that the trend in production rates observed in Fig. 3c is more attributable to varying ṅsweep/ṅoxidant than pO2. The pO2 in the sweep gas must be lower than pO2 in the oxidant stream at all points along the membrane to drive transfer of O2. At sufficiently low pO2, however, this parameter does not have a strong influence on the conversion of reactants, shown in Fig. S3 in the ESI.† In the range of pO2 observed in the experiments (0.2–0.9 Pa), the theoretical conversion of each reactant at constant ṅsweep/ṅoxidant is almost flat, while the experimental data points exhibit a trend due to varying relative sweep rates. In contrast, the same experimental data plotted against ṅsweep/ṅoxidant shown in Fig. 4b match the shape of the equilibrium limit curves.
In general, the results indicate that the reactor performance indeed approaches the thermodynamic limit for a countercurrent flow reactor. Importantly, the experimental conversion does not exceed the theoretical limit. Furthermore, the experimental points lie closer to the lower bound of the equilibrium region, suggesting that the simple heat transfer model is necessary and effective to estimate the reaction temperature. While the experimental conversion of H2O closely follows the lower bound of the predicted thermodynamic limit, the experimental conversion of CO2 falls short. The discrepancy is less than a factor of two and may be a result of the water–gas shift (WGS) reaction occurring at lower T downstream of the reactor, before the GC analysis. The WGS consumes some CO to produce additional H2 and is thus the difference of the CO2 and H2O dissociation reactions (eqn (2) minus eqn (1)):
| CO + H2O ↔ H2 + CO2 | (7) |
In this case, the GC measurements may not be representative of the composition in the reactor; the actual conversion of CO2 may have been higher, and the conversion of H2O lower, potentially equalizing the difference seen in Fig. 4 between the experimental data and the limit for each gas.
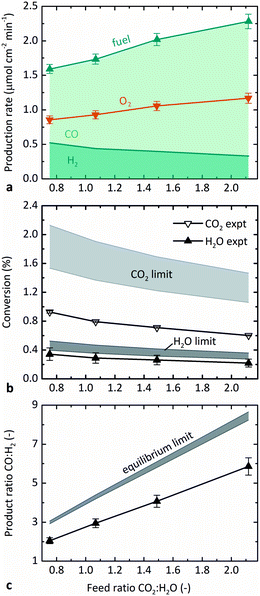
Fig. 5 illustrates the effect of the molar feed ratio, CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, on the: (a) steady-state average production rates of fuel and O2, (b) conversions of CO2 and H2O, and (c) molar ratio of the two fuels produced, CO
H2O, on the: (a) steady-state average production rates of fuel and O2, (b) conversions of CO2 and H2O, and (c) molar ratio of the two fuels produced, CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2. Fig. 5b and c show the comparison of the results measured experimentally with those predicted from thermodynamics. The relative flow rates of CO2 and H2O were varied while maintaining the steam feed rate at 5 g h−1 H2O, temperature at 1873 K, and pO2 at 0.5 Pa. Fig. 5a shows that the overall fuel production (sum of H2 and CO) increased with CO2
H2. Fig. 5b and c show the comparison of the results measured experimentally with those predicted from thermodynamics. The relative flow rates of CO2 and H2O were varied while maintaining the steam feed rate at 5 g h−1 H2O, temperature at 1873 K, and pO2 at 0.5 Pa. Fig. 5a shows that the overall fuel production (sum of H2 and CO) increased with CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, as did the production rate of CO, which occurred because the total feed rate and CO2 feed rate both increased. The production rate of H2, on the other hand, decreased with CO2
H2O, as did the production rate of CO, which occurred because the total feed rate and CO2 feed rate both increased. The production rate of H2, on the other hand, decreased with CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O. It must be emphasized that ṅsweep/ṅoxidant did not remain constant over experimentation, but rather decreased with CO2
H2O. It must be emphasized that ṅsweep/ṅoxidant did not remain constant over experimentation, but rather decreased with CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O because the flow rate of sweep gas remained constant. A constant flow rate of sweep gas is less effective at maintaining low pO2 as the amount of O2 to be removed increases. In the case of CO, the effect of increasing CO2 feed rate compensated for the decreasing sweep ratio, so that the net production rate increased. However, the H2 production decreased.
H2O because the flow rate of sweep gas remained constant. A constant flow rate of sweep gas is less effective at maintaining low pO2 as the amount of O2 to be removed increases. In the case of CO, the effect of increasing CO2 feed rate compensated for the decreasing sweep ratio, so that the net production rate increased. However, the H2 production decreased.
The confounding factors of changing both the total feed rate and the relative sweep rate are accounted for by plotting conversion instead of the production rate in Fig. 5b. As seen in Fig. 4, the absolute values of H2O conversion in Fig. 5b again match the model results better than those for CO2. The experimental conversions of both CO2 and H2O decreased slightly with increasing CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, in agreement with the trend predicted at equilibrium. There are two contributions to the negative trend in conversion. First, as already mentioned, ṅsweep/ṅoxidant decreased with CO2
H2O, in agreement with the trend predicted at equilibrium. There are two contributions to the negative trend in conversion. First, as already mentioned, ṅsweep/ṅoxidant decreased with CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, which decreased the conversion. However, the conversion of each reactant is predicted to decrease slightly with CO2
H2O, which decreased the conversion. However, the conversion of each reactant is predicted to decrease slightly with CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O even with a constant ṅsweep/ṅoxidant. The second reason for the trend is related to the difference in favorability of thermolysis of CO2 and H2O. As the feed ratio increases, a higher proportion of the feed is CO2, which has a higher conversion than H2O under these conditions. In fact, the overall conversion of reactants to products actually increased slightly with increasing CO2
H2O even with a constant ṅsweep/ṅoxidant. The second reason for the trend is related to the difference in favorability of thermolysis of CO2 and H2O. As the feed ratio increases, a higher proportion of the feed is CO2, which has a higher conversion than H2O under these conditions. In fact, the overall conversion of reactants to products actually increased slightly with increasing CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O. However, the O2 capacity of the sweep gas was unchanged and therefore the conversion of each individual reactant must decrease to balance the production of O2 with its removal. This result indicates that a feed of CO2 requires a higher relative sweep rate than an equal feed of H2O, because its higher potential conversion leads to a larger amount of O2 that must be removed.
H2O. However, the O2 capacity of the sweep gas was unchanged and therefore the conversion of each individual reactant must decrease to balance the production of O2 with its removal. This result indicates that a feed of CO2 requires a higher relative sweep rate than an equal feed of H2O, because its higher potential conversion leads to a larger amount of O2 that must be removed.
Consistent with Fig. 5a, Fig. 5c shows that the product ratio CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 increased with increasing feed ratio CO2
H2 increased with increasing feed ratio CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, as expected intuitively. Interestingly, CO
H2O, as expected intuitively. Interestingly, CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 is always greater than the corresponding CO2
H2 is always greater than the corresponding CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, which further confirms that dissociation of CO2 is more favorable than that of H2O under equivalent conditions. The observed experimental trend qualitatively matches equilibrium thermodynamics, though with a smaller slope, because the experimental conversion of CO2 is lower than predicted. In consideration of downstream processing, the Fischer–Tropsch synthesis favors a syngas feed with 1
H2O, which further confirms that dissociation of CO2 is more favorable than that of H2O under equivalent conditions. The observed experimental trend qualitatively matches equilibrium thermodynamics, though with a smaller slope, because the experimental conversion of CO2 is lower than predicted. In consideration of downstream processing, the Fischer–Tropsch synthesis favors a syngas feed with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 moles CO
2 moles CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2.37,38 According to Fig. 5c, the product ratio can be adjusted via the feed ratio, and a 1
H2.37,38 According to Fig. 5c, the product ratio can be adjusted via the feed ratio, and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 product ratio would require a feed ratio smaller than the minimum tested here.
2 product ratio would require a feed ratio smaller than the minimum tested here.
The maximum conversions observed experimentally were 1.0% CO2 and 0.4% H2O at 1873 K, ṅsweep/ṅoxidant = 5, and 0.2 Pa O2 (0.7% overall conversion of reactants). In general, the absolute values of both theoretical and experimental conversion were lower in the co-feed case tested here than in the pure-CO2 feed case tested previously,12 because the relative sweep rates were lower in this set of experiments. The base case ṅsweep/ṅoxidant was 8 in pure-CO2 experiments and 2.4 in these co-feed experiments. The relative sweep rate is a significant parameter for sweep gas operation, and the application of the countercurrent flow model was essential to accurately predict the behavior of the reactor. Furthermore, although there was no effort to optimize the efficiency of the reactor in these proof-of-concept experiments, ṅsweep/ṅoxidant also impacts efficiency because it determines how much sweep gas must be heated and circulated per unit fuel produced.
Conclusion
We have demonstrated steady-state splitting of a mixed feed containing CO2 and H2O into separate streams of syngas fuel and O2 using an isothermal tubular ceria membrane reactor driven by simulated concentrated solar radiation. The experimental results generally agreed with trends predicted by thermodynamics. The conversion of CO2 to CO was favored over H2O to H2, consistent with the energetics of the respective thermolysis reactions. The co-thermolysis of a mixture of CO2 and H2O is more complex than feeding either CO2 or H2O separately to the reactor, both experimentally and in the theoretical analysis. In the co-feed case, the mixture of CO2, H2O, CO, and H2 could undergo additional reactions, especially the reverse water–gas shift (RWGS). As seen in eqn (7), the WGS reaction is not independent of the two thermolysis reactions, and thus does not change the equilibrium conversion of each reactant from the pure-feed values. Other possible reactions were found to be negligible from the lack of by-products predicted by thermodynamics and measured experimentally under these conditions. The absence of by-products and a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of fuel
1 ratio of fuel![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) oxygen together confirmed 100% selectivity for the desired splitting reactions.
oxygen together confirmed 100% selectivity for the desired splitting reactions.
The solar thermochemical membrane reactor unifies both CO2 and H2O splitting in a single modular and scalable device and offers a technically viable pathway to single-step syngas production. However, determining an appropriate relative sweep rate is challenging in co-feed operation because the different favorability for thermolysis of CO2 and H2O implies different optimums for each species. In addition, these energetic differences mean that H2O needs to be fed in large excess to achieve a desirable syngas composition. Therefore, it may still be attractive to produce CO and H2 separately and mix them into syngas as needed. Furthermore, the single-step approach incorporated in the membrane reactor must compete with multistep cycles currently available. Thus, further R&D and alternative membrane configurations are needed to boost mass conversions and consequently reach favorable solar-to-fuel energy efficiencies, a challenge because T and pO2 determine the thermodynamic limits.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Swiss National Science Foundation (Ambizione Energy Grant No. 166883) and by the Chinese Academy of Sciences (International Collaboration Key Program award no. 182211KYSB20160043). We thank Brendan Bulfin for fruitful discussions and Patrick Basler and Simon Minder for supporting the experimental campaign.References
- N. S. Lewis, Science, 2016, 351, aad1920 CrossRef PubMed.
- G. A. Ozin, Adv. Mater., 2015, 27, 1957–1963 CrossRef CAS PubMed.
- J. A. Herron, J. Kim, A. A. Upadhye, G. W. Huber and C. T. Maravelias, Energy Environ. Sci., 2015, 8, 126–157 RSC.
- D. Marxer, P. Furler, J. Scheffe, H. Geerlings, C. Falter, V. Batteiger, A. Sizmann and A. Steinfeld, Energy Fuels, 2015, 29, 3241–3250 CrossRef CAS.
- W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, Science, 2010, 330, 1797–1801 CrossRef CAS PubMed.
- M. Romero and A. Steinfeld, Energy Environ. Sci., 2012, 5, 9234 RSC.
- Y. Hao, C. K. Yang and S. M. Haile, Phys. Chem. Chem. Phys., 2013, 15, 17084–17092 RSC.
- C. L. Muhich, B. W. Evanko, K. C. Weston, P. Lichty, X. Liang, J. Martinek, C. B. Musgrave and A. W. Weimer, Science, 2013, 341, 540–542 CrossRef CAS PubMed.
- L. J. Venstrom, R. M. De Smith, Y. Hao, S. M. Haile and J. H. Davidson, Energy Fuels, 2014, 28, 2732–2742 CrossRef CAS.
- E. A. Fletcher and R. L. Moen, Science, 1977, 197, 1050–1056 CrossRef CAS PubMed.
- J. E. Noring, R. B. Diver and E. A. Fletcher, Energy, 1981, 6, 109–121 CrossRef CAS.
- M. Tou, R. Michalsky and A. Steinfeld, Joule, 2017, 1, 146–154 CrossRef CAS PubMed.
- A. Evdou, L. Nalbandian and V. Zaspalis, J. Membr. Sci., 2008, 325, 704–711 CrossRef CAS.
- W. Jin, C. Zhang, X. Chang, Y. Fan, W. Xing and N. Xu, Environ. Sci. Technol., 2008, 42, 3064–3068 CrossRef CAS PubMed.
- L. Nalbandian, A. Evdou and V. Zaspalis, Int. J. Hydrogen Energy, 2009, 34, 7162–7172 CrossRef CAS.
- H. Wang, Y. Hao and H. Kong, Int. J. Energy Res., 2015, 39, 1790–1799 CrossRef CAS.
- X. Y. Wu, L. Chang, M. Uddi, P. Kirchen and A. F. Ghoniem, Phys. Chem. Chem. Phys., 2015, 17, 10093–10107 RSC.
- L. Zhu, Y. Lu and S. Shen, Energy, 2016, 104, 53–63 CrossRef CAS.
- T. C. Davenport, C.-K. Yang, C. J. Kucharczyk, M. J. Ignatowich and S. M. Haile, Energy Technol., 2016, 4, 764–770 CrossRef CAS.
- P. Furler, J. R. Scheffe and A. Steinfeld, Energy Environ. Sci., 2012, 5, 6098–6103 RSC.
- P. M. Geffroy, J. Fouletier, N. Richet and T. Chartier, Chem. Eng. Sci., 2013, 87, 408–433 CrossRef CAS.
- S. Ackermann, J. R. Scheffe and A. Steinfeld, J. Phys. Chem. C, 2014, 118, 5216–5225 CrossRef CAS.
- W. C. Chueh and S. M. Haile, Philos. Trans. R. Soc., A, 2010, 368, 3269–3294 CrossRef CAS PubMed.
- M. Mogensen, N. M. Sammes and G. A. Tompsett, Solid State Ionics, 2000, 129, 63–94 CrossRef CAS.
- A. Glück, R. Tamme, H. Kalfa and C. Streuber, Sol. Energy Mater., 1991, 24, 240–248 CrossRef.
- R. Bader, L. J. Venstrom, J. H. Davidson and W. Lipiński, Energy Fuels, 2013, 27, 5533–5544 CrossRef CAS.
- S. Brendelberger, H. von Storch, B. Bulfin and C. Sattler, Sol. Energy, 2017, 141, 91–102 CrossRef CAS.
- M. Ezbiri, K. M. Allen, M. E. Galvez, R. Michalsky and A. Steinfeld, ChemSusChem, 2015, 8, 1966–1971 CrossRef CAS PubMed.
- B. Bulfin, J. Vieten, C. Agrafiotis, M. Roeb and C. Sattler, J. Mater. Chem. A, 2017, 5, 18951–18966 RSC.
- W. He, H. Huang, J.-F. Gao, L. Winnubst and C.-S. Chen, J. Membr. Sci., 2014, 452, 294–299 CrossRef CAS.
- X. Tan, Y. Liu and K. Li, Ind. Eng. Chem. Res., 2005, 44, 61–66 CrossRef CAS.
- W. T. Welford and R. Winston, High Collection Nonimaging Optics, Academic Press, Inc., San Diego, 1989 Search PubMed.
- P. Furler, J. Scheffe, M. Gorbar, L. Moes, U. Vogt and A. Steinfeld, Energy Fuels, 2012, 26, 7051–7059 CrossRef CAS.
- Q. Jiang, Z. Chen, J. Tong, M. Yang, Z. Jiang and C. Li, Chem. Commun., 2017, 53, 1188–1191 RSC.
- B. Bulfin, Phys. Chem. Chem. Phys., 2019, 21, 2186–2195 RSC.
- M. W. Chase, C. A. Davies, J. R. Downey, D. J. Frurip, R. A. McDonald and A. N. Syverud, NIST-JANAF Thermochemical Tables: NIST Standard Reference Database 13, Standard Reference Data Program, National Institute of Standards and Technology, 1998, DOI:10.18434/T42S31.
- H. Schulz, Appl. Catal., A, 1999, 186, 3–12 CrossRef CAS.
- D. Leckel, Energy Fuels, 2009, 23, 2342–2358 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8re00218e |
| This journal is © The Royal Society of Chemistry 2019 |