Open Access Article
Open Access ArticleA manganese hydride molecular sieve for practical hydrogen storage under ambient conditions†
Leah
Morris
a,
James J.
Hales
b,
Michel L.
Trudeau
c,
Peter
Georgiev
d,
Jan Peter
Embs
 e,
Juergen
Eckert
e,
Juergen
Eckert
 f,
Nikolas
Kaltsoyannis
f,
Nikolas
Kaltsoyannis
 b and
David M.
Antonelli
b and
David M.
Antonelli
 *g
*g
aSustainable Environment Research Centre, University of South Wales, Pontypridd, CF37 4BD, UK
bSchool of Chemistry, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
cCenter of Excellence for Transportation Electrification and Energy Storage, Hydro-Quebec Research Institute, 1806 Boul. Lionel-Boulet, Varennes, Quebec J3X 1S1, Canada
dDepartment of Solid State Physics, Faculty of Physics, 5 Boul. James Bourchier, Sofia 1164, Bulgaria
eLaboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, CH-5232 Villigen, Switzerland
fDepartment of Chemistry and Biochemistry, Texas Tech University, P. O. Box 41061, Lubbock, TX 79406-1061, USA
gDepartment of Chemistry, Lancaster University, Lancaster, LA1 4YB, UK. E-mail: d.antonelli@lancaster.ac.uk
First published on 10th December 2018
Abstract
A viable hydrogen economy has thus far been hampered by the lack of an inexpensive and convenient hydrogen storage solution meeting all requirements, especially in the areas of long hauls and delivery infrastructure. Current approaches require high pressure and/or complex heat management systems to achieve acceptable storage densities. Herein we present a manganese hydride molecular sieve that can be readily synthesized from inexpensive precursors and demonstrates a reversible excess adsorption performance of 10.5 wt% and 197 kgH2 m−3 at 120 bar at ambient temperature with no loss of activity after 54 cycles. Inelastic neutron scattering and computational studies confirm Kubas binding as the principal mechanism. The thermodynamically neutral adsorption process allows for a simple system without the need for heat management using moderate pressure as a toggle. A storage material with these properties will allow the DOE system targets for storage and delivery to be achieved, providing a practical alternative to incumbents such as 700 bar systems, which generally provide volumetric storage values of 40 kgH2 m−3 or less, while retaining advantages over batteries such as fill time and energy density. Reasonable estimates for production costs and loss of performance due to system implementation project total energy storage costs roughly 5 times cheaper than those for 700 bar tanks, potentially opening doors for increased adoption of hydrogen as an energy vector.
Broader contextA viable hydrogen economy has thus far been hampered by the lack of convenient hydrogen storage solutions for long hauls and transportation/delivery infrastructure. Current approaches require high pressure and/or complex heat management systems to achieve acceptable storage densities. Development of hydrogen storage solutions operating at near ambient conditions can mitigate the complexity, cost and safety perception issues currently hindering the hydrogen economy. We have assembled a team of experts in both experimental and computational modelling approaches to synthesise and characterise a porous manganese hydride material, which projects to offer roughly four times the volumetric hydrogen storage capacity of 700 bar incumbents when used in a system at ambient temperature and moderate pressures, without the need for external heat management because of its unique nano-scale heat sinking mechanism. As a result of its highly-promising properties (including its use of the so-called “Kubas” mechanism for binding hydrogen) and the low projected cost of synthesis, we anticipate that our material may significantly lower commercial barriers to adoption of hydrogen fuel cells with respect to existing technologies and large-scale transportation of hydrogen will be facilitated. The properties of our new material also make hydrogen fuel cells an attractive alternative to lithium batteries in some applications, especially those involving long ranges. |
Introduction
For future market acceptance of hydrogen fuel cell vehicles or portable devices an efficient, low cost and practical hydrogen storage system and infrastructure suitable for all applications still needs to be developed.1,2 To achieve a driving range greater than 500 km in a fuel cell vehicle, about 5 kg of hydrogen is required. In the expensive carbon fiber 700 bar non-conformable hydrogen gas cylinders, which are employed in today's first generation hydrogen vehicles, 5 kg of hydrogen occupies a volume of about 125 L, thus placing unwanted constraints on the automobile design.3 A material-based hydrogen storage system gives the possibility of storing hydrogen at lower pressures with simplified thermal management requirements that may reduce both onboard and infrastructure system complexity and costs. While some metal hydrides approach practical performance levels, problems with heat management still thwart their applications.4 As a possible alternative, amorphous carbons and metal–organic frameworks (MOFs) have been explored owing to their projected low cost and ability to store hydrogen reversibly with fast kinetics at cryogenic temperatures.5 Storage using these materials at 77 K, however, has the practical problem of cooling cost and boil off due to the 5–13 kJ mol−1 heat release upon adsorption, which is significantly less than the 50–70 kJ mol−1 of typical hydrides but still enough to create practical problems.6 Thus, to use a MOF or hydride in a fuel cell vehicle, sophisticated heat management methods must be incorporated into the tank design and the need for cooling during refueling could create inconsistent fill rates and times. Cryogenic systems further complicate the fueling interface and drive significant extra cost into both the on-board tank and fueling infrastructure. For more detailed comparisons, a full table of representative hydrides and physisorption materials with their respective performances and desorption enthalpies has been compiled elsewhere.6 Because of the ideal binding enthalpies of σ-H2 (Kubas) binding to transition metals,7 it has been proposed that a material using this mechanism as the principal adsorption driving force may present a solution,8,9 however such materials would also have heat sinking issues on fueling due to their 20–30 kJ mol−1 binding enthalpies. So to facilitate broad scope implementation of fuel cell devices, a material is required which possesses high gravimetric and volumetric storage capacities under ambient conditions, and is both economical to produce and does not require extensive heat management to refuel. Such a material could also present a possible alternative to Li-batteries in portable devices, where rising costs and demand for energy storage are a concern.10Herein we present a manganese hydride molecular sieve (KMH-1 = Kubas Manganese Hydride-1) which can be prepared in a few simple steps from inexpensive precursors and possesses hydrogen storage performance which, even when estimates on system implementation are taken into consideration, may be sufficient to meet or surpass the US Department of Energy's (DOE) ultimate system targets of 6.5 wt% and 50 kgH2 m−3 for 5 kg of hydrogen.11 This is achieved using specifically tailored Kubas binding sites in an amorphous porous manganese hydride network which acts as its own intrinsic nanoscale heat sink, making external heat management requirements very limited or possibly even unnecessary.
Results and discussion
All hydrogen storage materials were prepared under argon by thermal hydrogenation at 373 K of a petroleum ether solution of bis(neopentyl) manganese.12 Elimination of alkane and formation of a metal hydride by hydrogenation of a transition metal alkyl is a well-known reaction13 and our proposed mechanism is shown in Fig. 1A. This method of synthesizing a solid-state transition metal hydride from a metal alkyl has been reported previously by our group for Ti, Cr, and V systems.14–17 The resulting black air sensitive solid (KMH-1 as synthesized) still contained hydrocarbon as evidenced by the infrared (IR) spectrum (Fig. S1, ESI†) and because of this was hydrogenated in the solid state at 373 K and 85 bar for 4 hours to give KMH-1 after 1st hydrogenation. Further hydrogenation at 413 K and 85 bar for 4 hours gave KMH-1 after 2nd hydrogenation, which still contained trace hydrocarbon by IR. In order to remove all hydrocarbon and streamline the synthesis process KMH-1 after 1st hydrogenation was cycled 54 times under repeated adsorption and desorption of hydrogen at 298 K up to 120 bar to give KMH-1 after cycling. All materials were extensively characterized and the hydrogen storage properties were investigated as discussed below.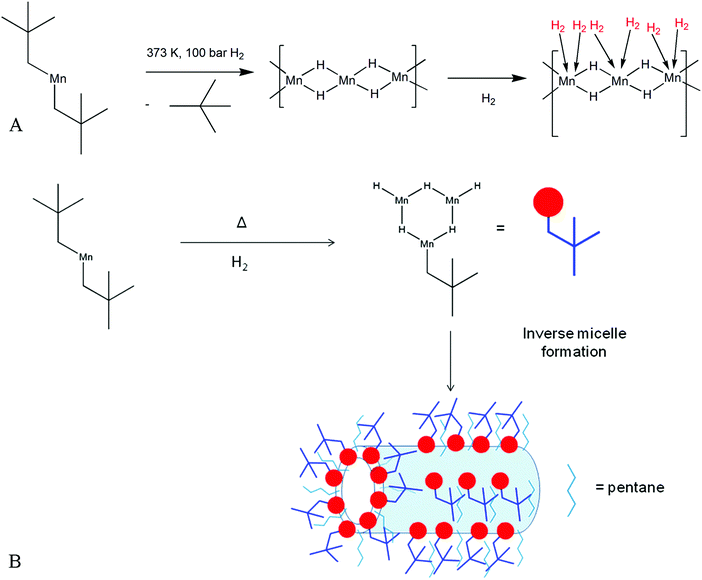 | ||
| Fig. 1 Synthesis scheme for KMH-1: (A) proposed mechanism for the formation of manganese hydride-based KMH-1 molecular sieve from bis(neopentyl) manganese; (B) schematic representation of KMH-1 nanostructure formation by an inverse micelle templating mechanism expected from self-assembly in a non-polar medium.19 | ||
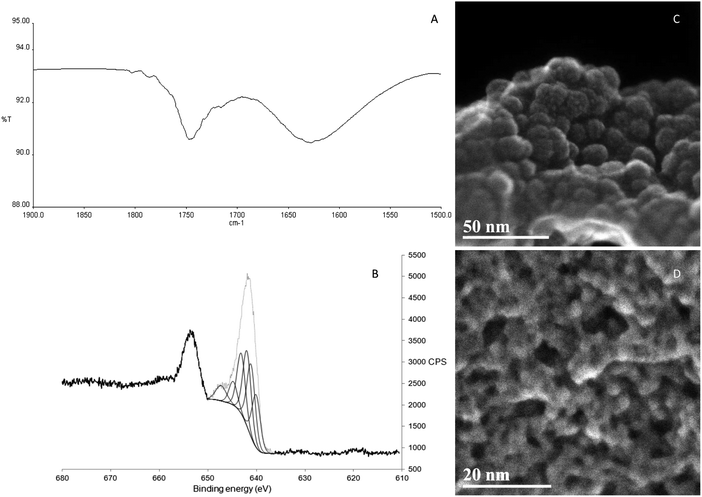
The IR spectra of KMH-1 as synthesized, KMH-1 after 1st hydrogenation, KMH-1 after 2nd hydrogenation, and KMH-1 after cycling (Fig. S1, ESI†) all show C–H stretches at 2964 cm−1. With successive hydrogenations the intensity of the C–H stretches decreases, which can be attributed to replacement of the neopentyl ligands with hydrides by hydrogenolysis. In the spectrum of KMH-1 after 1st hydrogenation there is a weak stretch at 1750 cm−1, which can be assigned to an Mn–H stretch on the basis of previous DFT calculations for a variety of homoleptic manganese hydride species, which predict bands in the region of 1600–1900 cm−1.18 In KMH-1 after 2nd hydrogenation (expansion in Fig. 2A) this band has increased in intensity and KMH-1 after cycling displays this same Mn–H stretch in the greatest intensity. Thermogravimetric analysis (TGA) of this family of KMH-1 materials was carried out to determine the hydrocarbon content (Fig. S2–S4, ESI†) and demonstrates significant weight loss with each successive hydrogenation. Nitrogen adsorption–desorption isotherms of all materials were conducted at 77 K to establish the surface area and porosity (see Fig. S5–S8 and Table S1, ESI†) and show a gradual increase of surface area from 1.2 m2 g−1 to 257 m2 g−1 upon successive hydrogenation. The full details of the TGA and nitrogen adsorption are discussed in the ESI.†
Scanning transmission electron microscopy in secondary electron mode (STEM-SE) of KMH-1 as synthesized is shown in Fig. 2C and shows raspberry-like clusters of nanospheres, suggesting an inverse micelle templated synthesis mechanism as illustrated in Fig. 1B.19 The STEM-SE of KMH-1 after 2nd hydrogenation confirms the uniform presence of porous channels of 5 nm or less in diameter (Fig. 2D and Fig. S9, ESI†) due to hydrogenation-induced hydrocarbon leaching. The powder X-ray diffraction (PXRD) of KMH-1 as synthesized revealed a small amount of crystallinity, probably due to the presence of a residual organic phase (Fig. S10, ESI†).
All materials after hydrogenation did not show any X-ray diffraction reflections and are thus amorphous with no long-range order (Fig. S11, ESI†). This is also true for other transition-metal alkyl hydride materials previously reported by our group.14–17 The Energy Dispersive X-ray Spectroscopy (EDS) for KMH-1 as synthesized (Fig. S12 and Table S2, ESI†) and KMH-1 after 2nd hydrogenation (Fig. S13 and Table S3, ESI†) confirms the principally manganese-based composition with small amounts of residual oxygen and Mg halide. X-ray Photoelectron Spectroscopy (XPS) was conducted to probe the oxidation states of the Mn in the material. KMH-1 after 2nd hydrogenation shows a broad emission in the Mn 2p3/2 region centered at 641 eV (Fig. 2B), which is assigned to a mixture of Mn(I) and Mn(II) species by comparison with the literature.20,21 The presence of Mn(I) in KMH-1 as synthesized (Fig. S14, ESI†) establishes that reduction of Mn(II) occurred in the initial thermal treatment of the neopentyl manganese precursor, either by hydrogenation or Mn–C bond homolysis, which is common in the thermal decomposition of metal alkyls.22,23 The sum of these techniques identifies the KMH-1 materials as non-stoichiometric manganese alkyl hydrides in an oxidation state between Mn(I) and Mn(II), with increasing meso- and microporosity and predominance of hydride over alkyl with successive hydrogenations until KMH-1 after cycling is highly porous and essentially alkyl-free.
The excess hydrogen adsorption–desorption isotherms at 298 K (Fig. 3A) for KMH-1 as synthesized, KMH-1 after 1st hydrogenation and KMH-1 after 2nd hydrogenation increase linearly with increasing pressure, without reaching saturation within the range of experiment. The initial material, KMH-1 as synthesized reached 1.57 wt% at 150 bar. KMH-1 after 1st hydrogenation absorbed 3 wt% at 150 bar, while KMH-1 after 2nd hydrogenation reached 7.26 wt% at 150 bar. The adsorption–desorption isotherms show slight hysteresis indicating a small kinetic barrier to fully desorb hydrogen from the material. The increased performance on loss of hydrocarbon can be attributed to loss of weight, improved hydrogen diffusion due to increased porosity and surface area, as well as more effective H2 binding to an M-H vs. an M-R site.7 With a xylene-displacement density of 1.88 g cm−3, 7.26 wt% corresponds to a volumetric capacity of 136 kgH2 m−3. Related Ti14 and Cr15 materials did not saturate at similar pressures, while those based on V16,17 reached saturation as high as 5.8 wt%. The reason for this is not understood, but may be due to varying amounts of physisorption present in the respective samples, i.e. the V-based materials possess much lower surface areas than their Ti, Cr, and Mn counterparts and are thus not expected to display an appreciable physisorption component. Volume calibration artefacts are ruled out because all experiments were conducted at a level of 2–3 mmol excess adsorption and we were able to obtain high accuracy and saturation at 2 mmol total excess adsorption at the same temperature and pressure with Carbon AX-21 (Fig. S15a, ESI†). Moreover, a “fouled” 40 mg sample of KMH-1 after 2nd hydrogenation sourced from an oxidized precursor solution demonstrated saturation at only 1.5 wt% at 60 bar (Fig. S15b, ESI†) with no further adsorption to the 100 bar limit of experiment, demonstrating freedom from virtual adsorption artefacts in our instrument down to levels of at least as low as 0.6 mmol total excess hydrogen adsorption.
As there was still hydrocarbon remaining in the material KMH-1 after 2nd hydrogenation, a sample of KMH-1 after 1st hydrogenation was put under repeated adsorption and desorption of hydrogen for 54 cycles as shown in Fig. 3B and Fig. S16 (ESI†). The sample reached a final performance of 10.5 wt% at 120 bar without saturation (Fig. 3C). Based on the molecular weight for MnH this corresponds to 2.9 H2 per Mn center. A MOF has recently been reported that binds 2 H2 per Mn center at cryogenic temperature,24 however there are no reports of metals with more than 2 bound H2 per metal. Because of the greater coordinative unsaturation and lower steric requirements of a homoleptic hydride as compared to a MOF, more H2 binding per metal site is not unexpected. While lower adsorption values might be expected based on the 257 m2 g−1 nitrogen surface area, this metric is only a useful indicator when physisorption is the dominant adsorption mechanism and hydrogen diffusion into pores too small for nitrogen penetration is not a contributing factor. Using a density of 1.88 g cm−3 the adsorption corresponds to a volumetric capacity of 197 kgH2 m−3, which compares to ca. 40 kgH2 m−3 for 700 bar tanks and is considerably higher than that for Mg2FeH6 (150 kgH2 m−3),1 the best performing hydride in this regard. However, this comparison can readily be rationalized by the observation that fully loaded KMH-1 possesses almost three times the molar H2-to-total metal ratio than Mg2FeH6.
The enthalpy of hydrogen adsorption of KMH-1 after 2nd hydrogenation was measured directly using an isothermal calorimeter. In this set up16 a hydrogen uptake measurement is conducted and the calorimeter collects the heat flow data simultaneously as the sample is dosed with hydrogen in increments up to 120 bar. To validate the results a calorimetric measurement of Carbon AX-21 at a similar level of 2 mmol total hydrogen adsorbed was also conducted. The calorimetric curves obtained were exothermic and decreased with increased surface coverage. The enthalpy of hydrogen adsorption for Carbon AX-21 measured using this method was −3.61 kJ mol−1 (Fig. S17, ESI†) which is in the region of ca. −4 kJ mol−1 reported for activated carbons.25 The enthalpy of hydrogen adsorption for KMH-1 after 2nd hydrogenation is +2.2 kJ mol−1, recorded at a value of 3 mmol excess adsorption. Unlike the data for AX-21 (Fig. S17, ESI†), the calorimetric curves (Fig. 3D) are endothermic and do not increase or decrease significantly with increased surface coverage. This supports the mechanism discussed at length previously and supported by computations and high-pressure Raman measurements15–17 in which the 20–40 kJ mol−1 H2 energy expected for Kubas binding of hydrogen8,9 is offset by twisting of the material as the pressure increases to open up new binding sites.26 A MOF has been reported that undergoes structural deformation on application of pressure and this deformation influences the adsorption properties.27 Due to this offset of heat energy, storage of hydrogen in KMH-1 is close to thermodynamically neutral. This provides an elegant solution to the practical problem of heat management in hydrogen storage tanks. Based on an estimated price of 10 USD per kg for KMH-1 with an expected loss in performance from system requirements, an energy storage cost of 3–4 $ per kW h can be projected, which is approximately 5 times cheaper than that for current 700 bar tanks for a 5 kgH2 system.28 Furthermore, while it is difficult to directly compare batteries and fuel cells, using an estimated price of 50 $ per kW for mass production of fuel cells,29 the complete fuel cell energy storage system projects as roughly 3–4 times less expensive than the current price of about 200 $ per kW h for lithium batteries.10
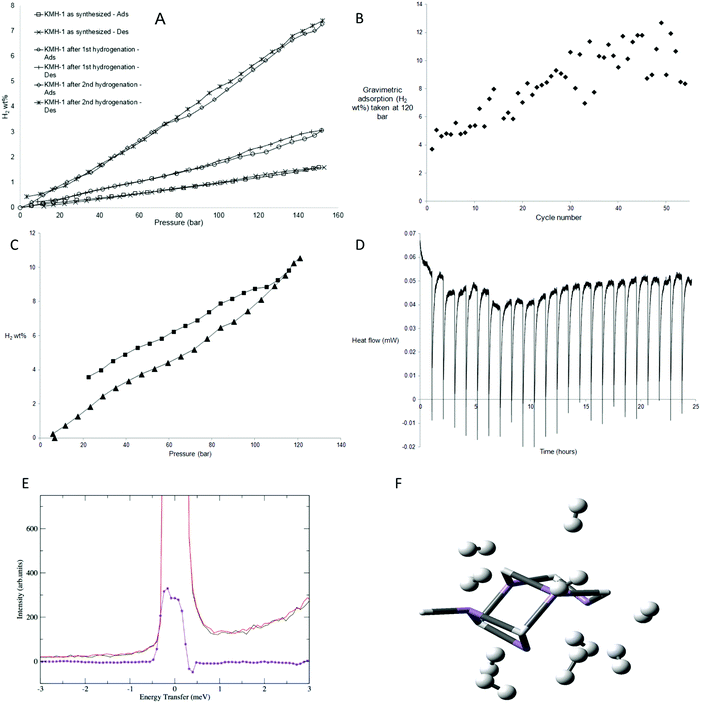 | ||
| Fig. 3 Hydrogen uptake by KMH-1: (A) excess hydrogen adsorption–desorption isotherms for KMH-1 materials recorded at 298 K at 2–3 mmol total excess adsorption; (B) cycle of 54 excess hydrogen adsorption and desorption isotherms up to 120 bar recorded at 298 K for KMH-1 at 2–3 mmol excess adsorption and scaled with a linear function to reflect gradual weight loss over the course of the measurement. Random scatter due to shorter equilibration times and high ΔP30 used during cycling; (C) adsorption–desorption isotherms for KMH-1 after cycling recorded at 298 K at 2.4 mmol excess adsorption; (D) calorimetric curves for KMH-1 after 2nd hydrogenation recorded at 313 K at 3 mmol excess adsorption; (E) INS spectra of KMH-1 after 2nd hydrogenation recorded at 1.5 K before and after H2 pressurization at 67 bar with the difference spectrum in violet. Sample was evacuated to remove weakly adsorbed H2; (F) computed structure of 10 H2 molecules bound to the Mn5H6 base structure with a representation of potential H2 binding sites in KMH-1. The base structure is rendered as tubes with the H2 units as balls and sticks. | ||
While high-pressure Raman measurements were used to confirm Kubas binding in closely analogous V, Cr, and Ti materials studied previously by our group,14–17 inelastic neutron scattering (INS) is a generally considered to be a more informative technique to explore hydrogen binding. Thus, to probe the mechanism of hydrogen binding more deeply, INS studies were performed on a sample of KMH-1 after 2nd hydrogenation; the results are shown in Fig. 3E. The essentially unresolved doublet peak at about zero energy transfer may be attributed to hydrogen bound to active adsorption sites. It was obtained by subtraction of the fully hydrogen loaded samples at 67 bar before and after re-activation, whereby the spectra of the non-adsorbed hydrogen is completely subtracted. The difference peak can be interpreted as showing rotational tunneling transitions for coordinated hydrogen at approximately ±0.4 meV in accordance with previous results on a large number of metal dihydrogen complexes.30 More specifically, INS results on the only stable Mn(II) dihydrogen complex Mn(I)CO(η2-H2)(dppe)231 show rotational tunneling transitions for H2 at ±0.5 meV. A barrier to rotation can be derived from the observed tunneling frequency if we assume that the reorientation takes place in a plane, and that the rotational potential is one of a double-minimum V2. If the rotational constant is adjusted for the H–H bond lengthening to 0.83 Å (as found in our DFT calculations) a two-fold barrier height of approximately 6.7 kJ mol−1 is obtained, in good agreement with our theoretical analysis (vide infra).
To investigate further the binding of H2 to KMH-1 and rationalize the adsorption and INS results, we turned to computational quantum chemistry, assuming a non-stoichiometric composition for KMH-1 between MnH2 and MnH, as supported by our data. To approximate behavior in an extended system, pentameric Mn hydride systems were modeled in addition to single Mn hydride molecules. Spin unrestricted density functional theory calculations were performed on monomeric and pentameric models of the H2 binding sites in KMH-1 using the PBE functional32,33 with Grimme's D3 dispersion corrections34 and the 6-311++G** basis set. We have previously employed the PBE/6-311++G** combination in studies of the Kubas binding of H2 to early first row transition metals.26 Recent benchmarking work has shown that generalized gradient approximation functionals, in conjunction with the D3 dispersion corrections, perform similarly to high level ab initio methods (CCSD(T)) for H2 binding to organic substrates decorated with metal atoms,35 transition metal oxide clusters,36 metal organic framework building units including transition metals,37 and graphene decorated with transition metals.38 All calculations were performed in the Gaussian 09 code, revision D.01.39 The geometries of the monomeric and pentameric manganese hydrides (hereafter referred to as base structure models, BSMs) were optimized without symmetry constraints, using the ultrafine integration grid and the very tight geometry convergence criteria: 2 × 10−6 a.u. for the maximum force, 10−6 a.u. for the RMS force, 6 × 10−6 a.u. for displacement, and 4 × 10−6 a.u. for the RMS displacement. All systems were studied in their high spin ground states, i.e. either Mn(II) with five unpaired electrons (upe) per metal center, or mixed Mn(II)/Mn(I) systems with five/four upe per Mn respectively. H2 units were introduced sequentially to the BSMs and the geometries were allowed to fully relax, without constraints, after each H2 addition. All structures were verified as true minima by harmonic vibrational frequency analysis. The converged Cartesian coordinates, SCF energies, hydrogen binding energies and enthalpies of all structures obtained are given in Tables S5–S11 (ESI†).
The hydrogen binding energies (HBE) were calculated using the following equation:
| HBE = E(BSM + nH2) − E(BSM) − nE(H2) |
Two key features of the binding of H2 to KMH-1 are (i) the extent to which the Kubas interaction plays a role and (ii) the maximum loading that can be achieved. Both of these have been assessed by examination of the geometries of the H2-loaded BSMs. For the former, we compare the Mn–H (H2) distances inside each H2 unit, and if the difference between the two is greater than 0.3 Å then we do not consider the binding as Kubas-like. Defining the maximum loading is not straightforward. For a three-dimensional cluster model, as more H2 bind, additional H2 units will experience the dispersion forces from ever-larger numbers of BSM + nH2 electrons. As such, an incoming H2 will always feel a weak attractive force. We have therefore chosen to take the maximum loading cut off as the point at which the shortest distance between an atom of an incoming H2 and the BSM + nH2 cluster is with a cluster-bound H2 unit, rather than with an atom of the BSM. We expect that this approach will provide a lower bound to the maximum H2 loading observed experimentally.
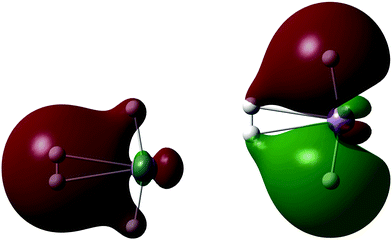
A single H2 binds to MnH2 (our monomeric BSM) with an HBE of 10.4 kJ mol−1 at the SCF level, with an enthalpy of 4.6 kJ mol−1. The H2 is oriented side-on to the almost linear MnH2 BSM, and Fig. 4 shows the two key Kohn–Sham molecular orbitals, which are characteristic of the synergic Kubas interaction.42 The left hand molecular orbital shows the donor interaction from the filled H2 σ bonding MO to a vacant Mn d orbital, and the right hand molecular orbital shows another, filled metal d orbital interacting in a π backbonding manner with the H2 σ* antibonding orbital. Note the involvement of the hydride ligands; this is an example of the previously observed cis-hydride effect in which the hydride ligands bend towards the H2 unit and participate in the bonding.43 We find a maximum load of 5 H2 on MnH2, where the average hydrogen binding energy (HBE) is 9.0 kJ mol−1 per H2 (enthalpy at 298 K of 4.8 kJ mol−1), consistent with measurements of MOFs with Mn(II) linkers, which can bind significant amounts of H2 only at cryogenic temperatures.24
To better mimic and rationalize experiment, we explored Mn hydride structures containing 5 Mn centers which are consistent with the KMH-1 XPS and IR data, i.e. the presence of Mn(I) emissions and terminal Mn–H stretches. Pentameric BSMs Mn5Hn (n = 6–10) were produced with between 0 and 4 formally Mn(I) centers. The reduced systems were generated by removing each of the hydrides from the Mn5H10 structure in turn and comparing the new structures’ SCF energies, choosing the most stable; this method was then repeated to generate the series. As the experimental IR data indicate the presence of terminal hydrides, if a structure lacked a terminal hydride it was discarded. The resulting Mn5H9 to Mn5H6 structures can be found in Fig. S18 (ESI†).
The XPS data for KMH-1 give the 2p3/2 orbital energies as a broad peak from 640–643 eV, with the emissions from 640–641 eV suggesting oxidation state of manganese lower than +2. We have examined the scalar energies of the Mn 2p orbitals for our reduced pentameric BSMs; see Table 1. The average 2p energy changes by cf. 2 eV from the all-Mn(II) system to that with four formal Mn(I) centers. Although the experimental and computational data differ in the absolute energies of the orbitals, the calculated energy range suggests that XPS data are consistent with a mixture of Mn(II) and Mn(I) centers.
| Number of Mn(I) present in the base structures | Minimum 2p orbital energy/eV | Maximum 2p orbital energy/eV | Average 2p orbital energy/eV |
|---|---|---|---|
| 0 | −626.9 | −628.0 | −627.5 |
| 1 | −626.6 | −627.3 | −627.0 |
| 2 | −626.2 | −626.5 | −626.3 |
| 3 | −625.4 | −626.5 | −625.8 |
| 4 | −625.4 | −626.4 | −625.6 |
The infrared spectrum of KMH-1 contains a broad peak at 1750 cm−1, attributed to a terminal Mn–H stretch. Frequency analysis of the optimized geometries for the Mn5H6 to Mn5H10 BSMs yielded the data in Table 2. The stretching frequencies, in all cases, are lower than those observed experimentally, but in acceptable agreement. In general the trend is for the stretching frequency to become smaller as the concentration of Mn(I) increases, with a difference of 23 cm−1 between the extremes of the model.
| Number of Mn(I) present in the base structures | Vibrational frequency of all the terminal Mn–H stretches | Average |
|---|---|---|
| 0 | 1684, 1691, 1700 | 1692 |
| 1 | 1679, 1684 | 1682 |
| 2 | 1651 | 1651 |
| 3 | 1670 | 1670 |
| 4 | 1669 | 1669 |
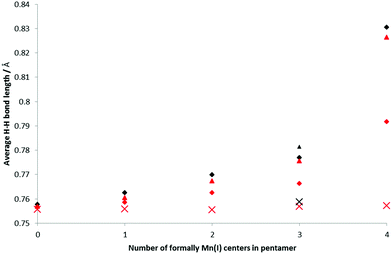
H2 binding to the BSMs was analyzed at 1 and 2 H2 per Mn center, i.e. loading levels similar to the conditions of the INS measurements and nearer to the experimental maximum loading. The bond length of free H2 is 0.752 Å at our chosen computational level. When bound in a Kubas-like fashion this bond length is expected to increase due to the back-donation from the metal d-orbital into the H2 σ*-orbital, though is not expected to change much on physisorption. Fig. 5 shows how the average H–H bond length varies with increasing concentration of Mn(I) in the BSMs. The smallest average H–H increase is for the all-Mn(II) system, and as the Mn atoms in the BSMs are reduced the average H–H distance increases, with the effect being less pronounced at greater loadings of H2. At 80% Mn(I) the bond lengthening effect is much stronger giving average bond lengths of 0.830 and 0.792 Å for loadings of 1 and 2 H2 per Mn, respectively.
Fig. 6 shows how the average Mn–H2 distance varies with increasing amounts of Mn(I) present in the BSM; these values were found by examining the shortest distances between a Mn in the BSM and the center of each H2 unit. The trend is for the distance between the H2 and Mn to decrease as the concentration of Mn(I) increases which suggests stronger bonds being formed. This is consistent with the stronger Kubas binding in the systems with more Mn(I). In all cases the distance is shorter for the smaller load as the strongest binding sites are occupied initially.
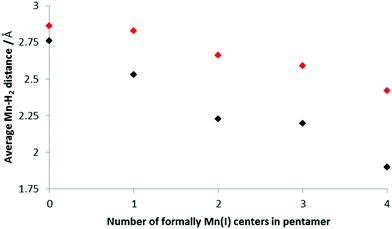 | ||
| Fig. 6 Average Mn–H2 distances for increasing concentrations of Mn(I); only the H closest to the Mn was considered. Black: 5 H2 bound to the base structure, red; 10 H2. | ||
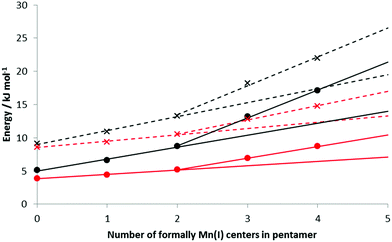
The HBEs (and enthalpies) increase as the number of formal Mn(I) in the BSM increases; Table 3 presents the data for loads of 5 and 10 H2 bound to the BSMs. With no Mn(I), average HBEs per H2 of 9.1 (5.1) kJ mol−1 and 8.6 (3.9) kJ mol−1 are found for loadings of 1 and 2 H2 per Mn respectively; this rises to 22.0 (17.2) kJ mol−1 and 14.8 (8.7) kJ mol−1 on Mn5H6 at the same loading levels; the structure of Mn5H6 with 2 H2 per Mn is shown in Fig. 3F. Fig. 7 shows how the binding energies and enthalpies increase with the amount of formal Mn(I) in the model. As discussed above, we do not believe a simple Mn5H5 model to be representative of KMH-1 and hence have used the data for the less reduced models to extrapolate a range of possible HBEs for a purely Mn(I) system. Specifically, trendlines generated from the first three points and last three points of the HBE data provide bounds for possible H2 binding energies and enthalpies to the 100% Mn(I) system. Since reversible room temperature binding of H2 is expected to occur between 20–30 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44,45 our calculations suggest an average Mn oxidation state for KMH-1 of cf. 1.2, consistent with findings that organometallic Mn(I) complexes with enthalpies of −52.2 kJ mol−1 achieve optimal reversible binding only at temperatures higher than 298 K.45 We conclude that an all-Mn(II) system is too high an oxidation state for optimal room temperature hydrogen storage,24 while all-Mn(I) is probably too low.
44,45 our calculations suggest an average Mn oxidation state for KMH-1 of cf. 1.2, consistent with findings that organometallic Mn(I) complexes with enthalpies of −52.2 kJ mol−1 achieve optimal reversible binding only at temperatures higher than 298 K.45 We conclude that an all-Mn(II) system is too high an oxidation state for optimal room temperature hydrogen storage,24 while all-Mn(I) is probably too low.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Data extrapolated producing a range of potential HBEs and enthalpies (see Fig. 7)
Data extrapolated producing a range of potential HBEs and enthalpies (see Fig. 7)
| Base structure | 5 H2 bound | 10 H2 bound | ||
|---|---|---|---|---|
| HBE | Enthalpy | HBE | Enthalpy | |
| Mn5H10 | 9.1 | 5.1 | 8.6 | 3.9 |
| Mn5H9 | 10.9 | 6.6 | 9.4 | 4.4 |
| Mn5H8 | 13.3 | 8.7 | 10.5 | 5.2 |
| Mn5H7 | 18.2 | 13.2 | 12.8 | 6.9 |
| Mn5H6 | 22.0 | 17.1 | 14.8 | 8.7 |
| Mn5H5* | 19.5–26.5 | 14.0–21.4 | 13.3–17 | 7.1–10.4 |
Applying the methodology to determine maximum loading level described above to Mn5H6 provides a maximum load of 2.2 H2 per metal center. This is lower than the 2.9 H2 per Mn observed by experiment (10.5 wt%), most likely because of the limitations of our cluster model in describing the full KMH-1 system and the expected contribution of physisorption in the isotherms, as discussed above, i.e. with greater loading levels the additional H2 are held closer to one another than to the base structure itself in a physisorption-like interaction. At the maximum H2 loading the HBE was found to be 14.0 (9.6) kJ mol−1, which is near the limit of plausible room temperature binding.
To further probe the likely oxidation state of Mn in KMH-1 and rationalize the INS results, we explored the barriers to rotation of H2 bound to our various BSMs. Barriers to H2 rotation were determined for one and five H2 units bound to MnH2 through a series of constrained geometry optimizations in which a single H2 molecule was rotated at 10° intervals such that it remained parallel to the H–Mn–H vector, all other geometric variables being allowed to relax at each angle interval. The maximum point of the energy curves thus generated for the MnH2 systems loaded singly and with five H2 are 3.1 and 2.0 kJ mol−1 respectively. The latter number is the average of the maximum for each of the five H2 rotating separately. The barriers to rotation of a single H2 bound to the various binding sites of the Mn5H10 BSM were determined in a different way. Constrained geometry optimizations proved problematic in these cases and so an alternative approach was adopted in which the H2 unit was rotated in 10° intervals with all other geometric variables remaining fixed; all further rotational calculations used this method. The barrier of the most strongly bound H2 was found to be 3.6 kJ mol−1 (relaxing to 2.5 kJ mol−1) with an average barrier of 1.6 kJ mol−1, from singly loaded Mn5H10, which lowered to 1.2 kJ mol−1 when allowed to relax.
To better mimic the conditions of the INS experiments, barriers were calculated for a single H2 rotating on the base Mn5H10 structure with five H2 units attached. This method provides an upper bound to the rotational barrier of 3.2 kJ mol−1 and averages 1.6 kJ mol−1 over the five H2, an example of the generated rotational barriers is presented in Fig. S19 (ESI†). The geometries of the maximum energy point of the energy surfaces thus generated were allowed to relax (keeping the H2 rotational angle fixed) and the energy difference with the 0° structure reduced to an average of 1.1 kJ mol−1.
Performing similar calculations on the other BSMs with 5 bound H2 units yielded the average rotational barriers given in Table 4. In general, the average rotational barrier increases as the base structure is reduced, to 9.3 kJ mol−1 with four formal Mn(I) centers. This is consistent with the increases in binding energies, and the structural data discussed above. Fig. 8 presents the correlation of average rotational barrier and HBE; the two datasets are well correlated with R2 = 0.92.
| Number of Mn(I) present in the base structure | Average/maximum H2 rotational barrier |
|---|---|
| 0 | 1.6/3.2 |
| 1 | 2.9/7.0 |
| 2 | 3.8/11.3 |
| 3 | 5.0/7.9 |
| 4 | 9.3 (16.0)/22.7 (42.8) |
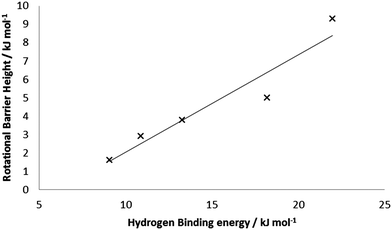 | ||
| Fig. 8 Correlation between average HBE and average rotational barrier for 5 H2 bound to Mn5Hn (n = 6–10). | ||
On the basis of the experimental INS data, which show a rotational barrier of 6.7 kJ mol−1, we expect an average oxidation state of cf. 1.2–1.4, in good agreement with that inferred from Table 4 (and from the binding energy data).
In summary, while cautioning that small molecular clusters cannot ever be perfect mimics of the KMH-1 family of materials, the computational data pleasingly support the conclusions from experiment, and suggest that KMH-1 contains substantial amounts of Mn(I), perhaps as much as 80%, and can absorb hydrogen in the same range demonstrated in our labs by experiment, with binding enthalpies favorable to room temperature reversibility.
Conclusion
In this work we have presented a porous manganese hydride material that can be synthesized easily in a few steps to give a hydrogen storage material that shows promise, even after reasonable estimates for losses due to implementation, in meeting or surpassing the US DOE system goals for gravimetric and volumetric capacity and possibly even competing with batteries in many energy storage applications. The material stores hydrogen reversibly under ambient conditions and as it is thermodynamically neutral will not require extensive engineering to utilize in on-board storage, in a wide variety of portable devices and even for large quantity transport (tube trailer or ship), while at the same time allowing a crucial decrease in the complexity and cost of the supporting infrastructure.Experimental section
General
All reagents were purchased from Sigma-Aldrich and used without further purification. Anhydrous diethyl ether and petroleum ether were purchased from Sigma Aldrich. Standard Schlenk techniques were used and all manipulations were performed in an argon glovebox or on a nitrogen Schlenk line. Solvents were monitored before use for absence of oxygen and moisture using titanocene and diethyl zinc. Manganese(II) chloride was dried by refluxing over thionyl chloride for 96 h followed by heating at 10−3 Torr at 200 °C for 4 h. Grade 6 hydrogen (99.9999% purity) purchased from Air Liquide was used for synthesis and hydrogenations. Reactions with hydrogen gas were carried out using either a stainless steel PARR hydrogenation vessel or the Hy-Energy PCT-Pro Sieverts apparatus purchased from Setaram. Bis(neopentyl) manganese was prepared according to the literature procedure12 using sublimed bis(neopentyl) magnesium instead of a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of the dialkylmagnesium and Grignard reagents. Bis(neopentyl) manganese is extremely air sensitive and solutions spontaneously turn green and then back to orange from oxidation on exposure to even trace amounts of oxygen in the glove box. Use of precursors solutions in which the green color has been detected leads to significantly lower hydrogen storage performance in the final KMH-1 product (Fig. S15b, ESI†). For this reason solutions must always be handled in a sealed system. Care must also be taken to perform multiple recrystallizations to ensure residual magnesium salts do not co-crystallize with the final organomanganese product.
50 mixture of the dialkylmagnesium and Grignard reagents. Bis(neopentyl) manganese is extremely air sensitive and solutions spontaneously turn green and then back to orange from oxidation on exposure to even trace amounts of oxygen in the glove box. Use of precursors solutions in which the green color has been detected leads to significantly lower hydrogen storage performance in the final KMH-1 product (Fig. S15b, ESI†). For this reason solutions must always be handled in a sealed system. Care must also be taken to perform multiple recrystallizations to ensure residual magnesium salts do not co-crystallize with the final organomanganese product.
Synthesis
In a typical preparation bis(neopentyl)manganese (2.37 g, 12 mmol) was stirred for 5 min in petroleum ether (150 mL) to give a red-brown solution. The solution was transferred to a stainless steel PARR hydrogenation vessel, which was then charged with 100 bar of H2. The reaction was stirred for 24 h at room temperature and then for a further 48 h at 100 bar H2 and 373 K. The reaction mixture was then filtered in the glove box and the precipitate dried at 373 K in vacuo for 4 h to afford a black air-moisture sensitive solid (KMH-1 as synthesized). The material was further hydrogenated in the solid state using the PCT-Pro for 4 h at 85 bar H2 and 423 K. Following this, the sample was evacuated at 373 K for 2 h and then allowed to cool to room temperature to give a black solid (KMH-1 after 1st hydrogenation). This sample was further hydrogenated in the solid state in the PARR vessel for 48 h at 85 bar H2 and 298 K followed by 2 h vacuum treatment at 373 K to give KMH-1 after 2nd hydrogenation. Since the IR showed that there was still hydrocarbon present in KMH-1 after 2nd hydrogenation, a 43 mg sample of KMH-1 after 1st hydrogenation was placed in the PCT-Pro and subjected to cycling of repeated adsorption and desorption of hydrogen up to 120 bar for 54 cycles to give KMH-1 after cycling. At this stage the sample weighed 22 mg and the IR showed only trace amounts of hydrocarbon remaining. Full characterization methods and details of background data are provided and discussed as ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the EPSRC EP/I004688/1, the Welsh Government A4B Program (HE 14 15 1002), University of South Wales, FCA US LLC, Hydro Quebec and the University of Manchester for funding. This work is based on experiments performed at the Swiss spallation neutron source SINQ, Paul Scherrer Institute, Villigen, Switzerland. Tarek Abdel-Baset is thanked for helpful conversations as well as Greg Kubas and Richard Andersen. We would also like to thank the Computational Shared Facility (CSF) at the University of Manchester for computational resources and associated support services. Finally we would like to thank Lisa Rodrigue for her technical assistance.Notes and references
- L. Schlapbach and A. Züttel, Hydrogen-storage materials for mobile applications, Nature, 2001, 414, 353 CrossRef CAS PubMed.
- P. Jena, Materials for hydrogen storage: past, present, and future, J. Phys. Chem. Lett., 2011, 2, 206 CrossRef CAS.
- D. Durbin and C. Malardier-Jugroot, Review of hydrogen storage techniques for on-board vehicle applications, Int. J. Hydrogen Energy, 2013, 38, 14595 CrossRef CAS.
- N. A. A. Rusman and M. Dahari, A review on the current progress of metal hydrides materials for solid state hydrogen storage applications, Int. J. Hydrogen Energy, 2016, 41, 12108 CrossRef CAS.
- J. Sculley, D. Yuan and H.-C. Zhou, The current status of hydrogen storage in metal-organic frameworks – updated, Energy Environ. Sci., 2011, 4, 2721 RSC.
- J. Yang, A. Sudik, C. Wolverton and D. J. Siegel, High capacity hydrogen storage materials: attributes for automotive applications and techniques for materials discovery, Chem. Soc. Rev., 2010, 39, 656 RSC.
- G. J. Kubas, Fundamentals of H2 binding and reactivity on transition metals underlying hydrogenase function and H2 production and storage, Chem. Rev., 2007, 107, 4152 CrossRef CAS PubMed.
- R. H. Crabtree, Dihydrogen complexation, Chem. Rev., 2016, 116, 8750 CrossRef CAS PubMed.
- Y. Zhou, Y.-H. Kim, A. C. Dillon, M. J. Heben and S. B. Zhang, Hydrogen storage in novel organometallic buckyballs, Phys. Rev. Lett., 2005, 94, 155504 CrossRef PubMed.
- B. Nykvist and M. Nilson, Rapidly falling costs of battery packs for electric vehicles, Nat. Clim. Change, 2015, 5, 329 CrossRef.
- US Department of Energy, Technical system targets: on board hydrogen storage for light-duty fuel cell vehicles, updated May 2017, https://energy.gov/eere/fuelcells/downloads/doe-targets-onboard-hydrogen-storage-systems-light-duty-vehicles.
- R. A. Andersen, E. Carmona-Guzman, J. F. Gibson and G. Wilkinson, Neopentyl, neophyl, and trimethylsilylmethyl compounds of manganese. Manganese(II) dialkyls; manganese(II) dialkyl amine adducts; tetra-alkyl manganate(II) ions and lithium salts; manganese(IV) tetra-alkyls, J. Chem. Soc., Dalton Trans., 1976, 2204 RSC.
- H. D. Kaesz and R. B. Saillant, Hydride complexes of the transition metals, Chem. Rev., 1972, 72, 231 CrossRef CAS.
- T. K. A. Hoang, L. Morris, M. L. Trudeau, D. Reed, D. Book and D. M. Antonelli, Observation of TiH5 and TiH7 in bulk-phase TiH3 gels for Kubas-type hydrogen storage, Chem. Mater., 2013, 25, 4765 CrossRef CAS.
- L. Morris, M. L. Trudeau, D. Reed, D. Book and D. M. Antonelli, Thermodynamically neutral Kubas-type hydrogen storage using amorphous Cr(III) alkyl hydride gels, Phys. Chem. Chem. Phys., 2015, 17, 9480 RSC.
- L. Morris, M. Trudeau, D. Reed, D. Book and D. M. Antonelli, High-pressure Raman and calorimetry studies of vanadium(III) alkyl hydrides for Kubas-type hydrogen storage, Chem. Phys. Chem., 2016, 17, 778 CrossRef.
- L. Morris, L. A. C. Smith and M. L. Trudeau, Synthesis and electrochemical evaluation of multivalent vanadium hydride gels for lithium and hydrogen storage, J. Phys. Chem. C, 2016, 120, 11407 CrossRef CAS.
- X. Wang and L. Andrews, Infrared spectra and DFT calculations for the gold hydrides AuH, (H2)AuH, and the AuH3 transition state stabilized in (H2)AuH3, J. Phys. Chem. A, 2003, 107, 4081 CrossRef CAS.
- L. Qi, Colloidal chemical approaches to inorganic micro- and nanostructures with controlled morphologies and patterns, Coord. Chem. Rev., 2010, 254, 1054 CrossRef CAS.
- J. C. Carver, G. K. Schweitzer and T. A. Carlson, Use of X-ray photoelectron spectroscopy to study bonding in Cr, Mn, Fe, and Co compounds, J. Chem. Phys., 1972, 57, 973 CrossRef CAS.
- Y. Umezawa and C. N. Reilley, Correlation of Mn charge state with the electrical resistivity of Mn doped indium tin oxide films, Anal. Chem., 1978, 50, 1290 CrossRef CAS.
- H. G. Alt, Photochemistry of alkyltransition-metal complexes, Angew. Chem., Int. Ed. Engl., 1984, 23, 766 CrossRef.
- R. R. Schrock and G. W. Parshal, s-alkyl and -aryl complexes of the group 4-7 transition metals, Chem. Rev., 1976, 76, 243 CrossRef CAS.
- T. Runcevski, M. T. Kapelewski, R. M. Torres-Gavosto, J. D. Tarver, C. M. Brown and J. R. Long, Adsorption of two gas molecules at a single metal site in a metal-organic framework, Chem. Commun., 2016, 52, 8251 RSC.
- P. Bernard and R. Chahine, Determination of the adsorption isotherms of hydrogen on activated carbons above the critical temperature of the adsorbate over wide temperature and pressure ranges, Langmuir, 2001, 17, 1950 CrossRef.
- C. V. J. Skipper, D. M. Antonelli and N. Kaltsoyannis, Are metal-metal interactions involved in the rising enthalpies observed in the Kubas binding of H2 to hydrazine linked hydrogen storage materials?, J. Phys. Chem. C, 2012, 116, 19134 CrossRef CAS.
- X. Zhao, B. Xiao, A. J. Fletcher, K. M. Thomas, D. Bradshaw and M. J. Rosseinsky, Hysteretic adsorption and desorption of hydrogen by nanoporous metal-organic frameworks, Science, 2004, 306, 1012 CrossRef CAS PubMed.
- It is anticipated that the favorable material properties of KMH-1 should yield system level gravimetric and volumetric levels that exceed any materials based system built to date and also exceed the incumbent 700 bar systems. Material properties of KMH-1 such as the low enthalpy, fast kinetics, and dense packaging will significantly reduce thermal management requirements/overhead typically seen in current sorbent/metal hydride systems. As a result, the system overhead penalty of 30–50% seen in current system could realistically decrease to 20–30%. As such, this system performance also compares favorably over 700 bar compressed H2 solutions. For example, a 700 bar tank containing 5.6 kg of hydrogen is 134 liters and contains 5.5 wt% and 40 kg m−3 H2 at a calculated cost of 2474.80 $ per tank and 22.94 $ per kW h for the system (see Table 6 in https://www.osti.gov/servlets/purl/1343975). 47 kg of KMH-1 stores 5 kg of hydrogen (10.5 wt%) at 120 bar at a volumetric density of 197 kg m−3, roughly 4 times greater than 700 bar assuming a reasonable 25% loss in performance on packing. The density of KMH-1 is 1.88 g cc−1, so 47 kg of KMH-1 occupies 25 liters of volume, and 32 liters assuming a 25% increase in volume on packing. A 32 liter Type 1 M150 Al tank supporting pressures up to 150 bar weighs 25 kg including the regulator and costs ca. $100.00, so the total weight of a KMH-1 tank holding 5 kg of hydrogen would be approximately 77 kg, providing 6.5 wt% storage at 120 bar. In terms of cost of KMH-1, since the bulk market cost of MnCl2 is 1.00 USD per kg and the other precursors such as magnesium and organic halides and solvents are similarly priced and available in bulk quantities, and the precursor cost and synthesis method by precipitation and thermal post treatment is comparable to common zeolites, a bulk price in the range of ZSM-5 (i.e. 2 USD per kg) is not unrealistic. For this reason a cost of 10 USD per kg represents a modest estimate for KMH-1. 47 kg KMH-1 would therefore cost $470.00 in addition to the $100.00 for the tank, giving a total of $570.00 to store 5 kgH2, or 3.00–4.00 $ per kW h for the system based on 33.33 kW h kg−1 for hydrogen. For a useful recent comparison of current 700 bar fuel cell vehicles (FCV) to battery electric vehicles (BEV) please see http://energypost.eu/the-lowdown-on-hydrogen-part-1-transportation/.
- M. A. Pellow, C. J. M. Emmott, C. J. Barrnhart and S. M. Benson, Hydrogen or batteries for grid storage? A net energy analysis, Energy Environ. Sci., 2015, 8, 1938 RSC.
- J. Eckert and G. J. Kubas, Barrier to rotation of the dihydrogen ligand in metal complexes, J. Phys. Chem., 1993, 97, 2378 CrossRef CAS.
- W. A. King, B. L. Scott, J. Eckert and G. J. Kubas, Reversible displacement of polyagostic interactions in 16e [Mn(CO)(R2PC2H4PR2)2]+ by H2, N2, and SO2. Binding and activation of h2-H2 trans to CO is nearly invariant to changes in charge and cis ligands, Inorg. Chem., 1999, 38, 1069 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Errata to Generalized Gradient Approximation Made Simple [Phys. Rev. Lett., 77, 3865, 1996], Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Kocman, P. Jurečka, M. Dubecký, M. Otyepka, Y. Cho and K. S. Kim, Choosing a density functional for modeling adsorptive hydrogen storage: reference quantum mechanical calculations and a comparison of dispersion-corrected density functionals, Phys. Chem. Chem. Phys., 2015, 17, 6423 RSC.
- J. Gebhardt, F. Viñes, P. Bleiziffer, W. Hieringer and A. Görling, Hydrogen storage on metal oxide model clusters using density-functional methods and reliable van der Waals corrections, Phys. Chem. Chem. Phys., 2014, 16, 5382–5392 RSC.
- A. Mavrandonakis, K. D. Vogiatzis, A. D. Boese, K. Fink, T. Heine and W. Klopper, Ab Initio Study of the Adsorption of Small Molecules on Metal-Organic Frameworks with Oxo-centered Trimetallic Building Units: The Role of the Undercoordinated Metal Ion, Inorg. Chem., 2015, 54, 8251–8263 CrossRef CAS PubMed.
- M. Manadé, F. Viñes, A. Gil and F. Illas, On the H2 Interaction on Transition Metal Adatoms Supported on Graphene: A Systematic Density Functional Study, Phys. Chem. Chem. Phys., 2018, 20, 3819–3830 RSC.
- M. J. Frisch, et al., Gaussian 09 Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J. Cha, C. H. Choi and N. Park, Ab initio study of Kubas-type dihydrogen fixation onto d-orbital states of Ca adatoms, Chem. Phys. Lett., 2011, 513, 256 CrossRef CAS.
- M. Samolia and T. J. Dhilip Kumar, Fundamental studies of H2 interaction with MAl3 clusters [M = Li, Sc, Ti, Zr], J. Alloys Compd., 2014, 588, 144 CrossRef CAS.
- G. J. Kubas, Metal dihydrogen and s-bond complexes, Kluwer/Plenum, New York, 2001 Search PubMed.
- B. Chaudret, G. Chung, O. Eisenstein, S. A. Jackson, F. J. Lahoz and J. A. Lopez, Preparation, x-ray molecular structure, and electronic structure of the first 16-electron ruthenium dihydrogen complexes RuH(H2)X(PCy3)2, J. Am. Chem. Soc., 1991, 113, 2314 CrossRef CAS.
- U. Eberle, M. Felderhoff and F. M. Schüth, Chemical and physical solutions for hydrogen storage, Angew. Chem., Int. Ed., 2009, 48, 6608 CrossRef CAS PubMed.
- D. G. Albrecht and B. Fultz, Evaluation of the thermodynamic properties of H2 binding in solid state dihydrogen complexes [Mn(h2-H2)(CO)dppe2][BArF24] (M = Mn, Tc, Re): an experimental and first principle study, J. Phys. Chem. C, 2012, 116, 22245 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Materials characterization details including IR, N2 adsorption–desorption, XRD, TGA/DTA, XPS, (S)TEM, EDS, INS, hydrogen adsorption–desorption, calorimetry, and background computational data. See DOI: 10.1039/c8ee02499e |
| This journal is © The Royal Society of Chemistry 2019 |