Ion transport mechanisms in bipolar membranes for (photo)electrochemical water splitting†
David A.
Vermaas
 *ab,
Sandra
Wiegman
a,
Tetsuro
Nagaki
a and
Wilson A.
Smith
*ab,
Sandra
Wiegman
a,
Tetsuro
Nagaki
a and
Wilson A.
Smith
 *a
*a
aDelft University of Technology, Department of Chemical Engineering, 2629 HZ Delft, The Netherlands. E-mail: d.a.vermaas@tudelft.nl; w.smith@tudelft.nl
bAquaBattery B.V., Lijnbaan 3C, 2352CK, Leiderdorp, The Netherlands
First published on 14th June 2018
Abstract
Bipolar membranes (BPMs) have attracted growing interest in electrochemical and photoelectrochemical systems, as they allow the unique ability to pair two different electrolytes which can be optimized for their respective oxidation and reduction reactions. Understanding the membrane voltage at a non-extreme pH gradient (ΔpH < 14) is an important step towards practical applications for electrochemical conversions, as many (photo-)electrodes and catalysts can only operate efficiently in a limited pH range. To obtain a better understanding of the individual effects that determine the BPM voltage, a complete series of experiments measuring the actual BPM voltage as a function of the pH, salt type/concentration, flow rate and current density is needed. In this paper, we present experimental results of voltage–current relations for a BPM using 16 different pH differences, 4 concentrations, 7 flow rates and permeation of 6 different ionic species. The results show that both ion cross-over and local diffusion boundary layers play important roles in the BPM voltage. We also show that the supporting electrolyte composition plays an important role, even more important than the pH itself, which is an important parameter to realize practical application of BPMs in electrochemical cells.
Introduction
In the quest for converting renewable electricity – from solar or other renewable sources – into chemical bonds, many electrocatalytic materials have been explored. Optimal electrochemical conditions for the anode are often incompatible with optimal electrochemical conditions for cathode materials. For example, in the water splitting reaction, many electrocatalysts used to drive the hydrogen evolution reaction (HER) show the lowest overpotentials in acidic media, while nearly all earth-abundant catalysts used to drive the oxygen evolution reaction (OER) at low overpotential are only stable under alkaline conditions.1 When considering the total voltage needed to drive the overall reaction, it is necessary to minimize the overpotentials and find stable working environments for both HER and OER reactions simultaneously. Recently, a bipolar membrane (BPM) was introduced to match an acidic catholyte with an alkaline anolyte.2,3A bipolar membrane consists of a negatively charged cation exchange layer (CEL) and a positively charged anion exchange layer (AEL), selective for the transport of only cations or anions, respectively. Hence, no salt ions should be able to pass through both layers, which results in the dissociation of water (H2O → H+ + OH−) at the interface of both membrane layers upon applying an electric field. Due to the water dissociation, protons are supplied to the catholyte, where they are (in an ideal case) consumed at the same rate in, for example, hydrogen evolution, while the hydroxides are supplied to the anolyte for the oxidation reaction. Hence, a different pH is conserved at either side of the membrane.
BPMs have been applied commercially for the production of acid and base (in bipolar membrane electrodialysis), and only explored for water electrolysis and CO2 electrolysis recently. Since 2014, commercial BPMs have been examined for water electrolysis,2–6 photo-electrolysis7–9 and CO2 reduction.10,11 High electricity-to-fuel or solar-to-fuel efficiencies have been obtained, even with Earth-abundant catalyst materials, due to the favourable pH environment for both anode and cathode.12 The pH difference over the membrane helps to reduce the overpotential for the hydrogen evolution reaction (HER) and the oxygen evolution reaction (OER), which can make the total cell voltage even lower than when applying no membrane or a monopolar ion exchange membrane.4,6
At an extreme pH difference (i.e., a catholyte at approximately pH 0 versus an anolyte at approximately pH 14), the process is well understood. In this case, a voltage of 0.83 V should be applied for dissociation of water in the BPM, and experiments are in fair agreement with that theory.13,14 Effectively, the bipolar membrane converts an electrical potential difference (in V) into a chemical potential difference (in terms of pH difference).
When using a pH difference other than 0–14, the process is less well understood. Several literature references suggest that an absolute electrical potential of 0.83 V is required for water dissociation in a BPM,3,14–17 referring to the thermodynamic potential difference to separate H2O into 1 M H+ and 1 M OH−. However, at non-extreme pH, the concentrations of H+ and OH− in the electrolyte are <1 M, which causes a sudden jump in concentration at the membrane–electrolyte interface. As a consequence, a Donnan potential arises at the membrane–electrolyte interfaces. As a result (see the theory section), the total membrane voltage should be equal to φBPM = 0.0591ΔpH, where ΔpH is the pH difference in the electrolytes.
Despite this theoretical analysis, experimental results have shown significant deviations from this theory.5,7 Membrane voltages have been measured to be lower7,14 and higher2,5 than the theoretical voltage, and seem to be dependent on the current density and the activity of the supporting electrolyte as well. It was observed that application of a BPM at non-extreme pH is subject to non-ideal behaviour of the membrane.6,7,17,18 Permeation of co-ions (i.e., ions different than H+ or OH−), such as potassium, has been observed, dependent on the current density.6 Moreover, mass transport from the membrane to the electrolyte creates a diffusion boundary layer adjacent to the BPM, which has been hypothesized to affect the membrane voltage.7
Understanding the membrane voltage at non-extreme pH is an important step to extend the practical applications for electrochemical conversions, as many (photo-)electrodes and catalysts operate in a limited non-extreme pH range.19–21 To obtain a better understanding of the individual effects that determine the BPM voltage, a complete series of experiments measuring the actual BPM voltage as a function of the pH, salt type, flow rate and current density is needed. We present experimental results of voltage–current relations for a BPM using 16 different pH differences, 4 concentrations, 7 flow rates and permeation of 6 different ionic species. The results show that both ion cross-over and local diffusion boundary layers play a role in the measured BPM voltage. We will show that the supporting electrolyte composition plays an important role, even more important than the pH itself, which is an important parameter to realize practical application of BPMs in electrolysis.
Theory
BPM Donnan potentials
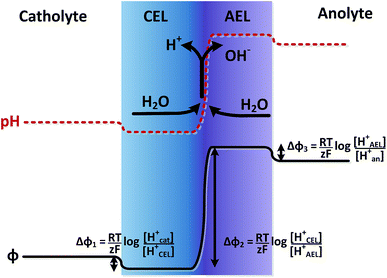
The potential difference over the bipolar membrane (BPM), which is comprised of a cation exchange layer (CEL) and anion exchange layer (AEL), is determined by three interfaces: the catholyte–CEL interface, the CEL–AEL interface and the AEL–anolyte interface. Donnan potentials arise at each interface, due to the sudden change in concentrations (and the diffusion related to that concentration change). It is assumed that the ion concentrations in the membrane layers are in the order of 1 M H+ in the CEL and 1 M OH− in the AEL, to balance the fixed charges in the membrane (which have a typical charge density of 1 meq g−1 H2O22,23). This also assumes implicitly that no other ion species are present in the BPM, which is acceptable when a significant electrical current is applied, as water dissociation produces H+ and OH− at the CEL–AEL interface.When an extreme pH difference (i.e., pH 0 in the catholyte and pH 14 in the anolyte) is used, the Donnan potentials at each of the membrane–electrolyte interfaces are close to zero because the H+ or OH− concentration in the electrolyte is then close to that in the membrane. When using non-extreme pH, the sudden change in proton concentration at both membrane–electrolyte interfaces causes a Donnan potential,24 and this Donnan potential at the membrane–electrolyte interface(s) is non-zero. The potentials are described schematically in Fig. 1. When adding the potentials at the catholyte–CEL interface, CEL–AEM interface and AEL–anolyte interface, the thermodynamically equilibrated voltage over the BPM, φBPM, must be equal to
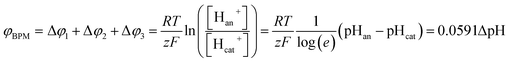 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485C mol−1), z is the charge valence (−) and the subscripts cat and an indicate the catholyte and anolyte, respectively.
485C mol−1), z is the charge valence (−) and the subscripts cat and an indicate the catholyte and anolyte, respectively.
Another way to understand that the thermodynamic potential difference over the BPM should depend on the pH is to consider very extreme acid and base concentrations, exceeding 1 M. As an example, if we consider a hypothetical case with a catholyte containing 10 M acid and an anolyte with 10 M base solution, the equilibrium potential at the hydrogen evolving cathode (in pH = −1) would be 0.059 V vs. SHE and at the oxygen evolving anode (in pH = 15) 0.343 V vs. SHE.25 When using an absolute membrane voltage of 0.83 V, the total cell voltage would be lower than 1.23 V, and would therefore be thermodynamically impossible. Hence, the thermodynamic potential difference over the BPM should be dependent (solely) on the pH difference over the membrane.
Limiting current
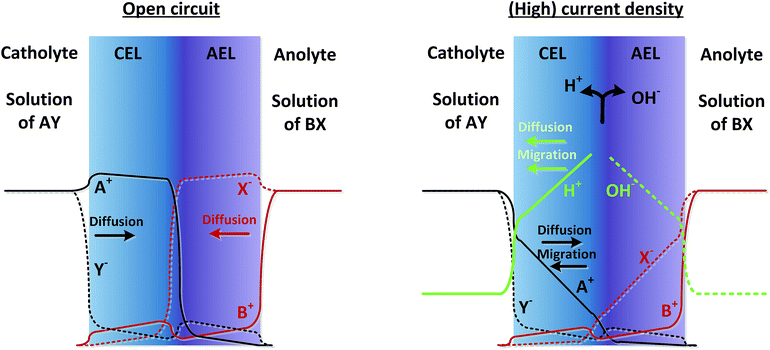
As real membranes are not perfectly selective, a small fraction of ions other than H+ or OH− do pass through the BPM. This is called co-ion permeation or ion cross-over. Ion cross-over is not necessarily dependent on the pH, as transport of most ionic species (e.g., K+, Cl−, etc.) does not influence the pH. In the early research on bipolar membranes, it was hypothesized that at low current density all charge is carried by co-ions, i.e. that no water dissociation occurs below a certain limiting current density.13–15,17 This non-ideal ion cross-over can cause deviations from the membrane voltage as described in eqn (1). At monopolar membranes, water dissociation occurs indeed only above a certain limiting current density, when the salt concentration at one side of the membrane is completely depleted due to concentration polarization.26,27 At the underlimiting current density, no water dissociation occurs at monopolar membranes. However, experiments with BPMs have shown that water dissociation in the current commercial BPMs carries charge even at very low current densities of 1 mA cm−2 or lower.6,7 At a current density of 0.5 mA cm−2, it is observed that 70–90% of the current is carried by water dissociation, which is due to co-ion cross-over. For higher current densities, the relative contribution of ion cross-over is smaller.6It can be hypothesized that at low current densities the concentration of co-ions in the membrane is larger (due to diffusion from the electrolyte), while at high current densities the migrational flux of H+ and OH− from the interface layer dominates the diffusion of co-ions into the membrane. This is illustrated in Fig. 2, where the relative concentrations of solution AY and BX are shown in black and red lines (solid lines for cations and dashed lines for anions). At open circuit, the ions from the electrolyte exchange into the adjacent layer of the BPM via diffusion. The jumps in concentration at the interfaces are due to the positive and negative fixed charge of the membrane material. Because the concentration of A+ and X− is significantly high in the CEL and AEL, respectively, some ions cross over. When a (high) current density is applied, the ions A+ and X− migrate out of the CEL to the catholyte, preventing cross-over. The only ion cross-over is therefore expected from the fluxes of B+ and Y−. These fluxes remain small when applying a current, because their concentrations in the membrane are small (and migration is proportional to the ion concentration). Therefore, the co-ion transport (i.e., Y− in the CEL and B+ in the AEL) can be expected as a rather constant flux via diffusion. As a consequence, the flux of H+ can dominate the charge transport in the CEL, and a similar argumentation causes OH− to dominate the charge transport in the AEL.
The concentration profiles in the membrane, for H+, OH− and co-ions, are obviously dependent on the pH at either side, the ion type (in particular the valence and diffusion coefficient) and their activity, approximated using the concentration. Hence, a systematic series of experiments with different pH, different salts and different concentrations are required to gain insight into the membrane potentials over a BPM and the ion transport within a BPM.
Results
Effect of pH
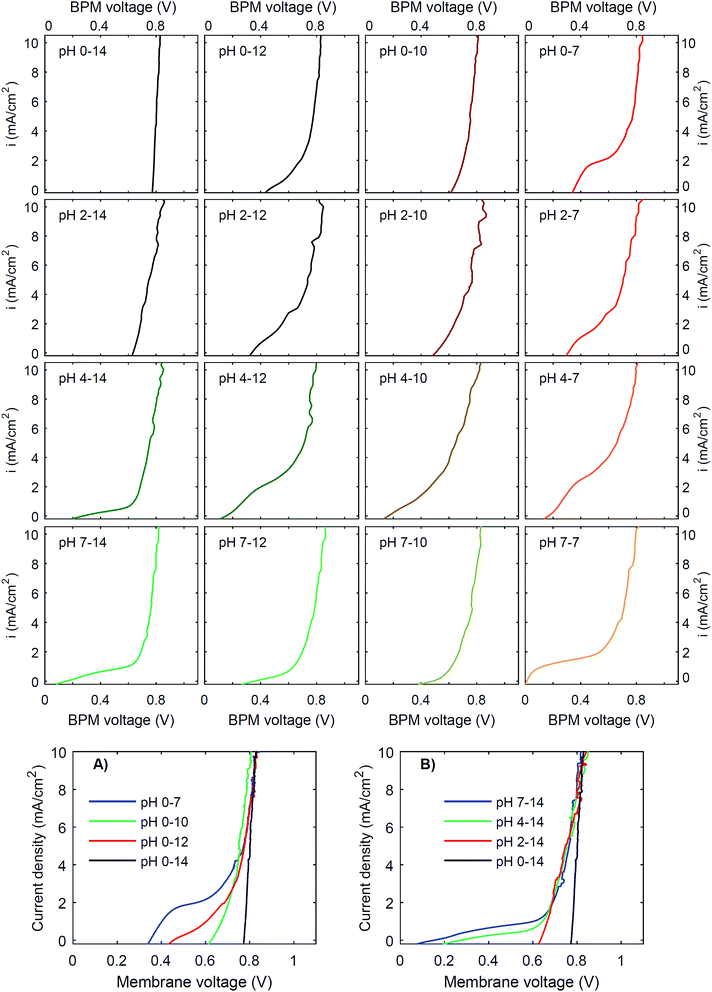
To investigate the effect of pH on the membrane potential, all combinations of pH 0, 2, 4 and 7 for the catholyte and pH 7, 10, 12 and 14 for the anolyte are tested with galvanodynamic scans and chronopotentiometry over the BPM. The complete set of I–V curves from galvanodynamic scans is shown in Fig. 3. To help understand the effect of varying pH, a selection of I–V curves using a fixed catholyte pH = 0 or a fixed anolyte pH = 14 is shown in Fig. 3A and B. Note that the pHs are approximated; exact pH values (due to non-unity activity coefficients) can be found in ESI Table S1.†Fig. 3 shows that when non-extreme pH differences are used across the BPM, i.e. ΔpH < 14, the I–V curve is non-linear, whereas a linear curve would be expected when just an ohmic resistance and a potential bias determine the curve. Only for the extreme pH difference (i.e., 0 vs. 14) is a steep linear line at approximately 0.83 V observed. The slope of this curve indicates that the resistance of the BPM plus the surrounding electrolyte (1 mm at either side) is approximately 6 Ω cm2. Based on the conductivity of the electrolytes (300 mS cm−1 and 190 mS cm−1 for 1 M H2SO4 and KOH, respectively28), the ohmic resistance of the BPM is approximately 5 Ω cm2. The cases of pH 2 vs. 14 and pH 0 vs. 10 are also reasonably linear but have a significantly lower membrane voltage at low current density. All other pH combinations show non-linear I–V curves.
Curve regimes
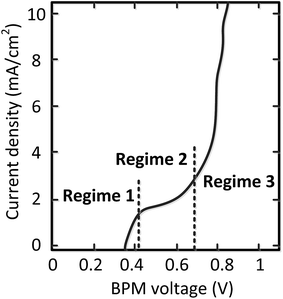
Detailed analysis of all the curves reveals 3 different regimes in the I–V curves over a BPM. The I–V curves do not always necessarily contain all 3 regimes; the case for pH 0 vs. 7 is most exemplary to clearly distinguish all regimes, indicated in Fig. 4.The 3 regimes correspond to the following phenomena:
(1) At conditions with low current density, the membrane potential is close to or lower than the thermodynamic potential for water dissociation based on the pH difference. This is illustrated by the membrane voltage obtained at 1 mA cm−2, which is compared to the theoretical value calculated using the Nernst equation, shown in Fig. 5A. The cases in which the membrane voltage is close to the thermodynamic potential difference (along the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line in Fig. 5A) follow the theory described before (i.e., φBPM = 0.0591ΔpH). This shows that the actual BPM voltage is indeed fairly close to the theoretical BPM, which means that the bulk pH determines the BPM voltage. Previous research showed that at these low current densities (≤1 mA cm−2), the majority of the charge is already carried by water dissociation (and 10–30% of the charge is carried by ion cross-over).6,7 In detail, the measured membrane voltage is for some cases lower than the theoretical value (data points below the 1
1 line in Fig. 5A) follow the theory described before (i.e., φBPM = 0.0591ΔpH). This shows that the actual BPM voltage is indeed fairly close to the theoretical BPM, which means that the bulk pH determines the BPM voltage. Previous research showed that at these low current densities (≤1 mA cm−2), the majority of the charge is already carried by water dissociation (and 10–30% of the charge is carried by ion cross-over).6,7 In detail, the measured membrane voltage is for some cases lower than the theoretical value (data points below the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 line). This trend can be due to the fact that part of the current is carried by co-ion permeation. In some cases, the measured membrane voltage is slightly higher than the theoretical value, due to ohmic losses and an early transition to regime 2.
1 line). This trend can be due to the fact that part of the current is carried by co-ion permeation. In some cases, the measured membrane voltage is slightly higher than the theoretical value, due to ohmic losses and an early transition to regime 2.
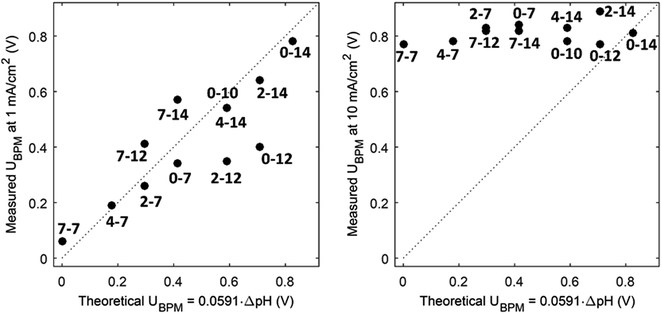 | ||
| Fig. 5 Measured potential versus thermodynamic membrane potential (φBPM = 0.0591ΔpH) for 12 cases, for a current density of 1 mA cm−2 (A) and 10 mA cm−2 (B). Measured voltages are obtained from chronopotentiometric series of 300 s, where the 10% percentile voltage is used. The use of the 10% percentile voltage level is to avoid overestimated voltages due to gas bubbles. Hence, the voltages can slightly deviate from the voltages from the cyclic voltammetry in Fig. 3. The numbers indicate the pH in the catholyte–anolyte. Default concentration is 1 M (pH 10 denotes 0.5 M), and Re = 12.5. | ||
(2) When increasing the current density, a plateau is observed in the I–V curve. We define the current density at which this plateau occurs (e.g., the plateau at 2 mA cm−2 for the case of pH 0 vs. 7) as the plateau current density. We explicitly do not use the term ‘limiting current density’, which is reserved for the case where no water dissociation occurs before this value in monopolar or bipolar membrane polarization.17,26,27 In contrast, in the BPM under study, water dissociation has also been observed as the main charge carrier in regime 1.
Fig. 3 shows that the plateau current density is not exclusively dependent on the pH but rather on the co-ion species. For example, the cases with pH 0 vs. 7 and pH 4 vs. 12 show a high plateau current density, while the case with pH 2 vs. 10 does not. The pH difference is in all cases similar, but the ionic species are different: the anolyte contains phosphate in case of pH 7 and 12, and borate in case of pH 10. To explain why the ΔpH cannot solely determine the I–V curve, non-ideal effects have to be taken into account. The next sections will discuss the individual effects of advection, electrolyte concentration and ion radius.
Moreover, the cases are not symmetrical, i.e. the case of pH 0 vs. 7 is significantly different from the case of pH 7 vs. 14, showing that ΔpH is alone not enough to describe the observed behavior. Sun et al.6 already noticed that the concentration polarization is more severe at the anolyte than at the catholyte, due to the high mobility of protons in the catholyte. In detail, Fig. 3 and 5 also show that phosphate-based ions at the anolyte increase the plateau current density. This can be due to the negative charge of the (di)hydrogen phosphate ions, which allows them to penetrate the AEL and its double layer, while they are excluded from the CEL and its double layer. Therefore, they may effectively act as a pH buffer inside the AEL and/or its double layer, keeping the local pH next to the AEL close to 7, but less effectively at the CEL, as we will discuss later. Also the differences in ion mobility and pKa will play a role.
(3) The third regime is the section of the I–V curve with an almost vertical line close to 0.8 V, which is observed for all curves at high current density. This resembles water dissociation at extreme pH at either membrane–solution interface. All 16 combinations in Fig. 3 show this regime at current densities >4 mA cm−2, leading to a membrane voltage of approximately 0.8 V for all cases (Fig. 5B). The small local fluctuations in the observed I–V curves in this regime are due to gas bubble formation.
When looking to these three regions, a major question remains as to how the plateau current density can be influenced, in order to optimally benefit from the low membrane voltage in regime 1. If the plateau could be lifted to a higher current density, while maintaining the faradaic efficiency for water dissociation, the practical utility of using a bipolar membrane at non-extreme pH would be largely increased.
Effect of advection
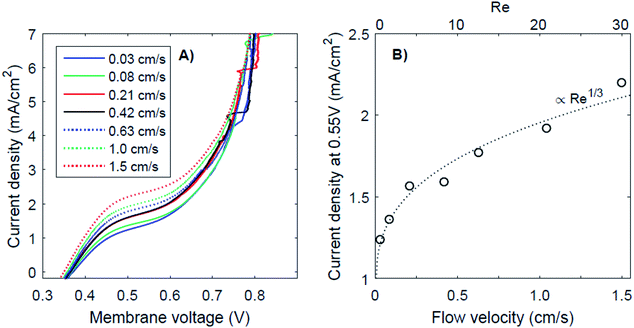
It has been proposed that (external) concentration polarization could cause the transition from regime 1 to regime 3. This effect is further examined for the case of pH 0 vs. 7, as this case shows the most pronounced plateau region. The I–V curves for this pH gradient with 7 different flow velocities are plotted in Fig. 6, together with the plateau current density (at a membrane voltage of 0.55 V) as a function of the flow velocity and Reynolds number (Re). Higher flow rates do raise the plateau current density (Fig. 6A), which supports the hypothesis that the transition from near-thermodynamic membrane voltages to a membrane voltage of approximately 0.8 V is related to a diffusion boundary layer for pH 0 vs. 7. At low flow velocity, the concentration at the membrane–solution interface deviates significantly from the concentration in the bulk due to concentration polarization. At higher flow rates, the diffusion boundary layer is thinner,29,30 which brings the concentration at the interface closer to that of the bulk. The flow cell used in this research provides the opportunity to control the advection in the catholyte and anolyte and demonstrates a dependency of the BPM I–V curve on the flow rate for the first time.The thickness of the diffusion boundary layer should be proportional to v−1/3 (v being the flow velocity)31 for Re < 1000, and, assuming that the current density indeed experiences a diffusion limitation, the current density should be proportional to Re1/3 for Re < 1000.29,32,33 This follows from the Sherwood relations for developed flow and undeveloped concentration boundary layers (see the ESI†). For higher Reynolds numbers (Re > 2000), theory predicts a transition to a regime in which the current density should be proportional to Re7/8. Our results are in good agreement with the expected concave trend for low Re (Fig. 6B).
It is expected that the plateau level of the current density increases further, proportional to Re1/3 first, and eventually proportional to Re7/8 for Re > 1000. Following this relation, a plateau with high current densities (i.e., >10 mA cm−2) requires very high flow rates (Re > 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), assuming that the electrode–membrane distance is kept constant. Such high flow rates are not practical as they will provide significant pumping losses for applications with large electrode areas.
000), assuming that the electrode–membrane distance is kept constant. Such high flow rates are not practical as they will provide significant pumping losses for applications with large electrode areas.
Effect of electrolyte concentration
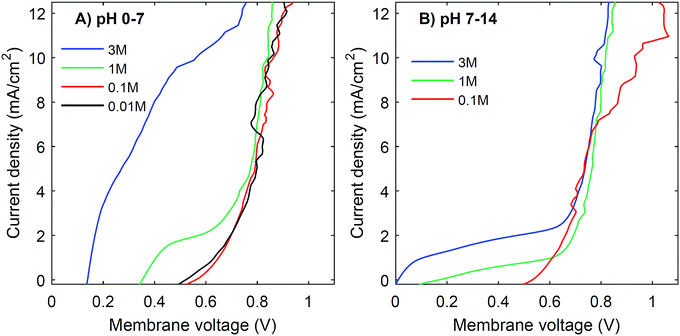
Another strategy to obtain a high current density at low membrane voltage is to increase the buffer concentration. Fig. 7 shows the I–V curves for concentrations of 0.01 M, 0.1 M, 1 M and 3 M of H2SO4 and K2HPO4/K2HPO4 and 0.1 M, 1 M and 3 M of KOH and K2HPO4/KH2PO4. The actual pH of the solutions is slightly dependent on the concentration of H2SO4 (pH between −0.5 and 2) and KOH (pH between 13 and 14.4), but these changes are relatively small compared to the difference with the electrolyte at the other side of the membrane (K2HPO4/KH2PO4 in all cases of pH 7).The curves for 0.01 M and 0.1 M show more noise in the I–V curves, and high membrane voltages for pH 7 vs. 14, due to an amplified effect of gas bubbles in combination with the low conductivity of the electrolyte. More importantly, the plateau current density is very sensitive to the concentration. In both cases, at concentrations of 0.1 M or lower, the I–V curve has a plateau current density near 0 mA cm−2, which causes the I–V curves to start at >0.5 V. In contrast, using 3 M salts gives a shift in the plateau current density to approximately 10 mA cm−2 (for pH 0 vs. 7) and 2 mA cm−2 (for pH 7 vs. 14), which is a four- to five-fold plateau current density compared to the default 1 M case.
Based on the observed strong sensitivity for the salt concentration and the slight effect of flow rate, we can judge the relation between the observed plateau current density and the diffusive boundary layer. In analogy to the limiting current density for monopolar membranes (which occurs when the salt in the diffusive boundary layer gets depleted), the expected limiting current density Ilim (in A m−2) would be obtained using the equation34–36
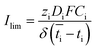 | (2) |
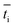 is the transport number of species i in the membrane (−), and ti is the transport number in water (−). We can consider the limit in current density for which the phosphate species can buffer the pH at the membrane–electrolyte interface, i.e. that a species of HPO42− takes up a proton and becomes H2PO4−. Using a value of zHPO42− = −2, DHPO42− = 6.9 × 10−10 m2 s−1, CHPO42− = 500 mol m−3, δ = 400 μm,34
is the transport number of species i in the membrane (−), and ti is the transport number in water (−). We can consider the limit in current density for which the phosphate species can buffer the pH at the membrane–electrolyte interface, i.e. that a species of HPO42− takes up a proton and becomes H2PO4−. Using a value of zHPO42− = −2, DHPO42− = 6.9 × 10−10 m2 s−1, CHPO42− = 500 mol m−3, δ = 400 μm,34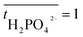 and tHPO42− = 0.12 gives Ilim = 19 mA cm−2. Note that HPO42− does not actually have to be transported through the membrane, but its conversion into H2PO4− is also resembled by
and tHPO42− = 0.12 gives Ilim = 19 mA cm−2. Note that HPO42− does not actually have to be transported through the membrane, but its conversion into H2PO4− is also resembled by 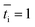 . The transport for HPO42− in the electrolyte is 0.12 because K+ has a 2.8× higher diffusion coefficient and 3× higher concentration than HPO42−. This limiting current density due to concentration polarization is an order of magnitude larger than the observed plateau current density. Also when using empirical relations between the flow rate and limiting current density for monopolar membranes,37 corrected for the diffusion coefficient in our research (K2HPO4/KH2PO4 instead of NaCl), a much higher limiting current density (30–45 mA cm−2) is expected.
. The transport for HPO42− in the electrolyte is 0.12 because K+ has a 2.8× higher diffusion coefficient and 3× higher concentration than HPO42−. This limiting current density due to concentration polarization is an order of magnitude larger than the observed plateau current density. Also when using empirical relations between the flow rate and limiting current density for monopolar membranes,37 corrected for the diffusion coefficient in our research (K2HPO4/KH2PO4 instead of NaCl), a much higher limiting current density (30–45 mA cm−2) is expected.
Although the existing theory on limiting current densities assumes the use of a monopolar membrane instead of a bipolar membrane, the basic concept of a depleting diffusive boundary layer in the electrolyte should be equal. As the plateau current density is at least an order of magnitude lower than the expected limiting current density, we cannot explain the plateau current density from a diffusive boundary layer only. As an alternative explanation for the observed plateau current density, the contribution of ion permeation to the current density is analyzed in the following section.
Effect of ion radius and valence
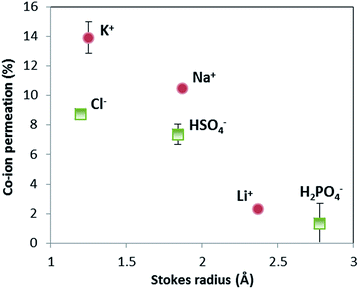
The selectivity of ion exchange membranes is largely dependent on the valence and hydrated radius of ions.38–40 Multivalent cations are weakly soluble under alkaline conditions; Ba(OH)2 is the best soluble multivalent hydroxide and has been investigated, but it precipitates with CO2 from the air and sulfates in the membrane (see ESI, Fig. S2 and S3†). Hence, we limit ourselves to the effect of hydrated radius. The ion cross-over is investigated for different cations (K+, Na+, and Li+) and different anions (HPO42−/H2PO4−, HSO4−/SO42−, and Cl−). The results of ion cross-over as a function of the hydrated radius are shown in Fig. 8.Fig. 8 shows that the cations contribute the most to the ion cross-over. The cations with the smallest hydrated ion radius (K+, then Na+, then Li+) show the highest ion cross-over, which can be expected due to the higher mobility and lower steric hindrance in the membrane. The relation between the Stokes radius for anions and its cross-over seems similar but is less reliable because of the changing valence dependent on the local pH for phosphate and sulfate.
It is important to note that phosphate shows hardly any cross-over (measured multiple times for the pH 0–7 case), and that sulfate and potassium ions have a similar cross-over in the pH 0–7 case compared to the pH 0–14 case (see ESI, Fig. S1†). When (potassium and sulfate) ion cross-over would cause the plateau current density, it would have been visible in the pH 0–14 case as well. The high plateau current density in the pH 0–7 case and the total absence of a plateau current density in the pH 0–14 case themselves indicate that the plateau current density cannot be solely explained by ion cross-over.
Effect of membrane selectivity
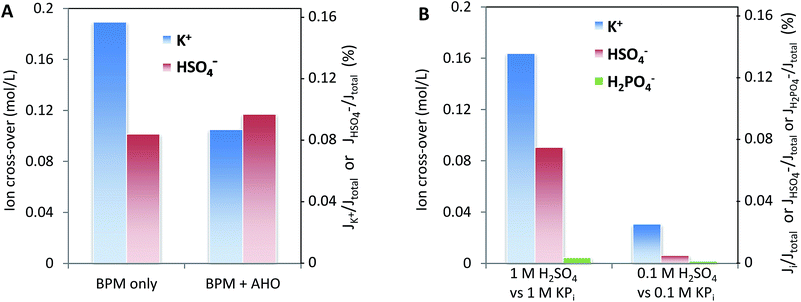
Fig. 8 may give the impression that cations, in particular K+ and Na+, permeate relatively more easily than anions. To assess whether this ion cross-over depends on the ion type, or is due to the specific membrane type (in this case a Fumatech BPM), we modified a Fumatech BPM with an extra selective anion exchange membrane on top of the AEL. We used a Selemion AHO membrane, which is known for its high selectivity and good chemical resistance against alkaline conditions. The results, illustrated in Fig. 9A, show that the ion cross-over for K+ is approximately halved when using an additional AHO membrane, while the sulfate cross-over is similar to that for the bare BPM membrane. This suggests that the higher cation permeation in Fig. 8 is caused by the specific characteristics of the chosen BPM (probably having a less selective AEL than CEL), and is not of fundamental nature.Fig. 9B shows that the salt concentration in the electrolyte strongly affects the ion cross-over. A 10× lower concentration gives approximately 4× lower ion cross-over. This is explained by the higher selectivity of the CEL and AEL: as the membrane charge density is a constant value, lower salt concentrations in the supporting electrolyte make the membrane charge density relatively larger.
Origin of distinct regimes in I–V curves
Both the appearance of a diffusive boundary layer (external concentration polarization) and the cross-over of salt ions are confirmed by the data obtained in this research. At the same time, both effects cannot fully explain the transition between the low membrane voltage at low current density (regime 1) for non-extreme pH differences, the plateau current density (regime 2) and the large membrane voltages at higher current density (regime 3).When speculating on the origin of the plateau current density, we should consider that the concentration gradients in the membrane itself may be larger than that in the adjacent electrolyte. Because the diffusion coefficients inside the membrane structure are easily an order of magnitude lower than those in the electrolyte and the membrane thickness is significant (>100 μm), a strong gradient in salt concentration can indeed appear within the membrane layers. Wilhelm et al.41 proposed a concentration profile for a BPM that faces a neutral non-buffered solution (NaCl) at either side, and used that theory for explaining the lower ion cross-over at higher current density.14 They also postulated that the ion concentrations in the membrane material show a large gradient (as in Fig. 2B), and referred to this phenomenon as internal concentration polarization, to distinguish it from (external) concentration polarization in the diffusive boundary layer.
The existence of a concentration gradient in the BPM has several effects. First, the concentrations of the salt species may reach zero at some point in the membrane layer. This reduces the relative ion cross-over, and also implies that bi-ionic potentials over the membrane layers may be established. When H+ is the dominant cation at the interface layer, and K+ the dominant cation at the electrolyte side of the CEL, a bi-ionic potential is established due to the different diffusivities of H+ and K+,42 which causes a diffusion potential. In the particular case of a membrane (layer) that faces different ratios of two co-ions at either side, this is referred to as a bi-ionic potential. Secondly, the chosen salt ions could play a pH-buffering role in the membrane layers (i.e., a weak acid that accepts a hydroxide ion inside the AEL and migrates out of the AEL to the anolyte) at low current density. This pH buffering inside the membrane layers may work in the same way as for reducing external concentration polarization: the actual pH then determines the BPM voltage. This would hold for low current density, while at high current density the concentration of buffering ion species would be too low to maintain a uniform pH within the membrane. Considering that the diffusion coefficient in the membrane material is an order of magnitude lower than that in the electrolyte, the limiting current density for this transport can be as low as 2 mA cm−2 (for 0.1 M H2PO4− in the membrane and 100 μm membrane layer), which is close to the observed plateau current density. This mechanism would work in particular for weak acid/base species that have an acid and conjugate base species both with a negative (or positive) charge, such that both acid and base are available at high concentrations in the same membrane layer. That would explain the most pronounced plateau in the I–V curves when using phosphate in the anolyte; both H2PO4− and HPO42− are negatively charged.
As the internal concentration polarization cannot be measured directly, this effect cannot be quantified from the existing experiments. Experiments with thinner BPMs and simulations of ion concentrations within the membrane, which are beyond the scope of this study, could give more insight into the origin of the plateau current density.
Conclusions
Bipolar membranes were investigated under various electrochemical conditions to measure the electrochemical response and ion cross-over as a function of the electrolyte pH, concentration, flow velocity, and ion type. It was found that at moderate pH gradients (ΔpH < 14), three distinct regions are seen in I–V curves, indicating that at low potentials/low current densities, it is possible to dissociate water at potentials lower than 0.83 V. It is critical to improve the current density at low potentials to enable the use of (photo)catalysts that can only operate at non-extreme pH. We show that the external concentration polarization and ion cross-over only partly explain the transition from the regime with membrane potential to a regime with high potential (0.83 V). Furthermore, comparing the same hydrated ion size, it was shown that cations permeated through the BPM in larger quantities than their corresponding salt anions. The results of this work show a clear picture of how relative electrolyte conditions can affect the potential drop across a BPM, offering a pathway for improving the selectivity of BPMs for electrochemical conversion applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Marijn Blommaert (TU Delft) for fruitful discussions and the Dutch Organisation for Scientific Research (NWO) for funding part of this research via a VIDI grant to W. A. Smith.References
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef PubMed.
- M. B. McDonald, S. Ardo, N. S. Lewis and M. S. Freund, ChemSusChem, 2014, 7, 3021–3027 CrossRef PubMed.
- N. M. Vargas-Barbosa, G. M. Geise, M. A. Hickner and T. E. Mallouk, ChemSusChem, 2014, 7, 3017–3020 CrossRef PubMed.
- J. Luo, D. A. Vermaas, D. Bi, A. Hagfeldt, W. A. Smith and M. Grätzel, Energy Environ. Sci., 2016 Search PubMed.
- R. S. Reiter, W. White and S. Ardo, J. Electrochem. Soc., 2016, 163, H3132–H3134 CrossRef.
- K. Sun, R. Liu, Y. Chen, E. Verlage, N. S. Lewis and C. Xiang, Adv. Energy Mater., 2016, 6, 1600379 CrossRef.
- D. A. Vermaas, M. Sassenburg and W. A. Smith, J. Mater. Chem. A, 2015, 3, 19556–19562 RSC.
- X. Zhou, R. Liu, K. Sun, Y. Chen, E. Verlage, S. A. Francis, N. S. Lewis and C. Xiang, ACS Energy Lett., 2016, 1, 764–770 CrossRef.
- S. Chabi, A. G. Wright, S. Holdcroft and M. S. Freund, ACS Appl. Mater. Interfaces, 2017, 9, 26749–26755 CrossRef PubMed.
- D. A. Vermaas and W. A. Smith, ACS Energy Lett., 2016, 1, 1143–1148 CrossRef.
- Y. C. Li, D. Zhou, Z. Yan, R. H. Gonçalves, D. A. Salvatore, C. P. Berlinguette and T. E. Mallouk, ACS Energy Lett., 2016, 1, 1149–1153 CrossRef.
- S. Chabi, K. M. Papadantonakis, N. S. Lewis and M. S. Freund, Energy Environ. Sci., 2017, 10, 1320–1338 RSC.
- J. J. Krol, Bipolar Membranes, Universiteit Twente, 1997 Search PubMed.
- F. G. Wilhelm, N. F. A. van der Vegt, H. Strathmann and M. Wessling, J. Membr. Sci., 2002, 199, 177–190 CrossRef.
- H. Strathmann, J. J. Krol, H. J. Rapp and G. Eigenberger, J. Membr. Sci., 1997, 125, 123–142 CrossRef.
- M. D. Eisaman, L. Alvarado, D. Larner, P. Wang, B. Garg and K. A. Littau, Energy Environ. Sci., 2011, 4, 1319–1328 RSC.
- A. M. Ashrafi, N. Gupta and D. Neděla, J. Membr. Sci., 2017, 544, 195–207 CrossRef.
- R. E. Moussaoui, G. Pourcelly, M. Maeck, H. D. Hurwitz and C. Gavach, J. Membr. Sci., 1994, 90, 283–292 CrossRef.
- J. Jin, K. Walczak, M. R. Singh, C. Karp, N. S. Lewis and C. Xiang, Energy Environ. Sci., 2014, 7, 3371–3380 RSC.
- F. F. Abdi, L. Han, A. H. M. Smets, M. Zeman, B. Dam and R. van de Krol, Nat. Commun., 2013, 4, 2195 CrossRef PubMed.
- J. W. Ager, M. Shaner, K. Walczak, I. D. Sharp and S. Ardo, Energy Environ. Sci., 2015, 8, 2811–2824 RSC.
- A. H. Galama, J. W. Post, M. A. Cohen Stuart and P. M. Biesheuvel, J. Membr. Sci., 2013, 442, 131–139 CrossRef.
- G. M. Geise, H.-S. Lee, D. J. Miller, B. D. Freeman, J. E. McGrath and D. R. Paul, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 1685–1718 CrossRef.
- H. Strathmann, Ion Exchange Membrane Separation Processes, Elsevier, 2004 Search PubMed.
- S. Z. Oener, S. Ardo and S. W. Boettcher, ACS Energy Lett., 2017, 2, 2625–2634 CrossRef.
- J. Balster, M. H. Yildirim, D. F. Stamatialis, R. Ibanez, R. G. H. Lammertink, V. Jordan and M. Wessling, J. Phys. Chem. B, 2007, 111, 2152–2165 CrossRef PubMed.
- J. J. Krol, M. Wessling and H. Strathmann, J. Membr. Sci., 1999, 162, 145–154 CrossRef.
- W. M. Haynes and D. R. Lide, CRC Handbook of Chemistry and Physics: a Ready-reference Book of Chemical and Physical Data, CRC Press, Boca Raton, Fla, 2011 Search PubMed.
- S. Pawlowski, P. Sistat, J. G. Crespo and S. Velizarov, J. Membr. Sci., 2014, 471, 72–83 CrossRef.
- Y. Tanaka, J. Membr. Sci., 2003, 216, 149–164 CrossRef.
- C. Larchet, S. Nouri, B. Auclair, L. Dammak and V. Nikonenko, Adv. Colloid Interface Sci., 2008, 139, 45–61 CrossRef PubMed.
- M. Isaacson and A. A. Sonin, Ind. Eng. Chem. Process Des. Dev., 1976, 15, 313–321 CrossRef.
- V. Geraldes and M. D. Afonso, J. Membr. Sci., 2010, 360, 499–508 CrossRef.
- P. Sistat and G. Pourcelly, J. Membr. Sci., 1997, 123, 121–131 CrossRef.
- N. W. Rosenberg and C. E. Tirrell, Ind. Eng. Chem., 1957, 49, 780–784 CrossRef.
- Y. Tanaka, Membr. Sci. Technol., 2007, 12, 245–270 Search PubMed.
- H.-J. Lee, H. Strathmann and S.-H. Moon, Desalination, 2006, 190, 43–50 CrossRef.
- M. Higa, A. Tanioka and K. Miyasaka, J. Membr. Sci., 1990, 49, 145–169 CrossRef.
- D. A. Vermaas, J. Veerman, M. Saakes and K. Nijmeijer, Energy Environ. Sci., 2014, 7, 1434–1445 RSC.
- T. Sata, J. Membr. Sci., 1994, 93, 117–135 CrossRef.
- F. G. Wilhelm, N. F. A. van der Vegt, M. Wessling and H. Strathmann, J. Electroanal. Chem., 2001, 502, 152–166 CrossRef.
- T. Sata, Ion Exchange Membranes: Preparation, Characterization, Modification and Application, RSC, Cambridge, 2004 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental setup details, sample analysis, Sherwood numbers and use of Ba(OH)2. See DOI: 10.1039/c8se00118a |
| This journal is © The Royal Society of Chemistry 2018 |