Open Access Article
Open Access ArticleInfluence of odd–even effect and intermolecular interactions in 2D molecular layers of bisamide organogelators†
Volga Kocasoy a,
Burcu Dedeoglu
a,
Burcu Dedeoglu *b,
Oznur Demir-Orduc and
Viktorya Aviyente
*b,
Oznur Demir-Orduc and
Viktorya Aviyente *a
*a
aDepartment of Chemistry, Bogazici University, 34342, Bebek, Istanbul, Turkey. E-mail: aviye@boun.edu.tr
bDepartment of Chemistry, Gebze Technical University, 41400, Gebze, Kocaeli, Turkey. E-mail: b.dedeoglu@gtu.edu.tr
cDepartment of Chemistry, Abant Izzet Baysal University, 14030, Golkoy, Bolu, Turkey
First published on 15th October 2018
Abstract
Organogelators have a wide range of use in everyday life including drug delivery and controlled release, surface coating and paper industry. In this study, a series of model bisamides have been analyzed as potential organogelators. These molecules are connected by odd and even numbered methylene units (n) in length ranging from 2 to 9. By constructing layers of those molecules along the growth direction we provide an insight into the self-assembly process. A complete systematic analysis of the computational results with B3LYP/6-311+G** suggests that the self-assembly of these potential organogelators is influenced by the odd–even effect, the relative direction of amide carbonyl groups, the bridging spacer chain length and the presence of a chiral alpha carbon. The aforementioned factors alter the strength of the intermolecular hydrogen bonds as well as the van der Waals interactions, which in turn may affect the self-assembly process of gelation and result in the formation of aggregates with different shapes. It is found that molecules with short central chains have an energetic preference for antiparallel arrangement over their parallel analogues as a result of stronger hydrogen bonding interactions. As the central chain elongates, the free energy difference between antiparallel and parallel structures decreases suggesting a compromise between hydrogen bonding and van der Waals interactions. The complete structural analysis suggests ribbon-like structures for achiral even-antiparallel and woven-like structures for odd-parallel systems, respectively. Upon creation of asymmetry on the alpha carbon, a twisted ribbon-like and a coiled coil-like structure are observed for even and odd systems, respectively. Our computational results are in accordance with the experimental results and provide an insight into the self-assembly of layers of bisamides.
Introduction
Gelation of organic molecules has been a milestone in materials chemistry. A specific type of these molecules, low molecular weight organogelators are known for their gelation properties of immobilizing a variety of organic solvents in their three dimensional infinite fibrillar networks.1–4 The ability to self-assemble into fibrous networks of such molecules like urethanes, amides, carbamates and ureas, has a wide range of uses in everyday life including drug delivery and controlled release and separation processes.5–7Gel structure is made of a colloidal phase and a dispersion medium which is the solvent. The colloids are mobile compared to solid and stationary compared to solution.8 Gelation enables immobilization of the organic solvent into 3D network by intermolecular interactions thus keeping the structure together. Physical gels form solutions upon heating and gelate back again upon cooling above and below their gel–sol transition temperature.9 This thermoreversible property enabling gel–sol transitions of the gels has applications most likely in areas such as photonic materials, cosmetics, fuel engineering and water purification via oil spill recovery.5,10,11
Self-assembly into nanosized fibrous structures is mainly driven by non-covalent forces between the layers of gelator molecules. These intermolecular interactions can be listed as hydrogen bonding, pi-stacking (in naphthalene, anthracene etc.), donor–acceptor interactions, hydrophobic forces and dispersion.10,12–16 Substances which contain the carbamate functional group have additional properties such as flexibility and strong adhesion with respect to their ability to form unidirectional and self-complementary intermolecular hydrogen bonds.2 Hence, due to their multifunctional utilities, the low molecular weight organogelators become an intensive focus of research in the field of self-assembly.
The chemical structure has a great influence on the gelation ability. For instance, the odd and even numbered methylene groups in aliphatic alkyl chain moieties in the low molecular weight organogelators, “the odd–even effect’’, is a widely observed and intensively studied phenomenon.17–20 Mukherjee and Biradha observed that a series of bis(pyridylcarboxamido)alkane derivatives having an odd number of carbon atoms in the alkyl spacer adopt twisted conformations, whereas the even ones have linear conformations.21 In another study, p-alkoxyphenyl substituted biscarbamate derivatives having odd numbered methylene units in their bridging alkyl spacer were shown to increase the ability of gelation.3 Interestingly, increasing the chain length in odd and even numbered units may influence the gelation in a completely different manner.3,11,12,22 For example, Sumiyoshi et al. claim that as the central spacer length increases, the odd numbered systems lead to an improved gelation. In contrast, for even numbered systems longer central spacer lengths result in the loss of gelation ability.12
Another structural aspect closely linked to the odd–even effect is the spatial arrangement of the amide groups, namely parallel and antiparallel arrangement.12 Sumiyoshi et al. examined the molecular assembly of bisamides connected by a bridging zigzag carbon chain. They studied the parallel and antiparallel arrangements of two amide groups that build upon the odd and even numbers of methylene units forming the alkyl chain which serves as the basis for the self-assembly of organogelators.12 Moreover, Kim and co-workers suggested that the odd numbered methylene units located in the bridging zigzag alkyl chain of a dicarbamate molecule result in a change in the direction of both of the terminal alkyl chains when compared to their even numbered analogues.2
Such structural features leading to a variety of intermolecular forces mediate the self-assembly process of gelation and eventually result in the formation of aggregates with different shapes. Sumiyoshi et al. reported that two amide moieties of an even number carbon chain diamide interact with each other through two pairs of hydrogen bonds with two other molecules in a plane resulting in the formation of ribbon-like aggregates. On the other hand, a diamide of an odd number carbon chain forms four independent hydrogen bonds with four other molecules not in a plane, which forms woven-like aggregates. Their structures mainly possess a hydrogen bonding core and a van der Waals interaction core which builds up overall skeleton of the self-assembly. The amide group plays the role of an intermolecular hydrogen-bonding core, and the alkyl side chains correspond to a van der Waals interaction core.
Previous approaches also revealed the influence of stereochemistry on the structure of aggregates upon introduction of chirality. They showed that achiral diamides form planar hydrogen-bonds whereas their analogous chiral molecules tend to form twisted layers with an improved gelation ability.1,12
Later on, Yamamoto et al. have shown that terminal functionalization of N,N′-didodecanoyl ethylenediamines inducing additional intermolecular interactions in the molecular self-assembly process provide more powerful low molecular weight gelators.23
In this study, density functional theory calculations are carried out to understand the factors that affect the molecular self-assembly of bisamide organogelator molecules (Scheme 1). Taking into consideration Sumiyoshi et al.'s study, we constructed a new series of model didocanoylamide of α,ω-alkylidenediamine layers having methyl groups at both ends connected by odd and even numbered methylene units (n) in length ranging from 2 to 9.12
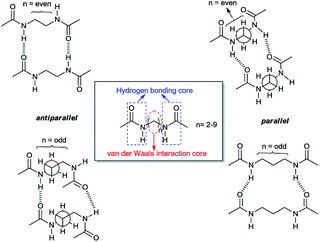 | ||
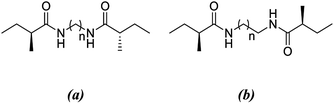
| Scheme 1 Antiparallel and parallel arrangements of the dimer with respect to the number of methylene units linking the two amide carbonyl groups. | ||
Methodology
All calculations are performed using the hybrid density functional B3LYP24–28 with 6-311+G** basis set in solution with the implicit solvent model IEFPCM29,30 (benzene) with ε = 2.27. Frequency analyses are performed on the B3LYP/6-311+G** optimized geometries to confirm the nature of the stationary points as minima (with all-real frequencies). The total stabilization energy emerging from the sum of interactions between the lone pair of O and the antibonding orbital of N–H is calculated by natural bond order analysis (NBO)31–33 at the B3LYP/6-311+G** level of theory. In order to probe the influence of non-covalent interactions, we performed dispersion corrected calculations using B3LYP-D3 (ref. 34–39) functional with 6-311+G** basis set in benzene. Single point calculations are computed at B3LYP/6-311+G**//B3LYP-D3/6-311+G** and B3LYP-D3/6-311+G**//B3LYP/6-311+G** levels of theory in benzene. All calculations are carried out by using the Gaussian 09 program package.40The model system used in this study is based on the experimentally studied series of didocanoylamides of α,ω-alkylidenediamines compounds.12 For computational simplicity, terminal methylene chains are replaced with single methyl groups. Antiparallel and parallel models are named as -anti and -para and the letter “n” is used to define the number of methylene units present at the central carbon chain. If the model is dimeric or trimeric, -d and -t is further included in the nomenclature of the model compounds.
Results and discussion
In previous experimental studies, Sumiyoshi et al. showed that increasing the central spacer length causes an improvement and a reduction in the gelation abilities of bisamide structures having odd and even numbered units, respectively. They observed this odd–even effect most clearly in benzene among other solvents used.12 Thus, we conducted our study on solvation with benzene. Moreover, Kim et al. investigated another type of self-assembling molecules namely dicarbamates and observed that their crystals show layered structural packing.2 Similarly in this study we have considered a layer by layer self-assembled molecules.Monomers, dimers and trimers
In order to probe the factors affecting the self assembly and thus the gelation abilities, we started by constructing a monolayer series of a model of the didocanoylamide of α,ω-alkylidenediamine system with single terminal methyl groups in both antiparallel and parallel arrangements having odd and even numbered bridging zigzag methylene chains (n).The antiparallel conformations (n = 2–9) of monomers are found to have lower dipole moments compared to their analogous parallel conformations (Table 1). The dipole moments (μ) of the antiparallel structures with odd numbered methylene units range from 1.4 to 1.8 while those with even numbered methylene units are almost zero. The parallel conformations with odd and even numbered methylene units have higher dipole moments ranging from 7.6 to 8.7 and exhibit a small variety for odd and even numbered methylene units. The calculated relative Gibbs free energies do not show a significant difference between antiparallel and parallel conformers regardless of the number of methylene units.
| Monomer | Dimer | Trimer | ||||||
|---|---|---|---|---|---|---|---|---|
| n-Anti/para | μ | Grel | n-Anti/para | μ | Grel | n-Anti/para | μ | Grel |
| 2-Anti | 0.0 | 0.0 | 2-Anti-d | 0.0 | 0.0 | 2-Anti-t | 0.0 | 0.0 |
| 2-Para | 7.6 | 1.6 | 2-Para-d | 19.1 | 4.0 | 2-Para-t | 31.2 | 5.3 |
| 3-Anti | 1.4 | 0.0 | 3-Anti-d | 2.4 | 0.0 | 3-Anti-t | 3.9 | 0.0 |
| 3-Para | 8.6 | 0.8 | 3-Para-d | 19.9 | 2.1 | 3-Para-t | 32.0 | 5.0 |
| 4-Anti | 0.0 | 0.6 | 4-Anti-d | 0.0 | 0.0 | 4-Anti-t | 0.0 | 0.0 |
| 4-Para | 8.3 | 0.0 | 4-Para-d | 19.8 | 2.6 | 4-Para-t | 31.8 | 1.6 |
| 5-Anti | 1.4 | 0.0 | 5-Anti-d | 2.6 | 0.0 | 5-Anti-t | 3.4 | 0.0 |
| 5-Para | 8.6 | 0.3 | 5-Para-d | 20.0 | 2.1 | 5-Para-t | 31.8 | 0.5 |
| 6-Anti | 0.0 | 0.0 | 6-Anti-d | 0.0 | 0.0 | 6-Anti-t | 0.5 | 0.0 |
| 6-Para | 8.4 | 0.2 | 6-Para-d | 19.7 | 1.9 | 6-Para-t | 31.5 | 0.5 |
| 7-Anti | 1.8 | 0.0 | 7-Anti-d | 2.1 | 0.0 | 7-Anti-t | 3.5 | 0.03 |
| 7-Para | 8.7 | 0.3 | 7-Para-d | 20.0 | 0.6 | 7-Para-t | 31.2 | 0.0 |
| 8-Anti | 0.3 | 0.0 | 8-Anti-d | 0.7 | 0.0 | 8-Anti-t | 0.5 | 0.2 |
| 8-Para | 8.4 | 0.3 | 8-Para-d | 20.0 | 2.6 | 8-Para-t | 31.6 | 0.0 |
| 9-Anti | 1.8 | 0.2 | 9-Anti-d | 2.4 | 0.2 | 9-Anti-t | 5.3 | 0.0 |
| 9-Para | 8.7 | 0.0 | 9-Para-d | 20.0 | 0.0 | 9-Para-t | 31.5 | 0.7 |
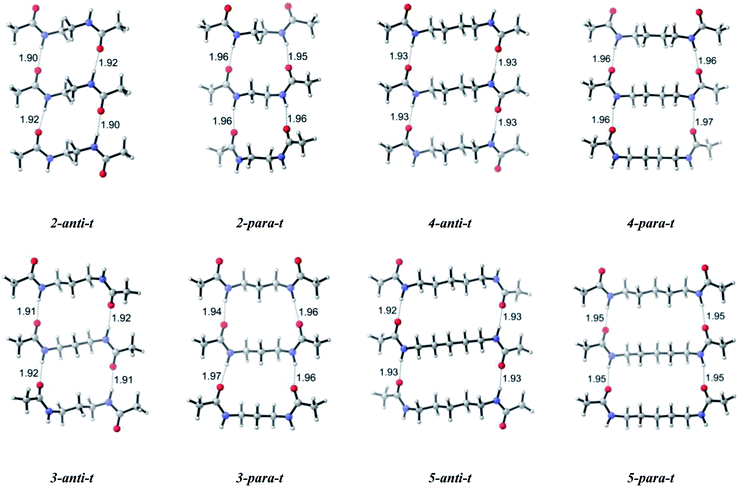
To increase our knowledge on self-assembly we built up a complementary second layer and turned our focus on dimeric systems (Scheme 1). Trends in dipole moments of the dimeric system are similar to the monomers, except for a significant increase in dipole moments of parallel conformations. For dimers, the calculated results show preference trends for antiparallel and parallel orientation of amide carbonyl groups: the antiparallel systems have lower relative Gibbs free energies compared to the parallel systems, except for n = 9 (Table 1). Such energetic difference favoring antiparallel arrangement can be attributed to the intermolecular interactions involving amide carbonyls of one layer and the amide hydrogens of the second layer. The hydrogen bond lengths are shorter for antiparallel and slightly longer for parallel systems (Table 2). This observation does not change with increasing chain length but becomes less pronounced as the chain length increases. Hence, attractive forces within dimers for antiparallel systems are dominant due to shorter interchain hydrogen bonds. Furthermore, hydrogen bonds in antiparallel conformations are less distorted with more linear N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interactions compared to those of parallel conformations. This situation is similar to the well known stability of antiparallel β sheets of polypeptides over parallel ones.41 It is noteworthy to indicate that the energy difference between antiparallel and parallel conformations with odd numbered of methylene units is less than that with even numbered methylene units; and in fact the energy difference with odd numbered methylene units disappears as the chain length increases. While the energy difference is 2.1 kcal mol−1 for n = 3 and n = 5, it decreases to 0.6 and −0.2 kcal mol−1 for n = 7 and n = 9.
C interactions compared to those of parallel conformations. This situation is similar to the well known stability of antiparallel β sheets of polypeptides over parallel ones.41 It is noteworthy to indicate that the energy difference between antiparallel and parallel conformations with odd numbered of methylene units is less than that with even numbered methylene units; and in fact the energy difference with odd numbered methylene units disappears as the chain length increases. While the energy difference is 2.1 kcal mol−1 for n = 3 and n = 5, it decreases to 0.6 and −0.2 kcal mol−1 for n = 7 and n = 9.
| a | b | |||||
|---|---|---|---|---|---|---|
| n-Anti/para | H⋯O (Å) | N⋯O (Å) | N–H⋯O (deg) | H⋯O (Å) | N⋯O (Å) | N–H⋯O (deg) |
| 2-Anti-d | 1.93 | 2.94 | 174.6 | 1.93 | 2.94 | 174.6 |
| 2-Para-d | 2.00 | 2.99 | 163.0 | 1.99 | 2.98 | 164.3 |
| 3-Anti-d | 1.94 | 2.95 | 171.3 | 1.94 | 2.95 | 171.3 |
| 3-Para-d | 1.99 | 2.99 | 168.3 | 1.99 | 2.99 | 168.3 |
| 4-Anti-d | 1.96 | 2.96 | 167.9 | 1.96 | 2.96 | 167.9 |
| 4-Para-d | 1.99 | 2.98 | 163.2 | 1.99 | 2.98 | 163.1 |
| 5-Anti-d | 1.96 | 2.97 | 173.1 | 1.97 | 2.99 | 180.0 |
| 5-Para-d | 1.98 | 2.98 | 167.4 | 1.98 | 2.98 | 167.4 |
| 6-Anti-d | 1.96 | 2.97 | 169.8 | 1.96 | 2.97 | 169.8 |
| 6-Para-d | 1.98 | 2.97 | 164.5 | 1.99 | 2.98 | 165.2 |
| 7-Anti-d | 1.97 | 2.97 | 168.9 | 1.97 | 2.97 | 169.2 |
| 7-Para-d | 1.98 | 2.98 | 167.7 | 1.98 | 2.98 | 167.7 |
| 8-Anti-d | 1.97 | 2.97 | 168.6 | 1.98 | 2.99 | 177.2 |
| 8-Para-d | 1.98 | 2.97 | 164.5 | 1.98 | 2.97 | 164.5 |
| 9-Anti-d | 1.97 | 2.97 | 168.9 | 1.97 | 2.97 | 169.0 |
| 9-Para-d | 1.98 | 2.98 | 167.9 | 1.98 | 2.98 | 168.0 |
For dimers having even numbered bridging methylene units, the energy difference of antiparallel–parallel systems is greater since antiparallel demonstrates a layer by layer fine packing and parallel systems are much distorted. The distortion level of parallel systems decreases as the even numbered chain length increases. For molecules having odd numbered bridging methylene units, an opposite trend is adopted and parallel structures pack better compared to their antiparallel analogues. However, antiparallel structures are not that much distorted, an indication of relatively similar free energies between the antiparallel–parallel systems with similar values of n.
Since gels are made up of infinite fibrillar networks by definition, increasing the layers of gelator molecules is necessary to broaden the understanding of gelation in these systems. Modeling of trimers affords a deeper understanding of self-assembly. The trimer structures yield regular orientations of gelator layers one on top of another (Fig. 1). The calculated results show that for n = 2 and n = 3, the antiparallel arrangement is highly selective over parallel and the corresponding difference in Gibbs free energies is greater compared to their dimers by 1.3 and 2.9 kcal mol−1 for n = 2 and n = 3, respectively (Table 1). However, for trimers when n increases the free energy difference between antiparallel and parallel systems decreases with a steeper acceleration as compared to dimers favoring antiparallel conformations.
The preference of antiparallel systems disappears regardless of the odd and even numbered bridging methylene units. Such a decrease in preference as the number of layers or as the number of bridging methylene units increase suggest that the 3D relative orientation of the layers is a compromise between the interaction of hydrogen bonding and van der Waals interaction cores. As the number of bridging methylene units or the number of layers is low, the interaction of hydrogen bonding cores dominates and the preference tilts towards antiparallel arrangements.
The dipole moments of antiparallel conformations of trimers are way less than parallel systems which indicates their lower free energies. However, this observation is insufficient to explain how parallel systems can possibly exist for n = 7 and n = 8 while having large dipole moments and will be discussed further in terms of intermolecular interactions.
In order to provide more accurate computational results on non-covalent intermolecular interactions, we added semi empirical dispersion correction proposed by Grimme to the B3LYP functional.34 As the system gets larger, the contribution of dispersion effect increases.37 Upon optimizations with B3LYP-D3, the original layer on top of another layer-structural trend followed by parallel systems-breaks down and forms entangled structures due to the increased number of non-covalent interactions (Fig. S1†). Also, the free energy values calculated with B3LYP/6-311+G**//B3LYP-D3/6-311+G** are larger as compared to their counterparts optimized with B3LYP/6-311+G** (Table S1†). Thus, the optimizations are carried out without the dispersion correction. Nevertheless, single point calculations at B3LYP-D3/6-311+G**//B3LYP/6-311+G** have been performed to monitor the effect of dispersion corrections on free energies and total stabilization energies (Table S2†). Due to the similar trends in energetics at the two levels of theory, the energetics reported here are B3LYP/6-311+G** and those that include dispersion correction (B3LYP-D3/6-311+G**//B3LYP/6-311+G**) are given in the ESI.†
The intermolecular hydrogen bonds for parallel systems are longer than those for antiparallel systems regardless of chain length. This effect can be attributed to the presence of stronger attractive forces in antiparallel systems. In previous experimental studies, Sumiyoshi et al. showed that increasing the central spacer length enables gelation specifically towards odd numbered parallel systems and directly relates the interlayer distance with gelation ability.12 Upon calculating the average interlayer distances (d, Å) by measuring the distances between the conjugate carbon atoms at the central carbon chains within achiral trimers (d1–d4 for even and d1–d2 for odd, Scheme 2), it is seen that the parallel arrangement of amide carbonyls yields longer d values irrespective of the odd–even effect. Furthermore, when n ≥ 5, keeping the lengthwise dominance of parallel, odd numbered systems have longer interlayer distances compared to the even numbered systems. Although the systems modeled in this study are not exactly similar to the ones used by Sumiyoshi et al.,12 we end up with a similar outcome where for odd values of n the trapping of solvent for gelation is favored (Fig. 2).
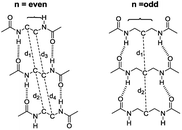 | ||
| Scheme 2 The interlayer distances between the conjugate carbon atoms at the central carbon chains. d is the average of the distances shown above. | ||
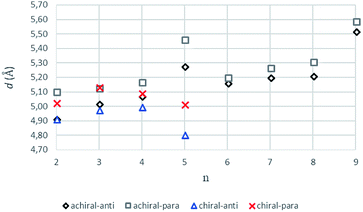 | ||
| Fig. 2 The average interlayer distance, d values (Å), for achiral (n = 2–9) and chiral (n = 2–5) trimers having antiparallel and parallel arrangements (B3LYP/6-311+G** (solvent = benzene)). | ||
For molecules having odd numbered methylene units and parallel arrangement of amide carbonyls, the longer distances within the van der Waals interaction cores keep the medium more stationary than a solution and more flexible than a solid. Thus, it provides the necessary environment for gelation. We expect improved role of intermolecular van der Waals interactions as the central alkyl chain elongates due to the increasing number of carbon atoms. We suspect that the presence of Waals interactions explains why the energetic difference between parallel and antiparallel systems decreases and even the former can dominate with increasing values of n although they possess larger dipole moments. Lengthening the alkyl spacer results in better assessed role of van der Waals interactions causing three dimentional growth. Hence, van der Waals interactions dominate over hydrogen bonding along growth direction.
Second order perturbation theory analysis of Fock matrix in NBO is carried out to determine the stabilization provided by hydrogen bonding in a quantitative form. Table 3 suggests that the antiparallel systems have greater stabilization energy compared to their parallel analogues. For the molecules having even numbered central alkyl chain, the energetic superiority of antiparallel arrangement over parallel is very obvious. In contrast, for molecules having odd numbered central alkyl chains both arrangements are closer in total stabilization energy. In addition, for n = odd as the chain length increases the anti–para selectivity in total stabilization energy decreases; for n = even first it increases and then decreases.
| n-Anti/para | Total stabilization energy | n-Anti/para | Total stabilization energy |
|---|---|---|---|
| 2-Anti-t | 44.1 (0.0) | 6-Anti-t | 56.2 (0.0) |
| 2-Para-t | 36.2 (7.9) | 6-Para-t | 39.2 (17.1) |
| 3-Anti-t | 45.9 (0.0) | 7-Anti-t | 42.8 (0.0) |
| 3-Para-t | 42.1 (3.8) | 7-Para-t | 41.1 (1.7) |
| 4-Anti-t | 48.6 (0.0) | 8-Anti-t | 48.7 (0.0) |
| 4-Para-t | 35.7 (13.0) | 8-Para-t | 40.1 (8.6) |
| 5-Anti-t | 44.3 (0.0) | 9-Anti-t | 42.6 (0.0) |
| 5-Para-t | 40.0 (4.3) | 9-Para-t | 40.9 (1.7) |
Growth
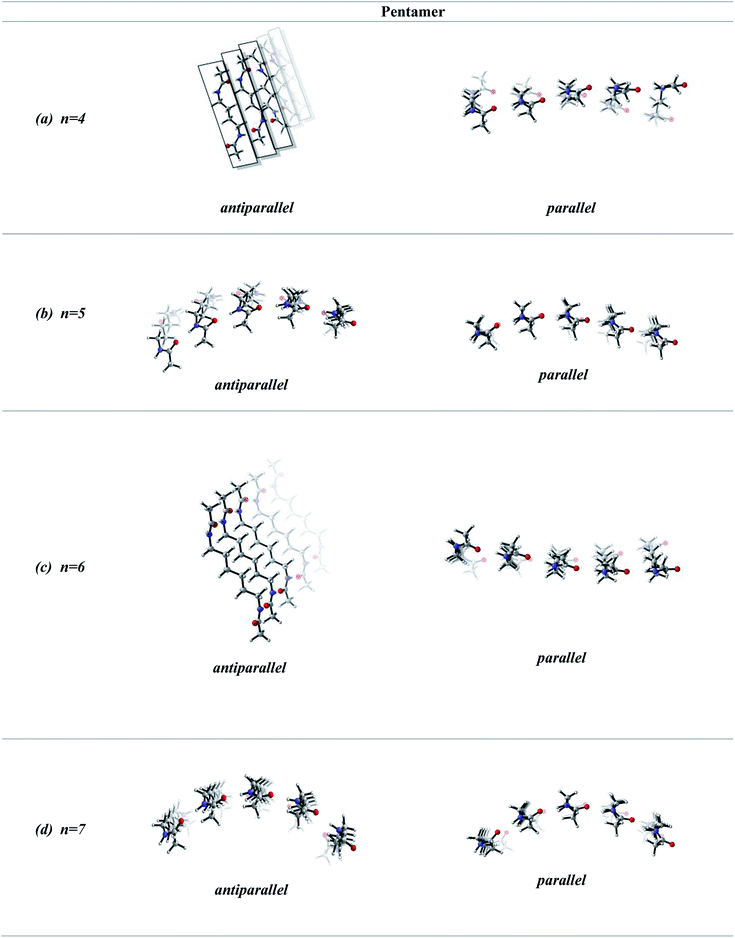
In order to screen the effect of growth on the molecular assembly, we studied the growth from dimer to pentamer for n = 2–3 in antiparallel and parallel structures (Fig. 3). Fig. 3a shows the packing of antiparallel molecules having two bridging methylene units. The packing motif is conserved throughout growth from dimer to pentamer. This arrangement suggests a layer by layer growth with a well-defined packing (Fig. 3a) and might be an indication of ribbon like shape. However, for the analogues parallel system, the fine regular packing is distorted for dimer, trimer, tetramer and pentamer structures (Fig. 3b). A twisting in the ribbon shape is clearly seen in Fig. 3b. As the chain length increases from n = 2 to n = 6, the same trend is observed for antiparallel and parallel conformations: regular packing for the former and twisting for the latter (Fig. 4a and c). Nevertheless, for antiparallel structures, a pleated appearance is observed after the addition of third layer.On the other hand, both antiparallel (Fig. 3c) and parallel (Fig. 3d) molecules having an odd number of methylene units display the formation of a curvature upon growth from dimer to pentamer. This observation might possibly be an indication of woven-like structures. There is a significant difference in antiparallel and parallel conformations with odd numbered methylene units. Although both exhibit curved structures, a slight twisting is evident in antiparallel structures while parallel ones possess a perfect curvature structure (Fig. 4).
Chirality
Previous works suggest that introduction of chirality twists the structures.1,12 We suspect that the fine packing of achiral antiparallel systems with even numbered methylene units in their central carbon chains eliminates twist formation. In order to understand why the achiral antiparallel systems do not undergo twisting, we modelled chiral conformers by creating asymmetry on the alpha carbon by the addition of a methyl and an ethyl group to our previous model (Scheme 3).12Introduction of chirality to the antiparallel systems distorts the layer by layer packing and twists the aggregates yielding structures like twisted ribbon and coiled coil structures for molecules having even and odd numbered methylene units within their central carbon chain, respectively (Fig. 5). The same trend is observed for parallel systems as well. Similarly, molecules having even numbered spacers twist into twisted ribbon-like and their odd numbered analogues twist into coiled coil-like structures. Hence, it is possible that creation of asymmetry on alpha carbon breaks down the fine packing and enables twisted geometries. When the interlayer distances within the layers of trimers are taken into account, it is noticed that the chiral molecules have shorter d values as compared to achiral molecules (Fig. 2). This observation can be attributed to molecule winding caused by the asymmetry of alpha carbon.12
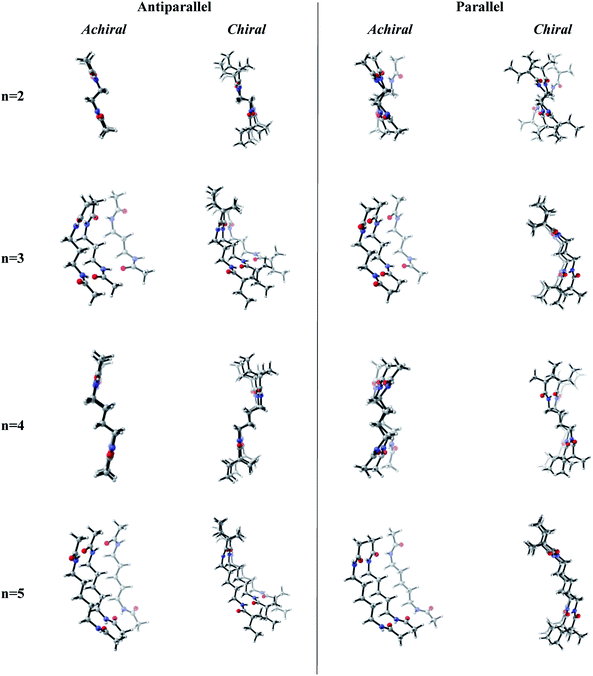 | ||
| Fig. 5 Optimized achiral vs. chiral trimers having antiparallel and parallel arrangements with n = 2–5 methylene units in central carbon chain. (B3LYP/6-311+G** (solvent = benzene)). | ||
Conclusions
Throughout our computations we had the task of rationalizing the factors that affect the molecular self-assembly and its role on gelation. A series of model didocanoylamide of α,ω-alkylidenediamine system having methyl groups at both ends connected by odd and even numbered methylene units (n) in length ranging from 2 to 9 were modeled in antiparallel and parallel arrangements depending on the direction of the amide carbonyl groups. We investigated the odd–even effect, the effect of antiparallel–parallel arrangement and the chirality in multilayers. Molecules having even numbered central spacers with antiparallel directed amide carbonyls groups have lower dipole moments compared to their parallel analogues. Therefore, antiparallel systems are energetically slightly preferred. As the central chain length increases, the free energy difference between anti and parallel structures decreases since both species are stabilized by van der Waals interactions. The gelation ability of the odd species has been attributed to the larger distance between chains which can easily accommodate the solvent. The complete structural analysis suggest ribbon-like and woven-like structures for achiral even-antiparallel and odd-parallel systems, respectively. Upon creation of asymmetry on the alpha carbon, a twisting of the ribbon-like geometry into the twisted ribbon-like and the woven-like geometry into the coiled coil-like structure, has been observed. Though experimental verification of our computational results is a challenge for the future, the results in this study provide useful information for the self-assembly of bisamide organogelators and thus are expected to contribute to the development of new sophisticated structures.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Bogazici University Research Funds (Project No: 14452). The computational resources and Parallel Run-Time Support are provided by CompecTA Ltd's Feynmangrid HPC cluster. (http://www.compecta.com/feynmangrid.html). All 3D structures were drawn using CYLview.42 All 2D structures were drawn using ChemBioDraw Ultra.43References
- N. Š. Vujičic, Z. Glasovac, N. Zweep, J. H. Van Esch, M. Vinkovic, J. Popovic and M. Žinic, Chem.–Eur. J., 2013, 19, 8558–8572 CrossRef PubMed.
- K. Kim, K. E. Plass and A. J. Matzger, J. Am. Chem. Soc., 2005, 127, 4879–4887 CrossRef CAS PubMed.
- Ö. Demir-Ordu, H. Şimşir and K. Alper, Tetrahedron, 2015, 71, 1529–1539 CrossRef.
- L. A. Estroff and A. D. Hamilton, Chem. Rev., 2004, 104, 1201–1217 CrossRef CAS PubMed.
- K. Wang, Q. Jia, F. Han, H. Liu and S. Li, Drug Dev. Ind. Pharm., 2010, 36, 1511–1521 CrossRef CAS PubMed.
- F. Plourde, A. Motulsky, A.-C. Couffin-Hoarau, D. Hoarau, H. Ong and J.-C. Leroux, J. Controlled Release, 2005, 108, 433–441 CrossRef CAS PubMed.
- S. Debnath, A. Shome, S. Dutta and P. K. Das, Chem.–Eur. J., 2008, 14, 6870–6881 CrossRef CAS PubMed.
- E. A. Hauser, J. Chem. Educ., 1948, 25, 461 CrossRef.
- M. M. K. Khan, PhD thesis, Carleton University, 2011.
- S. Khanna, M. K. Khan and P. Sundararajan, Langmuir, 2009, 25, 13183–13193 CrossRef CAS PubMed.
- Y. Wang, S. Wu, X. Yan, T. Ma, L. Shao, Y. Liu and Z. Guo, Chemosphere, 2017, 167, 178–187 CrossRef CAS PubMed.
- T. Sumiyoshi, K. Nishimura, M. Nakano, T. Handa, Y. Miwa and K. Tomioka, J. Am. Chem. Soc., 2003, 125, 12137–12142 CrossRef CAS PubMed.
- K. Hanabusa, M. Yamada, M. Kimura and H. Shirai, Angew. Chem., Int. Ed. Engl., 1996, 35, 1949–1951 CrossRef CAS.
- M. K. Khan and P. R. Sundararajan, J. Phys. Chem. B, 2011, 115, 8696–8706 CrossRef CAS PubMed.
- M. K. Khan and P. R. Sundararajan, J. Phys. Chem. B, 2013, 117, 5705–5717 CrossRef CAS PubMed.
- Ç. Ç. Cenker, P. H. H. Bomans, H. Friedrich, B. Dedeoğlu, V. Aviyente, U. Olsson, N. A. J. M. Sommerdijk and S. Bucak, Soft Matter, 2012, 8, 7463 RSC.
- F. Tao and S. L. Bernasek, Chem. Rev., 2007, 107, 1408–1453 CrossRef CAS PubMed.
- K. Aoki, M. Kudo and N. Tamaoki, Org. Lett., 2004, 6, 4009–4012 CrossRef CAS PubMed.
- T. Wang, Y. Li and M. Liu, Soft Matter, 2009, 5, 1066 RSC.
- J. Schneider, C. Messerschmidt, A. Schulz, M. Gnade, B. Schade, P. Luger, P. Bombicz and V. Hubert, Langmuir, 2000, 8575–8584 CrossRef CAS.
- G. Mukherjee and K. Biradha, Cryst. Growth Des., 2011, 11, 924–929 CrossRef CAS.
- G. Mukherjee and K. Biradha, J. Chem. Sci., 2014, 126, 1285–1290 CrossRef CAS.
- Y. Yamamoto, A. Oyanagi, A. Miyawaki and K. Tomioka, Tetrahedron Lett., 2016, 57, 5889–5892 CrossRef CAS.
- D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef.
- D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2008, 4, 297–306 CrossRef CAS PubMed.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS.
- A. Klamt, C. Moya and J. Palomar, J. Chem. Theory Comput., 2015, 11, 4220–4225 CrossRef CAS PubMed.
- J. K. Badenhoop and F. Weinhold, J. Chem. Phys., 1997, 107, 5406–5421 CrossRef CAS.
- J. K. Badenhoop and F. Weinhold, J. Chem. Phys., 1997, 107, 5422–5432 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- S. Ehrlich, J. Moellmann and S. Grimme, Acc. Chem. Res., 2013, 46, 916–926 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- L. A. Burns, Á. Vázquez-Mayagoitia, B. G. Sumpter and C. D. Sherrill, J. Chem. Phys., 2011, 134, 084107 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS PubMed.
- F. Mota, J. S. Miller and J. J. Novoa, J. Am. Chem. Soc., 2009, 131, 7699–7707 CrossRef CAS PubMed.
- M. J. Frisch, et al., GAUSSIAN 09 (Revision B.01), Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- A. Perczel, Z. Gáspári and I. G. Csizmadia, J. Comput. Chem., 2005, 26, 1155–1168 CrossRef CAS PubMed.
- Y. Legault, CYLview, 1.0b, Universite de Sherbrooke, 2009, (http://www.cylview.org) Search PubMed.
- ChemBioDraw Ultra, 13.0.0.3015, CambridgeSoft, 2012 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Structures, energetics and coordinates of output files. See DOI: 10.1039/c8ra06224b |
| This journal is © The Royal Society of Chemistry 2018 |