Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Direct estimation of the transfer integral for photoinduced electron transfer from TD DFT calculations†
Lluís
Blancafort
 a and
Alexander A.
Voityuk
a and
Alexander A.
Voityuk
 ab
ab
aInstitut de Química Computacional i Catàlisi and Departament de Química, Universitat de Girona, Facultat de Ciències, C/M. A. Capmany 69, 17003 Girona, Spain. E-mail: lluis.blancafort@udg.edu; alexander.voityuk@icrea.cat
bInstitució Catalana de Recerca i Estudis Avançats (ICREA), Barcelona 08010, Spain
First published on 10th November 2017
Abstract
The rate of photoinduced ET in molecular systems is controlled by electronic coupling of the locally excited and charge transfer states. We generalize the Bixon–Jortner–Verhoeven expression for electronic coupling to systems with a small energy gap and derive the transfer integral for charge separation in two model heterojunctions using the excitation energies and oscillator strengths computed with TD DFT. The estimated couplings are in good agreement with the reference values.
Photoinduced electron transfer (ET) in biomolecules and organic heterojunctions is of increasing interest.1–8 Charge transfer (CT) between donor (D) and acceptor (A) occurs by decay of an excited state of the donor D* via ET between the D and A sites, D*–A → D+A−. The ET rate is controlled by electronic coupling of the initial and final states. Several computational methods have been developed to derive the matrix element.9–18 These schemes, however, are not always accessible within a desired quantum mechanical (QM) model. For instance, to estimate the transfer integral between a locally excited (LE) state and a CT state with the Generalized Mullikene–Hush method,9 the transition dipole moment between these states is required. However, common programs like Gaussian 09
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 (and its newest version Gaussian 16) often do not provide the transition dipole moment between excited states computed with the time-dependent density functional theory (TDDFT) method and therefore cannot be employed to obtain the coupling. There are also other issues that often prevent the use of standard calculations of the transfer integral (in most cases one needs a special computational code to obtain the coupling). In this paper, we consider a simple approach that allows one to estimate the coupling matrix element from routine QM calculations.
19 (and its newest version Gaussian 16) often do not provide the transition dipole moment between excited states computed with the time-dependent density functional theory (TDDFT) method and therefore cannot be employed to obtain the coupling. There are also other issues that often prevent the use of standard calculations of the transfer integral (in most cases one needs a special computational code to obtain the coupling). In this paper, we consider a simple approach that allows one to estimate the coupling matrix element from routine QM calculations.
In their landmark study,20 Bixon, Jortner and Verhoeven derived the expression
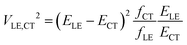 | (1) |
In this paper, we derive a more general expression
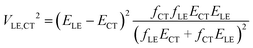 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 program, we carried out TDDFT calculations of excited state properties of the model and compare the coupling values derived using eqn (2) with reference data computed by the fragment charge difference (FCD) method.13
19 program, we carried out TDDFT calculations of excited state properties of the model and compare the coupling values derived using eqn (2) with reference data computed by the fragment charge difference (FCD) method.13
Let us consider a charge separation reaction D*A → D+–A−, where the donor molecule has a transition with strong light absorption. The corresponding LE state D* is the initial state of the reaction. The CT state D+–A− is generated by irradiation decay due to ET from the donor to the acceptor. The electronic interaction (coupling) of these pure states φLE and φCT with energies εLE and εCT determines the probability of the ET reaction. It also mixes φLE and φCT leading to “borrowing intensity” by the adiabatic CT (for more details see ref. 1). To express electronic coupling via spectroscopic parameters, eqn (2), we use the orthogonal transformation of the adiabatic states to diabatic states9,13 (its derivation is provided in the ESI†). This formula is obtained without any restriction on the energy gap |ELE − ECT|.
If the diabatic states of interest are in resonance, εLE = εCT, eqn (2) gives a well-known half-splitting formula for electronic coupling
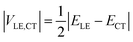 | (3) |
In contrast, eqn (1) overestimates the coupling by a factor of 2 (see Fig. 1).
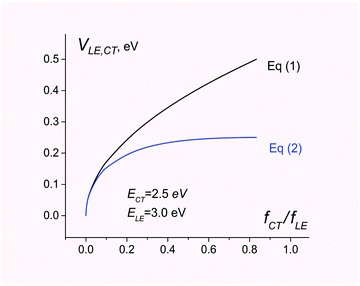 | ||
| Fig. 1 Electronic coupling for charge separation D*A → D+A− estimated using eqn (1) and (2). The energies of CT and LE states are set to 2.5 and 3.0 eV, respectively. The ratio of the CT and LE oscillator strength varies from 0 to ECT/ELE. | ||
Fig. 1 compares electronic couplings estimated with both eqn (1) and (2) for the 2-state model where ECT = 2.5 eV and ELE = 3.0 eV are kept constant but the ratio fCT/fLE is considered as a variable parameter.
As can be seen, eqn (1) and (2) give very similar results for fCT/fLE < 0.1. For larger values of fCT/fLE, eqn (1) overestimates the coupling.
If more than two diabatic states contribute to the LE and CT adiabatic states (for instance, the CT state is coupled with several LE states), a more complicated multi-state treatment has to be employed. Alternatively, the two state model can be modified to partially account for the multistate effects. If only two states, CT and LE, are coupled, transition dipole moments MCT and MLE are collinear, i.e. |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ| = 1, where γ is the angle between these vectors. Thus when a system with several interacting states is considered, the accuracy of the two-state scheme may be improved by using the projection of MCT on MLE instead of |MCT|. Then, the oscillator strength fCT in eqn (2) should be replaced by fCT
γ| = 1, where γ is the angle between these vectors. Thus when a system with several interacting states is considered, the accuracy of the two-state scheme may be improved by using the projection of MCT on MLE instead of |MCT|. Then, the oscillator strength fCT in eqn (2) should be replaced by fCT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ.
γ.
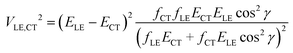 | (4) |
Eqn (2) and (4) provide comparable coupling values if |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ| > 0.7. The value of |cos
γ| > 0.7. The value of |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ| can also be used to decide whether the two-state model is applicable. If |cos
γ| can also be used to decide whether the two-state model is applicable. If |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ| < 0.7, the derived coupling may be inaccurate.
γ| < 0.7, the derived coupling may be inaccurate.
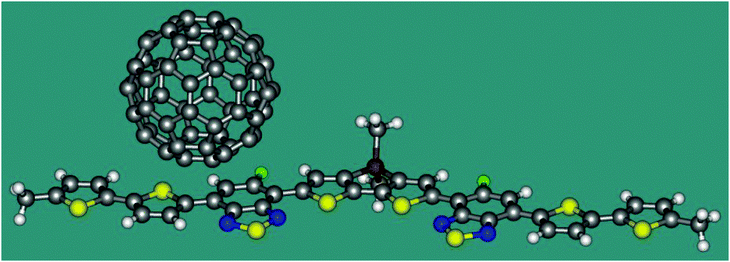
Now we apply eqn 2 in combination with TDDFT calculations to a model heterojunction shown in Fig. 2. The planar molecule containing thiophene and thiadiazole fragments is an electron donor. The C60 fullerene serves as an electron acceptor. The heterojunction is similar to that experimentally studied by Gelinas et al.21 Since ET coupling may strongly depend on the mutual position of the donor and acceptor, we estimate its value in two conformations of the complex, I and II, where the fullerene molecule is shifted from the centre of the donor by 7.9 and 3.4 Å, respectively. The distance between the plane of D and the lowest hexagon of C60 in both conformations is 3.20 Å. Cartesian coordinates of I and II are listed in the ESI.† The TDDFT calculations were carried out with the B3LYP functional and the 6-31G* basis set using the program Gaussian 09.19 The character of the excited states was analysed in terms of the transition density.22 The reference coupling values were derived using the Fragment Charge Difference method (FCD) and the calculated transition density.13
The first 3 transitions in both structures correspond to CT excitations. They are followed by a strongly absorbing LE state of the donor. The charge separation q in the CT states D+qA−q is close to 1e. Table 1 lists excited state properties of the lowest 4 states. As seen, the CT and LE excitation energies are similar in both structures. The LE state is found to be higher in energy by ca. 0.25 eV than the CT states. Its oscillator strength is quite strong, f ≈ 1.64, and depends on the position of the acceptor. In contrast, the oscillator strength of CT transitions differs substantially when passing from one state to another. For instance, its value for CT1 in complex I is larger by a factor of 5 than in II. There is a small charge separation in the LE states (q is 0.047 and 0.006 in structures I and II). In the CT states, q is always bigger than 0.94. In Table 1, we also compare electronic couplings estimated using eqn (2) with the reference data obtained by the FCD method.6,7 As seen there is good agreement between the obtained and the FCD values.
| Parameter | Complex I | Complex II | ||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | LE | CT1 | CT2 | CT3 | LE | CT1 | CT2 | CT3 |
a The two-state model is inaccurate because |cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ| < 0.7. γ| < 0.7.
|
||||||||
| E, eV | 1.605 | 1.332 | 1.355 | 1.363 | 1.621 | 1.367 | 1.382 | 1.389 |
| F | 1.6385 | 0.0480 | 0.0184 | 0.0076 | 1.6425 | 0.0091 | 0.0016 | 0.0096 |
| Q | 0.047 | 0.943 | 0.989 | 0.995 | 0.006 | 0.989 | 1.000 | 1.000 |
|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ| γ| |
0.998 | 0.930 | 0.878 | 0.591 | 0.950 | 0.666 | ||
| V, eqn (2), eV | 0.0495 | 0.0285 | 0.0178 | [0.0205]a | 0.0081 | [0.0190]a | ||
| V, eqn (4), eV | 0.0495 | 0.0265 | 0.0156 | [0.0121] | 0.0077 | [0.0127]a | ||
| V (FCD), eV | 0.0674 | 0.0246 | 0.0162 | [0.0291]a | 0.0055 | [0.0077]a | ||
We have generalized the Bixon–Jortner–Verhoeven formula to estimate the electronic coupling for photoinduced charge separation. Unlike the original equation, the modified formula may be applied also to systems with small energy gaps between the initial and final states. The quantities E and f required to estimate the coupling are directly available from quantum mechanical calculations and spectroscopic measurements. We have suggested to use the angle between the transition dipole moments of the states to decide whether the two-state approximation is applicable. Using TDDFT calculations we have demonstrated that the suggested formula gives reasonable estimates of electronic coupling for charge separation in heterojunctions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support of the Ministerio de Economía y Competitividad of Spain (project CTQ2015-69363-P), Generalitat de Catalunya (project number 2014SGR931), and Xarxa de Referència en Química Teòrica i Computacional.References
- M. Bixon and J. Jortner, in Electron Transfer-from Isolated Molecules to Biomolecules, ed. J. Jortner and M. Bixon, 1999, vol. 106, Pt 1, pp. 35–202 Search PubMed.
- J. L. Bredas, J. E. Norton, J. Cornil and V. Coropceanu, Acc. Chem. Res., 2009, 42, 1691–1699 CrossRef CAS PubMed.
- M. Gilbert and B. Albinsson, Chem. Soc. Rev., 2015, 44, 845–862 RSC.
- M. Rudolf, S. V. Kirner and D. M. Guldi, Chem. Soc. Rev., 2016, 45, 612–630 RSC.
- M. Pastore and F. De Angelis, in Multiscale Modelling of Organic and Hybrid Photovoltaics, ed. D. Beljonne and J. Cornil, 2014, vol. 352, pp. 151–236 Search PubMed.
- G. Bottari, M. A. Herranz, L. Wibmer, M. Volland, L. Rodriguez-Perez, D. M. Guldi, A. Hirsch, N. Martin, F. D'Souza and T. Torres, Chem. Soc. Rev., 2017, 46, 4464–4500 RSC.
- C. Curutchet and B. Mennucci, Chem. Rev., 2017, 117, 294–343 CrossRef CAS PubMed.
- T. Mirkovic, E. E. Ostroumov, J. M. Anna, R. van Grondelle, Govindjee and G. D. Scholes, Chem. Rev., 2017, 117, 249–293 CrossRef CAS PubMed.
- R. J. Cave and M. D. Newton, J. Chem. Phys., 1997, 106, 9213–9226 CrossRef CAS.
- A. A. Voityuk and N. Rosch, J. Chem. Phys., 2002, 117, 5607–5616 CrossRef CAS.
- J. E. Subotnik, S. Yeganeh, R. J. Cave and M. A. Ratner, J. Chem. Phys., 2008, 129 Search PubMed.
- M. Pavanello and J. Neugebauer, J. Chem. Phys., 2011, 135 Search PubMed.
- A. A. Voityuk, J. Phys. Chem. C, 2013, 117, 2670–2675 CAS.
- W. L. Liu, B. Lunkenheimer, V. Settels, B. Engels, R. F. Fink and A. Kohn, J. Chem. Phys., 2015, 143 Search PubMed.
- A. Kubas, F. Gajdos, A. Heck, H. Oberhofer, M. Elstner and J. Blumberger, Phys. Chem. Chem. Phys., 2015, 17, 14342–14354 RSC.
- A. A. Voityuk, J. Phys. Chem. A, 2017, 121, 5414–5419 CrossRef CAS PubMed.
- H. H. Chou, C. H. Yang, J. T. Lin and C. P. Hsu, J. Phys. Chem. C, 2017, 121, 983–992 CAS.
- J. Neugebauer, J. Chem. Phys., 2007, 126, 134116 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- M. Bixon, J. Jortner and J. W. Verhoeven, J. Am. Chem. Soc., 1994, 116, 7349–7355 CrossRef CAS.
- S. Gelinas, A. Rao, A. Kumar, S. L. Smith, A. W. Chin, J. Clark, T. S. van der Poll, G. C. Bazan and R. H. Friend, Science, 2014, 343, 512–516 CrossRef CAS PubMed.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06152h |
| This journal is © the Owner Societies 2017 |