Open Access Article
Open Access ArticleSearch for active and inactive ion insertion sites in organic crystalline materials
Harshan Reddy Gopidi abc,
Alae Eddine Lakraychiabc,
Abhishek A. Panchalabc,
Yiming Chenad,
Venkata Surya Chaitanya Kolluru
abc,
Alae Eddine Lakraychiabc,
Abhishek A. Panchalabc,
Yiming Chenad,
Venkata Surya Chaitanya Kolluru adh,
Jiaqi Wangae,
Ying Chen
adh,
Jiaqi Wangae,
Ying Chen af,
Jue Liu
af,
Jue Liu g,
Kamila Wiaderekae,
Maria K. Y. Chan
g,
Kamila Wiaderekae,
Maria K. Y. Chan ad,
Yan Yao*abc and
Pieremanuele Canepa
ad,
Yan Yao*abc and
Pieremanuele Canepa *abc
*abc
aEnergy Storage Research Alliance, Argonne National Laboratory, 9700 South Cass Avenue, Lemont, IL 60439, USA
bTexas Center for Superconductivity at the University of Houston, Houston, TX 77204, USA. E-mail: yyao4@central.uh.edu
cDepartment of Electrical and Computer Engineering, University of Houston, Houston, TX 77204, USA. E-mail: pcanepa@uh.edu
dCenter for Nanoscale Materials, Argonne National Laboratory, Lemont, IL 60439, USA
eX-ray Science Division, Argonne National Laboratory, Lemont, IL 60439, USA
fPhysical and Computational Sciences Directorate, Pacific Northwest National Laboratory, Richland, WA 99354, USA
gNeutron Sciences Directorate, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
hDepartment of Materials Science and Engineering, The Ohio State University, Columbus, OH 43210, USA
First published on 20th January 2026
Abstract
The position of mobile active and inactive ions, specifically ion insertion sites, within organic crystals, significantly affects the properties of organic materials used for energy storage and ionic transport. Identifying the positions of these atomic (and ionic) sites in an organic crystal is challenging, especially when the element has low X-ray scattering power, such as lithium (Li) and hydrogen, which are difficult to detect by powder X-ray diffraction. First-principles calculations, exemplified by density functional theory (DFT), are very practical for confirming the relative stability of ion positions in materials. However, the lack of effective strategies to identify ion sites in these organic crystalline frameworks renders this task extremely challenging. This work presents two algorithms: the (i) efficient location of ion insertion sites from extrema in electrostatic local potential and charge density (ELIISE), and the (ii) ElectRostatic InsertioN (ERIN), which leverage charge density and electrostatic potential fields accessed from first-principles calculations, combined with the Simultaneous Ion Insertion and Evaluation (SIIE) workflow. SIIE inserts all ions simultaneously—to determine ion positions in organic crystals. We demonstrate that these methods accurately reproduce known ion positions in 16 organic materials and identify previously overlooked low-energy sites in tetralithium 2,6-naphthalenedicarboxylate (Li4NDC), an organic electrode material, highlighting the importance of inserting all ions simultaneously, as in the SIIE workflow. These algorithms are also integrated with off-the-shelf machine learning potentials, yielding promising results comparable to first-principles findings.
1 Introduction
Understanding the structure of inorganic and organic-based materials containing electroactive elements, such as lithium (Li), sodium (Na), and zinc (Zn)1–14 is relevant for the development of the next generation of rechargeable battery technologies, which are prevalent in vehicular transportation, heavy-duty applications, and the supporting electrical grids.With the advent of the Rietveld methods,15–18 diffraction-based techniques using X-ray or neutron sources are commonly employed to determine the structures of energy materials. However, structural determinations through diffraction methods can be hindered by the weak scattering of X-rays by light elements, such as hydrogen and Li, which can partially occupy multiple crystallographic sites because of their high intrinsic mobility. In some cases, significant ion mobilities can cause the blurring of Bragg intensities.19,20 While neutron diffraction (ND) experiments enhance sensitivity to specific elements, e.g., light elements H and Li, ND experiments are significantly less available than X-ray diffraction analogues. ND still face challenges related to disorder, defects, and temperature-dependent site mixing.21
Organic electrode materials (OEMs) are promising for inexpensive and high-energy-density rechargeable batteries. Indeed, OEMs can provide three main benefits: (i) high material-level energy densities of 900–1000 kWh kg−1, (ii) a growing range of designs as shown by the variety of molecules studied so far, and (iii) potential benefits in sustainability and supply chains.6,22–28 One of the main challenges hindering the practical implementation of OEMs is a poor understanding of their structure–property relationships. The electrochemical reaction pathways of OEMs are typically interpreted based on simplistic molecular models, rather than describing these processes at the material level. These molecular-type OEM models are often paired with ex situ or operando XRD experiments, which frequently cannot reveal their underlying crystal structures and potential phase transformations.29–32 To date, only a handful of studies have resolved structures at both the charged and discharged (ion-containing) states of specific OEMs.23,33–37 For example, 1,4-benzoquinone (BQ) undergoes a phase transition from monoclinic (P21/c) to orthorhombic (P42/ncm) upon lithiation or sodiation, forming Li2BQ or Na2BQ,23,38 indicative of a biphasic reaction with substantial change in the molecular orientation, symmetry and the lattice parameters. By contrast, dilithium 2,6-naphthalene dicarboxylate (Li2NDC) retains a monoclinic (P21/c) structure upon complete lithiation (Li4NDC),34,35,39 following a biphasic intercalation reaction, with little change in molecular orientation and lattice parameters. However, distinguishing specific reaction mechanisms remains poorly understood in the OEM literature, mainly because structural data for the discharged state are scarce. In contrast, structural models for the charged state are often available.
A comprehensive understanding of OEM structures and their behavior across different ion content (i.e., different states of charge) remains crucial for bridging the gap between molecular-scale insights and crystalline materials with intrinsic periodicity. In general, this knowledge is essential for elucidating the physicochemical processes that govern electrochemical behavior, including phase transitions,23 voltage profiles,37 and mechanical degradation phenomena.36,40 However, accurate identification of the positions of mobile ions such as Li+, Na+, K+, Zn2+, and Mg2+, in organic crystalline frameworks, remains a significant experimental and computational challenge.29,33,35,36,41–49 This challenge arises primarily from the ample intermolecular space (void within the crystal framework) caused by weak intermolecular interactions, which are responsible for molecular assembly into organic molecular crystals.50,51 This results in numerous possible cation arrangements within the organic framework. Therefore, developing computational tools that accurately predict ion positions within the crystalline structures of organic materials is essential for breakthroughs and for unlocking hidden potential for rational materials design at the crystal level. While such approaches have been established for inorganic electrode materials,52–55 predictive search for ion sites in OEMs remains largely confined to the molecular scale and,46,56 to the best of our knowledge, has not yet been demonstrated for crystalline organic frameworks.
In this paper, we present two complementary computational algorithms and an ion insertion workflow for identifying the optimal active and inactive ion insertion sites within organic frameworks: (i) the Efficient Location of Ion Insertion Sites from Extrema (ELIISE) in electrostatic local potential and charge density, which identifies electrostatically stable ion positions by locating local extrema in electrostatic local potential and electronic charge density (CD) fields. (ii) The ElectRostatic InsertioN (ERIN), which, by following the electrostatic potential, iteratively places ions into electrostatically favorable regions of the unit cell until the entire cell volume is sampled. (iii) The Simultaneous Ion Insertion and Evaluation (SIIE), which inserts the ions simultaneously and evaluates to determine the correct structure. ELIISE and ERIN, in conjunction with SIIE, are applied with a library of 16 representative organic structures, illustrating their ability to automatically identify candidate ion sites within complex, flexible organic frameworks using limited computational resources. These predictions are subsequently refined using agnostic first-principles calculations, resulting in high-confidence ion positions, which provide crucial insights into ion coordination environments and other structural evidence. These predictive workflows establish a powerful toolkit for the systematic exploration of electroactive structures and their ion transport pathways, elucidating reaction mechanisms and guiding the rational design of materials for the development of competitive organic-based electrochemical devices, as well as the exploration of soft materials for other energy-storage applications.
2 Methods
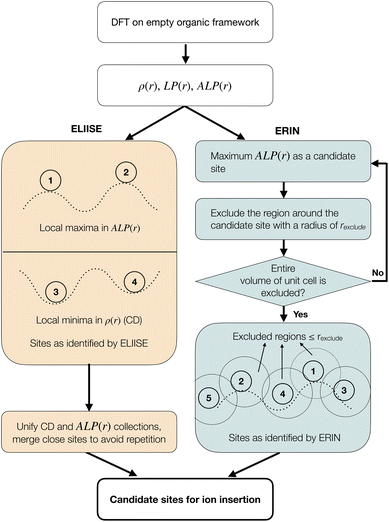
2.1. Finding candidate ion insertion sites in organic crystals: ELIISE and ERIN
Fig. 1 shows the identification of candidate ion sites using ELIISE and ERIN, which rely on the electronic charge density (CD, or ρ(r)) and the local electrostatic potential LP(r) of eqn (1), and the spherically averaged local potential, ALP(r), of eqn (2).| LP(r) = Vhartree(r) + Vionic(r); | (1) |
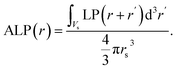 | (2) |
Both methodologies rely on an initial organic framework to compute LP(r) and CD. The choice of the initial organic framework is trivial when the organic framework of the discharged (ion-inserted) structure—i.e., the lattice parameters, the symmetry, and the atomic positions—is known. In such cases, only the precise determination of ion positions is necessary, as is often the case with lithium; here, ELIISE serves as an appropriate tool. In contrast, the more common scenario is when only the organic framework of the charged (ion-removed) phase is known. Under these circumstances, ERIN is recommended (see Discussion section for more details) as employing ELLISE may result in unreliable outcomes.
2.2. The efficient location of ion insertion sites from extrema in electrostatic local potential and charge density (ELIISE) method
The ELIISE method identifies candidate ion sites using both the CD and the spherically averaged local potential ALP(r), defined in eqn (2), within the empty (i.e., without any mobile species) organic framework from the discharged state.Following the ELIISE workflow in the left part of Fig. 1, the local potential and electronic CD are initially computed by performing a first-principles calculation without changing the atom positions (or changing the volume or cell shape of the material) of the empty organic framework. Subsequently, ELIISE identifies candidate active sites in an organic framework by identifying the local maxima and the local minima in the ALP(r) the CD fields, respectively. Fig. 1 shows a schematic diagram of the local minima in CD and local maxima in the ALP(r), which are used to identify candidate sites. We have concluded that a spherical average of the LP(r) provides the best predictions in terms of candidate ion sites, as it accounts for the finite size of inserted ions. Here, the empirical covalent radii of atoms by Slater57 appear to be a reliable option for defining this ion size. When different types of active species are involved in ion insertion, we imposed the empirical radius of the smaller atom for spherical averaging of the local potential. The candidate sites identified by both the CD and the ALP(r) descriptors are combined into a single collection. To avoid repetition of sites, spatially close sites are merged by calculating the geometric mean of their coordinates, as indicated in Fig. 1. The resulting sites are then ordered by their electrostatic stability, from most to least favorable, as determined by the ALP(r).
Large values of ALP(r) indicate regions that are electrostatically favorable for positively charged ions, typically near more electronegative (usually negatively charged) atoms within the crystal structure. Therefore, local maxima in ALP(r) naturally point to potential cation sites. Similarly, local minima in the CD usually occur in voids near more electronegative atoms. It is reasonable to assume that these electronegative atoms strongly attract electron density, leading to electron-deficient regions nearby, which are likely to form local minima in the charge density. Therefore, these minima in CD often correspond to favorable coordination environments for cations. An exception to this trend becomes evident when local minima occur within large structural voids, which are common in organic crystals and nanoporous materials. These voids may be too far from the organic framework to provide any stabilizing interactions for inserted ions. These situations can lead to surprisingly high Coulomb energies. To address this potential issue during the site search in both ELIISE and ERIN, we set cutoff distance thresholds to exclude regions that are either closer than the specified distance (e.g., 1.5 Å) or farther than ∼3 Å from atoms in the organic framework.
2.3. The ElectRostatic InsertioN (ERIN) method
In contrast to ELIISE, ERIN only requires the LP(r) (eqn (1)) of the organic framework, obtained from first-principles calculations. The ERIN approach in the right part of Fig. 1 only uses the spherically averaged local potential ALP(r) (eqn (2)) to explore electrostatic energy landscapes and systematically generates sparsely spaced candidate ion sites in a decreasing order of electrostatic favorability within the given unit cell. ERIN identifies and selects the site with the maximum ALP(r) value. Subsequently, ERIN excludes a spherical region within a user-defined radius, rexclude (e.g., 2 to 3 Å), around this site from future searches. Then, ERIN repeats the search for the site with the next highest value of ALP(r) to select as a candidate. This process is repeated iteratively until the entire volume of the unit cell is scanned systematically and excluded. The site search is performed independently within each symmetry-distinct region of the unit cell to identify candidate sites in all possible Wyckoff positions.2.4. Simultaneous ion insertion and evaluation (SIIE) workflow for candidate site insertion
Once ELIISE or ERIN identifies the candidate sites, the next step is to determine the optimal combination of sites that yield the expected stoichiometry of the system and is energetically viable. For this purpose, we introduce the Simultaneous Ion Insertion and Evaluation (SIIE) workflow, in which ions are introduced simultaneously within the organic framework to achieve the desired stoichiometry, as opposed to the sequential insertion method, where ions are inserted one at a time.52,58 In the SIIE workflow, if the organic framework of the discharged structure is known, its atoms are kept fixed during ion insertion, with only inserted ions and decorating hydrogen atoms (whose positions are typically unknown from standard XRD experiments) allowed to change. Otherwise, if only the organic framework of the charged phase is known, then both the ions and the organic framework are allowed to relax completely.As shown in Fig. 2a, SIIE uses the candidate ion insertion sites from the ELIISE or ERIN methods discussed in the previous sections as inputs. While ELIISE and ERIN provide sets of candidate ion positions, they do not determine the final configuration of ions in the discharged structure. In real systems, multiple symmetry-distinct sites may be occupied simultaneously, and therefore, the correct discharged state often results from a specific combination of these candidate sites.
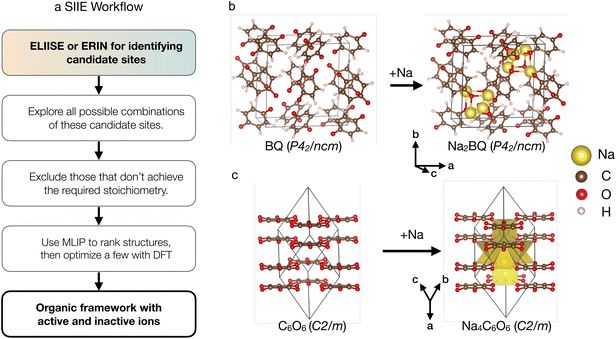 | ||
| Fig. 2 Workflow for the Simultaneous Ion Insertion and Evaluation (SIIE) method (a) and its application in two OEMs (b) disodium 1,4-benzoquinone (Na2BQ) and (c) tetrasodium rhodizonate (Na4C6O6). Combining SIIE with ELIISE, the Na-ion positions are located in two exemplary OEMs.38,62 | ||
Finding the right combination of candidate sites is challenging due to the large number of unique possibilities. Note that the number of possible combinations of predicted ion sites that produce the target ion content can grow combinatorially, in the range 10 to 106, which typically makes direct DFT evaluation of all combinations computationally infeasible.
To address this challenging task, we incorporate a machine learning interatomic potential (MLIP), such as MACE or Orb-v3,59–61 to screen thousands of configurations efficiently. Here, we use MACE to identify and remove high-energy structures. More details on how MACE and DFT are combined in the SIIE workflow are provided later (see Computational details section).
3 Results
3.1. Case studies: implementing the suggested workflows on example systems
To demonstrate the effectiveness of these algorithms, we showcase the application of the ELIISE (ERIN) + SIIE workflow to several model organic compounds. The accuracy of ELIISE + SIIE is verified by “rediscovering” the Na-ion sites in two known fully sodiated compounds: (i) the disodium 1,4-benzoquinone (P42/ncm, Na2BQ),38 and (ii) the tetra-sodium rhodizonate with formula Na4C6O6 (C2/m).62 Similarly, starting from the known dilithium 2,6-naphthalenedicarboxylate (P21/c, Li2NDC), using ERIN + SIIE, we predict Li positions in Li4NDC (tetra-lithium 2,6-naphthalenedicarboxylate),35,63 which contains two additional Li sites per formula unit (f.u.).Na4C6O6 (C2/m)62 is an oxocarbon-salt-based layered compound; it is a planar conjugated ring with six carbonyl oxygens, known to undergo a two-to-four electron reduction with Na.36 To test the ELIISE method, we first remove all Na atoms from Na4C6O6 and perform a static DFT calculation, at the volume and geometry available in literature, to calculate the electronic charge density and local electrostatic potential fields, and subsequently apply the ELIISE algorithm to find the possible sites for Na-ions (as described in Methods section 2.2).
The ELIISE algorithm yields nine symmetry-distinct Na sites with different multiplicities (Table S2). These candidate sites from ELIISE are then “funneled” into the SIIE workflow. We examine all possible combinations of sites from these nine symmetry-distinct candidates that produce the desired Na4C6O6 stoichiometry. This yields only 59 unique sodium configurations, for which we perform DFT and MACE optimizations to identify the most plausible Na-atom positions. To quantify the prediction accuracy of ELIISE + SIIE, we use a metric called the maximum atom displacement error (MADE), which is defined in eqn (3):
| MADE = max{|ri − rrefi|; i ∈ all active, inactive species} | (3) |
In practice, we interpret MADE values ≤ ∼0.4 Å as indicating correct predictions for all ions in the structure, while MADE values ≥ ∼0.4 Å suggest that at least one ion site has been predicted incorrectly. Among the predicted structures for Na4C6O6, the lowest-energy structure of Fig. 2c displays a MADE of ∼0.026 Å, indicating excellent agreement with the structure previously reported in the literature.62
In the second example, we investigate the structure of disodium 1,4-benzoquinone, Na2BQ38 (Fig. 2b), and the fully reduced (sodiated) form of a para-benzoquinone, i.e., BQ. In Na2BQ, the Na atom positions are available from the literature.38 In Fig. 2b, the Na2BQ features a highly open organic framework with large voids, making a brute-force search of the potential Na positions computationally expensive. Using ELIISE, we identify four symmetrically distinct candidate sites. Applying the SIIE workflow, we evaluate all combinations of these four symmetry-distinct ions that produce the stoichiometry of Na2BQ. This step yields only three valid configurations, which we used for further DFT structural relaxations (keeping the volume and shape fixed to the experimental structure of Na2BQ). The most stable structure with the lowest DFT total energy singled out with ELIISE + SIIE, shown in Fig. 2b, exhibits a MADE of ∼0.024 Å, demonstrating excellent agreement with the experimental Na positions.38
We tested our methods on a third structure, Li4NDC, which shares structural similarities with its precursor, Li2NDC,64 with 2 Li atoms per molecule. Prior experimental studies indicated that the NDC organic framework largely remains unchanged upon reaction with Li. Two structural arrangements of Li species, model 1 and model 2 (Fig. 3), have been proposed for Li4NDC.63 Models 1 and 2 preserve Li-ions in tetrahedral coordination sites as observed in Li2NDC64 (shown as Li1 in Fig. 3) and introduce new Li positions (shown as Li2 in Fig. 3), approaching composition Li4NDC (four Li atoms per molecule).
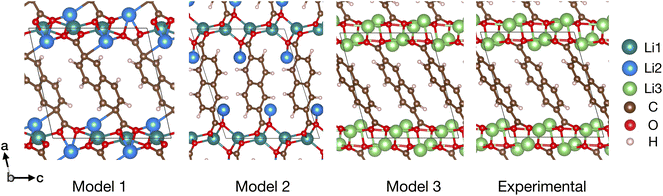 | ||
| Fig. 3 Li4NDC structures: model 1, model 2, model 3, and experimentally refined from single-crystal XRD.35 Different crystallographic Li sites are shown. | ||
Using ERIN with SIIE workflow, we predict the Li positions in Li4NDC based on the organic framework of Li2NDC as input. We recovered models 1 and 2, described in the literature. A close inspection of model 1 and model 2 reveals that these two structures reported in ref. 63 are different in the relative orientation of NDC molecules, as displayed in Fig. 3. However, this striking contrast is not highlighted in ref. 63, which suggests that model 1 and model 2 differ only in Li distribution but share the same molecular framework.
In addition to models 1 and 2, we identified a third model, model 3, as the lowest-energy structure, as determined by DFT minimization (and MACE). In model 3, the tetrahedral sites reported for Li2NDC are unoccupied, and all the Li atoms assume new crystallographic positions (collectively indicated as Li3 in Fig. 3), which are localized near the inorganic layer of the organic framework, consisting of oxygen atoms in NDC. These newly identified Li-atom positions in model 3 yield an electrostatically favorable arrangement of Li atoms relative to models 1 and 2 at the same composition. Quantitatively, DFT total-energy comparisons indicate that model 3 is energetically favored over models 1 and 2 by ∼100 meV per Li4H6C12O4 and ∼440 meV per Li4H6C12O4, respectively.
Indeed, model 3 is in excellent agreement with a recent study (appeared while drafting this paper) that used single-crystal XRD to refine the structure of Li4NDC.35 Because ERIN uses the organic framework of the charged state as input and optimizes all atomic positions, the MADE metric—measuring the prediction error in active species positions—appears unsuitable. Instead, a simple qualitative measure of similarity between two structures can be obtained by using the StructureMatcher (with the default parameters) as implemented in the Pymatgen library.65 Here, StructureMatcher indicated that model 3 qualitatively matches the recently reported experimental structure of Li4NDC.35 Alternatively, Table S4 shows a close match between the lattice parameters and atomic positions of experimental and predicted structures.
These three case studies, discussed in the previous paragraphs, collectively demonstrate the robustness of the ELIISE and ERIN methods when integrated with the SIIE workflow in accurately identifying ion positions across various organic electrode materials.
3.2. Assessing the accuracy of the ELIISE + SIIE approach
To assess the accuracy of the ELIISE + SIIE approach, we apply it to a diverse set of organic materials (16 in total) for which the organic framework and ion positions of the crystal structure are known from literature. Using MADE (eqn (3)) as a similarity metric we evaluate the performance of the ELIISE method with the SIIE workflow across 16 organic systems. These structure organic electrode materials, such as Li2NDC and Li4NDC (di and tetra lithium 2,6-naphthalene dicarboxylate),64 Li2BDC and Li4BDC (di and tetra lithium 1,4-benzene dicarboxylate),66 Li2BPDC (dilithium biphenyl dicarboxylate),67 Li2Mg-p-DHT (magnesium(2,5-dilithium-oxy)-terephthalate),33 Na2BQ (disodium hydroquinone),38 Na2C6O6 (disodium rhodizonate),68 and Na4C6O6 (tetra sodium rhodizonate),62 as well as other selected structures (see Table S1) were obtained from crystallographic databases, the Cambridge Crystallographic Data Centre (CCDC)69 and the Inorganic Crystal Structure Database (ICSD).70As shown in Fig. 4a, the lowest-energy structure identified by the SIIE workflow using ELIISE correctly reproduces the known ion positions in all tested cases, as measured by MADE, which is always ≤0.4 Å. Furthermore, Fig. 4b demonstrates that using a pre-trained machine-learning interatomic potential (MLIP), specifically MACE (used only to optimize the ion positions), yields correct predictions of ion positions, with MADE values consistently below ∼0.4 Å. This suggests that DFT-level structural relaxation may not be strictly necessary to determine the general location of inserted ions, thereby substantially reducing computational costs. Fig. S1 presents a similar assessment, but with predictions generated using ERIN + SIIE instead of ELIISE + SIIE, and only MACE was employed for optimizing ion positions. The MADE values in Fig. S1 show that ERIN + SIIE also accurately predicted the positions of all inserted ion sites for all 16 tested organic systems.
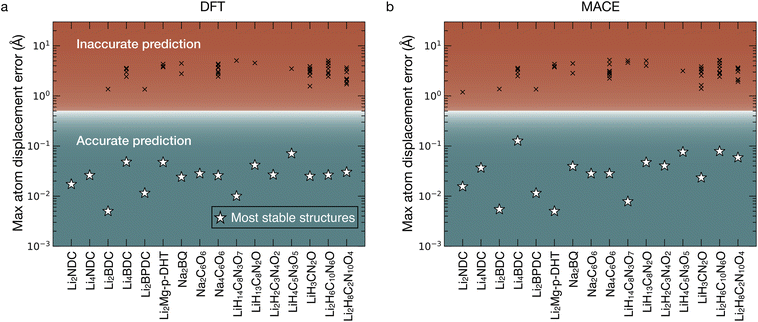 | ||
| Fig. 4 Accuracy of the predicted active ion positions with the proposed SIIE workflow and ELIISE. MADE (eqn (3)) values determined after optimization of ionic positions with (a) first-principles DFT and (b) the machine learned potential MACE. Stars indicate the most stable (lowest total energy) ion arrangements in each organic structure, and crosses indicate the thermodynamically unfavorable (high energy) structures. Details of reference structures reported in the literature are in Table S1. | ||
4 Discussion
Predicting ion positions in “soft” crystalline materials, such as organic electrode materials, remains a significant challenge due to the combination of large free volumes, weak intermolecular forces, and the dynamic nature of ion coordination. In this paper, we have developed two new methodologies, ELIISE and ERIN, and an ion insertion workflow, SIIE, designed to identify ion-insertion sites in organic structures. These include metal atoms, such as Na, Zn, and Mg, as well as light elements, for example, Li. Here, we discuss the advantages and disadvantages of implementing the ELIISE and ERIN algorithms to resolve unknown ion positions in crystal structures, where traditional structural techniques fail.ELIISE uses both the electronic charge density (CD) and the local electrostatic potential LP(r) derived from first-principles calculations of the empty organic framework. In combination, the CD and the LP(r) are used to find candidate crystallographic sites for light elements in these materials. However, since the CD and the LP(r) are intrinsically linked (as the latter is derived from atomic positions and the electronic charge density distribution), the independent use of the CD and the LP(r) often arrives at similar predictions for candidate ion sites. Since ELIISE directly identifies coordinating environments—regions surrounded by electronegative atoms in the organic frameworks—ELIISE appears most effective for systems in which the organic framework structure of the discharged (ion-inserted) phase is known. This signifies that prior experiments determining the space group, lattice constants, and atom positions of the organic framework (excluding the mobile ions) must be available. In some sense, this limits the capabilities of the ELIISE strategy. For example, if only the charged-phase structure of an organic system is available and significant structural changes and/or phase transitions are expected upon electrochemical reactions, using ELIISE may yield unreliable results.
To address the apparent limitation of ELIISE, we have developed an alternative method called ERIN. ERIN generates a sparse set of points that cover all possible Wyckoff sites, ranked from the electrostatically lowest-energy sites to the highest-energy sites. Therefore, ERIN should be applied when the structure of the organic framework, whose ion-inserted/discharged phases remain unknown. In such cases, the charged (empty) structure of the materials can be used as a starting point, assuming the unit cell of the pristine organic crystal shape and most of the symmetry remains unchanged or structural modifications occur gradually (for example, a displacive phase transition) upon reaction with Li (or sodium), which is typical of intercalation materials.
ELIISE identifies stationary sites (i.e., local minima) by populating the energy landscape; these sites are expected to be stationary points for ions in the potential created by the anion framework. In contrast, in ERIN, the identified sites are not necessarily located at energy minima – non-stationary sites, such as saddle points, on the potential energy surface, and may be mobile during structural relaxation. These non-stationary sites can perturb the organic framework during relaxation and promote structural changes that lead to a more stable discharged structure.
Even if the discharge phase does not involve phase transitions, the specific coordination environments and lattice parameters required to accommodate mobile metal atoms in the discharged organic framework may not be available in the charged organic framework. ERIN systematic electrostatic screening helps identify plausible insertion sites that would be hard to locate with ELIISE alone. Note, however, that ERIN predicts more candidate sites than ELIISE, resulting in a greater number of possible ion-vacancy arrangements to evaluate in the SIIE workflow.
Our study has focused on identifying plausible sites for cation insertion; however, with suitable modifications, these algorithms can also be used to locate anion positions in a crystal structure. For example, in the case of the ELIISE method, local minima in the ALP(r) should be used instead of local maxima. The approach remains the same when using CD. In ERIN, instead of selecting the maximum in the ALP(r) as a candidate site, the minimum in the ALP(r) should be chosen.
At its core, ERIN uses the Coulomb electrostatic potential to model the energy landscape and identify sites generated from electronic charge densities obtained from first-principles calculations. Other methods, such as machine learning interatomic potentials61,71,72 or bond valence sums73 appear viable for modeling and developing the potential energy landscape for ion insertion.
It is important to comment on some choices made in developing the averaged local potential, ALP(r), which uses a spherical averaging radius set in advance. We have observed that ion positions predicted from ALP(r) are generally insensitive to the precise value of this radius. However, because of the radius ionic size of the predicted sites, even a ∼10% change can modify the number of local extrema in ALP(r) and, consequently, the set of candidate sites identified by ELLISE. For ERIN, changes in the spherical averaging radius directly affect the predicted site positions by altering the underlying energy landscape. This sensitivity is not problematic, as ERIN is intended to generate a sparse set of representative ion sites rather than an exhaustive list. The exclusion radius in ERIN determines the total number of predicted ion sites. Increasing the radius reduces the number of distinct sites by merging nearby candidates. Thus, tuning the radius minimizes the number of ion combinations, increasing computational efficiency in the search. However, because of the MACE and DFT optimization steps, minor deviations from reasonable values are unlikely to affect the accuracy of ion-position predictions.
In general, when testing the ELIISE and ERIN algorithms on 16 previously known structures (Fig. 4 and S1), we demonstrated that these algorithms, in combination with the SIIE workflow, provide a reliable and systematic approach for accurately predicting unknown ion positions in organic frameworks.
Another important aspect is the integration of machine learning interatomic potentials (MLIPs), such as MACE, into the SIIE workflow. In principle, ERIN and ELIISE are applicable together with any foundational MLIP model, including M3GNET, CHGNET, and ORB-3, among others.61,71,72 This hybrid MLIP-DFT approach appears to be viable, significantly reducing the computational burden of exploring vast combinatorial site occupancies while providing sufficient accuracy in predicting ion positions. Furthermore, the ability of MLIPs to screen thousands of candidate configurations before subsequent, more accurate but computationally intensive refinements with first-principles calculations highlights a scalable pathway for high-throughput exploration of ion-insertion chemistries in soft systems, such as organic crystals, porous systems, metal–organic frameworks, and larger molecules with biological relevance.
In this vein, we have tested MACE predictions against DFT predictions for the same systems shown in Fig. 4. We have observed that, when the organic framework is fixed at the known discharged structure, identifying the structure with the lowest energy and correct ion arrangements using (MADE) with a prediction error within a tolerable range of 0.4 does not require DFT; foundational out-of-the-shelf MLIPs appear suited for this task. Here, we have only tested MACE.59,60 However, fine-tuning the foundational MLIPs with system-specific DFT data can provide even more accurate results.
The SIIE workflow appears limited when dealing with either amorphous structures or extremely large unit cells with low or no symmetry. In these cases, the number of possible ion combinations can be in the order of 104 to 106, requiring significant computational resources to evaluate total energies across all configurations, even with MACE. In this context, we had relied on the fact that candidate sites are ranked in decreasing order of electrostatic favorability, as indicated by the averaged local potential. Unfavorable sites are systematically excluded during the generation of ion combinations; this removal process continues until the number of valid ion combinations falls below the preset threshold (∼103). Developing more efficient yet accurate machine-learning potentials is a promising approach to address this issue in amorphous compositions, and considerable effort is currently devoted to this area.74–77
Aside from ELIISE and ERIN, the simultaneous insertion of ions, implemented in the SIIE workflow, is also essential for accurately finding discharged structures, as illustrated by the case study of Li4NDC. In Li4NDC, we proposed model 3, which yields the lowest DFT total energy (Fig. 3), and is lower than that of the previously proposed models 1 and 2.63 Before this work,55,63 other strategies, such as sequential insertion methods, have been proposed.52,58 In the sequential approach, a new model is created by inserting an atom at a new position within the unit cell, and the structure is then optimized. This process is repeated until the desired stoichiometry is achieved, thereby identifying a representative global minimum. The sequential approach can lead to incorrect selection of stable candidates because ions may become trapped in local minima of the potential energy surface.
Organic molecular crystals often exhibit polymorphism, resulting from different packing arrangements of the same molecule, including metastable ones.78,79 However, once the organic framework is established, ions are expected to occupy the most energetically favorable positions, as observed in all cases shown in Fig. 4, thus partially ignoring metastable effects. Therefore, the proposed workflows are effective when the discharged organic frameworks are known. When the discharge state is unknown, as in Li4NDC (where only the charged phase is known) lattice constants, crystal shape, and positions are allowed to vary during ion insertion. This can cause significant structural changes and different packing arrangements, potentially leading to the prediction of metastable or energetically favorable phases.
Current methods are limited because they either rely on the organic framework of the discharged structure or assume that the symmetry and unit cell of the discharged phase match those of the charged phase. In the case of Li4NDC, determining the optimal ion positions, starting from Li2NDC, was straightforward because the organic framework remained essentially unchanged during lithiation, i.e., the symmetry and unit cell of Li4NDC were commensurate with those of Li2NDC.
However, this is not the case for most systems. For example, when Li2BDC is lithiated to form Li4BDC, a symmetry reduction is observed.35 It involves doubling the unit cell along the stacking direction of the organic layers, accompanied by changes in the organic framework.35 Consequently, attempting to predict ion positions in Li4BDC by starting directly from the Li2BDC structure may produce an incorrect model structure. Na2-BQ and Na4C6O6 exemplify this type of structural change, undergoing phase transformations with altered unit cells (and symmetries) during discharge. Beyond the organic molecular crystals studied here, ion insertion has been shown to induce additional distortions, including octahedral tilting, phase separation, cell collapse, loss of crystallinity, and even phase changes, as observed in hybrid organic–inorganic metal halides and redox-active metal–organic frameworks.80–85
These cases highlight a broader challenge: it is often unclear whether a significant phase transition occurs during lithiation (or sodiation). When this uncertainty arises, a practical approach is first to predict ion positions based on the charged structure (i.e., the host in its oxidized or delithiated form). The resulting model can then be compared with experimental data, such as XRD or ND; if the simulated patterns are similar to the experimental patterns, the predicted structure can serve as a solid starting point for refinement.
However, if the comparison shows significant differences, it becomes necessary to explore alternative structural hypotheses. In such cases, one must generate and assess a set of candidate organic framework motifs to serve as initial models in the ERIN + SIIE workflow. Developing systematic methods for constructing and testing these organic framework variations appears crucial for reliably understanding the structural complexity of ion insertion in molecular crystals.
The issue of significant structural rearrangement or symmetry breaking is directly related to the problem of locating the global minimum on a structure's potential energy surface; for this, all possible structures must be examined, which entails solving global optimization problems. This goes beyond the simple task of determining ion positions discussed in the current work. Several strategies for identifying global minima in materials space have been proposed, including genetic algorithms, as implemented in USPEX,86–88 and particle swarm optimization, as implemented in CALYPSO.89–91 Recently, generative models aided by machine learning have emerged as an effective avenue for efficiently exploring complex potential energy landscapes and chemical spaces, such as those of organic/molecular crystals.92–95 These strategies are claimed to predict the positions of the organic framework and ions, thereby enabling a complete materials structure model.
For systems that amorphize during discharge, a realistic description of ion positions will ultimately require combining our structure-generation strategy with total-scattering measurements, melt-quench-type molecular dynamics (with machine learning), and possibly reverse Monte Carlo approaches to produce chemically meaningful, though not uniquely determined, models of the disordered Li environments.96–103
Besides XRD and ND for determining the structures of organic materials, solid-state nuclear magnetic resonance (ss-NMR) crystallography is another valuable tool that offers structural insights.104,105 The nascent application of ss-NMR in conjunction with first-principles calculations, termed NMR crystallography, has been used to establish the structure of functional materials.106
5 Conclusions
In summary, we have developed a computational framework for accurately predicting ion positions in organic materials, utilizing DFT-derived electrostatic and charge density fields with the ELIISE and ERIN algorithms and the SIIE workflow.Through case studies of Na4C6O6, Na2BQ, and Li4NDC, we showed that ELIISE and ERIN methodologies can reproduce ion positions known from the literature with sub-angstrom accuracy. Additionally, we demonstrate that these methodologies can uncover new, energetically favorable structural models that can improve our understanding of experimental observations.
We have demonstrated that computationally intensive DFT predictions are not a strong requirement for accurately identifying ion positions, and we have shown that machine-learned potentials provide sufficient accuracy for large-scale screening tasks.
Our results demonstrate that ELIISE and ERIN, combined with SIIE, are powerful and can significantly improve, if not augment, the limits of traditional structural characterization techniques. The framework proposed in this paper offers a pathway toward deeper mechanistic insights and the rational design of organic materials for next-generation functional materials. Moreover, MLIPs can efficiently screen thousands of candidate configurations initially, before performing more precise but computationally expensive refinements with first-principles methods. This approach offers a scalable pathway for high-throughput exploration of ion-insertion chemistries in soft systems, including organic crystals, porous materials, metal–organic frameworks, and larger biologically relevant molecules.
6 Computational details
All first-principles calculations presented in this work were performed using the density functional theory formalism, as implemented in the Vienna Ab initio Simulation Package (VASP).107–109 The PAW potentials describe the core electrons. Perdew, Burke, and Ernzerhof (PBE)110 was used to approximate the unknown DFT exchange and correlation XC functional. To account for van der Waals interactions, the empirical D3 method proposed by Grimme and collaborators, with Becke–Johnson (BJ) damping, was used.111,112VASP inputs prepared for geometry optimization and energy calculations closely followed the MITRelaxSet113 as available in pymatgen.65 The kinetic energy cutoff for the plane waves was set to 520 eV, and the total energy was converged to 10−5 eV per cell. Geometries (coordinates, volumes, and cell shapes) were considered converged when the forces on all atoms are lower than 0.05 eV Å−1. A Γ-centered Monkhorst–Pack114 grid with a density of 25 k-points per Å−1 for all systems. With these DFT settings, local potentials are computed as the sum of Ewald and Hartree parts, excluding the Exchange and Correlation (XC) contributions.
To reduce the number of structures for DFT optimization, MACE-MATPES-PBE-0 a machine-learned foundational model, based on MACE,59,60 with PFP-based PyTorch implementation of DFT-D3,111,112,115 was used to evaluate static total energy and/or optimize ion positions. Structural relaxations are carried out until the forces are converged below 0.03 eV Å−1.
When MACE is implemented in the SIIE workflow, it is used as follows:
(1) Generate all possible ion combinations. If the number of combinations exceeds a preset limit (∼103), they can be reduced systematically by excluding electrostatically unfavorable sites in ELIISE or ERIN before generating possible ion combinations.
(2) Use MACE to evaluate all the generated combinations.
(3) Select approximately ∼102 of the lowest-energy candidate structures for optimization of ion positions using MACE.
(4) From these structures, we select approximately 10 distinct lowest-energy structures for subsequent accurate DFT optimization of the atomic positions.
This hybrid approach, which combines the computational speed of MACE-based MLIPs with the accuracy of DFT, enables us to successfully identify the correct atomic configurations in organic frameworks with substantial structural complexity.
Author contributions
H. R. G.: conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, writing – original draft, writing – review & editing. A. E. L.: data curation, discussion, writing – original draft, writing – review & editing. A. A. P.: discussion, writing – review & editing. Y. C.: discussion, writing – review & editing. V. S. C. K.: discussion, writing – review & editing. L. J.: discussion, writing – review & editing. J. W.: discussion, writing – review & editing. Y. C.: discussion, writing – review & editing. K. W.: discussion, writing – review & editing. M. K. Y. C.: discussion, writing – review & editing. Y. Y.: funding acquisition, supervision, discussion, writing – review & editing. P. C.: conceptualization, funding acquisition, investigation, project administration, resources, supervision, visualization, writing – original draft, writing – review & editing.Conflicts of interest
Y. Y. has equity interests in LiBeyond, LLC and Solid Design Instruments, LLC. The University of Houston reviewed and approved his relationship in compliance with its conflict-of-interest policy. The remaining authors declare no competing interests.Data availability
Computational data related to this study, including Python scripts, input, and output files of the simulations, are available on GitHub at https://github.com/caneparesearch/data_site_finder.Supplementary information (SI) is available. See DOI: https://doi.org/10.1039/d5sc07602a.
Acknowledgements
This work is funded by the Energy Storage Research Alliance (ESRA) (DE-AC02-06CH11357), an Energy Innovation Hub funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences. We are grateful to the Research Computing Data Core at the University of Houston for assistance with the calculations presented in this work. This research utilized resources of the National Energy Research Scientific Computing Center (NERSC), a Department of Energy User Facility, supported by the NERSC award BES-ERCAP0031978. P. C. acknowledges the Welch Foundation under grants L-E-001-19921203, and E-2227-20250403. Work performed at the Center for Nanoscale Materials, a U.S. Department of Energy Office of Science User Facility, was supported by the U.S. DOE, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357.References
- A. E. Lakraychi, F. Dolhem, A. Vlad and M. Becuwe, Adv. Energy Mater., 2021, 11, 2101562 CrossRef CAS.
- Y. Zhang, P. Apostol, D. Rambabu, X. Guo, X. Liu, X. Lin, H. Xie, X. Chen, K. Robeyns, J. Wang, J. Wang and A. Vlad, Chem. Sci., 2025, 16, 1819–1825 RSC.
- Y. Lu and J. Chen, Nat. Rev. Chem., 2020, 4, 127–142 CrossRef CAS PubMed.
- H. Dai, L. Guan, M. Mao and C. Wang, Nature Reviews Clean Technology, 2025, 1, 493–510 Search PubMed.
- L. Zhao, A. E. Lakraychi, Z. Chen, Y. Liang and Y. Yao, ACS Energy Lett., 2021, 6, 3287–3306 Search PubMed.
- P. Poizot, J. Gaubicher, S. Renault, L. Dubois, Y. Liang and Y. Yao, Chem. Rev., 2020, 120, 6490–6557 Search PubMed.
- V. A. Blatov, L. Carlucci, G. Ciani and D. M. Proserpio, CrystEngComm, 2004, 6, 377–395 RSC.
- V. A. Blatov, A. P. Shevchenko and V. N. Serezhkin, J. Appl. Crystallogr., 2000, 33, 1193 CrossRef CAS.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586 CrossRef CAS.
- P. Canepa, G. Sai Gautam, D. C. Hannah, R. Malik, M. Liu, K. G. Gallagher, K. A. Persson and G. Ceder, Chem. Rev., 2017, 117, 4287–4341 CrossRef CAS.
- Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang, T. Chen, Z. Lun, Z. Rong, K. Persson and G. Ceder, Chem. Rev., 2021, 121, 1623–1669 CrossRef CAS PubMed.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Chem. Rev., 2014, 114, 11636–11682 Search PubMed.
- C. Delmas, Adv. Energy Mater., 2018, 8, 1703137 CrossRef.
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- R. B. Von Dreele and A. K. Cheetham, Proc. R. Soc. London, Ser. A, 1974, 338(1614), 311–326 Search PubMed.
- A. K. Cheetham and R. B. Von Dreele, Nat. Phys. Sci., 1973, 244, 139–140 CrossRef CAS.
- T. Runčevski and C. M. Brown, Cryst. Growth Des., 2021, 21, 4821–4822 CrossRef.
- D. S. Wimmer, K. M. Rießbeck, M. Seibald, D. Baumann, K. Wurst, G. Heymann and H. Huppertz, Dalton Trans., 2022, 51, 16465–16478 RSC.
- H. Buschmann, J. Dölle, S. Berendts, A. Kuhn, P. Bottke, M. Wilkening, P. Heitjans, A. Senyshyn, H. Ehrenberg, A. Lotnyk, V. Duppel, L. Kienle and J. Janek, Phys. Chem. Chem. Phys., 2011, 13, 19378 RSC.
- E. H. Kisi and C. J. Howard, Applications of Neutron Powder Diffraction, Oxford University Press, 2008 Search PubMed.
- T. Chen, H. Banda, L. Yang, J. Li, Y. Zhang, R. Parenti and M. Dincă, Joule, 2023, 7, 986–1002 CrossRef CAS.
- Y. Lu, H. Han, Z. Yang, Y. Ni, Z. Meng, Q. Zhang, H. Wu, W. Xie, Z. Yan and J. Chen, Natl. Sci. Rev., 2024, 11, nwae146 CrossRef CAS PubMed.
- H. Zhang, Y. Gao, X. Liu, Z. Yang, X. He, L. Li, Y. Qiao, W. Chen, R. Zeng, Y. Wang and S. Chou, Adv. Funct. Mater., 2022, 32, 2107718 CrossRef CAS.
- H. Dai, L. Guan, M. Mao and C. Wang, Nature Reviews Clean Technology, 2025, 1, 493–510 CrossRef.
- Y. Liang and Y. Yao, Joule, 2018, 2, 1690–1706 CrossRef CAS.
- J. Kim, Y. Kim, J. Yoo, G. Kwon, Y. Ko and K. Kang, Nat. Rev. Mater., 2022, 8, 54–70 CrossRef.
- A. Innocenti, H. Adenusi and S. Passerini, InfoMat, 2023, 5, e12480 Search PubMed.
- J. Wang, A. E. Lakraychi, X. Liu, L. Sieuw, C. Morari, P. Poizot and A. Vlad, Nat. Mater., 2021, 20, 665–673 Search PubMed.
- A. Jouhara, N. Dupré, A.-C. Gaillot, D. Guyomard, F. Dolhem and P. Poizot, Nat. Commun., 2018, 9, 4401 CrossRef PubMed.
- L. Sieuw, A. E. Lakraychi, D. Rambabu, K. Robeyns, A. Jouhara, G. Borodi, C. Morari, P. Poizot and A. Vlad, Chem. Mater., 2020, 32, 9996–10006 CrossRef CAS.
- L. Sieuw, A. Jouhara, É. Quarez, C. Auger, J.-F. Gohy, P. Poizot and A. Vlad, Chem. Sci., 2019, 10, 418–426 RSC.
- A. Jouhara, E. Quarez, N. Gautier, F. Boucher, E. Janod, N. Dupré, J. Gaubicher and P. Poizot, Energy Storage Mater., 2025, 81, 104456 CrossRef.
- N. Ogihara, N. Ohba and Y. Kishida, Sci. Adv., 2017, 3, e1603103 CrossRef PubMed.
- K. Griffiths, C. Cook, V. R. Seymour, R. J. Bragg, N. R. Halcovitch and J. M. Griffin, Chem. Commun., 2025, 61, 11991–11994 Search PubMed.
- M. Lee, J. Hong, J. Lopez, Y. Sun, D. Feng, K. Lim, W. C. Chueh, M. F. Toney, Y. Cui and Z. Bao, Nat. Energy, 2017, 2, 861–868 Search PubMed.
- X. Wu, S. Jin, Z. Zhang, L. Jiang, L. Mu, Y.-S. Hu, H. Li, X. Chen, M. Armand, L. Chen and X. Huang, Sci. Adv., 2015, 1, e1500330 CrossRef PubMed.
- U. Couhorn and R. Dronskowski, Z. Anorg. Allg. Chem., 2003, 629, 647–652 Search PubMed.
- L. Fédèle, F. Sauvage, S. Gottis, C. Davoisne, E. Salager, J.-N. Chotard and M. Becuwe, Chem. Mater., 2017, 29, 546–554 CrossRef.
- H. Kim, D.-H. Seo, G. Yoon, W. A. Goddard, Y. S. Lee, W.-S. Yoon and K. Kang, J. Phys. Chem. Lett., 2014, 5, 3086–3092 CrossRef CAS PubMed.
- D. Rambabu, T. Goossens, V. R. Bakuru, P. Apostol, F. Mairesse, T. Steenhaut, P. Beaujean, S. K. Mondal, X. Guo, Y. Zhang, S. Pal, R. Markowski, X. Lin, P. Xu, G. Chanteux, A. Kachmar, D. Tie, A. Ramackers, V. Frano, K. Robeyns, T. Kumar Maji, Y. Filinchuk, B. Champagne and A. Vlad, Chem, 2025, 102590 CAS.
- D. Rambabu, A. E. Lakraychi, J. Wang, L. Sieuw, D. Gupta, P. Apostol, G. Chanteux, T. Goossens, K. Robeyns and A. Vlad, J. Am. Chem. Soc., 2021, 143, 11641–11650 Search PubMed.
- L. Bernard, A. Jouhara, E. Quarez, Y. Levieux-Souid, S. Le Caër, P. Tran-Van, S. Renault and P. Poizot, Inorganics, 2022, 10, 62 Search PubMed.
- C. F. N. Marchiori, D. Brandell and C. M. Araujo, J. Phys. Chem. C, 2019, 123, 4691–4700 Search PubMed.
- Z. Lu and B. Zhu, in Computational Design of Battery Materials, ed. D. A. H. Hanaor, Springer International Publishing, Cham, 2024, vol. 150, pp. 187–210 Search PubMed.
- L. Liu, L. Miao, L. Li, F. Li, Y. Lu, Z. Shang and J. Chen, J. Phys. Chem. Lett., 2018, 9, 3573–3579 Search PubMed.
- É. Quarez, A. Jouhara, S. Grolleau, F. Dolhem, N. Dupré and P. Poizot, CrystEngComm, 2020, 22, 1653–1663 RSC.
- J. Wang, P. Apostol, D. Rambabu, X. Guo, X. Liu, K. Robeyns, M. Du, Y. Zhang, S. Pal, R. Markowski, F. Lucaccioni, A. E. Lakraychi, C. Morari, J.-F. Gohy, D. Gupta and A. Vlad, Sci. Adv., 2023, 9, eadg6079 CrossRef CAS PubMed.
- X. Guo, P. Apostol, X. Zhou, J. Wang, X. Lin, D. Rambabu, M. Du, S. Er and A. Vlad, Energy Environ. Sci., 2024, 17, 173–182 Search PubMed.
- C. Wang, Energy Environ. Mater., 2020, 3, 441–452 CrossRef CAS.
- A. N. Davis, K. Parui, M. M. Butala and A. M. Evans, Nanoscale, 2024, 16, 10142–10154 Search PubMed.
- J.-X. Shen, M. Horton and K. A. Persson, npj Comput. Mater., 2020, 6, 161 Search PubMed.
- Z. Rong, D. Kitchaev, P. Canepa, W. Huang and G. Ceder, J. Chem. Phys., 2016, 145, 074112 Search PubMed.
- N. E. R. Zimmermann, D. C. Hannah, Z. Rong, M. Liu, G. Ceder, M. Haranczyk and K. A. Persson, J. Phys. Chem. Lett., 2018, 9, 628–634 CrossRef CAS PubMed.
- R. Pascazio, Q. Chen, H. H. Li, A. D. Kaplan and K. A. Persson, Chem. Mater., 2025, 37, 6213–6226 Search PubMed.
- Y. Y. Zhang, Y. Y. Sun, S. X. Du, H.-J. Gao and S. B. Zhang, Appl. Phys. Lett., 2012, 100, 091905 CrossRef.
- J. C. Slater, J. Chem. Phys., 1964, 41, 3199–3204 CrossRef CAS.
- Y. Tateyama, A. Kagatsume, M. Yao, S. Matsuda and K. Uosaki, J. Phys. Chem. C, 2023, 127, 12867–12873 Search PubMed.
- I. Batatia, S. Batzner, D. P. Kovács, A. Musaelian, G. N. C. Simm, R. Drautz, C. Ortner, B. Kozinsky and G. Csányi, Nat. Mach. Intell., 2025, 7, 56–67 CrossRef PubMed.
- I. Batatia, D. Kovács, G. Simm, C. Ortner and G. Csányi, Apollo – University of Cambridge Repository, 2022, preprint, DOI:10.17863/CAM.111586.
- B. Rhodes, S. Vandenhaute, V. Šimkus, J. Gin, J. Godwin, T. Duignan and M. Neumann, arXiv, 2025, preprint, arXiv:2504.06231, DOI:10.48550/arXiv.2504.06231.
- T. Yamashita, H. Momida and T. Oguchi, J. Phys. Soc. Jpn., 2015, 84, 074703 CrossRef.
- N. Ogihara, T. Yasuda, Y. Kishida, T. Ohsuna, K. Miyamoto and N. Ohba, Angew. Chem., Int. Ed., 2014, 53, 11467–11472 CrossRef CAS PubMed.
- D. Banerjee, S. J. Kim and J. B. Parise, Cryst. Growth Des., 2009, 9, 2500–2503 CrossRef CAS.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- J. A. Kaduk, Acta Crystallogr., Sect. B:Struct. Sci., 2000, 56, 474–485 CrossRef PubMed.
- D. Banerjee, L. A. Borkowski, S. J. Kim and J. B. Parise, Cryst. Growth Des., 2009, 9, 4922–4926 Search PubMed.
- R. E. Dinnebier, H. Nuss and M. Jansen, Acta Crystallogr., Sect. E:Struct. Rep. Online, 2005, 61, m2148–m2150 CrossRef CAS.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- S. Rühl, in Materials Informatics, ed. O. Isayev, A. Tropsha and S. Curtarolo, Wiley, 1st edn, 2019, pp. 41–54 Search PubMed.
- B. Deng, P. Zhong, K. Jun, J. Riebesell, K. Han, C. J. Bartel and G. Ceder, Nat. Mach. Intell., 2023, 5, 1031–1041 CrossRef.
- C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728 CrossRef PubMed.
- H. Chen, L. L. Wong and S. Adams, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 2019, 75, 18–33 CrossRef CAS PubMed.
- B. Mortazavi, X. Zhuang, T. Rabczuk and A. V. Shapeev, Mater. Horiz., 2023, 10, 1956–1968 RSC.
- V. L. Deringer and G. Csányi, Phys. Rev. B:Condens. Matter Mater. Phys., 2017, 95, 094203 CrossRef.
- V. L. Deringer, N. Bernstein, A. P. Bartók, M. J. Cliffe, R. N. Kerber, L. E. Marbella, C. P. Grey, S. R. Elliott and G. Csányi, J. Phys. Chem. Lett., 2018, 9, 2879–2885 CrossRef CAS PubMed.
- L. C. Erhard, J. Rohrer, K. Albe and V. L. Deringer, npj Comput. Mater., 2022, 8, 90 CrossRef.
- A. J. Cruz-Cabeza, N. Feeder and R. J. Davey, Commun. Chem., 2020, 3, 142 CrossRef CAS PubMed.
- J. L. Andrews, E. Pearson, D. S. Yufit, J. W. Steed and K. Edkins, Cryst. Growth Des., 2018, 18, 7690–7700 CrossRef CAS.
- Y. Zhang, K. Chen, H. Guo, Y. Huang, W. Li, C. Wang and Y. Wang, Chem. Eng. J., 2022, 433, 133508 Search PubMed.
- T. Gong, X. Lou, E.-Q. Gao and B. Hu, ACS Appl. Mater. Interfaces, 2017, 9, 21839–21847 CrossRef CAS PubMed.
- W. Gou, Z. Xu, X. Lin, Y. Sun, X. Han, M. Liu and Y. Zhang, Materials, 2022, 15, 4186 Search PubMed.
- I. Ciria-Ramos, A. R. Neale, L. J. Hardwick, E. J. Juarez-Perez, I. Gascón and M. Haro, Dalton Trans., 2025, 54, 9714–9725 RSC.
- X. Ouyang, W. Chen, Y. Zhang, F. Zhang, Y. Zhuang, X. Jie, L. Liu and D. Wang, Phys. Rev. B, 2023, 108, L020103 Search PubMed.
- J. A. Dawson, A. J. Naylor, C. Eames, M. Roberts, W. Zhang, H. J. Snaith, P. G. Bruce and M. S. Islam, ACS Energy Lett., 2017, 2, 1818–1824 CrossRef CAS.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237 CrossRef CAS PubMed.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 094116 Search PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 Search PubMed.
- X. Shao, J. Lv, P. Liu, S. Shao, P. Gao, H. Liu, Y. Wang and Y. Ma, J. Chem. Phys., 2022, 156, 014105 Search PubMed.
- Z. Ye, N. Wang, J. Zhou and D. Ouyang, Innovation, 2024, 5, 100562 CAS.
- X. Luo, Z. Wang, P. Gao, J. Lv, Y. Wang, C. Chen and Y. Ma, npj Comput. Mater., 2024, 10, 254 Search PubMed.
- F. Liu, Z. Chen, T. Liu, R. Song, Y. Lin, J. J. Turner and C. Jia, iScience, 2024, 27, 110672 Search PubMed.
- P.-P. De Breuck, H.-C. Wang, G.-M. Rignanese, S. Botti and M. A. L. Marques, npj Comput. Mater., 2025, 11, 370 Search PubMed.
- V. L. Chevrier and J. R. Dahn, J. Electrochem. Soc., 2010, 157, A392 Search PubMed.
- V. L. Chevrier and J. R. Dahn, J. Electrochem. Soc., 2009, 156, A454 CrossRef CAS.
- B. Key, M. Morcrette, J.-M. Tarascon and C. P. Grey, J. Am. Chem. Soc., 2011, 133, 503–512 Search PubMed.
- M. K. Y. Chan, C. Wolverton and J. P. Greeley, J. Am. Chem. Soc., 2012, 134, 14362–14374 CrossRef CAS PubMed.
- M. W. Terban and S. J. L. Billinge, Chem. Rev., 2022, 122, 1208–1272 CrossRef CAS PubMed.
- S. J. L. Billinge, Philos. Trans. R. Soc., A, 2019, 377, 20180413 CrossRef CAS PubMed.
- R. L. McGreevy and P. Zetterström, J. Non-Cryst. Solids, 2001, 293–295, 297–303 Search PubMed.
- R. L. McGreevy and L. Pusztai, Mol. Simul., 1988, 1, 359–367 CrossRef.
- D. L. Bryce, IUCrJ, 2017, 4, 350–359 CrossRef CAS PubMed.
- K. D. M. Harris, Crystals, 2022, 12, 1277 CrossRef CAS.
- T. Whewell, V. R. Seymour, K. Griffiths, N. R. Halcovitch, A. V. Desai, R. E. Morris, A. R. Armstrong and J. M. Griffin, Magn. Reson. Chem., 2022, 60, 489–503 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 Search PubMed.
- A. Jain, G. Hautier, C. J. Moore, S. Ping Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2011, 50, 2295–2310 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- M. Friede, C. Hölzer, S. Ehlert and S. Grimme, J. Chem. Phys., 2024, 161, 062501 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |