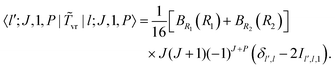A two-step quadrature-based variational calculation of ro-vibrational levels and wavefunctions of CO2 using a bisector-x molecule-fixed frame†
Received
14th February 2024
, Accepted 2nd April 2024
First published on 25th April 2024
Abstract
In this paper, we propose a new two-step strategy for computing ro-vibrational energy levels and wavefunctions of a triatomic molecule and apply it to CO2. A two-step method [J. Tennyson and B. T. Sutcliffe, Mol. Phys., 1986, 58, 1067] uses a basis whose functions are products of K-dependent “vibrational” functions and symmetric top functions. K is the quantum number for the molecule-fixed z component of the angular momentum. For a linear molecule, a two-step method is efficient because the Hamiltonian used to compute the basis functions includes the largest coupling term. The most important distinguishing feature of the two-step method we propose is that it uses an associated Legendre basis and quadrature rather than a K-dependent discrete variable representation. This reduces the cost of the calculation and simplifies the method. We have computed ro-vibrational energy levels with J up to 100 for CO2, on an accurate available potential energy surface which is known as the AMES-2 PES and present a subset of those levels. We have converged most levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to 0.0001 cm−1.
000 cm−1 to 0.0001 cm−1.
I. Introduction
Many variational methods have been proposed for computing solutions to the ro-vibrational Schröedinger equation for triatomic molecules1–11 and all of the components of the method we propose in this paper are known, but they have not previously been combined in the way we suggest. Our method is quadrature-based and simple and efficient. We demonstrate its advantages by computing ro-vibrational energy levels of CO2 up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the zero point energy.
000 cm−1 above the zero point energy.
The cornerstone of our approach is the two-step method of Tennyson and Sutcliffe.9 It shares many features with other contracted basis methods.2,12,13 In a two-step calculation, one first computes eigenfunctions, |v(K)〉, of a Hamiltonian, extracted from the full Hamiltonian, that depends on vibrational coordinates, but is also labelled by K, the quantum number associated with the molecule-fixed z component of the angular momentum. In the second step of the calculation, one computes eigenvalues and eigenvectors of a matrix representing the full Hamiltonian, in a basis of products of |v(K)〉 and symmetric top eigenfunctions |JKM〉. Instead of using the two-step method, one could use a basis of products of J = 0 eigenfunctions, |v(J=0)〉, and |JKM〉. The most important disadvantage of this approach for linear molecules is that matrix elements off-diagonal in |v(J=0)〉 are large. In many two-step calculations, the number of |v(K)〉 is independent of K. When the goal is to compute all states below some threshold, we show that it is better to choose the number of |v(K)〉 functions using a cut-off energy (and therefore use fewer functions when K is larger). We also note that if K is larger than some maximum value, no |v(K)〉 are required. The required number of |v(K)〉 functions depends more sensitively on K, and decreases more quickly with K, for linear molecules, because for linear molecules sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ in the term moved to the vibrational Hamiltonian is small where vibrational wavefunctions are large. We use Radau coordinates14,15 and a bisector-x molecule-fixed axis system. Both have been used before in two-step calculations.
θ in the term moved to the vibrational Hamiltonian is small where vibrational wavefunctions are large. We use Radau coordinates14,15 and a bisector-x molecule-fixed axis system. Both have been used before in two-step calculations.
The most important difference between our two-step method and the traditional two-step approach, as exemplified in the code DVR3D,5,6 is the primitive basis used to compute |v(K)〉. For the bend coordinate, DVR3D uses a K-dependent discrete variable representation (DVR) basis12,16,17 and we use an associated Legendre function (ALF) basis and a K-independent quadrature. Using an ALF basis obviates the need to transform matrix elements into a DVR and reduces the cost of the calculation. Using a DVR basis has the obvious advantage that the potential matrix is diagonal, however, it is straightforward and inexpensive to evaluate matrix-vector products (and hence compute eigenvalues and eigenvectors) with a potential matrix in the ALF basis by evaluating sums sequentially.10,17,18 Another difference between our approach and DVR3D is that we compute |v(K)〉 with an iterative eigensolver, which makes it possible to use large primitive bases. It is also possible using successive contractions, as in DVR3D, to use a large primitive basis, but successive contractions means extra steps in the calculation. These differences are most important when J is large.
The new combination of ideas is tested by using it to compute many energy levels of CO2. CO2 is a popular test molecule because it is an important greenhouse gas and a significant component of the atmospheres of many planets in our solar system.19,20 The spectrum of CO2 has been studied extensively.21–23 A complete line list for CO2 will be useful tool for studying environmental and physical conditions of planetary atmospheres. There are many theoretical calculations of ro-vibrational levels of CO2. The best and the most recent are those of Zak et al.,24 Huang et al.,25–27 and Yurchenko et al.28 All of these papers report a CO2 line list. Zak et al. used DVR3D which is a numerically exact method. Yurchenko et al. used a TROVE method with some approximations. Huang et al. use their VTET code which is also numerically exact. They use a multi-step contraction that incorporates stretch–bend coupling in the final diagonalization which is sub-optimal for CO2, because stretch–bend coupling is important. It is better to contract together all the vibrational coordinates in the first step, but this is costly for larger molecules.
II. Coordinates and kinetic energy operator
We use Radau coordinates14,15 because they simplify the kinetic energy operator (KEO). We attach molecule-fixed axes to CO2 by using the bisector-x embedding, in which the x-axis is antiparallel to the bisector vector R2![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 1 + R1
1 + R1![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 2. The z-axis is in the molecular plane with
2. The z-axis is in the molecular plane with ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 1 having a positive z component.
1 having a positive z component. ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 1 and
1 and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 2 are the Radau vectors see Fig. 1. The bisector-x KEO was first derived by Carter, Handy and Sutcliffe.29 Our KEO is different from theirs because the direction of the z-axis is reversed, and our molecule-fixed angular momentum operators satisfy the anomalous commutation relation (see ref. 30). We choose the bisector-x embedding because it makes it easy to exploit the symmetry of CO2 and reduces the ro-vibrational coupling. The ro-vibrational KEO we use has two parts: a vibrational term Tv and a ro-vibrational term Tvr,
2 are the Radau vectors see Fig. 1. The bisector-x KEO was first derived by Carter, Handy and Sutcliffe.29 Our KEO is different from theirs because the direction of the z-axis is reversed, and our molecule-fixed angular momentum operators satisfy the anomalous commutation relation (see ref. 30). We choose the bisector-x embedding because it makes it easy to exploit the symmetry of CO2 and reduces the ro-vibrational coupling. The ro-vibrational KEO we use has two parts: a vibrational term Tv and a ro-vibrational term Tvr,| | 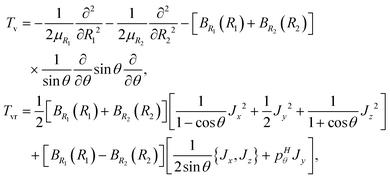 | (2) |
where| | 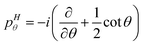 | (3) |
is a Hermitian momentum operator and BRi(Ri) = 1/(2μRiRi2). μRi are the masses of the atoms at the ends of the Radau vectors. The KEO is used with the volume element sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdR1dR2dθ
θdR1dR2dθ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βdαdβdγ. α, β, γ are Euler angles. The ro-vibrational term can be re-written in terms of G matrix elements
βdαdβdγ. α, β, γ are Euler angles. The ro-vibrational term can be re-written in terms of G matrix elements| | 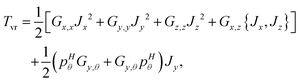 | (4) |
where the G matrix elements are functions of the shape coordinates and, according to eqn (2), are| | 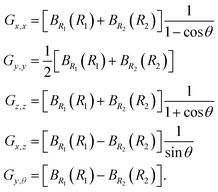 | (5) |
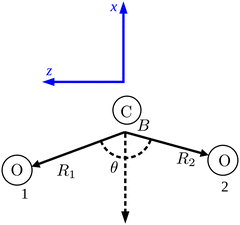 |
| | Fig. 1 The Radau coordinates (R1, R2, θ) and the bisector-x molecule-fixed frame (in blue). B is the canonical point. The dashed arrow is the bisector vector for θ. The origin of the molecule-fixed frame is not at the center of mass of the molecule for clarity. | |
When using Radau coordinates for a triatomic molecule it is also common to attach the molecular axis system so that the z axis is along a Radau vector. We call this a vector-z frame. Regardless of the embedding, some G matrix elements are singular at linear shapes. The vector-z frame has the advantage that basis functions can be chosen so that all KEO matrix elements are finite. For CO2, the bisector-x embedding has two advantages over the vector-z frame: (i) it allows full exploitation of the permutation symmetry of the O atoms; (ii) the ΔK = ±1 and ΔK = ±2 matrix elements are small since at the equilibrium geometry, where the molecule is linear, the former are zero because Gy,θ = Gx,z = 0 and the latter are zero because Gx,x = Gy,y.
III. Two-step variational calculation
We compute ro-vibrational energy levels and wavefunctions by using a two-step variational method. Each basis function is a product of a contracted vibrational function and a rotational function,|v(K)〉 is an eigenfunction of a modified “vibrational” Hamiltonian| | ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v = [ v = [![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v + V(R1,R2,θ)], v + V(R1,R2,θ)], | (7) |
| | 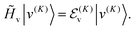 | (8) |
|JKM〉 is a symmetric top eigenfunction (or Wigner function). In the basis of eqn (6), ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v is diagonal, the off-diagonal elements of
v is diagonal, the off-diagonal elements of ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr are small, and convergence with respect to the size of the basis is very fast. We retain the |v(K)〉 for which the corresponding energy is less than a cut-off energy, Ecut.
vr are small, and convergence with respect to the size of the basis is very fast. We retain the |v(K)〉 for which the corresponding energy is less than a cut-off energy, Ecut.
To define the modified vibrational KEO, the full Hamiltonian
is rewritten
| | H = ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v + v + ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr, vr, | (10) |
by shifting a term from
Tvr into
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v
v. Matrix elements of coordinate dependent factors in the terms of the KEO are integrals that are computed by quadrature. The KEO of the modified “vibrational” Hamiltonian is designed so that, if the primitive basis functions, used to solve
eqn (8), are chosen correctly, all matrix elements of
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v
v in the primitive basis are finite. Some of the coordinate dependent factors in terms in
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr
vr are singular, but only where all wavefunctions have negligible amplitude. Such singularities are “unimportant”. Some authors discard DVR or quadrature points close to an unimportant singularity,
5,6,31 but this is unnecessary. We find that for CO
2, points close to the
θ = 0 singularity cause no problems. The KEO of
eqn (1) is singular at the equilibrium geometry where
θ = π and also at
θ = 0. The
θ = 0 singularity is unimportant because it corresponds to C–C–O which has a very high potential energy. The
θ = π singularity occurs in the factor
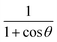
in
Gzz. To choose basis functions to deal with the important singularity, we use
| | 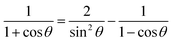 | (11) |
to rewrite
| | 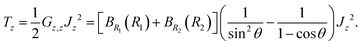 | (12) |
The modified vibrational KEO and the corresponding modified ro-vibrational KEO are
| | 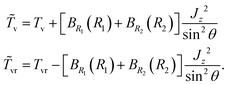 | (13) |
In the shared-
K associated Legendre function (ALF) basis
ΘKl(
θ), the matrix elements of
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v
v are finite because
| | 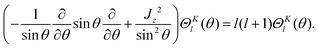 | (14) |
This two-step variational calculation method was first proposed by Tennyson and Sutcliffe
9 and used to compute high-
J levels of H
2D
+. The idea was subsequently used in many papers
24–27,32–37 to compute high-
J levels of triatomic molecules. We compute the |
v(K)〉 using the Lanczos algorithm.
Rather than using the two-step method, one could use a basis of products of J = 0 functions, |v(J=0)〉, and symmetric top functions. In this basis, off-diagonal matrix elements, 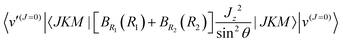 are large. In a two-step calculation, the term
are large. In a two-step calculation, the term 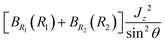 does not couple basis functions because it is included in the operator whose eigenfunctions are the |v(K)〉 basis functions. |v(K)〉 is like an eigenfunction of a 2-D harmonic oscillator with K = l2. This basis includes all the bending states
does not couple basis functions because it is included in the operator whose eigenfunctions are the |v(K)〉 basis functions. |v(K)〉 is like an eigenfunction of a 2-D harmonic oscillator with K = l2. This basis includes all the bending states 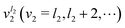 . For a given K = l2, the ground state of
. For a given K = l2, the ground state of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v is a state assigned to v2 = l2 = K.
v is a state assigned to v2 = l2 = K.
IV. Matrix elements in non-parity-adapted bases
A. Matrix elements in the non-parity-adapted primitive basis
The |v(K)〉 are computed for each K in a vibrational primitive basis| | 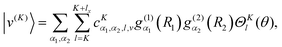 | (15) |
where ΘKl(θ) is an associated Legendre function (ALF) and 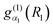 and
and 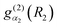 are discrete variable functions.17 In this section we present equations for matrix elements in the primitive basis each of whose functions is a product of the vibrational functions in eqn (15) and a non-parity adapted rotational function,
are discrete variable functions.17 In this section we present equations for matrix elements in the primitive basis each of whose functions is a product of the vibrational functions in eqn (15) and a non-parity adapted rotational function,| | 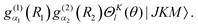 | (16) |
Matrix elements in the basis of eqn (6) are obtained from those in this subsection by transforming. The range of l is [K,K + lx]. lx is the maximum value of l when K = 0. In the following, the bend-rotation part of this basis function is denoted (dropping M)| | | |l;J,K〉 = ΘKl(θ)|JKM〉. | (17) |
In the basis of eqn (16) the matrix representing ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v is diagonal and its elements are
v is diagonal and its elements are
| | 〈l′;J,K|![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v|l;J,K〉 = [BR1(R1) + BR2(R2)]l(l + 1)δl′,l. v|l;J,K〉 = [BR1(R1) + BR2(R2)]l(l + 1)δl′,l. | (18) |
The matrix elements of the ro-vibrational term
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr
vr in the primitive basis are,
| | 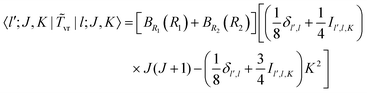 | (19) |
| | 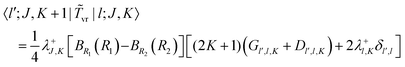 | (20) |
| | 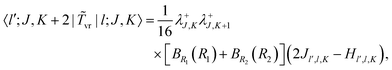 | (21) |
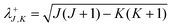
. The matrices
D,
G,
H,
I and
J are given in Appendix A of ref.
30. They are reproduced below,
| | 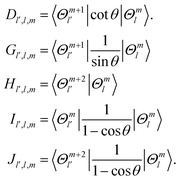 | (22) |
All these matrices can be computed numerically exactly with a Gauss Legendre quadrature except for
I. See ref.
30 for details. When
K = 0, matrix elements of
I are singular at
θ = 0. However, this singularity is unimportant because of the high potential at
θ = 0. One only needs accurate integrals in the region of configuration space in which wavefunctions are not negligible.
38 The matrix elements in
eqn (18)–(21) have been given in ref.
30, where the bisector-
z KEO (the bisector-
x KEO was not used) was used to compute the spectrum of an H
2O-atom complex, but in the second equation of
eqn (28) of ref.
30, there is a sign error: −2
λ+l,Kδl′,l should be +2
λ+l,Kδl′,l.
Note that G + D could be combined into one matrix by computing matrix elements of (1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/sin
θ)/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and that 2J − H could be combined into one matrix by computing matrix elements of (1 + cos
θ and that 2J − H could be combined into one matrix by computing matrix elements of (1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/(1 − cos
θ)/(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). We have not made these combinations because we want to give the matrix elements that are required for both the bisector-x and the bisector-z frames.30 Specifically, for the bisector-z frame, G − D is the matrix representing (1 − cos
θ). We have not made these combinations because we want to give the matrix elements that are required for both the bisector-x and the bisector-z frames.30 Specifically, for the bisector-z frame, G − D is the matrix representing (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/sin
θ)/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and it appears in ΔK = 1 matrix elements, and 2F − H is the matrix representing (1 − cos
θ and it appears in ΔK = 1 matrix elements, and 2F − H is the matrix representing (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/(1 + cos
θ)/(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and it appears in ΔK = 2 matrix elements.30
θ) and it appears in ΔK = 2 matrix elements.30
As noted after eqn (16), the maximum of l for the ALF basis is extended from lx to K + lx. This ensures that the bend basis size, lx + 1, is the same for each K since the minimum value of l is K. As a result, the quality of the converged vibrational levels is maintained for all K. Note, however, that as K becomes larger, fewer |v(K)〉 are retained because fewer of the corresponding energies are below Ecut. When J is much smaller than lx, it is fine to set the maximum value of l at lx. For each K, the integration over θ, required to calculate matrix elements of the potential, is done with at least Nθ = K + lx + 1 Gauss Legendre quadrature points. In fact, we use the same Jx + lx + 1 Gauss Legendre quadrature points for all K, Jx is the largest J. Using one set of points instead of a different set for each K gives us the advantage of needing to compute and store potential points only once. It would also be possible to use a K dependent Gauss Jacobi quadrature with only lx + 1 points (for each K), for which the points are determined by diagonalizing cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ in a ALF basis. If we used these points we would be doing a finite basis representation (FBR) calculation equivalent to the DVR calculation of DVR3D. Both quadratures allow one to evaluate potential matrix vector products with the sequential summation technique and use an iterative eigensolver to compute thousands of eigenstates |v(K)〉 directly in the 3D direct product primitive basis. The 3-D direct product basis is large, but that is not a problem if an iterative eigensolver is used. If a direct eigensolver used, it is common to reduce the size of the primitive basis by doing a series of diagonalizations and truncations.5,6,27,33
θ in a ALF basis. If we used these points we would be doing a finite basis representation (FBR) calculation equivalent to the DVR calculation of DVR3D. Both quadratures allow one to evaluate potential matrix vector products with the sequential summation technique and use an iterative eigensolver to compute thousands of eigenstates |v(K)〉 directly in the 3D direct product primitive basis. The 3-D direct product basis is large, but that is not a problem if an iterative eigensolver is used. If a direct eigensolver used, it is common to reduce the size of the primitive basis by doing a series of diagonalizations and truncations.5,6,27,33
B. Matrix elements in the non-parity-adapted contracted basis
Using the ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr matrix elements in Section IVA, it is straightforward to compute the matrix elements of the ro-vibrational Hamiltonian in the contracted basis. The diagonal elements are
vr matrix elements in Section IVA, it is straightforward to compute the matrix elements of the ro-vibrational Hamiltonian in the contracted basis. The diagonal elements are| | 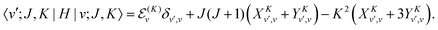 | (23) |
The matrix elements off-diagonal in K are| | 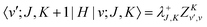 | (24) |
| | 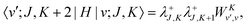 | (25) |
where| | | |v;J,K〉 ≡ |v(K)〉 |J,K〉 | (26) |
| | 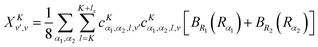 | (27) |
| | 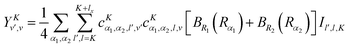 | (28) |
| | 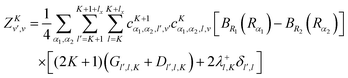 | (29) |
| | 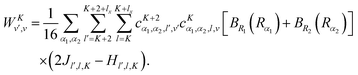 | (30) |
Although it is not indicated, the indices v and v′ in X and Y depend on K. The index v′ in Z depends on K + 1, and the index v′ in W depends on K + 2. Note that X, Y, Z, and W are independent of J. They are evaluated for K = 0, 1, …, Kmax and stored on disk in the first step. They are used in the second step calculation for all J. Kmax ≤ J, but for high J calculations, Kmax can be much smaller than J, eliminating the cost of calculating v(K) when K is between Kmax and J.
V. Parity symmetry and O–O permutation symmetry
A. Parity symmetry
To utilize the parity symmetry, we note that the parity operator does not affect the vibrational coordinates, but affects the rotational coordinates for the molecule-fixed frame we use,| | | E*(R1,R2,θ;α,β,γ) = (R1,R2,θ;π + α,π − β,π − γ). | (31) |
As a result,| | 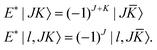 | (32) |
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) = −KThe parity-adapted (PA) primitive basis is therefore
= −KThe parity-adapted (PA) primitive basis is therefore| | 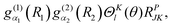 | (33) |
where| | 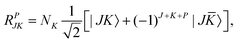 | (34) |
with NK = (1 + δK,0)−1/2. P = 0 and 1 correspond to even and odd parity, respectively, and K ≥ 0 for (−1)J+P = 1 and K ≥ 1 for (−1)J+P = −1. (−1)J+P = ±1 is called the spectroscopic parity e/f and is a popular label for linear molecules. RPJK is an eigenfunction of E*Matrix elements of rotational operators in the RPJK basis are given for example in ref. 39. They will be used to derive the KEO matrix elements in the PA primitive basis. We denote the angular part of the PA primitive basis by| | | |l;J,K,P〉 = ΘKl(θ)RPJK. | (36) |
Although the PA primitive basis for a triatomic is a product of a vibrational factor and rotational factor, this is not the case for molecules with more than three atoms.
B. O–O permutation symmetry
The O–O permutation symmetry operator (12) permutes atoms O1 and O2. The bisector-x frame is affected by (12) because the x-axis is unchanged and the y- and z-axes are flipped. The effect of (12) on the ro-vibrational coordinates is| | | (12)(R1,R2,θ;α,β,γ) = (R2,R1,θ;π + α,π − β, −γ). | (37) |
As a result,| | 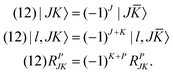 | (38) |
VI. Matrix elements in parity-adapted bases
A. Matrix elements in the parity-adapted primitive basis
The matrix elements of ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v in the PA primitive basis are the same as those in the primitive basis. Matrix elements of
v in the PA primitive basis are the same as those in the primitive basis. Matrix elements of ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr in the PA primitive basis are the same as those in the primitive basis except each is multiplied by a factor, FK = (1 + δK,0)1/2. They can be derived by taking advantage of the factorization in eqn (36) and using the matrix elements of rotational operators in the RPJK basis given in ref. 39. The results are
vr in the PA primitive basis are the same as those in the primitive basis except each is multiplied by a factor, FK = (1 + δK,0)1/2. They can be derived by taking advantage of the factorization in eqn (36) and using the matrix elements of rotational operators in the RPJK basis given in ref. 39. The results are| | 〈l′;J,K,P|![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v|l;J,K,P〉 = [BR1(R1) + BR2(R2)]l(l + 1)δl′,l v|l;J,K,P〉 = [BR1(R1) + BR2(R2)]l(l + 1)δl′,l | (39) |
| | 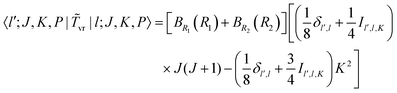 | (40) |
| | 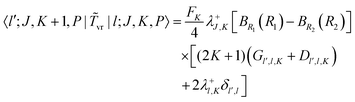 | (41) |
| | 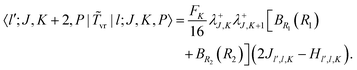 | (42) |
There is an additional special diagonal matrix element of ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr for K = 1 arising from Jx2 − Jy2 (there is no corresponding matrix element in the non-PA basis),
vr for K = 1 arising from Jx2 − Jy2 (there is no corresponding matrix element in the non-PA basis),
B. Matrix elements in the parity-adapted contracted basis
A PA contracted basis function is| | | |v;J,K,P〉 = |v(K)〉RPJ,K. | (43) |
The matrix elements of the ro-vibrational Hamiltonian in the PA contracted basis are the same as those in the contracted basis, eqn (23)–(30), except that the K-off-diagonal elements have an FK factor,| | 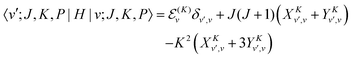 | (44) |
| | 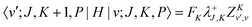 | (45) |
| | 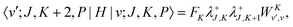 | (46) |
and there is a special diagonal matrix element for K = 1,| | 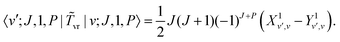 | (47) |
Note that there are two differences between the even and odd parity Hamiltonian matrices: (i) the K = 1 diagonal elements are different due to eqn (47); and (ii) when (−1)J+P = 1, the matrix has an additional K = 0 row and column. In the vector-z frame case, there are no special elements and the even and odd matrices differ only because when (−1)J+P = 1 there is an additional K = 0 row and column.
VII. Comparison with other methods
Many variational methods for computing energy levels of triatomic molecules exist. What is unique about the method we propose in this paper? Most variational methods have four basic components: (i) coordinates; (ii) primitive and contracted basis functions; (iii) matrix elements; (iv) a method for computing eigenvalues and eigenvectors of the Hamiltonian matrix. There are no papers using the combination of (i), (ii), (iii), and (iv) that we use suggest in this paper. Our combination is straightforward to implement and has advantages. In this section we compare our approach to approaches of other groups.
Carter and Handy (CH) were the first to use the bisector-x frame KEO in their calculation of energy levels of H2O32 and later of HCN.33 They also use the two-step method. Their coordinates are bond lengths and the bond angle. There is less potential coupling in bond coordinates than in Radau coordinates, but more kinetic coupling (the vibrational KEO has cross terms between the stretch coordinates and between stretch coordinates and the bend coordinate and additional ro-vibrational terms). The Radau KEO we use has fewer terms. CH used 1-D contracted basis functions and an optimised quadrature scheme.40,41 Instead, we use tri-diagonal Morse DVR functions for the stretches and ALF functions for the bend. CH did not publish equations for the matrix elements in the ALF basis. They use a direct eigensolver, which limits the size of the primitive basis they can use.
Tennyson and co-workers5,6 use the same bisector-x frame KEO, the same Radau coordinates, and a two-step method as we do in this paper. Their approach is implemented in the DVR3D code5,6 used in many calculations of triatomic molecules. Their method differs from ours in the choice of the primitive basis. To compute |v(K)〉, they use K-dependent DVR functions for the bend coordinate and we use ALF functions. The DVR3D bend basis functions are
| | 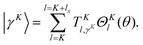 | (48) |
where
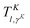
is a transformation matrix determined by diagonalizing the matrix representing cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ in the ALF basis.
17 Because we do not use a DVR for
θ, we must evaluate integrals by quadrature. If we used the Gauss-Jacobi quadrature that underlies the
K-dependent DVR used in DVR3D, then our Hamiltonian matrix and the matrix of DVR3D would be unitarily equivalent,
HDVR3D = (
TK)
T![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) vTK
vTK, where
![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) v
v is the matrix computed with Gauss-Jacobi quadrature. Instead, we use a
K-independent quadrature.
17 DVR3D computes matrices representing coordinate dependent factors
D,
G,
H,
I, and
J, in the ALF basis and then transforms them to the
K-dependent DVR. By using only the ALF, we obviate the need to transform all these matrices into the DVR. The transformation is a bit tricky because the DVR is
K-dependent which means that different transformation matrices must be used on the left and on the right. In Section 2.3 of ref.
42, it is noted that the cost of transforming into the DVR can be reduced by doing sums sequentially; we completely eliminate the transformation. In the first two-step paper
9 in 1986, a vector-
z frame and an ALF basis were used. DVR3D uses not only a different primitive basis but also a different contracted basis. As pointed out by Yan, Xie and Tian,
34 in the two-step calculation of DVR3D, the contracted functions computed in the first step are different for each
J,
K pair. The modified “vibrational” KEOs used by DVR3D and by Carter and Handy
32 include not only
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v
v, but also all
J2 and
Jz2 terms. In other words, they added the second and third terms on the RHS of
eqn (23). We find that most of the computation time is spent in the first-step of the calculation. If, as is true in our calculation, it is not necessary to recompute |
v(K)〉 for each value of
J, a lot of computer time is saved. Another difference between DVR3D and what we do is that we do not discard quadrature points close to the singularity.
The most accurate CO2 calculations have been done with a method developed by Schwenke and co-workers.25–27,35 It is quite different from our approach. They use different molecule-fixed axes, a different contraction scheme, and a direct eigensolver. They first contract together bend and rotation, then they contract their bend-rotation functions with a 1-D contracted antisymmetric stretch basis, finally they contract their bend-rotation-antisymmetric stretch functions with 1-D contracted symmetric stretch functions. They used the vector-z BF frame. Matrix elements off-diagonal in K are larger in the vector-z frame than in the bisector-x frame, but that coupling is accounted for in the first contraction and therefore not a problem. Schwenke and co-workers cannot use a symmetry-adapted primitive basis to set up their bend-rotation matrix because permuting the two O atoms changes their primitive functions (because they use the vector-z frame) in a complicated way. However the bend-rotation contracted functions are symmetric or antisymmetric under O–O permutation. They assign permutation symmetry labels to their bend-rotation contracted functions by analysing the functions at a set of points (see ref. 43). These symmetry-labelled bend-rotation contracted functions are then coupled to the symmetry-labelled contracted antisymmetric stretch functions to form the final symmetry-labelled basis functions. A disadvantage of their contraction scheme is that the important coupling between bend and symmetric stretch basis function is incorporated at the end of the calculation. On the other hand, an advantage is it can be used on molecules with more than three atoms. Everything is implemented in their VTET code. Their bend-rotation functions are similar to the rigid-bender functions of Bunker44 and to the bend-rotation functions used for methane in ref. 45. Schwenke et al. used an optimised quadrature scheme40,41 to compute matrix elements in their contracted basis. The nested contraction scheme makes it possible to calculate accurate ro-vibrational levels up to J = 150 and levels higher than 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 were converged. In this paper, we use their levels,27,46 called Huang2022 levels, as a benchmark to compare with our levels. The levels we received from them are published in ref. 27 and are used to generate the Ames-2021 line list.27 We also compare with their levels computed with a smaller basis on the same PES26 and call them Huang2017 levels.
000 cm−1 were converged. In this paper, we use their levels,27,46 called Huang2022 levels, as a benchmark to compare with our levels. The levels we received from them are published in ref. 27 and are used to generate the Ames-2021 line list.27 We also compare with their levels computed with a smaller basis on the same PES26 and call them Huang2017 levels.
Yurchenko and Mellor28,47 propose a TROVE method to compute ro-vibrational levels and wavefunctions of CO2. They also used the bisector-x frame and their treatment of the KEO is exact. However, they represent the potential with a 12th order Taylor expansion. They compared their energies with those computed with DVR3D24 on an earlier Ames-1 PES25 rather than the Ames-2 PES26 we are using. (They mistakenly stated that they used the Ames-2 PES.) Errors appear to be due to the Taylor series approximation. The largest error in their Table 1 is 0.0335 cm−1 for a J = 0 DVR3D level at 5667.6298 cm−1. The error of our calculation for this level is less than 1 × 10−5 cm−1.
Table 1 Calculation parameters for CO2
m
(C) = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 868.66175734604622 me 868.66175734604622 me |
m
(O) = 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.94559967216628 me 148.94559967216628 me |
1 Hartree = 219![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474.631482453 cm−1 474.631482453 cm−1 |
|
a
0 = 0.529177249 Å |
The two-step method with the ALF basis that is explained in this paper has been added to our RV3 code.48 The code computes the ro-vibrational energy levels, wavefunctions, and intensities of a three-atom molecule using a variety of basis functions including non-contracted bases, e.g. ALF and DVR bend bases, and contracted bases, e.g. a shared-K contracted basis |v(K)〉|JKM〉 (this work) a non shared-K contracted basis |v〉|JKM〉.38 All these bases can be used with the vector-z frame, the bisector-x frame, the bisector-z frame and the Eckart frame.
VIII. Results
The highly accurate Ames-2 PES26 was used in all calculations. The masses and constants are given in Table 1.46
A. Primitive basis optimization and primitive-basis convergence tests
We use a tridiagonal Morse(TDM) DVR basis for the stretch coordinates R1 and R2. Compared to a basis of Morse wavefunctions, it has the advantage that it is possible to define a corresponding DVR.49 The TDM basis depends on the values of parameters that appear in a Morse potential: De, ωe, and Re, and on a fourth parameter that is called γ in ref. 49 and α in ref. 50 and 51; α = 2γ. Here we use the α notation. The superscript of the associated Laguerre polynomials Lαn(y) in the TDM function is α. It is chosen as in ref. 49, so that the TDM basis spans the same space as the [A/2] bound states of the Morse oscillator. De, ωe, and Re are optimized to minimize low-lying J = 0 levels. For the optimization, lx is fixed at 50 which is more than enough for levels up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. A large (120) sine DVR basis provides the benchmark for the optimization. Our final parameters for the TDM basis are De = 65
000 cm−1. A large (120) sine DVR basis provides the benchmark for the optimization. Our final parameters for the TDM basis are De = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, ωe = 2170 cm−1, Re = 2.14a0. A = 4De/ωe = 119.82. The number of Morse bound states is [A/2] = 59. According to ref. 49, α = A − 2[A/2] = 1.82, if NRi ≥ 59; and α = A − 2NRi if NRi ≤ 59.
000 cm−1, ωe = 2170 cm−1, Re = 2.14a0. A = 4De/ωe = 119.82. The number of Morse bound states is [A/2] = 59. According to ref. 49, α = A − 2[A/2] = 1.82, if NRi ≥ 59; and α = A − 2NRi if NRi ≤ 59.
We determine the size of the primitive ALF basis, lx, by doing calculations with a small TDM basis. Our goal is to converge energy levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 with errors of 1 × 10−4 cm−1. We fix NR1 = NR2 = 28 and find that lx = 150 is enough to converge levels up to 20
000 cm−1 with errors of 1 × 10−4 cm−1. We fix NR1 = NR2 = 28 and find that lx = 150 is enough to converge levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to within 3 × 10−5 cm−1, by comparing with levels computed with lx = 200. Subsequently, with lx = 150 fixed, we test TDM DVR bases with up to NR1 = NR2 = 80. The basis with (NR1 = NR2,lx) = (50, 150) is chosen as our final primitive basis and is hereafter called basis I. Compared to levels computed with (NR1 = NR2,lx) = (80, 150), basis I converges almost all the J = 0 levels up to 20
000 cm−1 to within 3 × 10−5 cm−1, by comparing with levels computed with lx = 200. Subsequently, with lx = 150 fixed, we test TDM DVR bases with up to NR1 = NR2 = 80. The basis with (NR1 = NR2,lx) = (50, 150) is chosen as our final primitive basis and is hereafter called basis I. Compared to levels computed with (NR1 = NR2,lx) = (80, 150), basis I converges almost all the J = 0 levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to within 1 × 10−4 cm−1; the largest error is 0.00165 cm−1 at 19
000 cm−1 to within 1 × 10−4 cm−1; the largest error is 0.00165 cm−1 at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 cm−1. We refer to the difference between levels computed with the (NR1 = NR1,lx) = (50, 150) basis and with the (NR1 = NR1,lx) = (80, 150) basis as the primitive-basis error see Table 2. Basis I has 377
160 cm−1. We refer to the difference between levels computed with the (NR1 = NR1,lx) = (50, 150) basis and with the (NR1 = NR1,lx) = (80, 150) basis as the primitive-basis error see Table 2. Basis I has 377![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 functions, for J = 0.
500 functions, for J = 0.
Table 2 Testing the convergence of primitive vibrational bases. Δ15k/Δ20k are the maxium absolute differences for the A+ symmetry J = 0 vibrational levels up to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/20
000/20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, respectively, relative to the benchmark results obtained with the primitive basis NR1 = NR2 = 80 and lx = 150. The energies are in cm−1. The number of bend quadrature points is Nθ = lx + 1
000 cm−1, respectively, relative to the benchmark results obtained with the primitive basis NR1 = NR2 = 80 and lx = 150. The energies are in cm−1. The number of bend quadrature points is Nθ = lx + 1
| (NR1 = NR2,lx) |
N
bas
|
Δ
15k
|
Δ
20k
|
| (32, 120) |
108![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
0.00669 |
8.188 |
| (32, 150) |
154![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 624 624 |
0.00022 |
0.04900 |
| (50, 150) |
377![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
0.00003 |
0.00165 |
| (60, 150) |
543![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
0.00003 |
0.00027 |
| (80, 150) |
966![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
0 |
0 |
| Huang2017 |
|
0.00029 |
0.07551 |
| Huang2022 |
|
0.00102 |
0.00116 |
We have used the same masses and constants as those used by Huang et al.26,27 Nonetheless, there are still small differences between our levels and the levels of Huang2017 and Huang2022, for low-lying levels that should be fully converged in both calculations. For example, for levels up to 3000 cm−1, the largest difference is 0.0003 cm−1 for the level at 2548.36615 cm−1 (see Table S1 of ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52). This difference is certainly not due to convergence error in either calculation. We therefore consider any differences larger than 0.0003 cm−1 to be due to their basis set convergence error. In Table 2, we show that, for J = 0 levels below 20
52). This difference is certainly not due to convergence error in either calculation. We therefore consider any differences larger than 0.0003 cm−1 to be due to their basis set convergence error. In Table 2, we show that, for J = 0 levels below 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, the largest difference is 0.00116 cm−1 comparing to the Huang2022 levels and 0.07551 cm−1 comparing to the Huang2017 levels. The largest differences are in bold in Table S1 of ESI.†
000 cm−1, the largest difference is 0.00116 cm−1 comparing to the Huang2022 levels and 0.07551 cm−1 comparing to the Huang2017 levels. The largest differences are in bold in Table S1 of ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 This indicates that there are small convergence errors in their J = 0 levels. A list of all the J = 0 A+ levels is given in Table S1 of the ESI.†
52 This indicates that there are small convergence errors in their J = 0 levels. A list of all the J = 0 A+ levels is given in Table S1 of the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52
52
We could also compare levels computed with our primitive basis and those of Zak et al.,24 who used 30 slightly different TDM DVR basis functions for the stretches and lx = 120 and a different PES (Ames-1 PES). To estimate convergence errors of their calculation, we have determined that (using our TDM functions) the (NR1 = NR2,lx) = (30, 120) basis gives errors as large as 0.00669 cm−1 up to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and as large as 8.188 cm−1 up to 20
000 cm−1 and as large as 8.188 cm−1 up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. However, the goal of Zak et al. was to compute levels only up to 14
000 cm−1. However, the goal of Zak et al. was to compute levels only up to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 see Table 2.
500 cm−1 see Table 2.
B. Convergence of energies computed in the contracted basis
When J is large, rather than using the primitive basis, we use the contracted basis. The primitive basis of the previous paragraph (basis I) is used to compute the contracted basis functions. The convergence of the second step of the two-step calculation depends on the cut-off energy Ecut used to determine the size of the v(K) basis. As Ecut is increased, levels of the two-step calculations approach those computed in the primitive basis used to compute the v(K). We can therefore use a calculation done in the primitive basis to test the convergence of the two-step calculation, at least when J is not too large. The calculation with the primitive basis is much more costly than the two-step calculation. To compare the primitive (basis I) and 2-step levels, we use the J = 20 A+ symmetry levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. The primitive basis has 8
000 cm−1. The primitive basis has 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452
452![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 even-parity basis functions see Table 3 for details. We find that the contracted basis with Ecut = 30
500 even-parity basis functions see Table 3 for details. We find that the contracted basis with Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 is sufficient to converge levels up to 20
000 cm−1 is sufficient to converge levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to within 3.4 × 10−5 cm−1 see column 5 and 6 of Table 3. We therefore use Ecut = 30
000 cm−1 to within 3.4 × 10−5 cm−1 see column 5 and 6 of Table 3. We therefore use Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to compute all the levels reported in this paper, up to J = 100.
000 cm−1 to compute all the levels reported in this paper, up to J = 100.
Table 3 Testing the convergence of the two-step calculations with respect to the cutoff energy Ecut. The J = 20 A+ symmetry rovibrational levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (the number of levels is 2151) are used to do the test. Δ15k/Δ20k are the maxium absolute differences up to 15
000 cm−1 (the number of levels is 2151) are used to do the test. Δ15k/Δ20k are the maxium absolute differences up to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/20
000/20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, respectively, relative to the benchmark levels computed in the NR1 = NR2 = 50, lx = 170 primitive basis with Nθ = 171 and relative to two-step levels computed with Ecut = 38
000 cm−1, respectively, relative to the benchmark levels computed in the NR1 = NR2 = 50, lx = 170 primitive basis with Nθ = 171 and relative to two-step levels computed with Ecut = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. The size of the even-parity primitive basis is 8
000 cm−1. The size of the even-parity primitive basis is 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452
452![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500. The energies are in cm−1
500. The energies are in cm−1
|
E
cut
|
N
bas
|
Relative to Ecut = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Relative to the benchmark |
|
Δ
15k
|
Δ
20k
|
Δ
15k
|
Δ
20k
|
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 428 428 |
0.0 |
0.0 |
2.2 × 10−5 |
3.4 × 10−5 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
9185 |
2.0 × 10−9 |
2.8 × 10−6 |
2.2 × 10−5 |
3.4 × 10−5 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
6314 |
8.2 × 10−8 |
0.00017 |
2.2 × 10−5 |
0.00016 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
5513 |
3.1 × 10−7 |
0.00087 |
2.2 × 10−5 |
0.00085 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4809 |
1.7 × 10−6 |
0.00229 |
2.2 × 10−5 |
0.00227 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3581 |
1.5 × 10−5 |
0.06602 |
2.2 × 10−5 |
0.06602 |
| Huang2022 |
N/A |
0.00208 |
0.01966 |
0.00210 |
0.01966 |
Errors in the final energy levels can be caused by using a primitive basis and/or a Ecut that is too small. We estimate that the total error in the levels we report is about 0.0001 cm−1, for all levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. If one aims to converge only levels up to 15
000 cm−1. If one aims to converge only levels up to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, one can lower Ecut to at least 25
000 cm−1, one can lower Ecut to at least 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. When Ecut is large enough, the error in two-step eigenvalues compared to the corresponding primitive-basis eigenvalues decreases quickly as Ecut is increased. However, this two-step error is not the only error, there is also the primitive-basis error. For J = 20 A+, see Table 3, the largest eigenvalue difference between two-step calculations with Ecut = 30
000 cm−1. When Ecut is large enough, the error in two-step eigenvalues compared to the corresponding primitive-basis eigenvalues decreases quickly as Ecut is increased. However, this two-step error is not the only error, there is also the primitive-basis error. For J = 20 A+, see Table 3, the largest eigenvalue difference between two-step calculations with Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and Ecut = 15
000 cm−1 and Ecut = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 is Δ15k = 2.0 × 10−9 cm−1, but this does not imply that errors in two-step eigenvalues computed with Ecut = 15
000 cm−1 is Δ15k = 2.0 × 10−9 cm−1, but this does not imply that errors in two-step eigenvalues computed with Ecut = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 are 2.0 × 10−9 cm−1 because there is also primitive-basis error. In fact, the largest difference between two-step levels with Ecut = 15
000 cm−1 are 2.0 × 10−9 cm−1 because there is also primitive-basis error. In fact, the largest difference between two-step levels with Ecut = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and primitive-basis levels computed with the larger primitive basis (NR1 = NR2,lx) = (50, 180) primitive basis is 2.2 × 10−5 cm−1. When J is large, primitive-basis levels with the (NR1 = NR2,lx) = (50, 180) basis are not available. Convergence with respect to Ecut is not the full story.
000 cm−1 and primitive-basis levels computed with the larger primitive basis (NR1 = NR2,lx) = (50, 180) primitive basis is 2.2 × 10−5 cm−1. When J is large, primitive-basis levels with the (NR1 = NR2,lx) = (50, 180) basis are not available. Convergence with respect to Ecut is not the full story.
Many researchers, such as Carter and Handy,32,33 Zak et al.,24 Zuniga et al.,36,37 use a fixed number of v(K) functions for each K. This number is often called N. For a given J, this corresponds to Hamiltonian matrices of size N(J + 1) and NJ for (−1)J+P = 1 and −1, respectively. To limit the size of the matrices in the final diagonalization, it is common to use a smaller N when J is large. E.g., Zak et al.24 use N = 600 for J = 0–50 and N = 100 for J = 87–129.
Instead, we use Ecut to determine the number of v(K) functions for each K. According to perturbation theory, the importance of coupling between zeroth-order states v(K) and v′(K′) depends on the difference between their (zeroth-order) energies. Ecut therefore seems like a good criterion for determining the number of v(K) to retain. Ecut is also used in the work of Schwenke and co-workers.25–27 For each symmetry block, the number of v(K) we retain, denoted by N(K), decreases with K, because the corresponding energies are larger when K is larger see Table 4. A± levels (B± levels are Pauli forbidden) are computed from a basis of products of A± (B±) rotational functions RPJK and A+ (B+) v(K) functions. Because the A/B symmetry of the rotational functions RPJK alternates with K (see eqn (38)), the symmetry of v(K) must also alternate. We choose Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 in our final calculations and for a (−1)J+P = 1 calculation, N(K) is 885(A), 685(B), 787(A), 601(B) for K = 0, 1, 2, 3, respectively. It is 1(B), 3(A), 0(B), 1(A) for K = 39, 40, 41, 42, respectively. Clearly, there is no need to include v(K) functions when K > 42 and we therefore set Kmax is 42. The lowest level for each K is labelled by v2 = K, l2 = K. The fundamental bend frequency is 668 cm−1. At K = 42, only the lowest state with energy 29
000 cm−1 in our final calculations and for a (−1)J+P = 1 calculation, N(K) is 885(A), 685(B), 787(A), 601(B) for K = 0, 1, 2, 3, respectively. It is 1(B), 3(A), 0(B), 1(A) for K = 39, 40, 41, 42, respectively. Clearly, there is no need to include v(K) functions when K > 42 and we therefore set Kmax is 42. The lowest level for each K is labelled by v2 = K, l2 = K. The fundamental bend frequency is 668 cm−1. At K = 42, only the lowest state with energy 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 729 cm−1 is included see Table 4.
729 cm−1 is included see Table 4.
Table 4 The number of v(K) functions, N(K), with energies under Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 with symmetry A+ and B+. The last column is the energy of the lowest state for each K, which corresponds to v2 = K and l2 = K. The energies are relative to the ZPE of 2535.79929 cm−1
000 cm−1 with symmetry A+ and B+. The last column is the energy of the lowest state for each K, which corresponds to v2 = K and l2 = K. The energies are relative to the ZPE of 2535.79929 cm−1
|
K
|
N(K)(A+) |
N(K)(B+) |
Energy |
| 0 |
885 |
733 |
0.000 |
| 1 |
832 |
685 |
668.151 |
| 2 |
787 |
645 |
1338.251 |
| 3 |
737 |
601 |
2010.299 |
| 4 |
692 |
564 |
2684.298 |
| 5 |
647 |
526 |
3360.249 |
| 6 |
606 |
490 |
4038.151 |
| 7 |
567 |
454 |
4718.006 |
| 8 |
526 |
422 |
5399.814 |
| 9 |
491 |
389 |
6083.574 |
| 10 |
454 |
360 |
6769.287 |
| 11 |
420 |
331 |
7456.952 |
| 12 |
386 |
304 |
8146.568 |
| 13 |
359 |
278 |
8838.135 |
| 14 |
330 |
254 |
9531.651 |
| 15 |
301 |
232 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 227.115 227.115 |
| 16 |
275 |
209 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924.526 924.526 |
| 17 |
249 |
187 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623.882 623.882 |
| 18 |
227 |
169 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325.181 325.181 |
| 19 |
205 |
150 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028.421 028.421 |
| 20 |
184 |
135 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733.600 733.600 |
| 21 |
165 |
120 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440.714 440.714 |
| 22 |
147 |
104 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 149.761 149.761 |
| 23 |
132 |
92 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860.737 860.737 |
| 24 |
115 |
79 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 573.639 573.639 |
| 25 |
102 |
68 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288.463 288.463 |
| 26 |
89 |
59 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005.203 005.203 |
| 27 |
76 |
51 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 723.856 723.856 |
| 28 |
65 |
41 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444.415 444.415 |
| 29 |
55 |
35 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166.876 166.876 |
| 30 |
47 |
28 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891.231 891.231 |
| 31 |
38 |
23 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 617.475 617.475 |
| 32 |
31 |
18 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345.600 345.600 |
| 33 |
26 |
14 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075.600 075.600 |
| 34 |
20 |
10 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 807.467 807.467 |
| 35 |
16 |
7 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541.193 541.193 |
| 36 |
11 |
5 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276.770 276.770 |
| 37 |
9 |
3 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014.188 014.188 |
| 38 |
6 |
2 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 753.440 753.440 |
| 39 |
4 |
1 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 494.517 494.517 |
| 40 |
3 |
0 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237.409 237.409 |
| 41 |
1 |
0 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 982.106 982.106 |
| 42 |
1 |
0 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 728.599 728.599 |
Table 5 Comparison between our A+ symmetry levels and Huang2022 levels for select J. Δ15k/Δ20k are the maxium absolute differences between our levels and Huang2022 levels up to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/20
000/20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, respectively. Our levels are obtained from two-step calculations with Ecut = 30
000 cm−1, respectively. Our levels are obtained from two-step calculations with Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. A complete list of energy levels up to J = 100 is available from the authors
000 cm−1. A complete list of energy levels up to J = 100 is available from the authors
|
|
N
bas
|
N
level
|
Δ
15k
|
Δ
20k
|
|
J = 10(even) |
6605 |
1780 |
0.00184 |
0.00203 |
|
J = 20(even) |
9185 |
2151 |
0.00210 |
0.01966 |
|
J = 30(even) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014 014 |
2102 |
0.00207 |
0.05755 |
|
J = 40(even) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 133 133 |
1998 |
0.00205 |
0.10287 |
|
J = 50(even) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
1871 |
0.00205 |
0.04117 |
|
J = 60(even) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
1724 |
0.00201 |
0.02665 |
|
J = 70(even) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
1557 |
0.00182 |
0.02060 |
|
J = 74(even) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
1487 |
0.00181 |
0.01067 |
|
J = 80(even) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
1388 |
0.00180 |
0.00713 |
|
J = 90(even) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
1207 |
0.00150 |
0.00299 |
|
J = 100(even) |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134 134 |
1036 |
0.00147 |
0.00204 |
|
J = 11(even) |
6051 |
1554 |
0.00013 |
0.00152 |
|
J = 31(even) |
9152 |
1822 |
0.00012 |
0.02617 |
|
J = 75(even) |
9249 |
1260 |
0.00013 |
0.00581 |
We can directly compare our N with those of Zak et al.24 because we use the same coordinates and KEO and compute the same v(K). We use an ALF basis and they use a DVR basis, but this should not affect the required number of v(K). Since our J = 100 levels are well converged, we can be certain that there is no need to use N = 100 functions for K > 42 (we use zero). Moreover, using N = 100 functions for 0 ≤ K ≤ 41 is probably inadequate for small K. We have N = 885 for K = 0. Even though our final basis size is similar to theirs for computing J = 100 levels (they have 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 functions and we have 10
100 functions and we have 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134), we expect that our basis functions are better and our levels are better converged.
134), we expect that our basis functions are better and our levels are better converged.
Although in our final calculations, we use only |v(K)〉, K ≤ 42, we actually compute |v(K)〉 for higher K because they can be used to converge levels higher than those we publish in this paper. A good general rule of thumb is to choose Nθ (the number of Gauss Legendre quadrature points) to be at least one larger than the highest degree of the ALF basis. So we use Nθ = K + lx + 1. When K ≤ 50, we use Nθ = 201, regardless of K. For smaller values of K, we have more points than we need, but it is advantageous to evaluate the potential at a single set of points for all K ≤ 50. When 100 ≥ K > 50, we use Nθ = 251.
It is interesting to compare our basis sizes with the basis sizes in the calculation of Schwenke and co-workers. Take the J = 100 A+ calculation as an example with data from ref. 46. They use a series of intermediate contracted functions. To compute 1-D contracted bend functions for each K, up to K = 100, they use a large threshold at 0.6 Hartree (132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). A large threshold is required because in their scheme stretch–bend coupling is incorporated only at the end. They use 1371 bend-rotation eigenfunctions with energies less than 0.26 Hartree (57
000 cm−1). A large threshold is required because in their scheme stretch–bend coupling is incorporated only at the end. They use 1371 bend-rotation eigenfunctions with energies less than 0.26 Hartree (57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) (not 0.15 Hartree stated in their paper27). The 1371 bend-rotation functions are then coupled to stretch functions to make a final basis with 147
000 cm−1) (not 0.15 Hartree stated in their paper27). The 1371 bend-rotation functions are then coupled to stretch functions to make a final basis with 147![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 671 functions using a threshold of 0.3 Hartree (66
671 functions using a threshold of 0.3 Hartree (66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). Because they use a direct eigensolver, there are unable to calculate eigenvalues in a basis this large and they therefore truncate it keeping only 45
000 cm−1). Because they use a direct eigensolver, there are unable to calculate eigenvalues in a basis this large and they therefore truncate it keeping only 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 functions. We also use a direct eigensolver for the final diagonalization, but our final basis size has only about 10
000 functions. We also use a direct eigensolver for the final diagonalization, but our final basis size has only about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 basis functions and is determined with a single low threshold of Ecut = 30
000 basis functions and is determined with a single low threshold of Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. See Fig. 2 and Table 6, for a comparison of our levels with those of Huang et al. for J = 40.
000 cm−1. See Fig. 2 and Table 6, for a comparison of our levels with those of Huang et al. for J = 40.
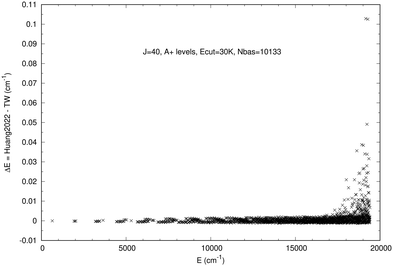 |
| | Fig. 2 Differences between Huang202246 and our levels (TW) for J = 40 A+ levels computed with Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. 000 cm−1. | |
Table 6 Comparison between our levels and Huang2022 levels for a select window of J = 40 A+ levels. Shown are the 1704th state to 1748th state. Δ22 = Huang2022 − TW. Δ17 = Huang2017 − TW. TW is this work. Our levels are obtained from two-step calculations obtained with Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. For our calculation, c1 and K are the coefficient of the dominant v(K) state and its K, respectively. c1 for the Huang calculation is the largest coefficient from their final diagonalization
000 cm−1. For our calculation, c1 and K are the coefficient of the dominant v(K) state and its K, respectively. c1 for the Huang calculation is the largest coefficient from their final diagonalization
|
i
|
TW |
Huang2022 |
Δ
22
|
Δ
17
|
TW |
Huang2022 |
|
c
1
|
K
|
c
1
|
| 1704 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156.7432 156.7432 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156.8461 156.8461 |
0.1029 |
1.1192 |
0.984 |
0 |
0.338 |
| 1705 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.7489 157.7489 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.7498 157.7498 |
0.0009 |
0.1299 |
0.794 |
10 |
0.365 |
| 1706 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.8551 157.8551 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.8552 157.8552 |
0.0001 |
4.1004 |
0.886 |
14 |
0.401 |
| 1707 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 162.3062 162.3062 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 162.3087 162.3087 |
0.0025 |
0.1802 |
0.785 |
6 |
0.303 |
| 1708 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166.7170 166.7170 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166.7163 166.7163 |
−0.0007 |
0.0018 |
0.993 |
14 |
0.462 |
| 1709 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170.7940 170.7940 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170.8160 170.8160 |
0.0220 |
1.3095 |
0.806 |
4 |
0.249 |
| 1710 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 172.7332 172.7332 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 172.7324 172.7324 |
−0.0008 |
0.1552 |
0.971 |
8 |
0.295 |
| 1711 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 173.1855 173.1855 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 173.1851 173.1851 |
−0.0004 |
0.0106 |
0.957 |
14 |
0.291 |
| 1712 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.2584 180.2584 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.2630 180.2630 |
0.0047 |
0.3436 |
0.811 |
2 |
0.268 |
| 1713 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186.0207 186.0207 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186.0239 186.0239 |
0.0032 |
0.2734 |
0.903 |
6 |
0.282 |
| 1714 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187.1353 187.1353 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187.1358 187.1358 |
0.0005 |
0.1136 |
0.805 |
9 |
0.376 |
| 1715 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 188.6595 188.6595 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 188.6603 188.6603 |
0.0008 |
0.0747 |
0.867 |
4 |
0.361 |
| 1716 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.5329 192.5329 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.5350 192.5350 |
0.0022 |
0.1184 |
0.791 |
7 |
0.429 |
| 1717 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.5890 192.5890 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.6090 192.6090 |
0.0200 |
1.2873 |
0.763 |
3 |
0.260 |
| 1718 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 196.8614 196.8614 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 196.8604 196.8604 |
−0.0010 |
0.0022 |
0.994 |
18 |
0.353 |
| 1719 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201.7280 201.7280 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201.7390 201.7390 |
0.0110 |
0.8847 |
0.677 |
5 |
0.223 |
| 1720 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 206.4734 206.4734 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 206.4784 206.4784 |
0.0050 |
0.2523 |
0.863 |
1 |
0.322 |
| 1721 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212.2731 212.2731 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212.2972 212.2972 |
0.0242 |
1.3899 |
0.532 |
3 |
0.209 |
| 1722 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 213.5329 213.5329 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 213.5324 213.5324 |
−0.0006 |
0.1487 |
0.904 |
0 |
0.186 |
| 1723 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214.9835 214.9835 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214.9825 214.9825 |
−0.0010 |
0.1143 |
0.995 |
14 |
0.391 |
| 1724 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217.7811 217.7811 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217.7800 217.7800 |
−0.0011 |
0.0010 |
0.996 |
22 |
0.394 |
| 1725 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218.7240 218.7240 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218.7257 218.7257 |
0.0017 |
0.0341 |
0.917 |
11 |
0.500 |
| 1726 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220.0152 220.0152 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220.0432 220.0432 |
0.0280 |
1.6477 |
0.673 |
1 |
0.177 |
| 1727 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224.8071 224.8071 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224.8136 224.8136 |
0.0064 |
0.5205 |
0.728 |
6 |
0.265 |
| 1728 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228.7026 228.7026 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228.7517 228.7517 |
0.0491 |
1.4633 |
0.935 |
2 |
0.281 |
| 1729 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229.7148 229.7148 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229.7182 229.7182 |
0.0034 |
1.7122 |
0.934 |
5 |
0.336 |
| 1730 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231.4000 231.4000 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231.4019 231.4019 |
0.0019 |
0.4021 |
0.965 |
9 |
0.480 |
| 1731 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231.9591 231.9591 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231.9579 231.9579 |
−0.0012 |
0.0002 |
0.999 |
26 |
0.511 |
| 1732 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232.9690 232.9690 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232.9710 232.9710 |
0.0020 |
0.0350 |
0.980 |
9 |
0.312 |
| 1733 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235.5377 235.5377 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235.5716 235.5716 |
0.0338 |
1.7576 |
0.782 |
0 |
0.229 |
| 1734 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237.4706 237.4706 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237.4699 237.4699 |
−0.0007 |
0.1428 |
0.895 |
2 |
0.218 |
| 1735 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238.2693 238.2693 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238.2712 238.2712 |
0.0019 |
0.0152 |
0.970 |
15 |
0.521 |
| 1736 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238.3057 238.3057 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238.3165 238.3165 |
0.0108 |
0.9118 |
0.879 |
6 |
0.405 |
| 1737 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242.5116 242.5116 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242.5141 242.5141 |
0.0025 |
0.2223 |
0.923 |
4 |
0.298 |
| 1738 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249.1103 249.1103 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249.1105 249.1105 |
0.0002 |
0.1479 |
0.968 |
8 |
0.510 |
| 1739 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252.0979 252.0979 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252.1000 252.1000 |
0.0021 |
0.0074 |
0.986 |
19 |
0.542 |
| 1740 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255.9739 255.9739 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255.9771 255.9771 |
0.0032 |
0.2162 |
0.846 |
2 |
0.372 |
| 1741 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258.6060 258.6060 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258.6083 258.6083 |
0.0023 |
0.0033 |
0.995 |
23 |
0.639 |
| 1742 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258.6561 258.6561 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258.6661 258.6661 |
0.0099 |
0.8936 |
0.787 |
0 |
0.277 |
| 1743 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261.5275 261.5275 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261.5360 261.5360 |
0.0084 |
0.5474 |
0.533 |
0 |
0.276 |
| 1744 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 263.8262 263.8262 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 263.8260 263.8260 |
−0.0002 |
0.0224 |
0.964 |
8 |
0.377 |
| 1745 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266.2800 266.2800 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266.2817 266.2817 |
0.0017 |
0.0648 |
0.938 |
1 |
0.280 |
| 1746 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266.7688 266.7688 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266.7862 266.7862 |
0.0174 |
1.3271 |
0.654 |
3 |
0.236 |
| 1747 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 274.1744 274.1744 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 274.1775 274.1775 |
0.0032 |
0.2293 |
0.844 |
2 |
0.268 |
| 1748 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277.6829 277.6829 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277.7854 277.7854 |
0.1025 |
3.8847 |
0.963 |
0 |
0.247 |
IX. Conclusion
In this paper, we propose a two-step method that uses an associated Legendre function basis and a K-independent quadrature. The advantage of the two-step idea is that the largest ro-vibrational term in the KEO does not have off-diagonal matrix elements in the |v(K)〉|JKM〉 basis. It is common to compute the |v(K)〉 functions in a basis of K-dependent DVR functions. A DVR seems appealing because the potential matrix in a DVR is diagonal. However, when using a K-dependent DVR, matrix elements of coordinate dependent factors in the KEO must be transformed from the ALF basis to the DVR. This is more complicated and more costly than using the ALF basis directly. If the ALF basis is used directly then these transformations are not necessary. However, when the ALF basis is used, it is necessary to either compute matrix-vector products with or calculate matrix elements of the potential. Fortunately, this is easily done, using a single set of (K-independent) quadrature points for all K, by evaluating sums sequentially.17,53–55 When one uses the ALF basis and quadrature (i.e. a finite basis representation17) rather than the corresponding DVR, one must transform the potential instead of the kinetic matrix. Whereas, transforming the kinetic matrix is complicated by the fact that the DVR is K-dependent, there is no need to use K-dependent points and weights when doing potential matrix elements by quadrature. Using a K-dependent DVR also requires evaluating the potential at different sets of points for each K. Another difference between our two-step method and the most popular two-step code5,6 is that we compute the |v(K)〉 with a Lanczos eigensolver. This makes it possible to use a large primitive basis whose functions are products of 1-D functions. The alternative is to use a sequence of contractions which works well, but requires additional steps. Iterative methods become essential for larger molecules, but are also useful for triatomics.
The two-step method was first used9 for H2D+, but it is most advantageous for linear molecules because the ro-vibrational coupling term incorporated into the Hamiltonian whose eigenfunctions are the |v(K)〉 basis functions is much larger for linear molecules. When it is large, the energies that correspond to |v(K)〉 increase rapidly with K (when K is increased to K + 1 the energy of the lowest |v(K)〉 increases by about the bend frequency). Because |v(K)〉 with large energies are less important, the number of |v(K)〉 which must be used to compute final energies and wavefunctions, below a chosen threshold, decreases with K. That number is actually zero if K is large enough. In some previous two-step calculations the number of |v(K)〉 has been chosen to be independent of K.
An efficient method for computing ro-vibrational levels of a linear triatomic molecule will also be useful for studying van der Waals complexes for which at least one of the constituents is a linear molecule. This is because a good basis is composed of products of intra- and inter-molecular functions.56,57
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work has been supported by the Natural Sciences and Engineering Research Council of Canada and the Digital Alliance of Canada. TC thanks the Jean d'Alembert fellowship program for its support at the Université Paris-Saclay. XGW thanks Donghui Zhang's group at the Dalian Institute of Chemical Physics for hospitality. We thank Xinchuan Huang and David Schwenke and Emil Zak for detailed and helpful discussions.
References
- G. D. Carney, L. L. Sprandel and C. W. Kern, Adv. Chem. Phys., 1978, 37, 305 CrossRef CAS.
- J. Tennyson, Comput. Phys. Rep., 1986, 4, 1 CrossRef.
- S. Carter and N. C. Handy, Comput. Phys. Commun., 1988, 51, 49 CrossRef CAS.
- P. Jensen, J. Mol. Spectrosc., 1988, 128, 478 CrossRef CAS.
- J. Tennyson, J. R. Henderson and N. G. Fulton, Comput. Phys. Commun., 1995, 86, 175 CrossRef CAS.
- J. Tennyson, M. A. Kostin, P. Barletta, G. J. Harris, O. L. Polyansky, J. Ramanlal and N. F. Zobov, Comput. Phys. Commun., 2004, 163, 85–116 CrossRef.
- D. W. Schwenke, J. Chem. Phys., 2015, 142, 144107 CrossRef PubMed.
- M. J. Bramley and N. C. Handy, J. Chem. Phys., 1993, 98, 1378–1397 CrossRef CAS.
- J. Tennyson and B. T. Sutcliffe, Mol. Phys., 1986, 58, 1067 CrossRef CAS.
- T. Carrington, J. Chem. Phys., 2017, 146, 120902 CrossRef PubMed.
- P. Sarkar, N. M. Poulin and T. Carrington, J. Chem. Phys., 1999, 110, 10269 CrossRef CAS.
- Z. Bačić and J. C. Light, Annu. Rev. Phys. Chem., 1989, 40, 469 CrossRef.
- M. Mladenovic, Spectrochim. Acta, Part A, 2002, 58, 809 CrossRef PubMed.
- F. T. Smith, Phys. Rev., 1960, 120, 1058 CrossRef.
- B. R. Johnson and W. P. Reinhardt, J. Chem. Phys., 1986, 85, 4538 CrossRef CAS.
- J. C. Light, I. P. Hamilton and J. V. Lill, J. Chem. Phys., 1985, 82(3), 1400–1409 CrossRef CAS.
- J. C. Light and T. Carrington Jr., Adv. Chem. Phys., 2000, 114, 263–310 CrossRef.
- J. M. Bowman, T. Carrington and H.-D. Meyer, Mol. Phys., 2008, 106, 2145–2182 CrossRef CAS.
- H. Massol,
et al.
, Space Sci. Rev., 2016, 205, 153 CrossRef CAS.
- M. Snels, S. Stefani, D. Grassi, G. Piccioni and A. Adriani, Planet. Space Sci., 2014, 103, 347 CrossRef CAS.
- I. E. Gordon,
et al.
, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 3 CrossRef CAS.
- B. Connor,
et al.
, Atmos. Meas. Tech., 2016, 9, 5227 CrossRef.
- F. Oyafuso,
et al.
, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 213 CrossRef CAS.
- E. J. Zak, J. Tennyson, O. L. Polyansky, L. Lodi, S. A. Tashkun and V. I. Perevalov, J. Quant. Spectrosc. Radiat. Transfer, 2016, 177, 31 CrossRef CAS.
- X. Huang, D. W. Schwenke, S. A. Tashkun and T. J. Lee, J. Chem. Phys., 2012, 136, 124311 CrossRef PubMed.
- X. Huang, D. W. Schwenke, R. S. Freedman and T. J. Lee, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 224 CrossRef CAS.
- X. Huang, D. W. Schwenke, R. S. Freedman and T. J. Lee, J. Phys. Chem. A, 2022, 126, 5940 CrossRef CAS PubMed.
- S. N. Yurchenko, T. M. Mellor, R. S. Freedman and J. Tennyson, Mon. Not. R. Astron. Soc., 2020, 496, 5282–5291 CrossRef CAS.
- S. Carter, N. C. Handy and B. T. Sutcliffe, Mol. Phys., 1983, 49, 745 CrossRef CAS.
- X.-G. Wang and T. Carrington, Jr., J. Chem. Phys., 2017, 146, 104105 CrossRef PubMed.
- J. Tennyson and B. Sutcliffe, Int. J. Quantum Chem., 1992, 42, 941–952 CrossRef CAS.
- S. Carter and N. C. Handy, J. Chem. Phys., 1987, 87, 4294 CrossRef CAS.
- S. Carter, N. C. Handy and I. M. Mills, Philos. Trans. R. Soc. London, Ser. A, 1990, 332, 309 CrossRef CAS.
- G. Yan, D. Xie and A. Tian, J. Phys. Chem., 1994, 98, 8870–8875 CrossRef CAS.
- H. Partridge and D. W. Schwenke, J. Chem. Phys., 1997, 106, 4618 CrossRef CAS.
- J. Zúñiga, A. Bastida, M. Alacid and A. Requena, J. Mol. Spectrosc., 2001, 205, 62 CrossRef PubMed.
- J. Cerezo, A. Bastida, A. Requena and J. Zúñiga, J. Quant. Spectrosc. Radiat. Transfer, 2014, 147, 233 CrossRef CAS.
- X.-G. Wang and T. Carrington Jr, Mol. Phys., 2012, 110(9–10), 825–835 CrossRef CAS.
- X.-G. Wang and T. Carrington, Jr., J. Chem. Phys., 2013, 138, 104106 CrossRef PubMed.
- D. W. Schwenke and D. G. Truhlar, Comput. Phys. Commun., 1984, 34, 57 CrossRef.
- S. Carter and N. C. Handy, Mol. Phys., 1986, 57, 175 CrossRef CAS.
- A. A. A. Azzam, J. Tennyson, S. N. Yurchenko and O. V. Naumenko, Mon. Not. R. Astron. Soc., 2016, 460, 4063–4074 CrossRef CAS.
- D. W. Schwenke, J. Phys. Chem., 1996, 100, 2867 CrossRef CAS.
- P. R. Bunker and J. M. R. Stone, J. Mol. Spectrosc., 1972, 41, 310–332 CrossRef CAS.
- X.-G. Wang and T. Carrington Jr., J. Chem. Phys., 2004, 121, 2937 CrossRef CAS PubMed.
-
X. Huang, private communication, November, 2023.
- S. N. Yurchenko and T. M. Mellor, J. Chem. Phys., 2020, 153, 154106 CrossRef CAS PubMed.
-
X. G. Wang and T. Carrington, RV3: A package of programs to compute rovi-brational levels and wavefunctions of triatomic molecules.
- H. Wei and T. Carrington Jr., J. Chem. Phys., 1992, 97, 3029 CrossRef CAS.
- J. Tennyson and B. T. Sutcliffe, J. Chem. Phys., 1982, 77, 406 Search PubMed.
- X.-G. Wang and T. Carrington, Jr., J. Chem. Phys., 2015, 143, 024303 CrossRef PubMed.
- ESI† for J = 0 A+ levels up to 20
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, and all the levels referred to in Table 5.
000 cm−1, and all the levels referred to in Table 5.
- M. J. Bramley and T. Carrington, Jr., J. Chem. Phys., 1993, 99, 8519 CrossRef CAS.
- U. Manthe and H. Köppel, J. Chem. Phys., 1990, 93, 345 CrossRef CAS.
- X.-G. Wang and T. Carrington, Jr., J. Chem. Phys., 2014, 141, 154106 CrossRef PubMed.
- P. M. Felker and Z. Bačić, J. Chem. Phys., 2019, 151, 024305 CrossRef PubMed.
- X.-G. Wang and T. Carrington, Jr., J. Chem. Phys., 2018, 148, 074108 CrossRef PubMed.
|
| This journal is © the Owner Societies 2024 |
 and
Tucker
Carrington
Jr
and
Tucker
Carrington
Jr

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to 0.0001 cm−1.
000 cm−1 to 0.0001 cm−1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the zero point energy.
000 cm−1 above the zero point energy.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ in the term moved to the vibrational Hamiltonian is small where vibrational wavefunctions are large. We use Radau coordinates14,15 and a bisector-x molecule-fixed axis system. Both have been used before in two-step calculations.
θ in the term moved to the vibrational Hamiltonian is small where vibrational wavefunctions are large. We use Radau coordinates14,15 and a bisector-x molecule-fixed axis system. Both have been used before in two-step calculations.![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 1 + R1
1 + R1![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 2. The z-axis is in the molecular plane with
2. The z-axis is in the molecular plane with ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 1 having a positive z component.
1 having a positive z component. ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 1 and
1 and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) 2 are the Radau vectors see Fig. 1. The bisector-x KEO was first derived by Carter, Handy and Sutcliffe.29 Our KEO is different from theirs because the direction of the z-axis is reversed, and our molecule-fixed angular momentum operators satisfy the anomalous commutation relation (see ref. 30). We choose the bisector-x embedding because it makes it easy to exploit the symmetry of CO2 and reduces the ro-vibrational coupling. The ro-vibrational KEO we use has two parts: a vibrational term Tv and a ro-vibrational term Tvr,
2 are the Radau vectors see Fig. 1. The bisector-x KEO was first derived by Carter, Handy and Sutcliffe.29 Our KEO is different from theirs because the direction of the z-axis is reversed, and our molecule-fixed angular momentum operators satisfy the anomalous commutation relation (see ref. 30). We choose the bisector-x embedding because it makes it easy to exploit the symmetry of CO2 and reduces the ro-vibrational coupling. The ro-vibrational KEO we use has two parts: a vibrational term Tv and a ro-vibrational term Tvr,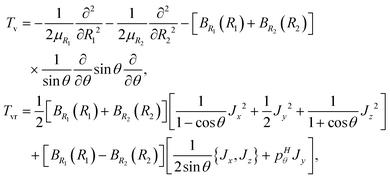
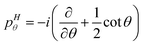
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θdR1dR2dθ
θdR1dR2dθ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βdαdβdγ. α, β, γ are Euler angles. The ro-vibrational term can be re-written in terms of G matrix elements
βdαdβdγ. α, β, γ are Euler angles. The ro-vibrational term can be re-written in terms of G matrix elements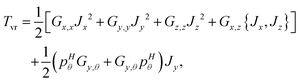
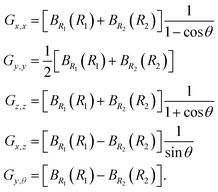
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v = [
v = [![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v + V(R1,R2,θ)],
v + V(R1,R2,θ)],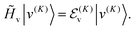
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v is diagonal, the off-diagonal elements of
v is diagonal, the off-diagonal elements of ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr are small, and convergence with respect to the size of the basis is very fast. We retain the |v(K)〉 for which the corresponding energy is less than a cut-off energy, Ecut.
vr are small, and convergence with respect to the size of the basis is very fast. We retain the |v(K)〉 for which the corresponding energy is less than a cut-off energy, Ecut.
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v +
v + ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr,
vr,![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v. Matrix elements of coordinate dependent factors in the terms of the KEO are integrals that are computed by quadrature. The KEO of the modified “vibrational” Hamiltonian is designed so that, if the primitive basis functions, used to solve eqn (8), are chosen correctly, all matrix elements of
v. Matrix elements of coordinate dependent factors in the terms of the KEO are integrals that are computed by quadrature. The KEO of the modified “vibrational” Hamiltonian is designed so that, if the primitive basis functions, used to solve eqn (8), are chosen correctly, all matrix elements of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v in the primitive basis are finite. Some of the coordinate dependent factors in terms in
v in the primitive basis are finite. Some of the coordinate dependent factors in terms in ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr are singular, but only where all wavefunctions have negligible amplitude. Such singularities are “unimportant”. Some authors discard DVR or quadrature points close to an unimportant singularity,5,6,31 but this is unnecessary. We find that for CO2, points close to the θ = 0 singularity cause no problems. The KEO of eqn (1) is singular at the equilibrium geometry where θ = π and also at θ = 0. The θ = 0 singularity is unimportant because it corresponds to C–C–O which has a very high potential energy. The θ = π singularity occurs in the factor
vr are singular, but only where all wavefunctions have negligible amplitude. Such singularities are “unimportant”. Some authors discard DVR or quadrature points close to an unimportant singularity,5,6,31 but this is unnecessary. We find that for CO2, points close to the θ = 0 singularity cause no problems. The KEO of eqn (1) is singular at the equilibrium geometry where θ = π and also at θ = 0. The θ = 0 singularity is unimportant because it corresponds to C–C–O which has a very high potential energy. The θ = π singularity occurs in the factor 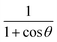 in Gzz. To choose basis functions to deal with the important singularity, we use
in Gzz. To choose basis functions to deal with the important singularity, we use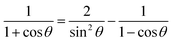
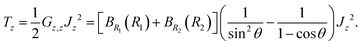
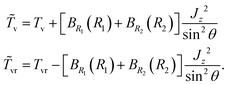
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v are finite because
v are finite because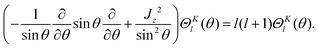
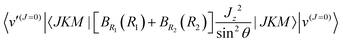 are large. In a two-step calculation, the term
are large. In a two-step calculation, the term 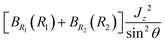 does not couple basis functions because it is included in the operator whose eigenfunctions are the |v(K)〉 basis functions. |v(K)〉 is like an eigenfunction of a 2-D harmonic oscillator with K = l2. This basis includes all the bending states
does not couple basis functions because it is included in the operator whose eigenfunctions are the |v(K)〉 basis functions. |v(K)〉 is like an eigenfunction of a 2-D harmonic oscillator with K = l2. This basis includes all the bending states 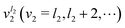 . For a given K = l2, the ground state of
. For a given K = l2, the ground state of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) v is a state assigned to v2 = l2 = K.
v is a state assigned to v2 = l2 = K.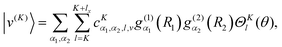
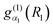 and
and 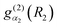 are discrete variable functions.17 In this section we present equations for matrix elements in the primitive basis each of whose functions is a product of the vibrational functions in eqn (15) and a non-parity adapted rotational function,
are discrete variable functions.17 In this section we present equations for matrix elements in the primitive basis each of whose functions is a product of the vibrational functions in eqn (15) and a non-parity adapted rotational function,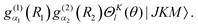
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v is diagonal and its elements are
v is diagonal and its elements are![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v|l;J,K〉 = [BR1(R1) + BR2(R2)]l(l + 1)δl′,l.
v|l;J,K〉 = [BR1(R1) + BR2(R2)]l(l + 1)δl′,l.![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr in the primitive basis are,
vr in the primitive basis are,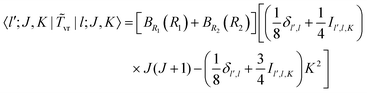
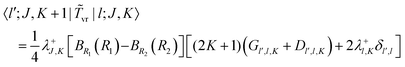
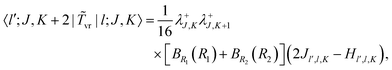
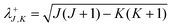 . The matrices D, G, H, I and J are given in Appendix A of ref. 30. They are reproduced below,
. The matrices D, G, H, I and J are given in Appendix A of ref. 30. They are reproduced below,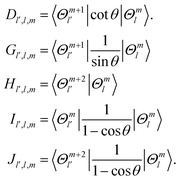
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/sin
θ)/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and that 2J − H could be combined into one matrix by computing matrix elements of (1 + cos
θ and that 2J − H could be combined into one matrix by computing matrix elements of (1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/(1 − cos
θ)/(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). We have not made these combinations because we want to give the matrix elements that are required for both the bisector-x and the bisector-z frames.30 Specifically, for the bisector-z frame, G − D is the matrix representing (1 − cos
θ). We have not made these combinations because we want to give the matrix elements that are required for both the bisector-x and the bisector-z frames.30 Specifically, for the bisector-z frame, G − D is the matrix representing (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/sin
θ)/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and it appears in ΔK = 1 matrix elements, and 2F − H is the matrix representing (1 − cos
θ and it appears in ΔK = 1 matrix elements, and 2F − H is the matrix representing (1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/(1 + cos
θ)/(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) and it appears in ΔK = 2 matrix elements.30
θ) and it appears in ΔK = 2 matrix elements.30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ in a ALF basis. If we used these points we would be doing a finite basis representation (FBR) calculation equivalent to the DVR calculation of DVR3D. Both quadratures allow one to evaluate potential matrix vector products with the sequential summation technique and use an iterative eigensolver to compute thousands of eigenstates |v(K)〉 directly in the 3D direct product primitive basis. The 3-D direct product basis is large, but that is not a problem if an iterative eigensolver is used. If a direct eigensolver used, it is common to reduce the size of the primitive basis by doing a series of diagonalizations and truncations.5,6,27,33
θ in a ALF basis. If we used these points we would be doing a finite basis representation (FBR) calculation equivalent to the DVR calculation of DVR3D. Both quadratures allow one to evaluate potential matrix vector products with the sequential summation technique and use an iterative eigensolver to compute thousands of eigenstates |v(K)〉 directly in the 3D direct product primitive basis. The 3-D direct product basis is large, but that is not a problem if an iterative eigensolver is used. If a direct eigensolver used, it is common to reduce the size of the primitive basis by doing a series of diagonalizations and truncations.5,6,27,33![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr matrix elements in Section IVA, it is straightforward to compute the matrix elements of the ro-vibrational Hamiltonian in the contracted basis. The diagonal elements are
vr matrix elements in Section IVA, it is straightforward to compute the matrix elements of the ro-vibrational Hamiltonian in the contracted basis. The diagonal elements are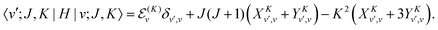
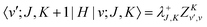
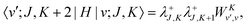
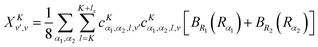
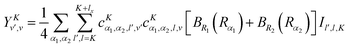
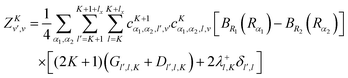
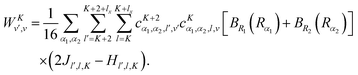
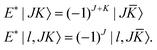
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) = −KThe parity-adapted (PA) primitive basis is therefore
= −KThe parity-adapted (PA) primitive basis is therefore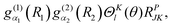
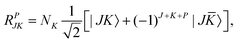
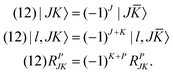
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v in the PA primitive basis are the same as those in the primitive basis. Matrix elements of
v in the PA primitive basis are the same as those in the primitive basis. Matrix elements of ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr in the PA primitive basis are the same as those in the primitive basis except each is multiplied by a factor, FK = (1 + δK,0)1/2. They can be derived by taking advantage of the factorization in eqn (36) and using the matrix elements of rotational operators in the RPJK basis given in ref. 39. The results are
vr in the PA primitive basis are the same as those in the primitive basis except each is multiplied by a factor, FK = (1 + δK,0)1/2. They can be derived by taking advantage of the factorization in eqn (36) and using the matrix elements of rotational operators in the RPJK basis given in ref. 39. The results are![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v|l;J,K,P〉 = [BR1(R1) + BR2(R2)]l(l + 1)δl′,l
v|l;J,K,P〉 = [BR1(R1) + BR2(R2)]l(l + 1)δl′,l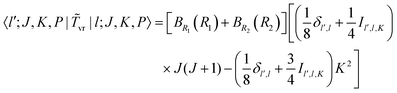
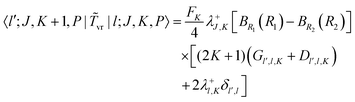
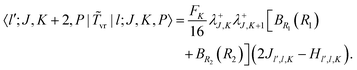
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) vr for K = 1 arising from Jx2 − Jy2 (there is no corresponding matrix element in the non-PA basis),
vr for K = 1 arising from Jx2 − Jy2 (there is no corresponding matrix element in the non-PA basis),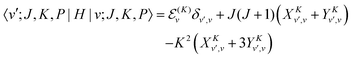
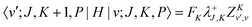
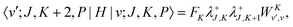
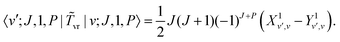
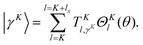
 is a transformation matrix determined by diagonalizing the matrix representing cos
is a transformation matrix determined by diagonalizing the matrix representing cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ in the ALF basis.17 Because we do not use a DVR for θ, we must evaluate integrals by quadrature. If we used the Gauss-Jacobi quadrature that underlies the K-dependent DVR used in DVR3D, then our Hamiltonian matrix and the matrix of DVR3D would be unitarily equivalent, HDVR3D = (TK)T
θ in the ALF basis.17 Because we do not use a DVR for θ, we must evaluate integrals by quadrature. If we used the Gauss-Jacobi quadrature that underlies the K-dependent DVR used in DVR3D, then our Hamiltonian matrix and the matrix of DVR3D would be unitarily equivalent, HDVR3D = (TK)T![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) vTK, where
vTK, where ![[H with combining tilde]](https://www.rsc.org/images/entities/b_char_0048_0303.gif) v is the matrix computed with Gauss-Jacobi quadrature. Instead, we use a K-independent quadrature.17 DVR3D computes matrices representing coordinate dependent factors D, G, H, I, and J, in the ALF basis and then transforms them to the K-dependent DVR. By using only the ALF, we obviate the need to transform all these matrices into the DVR. The transformation is a bit tricky because the DVR is K-dependent which means that different transformation matrices must be used on the left and on the right. In Section 2.3 of ref. 42, it is noted that the cost of transforming into the DVR can be reduced by doing sums sequentially; we completely eliminate the transformation. In the first two-step paper9 in 1986, a vector-z frame and an ALF basis were used. DVR3D uses not only a different primitive basis but also a different contracted basis. As pointed out by Yan, Xie and Tian,34 in the two-step calculation of DVR3D, the contracted functions computed in the first step are different for each J, K pair. The modified “vibrational” KEOs used by DVR3D and by Carter and Handy32 include not only
v is the matrix computed with Gauss-Jacobi quadrature. Instead, we use a K-independent quadrature.17 DVR3D computes matrices representing coordinate dependent factors D, G, H, I, and J, in the ALF basis and then transforms them to the K-dependent DVR. By using only the ALF, we obviate the need to transform all these matrices into the DVR. The transformation is a bit tricky because the DVR is K-dependent which means that different transformation matrices must be used on the left and on the right. In Section 2.3 of ref. 42, it is noted that the cost of transforming into the DVR can be reduced by doing sums sequentially; we completely eliminate the transformation. In the first two-step paper9 in 1986, a vector-z frame and an ALF basis were used. DVR3D uses not only a different primitive basis but also a different contracted basis. As pointed out by Yan, Xie and Tian,34 in the two-step calculation of DVR3D, the contracted functions computed in the first step are different for each J, K pair. The modified “vibrational” KEOs used by DVR3D and by Carter and Handy32 include not only ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) v, but also all J2 and Jz2 terms. In other words, they added the second and third terms on the RHS of eqn (23). We find that most of the computation time is spent in the first-step of the calculation. If, as is true in our calculation, it is not necessary to recompute |v(K)〉 for each value of J, a lot of computer time is saved. Another difference between DVR3D and what we do is that we do not discard quadrature points close to the singularity.
v, but also all J2 and Jz2 terms. In other words, they added the second and third terms on the RHS of eqn (23). We find that most of the computation time is spent in the first-step of the calculation. If, as is true in our calculation, it is not necessary to recompute |v(K)〉 for each value of J, a lot of computer time is saved. Another difference between DVR3D and what we do is that we do not discard quadrature points close to the singularity.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 were converged. In this paper, we use their levels,27,46 called Huang2022 levels, as a benchmark to compare with our levels. The levels we received from them are published in ref. 27 and are used to generate the Ames-2021 line list.27 We also compare with their levels computed with a smaller basis on the same PES26 and call them Huang2017 levels.
000 cm−1 were converged. In this paper, we use their levels,27,46 called Huang2022 levels, as a benchmark to compare with our levels. The levels we received from them are published in ref. 27 and are used to generate the Ames-2021 line list.27 We also compare with their levels computed with a smaller basis on the same PES26 and call them Huang2017 levels.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 868.66175734604622 me
868.66175734604622 me![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148.94559967216628 me
148.94559967216628 me![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474.631482453 cm−1
474.631482453 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. A large (120) sine DVR basis provides the benchmark for the optimization. Our final parameters for the TDM basis are De = 65
000 cm−1. A large (120) sine DVR basis provides the benchmark for the optimization. Our final parameters for the TDM basis are De = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, ωe = 2170 cm−1, Re = 2.14a0. A = 4De/ωe = 119.82. The number of Morse bound states is [A/2] = 59. According to ref. 49, α = A − 2[A/2] = 1.82, if NRi ≥ 59; and α = A − 2NRi if NRi ≤ 59.
000 cm−1, ωe = 2170 cm−1, Re = 2.14a0. A = 4De/ωe = 119.82. The number of Morse bound states is [A/2] = 59. According to ref. 49, α = A − 2[A/2] = 1.82, if NRi ≥ 59; and α = A − 2NRi if NRi ≤ 59.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 with errors of 1 × 10−4 cm−1. We fix NR1 = NR2 = 28 and find that lx = 150 is enough to converge levels up to 20
000 cm−1 with errors of 1 × 10−4 cm−1. We fix NR1 = NR2 = 28 and find that lx = 150 is enough to converge levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to within 3 × 10−5 cm−1, by comparing with levels computed with lx = 200. Subsequently, with lx = 150 fixed, we test TDM DVR bases with up to NR1 = NR2 = 80. The basis with (NR1 = NR2,lx) = (50, 150) is chosen as our final primitive basis and is hereafter called basis I. Compared to levels computed with (NR1 = NR2,lx) = (80, 150), basis I converges almost all the J = 0 levels up to 20
000 cm−1 to within 3 × 10−5 cm−1, by comparing with levels computed with lx = 200. Subsequently, with lx = 150 fixed, we test TDM DVR bases with up to NR1 = NR2 = 80. The basis with (NR1 = NR2,lx) = (50, 150) is chosen as our final primitive basis and is hereafter called basis I. Compared to levels computed with (NR1 = NR2,lx) = (80, 150), basis I converges almost all the J = 0 levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to within 1 × 10−4 cm−1; the largest error is 0.00165 cm−1 at 19
000 cm−1 to within 1 × 10−4 cm−1; the largest error is 0.00165 cm−1 at 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 cm−1. We refer to the difference between levels computed with the (NR1 = NR1,lx) = (50, 150) basis and with the (NR1 = NR1,lx) = (80, 150) basis as the primitive-basis error see Table 2. Basis I has 377
160 cm−1. We refer to the difference between levels computed with the (NR1 = NR1,lx) = (50, 150) basis and with the (NR1 = NR1,lx) = (80, 150) basis as the primitive-basis error see Table 2. Basis I has 377![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 functions, for J = 0.
500 functions, for J = 0.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/20
000/20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, respectively, relative to the benchmark results obtained with the primitive basis NR1 = NR2 = 80 and lx = 150. The energies are in cm−1. The number of bend quadrature points is Nθ = lx + 1
000 cm−1, respectively, relative to the benchmark results obtained with the primitive basis NR1 = NR2 = 80 and lx = 150. The energies are in cm−1. The number of bend quadrature points is Nθ = lx + 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900
900![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 624
624![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600
600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400
400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52). This difference is certainly not due to convergence error in either calculation. We therefore consider any differences larger than 0.0003 cm−1 to be due to their basis set convergence error. In Table 2, we show that, for J = 0 levels below 20
52). This difference is certainly not due to convergence error in either calculation. We therefore consider any differences larger than 0.0003 cm−1 to be due to their basis set convergence error. In Table 2, we show that, for J = 0 levels below 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, the largest difference is 0.00116 cm−1 comparing to the Huang2022 levels and 0.07551 cm−1 comparing to the Huang2017 levels. The largest differences are in bold in Table S1 of ESI.†
000 cm−1, the largest difference is 0.00116 cm−1 comparing to the Huang2022 levels and 0.07551 cm−1 comparing to the Huang2017 levels. The largest differences are in bold in Table S1 of ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 This indicates that there are small convergence errors in their J = 0 levels. A list of all the J = 0 A+ levels is given in Table S1 of the ESI.†
52 This indicates that there are small convergence errors in their J = 0 levels. A list of all the J = 0 A+ levels is given in Table S1 of the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52
52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and as large as 8.188 cm−1 up to 20
000 cm−1 and as large as 8.188 cm−1 up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. However, the goal of Zak et al. was to compute levels only up to 14
000 cm−1. However, the goal of Zak et al. was to compute levels only up to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 see Table 2.
500 cm−1 see Table 2.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. The primitive basis has 8
000 cm−1. The primitive basis has 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452
452![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 even-parity basis functions see Table 3 for details. We find that the contracted basis with Ecut = 30
500 even-parity basis functions see Table 3 for details. We find that the contracted basis with Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 is sufficient to converge levels up to 20
000 cm−1 is sufficient to converge levels up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to within 3.4 × 10−5 cm−1 see column 5 and 6 of Table 3. We therefore use Ecut = 30
000 cm−1 to within 3.4 × 10−5 cm−1 see column 5 and 6 of Table 3. We therefore use Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 to compute all the levels reported in this paper, up to J = 100.
000 cm−1 to compute all the levels reported in this paper, up to J = 100.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (the number of levels is 2151) are used to do the test. Δ15k/Δ20k are the maxium absolute differences up to 15
000 cm−1 (the number of levels is 2151) are used to do the test. Δ15k/Δ20k are the maxium absolute differences up to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/20
000/20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, respectively, relative to the benchmark levels computed in the NR1 = NR2 = 50, lx = 170 primitive basis with Nθ = 171 and relative to two-step levels computed with Ecut = 38
000 cm−1, respectively, relative to the benchmark levels computed in the NR1 = NR2 = 50, lx = 170 primitive basis with Nθ = 171 and relative to two-step levels computed with Ecut = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. The size of the even-parity primitive basis is 8
000 cm−1. The size of the even-parity primitive basis is 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452
452![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500. The energies are in cm−1
500. The energies are in cm−1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 428
428![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. If one aims to converge only levels up to 15
000 cm−1. If one aims to converge only levels up to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, one can lower Ecut to at least 25
000 cm−1, one can lower Ecut to at least 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. When Ecut is large enough, the error in two-step eigenvalues compared to the corresponding primitive-basis eigenvalues decreases quickly as Ecut is increased. However, this two-step error is not the only error, there is also the primitive-basis error. For J = 20 A+, see Table 3, the largest eigenvalue difference between two-step calculations with Ecut = 30
000 cm−1. When Ecut is large enough, the error in two-step eigenvalues compared to the corresponding primitive-basis eigenvalues decreases quickly as Ecut is increased. However, this two-step error is not the only error, there is also the primitive-basis error. For J = 20 A+, see Table 3, the largest eigenvalue difference between two-step calculations with Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and Ecut = 15
000 cm−1 and Ecut = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 is Δ15k = 2.0 × 10−9 cm−1, but this does not imply that errors in two-step eigenvalues computed with Ecut = 15
000 cm−1 is Δ15k = 2.0 × 10−9 cm−1, but this does not imply that errors in two-step eigenvalues computed with Ecut = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 are 2.0 × 10−9 cm−1 because there is also primitive-basis error. In fact, the largest difference between two-step levels with Ecut = 15
000 cm−1 are 2.0 × 10−9 cm−1 because there is also primitive-basis error. In fact, the largest difference between two-step levels with Ecut = 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and primitive-basis levels computed with the larger primitive basis (NR1 = NR2,lx) = (50, 180) primitive basis is 2.2 × 10−5 cm−1. When J is large, primitive-basis levels with the (NR1 = NR2,lx) = (50, 180) basis are not available. Convergence with respect to Ecut is not the full story.
000 cm−1 and primitive-basis levels computed with the larger primitive basis (NR1 = NR2,lx) = (50, 180) primitive basis is 2.2 × 10−5 cm−1. When J is large, primitive-basis levels with the (NR1 = NR2,lx) = (50, 180) basis are not available. Convergence with respect to Ecut is not the full story.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 in our final calculations and for a (−1)J+P = 1 calculation, N(K) is 885(A), 685(B), 787(A), 601(B) for K = 0, 1, 2, 3, respectively. It is 1(B), 3(A), 0(B), 1(A) for K = 39, 40, 41, 42, respectively. Clearly, there is no need to include v(K) functions when K > 42 and we therefore set Kmax is 42. The lowest level for each K is labelled by v2 = K, l2 = K. The fundamental bend frequency is 668 cm−1. At K = 42, only the lowest state with energy 29
000 cm−1 in our final calculations and for a (−1)J+P = 1 calculation, N(K) is 885(A), 685(B), 787(A), 601(B) for K = 0, 1, 2, 3, respectively. It is 1(B), 3(A), 0(B), 1(A) for K = 39, 40, 41, 42, respectively. Clearly, there is no need to include v(K) functions when K > 42 and we therefore set Kmax is 42. The lowest level for each K is labelled by v2 = K, l2 = K. The fundamental bend frequency is 668 cm−1. At K = 42, only the lowest state with energy 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 729 cm−1 is included see Table 4.
729 cm−1 is included see Table 4.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 with symmetry A+ and B+. The last column is the energy of the lowest state for each K, which corresponds to v2 = K and l2 = K. The energies are relative to the ZPE of 2535.79929 cm−1
000 cm−1 with symmetry A+ and B+. The last column is the energy of the lowest state for each K, which corresponds to v2 = K and l2 = K. The energies are relative to the ZPE of 2535.79929 cm−1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 227.115
227.115![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924.526
924.526![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 623.882
623.882![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325.181
325.181![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 028.421
028.421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733.600
733.600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440.714
440.714![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 149.761
149.761![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860.737
860.737![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 573.639
573.639![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288.463
288.463![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 005.203
005.203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 723.856
723.856![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444.415
444.415![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166.876
166.876![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 891.231
891.231![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 617.475
617.475![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345.600
345.600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075.600
075.600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 807.467
807.467![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 541.193
541.193![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276.770
276.770![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014.188
014.188![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 753.440
753.440![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 494.517
494.517![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237.409
237.409![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 982.106
982.106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 728.599
728.599![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000/20
000/20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, respectively. Our levels are obtained from two-step calculations with Ecut = 30
000 cm−1, respectively. Our levels are obtained from two-step calculations with Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. A complete list of energy levels up to J = 100 is available from the authors
000 cm−1. A complete list of energy levels up to J = 100 is available from the authors
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 014
014![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 133
133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134
134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 functions and we have 10
100 functions and we have 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 134), we expect that our basis functions are better and our levels are better converged.
134), we expect that our basis functions are better and our levels are better converged.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). A large threshold is required because in their scheme stretch–bend coupling is incorporated only at the end. They use 1371 bend-rotation eigenfunctions with energies less than 0.26 Hartree (57
000 cm−1). A large threshold is required because in their scheme stretch–bend coupling is incorporated only at the end. They use 1371 bend-rotation eigenfunctions with energies less than 0.26 Hartree (57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) (not 0.15 Hartree stated in their paper27). The 1371 bend-rotation functions are then coupled to stretch functions to make a final basis with 147
000 cm−1) (not 0.15 Hartree stated in their paper27). The 1371 bend-rotation functions are then coupled to stretch functions to make a final basis with 147![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 671 functions using a threshold of 0.3 Hartree (66
671 functions using a threshold of 0.3 Hartree (66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). Because they use a direct eigensolver, there are unable to calculate eigenvalues in a basis this large and they therefore truncate it keeping only 45
000 cm−1). Because they use a direct eigensolver, there are unable to calculate eigenvalues in a basis this large and they therefore truncate it keeping only 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 functions. We also use a direct eigensolver for the final diagonalization, but our final basis size has only about 10
000 functions. We also use a direct eigensolver for the final diagonalization, but our final basis size has only about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 basis functions and is determined with a single low threshold of Ecut = 30
000 basis functions and is determined with a single low threshold of Ecut = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. See Fig. 2 and Table 6, for a comparison of our levels with those of Huang et al. for J = 40.
000 cm−1. See Fig. 2 and Table 6, for a comparison of our levels with those of Huang et al. for J = 40.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1.
000 cm−1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. For our calculation, c1 and K are the coefficient of the dominant v(K) state and its K, respectively. c1 for the Huang calculation is the largest coefficient from their final diagonalization
000 cm−1. For our calculation, c1 and K are the coefficient of the dominant v(K) state and its K, respectively. c1 for the Huang calculation is the largest coefficient from their final diagonalization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156.7432
156.7432![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156.8461
156.8461![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.7489
157.7489![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.7498
157.7498![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.8551
157.8551![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157.8552
157.8552![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 162.3062
162.3062![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 162.3087
162.3087![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166.7170
166.7170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166.7163
166.7163![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170.7940
170.7940![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170.8160
170.8160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 172.7332
172.7332![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 172.7324
172.7324![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 173.1855
173.1855![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 173.1851
173.1851![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.2584
180.2584![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.2630
180.2630![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186.0207
186.0207![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 186.0239
186.0239![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187.1353
187.1353![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 187.1358
187.1358![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 188.6595
188.6595![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 188.6603
188.6603![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.5329
192.5329![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.5350
192.5350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.5890
192.5890![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.6090
192.6090![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 196.8614
196.8614![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 196.8604
196.8604![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201.7280
201.7280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201.7390
201.7390![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 206.4734
206.4734![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 206.4784
206.4784![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212.2731
212.2731![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 212.2972
212.2972![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 213.5329
213.5329![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 213.5324
213.5324![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214.9835
214.9835![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214.9825
214.9825![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217.7811
217.7811![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 217.7800
217.7800![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218.7240
218.7240![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218.7257
218.7257![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220.0152
220.0152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220.0432
220.0432![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224.8071
224.8071![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224.8136
224.8136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228.7026
228.7026![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228.7517
228.7517![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229.7148
229.7148![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229.7182
229.7182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231.4000
231.4000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231.4019
231.4019![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231.9591
231.9591![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231.9579
231.9579![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232.9690
232.9690![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 232.9710
232.9710![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235.5377
235.5377![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 235.5716
235.5716![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237.4706
237.4706![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 237.4699
237.4699![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238.2693
238.2693![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238.2712
238.2712![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238.3057
238.3057![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238.3165
238.3165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242.5116
242.5116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242.5141
242.5141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249.1103
249.1103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249.1105
249.1105![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252.0979
252.0979![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252.1000
252.1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255.9739
255.9739![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255.9771
255.9771![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258.6060
258.6060![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258.6083
258.6083![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258.6561
258.6561![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 258.6661
258.6661![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261.5275
261.5275![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 261.5360
261.5360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 263.8262
263.8262![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 263.8260
263.8260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266.2800
266.2800![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266.2817
266.2817![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266.7688
266.7688![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266.7862
266.7862![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 274.1744
274.1744![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 274.1775
274.1775![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277.6829
277.6829![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277.7854
277.7854![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, and all the levels referred to in Table 5.
000 cm−1, and all the levels referred to in Table 5.