Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Density functional theory methods applied to homogeneous and heterogeneous catalysis: a short review and a practical user guide
Valeria
Butera
ab
aCEITEC – Central European Institute of Technology Central European Institute of Technology, Brno University of Technology, Purkyňova 123, Brno 612 00, Czech Republic
bDepartment of Science and Biological Chemical and Pharmaceutical Technologies, University of Palermo, Palermo 90128, Italy. E-mail: valeria.butera@unipa.it
First published on 7th February 2024
Abstract
The application of density functional theory (DFT) methods in catalysis has been growing fast in the last few decades thanks to both the availability of more powerful high computing resources and the development of new efficient approximations and approaches. DFT calculations allow for the understanding of crucial catalytic aspects that are difficult or even impossible to access by experiments, thus contributing to faster development of more efficient and selective catalysts. Depending on the catalytic system and properties under investigation, different approaches should be used. Moreover, the reliability of the obtained results deeply depends on the approximations involved in both the selected method and model. This review addresses chemists, physicists and materials scientists whose interest deals with the application of DFT-based computational tools in both homogeneous catalysis and heterogeneous catalysis. First, a brief introduction to DFT is presented. Then, the main approaches based on atomic centered basis sets and plane waves are discussed, underlining the main differences, advantages and limitations. Eventually, guidance towards the selection of the catalytic model is given, with a final focus on the evaluation of the energy barriers, which represents a crucial step in all catalytic processes. Overall, the review represents a rational and practical guide for both beginners and more experienced users involved in the wide field of catalysis.
1. Introduction
Catalytic processes are fundamental to modern and sustainable chemistry. Catalysis refers to the process of enhancing the transformation rate of chemical compounds into other products in a selective manner. Therefore, a catalyst is a substance involved in the overall reaction mechanism and is capable of significantly lowering the activation energy of the “turnover-limiting step”, generally referred to as the rate-determining step. Furthermore, the structure of a catalyst can be designed to accelerate specific steps leading to target products, thus properly controlling the selectivity. Since the catalyst itself is recovered after the chemical reaction, becoming newly available for subsequent chemical transformations, the thermodynamic equilibrium of the reaction is unchanged. This allows for the conversion of large quantities of reactants using small amounts of catalyst under milder conditions than those required in the absence of the catalyst.Catalysts are usually divided into two main categories: homogeneous and heterogeneous catalysts. In the former case, several organic and metal-coordination compounds have been proposed as homogenous catalysts. On the other hand, solid surfaces of bulk organic and inorganic nanoparticles and 2D materials are mainly involved in heterogeneous catalysis. Very recently, a new class of catalysts has emerged, which consists of anchoring an active homogeneous catalyst on a solid support, thus obtaining the so-called “hybrid catalyst”.1–3 A different strategy based on the same idea of bridging heterogeneous catalysis and homogeneous catalysis led to the development of single atom catalysts (SACs),4–6 in which metal atoms are anchored to the support and act as the active center for the catalytic reaction. The fundamental idea behind these combined systems is that they might benefit from the individual properties of their homogeneous and heterogeneous constituents. Indeed, while homogeneous catalysts typically exhibit a high tunability of activity, they lack high stability and good electron transport often found in heterogeneous catalyst systems.
Based on the energy source, catalytic reactions can be categorized into three main different types: thermocatalysis, photocatalysis, and electrocatalysis. However, new emerging strategies that combine two modalities have emerged leading to, for example, electrophotocatalysis and photothermal catalysis. Depending on the nature of the catalytic system, specific computational techniques need to be applied accordingly: for example, the investigation of the photocatalytic activity can be achieved by using time-dependent DFT (TD-DFT),7 which allows for the correct description of the excited states formed upon adsorption of the light photons, the determination of excited state barriers, conical intersections and absorption spectra. Another method includes the GW approximation,8 which yields good results for bandgaps, but requires exceptional computational cost and it does not yield thermodynamic properties.
On the other hand, various descriptors have been used in predicting the electrocatalytic activities of electrocatalysts. Among them, the d-band center proposed by Nørskov et al.9,10 has been proved as a promising descriptor for rationalizing the electrocatalytic activity. A detailed analysis of the computational tools used for studying the photo- and electro-catalytic activity goes beyond the scope of this review and it can be found elsewhere.9,11
Computational modeling has been revealed to be a powerful tool for the mechanistic investigation of all kinds of catalytic systems through molecular and periodic simulations. The insights from computational studies are indeed used for the rational design of more catalytically active materials thus suggesting novel potential catalysts that can undergo subsequent experimental verification (see Fig. 1). Among the available computational methods, density functional theory (DFT)12,13 is the most commonly used due to the optimal compromise between accuracy and computational cost in comparison with the alternative semi-empirical methods (SEMs)14,15 and wavefunction-theory-based approaches (WFAs).16–18 Indeed, while SEMs are less accurate and robust but much faster, WFAs, such as coupled-cluster, are more accurate and robust but much slower. Furthermore, DFT can be employed in a “black-box” manner that does not require significant a priori knowledge of the system. Based on DFT results, a great deal of experimental phenomena can be elucidated at the atomic scale, thus allowing a wide range of catalytic features and properties to be tackled, such as estimation of adsorption energies, activation energy barriers, and electronic structure information.
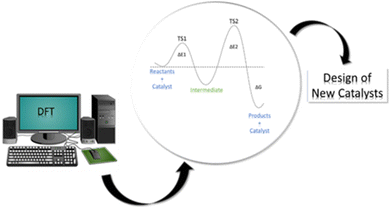 | ||
| Fig. 1 Schematic representation of the contribution of DFT approaches to the investigation of catalytic processes and the design of new catalysts. | ||
For example, according to the Brønsted–Evans−Polanyi (BEP) relation, the energy barriers of chemical reactions scale approximately linearly with the adsorption energies of the molecules.19,20 Therefore, the reliable prediction of adsorption energies is a key element for the search of new and more efficient catalysts.21 In this regard, accurate adsorption energies have been calculated by DFT methods and used as descriptors of the catalytic activity of a large number of systems.22–24 DFT studies have also addressed the computational screening of surface structures for the design of novel catalysts for a wide range of reactions, including methanation,25 ammonia synthesis26 and others.27,28
DFT computations were used to formulate a novel charge modulated switchable CO2 capture strategy (see Fig. 2) based on boron nitride (BN) nanosheets and nanotubes, whose CO2 adsorption/desorption can be controlled and reversed by modifying the charge state of the BN nanomaterials.29 Particularly, the authors demonstrated that CO2 molecules weakly adsorb on neutral BN; however, when excess electrons are injected into the sorbent material, the adsorption of CO2 molecules is dramatically enhanced. On the other hand, as the excess electrons are removed, the adsorbed CO2 is easily released. The authors also demonstrated the high selectivity of charged BN nanomaterials in the separation of CO2 from gas mixtures such as CO2/CH4 and CO2/H2. This work represents the first report supporting BN nanomaterials as effective capture/release CO2 materials, whose processes occur spontaneously without any barriers once the charge is injected into, or dismissed from, BN nanostructures. Even though the authors state that the DFT suggested modification of the charge state of BN nanomaterials can be easily achieved experimentally using electrochemical methods, electrospray, electron beam, or by gate voltage control, the high band gap of BN poses a challenge on how effectively the material can be charged. To overcome this issue, by means of DFT investigations, Tan and collaborators30 investigated borophene, a new type of two-dimensional (2D) boron sheet with a metallic behavior, and demonstrated that conductive borophene nanosheets are a highly promising candidate for charge modulated switchable CO2 capture. Moreover, these negatively charged borophene nanosheets are highly selective for separating CO2 from mixtures with CH4, H2, and/or N2. These theoretical studies open up the exploration of novel charge-modulated sorbent materials with higher selectivity, CO2 capture capacity, ideal thermodynamics and reversibility.
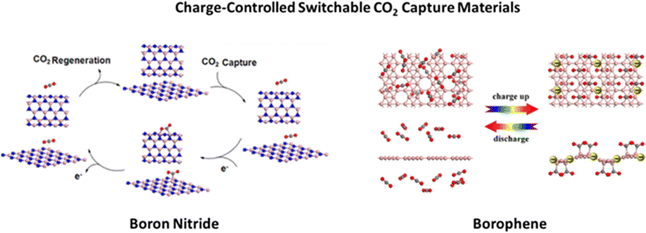 | ||
| Fig. 2 Charge-controlled switchable CO2 capture boron nitride and borophene materials proposed on the basis of DFT studies. Reproduced from ref. 29 and 30 with permission from American Chemical Society, copyright 2013 and 2017. | ||
Therefore, in the light of the crucial contribution of DFT calculations to catalysis, the main objective of this review is to give extensive guidance towards the application of DFT methods in computational catalysis. Particularly, a brief introduction to DFT is discussed first, followed by a discussion on DFT approaches based on atomic centered basis sets and plane waves, underlining the main differences, advantages and limitations. In the third paragraph, critical guidance towards the selection of the catalytic model is given. Eventually, a final focus on the evaluation of the energy barriers, which is a crucial step in catalytic processes, is discussed.
2. A brief introduction to DFT
Density functional theory (DFT) has emerged as an accurate first-principles alternative to quantum mechanical molecular investigations. DFT is primarily a theory of electronic ground state structures based on the electron density, ρ(r), as opposed to the many-electron wave function, Ψ(r, r2,…,rN). Since the density ρ(r) is a function of only three spatial coordinates (rather than the 3N coordinates of the wave function), density-functional theory is computationally feasible even for large systems. Moreover, contrary to the wavefunction, the electron density is a physical observable, and its integration over all space gives the total number of electrons N, as expressed in eqn (1):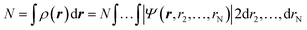 | (1) |
In the last l.h.s. of eqn (1), ρ(r) is expressed as a function of the wave function and, for this reason, it is defined as a “functional”. Indeed, a functional is a function of a function. In DFT, the functional is the electron density which is a function of space and time. As it will be discussed below, the electron density of a system uniquely determines the ground state energy and properties of a system.
The electron density at a particular position in space, ρ(r), can also be written in terms of the individual electron wave function as:
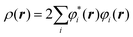 | (2) |
In eqn (2), the summation goes over all the individual electron wave functions, so the term inside the summation is the probability that an electron with individual wave function φi(r) is located at position r. The factor 2 appears because electrons have spin and the Pauli exclusion principle states that each individual electron wave function can describe two different electrons with different spins.
The entire field of density functional theory rests on two fundamental mathematical theorems proved by Kohn and Hohenberg. The first theorem states: “the ground-state energy is a unique functional of the electron density” or “the ground-state electron density uniquely determines all properties, including energy and wave function, of the ground state”. Unfortunately, although the first Hohenberg–Kohn theorem rigorously proves that a functional of the electron density exists and can be used to solve the Schrödinger equation, the theorem says nothing about its exact form. The second Hohenberg–Kohn theorem defines an important property of the functional: “the electron density that minimizes the energy of the overall functional is the true electron density corresponding to the exact solution of the Schrödinger equation”. If the “true” functional form was known, then we could vary the electron density until the energy from the functional is minimized, giving us a prescription for finding the relevant electron density. This variational principle is used in practice to provide approximate forms of the functional. The functional described by the Hohenberg–Kohn theorem can be written in terms of the single-electron wave functions φi(r) since these functions collectively define the electron density, ρ(r), as seen in eqn (2). In other words, electrons interact both with the other electrons and with the ‘external potential’.
The discussion above has emphasized that the density determines the external potential, which determines the Hamiltonian, which determines the wave function. And, of course, with the Hamiltonian and wave function in hand, the energy can be computed. However, if one attempts to proceed in this direction, there is no simplification over MO theory, since the final step is still the solution of the Schrödinger equation, and this is prohibitively difficult in most cases. The difficulty derives from the impossibility to describe the electron–electron interaction term in the Hamiltonian. In a key breakthrough, Kohn and Sham realized that things would be considerably simpler if only the Hamiltonian operator for a non-interacting system of electrons is employed. The crucial bit of cleverness, then, is to take as a starting point a fictitious system of non-interacting electrons that have for their overall ground-state density the same density as some real systems of interest where the electrons do interact. Next, we divide the energy functional into specific components to facilitate further analysis, in particular:
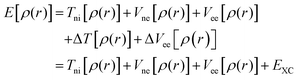 | (3) |
2.1. Conceptual density functional theory
Conceptual density functional theory (CDFT) is a DFT-subfield developed by Parr,31 whose application covers various subdisciplines of chemistry, ranging from organic to inorganic chemistry, from polymer to materials chemistry, and from catalysis to nanotechnology.Within CDFT relevant chemical concepts and principles can be extracted from the electron density to understand and predict the chemical behavior of a system.32 CDFT essentially relies on the fact that the ground state energy of an N-electron system as given by the Hohenberg–Kohn theorem can be considered to be depending on the number of electrons, N, and the external potential, v(r), which are themselves determined uniquely using the density, ρ(r). In this context, the responses of the system to changes of the number of its electrons and/or the external potential provide information about its reactivity. In other words, the partial derivatives of electron density and total energy, E, with respect to the number of electrons and external potentials allow for the determination of certain reactivity indices (or descriptors) from which it is possible to quantify the different chemical behaviours of a system. These reactivity indices can be divided into global reactivity indices including electronegativity (χ), chemical hardness (η), softness (S), electrophilicity (ω), chemical potential (μ), and polarizability (α), which elucidate the overall structure, reactivity, and bonding of molecular motifs, and local parameters such as local hardness (η(r)), local softness (s(r)), Fukui functions (f(r)), and local philicity (ω(r)), that define the site-selectivity of a molecule.33
3. Choice of the computational protocol
The accuracy of the DFT results deeply depends on the choice of the selected catalytic model and computational protocol, which in turn depends on the type of catalytic system.In the following, the main differences in terms of computational approaches and models for homogeneous, heterogeneous and hybrid catalysts will be discussed. Moreover, we will briefly discuss the main limits related to the considered DFT methods.
3.1. Basis sets in molecular systems
While a finite relatively low number of atoms are involved in homogeneous systems, this number becomes “infinitely” large in heterogeneous catalysts. Consequently, one of the main differences in treating such different systems is the use of appropriate basis sets. For molecular systems, the basis set is a set of functions used to describe the shape of the orbitals in an atom. Molecular orbitals and entire wave functions are created by taking linear combinations of basis functions and angular functions, which means that the functions should go toward zero as the distance between the nucleus and the electron becomes large. For example, Pople basis sets34–41 are among the most commonly used sets for molecular systems since they are often not demanding, and widely available in commercial packages, such as licensed Gaussian,42 and open-source ORCA.43,44Their typical notation is n-mxG, which implies that each core orbital is described by a single contraction of n Gaussian Type Orbital primitive functions, while each valence shell orbital is described by two contractions, one with m primitives and the other with x primitive. More accurate results for the computed geometries and vibrational frequencies can be achieved by the inclusion of polarization functions. The addition of polarization functions45 is indicated by * or **, where one single * means that d primitive functions are added to all the atoms but hydrogen, and ** includes also the addition of p primitives to hydrogen atoms. Referring to the above example, the notation will become n-mxG* or n-mxG**.
Omitting polarization functions on non-hydrogen atoms is a good strategy to significantly reduce the computational cost in systems where hydrogen does not take active part in the properties of interest. In this case, the error introduced by not including hydrogen polarization functions is often rather constant and, as the interest is usually in energy differences, tends to cancel out. On the other hand, when hydrogen atoms play a crucial role in the properties of interest, it is of course not a good idea to neglect polarization functions on hydrogen. Similarly, diffuse functions46 can be added by including + or ++ for diffuse function on all atoms rather than hydrogen or including hydrogen as well (n-mx+G or n-mx++G). These diffuse functions are primitives with small exponents, thus describing the shape of the wave function far from the nucleus. Diffuse functions are used for anions, which have larger electron density distributions. They are also used for describing interactions at long distances, such as van der Waals forces.
It is quite common to introduce mixed basis sets, in which more accurate basis sets are used for describing the “active” atoms that belong to the part of the molecule directly involved in the process under investigation, while the “spectator” atoms are instead described by less accurate basis sets. For example, in one of our works,47 the standard 6-311G* basis sets have been employed for all non-metal atoms of the investigated complex, except C and H atoms of the marginal phenyl rings, which have no crucial role in the catalytic activity. For these atoms, the smaller 6-31G basis sets have been used. Similar approaches were used also in ref. 48 and 49. However, a proper balance between the accuracy of the basis set(s) and the computational cost needs to be always taken into account in order to avoid artifacts and/or meaningless results. Maseras and collaborators50 investigated the effect of basis sets on a rhodium catalyst by using different sizes of basis sets for the ligand and the transition metal. The authors found that the use of a too small size of the ligand basis set in comparison to that of the transition metal reduces the accuracy of the structural parameters even in cases where the ligand has a marginal role in the catalytic mechanism. This interesting “ligand/TM basis set size relationship” and its impact on computational cost and accuracy add another level of complexity to calculations involving transition metal species.
Even though the literature offers a wide number of examples, it is always better to validate the chosen basis set(s) by comparing the accuracy of the obtained computational results with the available reported experimental data.
Another family of commonly used basis sets is known as basis sets of Ahlrichs and coworkers51 that, in Gaussian software,42 are indicated with the SV, SVP, TZV, and TZVP keywords, referring to the initial formations of the split valence and triple zeta basis sets from this group.52,53 Def2 basis sets represent the “newer” redefinitions of these basis sets,54,55 and they can be requested in Gaussian with the corresponding keywords: Def2SV, Def2SVP, Def2TZV, Def2TZVP, Def2QZV, Def2QZVP, and QZVP. The open-source ORCA43,44 also allows for the utilization of both older and newer Ahlrichs basis sets that can be combined with auxiliary basis sets for notably speeding up the calculations. However, the corresponding keywords are slightly different, and we direct the reader to consult the manual for detailed guidance.
Other classes of basis sets include the Dunning,56 Jensen,57,58 Sapporo59,60 and the atomic natural orbitals (ANOs).61 A complete list of all available basis sets for electronic structure calculations goes beyond the scope of this short review. However, we want to emphasize that the choice of the most suitable basis set strongly depends on the system and the main property under investigation. On the other hand, the balance between the accuracy and the computational cost should also be considered. Even though small systems allow for the selection of larger and more accurate basis sets, similar choice becomes impracticable when larger systems are under investigation. As a rule of thumb, the basis sets of double zeta quality with polarization might be suitable for getting accurate enough geometries, while more accurate energies can be obtained by performing single point (SP) calculations using more extended basis sets on the stationary point geometries. However, diffuse functions should always be included for systems containing anions. It is also worth mentioning that Ahlrichs basis sets are consistently available for a larger part of the periodic table and are also considered more efficient than Pople- and the Dunning-type sets for standard DFT treatments.62,63
3.2. Effective core potentials
Differently from semiempirical methods, in which core electrons are completely neglected and minimal basis sets are used for valence electrons, in ab initio methods all the electrons are usually represented. However, including all core electrons and their basis functions for heavy atoms is computationally demanding. Indeed, due to the rapid oscillation of the electron wave functions in the proximity to the nuclei, a large number of rapidly oscillating functions (a large set of Gaussians functions for GTO-based calculations) are required to adequately describe the core region. Since core electrons are not always particularly important in defining chemical bonding and other physical properties, they can be efficiently replaced by potential functions in the Hamiltonian referred to as effective core potentials (ECPs). These terms include the electron–electron repulsion of the replaced core orbitals, which is crucial for properly describing the properties of valence electrons.Moreover, for elements belonging to the lower half of the periodic table, scalar relativistic effects, such as relativistic mass defect and core orbital contraction spin coupling terms, become significant, and therefore they should not be neglected. The inclusions of these terms lead to the so-called relativistic effective core potentials (RECPs). Core potentials must be used along with a valence basis set that was created to accompany them. Some molecular properties may no longer be computed accurately if they are dependent on the electron density near the nucleus (i.e. NMR shielding). In such cases, the use of relativistic all electron calculations that include special Hamiltonians, such as X2C,64,65 ZORA,66,67 or DKH,68 might be needed.
It is worth mentioning that the term ECP is mostly used among the chemical community, while the physics community tends to prefer the term pseudopotential (PP), which will be briefly introduced below. ECPs or PPs are usually developed by considering an isolated atom of one element. However, a crucial property of ECP/PPs is transferability, based on which reliable results should be obtained when the chemical environment of the atom is changed without further adjustment of the ECP. Current DFT codes typically provide a library of ECPs and PPs that includes an entry for each (or at least most) element in the periodic table. Calculations that do not include the use of ECPs are instead referred to as all-electron calculations.
Many of the most efficient homogeneous catalysts consist of transition metal complexes. For these systems, the utilization of ECPs for describing heavy atoms might have great advantages in terms of cost/accuracy balance. When using ORCA, the utilization of ECPs is recommended when the system under investigation contains many heavy elements (heavier than Kr). In such cases, more accurate energies or property calculations can be obtained performing subsequent single-point calculations with an all-electron scalar relativistic approach. On the other hand, if only one heavy atom is present there is no significant advantage in introducing ECPs, while more accurate results, almost as fast, can be obtained using an all-electron relativistic approximation. Moreover, the use of ECPs is unadvised when the molecule does not contain elements heavier than Kr.
The relativistic compact Stuttgart/Dresden (SDD) effective core potential69–71 is largely used for precious metals, such as Ru19 and Pt,72,73 but it is also employed to describe the core electrons of non-precious transition metals, such as Zn74,75 and Ni,76 and heavier halogens such as iodine atoms.77,78 Sousa and collaborators79 found that use of SDD effective core potential has a very limited impact, in terms of accuracy, in the determination of metal–ligand bond lengths and angles in zinc-complexes, and it is a good and safe alternative to the use of an all-electron basis set. Another ECP widely employed in quantum chemistry is the Los Alamos National Laboratory (LANL2DZ) that was developed by Hay and Wadt.80–83 LANL2DZ basis sets are routinely employed to study transition metal compounds84–88 or clusters containing heavy elements.89–91
3.3. Basis set superposition error
Interaction or binding energies between two species (atoms or molecules) A and B are usually calculated as:| Eint = EAB(AB) − EA(A) − EB(B) | (4) |
| Eint = EAB(AB) − EAB(A) − EAB(B) | (5) |
A significant advantage of plane-wave basis sets discussed below is that they are independent of the nuclear positions. As a consequence, plane-wave based calculations are free of the basis set superposition error. In one of our works, we have compared the adsorption energy of one D-glucose molecule on a titanium dioxide (TiO2) surface using a localized atomic orbital scheme vs. plane waves.94 The results have underlined that, using localized atomic orbitals, the effect of the BSSE is a significant fraction of the interaction energy, and it should not be neglected. Indeed, the inclusion of BSSE leads to interaction energy values in perfect agreement with those obtained using PW-based calculations.
3.4. Basis sets in periodic systems
Methods based on plane-wave basis sets are suitable for the investigation of crystalline materials. For infinite systems, the molecular orbitals merge into bands, since the energy spacing between distinct levels vanishes. The electrons in a band can then be described by orbitals expanded in a basis set of plane waves (PW), which in three dimensions can be written as a complex function.In a perfect crystal, which is invariant under direct lattice translations, the values of a function will be identical at equivalent points on the lattice. Therefore, the electron density and the external potential of the unperturbed system keep the crystal periodicity: A(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = A(
) = A(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) +
+ ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) l)(A = n, Vext), and also the wavefunction assumes the same values at equivalent points of the lattice. The inherent periodicity of crystals can be exploited by invoking Bloch's theorem to express the wave function as a product of a phase factor by a function u
l)(A = n, Vext), and also the wavefunction assumes the same values at equivalent points of the lattice. The inherent periodicity of crystals can be exploited by invoking Bloch's theorem to express the wave function as a product of a phase factor by a function u![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) having the crystal periodicity as:
) having the crystal periodicity as:
φ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = ei ) = ei![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) · ·![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) u u![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ) | (6) |
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is periodic in space with the same periodicity of the supercell. The periodicity of u
) is periodic in space with the same periodicity of the supercell. The periodicity of u![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) means that it can be expanded in terms of a special set of PW. In other words, each orbital wavefunction is expressed as a linear combination of PW which differs by reciprocal lattice vectors:
) means that it can be expanded in terms of a special set of PW. In other words, each orbital wavefunction is expressed as a linear combination of PW which differs by reciprocal lattice vectors: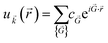 | (7) |
![[G with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0047_20d1.gif) = m1
= m1![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) 1 + m2
1 + m2![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) 2 + m3
2 + m3![[b with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0062_20d1.gif) 3 with integer values for mi (i = 1, 2, 3). These sets of vectors defined by
3 with integer values for mi (i = 1, 2, 3). These sets of vectors defined by ![[G with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0047_20d1.gif) in reciprocal space are defined so that for any real space lattice vector
in reciprocal space are defined so that for any real space lattice vector ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) i,
i, ![[G with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0047_20d1.gif) ·
·![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) i = 2πmi. The
i = 2πmi. The 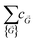 terms are the Fourier coefficients in the wavevector space.
terms are the Fourier coefficients in the wavevector space.
Therefore, by replacing eqn (7) into (6) we get:
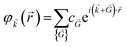 | (8) |
![[G with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0047_20d1.gif) is necessary. Fortunately, the latter issue can be addressed by considering that the functions appearing in eqn (8) have a simple interpretation as solutions of the Schrödinger equation, with kinetic energy:
is necessary. Fortunately, the latter issue can be addressed by considering that the functions appearing in eqn (8) have a simple interpretation as solutions of the Schrödinger equation, with kinetic energy: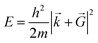 | (9) |
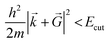 .
.
Therefore, the infinite sum then reduces to:
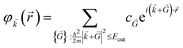 | (10) |
From the basic principles of Fourier analysis, the need for including wave vectors of increasing magnitude is connected to the smoothness of the function to be expanded: the smoother the function, the faster the expansion convergence. Functions that vary rapidly in space need a very large number of wave vectors to be described, when expanded in PW. The smoothly varying nature of Kohn–Sham states means that for insulators and semiconductors a well-converged sampling density can usually be achieved using a modest number of wavevectors. For metals, however, the abrupt change in the occupancy of each state with wavevector means that much denser grids are required.
E cut is the maximum allowed kinetic energy of the plane waves involved in the truncated sum eqn (9) and is a crucial parameter. On one hand, the larger the Ecut, the better the quality of the basis set, which tends to a complete one. On the other hand, the smaller the Ecut, the smaller the number of Fourier coefficients to be calculated and stocked in the computer memory. As a consequence, Ecut is determined through a compromise between numerical accuracy and computational cost. In practice, Ecut is the only parameter that adjusts the quality of the PW basis set. The choice should be done by looking at the behavior of several quantities (total energy, structural parameters, electronic structure, etc.) as a function of Ecut. As soon as they converge reasonably, the optimal Ecut is determined.
On the other hand, the idea of considering an infinite number of vectors k is replaced in practice by sampling the Bloch functions on a discrete mesh of wavevectors often referred to as k-points. This is possible because the wavefunction at points which are close together in k space does not change significantly, and therefore it can be represented by a representative point. Obviously, the denser the set of k vectors, the more accurate will be the result. One of the most known k sampling methods is the Monkhorst95 and Gamma methods.
Ideally, one should ensure that the calculation converges both in terms of the number of wavevectors k and Ecut. This should be done by performing some preliminary convergence tests in which the number of k-points is gradually increased while keeping Ecut fixed with a large value. Similarly, a dense fixed k-point mesh is used to get the converged Ecut value. In many ways, the parameter Ecut is easier to define than the k-points, as most packages will apply sensible default settings if no other information is supplied by the user. Just as with the k-points, it is a good practice to report the cutoff energy used in the calculations to allow people to easily reproduce the obtained results.
In conclusion, the main advantage of using PW basis sets is that each Bloch state is expressed as a Fourier series, whose basis functions are computed efficiently and straightforwardly. Moreover, the basis set is orthonormal and its size (and therefore accuracy) is controlled by a single parameter, the cut-off energy Ecut or equivalently wavevector Gcut. The ground state energy is variational with respect to Gcut, allowing the accuracy to be systematically improved simply by increasing Gcut. On the other hand, one of the main drawbacks of the approach is the much larger number of basis functions required in comparison with the use of localized basis sets. This notably increases the computational cost, particularly for the evaluation of the Fock exchange term as required by hybrid exchange–correlation functionals (see below). The second difficulty is in the representation of sharp peaks in the Kohn–Sham states, for example those occurring in the core regions near nuclei, and therefore the need for using pseudopotentials as discussed in the next paragraph.
3.5. Pseudopotentials
In analogy to that observed for molecular systems, where the inclusion of all core electrons for heavy atoms requires a large set of atomic localized functions, the explicit inclusion of core electrons in PW-based calculations is rather expensive. Therefore, as already mentioned, due to the rapid oscillation of the electron wave functions in the proximity of the nuclei, describing the core region adequately requires a large number of rapidly oscillating functions, i.e. a PW basis with very large Ecut. In order to reduce the computational cost, pseudopotentials (PPs) are used for smearing the nuclear charge and modelling the core electrons. Each pseudopotential contains the minimum energy cutoff that might be used in the calculations, and they are typically characterized by a “core radius”, rc (which may depend on the angular momentum of the valence orbitals). For distances smaller than rc, the potential is described by a suitable analytical function, typically a polynomial or spherical Bessel function, and the pseudo-wave function and its first and second derivatives are required to match those of the reference wave function at rc. As a consequence, pseudopotentials with small rc, named “hard” PPs, need more PW basis functions and higher cutoff energies for describing the region beyond rc, making the calculations computationally more demanding. On the other hand, “soft” PPs are characterized by larger rc, lower cutoff energies, and less PW basis functions. Even though soft PPs are less computationally demanding, a too large rc may significantly decreases the quality of the calculated results.One of the most widely used PPs is known as ultrasoft pseudopotentials (USPPs), developed by Vanderbilt.96 These pseudopotentials include Ecut values significantly lower than those of alternative approaches, whose reduced accuracy is balanced by the introduction of a set of empirical parameters. This latter aspect might limit the transferability of these pseudopotentials. For this reason, DFT codes based on their use typically include multiple USPPs with varying degrees of softness for some elements.
Another frozen core approach that avoids some of the disadvantages of USPPs is the projector augmented-wave (PAW) method, introduced by Blöchl97 and later adapted for plane-wave calculations by Kresse and Joubert.98 Their work shows that well-constructed USPPs and the PAW method provide essentially identical results in many cases and, just as importantly, these results are in good agreement with those from all-electron calculations. In materials with strong magnetic moments or with atoms that have large differences in electronegativity, the PAW approach gives more reliable results than USPPs.
In one of our recent works,99 we have applied the USPP method to pristine and doped/alloyed gallium nitride (GaN), proposed as an efficient photocatalyst for the CO2 reduction to value-added products. USPPs were also used in studies dealing with 2D materials100 and metal oxides101 underlying their applicability to describe a wide range of catalytic materials. Similarly, the PAW method has been widely applied to several classes of catalytic materials, ranging from the most studied TiO2 metal oxide94 to graphene102 and transition metal dichalcogenides (TMDC).103
While there is essentially no basis set error when using plane waves for expanding the orbitals, significant accuracy limitation arises from the employment of the pseudopotential to describe the core region. As a consequence, all molecular properties that depend directly on the core electrons (as in X-ray photoelectron spectroscopy) or the electron density near the nucleus (as in NMR shielding and coupling constants) cannot be properly described. Moreover, both the USPPs and PAW method are built based on the local density approximation (LDA) and the generalized gradient approximation (GGA) to the exchange–correlation (ex) energy functional. Therefore, calculations performed with the more recently developed XC functionals use PPs built from LDA or PBE atomic calculation. Their utilization might lead to inconsistent results for both total-energy and band-structure.104
3.6. Functionals
One of the most important differences between DFT calculations performed using spatially localized functions and periodic wave functions relies on the form of the exchange–correlation functional. DFT methods applied in computational chemistry are based on the re-introduction of orbitals, whose main flaw is the improved complexity from 3 to 3N variables, the re-emerged electron correlation term, and the consequent poor representation of the kinetic energy. As mentioned above, Kohn and Shan partially overtook the kinetic-energy problem by splitting this term into two parts: one that can be calculated exactly, and one consisting in a small correction term. The former is calculated under the assumption of non-interacting electrons and, as in the Hartree–Fock (HF) formalism, represents the main contribution to the total kinetic energy. The remaining kinetic energy contribution, associated with the interacting electrons, is absorbed into an exchange–correlation term, which includes also the interacting electrostatic term. A general DFT energy expression can be written as in eqn (11):| EDFT[ρ] = TS[ρ] + Ene[ρ] + J[ρ] + EXC[ρ] | (11) |
| EXC[ρ] = (T[ρ] − Ts[ρ]) + (Eee[ρ] − J[ρ]) | (12) |
In Kohn–Sham theory one major task is to derive approximations to the exchange–correlation energy functional, which is the only unknown term. As a consequence, the main difference between various DFT methods is the choice of the functional form for EXC. Even though the exchange–correlation potential, whose existence is guaranteed by the Hohenberg–Kohn theorem, is a unique functional, valid for all systems, its true form is not known (except for special cases, such as the uniform electron gas discussed below). For this reason, several functionals have been developed in the last few decades. The simplest classification divides the functionals into two main categories: non-empirical and empirical functionals. The former has been constructed to satisfy certain constraints in order to make use of the known exact constraints on the true Kohn–Sham functional. On the other hand, empirical functionals make use of some parameters that are obtained by fitting experimental or ab initio data.
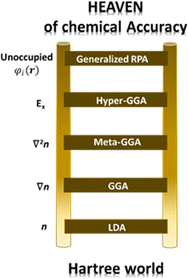
Perdew and co-workers105 have defined the so-called Jacob's ladder (see Fig. 3) based on which improved and more accurate functionals are placed at higher rungs, with the Schrödinger equation, solved without approximation, placed at the highest step. As anticipated above, the uniform electron gas represents the only case where the EXC functional can be derived exactly. In this case, the electron density is constant at all points in space. Similarly, the local density approximation (LDA) assumes variations of the density to be slow and treats the local density as a uniform electron gas and represents the first rung of Jacob's ladder. The second class of functional after the LDA includes information about the local electron density and the local gradient in the electron density, defining the so-called generalized gradient approximation (GGA). It is important to notice that the inclusion of more physical information in GGA in comparison with LDA leads, in principle, to more accurate functionals. However, their performance is not always better than LDA. In the third rung of Jacob's ladder are placed the meta-GGA functionals, which include the Laplacian (second derivative) of the density. Hybrid functionals (also known as hyper-GGAs) belong to the fourth rung of the ladder. These functionals combine some percent of the non-local, exact exchange-energy density with a GGA. Due to the numerical details associated with solving the Kohn–Sham equations in a plane-wave basis set, introducing the nonlocality of exact exchange greatly increases the numerical load of solving these equations, thus drastically limiting their usage in calculations based on plane waves. On the other hand, this issue is not so severe when localized basis sets are used, making hybrid functionals the most commonly used in quantum chemistry calculations with localized basis sets.
Two of the main drawbacks of DFT approximations are the self-interaction error (SIE) or delocalization error (DE) and the missing long-range correlation effects that will be discussed in more detail in the next paragraphs.
However, it is worth anticipating that the SIE is reduced in hybrid functionals where a fraction of approximate DFT exchange is replaced by Fock exchange. Another attempt to reduce the SIE is the utilization of range-separated functionals (RSs).106–108 In this approach, the exchange interaction is split into two components, a long-range (LR) coming from Hartree–Fock, and a short-range (SR) DFT component derived from local-density or generalized-gradient approximations (LDA or GGA). The range-separation parameter, ω, is then defined to set the distance at which the exchange term switches from HF to DFT. Based on the approach suggested by Kronik et al.,109–112 the optimal value of ω, which is found to be strongly system-dependent, can be tuned (giving the tuned range separated functionals) to fulfill Koopmans' theory113 for the first ionization energy. Alternatively, it can be determined to reproduce experimental data.114 The Heyd–Scuseria–Ernzerhof (HSE)115,116 functional is based on this approach; it is built by starting with the PBE functional and mixing a portion of exact exchange into only the short-range portion of the problem. Other commonly used RS functionals are ω-B97XD117 and CAM-B3LYP118 RS functionals.
One of the most recent functionals is the Strongly Constrained and Appropriately Normed (SCAN) meta-GGA functional119 that satisfies all the 17 known constraints for meta-GGA functionals and is constructed to be almost exact for the noble gases and jellium surfaces. Carter and co-workers found that the utilization of the SCAN functional accurately describes the oxidation energetics of binary transition metal oxides (TMOs). However, in order to get oxidation enthalpies comparable to experiment the Hubbard term, U, on the TM centers has to be introduced leading to the SCAN+U framework.120
Based on this description, it is clear that there is not a unique functional that is suitable for all systems. Reliable results and computational cost dramatically rely on the functional's selection. Therefore, the understanding of the main similarities and differences between the various functionals that are in common use is crucial for selecting the most suitable functional.
Moreover, guidance in selecting the correct functional can be obtained by carefully checking the literature. It is also highly advisable to first perform some benchmark studies, in which several functionals are used and the results are compared to any available experimental parameters. However, it is important to note that the results obtained by DFT studies greatly vary depending on the used method which might lead to diverse conclusions. The use of the right functional is not trivial and is still highly discussed between researchers not only for complicated systems but also for transition metal surfaces and complexes.
Among the hybrid functional, the most widely used in quantum chemistry is the B3LYP121–123 that, together with other hybrid DFT methods, in general achieves excellent results for equilibrium geometries124 across the periodic table. Vetere and collaborators125 performed geometry optimizations and harmonic frequency calculations of heavy metals using the GGA PBE126 and the corresponding hybrid PBE0.127 Both the functionals give better results than B3LYP, with PBE0 performing better than PBE for the reproduction of geometrical features, while both give similar good agreement for frequencies. On the other hand, the GGA BLYP121,122 functional has been reported to perform satisfactorily on modeling chemical reactions in comparison with hybrid or meta-GGA functionals128 for some oxides such as silica129 and metal oxides.130 The performance of B3LYP for both isomerization energies and heats of formation of organic molecules leads to an average error of about 3.0 kcal mol−1, which is reduced to 2.4 and 2.2 for heats of formation and isomerization energies, respectively, when dispersion forces (see below) are taken into account.131 In one of our last works,77 we found that the long range hybrid ω-B97XD132 functional tends to overestimate the calculated energy barriers with respect to hyper-GGA B3PW91133 and B3LYP for systems that involve organic molecules. Moreover, the adsorption energy of CO2 on GaN surfaces calculated at the B3LYP level of theory has been found to be similar to that obtained using the more accurate double hybrid PBE0DH134,135 functional that combines exact HF exchange with an MP2-like correlation to a DFT calculation. Thus, hybrid DFT methods provide a quantitative means of investigating reactive chemistry in a large range of systems.78,89,136–138 Two of the most widely used GGA functionals in calculations involving solids are the Perdew–Wang functional (PW91)139 and the Perdew–Burke–Ernzerhof functional (PBE).103 Even though most of the works dealing with periodic boundary conditions and plane waves still use the GGA functional, thanks to the High Performance Computing improvement that was fast achieved in the last few decades, the number of studies that include the HF exchange is rapidly increasing.140 Zaffran and Toroker141 have shown that standard DFT is sufficient to evaluate the geometry of the NiOOH material, but hybrid functionals are necessary to properly study the NiOOH electronic structure.
A bunch of approximations have been introduced to further overcome DFT limitations and they are currently widely available in different codes. Among these, inclusion of Hubbard terms and dispersion forces allow for very accurate results. These approximations will be shortly described in the following.
3.7. Self-interaction error
A systematic difficulty of DFT relies on the so-called SIE that results from an unphysical repulsive interaction of an electron with itself, which is due to the contribution of the electron to the total electron density. This error is not present in the HF method, since the spurious self-interaction energy is exactly cancelled out by the contributions to the energy from exchange. The same would happen in DFT if the exact Kohn–Sham functional was known. Since that is not the case, the incomplete cancellation of the self-interaction energy appears in any approximate DFT functional. One of the examples where the self-interaction error is significant is transition metal oxides. When these materials are modelled using DFT involving LDA and GGA approximations, exchange and correlation effects are not properly taken into account leading to not reliable results. A better description of metal oxide surfaces is provided by self-interaction correction (SIC)142–144 and GW approximations (GWA)145,146 but these methods are computationally very demanding and not appropriate for the large systems that are required for surface and cluster simulations. As mentioned above, the SIE is partially corrected in hybrid exchange functionals thanks to the inclusion of a percentage of the exact exchange energy in the EXC term, and range-separated functionals.A different approach, which has been proved particularly suitable for strongly correlated electron materials, is known as the DFT+U method or Hubbard method,147 which is of relatively computationally low cost and therefore applicable to extended systems. In this method, the underestimated electronic interactions are corrected by simply adding the semi-empirically tuned numerical parameter “U”. The method is also based on a combination between HF and DFT. Specifically, it combines a HF-like approach that takes into account the on-site Coulombic repulsion among localized d electrons by incorporating an extra energetic penalty for delocalization, with DFT for “everything else”. Following this scheme, a correction for electron self-interaction to the DFT energy is added by introducing two numerical parameters, U and J, which involve different aspects of self-interaction.
García-Mota and collaborators have reported that the inclusion of the Hubbard-U term to DFT (DFT+U) is necessary to reproduce the experimental trends observed in the oxygen evolution reaction (OER) activity of strongly correlated cobalt oxides.
Noteworthily, Barlocco et al.148 have investigated the role of functionals in predicting the activity of single atom catalysts (SAC) in the hydrogen and oxygen evolution reactions (HER and OER). Based on their findings, the authors highly recommend the use of the PBE+U approach to investigate systems that include transition metal (TM) atoms at the right of the first TM row, while the adoption of the standard PBE functional is found suitable for some 4d and 5d TM atoms.
3.8. Dispersion forces
Dispersion interactions, such as van der Waals interactions and London forces, are associated with interacting electrons that are spatially well separated. These attractive interactions are due to the dynamic correlations between fluctuating charge distributions. Since semi-local and hybrid functionals do not account for these interactions, they are not suitable for systems where these forces play an important role. In such cases, a correlation dispersion term should be added to the semi-local or hybrid functionals, leading to the resulting energy:| Evdw = Esem/hybXC + Edisp | (13) |
One possible way to include dispersion forces in DFT calculations is to incorporate empirical potentials of the form 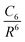 , where the C6 coefficients are pairwise atomic parameters, along with a dumped function, fdump. This method, developed by Grimme,149,150 is known as the dispersion-corrected DFT or DFT-D method. The oldest version, known as DFT-D2,151 has the form:
, where the C6 coefficients are pairwise atomic parameters, along with a dumped function, fdump. This method, developed by Grimme,149,150 is known as the dispersion-corrected DFT or DFT-D method. The oldest version, known as DFT-D2,151 has the form:
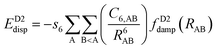 | (14) |
An alternative to Grimme's DFT-D2 is the empirical dispersion correction of Chai and Head-Gordon,152 which uses the same form but with a slightly different damping function.
The newer versions of Grimme's D2 method are the D3153 and D4154–156 corrections. The D3 version includes a similar potential to that in D2 with the addition of C8 terms:
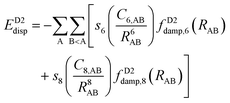 | (15) |
The more recent Becke–Johnson-damping version156 makes use of a different damping function, and it is usually referred to as DFT-D3(BJ).
Grimme and collaborators argued that the inclusion of dispersion correction is indispensable in any DFT treatment, and it should always be taken into account.157
4. Choice and validation of the catalyst model
As already mentioned, one of the main differences between homogeneous and heterogeneous catalysts is their size. The former contains a finite and relatively low number of atoms that, instead, becomes “infinitely” large in the latter. Due to their finite size, the real structure of a homogeneous catalyst is, in principle, easier to be modeled. However, many homogeneous catalysts, such as complexes of transition metals, consist of bulky organic substituents which notably increase the computational cost. In some cases, these substituents are necessary only to stabilize the structure of the catalyst and do not take active part in the catalytic process. In such cases, a common practice is to replace these bulkier groups with smaller ones, thus saving computational time and resources without affecting the validity of the results. For instance, in one of our works, the β-diketiminato ligand of Mg and Ca complexes used as an efficient catalyst for the dehydrogenation of dimethylamine–borane (DMAB) was simplified by replacing the two i-Pr substituents of the N-aryl groups with H atoms.158 Similarly, a simplified model of the [Rh(Ph2P(CH2)2-PPh2)(C6H5F)]+ complex, in which the phenyl rings of phosphine ligands have been replaced with less demanding methyl groups, has been used to explore the plausible reaction pathways of dehydrogenation/dehydrocoupling of amine-boranes.159As previously mentioned, the infinite number of atoms involved in heterogeneous catalysts is reduced when modeling these systems.160–163 Two main approaches are generally used: cluster approach (CA) and periodic boundary condition (PBC) calculations.
Both methods present advantages and disadvantages that are briefly described below.
The PBC approach allows for the investigation of extended surfaces and provides an accurate description of the structural properties of the surface and molecular adsorbates. Moreover, remarkably accurate solid-state properties such as equilibrium lattice constants, bulk moduli, cohesive energies, work functions, elastic and phonon properties, vacancy formation and surface energies can be achieved performing PBC calculations at the semilocal level of theory.164–168 However, as mentioned in previous paragraphs, these functionals fail in properly describing the exchange and correlation effects, leading to an inaccurate description of the electronic band gaps.169 Since more truthful exchange–correlation functionals are computationally expensive when used in PBC calculations, the most suitable alternative is the use of the DFT+U method described above. PBC calculations involving charged systems are problematic due to the spurious interactions between the charges in different periodic images that can affect the physical picture. Furthermore, the investigation of complex reaction mechanisms involving several stationary points is computationally more demanding with respect to CA. On the other hand, the CA allows for the use of hybrid functionals with lower computational cost, thus obtaining a more accurate description of the electronic properties. CAs are also more suitable for studying charged systems thanks to the possibility of adding/subtracting a charge carrier without suffering from interactions with similar charge carriers due to PBC.91,170 The reduced size of CA allows for the interception of all the stationary points, including the more complex transition states, at much lower computational cost. In some of our previous studies129,130,171 cluster models have been successfully used to investigate a wide range of catalytic reactions. It has to be pointed out that the selection of a cluster model is not trivial, and particular attention should be paid to the choice of the cluster size and the most suitable procedures to saturate the peripheral atoms.170 Indeed, a cluster may undergo strong deformations with respect to its starting structure and the dangling bonds at the termination may introduce spurious states in the surface's electronic structure, thus influencing its chemical reactivity. When such issues arise, two different strategies might be applied consisting in embedding the cluster (1) in a larger structure, which is treated with cheap empirical molecular mechanics methods172 or (2) in a network of polarizable Coulomb point charges, mimicking the long-range ionic network in a solid (electrostatic embedding).173
Additional difficulties in modelling heterogeneous systems with both the approaches need to be considered for proper model selection. In cases where no experimental information about the most stable phases of the crystal is given, different facets of the surfaces need to be taken into account. It is worth mentioning that the physical and chemical properties of the surface deeply depend on the particular crystallographic plane where the cleavage is performed. An estimation of the thermodynamic stability of the different structures can be obtained by calculating the formation energy reported by Person et al.,174 and defined as:
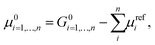 | (16) |
Eqn (16) has been widely used to evaluate the stability of target catalysts from the theoretical predictions175,176 as long as to guide the design of new catalysts.177
The number of atomic layers included in the slab should also be carefully assessed. Convergence tests should be performed to evaluate the number of layers that has to be considered in the model, while the size of the surface area should be chosen in order to accommodate the adsorbed molecules involved in the catalytic process and to avoid spurious interactions between their images. Moreover, the stoichiometric composition within the slab model should be taken into account.
Vacancy formation is very likely to occur in heterogeneous catalysts, such as O vacancies in metal oxides and N vacancies in nitride materials. It has been proved that vacancies play a crucial role in the activity of many catalytic systems160–163 and therefore their formation and effect on catalytic processes should not be neglected. Nevertheless, due to the inevitable oversimplification of real systems, calculations of homogeneous and heterogeneous systems are always afflicted with methodological errors. For this reason, it is highly recommended to connect theory with as many spectroscopic experiments as one can possibly obtain.
In hybrid systems, due to the presence of the active or inactive solid support to which the homogeneous catalyst is anchored, calculations based on PBC and CA are adopted. For example, García-Melchor and collaborators3 have studied the stability and activity of a homogeneous dimeric Ir complex catalyst that is attached onto the surface of the IrO2(110) heterogeneous catalyst. The authors have compared the activity of the hybrid catalyst to that of the corresponding homogeneous and heterogeneous constituents and found that there is not a significant loss of activity of the homogeneous catalysts after its anchoring to the oxide surfaces. To model the hybrid catalyst, the authors anchored this dimeric Ir complex on top of the IrO2(110) surface with a 6 × 2 periodicity through two oxygen atoms to the coordinatively unsaturated sites (CUS) of the surface. As a result of the considerable size of the combined system, calculations for this catalyst were performed at the Γ-point.
Despite their apparent simplicity, SACs are challenging to model due to their boundary nature between homogeneous and heterogenous catalysts. Similarly to homogeneous catalysts, SACs consist of individual atoms, whose chemical reactivity directly relates to their electron configuration and orbital diagram. On the other hand, as in heterogeneous catalysts, the strong interaction of the single atoms with the underlying support influences their charge spin state, and their overall chemical reactivity. Also in this case, approaches based on CA and PBC calculations are used to model these systems. A detailed discussion of pros and cons of both approaches can be found in references.178–180
Based on these considerations, it appears clear how the reliability of any presented results strongly relies on the accuracy of the selected model. Therefore, the choice of the model together with that of the computational protocol should always be guided by balancing accuracy and computational cost.
5. Determination of accurate energy barriers
One main aspect of catalysis is the efficiency of the conversion process leading to the formation of the desired products. Catalytic reactions proceed via several reaction steps in which reactants are converted into products by the involvement of intermediates and transition states (TSs), many of which are too unstable to be isolated experimentally. Therefore, while experimentally isolated species, which include the final products, do allow for the suggestion of plausible reaction mechanisms, they usually lack the possibility to picture all the subsequent reaction steps, thus limiting the detailed knowledge of the involved catalytic cycle. In this regard, DFT investigations have been proved to be of utmost importance since they allow for the interception of all relevant stationary points on the potential energy surfaces (PESs), thus representing a unique tool for identifying the missing structures and the related energy barriers. Moreover, different reaction paths leading to the same products can be hypothesized and explored by means of DFT calculations, and the most accessible pathway can be identified by determining the lowest activation barriers along with the corresponding involved rate determining states. This information is crucial for suggesting structural and electronic modification that leads to the design of new, more efficient catalysts. It should also be recalled that although local geometry optimization is a routine procedure in any DFT package, appropriate protocols are needed to identify the reaction pathways and the energy and geometry of the saddle point that connects two local minima in the potential energy surface of a given system. The availability, efficiency, and reliability of such protocols are clearly of uppermost importance when applying theoretical modeling to catalysis studies. Simm and collaborators181 have organized the plethora of strategies developed for the exploration of PESs into three classes: the first one includes methods in which, starting from a point on the PES, new TSs and intermediates are discovered by relying on local curvature information. This process is repeated until all relevant stationary points of the PESs are explored. In the class 2 methods, the starting point is a minimum energy structure from which new intermediates and TSs are obtained through the application of heuristics. Once a new intermediate is found, the minimum energy pathway (MEP) connecting it to the starting structure can be searched for. Eventually, the third class is based on the combination of chemical knowledge and intuition with ultrafast computer simulations in an interactive setting to efficiently explore intermediates and TSs of a PES. More details about all these methods can be found in references.181–1835.1. Transition state theory
A chemical reaction involves the rearrangement of nuclear configurations from the reactant state to the product state. For polyatomic molecules, an infinite number of possible rearrangement paths can, in principle, take place. Reactant molecules that have lots of energy could follow high energy paths, while low energy paths are involved in conversion of reactants with lower energy. Since a complete description of a chemical reaction including all these paths is challenging (because of the need to map out a multidimensional potential energy surface), a simplified approach, termed the transition state theory, is commonly employed. This approach is based on the identification of a saddle point (transition state) on the PES that corresponds to a maximum along a MEP for a particular reaction coordinate. The latter is a concerted vibration, characterized by an imaginary frequency value, involving two or few atoms of the molecular system, whose variation follows bond-breaking or a bond-formation.The most commonly applied algorithms for the transition state search can be divided into two main categories: methods based on the initial guess of the transition state (such as Quasi-Newton methods, Berny algorithms and Dimer methods), and those based on the optimized reactant and product structures (including the quadratic synchronous transit approach (QST), nudged elastic band (NEB) and climbing image NEB (CI-NEB)). The use of the former is highly recommended when the user has a clear idea of what the transition state structure should look like. Quasi-Newton methods require an initial estimate of the Hessian and implicitly assume that the potential energy surface has a quadratic shape. When the Berny algorithm is used the Hessian is computed incrementally, which further speeds up the calculation. On the other hand, the dimer method becomes advantageous if the product state on the MEP is not known. It has to be noticed that a poor initial guess can cause slow convergence or convergence to an incorrect structure or even failed to get a desired transition state. In such cases, the user can rely on double-ended interpolation techniques based on which the generation of the TS structure is performed by the algorithm starting from the known reactant and product. It has to be pointed out that these methods are more computationally demanding since they require the computation of additional calculations. For instance, when the NEB method is selected, the algorithm generates a number of images along the reaction path that are optimized by adding additional spring forces along the band between images. Each of these images finds the lowest energy while keeping equal spacing to the neighboring image.
Different to local optimization methods, double ended interpolation methods only converge to a close vicinity of the TS but do not precisely locate the TS. Therefore, these methods are usually combined with TS guess algorithms, such as the Berny optimization algorithm and dimer method mentioned above. The overall TS search is therefore divided into two steps: in the first one, the vicinity of a TS is located by a double ended interpolation method, while the second step refines the structure by a local TS optimization method.
Most common packages used in quantum chemistry and solid-state physics, such as Gaussian,42 ORCA,43,44 VASP184,185 and QuantumEspresso,186 allow for the utilization of both the methods that are easily accessible by specifying the corresponding keywords.
5.2. Energetic span model
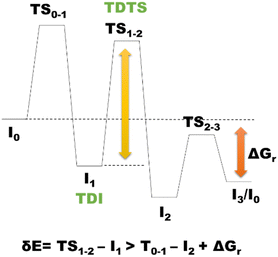
According to the energetic span model (ESM),187 the turnover frequency (TOF) of a catalytic event can be derived from electronic-structure calculations by identifying the energetic span of the cycle, δE, which is defined as the energy difference between the points of the highest and the lowest energy along the reaction profile corresponding to the complete catalytic cycle. Kozuch and Shaik188–191 extended this model by including the ΔGr of the reaction, and defining δEij as:Therefore, if the j-th transition state lies after the i-th intermediate, then δEij is just the energy difference among them; if j-th transition state precedes the i-th intermediate, then δEij is their energy difference minus the ΔGr. The highest value of δEij corresponds to the energy span of the cycle connecting the TOF-determining intermediate (TDI) and the TOF-determining transition state (TDTS) (see Fig. 4). The use of ESM is largely spreading.192–195 In some of our most recent works, ESM has been applied to determine the rate determining states involved in the catalytic formation of MeOH catalyzed by a homogeneous Ru complex19 and a heterogeneous catalyst based on GaN,171 along with the determination of the rate determining states involved in cyclic carbonate formation via CO2 insertion into epoxide catalyzed by organic molecules.77 The application of ESM to heterogeneous catalysis is hindered by several reasons,196 including the utilization of simplified catalyst models, such as infinite perfect periodic single crystal surfaces to represent the more complicated real catalysts, and the higher difficulty in intercepting transition states involved in heterogeneous catalysis with respect to molecular systems. Moreover, the ESM cannot be used for precise modeling of the kinetics of reactions involving several active sites197 such as in the case of heterogeneous catalysts, and last but not least, this model leads to the determination of the TOF, which is usually difficult measure in heterogeneous catalysis.
6. Conclusions and outlook
Thanks to the increasing computational power and improved computational methodologies, computational catalysis has become a powerful tool for studying, rationalizing, and even predicting the reactivity of a wide range of catalytic materials. Particularly, methods based on DFT has been proved crucial to get insights into the mechanistic details of catalytic reactions, allowing for the identification of active catalytic species, intermediates and transition states that are challenging to study via experimental approaches due to their high instability. However, there are still several challenges that limit the accuracy of the computational methodology, and therefore, the reliability of the obtained results. These challenges are mostly related to the complex nature of catalytic cycles and the precise reproduction of the catalyst model and conditions. In this regard, DFT studies are usually performed post experimentally to support and help rationalize the observed chemical reactivity. However, thanks to the extraordinary fast progress that computational methodologies have been achieving, it is highly auspicious that new implemented computational tools can be used for the development of novel reactions, innovative synthetic concepts, and more efficient catalysts. In this context, this review offers a practical guide for scientists that can contribute to the application and the further improvement of computational catalysis.Author contributions
The manuscript has been entirely written by Valeria Butera.Conflicts of interest
There are no conflicts to declare.Acknowledgements
V. B. thanks Prof. Giampaolo Barone for his precious suggestions that significantly contribute to enrich the content of this review. V. B. thanks Dr Hermann Detz for his constant support and advices. V. B. thanks also CzechNanoLab project LM2018110 and the e-INFRA CZ (ID:90254).Notes and references
- B. M. Klepser and B. M. Bartlett, Anchoring a molecular iron catalyst to solar-responsive WO3 improves the rate and selectivity of photoelectrochemical water oxidation, J. Am. Chem. Soc., 2014, 136, 1694–1697 CrossRef CAS PubMed.
- D. K. Zhong, S. Zhao, D. E. Polyansky and E. Fujita, Diminished photoisomerization of active ruthenium water oxidation catalyst by anchoring to metal oxide electrodes, J. Catal., 2013, 307, 140–147 CrossRef CAS.
- M. García-Melchor, L. Vilella, N. López and A. Vojvodic, Computationally Probing the Performance of Hybrid, Heterogeneous, and Homogeneous Iridium-Based Catalysts for Water Oxidation, ChemCatChem, 2016, 8, 1792–1798 CrossRef.
- A. C. M. Loy, S. Y. Teng, B. S. How, X. Zhang, K. W. Cheah, V. Butera, W. D. Leong, B. L. F. Chin, C. L. Yiin, M. J. Taylor and G. Kyriakou, Elucidation of single atom catalysts for energy and sustainable chemical production: Synthesis, characterization and frontier science, Prog. Energy Combust. Sci., 2023, 96, 101074 CrossRef.
- S. Liang, C. Hao and Y. Shi, The Power of Single-Atom Catalysis, ChemCatChem, 2015, 7, 2559–2567 CrossRef CAS.
- J. Hulva, M. Meier, R. Bliem, Z. Jakub, F. Kraushofer, M. Schmid, U. Diebold, C. Franchini and G. S. Parkinson, Unraveling CO adsorption on model single-atom catalysts, Science, 2021, 371, 375–379 CrossRef CAS PubMed.
- C. Adamo, D. Jacquemin, S. Adamo and C. Adamo, The calculations of excited-state properties with Time-Dependent Density Functional Theory, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- M. S. Hybertsen and S. G. Louie, Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390 CrossRef CAS PubMed.
- B. Hammer and J. K. Nørskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
- B. Hammer and J. K. Norskov, Why gold is the noblest of all the metals, Nature, 1995, 376, 238–240 CrossRef CAS.
- Ž. Kovačič, B. Likozar and M. Huš, Photocatalytic CO2 reduction: a review of ab initio mechanism, kinetics, and multiscale modeling simulations, ACS Catal., 2020, 10, 14984–15007 CrossRef.
- N. Argaman and G. Makov, Density functional theory: an introduction, Am. J. Phys., 2000, 68, 69–79 CrossRef CAS.
- R. G. Parr, Density Funct. Theory, 2003, 34, 631–656, DOI:10.1146/annurev.pc.34.100183.003215.
- N. D. Yilmazer and M. Korth, Comparison of molecular mechanics, semi-empirical quantum mechanical, and density functional theory methods for scoring protein-ligand interactions, J. Phys. Chem. B, 2013, 117, 8075–8084 CrossRef CAS PubMed.
- F. Bosia, P. Zheng, A. Vaucher, T. Weymuth, P. O. Dral and M. Reiher, Ultra-fast semi-empirical quantum chemistry for high-throughput computational campaigns with Sparrow, J. Chem. Phys., 2023, 158, 54118 CrossRef CAS PubMed.
- J. Čižek and J. Paldus, Coupled Cluster Approach, Phys. Scr., 1980, 21, 251 CrossRef.
- R. Berraud-Pache, F. Neese, G. Bistoni and R. Izsák, Computational Design of Near-Infrared Fluorescent Organic Dyes Using an Accurate New Wave Function Approach, J. Phys. Chem. Lett., 2019, 10, 4822–4828 CrossRef CAS PubMed.
- T. J. Martinez, M. Ben-Nun and R. D. Levine, Multi-electronic-state molecular dynamics: A wave function approach with applications, J. Phys. Chem. C, 1996, 100, 7884–7895 CrossRef CAS.
- S. Wang, B. Temel, J. Shen, G. Jones, L. C. Grabow, F. Studt, T. Bligaard, F. Abild-Pedersen, C. H. Christensen and J. K. Nørskov, Universal Brønsted-Evans-Polanyi relations for C–C, C–O, C–N, N–O, N–N, and O–O dissociation reactions, Catal. Lett., 2011, 141, 370–373 CrossRef CAS.
- M. M. Montemore and J. W. Medlin, Scaling relations between adsorption energies for computational screening and design of catalysts, Catal. Sci. Technol., 2014, 4, 3748–3761 RSC.
- F. Studt, F. Abild-Pedersen, T. Bligaard, R. Z. Sørensen, C. H. Christensen and J. K. Nørskov, Identification of non-precious metal alloy catalysts for selective hydrogenation of acetylene, Science, 2008, 320, 1320–1322 CrossRef CAS PubMed.
- J. Cheng and P. Hu, Utilization of the three-dimensional volcano surface to understand the chemistry of multiphase systems in heterogeneous catalysis, J. Am. Chem. Soc., 2008, 130, 10868–10869 CrossRef CAS PubMed.
- H. Falsig, B. Hvolbaek, I. S. Kristensen, T. Jiang, T. Bligaard, C. H. Christensen, J. K. Nørskov, C. B. Hvolbaek, I. S. Kristensen, T. Jiang, T. Bligaard, J. K. Nørskov, H. Falsig and C. H. Christensen, Trends in the Catalytic CO Oxidation Activity of Nanoparticles, Angew. Chem., Int. Ed., 2008, 47, 4835–4839 CrossRef CAS PubMed.
- H. Toulhoat and P. Raybaud, Kinetic interpretation of catalytic activity patterns based on theoretical chemical descriptors, J. Catal., 2003, 216, 63–72 CrossRef CAS.
- M. P. Andersson, T. Bligaard, A. Kustov, K. E. Larsen, J. Greeley, T. Johannessen, C. H. Christensen and J. K. Nørskov, Toward computational screening in heterogeneous catalysis: Pareto-optimal methanation catalysts, J. Catal., 2006, 239, 501–506 CrossRef CAS.
- C. J. H. Jacobsen, S. Dahl, B. G. S. Clausen, S. Bahn, A. Logadottir and J. K. Nørskov, Catalyst design by interpolation in the periodic table: Bimetallic ammonia synthesis catalysts [2], J. Am. Chem. Soc., 2001, 123, 8404–8405 CrossRef CAS PubMed.
- J. Greeley and M. Mavrikakis, Alloy catalysts designed from first principles, Nat. Mater., 2004, 3, 810–815 CrossRef CAS PubMed.
- P. Strasser, Q. Fan, M. Devenney, W. H. Weinberg, P. Liu and J. K. Nørskov, High throughput experimental and theoretical predictive screening of materials – A comparative study of search strategies for new fuel cell anode catalysts, J. Phys. Chem. B, 2003, 107, 11013–11021 CrossRef CAS.
- Q. Sun, Z. Li, D. J. Searles, Y. Chen, G. Lu and A. Du, Charge-controlled switchable CO2 capture on boron nitride nanomaterials, J. Am. Chem. Soc., 2013, 135, 8246–8253 CrossRef CAS PubMed.
- X. Tan, H. A. Tahini and S. C. Smith, Borophene as a Promising Material for Charge-Modulated Switchable CO2 Capture, ACS Appl. Mater. Interfaces, 2017, 9, 19825–19830 CrossRef CAS PubMed.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, Electronegativity: The density functional viewpoint, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity, Molecules, 2016, 21, 748 CrossRef PubMed.
- R. Pal and P. K. Chattaraj, Chemical reactivity from a conceptual density functional theory perspective, J. Indian Chem. Soc., 2021, 98, 100008 CrossRef CAS.
- J. S. Binkley, J. A. Pople and W. J. Hehre, Self-consistent molecular orbital methods. 21. Small split-valence basis sets for first-row elements, J. Am. Chem. Soc., 1980, 102, 939–947 CrossRef CAS.
- W. J. Hehre, K. Ditchfield and J. A. Pople, Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules, J. Chem. Phys., 2003, 56, 2257 CrossRef.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 2003, 54, 724 CrossRef.
- M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, Self-Consistent Molecular-Orbital Methods. 22. Small Split-Valence Basis Sets for Second-Row Elements, J. Am. Chem. Soc., 1982, 104, 2797–2803 CrossRef CAS.
- W. J. Pietro, M. M. Francl, W. J. Hehre, D. J. DeFrees, J. A. Pople and J. S. Binkley, Self-Consistent Molecular Orbital Methods. 24. Supplemented Small Split-Valence Basis Sets for Second-Row Elements, J. Am. Chem. Soc., 1982, 104, 5039–5048 CrossRef CAS.
- K. D. Dobbs and W. J. Hehre, Molecular orbital theory of the properties of inorganic and organometallic compounds 4. Extended basis sets for third-and fourth-row, main-group elements, J. Comput. Chem., 1986, 7, 359–378 CrossRef CAS.
- K. D. Dobbs and W. J. Hehre, Molecular orbital theory of the properties of inorganic and organometallic compounds 5. Extended basis sets for first-row transition metals, J. Comput. Chem., 1987, 8, 861–879 CrossRef CAS.
- K. D. Dobbs and W. J. Hehre, Molecular orbital theory of the properties of inorganic and organometallic compounds. 6. Extended basis sets for second-row transition metals, J. Comput. Chem., 1987, 8, 880–893 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani., V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. P. Jr., F. Ogliaro, M. J. Bearpark, J. J. Heyd, K. E. N. Brothers, N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Citation|Gaussian.com, https://gaussian.com/citation/ accessed 17 October 2022 Search PubMed.
- F. Neese and J. Wiley, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li–F, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- V. Butera, N. Russo and E. Sicilia, The role of chelating phosphine rhodium complexes in dehydrocoupling reactions of amine-boranes: A theoretical investigation attempting to rationalize the observed behaviors, ACS Catal., 2014, 4, 1104–1113 CrossRef CAS.
- V. Butera and H. Detz, Hydrogenation of CO2 to methanol by the diphosphine–ruthenium(II) cationic complex: a DFT investigation to shed light on the decisive role of carboxylic acids as promoters, Catal. Sci. Technol., 2021, 11, 3556–3567 RSC.
- V. Butera, N. Russo and E. Sicilia, Do rhodium bis(σ-amine-borane) complexes play a role as intermediates in dehydrocoupling reactions of amine-boranes?, Chem. – Eur. J., 2011, 17, 14586–14592 CrossRef CAS PubMed.
- F. Maseras, A. Liedós, M. Duran and J. Bertrán, Ab initio calculations on the [Rh(PH3)3Cl] system. Influence of the basis set on the structural and reactivity trends of transition-metal complexes, J. Chem. Soc., Faraday Trans., 1992, 88, 1111–1117 RSC.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- A. Schäfer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. IX. The atoms gallium through krypton, J. Chem. Phys., 1999, 110, 7667–7676 CrossRef CAS.
- F. Jensen, Polarization consistent basis sets. II. Estimating the Kohn–Sham basis set limit, J. Chem. Phys., 2002, 116, 7372–7379 CrossRef CAS.
- F. Jensen, Polarization consistent basis sets: Principles, J. Chem. Phys., 2001, 115, 9113–9125 CrossRef CAS.
- M. Sekiya, T. Noro, T. Koga and T. Shimazaki, Relativistic segmented contraction basis sets with core-valence correlation effects for atoms 57La through 71Lu: Sapporo-DK-nZP sets (n = D, T, Q), Theor. Chem. Acc., 2012, 131, 1–8 Search PubMed.
- T. Noro, M. Sekiya and T. Koga, Segmented contracted basis sets for atoms H through Xe: Sapporo-(DK)-nZP sets (n = D, T, Q), Theor. Chem. Acc., 2012, 131, 1–8 Search PubMed.
- P. O. Widmark, P. Å. Malmqvist and B. O. Roos, Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions – I. First row atoms, Theor. Chim. Acta, 1990, 77, 291–306 CrossRef CAS.
- F. Weigend, F. Furche and R. Ahlrichs, Gaussian basis sets of quadruple zeta valence quality for atoms H-Kr, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- M. Bursch, J. M. Mewes, A. Hansen and S. Grimme, Best-Practice DFT Protocols for Basic Molecular Computational Chemistry, Angew. Chem., Int. Ed., 2022, 61, e2022057 CrossRef PubMed.
- T. Saue, Relativistic Hamiltonians for Chemistry: A Primer, ChemPhysChem, 2011, 12, 3077–3094 CrossRef CAS PubMed.
- W. Liu, Handbook of relativistic quantum chemistry: With 150 figures and 87 tables, Handbook of Relativistic Quantum Chemistry, 2016, pp. 1–907 Search PubMed.
- C. Chang, M. Pelissier and P. Durand, Regular Two-Component Pauli-Like Effective Hamiltonians in Dirac Theory, Phys. Scr., 1986, 34, 394 CrossRef CAS.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic regular two-component Hamiltonians, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- M. Reiher, Relativistic Douglas–Kroll–Hess theory, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 139–149 CrossRef CAS.
- T. Leininger, A. Nicklass, H. Stoll, M. Dolg and P. Schwerdtfeger, The accuracy of the pseudopotential approximation. II. A comparison of various core sizes for indium pseudopotentials in calculations for spectroscopic constants of InH, InF, and InCl, J. Chem. Phys., 1996, 105, 1052–1059 CrossRef CAS.
- X. Cao and M. Dolg, Segmented contraction scheme for small-core lanthanide pseudopotential basis sets, THEOCHEM, 2002, 581, 139–147 CrossRef CAS.
- X. Cao and M. Dolg, Valence basis sets for relativistic energy-consistent small-core lanthanide pseudopotentials, J. Chem. Phys., 2001, 115, 7348–7355 CrossRef CAS.
- M. E. Alberto, V. Butera and N. Russo, Which one among the Pt-containing anticancer drugs more easily forms monoadducts with G and A DNA bases? A comparative study among oxaliplatin, nedaplatin, and carboplatin, Inorg. Chem., 2011, 50, 6965–6971 CrossRef CAS PubMed.
- T. Rasheed, S. A. Siddiqui, A. Kargeti, D. V. Shukla, V. Singh and A. K. Pandey, Exploration of superhalogen nature of Pt(CN)n complexes (n = 1–6) and their abilities to form supersalts and superacids: a DFT-D3 study, Struct. Chem., 2021, 32, 2209–2221 CrossRef CAS.
- A. S. M. Al-Janabi, M. M. Kadhim, A. I. A. Al-Nassiry and T. A. Yousef, Antimicrobial, computational, and molecular docking studies of Zn(II) and Pd(II) complexes derived from piperidine dithiocarbamate, Appl. Organomet. Chem., 2021, 35, e6108 CrossRef CAS.
- K. Groutchik, K. Jaiswal and R. Dobrovetsky, An air-stable, Zn2+-based catalyst for hydrosilylation of alkenes and alkynes, Org. Biomol. Chem., 2021, 19, 5544–5550 RSC.
- M. Dutta, H. K. Srivastava, A. Kumar, C. Hemant and A. Kumar, Rational design of pincer-nickel complexes for catalytic cyanomethylation of benzaldehyde: A systematic DFT study, J. Comput. Chem., 2021, 42, 1728–1735 CrossRef CAS PubMed.
- H. Detz and V. Butera, In-depth DFT insights into the crucial role of hydrogen bonding network in CO2 fixation into propylene oxide promoted by Biomass-Derived deep eutectic solvents, J. Mol. Liq., 2023, 380, 121737 CrossRef CAS.
- V. Butera and H. Detz, Cyclic Carbonate Formation from Epoxides and CO2Catalyzed by Sustainable Alkali Halide-Glycol Complexes: A DFT Study to Elucidate Reaction Mechanism and Catalytic Activity, ACS Omega, 2020, 5, 18064–18072 CrossRef CAS PubMed.
- S. F. Sousa, E. S. Carvalho, D. M. Ferreira, I. S. Tavares, P. A. Fernandes, M. J. Ramos and J. A. N. F. Gomes, Comparative analysis of the performance of commonly available density functionals in the determination of geometrical parameters for zinc complexes, J. Comput. Chem., 2009, 30, 2752–2763 CrossRef CAS PubMed.
- W. R. Wadt and P. J. Hay, Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- L. R. Kahn, P. Baybutt and D. G. Truhlar, Ab initio effective core potentials: Reduction of all-electron molecular structure calculations to calculations involving only valence electrons, J. Chem. Phys., 1976, 65, 3826–3853 CrossRef CAS.
- P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- P. J. Hay and W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- H. H. Hammud, K. T. Holman, M. Al-Noaimi, N. S. Sheikh, A. M. Ghannoum, K. H. Bouhadir, M. S. Masoud and R. K. Karnati, Structures of selected transition metal complexes with 9-(2-hydroxyethyl)adenine: Potentiometric complexation and DFT studies, J. Mol. Struct., 2020, 1205, 127548 CrossRef CAS.
- F. Sahan, M. Kose, C. Hepokur, D. Karakas and M. Kurtoglu, New azo-azomethine-based transition metal complexes: Synthesis, spectroscopy, solid-state structure, density functional theory calculations and anticancer studies, Appl. Organomet. Chem., 2019, 33, e4954 CrossRef.
- X. J. Qi, Y. Fu, L. Liu and Q. X. Guo, Ab initio calculations of thermodynamic hydricities of transition-metal hydrides in acetonitrile, Organometallics, 2007, 26, 4197–4203 CrossRef CAS.
- Y. Liu, A. Feng, R. Zhu and D. Zhang, New insights into the mechanism of synergetic photoredox/copper(I)-catalyzed carbocyanation of 1,3-dienes: a DFT study, Chem. Sci., 2023, 14, 4580–4588 RSC.
- S. C. Mandal and B. Pathak, Identifying the preferential pathways of CO2 capture and hydrogenation to methanol over an Mn(I)–PNP catalyst: a computational study, Dalton Trans., 2021, 50, 9598–9609 RSC.
- V. Butera and H. Detz, DFT Study of GaN Clusters Decorated with Rh and Pt Nanoparticles for the Photochemical Reduction of CO2, ACS Appl. Energy Mater., 2022, 5, 4684–4690 CrossRef CAS.
- P. Calaminici, A. M. Köster, T. Carrington, P. N. Roy, N. Russo and D. R. Salahub, V3: Structure and vibrations from density functional theory, Franck–Condon factors, and the pulsed-field ionization zero-electron-kinetic energy spectrum, J. Chem. Phys., 2001, 114, 4036–4044 CrossRef CAS.
- V. Butera and M. C. Toroker, Electronic Properties of Pure and Fe-Doped β-Ni(OH)2: New Insights Using Density Functional Theory with a Cluster Approach, J. Phys. Chem. C, 2016, 120, 12344–12350 CrossRef CAS.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Int. J. Interface Chem. Phys., 2006, 19, 553–566, DOI:10.1080/00268977000101561.
- V. Butera, A. Massaro, A. B. Muñoz-García, M. Pavone and H. Detz, D-Glucose Adsorption on the TiO2 Anatase (100) Surface: A Direct Comparison Between Cluster-Based and Periodic Approaches, Front. Chem., 2021, 9, 651 Search PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- I. Ritacco, M. Farnesi Camellone, L. Caporaso, H. Detz and V. Butera, Gallium Nitride-based Materials as Promising Catalysts for CO2 Reduction: A DFT Study on the Effect of CO2 Coverage and the Incorporation of Mg Doping or Substitutional In, ChemCatChem, 2023, 15, e202201171 CrossRef CAS.
- M. Chen, X. Yi, X. Hu, X. Zhou, J. Tian and X. Li, Correlation between the activity of Fe@(N, S, and P) doped graphene catalysts and the coordination environment: A density functional theory study, Int. J. Hydrogen Energy, 2023, 48, 171–179 CrossRef CAS.
- I. Ritacco, O. Sacco, L. Caporaso and M. F. Camellone, DFT Investigation of Substitutional and Interstitial Nitrogen-Doping Effects on a ZnO(100)-TiO2(101) Heterojunction, J. Phys. Chem. C, 2022, 126, 3180–3193 CrossRef CAS PubMed.
- Y. Yang, J. Li, C. Zhang, Z. Yang, P. Sun, S. Liu and Q. Cao, Theoretical Insights into Nitrogen-Doped Graphene-Supported Fe, Co, and Ni as Single-Atom Catalysts for CO2 Reduction Reaction, J. Phys. Chem. C, 2022, 126, 4338–4346 CrossRef CAS.
- H. Detz and V. Butera, Insights into the mechanistic CO2 conversion to methanol on single Ru atom anchored on MoS2 monolayer, Mol. Catal., 2023, 535, 112878 CrossRef CAS.
- P. Borlido, J. Doumont, F. Tran, M. A. L. Marques and S. Botti, Validation of Pseudopotential Calculations for the Electronic Band Gap of Solids, J. Chem. Theory Comput., 2020, 16, 3620–3627 CrossRef CAS PubMed.
- J. P. Perdew and K. Schmidt, Jacob's ladder of density functional approximations for the exchange-correlation energy, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
- A. Savin, On degeneracy, near-degeneracy and density functional theory, Theor. Comput. Chem., 1996, 4, 327–357 CAS.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Challenges for density functional theory, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- T. Körzdörfer and J. L. Brédas, Organic electronic materials: Recent advances in the dft description of the ground and excited states using tuned range-separated hybrid functionals, Acc. Chem. Res., 2014, 47, 3284–3291 CrossRef PubMed.
- T. Stein, H. Eisenberg, L. Kronik and R. Baer, Fundamental gaps in finite systems from eigenvalues of a generalized Kohn-Sham method, Phys. Rev. Lett., 2010, 105, 266802 CrossRef PubMed.
- T. Stein, L. Kronik and R. Baer, Reliable prediction of charge transfer excitations in molecular complexesusing time-dependent density functional theory, J. Am. Chem. Soc., 2009, 131, 2818–2820 CrossRef CAS PubMed.
- A. K. Manna, S. Refaely-Abramson, A. M. Reilly, A. Tkatchenko, J. B. Neaton and L. Kronik, Quantitative Prediction of Optical Absorption in Molecular Solids from an Optimally Tuned Screened Range-Separated Hybrid Functional, J. Chem. Theory Comput., 2018, 14, 2919–2929 CrossRef CAS PubMed.
- R. Baer, E. Livshits and U. Salzner, Tuned Range-Separated Hybrids in Density Functional Theory, Annu. Rev. Phys. Chem., 2010, 61, 85–109 CrossRef CAS PubMed.
- T. Koopmans, Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den Einzelnen Elektronen Eines Atoms, Physica, 1934, 1, 104–113 CrossRef.
- C. Halsey-Moore, P. Jena and J. T. McLeskey, Tuning range-separated DFT functionals for modeling the peak absorption of MEH-PPV polymer in various solvents, Comput. Theor. Chem., 2019, 1162, 112506 CrossRef.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Da Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J. Sun, A. Ruzsinszky and J. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- G. Sai Gautam and E. A. Carter, Evaluating transition metal oxides within DFT-SCAN and SCAN+U frameworks for solar thermochemical applications, Phys. Rev. Mater., 2018, 2, 95401 CrossRef CAS.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- A. Karton and P. R. Spackman, Evaluation of density functional theory for a large and diverse set of organic and inorganic equilibrium structures, J. Comput. Chem., 2021, 42, 1590–1601 CrossRef CAS PubMed.
- V. Vetere, C. Adamo and P. Maldivi, Performance of the ‘parameter free’ PBE0 functional for the modeling of molecular properties of heavy metals, Chem. Phys. Lett., 2000, 325, 99–105 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- G. T. De Jong, D. P. Geerke, A. Diefenbach and F. M. Bickelhaupt, DFT benchmark study for the oxidative addition of CH4 to Pd. Performance of various density functionals, Chem. Phys., 2005, 313, 261–270 CrossRef CAS.
- V. Butera, N. Fukaya, J. C. Choi, K. Sato and Y. K. Choe, Alkoxysilane production from silica and dimethylcarbonate catalyzed by alkali bases: A quantum chemical investigation of the reaction mechanism, Inorg. Chim. Acta, 2018, 482, 70–76 CrossRef CAS.
- V. Butera, Y. Tanabe, Y. Shinke, T. Miyazawa, T. Fujitani, M. Kayanuma and Y. K. Choe, Mechanistic investigation on ethanol-to-butadiene conversion reaction over metal oxide clusters, Int. J. Quantum Chem., 2021, 121, e26494 CrossRef CAS.
- J. Tirado-Rives and W. L. Jorgensen, Performance of B3LYP density functional methods for a large set of organic molecules, J. Chem. Theory Comput., 2008, 4, 297–306 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem. C, 1994, 98, 11623–11627 CrossRef CAS.
- J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- V. Butera, N. Russo, U. Cosentino, C. Greco, G. Moro, D. Pitea and E. Sicilia, Computational Insight on CO2 Fixation to Produce Styrene Carbonate Assisted by a Single-Center Aluminum(III) Catalyst and Quaternary Ammonium Salts, ChemCatChem, 2016, 8, 1167–1175 CrossRef CAS.
- M. D’Arienzo, L. Gamba, F. Morazzoni, U. Cosentino, C. Greco, M. Lasagni, D. Pitea, G. Moro, C. Cepek, V. Butera, E. Sicilia, N. Russo, A. B. Muñoz-García and M. Pavone, Experimental and Theoretical Investigation on the Catalytic Generation of Environmentally Persistent Free Radicals from Benzene, J. Phys. Chem. C, 2017, 121, 9381–9393 CrossRef.
- V. Butera, N. Russo and E. Sicilia, Hydrogen Release from Dialkylamine–Boranes Promoted by Mg and Ca Complexes: A DFT Analysis of the Reaction Mechanism, Chem. – Eur. J., 2014, 20, 5967–5976 CrossRef CAS PubMed.
- K. Burke, J. P. Perdew and Y. Wang, Derivation of a Generalized Gradient Approximation: The PW91 Density Functional, Electron. Density Funct. Theory, 1998, 81–111 CAS.
- N. Hernández-Haro, J. Ortega-Castro, Y. B. Martynov, R. G. Nazmitdinov and A. Frontera, DFT prediction of band gap in organic-inorganic metal halide perovskites: An exchange-correlation functional benchmark study, Chem. Phys., 2019, 516, 225–231 CrossRef.
- J. Zaffran and M. Caspary Toroker, Benchmarking Density Functional Theory Based Methods to Model NiOOH Material Properties: Hubbard and van der Waals Corrections vs Hybrid Functionals, J. Chem. Theory Comput., 2016, 12, 3807–3812 CrossRef CAS PubMed.
- T. Tsuneda and K. Hirao, Self-interaction corrections in density functional theory, J. Chem. Phys., 2014, 140, 18–513 CrossRef PubMed.
- J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- Z. Szotek, W. M. Temmerman and H. Winter, Application of the self-interaction correction to transition-metal oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 4029 CrossRef CAS PubMed.
- L. Reining, The GW approximation: content, successes and limitations, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1344 Search PubMed.
- F. Aryasetiawan and O. Gunnarsson, The GW method, Rep. Prog. Phys., 1998, 61, 237 CrossRef CAS.
- B. Himmetoglu, A. Floris, S. De Gironcoli and M. Cococcioni, Hubbard-corrected DFT energy functionals: The LDA+U description of correlated systems, Int. J. Quantum Chem., 2014, 114, 14–49 CrossRef CAS.
- I. Barlocco, L. A. Cipriano, G. Di Liberto and G. Pacchioni, Modeling Hydrogen and Oxygen Evolution Reactions on Single Atom Catalysts with Density Functional Theory: Role of the Functional, Adv. Theory Simul., 2022, 2200513 Search PubMed.
- S. Grimme, Density functional theory with London dispersion corrections, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- S. Grimme, Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- J. Da Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 dispersion coefficient model, J. Chem. Phys., 2017, 147, 34112 CrossRef PubMed.
- E. Caldeweyher, J. M. Mewes, S. Ehlert and S. Grimme, Extension and evaluation of the D4 London-dispersion model for periodic systems, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. Bursch, J. Mewes, A. Hansen and S. Grimme, Best-Practice DFT Protocols for Basic Molecular Computational Chemistry, Angew. Chem., Int. Ed., 2022, 61, e2022057 CrossRef PubMed.
- V. Butera, N. Russo and E. Sicilia, Hydrogen Release from Dialkylamine–Boranes Promoted by Mg and Ca Complexes: A DFT Analysis of the Reaction Mechanism, Chem. – Eur. J., 2014, 20, 5967–5976 CrossRef CAS PubMed.
- V. Butera, N. Russo and E. Sicilia, The role of chelating phosphine rhodium complexes in dehydrocoupling reactions of amine-boranes: A theoretical investigation attempting to rationalize the observed behaviors, ACS Catal., 2014, 4, 1104–1113 CrossRef CAS.
- J. Ye, J. Dai, D. Yang, C. Li, Y. Yan and Y. Wang, Interfacial engineering of vacancy-rich nitrogen-doped FexOy@MoS2 Co-catalytic carbonaceous beads mediated non-radicals for fast catalytic oxidation, J. Hazard. Mater., 2022, 421, 126715 CrossRef CAS PubMed.
- T. Zhang, S. Wu, N. Li, G. Chen and L. Hou, Applications of vacancy defect engineering in persulfate activation: Performance and internal mechanism, J. Hazard. Mater., 2023, 449, 130971 CrossRef CAS PubMed.
- J. Zhao, F. Li, H. Wei, H. Ai, L. Gu, J. Chen, L. Zhang, M. Chi and J. Zhai, Superior performance of ZnCoOx/peroxymonosulfate system for organic pollutants removal by enhancing singlet oxygen generation: The effect of oxygen vacancies, Chem. Eng. J., 2021, 409, 128150 CrossRef CAS.
- R. R. Ding, W. Q. Li, C. S. He, Y. R. Wang, X. C. Liu, G. N. Zhou and Y. Mu, Oxygen vacancy on hollow sphere CuFe2O4 as an efficient Fenton-like catalysis for organic pollutant degradation over a wide pH range, Appl. Catal., B, 2021, 291, 120069 CrossRef CAS.
- S. Jana, K. Sharma and P. Samal, Assessing the performance of the recent meta-GGA density functionals for describing the lattice constants, bulk moduli, and cohesive energies of alkali, alkaline-earth, and transition metals, J. Chem. Phys., 2018, 149, 164703 CrossRef PubMed.
- S. Jana, A. Patra and P. Samal, Assessing the performance of the Tao-Mo semilocal density functional in the projector-augmented-wave method, J. Chem. Phys., 2018, 149, 44120 CrossRef PubMed.
- Y. Mo, G. Tian and J. Tao, Performance of a nonempirical exchange functional from density matrix expansion: comparative study with different correlations, Phys. Chem. Chem. Phys., 2017, 19, 21707–21713 RSC.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- C. J. Cramer and D. G. Truhlar, Density functional theory for transition metals and transition metal chemistry, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816 RSC.
- H. Wang, A. Tal, T. Bischoff, P. Gono and A. Pasquarello, Accurate and efficient band-gap predictions for metal halide perovskites at finite temperature, npj Comput. Mater., 2022, 8, 1–13 CrossRef CAS.
- V. Butera and M. C. Toroker, Practical Cluster Models for a Layered β-NiOOH Material, Materials, 2017, 10, 480 CrossRef PubMed.
- V. Butera and H. Detz, Photochemical CO2 conversion on pristine and Mg-doped gallium nitride (GaN): a comprehensive DFT study based on a cluster model approach, Mater. Chem. Front., 2021, 5, 8206–8217 RSC.
- C. Bo and F. Maseras, QM/MM methods in inorganic chemistry, Dalton Trans., 2008, 2911–2919 RSC.
- A. O. Dohn, Multiscale electrostatic embedding simulations for modeling structure and dynamics of molecules in solution: a tutorial review, Int. J. Quantum Chem., 2020, 120, e26343 CrossRef CAS.
- K. A. Persson, B. Waldwick, P. Lazic and G. Ceder, Prediction of solid-aqueous equilibria: Scheme to combine first-principles calculations of solids with experimental aqueous states, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235438 CrossRef.
- J. Wu, S. Ma, J. Sun, J. I. Gold, C. Tiwary, B. Kim, L. Zhu, N. Chopra, I. N. Odeh, R. Vajtai, A. Z. Yu, R. Luo, J. Lou, G. Ding, P. J. A. Kenis and P. M. Ajayan, A metal-free electrocatalyst for carbon dioxide reduction to multi-carbon hydrocarbons and oxygenates, Nat. Commun., 2016, 7, 1–6 Search PubMed.
- Z. Zhang, J. Xiao, X. J. Chen, S. Yu, L. Yu, R. Si, Y. Wang, S. Wang, X. Meng, Y. Wang, Z. Q. Tian and D. Deng, Reaction Mechanisms of Well-Defined Metal–N4 Sites in Electrocatalytic CO2 Reduction, Angew. Chem., Int. Ed., 2018, 57, 16339–16342 CrossRef CAS PubMed.
- S. Kabir, K. Artyushkova, B. Kiefer and P. Atanassov, Computational and experimental evidence for a new TM–N3/C moiety family in non-PGM electrocatalysts, Phys. Chem. Chem. Phys., 2015, 17, 17785–17789 RSC.
- S. Tosoni, G. Di Liberto, I. Matanovic and G. Pacchioni, Modelling single atom catalysts for water splitting and fuel cells: a tutorial review, J. Power Sources, 2023, 556, 232492 CrossRef CAS.
- M. P. De Lara-Castells, A. O. Mitrushchenkov and H. Stoll, Combining density functional and incremental post-Hartree-Fock approaches for van der Waals dominated adsorbate-surface interactions: Ag2/graphene, J. Chem. Phys., 2015, 143, 102804 CrossRef PubMed.
- F. Cinquini, C. Di Valentin, E. Finazzi, L. Giordano and G. Pacchioni, Theory of oxides surfaces, interfaces and supported nano-clusters, Theor. Chem. Acc., 2007, 117, 827–845 Search PubMed.
- G. N. Simm, A. C. Vaucher and M. Reiher, Exploration of Reaction Pathways and Chemical Transformation Networks, J. Phys. Chem. C, 2019, 123, 385–399 CrossRef CAS PubMed.
- W. M. C. Sameera, S. Maeda and K. Morokuma, Computational Catalysis Using the Artificial Force Induced Reaction Method, Acc. Chem. Res., 2016, 49, 763–773 CrossRef CAS PubMed.
- A. L. Dewyer, A. J. Argüelles and P. M. Zimmerman, Methods for exploring reaction space in molecular systems, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1354 Search PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. De Gironcoli, P. Delugas, R. A. Distasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Kücükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-De-La-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- C. Amatore and A. Jutand, Mechanistic and kinetic studies of palladium catalytic systems, J. Organomet. Chem., 1999, 576, 254–278 CrossRef CAS.
- S. Kozuch and S. Shaik, How to conceptualize catalytic cycles? the energetic Span model, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS PubMed.
- S. Kozuch and J. M. L. Martin, What Makes for a Bad Catalytic Cycle? A Theoretical Study on the Suzuki-Miyaura Reaction within the Energetic Span Model, ACS Catal., 2011, 1, 246–253 CrossRef CAS.
- S. Kozuch, A refinement of everyday thinking: the energetic span model for kinetic assessment of catalytic cycles, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 795–815 CAS.
- S. Kozuch, S. E. Lee and S. Shaik, Theoretical analysis of the catalytic cycle of a nickel cross-coupling process: Application of the energetic span model, Organometallics, 2009, 28, 1303–1308 CrossRef CAS.
- C. M. Wang, Y. D. Wang, Y. J. Du, G. Yang and Z. K. Xie, Similarities and differences between aromatic-based and olefin-based cycles in H-SAPO-34 and H-SSZ-13 for methanol-to-olefins conversion: insights from energetic span model, Catal. Sci. Technol., 2015, 5, 4354–4364 RSC.
- Y. F. Wang, K. Li and G. C. Wang, Formic acid decomposition on Pt1/Cu (111) single platinum atom catalyst: Insights from DFT calculations and energetic span model analysis, Appl. Surf. Sci., 2018, 436, 631–638 CrossRef CAS.
- S. Bac and S. Mallikarjun Sharada, CO Oxidation with Atomically Dispersed Catalysts: Insights from the Energetic Span Model, ACS Catal., 2022, 12, 2064–2076 CrossRef CAS.
- J. Chen, Y. Chen, P. Li, Z. Wen and S. Chen, Energetic Span as a Rate-Determining Term for Electrocatalytic Volcanos, ACS Catal., 2018, 8, 10590–10598 CrossRef CAS.
- L. Falivene, S. M. Kozlov and L. Cavallo, Constructing Bridges between Computational Tools in Heterogeneous and Homogeneous Catalysis, ACS Catal., 2018, 8, 5637–5656 CrossRef CAS.
- S. Kozuch, A refinement of everyday thinking: the energetic span model for kinetic assessment of catalytic cycles, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 795–815 CAS.
| This journal is © the Owner Societies 2024 |