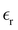Disentangling the molecular polarizability and first hyperpolarizability of methanol–air interfaces†
Tárcius N.
Ramos
 * and
Benoît
Champagne
* and
Benoît
Champagne

Theoretical Chemistry Lab, Unit of Theoretical and Structural Physical Chemistry, Namur Institute of Structured Matter, University of Namur, rue de Bruxelles, 61, B-5000 Namur, Belgium. E-mail: tarcius.nascimento@unamur.be
First published on 26th February 2024
Abstract
Liquid–air interfaces have extensive implications in different areas of interest because the dynamical processes at the interface can be different from those in bulk. Thus, its characterization, understanding, and control may be pivotal in advancing discoveries. However, characterizing the interface requires special and selective tools to avoid signals from the bulk region. This surface specificity and versatility is achieved by using the second harmonic generation (SHG) responses. This study adopts multiscale simulation methods to evaluate the surface SHG responses of methanol–air interfaces with submonolayer resolution tackled by sequentially using classical molecular dynamics simulations under different temperatures and then employing quantum chemistry methods to compute the molecular first hyperpolarizabilities (β). This approach ensures the configurational diversity required to evaluate the average β values. The main achievements are (i) a quasi-absence of surface sensitivity of the mean polarizability 〈α〉 with values about 2% larger than those obtained in bulk, (ii) conversely, smooth variations on the polarizability anisotropy Δα are observed up to the fourth molecular layer at around 20 Å from the interface, and (iii) narrow interfacial effects on the SHG responses, β(−2ω;ω,ω), which are limited to the first molecular layer (∼3.0 Å) and characterized by a high contrast in the βZZZ(−2ω;ω,ω) tensor component between the first and the subsequent layers. Similar trends are obtained at different temperatures or when increasing the number of methanol molecules treated at the quantum chemistry level, indicating the robustness of the approach for describing the dipolar molecular responses of air–liquid interfaces.
1. Introduction
Dynamic processes at liquid–air interfaces have extensive implications in a broad area of applications like catalysis, electrochemistry, and environmental science.1,2 Understanding and characterizing these interfacial phenomena is of paramount importance, as they may play a pivotal role in advancing discoveries. Notably, the interfacial water region exhibits larger reaction rate constants compared to the bulk phase, making it crucial in life sciences.2 However, optically probing these interfaces is challenging because the bulk signals often dominate the light–matter interaction responses, and surface-specific techniques are required to characterize these regions. The second harmonic generation (SHG) technique is a powerful optical tool to probe interfaces due to its surface specificity, versatility, and simplicity.3 SHG is a second-order nonlinear optical (NLO) phenomenon, which converts pairs of photons of ħω energy into photons of 2ħω energy. Its surface specificity, under the electric–dipole approximation, is related to the forbidden responses of media with inversion symmetry.4 Historically, the theory of surface SHG was formulated in 1962 by Bloembergen and Pershan,5 who extended the Maxwell's equations at the boundary of nonlinear media, one year after the first experimental observations of SHG.6 Since its formulation and owing to the development of controlled laser beams and more sensitive detectors,1–4,7–11 surface SHG has attracted much attention and has led to successful applications in a broad range of surface science disciplines.From the modeling point of view, the SHG responses of dynamical systems are calculated using a multiscale sequential approach,12 where (i) thermodynamically accessible structures are first produced using molecular dynamics (MD) simulations to probe the structural diversity and where (ii) the NLO responses are then evaluated using quantum chemistry (QC) methods. Similar approaches have also been applied to interfaces, where snapshots extracted from MD simulations have been used for calculating the SHG of lipid bilayers,13,14 functionalized materials,15,16 and liquid–air and liquid–liquid interfaces as well.17–20 An important aspect to tackle with these methods is the relationship between the microscopic first hyperpolarizability (β, a rank-3 tensor) and the corresponding macroscopic second-order NLO susceptibility (χ(2), a similar rank-3 tensor) of the interfaces. This relationship depends on orientational averages and is well-established for adsorbed molecules at interfaces.21 However, this is less the case for pure liquids, in which different assumptions of the averaging procedure lead to different results,19 and a consensus has not yet been reached to take into account the effects of intermolecular interactions. In general (for interfaces), the transformation from the microscopic to macroscopic responses has been performed by using the average orientational profile (from MD simulations) of the β tensor (determined at a given QC level) around the surface normal direction. This approach usually predicts NLO active regions beyond the first molecular layer thickness due to the interface roughness incorporated in the average orientational profile. Moreover, like pure liquids, whether the scattering units are individual molecules or clusters of molecules remains an open question. Indeed, the impact of the hyperpolarizability fluctuations has been observed in bulk liquid water,22 and this should also play a role at the interfaces.
The current study adopts multiscale simulation methods to evaluate the “microscopic” surface SHG responses of methanol–air interfaces. The submonolayer resolution of the surface SHG response is tackled by sequentially using classical MD simulations under different temperatures and then employing QC methods to compute the molecular first hyperpolarizabilities. In the later step, an increasing number of molecules is treated at the QC level and a decomposition scheme is employed. Moreover, identification and indexation of each molecule as belonging to a given molecular layer allows to disentangle the contribution of the first layers from those of the other layers and to capture a surface SHG monolayer resolution. Besides considering another liquid, this approach represents a step forward compared to our previous study on the water–air interface20 by including the temperature effects, the dependence on the number of molecules in the QC region, and analyses of property decomposition. In addition, it represents a step toward experimental results obtained for n-alcohols.23
This paper is organized as follows: a brief description of the NLO responses is presented and is followed by the details of the employed computational methods in the Methodology section. Next, the results and discussions are divided into reference bulk calculations and interfacial effects. The conclusions are finally drawn in the last section.
2. Methodology
2.1 Basics of nonlinear optical responses
Oscillating electric fields [![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω] interacting with matter give rise to induced dipole moments [Δ
ω] interacting with matter give rise to induced dipole moments [Δ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) (ωσ)], which are expressed in the form of Taylor expansions [T convention, eqn (1)]. The electric field perturbations on the molecular electronic structures are described by their “microscopic” properties associated with the linear response termed polarizability (α, a rank-2 tensor), and the nonlinear ones termed the first hyperpolarizability (β, a rank-3 tensor), the second hyperpolarizability (γ, a rank-4 tensor), and so on.
(ωσ)], which are expressed in the form of Taylor expansions [T convention, eqn (1)]. The electric field perturbations on the molecular electronic structures are described by their “microscopic” properties associated with the linear response termed polarizability (α, a rank-2 tensor), and the nonlinear ones termed the first hyperpolarizability (β, a rank-3 tensor), the second hyperpolarizability (γ, a rank-4 tensor), and so on.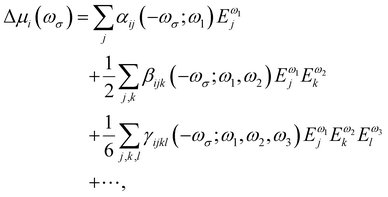 | (1) |
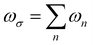 is the response angular frequency due to the perturbations.24
is the response angular frequency due to the perturbations.24
Several invariants are associated with the various macroscopic or observable properties. These are obtained from combining the tensor components. Here, the focus is on the so-called mean [〈α〉, eqn (2)] and anisotropic [Δα, eqn (3)] polarizability, and on the Hyper–Rayleigh Scattering (HRS)25 first hyperpolarizability [βHRS, eqn (4)] and its corresponding depolarization ratio [DR, eqn (5)]. The HRS experiment probes the incoherent responses by analyzing the intensities of the vertically-polarized (along Z) scattered light, which is usually collected at 90° angle with respect to the incident beam.25 The 〈β2ZZZ〉 response [eqn (6)] corresponds to the intensity obtained for a vertically-polarized incident light, whereas the 〈β2ZXX〉 response [eqn (7)] to the horizontally-polarized (along X) incident light.26 The lower-case indices [e.g., eqn (1)] define the molecular axes coordinates while the upper-case [e.g., eqn (4)] define the laboratory axes. The HRS technique was developed to measure the first hyperpolarizability of molecules in solutions, and, in our analysis, it is employed to monitor the variation of the SHG responses as well as the modification of “symmetry” effects between the bulk and interfacial regions. Additionally, the Cartesian components of the vectorial representation of β are given in eqn (8). This quantity is relevant for describing the β‖ response [eqn (9)], the ![[small beta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e115.gif) projection onto
projection onto ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) , which is associated with the electric field induced SHG (EFISHG) response. θ(μ,β) is the angle between
, which is associated with the electric field induced SHG (EFISHG) response. θ(μ,β) is the angle between ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) and
and ![[small beta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e115.gif) .
.
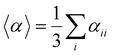 | (2) |
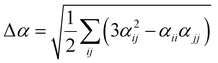 | (3) |
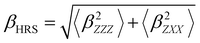 | (4) |
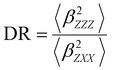 | (5) |
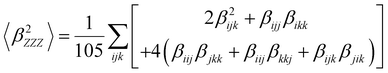 | (6) |
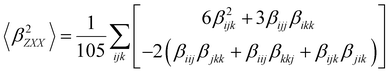 | (7) |
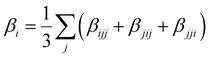 | (8) |
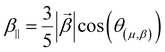 | (9) |
2.2 Molecular dynamic simulations
MD simulations were performed to sample energetically allowed configurations in the liquid phase. A cubic box was filled with 5000 methanol (MeOH) molecules, assuming a 0.8 g cm−3 density, resulting in a box edge of L = 69.3 Å. The MeOH molecules were represented by the OPLS-AA force field27 (in a.u.: qO = −0.683, qHO = 0.418, qC = 0.145, qHC = 0.040). Following a standard procedure, the atomic positions were first relaxed to minimize the potential energy of the initial structure using the steepest descent algorithm with a 350 kJ mol−1 nm−1 force tolerance criterium; second, the thermalization was performed in two steps. First, the dynamics was run for 2.5 ns within the NVT ensemble (at T = 300 K) and then for additional 2.5 ns within the NPT ensemble (P = 1 atm) at three temperatures (260, 280, and 300 K). Last, extra 30 ns of trajectories were created as the production step for each temperature within the NPT ensemble. The considered range of temperatures is far from the ∼175 K freezing point,28 ensuring the liquid phase of the MeOH. These MD simulations provide structures of the bulk MeOH phase. To simulate the interfaces, the Z-edge of the cubic boxes was then extended to 300 Å, creating a vacuum of about 230 Å between the two interfaces and ensuring slab conditions. The MeOH–air interface simulations were performed within the NVT ensemble for 30 ns.All the MD simulations were performed using the leap-frog integrator29 with a 1 fs time step. The short-range interactions were accounted for up to 14 Å distance, and long-range electrostatic corrections were incorporated by the smooth Particle–Mesh Ewald method.30 The Berendsen thermostat31 and barostat32 were coupled every 0.1 and 1.0 ps, respectively. The hydrogen bonds were constrained using the LINCS algorithm.33 All MD simulations were carried out on GROMACS.34,35 Snapshots of the bulk and slab simulation boxes are presented in Fig. 1.
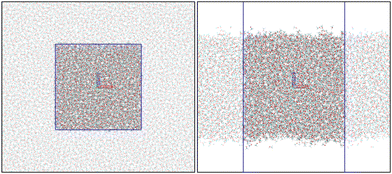 | ||
| Fig. 1 Snapshots from bulk (left) and slab (right) MD simulations. The blue lines identify the MD simulation boxes. The images were created using VMD.36 | ||
2.3 Classical trajectories analyses
Radial distribution functions (RDFs) are used to examine how the density of particles varies as a function of the distance between pairs of atoms. Its structures provide the average size of the coordination shells as well as the associated coordination numbers after integrating it.Hydrogen bond analysis is a helpful tool for understanding the intermolecular interactions. Geometrical criteria were used to assess these values. A hydrogen bond (H-bond) is assigned when the donor–acceptor distance is smaller than 3.5 Å and the donor–hydrogen–acceptor angle is larger than 140°. Layer-selective H-bond values were computed using the molecular layer index (described below) for disentangling the intralayer and interlayer interactions.
The static dielectric constant 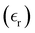 of the bulk phase was computed as an extra parameter to assess the accuracy of the molecular force field for describing the electrostatic environmental effects since they play a key role in modulating the NLO properties.
of the bulk phase was computed as an extra parameter to assess the accuracy of the molecular force field for describing the electrostatic environmental effects since they play a key role in modulating the NLO properties. 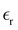 [eqn (10)] was estimated using the fluctuation of the dipole moment vector of the whole simulation box [
[eqn (10)] was estimated using the fluctuation of the dipole moment vector of the whole simulation box [![[M with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004d_20d1.gif) , eqn (11)], comprising N molecules within a V volume and under a T temperature following the expressions derived by Neumann.37 The computations were carried out using the MDAnalysis38 Python package.
, eqn (11)], comprising N molecules within a V volume and under a T temperature following the expressions derived by Neumann.37 The computations were carried out using the MDAnalysis38 Python package.
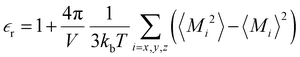 | (10) |
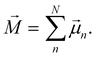 | (11) |
The interfacial density profile [ρ(Z)] along the direction of the normal to the interface describes a sigmoid function [eqn (12)] relating the density of the bulk-like region (ρcenter, termed as center, not to be confused with the bulk properties coming from the bulk reference MD simulations), the z-coordinate defining the interface position (z0 corresponds to ρ(z0) = ρcenter/2), and the interfacial thickness (D) corresponding to density change from 90% to 10%, which reflects the roughness of the interface.2
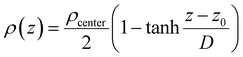 | (12) |
Molecular layers were defined by moving probe spheres of 1.5 Å radius from top to bottom inside the simulation boxes. Starting from above the interface, these probe spheres stop their movement when touching an atom, assigning it as belonging to the first molecular layer. After defining the molecules of the first molecular layer, they are removed and the probe movement resumes to define the second, third, and following molecular layers. The possible evaporated molecules are excluded from this procedure by a neighbor minimum distance criterion of 3.5 Å. This procedure is known as identification of the truly interfacial molecules (ITIM)39 and was performed using the Pytim40 package. Since the molecules are indexed as belonging to a given molecular layer through the whole trajectory, it becomes straightforward to compute their density profiles and the intralayer and interlayer properties, as well as to extract molecular clusters for the NLO computations.
2.4 Quantum chemistry calculations
Time-dependent density functional theory (TD-DFT) was employed in its linear and quadratic formalisms41 to compute the polarizabilities and first hyperpolarizabilities. Based on our previous results in describing the NLO properties of interfacial water molecules,20 the CAM-B3LYP42 exchange–correlation (XC) functional and the aug-cc-pVDZ43 basis set were used in the current study. In ref. 20, B3LYP and CAM-B3LYP XC functionals provided the same trends, while the aug-cc-pVDZ basis set gave a good compromise between CPU time and accuracy in comparison to aug-cc-pVTZ. Also, CAM-B3LYP has been reported to deliver good accuracy in simulating the NLO properties of small molecules.44 The environment effects were accounted for using the polarizable embedding (PE)45 approach and including the external effective field46 for the solvent embedding potential derived for MeOH47 (in a.u.: qO = −0.59543, qHO = 0.38068, qC = 0.18382, qHC = 0.01031, αO = 5.60297, αHO = 1.85100, αC = 6.42738, αHC = 2.50587). All calculations were performed with the Dalton software48,49 considering the frequently employed optical perturbation at 1064 nm wavelength.Additionally, the convergence of the optical properties as a function of the embedding size was investigated for both the bulk and the interface, with a QC region comprising only one MeOH molecule. These embeddings were spherical with a radius ranging from 15 Å to 30 Å, either considering a shell of charges and polarizabilities centered at the atoms or also, in addition, a second external shell of only point charges. All the NLO results reported in the following sections were obtained for a cluster encompassing N MeOH molecules (N = 1, 3, and 6) surrounded by 20 Å of polarizable and point charge sites. The left side of Fig. 2 shows a representative snapshot illustrating the interface model including the quantum region with N = 6 and the 20 Å embedding, while its right side shows a detailed picture of the cluster highlighting the central (vdW representation), the hydrogen-bonded (blue), and the first neighboring (orange) MeOH molecules.
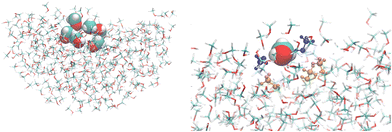 | ||
| Fig. 2 A snapshot illustrating the interfacial model used in the quantum chemical calculations. Left: A cluster with 6 MeOH molecules surrounded by 20 Å of polarizable embedding sites. Right: A detailed view of the cluster highlighting the central (vdW representation), the hydrogen-bonded (blue), and first neighbors (orange) MeOH molecules. The images were created using VMD.36 | ||
2.5 Decomposition into local properties
Partitioning the molecular properties could also help understanding its properties as a function of its constituents. It becomes more relevant when this decomposition is performed on extended systems, large molecules, or clusters of small molecules. Here, the local properties (LoProp) approach50 was employed to separate the β contribution of each MeOH molecule belonging to the quantum region. It allows to understand the impact of the hydrogen bonds and of the first neighbors on the first hyperpolarizability and to unravel how they affect the SHG interfacial signal. The dynamic β response decomposition is obtained by projecting the second-order electronic density perturbation into atomic basis functions, providing the β contribution of each atom. Therefore, the β response of each MeOH molecule of a cluster is obtained by summing its atomic contributions. These calculations were performed using the “LoProp for Dalton” program.513. Results and discussions
3.1 Structural analysis
Table 1 also lists the dielectric constants [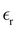 , eqn (10)], which decreases from ∼33 (at T = 260 K) to ∼26 (at T = 300 K) when increasing the temperature, presenting the same trend as that observed in experiments [36.88 (T = 278.15 K), 35.40 (T = 283.15 K), 33.30 (T = 293.15 K), 32.66 (T = 298.15 K), and 31.69 (T = 303.15 K)].54,55 One reason for this reasonable agreement between the theoretical results derived using the OPLS-AA charges originates from the fact that this force field has been designed to reproduce macroscopic properties associated with the potential energy surface.56 However, the dielectric constant depends also on the dipole moment surface of the system, that is, how the dipole moment of the system changes as a function of the nuclei coordinates. In terms of absolute values, classical non-polarizable force fields lack induction effects when predicting dielectric constants, and an empirical scaling factor of 1.26 usually leads to a better theoretical–experimental match.56 Applying this scaling factor modifies the values to 37.76 and 32.43 at T = 280 K and 300 K, respectively, in much better agreement with the experimental results. Alternatively,
, eqn (10)], which decreases from ∼33 (at T = 260 K) to ∼26 (at T = 300 K) when increasing the temperature, presenting the same trend as that observed in experiments [36.88 (T = 278.15 K), 35.40 (T = 283.15 K), 33.30 (T = 293.15 K), 32.66 (T = 298.15 K), and 31.69 (T = 303.15 K)].54,55 One reason for this reasonable agreement between the theoretical results derived using the OPLS-AA charges originates from the fact that this force field has been designed to reproduce macroscopic properties associated with the potential energy surface.56 However, the dielectric constant depends also on the dipole moment surface of the system, that is, how the dipole moment of the system changes as a function of the nuclei coordinates. In terms of absolute values, classical non-polarizable force fields lack induction effects when predicting dielectric constants, and an empirical scaling factor of 1.26 usually leads to a better theoretical–experimental match.56 Applying this scaling factor modifies the values to 37.76 and 32.43 at T = 280 K and 300 K, respectively, in much better agreement with the experimental results. Alternatively, 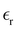 was also calculated using the PE (employed on the QC calculations) in order to evaluate how the model performs in predicting the dipole moment surface, which might affect the NLO responses. The induced dipole moments were calculated using the CPPE (C++ and Python library for PE) library,57 and they lead to values about 10% larger than those with the non-polarizable OPLS-AA but remain still smaller than the experimental results, i.e.,
was also calculated using the PE (employed on the QC calculations) in order to evaluate how the model performs in predicting the dipole moment surface, which might affect the NLO responses. The induced dipole moments were calculated using the CPPE (C++ and Python library for PE) library,57 and they lead to values about 10% larger than those with the non-polarizable OPLS-AA but remain still smaller than the experimental results, i.e., 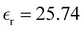 (OPLS-AA) and
(OPLS-AA) and 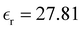 (PE) for T = 300 K.
(PE) for T = 300 K.
| Temperature | 260 K | 280 K | 300 K |
|---|---|---|---|
| ρ center [g cm−3] | 0.811 | 0.788 | 0.765 |
| D [Å] | 2.37 | 2.66 | 2.99 |
| Peak density [g cm−3] | |||
| L1 | 0.591 | 0.547 | 0.513 |
| L2 | 0.554 | 0.520 | 0.489 |
| L3 | 0.556 | 0.521 | 0.489 |
| L4 | 0.551 | 0.520 | 0.489 |
| Peak shift [Å] | |||
| L1 | 2.40 | 2.49 | 2.59 |
| L2 | 6.91 | 7.20 | 7.52 |
| L3 | 11.45 | 11.94 | 12.48 |
| L4 | 15.99 | 16.67 | 17.43 |
| HWHM [Å] | |||
| L1 | 3.03 | 3.30 | 3.58 |
| L2 | 3.14 | 3.38 | 3.65 |
| L3 | 3.12 | 3.36 | 3.62 |
| L4 | 3.12 | 3.37 | 3.63 |
The average numbers of H-bonds of MeOH were evaluated separately for the intralayer and interlayer contributions (Table 3). The number of intralayer H-bonds for the molecules belonging to L1 is around 1.25, which is larger than the corresponding intralayer values for deeper layers (∼0.9). These results indicate strong intralayer interactions at the topmost layer and suggest that L1 is ordered in a 2D-like network, as observed for the water interface.60 Moreover, the interlayer values are around 0.5, with slightly larger values between L1 and L2 because of the trend of each MeOH molecule to form almost 2 H-bonds and because the first layer interacts only with the second one. This trend is the same for the three temperatures. Yet, all these values decrease in a consistent way at higher temperatures, following the density evolution. Furthermore, the average values for the total number of H-bonds, encompassing both the intralayer and interlayer ones, are like those obtained in the bulk MD simulations already for L2. Thus, from the structural point of view, only L1 is distinguishable from the bulk, and therefore, one can assume it is the dominant contribution to the interfacial SHG responses.
| i | Li,i | Li,i+1 | Total |
|---|---|---|---|
| T = 260 K | |||
| 1 | 1.29 | 0.54 | 1.83 |
| 2 | 0.90 | 0.50 | 1.94 |
| 3 | 0.90 | 0.48 | 1.88 |
| T = 280 K | |||
| 1 | 1.25 | 0.51 | 1.76 |
| 2 | 0.89 | 0.46 | 1.86 |
| 3 | 0.90 | 0.46 | 1.81 |
| T = 300 K | |||
| 1 | 1.21 | 0.47 | 1.68 |
| 2 | 0.86 | 0.45 | 1.78 |
| 3 | 0.88 | 0.45 | 1.77 |
3.2 Linear and nonlinear optical responses
Additionally, for R = 15 Å and 20 Å, the linear and nonlinear properties were also probed at different temperatures to ensure convergence in these thermodynamic conditions. This assessment of the model was realized because the number of MeOH molecules is larger in denser regions (at lower T) and, therefore, may induce stronger interactions. Like T = 300 K, the results are very similar for R = 15 Å and 20 Å at the different temperatures (Table S2, ESI†). In addition, though 〈α〉 and βHRS hardly change with T, a smooth increase with the temperature is observed for β‖ and DR. The variation in β‖ are attributed to those in θ(μ,β). Owing to the similarity of results obtained with different embedding sizes (at different T), all the following NLO results are obtained with R = 20 Å. In fact, surrounding molecules are included provided that the position of their center-of-mass is less than 20 Å away from the center-of-mass of the central MeOH molecule. Since the QC part includes up to 6 molecules, this criterium ensures at least 15 Å embedding for each MeOH molecule. These results are presented in Table 4. In addition, Table S3 (ESI†) contains the linear and nonlinear optical properties obtained at different temperatures as a function of the number N of MeOH molecules in the QC region. For the examined properties, the reported values were obtained by dividing the total values by the number of MeOH molecules in the QC region.
| Property | T = 260 K | T = 280 K | T = 300 K |
|---|---|---|---|
| 〈α〉 | 20.39 ± 0.36 | 20.37 ± 0.39 | 20.37 ± 0.43 |
| Δα | 5.69 ± 1.94 | 6.67 ± 1.92 | 6.08 ± 1.80 |
|![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | | |
0.98 ± 0.08 | 0.95 ± 0.10 | 0.95 ± 0.10 |
| β ‖ | −12.26 ± 9.26 | −13.88 ± 9.61 | −14.54 ± 9.84 |
| θ (μ,β) | 109.95 ± 14.49 | 113.26 ± 14.98 | 113.57 ± 14.96 |
| β HRS | 26.73 ± 5.05 | 26.27 ± 4.94 | 26.59 ± 5.40 |
| DR | 4.25 ± 1.06 | 4.38 ± 1.15 | 4.43 ± 1.19 |
| β x | −6.86 ± 36.56 | 5.06 ± 34.21 | 4.12 ± 36.97 |
| β y | −0.86 ± 34.54 | −0.33 ± 35.24 | 2.87 ± 34.97 |
| β z | 7.15 ± 33.94 | −1.98 ± 35.84 | 1.00 ± 35.04 |
〈α〉 is weakly impacted by both the temperature and the number of QC molecules (Table 4 and Table S3, ESI†). It amounts to about 20.3 a.u. with differences smaller than 0.2 a.u. and a slight tendency to larger values at higher temperatures. Contrarily, increasing N induces a decrease in Δα (per molecule) from ∼6 a.u. for N = 1 to ∼2.5 a.u. for N = 6, indicating that the larger the cluster the more isotropic the response. Additionally, Δα is systematically smaller at T = 260 K. The magnitude of the dipole moment is also very similar over the range of temperatures, and it decreases with N by a factor of 2. On the NLO side, the ![[small beta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e115.gif) values (β‖ as well as its components) are oscillating around zero with large standard deviations, indicating its disappearance for a complete statistical sampling of an isotropic environment. Then, the βHRS values decrease with N (from 26 to 13, and to 10 a.u.), which suggests a fast convergence with N. Yet, slight variations with the temperature are observed. The DR ∼4.0–4.4 values indicate that the MeOH molecules closely behave like a 1-D harmonophore. In the case of β‖ no clear trend is observed when increasing T, except for N = 1 when the β‖ amplitude clearly increases with T. Experimentally, Campo et al.62 reported a βHRS value ∼12 a.u. at λ = 1072 nm for methanol solution at room temperature (using 1 a.u. = 8.639 × 10−33 esu and
values (β‖ as well as its components) are oscillating around zero with large standard deviations, indicating its disappearance for a complete statistical sampling of an isotropic environment. Then, the βHRS values decrease with N (from 26 to 13, and to 10 a.u.), which suggests a fast convergence with N. Yet, slight variations with the temperature are observed. The DR ∼4.0–4.4 values indicate that the MeOH molecules closely behave like a 1-D harmonophore. In the case of β‖ no clear trend is observed when increasing T, except for N = 1 when the β‖ amplitude clearly increases with T. Experimentally, Campo et al.62 reported a βHRS value ∼12 a.u. at λ = 1072 nm for methanol solution at room temperature (using 1 a.u. = 8.639 × 10−33 esu and 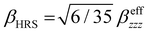 ). This fair agreement using the N = 1 model may be related to the fair description of the long-range interactions dictated by the dipole moment surface and the dielectric constant and mainly to the fair description of the short-range interactions associated with the hydrogen bonding molecules created by the PE model. This agreement becomes more accurate when considering more MeOH molecules in the QC region. Therefore, a systematic study of the dipole moment surface of different solutions and its effects on the NLO properties should clarify whether the scattering units are individual molecules or clusters of molecules.
). This fair agreement using the N = 1 model may be related to the fair description of the long-range interactions dictated by the dipole moment surface and the dielectric constant and mainly to the fair description of the short-range interactions associated with the hydrogen bonding molecules created by the PE model. This agreement becomes more accurate when considering more MeOH molecules in the QC region. Therefore, a systematic study of the dipole moment surface of different solutions and its effects on the NLO properties should clarify whether the scattering units are individual molecules or clusters of molecules.
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and a minimal effect on θ(μ,β) (a decrease of 0.7°). Nevertheless, a decrease of ∼5% is observed on the β‖ amplitude. These embedding effects are even smaller on βHRS and DR, where the average values change by less than 1% and 3%, respectively. The vectorial βx and βy values are oscillating around zero with large standard deviations, which contrasts with the distinct nonzero value of βz, characteristic of the interfacial symmetry. In summary, the results (Table S4, ESI†) are independent of the choice of the R values, and a sphere of radius 20 Å is also used on the following calculations to ensure at least 15 Å embedding for each MeOH molecule.
| and a minimal effect on θ(μ,β) (a decrease of 0.7°). Nevertheless, a decrease of ∼5% is observed on the β‖ amplitude. These embedding effects are even smaller on βHRS and DR, where the average values change by less than 1% and 3%, respectively. The vectorial βx and βy values are oscillating around zero with large standard deviations, which contrasts with the distinct nonzero value of βz, characteristic of the interfacial symmetry. In summary, the results (Table S4, ESI†) are independent of the choice of the R values, and a sphere of radius 20 Å is also used on the following calculations to ensure at least 15 Å embedding for each MeOH molecule.
Splitting the interfacial region into molecular layers allows for understanding on how the molecular property depends on its interfacial or bulk character. It also provides an evolution of the properties when going from L1 to L4. The data are presented in Table 5 for L1 and Tables S5–S7 (ESI†) for L2–L4, and in Fig. 4 and Fig. S5–S7 (ESI†). In general, the 〈α〉 values decrease (∼2%) toward the bulk reference value (∼20.3 a.u.) and present a very small increase with T. Yet, increasing N does not affect its values (i.e., its value per MeOH molecule). Similarly, from L1 to L4, Δα decreases by a 1.3–1.8 factor towards the bulk value (∼3 a.u. for N = 6). Increasing N leads to more isotropic (QC) clusters, therefore strongly affecting Δα, i.e., a decrease from 8.72 a.u. (N = 1) to 5.68 a.u. (N = 3), and to 4.49 a.u. (N = 6) for L1 at T = 300 K.
| Property | T = 260 K | T = 280 K | T = 300 K |
|---|---|---|---|
| N = 1 | |||
| 〈α〉 | 20.75 ± 0.42 | 20.71 ± 0.49 | 20.77 ± 0.53 |
| Δα | 9.96 ± 2.51 | 9.36 ± 2.71 | 8.72 ± 2.78 |
|![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | | |
0.94 ± 0.10 | 0.94 ± 0.09 | 0.91 ± 0.10 |
| β ‖ | −13.08 ± 9.66 | −14.21 ± 9.46 | −16.06 ± 10.70 |
| θ (μ,β) | 109.54 ± 14.50 | 112.89 ± 15.34 | 113.32 ± 14.79 |
| β HRS | 29.24 ± 5.93 | 27.92 ± 5.59 | 30.26 ± 6.15 |
| DR | 4.29 ± 1.15 | 4.39 ± 1.35 | 4.48 ± 1.17 |
| β x | −1.53 ± 40.55 | −6.12 ± 38.06 | 7.45 ± 36.73 |
| β y | −6.40 ± 41.19 | −1.68 ± 39.44 | 1.57 ± 43.72 |
| β z | −17.98 ± 29.64 | −14.37 ± 30.69 | −19.55 ± 36.79 |
| N = 3 | |||
| 〈α〉 | 20.61 ± 0.27 | 20.64 ± 0.27 | 20.73 ± 0.28 |
| Δα | 6.48 ± 2.18 | 6.40 ± 2.04 | 5.68 ± 1.96 |
|![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | | |
0.67 ± 0.20 | 0.61 ± 0.21 | 0.59 ± 0.20 |
| β ‖ | −1.86 ± 10.38 | 0.23 ± 11.32 | 0.53 ± 10.33 |
| θ (μ,β) | 94.68 ± 30.79 | 87.21 ± 34.45 | 86.94 ± 34.12 |
| β HRS | 15.95 ± 4.34 | 15.64 ± 3.96 | 15.41 ± 4.10 |
| DR | 4.54 ± 1.57 | 4.41 ± 1.45 | 4.16 ± 1.53 |
| β x | 1.08 ± 20.37 | −2.71 ± 21.98 | 1.15 ± 19.80 |
| β y | −2.35 ± 22.23 | 0.61 ± 18.92 | −2.14 ± 20.92 |
| β z | −16.84 ± 17.83 | −16.16 ± 17.42 | −13.96 ± 16.70 |
| N = 6 | |||
| 〈α〉 | 20.61 ± 0.19 | 20.66 ± 0.22 | 20.73 ± 0.22 |
| Δα | 4.82 ± 1.48 | 5.01 ± 1.54 | 4.49 ± 1.58 |
|![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | | |
0.46 ± 0.17 | 0.43 ± 0.16 | 0.41 ± 0.15 |
| β ‖ | −2.26 ± 9.25 | −1.68 ± 8.69 | −2.07 ± 8.05 |
| θ (μ,β) | 97.17 ± 33.48 | 94.56 ± 34.25 | 97.90 ± 30.78 |
| β HRS | 12.31 ± 3.49 | 11.96 ± 3.41 | 11.91 ± 3.34 |
| DR | 4.83 ± 1.46 | 4.66 ± 1.54 | 4.77 ± 1.44 |
| β x | −0.81 ± 15.06 | −2.22 ± 15.72 | −1.98 ± 14.81 |
| β y | 0.03 ± 15.46 | −0.09 ± 12.79 | −1.93 ± 16.63 |
| β z | −17.83 ± 13.14 | −16.97 ± 13.25 | −14.54 ± 12.76 |
On the other hand, no clear trends can be drawn for |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | and θ(μ,β) as a function of the molecular layer, even though |
| and θ(μ,β) as a function of the molecular layer, even though |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | decreases at higher temperatures and for larger N (due to the increased isotropicity of the QC region). |
| decreases at higher temperatures and for larger N (due to the increased isotropicity of the QC region). |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) | is almost constant, within 10%, as a function of the layer. Then, θ(μ,β) approaches 90° for N = 3 and 6, which is consistent with the decrease of β‖ (cos
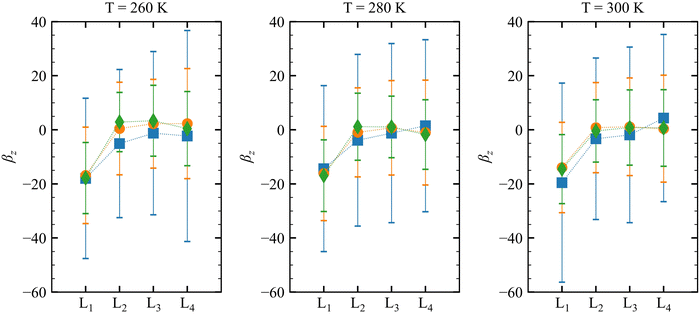
| is almost constant, within 10%, as a function of the layer. Then, θ(μ,β) approaches 90° for N = 3 and 6, which is consistent with the decrease of β‖ (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ(μ,β) tends to zero). Moreover, the β‖ values slightly oscillate from L1 to L4 and show an increase with T from L1 to L2. These small variations on β‖ as a function of the molecular layer go in opposite directions to the strong effects on βz in L1 (Fig. 4) because the dipole moment is preferentially oriented in the interfacial plane (perpendicular to the Z-direction). In general, the first hyperpolarizability vector is strongly affected by the symmetry and the molecular distributions, leading to large standard deviations. However, the standard error of the mean (SEM) associated to 100 sampled configurations amounts to 0.1 of the respective standard deviation (STD), allowing direct comparisons between the results. (
θ(μ,β) tends to zero). Moreover, the β‖ values slightly oscillate from L1 to L4 and show an increase with T from L1 to L2. These small variations on β‖ as a function of the molecular layer go in opposite directions to the strong effects on βz in L1 (Fig. 4) because the dipole moment is preferentially oriented in the interfacial plane (perpendicular to the Z-direction). In general, the first hyperpolarizability vector is strongly affected by the symmetry and the molecular distributions, leading to large standard deviations. However, the standard error of the mean (SEM) associated to 100 sampled configurations amounts to 0.1 of the respective standard deviation (STD), allowing direct comparisons between the results. (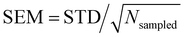 , where Nsampled = 100 is the number of sampled configurations in the QC calculations). The results obtained for βHRS show a small decrease as a function of the molecular layer and with N, but no direct relationship with the temperature. Moreover, all values are within the standard deviation error, indicating no distinction among the molecular layers. Analogously to β‖, the βHRS response is also not selective to the interface but for different reasons. The βHRS is originally used to evaluate the first hyperpolarizability of molecules in gas phase or in solution, where they present random orientations. This is not the case at the interface due to the preferential orientation of the molecules. However, the βHRS values are reported as a matter of comparison with the bulk values to help understanding the convergence of the molecular orientational average.
, where Nsampled = 100 is the number of sampled configurations in the QC calculations). The results obtained for βHRS show a small decrease as a function of the molecular layer and with N, but no direct relationship with the temperature. Moreover, all values are within the standard deviation error, indicating no distinction among the molecular layers. Analogously to β‖, the βHRS response is also not selective to the interface but for different reasons. The βHRS is originally used to evaluate the first hyperpolarizability of molecules in gas phase or in solution, where they present random orientations. This is not the case at the interface due to the preferential orientation of the molecules. However, the βHRS values are reported as a matter of comparison with the bulk values to help understanding the convergence of the molecular orientational average.
Table 6 collects the βZZZ, βZXX, and βXZX values as a function of N and of Li for T = 300 K, whereas those for T = 260 K and 280 K are in Tables S8 and S9 (ESI†). The βZZZ values of the first molecular layer are clearly distinct from the others with a small decrease between N = 1 and N = 6, and it dominates β with values one order of magnitude larger than βZXX and βXZX. Increasing N (from 1 to 6) narrows the data distribution and drives the values toward zero for L2–L4. These results also satisfy the Kleinman's rule for N = 1 and N = 6, where βZXX = βXZX far away from resonances.63 The projections onto the Z axis of the OH and CO bonds were computed for the N = 1 model at L1 to investigate the correlation between the βZZZ response and the MeOH orientation. Positive values of the projection indicate that the bond points upward [H of OH (O of CO) pointing towards increasing Z projection] and negative downward. About 70% of configurations present at least one of the two bonds pointing towards the bulk, while 50% present both bonds pointing downward. On the other hand, only 13% of the snapshots present both bonds pointing upward. More importantly, Fig. 5 shows that the βZZZ response follows the CO bond Z-orientation, and that negative βZZZ values originate from this preferential downward MeOH orientation.
| Property | N = 1 | N = 6 | N = 1(6) |
|---|---|---|---|
| L1 | |||
| β ZZZ | −17.78 ± 25.48 | −12.64 ± 8.80 | −31.14 ± 71.90 |
| β ZXX | −2.00 ± 12.35 | −1.21 ± 4.20 | −7.52 ± 109.54 |
| β XZX | −1.98 ± 12.39 | −1.21 ± 4.22 | −4.72 ± 20.67 |
| L2 | |||
| β ZZZ | −2.03 ± 17.31 | 0.67 ± 6.84 | −5.03 ± 67.87 |
| β ZXX | −0.98 ± 14.36 | −0.35 ± 4.74 | 17.13 ± 98.38 |
| β XZX | −0.97 ± 14.40 | −0.35 ± 4.74 | −7.42 ± 19.47 |
| L3 | |||
| β ZZZ | 0.17 ± 17.88 | 1.89 ± 8.98 | 0.21 ± 68.21 |
| β ZXX | −1.09 ± 12.37 | −0.64 ± 4.34 | −6.06 ± 90.07 |
| β XZX | −1.09 ± 12.39 | −0.65 ± 4.35 | −8.28 ± 17.61 |
| L4 | |||
| β ZZZ | 2.35 ± 19.10 | 1.09 ± 9.93 | −22.31 ± 71.65 |
| β ZXX | 0.37 ± 11.45 | −0.78 ± 4.33 | −0.25 ± 90.74 |
| β XZX | 0.37 ± 11.47 | −0.79 ± 4.34 | −8.20 ± 17.50 |
| L1 | |||
| χ (2) ZZZ | −7.27 ± 10.42 | −5.17 ± 3.60 | −12.73 ± 29.39 |
| χ (2) ZXX | −0.82 ± 5.05 | −0.49 ± 1.72 | −3.08 ± 44.78 |
| χ (2) XZX | −0.81 ± 5.07 | −0.49 ± 1.73 | −1.93 ± 8.45 |
| L1 − χ(2) values given in pm V−1 | |||
| χ (2) ZZZ | −14.14 ± 20.26 | −10.06 ± 7.00 | −24.77 ± 57.19 |
| χ (2) ZXX | −1.59 ± 9.82 | −0.96 ± 3.34 | −5.98 ± 87.12 |
| χ (2) XZX | −1.57 ± 9.86 | −0.96 ± 3.36 | −3.75 ± 16.44 |
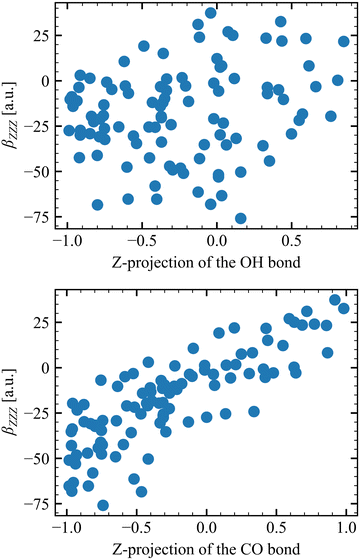 | ||
| Fig. 5 Correlation between the βZZZ response and the orientation of the OH (top) and CO (bottom) bond, as determined by their projections onto the Z axis. | ||
Then, the results obtained with N = 6 were decomposed to disentangle the individual contributions of the central MeOH molecule. These results, referred to as N = 1(6), lead to different conclusions. First, the data distributions are much broader, and the components are no longer specific to the interface. Indeed, by using the LoProp decomposition scheme, the trend of the components to become zero when going deeper and deeper toward the bulk is lost with average values larger than 5 a.u. and standard deviations up to 110 units. Moreover, βZZZ is not vanishing at L4, neither βZXX at L2. Furthermore, Kleinman's rule is also violated. These results evidently indicate that the decomposition scheme is not suitable for this study case and that it should be modified. This deficiency may be related to the number N of close MeOH molecules because it induces asymmetries in the individual contributions, and including the second solvation shell may improve the accuracy.
The same trends are observed for T = 260 K and 280 K, and no clear relationship can be drawn as a function of the temperature due to the large values of the standard deviations.
At the macroscopic scale, the optical responses are expressed as a power series of the polarization [B convention, eqn (13)] where the χ(n) is the nth order susceptibility tensor. Comparing eqn (13) with (1), a relationship between the macroscopic and microscopic responses is drawn [eqn (14)]. This relationship depends on the density of particles (ρN = ρNA/MM, where ρ is the mass density, MM the molar mass, and NA the Avogadro's number) and on the orientational average of the β tensor (〈β〉OR). 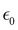 is the vacuum electric permittivity.
is the vacuum electric permittivity.
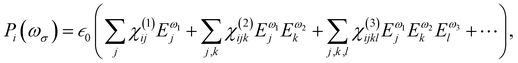 | (13) |
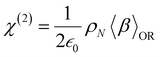 | (14) |
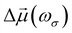 expansion might also affect the experimental measurements, e.g., the bulk quadrupole contributes for systems with weak interfacial dipolar signals.65
expansion might also affect the experimental measurements, e.g., the bulk quadrupole contributes for systems with weak interfacial dipolar signals.65
Looking for the macroscopic dipolar responses, the χ(2) values were estimated by multiplying the corresponding average βZZZ, βZXX, and βXZX components with the number density associated with the first molecular layer (Table 2). This is a reliable approximation because the average β values encompass the orientational averaging over the extracted snapshots and only the first molecular layer presents net β responses. At T = 300 K, the corresponding number density is ρN = 6.51 × 10−2 particles bohr−3. The χ(2) values of L1 are given at the bottom of Table 6 for experimental comparison purpose.
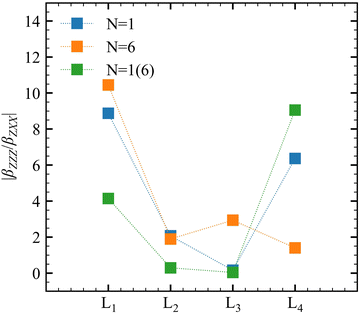
Experimentally, the χ(2)ZZZ/χ(2)ZXX ratio is often reported, and the corresponding βZZZ/βZXX quantities are plotted in Fig. 6 for the successive layers and for different QC schemes. Both N = 1 and N = 6 models predict large ratios (∼10) at the interface with a net decrease towards the bulk (∼2). The obtained values are comparable with the χ(2)ZZZ/χ(2)ZXX ratios (around 5) reported for longer alcohols ranging from butanol to undecanol.23 Using N = 1, an unexpectedly large value is observed for L4. It is ascribed to the large statistical fluctuations of these properties (between 10 and 20 a.u.). The ratios obtained using the N = 1(6) model are smaller than those obtained with N = 1 and N = 6, except for L4, which achieves a value of about 90 and is not reliable.
4. Conclusions
The second harmonic generation (SHG) responses of the methanol–air interface have been evaluated by adopting a sequential method, classical molecular dynamics (MD) then quantum chemistry (QC). This approach ensures the configurational diversity required to subsequently evaluate the average values of the first hyperpolarizability, which is a dynamical and symmetry-dependent property. Additionally, temperature effects on the linear and nonlinear optical responses have been studied. Within this approach, the molecular properties were disentangled as a function of molecular layers to which the MeOH molecules belong while different numbers of MeOH molecules were treated at the QC level. The main results are (i) the mean polarizability 〈α〉 is almost insensitive to the interface, with values about 2% larger than those obtained in bulk, (ii) conversely, a smooth decrease is observed in the polarizability anisotropy Δα, indicating a linear optical interface thickness of around 20 Å, corresponding to 4 MeOH molecular layers, (iii) for the molecular SHG responses, β(−2ω;ω,ω), the interfacial dependence is strong and limited to the first molecular layer (∼3.0 Å). This narrow interface is characterized by a high contrast in the βZZZ tensor component between the first (non-null values) and the subsequent (values toward zero) layers. Moreover, the average βZXX and βXZX values satisfy the Kleinman's symmetry rule within the dipolar molecular responses. Therefore, the model including six MeOH molecules (a central molecule plus its five nearest neighbors) in the QC region performs the best in capturing the SHG response of the methanol–air interface and its progression toward the bulk values. Furthermore, similar trends are obtained at different temperatures or when increasing the number of MeOH molecules treated at the QC level, which indicates the robustness of the employed approach for describing the dipolar molecular responses of air–liquid interfaces.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
TNR is a postdoctoral researcher of the Fonds de la Recherche Scientifique – FNRS. The calculations were performed on the computing facilities of the Consortium des Équipements de Calcul Intensif (CÉCI, https://www.ceci-hpc.be) and of the University of Namur under the grants 2.5020.11, U.G006.15, U.G011.22, U.G018.19, RW1610468, RW/GEQ2016, and RW2110213. The present research also benefited from computational resources made available on Lucia, the Tier-1 supercomputer of the Walloon Region, infrastructure funded by the Walloon Region under the grant agreement no. RW1910247.References
- J. Zhong, M. Kumar, J. Anglada, M. Martins-Costa, M. Ruiz-Lopez, X. Zeng and J. S. Francisco, Atmospheric spectroscopy and photochemistry at environmental water interfaces, Annu. Rev. Phys. Chem., 2019, 70, 45–69 CrossRef CAS PubMed.
- M. F. Ruiz-Lopez, J. S. Francisco, M. T. C. Martins-Costa and J. M. Anglada, Molecular reactions at aqueous interfaces, Nat. Rev. Chem., 2020, 4, 459–475 CrossRef CAS PubMed.
- Y. R. Shen, Surface properties probed by second-harmonic and sum-frequency generation, Nature, 1989, 337, 519–525 CrossRef CAS.
- Y. Shen, Optical second harmonic generation at interfaces, Annu. Rev. Phys. Chem., 1989, 40, 327–350 CrossRef CAS.
- N. Bloembergen and P. S. Pershan, Light waves at the boundary of nonlinear media, Phys. Rev., 1962, 128, 606–622 CrossRef.
- P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Generation of optical harmonics, Phys. Rev. Lett., 1961, 7, 118–119 CrossRef.
- R. J. Tran, K. L. Sly and J. C. Conboy, Applications of surface second harmonic generation in biological sensing, Annu. Rev. Anal. Chem., 2017, 10, 387–414 CrossRef CAS PubMed.
- K. B. Eisenthal, Liquid interfaces probed by second-harmonic and sum-frequency spectroscopy, Chem. Rev., 1996, 96, 1343–1360 CrossRef CAS PubMed.
- A. C. McGeachy, E. R. Caudill, D. Liang, Q. Cui, J. A. Pedersen and F. M. Geiger, Counting charges on membrane-bound peptides, Chem. Sci., 2018, 9, 4285–4298 RSC.
- R. Costa, C. M. Pereira, A. F. Silva, P.-F. Brevet and E. Benichou, Ordering and nonideality of air−ionic liquid interfaces in surface second harmonic generation, J. Phys. Chem. B, 2020, 124, 3954–3961 CrossRef CAS PubMed.
- G. C. Gschwend, A. Olaya and H. H. Girault, How to polarise an interface with ions: the discrete Helmholtz model, Chem. Sci., 2020, 11, 10807–10813 RSC.
- F. Castet, C. Tonnelé, L. Muccioli and B. Champagne, Predicting the second-order nonlinear optical responses of organic materials: the role of dynamics, Acc. Chem. Res., 2022, 55, 3716–3726 CrossRef CAS PubMed.
- N. A. Murugan, R. Apostolov, Z. Rinkevicius, J. Kongsted, E. Lindahl and H. Ågren, Association dynamics and linear and nonlinear optical properties of an n-acetylaladanamide probe in a POPC membrane, J. Am. Chem. Soc., 2013, 135, 13590–13597 CrossRef CAS PubMed.
- C. Bouquiaux, F. Castet and B. Champagne, Influence of the nature of the lipid building blocks on the second-order nonlinear optical responses of an embedded di-8-ANEPPS probe, J. Phys. Chem. B, 2023, 127, 528–541 CrossRef CAS PubMed.
- C. Wang, D. Liu and W. Lin, Metal–organic frameworks as a tunable platform for designing functional molecular materials, J. Am. Chem. Soc., 2013, 135, 13222–13234 CrossRef CAS PubMed.
- C. Tonnelé, B. Champagne, L. Muccioli and F. Castet, Nonlinear optical contrast in azobenzene-based self-assembled monolayers, Chem. Mater., 2019, 31, 6759–6769 CrossRef.
- T. T. Pham, A. Jonchère, J.-F. Dufrêche, P.-F. Brevet and O. Diat, Analysis of the second harmonic generation signal from a liquid/air and liquid/liquid interface, J. Chem. Phys., 2017, 146, 144701 CrossRef PubMed.
- Y. Foucaud, B. Siboulet, M. Duvail, A. Jonchere, O. Diat, R. Vuilleumier and J.-F. Dufrêche, Deciphering second harmonic generation signals, Chem. Sci., 2021, 12, 15134–15142 RSC.
- G. Le Breton, O. Bonhomme, P.-F. Brevet, E. Benichou and C. Loison, First hyperpolarizability of water at the air–vapor interface: a QM/MM study questions standard experimental approximations, Phys. Chem. Chem. Phys., 2021, 23, 24932–24941 RSC.
- T. N. Ramos and B. Champagne, Investigation of the second harmonic generation at the water–vacuum interface by using multi-scale modeling methods, ChemistryOpen, 2023, 12, e202200045 CrossRef CAS PubMed.
- A. A. Tamburello-Luca, P. Hébert, P. F. Brevet and H. H. Girault, Resonant-surface second-harmonic generation studies of phenol derivatives at air/water and hexane/water interfaces, J. Chem. Soc., Faraday Trans., 1996, 92, 3079–3085 RSC.
- G. Le Breton, O. Bonhomme, E. Benichou and C. Loison, Liquid water: when hyperpolarizability fluctuations boost and reshape the second harmonic scattering intensities, J. Phys. Chem. Lett., 2023, 14, 4158–4163 CrossRef CAS PubMed.
- R. Antoine, F. Bianchi, P. F. Brevet and H. H. Girault, Studies of water/alcohol and air/alcohol interfaces by second harmonic generation, J. Chem. Soc., Faraday Trans., 1997, 93, 3833–3838 RSC.
- T. Verbiest, K. Clays and V. Rodriguez, Second-order Nonlinear Optical Characterization Techniques: An Introduction, CRC Press, New York, 2009 Search PubMed.
- E. Hendrickx, K. Clays and A. Persoons, Hyper-Rayleigh Scattering in Isotropic Solution, Acc. Chem. Res., 1998, 31, 675–683 CrossRef CAS.
- F. Castet, E. Bogdan, A. Plaquet, L. Ducasse, B. Champagne and V. Rodriguez, Reference molecules for nonlinear optics: a joint experimental and theoretical investigation, J. Chem. Phys., 2012, 136, 024506 CrossRef PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- E. E. Roper, The freezing point of methanol; a simple type of cryostat applicable to freezing point determinations, J. Am. Chem. Soc., 1938, 60, 1693–1695 CrossRef CAS.
- R. W. Hockney, S. P. Goel and J. W. Eastwood, Quiet high-resolution computer models of a plasma, J. Comput. Phys., 1974, 14, 148–158 CrossRef.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: a linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, GROMACS: a message-passing parallel molecular dynamics implementation, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- D. van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: fast, flexible, and free, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. Neumann, Dipole moment fluctuation formulas in computer simulations of polar systems, Mol. Phys., 1983, 50, 841–858 CrossRef CAS.
- R. Gowers, M. Linke, J. Barnoud, T. Reddy, M. Melo, S. Seyler, J. Domański, D. Dotson, S. Buchoux, I. Kenney and O. Beckstein, Proceedings of the 15th Python in Science Conference, 2016, pp. 98–105 Search PubMed.
- L. B. Pártay, G. Hantal, P. Jedlovszky, Á. Vincze and G. Horvai, A new method for determining the interfacial molecules and characterizing the surface roughness in computer simulations. Application to the liquid–vapor interface of water, J. Comput. Chem., 2008, 29, 945–956 CrossRef PubMed.
- M. Sega, G. Hantal, B. Fábián and P. Jedlovszky, Pytim: a python package for the interfacial analysis of molecular simulations, J. Comput. Chem., 2018, 39, 2118–2125 CrossRef CAS PubMed.
- P. Sałek, O. Vahtras, T. Helgaker and H. Ågren, Density-functional theory of linear and nonlinear time-dependent molecular properties, J. Chem. Phys., 2002, 117, 9630–9645 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- F. Castet and B. Champagne, Assessment of DFT exchange–correlation functionals for evaluating the multipolar contributions to the quadratic nonlinear optical responses of small reference molecules, J. Chem. Theory Comput., 2012, 8, 2044–2052 CrossRef CAS PubMed.
- J. M. H. Olsen and J. Kongsted, Molecular properties through polarizable embedding, Adv. Quantum Chem., 2011, 61, 107–143 CrossRef CAS.
- N. H. List, H. J. A. Jensen and J. Kongsted, Local electric fields and molecular properties in heterogeneous environments through polarizable embedding, Phys. Chem. Chem. Phys., 2016, 18, 10070–10080 RSC.
- M. T. P. Beerepoot, A. H. Steindal, N. H. List, J. Kongsted and J. M. H. Olsen, Averaged Solvent Embedding Potential Parameters for Multiscale Modeling of Molecular Properties, J. Chem. Theory Comput., 2016, 12, 1684–1695 CrossRef CAS PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenaes, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjaergaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnaes, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CAS.
- Dalton, a molecular electronic structure program, Release Dalton2020.1, 2022, see https://daltonprogram.org.
- L. Gagliardi, R. Lindh and G. Karlström, Local properties of quantum chemical systems: the LoProp approach, J. Chem. Phys., 2004, 121, 4494–4500 CrossRef CAS PubMed.
- O. Vahtras, LoProp for Dalton, 2014 DOI:10.5281/zenodo.13276.
- D. L. Wertz and R. K. Kruh, Reinvestigation of the structures of ethanol and methanol at room temperature, J. Chem. Phys., 1967, 47, 388–390 CrossRef CAS.
- K. R. Wilson, R. D. Schaller, D. T. Co, R. J. Saykally, B. S. Rude, T. Catalano and J. D. Bozek, Surface relaxation in liquid water and methanol studied by X-ray absorption spectroscopy, J. Chem. Phys., 2002, 117, 7738–7744 CrossRef CAS.
- A. P. Gregory and R. N. Clarke, Traceable measurements of the static permittivity of dielectric reference liquids over the temperature range 5–50 °C, Meas. Sci. Technol., 2005, 16, 1506–1516 CrossRef CAS.
- M. Mohsen-Nia, H. Amiri and B. Jazi, Dielectric constants of water, methanol, ethanol, butanol and acetone: measurement and computational study, J. Solution Chem., 2010, 39, 701–708 CrossRef CAS.
- M. Jorge and L. Lue, The dielectric constant: Reconciling simulation and experiment, J. Chem. Phys., 2019, 150, 084108 CrossRef PubMed.
- M. Scheurer, P. Reinholdt, E. R. Kjellgren, J. M. Haugaard Olsen, A. Dreuw and J. Kongsted, CPPE: An open-source C++ and Python library for polarizable embedding, J. Chem. Theory Comput., 2019, 15, 6154–6163 CrossRef CAS PubMed.
- M. Matsumoto and Y. Kataoka, Molecular orientation near liquid–vapor interface of methanol: Simulational study, J. Chem. Phys., 1989, 90, 2398–2407 CrossRef CAS.
- M. Matsumoto and Y. Kataoka, Erratum: Molecular orientation near liquid–vapor interface of methanol [J. Chem. Phys. 90, 2398 (1989)], J. Chem. Phys., 1991, 95, 7782 CrossRef CAS.
- S. Pezzotti, A. Serva and M.-P. Gaigeot, 2D-HB-Network at the air–water interface: a structural and dynamical characterization by means of ab initio and classical molecular dynamics simulations, J. Chem. Phys., 2018, 148, 174701 CrossRef PubMed.
- J. Quertinmont, B. Champagne, F. Castet and M. H. Cardenuto, Explicit versus Implicit Solvation Effects on the First Hyperpolarizability of an Organic Biphotochrome, J. Phys. Chem. A, 2015, 119, 5496–5503 CrossRef CAS PubMed.
- J. Campo, F. Desmet, W. Wenseleers and E. Goovaerts, Highly sensitive setup for tunable wavelength hyper-Rayleigh scattering with parallel detection and calibration data for various solvents, Opt. Express, 2009, 17, 4587–4604 CrossRef CAS PubMed.
- D. A. Kleinman, Nonlinear Dielectric Polarization in Optical Media, Phys. Rev., 1962, 126, 1977–1979 CrossRef CAS.
- D. Zimdars and K. B. Eisenthal, Effect of solute orientation on solvation dynamics at the air/water interface, J. Phys. Chem. A, 1999, 103, 10567–10570 CrossRef CAS.
- S. Sun, J. Schaefer, E. H. G. Backus and M. Bonn, How surface-specific is 2nd-order non-linear spectroscopy?, J. Chem. Phys., 2019, 151, 230901 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Radial distribution functions, convergence of the vectorial β components, optical properties as a function of the molecular layer (figures and tables), and convergence of the optical properties as a function of the embedding size and number of methanol molecules treated at the quantum chemistry level. See DOI: https://doi.org/10.1039/d4cp00043a |
| This journal is © the Owner Societies 2024 |