Ta⁺ and Nb⁺ + CO₂: intersystem crossing in ion–molecule reactions

Abstract

The reactions of Ta⁺ and Nb⁺ with CO₂ proceed only by a highly efficient oxygen atom transfer reaction to the respective oxide at room temperature in the gas phase. Although the product spin states are not determined, thermochemistry dictates that they must be different from ground state quintet Ta⁺ and Nb⁺, implying that intersystem crossing (ISC) has occurred. Recent reactive scattering experiments found dominant indirect dynamics for the reaction with Ta⁺ hinting at a bottleneck along the reaction path. The question on the nature of the bottleneck, whether it involves a crossing point or a transition state, could not be finally answered because theory located both close to each other. Here, we aim at shedding further light onto the impact of intersystem crossing on the reaction dynamics and ultimately the reactivity of transition metal ion reactions in the gas phase. We employ a combination of thermal kinetics for Ta⁺ and Nb⁺ with CO₂ using a selected-ion flow tube (SIFT) apparatus and differential scattering cross sections for Nb⁺ + CO₂ from crossed-beam velocity map imaging. The reaction with niobium again shows dominant indirect dynamics and in general very similar dynamics compared to Ta⁺ + CO₂. At thermal energies, both reactions show sub-collisional rate constants with small negative temperature dependencies. Experiments are complemented by high level quantum chemical calculations of the minimum energy pathway. Statistical modelling well-reproduces the experimental thermal rate constants, and suggests that the Nb⁺ reaction is rate-limited by the intersystem crossing at thermal energies.

---

Introduction

In the gas phase, where confounding environmental factors can be eliminated, the mechanism of transition metal catalyzed reactions may often involve multi-state reactivity or in more specific cases two-state reactivity (TSR).^1,2 That is, total electron spin is not conserved along the entirety of the reaction path. Even in cases where the reactant and product ground states conserve spin, the rate-limiting step may occur on a potential surface with a different multiplicity.^2–4 Implicitly, these reactions involve intersystem crossings (ISC). While a large body of work in both experiment and theory has advanced understanding, the processes are sufficiently complicated that basic questions even for (seemingly simple) ion–molecule reactions involving intersystem crossing remain challenging.

Whether or not a given reaction may involve intersystem crossing is generally determinable through chemical intuition, known thermochemistry, or quantum chemical calculations. However, whether an intersystem crossing will occur efficiently or if it will be rate-limiting is generally not readily determinable except through experiment. An exceptional computational effort for the FeO⁺ + H₂ system,^4,5 a prototypical example of two-state reactivity,⁶ succeeded in matching experimental results^7,8 showing that while an intersystem crossing was required for this spin-conserving reaction to occur at room temperature, the intersystem crossing was not rate-limiting. Similar efforts for larger systems are challenging and have not been reported. Commonly, a reaction pathway is calculated using density functional theory (DFT). Although the uncertainties in DFT energies for transition-metal containing systems are large, the structures along the pathway are mostly reliable. Where an intersystem crossing is apparent, a minimum energy crossing point (MECP) is located and the spin–orbit coupling at the crossing point is calculated and the Massey parameter⁹ estimated. Where the value is large, the intersystem crossing is assumed to be efficient and where the value is small, the intersystem crossing is assumed to be inefficient. This approach, while tractable, is fraught. The crossing is a multi-dimensional seam, and the spin–orbit coupling may vary widely along this seam such that evaluating the MECP alone is insufficient. An example of this failure is the Ti⁺ + CH₃OH reaction in which calculations¹⁰ predicted an inefficient intersystem crossing, but experiment¹¹ showed an efficient one. Despite issues such as this being reported in the literature for many years, practical concerns have resulted in simplifying assumptions that appear to be poor. Simply put, transition metal-containing catalytic reactions are complicated and insight into ISC in these systems remains limited for systems with few atoms, much less larger real world systems for which analogous processes have been observed.^12–14 And even these small systems still pose challenges to experiment and theory alike.^15,16

The reduction of CO₂ to CO is of obvious importance to science and society as a whole. The set of bare transition metal cations that reduce CO₂ at room temperature is defined almost entirely by thermochemistry; those metal cations with oxygen affinities greater than that of CO (5.45 eV) react with measurable efficiency, while those with smaller oxygen affinities do not.¹⁷ The exceptions are V⁺ and As⁺, which do not produce VO⁺ or AsO⁺ despite the processes being slightly exothermic. Both reactions (1) and (2) are exothermic and have been observed at room temperature. The reactivity has relevance to active sites of real-world catalysts employing Nb-containing materials for CO₂ reduction via electrocatalytic, thermocatalytic, and photocatalytic processes.¹⁸

Nb⁺ + CO₂ → NbO⁺ + CO (1)

Ta⁺ + CO₂ → TaO⁺ + CO (2)

The kinetics of reaction (1) and (2) have been investigated previously both under thermal conditions at room temperature and as a function of collision energy. Bohme and co-workers found both reactions to be highly efficient at about a third of the capture rate.¹⁷ Sievers and Armentrout studied reaction (1) from ≈0.1 eV to 15 eV relative collision energy using a guided ion beam tandem mass spectrometer (GIB-MS) apparatus.¹⁹ Low energy collisions were consistent with a barrierless reaction and interpreted to be forming ground state triplet NbO⁺. At higher energies, excited state product channels opened, including the spin-conserved reaction to form quintet NbO⁺. At the highest collision energies studied, minor channels forming NbCO⁺ and NbO₂⁺ were observed. The authors intuited a reaction pathway involving an intersystem crossing near the [Nb⁺(CO₂)] entrance well. That pathway is quite similar to pathway found by later DFT studies.^20,21 For reaction (2), Schwarz and co-workers never directly measured the bi-molecular rate constant but inferred it to be capture limited or close to.²² Ion trap experiments also investigated the reaction of tantalum cluster cations with CO₂, although the rate constants appear unphysically large.²³

Recently, some of the present authors applied another experimental approach to the Ta⁺ + CO₂ reaction by recording energy and angle differential cross sections in a reactive scattering experiment in combination with high level ab initio calculations.¹⁵ Differential cross sections give insight into the atomic level rearrangement during a reactive collision, thereby probing the dynamics of a reaction.^24–27 If experiments are carried out under single collision conditions, energy and (angular) momentum conservation allow us to extract information on the molecular rearrangement during the reactive collision from the product ion velocity distribution. We can infer if a reaction is following direct dynamics, i.e. a reaction occurs upon impact, or if it is following a complex-mediated mechanism, which we refer to as indirect. Further, we can learn about how energy is redistributed between translational and internal degrees of freedom.^28–31 Weisshaar and co-workers were the first to investigate the dynamics of transition metal ions reacting with small molecules. However, their focus was on cobalt and nickel cations in reactions with C₃–C₄-hydrocarbons.^32,33 The recent experiments were the first to take a look at the dynamics of the oxygen atom transfer reaction involving carbon dioxide.¹⁵ The TaO⁺ product was scattered predominantly isotropically at relative collision energies of up to 2 eV. The found indirect dynamics were surprising considering the limited number of states to dispose the available energy into. The collision energy combined with more than 2 eV of energy released in the reaction makes up a considerable amount of energy available to the reacting system. We reasoned that during the lifetime of the pre-reaction complex collision energy could be efficiently redistributed into internal energy. Once the bottleneck is passed, the now released energy is partitioned into product translation.³⁴ In the calculated reaction pathway, the MECP is located very close to the relevant transition state (see Fig. 1). Both the transition state and the minimum energy crossing point are submerged with respect to the free reactants and pose no thermodynamic barrier. Further the spin–orbit coupling efficiency for the heavy 5d elements is considered to be unity. Thus, the bottleneck seems to be dynamical in nature, or in other words a kinetic effect.

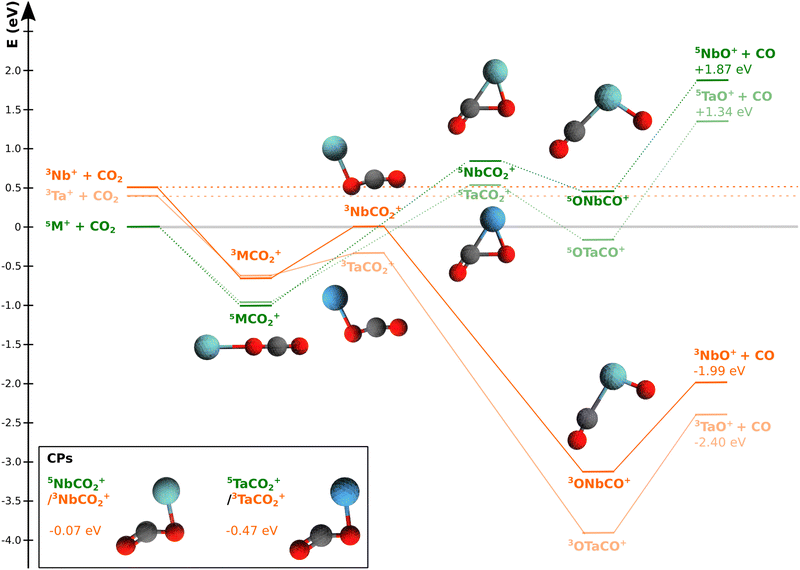Fig. 1 Potential energy profile along the suggested reaction coordinate for NbO⁺ + CO₂ → NbO⁺ + CO Structures of the stationary points along the minimum energy path are given, i.e for the pre-reaction and post-reaction complexes as well the transition states, for the quintet surface (green) and triplet (orange) surface (Nb = light blue, carbon = black, oxygen = red; structural data can be found in the ESI†). The orange coloured energy profile refers to the quintet state, while the energy profile of the triplet state is depicted in green. The reaction of Ta⁺ + CO₂ is given as comparison to Nb⁺ + CO in the same colour code but in shaded colours. Both energy profiles are referenced to ⁵M⁺ + CO₂. M is used whenever the energies of the respective states for Nb and Ta are close to indistinguishable from each other. Kinematic cut-offs are calculated using the presented reaction energies for the reaction of ⁵Nb⁺ and ³Nb⁺ to ³NbO⁺ (E(⁵Nb⁺) = −1.99 eV and E(³Nb⁺) = −2.41 eV). The potential energy profile for TaO⁺ + CO₂ is given as comparison.¹⁵ The inset shows the structures energies of the crossing points (CPs) from quintet to triplet and between Ta(dark blue) and Nb (light blue). All energies are relative to the free reactants in ground electronic state. The energies (not the structures) are calculated using the CCSD(T) method at the geometries optimized with MP2 and with CCSD. The aug-cc-pVTZ basis set was used for C, O, the ECP28MDF_AVTZ basis set for Nb, and ECP60MDF_AVTZ for Ta (see the Methods for details). The crossing points were optimized at the CCSD level.

Similar reactions to the title reactions have been studied by some of the authors using a combination of temperature variable selected-ion flow tube (SIFT) experiments and statistical modelling.^11,16,35,36 The rigorous treatment of the dynamics of transition metal ion molecule reaction is still not readily available. If the reaction, however, proceeds through a sufficiently long-lived intermediate, near complete ro-vibrational redistribution of energy can be assumed. That is, the reaction behaves statistical with respect to the isomerization and dissociation of the respective intermediate. Considering the correct treatment of angular momentum and reliable energetics, rate curves k(E,J) can be calculated. Bounds on the intersystem crossing lifetimes can be placed if experimental temperature dependent rates can be reproduced.³⁶ The Ti⁺ + CO₂ reaction displayed an unusual combination of low efficiency and small negative temperature dependence.¹⁶ Statistical modelling reproduced the results well assuming that an intersystem crossing was rate limiting and did not reproduce the data acceptably assuming instead that a transition state was rate limiting. In this picture, the intersystem crossing was treated as having a characteristic lifetime to a crossing occurring, in competition with possible isomerization or dissociation. The modeling fit the data assuming this lifetime was on the order of 10⁻⁷ s, with about an order of magnitude uncertainty. The same methodology showed very different intersystem crossing lifetimes in the reactions of Ti⁺ + O₂ and Ti⁺ + N₂O, varying from microseconds to sub-picoseconds.¹⁶

In the present study, we combine experimental and theoretical efforts for a deeper insight into the behaviour of the possible statistical behaviour of the oxygen atom transfer reaction between Ta⁺ and carbon dioxide and its lighter homologue niobium Nb⁺. Energetics along the reaction pathway have been calculated at the coupled cluster level of theory. The results give reliable input for the evaluation of energy partitioning in case of experimental differential cross sections and as input for the statistical modelling of the reaction rate and intersystem crossing rates. The results will be interpreted with respect to the possible and most probable bottleneck along the reaction pathway.

Methods

Experiment

Crossed beam velocity map imaging. Niobium cations Nb⁺ are crossed with a molecular beam of CO₂ under single collision conditions in the interaction region of a velocity map imaging spectrometer. The experimental set-up has been described in detail previously.¹⁵ Only a brief explanation will be given here. Ions are formed in a laser vaporization source^37,38 by focusing the 2^nd harmonic of a Nd:YAG laser (Innolas SpitLight, 532 nm, 20 Hz, ≈4 mJ per pulse) onto a rotating niobium target (Alfa Aesar, 99.97%). The generated plasma is swept up by a synchronized helium pulse (8 bar He, 40 μs; AirLiquide, alphagaz 1) oriented perpendicularly to the laser propagation direction. The source is operated such that Nb⁺ cations are formed and cluster formation is suppressed. The ions undergo on the order of 10⁴ collisions with helium before entering the high vacuum region of the source chamber which is insufficient to efficiently quench possible electronically excited states. For tantalum, we estimated an upper limit of electronically excited triplet states at 20% in accordance with estimations of comparable ion sources.^39,40 The laser vaporization source is oriented in line with the velocity map imaging (VMI) spectrometer.^41,42 Once the ions are transferred into the interaction region of the VMI, the ion beam is crossed at 150° with a synchronized molecular beam of pure CO₂ (AirLiquide, 99.995%) from a home-built piezo-electric valve. Product ions are mapped onto a position and time sensitive detector unit perpendicular to the scattering plane using velocity map imaging conditions.⁴³ We operate the VMI in a pulsed mode, i.e. the electrodes of the VMI spectrometer are switched from an off-set voltage to imaging settings about a 1 μs after the mean of ion and neutral beams pass the interaction region. The combination of a multi-channel plate stack, phosphor screen, and camera records the velocity components in the scattering plane, here denoted (v_x,v_y). The multi-channel plates are switched to single-ion counting conditions once the arrival time of the reactant ion beam is passed. A photo-multiplier tube records the arrival time of the ions, which contains information of the velocity along the z-direction. We can recover the 3D Newton sphere due to the cylindrical symmetry of the scattering geometry in the center-of-mass frame. We display the resulting 2D histograms weighted by the radial velocity v_r to be better comparable to sliced images.^41,42,44 The relative collision energy is adjusted by varying the potential off-set of the ion source relative to the DC off-set applied to the velocity map imaging lens stack. Relative collision energies were chosen to compare to the experiments of Ta⁺ + CO₂. Efforts were made to reach energies for which Sievers and Armentrout found the opening of new product states¹⁹ but the current experimental configuration did not allow lower or higher collision energies than the presented. On the lower limit, reliable control of the ion beam could no longer be achieved and at the higher limit the acceptance of the detector was reached. Scaling of the magnification settings would have resulted in additional challenges due to background from the ion beam. Both reactant beams are characterized by 2D velocity map imaging, in case of CO₂ after electron impact ionization. The 1σ-error of the collision energies due to velocity and angular spread of both input beams is between 65 to 140 meV for the presented experiments. Errors of the product ion velocity and respective energy distributions are obtained from Gaussian error propagation.⁴¹

Selected-ion flow tube. The variable-ion source, temperature-adjustable, selected-ion flow tube (VISTA-SIFT) and laser vaporization (LaVa) ion source used here have been described in detail previously.⁴⁵ Briefly, a rotating, translating diameter tantalum (ESPI Metals, 99.9%) or niobium rod (ESPI Metals, 99.9%) was vaporized and ionized using the 2^nd harmonic of a Nd:YAG laser (Litron) operating at 100 Hz. The ions were entrained in an expansion of argon (Matheson, 99.999%) from a high-speed pulsed valve (Parker Iota One) also operated at 100 Hz. Ions were transported using a series of quadrupolar ion guides to a quadrupole mass filter. Mass selected ions were transported using another series of quadrupolar ion guides and injected into a stainless steel, 1 m long, 7 cm diameter reaction flow tube via a Venturi inlet. The ions were entrained into a flow of helium (Matheson, 99.999%), typically 12 std. L min⁻¹ and 0.35 torr. The temperature of the flow tube was variable from 100–700 K using either liquid nitrogen pulsed through copper tubing braised to the outer wall or resistive heating elements wrapped around the exterior. CO₂ was added through a finger inlet 55 cm prior to the terminus of the flow tube via a mass flow meter (MKS) at a variable flow from 0.1 to 10 std. cm³ min¹. A typical reaction time was 2.5 ms. At the end of the flow tube, the bulk of the gas was removed using a Roots-style pump (Leybold) while the gas along the centre axis was sampled through a 4 mm aperture in a rounded, carbon-coated nosecone into a higher vacuum region. The ions were transported using a quadrupolar ion guide to the entrance of an orthogonally-accelerated time-of-flight mass spectrometer (Jordan TOF). Reactant and product ion abundances were monitored as a function of the neutral gas concentration. The mass-selected ions underwent 10⁴–10⁵ collisions with the buffer gas in the flow tube prior to introduction of the neutral reactant. For polyatomic species, this is sufficient to reliably quench to a thermal distribution at the temperature of the flow tube walls. For monatomic species, as was the case here, thermalization is less certain. Both Nb⁺ and Ta⁺ have a number of low-lying states.⁴⁶ While the experiment did not directly probe the state of the reactant ions, several observations suggest that the distributions were largely thermal. In all cases, the decay of the primary ion was well-described by a single exponential. The measured kinetics did not vary upon introducing N₂ or CO at 10¹³ cm⁻³ to the flow tube. The measured kinetics did not vary with varying ion source conditions and were consistent from day-to-day.

Theory

Quantum chemical calculations. Local minima and transition states were optimized using the coupled cluster singles and doubles (CCSD) method along with the aug-cc-pVTZ basis set on carbon and oxygen and the ECP28MDF_AVTZ basis set on Nb.⁴⁷ To obtain more reliable energies, singe-point re-calculation with non-iteratively included triplets, CCSD(T), was performed. The zero-point energy was included as calculated at the CCSD level. Due to convergence issues, the transition state in triplet spin multiplicity was optimized using Møller–Plesset perturbation theory, MP2 (Table S4, ESI† shows that the optimization method does not affect the relative energy considerably). We used the EasyMECP program⁴⁸ to localize the triplet/quintet minimum energy crossing point. While we succeeded to optimize the crossing point at the B3LYP/aug-cc-pVTZ level (with the gap of 17 kJ mol⁻¹ after CCSD(T) recalculation, lying 9.9 kJ mol⁻¹ below the entrance channel), the search for the triplet/quintet minimum energy at the CCSD level did not converge. Still, we localized a point with the 0.5 kJ mol⁻¹ energy difference between quintet and triplet surfaces at the CCSD/aug-cc-pVTZ level. This gap increases to 14 kJ mol⁻¹ after CCSD(T) single-point recalculation, the point lies below the energy of the entrance channel at −6.6 kJ mol⁻¹. Wave function stabilization was performed prior to each structure optimization. All calculations were performed in the Gaussian software package.⁴⁹

Statistical modeling. Full details of the statistical modeling are provided elsewhere.^16,36 Briefly, a reaction path was assumed defined by stationary points from the quantum chemical calculations. Unimolecular rate curves for possible isomerizations k(E,J) were calculated as well as for possible dissociations using the simplified statistical adiabatic channel model (SSACM). Initial conditions, reactant vibrations, rotations, relative kinetic energy, and impact parameter were selected stochastically from thermal distributions defined by a single temperature. The long-range potential was defined solely by electrostatic interactions. For each trial, if the kinetic energy exceeded the centrifugal barrier, a complex was assumed to be formed otherwise no reaction was assumed; this reproduced the Langevin–Gioumousis–Stevenson (LGS) capture rate constant.^50,51 For complex-forming reactions, the system evolved through competition of dissociation and isomerization with probabilities equal to the relative specific k(E,J). An ISC was treated as connecting two stationary points via a transition probability defined by an energy- and angular momentum-independent lifetime competing with relevant isomerization or dissociation. A sufficient number of trials, generally 10³–10⁶, were completed to reduce the statistical scatter to less than 1% in the rate constant.

Sudden vector projection (SVP). The Sudden Vector Projection (SVP) model^52,53 is based on the premise that the ability of a reactant mode in promoting the reaction is proportional to its coupling with the reaction coordinate at a transition state. Hence, the SVP values result from projection of the product modes onto the saddle point, respectively. They are unitless and range between 0 and 1. This assumption is reasonable for direct reactions in which the collision time is significantly shorter than that needed for intramolecular vibrational energy redistribution (IVR) of the reactants. The SVP can be considered as a generalization of the Polanyi rules for atom–diatom reactions,²⁹ which attribute the relative ability of reactant vibrational and translational excitation to enhance reactivity to the location of the transition state along the reaction path.

Results

Minimum energy pathway

The minimum energy reaction pathway for Nb⁺ + CO₂ → NbO⁺ + CO shows all features typical for an exothermic gas phase ion molecule reaction. The pre-reaction complex [MCO₂]⁺ is based on electrostatic interactions with the charge quadrupole interaction being the leading term.^21,54,55 The permanent negative quadrupole moment of CO₂ leads to a linear structure of the pre-reaction complex in both spin states (see Fig. 1). That the interaction is almost purely electrostatic can also be seen by the fact that the well-depth of [NbCO₂⁺] is the same as for [TaCO₂]⁺. The transition state on the quintet surface is characterized by an almost fully cleaved C–O bond and pre-formed products NbO⁺ and CO. It is a typical late transition state and endothermic by about one electron volt. As is well known, the reaction is facile at ambient temperatures.^17,19 The reaction starts on the quintet ground state and moves from there via intersystem crossing to the triplet state which features a much lower barrier compared to the quintet surface. The saddle point on the triplet surface is close in energy to the free ground-state reactants and located earlier along the reaction pathway. The CO₂ is bent by ≈15°. All this is in agreement with the Hammond postulate which states that such significant differences in barrier heights are only possible if the structures in both spin configurations are significantly different from each other.⁵⁶ This behaviour is well-known for transition metal mediated reactions and generally referred to as multi-state reactivity or two-state reactivity.² Recently, it has also been identified for metal-free systems with radical character.⁵⁷ In the present case, reaction (1) bypasses both transition states because the minimum energy crossing point is located after the triplet transition state and the quintet transition state is never reached. The deep minimum of the post-reaction complex is reached which can be characterized by the coordination of a CO molecule to the niobium oxide cation NbO⁺. The minimum energy pathway for the oxygen atom transfer reaction for Ta⁺ + CO₂ is given as comparison¹⁵ in Fig. 1. Structures of stationary points are shown in Fig. 1. Only minimal differences can be observed for tantalum and niobium (for structural data please see Table S3, ESI†).

The minimum energy pathway and the stationary points including crossing points have been investigated before with density functional theory.^19,20 The structures and general features of the surface agree with the known data from the literature. However, for a reliable analysis of the energy partitioning, we rely on the energies of the stationary points from theory which are prone to fluctuations depending on choice of parameters using DFT. Here, we present the stationary points calculated at coupled cluster CCSD(T) level. Our calculated reaction energy of −1.99 eV compares reasonably well with the experimental value of −1.68 eV from guided ion beam experiments.¹⁹ The energy needed to release the CO from the post-reaction complex [ONbCO]⁺ compares equally well to experimental values derived from collision induced dissociation experiments of [ONbCO]⁺ → NbO⁺ + CO which gave a dissociation energy of about 1 eV.¹⁹

Differential cross sections Nb⁺ + CO₂

Reactive scattering experiments have been performed for the niobium cation Nb⁺ and CO₂ forming NbO⁺ to record experimental differential cross sections which encode information on the underlying dynamics (see Fig. 2). Experiments have been conducted at 1.3 eV and 2.2 eV relative collision energy. At both energies, NbO⁺ ions are predominantly isotropically scattered around the center-of-mass at small velocities well away from the respective kinematic cut-offs. The kinematic cut-off is calculated as the maximum possible product ion velocity considering energy and momentum conservation. Ions with smaller velocities indicate that a fraction of the available energy is partitioned into ro-vibrational excitation of the molecular products NbO⁺ and CO. This agrees with the isotropic scattering which is a signature for a complex mediated mechanism in which an interaction complex between the reactants lives for several rotational periods before dissociating into products.^28,31 During this time transfer of energy from translational to internal degrees of freedoms is possible. In other words, the complex lifetime is much longer than the timescale of intromolecular vibrational energy redistribution (IVR). We want to point out two things. First, that that we work under single collision conditions and no energy can be dissipated to the environment. Secondly, that the reaction is exothermic by about 2 eV which makes more than 3 eV available to the reaction. The integrated angular distributions reveal slight asymmetries to the scattering distributions (Fig. 2c and d). While the NbO⁺ ions show some more intensity in the backward hemisphere at E_rel = 1.3 eV, at E_rel = 2.2 eV the trend shifts towards the forward hemisphere. The relative orientation of the reactant beams in the center-of-mass frame are illustrated by the Newton diagram at the top of Fig. 2. The forward hemisphere is defined by the initial direction of the neutral beam and corresponds to a scattering angle of θ = 0°–90° and the backward hemisphere accordingly to θ = 90°–180°, i.e., the initial direction of the ion beam. In the present case, the ion Nb⁺ (93 amu) is heavier than the neutral reactant CO₂ (44 amu). A direct rebound leads to a momentum reversal, meaning the niobium turns around. Thus, scattering into the forward hemisphere as seen at 2.2 eV indicates a direct rebound. At both energies, the scattering angles close to θ = 180° are obstructed due to signal from the ion beam leaking into the scattering signature. This is caused by the close arrival times of reactant and product ions at the detector and by the center-of-mass being located close to the ion beam incident position on the detector. The angular distribution for reaction (2) is added as a grey line in Fig. 2c and d for comparable relative collision energies of 1.4 eV and 2.0 eV¹⁵ for a direct comparison with the distribution for reaction (1). Both reactions show very similar angular distributions. The velocity cut used for evaluation of the energy distributions is indicated by the pink dashed lines. The cut in absolute velocity was chosen as the kinematic cut-off plus the 2σ-error of the product ion velocity from error propagation of the reactant beam velocity and angular spreads.⁴¹ The integrated energy distributions of the full scattering range (θ = 0°–180°) together with the 1σ-error is given in Fig. S1 (ESI†). NbO⁺ ions are scattered well within the kinematic cut-off of the ground state reaction and no significant product ion flux is seen outside the 2σ-error. In case of direct dynamics leading to scattering close to the kinematic cut-off, energy conservation arguments can be used for insight into the reactant beam composition. Due to the highly indirect nature of the reaction, we cannot conclude if NbO⁺ ions formed in reactions of electronically excited Nb⁺ ions. In case of Nb⁺ in its electronically excited triplet reacting, the reaction is spin conserving and follows the typical pathway of an exothermic ion–molecule reaction in the gas phase. At the investigated collision energies, we would expect direct dynamics to be dominant, i.e., a significantly more anisotropic angular distribution and less energy partitioning into internal excitation of the products.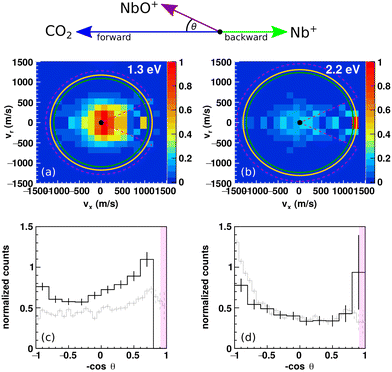

Fig. 2 Differential cross sections for Nb⁺ + CO₂ (a) and (b) product ion NbO⁺ velocity distributions at E_rel = 1.3 eV and 2.2 eV relative collision energy. Distributions are normalized relative to the bin of highest intensity. Kinematic cut-offs indicating the maximum possible energy partitioned into product translation are given by the green (quintet ground state) and orange (triplet excited state) rings. Product ions are mostly scattered isotropically around the center-of-mass with some asymmetry towards the backward plane at low collision energy and towards the forward plane at 2.2 eV. The Newton diagram at the top illustrates the relative orientation of the reactant beams in the center-of-mass frame used to display the velocity distributions. (c) and (d) Normalized integrated angular distributions. The area of the histograms is set to one. The gray histograms show the corresponding distributions for the reaction with tantalum. For θ ≤ 155° (cos θ ≤ 0.8) incomplete background subtraction leads to artifacts (pink shaded areas). The dashed pink lines (a) and (b) indicate the cuts used to calculate product energy distributions (see Methods). Angular integrated distributions for Ta⁺ + CO₂ → TaO⁺ + CO adapted from ref. 15.

Here, we show the fractions of the total energy available to the reaction which is partitioned into internal energy (Fig. 3a) and product ion translation (Fig. 3b). The total available energy is calculated as the sum of the relative collision energy E_rel and the energy of the triplet products with respect to the quintet reactants, ⁵Nb⁺ + CO₂ → ³NbO⁺ + CO. The relative energy partitioning between internal and translational energy is almost the same at both investigated collision energies, meaning that additional collision energy is mostly partitioned into internal excitation of either NbO⁺ or CO. We find a mean value of f_int ≈ 0.6. Energy distributions in absolute units of energy (here eV) are given in Fig. S1 (ESI†) including errors to the product ion energies. A direct comparison of both investigated collision energies is plotted in Fig. S2 (ESI†). The distributions for the reaction with tantalum are drawn as dashed lines as direct comparison. Similar to the angular distributions, the energy distributions are highly comparable. Slightly more energy seems to be channelled into product ion translation in case of niobium but within the experimental error we cannot conclude this to be significant.

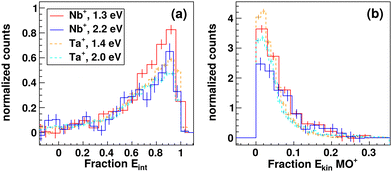Fig. 3 Comparison of energy partitioning for reactions with niobium and tantalum. Relative fractions of energy partitioned into (a) internal excitation of the products MO⁺ + CO and (b) product ion MO⁺ translation are given. The energy scale is set relative to the total available energy for each respective reaction. Histograms are each normalized to an area of one. Histograms in absolute energy scale including errors for the respective energy distributions from Gaussian error propagation are given in Fig. S1 (ESI†). Integrated energy distributions for Ta⁺ + CO₂ → TaO⁺ + CO adapted from ref. 15.

Both reactions encounter a bottleneck along the reaction pathway which leads to trapping with the associated life-time to redistribute energy. Considering the near constant kinetic energy release we reasoned in case of tantalum that the trapping happens on the reactant side and once the bottleneck is passed the reaction goes downhill and the products accelerate flying away from each other. This result is surprising because we have very exothermic four atom reactions combined with a reaction in which only a single atom is transferred. In case of direct dynamics, one could envision a classic heavy M⁺ – light O – heavy CO scenario as for example described by Polanyi.²⁹ However, our experimental differential cross sections give evidence for highly indirect dynamics. Therefore, we took a closer look at the thermal rate constants for the title reactions.

Thermal rate constants k(T) M⁺ + CO₂ (M = Nb, Ta)

Representative mass spectra and kinetics from the SIFT experiment are available in the ESI† (Fig. S4 and S6). Ta⁺ reacted to form only TaO⁺, which in turn reacted rapidly with CO₂ to yield TaO₂⁺. TaO₂⁺ associated with CO₂ to yield TaO₂⁺(CO₂)_1–3. Nb⁺ reacts similarly, but also producing small amounts of NbO⁺(CO₂)_1–3. Details of the sequential chemistry beyond reactions (1) and (2) are provided in the ESI.† The rate constants for reactions (1) and (2) from 200 to 600 K are shown in Fig. 4. Both reactions proceed at a significant fraction of the Langevin capture rate constant (Nb⁺: 6.8 × 10⁻¹⁰ cm³ s⁻¹; Ta⁺: 6.3 × 10⁻¹⁰ cm³ s⁻¹) with mild negative temperature dependence for each one. Over the measured range, the rate constants are well represented by (k_Ta⁺+CO2 = 4.5 ± 1.0 × 10⁻¹⁰ × (T/300)^−0.2±0.1 cm³ s⁻¹, k_Nb⁺+CO2 = 3.4 ± 0.9 × 10⁻¹⁰ × (T/300)^−0.7±0.2 cm³ s⁻¹).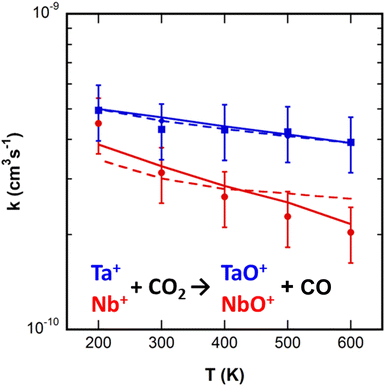

Fig. 4 Thermal rate constants derived from the SIFT measurements for reactions (1) (Nb⁺ + CO₂, red circles) and (2) (Ta⁺ + CO₂, blue squares). Curves are best-fits from statistical modelling (see text) assuming the reactions are rate-limited either by the transition state (dashed) or ISC (solid). Thin lines are Langevin–Gioumousis–Stevenson (LGS) capture rate constants.^50,51

In previous work, a statistical modeling approach was applied to the Ti⁺ + CO₂ → TiO⁺ + CO reaction.¹⁶ As for the systems here, the calculated minimum energy pathway is ambiguous as to whether a necessary intersystem crossing affects the kinetics. The measured Ti⁺ + CO₂ rate constants were smaller than for the Nb⁺ and Ta⁺ reactions reported here, and had a steeper negative temperature dependence, k_Ti⁺+CO2 = 5.5 ± 1.3 × 10⁻¹¹ × (T/300)^−1.1±0.2 cm³ s⁻¹. The experimental results were well-reproduced by assuming that the ISC was rate-limiting, while no reasonable fit to the data was possible assuming that the transition state was rate limiting. In the model, the ISC was not treated explicitly, but instead defined by an average lifetime to the crossing occurring, with that lifetime adjusted to fit the experimental data. For Ti⁺ + CO₂, that lifetime was on the order of 10⁻⁷ s.

For a statistical approach to be applicable, the initial complex must be sufficiently long-lived to allow for IVR to be near complete. Typical IVR timescales for small molecules are on the order of pico seconds but can be significantly longer. The calculated rate curves of the dissociation of the entrance complex back to reactants assuming phase-space behavior are shown in Fig. 5. At energies 1 to 2 eV above threshold, the rate constants are no larger than 10¹⁰ s⁻¹, indicating that a statistical treatment may be appropriate. The rate constants for dissociation into the free products from the post-reaction wells in both reactions are much larger (Fig. S7, ESI†) and should not occur statistically; however, this should not affect treatment of the earlier, rate-limiting step. It is likely that the statistical model can reproduce the general aspects of the kinetics, although non-statistical elements may well be present.

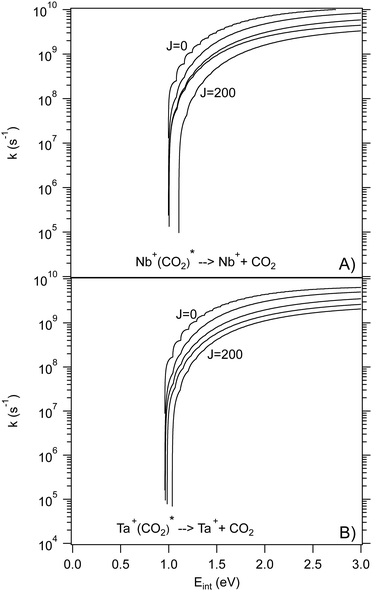Fig. 5 Calculated unimolecular rate curves for dissociation of (A) ⁵Nb⁺(CO₂) and (B) ⁵Ta⁺(CO₂) as a function of the internal energy of the complex for J = 0, 50, 100, 150, and 200.

The best-fits from statistical modeling for both systems are shown in Fig. 4. Scenarios were investigated assuming either the triplet transition state was rate-limiting, an ISC was rate-limiting, or both features contributed. The curves shown are the limiting cases. The calculated energetics for the complexes and the transition states relative to the separated reactants were varied along with the ISC lifetime. For reaction (2), Ta⁺ + CO₂, either scenario (or a combination) provide good fits to the experimental data, with best fit values shown in Table 1. For reaction (1), Nb⁺ + CO₂, an acceptable fit to the data is only achieved by assuming the ISC is rate-limiting. For reaction (2), the data are well fit assuming the triplet TS is −0.2 ± 0.1 eV below reactants (or more negative if ISC also contributes), in reasonable agreement with the calculated value. Alternatively, if the reaction is controlled by ISC alone, the data are fit by an average lifetime to a crossing of ≈10⁻⁹ s, which can be viewed as an upper limit if the TS also contributes. In comparison, the data for reaction (1), Nb⁺ + CO₂, are well fit assuming an average ISC lifetime of 10⁻⁸ s.

Table 1 Best-fit parameters for the reactions of M⁺ + CO₂ → MO⁺ + CO determined using statistical modelling under the scenarios described in the text. Energies are relative to separated ground-state reactants. Ab initio values for Ta⁺ + CO₂ from ref. 15

	Transition state energies (eV)				Lifetime (s)
	Statistical model	Ab initio
		Singlet	Triplet	Quintet
Ti^16					≈10^−7
Nb		0.15	± 0.00	0.84	10^−8
Ta	−0.2± 0.1	−0.07	−0.34	0.53	<10^−9

---

The thermal reactions are distinct from the beam measurements in that the spin-conserved products are always energetically prohibited. Additionally, the calculated spin-conserving quintet transition state is also energetically inaccessible. Singlet and triplet product states are accessible, although the experiment does not probe the nature of those states.

The 300 K rate constants reported here for reactions (1) and (2) (3.1 ± 0.9 × 10¹⁰ cm³ s⁻¹ and 4.5 ± 1.0 × 10¹⁰ cm³ s⁻¹, respectively) are ≈70–90% larger than those reported previously by Bohme and co-workers (1.8 ± 0.6 × 10¹⁰ cm³ s⁻¹ and 2.4 ± 0.8 × 10¹⁰ cm³ s⁻¹).¹⁷ This is a larger disagreement than is typical between the experiments. That the reactant ions are monoatomic and have low-lying electronic states causes concern that the reactant state distribution is non-thermal in one or both experiments, but the underlying cause of the discrepancy is not certain. For reaction (1), both the literature SIFT value and the present results are more efficient (0.26 and 0.47, respectively) relative to the LGS capture rate^50,51 than a guided ion beam measurement extrapolated to 300 K translational energy (0.12).¹⁹ The temperature dependence of reaction (1), T^−0.7±0.2, is in reasonable agreement with the translational energy dependence previously reported for the reaction of E^−1.0 ± 0.1,¹⁹ where T^x is equivalent to E^{x− 0.5}. Surprisingly, Armentrout has not published on reaction (2).

Discussion

Both reactions (1) and (2) occur at a substantial fraction of the LGS capture rate and show mild negative temperature dependencies in the rate constants, common occurrences for exothermic ion–molecule reactions. However, the observed reaction dynamics are dominated by indirect dynamics with a high fraction of ro-vibrational excitation of MO⁺ and/or CO. Additional collision energy seems to be almost exclusively partitioned into the internal excitation leading to a near constant kinetic energy release. This energy release is close to the energy difference between the entrance channel complex and the free products. A sufficiently long-lived entrance channel complex as is the case here, provides the explanation for both experimental observations because the long lifetime allows for efficient redistribution of energy within the entrance channel complex followed by a fixed amount of energy being released as product kinetic energy. The negative temperature dependence of the rate constant arises from competition between an entropically favoured dissociation back to reactants and an energetically favoured isomerization to the product well. Statistical treatment is often successful at quantitatively reproducing this effect by treating calculated transition state energies, which may have uncertainties on the order of hundreds of meV, as adjustable parameters.³⁶ For reaction (2), the statistical treatment reproduces the experimental rate constants well assuming a transition state energy only somewhat above that calculated. For reaction (1), the statistical treatment, regardless of input parameters, predicts a too shallow temperature dependence, indicating that the assumed reaction pathway involving that transition state is not dominant.

Instead, the statistical modelling suggests that reaction (1), Nb⁺ + CO₂, at thermal energies is rate-limited by the ISC, while the results for reaction (2), Ta⁺ + CO₂, are ambiguous and the reaction may be rate-limited by the ISC, a transition state, or a combination of both. Inspection of the calculated reaction pathways for the two reactions show qualitative similarity. In both cases, the ISC is calculated to be close to the transition state. The crossing point for reaction (1) is calculated at ≈0.1 eV lower than the transition state and in the product well. The calculated minimum energy path for reaction (1) then does not include any of the calculated transition states, instead the ISC deposits the reaction directly into the product well. This interpretation is consistent with the statistical modelling results; however, both the calculated minimum energy pathway and the statistical modelling are simplifications of a complicated reaction process, and the result cannot be viewed as definitive.

The dynamics of triatomic systems can often be rationalized under the Polanyi rules,²⁹ but these rules are not easily generalized to systems of more than three atoms. Attempting to apply those rules to the current systems by considering the product CO as a single unit suggests an “early” transition state (i.e. close to the reactant well). Under the Polanyi rules, such a potential surface will favour energy disposal into the NbO⁺ or TaO⁺ product vibrations, consistent with the observations here of excess energy being placed into internal modes. The sudden vector projection model (SVP) attempts to generalize the Polanyi rules to larger systems by comparing the vector of the critical mode at the transition state to the vectors of translational, rotational, and vibrational modes in the separated products or reactants.^53,58 SVP can only be applied where a process occurs promptly. Here, SVP may not appropriate to apply to the separated reactants, because the reaction proceeds through a long-lived intermediate. However, the dissociation of the exit channel complex is expected to be prompt due to the large exothermicity of the reaction and SVP can be applied. Under such circumstances, the energy disposal is largely dictated by the reaction coordinate at the saddle point, as implied by the SVP model. The SVP results for the [OTaOCO]⁺ → TaO⁺ + CO dissociation on the triplet or quintet surfaces are shown in Table 2.

Table 2 Results of the SVP model for the dissociation of the [TaOCO]⁺ transition state on the triplet and quintet surfaces. A graphical illustration of modes used in the SVP analysis is given in Fig. S8 (ESI)

	Triplet	Quintet
Translation	0.591	0.150
TaO^+ vibration	0.301	0.15
CO vibration	0.071	0.011
TaO^+ rotation	0.339	0.682
CO rotation	0.428	0.494

---

On the triplet surface, the SVP model indicates a preference for internal energy disposal, consistent with the experimental results. The TaO⁺ vibration is predicted to be excited, consistent with the Polanyi rules picture above, but primarily the internal energy disposal is expected to be in rotation. Interestingly on the quintet surface, which appears “later” than on the triplet surface, the vibrational excitation is predicted to be very small, consistent with the Polanyi rules, but the deposition into translation is predicted to decrease, inconsistent with the simple picture. The Nb⁺ system has not been treated by SVP, but the similarities between the Ta⁺ and Nb⁺ reaction path dictate that the SVP results would be very similar. In short, the observed dynamics are not inconsistent with the triplet transition state controlling the dynamics.

Conclusions

We presented a multi-method approach to investigate the nature of the bottleneck found for the oxygen atom transfer reactions between Nb⁺ and Ta⁺ with CO₂. Experimental differential cross sections from crossed beam imaging experiments show dominant indirect dynamics for Nb⁺ + CO₂ as found prior for Ta⁺ + CO₂. Despite both reactions involving only four atoms and being highly exothermic, we find a high fraction of internal excitation of NbO⁺ and CO as well as the additional collision energy being mostly partitioned into internal excitation. Only at about 2 eV relative collision energy some rebound dynamics set in. To conclude, both reactions show very similar dynamics which are dominated by indirect dynamics due to a bottleneck along the reaction path. To assess the nature of this bottleneck, we performed temperature dependent rate measurements in combination with statistical modelling. Both reactions show a mild negative temperature dependence which could be modelled using by our statistical approach. The model suggests the ISC as rate limiting for Nb⁺ + CO₂ but we cannot draw any conclusions for Ta⁺ + CO₂. Comparing the three M⁺ + CO₂ (M = Ti, Nb, Ta) reactions that have been investigated in this by combination of statistical modelling and temperature dependent rate constants, the derived ISC lifetimes do scale inversely with mass, consistent with the expectation that the ISC occurs more readily with increasing spin–orbit coupling. Our chemical intuition on if a reaction behaves (non-)statistical or statistical seem to be right as often as it is wrong.

Author contributions

M. E. H. and M. M. carried out the crossed beam experiments. M. E. H. and J. M. analysed the crossed beam data. T. W. R. L. and S. G. A. carried out the SIFT experiments. T. W. R. L., S. G. A. and B. C. S. analysed the SIFT data. N. S. S. performed the statistical modelling. M. O. performed and analysed the quantum chemical calculations, Y. L. and H. G. performed and analysed the SVP simulations, J. M., S. G. A. and N. S. S. supervised the experiments. J. M., M. O. and N. S. S. prepared the manuscript, J. M. and N. S. S. coordinated the study.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. M. thanks the Deutsche Forschungsgemeinschaft DFG (Project number 500279291) for support of this project and the EOARD Windows on Science programme (WOS232020). M. M. acknowledges support by the DFG through the SFB TRR88/3MET. The AFRL authors were supported through the Air Force Office of Scientific Research AFOSR-22RVCOR09. The computational results presented have been obtained using the HPC infrastructure LEO of the University of Innsbruck. H. G. acknowledges support by AFOSR (Grant No. FA9550-22-1-0350). M. E. H., M. M. and J. M. acknowledge and thank Roland Wester and Björn Bastian for providing the data analysis software package for the reactive scattering data. We thank Roland Wester and Albert A. Viggiano for valuable discussions of the presented results.

Notes and references

1. S. Shaik, Isr. J. Chem., 2020, 60, 938–956.
2. D. Schroeder, S. Shaik and H. Schwarz, Acc. Chem. Res., 2000, 33, 139–145.
3. D. Schroeder and H. Schwarz, Angew. Chem., Int. Ed. Engl., 1990, 29, 1433–1434.
4. S. Essafi, D. P. Tew and J. N. Harvey, Angew. Chem., Int. Ed., 2017, 56, 5790–5794.
5. J. N. Harvey and D. P. Tew, Int. J. Mass Spectrom., 2013, 354–355, 263–270.
6. D. Schroeder, A. Fiedler, M. F. Ryan and H. Schwarz, J. Phys. Chem., 1994, 98, 68–70.
7. S. G. Ard, R. S. Johnson, J. J. Melko, O. Martinez, N. S. Shuman, V. G. Ushakov, H. Guo, J. Troe and A. A. Viggiano, Phys. Chem. Chem. Phys., 2015, 17, 19709–19717.
8. S. G. Ard, J. J. Melko, O. Martinez, V. G. Ushakov, A. Li, R. S. Johnson, N. S. Shuman, H. Guo, J. Troe and A. A. Viggiano, J. Phys. Chem. A, 2014, 118, 6789–6797.
9. M. Desouter-Lecomte and J. C. Lorquet, J. Chem. Phys., 2008, 71, 4391–4403.
10. F. Zhang, W. Guo, L. Zhao, X. Lin, L. Zhang, H. Zhu and H. Shan, J. Phys. Chem. A, 2009, 113, 7103–7111.
11. B. C. Sweeny, S. G. Ard, D. C. McDonald II, O. Martinez Jr., A. A. Viggiano and N. S. Shuman, Chem. – Eur. J., 2017, 23, 11780–11783.
12. S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2011, 3, 19–27.
13. S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2012, 4, 511.
14. S. Shaik, S. Cohen, Y. Wang, H. Chen, D. Kumar and W. Thiel, Chem. Rev., 2010, 110, 949–1017.
15. M. Meta, M. E. Huber, T. Michaelsen, A. Ayasli, M. Ončák, R. Wester and J. Meyer, J. Phys. Chem. Lett., 2023, 14, 5524–5530.
16. B. C. Sweeny, B. A. Long, A. A. Viggiano, S. G. Ard and N. S. Shuman, J. Phys. Chem. A, 2022, 126, 859–869.
17. G. K. Koyanagi and D. K. Bohme, J. Phys. Chem. A, 2006, 110, 1232–1241.
18. J.-X. Gao, W.-J. Tian and H.-Y. Zhang, Tungsten, 2022, 4, 284–295.
19. M. Sievers and P. Armentrout, Int. J. Mass Spectrom., 1998, 179–180, 103–115.
20. S. Di Tommaso, T. Marino, F. Rondinelli, N. Russo and M. Toscano, J. Chem. Theory Comput., 2007, 3, 811–815.
21. D.-M. Han, G.-L. Dai, H. Chen, Y. Wang, A.-G. Zhong, C.-P. Lin and D. Chen, Int. J. Quantum Chem., 2011, 111, 2898–2909.
22. R. Wesendrup and H. Schwarz, Angew. Chem., Int. Ed. Engl., 1995, 34, 2033–2035.
23. N. Levin, J. T. Margraf, J. Lengyel, K. Reuter, M. Tschurl and U. Heiz, Phys. Chem. Chem. Phys., 2022, 24, 2623–2629.
24. P. Casavecchia, Rep. Prog. Phys., 2000, 63, 355.
25. K. Liu, Annu. Rev. Phys. Chem., 2016, 67, 91–111.
26. E. Carrascosa, J. Meyer and R. Wester, Chem. Soc. Rev., 2017, 46, 7498–7516.
27. X. Yang, D. C. Clary and D. M. Neumark, Chem. Soc. Rev., 2017, 46, 7481–7482.
28. D. R. Herschbach, Angew. Chem., Int. Ed. Engl., 1987, 26, 1221–1243.
29. J. C. Polanyi, Acc. Chem. Res., 1972, 5, 161.
30. Y. Lee, Science, 1987, 236, 793.
31. R. D. Levine, Molecular reaction dynamics, Cambridge University Press, 2009.
32. E. L. Reichert and J. C. Weisshaar, J. Phys. Chem. A, 2002, 106, 5563–5576.
33. S. S. Yi, E. L. Reichert, M. C. Holthausen, W. Koch and J. C. Weisshaar, Chem. – Eur. J., 2000, 6, 2232–2245.
34. R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534–538.
35. S. G. Ard, B. C. Sweeny, D. C. McDonald, A. A. Viggiano and N. S. Shuman, J. Phys. Chem. A, 2020, 124, 30–38.
36. S. G. Ard, A. A. Viggiano and N. S. Shuman, J. Phys. Chem. A, 2021, 125, 3503–3527.
37. V. E. Bondybey and J. H. English, J. Chem. Phys., 1981, 74, 6978–6979.
38. D. Proch and T. Trickl, Rev. Sci. Instrum., 1989, 60, 713–716.
39. M. A. Duncan, Rev. Sci. Instrum., 2012, 83, 041101.
40. J. Husband, F. Aguirre, P. Ferguson and R. B. Metz, J. Chem. Phys., 1999, 111, 1433–1437.
41. R. Wester, Phys. Chem. Chem. Phys., 2014, 16, 396–405.
42. S. Trippel, M. Stei, R. Otto, P. Hlavenka, J. Mikosch, C. Eichhorn, A. Lourderaj, J. Zhang, W. L. Hase, M. Weidemüller and R. Wester, J. Phys.: Conf. Ser., 2009, 194, 012046.
43. A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484.
44. J. Meyer, V. Tajti, E. Carrascosa, T. Györi, M. Stei, T. Michaelsen, B. Bastian, G. Czakó and R. Wester, Nat. Chem., 2021, 13, 977–981.
45. B. C. Sweeny, S. G. Ard, A. A. Viggiano and N. S. Shuman, J. Phys. Chem. A, 2019, 123, 4817–4824.
46. A. Kramida, Yu. Ralchenko, J. Reader and NIST ASD Team, NIST Atomic Spectra Database (version 5.11), 2023, [Online]. Available: https://physics.nist.gov/asd/ [Wed Jan 31 2024]. National Institute of Standards and Technology, Gaithersburg, MD. DOI: https://doi.org/10.18434/T4W30F.
47. K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, J. Chem. Phys., 2007, 126, 124101.
48. J. Rodríguez-Guerra, I. Funes-Ardoiz and F. Maseras, EasyMECP, Version v0.3.2, Zenodo, 2018.
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian Inc., Wallingford CT, 2016.
50. P. Langevin, Ann. Chem. Phys., 1905, 5, 245.
51. G. Gioumousis and D. P. Stevenson, J. Chem. Phys., 1958, 29, 294–299.
52. B. Jiang and H. Guo, J. Chem. Phys., 2013, 138, 234104.
53. H. Guo and B. Jiang, Acc. Chem. Res., 2014, 47, 3679–3685.
54. M. Sodupe, V. Branchadell, M. Rosi and C. W. Bauschlicher, J. Phys. Chem. A, 1997, 101, 7854–7859.
55. C. Heinemann, R. Wesendrup and H. Schwarz, Chem. Phys. Lett., 1995, 239, 75–83.
56. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338.
57. P. Recio, S. Alessandrini, G. Vanuzzo, G. Pannacci, A. Baggioli, D. Marchione, A. Caracciolo, V. J. Murray, P. Casavecchia, N. Balucani, C. Cavallotti, C. Puzzarini and V. Barone, Nat. Chem., 2022, 14, 1405–1412.
58. H. Song and H. Guo, ACS Phys. Chem. Au, 2023, 3, 406–418.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05549c

‡ These authors contributed equally to this work.

---