Correlated proton dynamics in hydrogen bonding networks: the benchmark case of 3-hydroxyglutaric acid

Abstract

Proton and hydrogen-bonded networks sustain a broad range of structural and charge transfer processes in supramolecular materials. The modelling of proton dynamics is however challenging and demands insights from prototypical benchmark systems. The intramolecular H-bonding networks induced by either protonation or deprotonation of 3-hydroxyglutaric acid provide intriguing case studies of correlated proton dynamics. The vibrational signatures associated with the fluxional proton bonding and its coupling with the hydroxyglutaric backbone are investigated here with infrared action ion spectroscopy experiments and Born–Oppenheimer molecular dynamics (BOMD) computations. Despite the formally similar symmetry of protonated and deprotonated hydroxyglutaric acid, the relative proton affinities of the oxygen centers of the carboxylic and carboxylate groups with respect to that of the central hydroxyl group lead to distinct proton dynamics. In the protonated acid, a tautomeric arrangement of the type HOCO·[HOH]⁺·OCOH is preferred with the proton binding tighter to the central hydroxyl moiety and the electronic density being shared between the two nearly symmetric H-bonds with the carboxylic end groups. In the deprotonated acid, the asymmetric [OCO]⁻·HO·HOCO configuration is more stable, with a stronger H-bonding on the bare carboxylate end. Both systems display active backbone dynamics and concerted Grothuss-like proton motions, leading to diffuse band structures in their vibrational spectra. These features are accurately reproduced by the BOMD computations.

---

1 Introduction

The acid–base activity and the electrochemical responses of organic and biomolecular materials are often driven by proton transfer across coupled H-bonding networks.^1–4 The rationalization of the mechanisms involved in charge transfer and predicting its efficiency are challenged by its intrinsically dynamic and anharmonic nature, and by the typical complexity of the extended supramolecular frameworks that sustain the process. Since this is commonly beyond the reach of first-principles quantum chemistry, cost-effective modeling strategies are sought that capture the essential features of H-bonding and proton dynamics, eventually leading to fair, intuitive approximations to the actual mesoscopic behavior. A variety of quantum-chemical and molecular dynamics approaches have been devised to gain insights into proton sharing and eventual transfer between neighboring electronegative centers.^5–11 The application of these methodologies to well-defined molecular systems of limited size provides a valuable route towards the screening of efficient and scalable modeling schemes.^12–16

This study focuses on the proton dynamics taking place within neighbouring intramolecular H bonds. 3-Hydroxyglutaric acid is chosen as case study, as it provides an outstanding framework in which both protonation and deprotonation trigger a nearly symmetric intramolecular H-bonding that promotes a concerted motion of the two H nuclei in the adjacent bonds. Fig. 1 illustrates this scenario by depicting the lowest-energy configurations adopted by (isolated) neutral 3-hydroxyglutaric acid and by its protonated and deprotonated forms (henceforth denoted M⁰, [M+H]⁺ and [M–H]⁻, respectively). Protonation of the molecule induces a strongly H-bonded configuration in which a central [HOH]^δ+ moiety retains the proton and interacts with the oxygen atoms of the two C=O carboxylic groups. Interestingly, this leads to a roughly symmetric distribution of electronic density in the two H-bonds, which makes the location of the proton in either bond indistinguishable. Deprotonation of the acid also leads to a configuration that can be similarly visualized, although in terms of carboxylate end groups, in this case resulting in an asymmetric H-bonding tautomeric arrangement. In both [M+H]⁺ and [M–H]⁻, the motion of the H-nuclei along the two H-bonds is modulated by the relative proton affinities of the central hydroxyl group and of the carboxylic or carboxylate moieties. Fig. 1 also depicts the complex of 3-hydroxyglutaric acid with Li⁺ (henceforth, [M+Li]⁺), which is included in this work as a reference system featuring more rigid electrostatic interactions.

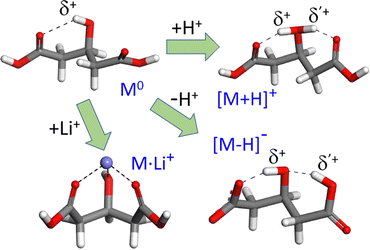Fig. 1 Most stable gas-phase conformations of neutral 3-hydroxyglutaric acid (M⁰) and of the most stable tautomers of its protonated and deprotonated forms (C⁰₁, C₁⁺ and C₁⁻, respectively, see Fig. 4 for additional low-energy configurations). Both protonation or deprotonation trigger an H-bonding network with active proton dynamics, as discussed throughout this work. The more rigid electrostatic Li⁺ complex is included in the investigation as reference.

The structural properties and the dynamical behavior of the three ionic systems, [M+H]⁺, [M–H]⁻ and [M+Li]⁺, are probed in this study through the vibrational signatures exposed in infrared action ion spectroscopy measurements under isolated conditions at room temperature. It will be shown that the electrostatic Li⁺ complex can be described fairly accurately with static quantum chemical approaches. In contrast, the spectral positions and broadenings of the vibrational bands in the H-bonded systems demand a modeling framework that captures proton delocalization effects. Born–Oppenheimer molecular dynamics is found to perform remarkably well in this scenario, thus providing a valuable link between the dynamic structural features of H-bonded networks and the associated experimental observables.

2 Materials and methods

2.1 IRMPD experiments

Infrared multiple photon dissociation (IRMPD) spectra were recorded for lithiated, protonated and deprotonated 3-hydroxyglutaric acid (m/z= 155, 149 and 147, respectively). The complexes were produced by electrospray ionization of 100 μM solutions of the 3-hydroxyglutaric acid in 1 : 1 methanol : water. Trifluoroacetic acid or LiOH were added to stabilize the cationic complexes. Ions were isolated in a quadrupole ion trap mass spectrometer (Bruker AmaZon Speed) at room temperature for spectroscopic interrogation, as described elsewhere.¹⁷

The IRMPD experiments covered a broad spectral range, 700–3800 cm⁻¹, in order to probe vibrational modes of the hydroxyglutaric/glutarate backbone, along with those associated with the intramolecular H-bonding network. The free electron laser FELIX was operated with two different electron beam energies (35 MeV and 46 MeV), to generate infrared radiation in partially overlapping spectral regions, namely 700–2000 cm⁻¹ and 1200–3800 cm⁻¹. The ions were irradiated with a single FELIX pulse, which consists of a 5 microsecond long train of micropulses at a repetition rate of 1 GHz. The spectral bandwidth was ∼0.5% of the central IR frequency. Pulse energies were typically between 20–100 mJ pulse⁻¹, although they dropped to values of ∼5 mJ pulse⁻¹ in the high energy end of the spectrum (>3700 cm⁻¹).

When the laser frequency is in resonance with a vibrational transition of the isolated ion, multiple photon absorption occurs, resulting in fragmentation. The main fragmentation product detected in the mass spectra were as follows: m/z 131 and 113 for [M+H]⁺ (water losses); m/z 85 for [M–H]⁻ (loss of water and CO₂); m/z 95 for [M+Li]⁺ (loss of CH₂–COOH). Each IRMPD spectrum was produced from the corresponding precursor intensity (I_p) and the product ion intensities (I_f) by plotting the photofragmentation yield  ln(I_p/[I_p+ΣI_f]) as a function of the IR frequency. The yield was linearly corrected for the laser pulse energy.¹⁸

2.2 Computations

The low-energy conformational and tautomeric landscapes of the M⁰, [M+H]⁺, [M–H]⁻ and [M+Li]⁺ systems were explored with density functional theory (DFT), ab initio MP2 and coupled-cluster CCSD(T) computations. Geometric optimizations were sequentially performed with the 6-311++G(d,p) and aug-cc-pVTZ basis sets. A broad range of functionals were tested. The B3LYP-D3(BJ)¹⁹ functional (including the D3 empirical dispersion correction with Becke–Johnson damping²⁰) was employed in static DFT and in the Born–Oppenheimer molecular dynamics computations (BOMD) described below. Additional DFT computations were perfomed for all conformers/tautomers with the range-separated functional ωB97xD,²¹ the global hybrid functional MN15²² and the double-hybrid functional B2PLYP-D3(BJ).²³ In view of apparent discrepancies of the computations with experiment for the deprotonated 3-hydroxyglutarate system (see below), an extended series of double-hybrid functionals were tested, namely B2GP-PLYP-D3(BJ),²⁴ DSD-BLYP-D3(BJ),^25,26 PWPB85-D3(BJ),²⁶ DSD-PBEP86-D3(BJ)²⁷ and PBE-QIDH-D3(BJ).^28,29 These double-hybrid functionals range among the most accurate approaches for the description of inter- and intramolecular non-covalent interactions within the framework of extensive databases of molecular properties (e.g., GMTKN55).^26,30,31

The effect of solvation was assessed for particular cases by means of the implicit solvent polarizable continuum model (PCM),³² for water (ε = 78.355) and methanol (ε = 32.688). Free energies under solvation were calculated using the thermodynamic cycle outlined in previous studies.^33,34

Born–Oppenheimer molecular dynamics (BOMD) computations were performed for the ionic system, within the framework of the CP2K code.³⁵ The BOMD computations employed the B3LYP functional with the double-ζ DZVP basis set, the D3(BJ) dispersion correction and the Goedecker, Teter and Hutter pseudopotentials.³⁶ The cut-off radius for the pair potential was set to 12.5 Å and a cubic cell of side length 25 Å was employed for the isolated complex. The plane wave cutoff was set to 400 Ry while the relative cutoff for the Gaussian grid to 50 Ry. The electrostatic contribution was calculated by solving the Poisson equation with cluster boundary conditions from the translational invariant Martyna–Tuckerman scheme.³⁷ The initial angular velocity was set to zero and the center-of-mass was fixed. The complexes were equilibrated in the NVT ensemble at 350 K, with the CSVR thermostat (canonical sampling through velocity rescaling) for 5 ps. Subsequently, a computation in the NVE ensemble was performed to monitor the dynamics of the complexes over 200 ps, with a timestep of 0.5 fs. During this latter NVE stage, the temperature fluctuated with a standard deviation of 40–50 K in all computations. Additional BOMD computations were performed for deuterated variants of the systems under study and also at low temperature (20 K) to aid in the assignment of spectral signatures and in the assessment of homogeneous brodening effects.

Infrared spectra were produced from the BOMD trajectories with the TRAVIS analyzer package,³⁸ based on the Fourier transform of the time correlation function of the molecular dipole moment evaluated from the maximally localized Wannier functions.³⁹ For comparison with experiment, the BOMD spectra shown throughout the paper include scaling factors of 0.985 and 0.965 for the wavenumbers below and above 2000 cm⁻¹, respectively. Similarly, the fundamental frequencies predicted by the DFT B3LYP computations were scaled by 0.975 and 0.955 in the same spectral ranges. Such scaling factors were chosen as to match the position of the narrow bands observed experimentally for the [M+Li]⁺ system and are consistent with common recommendations.⁴⁰

Relaxed potential energy surfaces (PES) were computed at the B3LYP-D3(BJ)/6-311++G(d,p) level to aid in the rationalization of the intramolecular dynamics. In these calculations, the structural parameter of interest is scanned while all other degrees of freedom of the molecular system are allowed to equilibrate to their configuration of minimum energy. Specifically, two parameters were scanned in separate computations: (i) the proton positions along the intramolecular H-bonds and (ii) the dihedral angles of the 3-hydroxy glutaric backbone.

3 Results and discussion

3.1 General features of the IRMPD spectra

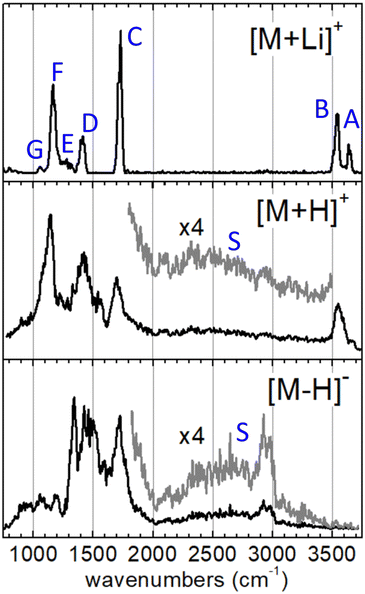
The IRMPD spectra measured for the [M+Li]⁺, [M+H]⁺ and [M–H]⁻ systems are represented in Fig. 2. The spectrum of the [M+Li]⁺ complex displays an ensemble of narrow bands (labelled A–G) that can be assigned to vibrational modes of the 3-hydroxyglutaric acid backbone: O–H stretching of the central hydroxyl (A) and the terminal carboxylic acid groups (B), C=O stretching (C), CH₂ scissoring (D), C–C stretching, mixed with CH/CH₂ wagging and C–O–H bending (E), C–OH stretching and bending in the carboxylic group (F), and C–C stretching mixed with C–O stretching in the central hydroxyl moiety (G). Fig. 3 illustrates how these assignments are supported by the good agreement between the IRMPD measurement and the IR spectra predicted for the [M+Li]⁺ system by the DFT and the BOMD computations (both with the B3LYP functional). It can be concluded that the two computational methodologies reproduce accurately the intrinsic bond strengths and vibrational modes of 3-hydroxyglutaric acid in structurally static complexes, such as [M+Li]⁺.

Fig. 2 IRMPD spectra measured for 3-hydroxyglutaric acid in lithiated, [M+Li]⁺, protonated, [M+H]⁺, and deprotonated, [M–H]⁻, forms. See text for an assignment of the backbone vibrational modes associated to bands A–G in the reference spectrum of the [M+Li]⁺ complex. In the spectra of [M+H]⁺ and [M–H]⁻ the backbone vibrational bands are appreciably broadened. In addition, the stretching modes of the H-bonding network give rise to specific diffuse bands covering an ample spectral range (denoted S and magnified for better visual appreciation).

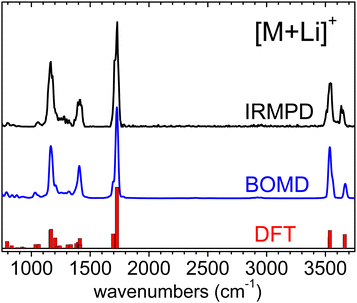Fig. 3 Experimental IRMPD spectrum measured for the [M+Li]⁺ complex and corresponding vibrational spectrum produced from the BOMD computation. The fundamental frequencies predicted by the B3LYP-D3(BJ)/6-311++G(d,p) computation are depicted as a bar diagram for reference. See the lowest energy conformation in Fig. 1. Frequency scaling factors have been applied to the computational spectra as described in Section 2.

The inspection of the time evolution of the BOMD trajectory computed for the [M+Li]⁺ system corroborates the static nature of the robust three-fold coordinated arrangement induced by the strong electrostatic interactions between Li⁺ and the oxygen atoms of the molecular substrate. The distributions of O–Li⁺ distances and of dihedral angles of the glutaric backbone derived from the BOMD computation (not shown) are narrow, with standard deviations of around 0.1 Å and 15°, respectively.

The IRMPD spectra of the H-bonded systems [M+H]⁺ and [M–H]⁻ display vibrational bands with significantly broadened envelopes. Whereas bands C–G described above can be partly recognized, the vibrational signatures of these two systems are clearly spread over broader spectral ranges, suggesting a more fluxional structural behavior. It will be argued that the observed band broadenings are caused by perturbation of the bond strengths across the 3-hydroxyglutaric/glutarate backbone, induced by the dynamic H-bonding network. In addition, proton delocalization along the H-bonds leads to characteristic very diffuse bands associated with O–H^δ+ stretching, which for the present systems extend over the entire 2000–3500 cm⁻¹ spectral range (bands S, magnified ×4 in Fig. 2). These features are discussed in depth below, in the light of the active proton dynamics exposed by the BOMD computations. It is also worth remarking that band B, associated with the stretching of the non-interacting O–H bond of the carboxylic groups is apparent in the IRMPD spectrum of [M+H]⁺ at 3500–3600 cm⁻¹, as a sharp non-diffuse peak. In contrast, the spectrum of [M–H]⁻ displays no peaks in that region, indicating that all of its OH groups are dominantly involved in intramolecular bonding, as illustrated in Fig. 1.

3.2 The concerted proton sharing scenario

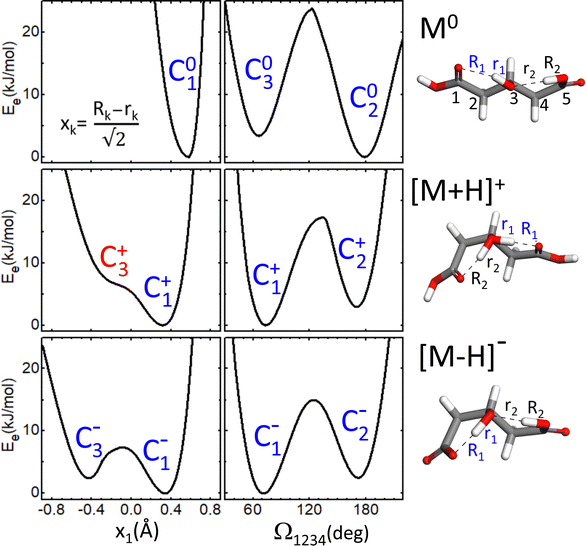
As a first step towards the rationalization of the diffuse vibrational band structures and the underlying proton dynamics, the configurational landscape of 3-hydroxyglutaric acid and of its protonated and deprotonated forms are mapped. Static computations at different levels of theory were performed to assess the relative stability of the low-energy conformers and tautomers and the potential energy barriers between them. The computations include optimizations with DFT employing an ample variety of hybrib and double-hybrid functionals, as well as with ab initio MP2. In addition, single-point coupled-cluster CCSD(T) computations on the equilibrium MP2 configurations were performed. Such variety of methods was applied with the aim of screening the level of theory required to describe the benchmark H-bonding network under study.

Fig. 4 shows the lowest energy configurations of 3-hydroxyglutaric acid in neutral, protonated and deprotonated configurations. The corresponding relative energies at the different levels of theory explored are provided in Table 1. Atomic coordinates of the different configurations are included in the ESI.†Fig. 5 depicts relaxed potential energy surfaces (PES) associated with the motion of one proton along the H-bond, connecting different tautomers (such as C₂⁺↔C₃⁺, or C₂⁻↔C₃⁻). Proton positions are described in terms of the asymmetric stretching coordinate, denoted x and defined from the O–H^δ+–O distances as described in Fig. 5. In addition, PESs are also shown for continuous changes in one dihedral angle, connecting linear and bent backbone conformations. The PES were in all cases computed at the B3LYP/6-311++G(d,p) level in order to provide a close link with the BOMD computations described below, which were performed with the same functional.

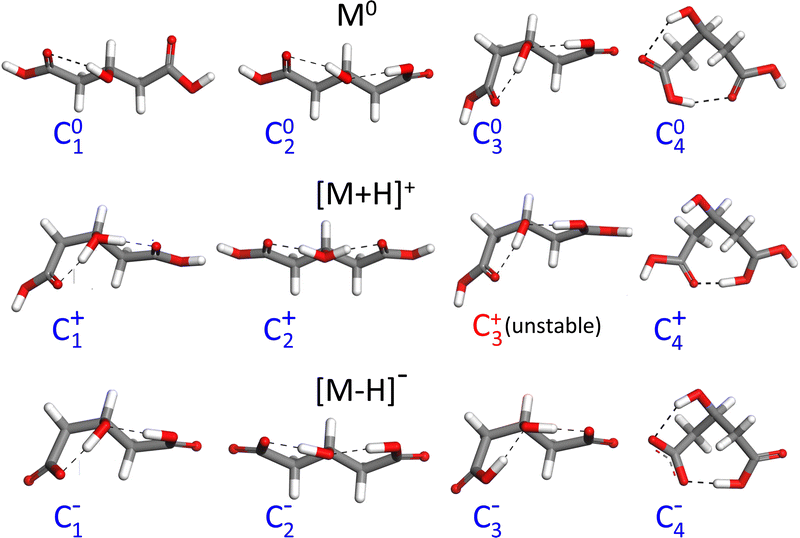Fig. 4 Lowest-energy configurations and prototypical higher energy ones of neutral 3-hydroxyglutaric acid (M⁰) and of its protonated ([M+H]⁺) and deprotonated ([M–H]⁻) forms. Relative energies of the tautomers and conformers at different levels of theory are listed in Table 1.

Table 1 Relative free energies (electronic energies in parenthesis, in kJ mol⁻¹) of the most stable configurations of the M⁰, [M+H]⁺, [M–H]⁻ 3-hydroxy glutaric systems (see Fig. 4), computed at different levels of theory, in all cases with the aug-cc-pVTZ basis set. The bottom row provides the relative energies of the C₄⁻ configuration for the double-hybrid functionals tested in this study (in all cases with D3(BJ) dispersion correction). (C₄⁻)_solv indicates the relative free energy in aqueous solution (methanol solution in brackets), as calculated from the thermodynamic cycle within the PCM method

Method	B3LYP-D3(BJ)	ωB97xD	MN15	B2PLYP	MP2	CCSD(T)
C^01	0	0	0	0	0	0
C^02	+3.1 (−2.2)	+3.4 (−1.6)	+3.1 (−1.7)	+4.3 (+1.8)	+4.5 (−0.6)	(−0.6)
C^03	+7.5 (+0.8)	+8.3 (+1.4)	+7.8 (+1.3)	+9.2 (+2.8)	+8.8 (+2.4)	(+2.7)
C^04	+12 (+3.4)	+12 (+3.9)	+11 (+1.7)	+15 (+5.4)	+13 (+3.9)	(+5.0)
C1^+	0	0	0	0	0	0
C2^+	+2.1 (+3.4)	+2.9 (+3.4)	+0.0 (+1.7)	+1.7 (+2.8)	+2.5 (+3.6)	(+3.0)
C4^+	+20 (+21)	+16 (+18)	+20 (+22)	+22 (+24)	+23 (+27)	(+24)
C1^−	0	0	0	0	0	0
C2^−	+0.4 (+2.2)	+0.4 (+2.2)	−0.2 (+2.3)	+0.3 (+2.2)	+1.3 (+3.4)	(+2.9)
C3^−	+1.8 (+2.4)	+2.2 (+2.6)	+2.4 (+3.2)	+2.2 (+2.6)	+1.7 (+2.7)	(+3.1)
C4^−	−5.2 (−10)	−6.8 (−12)	−10 (−15)	−7.6 (−11)	−6.1 (−12)	(−13)
(C4^−)solv	+2.9 [+2.5]	+2.2 [+1.7]			−0.1 [−0.5]

---

Method	B2PLYP	B2GP-PLYP	DSD-BLYP	PWPB95	DSD-PBEP86	PBE-QIDH
C4^−	−7.6 (−11)	−9.5 (−12)	−10 (−12)	−8.3 (−13)	−7.4 (−12)	−6.3 (−10)

---

Fig. 5 Relaxed potential electronic energy surfaces (PES) computed at the B3LYP-D3(BJ)/6-311++G(d,p) level for neutral 3-hydroxyglutaric acid (M⁰) and for its protonated ([M+H]⁺) and deprotonated ([M–H]⁻) forms. The PES are associated with the scan of the asymmetric stretching coordinate x₁ (left-hand panels), or of the dihedral angle Ω₁₂₃₄ (right-hand panels). See labelling of the H-bond distances and numbering of the C atoms in the representation of the corresponding molecular configurations.

The neutral molecule in its lowest energy conformer (C⁰₁) displays an intramolecular H-bond with the central hydroxyl group as donor. Fig. 5 shows that proton motion within this bond is hindered by a deep and narrow potential energy well that keeps the proton close to its equilibrium position in the covalent O–H hydroxyl bond. In a close lying conformation, C⁰₂, a second comparably weaker H-bond is formed with a carboxylic acid group in anti configuration as donor. The C⁰₂ conformation features a roughly linear backbone (dihedral angles Ω₁₂₃₄ = Ω₅₄₃₂ ≈ 175°; see atom numbering in Fig. 5). The similar H-bonding arrangement C⁰₃, with a bent backbone (Ω₁₂₃₄ ≈ 65° and Ω₅₄₃₂ ≈ 175°) lies higher in energy, despite the improved orientation of the CH₂ groups to avoid mutual repulsions. Finally, it is found that the direct H-bonding of the two carboxylic acid groups (conformer C⁰₄) is not favoured at any level of theory.

The structural features just described for the neutral 3-hydroxyglutaric acid change qualitatively upon protonation or deprotonation, as illustrated in Fig. 4. The bent backbone configurations of [M+H]⁺ and [M–H]⁻ (C₁⁺ and C₁⁻, respectively) are favoured with respect to the linear ones (C₂⁺ and C₂⁻) at most levels of theory and the barrier between the bent and linear configurations is significantly lower than in the neutral molecule. In addition, the effective potential energy surface for the motion of the proton along the H-bonds flattens appreciably. It will be shown that this constitutes a particularly relevant feature, as it triggers an active concerted proton difussion along the two H bonds. In the most stable configuration of [M+H]⁺, C₁⁺, both protons are bound to the central O atom and the transfer of either one of them to an end carbonyl group, while facilitated by the shallow potential energy surface, does not lead to a stable configuration with a pronounced energy well on the PES (e.g. configuration C₃⁺). The analogous configuration C₁⁻ of the anionic [M–H]⁻ system features two-fold H-bonding: a weaker H-bond between one carboxylic acid in anti configuration with the O atom of the hydroxyl group, and a stronger one between the hydroxyl proton and the carboxylate terminal. There is a relatively low barrier for a concerted motion of the two H nuclei, transforming conformation C₁⁻ into C₃⁻, although the latter one is higher in energy by ca. 2 kJ mol⁻¹ at all levels of theory.

A remarkable finding for the deprotonated [M–H]⁻ system is that the most stable configuration predicted at all levels of theory is actually C₄⁻, which features a shared proton bond between the two carboxylate end groups, complemented by a weaker H-bonding interaction of the hydroxyl group. This configuration resembles qualitatively the one adopted by deprotonated glutaric acid.⁴¹ From Table 1, it can be noted that the analogous configurations C⁰₄ in M⁰ and C₄⁺ in [M+H]⁺ are in contrast appreciably high in energy. We argue below that the experimental results do not support a dominant contribution of the C₄⁻ conformation to the recorded spectra.

3.3 Spectral signatures of proton delocalization

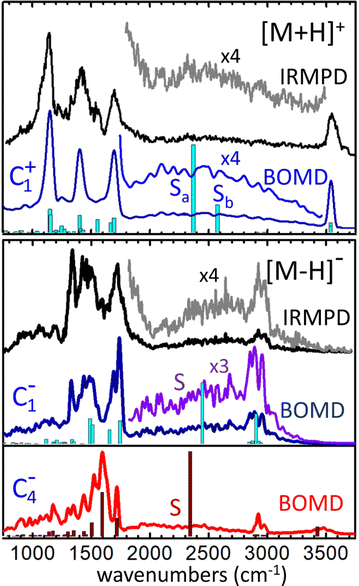
The infrared spectra derived from the BOMD computations for the [M+H]⁺ and [M–H]⁻ systems are depicted in Fig. 6 along with the corresponding IRMPD spectra. The fundamental frequencies predicted by the static B3LYP computation for relevant conformers are also included for reference.

Fig. 6 Experimental IRMPD spectra measured for the [M+H]⁺ cation and the [M–H]⁻ anion, and corresponding spectra produced from the BOMD computations seeded with the C₁⁺, C₁⁻ and C₄⁻ conformers, as indicated. The diffuse band in the central part of the spectra are amplified by the indicated factors for better visualization. The fundamental frequencies predicted by the B3LYP-D3(BJ)/6-311++G(d,p) computations for the same conformers are depicted as bar diagrams for reference. Frequency scaling factors have been applied to the computational spectra as described in Secttion 2.

For [M+H]⁺, the BOMD computation was initated from the C₁⁺ configuration. Nevertheless, the system ocassionally transited to the C₂⁺ and C₃⁺ tautomeric conformations during the 200 ps trajectory, as discussed below in detail. The BOMD spectrum resembles accurately the position of the backbone vibrational bands in the fingerprint region (800–2000 cm⁻¹), as well as the OH stretching band at 3550 cm⁻¹ of the free acid groups. Moreover, the BOMD computation reproduces correctly the diffuse band covering 1800–3500 cm⁻¹, produced by the stretching vibrational modes associated with the H-bonding network. The B3LYP computation predicts harmonic frequencies for the asymmetric and symmetric stretching modes of the central HOH moiety of conformer C₁⁺ at ca. 2400 and 2600 cm⁻¹, respectively, matching the central region of the band. The close agreement between the BOMD and IRMPD spectra is certainly remarkable and provides strong support for the conformational dynamics discussed below, which show that the loose distribution of the protons within the OHOHO network blurs the stretching vibrational energies, leading to the diffuse band observed experimentally.

A complementary BOMD computation was performed for the d₄-deuterated variant of [M+H]⁺, in order to explore isotopic effects on the vibrational signatures and confirm band assignments. The BOMD spectrum derived from this computation is shown in Fig. S1b of the ESI.† Even though the d₄-isotopologue was not measured experimentally, the BOMD computation serves to expose isotopic effects on band positions and broadenings. It is observed that the carboxylic acid CO–D stretching and angle bending bands (bands B and F) are consistently red-shifted with respect to the analogous CO–H bands, by ca. 1000 cm⁻¹ and 150 cm⁻¹, respectively. Band S (shaded in Fig. S1a and b for a better visualization, ESI†) is predicted by BOMD to shift to lower frequencies by ca. 800 cm⁻¹ upon deuteration of the protonated moiety. This band remains appreciably broad in the deuterated isotopologue; nevertheless the slower dynamics of the proton bond for [D–O–D]⁺ in comparison to [H–O–H]⁺, due to the heavier deuteron, reduces the bandwidth by a factor of roughly 2.

An additional prospective BOMD computation was carried out for [M+H]⁺ at low temperature (20 K), seeking to assess the roles of inhomogenous or intrinsic homogeneous band broadenings in this type of proton-bonded systems. The BOMD spectrum derived from this low temperature computation appears to converge to the harmonic spectrum from static DFT, as shown in Fig. S1c (ESI†). It features band envelopes for the main backbone vibrational modes that are roughly a factor of three narrower than their counteparts in the computation at 350 K. The reduced broadening indicates that the three-band structure observed in the fingerprint region at room temperature (bands C, D, F at 1100–1800 cm⁻¹) receives contribution from at least five narrower bands, associated with contributions from COH, CH₂ bending and C–C and C=O stretching vibrations. Remarkably, the 20 K BOMD spectrum displays two sharp bands centered at 2360 and 2650 cm⁻¹ (denoted S_a, S_b), that are associated with the stretching modes of each of the two O–H^δ+ bonds in the [H–O–H]⁺ proton bonding moiety. These bands resemble nicely the two harmonic frequencies predicted by static DFT, with a red-shift of ca. 100 cm⁻¹. The contrast between the sharp bands S_a and S_b at 20 K with the broad band S at 350 K suggests that band broadenings at room temperature are related with dynamic proton motions along the intramolecular bonds, resulting in an indefinition of the stretching frequency (inhomogeneous braodening). The actual behavior of the system at low temperature should be confirmed in experiments conducted at cryogenic temperatures, as quantum nuclear effects (e.g., zero-point energy and tunneling) not accounted for in the BOMD computation may lead to substantial homogeneous band broadening effects as observed for related systems.⁴³

We now focus on the BOMD computations for the deprotonated system [M–H]⁻. In this case, separate computations were seeded with either the C₁⁻ or the C₄⁻ configuration. The electronic energy of C₄⁻ during the BOMD trajectory was on average ∼10 kJ mol⁻¹ lower than C₁⁻, which agrees with the static DFT prediction using the B3LYP functional. The C₁⁻ conformation was found to be connected dynamically with the C₂⁻ conformation (through dihedral angle bending) and with the C₃⁻ tautomer (through proton motions along the intramolecular H-bond), but not to C₄⁻. The C₄⁻ conformation was robustly isolated from the rest, so that the main structural changes during the dynamics were in this case related to proton motion between the two carboxylate groups and to rotation of the COH hydroxyl moiety. Fig. 6 shows that the C₁⁻-seeded BOMD computation yields an excellent agreement with the IRMPD spectrum over the entire spectral region explored. In the fingerprint region, the band at 1120 cm⁻¹ observed for [M+H]⁺ (C–OH stretching and bending in the carboxylic group) is replaced by a band at 1320 cm⁻¹ (assigned to stretching of the H-bonded C=O, mixed with CH₂ wagging). The high energy spectral region features a broad diffuse band extending over 1800–3300 cm⁻¹, overlapping with a comparably narrower band centered at 2920 cm⁻¹. These experimental signatures are accurately reproduced in the BOMD computation and correlate with the position of the fundamental frequencies predicted by the B3LYP DFT computation. The combined computational information allows to assign the broader and more diffuse band to the stretching of the H bond between the hydroxyl group (donor) and the carboxylate group (acceptor), and the narrower band to the similar stretching vibrations in the complementary and weaker H bond between the anti carboxylic acid group (donor) and the O atom of the hydroxyl group (acceptor), on top of lower-intensity C–H streching transitions.

Somewhat unexpectedly, Fig. 6 shows the C₄⁻-seeded BOMD computation produces an IR spectrum with band structures at odds with the most intense features of the experimental IRMPD spectrum. For instance, the intense BOMD band with a maximum at 1600 cm⁻¹ does not correspond to any of the main experimental bands. The computations assign this band to the asymmetric streching mode of the COO⁻ carboxylate moiety. The analogous vibrational mode in conformer C₁⁻ is located at 1700 cm⁻¹, in good agrement with experiment. Moreover, the weakly H-bonded hydroxyl group in C₄⁻ results in an O–H stretching transition at ca. 3450 cm⁻¹, where the experiment shows negligible vibrational activity. This suggests that the C₄⁻ configuration does not have a dominant contribution to the ion population formed in the trap, although a marginal population cannot be ruled out. A minor contribution from C₄⁻ would be for instance consistent with the IRMPD intensity observed between peaks at 1600 cm⁻¹, which seems to be underestimated by the C₁⁻ computation. Also, a marginal participation of C₄⁻ could preclude the detection of the OH stretching band at 3450 cm⁻¹, due to the dynamic broadening predicted for this band by the BOMD computation.

This apparent contradiction between the low relative energy of the C₄⁻ configuration and its minor presence in the experiment could be attributed to inaccuracies in the computational approaches tested in this work, that would overestimate the relative stability of this conformer. Motivated by this discrepancy, the stability of C₄⁻ relative to C₁⁻ was investigated with an ample varity of hybrid and double-hybrid functionals, along with the MP2 and CCSD(T), leading to the energies listed in Table 1. It is found that all computational approaches are coincident in the greater stability of the C₄⁻ configuration by 6–10 kJ mol⁻¹.

An alternative plausible explanation for a low relative abundance of C₄⁻ in the experiments would be that this configuration of the isolated [M–H]⁻ anion is not produced efficiently under the electrospray ionization conditions presently employed. In the electrospray ionization method, species in solution (here water/methanol) are brought into the gas phase through rapid evaporative desolvation of charged droplets. Depending on the molecular system under study, conformations that are stable in solution may be kinetically trapped and retained in the gas phase within the ∼100 ms timescale of the IRMPD experiment.⁴² The deprotonation of the neutral acid in a preformed C⁰₁ or C⁰₂ configuration can be expected to result in the similar C₂⁻ configuration of the [M–H]⁻ anion, eventually relaxing to C₁⁻. Interestingly, the implicit solvent computations indicate that the C₁⁻ conformation becomes roughly isoenergetic to the C₄⁻ one in water and methanol solution in the MP2 computation (see Table 1). At the B3LYP and ωB97xD levels, C₁⁻ is even more stable by ca. +2–3 kJ mol⁻¹. If the [M–H]⁻ anion is transferred to the gas phase dominantly in the C₁⁻ conformation, it is likely that it will be probed in that conformation in the IRMPD measurement. Relaxation of C₁⁻ to the lower energy C₄⁻ configuration would be prevented by a substantial barrier; indeed, we remark that such relaxation process was not observed in the C₁⁻-seeded BOMD computation, despite the fluxional features displayed by the anion.

3.4 BOMD conformational dynamics

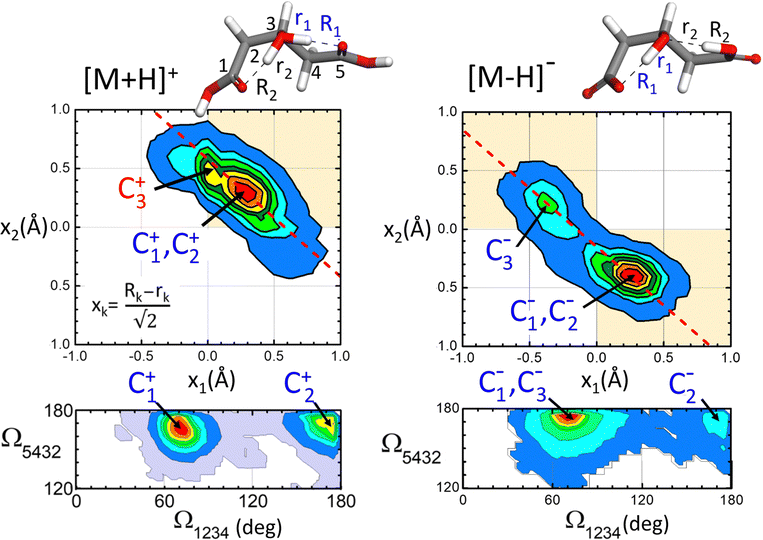
The conformational dynamics of the [M+H]⁺ and [M–H]⁻ systems assessed by the BOMD computations are illustrated in Fig. 7, which shows the probability distribution of the positions of the protons involved in H-bonding (top panels) and of that of the dihedral angles of the hydroxyglutaric acid backbone (bottom panels). The proton distribution is depicted as a contour plot confronting the asymmetric O–H–O stretching coordinates along the two adjacent H-bonds, x₁ and x₂. A similar contour plot represents the distribution of backbone configurations in terms of the dihedral angles Ω₁₂₃₄ and Ω₅₄₃₂ (Ω ∼ 180° for a linear backbone configuration). Only BOMD computations seeded with the C₁⁺ and C₁⁻ conformations are considered in this discussion as they appear to be most relevant to rationalize the present experiments. Relevant types of dynamic structural changes undegone by the two systems are illustrated by means of video animations of time windows of the computed BOMD trajectories, included in the ESI.†

Fig. 7 Probability distributions for the position of the protons along the H-bonding network (top panels) and for the dihedral angles Ω₁₂₃₄/Ω₅₄₃₂ of the hydroxyglutaric backbone (bottom panels) produced from the BOMD computation for the [M+H]⁺ cation and the [M–H]⁻ anion. The shaded quadrants and the dashed line (slope −1) are meant to guide the eye in observing the proton locations and motions in the x₁ − x₂ diagram. The asymmetric O–H–O bond stretching coordinate x_k is defined in the inset. See labelling of the H-bond distances and numbering of the C atoms in the upper molecular representations.

For [M+H]⁺, the proton distribution shows a probability distribution for proton location with a maximum at x₁ ≈ x₂ ≈ +0.3 Å, which correlates with the structures of the two lowest energy conformations C₁⁺ and C₂⁺ (recall that a positive value of x indicates a proton closer to the central O atom than to an O atom of any of the terminal groups). Interestingly, the overall envelope of the probability distribution is oriented along an axis of slope −1, as indicated by the dash line in the contour plot. This feature is indicative of a concerted asymmetric motions of the two protons: when one of the protons departs from the central O atom to approach a carboxylic group, thereby moving toward negative x values, the other proton binds tighter to the central atom reaching more positive values of x (see animation ‘p-proton.mp4’ in the ESI†).

The [M–H]⁻ system displays a qualitatively different proton distribution. In this case, two asymmetric probability maxima are observed, a dominant one at (x₁,x₂) ≈ (+0.3 Å, −0.4 Å) associated with conformations C₁⁻ and C₂⁻ and a less prominent one at (−0.4 Å, +0.3 Å) related to C₃⁻. Both maxima are again connected by an axis of slope −1, indicating a concerted motion of the protons. In this case the transfer of the proton to the carboxylate group induces the deprotonation of the opposite carboxylic acid group, so that the central hydroxyl moiety keeps its entity (see animation ‘m-proton.mp4’ in the ESI†).

As for the hydroxyglutaric backbone configuration, the dihedral angle distributions of both the [M+H]⁺ and [M–H]⁻ systems display two maxima related to the bent and the linear conformations, with Ω₁₂₃₄ ≈ 75° and 175°, respectively. Whereas the bent configuration is clearly dominant, the presence of the two types of conformations in the BOMD trajectory indicates that they are connected through thermal fluctuations at room temperature (see animation ‘p-angle.mp4’ in the ESI†).

The active internal dynamics of the [M+H]⁺ and [M–H]⁻ ions provide a plausible framework to rationalize the broadened and diffuse band structures observed in the experimental IRMPD spectra. On the one hand, the stretching and bending vibrational modes of the hydroxyglutaric acid backbone, mainly observed in the fingerprint spectral region (<2000 cm⁻¹) are perturbed by the configurational changes that take place recurrently at room temperature. On the other hand, proton delocalization along the intramolecular bonds produces the diffuse band structures that extend over the central part of the spectral window investigated (ca. 1800–3200 cm⁻¹).

4 Conclusions

Protonated and deprotonated 3-hydroxyglutaric acid, [M+H]⁺ and [M–H]⁻, have been investigated as benchmarks of fluxional molecular systems with neighboring intramolecular proton bonds. Under isolated room temperature conditions of the ions, vibrational signatures of proton and backbone dynamics are observed in terms of broadened and diffuse band structures over the spectral range 700–3800 cm⁻¹. In general terms, the observed band broadenings arise from the distortion of the bond strengths in the 3-hydroxyglutaric/glutarate backbone induced by the dynamic H-bonding network. Moreover, the O–H^δ+ stretching modes produce particularly broad diffuse bands extending over the entire 2000–3500 cm⁻¹ range, as a consequence of proton delocalization along the H-bonds.

Whereas the average position of most bands is well accounted for by DFT and MP2 computations, ab initio molecular dynamics reproduce with remarkable accuracy their complex precise envelopes. This provides mutual support to the IRMPD and BOMD approaches in that they are reliable methods to probe the inherently anharmonic vibrational features associated with proton bonding at room temperature. IRMPD is a sequential one-photon process that benefits from laser pulse trains appropriately matching the time scale of internal energy redistribution. Nevertheless, IRMPD relies on molecular fragmentation processes that may be complex and affect the spectral response. This and recent investigations^15,16 suggest that band broadenings observed in IRMPD spectra are intrinsinsic to proton-bonded systems. BOMD relies on the accurate description of the relevant energetics by DFT and management of the dipole autocorrelation function, which is here described in terms of maximally localized Wannier functions.³⁹ Alternative approaches have been outlined to elucidate anharmonicity and band broadenings intrinsic to proton bonding at cryogenic temperatures, that are based on the determination of vibrational frequencies with hamiltonians of reduced dimensionality.⁴³

The C₁⁺–C₃⁺ and C₁⁻–C₃⁻ configurational landscapes probed by the present experiments lay out a two-fold H-bonded molecular framework featuring concerted proton motions along the bonds. As a consequence of the symmetry of 3-hydroxyglutaric acid, the two intramolecular H-bonds adopt a dynamically changing ‘proton character’, depending on the relative proximity of the H nuclei to the carboxylic/carboxylate and hydroxyl moieties and the associated rearrangement of electronic density. Protonation of the 3-hydroxyglutaric acid prompts two roughly indistinguishable intramolecular bonds, with properties midway between those of a proton bond and those of a conventional H-bond. Hence, the question of where the added proton is in the molecule becomes meaningless. The two bonds are actually not equivalent because the symmetry is broken by the bent backbone configuration. Such breaking of symmetry has a moderate impact in [M+H]⁺ but it induces a significant configurational bias in [M–H]⁻, favoring a particular H-bonding orientation (x₁ > 0, x₂ < 0; configuration C₁⁻) over its reverse counterpart (C₃⁻).

In the light of the present study, it can be concluded that proton dynamics in 3-hydroxyglutaric acid and its protonated and deprotonated variants captures fundamental features of proton bonded molecular materials. The concerted proton dynamics exposed by the associated vibrational signatures are expected to resemble those of key stages of Grotthus-like proton transfer processes in extended molecular networks. Loose-proton bonding remains as a structural motif of great chemical relevance to be further elucidated in well-defined molecular benchmark systems under controlled conditions.

Author contributions

All authors have collaboratively contributed equally to the different aspects of the investigation and the writing of the manuscript.

Conflicts of interest

The authors have no confict of interest to declare.

Acknowledgements

The authors acknowledge ERDF funding from the Government of Spain (projects TED2021-130683B-C21 and PID2022-136919NA-C33, and the Salvador de Madariaga visiting felowship PRX21/00549). The FELIX free-electron laser laboratory is supported by the Nederlandse Organisatie voor Wetenschappelijk Onderzoek and receives funding from the European Community's Horizon 2020 research and innovation program under grant agreement 871124. We are indebted to the high-performance computing service C3UPO of Universidad Pablo de Olavide.

References

1. M. Meot-Ner, Chem. Rev., 2012, 112, PR22–PR103.
2. O. F. Mohammed, D. Pines, J. Dreyer, E. Pines and E. T. J. Nibbering, Science, 2005, 310, 83–86.
3. D. G. Nocera, J. Am. Chem. Soc., 2022, 144, 1069–1081.
4. L. Catacuzzeno, F. Conti and F. Franciolini, J. Gen. Physiol., 2023, 155, e202313380.
5. S. Raghunathan and S. A. K. Nakirikanti, Mach. Learn.: Sci. Technol., 2023, 4, 035006.
6. Y. Zhang, X. Xu, N. Yang, Z. Chen and Y. Yang, J. Chem. Phys., 2023, 158, 231101.
7. R. E. Warburton, A. V. Soudackov and S. Hammes-Schiffer, Chem. Rev., 2022, 122, 10599–10650.
8. A. W. Sakti, Y. Nishimura and H. Nakai, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 10, e1419.
9. D. C. Marinica, G. Grégoire, C. Desfrançois, J. P. Schermann, D. Borgis and M. P. Gaigeot, J. Phys. Chem. A, 2006, 110, 8802–8810.
10. X. Li, D. T. Moore and S. S. Iyengar, J. Chem. Phys., 2008, 128, 184308.
11. D. Boutwell, D. Pierre-Jacques, O. Cochran, J. Dyke, D. Salazar, C. Tyler and M. Kaledin, J. Phys. Chem. A, 2022, 126, 583–592.
12. J. R. Roscioli, L. R. McCunn and M. A. Johnson, Science, 2007, 316, 249–254.
13. J. Oomens, G. Berden, J. Martens and T. H. Morton, Int. J. Mass Spectrom., 2017, 418, 188–192.
14. D. A. Thomas, M. Marianski, E. Mucha, G. Meijer, M. A. Johnson and G. von Helden, Angew. Chem., Int. Ed., 2018, 57, 10615–10619.
15. F. Gámez, J. R. Avilés-Moreno, G. Berden, J. Oomens and B. Martínez-Haya, Phys. Chem. Chem. Phys., 2021, 23, 21532–21543.
16. B. Martínez-Haya, J. R. Avilés-Moreno, F. Gámez, J. Martens, J. Oomens and G. Berden, J. Phys. Chem. Lett., 2023, 14, 1294–1300.
17. J. Martens, G. Berden, C. R. Gebhardt and J. Oomens, Rev. Sci. Instrum., 2016, 87, 103108.
18. G. Berden, M. Derksen, K. J. Houthuijs, J. Martens and J. Oomens, Int. J. Mass Spectrom., 2019, 443, 1–8.
19. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
20. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
21. J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106.
22. H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051.
23. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
24. A. Karton, A. Tarnopolsky, J. F. Lamere, G. C. Schatz and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 12868–12886.
25. S. Kozuch, D. Gruzman and J. M. L. Martin, J. Phys. Chem. C, 2010, 114, 20801–20808.
26. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309.
27. S. Kozuchm and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104–20107.
28. E. Brémond, J. C. Sancho-García, A. J. Pérez-Jímenez and C. Adamo, J. Chem. Phys., 2014, 141, 031101.
29. J. C. Sancho-García, E. Brémond, M. Savarese, A. J. Pérez-Jímenez and C. Adamo, Phys. Chem. Chem. Phys., 2017, 19, 13481–13487.
30. N. Mehta, M. Casanova-Páez and L. Goerigk, Phys. Chem. Chem. Phys., 2018, 20, 23175–23194.
31. A. Najibi, M. Casanova-Páez and L. Goerigk, J. Phys. Chem. A, 2021, 125, 4026–4035.
32. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
33. T. Dudev and C. Lim, J. Am. Chem. Soc., 2000, 122, 11146–11153.
34. E. da Silva, H. F. Svendsen and K. M. Merz, J. Phys. Chem. A, 2009, 113, 6404–6409.
35. T. D. Kühne, et al. , J. Chem. Phys., 2020, 152, 194103.
36. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
37. G. Martyna and M. Tuckerman, Chem. Phys., 1999, 110, 2810–2821.
38. M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023.
39. M. Sharma, Y. Wu and R. Car, Int. J. Quantum Chem., 2003, 95, 821–829.
40. NIST Computational Chemistry Comparison and Benchmark Database. NIST Standard Reference Database Number 101 (release 22, may 2022). Russell D. Johnson III (ed.). https://cccbdb.nist.gov/vibscalejust.asp (accessed 20 August 2023).
41. F. Thaunay, F. Calvo, E. Nicol, G. Ohanessian and C. Clavaguéra, ChemPhysChem, 2019, 20, 803–814.
42. J. D. Steill and J. Oomens, J. Am. Chem. Soc., 2009, 131, 13570–13571.
43. L. Chen, E. L. Sibert III and J. A. Fournier, J. Phys. Chem. A, 2023, 127, 3362–3371.

---

Footnote

† Electronic supplementary information (ESI) available: Video animations of BOMD trajectories, illustrating intermolecular proton motions and changes in hydroxyglutaric backbone dihedral angles. Atomic coordinates of low energy conformers. Additional BOMD IR spectra. See DOI: https://doi.org/10.1039/d3cp04514e

---