Open Access Article
Open Access ArticleThree-dimensional ordering of water molecules reflecting hydroxyl groups on sapphire (001) and α-quartz (100) surfaces†
Sho
Nagai
a,
Shingo
Urata
 b,
Kent
Suga
a,
Takeshi
Fukuma
b,
Kent
Suga
a,
Takeshi
Fukuma
 cd,
Yasuo
Hayashi
a and
Keisuke
Miyazawa
cd,
Yasuo
Hayashi
a and
Keisuke
Miyazawa
 *cd
*cd
aInnovative Technology Laboratories, AGC Inc., 1-1 Suehiro-cho, Tsurumi-ku, Yokohama, Kanagawa 230-0045, Japan
bPlanning Division, AGC Inc., 1-1 Suehiro-cho, Tsurumi-ku, Yokohama, Kanagawa 230-0045, Japan
cFaculty of Frontier Engineering, Kanazawa University, Kakuma-machi, Kanazawa 920-1192, Japan. E-mail: k.miyazawa@staff.kanazawa-u.ac.jp
dNano Life Science Institute (WPI-NanoLSI), Kanazawa University, Kakuma-machi, Kanazawa 920-1192, Japan
First published on 19th July 2023
Abstract
Water molecules on oxide surfaces influence the chemical reactivity and molecular adsorption behavior of oxides. Herein, three-dimensional atomic force microscopy (3D-AFM) and molecular dynamics simulations are used to visualize the surface hydroxyl (OH) groups and their hydration structures on sapphire (001) and α-quartz (100) surfaces at the atomic-scale. The obtained results revealed that the spatial density distributions and hydrogen-bonding strengths of surface OH groups affect their local hydration structures. In particular, the force curves obtained by 3D-AFM suggest that the hydration forces of water molecules intensify at sites where water molecules strongly interact with the surface OH groups. The insights obtained in this study deepen our understanding of the affinities of Al2O3 and SiO2 for water molecules and contribute to the use of 3D-AFM in the investigation of atomic-scale hydration structures on various surfaces, thereby benefiting a wide range of research fields dealing with solid–liquid interfaces.
1 Introduction
The chemical reactivity, molecular adsorption behavior, and other interfacial properties of oxides, e.g., the HF etching rate1,2 and the biomaterial affinity3,4 of SiO2, are affected by water molecules on oxide surfaces. Given that these interfacial properties are influenced by local interactions between the material surface and water molecules, a deep understanding of the atomic-scale surface structures and their hydration structures is crucial for the design of surface functions. In particular, oxide surfaces usually have polar hydroxyl (OH) groups that strongly interact with water molecules by forming complex hydrogen-bonded networks, which highlight the need for clarifying the local distributions of such surface OH groups and water molecules. The interactions between OH groups and water molecules on oxide surfaces have been widely studied using X-ray reflectivity,5–7 sum-frequency generation infrared spectroscopy8–10 and nuclear magnetic resonance spectroscopy.3,11 These methods provide quantitative information on atomic-scale density distributions, interaction strengths, and relaxation times of water molecules on surfaces, but provide only data averaged over the submicrometer-scale in the lateral direction because of the limited lateral resolution. Therefore, the atomic-scale spatial distributions of water molecules adsorbed on oxide surfaces in real space remain unclear despite numerous related theoretical studies employing computational methods, such as molecular dynamics (MD)12,13 and first-principles simulations.14–16Three-dimensional atomic force microscopy (3D-AFM) was developed as an effective method for investigating local hydration structures.17,18 In 3D-AFM, a frequency shift (Δf) induced by the interaction force applied to an AFM tip is measured during tip 3D scanning at a solid–liquid interface to generate a 3D-Δf image with atomic-scale local contrasts reflecting the local density distributions of water molecules on a sample surface. Previous studies using 3D-AFM have revealed a strong correlation between simulated hydration structures and 3D-Δf images of mica,17–19 calcite,20–23 fluorite,24,25 clinochlore,26 and albite.27 These studies used layered compounds or cleavable crystalline materials, as their surface cleavage easily affords atomically flat and clean surfaces suitable for 3D-AFM measurements. However, this technique has not been extensively applied to oxides, such as SiO2 and Al2O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28,29 despite their importance in glass and cement production, mainly because these oxides cannot be cleaved and easily processed to produce atomically flat and clean surfaces. Thus, a detailed analysis of the local water density distributions and OH group structures on oxide surfaces remains a challenge.
28,29 despite their importance in glass and cement production, mainly because these oxides cannot be cleaved and easily processed to produce atomically flat and clean surfaces. Thus, a detailed analysis of the local water density distributions and OH group structures on oxide surfaces remains a challenge.
Sapphire contains crystalline Al2O3 featuring six-fold-coordinated Al. The sapphire (001) surface has been widely studied and its atomic-scale structure has been revealed using X-ray reflectivity.5,30 The topmost surface of sapphire (001) in water is thought to be hydroxylated31 with densely packed OH groups30 (Fig. 1a) forming a planar arrangement (Fig. 1b). α-quartz (100) is a major crystal of SiO2 and includes an array of SiO4 tetrahedra. In contrast to sapphire (001), the surface structure of α-quartz (100) has not been well investigated. The few related density functional theory (DFT)14,32 and X-ray reflectivity7 studies suggest that the α-quartz (100) surface features OH groups arranged in a zigzag hydrogen-bonded structure (Fig. 1c) consisting of periodically alternating strong and weak hydrogen bonds.32 The corresponding cross-sectional view (Fig. 1d) shows that the OH groups protruded from the Si atoms on the α-quartz (100) surface.
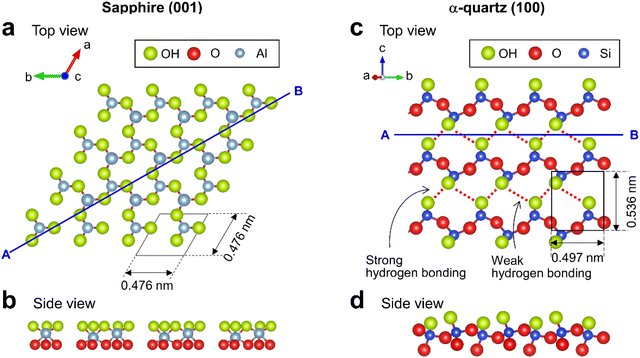 | ||
| Fig. 1 Crystal structures of sapphire (001) and α-quartz (100) surfaces. (a and c) Top and (b and d) side views of (a and b) sapphire (001) and (c and d) α-quartz (100) surfaces visualized using VESTA.33 | ||
Herein, the local hydration structures of the Al2O3 and SiO2 surfaces were investigated using 3D-AFM for sapphire (001) and α-quartz (100) as model samples. The relationship between the surface OH groups and water density distributions on the surfaces was also investigated by comparison with the MD simulation results. Furthermore, the adsorption forces of the water molecules on the surfaces were quantitatively analyzed using force curves obtained by 3D-AFM.
2 Methods
2.1 AFM experiment
Commercially available sapphire (001) substrates with a step-and-terrace structure (Adamant Namiki Precision Jewel Co., Ltd, Japan) were cut and stored in ultrapure water prior to AFM measurements. α-quartz (100) substrates (SOY101005S2, MTI Corporation, Japan) were etched by immersion into a 12% HF solution for 5 h, and then rinsed and stored in ultrapure water prior to AFM measurements. The sample was placed on a sample holder using carbon tape. Subsequently, 50 μL of ultrapure water was dropped onto the sample surface.AFM measurements were performed using a home-built frequency-modulation atomic force microscopy (FM-AFM) equipped with an ultralow-noise cantilever deflection sensor and a highly stable photothermal excitation system.17 A phase-locked loop circuit (OC4, SPECS, Germany) was used for oscillating the cantilever at its resonance frequency (f0). The AFM head was controlled using a commercially available controller (ARC2, Asylum Research, USA). A commercially available cantilever (AC55, OLYMPUS CORPORATION, Japan) was used without any modifications. To measure the crystal surface structures in water, FM-AFM images were acquired and processed using Igor Pro (ver. 6.3.8.1, Wave Metrics Inc., USA). 3D scanning force microscopy (3D-SFM)17 was used to acquire 3D force images for all surfaces. In the 3D-SFM measurements, the 3D distribution of the frequency shift (Δf) was obtained by tip 3D scanning at a solid–liquid interface. 3D-Δf images were acquired for regions with dimensions of 4 × 4 × 2 nm on the substrate surfaces at a resolution of 64 × 64 × 256 voxels in 53 s. The amplitudes of the oscillated cantilever in 3D-SFM measurements were 143.2 pm for sapphire (001) and 89.1 pm for α-quartz (100). The 3D-Δf images were processed using an averaging filter in the XY-plane with a size of 3 × 3 pixels and interpolated four times in the X- and Y-directions using linear interpolation using the home-made analysis software LabVIEW (National Instruments, USA). Sader's method34 was used to convert the Δf curves into force curves for the quantitative analysis of the hydration forces of water molecules on both surfaces.
2.2 MD simulations
The sapphire (001) and α-quartz (100) substrates were composed of 7 × 7 × 2 and 6 × 6 × 4 unit cells, respectively. The as-cut substrate models had two surfaces with exposed oxygen atoms, and 2000 water molecules, as shown in Fig. S1 in the ESI.† In total, 8891 and 7620 atoms were included in the models, respectively. During the simulations, the atoms within 5 Å from the bottom were fixed, and the pressure was controlled at 0.1 MPa in the Z-direction under an isobaric-isothermal ensemble. The water density was then analyzed using trajectories for 2.5 ns following the 1 ns equilibration simulations at 300 K. MD simulations were performed using the LAMMPS package35 with ReaxFF force fields36–38 because the reactive force field automatically generates silanol and aluminol at the surfaces. A Nosé–Hoover thermostat39 and barostat40 were employed, and the atom motion was integrated with a time step of 0.25 fs.To observe the water mobility, the residence autocorrelation of water molecules in a slab layer was analyzed using the following definition:
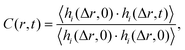 | (1) |
| KKW(t) = exp[−(t/τ)β]. | (2) |
3 Results
3.1 Sapphire (001) and α-quartz (100) surface structures
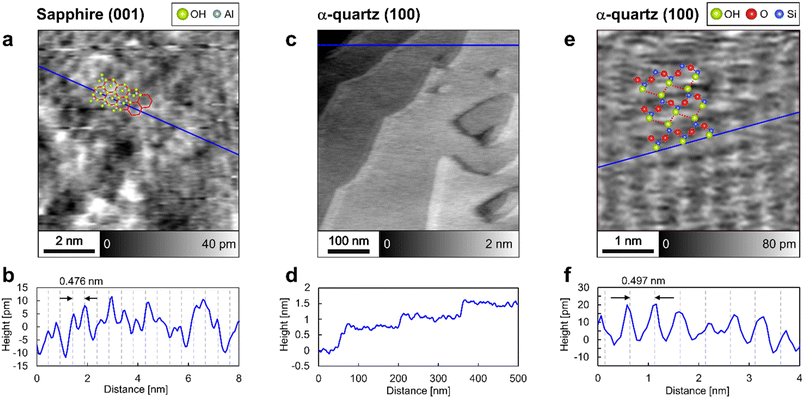
The surface structures of sapphire (001) and α-quartz (100) were analyzed by frequency-modulation atomic force microscopy (FM-AFM) in ultrapure water. Fig. 2a shows an atomic-scale height image of the sapphire (001) surface, revealing the presence of periodic honeycomb-like structures, whereas Fig. 2b presents the height profile obtained along the blue line in Fig. 2a. The periodic structures in Fig. 2b agree with the sapphire (001) unit with a lattice size of 0.476 nm, suggesting that the peak-to-peak distance reflects the crystal structure. The honeycomb-like contrasts in Fig. 2a are consistent with those obtained in previous studies using contact-mode AFM in air41 and probably indicate the presence of vertically oriented Al–O–H groups,41 as predicted using DFT calculations.15,16Fig. 2c and d show the step-and-terrace structure of the α-quartz (100) surface. The single step height (∼0.4 nm according to Fig. 2d) corresponds to the thickness of two SiO4 tetrahedral units.7 In Fig. 2c, shadow effects at the step edges are observed; however, this is caused by the slightly higher feedback gain during the AFM measurement (see Fig. S2 in the ESI†). Further magnification of the flat terrace region reveals lattice-like periodic structures (Fig. 2e and f) that form a rectangular lattice with a period (∼0.5 nm according to Fig. 2f) closely matching the unit lattice length of α-quartz (100). Thus, the FM-AFM images in Fig. 2 exhibit a strong correlation with the crystal structures of sapphire (001) and α-quartz (100) surfaces. We interpret that the atomic-scale contrasts in Fig. 2a and e show the surface OH groups. Thus, the predicted atomistic structures were superimposed on these images. However, it is difficult to determine whether the sample surfaces or their hydration structures are visualized in the FM-AFM images. Thus, comprehensive 3D analysis using 3D-AFM is necessary to understand the 3D interfacial structures on both sapphire (001) and α-quartz (100) surfaces.3.2 Z profiles of hydration structures
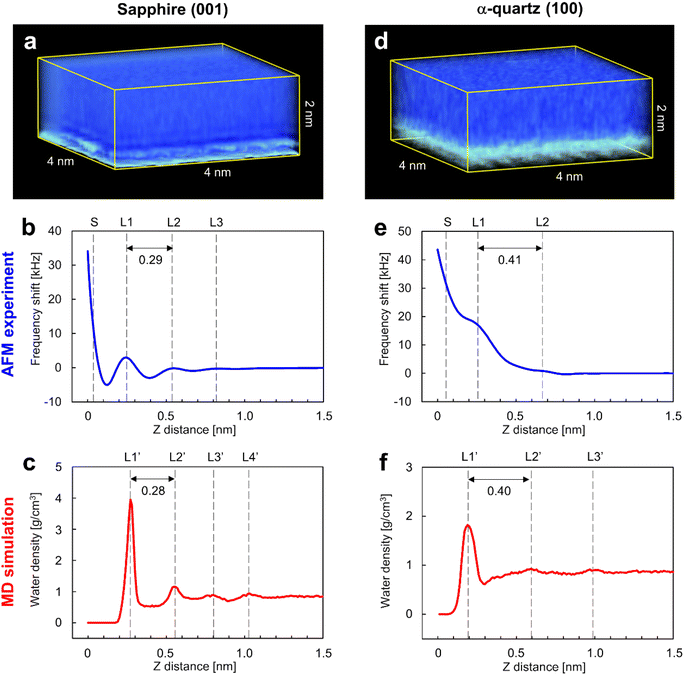
Fig. 3a and d show the 3D visualizations of the Δf distributions measured by 3D-AFM on the sapphire (001) and the α-quartz (100) surfaces, respectively, revealing atomic-scale local contrasts near the surfaces in both cases (bottom sides in Fig. 3a and d). An accidental tip change during 3D-AFM measurement caused changes in the atomic-scale contrasts in the 3D-Δf images. Thus, we excluded areas including discontinuous atomic-scale contrasts from the 3D-Δf images and obtained the cropped 3D-Δf images of 4 × 2 × 2 nm (64 × 32 × 256 voxels) for sapphire (001) and 4 × 3.06 × 2 nm (64 × 49 × 256 voxels) for α-quartz (100) with continuous atomic-scale contrasts. Fig. 3b and e present the laterally averaged Δf curves calculated for both surfaces from the 3D-Δf images and plotted against the vertical distance from the surface side (Z), which represents the relative distance of the vertical tip position in the 3D-AFM experiment. These force curves were averaged over the XY pixel size of each 3D-Δf image (64 × 32 = 2048 points for sapphire (001) and 64 × 49 = 3136 points for α-quartz (100)). Fig. 3c and f show the laterally averaged water density (ρ) profiles of the sapphire (001) and α-quartz (100) surfaces calculated using MD simulations, respectively. The zero position of the ρ profile indicates the vertical position of the top surface of each crystal.The Δf curve of the sapphire (001) surface (Fig. 3b) shows oscillatory profiles, including three repulsive peaks (L1–L3), with a distance between L1 and L2 of 0.29 nm. Similarly, the ρ profile in Fig. 3c shows oscillatory profiles, indicating local hydration layers (L1′–L4′) with a distance between L1′ and L2′ of 0.28 nm. These findings indicate a strong correlation between the Δf and ρ profiles of the sapphire (001) surface, suggesting that L1–L3 in the Δf curve in Fig. 3b represent repulsive peaks generated when the tip penetrates the hydration layers on the sapphire (001) surface (L1′–L3′). The spacings between the L1 and L2 layers in both Δf and ρ profiles of the sapphire (001) surface are consistent with the results of previous X-ray reflectivity5 and AFM42 studies. After the L1 layer was penetrated, Δf significantly increased because of the direct interaction between the tip and the sapphire (001) surface. The Δf curve of the α-quartz (100) surface (Fig. 3e) shows a long-range repulsive profile with small peaks (L1–L2). The distance between L1 and L2 was determined as 0.41 nm. Similarly, the ρ profile (Fig. 3f) shows oscillatory profiles, indicating local hydration layers (L1′–L3′). The distance between L1′ and L2′ was determined as 0.40 nm. These results suggest a strong correlation between the Δf and ρ profiles for the α-quartz (100) surface. Consequently, the L1–L2 peaks in the Δf curve in Fig. 3e correspond to the hydration layers on the sapphire (001) surface (L1′–L2′) in Fig. 3f.
The spacings between the repulsive peaks in the Δf curves agreed with the ρ profiles calculated using MD simulations on both surfaces, and these peaks were therefore concluded to represent the forces associated with the tip penetrating several hydration layers on the sapphire (001) and α-quartz (100) surfaces. The hydration layers away from the surfaces (L4′ in Fig. 3c and L3′ in Fig. 3f) do not appear in the Δf curves because the penetration forces of the hydration layer are weak owing to the higher mobility of water molecules and the lower water density in the hydration layer away from the sample surface. Generally, hydration structures near a surface (such as L1–L3) have higher water density distributions than bulk water, and the mobility of water molecules in the hydration layer is weak because of the strong interactions between the sample surface and water molecules in the hydration layer. 3D-AFM generally enables the visualization of the time-averaged local hydration structures of strongly hydrated water molecules on the surface. Meanwhile, it is difficult to detect the hydration structure with a lower density distribution, which has higher mobility of water molecules (very similar to bulk water) away from the surface, using the current force sensitivity of AFM systems. It may be possible to visualize weakly hydrated structures by further improvement of AFM instruments, such as miniaturizing the cantilever to reduce the noise component or by improving image processing to enhance weak hydration structures.
To investigate the effect of the surfaces on water mobility, the autocorrelation function of water residence was analyzed along the Z-axis using extra MD trajectories of 100 ps (see Fig. S3 in the ESI†). According to Fig. S3,† it is clear that the water molecules located closer to the surfaces maintain their positions for a longer time for both surfaces. The influence of both surfaces on the water mobility almost disappeared at approximately Z = 1.0 nm, whereas the reduction rate of the relaxation time for α-quartz (100) was less steep than that for sapphire (001). The relaxation times of water molecules at Z-distances greater than 0.8 nm are less than 2 ps, indicating that it is difficult to visualize a hydration structure formed by such highly mobile water molecules with a short relaxation time of less than 2 ps, with the current force sensitivity of the AFM system.
3.3 Local structures of surface OH groups and hydrated water molecules
To investigate the local hydration structures on the sapphire (001) and the α-quartz (100) surfaces in detail, we extracted XY and Z cross-sections from the 3D-Δf images. The XY cross-section extracted from the 3D-Δf image of the sapphire (001) surface at Z position S (Z = 0.03 nm) in Fig. 3b shows honeycomb structures (Fig. 4a, red line). The superimposed model of the OH groups on the sapphire (001) surface in Fig. 4a corresponds to the atomic-scale honeycomb contrast of the surface OH groups. The Z cross-section extracted from the 3D-Δf image along the dotted line in Fig. 4a shows three hydration layers (Fig. 4b, L1–L3), similar to the averaged Δf curve indicated in Fig. 3b. In Fig. 4b, the local Δf distributions are indicated by dotted lines, and the water molecules in these areas are expected to be partially concentrated on the surface OH groups.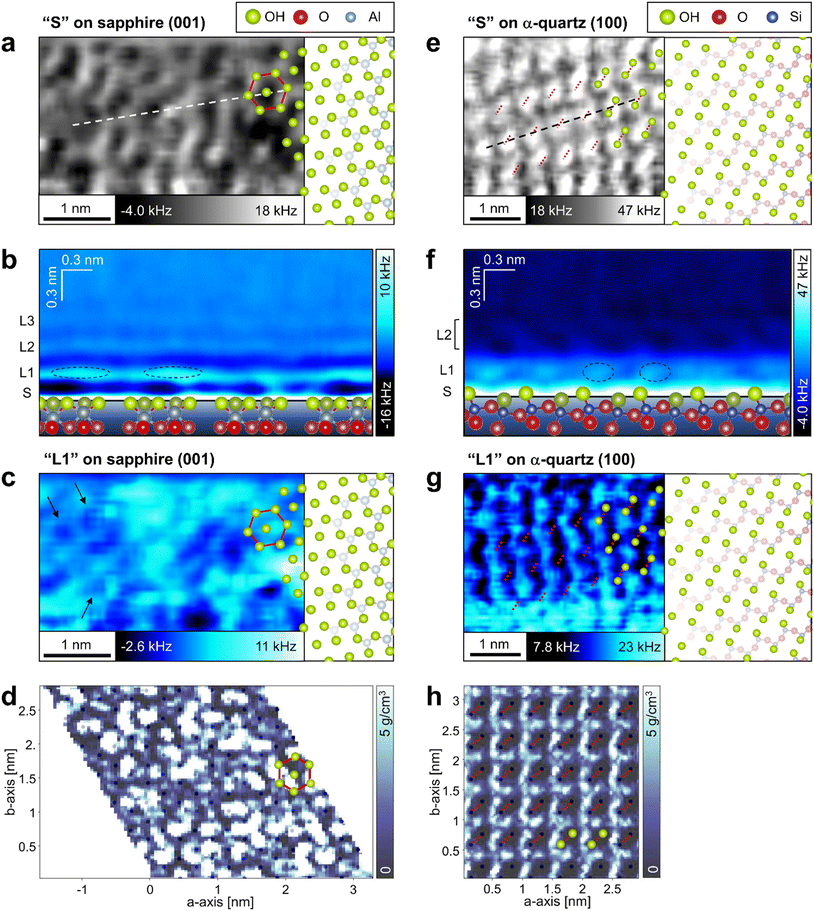 | ||
| Fig. 4 Local water density distributions on the sapphire (001) and the α-quartz (100) surfaces. (a, c, d, e, g and h) XY and (b and f) Z cross-sections extracted from (a, b, c, e, f and g) 3D-Δf images obtained using 3D-AFM and (d and h) 3D-ρ images calculated using MD simulations for (a–d) sapphire (001) and (e–h) α-quartz (100) surfaces, respectively. The XY cross-sections are extracted at positions (a and e) S and (c, d, g and h) L1 as indicated in Fig. 3b, c, e and f. The Z cross-sections in b and f are extracted along the dotted line in a and e. The hexagonal structure in sapphire (001) and the strongly hydrogen-bonded OH groups in α-quartz (100) are indicated by red lines or dotted lines in a, c, d, e, g and h. | ||
The XY cross-section extracted from the 3D-Δf image of α-quartz (100) at Z position S (Z = 0.05 nm) in Fig. 3e reveals elliptical lattices with bright spots (Fig. 4e, red dotted lines). The periodic distances of the lattice contrasts are consistent with the size of the α-quartz (100) unit cell. In addition, the atomic-scale contrasts correspond to the hydrogen-bonded OH groups, as indicated by the atomic models of the quartz (100) surface in Fig. 4e. This result agrees with those of previous DFT calculations14,32 and X-ray reflectivity measurements.7Fig. 4f shows the Z cross-section extracted from the 3D-Δf image along the black dashed line in Fig. 4e. On the α-quartz (100) surface, the Δf distributions show a checkerboard and vertically tilted patterns (Fig. 4f, L1 and L2), whereas a layered distribution is observed on the sapphire (001) surface (Fig. 4b). The vertically tilted structures in L2 were visualized even in raw data without a filtering process (see Fig. S4 in the ESI†). Although the peak-to-peak distances between L1 and L2 in Fig. 3e and f are relatively separate (0.41 nm), hydrated water molecules exist between L1 and L2 and fill this space by forming tilted hydration structures. It is difficult to understand such complicated local hydration structures with the laterally averaged 1D-Δf and ρ profiles shown in Fig. 3e and f. Thus, three-dimensional analysis by 3D-AFM is necessary to understand the atomic-scale local hydration structures in 3D real space. To clarify the relationship between the arrangement of surface OH groups and the in-plane ordering of water molecules, we compared the distributions of water molecules calculated using MD simulations at the L1 layer with the results of the 3D-AFM measurements for both surfaces. Fig. 4c and g show the XY cross-sections extracted from 3D-Δf images at the L1 layer for each crystal surface, whereas Fig. 4d and h present the XY cross-sections extracted from 3D-ρ images calculated using MD simulations at position L1. The honeycomb-like structure of sapphire (001) depicted in Fig. 4a is superimposed in Fig. 4c and d, and the strongly hydrogen-bonded OH groups of α-quartz (100) are superimposed in Fig. 4g and h (red dotted lines). The black dots in Fig. 4d and h represent the positions of oxygen (corresponding to the OH groups) on the topmost surfaces of the crystals.
For sapphire (001), both AFM experiments and MD simulations revealed the presence of uniform and non-uniform local hydration structures, as shown in Fig. 4c and d. Uniform ring-like local contrasts are partially observed, as indicated by the arrows in Fig. 4c. This hexagonal hydration structure was predicted using previous DFT calculations.15,16 The non-uniform contrast in sapphire (001) is due to the higher dynamics of the surface OH groups on sapphire (001).45 The locality of these OH states on the sapphire (001) surface contributes to the generation of irregularities in the atomic-scale local contrast of the L1 hydration layer.
For α-quartz (100), the XY cross-sections in Fig. 4g and h exhibit atomic-scale periodic structures, and the higher contrast regions are localized at positions that are not just above the surface OH groups. The lower contrasts just above the OH groups suggest a lower water density in the OH groups. This result is consistent with that of a previous DFT study.14
3.4 Relationship between force curves and hydration forces
A quantitative analysis of the force curves measured by 3D-AFM was performed to compare the hydration forces at the adsorption sites of water molecules on the surfaces. Fig. 5a and c are the averaged force curves for the sapphire (001) and the α-quartz (001) surfaces with superimposed double-exponential fittings. Fig. 5b and d show the XY cross-sections obtained from the 3D-Δf images similar to Fig. 4a and e. For the sapphire (001) surfaces in Fig. 5b, atomic-scale sites from (1) to (3) were determined. Sites (1) and (2) correspond to the vertices of the hexagonal structure, whereas site (3) corresponds to the center of the hexagonal structure. For the α-quartz (100) surface in Fig. 5d, sites (1), (2), and (3) correspond to the positions between the two strongly hydrogen-bonded OH groups, the central position of the four OH groups, and the position just above the strongly hydrogen-bonded OH groups, respectively. Force curves were converted from the Δf curves using Sader's method.34 The averaged force curves were obtained by averaging the force curves obtained at sites (1)–(3) in Fig. 5b and d. For averaging the force curves, three force curves were acquired at each of the sites (1)–(3) indicated in Fig. 5b for sapphire (001), and five force curves were acquired at each of the sites (1)–(3) indicated in Fig. 5d for α-quartz (001). For clarity, the force curves were visualized by adding offsets to the vertical axis (Fig. 5a and c). The force curves include several types of tip–sample interactions such as short-range repulsive forces against the surface, attractive van der Waals force, solvation force (i.e., penetration of water or solvation molecules in liquid) and electric double-layer forces.24,43,44 Herein, the tip–surface interaction was approximated by fitting it to an exponential function, as described in previous studies,17,24,26,44 and this function was subsequently subtracted from the original force curves (Fig. 5e and f).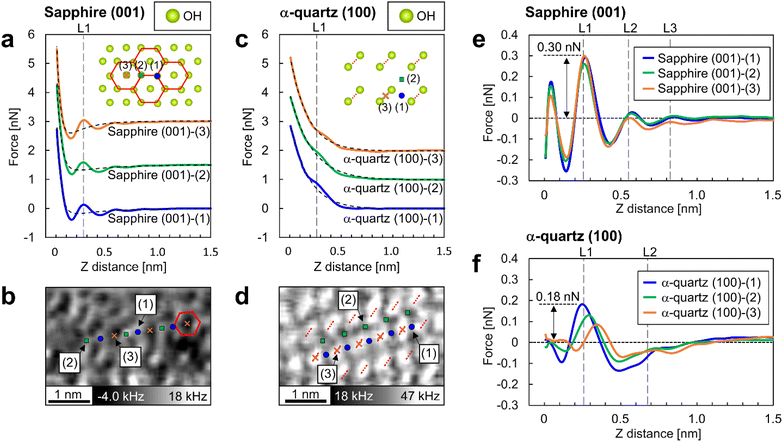 | ||
| Fig. 5 Short-range force curves on sapphire (001) and α-quartz (100) surfaces. (a and c) Averaged force curves on sapphire (001) and α-quartz (100) surfaces with superimposed double-exponential fittings. The inset atomic models depict the crystal structures of the OH groups on each surface. The averaged force curves were calculated by averaging the force curves obtained at sites (1)–(3). In (a), sites (1) and (2) correspond to the vertices of the hexagonal structure, whereas site (3) corresponds to the center of this structure. In (c), sites (1), (2), and (3) correspond to a position between two strongly hydrogen-bonded OH groups, the central position of the four OH groups, and a position directly above the strongly hydrogen-bonded OH groups, respectively. (b and d) XY cross-sections taken from the 3D-Δf images (identical to the images in Fig. 4a and e) at position S in Fig. 3b and e for each crystal. Similar to a and c, the atomic positions at sites (1)–(3) are indicated on the XY cross sections. (e and f) Short-range force curves for each site on the sapphire (001) and α-quartz (100) surfaces after the subtraction of long-range interactions. | ||
The force curves for sapphire (001) in Fig. 5a reveal an attractive force at Z-distances of less than 0.5 nm and a strong repulsive force closer to the surface, whereas the force curves for α-quartz (100) in Fig. 5c show monotonic increase profiles. These long-range interactions are explained by the surface charges of the Si tip and both sapphire (001) and α-quartz (100) surfaces (see Table 1 in the ESI†). For the short-range forces of sapphire (001) in Fig. 5e, the force peaks at position L1 in all force curves show higher values of 0.22–0.31 nN. Force peaks were also observed at positions L2 and L3; however, the related peak values were lower than those at position L1. For the short-range force curves of α-quartz (100) in Fig. 5f, the force curves at sites (1) and (2) showed higher values at position L1, whereas a much weaker force was measured at the slightly shifted Z position at site (3). This behavior reflects that the hydration structure on the α-quartz (100) surface is much more site-dependent than that on the sapphire (001) surface, as shown in Fig. 4b and f. In addition, the peak force values for penetrating the L1–L3 hydration layers on sapphire (001) exceed those observed for α-quartz (100). In particular, the force required to penetrate the L1 hydration layer on sapphire (001) is approximately twice that required for quartz (100).
4 Discussion
4.1 Relationship between surface OH groups and their hydration structures
In this study, we compared the 3D hydration structures on sapphire (001) and α-quartz (100) surfaces using 3D-AFM. For sapphire (001), although the L1 layer was partially structured as a ring-like shape because of the Al–O–H at the surface,15,16,45,46 the overall L1 hydration layer was not uniform in the XY-plane (Fig. 4c), possibly because of the imperfect honeycomb arrangement of the vertically oriented OH groups on the sapphire (001) surface. Given that the OH groups serve as primary adsorption sites for water molecules, even a minor structural deviation of the states of the OH groups could alter the hydrogen-bonding network, disrupting the in-plane water density distributions from an ideal honeycomb structure. For α-quartz (100), the L1 layer exhibits a uniform structure in the XY plane. 3D-AFM experiments revealed that a higher force was necessary to penetrate the L1 layer at site (1) (Fig. 5f). This site is associated with the location of the weakly hydrogen-bonded OH groups on the surface. Thus, water molecules were stably adsorbed onto the surface OH groups on this site. The above results indicate that the hydration structures on oxide surfaces are influenced not only by the lateral periodicity of the surface OH groups, as previously proposed,26,27 but also by their spatial density distributions and hydrogen-bonding strengths.4.2 Affinity of oxide surfaces for water molecules
When calculating the hydration forces of water molecules on each surface from the force peak values necessary for penetrating the L1 layer on each surface, we found that the force peak of L1 on sapphire (001) and α-quartz (100) were 0.31 nN (Fig. 5e) and 0.15 nN (Fig. 5f), respectively. Considering the ideal situation of in-liquid AFM measurements using a water molecule tip, as proposed in the solvent tip approximation model,47 these force peaks are interpreted as the force required to displace a water molecule directly interacting with the surface OH groups (i.e., the hydration force of a water molecule on a surface). These findings qualitatively suggest that the sapphire (001) surface has higher affinity for water than the α-quartz (100) surface. It is reasonable to assume that the AFM tip has a certain radius of curvature and is expected to interact with the water molecules surrounding the tip apex during AFM experiments.24,26 Thus, strictly speaking, the absolute magnitude of the interaction between the OH groups and water molecules determined from the 3D-AFM data could be overestimated because of the variations in water density distributions just under the tip apex. Therefore, a comprehensive discussion of the hydration forces based on 3D-AFM data requires careful verification of the number of water molecules interacting with the tip. This verification should be conducted in combination with both AFM simulation42,48–50 and theoretical modeling.515 Conclusion
We successfully visualized the 3D hydration structures of non-cleavable sapphire (001) and α-quartz (100) oxide surfaces using 3D-AFM, showing that these hydration structures are affected by the spatial density distributions and hydrogen-bonding strengths of the surface OH groups. Quantitative analysis of the force curves suggested that the hydration force of the water molecules was higher at sites where these molecules strongly interacted with the surface OH groups. These insights improve our understanding of the affinities of Al2O3 and SiO2 for water molecules. Furthermore, this study contributes to the application of 3D-AFM in exploring atomic-scale hydration structures on various surfaces, and hence, to a wide range of solid–liquid interfacial research fields.Author contributions
S. N., K. S., and K. M. performed experiments and sample preparations. S. U. performed simulations. S. N., S. U., and K. M. wrote the manuscript. S. N., Y. H., T. F., and K. M. conceptualized and supervised this work, acquired funding, and wrote and revised the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from JSPS KAKENHI (No. 22K14603), JST ACT-X (No. JPMJAX20BH), and World Premier International Research Center Initiative (WPI), MEXT, Japan. We would like to thank Editage (https://www.editage.com) for English language editing.References
- J. K. Kang and C. B. Musgrave, J. Chem. Phys., 2002, 116, 275–280, DOI:10.1063/1.1420729.
- C. R. Helms and B. E. Deal, J. Vac. Sci. Technol., A, 1992, 10, 806–811, DOI:10.1116/1.577676.
- I. B. Shir, S. Kababya and A. Schmidt, J. Phys. Chem. C, 2012, 116, 9691–9702, DOI:10.1021/jp302431t.
- J. Schneider and L. C. Ciacchi, J. Am. Chem. Soc., 2012, 134, 2407–2413, DOI:10.1021/ja210744g.
- J. G. Catalano, Geochim. Cosmochim. Acta, 2011, 75, 2062–2071, DOI:10.1016/j.gca.2011.01.025.
- J. G. Catalano, C. Park, Z. Zhang and P. Fenter, Langmuir, 2006, 22, 4668–4673, DOI:10.1021/la060177s.
- M. L. Schlegel, K. L. Nagy, P. Fenter and N. C. Sturchio, Geochim. Cosmochim. Acta, 2002, 66, 3037–3054, DOI:10.1016/S0016-7037(02)00912-2.
- L. Dalstein, E. Potapova and E. Tyrode, Phys. Chem. Chem. Phys., 2017, 19, 10343–10349, 10.1039/c7cp01507k.
- A. Myalitsin, S. Urashima, S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Phys. Chem. C, 2016, 120, 9357–9363, DOI:10.1021/acs.jpcc.6b03275.
- S. Urashima, T. Uchida and H. Yui, Phys. Chem. Chem. Phys., 2020, 22, 27031–27036, 10.1039/d0cp03207g.
- S. A. Carroll, R. S. Maxwell, W. Bourcier, S. Martin and S. Hulsey, Geochim. Cosmochim. Acta, 2002, 66, 913–926, DOI:10.1016/S0016-7037(01)00827-4.
- Q. A. Besford, A. J. Christofferson, J. Kalayan, J. U. Sommer and R. H. Henchman, J. Phys. Chem. B, 2020, 124, 6369–6375, DOI:10.1021/acs.jpcb.0c04545.
- D. Argyris, T. Ho, D. R. Cole and A. Striolo, J. Phys. Chem. C, 2011, 115, 2038–2046, DOI:10.1021/jp109244c.
- F. Musso, P. Ugliengo and M. Sodupe, J. Phys. Chem. A, 2011, 115, 11221–11228, DOI:10.1021/jp203988j.
- P. Thissen, G. Grundmeier, S. Wippermann and W. G. Schmidt, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 1–6, DOI:10.1103/PhysRevB.80.245403.
- V. A. Ranea, I. Carmichael and W. F. Schneider, J. Phys. Chem. C, 2009, 113, 2149–2158, DOI:10.1021/jp8069892.
- T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 016101, DOI:10.1103/PhysRevLett.104.016101.
- K. Kobayashi, N. Oyabu, K. Kimura, S. Ido, K. Suzuki, T. Imai, K. Tagami, M. Tsukada and H. Yamada, J. Chem. Phys., 2013, 138, 184704, DOI:10.1063/1.4803742.
- D. Martin-Jimenez, E. Chacon, P. Tarazona and R. Garcia, Nat. Commun., 2016, 7, 12164, DOI:10.1038/ncomms12164.
- H. Imada, K. Kimura and H. Onishi, Langmuir, 2013, 29, 10744, DOI:10.1021/la402090w.
- T. Fukuma, B. Reischl, N. Kobayashi, P. Spijker, F. F. Canova, K. Miyazawa and A. S. Foster, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 155412, DOI:10.1103/PhysRevB.92.155412.
- H. Söngen, B. Reischl, K. Miyata, R. Bechstein, P. Raiteri, A. L. Rohl, J. D. Gale, T. Fukuma and A. Kühnle, Phys. Rev. Lett., 2018, 120, 116101, DOI:10.1103/PhysRevLett.120.116101.
- K. Miyazawa, J. Tracey, B. Reischl, P. Spijker, A. S. Foster, A. L. Rohl and T. Fukuma, Nanoscale, 2020, 12, 12856–12868, 10.1039/d0nr02043e.
- K. Miyazawa, N. Kobayashi, M. Watkins, A. L. Shluger, K. Amano and T. Fukuma, Nanoscale, 2016, 8, 7334–7342, 10.1039/c5nr08092d.
- K. Miyazawa, M. Watkins, A. L. Shluger and T. Fukuma, Nanotechnology, 2017, 28, 245701, DOI:10.1088/1361-6528/aa7188.
- K. Umeda, L. Zivanovic, K. Kobayashi, J. Ritala, H. Kominami, P. Spijker, A. S. Foster and H. Yamada, Nat. Commun., 2017, 8, 2111, DOI:10.1038/s41467-017-01896-4.
- K. Umeda, K. Kobayashi, T. Minato and H. Yamada, Langmuir, 2018, 34, 9114–9121, DOI:10.1021/acs.langmuir.8b01340.
- T. Hiasa, K. Kimura, H. Onishi, M. Ohta, K. Watanabe, R. Kokawa, N. Oyabu, K. Kobayashi and H. Yamada, J. Phys. Chem. C, 2010, 114, 21423–21426, DOI:10.1021/jp1057447.
- P. J. Molino, D. Yang, M. Penna, K. Miyazawa, B. R. Knowles, S. MacLaughlin, T. Fukuma, I. Yarovsky and M. J. Higgins, ACS Nano, 2018, 12, 11610–11624, DOI:10.1021/acsnano.8b06856.
- P. J. Eng, T. P. Trainor, G. E. Brown Jr., G. A. Waychunas, M. Newville, S. R. Sutton and M. L. Rivers, Science, 2000, 288, 1029–1033, DOI:10.1126/science.288.5468.1029.
- V. Coustet and J. Jupille, Surf. Sci., 1994, 307–309, 1161–1165 CrossRef CAS.
- O. Tsendra, A. M. Scott, L. Gorb, A. D. Boese, F. C. Hill, M. M. Ilchenko, D. Leszczynska and J. Leszczynski, J. Phys. Chem. C, 2014, 118, 3023–3034, DOI:10.1021/jp406827h.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276, DOI:10.1107/S0021889811038970.
- J. E. Sader, T. Uchihashi, M. J. Higgins, A. Farrell, Y. Nakayama and S. P. Jarvis, Nanotechnology, 2005, 16, S94–S101, DOI:10.1088/0957-4484/16/3/018.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19, DOI:10.1006/jcph.1995.1039.
- A. C. T. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409, DOI:10.1021/jp004368u.
- S. Hong and A. C. T. Van Duin, J. Phys. Chem. C, 2016, 120, 9464–9474, DOI:10.1021/acs.jpcc.6b00786.
- S. H. Hahn, J. Rimsza, L. Criscenti, W. Sun, L. Deng, J. Du, T. Liang, S. B. Sinnott and A. C. T. van Duin, J. Phys. Chem. C, 2018, 122, 19613–19624, DOI:10.1021/acs.jpcc.8b05852.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519, DOI:10.1063/1.447334.
- M. E. Tuckerman, J. Alejandre, R. López-Rendón, A. L. Jochim and G. J. Martyna, J. Phys. A: Math. Gen., 2006, 39, 5629–5651, DOI:10.1088/0305-4470/39/19/S18.
- Y. Gan, E. J. Wanless and G. V. Franks, Surf. Sci., 2007, 601, 1064–1071, DOI:10.1016/j.susc.2006.11.057.
- D. Argyris, A. Phan, A. Striolo and P. D. Ashby, J. Phys. Chem. C, 2013, 117, 10433–10444, DOI:10.1021/jp400370g.
- J. N. Israelachvili, Intermolecular and Surface Forces, Acad. Press Ltd., London, 2nd edn, 1992 Search PubMed.
- J. I. Kilpatrick, S. H. Loh and S. P. Jarvis, J. Am. Chem. Soc., 2013, 135, 2628–2634, DOI:10.1021/ja310255s.
- K. C. Hass, W. F. Schneider, A. Curioni and W. Andreoni, J. Phys. Chem. B, 2000, 104, 5527–5540, DOI:10.1021/jp000040p.
- R. Wang, M. DelloStritto, R. C. Remsing, V. Carnevale, M. L. Klein and E. Borguet, J. Phys. Chem. C, 2019, 123, 15618–15628, DOI:10.1021/acs.jpcc.9b03054.
- M. Watkins and B. Reischl, J. Chem. Phys., 2013, 138, 154703, DOI:10.1063/1.4800770.
- B. Reischl, M. Watkins and A. S. Foster, J. Chem. Theory Comput., 2013, 9, 600–608, DOI:10.1021/ct3008342.
- K. Kobayashi, Y. Liang, K. Amano, S. Murata, T. Matsuoka, S. Takahashi, N. Nishi and T. Sakka, Langmuir, 2016, 32, 3608–3616, DOI:10.1021/acs.langmuir.5b04277.
- B. Reischl, P. Raiteri, J. D. Gale and A. L. Rohl, J. Phys. Chem. C, 2019, 123, 14985–14992, DOI:10.1021/acs.jpcc.9b00939.
- K. Amano, Y. Liang, K. Miyazawa, K. Kobayashi, K. Hashimoto, K. Fukami, N. Nishi, T. Sakka, H. Onishie and T. Fukuma, Phys. Chem. Chem. Phys., 2016, 18, 15534–15544, 10.1039/c6cp00769d.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr02498a |
| This journal is © The Royal Society of Chemistry 2023 |