Non-centrosymmetric Weyl semimetal state and strain effect in the twisted-brick phase transition metal monochalcogenides†
Jia-Fang
Wu
 a,
Sha-Sha
Ke
*a,
Yong
Guo
b,
Huai-Wu
Zhang
a and
Hai-Feng
Lü
a,
Sha-Sha
Ke
*a,
Yong
Guo
b,
Huai-Wu
Zhang
a and
Hai-Feng
Lü
 *ab
*ab
aSchool of Physics and State Key Laboratory of Electronic Thin Films and Integrated Devices, University of Electronic Science and Technology of China, Chengdu 610054, China. E-mail: keshasha@uestc.edu.cn; lvhf04@uestc.edu.cn
bDepartment of Physics and State Key Laboratory of Low-Dimensional Quantum Physics, Tsinghua University, Beijing 100084, China
First published on 12th January 2023
Abstract
Weyl semimetals are a class of gapless electronic excitation topological quantum materials upon breaking time-reversal or inversion symmetry. Here, we demonstrate the existence of the Weyl semimetal state in the non-centrosymmetric twisted-brick phase MoTe theoretically. The topological properties and strain effects of MoTe have been systematically studied based on first-principles calculations and the Wannier-based tight-binding method. In the absence of spin–orbit coupling (SOC), MoTe exhibits gapless nodal loop states related to the mirror reflection symmetry. When the SOC is turned on, the two nodal loops split into 22 pairs of Weyl points (WPs) with opposite chirality. When the effect of uniaxial (εz) strain is taken into account, the Weyl semimetal phase of MoTe shows great robustness and striking tunable topological strength. In particular, the total number of WPs changes significantly under strain. MoTe under +4% and +8% uniaxial strains have only four pairs of WPs with a relatively large separation in momentum space. These results show that MoTe under weak strain is a promising partly ideal type I Weyl semimetal candidate, while the isolog structure WTe both opens a direct gap with and without SOC, showing a compensated semimetal state.
1. Introduction
The discovery of exotic topological states of matter is an active research field in condensed matter physics and materials science in the past decade. Topological materials such as topological insulators1 and topological semimetals (TSMs) have potential applications in the spintronic field due to their novel physical properties. Three dimensional (3D) topological semimetal phases are the phases of matter with gapless electronic excitations that are protected by topology and symmetry,2 in which the conduction and valence bands can cross each other either at discrete points (Dirac/Weyl semimetal)3–7 or along a closed curve (nodal line/loop semimetal).8–13 The gapless phases of 3D Weyl semimetal (WSM) are usually characterized by the 2D discontinuous Fermi surface boundary states (Fermi arcs) on the surfaces Brillouin zone (BZ).2 The surface arc depends sensitively on the protected double degeneracy WPs near the Fermi level due to which the low-energy electron quasiparticles exhibit pseudospin, linear dispersions, and other features. Furthermore, the twofold degeneracy WPs suggests that WPs can only appear when the spin-doublet degeneracy of the bands is eliminated, which means that the time-reversal symmetry (TRS) or the inversion symmetry (IS) of the system should be broken. The chirality of WPs is also considered a topological charge analogous to the monopole or anti-monopole of Berry curvature. It can be quantized by the total Berry flux through a momentum space surface containing a single WP. Moreover, WSM is robust against any weak perturbation that preserves translational symmetry.14 An exchange field or slight lattice distortion can only shift the positions of WPs.4Recently, efficiently mass-searching topological materials by symmetry-based indicator and topological quantum chemical methods has attracted increasing attention, such as centrosymmetric nonmagnetic topological systems15–17 and magnetic topological systems.18 However, it cannot detect strongly correlated electronic systems whose low-energy quasiparticles are Dirac/Weyl fermions and non-centrosymmetric systems, whose band inversion is away from certain high-symmetry points. Non-centrosymmetric systems provide a promising arena to realize ideal Weyl semimetals with potential applications for low-power and high-speed electronics. Currently, there are several representative proposals for WSM systems that involve nonmagnetic materials by breaking the spatial IS.19 The first proposal to realize non-centrosymmetric WSM in condensed-matter materials was suggested in ref. 20–22 for the TaAs family, where 12 pairs of WPs were derived from the nonzero mirror Chern numbers for two of the mirror-invariant planes. The Td phase layered transition metal dichalcogenides (TMDs) discussed in ref. 23 and 24 is an example of a type-II Weyl semimetal, which in its incarnation demonstrates that the distribution of the WPs is found to be very sensitive to the lattice parameters. A magnetic non-centrosymmetric system PrAlGe was then proposed, which hosts the emergent topological properties of Weyl fermions by photoemission-based spectroscopy and magneto-transport.25 The transition metal monochalcogenides (TMMs) system MoTe26,27 and W2SeS28 were also proposed, in which 4 and 12 pairs of WPs due to band-crossing appear when the systems are with SOC, respectively. Recent experimental and theoretical studies on the non-centrosymmetric LaAlSi29 and LaAlGe30 unveiled the signatures of the type-I and type-II Weyl states. Undoubtedly, it is still an important task to search for WSM in non-centrosymmetric systems.
In this work, using density functional theory (DFT) calculations and the Wannier-based tight-binding method, we systematically studied the topological electronic properties and strain effects of the non-centrosymmetric twisted-brick phase TMMs, MoTe, and WTe. We mainly focused on the Pmn21-MoTe system, which presents a clear nodal loop state and WSM state near the Fermi level when SOC is absent and present, respectively. For completeness, we also carried out some calculations on the optimized WTe, such as energy bands with/without SOC, and the crossing points between the conduction band (CB) and the valence band (VB). The results show that WTe is a compensated semimetal with and without SOC. Moreover, we find that the topological properties in MoTe can be strikingly tuned by strain; thus, the WPs in MoTe are controllable.
The paper is organized as follows. In Section 2, we first described the crystal structural features and the stabilities of twisted-brick phase MoTe/WTe. Then, we provided the computational methods used. Next, we have considered the electronic properties and symmetries of MoTe and WTe. In Section 3, we investigated the effects of SOC on the topological properties of MoTe. At the end of this section, we discussed in detail the effects of uniaxial strain on the topological properties of MoTe, such as the total number of WPs, the average energy of WPs, and the length of the Fermi arc. Finally, we gave a summary in Section 4.
2. Calculation methods and crystal structure
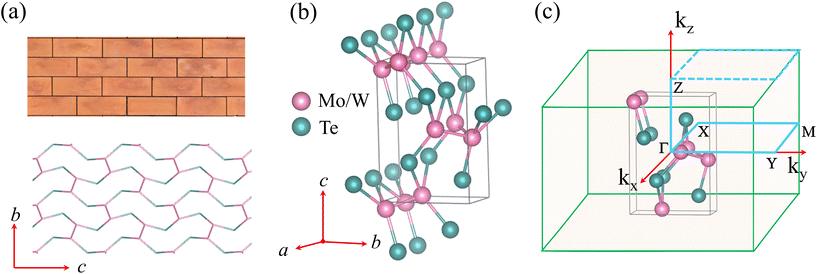
To predict the “twisted-brick” phase MoTe/WTe hosting non-centrosymmetric topological WSM, we carried out the structural optimization and electronic structure calculations using density functional theory (DFT)31 based on the projector-augmented wave method as implemented in the Vienna Ab initio Simulation Package (VASP) code.32 The plane-wave kinetic energy cutoff is set at 550 eV. The exchange–correlation interaction was handled in the generalized gradient approximation parametrized by Perdew–Burke–Ernzerhof (PBE).33 The Brillouin zones are sampled with 10 × 6 × 4 Monkhorst–Pack special k-point meshes for MoTe/WTe bulk. During structural relaxation, all lattices and atoms are fully relaxed until the Hellmann–Feynman forces are less than the convergence criteria of 0.001 eV Å−1. The dynamic properties of MoTe and WTe were obtained by the DFPT method, which is realized in the Phonopy package.34 The effect of with and without SOC interactions both are considered in the calculations of electronic structures. The novel topological properties of both MoTe and WTe are obtained by tight-binding (TB) models within maximum localized Wannier functions (MLWF),35 as implemented in the software package Wannier90.36 We chose Mo-d/W-s, d, and Te-p orbitals as the initial orbitals and projected them into localized Wannier orbitals to accurately reproduce the DFT-based bands near the Fermi energy. The identification of the positions of WPs and the nodal loops, the Berry curvature in the BZ, and the surface states are calculated by the WannierTools software package.37 Also, all the crystal structures are plotted using the VESTA software.38Both MoTe and WTe crystallize in the non-symmorphic space group Pmn21 (No. 31), which lacks inversion symmetry. The optimized lattice parameters of MoTe (WTe) are a = 3.279 Å, b = 5.794 Å, and c = 8.830 Å (a = 3.302 Å, b = 5.942 Å, and c = 8.721 Å). All the atoms are located at the 2a Wyckoff position of the Pmn21 space group; the reduced positions are shown in Table 1. The “twisted-brick” phase is named because the side view of the twisted-brick phase is like a wall stacked with twisted bricks, as illustrated in Fig. 1(a). The bulk BZ is shown in Fig. 1c, where high symmetry points are noted. The symmetries in the twisted-brick phase are generated by the following symmetry operations: (i) identity operation E, (ii) the mirror reflection Myz, which is a reflection around the x = 0 plane,
| Myz: (x,y,z) → (−x,y,z), | (1) |
| Atom | Wyck. | x | y | z | Atom | Wyck. | x | y | z |
|---|---|---|---|---|---|---|---|---|---|
| Mo (1) | 2a | 0.5 | 0.65 | 0.03 | W (1) | 2a | 0 | 0.64 | 0.03 |
| Mo (3) | 2a | 0.5 | 0.05 | 0.45 | W (3) | 2a | 0 | 0.07 | 0.46 |
| Te (1) | 2a | 0.5 | 0.33 | 0.80 | Te (1) | 2a | 0 | 0.34 | 0.79 |
| Te (3) | 2a | 0.5 | 0.18 | 0.15 | Te (3) | 2a | 0 | 0.17 | 0.15 |
(iii) the glide reflection ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) xz, which consists of y = 0 plane reflection, followed by a/2 translation along the x axis and c/2 translation along the z axis,
xz, which consists of y = 0 plane reflection, followed by a/2 translation along the x axis and c/2 translation along the z axis,
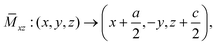 | (2) |
and (iv) the twofold screw rotation ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 2z, which consists of π rotation around the z = c/2 line, followed by a/2 translation along the x axis.
2z, which consists of π rotation around the z = c/2 line, followed by a/2 translation along the x axis.
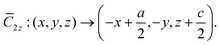 | (3) |
The symmetries are the same as that of Td-WTe2 and MoTe2 (layered TMDs) identified as the typical type-II Weyl semimetals. The twisted-brick XTe (X = W, Mo) is a bulk structure without layers and with broken inversion symmetry. For the brick phase, a relatively simpler brick system, odd-atomic-layer Bi, is predicted to be a Dirac-line semimetal protected by symmetries in first-principles calculation.39 In addition, in the optical lattice, the tilted brick-wall system exhibits a sequence of topological phase transitions.40
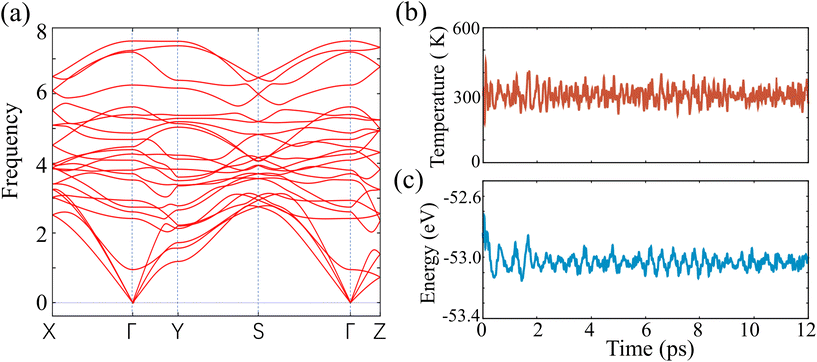
The symmetry of the nonsymmorphic Pmn21 space group in the twisted-brick structure plays an important role in protecting the topological phases, which satisfies the requirement for generating WPs because it has broken inversion symmetry. It is important to note here that the mirror planes Myz and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) xz contain the rotation z axis, which belongs to the C2v point group. In addition, we confirmed the lattice dynamic stability and thermal stability of MoTe (see Fig. 2) and WTe (see ESI†) by calculating the phonon spectrum and a long-timescale AIMD simulation, respectively. We can see clearly that the phonon dispersion bands of MoTe have no negative frequencies, as shown in Fig. 2a, which indicates that the optimized twisted-brick structures are dynamically stable. The temperature and the total energy per unit cell of MoTe exhibit thermal fluctuations around the average up to 12 ps, as shown in Fig. 2(b and c). In addition, we also presented the phonon, temperature, and total energy dispersions for MoTe under εz = +4% and +8% strain to identify their dynamic stability and thermal stability (see details in Section 4 of the ESI†).
xz contain the rotation z axis, which belongs to the C2v point group. In addition, we confirmed the lattice dynamic stability and thermal stability of MoTe (see Fig. 2) and WTe (see ESI†) by calculating the phonon spectrum and a long-timescale AIMD simulation, respectively. We can see clearly that the phonon dispersion bands of MoTe have no negative frequencies, as shown in Fig. 2a, which indicates that the optimized twisted-brick structures are dynamically stable. The temperature and the total energy per unit cell of MoTe exhibit thermal fluctuations around the average up to 12 ps, as shown in Fig. 2(b and c). In addition, we also presented the phonon, temperature, and total energy dispersions for MoTe under εz = +4% and +8% strain to identify their dynamic stability and thermal stability (see details in Section 4 of the ESI†).
3. Results and discussion
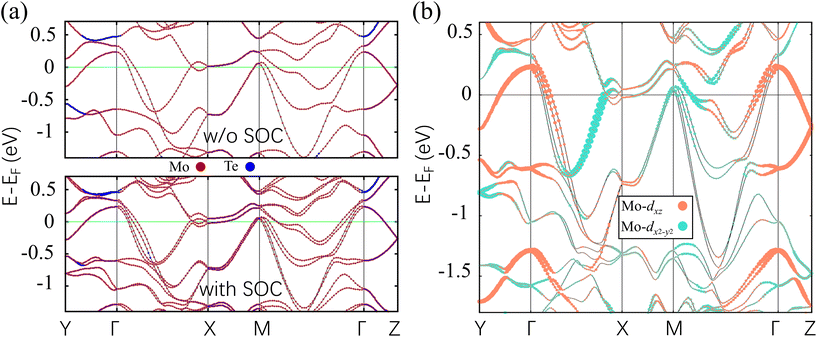
We first obtained the band structure of WTe without and with SOC by first-principles calculation and plotted it along the high-symmetry directions (see details in Section 1 of the ESI†). The results show that the band structure of WTe in the absence/presence of SOC both have a small direct gap with small trivial Fermi pockets along the high-symmetry line, exhibiting a compensated semimetal state. For MoTe, the results of first-principles calculation are summarized in Fig. 3. In the absence of SOC, the occupied band N and the band N + 1 cross each other twice along the Y–Γ line, which is indicated in the upper panel of Fig. 3a. The bands N + 2 and the N + 3 have no crossing points along the Y–Γ–X–M–Γ–Z line. There is a gap of 18.6 meV between the N + 2 and N + 3 bands along the Γ–X line at the suspected crossing points. By calculating the crossing points between the band N and the band N + 1 in the whole BZ, all the crossing points form two closed curves in the mirror Myz plane, which can be confirmed by the 3D band dispersions, as illustrated in Fig. 4. Actually, the two crossing points along the Y–Γ line are a part of one closed curve in the mirror Myz plane. The orbital-resolved analysis shows that the bands near the Fermi energy are mainly composed of Mo-5d orbitals, which have a large SOC effect. The nodal loop states of MoTe without SOC are double-checked by the HSE06 functional (see details in Section 2 of the ESI†). Identical conclusions were obtained in the HSE06 band structure. When SOC turns on, the degeneracy of the band structure is broken, and the electronic band structures are modified strongly. The bands open a gap and form discrete touching points on the non-symmetrical lines and planes, as plotted at the bottom of Fig. 3a. Due to the non-centrosymmetry and the SOC effect in MoTe, the energy bands are nondegenerate except for the time-reversal invariant points and lines of high symmetry. It should be pointed out that we determined the location of the possible touching points by searching the Wannier tight-binding bands throughout the BZ since band crossing points are away from certain high symmetry points and lines in the presence of SOC.We further verify the contribution of the orbitals of the Mo atom to the bands near the Fermi level and identify the band inversion. From Fig. 3a, we conclude that the low-energy bands are mostly dominated by the contribution of the Mo-5d orbitals with a small Te-p orbitals admixture. We further performed an analysis of each orbital contribution of Mo 5d. From the results, we obtained that the crossing bands are mainly composed of the Mo-dx2−y2 and Mo-dxz orbitals. Particular emphasis is placed on the band inversion features near the Fermi level along the high symmetry line Γ–X, which can be indicated by orange and turquoise dots in Fig. 3b. Hence, there is a nontrivial band inversion between the Mo-dx2−y2 and Mo-dxz orbitals in the twisted-brick phase MoTe. Similar to many other typical WSMs, the topological phase in the MoTe system results from a band-inversion phenomenon in the absence of SOC (see details in Section 3 of the ESI†). At the same time, the two nontrivial nodal loops in the kx = 0 mirror plane are symmetry-protected. When the SOC is considered, the nodal loops will split into pairs of WPs.
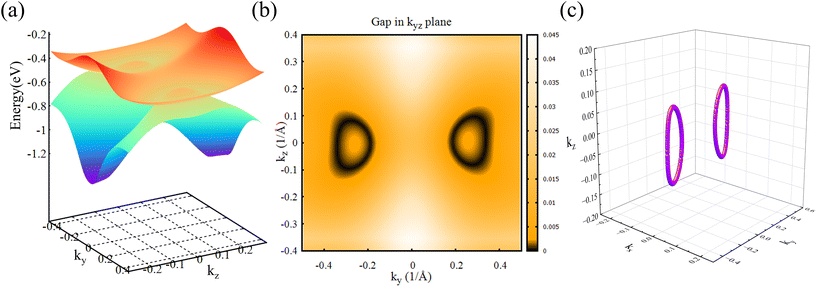
We first consider in detail the crossing points of MoTe at generic momenta (GM) points in the absence of SOC. The locations of all crossing points between the lowest CB and the top VB and the shape of the crossing points were obtained by the Wannier-based tight-binding method, as shown in Fig. 4. The results show that the crossing points are not independent, and it is residing on a nodal ring in the kx = 0 plane (see Fig. 4c). The 3D energy bands around the nodal loop in plane kyz is as shown in Fig. 4a, which reveals that the band crossing points in the plane form two closed nodal rings. It is also found that the energy of the crossing points is linear with slight energy variation along the loop. To clarify the feature of the nodal loops, the energy gap ΔE (kx, kz) between the two crossing bands is shown in Fig. 4b. It should be pointed out that the nodal ring of the current MoTe system is protected by the mirror reflection Myz in the absence of SOC. We can see that the loops are located in the mirror-invariant kx = 0 plane. The two crossing bands have opposite mirror eigenvalues, which means that the points will break away from the mirror symmetry protection as it moves away from the mirror plane. As a conclusion, in the absence of SOC, the twisted-brick phase MoTe is with topological nontrivial electronic states exhibiting two nodal loops around the Fermi level. Notably, the topological nodal loop states will change when SOC is considered.
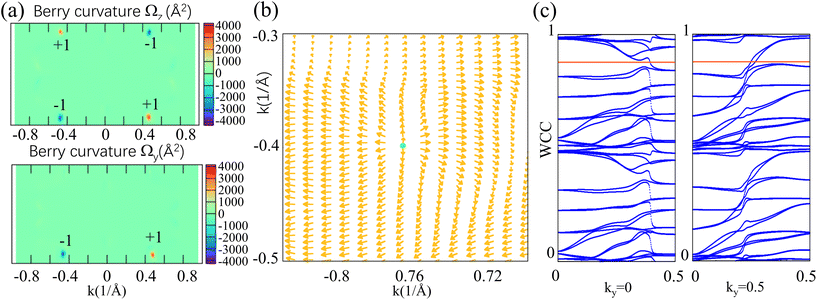
Including SOC in calculation leads to a dramatic change of the band structure near the Fermi level of MoTe. Our calculation shows that the previous nodal loops in the kyz plane are partially gapped in the presence of SOC, and the nodal loops split into 22 pairs of Weyl nodes with opposite chirality. To check the chirality of the WPs, we obtained the Berry curvature around them by the Wannier-based tight-binding method. Considering only the occupied bands as a joint band manifold, the discrete k mesh as the integration, and a series of close space points kj as the closed curve, the formalism of the Berry phase ϕ and Berry curvature Ω are as follows
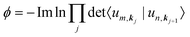 | (4) |
| Ωmn,αβ = −2Im〈∂αum,k|∂βun,k〉 | (5) |
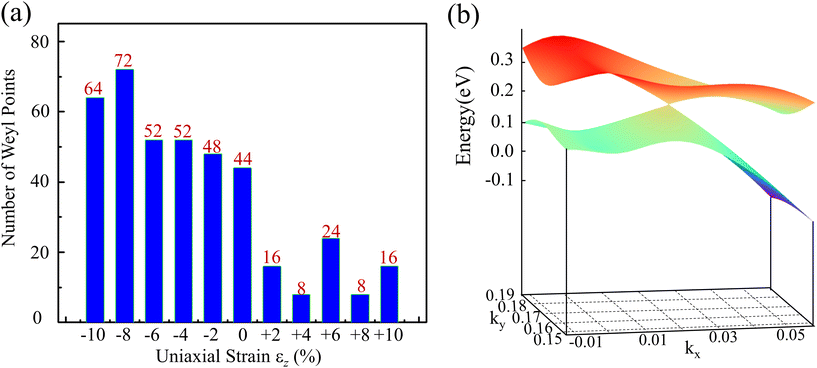
When SOC turns on, the two nodal loops split into 22 pairs of WPs. However, it is potentially more complicated with a higher number of WPs, and the minimum numbers of WPs in nonmagnetic Weyl semimetals are four. We thus propose an effective modulation way to optimize the topological properties of WSMs utilizing the strain effects, such as uniaxial strain along the z-axis (εz). We mainly focus on the changes in WPs within the −10% to +10% strain range, including the number of WPs (see Fig. 6a), the average energy of WPs and the k space distance (Δk) between a pair of WPs (see details in Section 5 of the ESI†). Our calculation shows that the number of WPs decreases rapidly under tensile strain. In particular, the numbers are both reduced to eight under εz = +4% and +8% tensile strain. We pinpoint the WPs’ locations of MoTe under εz = +4% and +8% tensile strain, as shown in Table 2. The coordinates and chirality of WPs under εz = +4% and +8% strain fully satisfy time-reversal symmetry and Myz mirror symmetry, which support the result of symmetry protection. At the same time, through the two symmetries, we can obtain the eight WPs coordinates from the two irreducible nodes, as given in Table 2. In addition, the total number of WPs always changes with a multiple of four (see Fig. 6a), which further highly reflects the symmetry protected by time-reversal symmetry and mirror symmetry (see ESI† for the discussion of strain effects in Section 5). Intriguingly, the length of the Fermi arc between the Weyl nodes changes larger under strain. Usually, an increasing Δk between WPs leads to the length of the Fermi arc and the topological strength than before. The Δk decreases first and then increases as the strain varies from compressive to tensile. For example, under εz = −6% strain, the k space separation Δk is found to be as large as 1.08 Å−1. Another useful quantity is the average energy of WPs. It is interesting to note that in contrast to the evolution of Δk (Fig. 5S†), the energy of WPs shows a non-monotonous function of uniaxial strain. At +10% strain, the average energy of WPs is found to be as large as 0.24 eV. The energy is about −1.10 eV at 0% strain. Besides, we have checked the type of the Weyl cones under εz = +4% and +8% tensile strain. Our calculation clearly shows that constant energy surfaces are closed rather than open, which illustrates that WPs are type I Weyl cones, as seen in Fig. 6b.
| Strain | Symmetry | Nodes | Coordinates kx(2π/a), ky(2π/b), kz(2π/c) | Δk (Å−1) | Chirality | |
|---|---|---|---|---|---|---|
| ε z | +4% | M yz + | WP1 | (0.026, 0.170, 0.079) | 0.36 | −1 |
| WP2 | (−0.001, 0.114, −0.0587) | 0.26 | −1 | |||
| +8% | M yz + | WP1 | (0.033, 0.189, 0.124) | 0.45 | −1 | |
| WP2 | (0.035, 0.188, −0.129) | 0.46 | −1 | |||
There are several major characteristics for the WPs under εz = +4% and +8% tensile strain. Firstly, the number of WPs is both 8, which is one-third of the number in the typical non-centrosymmetric WSM TaAs.22 Secondly, the energy dispersion around WPs formed a closed Fermi surface with a standard Weyl cone along the certain k direction, which pointed out the WPs observed in the MoTe material under strain are type I fermions. By the way, the Fermi arcs of these WPs under εz = +4%, and +8% reside entirely above the Fermi energy, which can be observed by the pump–probe angle-resolved photoemission spectroscopy (ARPES) technique.41 Furthermore, the WPs have a relatively large separation in momentum space, which is one property of ideal WSMs. The maximal separations between two WPs under εz = +4% and +8% strain with opposite chirality are 0.36 Å−1 and 0.46 Å−1, as shown in Table 2, respectively. It is observed that the separations are larger than some typical WSMs, such as TaAs ∼0.074 Å−1,22 MoTe2 ∼ 0.042 Å−1,4 and W2SeS ∼ 0.24 Å−1.28
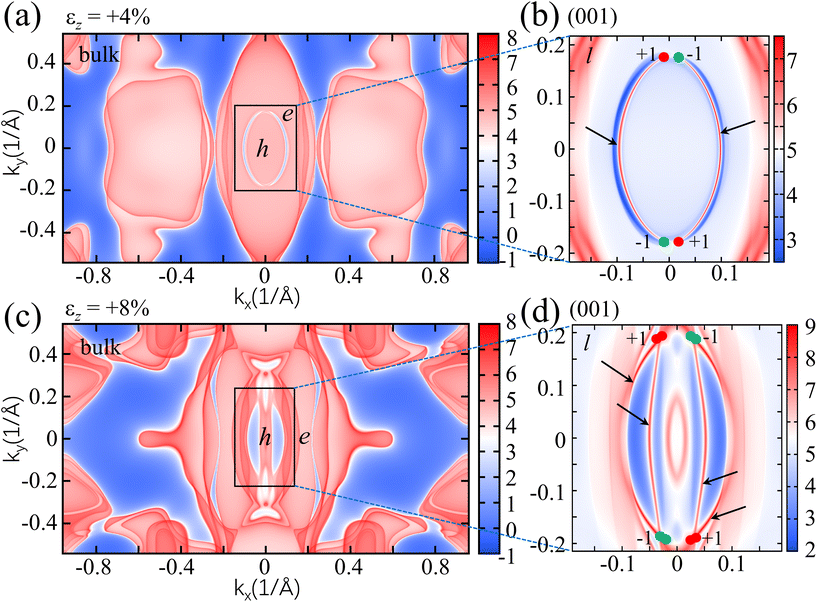
We have shown that applying small uniaxial strain along the z direction in twisted-brick MoTe can give rise to partly ideal type I WSM with only four pairs of Weyl nodes. Unique surface states with connected Fermi arcs can be found on the surface of a Weyl semimetal. We have computed the surface states for the (001) surface under εz = +4% and +8% tensile strain, as shown in Fig. 7. Both the bulk surface states exhibit a small hole-like pocket around the point Γ and a large electron-like pocket along the line Γ−X. It can be seen that the Weyl nodes are connected by the Fermi arc. In addition, the connectivity pattern of the Fermi arc under εz = +4% and +8% strain is shown in Fig. 7(b) and (d), respectively. Compared to other proposed WSM materials, this connectivity pattern guarantees the length of the Fermi arc, which greatly facilitates their detection in experiments. A very interesting point of the Fermi arc under εz = +4% strain is that the surface Fermi arcs form an approximately closed loop, as shown in Fig. 7b, which is similar to the Fermi arc shapes of TaAs.22 The connectivity pattern of Fermi arcs is associated with exotic electron transport properties, which are expected to be verified in future experiments.
4. Conclusion
In conclusion, we theoretically report the topological properties and elucidated the strain effect on non-centrosymmetric twisted-brick compounds MoTe/WTe. Our calculations found that the MoTe compound appears a nontrivial nodal loop state in the mirror-invariant kx = 0 plane in the absence of SOC. The nodal loop shows type-I band crossings. When SOC is considered, the nodal loops of MoTe are split into 22 pairs of WPs with opposite chirality. We found that the WSM phase of MoTe with SOC is robust against uniaxial strain along the z direction in the -10% –10% range. At the same time, the total number, average energy, and location of WPs can be controlled by the strain strength. Very interestingly, at εz = +4% and +8%, the total number of WPs reduced to four pairs. Therefore, the strain effect can tune the WPs to generate or annihilate new WPs. In addition, all the WPs located on the kx ≠ 0 planes are related by time-reversal symmetry and Myz mirror symmetry. Also, all WPs are type I fermions. We also show that the strain can tune the length of the Fermi arc of MoTe, reaching approximately of the order of magnitude 0.1 Å−1, which can be observed by pump–probe ARPES experiments. Also, the average energy of WPs shows a non-monotonous function of uniaxial strain. Remarkably, we revealed that WTe shows a compensated semimetal state with and without SOC. This study unveils the topological electronic properties of MoTe/WTe and further extends the promising material candidate of the ideal type I WSM with centrosymmetric breaking.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Natural Science Foundation of China under Grants No. 12074209 and No. 12274063, the Fundamental Research Funds for the Central Universities (No. ZYGX2019J100), and the Open Project of State Key Laboratory of Low-Dimensional Quantum Physics (Grant No. KF202008). The numerical calculations in this paper have been done on Hefei advanced computing center.References
- Z. Guo, X. Hao, J. Dong, H. Li, Y. Gong, D. Yang, J. Liao, S. Chu, Y. Li, X. Li and D. Chen, Nanoscale, 2020, 12, 22710–22717 RSC.
- N. P. Armitage, E. J. Mele and A. Vishwanath, Rev. Mod. Phys., 2018, 90, 015001 CrossRef CAS.
- T. O. Wehling, A. M. Black-Schaffer and A. V. Balatsky, Adv. Phys., 2014, 63, 1–76 CrossRef CAS.
- Z. Wang, D. Gresch, A. A. Soluyanov, W. Xie, S. Kushwaha, X. Dai, M. Troyer, R. J. Cava and B. A. Bernevig, Phys. Rev. Lett., 2016, 123(18), 186401 CrossRef PubMed.
- A. L. D. F. Liu, E. K. Liu, Q. N. Xu, Y. W. Li, C. Chen, D. Pei, W. J. Shi, S. K. Mo, P. Dudin, T. Kim, C. Cacho, G. Li, Y. Sun, L. X. Yang, Z. K. Liu, S. S. P. Parkin, C. Felser and Y. L. Chen, Science, 2019, 365(6459), 1282–1285 CrossRef PubMed.
- N. Morali, R. Batabyal, P. K. Nag, E. Liu, Q. Xu, Y. Sun, B. Yan, C. Felser, N. Avraham and H. Beidenkopf, Science, 2019, 365(6459), 1286–1291 CrossRef CAS PubMed.
- X. Wang, D. Pan, Q. Zeng, X. Chen, H. Wang, D. Zhao, Z. Xu, Q. Yang, J. Deng, T. Zhai, G. Wu, E. Liu and J. Zhao, Nanoscale, 2021, 13, 2601–2608 RSC.
- Y. Kim, B. J. Wieder, C. L. Kane and A. M. Rappe, Phys. Rev. Lett., 2015, 115, 036806 CrossRef PubMed.
- T. Bzdusek, Q. Wu, A. Ruegg, M. Sigrist and A. A. Soluyanov, Nature, 2016, 538, 75–78 CrossRef CAS PubMed.
- B. Feng, B. Fu, S. Kasamatsu, S. Ito, P. Cheng, C. C. Liu, Y. Feng, S. Wu, S. K. Mahatha, P. Sheverdyaeva, P. Moras, M. Arita, O. Sugino, T. C. Chiang, K. Shimada, K. Miyamoto, T. Okuda, K. Wu, L. Chen, Y. Yao and I. Matsuda, Nat. Commun., 2017, 8, 1007 CrossRef PubMed.
- B. Feng, R. W. Zhang, Y. Feng, B. Fu, S. Wu, K. Miyamoto, S. He, L. Chen, K. Wu, K. Shimada, T. Okuda and Y. Yao, Phys. Rev. Lett., 2019, 123, 116401 CrossRef CAS PubMed.
- W. Meng, W. Liu, X. Zhang, Y. Liu, X. Dai and G. Liu, Nanoscale, 2021, 13, 3194–3200 RSC.
- P. Yan, T. Ouyang, C. He, J. Li, C. Zhang, C. Tang and J. Zhong, Nanoscale, 2021, 13, 3564–3571 RSC.
- Y. Sun, S.-C. Wu and B. Yan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 115428 CrossRef.
- T. Zhang, Y. Jiang, Z. Song, H. Huang, Y. He, Z. Fang, H. Weng and C. Fang, Nature, 2019, 566, 475–479 CrossRef CAS PubMed.
- M. G. Vergniory, L. Elcoro, C. Felser, N. Regnault, B. A. Bernevig and Z. Wang, Nature, 2019, 566, 480–485 CrossRef CAS PubMed.
- F. Tang, H. C. Po, A. Vishwanath and X. Wan, Nature, 2019, 566, 486–489 CrossRef CAS PubMed.
- Y. Xu, L. Elcoro, Z. D. Song, B. J. Wieder, M. G. Vergniory, N. Regnault, Y. Chen, C. Felser and B. A. Bernevig, Nature, 2020, 586, 702–707 CrossRef CAS PubMed.
- H. Gao, J. Strockoz, M. Frakulla, J. W. F. Venderbos and H. Weng, Phys. Rev. B, 2021, 103, 205151 CrossRef CAS.
- L. X. Yang, Z. K. Liu, Y. Sun, H. Peng, H. F. Yang, T. Zhang, B. Zhou, Y. Zhang, Y. F. Guo, M. Rahn, D. Prabhakaran, Z. Hussain, S. K. Mo, C. Felser, B. Yan and Y. L. Chen, Nat. Phys., 2015, 11, 728–732 Search PubMed.
- B. Q. Lv, H. M. Weng, B. B. Fu, X. P. Wang, H. Miao, J. Ma, P. Richard, X. C. Huang, L. X. Zhao, G. F. Chen, Z. Fang, X. Dai, T. Qian and H. Ding, Phys. Rev. X, 2015, 5, 031013 Search PubMed.
- H. Weng, C. Fang, Z. Fang, B. A. Bernevig and X. Dai, Phys. Rev. X, 2015, 5, 011029 Search PubMed.
- J. Jiang, Z. K. Liu, Y. Sun, H. F. Yang, C. R. Rajamathi, Y. P. Qi, L. X. Yang, C. Chen, H. Peng, C. C. Hwang, S. Z. Sun, S. K. Mo, I. Vobornik, J. Fujii, S. S. Parkin, C. Felser, B. H. Yan and Y. L. Chen, Nat. Commun., 2017, 8, 13973 Search PubMed.
- P. Hein, S. Jauernik, H. Erk, L. Yang, Y. Qi, Y. Sun, C. Felser and M. Bauer, Nat. Commun., 2020, 11, 2613 Search PubMed.
- D. S. Sanchez, G. Chang, I. Belopolski, H. Lu, J. X. Yin, N. Alidoust, X. Xu, T. A. Cochran, X. Zhang, Y. Bian, S. S. Zhang, Y. Y. Liu, J. Ma, G. Bian, H. Lin, S. Y. Xu, S. Jia and M. Z. Hasan, Nat. Commun., 2020, 11, 3356 Search PubMed.
- J. F. Wu, S. S. Ke, Y. Guo, H. W. Zhang and H. F. Lu, Phys. Chem. Chem. Phys., 2021, 23, 23196–23202 RSC.
- L. Meng, J. Wu, Y. Li and J. Zhong, J. Mater. Chem. C, 2019, 7, 12151–12159 RSC.
- L. Meng, J. Wu, Y. Li, L. Zhao and J. Zhong, Phys. Rev. B, 2019, 100, 155151 CrossRef CAS.
- H. Su, X. Shi, J. Yuan, Y. Wan, E. Cheng, C. Xi, L. Pi, X. Wang, Z. Zou, N. Yu, W. Zhao, S. Li and Y. Guo, Phys. Rev. B, 2021, 103, 165128 CrossRef CAS.
- M. Corasaniti, R. Yang, Z. Hu, M. Abeykoon, C. Petrovic and L. Degiorgi, Phys. Rev. B, 2021, 104, L121112 CrossRef CAS.
- P. J. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33(12), 8822 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419–1475 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699 CrossRef CAS.
- Q. Wu, S. Zhang, H.-F. Song, M. Troyer and A. A. Soluyanov, Comput. Phys. Commun., 2018, 224, 405–416 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- D. Guo, P. Guo, S. Tan, M. Feng, L. Cao, Z.-X. Liu, K. Liu, Z.-Y. Lu and W. Ji, Sci. Bull., 2022, 67, 1954–1957 CrossRef CAS PubMed.
- A. R. Kolovsky, Phys. Rev. A, 2018, 98, 013603 CrossRef CAS.
- I. Belopolski, P. Yu, D. S. Sanchez, Y. Ishida, T. R. Chang, S. S. Zhang, S. Y. Xu, H. Zheng, G. Chang, G. Bian, H. T. Jeng, T. Kondo, H. Lin, Z. Liu, S. Shin and M. Z. Hasan, Nat. Commun., 2017, 8, 942 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr04946e |
| This journal is © The Royal Society of Chemistry 2023 |