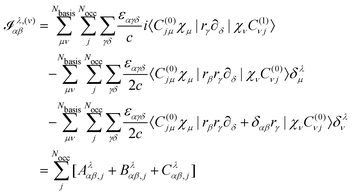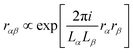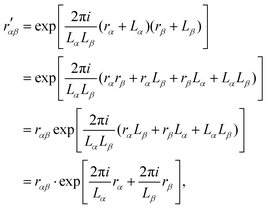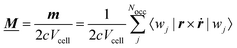DOI:
10.1039/D2CP05991F
(Perspective)
Phys. Chem. Chem. Phys., 2023,
25, 14672-14685
The position operator problem in periodic calculations with an emphasis on theoretical spectroscopy
Received
23rd December 2022
, Accepted 12th May 2023
First published on 22nd May 2023
Abstract
In this article, we present the challenges that arise when carrying out spectroscopic simulations within periodic boundary conditions. We present approaches which were proposed in the literature for the calculation of the extension of the electric dipole moment to periodic systems. Further, we describe the challenges arising for the simulation of magnetic properties within periodic boundary conditions and for the simulation of nuclear magnetic resonance shielding tensors and related quantities. Furthermore, issues arising in periodic implementations of vibrational circular dichroism spectroscopy are described, especially for the case of atom-centered basis functions and nuclear velocity perturbation theory.
1. Introduction
For many types of simulations in electronic structure theory Periodic Boundary Conditions (PBC) are an important tool. Instead of being limited to isolated molecules or clusters, PBC allow for the simulation of extended and condensed phase systems. This includes simulations of periodic systems such as (molecular) crystals in the field of solid-state physics, liquid phase systems consisting of molecules, and interfaces between, for example, solid and liquid phases as present at solvated surfaces. In the case of crystals, usually plane wave basis sets are employed with k-point sampling in reciprocal space to capture the band structure, phonons, and other properties of a system defined in terms of a primitive unit cell. Applying additionally a supercell approach, one can reduce the number of k-points needed, as well as study defects in solid state systems.1
For applications in chemistry, usually a large supercell consisting of a mixture of solvent and solute molecules is employed in order to study the liquid phase. Such systems are not periodic in the sense that their infinite repetitions in all directions give rise to certain electronic properties, but rather the presence of boundary surfaces is avoided by applying PBC. In this way, each individual molecule in the system “sees” a solvation shell around it, emulating a macroscopic system. In ab initio molecular dynamics (AIMD) simulations, atoms are allowed to leave the simulation box through a boundary and reemerge on the opposite side of the box. When covalent bonds are formally broken by such a movement, the minimum image convention is applied to define the environment of an atom in terms of the minimum distance to all other atoms. In this way, each atom is at the center of its own virtual simulation box.1
A well-known problem for the implementation of PBC is the so-called position operator problem.2 Considering a finite but infinitely often repeating simulation box, the distance dAB between two objects centered at points A and B in the simulation box is not well defined. In fact, infinitely many distance vectors may be defined by considering all periodic images of the two objects. Usually, this problem is solved, for classical particles, by enforcing the minimum image convention. In the case of the electronic position operator (r) the situation is worse: in order to calculate the expectation value of the position operator over a (periodic) orbital ϕj(r), the integral
| | 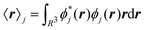 | (1) |
has to be evaluated. Such integrals are needed, for example, when the expectation value of the electric dipole moment is calculated in order to obtain Infrared (IR) intensities. For the sake of simplicity, we do not include explicitly occupation numbers into the formulas in this work. The operator
r is unbounded under PBC and as such the value of the integral is not defined. Different solutions to this problem have been proposed in the literature.
3–7
There are several ways to obtain response properties with respect to the interaction with electric and magnetic field. For one, one can calculate properties by applying a finite field of varying strength to obtain derivatives of the total energy with respect to the electric and magnetic field. Secondly, perturbation theory can be applied. While there are various formulations resulting in different working equations, usually an expansion of the quantities entering the electronic structure problem (the orbitals, the operators and the corresponding matrix elements) is carried out. In the often employed Sternheimer equation or Coupled Perturbed Kohn Sham (CPKS) approach, the working equation for the perturbation calculation takes a form similar to8–12
| | (![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (0) − εj)|ϕ(1)j〉 = − (0) − εj)|ϕ(1)j〉 = −![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (1)|ϕ(0)j〉, (1)|ϕ(0)j〉, | (2) |
where
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (0)
(0) is the ground state Hamiltonian operator,
ϕ(0)/(1)j is an unperturbed/perturbed Molecular Orbital (MO), and
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (1)
(1) is referred to as the perturbation operator. If the perturbation operator leads to real-valued (or complex) perturbed MOs, the effect of the perturbed electron density must be considered during the response calculation. If, on the other hand, the resulting perturbed MOs are purely imaginary and do not contribute to the real space density, no coupling appears in
eqn (2) and the equation can in principle be solved for the perturbed orbitals |
ϕ(1)j〉 in a single step. In some cases the coupled treatment for the atomic displacements can be avoided, such as the simulation of IR intensities, by employing an analytical CPKS scheme.
13
An approach based on perturbation theory might be combined with finite differences in order to obtain higher derivatives in a mixed approach. Finally, in dynamic calculations, spectra are obtained from time-correlation functions of the expectation values of the different electric and magnetic moments. This can apply to a real-time propagation of the electronic structure as in time-dependent (TD)-Density Functional Theory (DFT), or to a time propagation of the nuclear coordinates in (ab initio) molecular dynamics simulations.14 Approaches based on real-time propagation can also be combined with finite differences.15
In this review article, we define the arising problems when calculating integrals such as the one in eqn (1) and the solutions to the position operator problem in the context of various property calculations. We will focus the discussion on implementations in the framework of KS DFT and additional difficulties that arise when applying perturbation theory to the generalized eigenvalue problem of DFT. Throughout this manuscript we employ Hartree atomic units, unless stated otherwise.
2. The position operator for polarization
The electronic position operator r appears in different fields of electronic structure theory. The most direct application is the evaluation of its expectation value for the calculation of the electronic part of the electric dipole moment d and the bulk polarization per unit cell, P,16| | 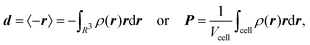 | (3) |
where ρ(r) is the charge density and Vcell the volume of the unit cell in a periodic calculation. The definitions given in eqn (3) are not applicable in PBC. The closely related electric dipole–electric dipole polarizability tensor is given in a non-PBC framework by17| | 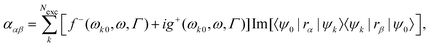 | (4) |
where the sum goes over the Nexc excited states, {ψk} are the electronic wave functions of the kth excited state, and ψ0 is the electronic ground state wave function. In eqn (4), the terms f− and g+ are defined in terms of the energy difference between the ground-state and excited state, ωk0, the frequency of incident light, ω, and the life-time of the excitation Γ.15,18 Electric dipole moment integrals, for non-periodic calculations, and bulk polarization integrals, for periodic calculations, are not only needed for the calculation of the polarizability,19–22 but also for the simulation of vibrational and electronic spectra such as IR spectra,13,23,24 Vibrational Circular Dichroism (VCD) spectra,25,26 Raman spectra,17,27–32 and Raman Optical Activity (ROA) spectra,15,33 sum frequency generation spectra,34,35 and two-dimensional IR spectroscopy.36
For the evaluation of properties that are related to the electric dipole moment and to the polarization, a light-matter interaction Hamiltonian is usually applied. In the standard formulation and dipole approximation, the Hamiltonian reads
where
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
is the system's ground state Hamiltonian operator which is extended by the interaction of the electric dipole moment
μ with the electric field
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif)
. Derivatives of the electronic energy with respect to the electric field thus depend on the electric dipole moment and its derivatives. Often applied theories in this context are time-dependent DFT and perturbation theory, which can also be combined.
It is clear that the different properties that depend on the electronic position operator r are of great interest to a wide range of researches aiming to calculate electronic properties. The application to periodic systems is of special interest, because in most experimental setups condensed systems are studied as opposed to gases. In the following sections, we will outline the different solutions that have been proposed in the literature to tackle the ill-definition of the position operator in extended systems.
2.1 Modern theory of polarization
The calculation of the bulk polarization per unit cell, P, is not possible by eqn (3) because different choices of the unit cell lead to different numerical values of P.16 The solution to this inconsistency can be found in the Modern Theory of Polarization.16 In this theory, it has been shown that differences in the polarization, such as, for example, its derivatives, can be obtained by calculating the polarization according to| | 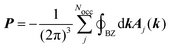 | (6) |
where the sum goes over all occupied bands, the integral is taken over a closed loop in k-space and Aj(k) is the Berry connection, defined asand the matrix elements are calculated over the cell-periodic Bloch functions {ujk(r)}. In order to calculate the gradient of the Bloch function with respect to k, a finite differences scheme can be applied by considering multiple calculations at different values for k, or perturbation theory can be applied.37 By applying perturbation theory in explicitly k-dependent formulations of DFT, the effect of an electric field has been considered for calculations of e.g. polarizabilities and hyperpolarizabilities,19–22 IR13,24 and vibrational Raman spectra,27–31 and second harmonic generation.38 Generally, the Berry phase φBerry can be calculated as the line integral of the Berry connection along a closed loop in reciprocal space as| | 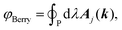 | (8) |
where the integral is taken over the boundary P of a surface along the adiabatic parameter λ. The Berry phase in eqn (8) is a gauge-invariant quantity, up to the so-called quantum of polarization,16,39 while the Berry connection (eqn (7)) is gauge-dependent. In addition to the phase indeterminacy, properties based on the polarization can also include surface effects.40 Each component of the polarization can take multiple values, corresponding to different branches of the logarithm (see eqn (9)), so that the total polarization can take more than one value. In a simplified picture, considering only the Γ-point (k = 0) in a KS-DFT framework, the Berry phase can be calculated as2,41| | 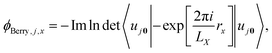 | (9) |
where LX is the length of an orthorhombic unit cell in x-direction, and rx is the x-component of the electronic position operator. It can be seen in eqn (9), that the bulk polarization, is only defined up the so-called quantum of polarization, due to the freedom to choose any branch of the logarithm. The expressions for the other two Cartesian directions are found analogously. The bulk polarization in the Γ-point limit is then given by| | 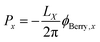 | (10) |
and analogously for the Cartesian y- and z-direction. For further details on the derivation, as well as the extension to arbitrary unit cell shapes, we refer to the literature.16,41 The expressions derived by the modern theory of polarization are routinely applied to calculate the expectation value of the bulk polarization, for example in calculations of Raman spectra,17,32,42–44 Born effective charges and IR spectra,13,45–49 ferroelectric materials,46,50–53 piezoelectricity,54–56 dielectric constants,47,57 the (anomalous) Hall effect,58,59 magnetoelectric responses,60 and sum frequency generation spectra.34,35
As pointed out e.g. by Springborg et al.,61 extending work by Tasker,62 the polarization per unit cell of real systems includes also terms dependent on the surfaces and as such it can in effect obtain any physically reasonable value, i.e. not just differing by a quantum of polarization except for quasi-1D systems.
The Berry phase formalism can also be applied to calculate the polarization,63 magnetoelectric response,64,65 piezoelectric tensors,66 and dielectric susceptibility tensors66,67 due to finite (time-dependent) electric fields. In such approaches, a finite field strength allows for the calculation of non-linearities of the electromagnetic response.
2.2 Maximally localized Wannier functions
A concept that is closely related to the modern theory of polarization, are Maximally Localized Wannier Functions (MLWFs). Wannier functions {wnR} can be obtained by applying a unitary transformation to the Bloch functions {unk} which are periodic in reciprocal space. The transformation matrix ![[U with combining low line]](https://www.rsc.org/images/entities/b_i_char_0055_0332.gif) (k), that defines the Wannier functions
(k), that defines the Wannier functions| | 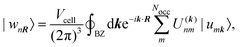 | (11) |
where R is a lattice vector, can be choosen freely and is optimized to minimize a spread functional, such as the Foster–Boys criterion68| | 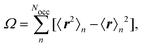 | (12) |
where the expectation values are calculated over the occupied Wannier functions (eqn (11)). The resulting functions are the MLWFs which are localized in space around the Wannier center 〈r〉n and decay exponentially with the distance from the Wannier center.69,70 The evaluation of the spread functional given in eqn (12) is not possible by considering the regular electronic position operator. Instead, the modern theory of polarization is applied to obtain for the expectation values in eqn (12)71| | 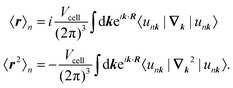 | (13) |
The result that is obtained for the bulk polarization using MLWFs is given by| | 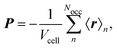 | (14) |
which is equivalent to the expression in eqn (6). While the Berry phase expressions for the polarization can only be applied to the calculation of expectation values of the polarization, the advantage of employing MLWFs is that additional information becomes available from each of the MLWFs. Properties, such as the dipole strengths for IR absorption, can be calculated for each MLWF individually. In this way, the total expectation value can be partitioned into contributions from each center, or groups of Wannier centers centered around individual bonds and atoms, functional groups, or molecules. This approach is not limited to periodic systems and has been applied to IR spectra,23,49,72–79 VCD spectra calculations,80 Raman spectra calculations,32,74,81 ROA spectra calculations,33 SFG spectra calculations,34,82–84 high harmonic generation in crystals,85 Hall conductivities,86,87 the magnetoelectric polarizability tensor,88 Magnetic Circular Dichroism (MCD) spectra89 of ferroelectrics,90 piezoelectric constants,56 the shift-current response in piezoelectric crystals,91 and dielectric constants.76,77,92
MLWFs have not only been used to calculate the bulk polarization and molecular polarizabilities, but have been also applied to magnetic properties. Because the modern theory of polarization, and hence MLWFs, can not be directly extended to the calculation of the magnetic dipole moments and electronic currents, ad hoc generalizations must be made. One proposed solution is the definition of a saw-tooth operator.7 The position operator is recast as
for each orbital, such that the orbital is located in the center of a virtual box with dimensions
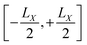
(and analogous for the other two directions). Around the center of this cell, the position operator is defined in the usual way, and at the boundaries the position operator goes from +
LX/2 to −
LX/2. Whether this change is smooth or abrupt does not matter theoretically because the Wannier function
wj(
r) is assumed to be zero in this region (see
Fig. 1).
7 It was shown by Springborg
et al. that the saw-tooth operator is not a general solution for the position operator problem in periodic systems.
93 This is due to the fact that the saw-tooth operator omits current terms due to the intercellular charge flow as was shown for a one dimensional Hückel model.
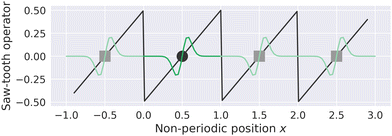 |
| | Fig. 1 The saw-tooth operator (eqn (15)) is shown for a simulation cell with length L = 1 and a MLWF centered at 0.5. The saw-tooth operator is plotted as a straight black line, the position of the Wannier center in the home cell is shown as a black circle, and a schematic Wannier function is plotted in dark green in the home cell. The periodic images of the Wannier center and Wannier function are plotted as gray squares and light green lines, respectively. The saw-tooth operator is discontinuous at the boundary, but could also be smoothed (see ref. 7). The units in this figure are arbitrary. | |
2.3 Velocity gauge
Another option for the calculation of the expectation value of the electric dipole moment is the velocity gauge.42 The velocity (or electric current operator) can be calculated as the Heisenberg time derivative of the position operator as94–96| | 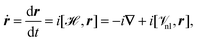 | (16) |
where ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) nl collects all non-local potentials, such as pseudopotentials, that appear in the Hamiltonian and do not commute with r. The first term in eqn (16) is due to the commutator of the kinetic energy operator with the position operator. Because the operator in eqn (16) is well-defined in PBC, it offers another way for the calculation of the expectation value of the electronic position operator. A property of the operator in eqn (16) is that it is purely imaginary. For this reason, a complex electron density matrix must be employed to obtain non-vanishing expectation values. This can be achieved, for example, by TD-DFT42,97 or imaginary perturbations.98 Additionally, the equality
nl collects all non-local potentials, such as pseudopotentials, that appear in the Hamiltonian and do not commute with r. The first term in eqn (16) is due to the commutator of the kinetic energy operator with the position operator. Because the operator in eqn (16) is well-defined in PBC, it offers another way for the calculation of the expectation value of the electronic position operator. A property of the operator in eqn (16) is that it is purely imaginary. For this reason, a complex electron density matrix must be employed to obtain non-vanishing expectation values. This can be achieved, for example, by TD-DFT42,97 or imaginary perturbations.98 Additionally, the equality| | | 〈a|ṙ|b〉 = −i(Eb − Ea) 〈a|r|b〉 | (17) |
for two eigenstates |a〉 and |b〉 with corresponding energy eigenvalues Ea and Eb is only fulfilled for exact wavefunctions, and otherwise the position operator and velocity operator do not yield identical results.94 Special care has to be taken in the evaluation of the commutator of the position operator and the non-local (pseudo)potential operator in eqn (16) to ensure correct results.42,96,99
Similar to the MLWF approach, the application of the velocity dipole operator is not limited to periodic systems but can also be used to remove gauge dependencies in non-periodic simulations. The velocity gauge operator has been succesfully applied in the calculation of absorption spectra from the X-ray to IR region,25,42,100–102 photoinduced processes,103 excited state dipole moments,100 high harmonic generation,104,105 electron scattering experiments,106 optical rotation tensors,107,108 VCD spectra,25,26 Electronic Circular Dichroism (ECD) spectra,42,96 ROA spectra,33,109–113 and dielectric constants.114
2.4 Local electric dipole moments via embedding
Another approach for calculation of local electric dipole moments in periodic system has been presented, which is based on DFT embedding. In this scheme, a periodic system is partitioned into subsystems via periodic subsystem DFT.79 It can be shown that the Berry phase formula can be replaced by the usual position operator in an embedding framework, by expanding the exponential in terms of the inverse cell lengths as| | 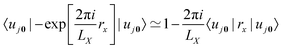 | (18) |
leading, for orthorombic unit cells, to the expression| | 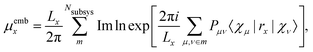 | (19) |
where the first sum goes over the Nsubsys subsystems, the second sum goes over all basis functions which were assigned to the subsystem m, and Pμν are the matrix elements of the density matrix. This approach has been applied to the calculation of IR spectra of liquids, molecules solvated in water, and molecules adsorbed on a rutile TiO2 surface.79 A similar approach was also used to simulate absorption spectra of a molecule solvated in water and a liquid mixture via RT-TDDFT simulations, also employing MLWFs.49
2.5 Redefinition of the position operator
Another approach, based on redefining the position operator to be consistent with PBC, was proposed in the literature.115 Recognizing, that the usual form of the position operator cannot be applied under PBC, a new definition has to be found. In a seminal paper by Resta,2 the expectation value of the electronic position operator was given by| | 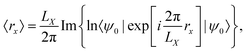 | (20) |
where ψ0 is the ground state electronic wave function, which coincides with the Berry phase definition116–119 of the polarization in the Γ-point limit.41 Berger and co-workers recently expanded this definition of the expectation value to the definition of the position operator itself115 by defining a complex position| | 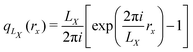 | (21) |
which is a continuous and periodic function of the position operator rx. This position operator fulfills the criteria, that it (1) is invariant with respect to translation by a unit cell, (2) reduces to the regular position operator in the limit of infinite cell size LX → ∞, (3) distances defined in terms of eqn (21) are real and gauge-invariant, and (4) is a one-particle operator. The uniqueness of the operator in eqn (21), up to an additive constant and modulo a phase factor, was proven as well.120 The complex position operator (eqn (21)) that has been proposed, notably, allows for a periodic definition of the electric quadrupole integrals as can be seen by calculating the product of position operators as| | 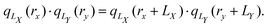 | (22) |
Whether the operator defined in eqn (22) is, in fact, a physically meaningful definition of electric quadrupole moments remains to be seen. The complex position operator given in eqn (21) has so far been applied to the calculation of the polarization and the localization tensors (see eqn (12)), where the Resta-type in eqn (20)2, Berry-type in eqn (9),41 and complex position operator in eqn (21)115 coincide anyways (in the Γ-point limit).115,120
3. The position operator for magnetic properties in a periodic framework
In Section 2, different ways for the calculation of the expectation value of the electric dipole moment operator and closely related properties such as the electric dipole–electric dipole polarizability were presented. In many cases, not only the electric dipole but also integrals related to magnetic properties such as the magnetic dipole moment must be evaluated. In the context of this manuscript, the magnetic properties can be divided in two sections. For one, there is chiral spectroscopy that relies on the evaluation of the magnetic dipole operator or polarizability tensors such as the electric dipole–magnetic dipole polarizability tensor, which are needed for e.g. ECD,121 VCD,122 and ROA122 spectroscopic calculations. On the other hand, there is the calculation of nuclear magnetic resonance (NMR) chemical shielding tensors and electron paramagnetic resonance (EPR) g-tensors which are due to electronic currents induced by magnetic fields.
The minimal-coupling Hamiltonian operator in the presence of a magnetic vector potential can be written as
| | 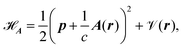 | (23) |
where
A is the magnetic vector potential, and all remaining potentials are collected in
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif)
(
r). The magnetic vector potential for a uniform magnetic field
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
depends on
r and is given by
| | 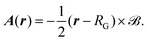 | (24) |
Considering only the terms linear in the vector potential and inserting
eqn (24) into
eqn (23) one obtains the magnetic field dependent Hamiltonian
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
| | 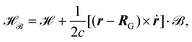 | (25) |
where
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
is the ground state Hamiltonian that is usually employed, we introduced the gauge origin
RG, and
ṙ is defined as in
eqn (16). In principle, an arbitrary gauge origin can be employed in molecular simulations, due to the gauge freedom of the vector potential which is only defined up to the gradient of a function
β(
r), called the gauge function.
123 The magnetic field can be derived from the magnetic vector potential by
| | ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = ∇ × A = ∇ × [A + ∇β(r)]. = ∇ × A = ∇ × [A + ∇β(r)]. | (26) |
The Schrödinger equation, including the operators and wave function, can be gauge transformed according to
| | 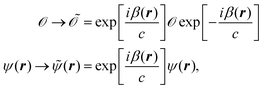 | (27) |
which does not change the expectation values. For calculations involving magnetic fields, one can take advantage of the gauge transformation in
eqn (27) by applying it to the Atomic Orbital (AO) basis. This modified basis set includes an explicit dependence on the vector potential and is called Gauge Including Atomic Orbitals (GIAOs). The GIAOs are given by
98,124| | 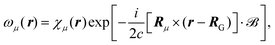 | (28) |
where the GIAOs {
ωμ} are derived from the atomic orbital basis {
χμ}, and the exponential phase factor includes the position
Rμ where the basis function is centered. In this way, the AOs are gauge transformed so that the atomic center of each basis function is used as the gauge origin respectively in order to reduce the dependence of results on the gauge freedom. The magnetic field in
eqn (28) can either be set to a finite value
125 or only applied in perturbative schemes where related quantities are taken in the limit of vanishing magnetic field.
126
3.1 Modern theory of magnetization
A formalism closely related to the modern theory of polarization is the modern theory of magnetization which aims to reformulate the expressions for the expectation value of the magnetic dipole operator m and the bulk magnetization M127| | 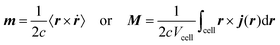 | (29) |
in a way that leads to physically meaningful values under PBC. For this purpose, the magnetization is partitioned into a local circulation (LC) and itinerant circulation (IC) contribution.127,128 The IC contribution to the orbital magnetization can be formulated in terms of a sum over surface Wannier functions or alternatively it can be written in terms of k-space integrals and the Berry connection as127| | 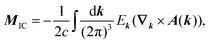 | (30) |
where A(k) is the Berry connection. The LC contribution to the orbital magnetization can be written as| | 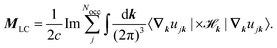 | (31) |
Both contributions can be combined to arrive at| | 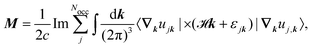 | (32) |
where ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) k is the k-dependent Hamiltonian operator, Ek is the corresponding total energy, εjk are the orbital energies, and the integrals are taken over the Nocc occupied Bloch orbitals uj,k.6 The formula in eqn (32) is only applicable to noninteracting zero-Chern-number insulators in a vanishing magnetic field,127 although these limitations have been lifted in subsequent publications.129–131 Test calculations have shown that the results obtained from eqn (32) match with the results obtained from finite systems using the Haldane model Hamiltonian.6,132 An important difference compared to eqn (6) is that no quantum of magnetization appears in the modern theory of magnetization and the results are completely defined by eqn (32). The formulas resulting from the modern theory of magnetization have been applied for the calculation of NMR shifts in water133 and a set of small molecules,134 SiO2 polymorphs and an organometallic system,135 and aromatic hydrocarbons.136 Calculations of EPR g tensors were carried out for radicals and paramagnetic defects in solids.137 Other derivatives of the orbital magnetization are related to the quantum spin Hall effect138,139 and the magnetoelectric polarizability,140 among others.128
k is the k-dependent Hamiltonian operator, Ek is the corresponding total energy, εjk are the orbital energies, and the integrals are taken over the Nocc occupied Bloch orbitals uj,k.6 The formula in eqn (32) is only applicable to noninteracting zero-Chern-number insulators in a vanishing magnetic field,127 although these limitations have been lifted in subsequent publications.129–131 Test calculations have shown that the results obtained from eqn (32) match with the results obtained from finite systems using the Haldane model Hamiltonian.6,132 An important difference compared to eqn (6) is that no quantum of magnetization appears in the modern theory of magnetization and the results are completely defined by eqn (32). The formulas resulting from the modern theory of magnetization have been applied for the calculation of NMR shifts in water133 and a set of small molecules,134 SiO2 polymorphs and an organometallic system,135 and aromatic hydrocarbons.136 Calculations of EPR g tensors were carried out for radicals and paramagnetic defects in solids.137 Other derivatives of the orbital magnetization are related to the quantum spin Hall effect138,139 and the magnetoelectric polarizability,140 among others.128
The modern theory of magnetization considers only the orbital magnetization, so that spin-dependent terms must be considered separately. Furthermore, it has been shown that the orbital magnetization of infinite periodic systems under a homogeneous magnetic field, depending on k-derivatives of the Bloch orbitals (see eqn (32)), can be obtained from the bulk electron density alone,141,142 while the same is not true for large finite systems exposed to a magnetic field, where the orbital magnetization is shape-dependent.39,141,143,144
3.2 Nuclear magnetic and electron paramagnetic resonance
The elements of the chemical shift tensor of the nucleus λ are given by| | 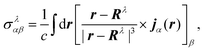 | (33) |
where Rλ is the position of the nucleus, and jα is the current density induced by a homogeneous magnetic field applied along the Cartesian α-direction. The induced current density is calculated for each point in real space as7| | 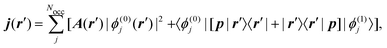 | (34) |
where ϕ(0)/(1)j is the jth the unperturbed/perturbed KS orbital, p is the linear momentum operator, and the first contribution is referred to as the diamagnetic term and the second contribution as the paramagnetic term. Both contributions in eqn (34) depend on the choice of gauge, while the total current should be gauge-independent.7 The EPR g-tensor components are given by145| | 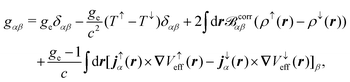 | (35) |
where δαβ is the Kronecker-delta, ge is the free-electron g value, ↑ and ↓ denote the two spin channels, and T↑, j↑α(r), and ρ↑ are the unperturbed kinetic energy, induced current density, and electron density of the spin-↑ channel, respectively. V↑eff is an effective potential felt by the spin-↑ electrons. The vector ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) corrα in eqn (35) is the magnetic field originating from the induced current density jα
corrα in eqn (35) is the magnetic field originating from the induced current density jα| | 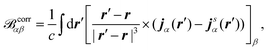 | (36) |
where jsα = (j↑α(r) − j↓α(r)) is a self-interaction correction.145 Different approaches for the calculation of the tensors in eqn (33) and (35) have been applied. Weber et al. applied perturbation theory in combination with MLWFs.145 In this scheme, three different perturbation operators (see eqn (2)), labeled ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) L,
L, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) p, and
p, and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) Δi, must be considered which are given by
Δi, must be considered which are given by| | 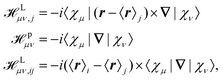 | (37) |
where {χμ} are the atom-centered basis functions and {〈r〉i} are the Wannier centers obtained by the modern theory of polarization. Although the ill-defined position operator appears both in the sought-for tensors as well as in the perturbation operators in eqn (37), the application of MLWFs has proven to be an effective way to simulate the NMR and EPR tensors in periodic systems in the Γ-point limit. For this purpose, the equations are reformulated such that the Wannier centers {〈r〉j} appear in the response equations.145 Such an approach might be referred to as a Wannier gauge method, or as an individual gauge for localized orbitals (IGLO) approach as used in non-periodic calculations,146–149 where the response to the magnetic field and the induced current corresponding to each orbital is calculated with different gauge origins set for each orbital.
Another approach is the continuous set of gauge transformations (CSGT) method. In the “RG = r′” variant of CSGT,3,150–152 for each point in space r′ the current density jα(r′) (eqn (34)) is calculated with the gauge origin RG set equal to r′. Applying this gauge, the diamagnetic contribution to the current vanishes analytically and only the paramagnetic term remains. The same result is obtained more rigorously by writing the magnetic properties in terms of current densities, yielding a gauge-invariant formulation where the diamagnetic and paramagnetic terms are treated on equal footing.153 In this approach the first two perturbation operators in eqn (37) have to be evaluated, in principle for each point in real space. By also including the third perturbation operator in eqn (37), the computational cost can be reduced significantly such that only nine sets of expansion coefficients are needed in total to evaluate eqn (33) (for the three operators in three directions each).7 The ill-definition of the position operator under PBC is in this case circumvented by localizing the bands and applying a saw-tooth operator (see Fig. 1) around the Wannier center of each band. The working equations and perturbation look similar to the IGLO approach from ref. 145, but in fact a different gauge is applied.7 The individual gauges for atoms in molecules (IGAIM) method is a derivative of the CSGT method,154 where the gauge origin is set to the atom of interest,150–152 although this approach has not been applied to periodic systems to our knowledge.
An implementation for the calculation of periodic NMR spectra has also been presented by Ziegler and co-workers which is based on GIAOs.155 The approach is based on the formulation of NMR shiedling tensors as the second derivative of the energy with respect to an external magnetic field and the magnetic dipole moment
| | 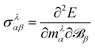 | (38) |
where
E is the system's electronic energy, and the nuclear magnetic dipole moment
mλ, of atom
λ is defined for one atom in the unit cell and the conditionally convergent sum over all lattice vectors is carried out
via analytic continuation techniques.
155 The derivative with respect to the external magnetic field is carried out analytically by perturbation theory, relying on GIAOs. The contributions to the NMR shielding tensor are made gauge invariant by employing the recipe of Fukui,
156 relying on the fact that the current density of the probe atom vanishes at the cell boundary.
155 The derivative with respect to the nuclear magnetic moment on the other hand is carried out numerically, by varying the nuclear magnetic dipole moment and applying a finite differences formula.
Pickard and Mauri presented an implementation of periodic NMR tensors in the gauge including projector augmented wave (GIPAW) framework which is based on the Green's-function approach and the construction of a Hamiltonian that has the required translational invariance.99 The contributions due to the use of norm-conserving pseudopotentials and the gauge of the projectors applied in the pseudopotentials were taken into account in this implementation. As mentioned by the authors of ref. 99, the applicability to periodic simulations is only given because the arising operators are short-ranged, and thus the ill-definition of the position operator at large distances from the studied nucleus can be safely ignored. The implementation was later also expanded to ultrasoft pseudopotentials.133
Another approach for solving the problem of the missing periodicity of the magnetic vector potential (see eqn (23) and (24)) was presented by Mauri et al. reyling on explicitly k-dependent calculations including a finite magnetic field that is modulated by a finite wavelength q.157 The magnetic field is defined explicitly as
| | 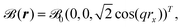 | (39) |
with the field strength
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 0
0. By carrying out calculations for different values of
q, an extrapolation can be carried out towards the limit
q → 0, corresponding to the case of a homogenous magnetic field. This approach was applied to the calculation of the magnetic susceptibility defined as
157,158| | 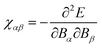 | (40) |
as well as to the NMR chemical shift of diamond and diamondlike amorphous carbon,
159,160 and carbon nitride compounds.
161 For the evaluation of
eqn (40) using the applied field (
eqn (39)), terms arise which individually diverge. By exploiting the
f-sum rule, the terms can be combined to yield a single non-diverging expression for the magnetic susceptibility. Alternatively, time-dependent current-DFT
4 can be applied to obtain fundamentally periodic responses to magnetic
162 and electric fields.
163
4. The position operator problem for periodic VCD calculations
4.1 Circular dichroism spectra and the magnetic dipole
Circular dichroism (CD) spectroscopies rely on the difference of absorption of left- and right-circularly polarized light by a sample. In ECD spectroscopy, light in the ultraviolet (UV), visible (Vis), and near-infrared (NIR) range is used to probe e.g. the secondary structure of proteins, charge-transfer transitions, and the electronic structure of metal complexes, by inducing electronic transitions. Vibrational CD (VCD) instead relies on the vibronic coupling induced by IR radiation. When circularly polarized light hits a chiral sample, the helicity of the (electro)magnetic field interacts with the sample and induces a circulation of charge. The intensity of this effect differs depending on whether the chirality of the field and sample are the same or opposite, which gives rise to ECD and VCD spectroscopy. In MCD spectroscopy, a strong magnetic field is applied parallel to the propagation axis of the incident light which induces a CD in materials that do not generally have to be chiral.164 Often very weak transitions in optical absorption spectra are enhanced by an applied magnetic field.164
The expectation value of the electronic part of the magnetic dipole moment operator in non-periodic systems is given by7,145
| | 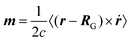 | (41) |
where
ṙ is the velocity operator (see
eqn (16)). We will focus only on the electronic contributions to the magnetic dipole moment henceforth. Both mentioned operators, the electric dipole moment (
eqn (3)), the magnetic dipole moment (
eqn (41)) – as well as the electric quadrupole moment which is not shown here – depend on the position operator and thus on the choice of the gauge origin
RG. For the calculation of the optical rotary power, the rotation of the light's plane of polarization by the sample, an approach similar to ref.
157 was presented recently.
165 Additionally to an explicit periodic magnetic field and a subsequent extrapolation to the limit of a homogeneous magnetic field, which was also used by Mauri
et al.,
157 a perturbative treatment of the
k-derivatives of the Bloch functions was applied for the calculation of the optical rotary power of H
2O
2 polymers, enforcing also the Hermiticity of the arising operators, resulting in gauge-invariant rotary powers.
165
The simulation of VCD spectra usually relies on perturbation theory and involves the magnetic field or nuclear velocity perturbation theories (MFP126,166 and NVP,25 respectively). Similar to response theory for electronic transitions42 one can think of VCD spectra as the coupling of a system's vibrational motion to a magnetic field, which induces an electronic current j(r). Alternatively, on can think of a magnetic field that is induced by an already present electronic current. Both descriptions can be related to each other by energy gradient theory.98
In perturbative schemes, the quantity that is needed for the calculation of VCD spectra is the rotational strength Ri which is related to the Atomic Axial Tensors (AATs). To our knowledge only one periodic implementation for VCD exists so far, which is based on the nuclear velocity perturbation (NVP) in the plane-wave code CPMD.80 Generally, either the magnetic field perturbation (MFP)166 or the NVP25,26,98 can be applied in order to obtain the rotational strengths necessary to calculate VCD spectra. While the MFP is based on GIAOs (eqn (28)) and a magnetic field dependent perturbation operator (eqn (25)), the NVP is based on velocity-gauge including atomic orbitals {![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) μ} – when atom-centered basis functions are employed – and the complete adiabatic Hamiltonian
μ} – when atom-centered basis functions are employed – and the complete adiabatic Hamiltonian ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) CA
CA
| | ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) μ(r) = χμ(r) μ(r) = χμ(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[i(r − RG)·Ṙμ] exp[i(r − RG)·Ṙμ] | (42) |
| | 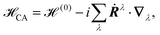 | (43) |
where
Ṙμ is the velocity of the atom on which the
μth basis function is centered, the sum in
eqn (43) goes over all atoms
λ, and
∇λ is the gradient with respect to the nuclear coordinate of the
λth atom. As can be seen in
eqn (25), (28) and (42), both the MFP and NVP have explicit dependencies on the position operator, and thus on the gauge origin, which poses serious problems for periodic implementations, especially when atom centered basis sets are employed.
The electronic contribution to the AATs in the MFP and NVP case is given by
| | 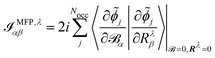 | (44) |
and
| | 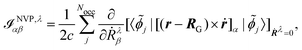 | (45) |
respectively, where {
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) j
j} are the MOs including the gauge factors (see
eqn (28) and (42)), and in the MFP, the position operator enters in
eqn (44) through the orbitals perturbed with respect to the magnetic field (see
eqn (28)), while in the NVP, the position operator enters in
eqn (45) through the magnetic dipole moment operator and the orbitals perturbed with respect to nuclear velocities.
As can be seen in the equations for VCD spectra in the MFP (eqn (44) and (28)) and in the NVP (eqn (45) and (42)), and for NMR and EPR spectra (eqn (33) and (37)), the properties and perturbation operators depend explicitly on the electronic position operator, and thus on the specification of a gauge origin RG.
The origin of the magnetic dipole operator (eqn (41)) can be defined in different gauges when evaluating matrix elements of the form 〈a|m|b〉. In molecular simulations, the direct choice is the common origin (CO) gauge. In this case, the position operator is referenced to the same origin for the whole calculation. Natural choices for the origin are the zero vector or the system's center of mass. Alternatively, a distributed origin (DO) gauge can be employed to reduce the dependence of resulting spectra on the coordinate system. This can refer to an approach such as the previously mentioned GIAOs, where each basis function has its own gauge origin. Alternatively, in perturbation calculations, where derivatives with respect to nuclear coordinates or velocities are taken (as in eqn (44) and (45)), a separate gauge origin can be set for each of the nuclear derivatives such that eqn (44) and (45) become
| | 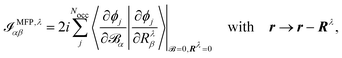 | (46) |
where the position operator
r enters through the derivative of the MO with respect to the magnetic field, and
| | 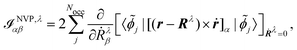 | (47) |
for the MFP and NVP expressions for the AATs. Further choices for the gauge are the IGLO,
146 where the gauge origin is not fixed per basis function or atom, but rather per orbital. The corresponding expression for the electronic contribution to the NVP AAT would in this case read
| | 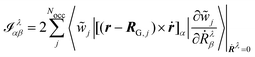 | (48) |
where
RG,j is the gauge origin of the
jth localized orbital, after applying a localization procedure to the MOs {
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) j
j} to obtain the Wannier functions {
![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) j
j}. A natural choice for the gauge origin in periodic systems is the corresponding Wannier center
RG,j = 〈
r〉
j,
167 although, as mentioned previously, this is not a general solution for the ill-definition of the magnetic dipole operator in periodic systems. For instance, a theoretical formulation that is gauge-invariant does not imply that the results are correct under PBC.
165
4.2 Vibrational circular dichroism from density functional perturbation theory
We assume a periodic electronic structure calculation carried out in the framework of KS-DFT in the Γ point limit for insulating systems. Generally, when a non-orthogonal set of basis functions is used, the electronic structure problem takes the form of a generalized eigenvalue problemwith the Hamiltonian matrix H, the MO coefficients C, the overlap matrix ![[S with combining low line]](https://www.rsc.org/images/entities/b_i_char_0053_0332.gif) , and the electronic energy matrix E. In our case, we define the Hamiltonian matrix, generally, by the matrix elements of the KS Hamiltonian operator
, and the electronic energy matrix E. In our case, we define the Hamiltonian matrix, generally, by the matrix elements of the KS Hamiltonian operator ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) KS as
KS as| | Hμν = 〈χμ|![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) KS|χν〉 = 〈χμ| KS|χν〉 = 〈χμ|![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) + + ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) |χν〉, |χν〉, | (50) |
where {χμ} are atom-centered basis functions, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is the kinetic energy operator, and we collect all arising potentials in
is the kinetic energy operator, and we collect all arising potentials in ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) . The potential energy operator
. The potential energy operator ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) includes the electrostatic interactions, which are usually calculated via Ewald summation,168 the pseudopotentials, and the DFT exchange–correlation potential. Although hybrid exchange–correlation functionals, including a fraction of exact Hartree–Fock exchange, could be applied, this has not been done so far for the NVPT. The solutions of eqn (49) are the KS-MO coefficients Cj for the jth KS orbital (ϕj) from which the real space electron density n(r) is calculated as
includes the electrostatic interactions, which are usually calculated via Ewald summation,168 the pseudopotentials, and the DFT exchange–correlation potential. Although hybrid exchange–correlation functionals, including a fraction of exact Hartree–Fock exchange, could be applied, this has not been done so far for the NVPT. The solutions of eqn (49) are the KS-MO coefficients Cj for the jth KS orbital (ϕj) from which the real space electron density n(r) is calculated as| | 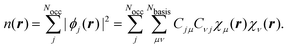 | (51) |
Due to simplicity, we limit the discussion to the Γ-point of the Brillouin zone and assume real MO-coefficients and basis functions. We carried out a basis set expansion of the KS-MOs in eqn (51) by| | 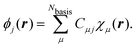 | (52) |
When the potentials in eqn (50) are defined periodically, the resulting KS orbitals are periodic, too, and fulfill Born-von Kármán boundary conditions:169for any integer vector n representing a periodic image of the home cell n = (0,0,0)T, where L are the lattice vectors. We assume that a large supercell is employed.
We will focus on the NVPT25 in the Complete Adiabatic (CA) formalism, as proposed by Nafie.98 For the evaluation of VCD spectra, the magnetic dipole moments need to be calculated. For this purpose, we define the AAT for the atom λ in the Cartesian directions α and β as
| | 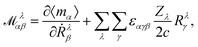 | (54) |
where the magnetic dipole moment operator
m is given by
eqn (41).
In eqn (54), Ṙλ and Zλ are the velocity and effective charge of the λth nucleus, 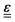 is the Levi-Civita symbol, c is the speed of light in atomic units, and the sums in eqn (54) go over the atoms λ and the Cartesian directions γ. The magnetic dipole moment operator (eqn (41)) is defined in terms of the electronic position operator r and the electronic velocity operator ṙ (eqn (16)). The latter is calculated as the Heisenberg time derivative of the electronic position operator.94,96 Within a static approach in the harmonic approximation, the VCD spectrum of a system is defined in terms of the vibrational normal mode frequencies {ωv} and the rotational strengths {Rv} that are given by
is the Levi-Civita symbol, c is the speed of light in atomic units, and the sums in eqn (54) go over the atoms λ and the Cartesian directions γ. The magnetic dipole moment operator (eqn (41)) is defined in terms of the electronic position operator r and the electronic velocity operator ṙ (eqn (16)). The latter is calculated as the Heisenberg time derivative of the electronic position operator.94,96 Within a static approach in the harmonic approximation, the VCD spectrum of a system is defined in terms of the vibrational normal mode frequencies {ωv} and the rotational strengths {Rv} that are given by
| | 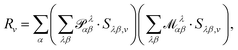 | (55) |
where
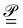
is the Atomic Polar Tensor (APT),
170,171![[S with combining low line]](https://www.rsc.org/images/entities/b_i_char_0053_0332.gif) v
v is the mass-weighted transformation matrix from Cartesian coordinates to normal mode coordinates, and
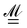
ist the AAT as defined in
eqn (54).
The expectation value of eqn (41) is inaccessible from a wave function obtained in a standard Born–Oppenheimer calculation, because it vanishes due to symmetry. A perturbation can be applied to the system to recover the effects of the current density j(r). To achieve this, an imaginary correction to the KS-MOs has been applied using Density Functional Perturbation Theory (DFPT),9,23 and the CA Hamiltonian ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) CA (see eqn (43)) in combination with velocity-gauge including atomic orbitals (see eqn (42)).25,98 The basis functions in eqn (42) can be Gaussian-type orbitals, Slater-type orbitals, or numerical basis functions. A perturbative expansion of the generalized eigenvalue equation (eqn (49)) leads to the Sternheimer equation23,172
CA (see eqn (43)) in combination with velocity-gauge including atomic orbitals (see eqn (42)).25,98 The basis functions in eqn (42) can be Gaussian-type orbitals, Slater-type orbitals, or numerical basis functions. A perturbative expansion of the generalized eigenvalue equation (eqn (49)) leads to the Sternheimer equation23,172
| | 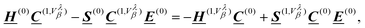 | (56) |
where the superscript “(0)” refers to the unperturbed ground state quantities and the superscript “(1,
Vλβ)” is a shorthand notation for
| | 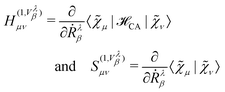 | (57) |
in the case of the Nuclear Velocity Perturbation Theory (NVPT), but could also refer to a magnetic field derivative (∂/∂
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) α
α) when GIAOs
124 are employed. Comparing
eqn (57) and (42) it becomes clear, that the position operator enters into the derivatives of the Hamiltonian and overlap matrix. Even though the KS Hamiltonian matrix elements (see
eqn (50)) fulfill the Born-von Kármán boundary conditions, this is not the case for the Sternheimer equation due to the arising position operators.
It was previously suggested that the application of MLWFs can avoid the ill-definition of the position operator and the corresponding response calculations for NMR spectroscopy.7 The exponential decay of the Wannier functions in combination with the
| | 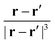 | (58) |
dependency of the induced magnetic field (
eqn (36)) and NMR shieldings (
eqn (33)) allows for ignoring the unphysical discontinuity of the saw-tooth operator. In the position operator-dependent perturbation operator (
r ×
∇, in this case), a separate coordinate system is defined for each MO so that the
jth position operator is given by
eqn (15).
145
In the framework of NVPT using MLWFs, the Sternheimer equation (eqn (56)) rewritten in terms of matrix elements is given by
| | 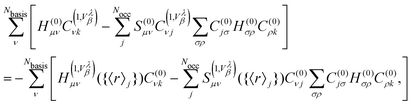 | (59) |
where we explicitly show the dependence of the terms in
eqn (57) on the Wannier centers for the case that MLWFs are employed. In this framework, the second term on the LHS of
eqn (56) and the second term on the RHS of
eqn (56) lead to a mixing of the different gauge origins. This additional complexity can necessitate the application of an additional correction operator along similar lines as properties in
eqn (37) for NMR.
Applying an orthogonal basis set formally eliminates the overlap matrix ![[S with combining low line]](https://www.rsc.org/images/entities/b_i_char_0053_0332.gif) from the generalized eigenvalue equation (eqn (49)). The overlap matrix derivative still appears in eqn (56), though, and contributes a position operator-dependent phase factor.
from the generalized eigenvalue equation (eqn (49)). The overlap matrix derivative still appears in eqn (56), though, and contributes a position operator-dependent phase factor.
4.3 Evaluation of properties
Turning our attention to the magnetic dipole moment operator integrals, in the NVPT the expression for the electronic contribution to the AATs is given by25| | 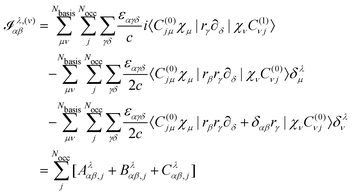 | (60) |
if we assume that no nonlocal potentials are present in the calculation.25 In the first term, Aλαβ,j, we assume that the Sternheimer equation for the kth MO was solved using the kth Wannier center 〈r〉j as the gauge origin. The matrix element should then be evaluated as| | | 〈C(0)jμχμ|(rγ − 〈r〉j,γ)·∂δ|χνC(1)νj〉. | (61) |
The terms Bλαβ,j and Cλαβ,j, on the other hand, include quadrupolar integrals of the form 〈χμ|rβrγ∂δ|χν〉. Such multipolar integrals are not well-defined in the bulk.173 Three proposal were made to extend Resta's periodic position operator.2 Wheeler et al. suggest extending the exponential function directly for the quadrupole integrals as174| | 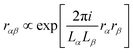 | (62) |
which can be shown not to be periodic, by inserting rα → rα + Lα and rβ → rβ + Lβ| | 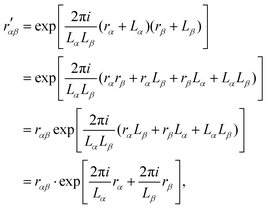 | (63) |
where one can see that the quadrupole in a periodic image of the home cell accumulates a phase factor and is thus not strictly periodic.173,175 Further, it was shown that neither a Resta-type nor a Berry-type formula for bulk quadrupole moments exists.173 Kang et al. instead propose to define the bulk multipole moments in terms of closed Wilson loops.176 A third proposal due to Balduff and Caricato177 relies on enforcing the translational invariance of the matrix elements corresponding to the electric quadrupole moment operator. By evenly distributing the non-hermitian part of the electric quadrupole matrix elements between the matrix itself and its adjoint element, a Hermitian electric quadrupole matrix is obtained. In any case, the mentioned definitions of multiple moments for periodic systems are only concerned with the expectation values of the multipole operators in the whole bulk, while in eqn (54) the multipole integrals are needed in the AO basis and including basis function derivatives.
Notably, the aforementioned issues do not arise when the basis functions do not carry a gauge dependence, as was demonstrated in the formulation of NVPT using only plane waves as a basis.26,178 In this case, no technical issues arise in the formulation of the Sternheimer equation and the definition of the APTs, since the IGLO approach can be applied to the formula for the AATs (eqn (54)). It was shown, though, that extensive post-processing is necessary to obtain gauge-invariant and physically meaningful VCD spectra.178 As such, the application of a plane wave basis set does not offer a straightforward, black-box implementation for VCD spectra.
We now want to focus on the more general problem of defining a bulk magnetization (the magnetic dipole moment per volume) that is implied when carrying out periodic VCD simulations. In analogy to the modern theory of polarization,41 the modern theory of orbital magnetization130 has emerged recently. It has been shown that the evaluation of the magnetization over bulk Wannier functions results only in the local circulation (LC) contribution to the orbital magnetization. The itinerant contribution (IC), arising from the surface contributions, is absent from the expression130
| | 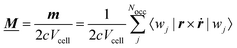 | (64) |
and must be considered separately. As such, the Wannier function approach alone is not sufficient to recover the whole bulk magnetization, as discussed in Section 3.1.
5. Conclusion
In this review article we have presented an overview of the different strategies that have been developed to overcome the difficulties arising in periodic implementations involving the position operator in the presence of PBC. The polarization, as well as the electric dipole polarizabilities, suffer from the arbitrary choice of the origin of the electronic position operator. The most often employed remedies for this problem are based on the Berry phase formalism and the modern theory of polarization. In these schemes, the bulk polarization is not expressed in terms of the usual dipole moment operator, but rather in terms of k-derivatives of cell periodic Bloch functions. An equivalent formulation relies on MLWFs that are computed via the Berry phase and lead to an expression for the bulk polarization that is identical to the Berry phase formula. For the electric dipole polarizabilities and quantities related to the electric dipole moment operator, the MLWFs lead to the IGLO (or Wannier gauge) method that is especially useful in perturbation calculations. Another approach not directly related to the Berry phase, is the velocity gauge which replaces the electronic position operator by its Heisenberg time derivative which is unproblematic in periodic systems and often employed in TD-DFT calculations of electric dipole–electric dipole polarizabilities and electric transition dipole moments. Additionally, some results have been presented which rely on periodic DFT embedding for the calculation of local electric dipole moments in periodic systems.
In the case of magnetic properties, the CSGT method has been applied to the simulation of NMR and EPR shifts as well as the closely related magnetic susceptibility tensors obeying PBC. These methods have also been combined with MLWFs, taking advantage of the short-ranged nature of the electronic current. GIAOs have also been used to carry out simulations with finite magnetic fields as well as perturbation calculations of finite systems. We have also described particular challenges for the calculation of periodic VCD spectra with an emphasis on the NVPT and atom-centered basis functions. The only documented implementation of periodic VCD spectra has been carried out in a plane wave code using the CA formalism in the velocity gauge in combination with MLWFs. Whether such an implementation is complete, in the sense that it includes also the surface contributions of the bulk magnetization, is not clear.
Another promising route for the implementation of the electronic current density in periodic system is current-DFT.179,180 In this approach, the DFT exchange–correlation functional is defined in terms of the applied magnetic vector potential, leading to a gauge-invariant and periodic theory of DFT in presence of finite magnetic fields.153
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Funding from the University of Zurich is gratefully acknowledged.
Notes and references
- P. Kratzer and J. Neugebauer, Front. Chem., 2019, 7 DOI:10.3389/fchem.2019.00106.
- R. Resta, Phys. Rev. Lett., 1998, 80, 1800–1803 CrossRef CAS.
- T. A. Keith and R. F. W. Bader, Chem. Phys. Lett., 1993, 210, 223–231 CrossRef CAS.
- J. A. Berger, P. L. de Boeij and R. van Leeuwen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035116 CrossRef.
- S. Luber, J. Chem. Phys., 2014, 141, 234110 CrossRef PubMed.
- R. Resta, J. Phys.: Condens. Matter, 2010, 22, 123201 CrossRef PubMed.
- D. Sebastiani and M. Parrinello, J. Phys. Chem. A, 2001, 105, 1951–1958 CrossRef CAS.
- A. Beérces, R. M. Dickson, L. Fan, H. Jacobsen, D. Swerhone and T. Ziegler, Comput. Phys. Commun., 1997, 100, 247–262 CrossRef.
- X. Gonze, Phys. Rev. A, 1995, 52, 1096–1114 CrossRef CAS PubMed.
- G. D. Mahan, Phys. Rev. A, 1980, 22, 1780–1785 CrossRef CAS.
- J. L. Dodds, R. McWeeny and A. J. Sadlej, Mol. Phys., 1977, 34, 1779–1791 CrossRef CAS.
- A. Putrino, D. Sebastiani and M. Parrinello, J. Chem. Phys., 2000, 113, 7102–7109 CrossRef CAS.
- L. Maschio, B. Kirtman, R. Orlando and M. Reèrat, J. Chem. Phys., 2012, 137, 204113 CrossRef PubMed.
- E. Ditler and S. Luber, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1605 CAS.
- J. Mattiat and S. Luber, J. Chem. Phys., 2019, 151, 234110 CrossRef PubMed.
-
D. Vanderbilt, Berry Phases in Electronic Structure Theory: Electric Polarization, Orbital Magnetization and Topological Insulators, Cambridge University Press, Cambridge, England, UK, 2018 Search PubMed.
- J. Mattiat and S. Luber, J. Chem. Theory Comput., 2021, 17, 344–356 CrossRef CAS PubMed.
- L. Jensen, J. Autschbach, M. Krykunov and G. C. Schatz, J. Chem. Phys., 2007, 127, 134101 CrossRef CAS PubMed.
- P. Otto, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 10876–10885 CrossRef PubMed.
- P. Otto, F. L. Gu and J. Ladik, J. Chem. Phys., 1999, 110, 2717–2726 CrossRef CAS.
- L. Maschio, M. Rérat, B. Kirtman and R. Dovesi, J. Chem. Phys., 2015, 143, 244102 CrossRef PubMed.
- M. Ferrero, M. Rérat, R. Orlando and R. Dovesi, J. Comput. Chem., 2008, 29, 1450–1459 CrossRef CAS PubMed.
- E. Ditler, C. Kumar and S. Luber, J. Chem. Phys., 2021, 154, 104121 CrossRef CAS PubMed.
- R. Dovesi, M. De La Pierre, A. M. Ferrari, F. Pascale, L. Maschio and C. M. Zicovich-Wilson, Am. Mineral., 2011, 96, 1787–1798 CrossRef CAS.
- E. Ditler, T. Zimmermann, C. Kumar and S. Luber, J. Chem. Theory Comput., 2022, 18, 2448–2461 CrossRef CAS PubMed.
- A. Scherrer, R. Vuilleumier and D. Sebastiani, J. Chem. Theory Comput., 2013, 9, 5305–5312 CrossRef CAS PubMed.
- L. Maschio, B. Kirtman, M. Rérat, R. Orlando and R. Dovesi, J. Chem. Phys., 2013, 139, 164101 CrossRef PubMed.
- L. Maschio, R. Demichelis, R. Orlando, M. De La Pierre, A. Mahmoud and R. Dovesi, J. Raman Spectrosc., 2014, 45, 710–715 CrossRef CAS.
- C. S. Praveen, L. Maschio, M. Rérat, V. Timon and M. Valant, Phys. Rev. B, 2017, 96, 165152 CrossRef.
- L. Maschio, B. Kirtman, S. Salustro, C. M. Zicovich-Wilson, R. Orlando and R. Dovesi, J. Phys. Chem. A, 2013, 117, 11464–11471 CrossRef CAS PubMed.
- M. De La Pierre, C. Carteret, L. Maschio, E. André, R. Orlando and R. Dovesi, J. Chem. Phys., 2014, 140, 164509 CrossRef PubMed.
- S. Luber, M. Iannuzzi and J. Hutter, J. Chem. Phys., 2014, 141, 094503 CrossRef PubMed.
- S. Luber, Phys. Chem. Chem. Phys., 2018, 20, 28751–28758 RSC.
- M. Sulpizi, M. Salanne, M. Sprik and M.-P. Gaigeot, J. Phys. Chem. Lett., 2013, 4, 83–87 CrossRef CAS PubMed.
- S. Luber, J. Phys. Chem. Lett., 2016, 7, 5183–5187 CrossRef CAS PubMed.
- S. Imoto, S. S. Xantheas and S. Saito, J. Phys. Chem. B, 2015, 119, 11068–11078 CrossRef CAS PubMed.
- M. Rérat, L. Maschio, B. Kirtman, B. Civalleri and R. Dovesi, J. Chem. Theory Comput., 2016, 12, 107–113 CrossRef PubMed.
- M. Rérat, P. Karamanis, B. Civalleri, L. Maschio, V. Lacivita and B. Kirtman, Theor. Chem. Acc., 2018, 137, 1–15 Search PubMed.
- R. Bianco and R. Resta, Phys. Rev. Lett., 2013, 110, 087202 CrossRef PubMed.
- M. Molayem, M. Springborg and B. Kirtman, Phys. Chem. Chem. Phys., 2017, 19, 24724–24734 RSC.
-
R. Resta and D. Vanderbilt, Physics of Ferroelectrics, Springer, Berlin, Germany, 2007, pp. 31–68 Search PubMed.
- J. Mattiat and S. Luber, J. Chem. Theory Comput., 2022, 18, 5513–5526 CrossRef CAS PubMed.
- M. Pagliai, C. Cavazzoni, G. Cardini, G. Erbacci, M. Parrinello and V. Schettino, J. Chem. Phys., 2008, 128, 224514 CrossRef PubMed.
- A. Putrino and M. Parrinello, Phys. Rev. Lett., 2002, 88, 176401 CrossRef PubMed.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368 CrossRef CAS.
- D. Sánchez-Portal, I. Souza and R. M. Martin, AIP Conference Proceedings, 2000, 535, 111–120 CrossRef.
- M. De La Pierre, R. Orlando, L. Maschio, K. Doll, P. Ugliengo and R. Dovesi, J. Comput. Chem., 2011, 32, 1775–1784 CrossRef CAS PubMed.
- I. Souza and R. M. Martin, Phys. Rev. Lett., 1998, 81, 4452–4455 CrossRef CAS.
- L. Schreder and S. Luber, J. Chem. Phys., 2021, 155, 134116 CrossRef CAS PubMed.
- K. T. Butler, J. M. Frost and A. Walsh, Energy Environ. Sci., 2015, 8, 838–848 RSC.
- J. B. Neaton, C. Ederer, U. V. Waghmare, N. A. Spaldin and K. M. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 014113 CrossRef.
- R. Resta, Modell. Simul. Mater. Sci. Eng., 2003, 11, R69 CrossRef CAS.
- S. Massidda, M. Posternak, A. Baldereschi and R. Resta, Phys. Rev. Lett., 1999, 82, 430–433 CrossRef CAS.
- D. Vanderbilt, J. Phys. Chem. Solids, 2000, 61, 147–151 CrossRef CAS.
- A. Dal Corso, R. Resta and S. Baroni, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 16252–16256 CrossRef CAS PubMed.
- Y. Noel, C. M. Zicovich-Wilson, B. Civalleri, P. D'Arco and R. Dovesi, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 014111 CrossRef.
- F. Bernardini, V. Fiorentini and D. Vanderbilt, Phys. Rev. Lett., 1997, 79, 3958–3961 CrossRef CAS.
- T. Rauch, T. Olsen, D. Vanderbilt and I. Souza, Phys. Rev. B, 2018, 98, 115108 CrossRef CAS.
- T. Olsen and I. Souza, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 125146 CrossRef.
- A. Malashevich, S. Coh, I. Souza and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 094430 CrossRef.
- M. Springborg, M. Zhou, M. Molayem and B. Kirtman, J. Phys. Chem. C, 2018, 122, 11926–11932 CrossRef CAS.
- P. W. Tasker, J. Phys. C-Solid State Phys., 1979, 12, 4977 CrossRef CAS.
- I. Souza, J. Íñiguez and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 085106 CrossRef.
- A. Malashevich, I. Souza, S. Coh and D. Vanderbilt, New J. Phys., 2010, 12, 053032 CrossRef.
- A. Malashevich, D. Vanderbilt and I. Souza, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 092407 CrossRef.
- I. Souza, J. Íñiguez and D. Vanderbilt, Phys. Rev. Lett., 2002, 89, 117602 CrossRef PubMed.
- E. Roman, J. R. Yates, M. Veithen, D. Vanderbilt and I. Souza, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245204 CrossRef.
- J. M. Foster and S. F. Boys, Rev. Mod. Phys., 1960, 32, 300–302 CrossRef CAS.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419–1475 CrossRef CAS.
- C. Brouder, G. Panati, M. Calandra, C. Mourougane and N. Marzari, Phys. Rev. Lett., 2007, 98, 046402 CrossRef PubMed.
-
E. Blount, in E. Blount, ed. F. Seitz and D. Turnbull, Academic Press, 1962, vol. 13 of Solid State Physics, pp. 305–373 Search PubMed.
- A. Esser, H. Forbert and D. Marx, Chem. Sci., 2018, 9, 1560–1573 RSC.
- M. Masia, H. Forbert and D. Marx, J. Phys. Chem. A, 2007, 111, 12181–12191 CrossRef CAS PubMed.
- M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622 RSC.
- I. Souza, R. M. Martin, N. Marzari, X. Zhao and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15505–15520 CrossRef CAS.
- C. M. Zicovich-Wilson, F. J. Torres, F. Pascale, L. Valenzano, R. Orlando and R. Dovesi, J. Comput. Chem., 2008, 29, 2268–2278 CrossRef CAS PubMed.
- L. Valenzano, Y. Noël, R. Orlando, C. M. Zicovich-Wilson, M. Ferrero and R. Dovesi, Theor. Chem. Acc., 2007, 117, 991–1000 Search PubMed.
- C. M. Zicovich-Wilson, F. Pascale, C. Roetti, V. R. Saunders, R. Orlando and R. Dovesi, J. Comput. Chem., 2004, 25, 1873–1881 CrossRef CAS PubMed.
- S. Luber, J. Chem. Phys., 2014, 141, 234110 CrossRef PubMed.
- A. Scherrer, R. Vuilleumier and D. Sebastiani, J. Chem. Phys., 2016, 145, 084101 CrossRef PubMed.
- Q. Wan, L. Spanu, G. A. Galli and F. Gygi, J. Chem. Theory Comput., 2013, 9, 4124–4130 CrossRef CAS PubMed.
- F. Creazzo, D. R. Galimberti, S. Pezzotti and M.-P. Gaigeot, J. Chem. Phys., 2019, 150, 041721 CrossRef PubMed.
- C. Liang, J. Jeon and M. Cho, J. Phys. Chem. Lett., 2019, 10, 1153–1158 CrossRef CAS PubMed.
- Q. Wan and G. Galli, Phys. Rev. Lett., 2015, 115, 246404 CrossRef PubMed.
- R. E. F. Silva, F. Martín and M. Ivanov, Phys. Rev. B, 2019, 100, 195201 CrossRef CAS.
- J. H. Ryoo, C.-H. Park and I. Souza, Phys. Rev. B, 2019, 99, 235113 CrossRef CAS.
- X. Wang, J. R. Yates, I. Souza and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195118 CrossRef.
- A. Malashevich and I. Souza, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 245118 CrossRef.
- I. Souza and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 054438 CrossRef.
- J. R. Yates, X. Wang, D. Vanderbilt and I. Souza, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195121 CrossRef.
- J. Ibañez-Azpiroz, S. S. Tsirkin and I. Souza, Phys. Rev. B, 2018, 97, 245143 CrossRef.
- M. Sharma, R. Resta and R. Car, Phys. Rev. Lett., 2007, 98, 247401 CrossRef PubMed.
- M. Springborg, B. Kirtman and Y. Dong, Chem. Phys. Lett., 2004, 396, 404–409 CrossRef CAS.
- A. F. Starace, Phys. Rev. A, 1971, 3, 1242–1245 CrossRef.
- A. F. Starace, Phys. Rev. A, 1973, 8, 1141–1142 CrossRef.
- J. Mattiat and S. Luber, Chem. Phys., 2019, 527, 110464 CrossRef CAS.
- J. Mattiat and S. Luber, Helv. Chim. Acta, 2021, 104, e2100154 CrossRef CAS.
- L. A. Nafie, J. Chem. Phys., 1992, 96, 5687–5702 CrossRef CAS.
- C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101 CrossRef.
- R. Sarkar, M. Boggio-Pasqua, P.-F. Loos and D. Jacquemin, J. Chem. Theory Comput., 2021, 17, 1117–1132 CrossRef CAS PubMed.
- P. J. Lestrange, F. Egidi and X. Li, J. Chem. Phys., 2015, 143, 234103 CrossRef PubMed.
- C. Gougoussis, M. Calandra, A. P. Seitsonen and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 075102 CrossRef.
- H. M. Dong, K. Han and W. Xu, J. Appl. Phys., 2014, 115, 063503 CrossRef.
- Y. J. Chen and B. Hu, Phys. Rev. A, 2009, 80, 033408 CrossRef.
- Y.-C. Han and L. B. Madsen, Phys. Rev. A, 2010, 81, 063430 CrossRef.
- C. Chang and E. J. Robinson, J. Phys. B: At. Mol. Phys., 1987, 20, 963 CrossRef CAS.
- T. D. Crawford, Theor. Chem. Acc., 2006, 115, 227–245 Search PubMed.
- T. D. Crawford, M. C. Tam and M. L. Abrams, J. Phys. Chem. A, 2007, 111, 12057–12068 CrossRef CAS PubMed.
- S. Luber and M. Reiher, Chem. Phys., 2008, 346, 212–223 CrossRef CAS.
- S. Luber, J. Neugebauer and M. Reiher, J. Chem. Phys., 2010, 132, 044113 CrossRef PubMed.
- S. Luber and M. Reiher, J. Phys. Chem. B, 2010, 114, 1057–1063 CrossRef CAS PubMed.
- S. Luber, J. Phys. Chem. A, 2013, 117, 2760–2770 CrossRef CAS PubMed.
- S. Luber, J. Chem. Theory Comput., 2017, 13, 1254–1262 CrossRef CAS PubMed.
- S. Baroni and R. Resta, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 7017–7021 CrossRef CAS PubMed.
- E. Valença Ferreira de Aragão, D. Moreno, S. Battaglia, G. L. Bendazzoli, S. Evangelisti, T. Leininger, N. Suaud and J. A. Berger, Phys. Rev. B, 2019, 99, 205144 CrossRef.
- E. Yaschenko, L. Fu, L. Resca and R. Resta, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 1222–1229 CrossRef CAS.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651–1654(r) CrossRef CAS PubMed.
- R. Resta, Rev. Mod. Phys., 1994, 66, 899–915 CrossRef CAS.
- G. Ortiz and R. M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14202–14210 CrossRef CAS PubMed.
- S. Evangelisti, F. Abu-Shoga, C. Angeli, G. L. Bendazzoli and J. A. Berger, Phys. Rev. B, 2022, 105, 235201 CrossRef CAS.
- G. Pescitelli and T. Bruhn, Chirality, 2016, 28, 466–474 CrossRef CAS PubMed.
-
L. A. Nafie, Vibrational Optical Activity: Principles and Applications, Wiley, Hoboken, NJ, USA, 2011 Search PubMed.
-
J. D. Jackson, Classical Electrodynamics, John Wiley & Sons, Nashville, TN, 3rd edn, 1998 Search PubMed.
- F. London, J. Phys. Radium, 1937, 8, 397–409 CrossRef CAS.
- M. Krykunov and J. Autschbach, J. Chem. Phys., 2005, 123, 114103 CrossRef PubMed.
- P. J. Stephens, J. Phys. Chem., 1987, 91, 1712–1715 CrossRef CAS.
- T. Thonhauser, D. Ceresoli, D. Vanderbilt and R. Resta, Phys. Rev. Lett., 2005, 95, 137205 CrossRef CAS PubMed.
-
T. Thonhauser, ArXiv e-prints, 2011.
- J. Shi, G. Vignale, D. Xiao and Q. Niu, Phys. Rev. Lett., 2007, 99, 197202 CrossRef PubMed.
- D. Ceresoli, T. Thonhauser, D. Vanderbilt and R. Resta, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 024408 CrossRef.
- D. Ceresoli and R. Resta, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 012405 CrossRef.
- F. D. M. Haldane, Phys. Rev. Lett., 1988, 61, 2015–2018 CrossRef CAS PubMed.
- J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401 CrossRef.
- T. Thonhauser, D. Ceresoli, A. A. Mostofi, N. Marzari, R. Resta and D. Vanderbilt, J. Chem. Phys., 2009, 131, 101101 CrossRef.
- D. Ceresoli, N. Marzari, M. G. Lopez and T. Thonhauser, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 184424 CrossRef.
- T. Thonhauser, D. Ceresoli and N. Marzari, Int. J. Quantum Chem., 2009, 109, 3336–3342 CrossRef CAS.
- D. Ceresoli, U. Gerstmann, A. P. Seitsonen and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 060409 CrossRef.
- S. Murakami, Phys. Rev. Lett., 2006, 97, 236805 CrossRef PubMed.
- N. R. Cooper and A. Stern, Phys. Rev. Lett., 2009, 102, 176807 CrossRef CAS PubMed.
- A. M. Essin, J. E. Moore and D. Vanderbilt, Phys. Rev. Lett., 2009, 102, 146805 CrossRef PubMed.
- M. Springborg, M. Molayem and B. Kirtman, J. Chem. Phys., 2017, 147, 104101 CrossRef PubMed.
- A. Marrazzo and R. Resta, Phys. Rev. Lett., 2016, 116, 137201 CrossRef PubMed.
-
R. Bianco and R. Resta, ArXiv e-prints, 2015.
- K.-T. Chen and P. A. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195111 CrossRef.
- V. Weber, M. Iannuzzi, S. Giani, J. Hutter, R. Declerck and M. Waroquier, J. Chem. Phys., 2009, 131, 014106 CrossRef PubMed.
- M. Buehl, N. J. R. Van Eikema Hommes, P. V. R. Schleyer, U. Fleischer and W. Kutzelnigg, J. Am. Chem. Soc., 1991, 113, 2459–2465 CrossRef CAS.
- R. Born and H. W. Spiess, Macromolecules, 1995, 28, 7785–7795 CrossRef CAS.
- V. G. Malkin, O. L. Malkina and D. R. Salahub, Chem. Phys. Lett., 1993, 204, 87–95 CrossRef CAS.
- C. van Wuüllen and W. Kutzelnigg, Chem. Phys. Lett., 1993, 205, 563–571 CrossRef.
- T. A. Keith and R. F. W. Bader, Chem. Phys. Lett., 1992, 194, 1–8 CrossRef CAS.
- P. Lazzeretti, M. Malagoli and R. Zanasi, Chem. Phys. Lett., 1994, 220, 299–304 CrossRef CAS.
- N. H. Werstiuk and J. Ma, Can. J. Chem., 1996, 74, 875–884 CrossRef.
- N. Raimbault, P. L. de Boeij, P. Romaniello and J. A. Berger, Phys. Rev. Lett., 2015, 114, 066404 CrossRef CAS PubMed.
- P. R. Rablen, S. A. Pearlman and J. Finkbiner, J. Phys. Chem. A, 1999, 103, 7357–7363 CrossRef CAS.
- D. Skachkov, M. Krykunov, E. Kadantsev and T. Ziegler, J. Chem. Theory Comput., 2010, 6, 1650–1659 CrossRef CAS PubMed.
- H. Fukui, Magn. Reson. Rev., 1987, 11, 205–274 CAS.
- F. Mauri and S. G. Louie, Phys. Rev. Lett., 1996, 76, 4246–4249 CrossRef CAS PubMed.
- F. Mauri, B. G. Pfrommer and S. G. Louie, Phys. Rev. Lett., 1996, 77, 5300–5303 CrossRef CAS PubMed.
- F. Mauri, B. G. Pfrommer and S. G. Louie, Phys. Rev. Lett., 1997, 79, 2340–2343 CrossRef CAS.
- F. Mauri, B. G. Pfrommer and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 2941–2945 CrossRef CAS.
- Y.-G. Yoon, B. G. Pfrommer, F. Mauri and S. G. Louie, Phys. Rev. Lett., 1998, 80, 3388–3391 CrossRef CAS.
- N. T. Maitra, I. Souza and K. Burke, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 045109 CrossRef.
- C. A. Ullrich and G. Vignale, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 245102 CrossRef.
- P. J. Stephens, Annu. Rev. Phys. Chem., 1974, 25, 201–232 CrossRef CAS.
- M. Rérat and B. Kirtman, J. Chem. Theory Comput., 2021, 17, 4063–4076 CrossRef PubMed.
- P. J. Stephens, J. Phys. Chem., 1985, 89, 748–752 CrossRef CAS.
- S. Jähnigen, A. Zehnacker and R. Vuilleumier, J. Phys. Chem. Lett., 2021, 12, 7213–7220 CrossRef PubMed.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
-
N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, Rinehart and Winston, 1976 Search PubMed.
- C. Lee and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14730–14731 CrossRef CAS PubMed.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355–10368 CrossRef CAS.
- R. M. Sternheimer, Phys. Rev., 1954, 96, 951–968 CrossRef CAS.
- S. Ono, L. Trifunovic and H. Watanabe, Phys. Rev. B, 2019, 100, 245133 CrossRef CAS.
- W. A. Wheeler, L. K. Wagner and T. L. Hughes, Phys. Rev. B, 2019, 100, 245135 CrossRef CAS.
- P. L. Silvestrelli and M. Parrinello, J. Chem. Phys., 1999, 111, 3572–3580 CrossRef CAS.
- B. Kang, K. Shiozaki and G. Y. Cho, Phys. Rev. B, 2019, 100, 245134 CrossRef CAS.
- T. Balduf and M. Caricato, J. Chem. Phys., 2022, 157, 214105 CrossRef CAS PubMed.
- S. Jähnigen, A. Zehnacker and R. Vuilleumier, J. Phys. Chem. Lett., 2021, 12, 7213–7220 CrossRef PubMed.
-
G. Vignale, M. Rasolt and D. J. W. Geldart, Advances in Quantum Chemistry, Academic Press, Cambridge, MA, USA, 1990, vol. 21, pp. 235–253 Search PubMed.
- M. Ferconi and G. Vignale, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 14722–14725(R) CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Johann
Mattiat
,
Johann
Mattiat
 and
Sandra
Luber
and
Sandra
Luber
 *
*
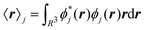
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (0) − εj)|ϕ(1)j〉 = −
(0) − εj)|ϕ(1)j〉 = −![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (1)|ϕ(0)j〉,
(1)|ϕ(0)j〉,![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (0) is the ground state Hamiltonian operator, ϕ(0)/(1)j is an unperturbed/perturbed Molecular Orbital (MO), and
(0) is the ground state Hamiltonian operator, ϕ(0)/(1)j is an unperturbed/perturbed Molecular Orbital (MO), and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (1) is referred to as the perturbation operator. If the perturbation operator leads to real-valued (or complex) perturbed MOs, the effect of the perturbed electron density must be considered during the response calculation. If, on the other hand, the resulting perturbed MOs are purely imaginary and do not contribute to the real space density, no coupling appears in eqn (2) and the equation can in principle be solved for the perturbed orbitals |ϕ(1)j〉 in a single step. In some cases the coupled treatment for the atomic displacements can be avoided, such as the simulation of IR intensities, by employing an analytical CPKS scheme.13
(1) is referred to as the perturbation operator. If the perturbation operator leads to real-valued (or complex) perturbed MOs, the effect of the perturbed electron density must be considered during the response calculation. If, on the other hand, the resulting perturbed MOs are purely imaginary and do not contribute to the real space density, no coupling appears in eqn (2) and the equation can in principle be solved for the perturbed orbitals |ϕ(1)j〉 in a single step. In some cases the coupled treatment for the atomic displacements can be avoided, such as the simulation of IR intensities, by employing an analytical CPKS scheme.13
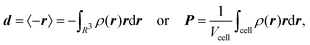
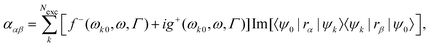
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) LM =
LM = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) − μ·
− μ·![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) ,
,![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) is the system's ground state Hamiltonian operator which is extended by the interaction of the electric dipole moment μ with the electric field
is the system's ground state Hamiltonian operator which is extended by the interaction of the electric dipole moment μ with the electric field ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) . Derivatives of the electronic energy with respect to the electric field thus depend on the electric dipole moment and its derivatives. Often applied theories in this context are time-dependent DFT and perturbation theory, which can also be combined.
. Derivatives of the electronic energy with respect to the electric field thus depend on the electric dipole moment and its derivatives. Often applied theories in this context are time-dependent DFT and perturbation theory, which can also be combined.
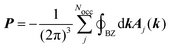
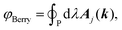
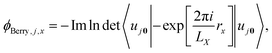
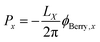
![[U with combining low line]](https://www.rsc.org/images/entities/b_i_char_0055_0332.gif) (k), that defines the Wannier functions
(k), that defines the Wannier functions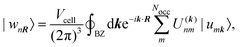
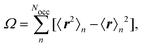
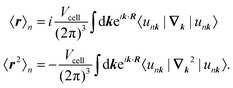
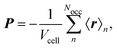
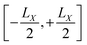 (and analogous for the other two directions). Around the center of this cell, the position operator is defined in the usual way, and at the boundaries the position operator goes from +LX/2 to −LX/2. Whether this change is smooth or abrupt does not matter theoretically because the Wannier function wj(r) is assumed to be zero in this region (see Fig. 1).7 It was shown by Springborg et al. that the saw-tooth operator is not a general solution for the position operator problem in periodic systems.93 This is due to the fact that the saw-tooth operator omits current terms due to the intercellular charge flow as was shown for a one dimensional Hückel model.
(and analogous for the other two directions). Around the center of this cell, the position operator is defined in the usual way, and at the boundaries the position operator goes from +LX/2 to −LX/2. Whether this change is smooth or abrupt does not matter theoretically because the Wannier function wj(r) is assumed to be zero in this region (see Fig. 1).7 It was shown by Springborg et al. that the saw-tooth operator is not a general solution for the position operator problem in periodic systems.93 This is due to the fact that the saw-tooth operator omits current terms due to the intercellular charge flow as was shown for a one dimensional Hückel model.

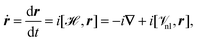
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) nl collects all non-local potentials, such as pseudopotentials, that appear in the Hamiltonian and do not commute with r. The first term in eqn (16) is due to the commutator of the kinetic energy operator with the position operator. Because the operator in eqn (16) is well-defined in PBC, it offers another way for the calculation of the expectation value of the electronic position operator. A property of the operator in eqn (16) is that it is purely imaginary. For this reason, a complex electron density matrix must be employed to obtain non-vanishing expectation values. This can be achieved, for example, by TD-DFT42,97 or imaginary perturbations.98 Additionally, the equality
nl collects all non-local potentials, such as pseudopotentials, that appear in the Hamiltonian and do not commute with r. The first term in eqn (16) is due to the commutator of the kinetic energy operator with the position operator. Because the operator in eqn (16) is well-defined in PBC, it offers another way for the calculation of the expectation value of the electronic position operator. A property of the operator in eqn (16) is that it is purely imaginary. For this reason, a complex electron density matrix must be employed to obtain non-vanishing expectation values. This can be achieved, for example, by TD-DFT42,97 or imaginary perturbations.98 Additionally, the equality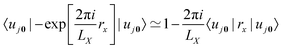
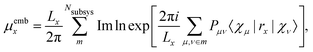
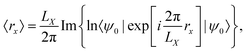
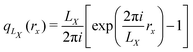
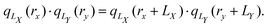
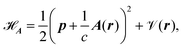
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) (r). The magnetic vector potential for a uniform magnetic field
(r). The magnetic vector potential for a uniform magnetic field ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) depends on r and is given by
depends on r and is given by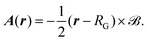
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif)
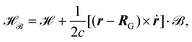
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) is the ground state Hamiltonian that is usually employed, we introduced the gauge origin RG, and ṙ is defined as in eqn (16). In principle, an arbitrary gauge origin can be employed in molecular simulations, due to the gauge freedom of the vector potential which is only defined up to the gradient of a function β(r), called the gauge function.123 The magnetic field can be derived from the magnetic vector potential by
is the ground state Hamiltonian that is usually employed, we introduced the gauge origin RG, and ṙ is defined as in eqn (16). In principle, an arbitrary gauge origin can be employed in molecular simulations, due to the gauge freedom of the vector potential which is only defined up to the gradient of a function β(r), called the gauge function.123 The magnetic field can be derived from the magnetic vector potential by![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) = ∇ × A = ∇ × [A + ∇β(r)].
= ∇ × A = ∇ × [A + ∇β(r)].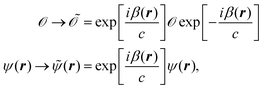
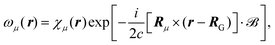
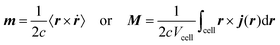
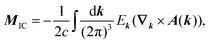
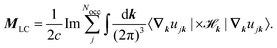
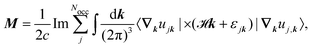
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) k is the k-dependent Hamiltonian operator, Ek is the corresponding total energy, εjk are the orbital energies, and the integrals are taken over the Nocc occupied Bloch orbitals uj,k.6 The formula in eqn (32) is only applicable to noninteracting zero-Chern-number insulators in a vanishing magnetic field,127 although these limitations have been lifted in subsequent publications.129–131 Test calculations have shown that the results obtained from eqn (32) match with the results obtained from finite systems using the Haldane model Hamiltonian.6,132 An important difference compared to eqn (6) is that no quantum of magnetization appears in the modern theory of magnetization and the results are completely defined by eqn (32). The formulas resulting from the modern theory of magnetization have been applied for the calculation of NMR shifts in water133 and a set of small molecules,134 SiO2 polymorphs and an organometallic system,135 and aromatic hydrocarbons.136 Calculations of EPR g tensors were carried out for radicals and paramagnetic defects in solids.137 Other derivatives of the orbital magnetization are related to the quantum spin Hall effect138,139 and the magnetoelectric polarizability,140 among others.128
k is the k-dependent Hamiltonian operator, Ek is the corresponding total energy, εjk are the orbital energies, and the integrals are taken over the Nocc occupied Bloch orbitals uj,k.6 The formula in eqn (32) is only applicable to noninteracting zero-Chern-number insulators in a vanishing magnetic field,127 although these limitations have been lifted in subsequent publications.129–131 Test calculations have shown that the results obtained from eqn (32) match with the results obtained from finite systems using the Haldane model Hamiltonian.6,132 An important difference compared to eqn (6) is that no quantum of magnetization appears in the modern theory of magnetization and the results are completely defined by eqn (32). The formulas resulting from the modern theory of magnetization have been applied for the calculation of NMR shifts in water133 and a set of small molecules,134 SiO2 polymorphs and an organometallic system,135 and aromatic hydrocarbons.136 Calculations of EPR g tensors were carried out for radicals and paramagnetic defects in solids.137 Other derivatives of the orbital magnetization are related to the quantum spin Hall effect138,139 and the magnetoelectric polarizability,140 among others.128
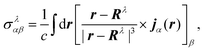
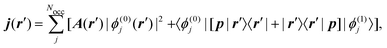
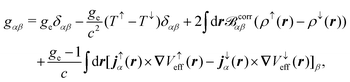
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) corrα in eqn (35) is the magnetic field originating from the induced current density jα
corrα in eqn (35) is the magnetic field originating from the induced current density jα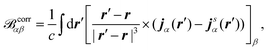
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) L,
L, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) p, and
p, and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) Δi, must be considered which are given by
Δi, must be considered which are given by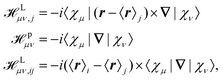
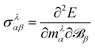
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) 0. By carrying out calculations for different values of q, an extrapolation can be carried out towards the limit q → 0, corresponding to the case of a homogenous magnetic field. This approach was applied to the calculation of the magnetic susceptibility defined as157,158
0. By carrying out calculations for different values of q, an extrapolation can be carried out towards the limit q → 0, corresponding to the case of a homogenous magnetic field. This approach was applied to the calculation of the magnetic susceptibility defined as157,158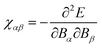
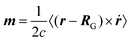
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) μ} – when atom-centered basis functions are employed – and the complete adiabatic Hamiltonian
μ} – when atom-centered basis functions are employed – and the complete adiabatic Hamiltonian ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) CA
CA![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) μ(r) = χμ(r)
μ(r) = χμ(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[i(r − RG)·Ṙμ]
exp[i(r − RG)·Ṙμ]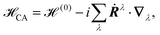
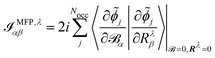
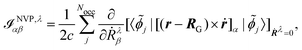
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) j} are the MOs including the gauge factors (see eqn (28) and (42)), and in the MFP, the position operator enters in eqn (44) through the orbitals perturbed with respect to the magnetic field (see eqn (28)), while in the NVP, the position operator enters in eqn (45) through the magnetic dipole moment operator and the orbitals perturbed with respect to nuclear velocities.
j} are the MOs including the gauge factors (see eqn (28) and (42)), and in the MFP, the position operator enters in eqn (44) through the orbitals perturbed with respect to the magnetic field (see eqn (28)), while in the NVP, the position operator enters in eqn (45) through the magnetic dipole moment operator and the orbitals perturbed with respect to nuclear velocities.
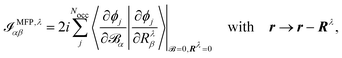
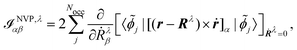
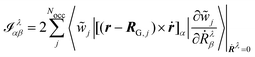
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) j} to obtain the Wannier functions {
j} to obtain the Wannier functions {![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) j}. A natural choice for the gauge origin in periodic systems is the corresponding Wannier center RG,j = 〈r〉j,167 although, as mentioned previously, this is not a general solution for the ill-definition of the magnetic dipole operator in periodic systems. For instance, a theoretical formulation that is gauge-invariant does not imply that the results are correct under PBC.165
j}. A natural choice for the gauge origin in periodic systems is the corresponding Wannier center RG,j = 〈r〉j,167 although, as mentioned previously, this is not a general solution for the ill-definition of the magnetic dipole operator in periodic systems. For instance, a theoretical formulation that is gauge-invariant does not imply that the results are correct under PBC.165
![[H with combining low line]](https://www.rsc.org/images/entities/b_i_char_0048_0332.gif)
![[C with combining low line]](https://www.rsc.org/images/entities/b_i_char_0043_0332.gif) =
= ![[S with combining low line]](https://www.rsc.org/images/entities/b_i_char_0053_0332.gif)
![[C with combining low line]](https://www.rsc.org/images/entities/b_i_char_0043_0332.gif)
![[E with combining low line]](https://www.rsc.org/images/entities/b_i_char_0045_0332.gif) ,
,![[S with combining low line]](https://www.rsc.org/images/entities/b_i_char_0053_0332.gif) , and the electronic energy matrix E. In our case, we define the Hamiltonian matrix, generally, by the matrix elements of the KS Hamiltonian operator
, and the electronic energy matrix E. In our case, we define the Hamiltonian matrix, generally, by the matrix elements of the KS Hamiltonian operator ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) KS as
KS as![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) KS|χν〉 = 〈χμ|
KS|χν〉 = 〈χμ|![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) +
+ ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) |χν〉,
|χν〉,![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is the kinetic energy operator, and we collect all arising potentials in
is the kinetic energy operator, and we collect all arising potentials in ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) . The potential energy operator
. The potential energy operator ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) includes the electrostatic interactions, which are usually calculated via Ewald summation,168 the pseudopotentials, and the DFT exchange–correlation potential. Although hybrid exchange–correlation functionals, including a fraction of exact Hartree–Fock exchange, could be applied, this has not been done so far for the NVPT. The solutions of eqn (49) are the KS-MO coefficients Cj for the jth KS orbital (ϕj) from which the real space electron density n(r) is calculated as
includes the electrostatic interactions, which are usually calculated via Ewald summation,168 the pseudopotentials, and the DFT exchange–correlation potential. Although hybrid exchange–correlation functionals, including a fraction of exact Hartree–Fock exchange, could be applied, this has not been done so far for the NVPT. The solutions of eqn (49) are the KS-MO coefficients Cj for the jth KS orbital (ϕj) from which the real space electron density n(r) is calculated as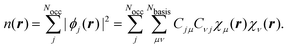
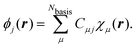
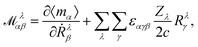
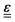 is the Levi-Civita symbol, c is the speed of light in atomic units, and the sums in eqn (54) go over the atoms λ and the Cartesian directions γ. The magnetic dipole moment operator (eqn (41)) is defined in terms of the electronic position operator r and the electronic velocity operator ṙ (eqn (16)). The latter is calculated as the Heisenberg time derivative of the electronic position operator.94,96 Within a static approach in the harmonic approximation, the VCD spectrum of a system is defined in terms of the vibrational normal mode frequencies {ωv} and the rotational strengths {Rv} that are given by
is the Levi-Civita symbol, c is the speed of light in atomic units, and the sums in eqn (54) go over the atoms λ and the Cartesian directions γ. The magnetic dipole moment operator (eqn (41)) is defined in terms of the electronic position operator r and the electronic velocity operator ṙ (eqn (16)). The latter is calculated as the Heisenberg time derivative of the electronic position operator.94,96 Within a static approach in the harmonic approximation, the VCD spectrum of a system is defined in terms of the vibrational normal mode frequencies {ωv} and the rotational strengths {Rv} that are given by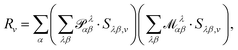
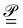 is the Atomic Polar Tensor (APT),170,171
is the Atomic Polar Tensor (APT),170,171![[S with combining low line]](https://www.rsc.org/images/entities/b_i_char_0053_0332.gif) v is the mass-weighted transformation matrix from Cartesian coordinates to normal mode coordinates, and
v is the mass-weighted transformation matrix from Cartesian coordinates to normal mode coordinates, and 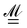 ist the AAT as defined in eqn (54).
ist the AAT as defined in eqn (54).
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) CA (see eqn (43)) in combination with velocity-gauge including atomic orbitals (see eqn (42)).25,98 The basis functions in eqn (42) can be Gaussian-type orbitals, Slater-type orbitals, or numerical basis functions. A perturbative expansion of the generalized eigenvalue equation (eqn (49)) leads to the Sternheimer equation23,172
CA (see eqn (43)) in combination with velocity-gauge including atomic orbitals (see eqn (42)).25,98 The basis functions in eqn (42) can be Gaussian-type orbitals, Slater-type orbitals, or numerical basis functions. A perturbative expansion of the generalized eigenvalue equation (eqn (49)) leads to the Sternheimer equation23,172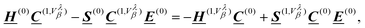
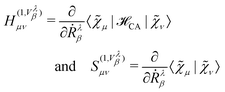
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) α) when GIAOs124 are employed. Comparing eqn (57) and (42) it becomes clear, that the position operator enters into the derivatives of the Hamiltonian and overlap matrix. Even though the KS Hamiltonian matrix elements (see eqn (50)) fulfill the Born-von Kármán boundary conditions, this is not the case for the Sternheimer equation due to the arising position operators.
α) when GIAOs124 are employed. Comparing eqn (57) and (42) it becomes clear, that the position operator enters into the derivatives of the Hamiltonian and overlap matrix. Even though the KS Hamiltonian matrix elements (see eqn (50)) fulfill the Born-von Kármán boundary conditions, this is not the case for the Sternheimer equation due to the arising position operators.
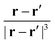
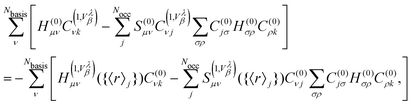
![[S with combining low line]](https://www.rsc.org/images/entities/b_i_char_0053_0332.gif) from the generalized eigenvalue equation (eqn (49)). The overlap matrix derivative still appears in eqn (56), though, and contributes a position operator-dependent phase factor.
from the generalized eigenvalue equation (eqn (49)). The overlap matrix derivative still appears in eqn (56), though, and contributes a position operator-dependent phase factor.