Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding catalytic CO2 and CO conversion into methanol using computational fluid dynamics†
Stylianos
Kyrimis
 ,
Matthew E.
Potter
,
Matthew E.
Potter
 ,
Robert
Raja
,
Robert
Raja
 * and
Lindsay-Marie
Armstrong
* and
Lindsay-Marie
Armstrong
 *
*
University of Southampton, University Road, Highfield, Southampton, SO17 1BJ, UK. E-mail: r.raja@soton.ac.uk; l.armstrong@soton.ac.uk
First published on 28th January 2021
Abstract
The kinetics of methanol synthesis from a mixture of CO2/CO/H2 have been widely studied in the literature. Yet the role of direct CO hydrogenation is still unclear, in terms of predicting and developing an accurate kinetic model. To investigate, a computational fluid dynamics model has been developed, incorporating two distinct kinetic models, one which includes CO hydrogenation and one which does not. Including CO hydrogenation in the kinetic model provides a more complex interaction between the three involved reactions and can better predict potential inhibitions caused by the presence of H2O. This, however, increases the complexity of the kinetic model. The benefit of applying a fluid dynamics model to study fixed bed reactors is demonstrated, as it offers unique insights into the spatial species concentration, temperature variations, and reaction rate magnitudes. The validated model is shown to be a powerful interrogative tool, capable of supporting system optimization across the catalyst and reactor engineering sectors.
Introduction
Increasing greenhouse gas emissions continually motivate research into offsetting anthropogenic emissions. Carbon Capture and Utilisation (CCU) has great potential in the long-term mitigation of CO2 emissions,1 especially when applied to the large scale production of fuels or bulk chemicals, such as the methanol (MeOH) economy concept, outlined by Olah et al.2 Here, captured CO2 can act as a MeOH feedstock, either through its direct hydrogenation, eqn (1), or through a two-step process where CO is initially produced through the Reverse Water–Gas Shift (RWGS) reaction, eqn (2), followed by subsequent CO hydrogenation to MeOH, eqn (3). By nature, the forward rate of all three reactions is exothermic, while their reverse rate is endothermic.| R1: CO2 + 3H2 ↔ CH3OH + H2O, −49.2 kJ mol−1 | (1) |
| R2: CO + H2O ↔ CO2 + H2, −41.2 kJ mol−1 | (2) |
| R3: CO + 2H2 ↔ CH3OH, −90.8 kJ mol−1 | (3) |
Due to its use as an energy resource, solvent, and chemical precursor,3–5 around 40 million tons of MeOH are produced annually.4 The vast majority is produced from a mixture of CO2/CO/H2 at temperatures of 200–300 °C and pressures above 30 bar.4,6 Typically, this is achieved with a multi-component Cu/ZnO/Al2O3 catalyst, where metallic Cu acts as a binding site for CO2 and/or CO and ZnO acts as a binding site for H2/H2O.7–9 Despite significant work, MeOH synthesis is challenging to control, as it is governed by the equilibria of the involved reactions, eqn (1)–(3). Because of its importance, research on MeOH synthesis from CO2/CO is diverse and has focused on areas such as the impact of different catalyst synthesis processes,10,11 alternative and optimized catalysts for increased selectivity and conversion,12–18 catalyst sintering and recovery,19,20 and optimal operating conditions.21–23 Another key area is the design and optimization of the reactor itself, which is particularly important when employing large-scale reactors.24–27 Scaling up chemical reactors can prove challenging, especially regarding management of the inherent heat and mass transfer effects. In highly exothermic reactions, such as MeOH synthesis, effective heat transfer is crucial to avoid catalyst sintering and/or runaway conditions.22,26 Investigating such processes typically requires either costly large scale demonstration experiments, or theoretical investigations.
Computational Fluid Dynamics (CFD) models have been instrumental in supporting the scale up modelling of different chemical reactor types, such as fixed bed,28,29 thermochemical30,31 and fluidised bed32,33 reactors. Apart from their potential as a reactor design and optimization tool, CFD models also have many benefits as an investigation tool. Unlike DFT,34–37 Aspen,9,38 and Matlab8,21,39 models, CFD considers local variations in flow properties, such as temperature, pressure, and diffusion, along with species concentrations, to evaluate chemical reactions. In addition, CFD models offer a dynamic, in situ representation of the distribution, conversion and spatial transfer of chemical species. Working alongside experiments, they have the potential to guide novel catalyst and/or reactor design. As with any model, the accuracy of the CFD simulations depends on the methodology and assumptions considered for the different transfer effects. As such, before being applied, initial validation with available experimental data is crucial.
Key aspects of MeOH synthesis investigations are the precise mechanisms and kinetics, which have been a controversial topic in the literature.
One of the earlier arguments questioned whether CO or CO2 was the carbon source for MeOH. Isotope labelling studies concluded that MeOH is produced mainly from CO2, while CO hydrogenation, eqn (3), is comparatively small.40–42 This has also been confirmed by different studies.23,34 With this realisation, the perceived role of CO hydrogenation became less important when developing kinetic models (KMs) for MeOH synthesis. In fact, some KMs chose to omit it entirely, instead focussing purely on eqn (1) and (2). The exclusion of direct CO hydrogenation seems counter-intuitive, since CO hydrogenation, while less impactful than CO2 hydrogenation, can still occur. Its significance, however, varies greatly in the literature; as an example, Grabow and Mavrikakis34 predicted ∼1/3 of MeOH being produced from CO, while Sahibzada et al.23 predicted that MeOH synthesis from CO2 may be 20 times higher than MeOH synthesis from CO. Grabow and Mavrikakis34 investigated the Cu(111) surface of the commercial catalyst, while in the DFT study of Higham et al.,37 the Cu(110) and the Cu(100) facets were investigated instead; it was identified that the Cu(110) and Cu(100) facets could be even more active for CO2 dissociation into CO and subsequent hydrogenation to MeOH37 compared to the Cu(111) facet, yet the impact of CO hydrogenation in MeOH synthesis was not defined. Wilkinson et al.43 investigated the species concentration at different lengths along the catalytic bed, by having different catalyst loads in the reactor each time. The conclusions seem to indicate that the Forward Water–Gas Shift (FWGS) reaction followed by MeOH synthesis is a more favourable pathway for CO compared to direct hydrogenation. It is easy to see from these reports that to date, there is still no definitive consensus on how impactful CO hydrogenation is in MeOH synthesis.
Another uncertainty concerned the active catalytic site for CO and CO2 adsorption. Graaf et al.7,44 introduced a KM based on a dual-site Langmuir–Hinshelwood mechanism, where CO and CO2 adsorb competitively on the first site and H2 and H2O adsorb competitively on the second site. Graaf’s KM has since become one of the most widely used models for MeOH synthesis kinetic investigations,6,12,13,25,38,45 even though it is known to underestimate experimental MeOH synthesis rates.6 However, different studies proposed that CO and CO2 follow a non-competitive route to MeOH, with CO adsorbing on Cu1+ sites and CO2 adsorbing on Cu0 sites.8,23 Based on this, Park et al.46 proposed an alternative KM, as shown in eqn (4)–(6) which refer to reactions R1–R3 in eqn (1)–(3), respectively. In this KM, CO2 and CO hydrogenation rates (eqn (4) and (6), respectively) are independent from one another. To define the kinetic constants, the authors ran an extensive experimental session with the commercial Cu/ZnO/Al2O3 catalyst in a fixed bed reactor, by varying the CO/CO2/H2 feed composition, total flow rate, operating temperature and pressure.
Kinetic model from Park et al. : 46
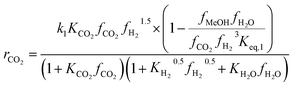
| (4) |
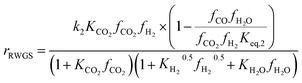
| (5) |
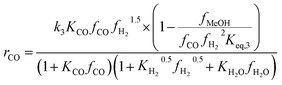
| (6) |
Park’s KM was validated in a subsequent paper, where it was integrated into a CFD model, with the focus on investigating the thermal behaviour of a fixed bed reactor.47 As a result of these findings, the authors proposed an alternate bayonet-type reactor be used, which demonstrated an enhanced thermal profile, reducing the peak temperature reached in the bed, and achieving a higher MeOH conversion. Their study demonstrated how CFD can guide experimental procedure. In another recent paper, a hybrid Cu/ZnO/Al2O3–ferrierite catalyst, used for direct DME synthesis from syngas via a MeOH intermediate, was investigated.48 The study incorporated Park’s KM into a Matlab code which investigated the mechanistic implications of the hybrid catalyst, thus identifying MeOH synthesis as the primary rate controlling step whilst complementing the experimental study. This required the kinetic constants of Park’s reaction rates to be re-evaluated for this new hybrid catalyst.
Another widely studied KM,49–51 proposed by Bussche and Froment,52 assumed all reactions to occur only on the Cu catalytic sites. Here, CO hydrogenation is omitted, as MeOH is assumed to be exclusively synthesised from CO2. In this KM, CO participates only through the FWGS reaction, serving as a CO2 precursor for subsequent conversion to MeOH.
To identify which of the available models is better suited to predicting experimental results, several studies have compared them. Nestler et al.53 and Wilkinson et al.43 both compared the Bussche and Graaf KMs, but did not consider Park’s KM.46 Both concluded that Bussche’s KM is more accurate, as the kinetic constants of Graaf’s model were derived for an older, less active version of the commercial MeOH synthesis catalyst.53 Following this, Nestler et al.53 insisted that these KMs are only suitable for the specific range of pressures, stoichiometric numbers and CO/CO2 ratios from which they were derived. They should not be extrapolated outside this range to minimise the simulation errors. Here, an alternative KM was also proposed using eqn (7) and (8), by applying a parameter fitting to the experimental data set produced by Park et al.46 Nestler’s KM was established to be applicable to a wide range of industrially relevant MeOH synthesis operating conditions, specifically a pressure range of 50–80 bar, temperature range of 473–593 K, and a varying range of CO2, CO, and H2 feed compositions, including pure CO2 feeds with no initial CO content.53 Similar to Bussche’s model, Nestler’s KM does not consider direct CO hydrogenation, yet CO adsorption on an active site is considered.
Kinetic model from Nestler et al. : 53
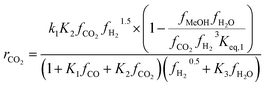
| (7) |
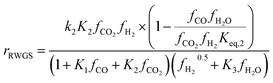
| (8) |
On first sight, the main difference between Park’s KM (eqn (4)–(6)) and Nestler’s KM (eqn (7) and (8)) is the inclusion of CO hydrogenation. Yet, they also have some additional mechanistic differences. The denominator of both KMs represents the adsorption of species on the active sites; as previously stated, Park’s KM, eqn (4)–(6), considers CO2 and CO to have two distinct sites, as the adsorption of one is independent from the adsorption of the other, i.e. the denominator of rCO2 depends only on CO2 while the denominator of rCO depends only on CO. Nestler’s KM, eqn (7) and (8), considers a common catalytic adsorption site for CO and CO2, as the denominator of rCO2 depends on the fugacity, here assumed to be equal to the partial pressure, of both CO2 and CO. Both models consider a common site for H2 and H2O. The reaction rate of the RWGS reaction is dependent only on the adsorption of CO2 in Park’s KM, while Nestler’s KM considers both CO and CO2. Overall, Park’s KM considers three distinct active sites, while Nestler’s KM considers two.
As previously mentioned, CFD models can be used as an investigative tool, since their predicted flow profile can indicate the trends and the mechanisms of chemical reactions. In our previous work, one such CFD model was applied to study ethanol dehydration to ethylene on a fixed bed reactor using a SAPO-34 catalyst.54 By combining experimental and CFD studies, it was possible to identify the preferable mechanistic pathway of ethanol dehydration. Here, the previously presented CFD model will be adapted and applied to investigate the kinetic mechanisms of MeOH synthesis, using the KMs of Park and Nestler. To compare and validate the two KMs, in terms of species interactions and shifts in the chemical equilibrium, the experimental results previously presented by Park et al.46 will be used. The validation in this paper will focus mainly on the mechanistic implications of changing the composition of the feed gas, rather than the operating temperature, flow rate, and pressure. Thus, only the experimental runs with temperature of 523 K, flow rate of 8000 mL gcat−1 h−1, and pressure of 50 bar are considered. Noticeably, both models were derived by fitting their parameters to the same experimental setup and results, those of Park et al.,46 yet they assume different reaction mechanisms and roles for CO. Identification of the strengths and internal inconsistencies in these mechanisms can provide key information regarding the impact of CO hydrogenation in MeOH synthesis.
Computational model
In this section, the computational geometry, which is based on the experimental setup of Park et al.,46 will be presented. In addition, the methodology used to implement diffusion transfer and the KMs of Park and Nestler are analysed. Details of the computational theory and the setup of the porous medium, the boundary conditions, and the solution setup are presented in the ESI.†Computational geometry
The Ansys® Academic Research, release 2019 R2, simulation software was used for this study, with Fluent as the computational code. A 3D cylindrical geometry was designed with the same dimensions as the fixed bed used in the experimental setup of Park et al.,46 where 0.4 g of Cu/ZnO/Al2O3 catalyst (assumed density 1775 kg m−3)52 was loaded in a 7 mm inner-diameter reactor tube. The estimated height for the cylindrical packed bed, based on the aforementioned density and the estimated volumetric porosity (see ESI†), is 15.6 mm. In the experimental setup, the catalyst was diluted with 1.2 g of inert Al2O3 as a means to limit the exothermicity of the reaction. These inert species will also affect the flow dynamics and overall pressure drop along the packed bed. However, implementing the inert Al2O3 diluent into the current porous medium model would increase the complexity of the code, since inert species should be defined as unreactive computational elements, homogeneously mixed with reactive elements. Thus, in the considered geometry, these inert species were not considered. The generated mesh consists of cubic elements of 0.1 mm in size, resulting in a total of 627k elements. The schematics of the reactor, along with the generated mesh, are presented in Fig. A1 of the ESI.† In addition, a mesh independency study is also presented in the ESI.† This study, apart from justifying the decision for the chosen mesh element size, also indicates the refinement necessary to accurately capture the flow characteristics while minimizing errors and/or computational time.A steady-state simulation was considered, with laminar conditions assumed, since the estimated Reynolds number is ≤15. This aligns with the classification of “steady laminar inertial flow” for packed beds as outlined by Dixon et al.55
Diffusion transfer
Inter and intra-particle diffusion transfer is a key parameter in chemical systems, as it is inherently connected to the reaction regime. Diffusion transfer within a catalytic bed follows three distinct mechanisms, as described by Krishna:56 (a) bulk diffusion, (b) Knudsen diffusion, and (c) surface diffusion. Bulk diffusion refers to the transport of species within the empty space of the porous network. It is governed by the relative motion of individual species of a mixture, i.e. molecular collisions, based on their concentration gradients and diffusion coefficients.56,57 Knudsen diffusion refers to diffusion transfer of species in the proximity of the catalyst surface or in intra-particle space, and is governed by molecule–catalytic surface collisions.56 Finally, surface diffusion refers to the adsorption and diffusion/migration of molecular species on the catalyst active sites.56 As all three diffusion mechanisms impact the flow profile and the reaction mechanisms, they should be implemented in the CFD solution.The porous medium model of Fluent does not consider the existence of solid catalytic particles.58 Each computational element is considered to be an entirely homogeneous “fluid” zone with a momentum sink applied, as a result of the existence of pores, rather than having dedicated fluid and solid subzones. Unfortunately, this restriction does not allow the definition of intra-particle space.
Catalytic particles smaller than 0.35 mm, and especially of the size considered here, 0.2 mm, do not suffer from intra-particle diffusion limitations.13,44 As such, the reaction is governed by the kinetics, where external mass transport is key,59 so a volumetric diffusion transfer approach, such as the one offered by Fluent, is not unreasonable. For an accurate and realistic flow profile, however, both bulk and Knudsen diffusion transfer must still be considered; it has been observed that Knudsen diffusivity predominates at lower pressures (10 bar), while bulk diffusivity predominates at higher pressures (100 bar).44 In the considered experimental runs of Park et al.,46 the operating pressure is 50 bar, so both diffusion mechanisms will contribute. Regarding the third diffusion mechanism, surface diffusion, the studied KMs were defined by considering the adsorption of species on active sites. Thus, even though migration of adsorbed species on neighbouring sites is not individually accounted for, surface diffusion mechanisms are already implemented in the reaction kinetics.
While Fluent’s code considers bulk diffusivity,60 its user-interface (UI) does not directly allow the combination of bulk and Knudsen diffusivities. Dixon et al.61–63 carried out a discrete element CFD model which combined the bulk and Knudsen diffusivities in the form of the dusty-gas diffusion correlation, initially introduced by Hite and Jackson.64 This was possible through the use of Fluent’s scalar equation theory. A similar methodology to that of Dixon et al.61–63 is considered here as well. The methodology to implement it into the CFD model is presented in detail in the ESI.†
Chemical reactions
Chemical reactions are applied volumetrically through User-Defined Functions (UDFs), i.e. external user codes, as a source term in the conservation equation of the scalar quantities (see ESI†). This source term is dependent on the reaction rate defined in the considered KMs of Park and Nestler, and follows the general equation form for chemical reactions60 in Fluent: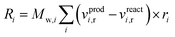 | (9) |
The reaction source term in Fluent, eqn (9), is applied in units of kg m−3 s−1, so the reaction rate constants calculated from the respective KMs should be modified accordingly.
The reaction constants follow the form of Arrhenius equations, and their values are presented in the ESI† for both KMs. The equilibrium constants for the reaction rates, Keq,1, Keq,2, and Keq,3, are taken from Graaf and Winkelman.65 They are also presented in the ESI.†
In Fluent’s code, it is common practice to define the carrier gas, argon in this case, as the bulk species.58 The bulk species mass fraction is always such that the mass balance of species is preserved, meaning that the sum of all species mass fractions doesn’t go above unity. For the scalar quantities, however, the conservation law is not ensured, and it must be enforced, as both diffusion and chemical reaction sources are applied directly on the scalar equations. Two mass balance conservation conditions are considered at the end of each iteration, one which forces the sum of all 6 scalars (φCO2, φCO, φH2, φH2O, φMeOH, φAr) to be equal to unity and a secondary one which forces the reactant and the product scalars to be equal to the initial mass fraction of the feedstock (φCO2/φCO/φH2). After the conservation law is applied, the species mass fractions are replaced with the values of the scalar quantities, i.e. Yi = φi, to complete the iteration.
The experimental runs considered from Park et al.46 are presented in Table 1. The stoichiometric number, SN, and the carbon oxide ratio, COR, are defined as follows:53
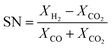 | (10) |
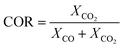 | (11) |
| Composition of feed gas | Mass fractions [%] | SN | COR | |||
|---|---|---|---|---|---|---|
| CO2 | CO | H2 | Ar | |||
| Feed 13 | 77.6 | 0.0 | 10.7 | 11.7 | 2 | 1 |
| Feed 14 | 52.1 | 22.8 | 10.3 | 14.8 | 1.96 | 0.59 |
| Feed 15 | 37.4 | 36.8 | 10.4 | 15.4 | 2 | 0.39 |
| Feed 23 | 33.4 | 37.8 | 11.9 | 16.9 | 2.44 | 0.36 |
| Feed 25 | 29.0 | 33.2 | 22.0 | 15.8 | 5.57 | 0.36 |
| Temperature: 523 K, pressure: 50 bar, space velocity: 8000 mL gcat−1 h−1 | ||||||
A selection of cases taken from Park et al.46 were chosen to focus on. The selected feeds cover a range of SN and COR numbers. Feeds with 0 mol% CO2 were not considered, as the model of Nestler was derived by excluding these feeds.
Results
Model validation
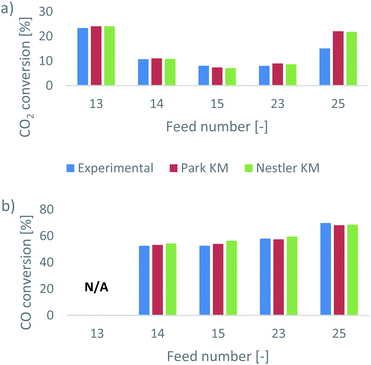
Park et al.46 presented their results as CO2 and CO conversions at the outlet of the reactor. In addition, they identified whether equilibrium was reached for the feed gas compositions or not. This information can be used to validate the two kinetic models. The comparative results, presented as the experimental and predicted CO2 and CO conversions at the outlet, are shown in Fig. 1. In Tables A3 and A4 of the ESI,† the expected outlet mass fractions of CO2 and CO, respectively, based on the experimental conversions, are presented, alongside the respective predictions and relative errors of the two KMs. For feed 13, calculating the CO conversion is not applicable, as the initial CO content is 0; the presented conversions are calculated based on the difference between the final and the initial mass fractions of the species.Interestingly, both KMs present a very good agreement with the experimental results, for a range of different feed compositions. Overall, Nestler’s KM has a smaller error in its CO2 prediction and a larger error in its CO prediction, compared to Park’s KM (Tables A3 and A4, ESI†). Specifically, Nestler’s KM tends to overestimate the CO conversion. Larger overall errors for both models appear only in feed 25, where the SN increases. It appears that while both models have a similar accuracy when the CO2/CO ratio changes, this is not the case for when the SN changes. Still, however, the error for both models is well below 10% in all cases. Nestler’s KM was defined for an SN ratio of up to 3.5,53 so feed 25, with an SN ratio of 5.6, falls outside its definition range. Therefore, the result that Nestler’s KM has a smaller error compared to Park’s KM in feed 25 further supports the authors’ claim that this model can be accurately applied to a wide range of industrially relevant operating conditions.
According to the experimental results of Park et al.,46 feeds 13 and 15 do not reach equilibrium, while the remaining three feeds do. To identify if the models can predict equilibrium as well, the mass fractions of the species along the axial direction of the reactor are investigated, as predicted from the two KMs. These are all presented in the ESI,† in the dedicated results section for each feed.
The equilibrium depth varies along the bed as a result of the feed composition and of the considered KM. For feed 13 (Fig. A2 in the ESI†), Park’s KM predicts that equilibrium is reached early in the bed, while in Nestler’s KM, the species have almost reached equilibrium by the exit of the reactor, as indicated by the upward trends of MeOH and of H2O. On the other hand, for feed 15 (Fig. A13, ESI†), the opposite is true; Nestler’s KM predicts an early equilibrium depth, while equilibrium is not reached in Park’s KM. In most other cases, equilibrium is reached for both models, but Nestler’s KM predicts equilibrium slightly earlier in the catalytic bed compared to Park’s KM.
It is noteworthy that while the exit compositions predicted from the two KMs are almost identical, the predicted species profiles within the reactor differ significantly. As such, a simple prediction of the exit CO2/CO conversions and whether or not equilibrium is reached leads to a valuable comparison. Yet, without non-invasive in situ composition tracking of the experimental setup, it is hard to validate the two profiles. The two models reach comparable outlet results by following discrete reaction mechanisms, and the disparities in the CO prediction are not sufficient to prefer one model over the other. For this purpose, the flow and reaction profiles within the catalytic bed should be examined and compared for the two KMs, which is an additional benefit offered by CFD models. Through this investigation, the predicted favourable mechanistic pathways can be evaluated according to kinetic studies available in the literature. This can evaluate the validity of the considered reaction mechanisms and identify potential weaknesses in the available models. For this investigation, two different feed compositions were selected, feed 23 and feed 13. The latter is important to consider as well, as pure CO2 feeds with no initial CO content are important for CCU studies.
Flow profile within the catalytic bed: feed 23
The species mass fractions along a 2D plane surface in the centre of the reactor are presented in Fig. 2 for feed 23. In addition, the rates of reactions R1–R3, in terms of CO2 (R1 and R2) and CO (R3) rate of change, are presented in Fig. 3. Here a positive rate of change is associated with the production of that species, whereas a negative rate of change refers to its consumption. Specifically for R2, a negative rate is associated with the RWGS pathway (CO2 consumption).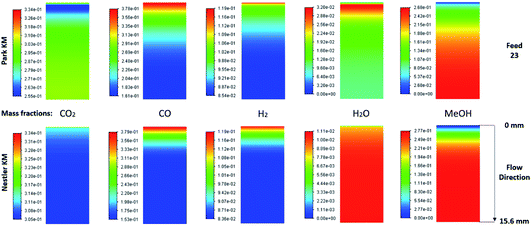 | ||
| Fig. 2 Mass fractions of species along a 2D plane surface in the centre of the reactor for feed 23, predicted from both KMs. | ||
 | ||
| Fig. 3 Rates of reaction for feed 23, predicted from (a) Park’s KM for CO2 (R1 and R2) and CO (R3) and from (b) Nestler’s KM for CO2 (R1 and R2). | ||
Nestler’s KM predicts that the rate of CO2 hydrogenation and the rate of FWGS reaction are of similar magnitude. The species reach equilibrium early in the bed, with CO almost instantly compensating the amount of CO2 consumed for MeOH synthesis.
In Park’s KM, for CO, its conversion to CO2 is a more favourable pathway than its direct hydrogenation to MeOH. Surprisingly, the mass fraction of H2O follows an inverse relationship to that of CO2; H2O reaches a peak value early in the bed, followed by its consumption, along with CO, in the FWGS reaction to supply enough CO2 for MeOH synthesis. The rate of CO2 hydrogenation is quite high near the entrance, thus producing MeOH and H2O. This leads to a big spike in the maximum H2O mass fraction, which is almost triple the respective value predicted from Nestler’s KM (Fig. 2). This sudden peak in H2O inhibits MeOH synthesis from CO2 and drives the FWGS reaction, as seen from the relative magnitudes of the rates of change of reactions R1 and R2. The inhibitory effect of H2O in the MeOH synthesis reaction is well known, as it has a detrimental effect on the equilibrium.4,7,23,42
In this case, the outlet mass fractions of the different species predicted from the two models have a much larger variation compared to those of feed 13. Nestler’s KM predicts 5% less CO and H2O and 3.1% more MeOH at the exit of the reactor, compared to Park’s KM, so the inhibitory effect of H2O is not as pronounced in Nestler’s case.
The local temperature variations in the centreline of the reactor, for feed 23, are presented in the ESI (Fig. A19†). The temperature values correspond to the local variation from the 523 K operating temperature. In addition, the energy released specifically from chemical reactions is also shown (Fig. A20 and A21†), with positive energy release associated with an energy source or exothermicity, and negative energy release associated with an energy sink or endothermicity. Both KMs predict a similar temperature profile, with a local temperature increase early in the bed, where the magnitudes for the exothermic reactions, MeOH synthesis-R1 and FWGS-R2, are the highest. Interestingly, Nestler’s KM predicts a higher local temperature variation profile, despite omitting CO hydrogenation, which is the most exothermic reaction. Park’s KM predicts that the magnitude of the CO hydrogenation rate is much smaller compared to the other two reactions early in the bed (Fig. 3), however, due to its significant exothermicity (−90 kJ mol−1), its contribution as an energy source is even larger than that of the FWGS reaction (Fig. A20 in the ESI†). As with all feeds, with the exception of the temperature variation predicted from Nestler’s KM for feed 13, the hotspot location is early in the catalytic bed.
Flow profiles within the catalytic bed: feed 13
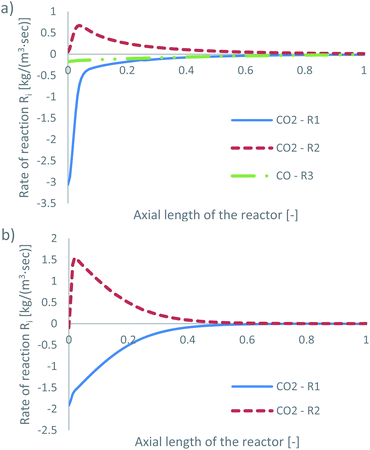
The species mass fractions along a 2D plane surface in the centre of the reactor are presented in Fig. 4 for feed 13, which has no CO in the initial feed. The rates of reactions R1–R3, in terms of CO2 (R1 and R2) and CO (R3) rate of change, are presented in Fig. 5.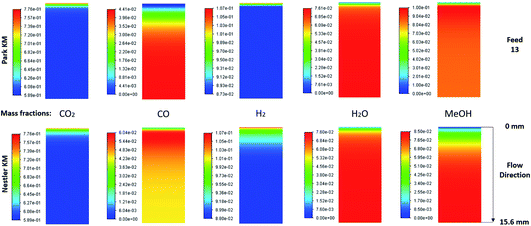 | ||
| Fig. 4 Mass fractions of species along a 2D plane surface in the centre of the reactor, for feed 13, predicted from both KMs. | ||
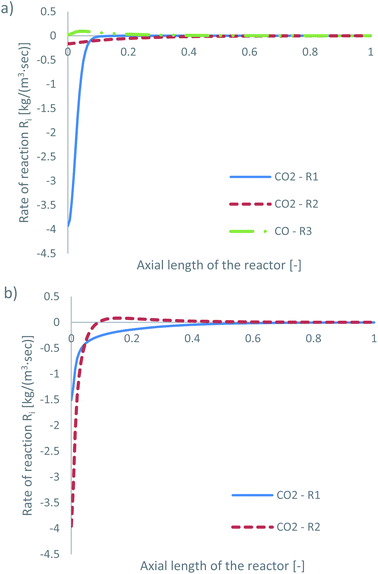 | ||
| Fig. 5 Rates of reaction for feed 13, predicted from (a) Park’s KM for CO2 (R1 and R2) and CO (R3) and from (b) Nestler’s KM for CO2 (R1 and R2). | ||
Park’s KM predicts that CO2 hydrogenation is more important early in the bed, causing MeOH to reach a peak value before being consumed to produce CO. Specifically, CO is produced evenly from RWGS (52.87%) and MeOH decomposition (47.13%), while no CO is consumed in this case to produce MeOH. However, Nestler’s KM predicts that initially the RWGS reaction dominates with a higher rate than CO2 hydrogenation. In this KM, the peak CO concentration is predicted to be early in the bed, followed by its consumption in the FWGS reaction. Unsurprisingly, in both models, at 0 mol% initial CO concentration, production of CO takes priority, as opposed to MeOH production. This confirms the observations in the literature that low CO mixtures are not as effective for MeOH synthesis.13,39
Kunkes et al.66 showed, through H/D isotope substitution experiments, that CO is not produced from MeOH decomposition, but instead only through the RWGS reaction. Though in their work, the feed gas composition included both CO and CO2 with concentrations of 6% and 8%, respectively. In all other feeds where CO is initially present in the feed gas, CO is not produced from MeOH decomposition but only through the RWGS reaction. As such, the possibility that MeOH decomposes to form CO, in the absence of CO, cannot be dismissed. A parametric study to investigate how the initial mass fraction of CO in the feed affects the rate of MeOH synthesis/decomposition for R3 will be presented in a following section.
The local temperature variation in the centreline of the reactor, for both KMs, is presented in the ESI (Fig. A3†). The energy released by the chemical reactions is also shown in Fig. A4 and A5 of the ESI.† As predicted from Park’s KM, a large amount of energy is released early in the bed, due to the exothermic nature and significant magnitude of R1. As the rates of the RWGS and of MeOH decomposition for CO production, i.e. reverse R3, are much smaller compared to that of R1, their endothermicity cannot balance the exothermicity of R1, causing a temperature increase early in the bed. Deeper into the bed, the reaction rate magnitudes of all three reactions drop, along with the local temperature variation. Nestler’s KM predicts a significantly different local temperature variation profile; since the RWGS reaction, R2, is the only reaction which produces CO in Nestler’s KM, its magnitude is larger early in the bed compared to that of MeOH synthesis, R1. This results in an overall energy sink and a local temperature decrease.
When examining the 2D plane surface of the temperature variation, Fig. A3,† uneven local variations were observed in Nestler’s case; specifically, variations where both the radial and the axial temperature present random fluctuations that don’t match the species flow profile (Fig. 4) and the reaction rate profile (Fig. 5). Such profiles are usually associated with numerical errors, mainly caused by mesh quality. Yet, all other feed compositions for both KMs, including feed 13 with Park’s KM, present a uniform temperature variation profile with a smooth transition, which follows their respective species flow profiles. To investigate further the reason for this numerical error, and to eliminate the possibility that mesh quality was the reason for the inaccuracies, a mesh independency study was performed for feed 13 as well. Following the same procedure as the mesh independency study presented in the ESI,† a total of 5 different meshes are investigated, with total mesh element counts of roughly 100k, 300k, 600k (baseline), 900k and 1200k. The temperature variation profiles along the 5 different meshes are presented in Fig. 6. In all five cases, Park’s KM presents a smooth temperature transition along the bed. In Nestler’s KM, however, the fluctuating temperature profile not only persists but also changes across the different mesh cases. It is important to identify the source of the temperature profile difference between the two KMs, as it can be caused by a variety of reasons.
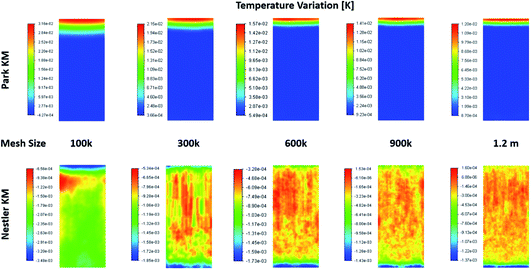 | ||
| Fig. 6 Temperature variation profiles along a 2D plane in the centre of the reactor, predicted from the two KMs, according to the total mesh size. | ||
One reason could be the existence of reverse flow at the outlet of the reactor, observed in Nestler’s KM (Fig. 6), which affects the local temperature variation. A description of what the reverse flow is and how it affects the flow is presented in the mesh independency study in the ESI.† In sum, it is limited only in the near-outlet region, above the 0.9 axial length of the reactor, and its impact is negligible in the flow profile of the main catalytic body. Thus, it cannot be the reason for the inconsistent temperature profile observed along the catalytic bed. In addition, poor mesh quality can also be excluded as a potential cause, as the mesh quality of the 600k mesh is sufficient to minimize numerical errors (see ESI†). These conclusions allow us to eliminate the possibility that the temperature fluctuations are caused by bad mesh quality or incorrect model setup. Their potential cause can thus be limited to the KM itself.
The mass fractions of all species and in all feeds in the outlet are almost identical to their respective experimental values, signifying that the kinetic constants are accurately defined for both KMs. Yet the flow profiles of the species, especially of CO and MeOH, differ significantly between the two KMs (Fig. A31, ESI†). This difference is key, as it originates from the considered reaction mechanisms and causes two distinct reaction equilibrium, as well as local temperature, profiles. The only main mechanistic difference between the two KMs, then, is the existence of R3. The local temperature variation is dependent on the local balance between endothermic and exothermic reactions; as feed 13 has no initial CO content, the equilibrium of the involved reactions is forced towards its production. In Park’s KM, two different reactions are responsible for CO production, RWGS and MeOH decomposition, which both take place simultaneously. In Nestler's KM, however, the exclusion of a direct pathway between CO and MeOH, i.e. R3, means that the local species equilibrium (CO2, CO and MeOH) is dependent on a single intermediate species, CO2..
Undoubtedly, the accurate prediction of the correct temperature profile is crucial for large-scale reactors to avoid catalyst sintering, so identifying the error is key for future modeling investigations. This is another instance where CFD can act as a guide for future experimental investigations. One of these two temperature profiles is unrealistic, and that can be experimentally confirmed. Following the experimental investigation, a more educated decision can be made on which of the two KMs results in a more realistic species and temperature profile and which mechanisms are key for feeds with no initial CO content.
MeOH production from CO2 or CO?
Including an expression for CO hydrogenation in the KM can be beneficial for investigating questions that have been set in the literature regarding its overall role in the MeOH synthesis process. Specifically, it quantifies the amount of MeOH synthesised directly from CO. Furthermore, preferable pathways for the conversion of CO into MeOH, i.e. direct hydrogenation or a combination of the FWGS reaction and CO2 hydrogenation, can be subsequently considered.In Table 2, a comparison of MeOH synthesis from CO2 and CO is presented, as predicted from Park’s KM. The presented percentage values are estimated volumetrically in the entire reactor. It is important to note that in feed 13, MeOH is volumetrically produced from CO2 and then is consumed to produce CO. So the negative percentage value for CO and the >100% value for CO2 are associated with the mechanistic pathways of MeOH.
| Park KM – Volumetric MeOH production from CO2 and CO | ||
|---|---|---|
| Feed number | MeOH from CO2 | MeOH from CO |
| 13 | 127.53% | −27.53% |
| 14 | 67.28% | 32.72% |
| 15 | 63.23% | 36.77% |
| 23 | 58.58% | 41.42% |
| 25 | 61.17% | 38.83% |
| Average values (excluding feed 13) | 62.57% | 37.44% |
As can be seen, MeOH is produced predominantly from CO2, with a percentage of 62.6%, as opposed to 37.4% of it being synthesised from CO. This agrees with the literature studies that identify CO2 as the main source of MeOH.23,34,40–42 In the kinetic study of Grabow and Mavrikakis,34 for the experimental conditions of T: 499.3 K, P: 29.9 bar, SN: 8.53, and COR: 0.47, they predicted 2/3 of MeOH to be produced from CO2 and the remaining MeOH to be produced from CO. Their prediction is in excellent agreement with this kinetic model, though their reaction conditions differ from those considered here. As can be seen in Table 2, composition variations (with the exception of feed 13) don’t significantly affect the amount of MeOH produced from CO2 and from CO. Changing the reaction temperature and pressure, however, will definitely affect the relative balance of the three reaction pathways and possibly alter the amount of MeOH produced from CO. More investigation is required with the produced CFD models to see how MeOH production from CO2/CO changes with variations in the operating conditions.
Preferable pathway for CO: RWGS or direct CO hydrogenation?
As already mentioned, the preferable pathway for CO can be investigated with the kinetic model of Park, since CO hydrogenation is included in the rate equation. To evaluate the preferable pathway for CO, the volumetric CO consumption in the FWGS reaction (R2) and in CO hydrogenation (R3) is presented in Table 3. In addition, the CO consumption in R2 and R3 along the centreline of the catalytic bed for feed 23 is presented in Fig. 7.| Volumetric CO consumption | ||
|---|---|---|
| Feed | FWGS – R2 | CO Hydrog. – R3 |
| 14 | 56.79% | 43.21% |
| 15 | 59.59% | 40.41% |
| 23 | 58.78% | 41.22% |
| 25 | 53.66% | 46.34% |
| Average | 57.21% | 42.79% |
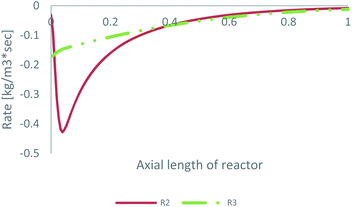 | ||
| Fig. 7 CO consumption in the FWGS reaction (R2) and in CO hydrogenation (R3) for feed 23, predicted from Park’s KM. | ||
The preferable pathway for CO to MeOH is through conversion to CO2, through the FWGS reaction, rather than through direct hydrogenation. The main difference between the two reaction pathways is the large magnitude of the FWGS reaction early in the bed, which, as seen earlier, is mainly driven by the fast CO2 hydrogenation rate. Later in the bed, the two reaction pathways have a similar contribution to CO consumption.
It has been demonstrated in the literature that CO2 hydrogenation, in both experiments and in models, is undoubtedly more important in MeOH production.40,41,52 The KM of Park agrees with this result, yet it predicts significant CO consumption for MeOH synthesis as well. In several kinetic models, however, such as those of Bussche and Froment and of Nestler, it is assumed that CO hydrogenation is negligible in the overall mechanisms of MeOH synthesis. The kinetic model of Park predicts otherwise, as CO is consumed in almost equal amounts in both the FWGS reaction and CO hydrogenation. In the kinetic study of Grabow and Mavrikakis34 it was predicted that only 28% of total CO is consumed by the FWGS reaction, while the rest was consumed by CO hydrogenation. Again, it is difficult to extrapolate these conclusions to the results observed here, due to the vastly different experimental conditions considered. Other studies predict that the kinetics of the WGS reaction are much faster than those of the hydrogenation reaction13 but that is not necessarily indicative of the preferable CO consumption pathway, or their relative difference.
Connection between initial CO mass fraction and MeOH synthesis
Specifically for feed 13, where there is no CO in the initial feed, it was observed that a significant amount of the produced MeOH (27.5% in Table 2) is consumed to produce CO. Obviously, this is detrimental to the efficiency of a MeOH synthesis system. The produced CFD model can be used as a parametric analysis tool to investigate the minimum required initial CO mass fraction to negate MeOH decomposition and only drive MeOH synthesis. The KM of Park was used for this parametric study. The volumetric production of MeOH from CO2 and CO, according to the initial mass fraction of CO in the feed gas, is presented in Table 4. In addition, the CO rate of change for reaction R3, presented as the consumption of CO, is shown in Fig. 8.| Park KM – volumetric production of MeOH | ||
|---|---|---|
| Initial CO mass fraction | Magnitude of R1 (MeOH from CO2) | Magnitude of R3 (MeOH from CO) |
| 0.0 (feed 13) | 127.53% | −27.53% |
| 0.01 | 120.09% | −20.09% |
| 0.02 | 113.51% | −13.51% |
| 0.03 | 107.69% | −7.69% |
| 0.04 | 102.54% | −2.54% |
| 0.05 | 97.98% | 2.02% |
| 0.06 | 93.93% | 6.07% |
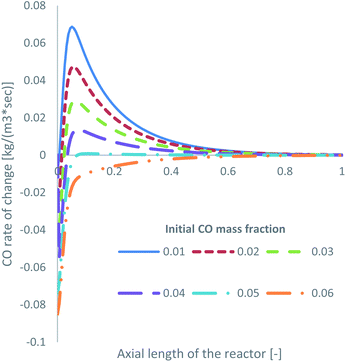 | ||
| Fig. 8 Rate of change of R3 along the axial length of the reactor, according to the initial mass fraction of CO. | ||
MeOH decomposition to CO occurs up until an approximate initial CO mass fraction of around 0.05, or a 2.5% initial mol fraction. Even at a mass fraction of 0.05, early in the bed, and after the initial spike in MeOH production in the entrance of the reactor, some MeOH is decomposed to produce CO. When the initial mass fraction of CO is 0.06, or 3.0 mol%, the rate of R3 primarily drives towards MeOH synthesis rather than towards MeOH decomposition. This demonstrates the benefits of cofeeding CO and CO2, which have also been observed in the literature for both low CO13,39 and low CO2 (ref. 22, 34 and 67) initial content.
From the results of the different feeds studied here, it seems that MeOH decomposes to CO only at very low initial CO mass fractions in the feed gas. In all other cases, MeOH synthesis takes place exclusively. This agrees with the results of Kunkes et al.66 where CO production takes place as a result of the RWGS reaction rather than through MeOH decomposition.
Discussion
One of the most important conclusions that can be reached from this study is the mechanisms for MeOH synthesis from CO2. In the paper of Wilkinson et al.,43 it was experimentally observed that early in the bed, CO2 is consumed to produce MeOH and H2O through direct hydrogenation. Deeper in the bed, CO2 and H2O reach a steady level and CO consumption replaces CO2 consumption. In addition, the production rate of MeOH is faster earlier in the bed than later.43 All these conclusions agree with the mechanisms predicted from both models, as seen from the species mass fractions along the bed; this indicates that both models provide reasonable results and the final compositions predicted are close both to each other and to the experimental results. This, however, makes validation of the two models much harder, as this validation requires either a dedicated experimental run or general observations in the literature.For the latter, these observations are hard to use as validation for the mechanisms, since experimental conditions and setups vary. Grabow and Mavrikakis34 stated that conclusions regarding the main carbon source for MeOH can only be made for specific conditions and cannot be generalised. The same applies to reaction mechanisms, especially since the errors of the various kinetic models increase outside the operating range for which they were defined.53
In the current model comparison, some discrepancies could be seen in feed 23, where Nestler’s model predicted 3% more MeOH and 5% more CO and H2O compared to Park’s KM. This result could not be validated with the experimental results of Park et al.46 Actually, this result was fundamentally related to the preferable reaction mechanisms and whether H2O inhibition takes place or not. Conclusively, being able to experimentally identify the physical trends of the different involved species is as important as the actual species values under distinct experimental conditions. The experimental procedure followed by Wilkinson et al.43 is a great example of the former.
Dedicated experimental runs to define the reaction mechanisms, given in a form that can be usable by various kinetic investigation methodologies, i.e. DFT, kinetic Monte Carlo and CFD, will be crucial for reaching a common understanding. Especially for papers where experimental results are used to establish new kinetic models, thorough investigations and results are required. In addition, combining our available investigative methods can lead to invaluable information regarding the MeOH synthesis process. As an example, Higham et al.37 predicted that CO2 could bond dissociatively on Cu(110) and Cu(100) facets, thus initialising CO hydrogenation on these sites. Yet the adsorption of CO feedstock on these facets was not considered. Park’s KM considers that CO2 and CO adsorb non-competitively on Cu sites while Nestler’s KM considers competitive adsorption of CO2 and CO. The role of these adsorption sites cannot be identified with the CFD model but DFT models are better suited for such investigations. Following the identification of the accurate micro-scale mechanisms, more accurate KMs can then be experimentally established, and their validation on both the local and the reactor scale can be verified with CFD tools. Here, the role of CFD was to investigate the kinetic mechanisms of MeOH synthesis from CO2/CO/H2 throughout the catalytic bed. The produced results can now be used to guide the experimental setup, which in turn can investigate the gas compositions at different reactor lengths. This can help validate the two KMs better and increase our understanding of the overall kinetics. After further validation, the CFD model can also be used as a predictive tool for the identification of temperature hotspots or for process optimisation, e.g. if the equilibrium depth can be predicted beforehand, this can help minimise the total catalyst load required. In general, collective and combined research with the available investigative methods has the potential to accelerate scientific understanding.
This leaves the question of which of the two KMs is more accurate and produces more reasonable results. Unfortunately, the answer is not straightforward. In their paper, Slotboom et al.68 compared several kinetic models, including those of Graaf and of Bussche and Froment, to determine their ability to predict experimental results. They separated the kinetic models into four groups, according to the mechanisms the KMs used to predict MeOH synthesis. They concluded that it is not the inclusion of CO hydrogenation that is key to predicting MeOH synthesis, but rather considering at least two distinct active sites, i.e. adsorption of CO on catalytic sites should also be considered. The considered KMs fundamentally consider three (Park’s KM) and two (Nestler’s KM) active sites, which allows both models to give accurate predictions. One of the criteria set by Slotboom et al.68 for choosing between models is the number of parameters necessary to define that model. The model of Park requires 10 parameters to be experimentally defined, while that of Nestler requires only 7. This makes the model of Nestler easier to use and implement.
In reality, though, choosing between these two models depends on the operating conditions and the expected investigation outcomes. The errors of Nestler’s KM decrease as the COR ratio increases, so for feed compositions with high CO2 content, Nestler’s KM is expected to give a more accurate prediction, especially for the CO2 species. In addition, Nestler’s KM presented a smaller error in its prediction for the high SN ratio case, compared to Park’s KM. As this model was defined to be applicable to a wide industrially relevant operating range, this benefit can be a great asset when deciding the most suitable model. Finally, it is easier to adapt to different experimental setups, as it only requires 7 parameters to be defined. However, it is important to consider that for feeds with no initial content of CO, inaccuracies in the predicted temperature profile can occur. The model of Park can more accurately predict feeds with low COR number. In addition, the inclusion of CO hydrogenation in the KM provides a more comprehensive mechanistic understanding of the effects, the interactions, the inhibitions, and the overall equilibrium of the involved reactions and species. In addition, as this model considers three active sites, from a catalyst design/optimization point of view, it can better guide experimental efforts to optimize the catalyst with the goal of promoting a different mechanism, e.g. to enhance the rate of CO2 or CO hydrogenation. However, its requirement for 10 parameters makes this model’s adaptation to different experimental conditions more challenging.
Conclusions
Methanol synthesis from a mixture of CO2/CO/H2 has been widely studied for its kinetics and reaction equilibria. In this paper, two of the available kinetic models in the literature, those of Park et al.46 and Nestler et al.,53 are compared using a CFD simulation. The kinetic models are validated, based on previously published experimental results, in terms of their mechanistic predictions within the catalytic bed. As has also been observed in the literature, CO2 is converted early in the bed to MeOH but reaches a steady state soon after. CO consumption then replaces CO2 consumption, as it is converted to MeOH either through the FWGS reaction and subsequent (CO2) hydrogenation or through direct hydrogenation. The inclusion of CO hydrogenation in the kinetic model of Park offers more detailed mechanistic insights in terms of the interactions, the inhibitions, and the equilibrium of the involved reactions. However, Nestler’s kinetic model offers a broader applicability, as it was defined for a wide range of industrially relevant operating conditions.The benefits of applying a validated CFD model as an investigation method were demonstrated. The presented CFD model offers a realistic representation of the spatial profiles of local species concentrations, temperature variations, and reaction rate magnitudes. Data such as this are hard to acquire experimentally, as non-invasive and in situ experimental setups have limited applicability. More importantly, the CFD model can detect internal inconsistencies in the applied kinetic models or key mechanisms for the MeOH synthesis process at low initial CO content, thus paving the way for further dedicated and educated experimental investigations. In combination with these experimental runs, it can be used to increase our understanding of the methanol synthesis process, and in turn, act as a guide for catalyst design and reactor engineering. Especially for large scale chemical reactors, where knowledge of spatial heat and mass transfer is crucial to avoid runaway conditions, accurate CFD models can play a decisive role.
Nomenclature
Symbols
| f i | Fugacity of species i, [bar] |
| K eq,i | Equilibrium constant of reaction i, [variable units] |
| k i | Reaction rate constant for reaction i, [variable units] |
| K i | Adsorption constant for species i, [bar−1] |
| M w,i | Molecular weight of species i, [kg kmol−1] |
| R | Universal gas constant, [J kmol−1 K−1] |
| P | Pressure, [Pa] |
| r i | Reaction rate based on the respective kinetic model, [kmol m−3 s−1] |
| R i | Reaction source term, [kg m−3 s−1] |
| T | Temperature, [K] |
| v prod i,r | Stoichiometric coefficient of product species i in reaction r |
| v react i,r | Stoichiometric coefficient of reactant species i in reaction r |
| X i | Molar fraction of species i |
| Y i | Mass fraction of species i |
Greek symbols
| φ i | Scalar quantity of species i |
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors would like to thank the Southampton Marine & Maritime Institute for their PGR studentship funding.References
- R. M. Cuéllar-Franca and A. Azapagic, J. CO2 Util., 2015, 9, 82–102 Search PubMed.
- G. A. Olah, Angew. Chem., Int. Ed., 2013, 52, 104–107 Search PubMed.
- X. Zhen and Y. Wang, Renewable Sustainable Energy Rev., 2015, 52, 477–493 Search PubMed.
- J. M. Thomas and W. J. Thomas, Principles and practice of heterogeneous catalysis, Wiley-VCH, 2nd edn, 2015 Search PubMed.
- T. Weimer, K. Schaber, M. Specht and A. Bandi, Energy Convers. Manage., 1996, 37, 1351–1356 Search PubMed.
- N. Rezaie, A. Jahanmiri, B. Moghtaderi and M. R. Rahimpour, Chem. Eng. Process., 2005, 44, 911–921 Search PubMed.
- E. J. S. G. H. Graaf and A. A. C. M. Beenackers, Chem. Eng. Sci., 1988, 43, 3185–3195 Search PubMed.
- H.-W. Lim, M.-J. Park, S.-H. Kang, H.-J. Chae, J. W. Bae and K.-W. Jun, Ind. Eng. Chem. Res., 2009, 48, 10448–10455 Search PubMed.
- N. Park, M.-J. Park, K.-S. Ha, Y.-J. Lee and K.-W. Jun, Fuel, 2014, 129, 163–172 Search PubMed.
- R. A. Koeppel, A. Baiker and A. Wokaun, Appl. Catal., A, 1992, 77–102, DOI:10.1016/0926-860x(92)80340-i.
- Z.-S. Hong, Y. Cao, J.-F. Deng and K.-N. Fan, Catal. Lett., 2002, 82, 37–44 Search PubMed.
- X. An, J. Li, Y. Zuo, Q. Zhang, D. Wang and J. Wang, Catal. Lett., 2007, 118, 264–269 Search PubMed.
- X. An, Y. Zuo, Q. Zhang and J. Wang, Chin. J. Chem. Eng., 2009, 17, 88–94 Search PubMed.
- I. A. Fisher, H. C. Woo and A. T. Bell, Catal. Lett., 1997, 44, 11–17 Search PubMed.
- T. C. Schilke, I. A. Fisher and A. T. Bell, J. Catal., 1999, 184, 144–156 Search PubMed.
- A. Gotti and R. Prins, J. Catal., 1998, 175, 302–311 Search PubMed.
- X. Jiang, Y. Jiao, C. Moran, X. Nie, Y. Gong, X. Guo, K. S. Walton and C. Song, Catal. Commun., 2019, 118, 10–14 Search PubMed.
- X. Jiang, N. Koizumi, X. Guo and C. Song, Appl. Catal., B, 2015, 170–171, 173–185 Search PubMed.
- I. Sierra, J. Ereña, A. T. Aguayo, J. M. Arandes and J. Bilbao, Appl. Catal., B, 2010, 94, 108–116 Search PubMed.
- J. Ereña, I. Sierra, M. Olazar, A. G. Gayubo and A. T. Aguayo, Ind. Eng. Chem. Res., 2008, 47, 2238–2247 Search PubMed.
- A. Ateka, P. Pérez-Uriarte, M. Gamero, J. Ereña, A. T. Aguayo and J. Bilbao, Energy, 2017, 120, 796–804 Search PubMed.
- M. Shahrokhi and G. R. Baghmisheh, Chem. Eng. Sci., 2005, 60, 4275–4286 Search PubMed.
- M. Sahibzada, I. S. Metcalfe and D. Chadwick, J. Catal., 1998, 174, 111–118 Search PubMed.
- S. Arab, J.-M. Commenge, J.-F. Portha and L. Falk, Chem. Eng. Res. Des., 2014, 92, 2598–2608 Search PubMed.
- F. Manenti, S. Cieri and M. Restelli, Chem. Eng. Sci., 2011, 66, 152–162 Search PubMed.
- F. Manenti, S. Cieri, M. Restelli and G. Bozzano, Comput. Chem. Eng., 2013, 48, 325–334 Search PubMed.
- M. J. Bos and D. W. F. Brilman, Chem. Eng. J., 2015, 278, 527–532 Search PubMed.
- X. Zhou, Y. Duan, X. Huai and X. Li, Particuology, 2013, 11, 715–722 Search PubMed.
- A. G. Dixon and M. Nijemeisland, Ind. Eng. Chem. Res., 2001, 40, 5246–5254 Search PubMed.
- P. Pandi and P. Le Clercq, Numerical Simulation of Heat Transfer in a 3D Cavity-Receiver, Proceedings of the ASME 2015 9th International Conference on Energy sustainability, 2015, DOI:10.1115/ES2015-49355.
- S. Kyrimis, P. L. Clercq and S. Brendelberger, AIP Conf. Proc., 2019, 2126, 180013 Search PubMed.
- L. M. Armstrong, S. Gu and K. H. Luo, Int. J. Heat Mass Transfer, 2010, 53, 4949–4959 Search PubMed.
- L. M. Armstrong, K. H. Luo and S. Gu, Chem. Eng. J., 2010, 160, 239–248 Search PubMed.
- L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384 Search PubMed.
- M. Behrens, F. Studt, I. Kasatkin, S. Kuhl, M. Havecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B. L. Kniep, M. Tovar, R. W. Fischer, J. K. Norskov and R. Schlogl, Science, 2012, 336, 893–897 Search PubMed.
- S. Kattel, B. Yan, Y. Yang, J. G. Chen and P. Liu, J. Am. Chem. Soc., 2016, 138, 12440–12450 Search PubMed.
- M. D. Higham, M. G. Quesne and C. R. A. Catlow, Dalton Trans., 2020, 49, 8478–8497 Search PubMed.
- A. A. Kiss, J. J. Pragt, H. J. Vos, G. Bargeman and M. T. De Groot, Chem. Eng. J., 2016, 284, 260–269 Search PubMed.
- X. An, Y.-Z. Zuo, Q. Zhang, D.-Z. Wang and J.-F. Wang, Ind. Eng. Chem. Res., 2008, 47, 6547–6554 Search PubMed.
- G. Liu, D. Willcox, M. Garland and H. H. Kung, J. Catal., 1985, 96, 251–260 Search PubMed.
- G. C. Chinchen, P. J. Denny, D. G. Parker, M. S. Spencer and D. A. Whan, Appl. Catal., 1987, 30, 333–338 Search PubMed.
- M. Saito, T. Fujitani, M. Takeuchi and T. Watanabe, Appl. Catal., A, 1996, 138, 311–318 Search PubMed.
- S. K. Wilkinson, L. G. A. Van De Water, B. Miller, M. J. H. Simmons, E. H. Stitt and M. J. Watson, J. Catal., 2016, 337, 208–220 Search PubMed.
- G. H. Graaf, H. Scholtens, E. J. Stamhuis and A. A. C. M. Beenackers, Chem. Eng. Sci., 1990, 45, 773–783 Search PubMed.
- A. Montebelli, C. G. Visconti, G. Groppi, E. Tronconi, C. Ferreira and S. Kohler, Catal. Today, 2013, 215, 176–185 Search PubMed.
- N. Park, M.-J. Park, Y.-J. Lee, K.-S. Ha and K.-W. Jun, Fuel Process. Technol., 2014, 125, 139–147 Search PubMed.
- M. Son, Y. Woo, G. Kwak, Y.-J. Lee and M.-J. Park, Int. J. Heat Mass Transfer, 2019, 145, 118776 Search PubMed.
- J. Park, Y. Woo, H. S. Jung, H. Yang, W. B. Lee, J. W. Bae and M.-J. Park, Catal. Today, 2020 DOI:10.1016/j.cattod.2020.06.023.
- W. Li, Y. Zhuang, L. Liu, L. Zhang and J. Du, J. Cleaner Prod., 2020, 274, 123153 Search PubMed.
- T. B. H. Nguyen and E. Zondervan, J. CO2 Util., 2019, 34, 1–11 Search PubMed.
- D. Mignard and C. Pritchard, Chem. Eng. Res. Des., 2008, 86, 473–487 Search PubMed.
- K. M. V. Bussche and G. F. Froment, J. Catal., 1996, 161, 1–10 Search PubMed.
- F. Nestler, A. R. Schütze, M. Ouda, M. J. Hadrich, A. Schaadt, S. Bajohr and T. Kolb, Chem. Eng. J., 2020, 394, 124881 Search PubMed.
- M. E. Potter, L.-M. Armstrong and R. Raja, Catal. Sci. Technol., 2018, 8, 6163–6172 Search PubMed.
- A. G. Dixon, M. Nijemeisland and E. H. Stitt, Adv. Chem. Eng., 2006, 31, 307–389 Search PubMed.
- R. Krishna, Chem. Eng. Sci., 1993, 48, 845–861 Search PubMed.
- E. B. Poling, M. J. Prausnitz and P. J. O’Connell, Properties of Gases and Liquids, McGraw-Hill Education, New York, 5th edn, 2001 Search PubMed.
- ANSYS Inc., Fluent User’s Guide, 2013, Release 15.0 Search PubMed.
- S. H. Fogler, Elements of Chemical Reaction Engineering, Pearson, 4th edn, 2006 Search PubMed.
- ANSYS Inc., Fluent Theory Guide, 2013, Release 15.0 Search PubMed.
- M. E. Taskin, A. Troupel, A. G. Dixon, M. Nijemeisland and E. H. Stitt, Ind. Eng. Chem. Res., 2010, 49, 9026–9037 Search PubMed.
- A. G. Dixon, M. E. Taskin, M. Nijemeisland and E. H. Stitt, Ind. Eng. Chem. Res., 2010, 49, 9012–9025 Search PubMed.
- A. G. Dixon, Chem. Eng. Sci., 2017, 168, 156–177 Search PubMed.
- R. H. Hite and R. Jackson, Chem. Eng. Sci., 1977, 32, 703–709 Search PubMed.
- G. H. Graaf and J. G. M. Winkelman, Ind. Eng. Chem. Res., 2016, 55, 5854–5864 Search PubMed.
- E. L. Kunkes, F. Studt, F. Abild-Pedersen, R. Schlögl and M. Behrens, J. Catal., 2015, 328, 43–48 Search PubMed.
- C. V. Ovesen, B. S. Clausen, J. Schiøtz, P. Stoltze, H. Topsøe and J. K. Nørskov, J. Catal., 1997, 168, 133–142 Search PubMed.
- Y. Slotboom, M. J. Bos, J. Pieper, V. Vrieswijk, B. Likozar, S. R. A. Kersten and D. W. F. Brilman, Chem. Eng. J., 2020, 389, 124181 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Including computational theory, model setup, and further computational results for the different considered feeds. See DOI: 10.1039/d0fd00136h |
| This journal is © The Royal Society of Chemistry 2021 |