Structure determination of modulated structures by powder X-ray diffraction and electron diffraction
Zhengyang
Zhou
ac,
Lukáš
Palatinus
*b and
Junliang
Sun
*a
aCollege of Chemistry and Molecular Engineering, Peking University, Beijing 100871, People's Republic of China
bInstitute of Physics of the CAS, v.v.i., Na Slovance 2, 182 21 Prague, Czech Republic. E-mail: palat@fzu.cz
cCollege of Chemistry and Chemical Engineering, Chongqing University, Chongqing 400044, People's Republic of China
First published on 2nd September 2016
Abstract
Since the first discovery and description of materials, whose structures are not periodic, enormous efforts have been made in studying these aperiodic structures. With these efforts including the development of superspace group theory and structure solution algorithms, numerous incommensurately modulated structures which represent the vast majority of known aperiodic structures have been determined with single crystal X-ray diffraction data. However, the determination of modulated structures remains very difficult for polycrystalline materials. Powder X-ray diffraction and electron microscopy techniques yield remarkable information for polycrystalline materials. By combining these two methods, modulated structures of polycrystalline materials that impede solution by conventional methods can be determined. The power of these methods is illustrated with the examples of the determination of modulated structures of polycrystalline materials.
Introduction to the international collaborationElectron diffraction methods have made enormous progress over the last decade. The determination of some structures using solely electron diffraction (ED) techniques, or in combination with powder X-ray diffraction (PXRD) has now become convenient. However, the analysis of complex structures is far from routine even with high-quality single crystal X-ray diffraction (SXRD) data, and the structure analysis of complex structures from ED and/or PXRD data is more challengeable. The international collaborative researching projects of our group and of Lukáš focus on synthetizing some new compounds which have some interesting functions and developing routine PXRD and ED methods to simplify the determination of complex structures of these new compounds. |
1. Introduction
Since the first discovery and description of materials, whose structures are not periodic,1 enormous efforts have been made in studying these aperiodic structures. With these efforts including the development of superspace group theory2–16 and structure solution algorithms,17–21 numerous incommensurately modulated structures (IMS) which represent the vast majority of known aperiodic structures have been determined with single crystal X-ray diffraction (SXRD) data. However, the determination of modulated structures (MS) remains very difficult for polycrystalline materials.For polycrystalline materials, single crystals large enough for SXRD are not available and materials are then often studied by powder X-ray diffraction (PXRD). Reflections from differently oriented crystallites are measured simultaneously, so reflections with similar d-values are overlapped in the powder X-ray diffraction pattern, which hinders structure solution by PXRD methods. Compared to X-ray diffraction, electron diffraction (ED) patterns can be obtained from extremely small crystals. Therefore, the crystal size limitation of X-ray crystallography is not a problem for electron diffraction with a transmission electron microscope (TEM). But dynamical diffraction effects always present in ED seriously complicate the quantitative analysis of ED patterns for the determination of structures. By making a general survey of the characteristics of PXRD and ED, it is found that these two techniques are remarkably complementary,22 and several ways of combining them have been successfully used to address MS that can't be solved by either method alone.
In this review the structure analysis of MS is focused. We first outline basic concepts used in the structure determination of MS. Then the methods used to analyze the MS of polycrystalline materials are described together with examples of the determination of the MS of polycrystalline materials.
2. Basic concepts
2.1. (1 + 1)D MS
The MS can be described as a section through a hypothetical higher-dimensional structure periodic in a superspace.2–16 The simplest crystalline system: the 1D single atom chain with the unit cell c1 (Fig. 1a) is used to understand this idea. In Fig. 1b, the arrows indicate the modulations of atomic positions, the hatch marks indicate the original atomic positions (average positions), and the small solid circles indicate the atom positions after modulation (real positions).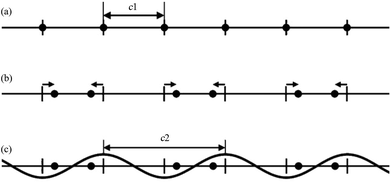 | ||
| Fig. 1 A simple 1D modulated system. (a) Before modulation: all atoms (filled circles) lie equally spaced along a straight line. (b) After modulation: half the atoms shift to the left, and half to the right (arrows). (c) Modulation in (b) represented as a simple cosine function. Reproduced with permission from ref. 16. Copyright 2007 Wiley-VCH. | ||
Although the modulation of the 1D atom chain is shown in Fig. 1b, an alternative view being of greater utility was found. In this alternative view, the arrows of Fig. 1b were replaced by simple curves (sinusoidal wave with wavelength c2) (Fig. 1c). If the ratio γ (γ = c1/c2) between c1 and c2 is rational, the structure becomes commensurately modulated. If the ratio γ is irrational, the structure becomes incommensurately modulated. With this convention in mind, the atoms originally located at the average positions were moved either to the left or to the right. Atoms shifted to the left are represented by positive values of this sinusoidal curve, whereas negative values represent the shift to the right.
Such a modulated 1D atom system (Fig. 1c) can be treated as a section through a hypothetical (1 + 1)D crystal. The second 1 in (1 + 1)D is used to distinguish the number of physically unreal axes. To illustrate this, the following mathematical artifice is introduced.
The positional modulation functions of Fig. 1c were rotated by 90° around every original atomic position (Fig. 2). Then the MS turns to a (1 + 1)D crystal. xs1 and xs2 are the cell axes of this crystal. The period of xs2 is c2, and the period of xs1 is discussed below. Then periodic curved lines are used to replace the points to describe atomic positions.
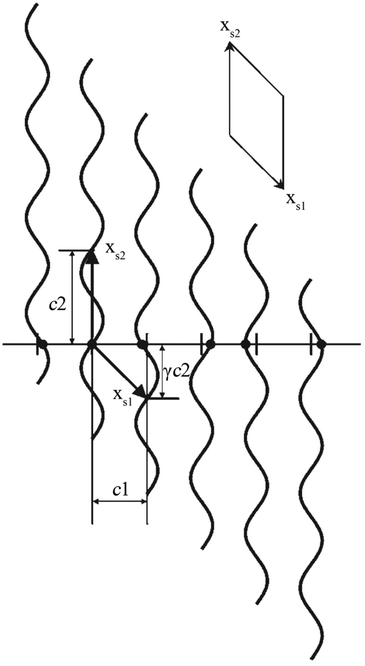 | ||
| Fig. 2 A simple 1D MS represented as a (1 + 1)D crystal. Atoms (filled circles) lie at the intersection of the horizontal line (the physical space) with a set of vertical periodic displacement functions. Drawn in this fashion, an oblique 2D unit cell with unit cell vectors xs1 and xs2 can be discerned. Reproduced with permission from ref. 16. Copyright 2007 Wiley-VCH. | ||
As the 1D modulated system is the section through the (1 + 1)D system along the horizontal physical axis, the interpretation of this only horizontal physical axis should not be changed. But the unit scale of the vertical axis without any physical meaning can be changed discretionarily at will. The unit length is the easiest choice so that c2 is of length unity. Through this simple transformation, the unit cell of this (1 + 1)D crystal can be expressed as
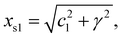 | (2-1) |
| xs2 = 1, | (2-2) |
| α = cot−1(c1/γ). | (2-3) |
It should be noted that CMS in this review are all described in a higher-dimensional space, but they can also be described in a supercell.
2.2. (3 + d)D MS
According to the (1 + 1)D MS mathematical artifice, the actual MS can also be described as a section through a hypothetical higher-dimensional structure periodic in a (3 + d)D superspace. The basis vectors in the (3 + d)D direct superspace are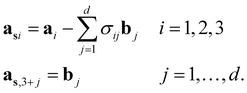 | (2-4) |
The {a1, a2, a3} are the basis vectors in the physical space. The σij are the components of the modulation vectors.
Then, the generalized electron density ρs(xs) in the superspace is a periodic function of the superspace vectors xs, with a periodicity provided by the basis vectors {as1, as2, as3, …, as,3+d}. The electron density in the physical space ρ(x) can be obtained as the physical space section of ρs(xs).12
The structure factors Fs(Hs) in the reciprocal superspace can be obtained by Fourier transformation of the generalized electron density ρs(xs). According to the properties of Fourier transformation, Fs(Hs) is a periodic function of the reciprocal superspace vectors Hs, with a periodicity provided by the basis vectors {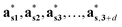 }. The relationships between the basis vectors in the reciprocal superspace and direct superspace are:
}. The relationships between the basis vectors in the reciprocal superspace and direct superspace are:
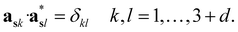 | (2-5) |
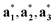 } can be considered as a projection onto the physical reciprocal space from the structure factors Fs(Hs). The relationships between the basis vectors in the (3 + d)D reciprocal superspace and those in the physical reciprocal space can be expressed as
} can be considered as a projection onto the physical reciprocal space from the structure factors Fs(Hs). The relationships between the basis vectors in the (3 + d)D reciprocal superspace and those in the physical reciprocal space can be expressed as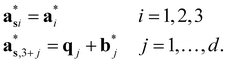 | (2-6) |
The 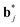 (j = 1, …, d) are unit vectors which are perpendicular to the reciprocal space {
(j = 1, …, d) are unit vectors which are perpendicular to the reciprocal space {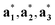 }. qj are the wave vectors of the modulation waves defined as
}. qj are the wave vectors of the modulation waves defined as
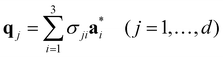 | (2-7) |
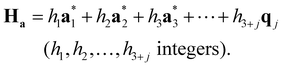 | (2-8) |
Fig. 3 shows the HRTEM image and corresponding FT patterns of KNd(MoO4)2.23 The modulation vector q of KNd(MoO4)2 is 0.57789(4)a* − 0.14748(6)b* (a = 5.5202(2), b = 5.33376(5), c = 11.8977(3) Å and γ = 90.9591(7)°). It is obvious that the direction of the modulation wave is parallel to the direction of the modulation vector q, and the wavelength is reciprocal to the length of the modulation vector.
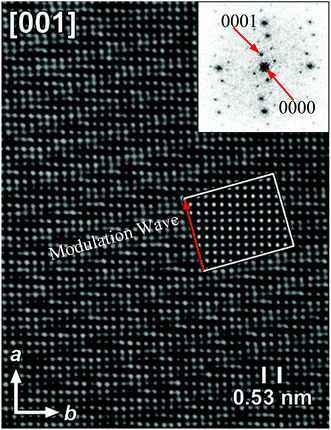 | ||
| Fig. 3 [001] HRTEM image and the corresponding FT pattern of the incommensurately modulated KNd(MoO4)2. The inset represents a calculated image based on the model, for a focus value of −60 nm and a thickness of 2 nm. Reproduced with permission from ref. 23. Copyright 2006 American Chemical Society. | ||
The relationship between the physical space and superspace is summarized in Fig. 4.12
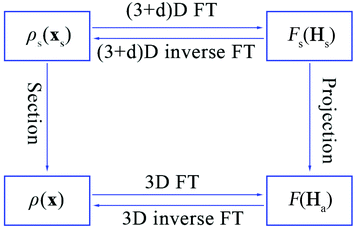 | ||
| Fig. 4 The relationship between the electron density and structure factors is given by Fourier transform (FT) in the 3D or (3 + d)D space. | ||
2.3. Symmetry in the superspace
The generalized electron density in a direct superspace is a periodic function of the superspace vectors xs, with a periodicity provided by the basis vectors {as1, as2, as3, …, as,3+d}. It thus follows that such a representation of an MS has symmetries according to a (3 + d)D superspace group.2–4 It should be noted that not all (3 + d)D space groups are possible as the symmetry for an MS. Those denoted as superspace groups for d = 1 were provided by Janner, Janssen and De Wolff,4,5,8,9 and for (3 + 2)D and (3 + 3)D were derived by Yamamoto,24,25 and recently comprehensive tables have been derived and made available on-line by Stokes, Campbell and van Smaalen.262.4. Reflection conditions in the superspace
Let us consider the set of symmetry operators {Rs|τs}, which form the superspace group of the structure. In complete analogy to the standard periodic case, the structure factors in the superspace transform according to| F(HsRs) = F(Hs)exp(−2πiHs·τs). | (2-9) |
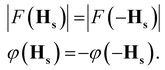 | (2-10) |
Conditions (2)–(9) must be obeyed also by all structure factors with a diffraction vector that fulfills the condition HsRs = Hs.8 Either F(Hs) is zero (an extinction), or the phase must be equal. The latter condition provides the reflection conditions, given by
| Hs·τs = n. n integers | (2-11) |
3. Determination of MS
3.1. PXRD
The PXRD diagram is a 1D projection of the reflections in the reciprocal space (Fig. 5). The reflection overlap is the greatest drawback of PXRD. The problem can be reduced by collecting high resolution data at a synchrotron facility. But the high resolution data cannot change the essence of PXRD. For the MS, the reflection overlap in PXRD is much more serious, because there the projection is not from a 3D lattice, but from a (3 + d)D lattice. To the best of our knowledge, there has been no fully ab initio structure solution in the superspace from PXRD so far.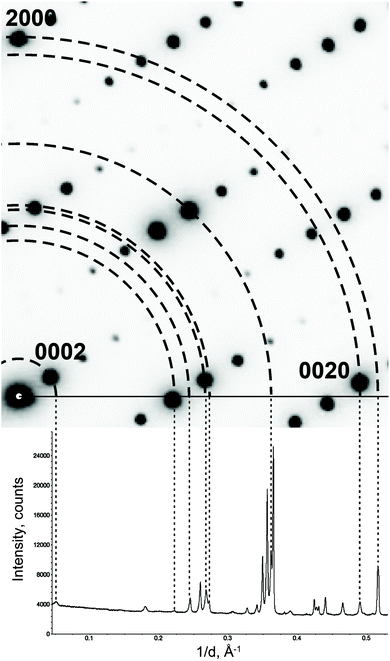 | ||
| Fig. 5 Projecting an electron diffraction pattern on a powder X-ray diffraction pattern. Note that not all reflections on the powder pattern are present on the electron diffraction pattern. These reflections belong to other reciprocal lattice sections. Reproduced with permission of the International Union of Crystallography from ref. 27. | ||
Although the reflection overlap hinders the ab initio structure solution of MS, MS determination by refinement is probable. A commonly known structure type is treated as the origin model of the refinement of MS. The amplitudes of the positional and occupational modulation functions are generally obtained in the refinement starting from arbitrary small values and verified against the Fourier maps in the superspace. There are more than 35 MS that have been refined against PXRD and/or NPD in the superspace in the period of 1989–2014.28–63 It might not be comprehensive, but might be sufficiently representative to obtain the importance of PXRD which are widely employed for the analysis of MS.
3.2. ED
ED patterns can be obtained from small individual single crystals of the material that constitute the powder sample. Based on the crystal orientation during the data collection, the ED data collection can be divided into two main approaches: collection of zone-axis patterns and acquisition of 3D diffraction data.To make the quantitative determination of structures from ED patterns true, a method called precession electron diffraction (PED) was introduced 20 years ago.64 In the PED method (Fig. 6), the electron beam is rocked in a hollow cone (at a fixed angle to the optic axis) above the sample and then de-rocked below the sample. With this method, only a few reflections are excited simultaneously and the intensities are integrated over many orientations of the incident beam.65
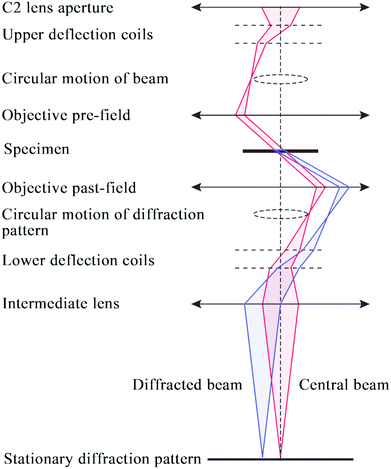 | ||
| Fig. 6 Schematic ray diagram for precession electron diffraction (PED), illustrating the rocking/de-rocking action of the beam before and after the specimen.65 | ||
3.2.1.1. CaEu2(WO4)4. In view of the first determination of MS by zone-axis ED in the superspace,66 eight zone-axis PED patterns were collected, resulting in a dataset with 406 main reflections and 51 satellite reflections.
The intensities of these reflections were used to refine the (3 + 1)D MS. At the beginning of the refinement, a rigid body approximation for the WO4 tetrahedra was applied. After the convergence was achieved, the rigid body constraints were replaced by soft constraints on W–O distances, and the atomic coordinates of W and O atoms were refined. The positional modulations of all atoms were not refined due to the limited amount of observed satellites. By analogy to the known structure modulations in other scheelite-type oxides, the modulation was assumed to be essential for ordering of the cation vacancies.67–71 The occupational modulations of Ca and Eu atoms were therefore introduced and refined with crenel functions.72 The refinement was finally converged with a value of Rall = 17.9%, which is well acceptable for PED data. Fig. 7 shows the occupational modulations of Ca and Eu obtained from the refinement. Fig. 8 shows the cation-vacancy ordering in the 7a × 9b × 1c commensurate approximant.
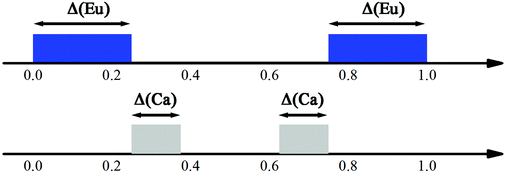 | ||
| Fig. 7 Schematic view of the crenel domains in the superspace. The Eu domain (blue) is centered at x04 = 0 with Δ = 1/2. Two crenel domains of Ca (grey) are centered at x04 = 5/16 and 11/16 with Δ = 1/8, respectively. Reproduced with permission from ref. 66. Copyright 2013 American Chemical Society. | ||
 | ||
| Fig. 8 Outline of cation-vacancy ordering in the 7a × 9b × 1c commensurate approximant. WO4 tetrahedra are not shown. The dimers (marked in orange) and trimers (marked in yellow) of the vacant cationic columns are marked with red rectangles. Reproduced with permission from ref. 66. Copyright 2013 American Chemical Society. | ||
3.2.2.1. ADT. In an ADT method, the data is acquired through sequentially tilting a selected crystal around an arbitrary crystallographic axis with a variable tilt step down to 0.1 degree.87 Such a data set may miss main crystallographic zones, but as it includes a large number of high-index reflections, the overall number of collected reflections is typically higher than that achieved by manual electron diffraction data collection. So ADT data contains nearly all reflections present in the covered wedge of the reciprocal space.
3.2.2.2. RED. The RED method combines coarse goniometer tilts (∼2.0°) with fine electron beam tilt steps (usually ∼0.10°–0.40°) for electron diffraction pattern collection. This is similar to collecting the single crystal X-ray diffraction data by the rotation method with a 2D area detector. RED data collection is controlled using the RED data collection software package.90 Typically, more than 1000 ED frames are collected in about one hour and used for structure determination.
3.2.2.3. IEDT. Integrated electron diffraction tomography is very similar to the previous methods. However, the rotation of the crystal around the tilt axis is continuous and diffraction is recorded during the tilting of the crystal. Each recorded pattern is thus an integration of the reciprocal space over a small tilt range. This data collection strategy is closest to the standard data collection used in SXRD data collection.
All EDT methods have been applied successfully to the phase identification and structure determination of a variety of 3D periodic materials,87,88,90,92–99 but so far no MS has been determined purely with EDT data in the superspace.
3.2.3.1. η′-Cu3+x(Si, Ge). In the case of η′-Cu3+x(Si, Ge),101 a single crystal was tilted in steps of 1° (−31° to 50°), and in each step two 2° precession angle electron diffraction patterns (200 ms exposure and 5 s exposure) used to accurately extract the intensities of both the strong and the weak reflections were collected.
The reflections extracted from PEDT data (Fig. 9) belonging to the Laue class ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m (Rint(
1m (Rint(![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m) = 16.75%) were indexed with a hexagonal basic unit cell corresponding to η-Cu3+xSi with two modulation vectors q1 = α(a* + b*) + 1/3c* and q2 = −2αa* + αb* + 1/3c*. The value of α was determined from the positions of the spots in the [001] zone axis SAED to be 0.244(1).
1m) = 16.75%) were indexed with a hexagonal basic unit cell corresponding to η-Cu3+xSi with two modulation vectors q1 = α(a* + b*) + 1/3c* and q2 = −2αa* + αb* + 1/3c*. The value of α was determined from the positions of the spots in the [001] zone axis SAED to be 0.244(1).
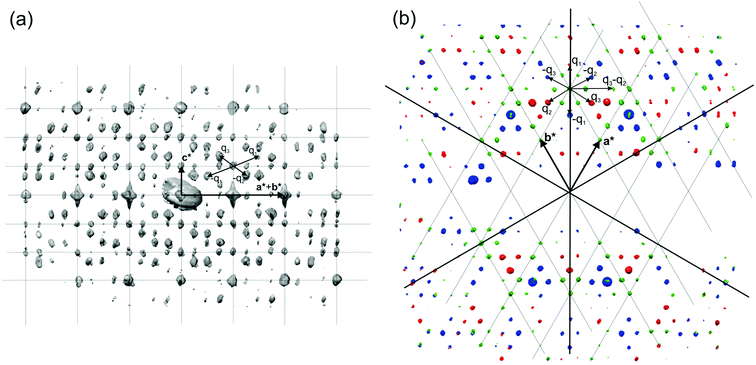 | ||
| Fig. 9 3D distribution of diffracted intensities in the reciprocal space. (a) Projection along a*–b* with the basic unit cell and modulation vectors is indicated. Vectors q3 and −q2 point partly toward the reader (cf. part b of this figure); other vectors lie in the plane of the drawing. (b) Three layers viewed along c*. Blue, l = 2/3; green, l = 1; red, l = 4/3. Reproduced with permission from ref. 101. Copyright 2011 American Chemical Society. | ||
The structure of η′-Cu3+x(Si, Ge) was solved by charge flipping in the superspace.20 As the charge flipping algorithm is independent of the (super)space group symmetry, it is possible to obtain symmetry information by analysis of the reconstructed electron density.21 This procedure found the superspace group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1m(α, α, 1/3)000(−2α, α, 1/3)000, in agreement with the diffraction symbol determined from the diffraction data. Based on the ab initio reconstructed superspace electron density, the MS was described as sheets of Cu clusters separated by honeycomb layers of mixed Si/Ge positions. The shape of the Cu clusters in the sheets strongly varied with the modulation phase, and the predominant form was an icosahedron. The striving of the Cu layers to form icosahedral clusters was deemed to be the main driving force of the modulation.101
1m(α, α, 1/3)000(−2α, α, 1/3)000, in agreement with the diffraction symbol determined from the diffraction data. Based on the ab initio reconstructed superspace electron density, the MS was described as sheets of Cu clusters separated by honeycomb layers of mixed Si/Ge positions. The shape of the Cu clusters in the sheets strongly varied with the modulation phase, and the predominant form was an icosahedron. The striving of the Cu layers to form icosahedral clusters was deemed to be the main driving force of the modulation.101
Later investigations showed that the honeycomb layers were not formed purely by Si/Ge, but that they were in fact a mixture of Cu and Si/Ge.15 The determination of this disorder was beyond the sensitivity of the electron diffraction data.
The MS determination of η′-Cu3+x(Si, Ge) was the first time that three-dimensional electron diffraction data with a high coverage of the reciprocal space was used for the solution of MS employing the charge flipping algorithm in the superspace.
3.3. Combination of ED and PXRD
Although the recent developments in ED have led to a number of structure determinations,66,73–85,100 the residual dynamical effects present in the ED data are still too strong to allow for accurate structure determination using kinematic theory. As an example of the limitation of ED data, the occupancy factors of Ca and Eu in CaEu2(WO4)4 are in fact modulated harmonically,102 but the residual dynamical effects in PED introduce an apparently complete ordering of Ca, Eu and vacancies. It is thus desirable, where possible, to combine the results of ED with other methods.3.3.1.1. Ba0.85Ca2.15In6O12. The first combination of zone-axis ED and PXRD to determine MS in the superspace was performed on the mixed metal oxide Ba0.85Ca2.15In6O12.103 Most of the peaks in the PXRD pattern could be indexed with a hexagonal unit cell (P63/m, a = b = 9.8880(1) and c = 3.2170(1) Å), but a few smaller peaks were not indexed. Therefore, zone-axis ED data were used to confirm the unit cell and symmetry. The reflections in the [001] zone axis SAED pattern (Fig. 10a) were compatible with the hexagonal unit cell. The [100] zone axis SAED pattern (Fig. 10b) contained satellite reflections. In Fig. 10b, intense satellites were observed along q1 = 1/3a* + 1/3b* + γc* and q2 = 1/3a* + 1/3b* − γc*. However, no mixed satellites of the type q1 + q2 could be observed. The diffraction pattern was therefore interpreted as stemming from at least two twin domains, and the MS of Ba0.85Ca2.15In6O12 was determined as (3 + 1)D. The choice of only one modulation vector, q = 1/3a* + 1/3b* + γc*, was not compatible with a (3 + 1)D hexagonal class superspace group and was only compatible with the trigonal class superspace group P3(1/3, 1/3, γ) or P
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) (1/3, 1/3, γ). When all of this information was included in the refinements of PXRD and NPD, the MS could be determined.
(1/3, 1/3, γ). When all of this information was included in the refinements of PXRD and NPD, the MS could be determined.
 | ||
| Fig. 10 Electron diffraction pattern of Ba0.85Ca2.15In6O12. (a) [001] zone axis. (b) [100] zone axis showing extra spots appearing near the main spots of the hexagonal lattice. Reproduced with permission of the International Union of Crystallography from ref. 103. | ||
3.3.1.2. PbBiNb5O15. This example dates twenty years after the determination of MS of Ba0.85Ca2.15In6O12, and it illustrates how the developments of the methodology and of the light sources have enabled tackling more complex problems of MS determination in the superspace.
Fig. 11 shows the zone-axis ED patterns of the compounds PbBiNb5O15 (PBN).104 In Fig. 11a, the diffraction pattern of PBN is similar to the [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] zone SAED patterns of other (3 + 2)D tetragonal TTB compounds.105 The main reflections and satellite reflections can be indexed by the basic TTB cell (a = b ≈ 12.5, c ≈ 3.9 Å) and modulation vector α(a* + b*) + γc* (α ≈ 0.3, γ = 0.5), respectively. In order to determine the superspace group of PBN, RED data was collected from the sample which was selected by the second biggest selected area aperture (diameter 500 nm). Fig. 11b is the reconstructed 3D reciprocal space viewed along the c* axis. Although there are two orthogonal modulation wave vectors in Fig. 11b, it is hard to say that the MS of PBN is (3 + 2)D. Twinning, which is a notorious problem in MS determination, can also generate a similar pattern. In order to circumvent the effect of twinning, the smallest selected area aperture (diameter 100 nm) was used to select different areas to obtain SAED patterns. It is obvious that the [001] zone SAED pattern of PBN (Fig. 11c) doesn't agree with the (3 + 2)D tetragonal symmetry. There is no modulation vector along α(a* − b*) + γc*. Thus PBN is a (3 + 1)D orthorhombic TTB compound.
0] zone SAED patterns of other (3 + 2)D tetragonal TTB compounds.105 The main reflections and satellite reflections can be indexed by the basic TTB cell (a = b ≈ 12.5, c ≈ 3.9 Å) and modulation vector α(a* + b*) + γc* (α ≈ 0.3, γ = 0.5), respectively. In order to determine the superspace group of PBN, RED data was collected from the sample which was selected by the second biggest selected area aperture (diameter 500 nm). Fig. 11b is the reconstructed 3D reciprocal space viewed along the c* axis. Although there are two orthogonal modulation wave vectors in Fig. 11b, it is hard to say that the MS of PBN is (3 + 2)D. Twinning, which is a notorious problem in MS determination, can also generate a similar pattern. In order to circumvent the effect of twinning, the smallest selected area aperture (diameter 100 nm) was used to select different areas to obtain SAED patterns. It is obvious that the [001] zone SAED pattern of PBN (Fig. 11c) doesn't agree with the (3 + 2)D tetragonal symmetry. There is no modulation vector along α(a* − b*) + γc*. Thus PBN is a (3 + 1)D orthorhombic TTB compound.
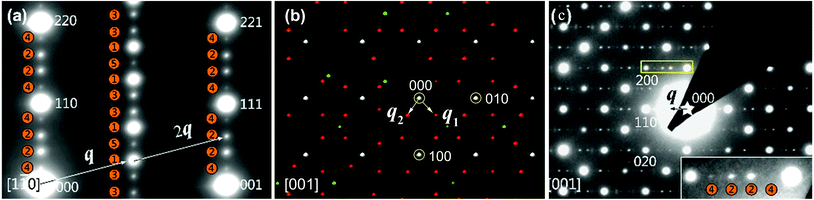 | ||
Fig. 11 Electron diffraction pattern of PbBiNb5O. (a) SAED patterns along [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0]TTB showing different orders of satellite reflections, which are positioned in both l = 0 and l = 1/2 planes. The numbers in the orange circles represent the orders of modulation and q is the modulation vector. The indices are labeled on the basis of a basic TTB cell. (b) The reconstructed 3D reciprocal space view along the c* axis. The white, red, and green spots indicate the main reflections, first order, and higher order satellite reflections respectively. There are two orthogonal modulation wave vectors: q1 and q2. (c) SAED patterns along [001]TTB. Reproduced with permission from ref. 104. Copyright 2015 American Chemical Society. 0]TTB showing different orders of satellite reflections, which are positioned in both l = 0 and l = 1/2 planes. The numbers in the orange circles represent the orders of modulation and q is the modulation vector. The indices are labeled on the basis of a basic TTB cell. (b) The reconstructed 3D reciprocal space view along the c* axis. The white, red, and green spots indicate the main reflections, first order, and higher order satellite reflections respectively. There are two orthogonal modulation wave vectors: q1 and q2. (c) SAED patterns along [001]TTB. Reproduced with permission from ref. 104. Copyright 2015 American Chemical Society. | ||
According to the SAED patterns, the nonpolar space groups C222 (no. 21) and Cmmm (no. 65), and polar space groups Cmm2 (no. 35, polar axis along the c axis) and Cm2m (or C2mm, no. 38, polar axis along b or a) are all compatible with the reflection conditions. The nonpolar space groups were excluded due to the existence of the second harmonic generation (SHG) signal and ferroelectric behavior for PBN.
In situ synchrotron radiation PXRD data in the temperature range of −73 to 427 °C were applied to study the polar axis. The nearly linear thermal expansion behavior of the c axis and the nonlinear trends of both a and b axes (Fig. 12) indicate a polar axis within the a–b plane. Finally, the exact direction of the polar axis (along b) was determined based on the physical property perspective that the ferroelectric long-range ordering tends to elongate the polar axes in pseudo-cubic or pseudo-tetragonal structures.104
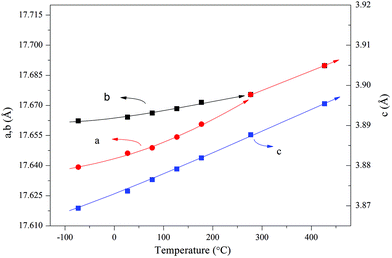 | ||
| Fig. 12 Thermal expansion behavior obtained by the Le Bail fitting of the in situ synchrotron radiation PXRD data. The solid lines are a guide to the eye. Reprinted with permission from ref. 104. Copyright 2015 American Chemical Society. | ||
The modulation vector q (0.61199(8)a* + 0.5c*) was determined by the Le Bail fitting against the room temperature synchrotron radiation PXRD. Thus the (3 + 1)D superspace group of PBN is Cm2m(α 0 0.5)000 (a = 17.65852(10), b = 17.67709(10), c = 3.87645(3)).
When all of this information was included in the refinements of synchrotron radiation PXRD and anomalous dispersion PXRD data, the exact shapes of the occupational modulations of Bi and Pb atoms and positional modulations of all atoms were determined.
Through the examples of Ba0.85Ca2.15In6O12 and PBN, it is obvious that zone-axis ED and PXRD are remarkably complementary. The reflection overlap of PXRD hinders the detection of satellite reflections, finding the components of the modulation vector(s) and analyzing the superspace symmetry. The dynamical effect of zone-axis ED makes the quantitative determination of MS hard. Therefore zone-axis ED patterns are used to detect satellite reflections, to find the components of the modulation vector(s) and to determine the superspace symmetry exactly, and PXRD are used to refine modulation vector(s) and modulation functions (positional and occupational). In addition, zone-axis ED and PXRD are most conveniently achieved, so the combination of zone-axis ED and PXRD becomes the most common method to determine MS of polycrystalline materials in the superspace. There are more than 12 MS that have been determined with this combination in the superspace in the period of 1996–2015.23,102–104,106–114
3.3.2.1. Bi5Nb3O15. The first determination of MS by PEDT and PXRD in the superspace appeared in the structure determination of Bi5Nb3O15.115 The analysis of zone-axis patterns as well as the 3D reciprocal space reconstructions from data obtained by PEDT, the structure was found to be orthorhombic with the modulation vector q = 0.1758(6)b*. The analysis of systematic absences indicated the presence of a b-glide perpendicular to c. The solution was obtained from the PEDT data by the program Superflip using charge flipping in the superspace. The solution revealed the stacking of perovskite blocks separated by [Bi2O2] slabs along c, typical for Aurivillius phases, but the structure contains additional shears, which lead to the presence of both continuous and discontinuous perovskite slabs in the structure (Fig. 13). The superspace electron density was used to construct the initial structure model, including some (but not all) oxygen positions. The missing oxygen positions were added based on the known crystal chemistry of the related phases. This model was then confirmed by Rietveld refinement against PXRD data.
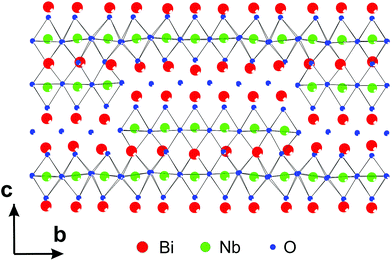 | ||
| Fig. 13 Part of the structure of Bi5Nb3O15 showing both the continuous and discontinuous perovskite blocks and [Bi2O2] slabs. Reproduced with permission from ref. 115. Copyright 2013 American Chemical Society. | ||
4. Summary and future
Electron diffraction methods have made enormous progress over the last decade. The determination of periodic structures using solely ED techniques, or in combination with PXRD has now become almost routine. However, the analysis of MS is far from routine even with high-quality SXRD data, and the structure analysis of MS from ED and/or PXRD data is a real challenge. In this review we summarize the methods used for this purpose and we illustrate a series of examples to show that it is nowadays possible to obtain detailed structural information on MS in this way.The main hindrance in accurate structure determination from electron diffraction data is the presence of dynamical diffraction effects. To obtain accurate structure models, these effects need to be taken into account during structure refinement. The method of dynamical refinement from electron diffraction data has recently been developed83,86 and successfully applied to periodic structures.116,117 The generalization of the method for MS in the superspace is under development. Once finished, it should be possible to obtain accurate and detailed structural information on MS from electron diffraction data collected on a single nanocrystal.
Acknowledgements
This work was supported by the Natural Science Foundation of China (21321001 and 21527803) and the National Basic Research Program of China (2013CB8933402).References
- G. D. Preston, Proc. R. Soc. London, Ser. A, 1938, 167, 526–538 CrossRef CAS.
- P. M. De Wolff, Acta Crystallogr., Sect. A: Found. Crystallogr., 1974, 30, 777–785 CrossRef.
- P. M. De Wolff, Acta Crystallogr., Sect. A: Found. Crystallogr., 1977, 33, 493–497 CrossRef.
- A. Janner and T. Janssen, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 15, 643–658 CrossRef CAS.
- A. Janner and T. Janssen, Phys. A, 1979, 99, 47–76 CrossRef.
- A. Janner and T. Janssen, Acta Crystallogr., Sect. A: Found. Crystallogr., 1980, 36, 399–408 CrossRef.
- A. Janner and T. Janssen, Acta Crystallogr., Sect. A: Found. Crystallogr., 1980, 36, 408–415 CrossRef.
- P. M. De Wolff, T. Janssen and A. Janner, Acta Crystallogr., Sect. A: Found. Crystallogr., 1981, 37, 625–636 CrossRef.
- A. Janner, T. Janssen and P. M. de Wolff, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1983, 39, 658–666 CrossRef.
- T. Janssen, Acta Crystallogr., Sect. A: Found. Crystallogr., 1986, 42, 261–271 CrossRef.
- A. Janner, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 13206–13214 CrossRef.
- S. Van Smaalen, Crystallogr. Rev., 1995, 4, 79–202 CrossRef CAS.
- I. Orlov, L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2008, 41, 1182–1186 CrossRef CAS.
- T. Janssen and A. Janner, Acta Crystallogr., Sect. B: Struct. Sci., 2014, 70, 617–651 CrossRef CAS PubMed.
- C. A. Corrêa, M. Poupon, J. Kopeček, V. Dřínek, P. Brázda, M. Klementová and L. Palatinus, Preparation.
- J. Sun, S. Lee and J. Lin, Chem. – Asian J., 2007, 2, 1204–1229 CrossRef CAS PubMed.
- Q. Hao, Y.-w. Liu and H.-f. Fan, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1987, 43, 820–824 CrossRef.
- S.-B. Xiang, H.-F. Fan, X.-J. Wu, F.-H. Li and Q. Pan, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1990, 46, 929–934 CrossRef.
- A. Altomare, C. Giacovazzo, A. Grazia, G. Moliterni and R. Rizzi, J. Res. Natl. Inst. Stand. Technol., 2004, 109, 125–132 CrossRef CAS PubMed.
- L. Palatinus, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2004, 60, 604–610 CrossRef PubMed.
- L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- L. B. McCusker and C. Baerlocher, Chem. Commun., 2009, 1439–1451, 10.1039/B821716E.
- V. A. Morozov, A. V. Arakcheeva, G. Chapuis, N. Guiblin, M. D. Rossell and G. Van Tendeloo, Chem. Mater., 2006, 18, 4075–4082 CrossRef CAS.
- A. Yamamoto, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1996, 52, 509–560 CrossRef.
- A. Yamamoto, Ferroelectrics, 2001, 250, 139–142 CrossRef CAS.
- H. T. Stokes, B. J. Campbell and S. van Smaalen, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2011, 67, 45–55 CrossRef CAS PubMed.
- D. Batuk, M. Batuk, A. M. Abakumov and J. Hadermann, Acta Crystallogr., Sect. B: Struct. Sci., 2015, 71, 127–143 CAS.
- A. Hédoux, D. Grebille and P. Garnier, Phys. Rev. B: Condens. Matter, 1989, 40, 10653–10656 CrossRef.
- A. Yamamoto, M. Onoda, E. Takayama-Muromachi, F. Izumi, T. Ishigaki and H. Asano, Phys. Rev. B: Condens. Matter, 1990, 42, 4228–4239 CrossRef CAS.
- N. Rivezzi and P. Sciau, J. Solid State Chem., 1998, 139, 332–341 CrossRef CAS.
- M. Onoda, M. Ishii, P. Pattison, K. Shibata, A. Yamamoto and G. Chapuis, J. Solid State Chem., 1999, 146, 355–362 CrossRef CAS.
- C. Bougerol-Chaillout, P. Bordet, J. F. Bérar, C. Darie and S. Pachot, Phys. C, 2000, 341, 479–480 CrossRef.
- M. Dusek, V. Petricek, M. Wunschel, R. E. Dinnebier and S. van Smaalen, J. Appl. Crystallogr., 2001, 34, 398–404 CrossRef CAS.
- G. Baldinozzi, J.-M. Raulot and V. Petricek, MRS Online Proc. Libr., 2002, 755, DD12.18 Search PubMed (16 pages).
- P. Boullay, N. Ténèze, G. Trolliard, D. Mercurio and J. M. Perez-Mato, J. Solid State Chem., 2003, 174, 209–220 CrossRef CAS.
- H. A. Graetsch, Z. Kristallogr. – Cryst. Mater., 2003, 218, 531 CAS.
- C. Hejny and M. I. McMahon, Phys. Rev. Lett., 2003, 91, 215502 CrossRef CAS PubMed.
- T. Hoche, S. Esmaeilzadeh, R. Uecker, S. Lidin and W. Neumann, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 209–216 Search PubMed.
- N. A. Jordan, P. D. Battle, S. van Smaalen and M. Wunschel, Chem. Mater., 2003, 15, 4262–4267 CrossRef CAS.
- T. Kenichi, S. Kyoko, F. Hiroshi and O. Mitsuko, Nature, 2003, 423, 971–974 CrossRef CAS PubMed.
- A. Leineweber, J. Solid State Chem., 2004, 177, 1197–1212 CrossRef CAS.
- A. Graetsch Heribert and M. Brunelli, Z. Kristallogr. – Cryst. Mater., 2005, 220, 606 Search PubMed.
- C. Hejny, L. F. Lundegaard, S. Falconi, M. I. McMahon and M. Hanfland, Phys. Rev. B: Condens. Matter, 2005, 71, 020101 CrossRef.
- Y. Michiue, A. Yamamoto and M. Tanaka, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 737–744 Search PubMed.
- L. Righi, F. Albertini, G. Calestani, L. Pareti, A. Paoluzi, C. Ritter, P. A. Algarabel, L. Morellon and M. Ricardo Ibarra, J. Solid State Chem., 2006, 179, 3525–3533 CrossRef CAS.
- J. Schefer, D. Schaniel, V. Pomjakushin, U. Stuhr, V. Petříček, T. Woike, M. Wöhlecke and M. Imlau, Phys. Rev. B: Condens. Matter, 2006, 74, 134103 CrossRef.
- H. Fujihisa, Y. Akahama, H. Kawamura, Y. Ohishi, Y. Gotoh, H. Yamawaki, M. Sakashita, S. Takeya and K. Honda, Phys. Rev. Lett., 2007, 98, 175501 CrossRef.
- A. Graetsch Heribert, Z. Kristallogr. – Cryst. Mater., 2007, 222, 226 Search PubMed.
- A. K. Larsson, F. J. García-García and R. L. Withers, J. Solid State Chem., 2007, 180, 1093–1102 CrossRef CAS.
- A. K. Larsson, L. Noren, R. L. Withers and H. Rundlöf, J. Solid State Chem., 2007, 180, 2723–2733 CrossRef CAS.
- L. Righi, F. Albertini, L. Pareti, A. Paoluzi and G. Calestani, Acta Mater., 2007, 55, 5237–5245 CrossRef CAS.
- F. Damay, J. Rodriguez-Carvajal, D. Andre, F. Dunstetter and H. Szwarc, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 589–595 CAS.
- D. C. Fredrickson, S. Lidin, G. Venturini, B. Malaman and J. Christensen, J. Am. Chem. Soc., 2008, 130, 8195–8214 CrossRef CAS PubMed.
- L. Righi, F. Albertini, E. Villa, A. Paoluzi, G. Calestani, V. Chernenko, S. Besseghini, C. Ritter and F. Passaretti, Acta Mater., 2008, 56, 4529–4535 CrossRef CAS.
- A. Leineweber, J. Solid State Chem., 2009, 182, 1846–1855 CrossRef CAS.
- W. Slawinski, R. Przenioslo, I. Sosnowska, M. Bieringer, I. Margiolaki and E. Suard, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 535–542 CAS.
- L. Righi, P. Lázpita, J. Gutierrez, J. M. Barandiaran, V. A. Chernenko and G. Calestani, Scr. Mater., 2010, 62, 383–386 CrossRef CAS.
- G. Deng, V. Pomjakushin, V. Petříček, E. Pomjakushina, M. Kenzelmann and K. Conder, Phys. Rev. B: Condens. Matter, 2011, 84, 144111 CrossRef.
- A. Arakcheeva, D. Logvinovich, G. Chapuis, V. Morozov, S. V. Eliseeva, J.-C. G. Bunzli and P. Pattison, Chem. Sci., 2012, 3, 384–390 RSC.
- R. J. Husband, I. Loa, G. W. Stinton, S. R. Evans, G. J. Ackland and M. I. McMahon, Phys. Rev. Lett., 2012, 109, 095503 CrossRef CAS PubMed.
- S. Kawaguchi, H. Ishibashi, N. Tsuji, J. Kim, K. Kato, M. Takata and Y. Kubota, J. Phys. Soc. Jpn., 2013, 82, 064603 CrossRef.
- S. Sanjay, J. Nayak, R. Abhishek, R. Parasmani, H. H. Adrian, S. R. Barman and P. Dhananjai, J. Phys.: Condens. Matter, 2013, 25, 212203 CrossRef PubMed.
- S. Singh, V. Petricek, P. Rajput, A. H. Hill, E. Suard, S. R. Barman and D. Pandey, Phys. Rev. B: Condens. Matter, 2014, 90, 014109 CrossRef.
- R. Vincent and P. A. Midgley, Ultramicroscopy, 1994, 53, 271–282 CrossRef CAS.
- P. A. Midgley and A. S. Eggeman, IUCrJ, 2015, 2, 126–136 CrossRef CAS PubMed.
- V. A. Morozov, A. Bertha, K. W. Meert, S. Van Rompaey, D. Batuk, G. T. Martinez, S. Van Aert, P. F. Smet, M. V. Raskina, D. Poelman, A. M. Abakumov and J. Hadermann, Chem. Mater., 2013, 25, 4387–4395 CrossRef CAS.
- W. Jeitschko, Acta Crystallogr., Sect. B: Struct. Sci., 1973, 29, 2074–2081 CrossRef CAS.
- A. F. van den Elzen and G. D. Rieck, Acta Crystallogr., Sect. B: Struct. Sci., 1973, 29, 2433–2436 CrossRef CAS.
- K. Boulahya, M. Parras and J. M. González-Calbet, Eur. J. Inorg. Chem., 2005, 2005, 967–970 CrossRef.
- M. M. Wu, J. Peng, Y. Z. Cheng, H. Wang, Z. X. Yu, D. F. Chen and Z. B. Hu, Solid State Sci., 2006, 8, 665–670 CrossRef CAS.
- S.-F. Wang, K. Koteswara Rao, Y.-R. Wang, Y.-F. Hsu, S.-H. Chen and Y.-C. Lu, J. Am. Ceram. Soc., 2009, 92, 1732–1738 CrossRef CAS.
- V. Petricek, A. van der Lee and M. Evain, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 529–535 CrossRef.
- B. S. Berg, V. Hansen, P. A. Midgley and J. Gjønnes, Ultramicroscopy, 1998, 74, 147–157 CrossRef CAS.
- J. Gjønnes, V. Hansen, S. J. Andersen, C. D. Marioara and X. Z. Li, Z. Kristallogr. – Cryst. Mater., 2003, 218, 293 Search PubMed.
- C. S. Own, L. D. Marks and W. Sinkler, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2006, 62, 434–443 CAS.
- T. E. Weirich, J. Portillo, G. Cox, H. Hibst and S. Nicolopoulos, Ultramicroscopy, 2006, 106, 164–175 CrossRef CAS PubMed.
- D. L. Dorset, C. J. Gilmore, J. L. Jorda and S. Nicolopoulos, Ultramicroscopy, 2007, 107, 462–473 CrossRef CAS PubMed.
- P. Boullay, V. Dorcet, O. Pérez, C. Grygiel, W. Prellier, B. Mercey and M. Hervieu, Phys. Rev. B: Condens. Matter, 2009, 79, 184108 CrossRef.
- C. S. Birkel, E. Mugnaioli, T. Gorelik, U. Kolb, M. Panthöfer and W. Tremel, J. Am. Chem. Soc., 2010, 132, 9881–9889 CrossRef CAS PubMed.
- M. Gemmi, H. Klein, A. Rageau, P. Strobel and F. Le Cras, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 60–68 CAS.
- J. Hadermann, A. M. Abakumov, A. A. Tsirlin, V. P. Filonenko, J. Gonnissen, H. Tan, J. Verbeeck, M. Gemmi, E. V. Antipov and H. Rosner, Ultramicroscopy, 2010, 110, 881–890 CrossRef CAS PubMed.
- P. Roussel, L. Palatinus, F. Belva, S. Daviero-Minaud, O. Mentre and M. Huve, J. Solid State Chem., 2014, 212, 99–106 CrossRef CAS.
- L. Palatinus, C. A. Correa, G. Steciuk, D. Jacob, P. Roussel, P. Boullay, M. Klementova, M. Gemmi, J. Kopecek, M. C. Domeneghetti, F. Camara and V. Petricek, Acta Crystallogr., Sect. B: Struct. Sci., 2015, 71, 740–751 CAS.
- M. Colmont, L. Palatinus, M. Huvé, H. Kabbour, S. Saitzek, N. Djelal and P. Roussel, Inorg. Chem., 2016, 55, 2252–2260 CrossRef CAS PubMed.
- H. Klein, Z. Kristallogr. – Cryst. Mater., 2013, 228, 35 CrossRef CAS.
- L. Palatinus, V. Petricek and C. A. Correa, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2015, 71, 235–244 CrossRef CAS PubMed.
- U. Kolb, T. Gorelik, C. Kübel, M. T. Otten and D. Hubert, Ultramicroscopy, 2007, 107, 507–513 CrossRef CAS PubMed.
- U. Kolb, T. Gorelik and M. T. Otten, Ultramicroscopy, 2008, 108, 763–772 CrossRef CAS PubMed.
- D. Zhang, P. Oleynikov, S. Hovmöller and X. Zou, Z. Kristallogr. – Cryst. Mater., 2010, 225, 94 CAS.
- W. Wan, J. Sun, J. Su, S. Hovmoller and X. Zou, J. Appl. Crystallogr., 2013, 46, 1863–1873 CAS.
- M. Gemmi, M. G. I. La Placa, A. S. Galanis, E. F. Rauch and S. Nicolopoulos, J. Appl. Crystallogr., 2015, 48, 718–727 CAS.
- D. Shi, B. L. Nannenga, M. G. Iadanza and T. Gonen, eLife, 2013, 2, e01345 Search PubMed.
- B. L. Nannenga, D. Shi, J. Hattne, F. E. Reyes and T. Gonen, eLife, 2014, 3, e03600 Search PubMed.
- B. L. Nannenga, D. Shi, A. G. W. Leslie and T. Gonen, Nat Meth, 2014, 11, 927–930 CAS.
- W. Hua, H. Chen, Z.-B. Yu, X. Zou, J. Lin and J. Sun, Angew. Chem., Int. Ed., 2014, 53, 5868–5871 CrossRef CAS PubMed.
- J. Hattne, F. E. Reyes, B. L. Nannenga, D. Shi, M. J. de la Cruz, A. G. W. Leslie and T. Gonen, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2015, 71, 353–360 CAS.
- Y. Yun, X. Zou, S. Hovmoller and W. Wan, IUCrJ, 2015, 2, 267–282 CrossRef CAS PubMed.
- H. Chen, J. Ju, Q. Meng, J. Su, C. Lin, Z. Zhou, G. Li, W. Wang, W. Gao, C. Zeng, C. Tang, J. Lin, T. Yang and J. Sun, J. Am. Chem. Soc., 2015 DOI:10.1021/jacs.5b03685.
- D. Shi, B. L. Nannenga, M. J. de la Cruz, J. Liu, S. Sawtelle, G. Calero, F. E. Reyes, J. Hattne and T. Gonen, Nat. Protocols, 2016, 11, 895–904 CAS.
- E. Mugnaioli, T. Gorelik and U. Kolb, Ultramicroscopy, 2009, 109, 758–765 CrossRef CAS PubMed.
- L. Palatinus, M. Klementová, V. Dřínek, M. Jarošová and V. Petříček, Inorg. Chem., 2011, 50, 3743–3751 CrossRef CAS PubMed.
- A. M. Abakumov, V. A. Morozov, A. A. Tsirlin, J. Verbeeck and J. Hadermann, Inorg. Chem., 2014, 53, 9407–9415 CrossRef CAS PubMed.
- G. Baldinozzi, F. Goutenoire, M. Hervieu, E. Suard and D. Grebille, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52, 780–789 CrossRef.
- K. Lin, Z. Zhou, L. Liu, H. Ma, J. Chen, J. Deng, J. Sun, L. You, H. Kasai, K. Kato, M. Takata and X. Xing, J. Am. Chem. Soc., 2015, 137, 13468–13471 CrossRef CAS PubMed.
- L. A. Bursill and P. J. Lin, Acta Crystallogr., Sect. B: Struct. Sci., 1987, 43, 49–56 CrossRef.
- P. Boullay, D. Grebille, M. Hervieu, B. Raveau and E. Suard, J. Solid State Chem., 1999, 147, 450–463 CrossRef CAS.
- N. V. Tarakina, A. P. Tyutyunnik, V. G. Zubkov, T. V. D'Yachkova, Y. G. Zainulin, H. Hannerz and G. Svensson, Solid State Sci., 2003, 5, 983–994 CrossRef CAS.
- V. A. Morozov, A. V. Mironov, B. I. Lazoryak, E. G. Khaikina, O. M. Basovich, M. D. Rossell and G. Van Tendeloo, J. Solid State Chem., 2006, 179, 1183–1191 CrossRef CAS.
- D. Pauwels, F. Weill, A. Tressaud and A. Demourgues, Chem. Mater., 2006, 18, 6121–6131 CrossRef CAS.
- A. M. Abakumov, M. D. Rossell, O. Y. Gutnikova, O. A. Drozhzhin, L. S. Leonova, Y. A. Dobrovolsky, S. Y. Istomin, G. V. Tendeloo and E. V. Antipov, Chem. Mater., 2008, 20, 4457–4467 CrossRef CAS.
- A. Arakcheeva, P. Pattison, G. Chapuis, M. Rossell, A. Filaretov, V. Morozov and G. Van Tendeloo, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 160–171 CAS.
- V. A. Morozov, A. V. Arakcheeva, V. V. Konovalova, P. Pattison, G. Chapuis, O. I. Lebedev, V. V. Fomichev and G. Van Tendeloo, J. Solid State Chem., 2010, 183, 408–418 CrossRef CAS.
- D. A. Rusakov, A. M. Abakumov, K. Yamaura, A. A. Belik, G. Van Tendeloo and E. Takayama-Muromachi, Chem. Mater., 2011, 23, 285–292 CrossRef CAS.
- A. M. Abakumov, R. Erni, A. A. Tsirlin, M. D. Rossell, D. Batuk, G. Nénert and G. V. Tendeloo, Chem. Mater., 2013, 25, 2670–2683 CrossRef CAS.
- P. Boullay, L. Palatinus and N. Barrier, Inorg. Chem., 2013, 52, 6127–6135 CrossRef CAS PubMed.
- M. Colmont, L. Palatinus, M. Huvé, H. Kabbour, S. Saitzek, N. Djelal and P. Roussel, Inorg. Chem., 2016, 55, 2252–2260 CrossRef CAS PubMed.
- C. A. Corrêa, M. Klementová, V. Dřínek, J. Kopeček and L. Palatinus, J. Alloys Compd., 2016, 672, 505–509 CrossRef.
| This journal is © the Partner Organisations 2016 |



