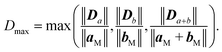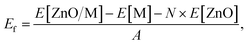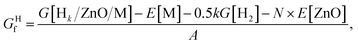Tunable properties and composition of ZnO films supported on metal surfaces†
Yizhen
Song‡
 ,
Paulo C. D.
Mendes‡
,
Paulo C. D.
Mendes‡
 and
Sergey M.
Kozlov
and
Sergey M.
Kozlov
 *
*
Department of Chemical and Biomolecular Engineering, College of Design and Engineering, National University of Singapore, 119260, Singapore. E-mail: sergey.kozlov@nus.edu.sg
First published on 29th May 2023
Abstract
Oxide overlayers covering metal supports find applications in sensors, catalysis, microelectronics, and optical devices. For example, depending on the choice of metal support, ZnO films may serve as sensors for hydrogen or ethanol and exhibit catalytic activity in CO oxidation or methanol synthesis, which is catalyzed in the chemical industry by intensely studied Cu–ZnO catalysts. Here, we apply density functional (DFT) calculations to characterize the properties of periodic ZnO monolayers supported on close-packed surfaces of various metals (Mo, Ru, Pd, Pt, Cu, Ag, Au, Sn, and Pb) under oxidative, ambient, and hydrogenation conditions. Thermodynamic analysis revealed high stability of the films on most metals, except highly reactive Mo and insufficiently reactive Sn and Pb. Metal–oxide interactions are found to have a significant and locally uneven effect on the electronic structure of ZnO. Compared to pristine ZnO, the supported ZnO films show a higher propensity for H adsorption and O vacancy formation, whose energies may be tuned by more than 1 eV depending on the choice of metal support. As a result, under hydrogenation conditions supported ZnO films are calculated to adsorb significant quantities of H or develop O vacancies, unlike pristine ZnO. The calculations reveal how the composition, stability and reactivity of ZnO films are affected by the metal support and provide guidelines for the rational design of ZnO–metal interfaces.
Introduction
Due to their diverse mechanical, thermal, and electronic properties,1 oxide films are applied in microelectronics,2 photonics and plasmonics,3 passivation,4 biotechnologies,5 and catalysis.6 Often thin oxide films are mechanically stabilized by supports, which can change the properties and stability of the films through electronic interactions and induced structural changes.7 Metals are particularly attractive as supports for oxide films because metal supports facilitate the synthesis of oxide films and may induce promising optical and/or catalytic properties in them.8 For example, metal supports can stabilize (hydroxy)oxide films with uncommon stoichiometries under electrochemical conditions and increase their activity in the hydrogen evolution reaction.9,10 Some catalysts may also develop oxide films grown on the metal phase under reaction conditions through hydroxylation or overlayer formation mechanisms11 leading to strong metal–support interaction phenomena, which profoundly change the activity of the catalysts.11–13Among numerous oxides, ZnO has been intensely studied due to its applications in optical,14 piezoelectric,15 and sensing devices.16 Moreover, ZnO nanostructures can be easily synthesized and integrated with other semiconductors.17 For instance, ZnO composites with Ag and Au can be used as highly effective ethanol sensors, whereas nanocomposites of ZnO with Pd can be used for hydrogen detection.18,19 Moreover, ZnO nanomaterials in contact with Cu, Pd, Pt, and Ag find many applications in heterogeneous catalysis,6,20 such as industrial production of methanol on Cu–ZnO catalysts through the reduction of CO and CO2.21,22 Currently great scientific attention is focused on improving these catalysts for the direct use of concentrated CO2 as a feedstock, which requires a detailed understanding of the interactions between ZnO and Cu.21,23 Although the role of ZnO in Cu–ZnO catalyst is known to extend beyond the stabilization of Cu particles against agglomeration,24,25 the catalytic roles of CuOx, CuZn alloys, and ZnO oxide films or islands on Cu particles are still under scrutiny.22,26,27 In particular, some studies suggest that ZnO films formed on Cu nanoparticles under reaction conditions serve as the catalytically active phase in methanol synthesis on Cu–ZnO.28,29 In addition, ZnO/Au catalysts were reported to be highly selective to methanol during CO2 reduction.30
In turn, the combination of Pd with ZnO is a promising catalyst for the steam reforming of methanol.31,32 However, the structure of Pd–ZnO catalysts is still debated, since ZnO overlayers, metallic Pd, and PdZn alloy may form under reaction conditions and expose catalytically active sites.33–35 For example, some studies suggest that ZnO overlayers over Pd catalysts can be as active or even more active than PdZn alloys in methanol steam reforming.35,36 The composites of ZnO and Pd and Pt are also relevant in the oxidation of CO, a critical reaction to control the pollution from combustion engines.37,38 The high CO oxidation activity of ZnO/Pt was ascribed to strong CO binding to Pt sites, which could not be achieved on ZnO/Ag and ZnO/Au catalysts.6
Such interest in the applications of ZnO overlayers in catalysis motivated many experimental studies of the basic properties of ZnO films supported on various metals, including Cu,39 Pd,40 Ag,6,41 Pt,38,42 and Au.39,43,44 The studies show that the metal support can significantly affect the reactivity of the ZnO films.45 For example, Au, Pt, and Ru were shown to affect the binding strength of CO and NH3 on supported ZnO films.7 Moreover, the morphology of ZnO films supported on transition metals may change under reaction conditions, which makes the design and optimization of the catalytic properties of supported oxide films very challenging.42 Particularly important is the stability of continuous oxide films, as the perimeter sites on the oxide nanoflakes or nanoislands supported on transition metals may be highly active in desired or undesired reactions.6,46 Previous computational studies also found metal–oxide interactions to profoundly affect the electronic structure and reactivity of ZnO films supported on (111) surfaces of Cu, Ag, and Au with experimentally observed lattice matchings. For example, the presence of metal support was shown to affect the charge state47 and infrared spectra48 of various species adsorbed on ZnO films as well as the electronic structure of O vacancies49 and various dopants in them.50
Supports also strongly affect the geometric structure of ZnO films. In the absence of any support, ZnO films are predicted to adopt a graphitic structure,51 which was experimentally observed in ZnO nanoflakes.52 For thick films of several ZnO layers, the wurtzite structure with tetrahedral coordination of Zn and O, tends to be more stable than graphitic, and a body-centred tetragonal phase was also suggested for films thicker than 4 ZnO layers.53 Similar changes between the wurtzite and graphitic structures were also observed in ZnO films supported on metal surfaces.40,43,54,55 Lattice strain from the support can regulate the stable phase of the film at various thicknesses.7 Calculations showed that unstrained freestanding ZnO forms graphitic slabs with a thickness of up to 16 layers, while a tensile strain of 5% stabilizes up to 32 layers of the graphitic phase. In turn, compressive strain tends to improve the relative stability of a wurtzite-like phase, as suggested by the instability of the graphitic ZnO under a compressive strain of 10%.56,57 In turn, the film structure strongly affects the electronic properties of the film, such as band gap, because p orbitals hybridize differently in the wurtzite and graphitic structures.56
The strong dependency of various structural and chemical properties of ZnO films on the choice of metal support opens opportunities for tailoring their properties for specific applications. However, the rational design of metal supports for ZnO films requires a precise understanding of the interactions on metal–oxide interfaces, which is hard to obtain using available experimental techniques. Here, we characterize the geometric and electronic structures of metal-supported ZnO films as well as their composition under oxidative, ambient, and hydrogenation conditions and reactivity towards H and O using density functional (DFT) calculations. Namely, we studied films based on graphitic ZnO, as well as ZnO(0001) and (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) wurtzite surfaces on the following close-packed metal surfaces: Cu(111), Pt(111), Au(111), Ru(0001), Pd(111), Ag(111), α-Sn(111), Pb(111), and Mo(110). We chose these supports because they are expected to remain metallic under hydrogenation conditions of methanol synthesis due to their less exothermic oxidation compared to ZnO.58,59 Whereas ZnO films on Cu,39 Pd,40 Ag,6,41 Pt,38,42 and Au39,43,44 supports were previously considered in experimental studies, we could not find such studies for ZnO films on Ru, Sn, Pb, and Mo surfaces. The variety of considered metal supports allows us to establish trends in their effects on the properties of ZnO films. In this work, we consider lattice matchings between ZnO films and metal surfaces that were either observed experimentally or calculated to be highly thermodynamically stable and discuss the effect of chosen lattice matching on the calculated results. Finally, we evaluate the implications of metal–oxide interactions for the composition, properties, and thermodynamic stability of the ZnO films in various environments. Our study aims to fill the gaps in the experimental characterization of ZnO films supported on metals and to facilitate the development of ZnO/metal composites for applications in thermal and photocatalysis, sensing, and other fields.
0) wurtzite surfaces on the following close-packed metal surfaces: Cu(111), Pt(111), Au(111), Ru(0001), Pd(111), Ag(111), α-Sn(111), Pb(111), and Mo(110). We chose these supports because they are expected to remain metallic under hydrogenation conditions of methanol synthesis due to their less exothermic oxidation compared to ZnO.58,59 Whereas ZnO films on Cu,39 Pd,40 Ag,6,41 Pt,38,42 and Au39,43,44 supports were previously considered in experimental studies, we could not find such studies for ZnO films on Ru, Sn, Pb, and Mo surfaces. The variety of considered metal supports allows us to establish trends in their effects on the properties of ZnO films. In this work, we consider lattice matchings between ZnO films and metal surfaces that were either observed experimentally or calculated to be highly thermodynamically stable and discuss the effect of chosen lattice matching on the calculated results. Finally, we evaluate the implications of metal–oxide interactions for the composition, properties, and thermodynamic stability of the ZnO films in various environments. Our study aims to fill the gaps in the experimental characterization of ZnO films supported on metals and to facilitate the development of ZnO/metal composites for applications in thermal and photocatalysis, sensing, and other fields.
Computational methodology and details
Spin-unpolarized (if not specified otherwise) calculations employed the PBE exchange–correlation functional60 implemented in the Vienna Ab initio Simulation Package (VASP).61,62 The projected augmented wave63,64 method was employed to solve the Kohn–Sham equations. The plane-wave cut-off energy for all calculations was set to 400 eV, as recommended for O atoms. We tested various Hubbard parameters65 (U–J) proposed for ZnO in previous studies66–68 and selected 4.7 eV for the Zn d-states, which provides a balanced description of both lattice parameters and band gap in wurtzite ZnO (Fig. S1†). Dispersive interactions are expected to be important for the accurate description of films on metal surfaces.43,69 Here, to improve the description of dispersive interactions, we employed the pair-wise additive zero-damping D3 van der Waals corrections with the default parameters available in VASP.70 The dispersive corrections decreased the corrugation of metal-supported ZnO films by shortening metal–oxide distances in the regions of weak binding and had a moderate effect on the reactivity of the films (Table S1†). The chosen computational approach yielded lattice parameters of a0 = 3.21 Å and c0 = 5.17 Å for wurtzite ZnO bulk.Only the Γ-point in the reciprocal space was considered in calculations of gas-phase H2, triplet O2, and H2O molecules. Our convergence tests of the adsorption energy of a hydrogen atom on a 9/16 (i.e. 3 × 3/4 × 4) supercell of graphitic ZnO(0001)/Cu(111) versus k-mesh sampling yielded results converged within 0.03 eV for a k-mesh built from 3 × 3 × 1 subdivisions (Table S2†). Equally dense k-mesh subdivisions were used for other ZnO/metal systems (Table S3†). To calculate the electronic density of states (DOS), the k-mesh parameters along the surface lattice vectors were multiplied by 8. During geometry optimization, all atomic coordinates were relaxed with the convergence criteria of |0.03| eV Å−1 for the forces on each atom, except for the atoms in the bottom layer of the metal slab, which were fixed in the experimental lattice positions. Thus, the positions of the atoms at the metal–oxide interface were fully optimized. For each self-consistent iteration, the total electronic energy was converged to 10−5 eV.
The work function changes upon formation of ZnO/M were calculated including the dipole correction71 (Table S1†) as Δϕ = ϕZnO/M − ϕM, where ϕZnO/M and ϕM are the differences between the electrostatic potential in vacuum and the Fermi energy for ZnO film supported on metal M and pristine metal surface, respectively. Effective charges are calculated with the Bader method.72–74 The charge density difference produced by the metal–oxide interaction was calculated as
| Δρ(r) = ρZnO/M − ρZnO − ρM, |
Model design
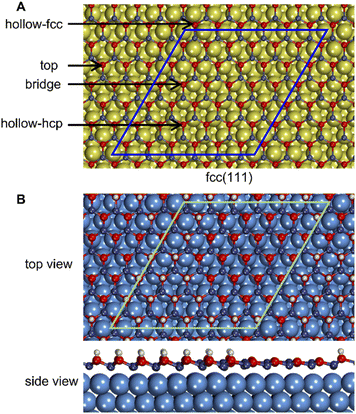
ZnO monolayers, metal surfaces, and ZnO/metal interfaces were constructed using a vacuum region of about 11 Å and experimental lattice parameters (3.15 Å for Mo, 2.71 and 4.28 Å for Ru; 3.89 Å for Pd; 3.92 Å for Pt; 3.61 Å for Cu; 4.09 Å for Ag; 4.08 Å for Au; 6.49 Å for Sn; 4.95 Å for Pb; 3.25 Å and 5.21 Å for wurtzite ZnO).76–78 Metal slabs consisted of 4 layers. Three different types of continuous ZnO monolayer films were investigated, namely, a graphitic ZnO film, gr-ZnO(0001), and two films formed from wurtzite layers wz-ZnO(0001) and wz-ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0). The hexagonal gr-ZnO(0001) was built with O and Zn atoms in a common plane adopting in-plane lattice constants of a0 = b0 = 3.303 Å (dZn–O = 1.91 Å) based on reports by other authors for supported ZnO films.41,54,79 Although the initial structures of wz-ZnO(0001) films featured Zn and O atoms located in different planes, all atoms approached a common plane after geometry optimization. The initial ZnO–metal distances were set to about 2.30 Å before local optimization. For consistency, we initiated all our calculations of wz-ZnO(0001) film from a configuration with Zn closer to the vacuum and O closer to the metal. Translations of the oxide film changing the lateral alignment between the metal and the oxide affected the total energies of the system by less than 40 meV and were not considered further (Fig. S2†).
0). The hexagonal gr-ZnO(0001) was built with O and Zn atoms in a common plane adopting in-plane lattice constants of a0 = b0 = 3.303 Å (dZn–O = 1.91 Å) based on reports by other authors for supported ZnO films.41,54,79 Although the initial structures of wz-ZnO(0001) films featured Zn and O atoms located in different planes, all atoms approached a common plane after geometry optimization. The initial ZnO–metal distances were set to about 2.30 Å before local optimization. For consistency, we initiated all our calculations of wz-ZnO(0001) film from a configuration with Zn closer to the vacuum and O closer to the metal. Translations of the oxide film changing the lateral alignment between the metal and the oxide affected the total energies of the system by less than 40 meV and were not considered further (Fig. S2†).
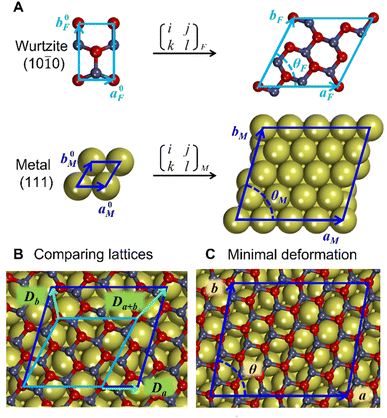
Similarly to previous studies, the atomic structures of ZnO film on metal surfaces were designed through lattice matching minimizing the strain generated on the interface.9,11,45,80–83 In this study, the strain was applied to the oxide film whose lattice parameters were adjusted to match the lattice parameters of the unstrained metal support. To find the combination that minimizes the deformation of the film, we wrote a python code that scanned all surface lattice transformation matrices with elements in the range of [−9, 9]. The resulting list of composite surface cells was ordered by ZnO deformation, from which we manually selected the cell yielding the lowest deformation, computationally feasible model size, and angles of about 30 degrees or more between lattice vectors to ensure sufficient lateral distances between periodic images. After transformation, the lattice vectors of the metal support, [aM, bM], and ZnO film, [aF, bF], were aligned along the a vectors, and the deformation vectors, D, were calculated as illustrated in Fig. 1,
| Da = (aM − aF, 0), |
Db = (bM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θM − bF θM − bF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θF, bM θF, bM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θM − bF θM − bF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θF), θF), |
Da+b = (bM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θM − bF θM − bF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θF + aM − aF, bM θF + aM − aF, bM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θM − bF θM − bF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θF). θF). |
Similar equations were used to calculate D vectors for lattices aligned along bM and bF. The combinations with the lowest possible film strains were selected by minimizing the maximum value, Dmax, between the deformations of the film relative to the lattice parameters of the metal surface,
The obtained structures are summarized in Table 1 labelled in terms of the number of stacked unit cells of the monolayer ZnO film and metal support in the ZnO/metal cell. Some of the performed calculations involved supercells of the obtained structures, e.g., 36/64 ZnO/Cu corresponds to 2 × 2 supercell of 9/16 ZnO/Cu. The computational efficiency of the lattice matching procedure was improved by eliminating combinations of unit cells with drastically different areas employing a well-known area-matching algorithm.84
| Metal support | Experimentally observed ZnO/metal | Lowest deformation gr-ZnO(0001)/metal | Lowest deformation wz-ZnO(0001)/metalb | Lowest deformation wz-ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0)/metal 0)/metal |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ZnO/M (units) | D max (%) | E f (eV nm−2) | ZnO/M (units) | D max (%) | E f (eV nm−2) | ZnO/M (units) | D max (%) | E f (eV nm−2) | ZnO/M (units) | D max (%) | E f (eV nm−2) | |
| a For the reference freestanding gr-ZnO(0001), the formation energy is of 4.89 eV nm2. b ZnO structure becomes graphitic upon geometry optimization. c For Pd, lowest deformation and experimental cells coincide ref. 40. d Ref. 38 and 42. e Ref. 39. f For Ag, lowest deformation and experimental cells coincide ref. 6 and 41. g Ref. 39 and 43. | ||||||||||||
| Mo(110) | 32/43 | 0.11 | Unstable | 30/39 | 0.31 | Unstable | 32/38 | 0.77 | Unstable | |||
| Ru(0001) | 43/64 | 0.09 | −4.82 | 25/36 | 0.06 | −4.62 | 20/27 | 0.91 | −4.36 | |||
| Pd(111) | 25/36c | 0.07 | −4.47 | 25/36c | 0.07 | −4.47 | 28/39 | 0.11 | −4.67 | 28/36 | 0.47 | −4.10 |
| Pt(111) | 25/36d | 0.70 | −4.00 | 19/27 | 0.04 | −4.39 | 27/37 | 0.16 | −4.53 | 22/28 | 0.51 | −4.42 |
| Cu(111) | 9/16e | 2.95 | −0.50 | 31/52 | 0.09 | −1.47 | 13/21 | 0.17 | −1.43 | 18/27 | 0.41 | −0.73 |
| Ag(111) | 49/64f | 0.07 | −1.97 | 49/64f | 0.07 | −1.97 | 31/39 | 0.19 | −2.11 | 24/28 | 0.31 | −1.20 |
| Au(111) | 49/64g | 0.18 | −2.34 | 16/21 | 0.07 | −2.46 | 31/39 | 0.44 | −2.61 | 24/28 | 0.48 | −1.49 |
| Sn(111) | 52/27 | 0.12 | 1.70 | 31/16 | 1.42 | 1.71 | 30/14 | 1.84 | 2.01 | |||
| Pb(111) | 64/57 | 0.01 | 1.60 | 36/31 | 0.06 | 1.41 | 30/24 | 0.84 | 2.34 | |||
In some cases, we identified structures of ZnO/metal interfaces that yielded strains much smaller or calculated thermodynamic stability much higher than ZnO/metal interfaces observed experimentally. Both experimentally observed and the most thermodynamically stable lattice matchings were included in the analysis. In general, experimental studies tend to report supercells where lattice vectors of metal and oxide unit cells are aligned with each other.6,38–43 Although our method identified numerous interface structures with aligned vectors, our study focuses on the most thermodynamically stable film structures with the lowest formation energy instead. A detailed analysis of the discrepancies between the results of our lattice matching method and the experimental observations is hindered by the intrinsic inaccuracies in the lattice parameters and binding energies calculated by the employed exchange–correlation functional.
Thermodynamic analysis
The formation energies of metal-supported ZnO films were defined aswhere N is the total number of atoms in the ZnO film, A is the area of the ZnO/M cell in nm2, E[ZnO/M] and E[M] are the total electronic energies of the ZnO/M composite and isolated metal support slab, and E[ZnO] is the total electronic energy per atom of the wurtzite ZnO bulk.
For hydrogenated films, the formation energy was calculated as
| Gvac[O] = E[ZnxOx−v/M] + 0.5 × G[O2] − G[ZnxOx−v+1/M], |
| Gredvac[O] = E[ZnxOx−v/M] + G[H2O] − G[ZnxOx−v+1/M] − G[H2] |
The Gibbs adsorption energy of H was calculated as
| Gad[H] = G[H/ZnO/M] − E[ZnO/Cu] − G[H2]/2, |
In turn, O and OH adsorption energies under ambient (or oxidation) and reducing conditions were calculated as
| Gad[O] = E[ZnxOx−v+1/M] − G[ZnxOx−v/M] − 0.5 × G[O2], |
| Gredad[O] = G[ZnxOx−v+1/M] + G[H2] − E[ZnxOx−v/M] − G[H2O], |
| Gad[OH] = G[H/ZnxOx−v+1/M] − E[ZnxOx−v/M] − G[H2O]/2 − G[O2]/4, |
| Gredad[OH] = G[H/ZnxOx−v+1/M] + G[H2]/2 − E[ZnxOx−v/M] − G[H2O]. |
Gibbs free energy corrections within the ideal gas and harmonic approximations were calculated at ambient conditions (T = 298.15 K, p[O2] = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 612.2 Pa, p[H2O] = 3171.5 Pa), typical hydrogenation conditions of methanol synthesis (T = 525 K, p[H2] = 1.5 MPa, p[H2O] = 0.05 MPa) and oxidative conditions of CO oxidation (T = 450 K, p[O2] = 5000 Pa) found in the literature.6,21–23,29,85–87 The Gibbs free energies were calculated as
612.2 Pa, p[H2O] = 3171.5 Pa), typical hydrogenation conditions of methanol synthesis (T = 525 K, p[H2] = 1.5 MPa, p[H2O] = 0.05 MPa) and oxidative conditions of CO oxidation (T = 450 K, p[O2] = 5000 Pa) found in the literature.6,21–23,29,85–87 The Gibbs free energies were calculated as
| G = E + ZPE + ∫CPdT − TS, |
Results and discussion
The reduced dimensionality and metal–support interactions were observed to result in important structural changes in thin ZnO films supported on metals, which lead to the emergence of the graphitic ZnO phase.40,43,52,54,55 Similarly to previous studies, ZnO films based on wurtzite (0001) structure became planar and adapted a structure very similar to the graphitic ZnO,51 whereas wurtzite ZnO monolayers supported on metal surfaces retained corrugated structure. For Mo(110), no stable structures of ZnO monolayers were identified because oxygen atoms moved away from ZnO and formed Mo–O bonds of approximately 2.15 Å (Fig. S3†). The migration of O atoms to Mo was calculated for all considered types of ZnO films, including a thicker graphitic film containing 4 ZnO layers, which had fewer O atoms displaced but still displayed the deformed ZnO structure at the interface (Fig. S3†). Strong interactions between Mo and O are in line with the higher oxophilicity of Mo compared to the other metals.90 Therefore, our results suggest that ZnO films on Mo are either unstable or differ significantly from the ZnO structures on other metals.Formation energies of metal-supported ZnO films
The driving force for the formation of ZnO films on metal surfaces in the experiment can be evaluated through the calculation of formation energies of supported ZnO films with respect to ZnO bulk (Table 1). The most thermodynamically stable supported ZnO films were obtained through the lattice matching of gr-ZnO(0001) and wz-ZnO(0001) films, whereas wz-ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) films showed low thermodynamic stability and were not considered further. The stability of ZnO films on metal surfaces is found to strongly depend on the group of the metal element. Pt-group metals and Ru bind ZnO rather strongly in the order Pt < Pd < Ru and yield film formation energies around −4 eV nm−2, suggesting the facile formation of ZnO films on these metals. In turn, the exothermicity of ZnO film formation on coinage metals is significantly weaker and grows in the order Cu < Ag < Au. In particular, ZnO films on Cu are calculated to be only slightly more stable than bulk ZnO, which may explain the significant time required for their formation in industrial Cu–ZnO catalysts for methanol synthesis.91 In turn, the formation of ZnO films is endothermic on group 14 sp-metals, Sn and Pb, indicating possible challenges in the experimental synthesis of ZnO films on these metals due to their lower reactivity.
0) films showed low thermodynamic stability and were not considered further. The stability of ZnO films on metal surfaces is found to strongly depend on the group of the metal element. Pt-group metals and Ru bind ZnO rather strongly in the order Pt < Pd < Ru and yield film formation energies around −4 eV nm−2, suggesting the facile formation of ZnO films on these metals. In turn, the exothermicity of ZnO film formation on coinage metals is significantly weaker and grows in the order Cu < Ag < Au. In particular, ZnO films on Cu are calculated to be only slightly more stable than bulk ZnO, which may explain the significant time required for their formation in industrial Cu–ZnO catalysts for methanol synthesis.91 In turn, the formation of ZnO films is endothermic on group 14 sp-metals, Sn and Pb, indicating possible challenges in the experimental synthesis of ZnO films on these metals due to their lower reactivity.
Geometric analysis of ZnO monolayer supported on metals
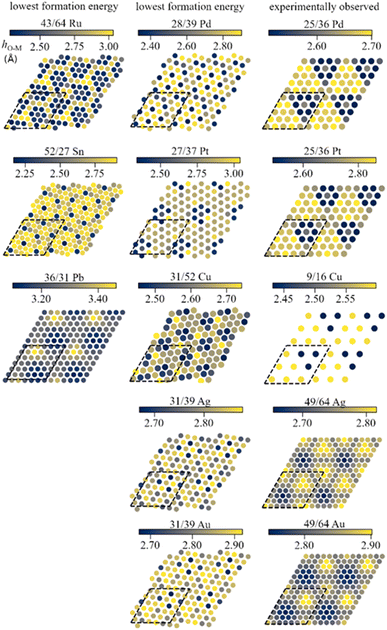
The mismatch between lattice parameters of the ZnO and metal surface unit cells introduces variations between metal–oxide distances in various regions, which modulates the strength of local metal–oxide interactions. All metal-supported ZnO films adopt a graphitic structure with the distances between the planes occupied by Zn and O atoms below 0.2 Å, which is much smaller than 0.63 Å of the wurtzite structure (Table S4†).The local structure of supported ZnO films can be understood from the analysis of the local distances from O atoms to the planes of metal surfaces, i.e., the height of O atoms above the surface (Fig. 2). Such distances form familiar moire patterns when lattice vectors of oxide and metal unit cells are aligned in the ZnO/M superstructure, whereas the patterns become more complex for superstructures with misaligned lattice vectors. The latter structures also tend to show a higher corrugation of the ZnO films compared to the structures with aligned unit cell vectors, which can be tentatively attributed to more heterogeneous metal–oxide interactions in different parts of the film. For most metals, the lowest elevation of O atoms above the plane corresponds to O positions directly above on-top sites on the metal surface, which results in the shortest O–M bonds (Fig. S4 and S5†). However, the O–M heights for 49/64 cells of ZnO on Au(111) and Ag(111) surfaces show the opposite trends with O atoms above top sites exhibiting the highest elevation above the metal plane. Remarkably, similar lattice matchings may produce either similar (e.g., for ZnO/Ag and ZnO/Au) or distinct (e.g. for 25/36 ZnO/Pd and ZnO/Pt) patterns of O elevation above the metal surface.
Electronic structure of supported ZnO films
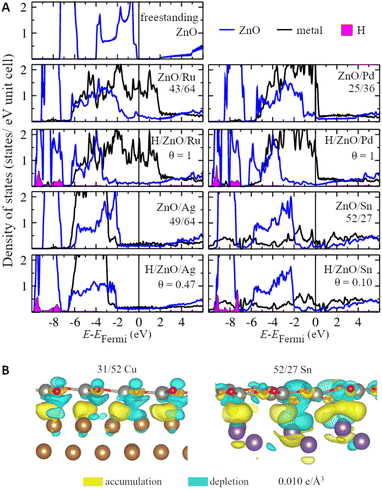
Strong and heterogeneous metal–support interactions also modify the electronic structure of ZnO films on metal surfaces. Representative densities of states of the supported ZnO films for metals representing each studied group of the periodic table are shown in Fig. 3. Whereas freestanding ZnO films are calculated to have a band gap of 1.9 eV with the employed computational parameters, supported ZnO films feature hybridized metal–oxide states in the vicinity of the Fermi level, which leads to the absence of the band gap. The broadening of the ZnO bands due to interaction with the metal atoms is more notable on Pt and Ru supports, which are also the metal supports with the most negative formation energies of ZnO films. In turn, less reactive metals such as Ag, Au, Sn, and Pb have less significant effects on the ZnO DOS. Note that similar conclusions can be reached from the analysis of various lattice matchings between ZnO films and metal supports (Fig. S6 and S7†). The modulation of the magnitude of metal–oxide interactions due to the superposition of the oxide and metal lattices can be also observed in the locally projected DOS. For example, the average energy of O 2p states may vary by up to 0.9 eV with the position of the O atom within supported ZnO films (Fig. S8†). Such variation also leads to a significant and complex variation in the chemical reactivities of these O atoms discussed below. Thus, our results indicate that metal supports profoundly affect both the local and average electronic structure of ZnO films and, as a result, can tune various properties of the films.Although charge transfer is considered to be one of the most important components of metal–oxide interactions,92,93 its value is calculated to be negligible for pristine ZnO films supported on all considered metals (Table S4†). At the same time, ZnO films are calculated to change the work function of metal supports by 0.1–0.4 eV, which indicates significant charge polarization on the metal–oxide interfaces (Table S5†). Namely, charge density difference plots reveal electron accumulation in the region between Zn and surface metal atoms as well as significant polarization of the electron density in O atoms (Fig. 3). Moreover, the analysis of charge density difference plots of ZnO films supported on Sn reveals that the electron polarization may be significant only in the regions of the films directly above protruding surface metal atoms and may not extend to the regions remote from them. Thus, the charge polarization in ZnO films may be tuned to a significant extent using supports with complex surface structures.94,95
Hydrogenation of ZnO films supported on metal surfaces
Transition metal supports significantly affect how ZnO films interact with the environment in various applications. For example, CO2 hydrogenation on ZnO-based catalysts takes place under ∼1.5 MPa H2 pressure. Such reaction environment will have little effect on the composition of pristine ZnO due to very endothermic H adsorption on it with Gad[H] = 1.15 eV and 0.12 eV calculated for 3 × 3 supercells of gr-ZnO films and 4-layer wurtzite ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) slabs, respectively. However, certain metal supports can facilitate the hydrogenation of ZnO films by providing an electron reservoir and facilitating their charge balance (Fig. 4, Table S6†).
0) slabs, respectively. However, certain metal supports can facilitate the hydrogenation of ZnO films by providing an electron reservoir and facilitating their charge balance (Fig. 4, Table S6†).
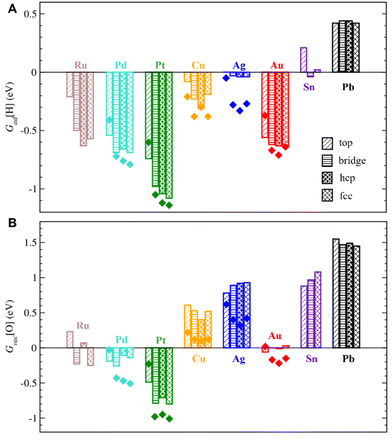
Under hydrogenation conditions, the strongest H adsorption is calculated on ZnO films supported on Pt and Pd, which are among the metals with the strongest interactions with ZnO (Fig. 4). In particular, ZnO films on Pt are calculated to bind H atoms ∼ 2.3 eV more strongly compared to unsupported ZnO films. H adsorption is calculated to be also feasible and exothermic on ZnO films supported by coinage metals, such as Cu, Ag, and Au, despite their much weaker interactions with ZnO films. Even Sn and Pb supports considerably increase binding strength of H on ZnO compared to unsupported ZnO films. Thus, both d- and p-metals can serve as electron reservoirs with a strong effect of 0.7–2.3 eV on H adsorption on supported ZnO films.
Moreover, the heterogeneous nature of metal–oxide interactions (Fig. 2) results in the dependency of the adsorption properties of various ZnO sites on their position above the metal surface (e.g., above top, bridge, hcp, and fcc sites) as illustrated in Fig. 5 for fcc metals with other surfaces represented in Fig. S9.† Since the position of the film is not always perfectly aligned to the sites on metal surfaces, the metal sites below the film were classified using the triangulation method.85 On all supported ZnO films except ZnO/Sn, H prefers to adsorb on O atoms above threefold hollow hcp or fcc sites on metal surfaces, whereas O atoms above top sites on metal surfaces are calculated to be the least reactive towards H (Fig. 4). Note that this observation is valid for supports where O atoms above top sites show both the highest and the lowest elevation above the surface. For some metal supports, the variation of H binding energies on various sites can reach 0.54 eV. Thus metal–oxide interactions are calculated to critically change both the average and local reactivity of ZnO films.
Note that H adsorption energies are calculated to be somewhat different on supported ZnO films with experimentally observed and the most stable lattice matchings with differences below 0.1 eV for most metal supports except Ag, where the difference reaches ∼0.3 eV. Our results also show that the effect of lattice matching on H binding energies depends on the location of adsorption sites above the metal surface and may be related to the configuration of the underlying metal atoms below the ZnO film.
For example, metal–oxide interactions may result in high and uneven coverage of H on supported ZnO films. Whereas under hydrogenation conditions H coverage on ZnO films supported on Pt, Ru, and Pd may reach 1 ML, it is calculated to be above 0.75 ML on ZnO films supported on Cu and Au (Table S6†). Small quantities of H around 0.1 ML can also adsorb on ZnO/Sn system, whereas no H atoms would adsorb on ZnO/Pb. Interestingly, the saturation coverage of H on Ag-supported ZnO films was calculated to strongly depend on the employed lattice matching changing from 0.13 ML on the most stable 31/39 ZnO/Ag cells to 0.47 ML in the experimentally observed 49/64 ZnO/Ag structures. Furthermore, hydrogenation stabilizes ZnO films supported on transition metals, making their formation energies significantly more exothermic (Table S6†), which enhances the thermodynamic driving force for the formation of ZnO, or more precisely ZnOHx, overlayers on metal surfaces under hydrogenation conditions in the experiment. Similar stabilization upon hydrogenation was calculated previously for ZnO nanoribbons supported on Cu(111).46 Upon adsorption, H atoms become charged by ∼0.55 a.u., which decreases the positive charge on Zn atoms by ∼0.15 a.u. and induces a negative charge of around 0.1–0.2 a.u. on the surface metal atoms, resulting in more significant charge transfer between the metal and the film (Table S4†). The ability of metal atoms to accept electrons coming from H atoms is likely to be one of the key factors enabling exothermic H adsorption on ZnO films supported on transition metals.
The adsorption of H atoms also profoundly changes the electronic and geometric structure of the supported ZnO films. For example, hydrogenation of ZnO films shifts their DOS by about 1 eV to lower energies compared to the DOS of pristine films (Fig. 3) without changing much the DOS of underlying metal atoms.
More importantly, the hydrogenation of ZnO films disrupts the graphitic structure of ZnO films. When OH is formed upon the adsorption of one H atom on ZnO, the O atom is plucked out of the ZnO plane by 25–40 pm. For the fully hydrogenated films, the whole film shows a bent ZnO film forming a zigzag structure where Zn is closer to the metal than the OH groups with the distance between O and Zn planes of about 1 Å, irrespective of the support. Interestingly, supported ZnO films with submonolayer H coverage exhibit regions with both bent and graphitic structures of ZnO films (Fig. 5). Therefore, local variations in H coverage and film structure further accentuate the heterogeneity of the film properties due to the formation of a periodic superlattice with the metal surface.
Formation of oxygen vacancies in ZnO supported on metals
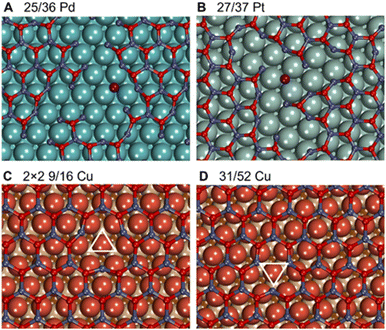
Metal–oxide interactions may also lead to the formation of O vacancies in oxides, which often increases their catalytic activity in reduction reactions.96,97 On 3 × 3 nonpolar ZnO slabs and 3 × 3 freestanding graphitic ZnO films, O vacancy formation is highly endothermic by 0.77 eV and 1.62 eV under hydrogenation conditions, respectively (Table S7†). Similarly high O vacancy formation energies of 0.88 eV and 1.14 eV are calculated in ZnO films on Sn and Pb supports, which exhibit weak metal–oxide interactions with ZnO. However, transition metal supports strongly stabilize O vacancies in ZnO films and enable their formation under methanol synthesis conditions. In particular, the formation of O vacancies becomes exothermic by 0.25 eV, 0.51 eV, and 1.01 eV in ZnO films supported on Ru, Pd, and Pt, respectively, which exhibit the most exothermic formation energies of ZnO films. Weaker interactions between ZnO and coinage metals like Cu and Ag result in mildly endothermic O vacancy formation energy under hydrogenation conditions, whereas ZnO/Au can exhibit O vacancy formation energies exothermic by just 0.22 eV. Note that some metals may stabilize O vacancies in ZnO to the extent that undermines the stability and integrity of ZnO films. For example, ZnO films were calculated to break under hydrogenation conditions on Pt supports as well as in the experimentally observed 25/36 ZnO/Pd system (Fig. 6), which is in line with previous studies.42,98 Other supports such as Ru and Au may stabilize up to 0.2 ML of O vacancies in ZnO films under hydrogenation conditions. However, none of the metal supports stabilizes O vacancies in ZnO films sufficiently to enable their formation under ambient or oxidative conditions.The formation of O vacancies in supported ZnO films was calculated to significantly depend on the chosen lattice matching between the metal and the oxide. For example, under hydrogenation conditions O vacancy formation energy is calculated to be endothermic by ∼0.1 eV in 2 × 2 supercells of experimentally observed 9/16 ZnO/Cu structures, whereas it increases to ∼0.4 eV in more thermodynamically stable 31/52 ZnO/Cu cells. We attribute such unusual dependency of O vacancy formation energies on the lattice matching details to structural rearrangements around O vacancies in ZnO films (Fig. 6). In general, the low-coordinated Zn atoms approach the surface by around 0.3 Å upon the vacancy formation forming strong bonds with the metal support. The different arrangement of metal atoms below the O vacancy in both cases resulted in different environments for adjacent Zn atoms and their different lateral displacements during geometry optimization. For instance, the 135° angles between O–Zn–O atoms around the vacancy in 2 × 2 9/16 ZnO/Cu are significantly larger than the 120° angles in 31/52 ZnO/Cu and pristine films without vacancies. The most pronounced effect of the lattice matching on O vacancy formation energies is calculated for ZnO films supported on Ag, where experimentally observed 49/64 ZnO/Ag structures exhibit 0.46 eV lower values than more stable 31/39 ZnO/Ag cells.
In principle, O vacancies could also form in hydrogenated ZnO films through the reaction of a surface OH group with H to form a water molecule. However, such process was calculated to be endothermic for all considered supported ZnO films (Table S8†). Thus, ZnO films are more likely to be reduced through the accumulation of surface H atoms rather than through the formation of O vacancies under hydrogenation conditions.
O and OH adsorption on supported ZnO films
Whereas reductive conditions facilitate the formation of O vacancies in ZnO, one could expect the presence of additional O atoms on ZnO surfaces under ambient or oxidative conditions. Although O adsorption is endothermic by more than 1 eV and 3 eV on ZnO surfaces and unsupported films, respectively, it may become exothermic on metal-supported ZnO films. For example, our calculations demonstrate the feasibility of O adsorption on ZnO films supported on Cu, Ag, Sn, and Pb with binding energies of −0.88 eV, −0.39 eV, −1.34 eV, and −1.11 eV under ambient conditions, respectively (Table S9†). In addition, some O atoms may adsorb on ZnO films on Pt due the proximity of calculated Gibbs adsorption energies to zero. Such strong O adsorption on metal-supported ZnO films could be rationalized by the metal–oxide charge transfer that helps to maintain charge balance in the film with an additional O2− on its surface. Interestingly, O adsorption on ZnO films supported on Ru, Pt, Cu, Au, and Sn may result in some O atoms moving from the oxide to the metal surface, which could be attributed to their higher oxophilicity compared to stoichiometric ZnO. Such reconstruction of ZnO films becomes more pronounced upon the adsorption of multiple O atoms.For comprehensiveness, we also consider the binding strength of OH species on ZnO films, which is relevant for their hydroxylation99–101 and transformation in ZnOxHy films under certain conditions (Table S10†).11 Although all considered metals stabilize OH on supported ZnO films compared to pristine ZnO, the magnitude of stabilization varies by more than 1.2 eV and does not correlate with the metal position in the periodic table. The strongest binding of OH is calculated on ZnO/Sn and ZnO/Pb models followed by ZnO/Ru. In turn, the weakest OH binding is calculated on ZnO/Au followed by ZnO/Pd.
Note that several corrections were proposed to the DFT energy of O2 molecules.102,103 For example, the energy of O2 molecules can be adjusted by 0.39 eV to higher values in order to make the calculated Gibbs energy of water formation to match with the value measured experimentally. Such correction would shift the values of O vacancy formation energies, O adsorption energies, and OH adsorption energies in Tables S6, S7, and S9,† by 0.195 eV, −0.195 eV, and −0.098 eV, respectively, without significant effect on the main conclusions of this study.
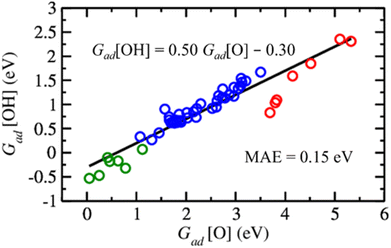
For the rational design of ZnO-based catalysts, it is also important to note that the Gibbs adsorption energies of O versus OH on metal-supported ZnO films follow an approximately linear relationship (Fig. 7), i.e., structures and sites with strong O adsorption also favour OH adsorption. To make our analysis more comprehensive, we include binding energies of O and OH species to O vacancies in ZnO films supported on metals calculated from the data discussed above. As expected,104 the variation in the OH binding energies is around twice less than the variation in O binding energies among the considered ZnO films on metal surfaces. Also, the strength of the obtained correlation with a mean absolute error of 0.15 eV is similar to the scaling relations obtained in other studies.105,106 Thus, metal–oxide interactions in supported ZnO films preserve the scaling relations between O and OH binding energies. At the same time, the choice of transition metal support allows one to tune H binding energies by more than 1 eV and O vacancy formation energies by more than 1.3 eV for a given application (Tables S6 and S9†). The variation of H and O binding energies is further increased by the dependency of properties of the sites on ZnO films on their position above the metal support (Fig. 4).
Conclusions
Metal surfaces profoundly affect the properties of ZnO films supported on them, which makes ZnO/M composites promising for many applications such as sensing and catalysis. Supported ZnO films are calculated to be significantly more stable than bulk ZnO on Ru, Pd, and Pt, and slightly more stable than bulk ZnO on Cu, Ag, and Au. The thermodynamic stability of supported ZnO films is undermined by insufficiently strong interactions with Sn and Pb and exceedingly strong interactions with Mo surfaces, which abstracted O atoms from the films. Unlike ZnO crystals with wurtzite structure, thin ZnO films supported on metals have graphitic structures and no band gap.Metal–oxide interactions facilitate H adsorption on ZnO films and O vacancy formation in them. Whereas some concentration of O vacancies under hydrogenation conditions can be expected in ZnO films supported on Ru and Au, the high amount of O vacancies formed in ZnO films on Pd and Pt may undermine their structural integrity. Although pristine ZnO surfaces or films weakly interact with H atoms, ZnO films supported on transition metals adsorb significant (up to 1 ML) amounts of H atoms on their surface under hydrogenation conditions because metal surface helps to maintain charge balance in H-covered ZnO. Submonolayer H coverage on supported ZnO films results in the coexistence of H-covered and bare areas within the same film. Note that hydrogenation of supported ZnO films corrugates their structure and greatly hinders the formation of O vacancies in them. More importantly, hydrogenated ZnO films on transition metals are calculated to be significantly more thermodynamically stable compared to pristine films, which would increase the thermodynamic driving force for film formation under hydrogenation conditions in the experiment.
The mismatch between lattice parameters of ZnO and metal surfaces induces significant variations in the local properties of the supported ZnO films, such as the elevation above the surface or the electronic structure of atoms composing the film. The binding energies of H atoms and O vacancy formation energies are also calculated to vary among sites within each supported film by up to 0.8 eV depending on the alignment of the sites with the underlying metal atoms. The employed lattice matching also significantly affected the calculated binding energies of H and O to the supported films by up to 0.3 eV.
Overall, metal–oxide interactions are shown to be a valuable tool to modify the electronic structure and the interaction energies of the ZnO films with H and O species by up to 1.4 eV. Thus, the rational choice of metal support for ZnO films is suggested as a promising strategy for tuning their properties for various applications based on the fundamental understanding of the metal–oxide interactions obtained in this study.
Author contributions
S. Y. performed most calculations while P. C. D. M. developed programming scripts. S. Y. and P. C. D. M. analysed the data. S. M. K. conceptualized and supervised the project. All authors worked on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work received funding from the National Research Foundation under the NRF Fellowship NRFF13-2021-0126. The computational work for this article was partially performed on resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg).References
- G. Barcaro and A. Fortunelli, Phys. Chem. Chem. Phys., 2019, 21, 11510–11536 RSC.
- H. P. Quiroz, J. A. Calderón and A. Dussan, J. Alloys Compd., 2020, 840, 155674 CrossRef CAS.
- H. Khamh, E. Sachet, K. Kelly, J.-P. Maria and S. Franzen, J. Mater. Chem. C, 2018, 6, 8326–8342 RSC.
- H. Cho, P. Pujar, Y. I. Cho, S. Hong and S. Kim, Adv. Electron. Mater., 2022, 8, 2101012 CrossRef CAS.
- J. Yang, M. Wang, X. Li, Z. Dong, X. Zhou, J. Luan, Y. Guo and Y. Xue, J. Appl. Biomater. Funct. Mater., 2022, 20, 1–10 CAS.
- Q. Pan, B. H. Liu, M. E. McBriarty, Y. Martynova, I. M. N. Groot, S. Wang, M. J. Bedzyk, S. Shaikhutdinov and H.-J. Freund, Catal. Lett., 2014, 144, 648–655 CrossRef CAS.
- L. Lin, Z. Zeng, Q. Fu and X. Bao, AIP Adv., 2020, 10, 125125 CrossRef CAS.
- P. C. D. Mendes, Y. Song, W. Ma, T. Z. H. Gani, K. H. Lim, S. Kawi and S. M. Kozlov, Adv. Phys.: X, 2023, 8, 2175623 Search PubMed.
- Z. Zeng, K.-C. Chang, J. Kubal, N. M. Markovic and J. Greeley, Nat. Energy, 2017, 2, 17070 CrossRef CAS.
- J. A. Bau, S. M. Kozlov, L. M. Azofra, S. Ould-Chikh, A.-H. Emwas, H. Idriss, L. Cavallo and K. Takanabe, ACS Catal., 2020, 10, 12858–12866 CrossRef CAS.
- K. J. Sawant, Z. Zeng and J. P. Greeley, Chem. Sci., 2023, 14, 3206–3214 RSC.
- P. Lackner, J. I. J. Choi, U. Diebold and M. Schmid, J. Mater. Chem. A, 2019, 7, 24837–24846 RSC.
- S. Shaikhutdinov, Catal. Lett., 2018, 148, 2627–2635 CrossRef CAS.
- D. K. Sharma, S. Shukla, K. K. Sharma and V. Kumar, Mater. Today: Proc., 2022, 49, 3028–3035 CAS.
- A. T. Le, M. Ahmadipour and S.-Y. Pung, J. Alloys Compd., 2020, 844, 156172 CrossRef CAS.
- V. S. Bhati, M. Hojamberdiev and M. Kumar, Energy Rep., 2020, 6, 46–62 CrossRef.
- Ü. Özgür, Ya. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Dogan, V. Avrutin, S.-J. Cho and H. Morkoç, J. Appl. Phys., 2005, 98, 41301 CrossRef.
- M. J. Ahemad, T. D. Le, D.-S. Kim and Y.-T. Yu, Sens. Actuators, B, 2022, 359, 131595 CrossRef CAS.
- T. T. D. Nguyen, D. V. Dao, D.-S. Kim, H.-J. Lee, S.-Y. Oh, I.-H. Lee and Y.-T. Yu, J. Colloid Interface Sci., 2021, 587, 252–259 CrossRef CAS PubMed.
- S. Chen, A. M. Abdel-Mageed, C. Mochizuki, T. Ishida, T. Murayama, J. Rabeah, M. Parlinska-Wojtan, A. Brückner and R. J. Behm, ACS Catal., 2021, 11, 9022–9033 CrossRef CAS.
- R. Guil-López, N. Mota, J. Llorente, E. Millán, B. Pawelec, J. L. G. Fierro and R. M. Navarro, Materials, 2019, 12, 3902 CrossRef PubMed.
- L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384 CrossRef CAS.
- B. Liang, J. Ma, X. Su, C. Yang, H. Duan, H. Zhou, S. Deng, L. Li and Y. Huang, Ind. Eng. Chem. Res., 2019, 58, 9030–9037 CrossRef CAS.
- G. Wang, F. Luo, L. Lin and F. Zhao, React. Kinet., Mech. Catal., 2021, 132, 155–170 CrossRef CAS.
- S. Zander, E. L. Kunkes, M. E. Schuster, J. Schumann, G. Weinberg, D. Teschner, N. Jacobsen, R. Schlögl and M. Behrens, Angew. Chem., Int. Ed., 2013, 52, 6536–6540 CrossRef CAS PubMed.
- P. Amann, B. Klötzer, D. Degerman, N. Köpfle, T. Götsch, P. Lömker, C. Rameshan, K. Ploner, D. Bikaljevic, H.-Y. Wang, M. Soldemo, M. Shipilin, C. M. Goodwin, J. Gladh, J. Halldin Stenlid, M. Börner, C. Schlueter and A. Nilsson, Science, 2022, 376, 603–608 CrossRef CAS PubMed.
- J. Schumann, J. Kröhnert, E. Frei, R. Schlögl and A. Trunschke, Top. Catal., 2017, 60, 1735–1743 CrossRef CAS.
- D. Li, F. Xu, X. Tang, S. Dai, T. Pu, X. Liu, P. Tian, F. Xuan, Z. Xu, I. E. Wachs and M. Zhu, Nat. Catal., 2022, 5, 99–108 CrossRef CAS.
- S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355, 1296–1299 CrossRef CAS PubMed.
- Y. Hartadi, D. Widmann and R. J. Behm, ChemSusChem, 2015, 8, 456–465 CrossRef CAS PubMed.
- Y. Chin, Catal. Today, 2002, 77, 79–88 CrossRef CAS.
- E. S. Ranganathan, S. K. Bej and L. T. Thompson, Appl. Catal., A, 2005, 289, 153–162 CrossRef CAS.
- C. Ziegler, S. Klosz, L. Borchardt, M. Oschatz, S. Kaskel, M. Friedrich, R. Kriegel, T. Keilhauer, M. Armbrüster and A. Eychmüller, Adv. Funct. Mater., 2016, 26, 1014–1020 CrossRef CAS.
- M. Heggen, S. Penner, M. Friedrich, R. E. Dunin-Borkowski and M. Armbrüster, J. Phys. Chem. C, 2016, 120, 10460–10465 CrossRef CAS.
- M. Friedrich, S. Penner, M. Heggen and M. Armbrüster, Angew. Chem., Int. Ed., 2013, 52, 4389–4392 CrossRef CAS PubMed.
- J. Xu, X. Su, X. Liu, X. Pan, G. Pei, Y. Huang, X. Wang, T. Zhang and H. Geng, Appl. Catal., A, 2016, 514, 51–59 CrossRef CAS.
- P. Kast, M. Friedrich, F. Girgsdies, J. Kröhnert, D. Teschner, T. Lunkenbein, M. Behrens and R. Schlögl, Catal. Today, 2016, 260, 21–31 CrossRef CAS.
- Y. Martynova, B.-H. Liu, M. E. McBriarty, I. M. N. Groot, M. J. Bedzyk, S. Shaikhutdinov and H.-J. Freund, J. Catal., 2013, 301, 227–232 CrossRef CAS.
- X. Zhao, H. Chen, H. Wu, R. Wang, Y. Cui, Q. Fu, F. Yang and X. Bao, Acta Phys.-Chim. Sin., 2018, 34, 1373–1380 CAS.
- G. Weirum, G. Barcaro, A. Fortunelli, F. Weber, R. Schennach, S. Surnev and F. P. Netzer, J. Phys. Chem. C, 2010, 114, 15432–15439 CrossRef CAS.
- C. Tusche, H. L. Meyerheim and J. Kirschner, Phys. Rev. Lett., 2007, 99, 026102 CrossRef CAS PubMed.
- B.-H. Liu, M. E. McBriarty, M. J. Bedzyk, S. Shaikhutdinov and H.-J. Freund, J. Phys. Chem. C, 2014, 118, 28725–28729 CrossRef CAS.
- X. Deng, K. Yao, K. Sun, W.-X. Li, J. Lee and C. Matranga, J. Phys. Chem. C, 2013, 117, 11211–11218 CrossRef CAS.
- F. Tumino, C. S. Casari, M. Passoni, C. E. Bottani and A. L. Bassi, Nanotechnology, 2016, 27, 475703 CrossRef CAS PubMed.
- S. Tosoni, C. Li, P. Schlexer and G. Pacchioni, J. Phys. Chem. C, 2017, 121, 27453–27461 CrossRef CAS.
- K. Mondal, Megha, A. Banerjee, A. Fortunelli, M. Walter and M. Moseler, J. Phys. Chem. C, 2022, 126, 764–771 CrossRef CAS.
- H. V. Thang, S. Tosoni and G. Pacchioni, ACS Catal., 2018, 8, 4110–4119 CrossRef CAS.
- M. Andersen, X. Yu, M. Kick, Y. Wang, C. Wöll and K. Reuter, J. Phys. Chem. C, 2018, 122, 4963–4971 CrossRef CAS.
- H. V. Thang and G. Pacchioni, J. Phys. Chem. C, 2018, 122, 20880–20887 CrossRef CAS.
- H. V. Thang and G. Pacchioni, Phys. Chem. Chem. Phys., 2019, 21, 369–377 RSC.
- F. Claeyssens, C. L. Freeman, N. L. Allan, Y. Sun, M. N. R. Ashfold and J. H. Harding, J. Mater. Chem., 2005, 15, 139–148 RSC.
- K. B. Tom, S. Lin, L. F. Wan, J. Wang, N. Ahlm, A. T. N'Diaye, K. Bustillo, J. Huang, Y. Liu, S. Lou, R. Chen, S. Yan, H. Wu, D. Jin, H. Yuan, D. Prendergast and J. Yao, ACS Nano, 2018, 12, 7554–7561 CrossRef CAS PubMed.
- L. Lin, Z. Zeng, Q. Fu and X. Bao, Chem. Sci., 2021, 12, 15284–15290 RSC.
- H. Ta, L. Zhao, D. Pohl, J. Pang, B. Trzebicka, B. Rellinghaus, D. Pribat, T. Gemming, Z. Liu, A. Bachmatiuk and M. Rümmeli, Crystals, 2016, 6, 100 CrossRef.
- V. Schott, H. Oberhofer, A. Birkner, M. Xu, Y. Wang, M. Muhler, K. Reuter and C. Wöll, Angew. Chem., Int. Ed., 2013, 52, 11925–11929 CrossRef CAS PubMed.
- D. Wu, M. G. Lagally and F. Liu, Phys. Rev. Lett., 2011, 107, 236101 CrossRef PubMed.
- B. Bieniek, O. T. Hofmann and P. Rinke, Appl. Phys. Lett., 2015, 106, 131602 CrossRef.
- C. Sun, L. Yan, B. Yue, H. Liu and Y. Gao, J. Mater. Chem. C, 2014, 2, 9283–9293 RSC.
- R. A. Robie, B. S. Hemingway and J. R. Fisher, Thermodynamic properties of minerals and related substances at 298.15 K and 1 bar (105 pascals) pressure and at higher temperatures, U. S. G. P. O, 1978 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- A. Janotti and C. G. V. de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165202 CrossRef.
- G. Barcaro, I. O. Thomas and A. Fortunelli, J. Chem. Phys., 2010, 132, 124703 CrossRef PubMed.
- A. Calzolari, A. Ruini and A. Catellani, J. Am. Chem. Soc., 2011, 133, 5893–5899 CrossRef CAS PubMed.
- H. V. Thang and G. Pacchioni, ChemNanoMat, 2019, 5, 932–939 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1994 Search PubMed.
- R. F. W. Bader, Theor. Chem. Acc., 2001, 105, 276–283 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, Inc., New York, 8th edn, 2005 Search PubMed.
- J. Ihm and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 1576–1579 CrossRef CAS.
- Ü. Özgür, Ya. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Doğan, V. Avrutin, S.-J. Cho and H. Morkoç, J. Appl. Phys., 2005, 98, 041301 CrossRef.
- H. Chen, L. Lin, Y. Li, R. Wang, Z. Gong, Y. Cui, Y. Li, Y. Liu, X. Zhao, W. Huang, Q. Fu, F. Yang and X. Bao, ACS Catal., 2018, 9, 1373–1382 CrossRef.
- P. Lazić, Comput. Phys. Commun., 2015, 197, 324–334 CrossRef.
- S. Moayedpour, D. Dardzinski, S. Yang, A. Hwang and N. Marom, J. Chem. Phys., 2021, 155, 034111 CrossRef CAS PubMed.
- F. Therrien, P. Graf and V. Stevanović, J. Chem. Phys., 2020, 152, 74106 CrossRef CAS PubMed.
- N. T. Taylor, F. H. Davies, I. E. M. Rudkin, C. J. Price, T. H. Chan and S. P. Hepplestone, Comput. Phys. Commun., 2020, 257, 107515 CrossRef CAS.
- A. Zur and T. C. McGill, J. Appl. Phys., 1984, 55, 378–386 CrossRef CAS.
- S. Kuld, M. Thorhauge, H. Falsig, C. F. Elkjaer, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2016, 352, 969–974 CrossRef CAS PubMed.
- B. Yang, C. Liu, A. Halder, E. C. Tyo, A. B. F. Martinson, S. Seifert, P. Zapol, L. A. Curtiss and S. Vajda, J. Phys. Chem. C, 2017, 121, 10406–10412 CrossRef CAS.
- M. Mahapatra, R. A. Gutiérrez, J. Kang, N. Rui, R. Hamlyn, Z. Liu, I. Orozco, P. J. Ramírez, S. D. Senanayake and J. A. Rodriguez, Surf. Sci., 2019, 681, 116–121 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- K. P. Kepp, Inorg. Chem., 2016, 55, 9461–9470 CrossRef CAS PubMed.
- D. Laudenschleger, H. Ruland and M. Muhler, Nat. Commun., 2020, 11, 3898 CrossRef PubMed.
- K. M. Neyman and S. M. Kozlov, NPG Asia Mater., 2022, 14, 59 CrossRef CAS.
- G. T. Kasun Kalhara Gunasooriya and M. Saeys, in Nanotechnology in Catalysis, ed. M. Van de Voorde and B. Sels, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2017, pp. 209–224 Search PubMed.
- J. Goniakowski and C. Noguera, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155433 CrossRef.
- L. Sementa, G. Barcaro, F. R. Negreiros, I. O. Thomas, F. P. Netzer, A. M. Ferrari and A. Fortunelli, J. Chem. Theory Comput., 2012, 8, 629–638 CrossRef CAS PubMed.
- K. Lee, U. Anjum, T. P. Araújo, C. Mondelli, Q. He, S. Furukawa, J. Pérez-Ramírez, S. M. Kozlov and N. Yan, Appl. Catal., B, 2022, 304, 120994 CrossRef CAS.
- A. Bavykina, I. Yarulina, A. J. Al Abdulghani, L. Gevers, M. N. Hedhili, X. Miao, A. R. Galilea, A. Pustovarenko, A. Dikhtiarenko, A. Cadiau, A. Aguilar-Tapia, J.-L. Hazemann, S. M. Kozlov, S. Oud-Chikh, L. Cavallo and J. Gascon, ACS Catal., 2019, 9, 6910–6918 CrossRef CAS.
- J. Gao, K. J. Sawant, J. T. Miller, Z. Zeng, D. Zemlyanov and J. P. Greeley, ACS Appl. Mater. Interfaces, 2021, 13, 35113–35123 CrossRef CAS PubMed.
- N. Su, R. Mu, H. Wu, R. Zhang, S. Zhao, Y. Li, Q. Fu and X. Bao, Appl. Surf. Sci., 2020, 503, 144204 CrossRef CAS.
- I. Orozco, E. Huang, R. A. Gutiérrez, Z. Liu, F. Zhang, M. Mahapatra, J. Kang, H. Kersell, S. Nemsak, P. J. Ramírez, S. D. Senanayake, P. Liu and J. A. Rodriguez, J. Phys. D: Appl. Phys., 2019, 52, 454001 CrossRef CAS.
- H. Wu, Q. Fu, Y. Li, Y. Cui, R. Wang, N. Su, L. Lin, A. Dong, Y. Ning, F. Yang and X. Bao, Nano Res., 2019, 12, 2348–2354 CrossRef CAS.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- Q. Zhang and A. Asthagiri, Catal. Today, 2019, 323, 35–43 CrossRef CAS.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS PubMed.
- L. Falivene, S. M. Kozlov and L. Cavallo, ACS Catal., 2018, 8, 5637–5656 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Complementary analyses and data. See DOI: https://doi.org/10.1039/d3ta01940c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2023 |